An Improved Comprehensive Atomization Model for Pressure Swirl Atomizers
Abstract
1. Introduction
2. Model Formulation
2.1. Internal Flow Sub-Model
2.2. Liquid Sheet Instability Sub-Model
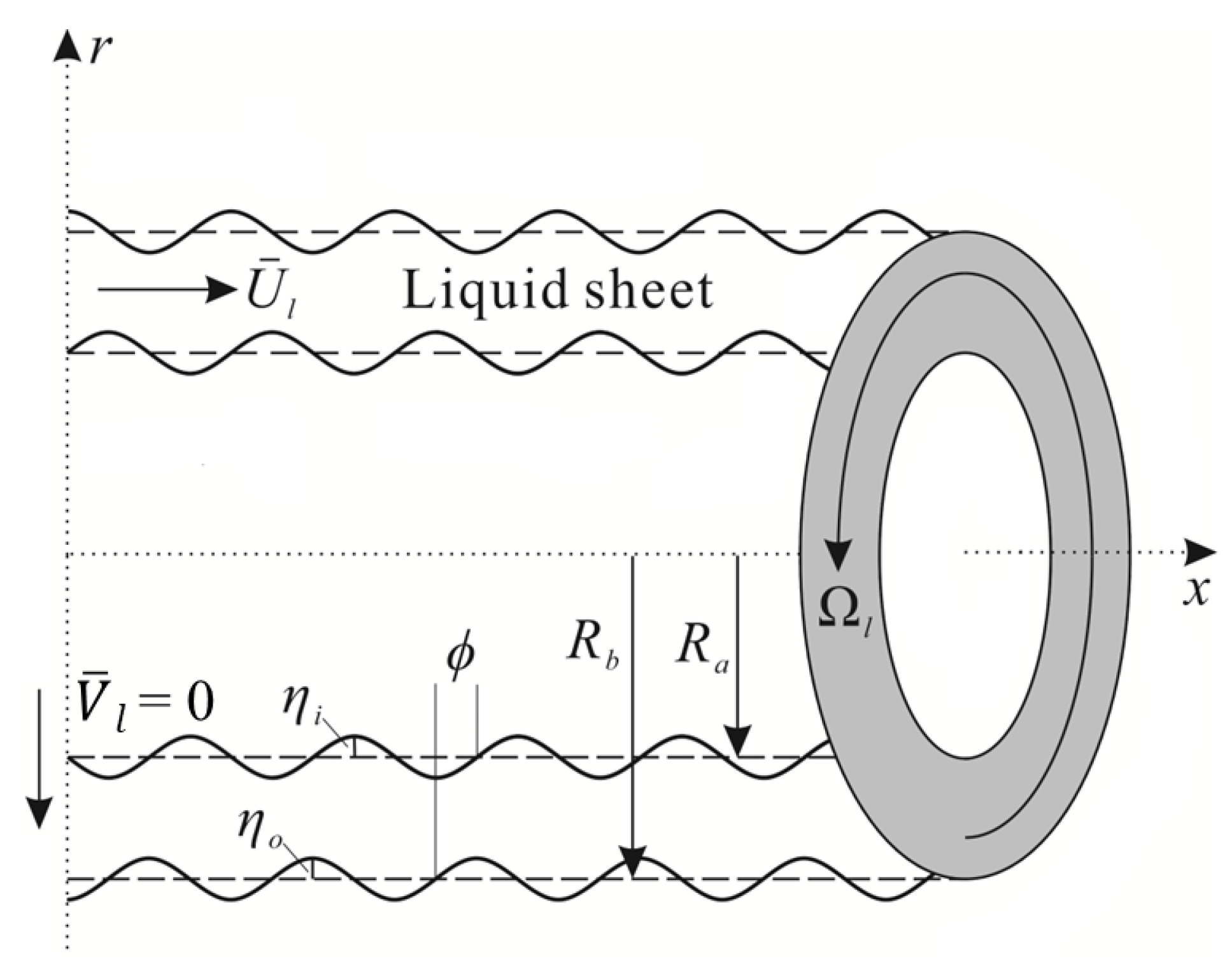
2.2.1. Problem Formulation
2.2.2. Governing Equations
2.2.3. Boundary Conditions
2.2.4. Formulation and Solution of the Dispersion Relation
2.3. Primary Atomization Sub-Model
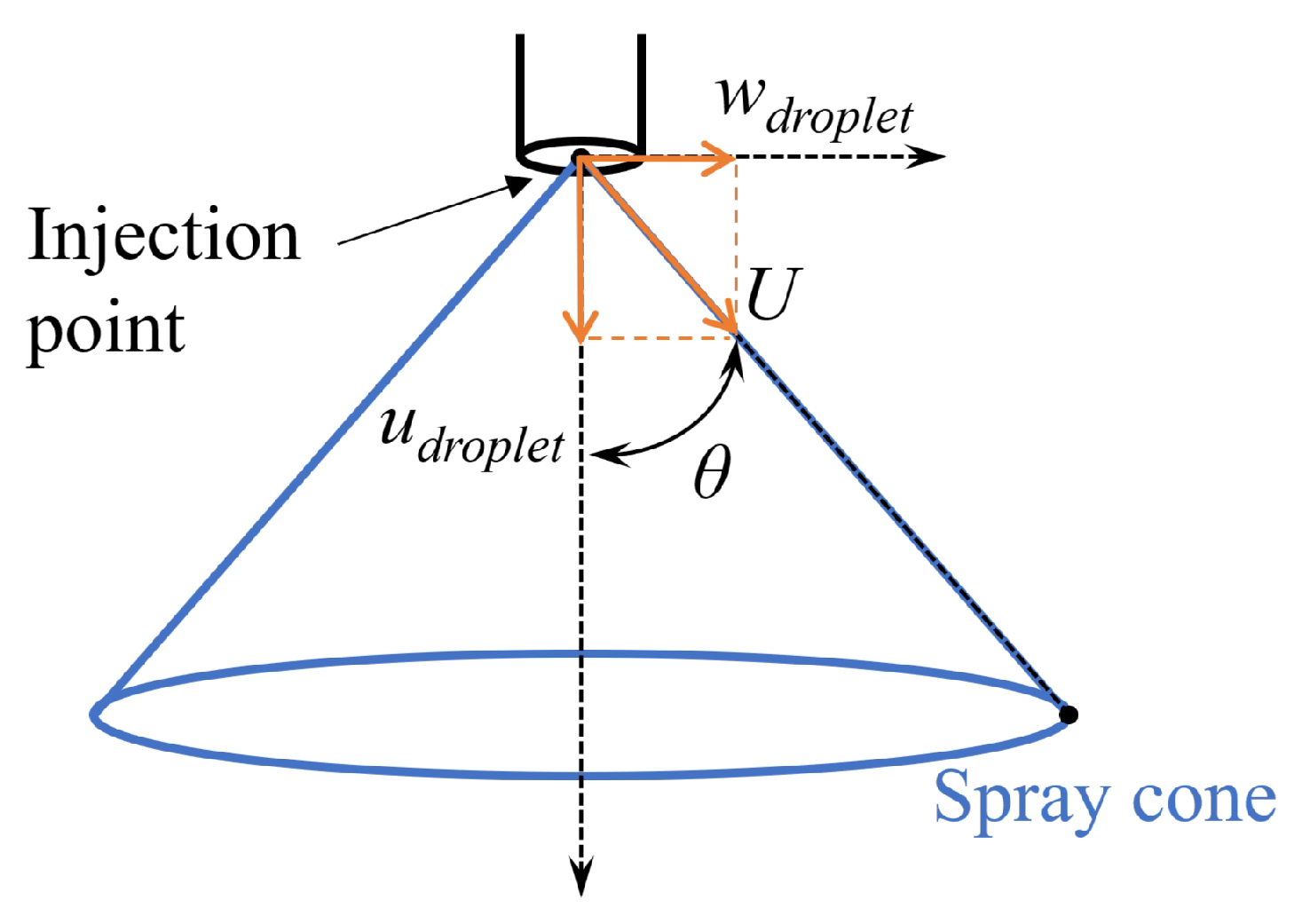
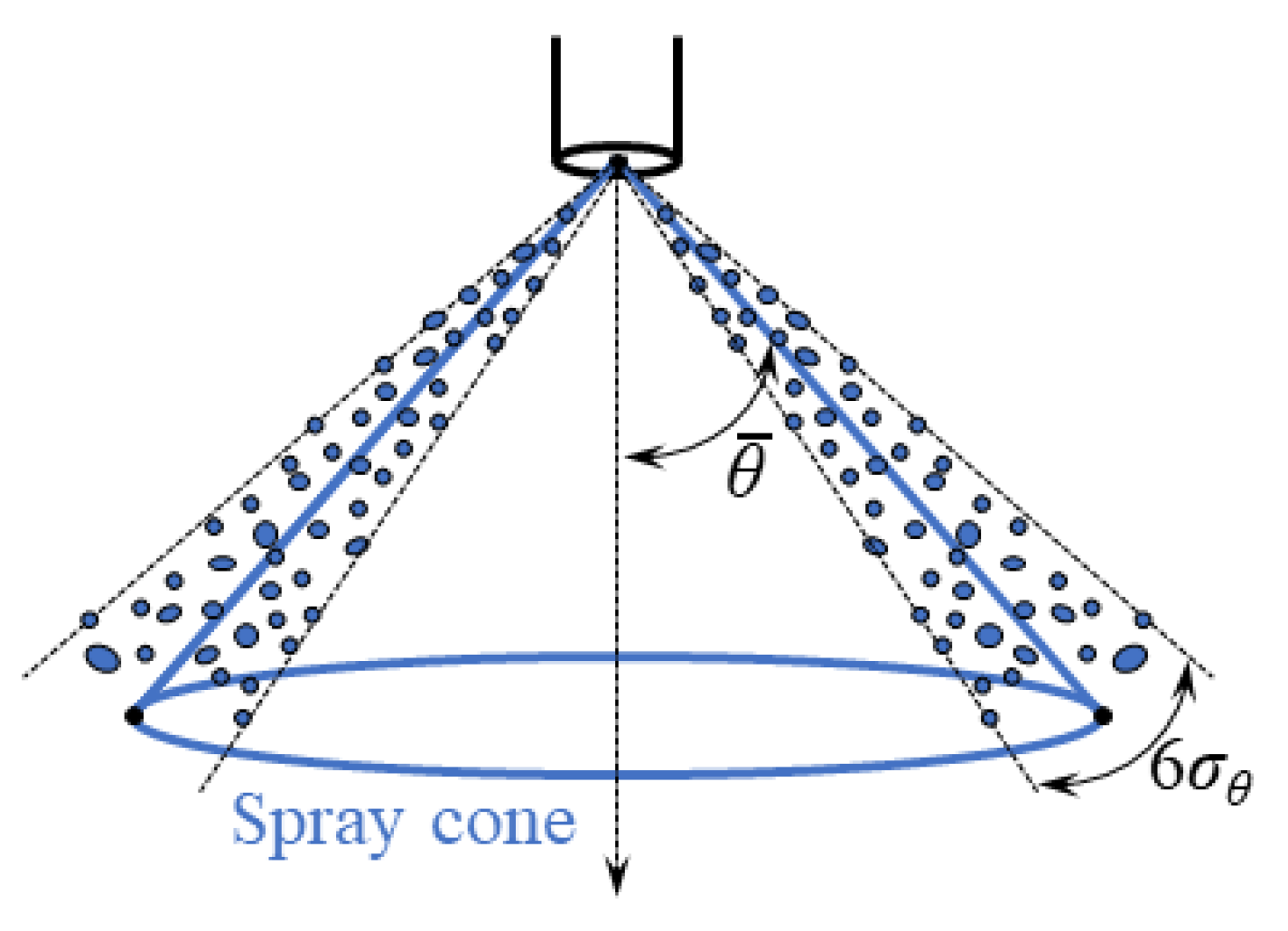
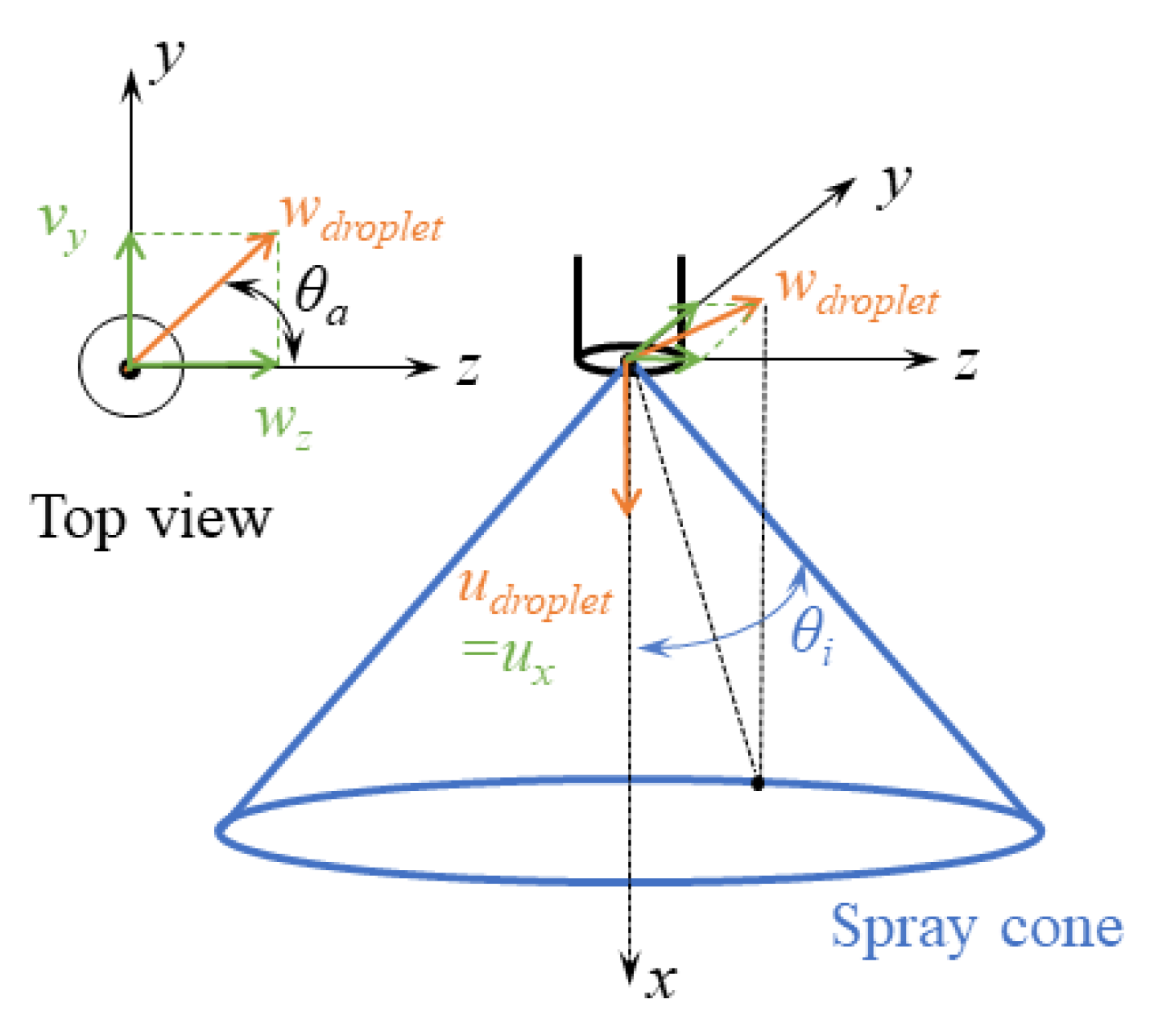
2.4. Droplet Velocity Sub-Model
2.5. Summary of the Comprehensive Atomization Model for Pressure Swirl Atomizers
3. Model Implementation
4. Experimental Testing Methods
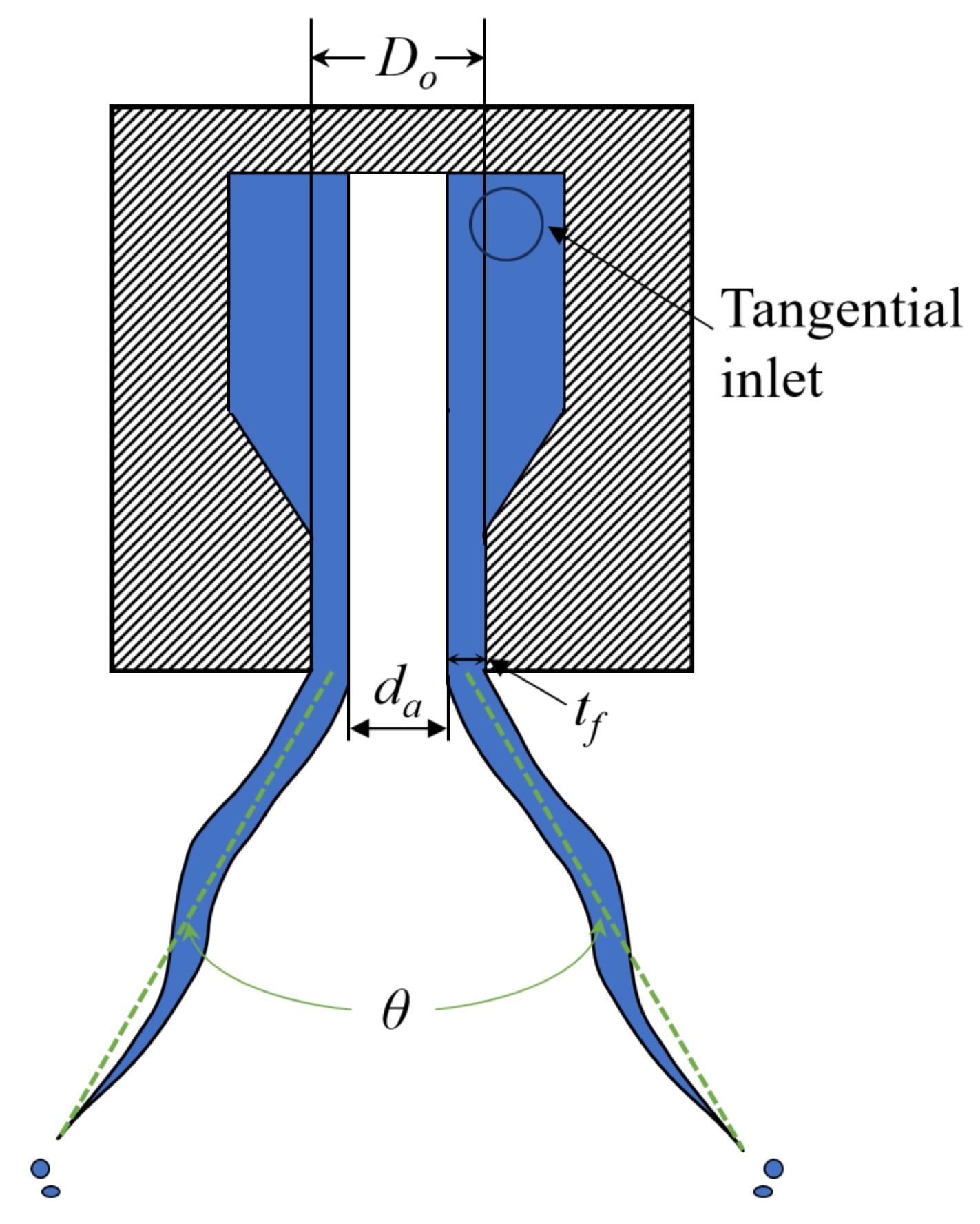
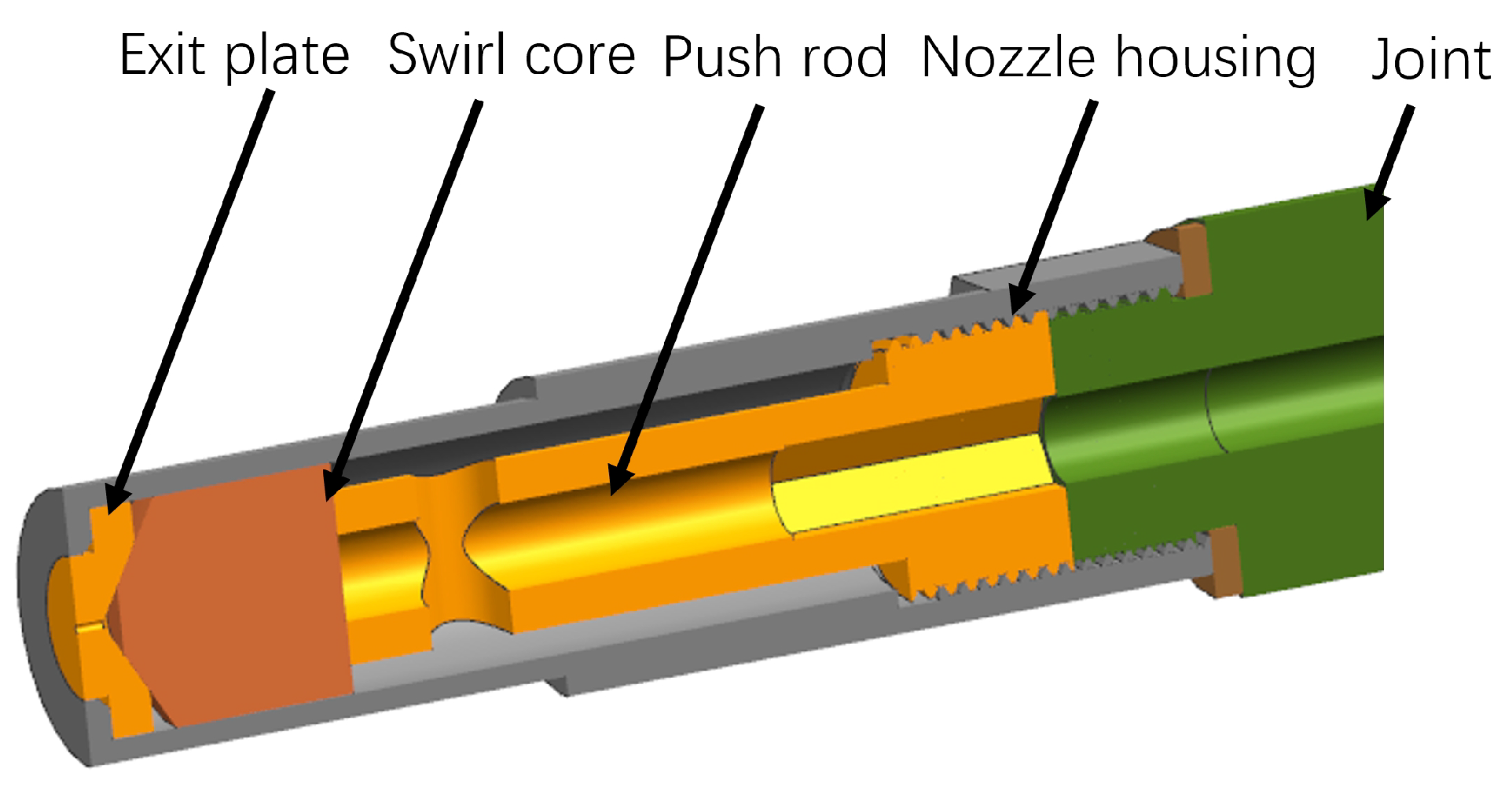
4.1. Pressure Swirl Atomizer
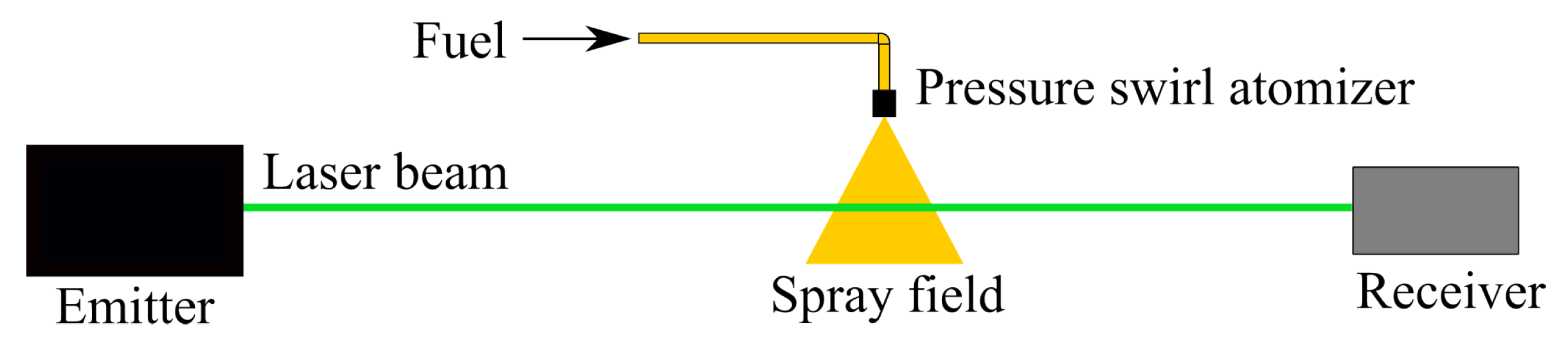
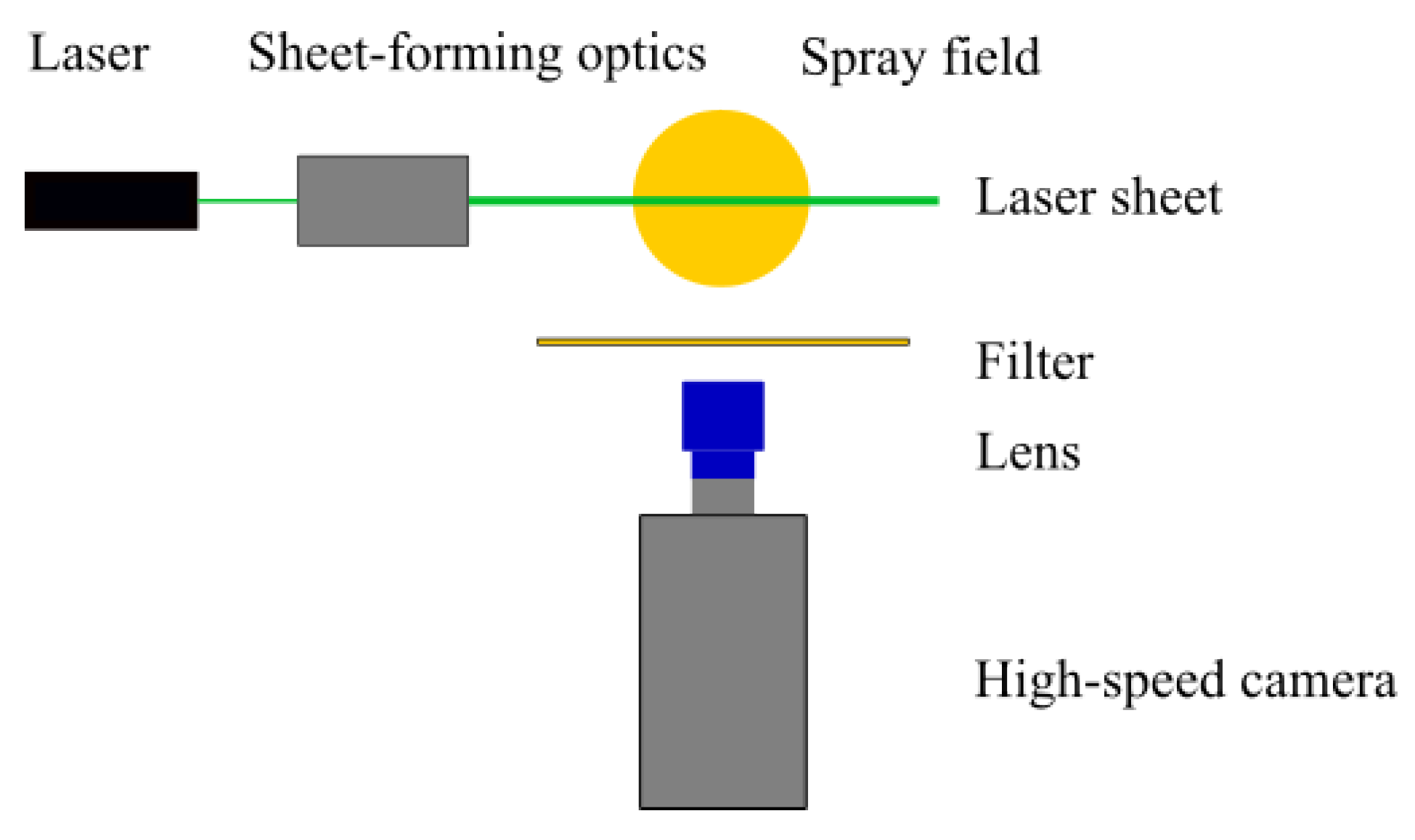
4.2. Laser Diagnostics
5. Results and Discussion
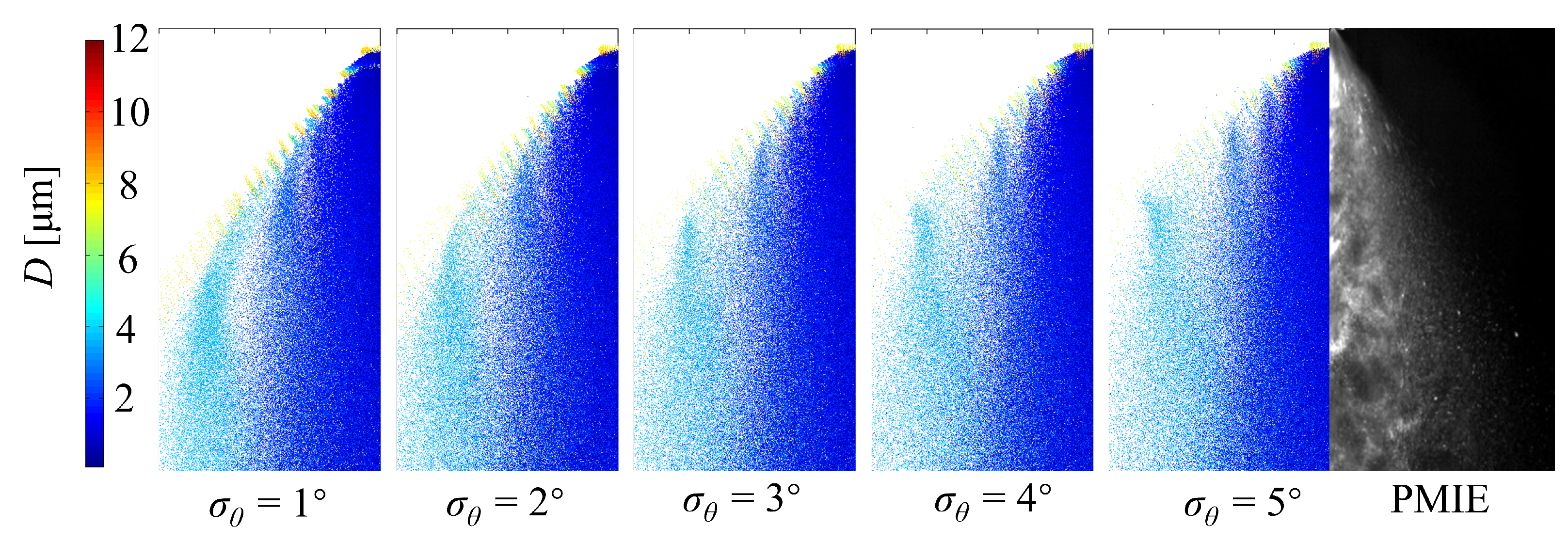
5.1. Linear Instability of the Annular Liquid Sheet
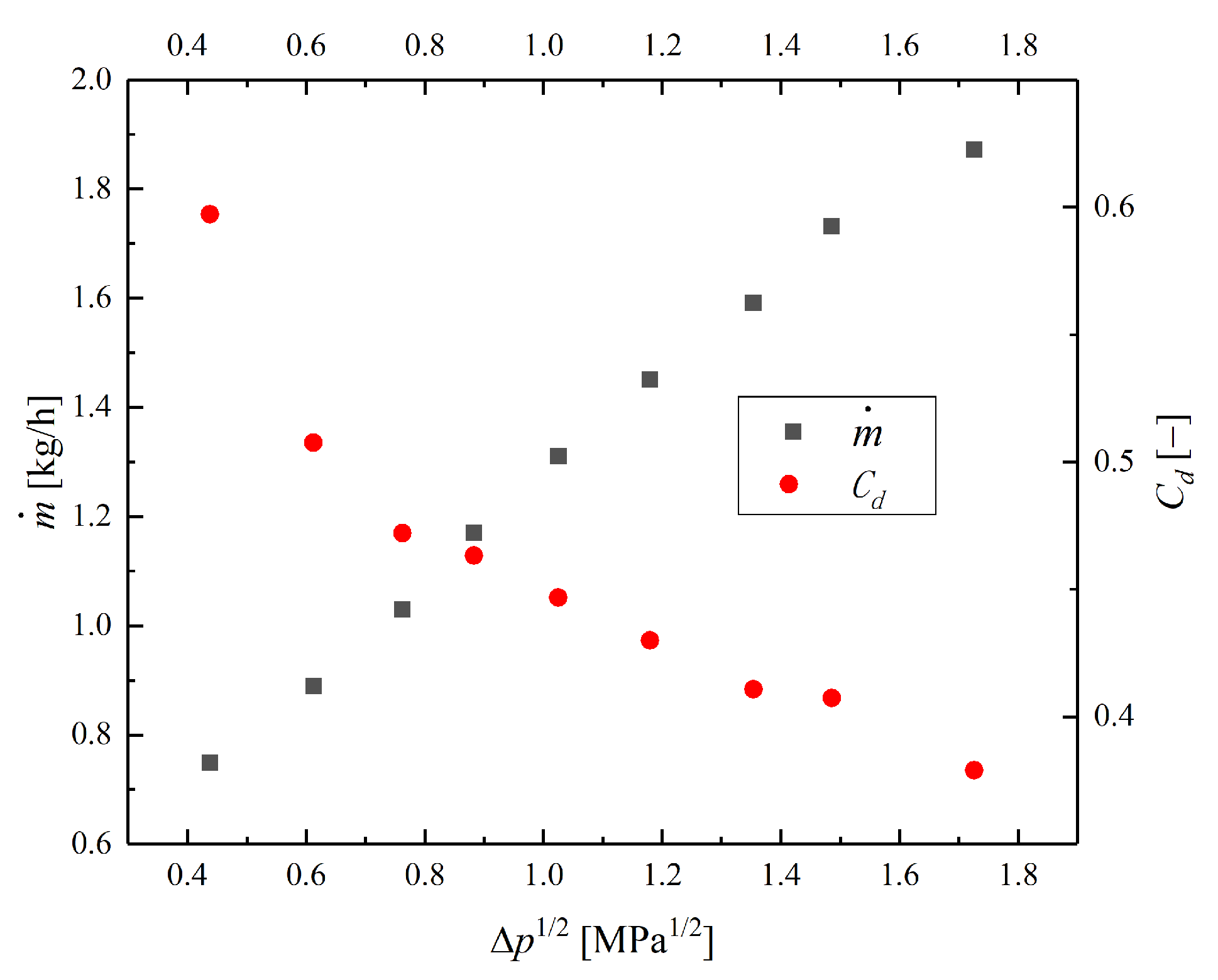
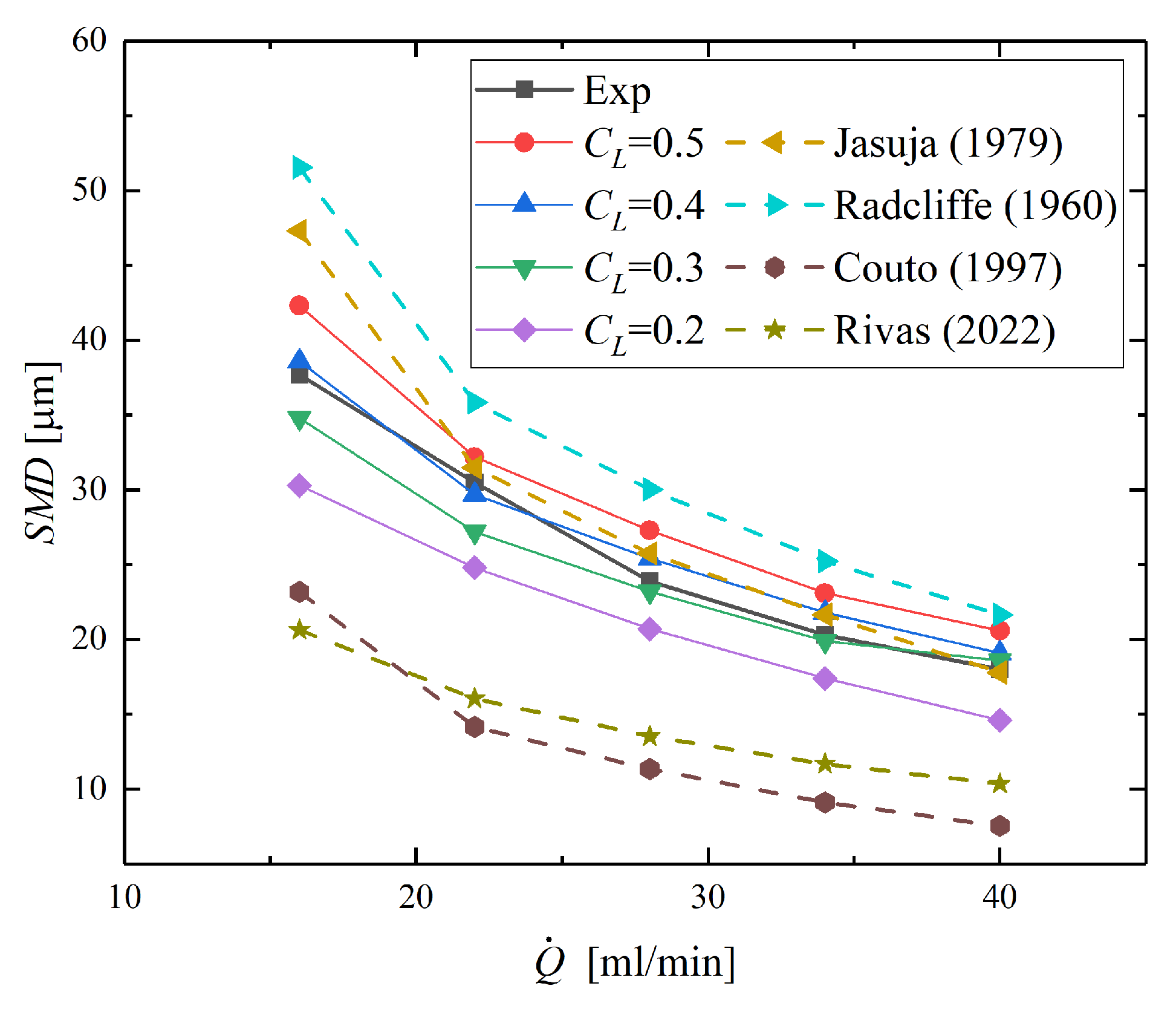
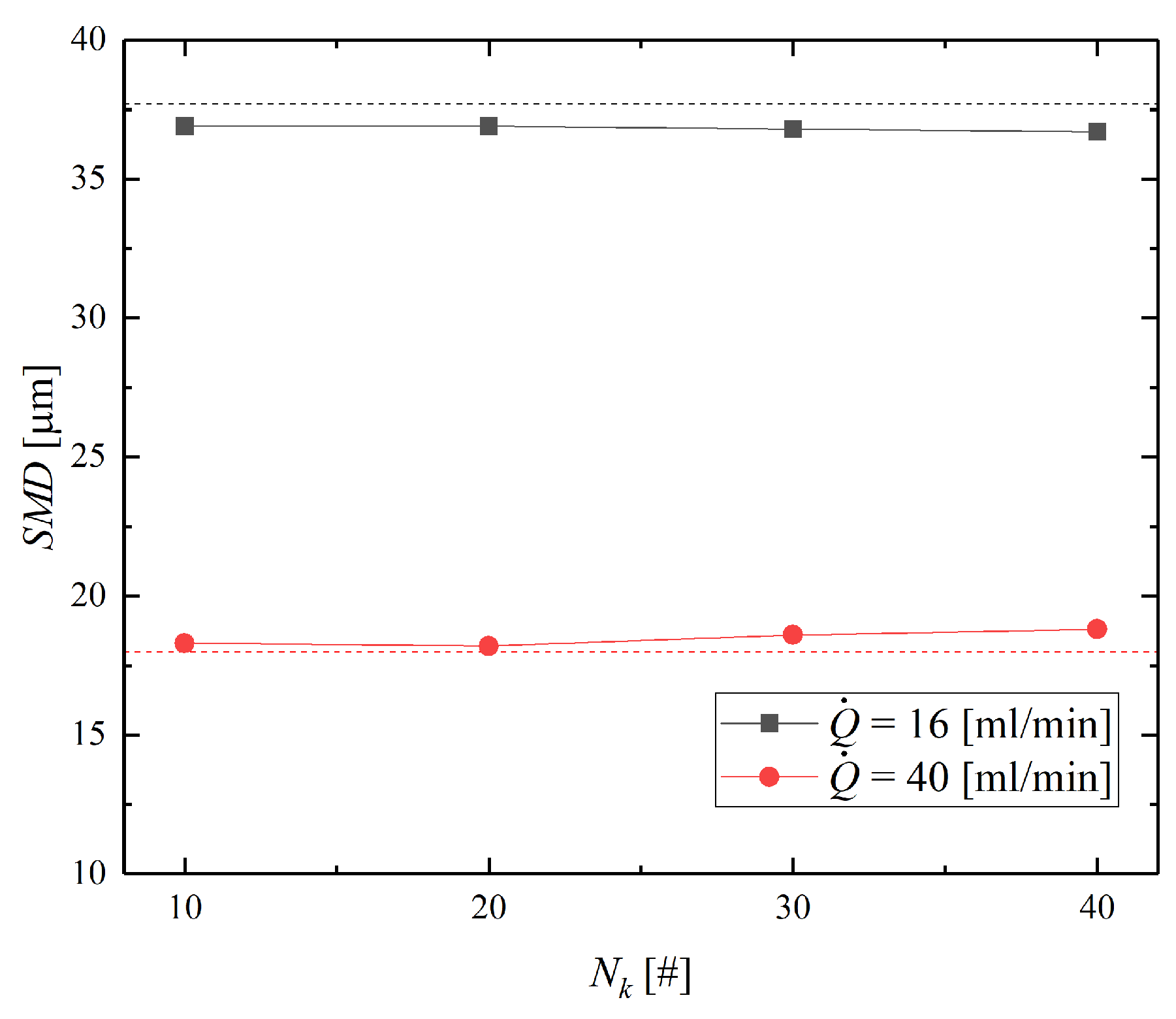
5.2. Effect of Model Parameters on the Prediction of
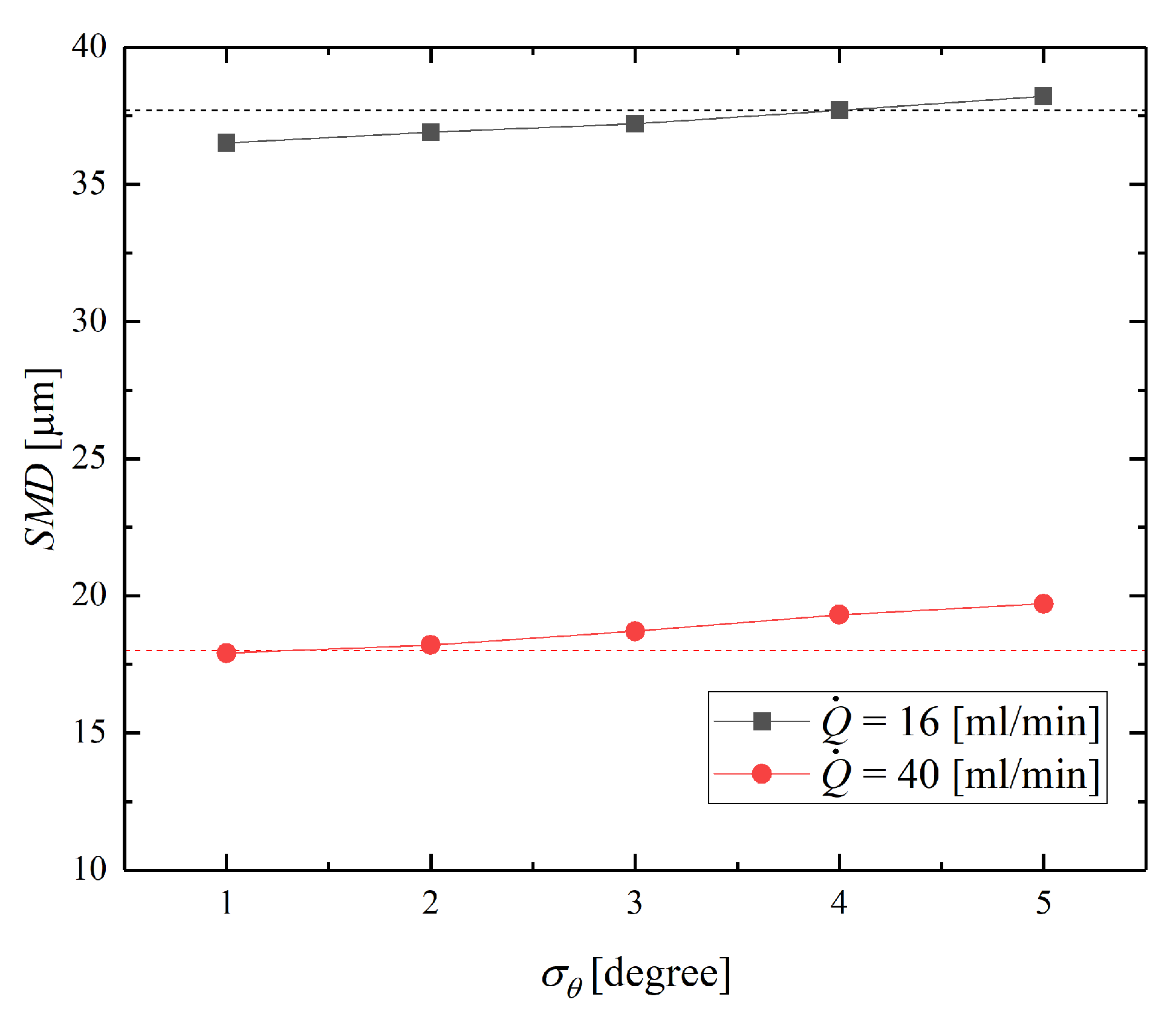
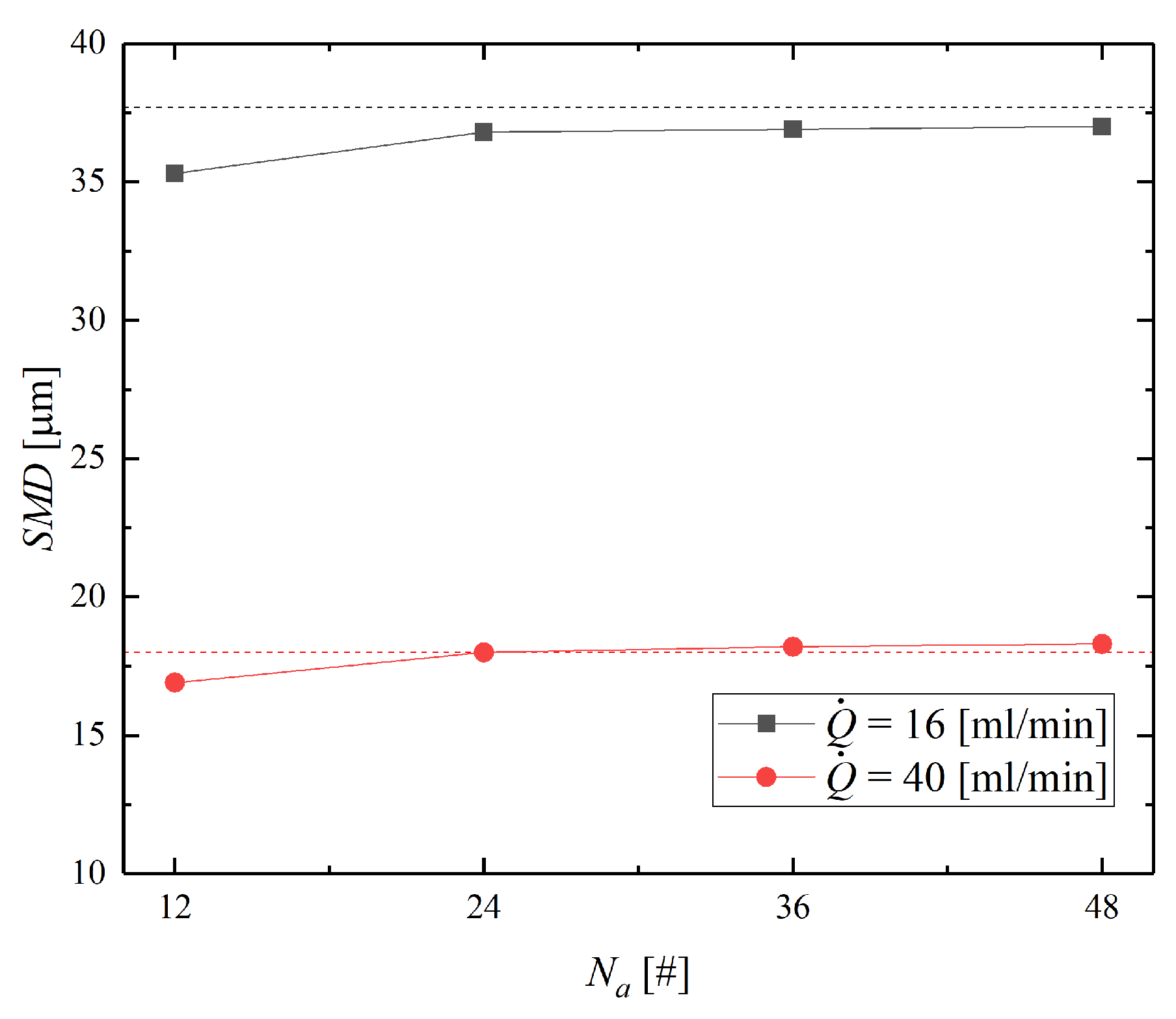
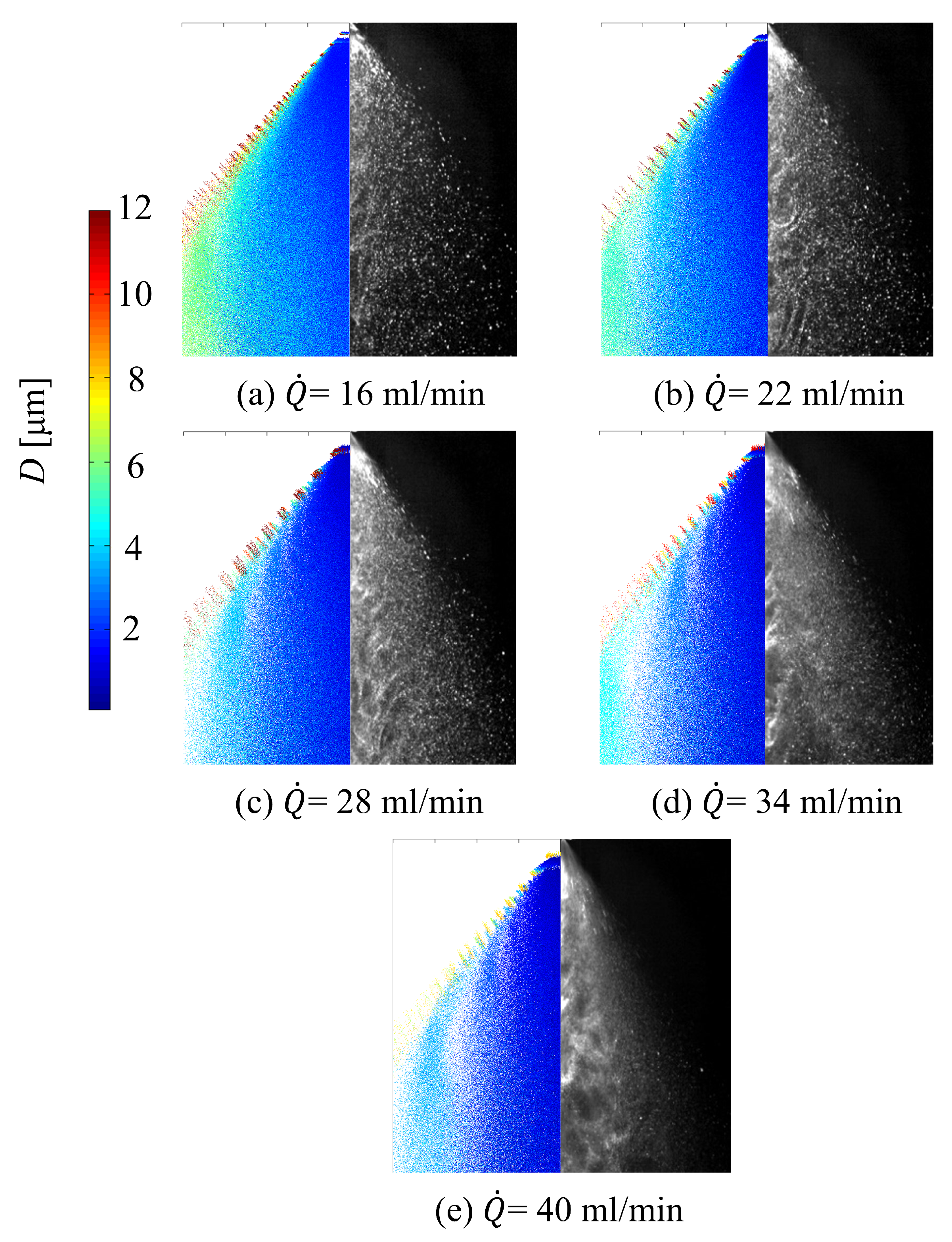
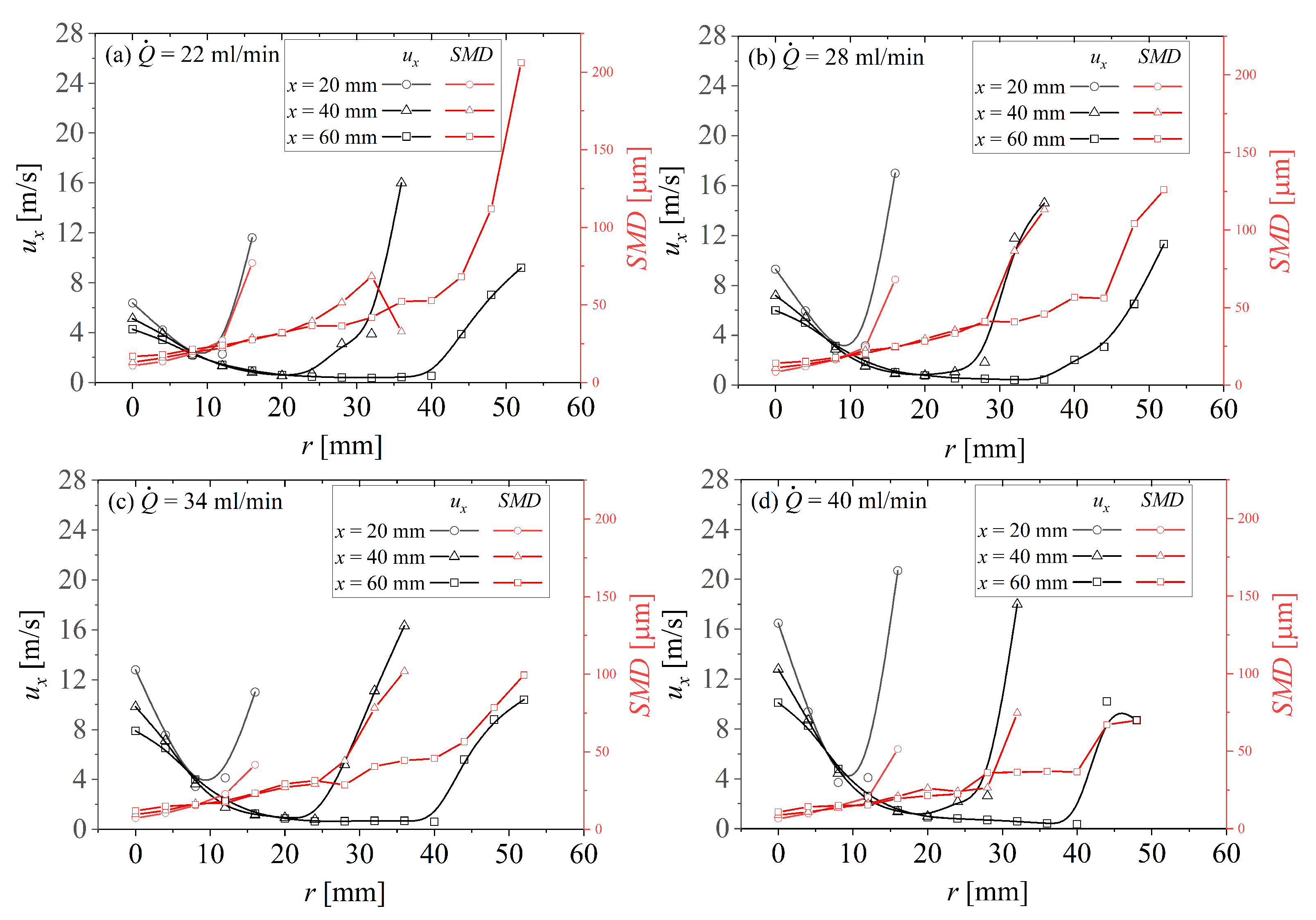
5.3. Effect of Model Parameters on the Simulation Results of the Spray Field
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | aera |
| discharge coefficient | |
| ligament constant | |
| atomizer outlet diameter | |
| air core diameter | |
| F | interface function |
| g | density ratio |
| h | ratio of the inner to outer radius of the annular liquid sheet |
| k | axial wave number |
| mass flow rate | |
| N | number of groups |
| n | azimuthal wave number |
| unit normal interface vector | |
| p | pressure |
| volume flow rate | |
| inner radius of the liquid sheet | |
| outer radius of the liquid sheet | |
| Reynolds number | |
| liquid sheet thickness | |
| U | total velocity magnitude of droplet |
| mean axial velocity | |
| instantaneous velocity vector | |
| mean tangential velocity | |
| Weber number | |
| Y | mass flow rate ratio |
| Greek Symbols | |
| swirl strength of the liquid sheet | |
| complex wave frequency | |
| phase difference between the disturbances on two interfaces | |
| liquid sheet area coefficient | |
| density | |
| surface tension coefficient | |
| spray dispersion angle | |
| spray half angle | |
| radial displacement of the interface | |
| dynamic viscosity | |
| wavelength | |
| subscripts | |
| a | air |
| l | liquid |
| o | outlet |
| s | swirl |
| Abbreviations | |
| CFD | computational fluid dynamics |
| ODE | ordinary differential equations |
| PSA | pressure swirl atomizer |
| SMD | sauter mean diameter |
References
- Yu, S.H.; Si, H.Q.; Chen, C.; Wang, S.J.; Japhet, J.J. Experimental investigation on the impact of air flow rates and back pressures on kerosene microscopic spray characteristics discharged from an air-assisted pressure-swirl atomizer. Int. Commun. Heat Mass Transf. 2024, 151, 107247. [Google Scholar] [CrossRef]
- Leng, X.Y.; Yang, S.; Deng, Y.C.; Jin, Y.; He, Z.X.; Yan, X.S.; Feng, Z.H.; Li, C.; Wang, Q.; Long, W.Q. An experimental study on the in-nozzle cavitating flow and near-field breakup of spirally grooved hole nozzles. Int. Commun. Heat Mass Transf. 2022, 139, 106406. [Google Scholar] [CrossRef]
- Duan, R.Z.; Du, J.B.; Fu, Q.F.; Yue, Y.H.; Liu, T.; Liu, L.S. Investigation on pressure-swirl atomization for cooling and efficiency improvement of photovoltaic module. Appl. Therm. Eng. 2024, 244, 122720. [Google Scholar] [CrossRef]
- Zhang, X.G.; Qiao, W.T.; Gao, Q.X.; Zhang, D.W.; Yang, L.J.; Fu, Q.F. Experimental study on the dynamic characteristics of gas-centered swirl coaxial injector under varying ambient pressure. Aerospace 2023, 10, 257. [Google Scholar] [CrossRef]
- He, C.M.; Luo, W.H.; Zhang, P.; He, Z.X.; Yue, L.J. Spray combustion characteristics of a gas-liquid pintle injector with variable swirl intensities. Phys. Fluids 2023, 35, 097111. [Google Scholar] [CrossRef]
- Tharakan, T.J.; Mukhopadhyay, A.; Datta, A.; Milind, A.J. Trends in comprehensive modeling of spray formation. Int. J. Spray Combust. Dyn. 2013, 5, 123–180. [Google Scholar] [CrossRef]
- Jasuja, A.K. Atomization of crude and residual fuel oils. J. Eng. Gas Turbines Power 1979, 101, 250–258. [Google Scholar] [CrossRef]
- Kennedy, J.B. High weber number SMD correlations for pressure atomizers. J. Eng. Gas Turbines Power 1986, 108, 191–195. [Google Scholar] [CrossRef]
- Ballester, J.; Dopazo, C. Drop size measurements in heavy oil sprays from pressure swirl nozzles. At. Sprays 1996, 6, 377–408. [Google Scholar]
- Kang, Z.T.; Wang, Z.G.; Li, Q.L.; Cheng, P. Review on pressure swirl injector in liquid rocket engine. Acta Astronaut. 2018, 145, 174–198. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 135–145. [Google Scholar]
- Wang, X.F.; Lefebvre, A.H. Mean drop sizes from pressure swirl nozzles. J. Propuls. Power 1987, 3, 11–18. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Hydrodynamics, 1st ed.; Hemisphere: Washington, DC, USA, 1983. [Google Scholar]
- Dombrowski, N.; Johns, W.R. The aerodynamic instability and disintegration of viscous liquid sheets. Chem. Eng. Sci. 1963, 18, 203–214. [Google Scholar] [CrossRef]
- Xiao, W.; Huang, Y. Improved semiempirical correlation to predict sauter mean diameter for pressure swirl atomizers. J. Propuls. Power 2014, 30, 1628–1635. [Google Scholar]
- Chu, C.C.; Chou, S.F.; Lin, H.I.; Liann, Y.H. Theoretical analysis of heat and mass transfer in swirl atomizers. Heat Mass Transf. 2007, 43, 1213–1224. [Google Scholar] [CrossRef]
- Couto, H.S.; Carvalho, J.A., Jr.; Bastos-Netto, D. Theoretical formulation for sauter mean diameter of pressure swirl atomizers. J. Propuls. Power 1997, 13, 691–696. [Google Scholar] [CrossRef]
- Jafari, S.; Kebriaee, A.; Sohrabi, S. A comprehensive predictive model to anticipate droplets size distribution in pressure swirl atomizer. In Proceedings of the ILASS-Europe 2017, Valencia, Spain, 6–8 September 2017; p. 4845. [Google Scholar]
- Som, S.K.; Mukherjee, S.G. Theoretical and experimental investigations on the formation of air core in a swirl spray atomizing nozzle. Appl. Sci. Res. 1980, 36, 173–196. [Google Scholar] [CrossRef]
- Amini, G. Liquid flow in a simplex swirl nozzle. Int. J. Multiph. Flow 2016, 79, 225235. [Google Scholar] [CrossRef]
- Tharakan, T.J.; Ramamurthi, K.; Balakrishnan, M. Nonlinear breakup of thin liquid sheets. Acta Mech. 2002, 156, 29–46. [Google Scholar] [CrossRef]
- Herrero, E.P.; Del Valle, E.M.M.; Galan, M.A. Instability study of a swirling annular liquid sheet of polymer produced by air-blast atomization. Chem. Eng. J. 2007, 133, 69–77. [Google Scholar] [CrossRef]
- Rivas, J.R.; Pimenta, A.P.; Lessa, J.S.; Rivas, G.R. An improved theoretical formulation for Sauter mean diameter of pressure-swirl atomizers using geometrical parameters of atomization. Propuls. Power Res. 2022, 2, 007. [Google Scholar]
- Yan, K.; Ning, Z.; Lü, M.; Sun, C. Study on Droplet Size and Velocity Distributions of a Pressure Swirl Atomizer Based on the Maximum Entropy Formalism. Entropy 2015, 17, 580–593. [Google Scholar] [CrossRef]
- Senecal, P.K.; Schmidt, D.P.; Nouar, I.; Rutland, C.J.; Reitz, R.D.; Corradini, M.L. Modeling high-speed viscous liquid sheet atomization. Int. J. Multiph. Flow 1999, 25, 1073–1097. [Google Scholar] [CrossRef]
- Moon, Y.; Kim, D.; Yoon, Y. Improved spray model for viscous annular sheets in a swirl injector. J. Propuls. Power 2010, 26, 267–279. [Google Scholar] [CrossRef]
- Maly, M.; Slama, J.; Cejpek, O.; Jedelsky, J. Searching for a Numerical Model for Prediction of Pressure-Swirl Atomizer Internal Flow. Appl. Sci. 2022, 12, 6357. [Google Scholar] [CrossRef]
- Qian, W.J.; Hui, X.; Zhang, C.; Xu, Q.H.; Lin, Y.Z.; Sung, C.J. A numerical study of the internal flow in a pressure swirl atomizer. In Proceedings of the ASME Turbo Expo 2017, Charlotte, NC, USA, 26–30 June 2017. GT2017-64149. [Google Scholar]
- Sakman, A.T.; Jog, M.A.; Jeng, S.M.; Benjamin, M.A. Parametric study of simplex fuel nozzle internal flow and performance. AIAA J. 2000, 38, 1214–1218. [Google Scholar] [CrossRef]
- Giffen, E.; Muraszew, A. The Atomisation of Liquid Fuels; Chapman & Hall: London, UK, 1953; pp. 67–115. [Google Scholar]
- Khavkin, Y.I. The Theory and Practice of Swirl Atomizers; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Bazarov, V.; Yang, V.; Puri, P. Design and Dynamics of Jet and Swirl Injectors; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004; pp. 19–103. [Google Scholar]
- Ronceros, J.; Raymundo, C.; Ayala, E.; Rivera, D.; Vinces, L.; Ronceros, G.; Zapata, G. Study of internal flow in open-end and closed pressure-swirl atomizers with variation of geometrical parameters. Aerospace 2023, 10, 930. [Google Scholar] [CrossRef]
- Hui, X.; Qian, W.J.; Lin, Y.Z.; Zhang, C.; Wang, J.C. Effects of liquid and air swirls on the three-dimensional instability of an annular viscous liquid sheet. Fuel 2021, 292, 120227. [Google Scholar] [CrossRef]
- Liao, Y.; Sakman, A.T.; Jeng, S.M.; Jog, M.A.; Benjamin, M.A. A comprehensive model to predict simplex atomizer performance. J. Eng. Gas Turbines Power 1999, 121, 285–294. [Google Scholar] [CrossRef]
- Qian, W.J.; Lin, Y.Z.; Hui, X. Effect of heat and mass transfer on the instability of an annular liquid sheet. Int. J. Heat Mass Transf. 2019, 143, 118499. [Google Scholar] [CrossRef]
- Liu, L.H.; Fu, Q.F.; Yang, L.J. Theoretical atomization model of liquid sheet generated by coaxial swirl injectors. Int. J. Multiph. Flow 2021, 142, 103725. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.J.; Wang, X.D. Theoretical and experimental study of the dynamics of a liquid swirl injector. J. Propuls. Power 2010, 26, 94–101. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.J. Theoretical investigation of the dynamics of a gas-liquid coaxial swirl injector. J. Propuls. Power 2011, 27, 144–150. [Google Scholar]
- Radcliffe, A. Fuel injection. In High Speed Aerodynamics and Jet Propulsion; Princeton University Press: Princeton, WV, USA, 1960. [Google Scholar]
- Hinterbichler, H.; Steiner, H.; Brenn, G. Self-similar pressure-atomized sprays. J. Fluid Mech. 2020, 889, A17. [Google Scholar] [CrossRef]






| h | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.192 | 16 | 0.208 | 0.597 | 0.0781 | 0.0409 | 17.4 | 14.6 | 0.434 | 807 | 766 | 539 |
| 0.581 | 22 | 0.286 | 0.472 | 0.0924 | 0.0338 | 27.3 | 22.9 | 0.513 | 1267 | 1889 | 1330 |
| 1.05 | 28 | 0.364 | 0.447 | 0.0952 | 0.0324 | 35.9 | 30.1 | 0.529 | 1665 | 3265 | 2298 |
| 1.83 | 34 | 0.442 | 0.411 | 0.0992 | 0.0304 | 45.7 | 38.4 | 0.551 | 2120 | 5291 | 3724 |
| 2.98 | 40 | 0.520 | 0.379 | 0.103 | 0.0286 | 56.3 | 47.3 | 0.571 | 2613 | 8041 | 5659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, W.; Wang, J.; Hui, X.; Yang, S.; Cheng, R.; Wang, P. An Improved Comprehensive Atomization Model for Pressure Swirl Atomizers. Aerospace 2024, 11, 658. https://doi.org/10.3390/aerospace11080658
Qian W, Wang J, Hui X, Yang S, Cheng R, Wang P. An Improved Comprehensive Atomization Model for Pressure Swirl Atomizers. Aerospace. 2024; 11(8):658. https://doi.org/10.3390/aerospace11080658
Chicago/Turabian StyleQian, Weijia, Jinduo Wang, Xin Hui, Siheng Yang, Ruyue Cheng, and Ping Wang. 2024. "An Improved Comprehensive Atomization Model for Pressure Swirl Atomizers" Aerospace 11, no. 8: 658. https://doi.org/10.3390/aerospace11080658
APA StyleQian, W., Wang, J., Hui, X., Yang, S., Cheng, R., & Wang, P. (2024). An Improved Comprehensive Atomization Model for Pressure Swirl Atomizers. Aerospace, 11(8), 658. https://doi.org/10.3390/aerospace11080658








