Abstract
The airfoil is the foundation of an aircraft, and its characteristics have a significant impact on those of the aircraft. Conventional airfoil design mainly focuses on improving aerodynamic performance, while flying wing airfoil designs should also consider layout stability and stealth performance. The design requirements for an airfoil vary with its position on the flying wing layout aircraft based on corresponding spanwise flow field characteristics. By analyzing the spanwise flow characteristics of the flying wing, partition design models for flying wing airfoils were established in this study, and a series of flying wing airfoil designs that consider aerodynamics and aerodynamic/stealth were implemented. Then, the designed airfoils were configured on a three-dimensional X-47B layout for testing and verification. The results showed that the aerodynamic design and the aerodynamic/stealth design exhibited significant improvements in terms for aerodynamic and longitudinal trimming characteristics. However, the cruise drag performance of the aerodynamic/stealth design was slightly worse than that of the aerodynamic design, although the longitudinal moment trimming characteristics were basically the same. The stealth characteristics of the aerodynamic/stealth design had significant advantages, indicating that there were weak contradictions between the aerodynamic, stealth, and trimming requirements in the design of the flying wing.
1. Introduction
The airfoil is a basic element that constitutes the wings, tail, and helicopter rotors of an aircraft. Its simple shape enables complex aerodynamic phenomena and flow mechanisms such as shock waves, separation, and vortices to occur [1]. By changing the lift, drag, moment, and radar cross section (RCS) characteristics of the lift or control surface, the airfoil affects the cruise speed, control performance, aerodynamics, and stealth efficiency of the aircraft during all flight stages. Therefore, the airfoil is an important foundation for supporting the development of aviation aircraft [2,3,4,5].
On the one hand, the characteristics of the flying wing airfoil have a more profound impact on the performance of the aircraft due to the integration of the wing body [4,6,7,8]. On the other hand, in response to the increasingly refined design requirements of advanced aircraft, airfoil design has always been an important part of aircraft aerodynamic design, and research on its design theory and methods has received continued attention from designers [1,2,3,5,8,9,10,11,12,13,14].
Aircraft longitudinal moment trimming refers to the use of devices to fine-tune the operating surfaces (ailerons, elevators, and tails) in order to achieve the goal of stabilizing the aircraft’s attitude and heading. However, for wing layout aircraft, due to the lack of tail fins, the flying wing airfoil design must consider the requirements for longitudinal moment trimming, and the moment characteristics of the airfoil are closely related to its camber distribution [7,15,16]. Early flying wing aircraft, such as the YB-49, operated under subsonic cruising states, and the flow field across the wing surface was simple; however, pitch moment trimming would become the prime problem in its aerodynamic design. Therefore, the YB-49 adopted zero-curvature NACA 65-series symmetrical airfoils (such as NACA 65,3-018) for both the inner and outer wing segments [17,18].
As the cruising speed of the aircraft increased to transonic or even high transonic speeds, the aerodynamic load on the outer wing segment increased, leading to a sharp increase in the aircraft’s negative moment coefficient. In order to meet the requirements of pitch moment trimming, the BWB-450 adopted an airfoil with reverse camber of the trailing edge on the inner wing [16], which increased negative loading on the trailing edge to provide a positive moment coefficient, while the outer wing adopted a supercritical airfoil combined with a torsional distribution to reduce pressure drag. However, the airfoil with reverse camber resulted in losses in cruise aerodynamic performance. To solve this issue, the silent aircrafts SAX-29 and SAX-40 adopted airfoils with frontal positive camber on the lower surface of the leading edge to achieve longitudinal moment trimming without a horizontal tail, with no lift loss and the ability maintain a higher static margin (6% to 9.5%) during cruising [19,20]. In addition to pitch moment trimming and aerodynamic characteristics, stealth characteristics should also be taken into consideration in flying wing airfoil design. The stealth design requires the frontal shape of the airfoil to be a clear “eagle beak” feature, effectively avoiding mirror reflection caused by pitch incidence, and thereby reducing the RCS of the entire aircraft [21,22,23]. The aerodynamic loading brought about by the “eagle beak” shape can generate a large positive moment to meet the longitudinal moment trimming requirements, resulting in a good balance between the trimming performance and stealth performance of the flying wing layout [24].
In summary, the shaping of an aircraft has a significant influence on both scattering characteristics and aerodynamic performance, and a balance between aerodynamic and stealth performance is essential in aircraft design. Therefore, coupled aerodynamic and stealth optimization is attracting more attention. However, this multidisciplinary design approach leads to various requirements for the shape of airfoils at different spanwise stations, which cannot be met using traditional airfoil design models for flying wings. Since the beginning of this century, many meaningful studies have been carried out on flying wing airfoil design. Liebeck et al. [7] obtained the ideal velocity distribution of a subsonic airfoil and then designed the LW109A airfoil with a reverse camber trailing edge on the inboard of the BWB-450. Li Long et al. [4] optimized the aerodynamics of a flying wing airfoil by using an improved genetic algorithm to improve the lift-to-drag ratio and decrease the moment coefficient. Huang Jiangtao et al. [25] utilized the Principal Component Analysis (PCA) reduction method for the multidisciplinary optimization of flying wing airfoils. Pambagjo et al. [26] used NASA’s supercritical airfoil as the basis and adopted the residual correction method based on the small perturbation velocity equation to design airfoil profiles at different station positions within the wing layout. The designed airfoil had typical supercritical characteristics. Based on the layout of the Multidisciplinary Optimization Blended (MOB) wing body project, Peigin et al. [27] utilized a global optimization method based on surrogate models to carry out a single-point and multi-point design of an airfoil in a three-dimensional environment, respectively. Hileman et al. [20] combined the design requirements of the inner and outer wing sections of an airfoil and used MSES 2.0 software to carry out the inverse design of a silent passenger aircraft airfoil. Li Peifeng et al. [28] used the Direct Iterative Surface Curvature (DISC) method to design the sectional profile of an outer wing on a large flying wing layout aircraft in order to weaken the shock wave drag of the outer wing. Kuntawala et al. [29] utilized the Free Form Deformation (FFD) method based on spline curves and the adjoint gradient method to carry out the aerodynamic design of airfoils on a flying wing layout. Kanazaki et al. designed an airfoil for a low-aspect-ratio flying wing based on the Efficient Global Optimization (EGO) method. Thomas et al. [30] compared the wing design of a wide body and narrow body flying wing layout passenger aircraft and compared their aerodynamic efficiency and fuel efficiency. Martins et al. [31] designed a flying wing layout aircraft that considered aerodynamics, trim, and maneuverability and optimized the airfoils at three stations. Qin et al. [6] used gradient optimization methods with classic airfoil design models for the airfoil design and then used the obtained results as initial values to achieve a more refined design of the wing layout in a three-dimensional environment, achieving a combination of two-dimensional and three-dimensional conditions for aerodynamic airfoil design.
These studies have made important contributions towards the optimization of flying wing airfoil design. However, certain problems remain that need further attention. First, the studies mentioned above mainly focused on the airfoil design requirements for the central body. Moreover, some work investigated the design optimization of airfoils in multiple positions using a 3D layout. Thus, as there was no detailed partitioning of the flying wing, a comparison of the distinct design requirements of the flying wing airfoil at various positions could not be conducted. Second, the influence of the aerodynamics, stealth, and trimming characteristics of airfoils designed for different spanwise positions on the flying wing performance has not been studied. Therefore, the main contributions of the current paper are (1) the establishment of flying wing airfoil partition design models; (2) the performance of airfoil optimizations that consider aerodynamics and aero/stealth requirements; and (3) the study of the influence of different station airfoils on flying wing layout characteristics. The remainder of the paper is organized as follows. Research on the airfoil design model used in this work is described in Section 2. The optimization, considering aerodynamics and aerodynamics/stealth, is presented in Section 3. Section 4 concludes the paper with a summary.
2. Research on Airfoil Design Model Based on Spanwise Flow
2.1. Problem Formulation
In order to analyze the spanwise aerodynamic characteristics of the flying wing under the high-speed cruise state, a typical double-sweep flying wing based on X-47B is selected, as shown in Figure 1, with an inboard sweep angle of 55° and an outboard sweep angle of 36°. The parameters of the baseline aircraft are summarized in Table 1: the coordinate of the nose was (0, 0, 0). The aerodynamic and electromagnetic evaluation conditions are summarized in Table 2.
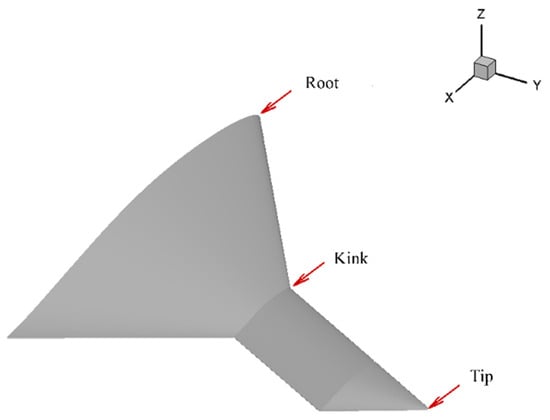
Figure 1.
Spanwise zoning of flying wing.

Table 1.
Layout parameters of the baseline aircraft.

Table 2.
Computation states.
The NACA 65,3-018 airfoil is selected as the basis to generate NACA 65,3-series airfoils with relative thicknesses of 14%, 13%, and 11% adopted for the various positions of the flying wing. The NACA 65,3-018 airfoil is the baseline airfoil of the YB-49 aircraft.
In this paper, a parallel CFD solver, CFL3D 6.7 [32], is adopted to evaluate the aerodynamic characteristics of two-dimensional (2D) airfoils and three-dimensional (3D) layouts. CFL3D 6.7 is a structured-grid, cell-centered, upwind-biased, Reynolds-averaged Navier–Stokes (RANS) code. It can be run in parallel on multiple grid zones with point-matched, patched, overset, or embedded connectivities. Both multigrid and mesh sequencing are available in time-accurate or steady-state modes. CFL3D 6.7is especially good for the computation of transonic statements, which makes it suitable for use in this study. The RCS characteristics are evaluated via FEKO 2021 employing the Multilevel Fast Multipole Method (MLFMA). FEKO 2021 is the first algorithm in the world to successfully apply the numerical Method of Moments (MOMs) and introduce the Multilayer Fast Multipole (MLFMM) on top of it. This method makes it possible to accurately analyze the problem of large-sized electrical objects. FEKO 2021 supports the finite element method (FEM) and solves the problem of a mixture of MLFMM and FEM, and the MLFMM + FEM hybrid algorithm can solve the problem of large electrical dimensions with highly inhomogeneous dielectrics. The space between the MLFMM region (e.g., the radiation region) and the FEM region (e.g., the media region) does not need to be meshed, which makes the matrix small in size and therefore require few computational resources.
2.2. Study on the Spanwise Flow Mechanism of Flying Wing Layout
Table 3 shows the aerodynamic and stealth performance of the BaseModel under the evaluation states. Given the center of gravity (C.G.) around the middle of the root section, the BaseModel equipped with symmetrical airfoils obtains a large negative pitch moment coefficient. There is a strong shock wave across the middle part on the upper surface. As for stealth performance, there are two obvious peak angles within the frontal sector at . In the yaw direction, it is typical to pay attention to the frontal sector at .

Table 3.
Computational results for X-47B layout.
Figure 2 shows the pressure distribution contour of the X-47B layout, with the left side showing the pressure distribution on the upper surface and the right side showing the pressure distribution on the lower surface. In the current computational state, the pressure distribution in the inner wing section is relatively gentle, and obvious shock waves occur in the outer wing. Figure 3 and Figure 4 show the corresponding spanwise lift coefficient distribution and circulation distribution, respectively. The local lift coefficient of the inboard wing is relatively small, and it gradually increased along the span length until reaching its maximum in the outboard wing.
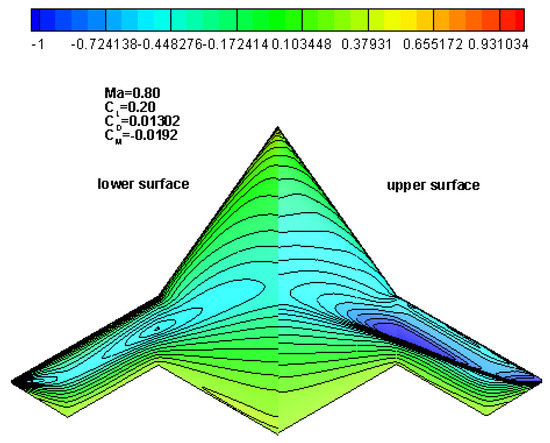
Figure 2.
Pressure distribution contour map.
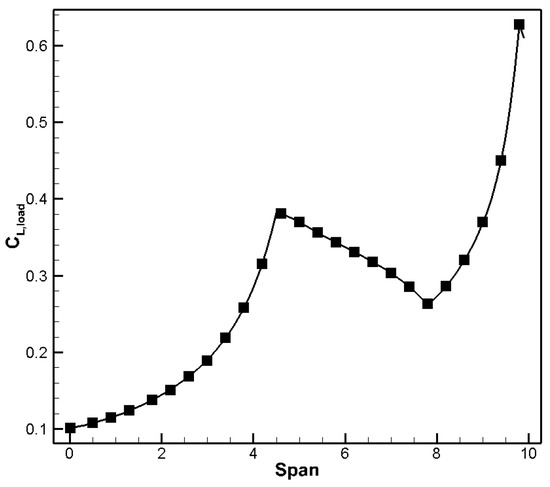
Figure 3.
Spanwise lift coefficient distribution.
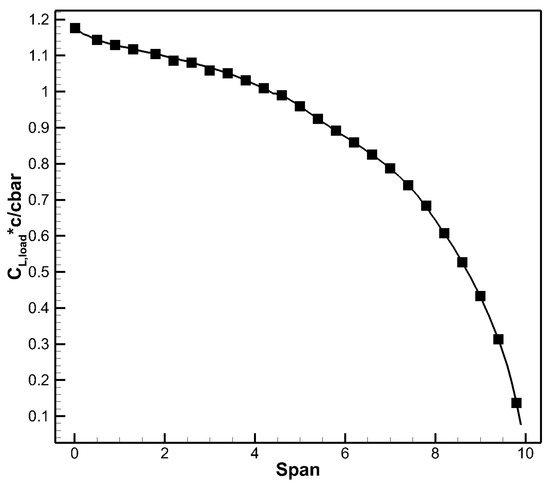
Figure 4.
Spanwise circulation distribution.
Although the thickness of the inboard position of the flying wing is large, no significant shock wave occurred due to its large sweep angle. However, the high lift of the outer wing section leads to strong shock waves in the middle area of the flying wing, spanning the entire outboard wing and extending to the wing tip. The difference in the local chord length of various positions results in a gradual reduction in the local load from the inboard wing to the outboard, as shown in Figure 4, presenting an approximate triangular distribution, which reflects the balance between shock drag and induced drag.
In summary, for the tailless flying wing, the central body region (the region around the root) and middle region (the region around the kink) undertakes the task of pitch moment trimming, while the middle region to wing tip region represent the key point for aerodynamic drag reduction, which make the design requirements for the flying wing airfoils for various positions differ from each other.
2.3. Design Requirements of Flying Wing Layout Airfoil
Traditional aircraft require good cruising aerodynamic efficiency and takeoff and landing performance. Thus, the general requirements of their airfoils are as follows:
- (1)
- Throughout the entire range, the airfoil must have a high cruising lift-to-drag ratio, good drag divergence characteristics and a small compressible drag increment.
- (2)
- There must be sufficient buffet boundaries to ensure that the aircraft does not exhibit buffet within a certain range beyond the cruising Mach number.
- (3)
- The positive moment coefficient should be designed within a certain range to reduce trimming drag.
Compared with traditional aircraft, the flying wing has stricter requirements in terms for aerodynamic airfoil design. Based on traditional aerodynamic characteristics, the requirements for pitch moment trimming characteristics and boundary characteristics are greater. Specifically, the design requirements are as follows:
- (1)
- Due to the lack of a tail and the complex control surface settings, the flying wing airfoil needs to achieve moment self-trimming at the cruise design states as much as possible to alleviate the pressure on aircraft control and facilitate the design of the aircraft control system.
- (2)
- High transonic and even supersonic cruising are important trends in the future development of aircraft. However, the loading requirements of the flying wing necessitate a much thicker airfoil, so it is necessary to improve the drag divergence characteristics of the airfoil to achieve better aircraft cruising efficiency and to meet the buffet boundaries.
- (3)
- The flying wing integrates the wing and fuselage; thus, the inboard bears the loading requirements and requires greater volume and thickness.
In addition to the aerodynamic design requirements, the flying wing also requires collaborative design from other disciplines, such as stealth [22]. Stealth characteristics are directly related to the combat capability and battlefield survival ability of military aircraft [33]. As a low-RCS layout, flying wings need to integrate the influence of RCS into the airfoil design stage to fully leverage their layout advantages.
It is usually difficult to fulfill the multidisciplinary requirements of flying wing airfoils simultaneously. However, the performance requirements for the different spanwise positions on the flying wing are distinct, meaning that the design requirements for each airfoil are also different. With this in mind, it becomes necessary to establish design models for flying wing airfoils used in different spanwise positions and to carry out the optimization design separately. Based on the above analysis, a three-dimensional partitioning airfoil design concept based on the X-47B was established. The layout is decomposed into the wing root area (root), wing kink area (kink), and wing tip area (tip), and a series of airfoil design models are proposed to meet the design requirements of the entire aircraft. For a military flying wing layout with high demand for aerodynamic and stealth characteristics, its airfoils should generally meet the following requirements:
- (1)
- The central body zone, also known as the wing root zone, is a region where the airfoil should not only meet the loading requirements but also have good lift–drag characteristics and stealth characteristics. In addition, a certain amount of positive moment is also required to promote the longitudinal moment trimming of the entire aircraft.
- (2)
- Shock waves generally occur in the kink zone. Therefore, in addition to ensuring loading requirements, the airfoil design in this region should have good cruise lift–drag characteristics and drag divergence characteristics. Moreover, this region is close to the center of gravity, and it is necessary to decrease the negative moment or even increase the positive moment to meet the pitch moment trimming requirements.
- (3)
- The airfoil in the tip zone should increase the cruising lift/drag ratio, achieving good cruising efficiency and exhibiting good stealth performance.
The above discussion shows that the design requirements for airfoils on the inboard and outboard wing are mostly different. In terms for aerodynamic design, for the airfoil on the outboard wing, the main focus is to reduce cruise drag and improve stealth characteristics to ensure high cruise efficiency. The inboard wing airfoil needs a high positive moment coefficient to neutralize the negative moment generated by the outboard wing, achieving pitch moment self-trimming in the cruise state.
3. Optimization Studies
In this part of the study, aerodynamic and aerodynamic/stealth optimizations of airfoils in different positions are performed. The first optimization considers aerodynamics, with research being conducted to determine how the transonic aerodynamic and moment performance of the airfoils would affect that of the flying wing. The second optimization considers aerodynamics and stealth in combination, with the aim of determining the influence of the airfoils’ aerodynamic/stealth performance on that of the flying wing.
In all optimizations, the design variables are the z-coordinates of the Class Shape function Transformation (CST) parameterization [34], with 36 shape parameters in total. The Niching-based Adaptive Space Reduction (NASR) method [24] based on the Kriging model [35] is adopted to obtain the design results.
3.1. CFD Validations
CFL3D is a finite-volume multi-block solver for the RANS and Euler equations. The RANS equation with the Shear Stress Transport (SST) two-equation turbulence model is adopted as a high-fidelity numerical method, and the Euler equation is the low-fidelity numerical method. The current study uses the second-order Roe scheme augmented with artificial viscosity for the spatial discretization and the implicit approximate factorization method for time marching.
To test and verify whether the CFD solver CFL3D for aerodynamic analysis is accurate and the optimization is not driven to unphysical solutions due to CFD solver errors, the CFD solver validation based on an RAE2822 airfoil, which was provided by National Aeronautics and Space Administration (NASA), Washington, DC, USA, is carried out and is presented in this section.
The RAE2822 airfoil is a classic validation example used by the AGARD and EUROVAL project teams. The calculation states selected in this study are , , and . Three different densities of grids (coarse, medium, and fine) are used, respectively. The grid topology is C-type, and the grid parameters are shown in Table 4. The grid is shown in Figure 5.

Table 4.
RAE2822 airfoil calculation grid parameters.
Figure 5.
RAE2822 computational grid.
Figure 6 shows a comparison between the pressure distribution of the RAE2822 airfoil numerical calculation and the wind tunnel test results. The calculation results using medium and fine grids are in good agreement with the test results and could accurately calculate the position and intensity of the shock wave. However, the shock wave position calculated using coarse grids is higher and the shock wave intensity is weaker. Figure 7 shows the comparison between the calculated friction distribution of the RAE2822 airfoil and the experimental results. The friction distribution of the three grid calculations is in good agreement with the experimental data, but there is a certain deviation at the shock wave. Table 5 presents a comparison between the numerical calculation and the wind tunnel test results. The lift and drag coefficients calculated using medium and fine grids have high simulation accuracy.
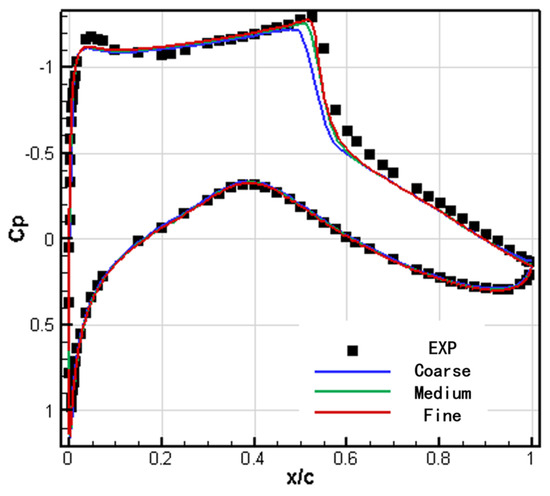
Figure 6.
Comparison of pressure distribution on airfoils.
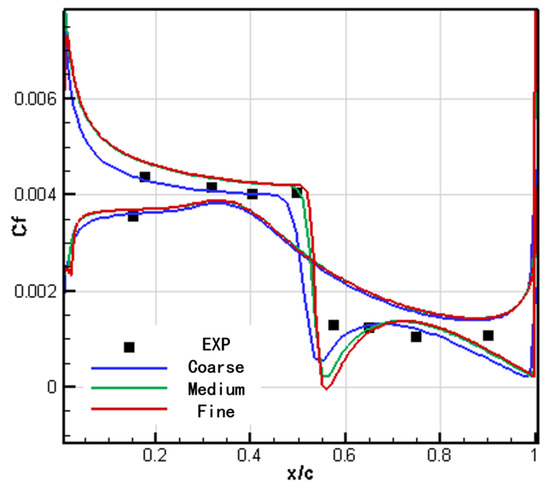
Figure 7.
Comparison of wing friction distribution.

Table 5.
Comparison of numerical calculation and wind tunnel test results for RAE2822 airfoil.
3.2. Aerodynamic Optimization
3.2.1. Aerodynamic Optimization of Root Airfoil
The design status of the central body zone (root) airfoil is . The baseline airfoil was the NACA 65,3-014 airfoil with a relative thickness of 14%, and its aerodynamic characteristics required an increase in lift–drag characteristics, while maintaining the positive moment coefficient. The problem can be expressed as a nonlinear optimization problem:
A comparison of the computational results is shown in Table 6. Compared to the baseline airfoil NACA 65,3-014, the drag coefficient of the designed airfoil, named Aero_RootOpt, reduced by 2 counts, and the moment coefficient reached 0.0308, meeting the constraint.

Table 6.
Comparison for aerodynamic results of root airfoil.
A comparison between the airfoil profile shape and pressure coefficient distribution is shown in Figure 8 and Figure 9, respectively. In the current state, there is no significant shock wave in the NACA 65,3-014 airfoil, and the pressure recovery is gentle. In order to meet the moment coefficient constraint, the leading-edge camber of the designed airfoil increases, showing obvious positive loading, and the trailing-edge camber decreases, resulting in negative loading. By combining the change in aerodynamic loading, the positive moment coefficient requirement is fulfilled. The pressure recovery on the upper surface of the Aero_RootOpt airfoil is gentle, and the low-pressure area moves slightly forward, as shown in Figure 10. Comparisons of the drag and moment characteristics are shown in Figure 11 and Figure 12, respectively, from which it can be observed that Aero_RootOpt maintains good drag characteristics and positive moment characteristics from Ma0.60 to 0.69, with little fluctuation in the moment coefficient.
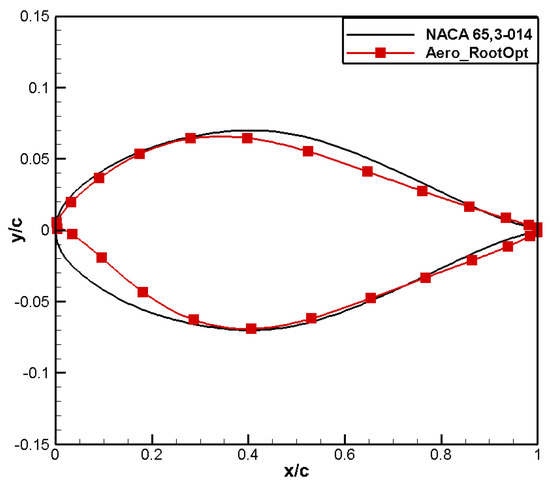
Figure 8.
Comparison of airfoil shape for aero root airfoil.
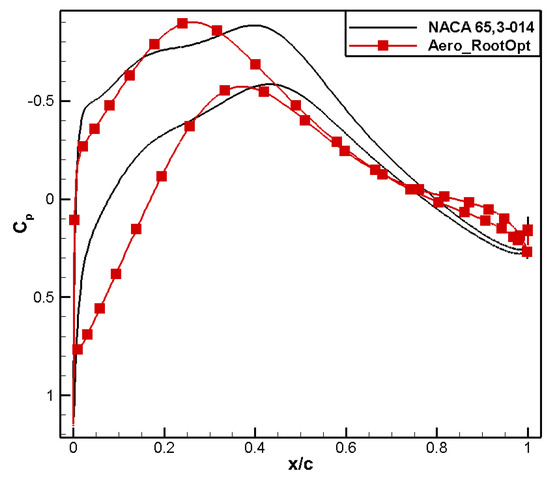
Figure 9.
Comparison of pressure coefficient distribution for aero root airfoil.
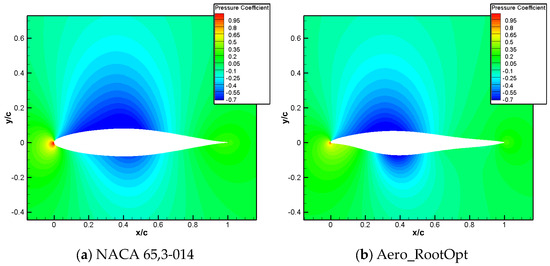
Figure 10.
Comparison of pressure distribution for aero root airfoil.
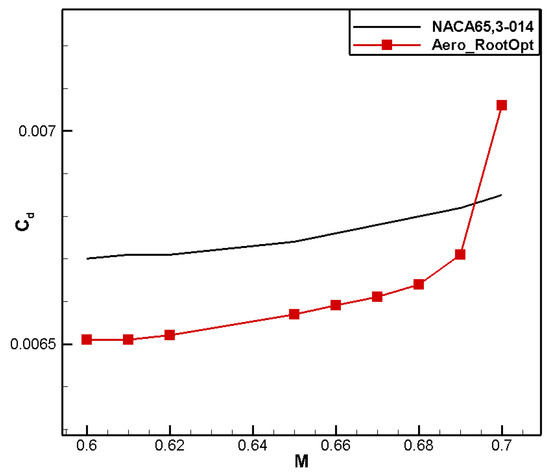
Figure 11.
Comparison of drag characteristics for aero root airfoil.
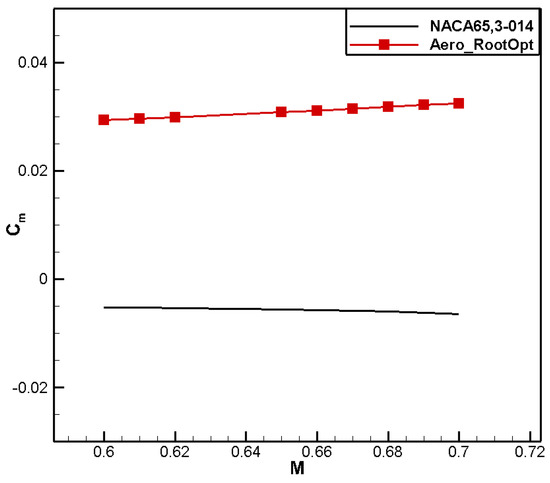
Figure 12.
Comparison of moment characteristics for aero root airfoil.
Aero_RootOpt is assembled onto the central body of the X-47B to form the layout AeroOpt1, and Table 7 shows a comparison of the computational results. Compared to BaseModel, the drag coefficient for aeroOpt1 reduced by 7.8 counts, and the pitch moment coefficient increases from −0.0192 to −0.0058. Figure 13 presents a comparison of the pressure distribution contours. Compared to the BaseModel, the low-pressure zone on the inboard wing for aeroOpt1 expands forward, and the pressure recovery at the trailing edge becomes more gentle. The shock drag on the middle wing area is significantly reduced; however, a strong shock wave still occurs on the outboard wing.

Table 7.
Computational results for layout with aero root airfoil.
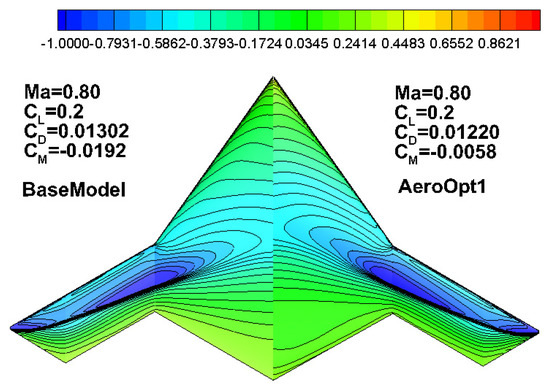
Figure 13.
Pressure distribution of BaseModel (left) and AeroOpt1 (right).
3.2.2. Aerodynamic Optimization of Kink Airfoil
The design state of the airfoil in the kink position is , and the baseline airfoil is NACA 65,3-013. The kink airfoil requires improvements to the lift–drag characteristics and drag divergence characteristics in the cruise state while maintaining a positive pitch moment. The design model is shown in Equation (2).
The comparison of computational results is shown in Table 8. Compared to the baseline airfoil NACA 65,3-013, the drag coefficient of the optimized airfoil, named Aero_KinkOpt, is reduced by 16 counts and the moment coefficient reaches 0.0100, meeting the design constraint.

Table 8.
Comparison for aerodynamic results for aero kink airfoil.
A comparison of the airfoil profile shapes is presented in Figure 14, from which it can be observed that, compared to that of NACA 65,3-013, the leading-edge radius for aero_KinkOpt decreases slightly, and the upper surface shape tends to be flatter—a shape conducive to pressure recovery. At the same time, the maximum thickness position moves backward and the trailing-edge thickness increases. Figure 15 shows that the suction peak for aero_KinkOpt increases at the leading edge, and the strong shock wave on the upper surface is transformed into a dual weak shock wave. In addition, due to the drastic changes on the lower surface, a weak shock wave appears, as shown in Figure 16. At the same time, the shock wave position shifts forward, which is beneficial for improving its drag divergence characteristics, as shown in Figure 17. In order to meet the positive moment constraint, the leading edge of the designed airfoil exhibits obvious positive loading characteristics, and the phenomenon of alternating positive and negative loading at the trailing edge occurs. Figure 18 shows that Aero_KinkOpt maintains good positive moment characteristics within the Mach number range of 0.70–0.76.
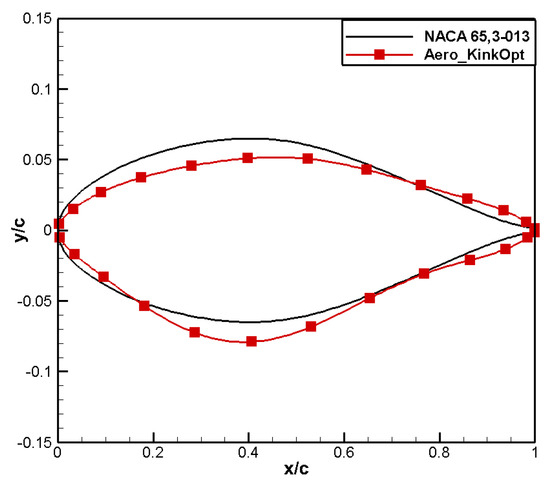
Figure 14.
Comparison of airfoil shape for aero kink airfoil.
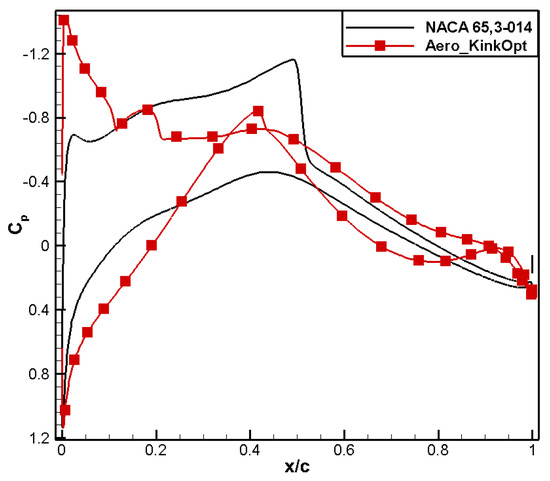
Figure 15.
Comparison of pressure distribution for aero kink airfoil.
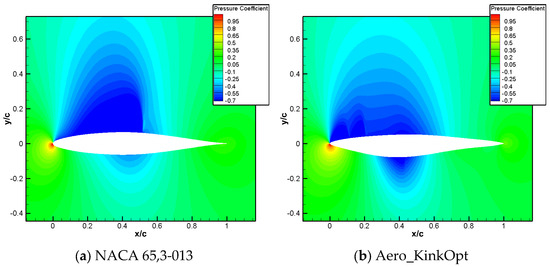
Figure 16.
Comparison of pressure distribution for aero kink airfoil.
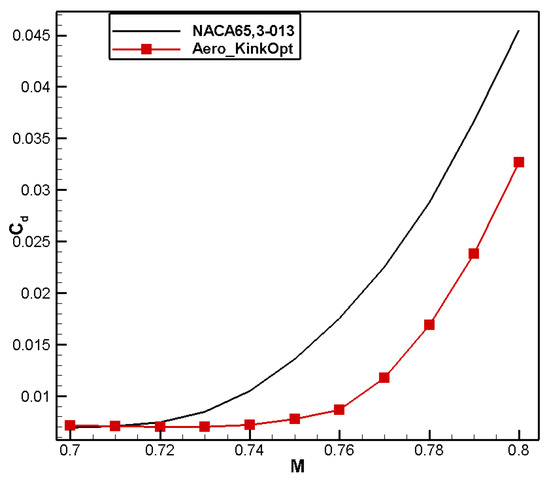
Figure 17.
Comparison of drag characteristics for aero kink airfoil.
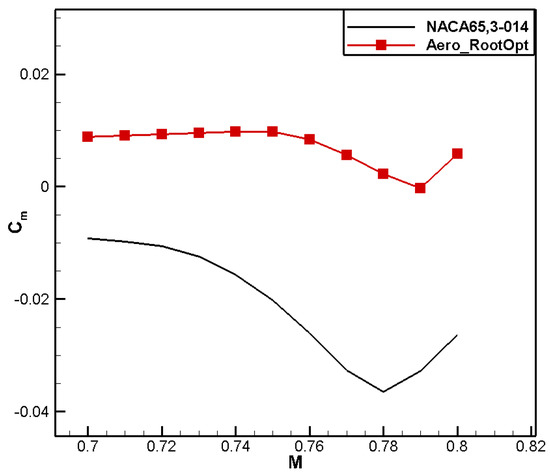
Figure 18.
Comparison of moment characteristics for aero kink airfoil.
The Aero_KinkOpt airfoil is assembled in the middle area of the X-47B to form the layout AeroOpt2. Table 9 presents the comparisons between the aerodynamic calculation results. Compared to AeroOpt1, the drag coefficient for aeroOpt2 reduced to 113.8 counts, and the pitch moment coefficient increases from −0.0058 to −0.0025, further improving the pitch moment trimming characteristics. Figure 19 shows that, compared to AeroOpt1, the shock waves in the middle and outboard wing for aeroOpt2 are significantly weakened, and the shock wave in the outboard wing moves slightly forward.

Table 9.
Computational results for layout with aero root and kink airfoil.
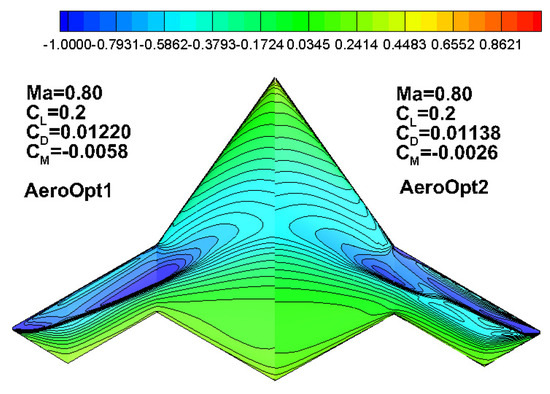
Figure 19.
Pressure distribution for aeroOpt1 (left) and AeroOpt2 (right).
3.2.3. Aerodynamic Optimization of Tip Airfoil
The design requirements for the tip airfoil are to reduce drag and enhance drag divergence characteristics, with the constraint being that the moment coefficient of the designed airfoil should be no less than that of the baseline airfoil NACA 65,3-011, while keeping the maximum thickness unchanged. The design status is , and the design model is shown in Equation (3).
The comparison results for the two airfoils are shown in Table 10. Compared to NACA 65,3-011, the drag coefficient for aero_TipOpt is reduced by 1 count since there is no significant shock wave in the pressure coefficient distribution of the baseline airfoil under low transonic load calculations, so the lift–drag characteristic is basically maintained. The moment coefficient reaches −0.0021, meeting the design requirements.

Table 10.
Comparison for aerodynamic results for aero tip airfoil.
A comparison of the shape of the airfoils is shown in Figure 20. Compared to NACA 65,3-011, the leading-edge radius for aero_TipOpt decreases, while the upper surface on the leading edge tends to be flat. The maximum thickness position moves back, and the thickness of the trailing edge increases. A comparison of the pressure coefficient distribution is shown in Figure 21. Compared to the baseline airfoil, the suction peak on the leading edge of the optimized airfoil is significantly weakened, and the baseline airfoil begins to recover pressure at 40% chord. The optimized airfoil recovers at 20% and 60% chord, respectively, which is beneficial for improving the drag divergence characteristics. Figure 22 and Figure 23 show that the drag divergence Mach numbers of the Aero_TipOpt and the NACA 65,3-011 airfoils are both 0.76, but Aero_TipOpt has better drag characteristics and maintains good moment characteristics, as shown in Figure 24.
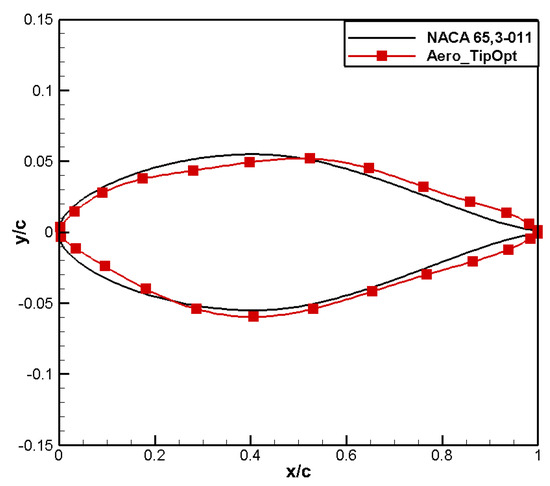
Figure 20.
Comparison of airfoil shape for aero tip airfoil.
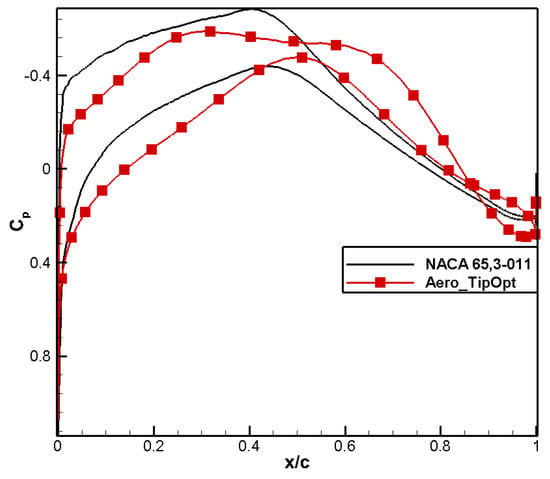
Figure 21.
Comparison of pressure distribution for aero tip airfoil.
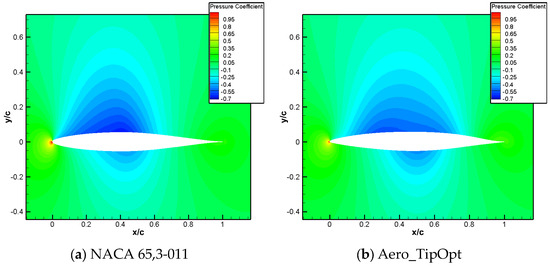
Figure 22.
Comparison of pressure distribution for aero tip airfoil.
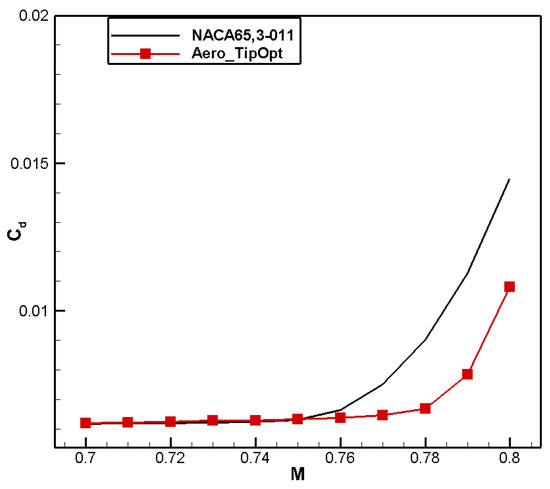
Figure 23.
Comparison of drag characteristics for aero tip airfoil.
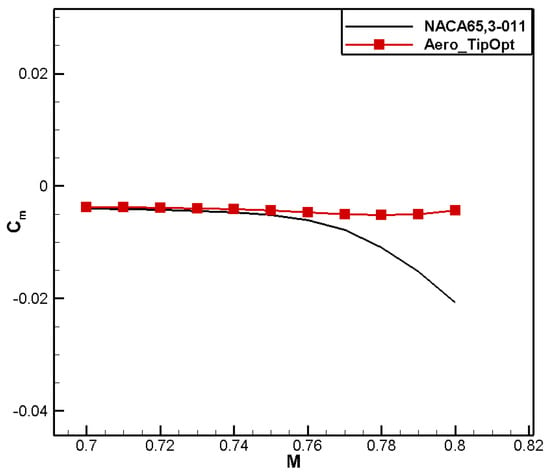
Figure 24.
Comparison of moment characteristics for aero tip airfoil.
The Aero_TipOpt airfoil is assembled onto the wing tip area of the X-47B to form AeroOpt3, and comparisons are made with other layouts, as shown in Table 11. Compared to AeroOpt2, the drag coefficient for aeroOpt3 reduces by 0.9 counts, and the moment coefficient increases to −0.0009, achieving balanced pitch moment trimming. Figure 25 shows that the shock wave intensity in the tip region for aeroOpt3 is weakened, and the pressure recovery at the trailing edge is much gentler.

Table 11.
Computational results for layout with aero root, kink and tip airfoil.
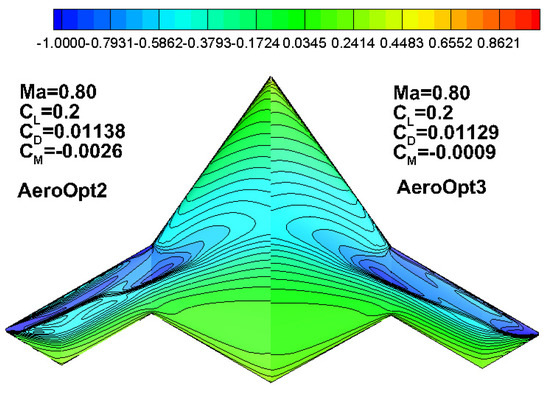
Figure 25.
Pressure distribution for aeroOpt2 (left) and AeroOpt3 (right).
3.3. Aerodynamic/Stealth Optimization
In this section, the aerodynamic and stealth performance of airfoils at the root, kink, and tip positions of the flying wing are considered, respectively. The aerodynamic design conditions and constraints of all airfoils are same as those in the previous section. The stealth objective is the average RCS in the frontal edge, i.e., , at the frequency of 9 GHz. How the airfoils’ aerodynamic/stealth performance affect those of the three-dimensional (3D) configuration are investigated. The RCS evaluation condition of the 3D model is also at f = 9 GHz in the frontal sector at in the pitch direction and at in the yaw direction.
3.3.1. Aerodynamic/Stealth Optimization of Root Airfoil
The stealth characteristics require a decrease in the average forward degree at an incident frequency of 9 GHz; a schematic diagram of the incident angle is shown in Figure 26. Therefore, the design objective is to reduce drag and improve the forward RCS characteristics of the airfoil. The drag coefficient and the frontal average RCS are normalized by the values of the baseline airfoil, as described in Equation (4), where and are the weight factors and is the average value of RCS. The designers could trade off the multidisciplinary conflicts by selecting different weight factors. Ref. [36] is a study of the influence on the design results using different values of the weight factor, and we adopt a similar object function, where and are used. This weighted method is also adopted in the subsequent sections.
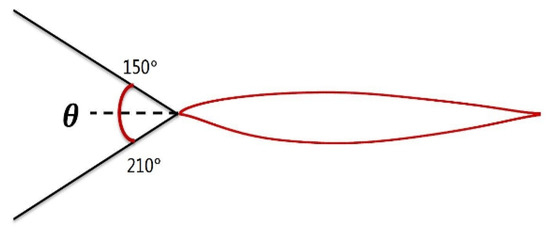
Figure 26.
Sketch of incident angle.
Table 12 shows that the drag coefficient of the optimized airfoil, named Aero/RCS_RootOpt, is larger than that for aero_RootOpt by 1 count, and the moment coefficient remains basically unchanged. In addition, the frontal average RCS decreases by 68.5% compared to the baseline airfoil.

Table 12.
Comparison for aerodynamic/stealth results for aero/stealth root airfoil.
Figure 27 shows that the shape trend for aero/RCS_RootOpt is similar to that for aero_RootOpt: the leading-edge radius decreases and the leading-edge positive camber and trailing-edge negative camber increase. However, Aero/RCS_RootOpt has a smaller leading-edge radius and exhibits an “eagle beak” feature, resulting in a significant decrease in its leading-edge suction peak, as shown in Figure 27. In addition, the low-pressure area on the surface for aero/RCS_RootOpt moves forward, contributing to pressure recovery, as shown in Figure 28. Due to the decrease in the leading-edge radius, the positive loading of the leading edge is less than for Aero_RootOpt, and in order to meet the constraint of positive moment, the trailing edge needs to provide more negative loading, resulting in an extension of the negative lift area of the trailing edge, as shown in Figure 29, which would adversely affect the lift–drag characteristics. Figure 30 and Figure 31 show that the drag characteristic for aero/RCS_RootOpt is significantly better than NACA 65,3-014 but slightly worse than Aero_RootOpt. Moreover, the positive moment characteristics of these two optimized airfoils are basically the same. Figure 32 presents a comparison of the frontal RCS of the airfoils. Compared to NACA 65,3-014, the RCS of the Aero_RootOpt and the Aero/RCS_RootOpt airfoils significantly reduces at all angles, but the leading-edge radius on the upper surface of the Aero_RootOpt airfoil is larger than that on the lower surface, resulting in a larger peak on the upper surface. The peaks on the upper and lower surfaces for aero/RCS_RootOpt are closer, resulting in better RCS characteristics.
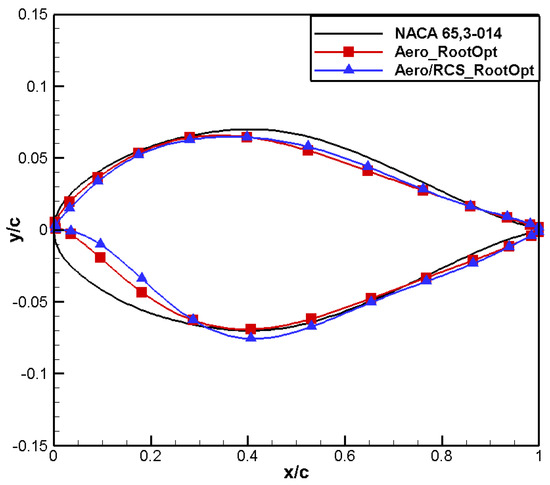
Figure 27.
Comparison of airfoil shape for aero/stealth root airfoil.
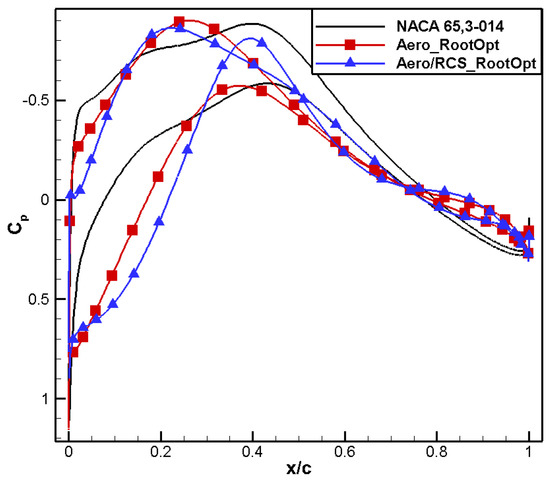
Figure 28.
Comparison of pressure coefficient distribution for aero/stealth root airfoil.
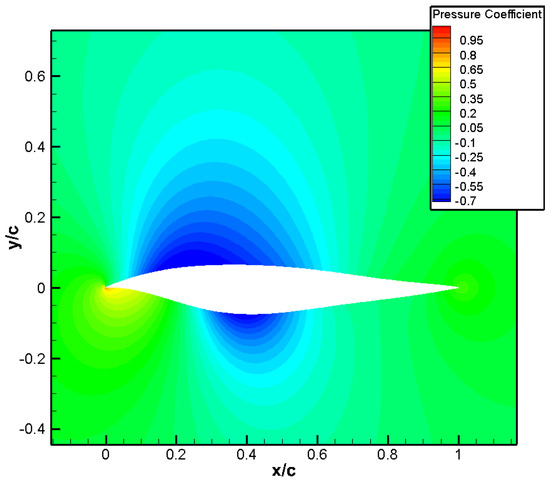
Figure 29.
Pressure distribution of optimized airfoil for aero/stealth root airfoil.
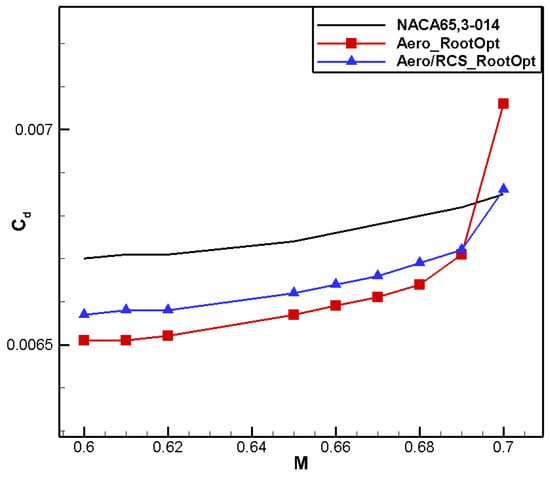
Figure 30.
Comparison of drag characteristics for aero/stealth root airfoil.
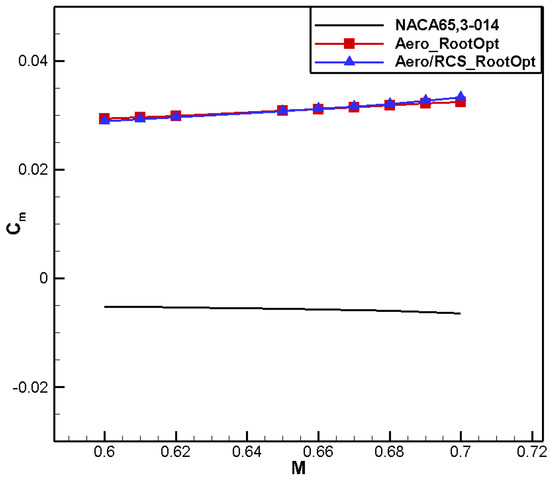
Figure 31.
Comparison of moment characteristics for aero/stealth root airfoil.

Figure 32.
Comparison of frontal RCS for aero/stealth root airfoil.
The Aero/RCS_RootOpt airfoil is assembled onto the central body area of the X-47B to form the layout for aero/RCSOpt1. Table 13, Table 14 and Table 15 list the comparisons of the layout airfoil scheme and calculation results, respectively. Compared to AeroOpt1, Aero/RCSOpt1 exhibits a slight loss in the lift–drag characteristics at the design point, with an increase in the drag coefficient of 1.4 counts. The moment coefficients remain consistent, both being −0.0058; the average RCS for aero/RCS_RootOpt in the yaw direction decreases from 1.0780 to −2.9281 and decreases from −29.8037 to −30.1186 in the pitch direction. This is due to the fact that the local chord length of the root station airfoil is the longest and the spanwise size is relatively large, which significantly affects the shape of the inboard wing. Therefore, the stealth design of the root station airfoil significantly improves the RCS characteristics in the pitch and yaw directions of the three-dimensional layout.

Table 13.
Airfoil plan.

Table 14.
Aerodynamic computational results for layout with aero/stealth root airfoil.

Table 15.
Stealth computational results for layout with aero/stealth root airfoil.
Figure 33 shows the pressure distribution contour trend for aero/RCSOpt1 as being similar to that for aeroOpt1, with the low-pressure area of the inboard wing expanding forward and the pressure recovery at the trailing edge being much gentler. There are strong shock waves in the outboard wing. The yaw RCS characteristics and pitch RCS characteristics of each layout are evaluated, and the calculation results are shown in Figure 34 and Figure 35. In the pitch direction, the RCS for aero/RCSOp1 significantly improves; in the yaw direction, the RCS peak position and RCS angle variation characteristics for aero/RCSOp1 and the baseline are relatively similar, but the peak values for aero/RCSOp1 are significantly lower than that of BaseModel.
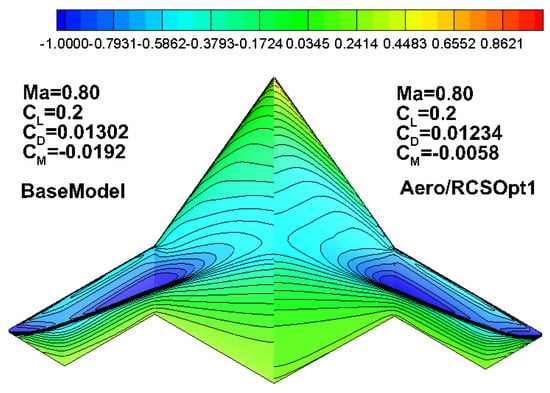
Figure 33.
Pressure distribution of BaseModel (left) and Aero/RCSOpt1 (right).
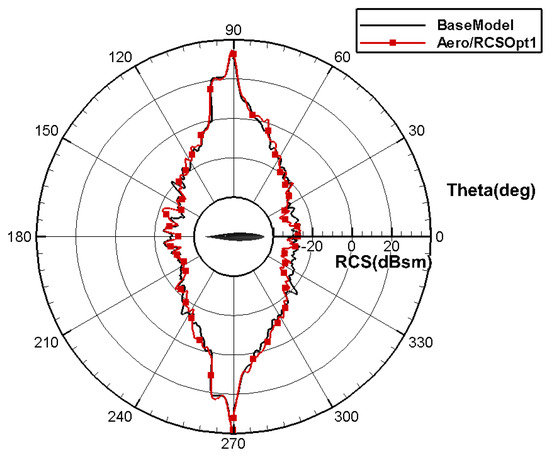
Figure 34.
Comparison of RCS in the pitch direction for layout with aero/stealth root airfoil.
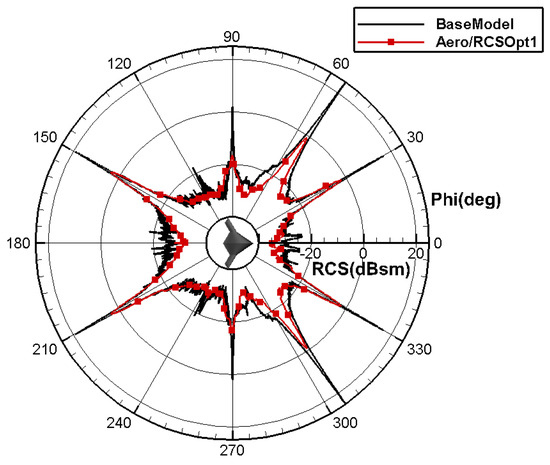
Figure 35.
Comparison of RCS in the yaw direction for layout with aero/stealth root airfoil.
3.3.2. Aerodynamic/Stealth Optimization of Kink Airfoil
The aerodynamic design state of the kink airfoil based on NACA 65,3-013 is the same as that for the aerodynamic optimization. The stealth design requirement is to reduce the RCS in the frontal sector at an incident frequency of 9 GHz. Therefore, the design objective is to reduce the drag coefficient and improve the frontal RCS characteristics of the airfoil, with a moment coefficient of no less than 0.01 and no reduction in the maximum thickness. The design model is shown in Equation (5), where and .
The computation results are shown in Table 16. Compared to Aero_KinkOpt, Aero/RCS_KinkOpt has a slight loss in lift–drag characteristics, with an increase of 1 count for the drag coefficient. The moment coefficients of these two optimized airfoils are 0.01, and the frontal average RCS for aero/RCS_KinkOpt reduces to 0.0040.

Table 16.
Comparison for aerodynamic/stealth results for aero/stealth kink airfoil.
Figure 36 shows that the upper surface shape variation trends for aero/RCS_KinkOpt and Aero_KinkOpt are similar: the upper surface shape tends to be flatter, with the maximum thickness position moving backward, and the trailing edge thickness increases. However, Aero/RCS_KinkOpt has a smaller leading-edge radius, resulting in a lower leading-edge suction peak. In addition, the contradiction between the positive moment constraint and the stealth design requirement leads to the loss in the lift–drag characteristics. The position of the weak shock wave on the upper surface is more backward, while the pressure recovery on the lower surface is more gentle, as shown in Figure 37 and Figure 38, respectively.
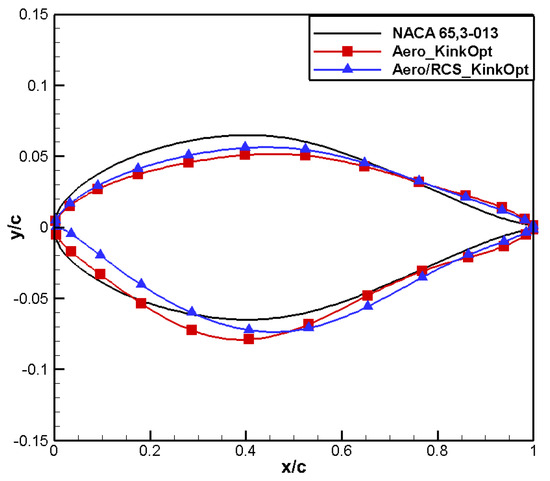
Figure 36.
Comparison of airfoil shape for aero/stealth kink airfoil.
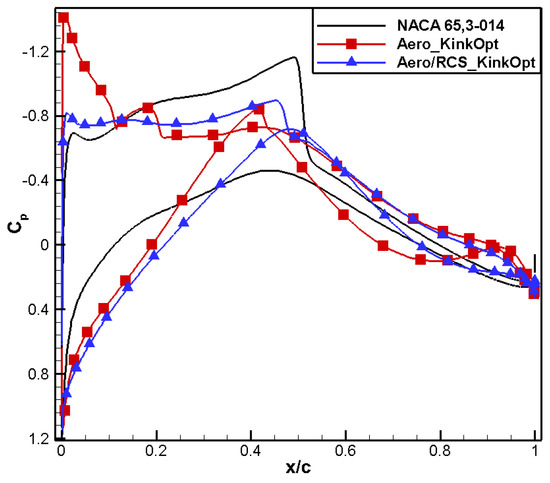
Figure 37.
Comparison of pressure distribution for aero/stealth kink airfoil.
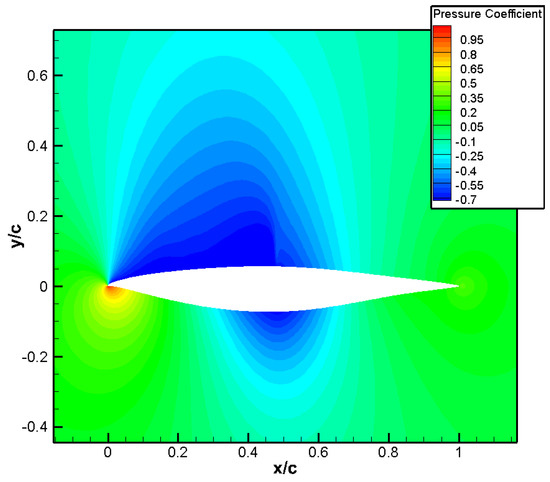
Figure 38.
Pressure distribution for aero/stealth kink airfoil.
From Figure 39, it is seen that the drag divergence Mach number of the Aero/RCS_KinkOpt airfoil reaches 0.75, which is significantly worse than that for aero_KinkOpt. Figure 40 shows that the pitch moment coefficient of the Aero/RCS_KinkOpt and the Aero_KinkOpt airfoils remains basically consistent within the Mach number range of 0.70–0.74, with a slightly smaller positive moment in the range of 0.75–0.76. The comparison of the frontal RCS provided in Figure 41 shows that the RCS value for aero/RCS_KinkOpt significantly reduces at all angles, and there is no significant difference in the peak values between the upper and lower surfaces.
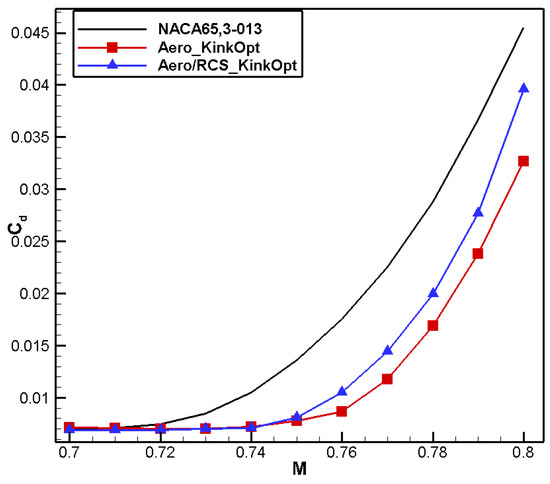
Figure 39.
Comparison of drag characteristics for aero/stealth kink airfoil.
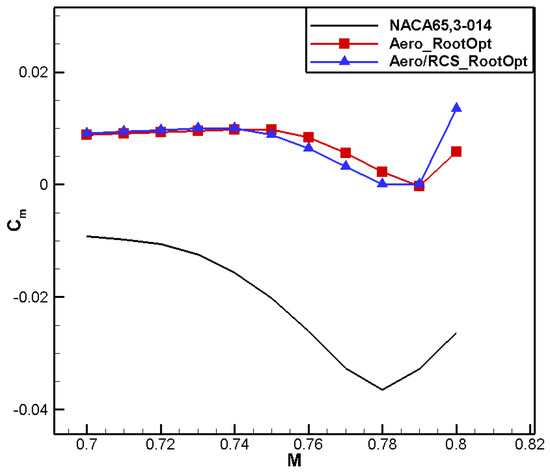
Figure 40.
Comparison of moment characteristics for aero/stealth kink airfoil.
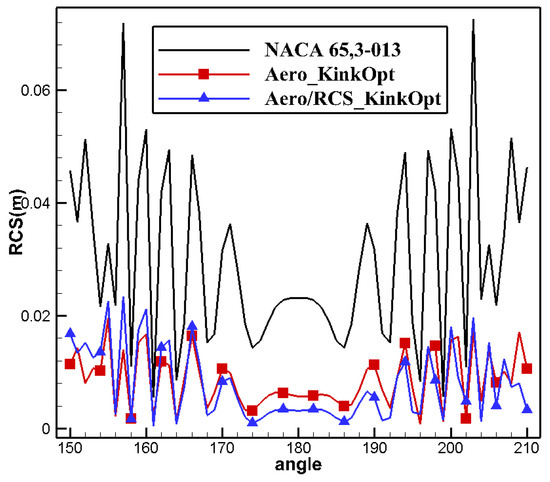
Figure 41.
Frontal RCS for aero/stealth kink airfoil.
Table 17 provides the airfoil plan for all layouts, and the calculation results are shown in Table 18 and Table 19. Compared to Aero/RCSOpt1, the aerodynamic and stealth characteristics for aero/RCSOpt2 significantly improve at the current state: the drag coefficient at the design point reduces by 6.6 counts and the moment coefficient decreases from −0.0058 to −0.0022, further improving the pitch moment trimming characteristics. In addition, the average RCS is decreased by −1.593 in the pitch direction and −1.8555 in the yaw direction. Compared to AeroOpt2, the drag coefficient for aero/RCSOpt2 is increased by 3 counts, resulting in a loss of lift–drag characteristics. Figure 42 shows that the shock wave intensity in the middle region and outboard wing for aero/RCSOpt2 is weakened, and the shock wave position in the outboard wing moves forward and the pressure recovery at the trailing edge is much gentler. The average RCS decreases by −1.3382 in the pitch direction and −4.408 in the yaw direction, resulting in a significant improvement in the RCS characteristics, as shown in Figure 43 and Figure 44.

Table 17.
Airfoil plan.

Table 18.
Aerodynamic computational results for layout with aero/stealth root and kink airfoil.

Table 19.
Stealth computational results for layout with aero/stealth root and kink airfoil.
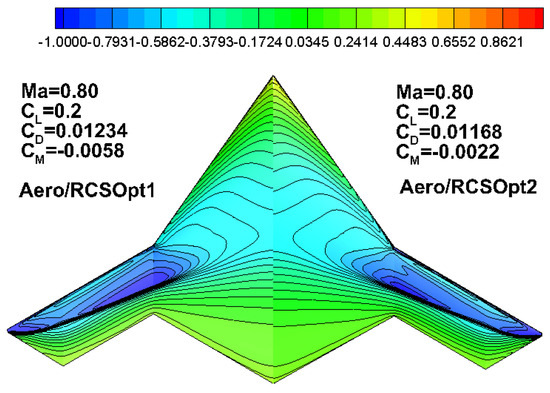
Figure 42.
Pressure distribution for aero/RCSOpt1 (left) and Aero/RCSOpt2 (right).
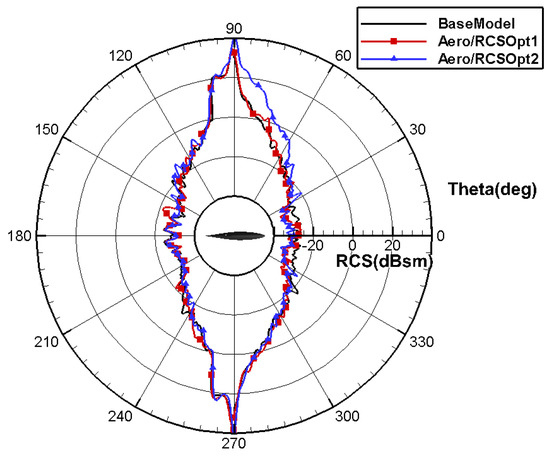
Figure 43.
Comparison of RCS in the pitch direction for layout with aero/stealth root and kink airfoil.
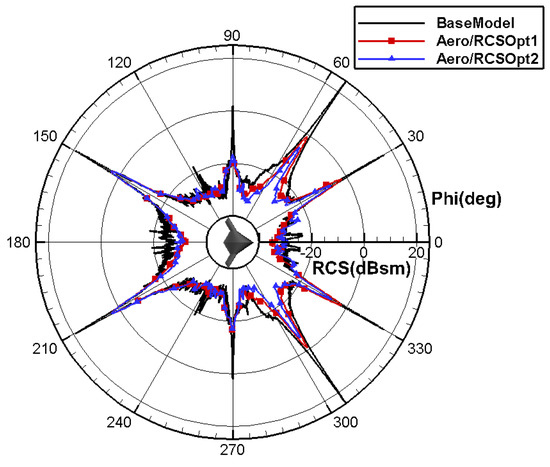
Figure 44.
Comparison of RCS in the yaw direction for layout with aero/stealth root and kink airfoil.
3.3.3. Aerodynamic/Stealth Optimization of Tip Airfoil
The aerodynamic design requirements for the tip airfoil are drag reduction and drag divergence characteristics, and the constraint is that the moment coefficient of the optimized airfoil should be larger than that of the baseline airfoil, with the maximum thickness being maintained. The stealth design requirements remain the same as before. The design model is shown below, where and .
Table 20 shows that the drag coefficient for aero/RCS_TipOpt is the same as that for aero_TipOpt, with a moment coefficient of 0.0017, meeting the moment constraint. The frontal RCS characteristic is significantly improved, reducing to 0.0032.

Table 20.
Comparison for aerodynamic/stealth results for aero/stealth tip airfoil.
From Figure 45, it can be observed that the shape variation trends for aero/RCS_TipOpt and Aero_TipOpt are similar on the upper surface, but on the lower surface, there is a significant difference in that the leading-edge radius for aero/RCS_TipOpt is much smaller, resulting in positive loading characteristics, as shown in Figure 46. The pressure coefficient distribution for aero/RCS_TipOpt is close to that for aero_TipOpt: the suction peak decreases and exhibits two pressure recovery zones, which are beneficial for improving the drag divergence characteristics. However, the low-pressure area on the lower surface of the Aero/RCS_TipOpt airfoil moves towards the leading edge, resulting in gentler pressure recovery, as shown in Figure 47. Figure 48 and Figure 49 show comparisons of the drag divergence characteristics and moment characteristics, respectively. The results demonstrate that the drag characteristics for aero/RCS_TipOpt are basically the same as for Aero_TipOpt, with better positive moment characteristics. In addition, the frontal RCS for aero/RCS_TipOpt significantly reduces at all angles, and there is no significant difference in the peak values between the upper and lower surfaces, as shown in Figure 50.
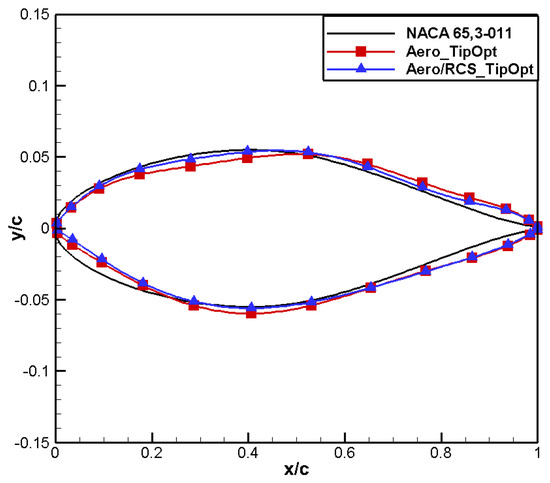
Figure 45.
Comparison of airfoil shape for aero/stealth tip airfoil.
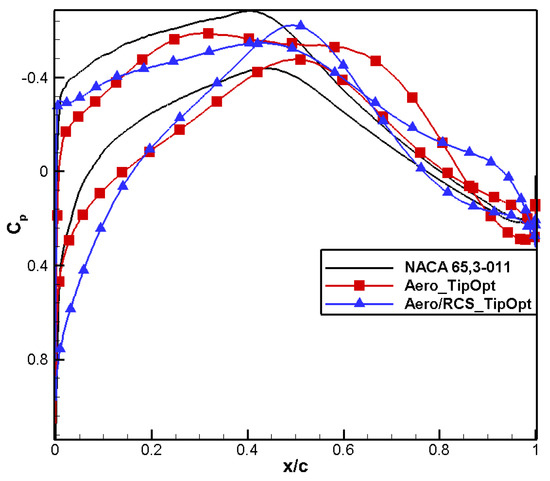
Figure 46.
Comparison of pressure distribution for aero/stealth tip airfoil.
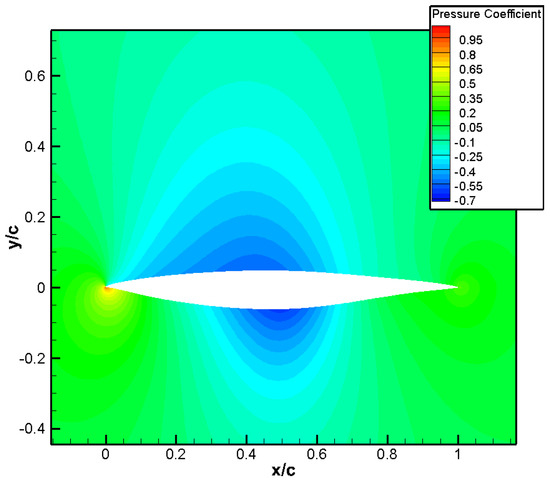
Figure 47.
Pressure distribution for aero/stealth tip airfoil.
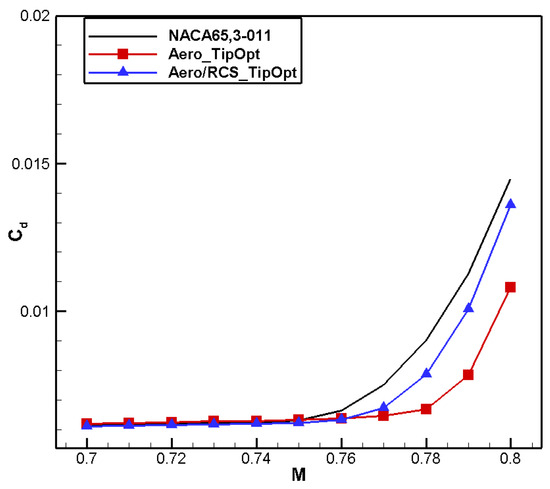
Figure 48.
Comparison of drag characteristics for aero/stealth tip airfoil.
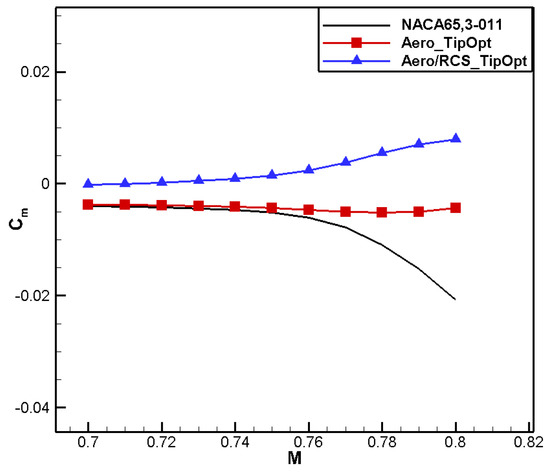
Figure 49.
Comparison of moment characteristics for aero/stealth tip airfoil.
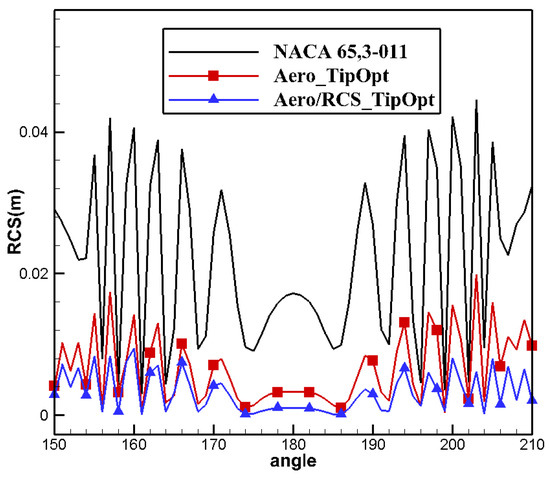
Figure 50.
Frontal RCS for aero/stealth tip airfoil.
The layout scheme and calculation results are shown in Table 21, Table 22 and Table 23. Compared to Aero/RCOpt2, Aero/RCOpt3 maintains the lift–drag characteristics at the design point, with a reduction of 0.9 counts for the drag coefficient. The moment coefficient reaches −0.0002, basically achieving pitch moment trimming. The stealth characteristics are further improved, with a decrease of −0.7645 in the average RCS value in the pitch direction and −2.86 in the yaw direction. As shown in Figure 51, the shock wave position of the outboard wing for aero/RCSOpt3 continues to move forward, while the shock wave intensity remains unchanged. The RCS performance of the 3D layout significantly improves, as shown in Figure 52 and Figure 53. Compared to the RCS improvement in the pitch direction, there is a more significant improvement in the yaw direction. This is because the flow scale of the 3D layout at the tip station is very small, but the span scale of the 3D layout is relatively large. Therefore, the design of the tip station airfoil has a significant impact on the RCS in the yaw direction. Compared to AeroOpt3, Aero/RCSOpt3 exhibits a loss of lift–drag characteristics, with an increment of 3 counts for the drag coefficient. The pitch moment trimming characteristics are basically consistent, and a significant improvement is observed in terms of RCS characteristics.

Table 21.
Airfoil plan.

Table 22.
Aerodynamic computational results for layout with aero/stealth root, kink and tip airfoil.

Table 23.
Stealth computational results for layout with aero/stealth root, kink and tip airfoil.
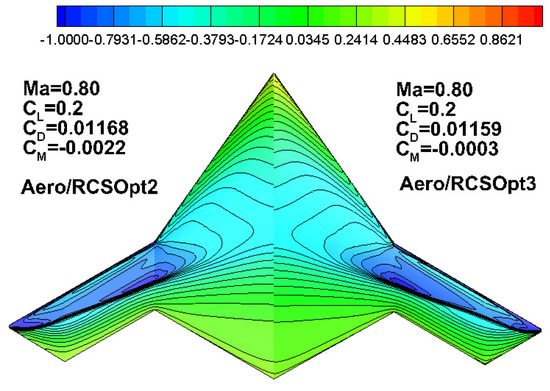
Figure 51.
Pressure distribution for aero/RCSOpt2 (left) and Aero/RCSOpt3 (right).
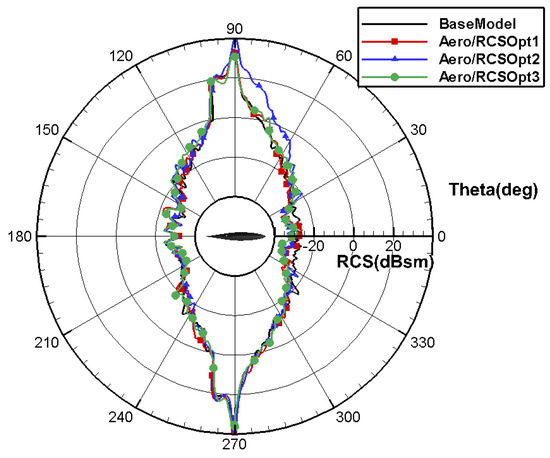
Figure 52.
Comparison of RCS in the pitch direction for layout with aero/stealth root, kink and tip airfoil.
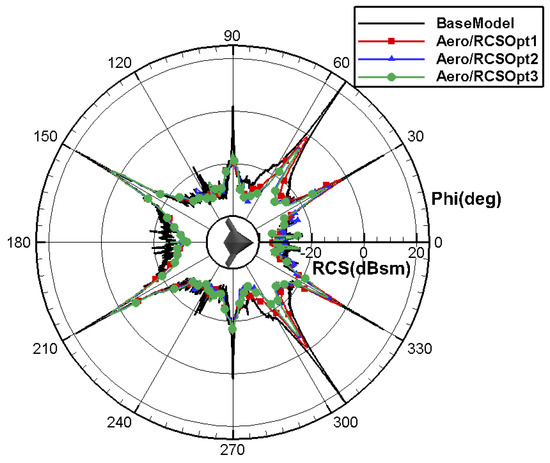
Figure 53.
Comparison of RCS in the yaw direction for layout with aero/stealth root, kink and tip airfoil.
4. Conclusions
This study investigates the design of an airfoil for a flying wing layout. Based on the X-47B flying wing layout, the spanwise aerodynamic characteristics of a double-sweep flying wing during a high-speed cruising state are analyzed, and the multidisciplinary design requirements of the airfoils at the root, kink, and tip positions of the flying wing are refined in order to establish the corresponding design models. Then, optimization of the aerodynamics and aerodynamics/stealth of the airfoils is carried out, respectively. Finally, the optimized airfoils are configured using the X-47B flying wing layout for verification. The main conclusions are summarized as follows:
- (1)
- The root airfoil should not only fulfill the loading requirements but must also have good lift–drag characteristics and stealth characteristics. In addition, a certain positive moment is needed to promote the pitch moment trimming of the layout. The kink airfoil should have good cruising lift–drag and drag divergence characteristics in addition to stealth characteristics, and it is also necessary to reduce the negative moment as much as possible. The tip airfoil requires a reduction in cruising drag and improved stealth performance.
- (2)
- In aerodynamic optimizations, Aero_RootOpt can decrease the negative moment coefficient in a 3D layout, improving its pitch moment trimming performance. In addition, the aerodynamic loading distribution on the inboard wing can be adjusted to improve the lift–drag characteristics in a cruise state. Aero_KinkOpt can weaken strong shock waves on the outboard wing of the 3D layout. On this basis, the pitch moment trimming characteristics could be further improved. The shock wave intensity in the wing tip region can be weakened by Aero_TipOpt, improving the lift–drag characteristics of the 3D layout, and the pitch moment can be trimmed.
- (3)
- In aerodynamic/stealth optimizations, the negative moment coefficient of the 3D layout can be decreased using Aero/RCS_RootOpt, thus improving the pitch moment trimming characteristics. The lift–drag characteristics are also improved under the cruising state, as well as the RCS characteristics in the pitch and yaw directions. The stealth characteristics of the 3D layout could be further improved through the use for aero/RCS_KinkOpt, and the aerodynamic lift–drag characteristics and pitch moment trimming characteristics can also be enhanced. Aero/RCS_TipOpt had little effect on improving the lift–drag characteristics of the 3D layout, but it did improve the stealth characteristics, especially in the yaw direction.
- (4)
- The calculation results shows that the aerodynamic characteristics and pitch moment trimming characteristics of the aerodynamic design and the aerodynamic/stealth design are significantly improved. The pitch moment trimming characteristics are basically the same. In addition, the cruise lift–drag characteristics of the aerodynamic/stealth design are slightly worse than those of the aerodynamic design, indicating that there are weak conflicts between aerodynamics and stealth in the flying wing layout design. This is because the pitch moment constraint relies on positive loading at the leading edge and negative loading at the trailing edge; moreover, the improvement in the stealth characteristics tends to result in a decrease in the leading-edge radius, leading to a decrease in positive loading on the leading edge. To meet the pitch moment constraint, more negative loading would be required on the trailing edge, which would then cause a loss for aerodynamic characteristics.
- (5)
- The aerodynamic and stealth characteristics of the flying wing airfoils during transonic cruise are also researched in this study. However, an understanding for aerodynamic characteristics during aircraft takeoff and landing is also essential, as these characteristics can further complicate airfoil design. In future work, studies on the optimization for aerodynamics and stealth in flying wing airfoils that takes into consideration takeoff, landing, and cruise will be carried out. In addition, structural elasticity is another problem faced when designing wings for practical applications [37]. For a swept wing, under the combined action of elastic wing bending and torsion, the effective angle of attack of the wing decreases, leading to a decrease in the lift coefficient. Therefore, the aerodynamic characteristics of a theoretically designed wing may differ from those of an actual elastic wing. If a designed wing is applied in wind tunnel testing and practical applications, the influence of structural elasticity must be considered.
Author Contributions
Conceptualization, W.Z. and K.Z.; methodology, W.Z. and L.Z.; validation, R.Z. and B.S.; formal analysis, Z.G.; writing—original draft preparation, W.Z.; writing—review and editing, W.Z.; visualization, L.Z.; project administration, K.Z.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Key Laboratory Funding [grant number 614220121020128].
Data Availability Statement
The specific values of the parameters and the details of the methodology are included in the paper. If the reader is interested, the corresponding author can provide additional information.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martins, J.R.R.A. Perspectives on aerodynamic design optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute for aeronautics and Astronautics: Reston, FL, USA, 2020. [Google Scholar]
- Jameson, A.; Reuther, J. Control theory based airfoil design using the Euler equations. In Proceedings of the 5th Symposium on Multidisciplinary Analysis and Optimization, Panama City Beach, FL, USA, 7–9 September 1994; p. 4272. [Google Scholar]
- Sobieczky, H. Parametric airfoils and wings. In Recent Development for Aerodynamic Design Methodologies: Inverse Design and Optimization; Vieweg Teubner Verlag: Berlin, Germany, 1999; pp. 71–87. [Google Scholar]
- Li, L.; Xu, Y.; Sun, M.; Huang, H.; Zhang, B.S.; Destech Publications, I. Airfoil Optimization Design of Flying Wing Configuration. In Proceedings of the 2015 International Conference on Mechanical Science and Mechanical Design, MSMD 2015, Changsha, China, 14–16 August 2015; pp. 418–422. [Google Scholar]
- Gao, C.; Gao, Z.; Li, S. Research on Airfoil Design Space and the Application of Niching Techniques in Airfoil Design. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0722. [Google Scholar]
- Qin, N. Aerodynamic studies for blended wing body aircraft. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002; p. 5448. [Google Scholar]
- Liebeck, R. Blended wing body design challenges. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2659. [Google Scholar]
- Rani, S.S.; Raj, S.R.; Rakshith, G.R.; Paragi, C.S.; Somashekar, V. Numerical Investigation for Selection of Airfoil with Regard to Flying Wing Applications. Int. J. Fluid Mech. Res. 2022, 49, 59–70. [Google Scholar] [CrossRef]
- Cook, P.H.; Firmin, M.C.P.; McDonald, M.A.; Establishment, R.A. Aerofoil RAE 2822: Pressure Distributions, and Boundary Layer and Wake Measurements; AGARD Advisory Report AR-138; Advisory Group for Aerospace Research and Development: Neuilly sur Seine, France, 1979. [Google Scholar]
- Pan, Y.; Huang, J. Influences of airfoil profile on lateral-directional stability of aircraft with flying wing layout. Aircr. Eng. Aerosp. Technol. 2019, 91, 1011–1017. [Google Scholar] [CrossRef]
- Achour, G.; Sung, W.J.; Pinon-Fischer, O.J.; Mavris, D.N. Development of a conditional generative adversarial network for airfoil shape optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 2261. [Google Scholar]
- Liu, Z.; An, W.; Qu, X.; Liu, X.; Lyu, H. Portfolio-Based Bayesian Optimization for Airfoil Design. AIAA J. 2021, 59, 1975–1989. [Google Scholar] [CrossRef]
- Liu, Z.; Qu, X.; Liu, X.; Lyu, H. Correlation-concerned Bayesian optimization for multi-objective airfoil design. Aerosp. Sci. Technol. 2022, 129, 107867. [Google Scholar] [CrossRef]
- Feng, C.; Chen, S.S.; Yuan, W.; Li, Z.; Gao, Z.H. A wide-speed-range aerodynamic configuration by adopting wave-riding-strake wing. Acta Astronaut. 2023, 202, 442–452. [Google Scholar] [CrossRef]
- Wakayama, S. Blended-wing-body optimization problem setup. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000; p. 4740. [Google Scholar]
- Liebeck, R. Design of the blended wing body subsonic transport. J. Aircr. 2004, 41, 10–25. [Google Scholar] [CrossRef]
- Sears, W. Flying-wing airplanes-The XB-35/YB-49 program. In Proceedings of the Symposium, The Evolution of Aircraft Wing Design, Dayton, OH, USA, 18–19 March 1980; p. 3036. [Google Scholar]
- Robinson, R.C. High-Speed Aerodynamic Characteristics of a 1/7-Scale Model of the Northrop YB-49 Airplane; NACA-RM_A7C13; Langley Research Center: Hampton, VA, USA, 1947. Available online: https://ntrs.nasa.gov/citations/20030063936 (accessed on 3 July 2024).
- Diedrich, A.; Hileman, J.; Tan, D.; Willcox, K.; Spakovszky, Z. Multidisciplinary design and optimization of the silent aircraft. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 1323. [Google Scholar]
- Hileman, J.; Spakovszky, Z.; Drela, M.; Sargeant, M. Airframe design for” silent aircraft”. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 453. [Google Scholar]
- Lee, D.; Gonzalez, L.F.; Srinivas, K.; Auld, D.; Wong, K.C. Aerodynamic/RCS shape optimisation of unmanned aerial vehicles using hierarchical asynchronous parallel evolutionary algorithms. In Proceedings of the 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006; p. 3331. [Google Scholar]
- Zhou, L.; Huang, J.; Gao, Z.; Zhang, W. Three-Dimensional Aerodynamic/Stealth Optimization Based on Adjoint Sensitivity Analysis for Scattering Problem. AIAA J. 2020, 58, 2702–2715. [Google Scholar] [CrossRef]
- Taj, Z.U.D.; Bilal, A.; Awais, M.; Salamat, S.; Abbas, M.; Maqsood, A. Design exploration and optimization for aerodynamics and radar cross section for a fighter aircraft. Aerosp. Sci. Technol. 2023, 133, 108114. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, Z.; Wang, C.; Xia, L. The niching-based adaptive space reconstruction method for airfoil aerodynamic/stealth design. Struct. Multidiscip. Optim. 2023, 66, 159. [Google Scholar] [CrossRef]
- Huang, J.; Zhu, Z.H.O.U.; Zhenghong, G.A.O.; Zhang, M.; Lei, Y.U. Aerodynamic multi-objective integrated optimization based on principal component analysis. Chin. J. Aeronaut. 2017, 30, 1336–1348. [Google Scholar] [CrossRef]
- Pambagjo, T.; Nakahashi, K.; Obayashi, S.; Matsushima, K. Aerodynamic design of a medium size blended-wing-body airplane. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 129. [Google Scholar]
- Peigin, S.; Epstein, B. Computational fluid dynamics driven optimization of blended wing body aircraft. AIAA J. 2006, 44, 2736–2745. [Google Scholar] [CrossRef]
- Peifeng, L.I.; Zhang, B.; Yingchun, C.; Changsheng, Y.U.A.N.; Yu, L.I.N. Aerodynamic design methodology for blended wing body transport. Chin. J. Aeronaut. 2012, 25, 508–516. [Google Scholar]
- Kuntawala, N.B. Aerodynamic Shape Optimization of a Blended-Wing-Body Aircraft Configuration; University of Toronto: Toronto, ON, Canada, 2011. [Google Scholar]
- Reist, T.A.; Zingg, D.W. Aerodynamic design of blended wing-body and lifting-fuselage aircraft. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3874. [Google Scholar]
- Lyu, Z.; Martins, J.R. Aerodynamic design optimization studies of a blended-wing-body aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef]
- CFL3D Version 6.7 Website. Available online: https://nasa.github.io/CFL3D/ (accessed on 11 December 2023).
- Wei, Z.; Zhenghong, G.; Lin, Z.; Jun, D.; Lu, X.; Yingtao, Z. Research on Multimodality in Aerodynamic/Stealth Airfoil Design Optimization. In Proceedings of the 2021 12th International Conference on Mechanical and Aerospace Engineering (ICMAE), Athens, Greece, 16–19 July 2021; pp. 384–393. [Google Scholar]
- Kulfan, B.; Bussoletti, J. “ Fundamental” parameteric geometry representations for aircraft component shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; p. 6948. [Google Scholar]
- Simpson, T.W.; Mauery, T.M.; Korte, J.J.; Mistree, F. Kriging models for global approximation in simulation-based multidisciplinary design optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef]
- Li, M.; Bai, J.; Li, L.; Meng, X.; Liu, Q.; Chen, B. A gradient-based aero-stealth optimization design method for flying wing aircraft. Aerosp. Sci. Technol. 2019, 92, 156–169. [Google Scholar] [CrossRef]
- Ahmad, D.; Ajaj, R.M. A multiaxial fracture of ecoflex skin with different shore hardness for morphing wing application. Polymers 2023, 15, 1526. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).