Design of Entire-Flight Pinpoint Return Trajectory for Lunar DRO via Deep Neural Network
Abstract
1. Introduction
2. Dynamics
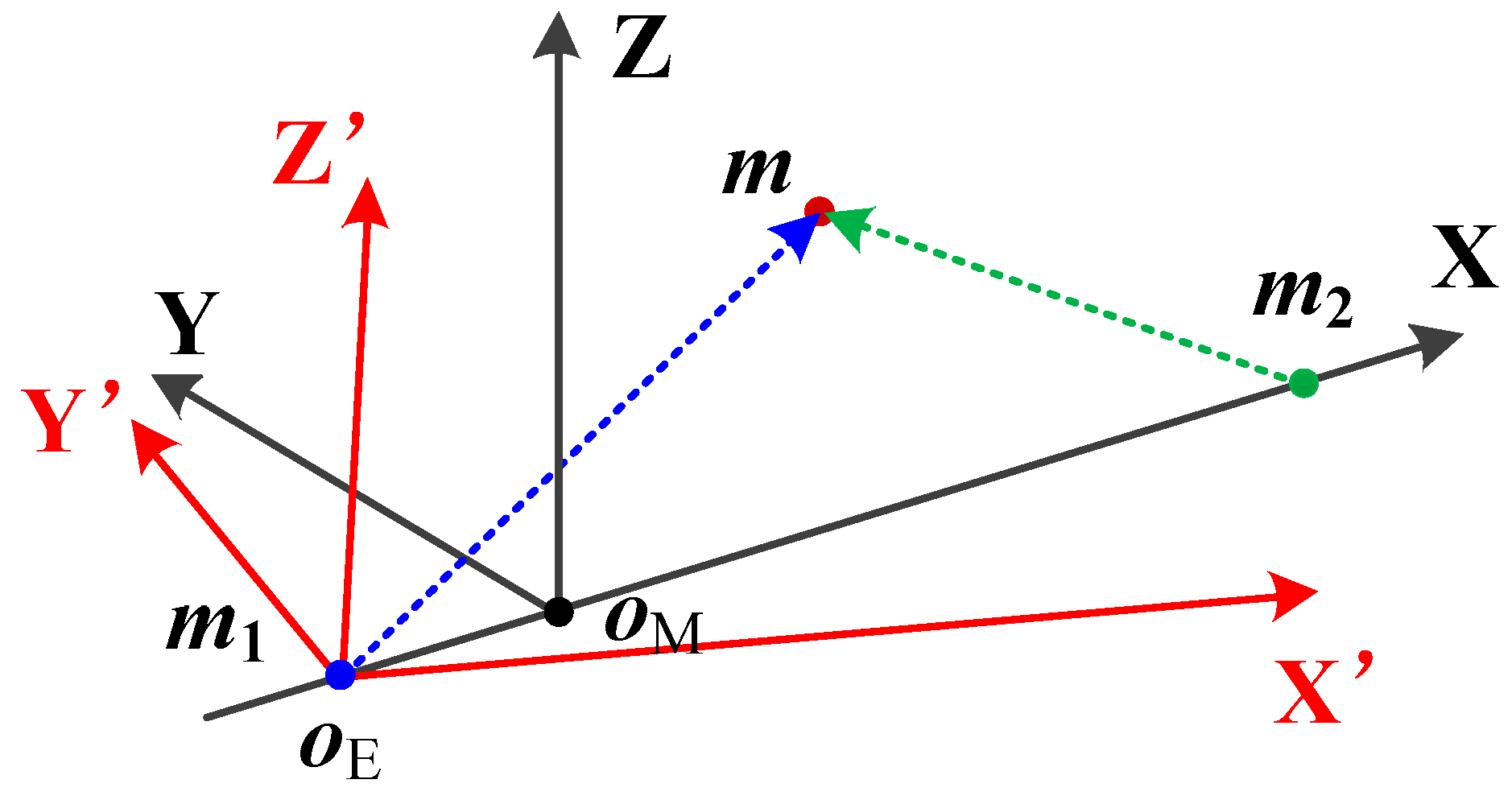
2.1. Dynamic Model in Cis-Lunar Space
2.2. Aerodynamic Model of Earth Re-Entry
2.2.1. Aerodynamic Model of Earth Atmosphere Entry
2.2.2. Aerodynamic Effects of the Re-Entry Capsule
3. Design Method for Entire-Flight Moon–Earth Pinpoint Return Trajectory
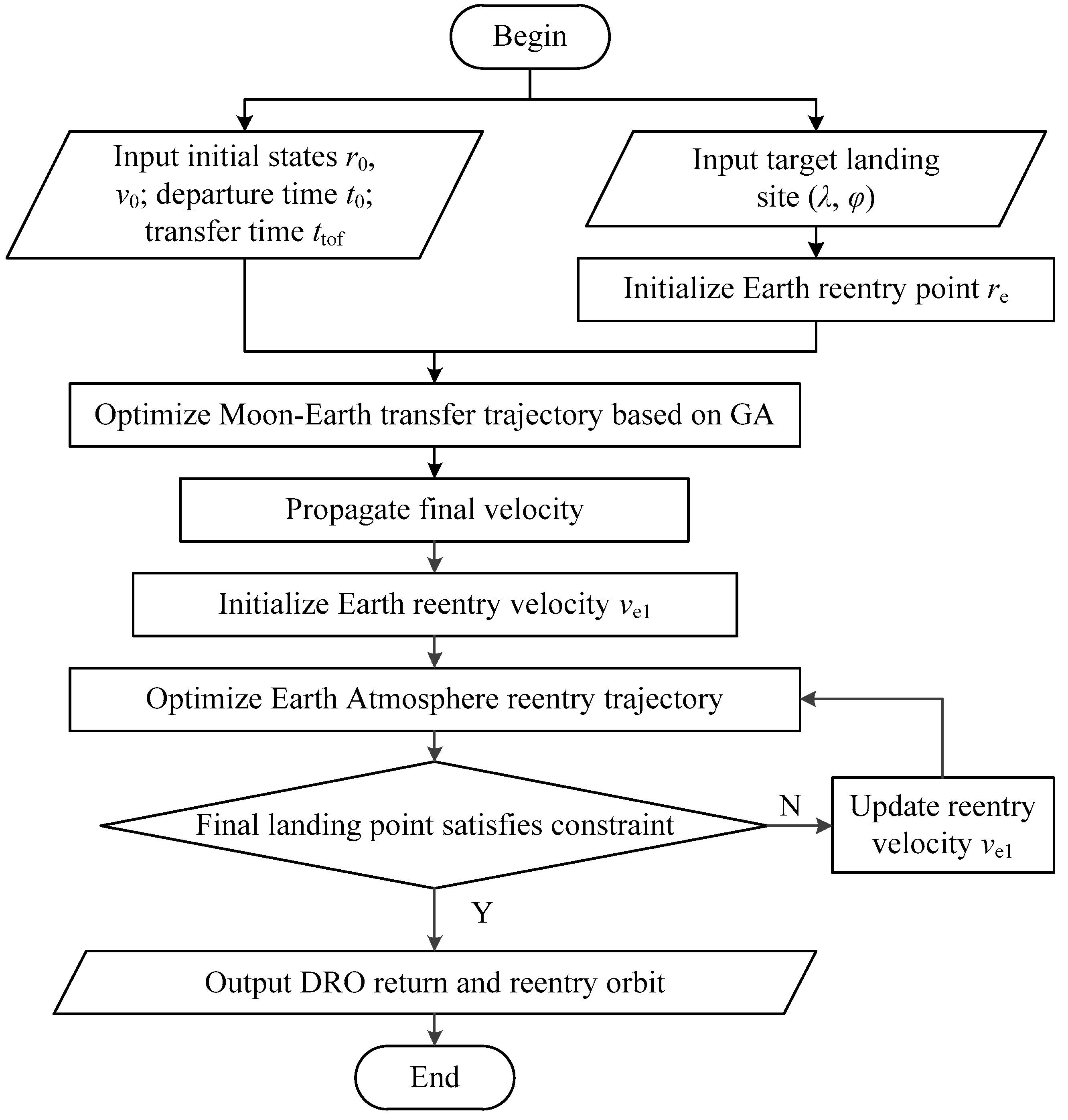
3.1. Global Optimization Framework for Entire-Flight Lunar DRO Pinpoint Return Trajectory
- (1)
- Input the initial state, time epoch, and desired transfer time of the re-entry capsule in the lunar DRO;
- (2)
- Input the target landing site for capsule pinpoint landing;
- (3)
- Initialize the Earth re-entry point re;
- (4)
- Solve the fuel-optimal multi-impulse Moon–Earth transfer trajectory and propagate the final velocity when approaches the re-entry point;
- (5)
- Initialize the Earth re-entry velocity Ve1;
- (6)
- Solve the optimal control Earth atmosphere re-entry trajectory and propagate the final landing point of the capsule;
- (7)
- Calculate the difference between the desired landing site and the final landing point as the landing error;
- (8)
- If the landing error violates the constraint, update the re-entry velocity and go back to step (6); otherwise output the entire lunar DRO return trajectory;
- (9)
- Optimize the Earth re-entry point to obtain the optimal entire-flight DRO pinpoint return trajectory.
3.2. Optimization of Lunar DRO Moon–Earth Transfer Trajectory
3.2.1. Optimization Method for Moon–Earth Transfer Trajectory
3.2.2. Trajectory Correction of Moon–Earth Transfer Trajectory
- (1)
- Taking the CR3BP transfer trajectory as a reference, the initial state for trajectory correction is set as with a flight time of ttof. The desired final position is the same as the final position of this transfer segment, including single-impulse mode and double-impulse mode.
- (2)
- An impulse correction is introduced in the initial velocity. Then, the accurate final state under the ephemeris model can be propagated.where g(·) represents the orbital propagation under the accurate ephemeris dynamical model.
- (3)
- The difference between the accurate final position and the desired final position is obtained. The Jacobian matrix for differential correction is defined as follows:where [δxf; δyf; δzf] represents the position difference.
- (4)
- The ΔV correction for the initial velocity can be obtained as:The initial velocity is corrected as .
3.3. Optimization of Pinpoint Re-Entry Trajectory for Earth Atmospheric Re-Entry Stage
3.3.1. Optimization Method for Earth Re-Entry Trajectory
3.3.2. Correction of Pinpoint Re-Entry Trajectory
- (1)
- Taking the optimal control re-entry trajectory with respect to the final state of the Moon–Earth transfer trajectory as a reference, the initial state is set as with a flight time of ttof. The desired final position is the same as the pinpoint landing site;
- (2)
- An impulse correction is introduced in the initial re-entry velocity. Then, the optimal control re-entry trajectory is solved using the optimization method in Section 3.3.1. The landing point of the optimal control re-entry trajectory is obtained;
- (3)
- The Jacobian matrix J is calculated between the landing point and the desired landing site. The correction of the re-entry velocity is then obtained.
4. Intelligent Landing Point Prediction of Atmospheric Re-Entry Trajectory
4.1. Deep Neural Network
- (1)
- A dataset is built by collecting training samples. For a landing point prediction network, the training samples are optimal control pinpoint re-entry trajectory. However, due to the difference in scale of input and output parameters, sensitivities of the DNN for parameters are different, resulting in gradient explosion or vanishing gradients. Therefore, in order to improve the numerical stability of the model and facilitate learning and convergence, normalizations of parameters are executed. Since training samples are evenly distributed based on the classical grid method, a min–max scaling method is employed to normalize the input and output parameters and eliminate the parameter differences in scales. During the training of the DNN, a ratio of 7:1:2 is applied to divide the original dataset into training, validating, and testing sets.
- (2)
- Training samples p are input into the neural network for forward propagation. The value of the input node i is denoted as . The output of the j-th node in the hidden layer can be calculated by:where denotes the connection weight between the i-th node in the input layer and the j-th node in the hidden layer; is the bias on the j-th node in the hidden layer; and is the activation function of the hidden layer. Similarly, the propagation process between multiple hidden layers follows a similar process.A rectified linear unit (ReLU) activation function is a type of left-bounded activation function, and it possesses a derivative of 1 when the input is greater than zero. This design addresses the issue of gradient vanishing encountered in other activation functions. The ReLU is given by:
- (3)
- The output of the k-th node in the output layer is denoted aswhere represents the connection weight between the j-th node in the s-th hidden layer and the k-th node in the output layer; denotes the bias on the j-th node in the s-th hidden layer. Note that the output layer does not have an activation function.
- (4)
- The difference between the output qf of the DNN and the actual value q is evaluated. A mean square error (MSE) loss function is employed for back-propagation. The lost function is shown as follows:where m is the number of samples.The correction amount is given as:where indicates the learning rate of DNN.The corrected weight isSimilarly, can be illustrated as:
- (5)
- Network parameters are updated where an Adam optimization algorithm is employed to minimize the loss function. Its uniqueness lies in its ability to dynamically adjust the learning rate for each parameter, calculating different adaptive learning rates for different parameters. By introducing momentum and adaptive learning rates, the Adam algorithm effectively updates network parameters during training, contributing to improved training effectiveness. Additionally, the Adam algorithm requires less memory, significantly speeding up the training process [28].
- (6)
- The network parameters are updated by iterating the steps (1)–(5). The validation is performed every 10 iterations. This process repeats until the error reaches the specified tolerance or the maximum number of iterations.
- (7)
- After completing all iterations, the neural network with the smallest validation set error is selected as the neural network output. This network provides the optimal weight and bias information for each layer.
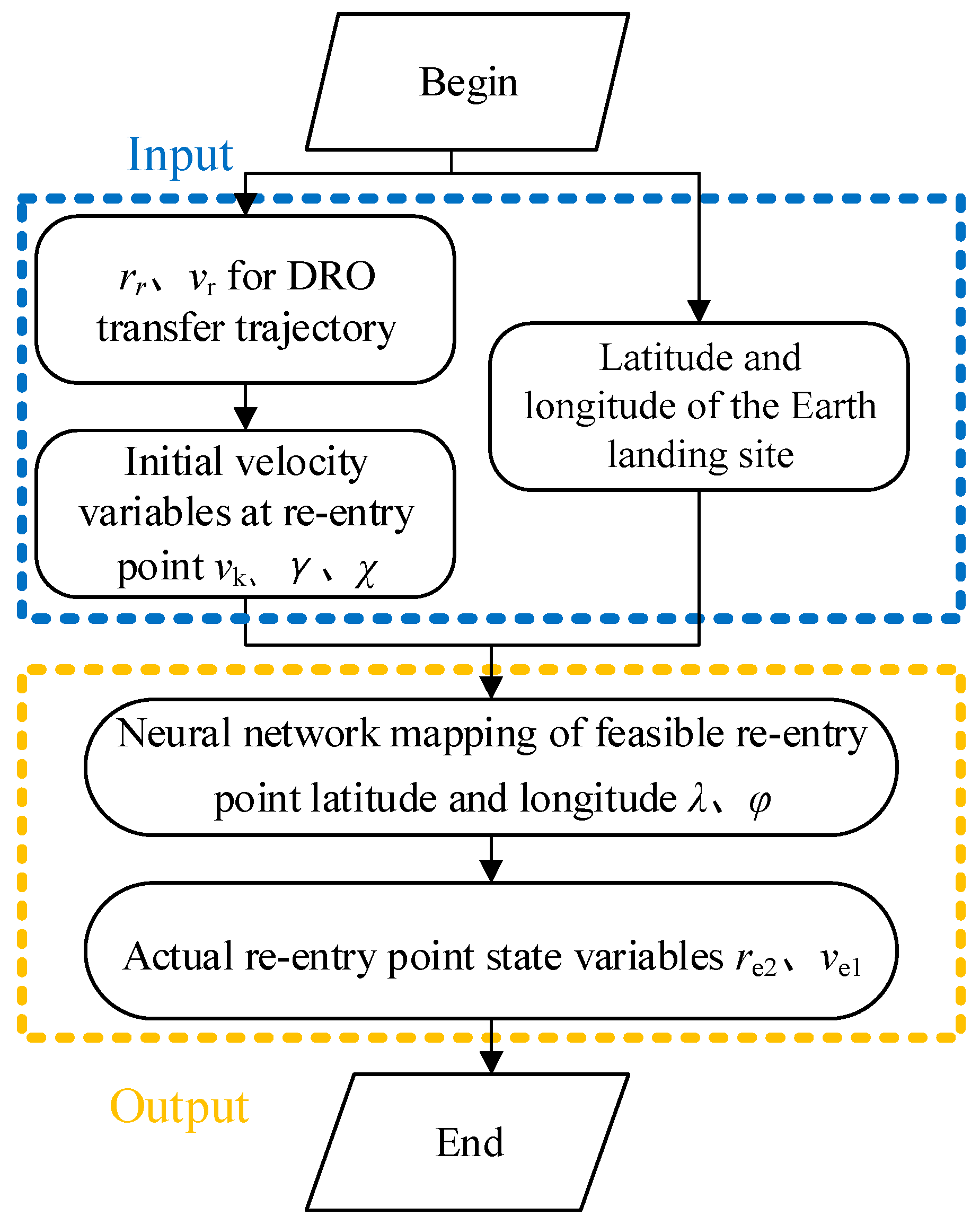
4.2. DNN-Based Landing Point Prediction Method
5. Simulation and Analysis
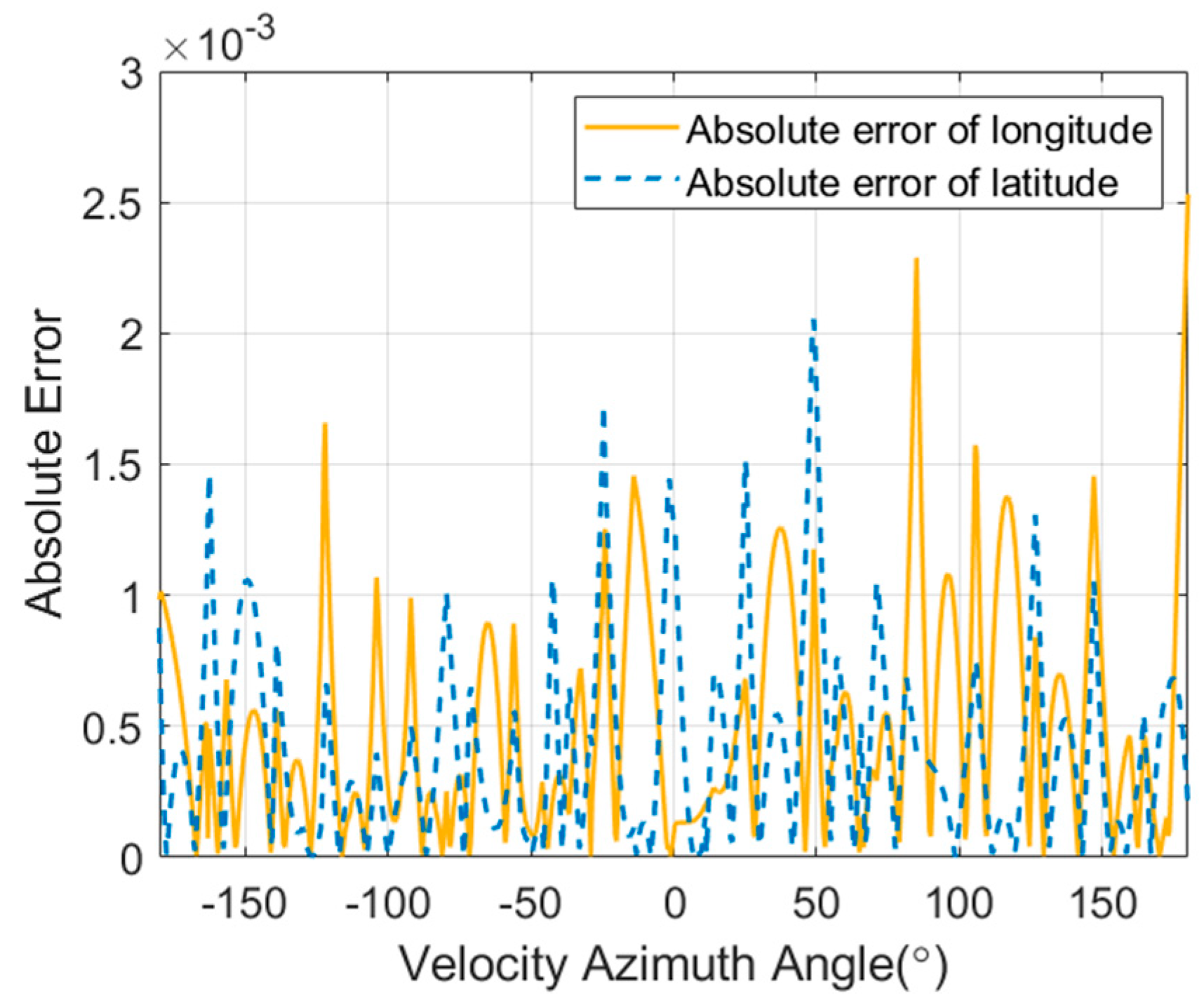
5.1. Validation of DNN-Based Landing Point Prediction Method
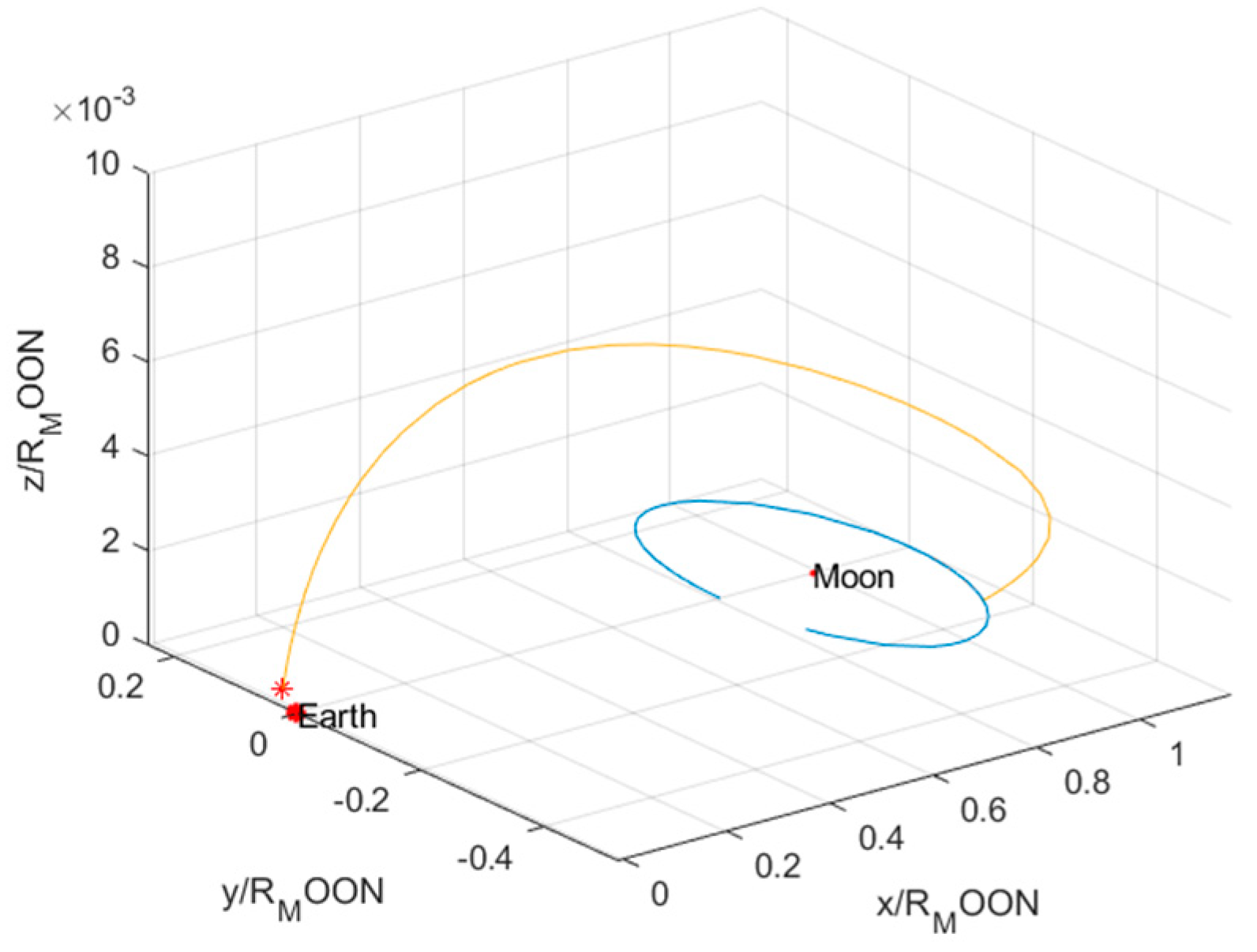
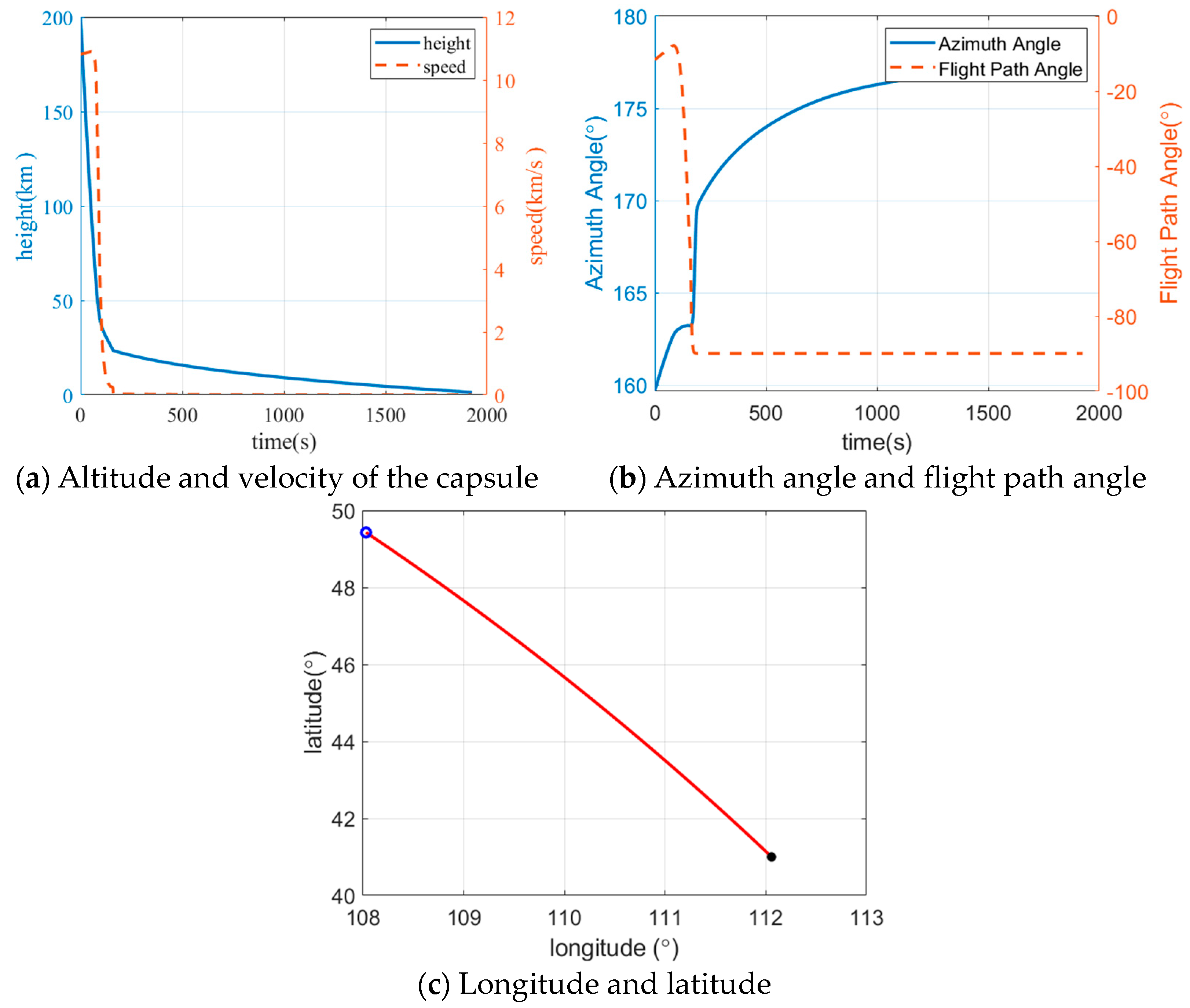
5.2. Validation of Global Optimization of the Lunar Return Trajectory
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lopez, F.; Mauro, A.; Mauro, S.; Monteleone, G.; Sfasciamuro, D.E.; Villa, A. A Lunar-Orbiting Satellite Constellation for Wireless Energy Supply. Aerospace 2023, 10, 919. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, M.; Shi, Y.; Zhang, H. Midcourse correction of Earth-Moon distant retrograde orbit transfer trajectories based on high-order state transition tensors. Astrodynamics 2023, 7, 335–349. [Google Scholar] [CrossRef]
- Burns, J.O.; Mellinkoff, B.; Spydell, M.; Fong, T.; Kring, D.A.; Pratt, W.D.; Cichan, T.; Edwards, C.M. Science on the lunar surface facilitated by low latency telerobotics from a Lunar Orbital Platform-Gateway. Acta Astronaut. 2019, 154, 195–203. [Google Scholar] [CrossRef]
- Zhang, P.; Dai, W.; Niu, R.; Zhang, G.; Liu, G.; Liu, X.; Bo, Z.; Wang, Z.; Zheng, H.; Liu, C.; et al. Overview of the Lunar In Situ Resource Utilization Techniques for Future Lunar Missions. Space Sci. Technol. 2023, 3, 37. [Google Scholar] [CrossRef]
- Lu, L.; Li, H. Three-Impulse Return Orbit Design and Characteristic Analysis for Manned Lunar Missions. IEEE Access 2020, 8, 154256–154268. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J.; Zhou, Y.; Sun, K. Assessment of radiative heating for hypersonic earth reentry using nongray step models. Aerospace 2022, 9, 219. [Google Scholar] [CrossRef]
- Singh, S.K.; Junkins, J.L.; Majji, M.; Taheri, E. Rapid accessibility evaluation for ballistic lunar capture via manifolds: A Gaussian process regression application. Astrodynamics 2022, 6, 375–397. [Google Scholar] [CrossRef]
- Lu, P.; Wang, Y.; Cui, S. Near Rectilinear Halo Orbits and Transfer Trajectories in the Jupiter–Europa System. J. Guid. Control Dyn. 2024, 1–10. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhao, M. Universal method for designing periodic orbits by homotopy classes in the elliptic restricted three-body problem. Astrodynamics 2024, 8, 175–188. [Google Scholar] [CrossRef]
- Lin, M.; Xu, M. Entire flight trajectory design for temporary reconnaissance mission. Trans. Jpn. Soc. Aeronaut. Space Sci. 2017, 60, 137–151. [Google Scholar] [CrossRef]
- Wu, S.; Tian, B.; Li, Z. Full-stage Reentry Trajectory Optimization for Reusable Launch Vehicle. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 3489–3494. [Google Scholar]
- Salmaso, F.; Trisolini, M.; Colombo, C. A machine learning and feature engineering approach for the prediction of the uncontrolled re-entry of space objects. Aerospace 2023, 10, 297. [Google Scholar] [CrossRef]
- Ben, L.Y.; Yan, L.L.; Xie, X.H.; Zhang, R.; Wang, G. Design of Moon-to-Earth transfer orbit with direct atmospheric reentry. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 287–293. [Google Scholar]
- Zhang, R.; Wang, Y.; Zhang, C.; Zhang, H. The transfers from lunar DROs to Earth orbits via optimization in the four body problem. Astrophys. Space Sci. 2021, 366, 49. [Google Scholar] [CrossRef]
- Robinson, S.; Geller, D. A simple targeting procedure for lunar trans-earth injection. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6107. [Google Scholar]
- He, B.; Li, H.; Shen, H.; Peng, Q. Coupled design of landing window and point return orbit for manned lunar landing mission. J. Natl. Univ. Def. Technol. 2017, 39, 11–16. [Google Scholar]
- Li, Y.; Xin, X.; Hou, X. Two-maneuver indirect contingency return from a low lunar orbit. Chin. J. Aeronaut. 2023, 36, 115–127. [Google Scholar] [CrossRef]
- Jia, F.; Peng, Q.; Zhou, W.; Li, X. Integrated Design of Moon-to-Earth Transfer Trajectory Considering Re-Entry Constraints. Appl. Sci. 2022, 12, 8716. [Google Scholar] [CrossRef]
- Dong, T.; Luo, Q.; Han, C. Bayesian Optimization of crewed lunar free return abort trajectory. Acta Astronaut. 2022, 201, 288–301. [Google Scholar] [CrossRef]
- Whitmore, S.; Banks, D.; Andersen, B.; Jolley, P. Direct-entry, aerobraking, and lifting aerocapture for human-rated lunar return vehicles. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 1033. [Google Scholar]
- D’Amato, E.; Notaro, I.; Panico, G.; Blasi, L.; Mattei, M.; Nocerino, A. Trajectory planning and tracking for a re-entry capsule with a deployable aero-brake. Aerospace 2022, 9, 841. [Google Scholar] [CrossRef]
- Li, S.; Zhu, Q.; Wang, W.; Li, Z.; Cai, C.; Qin, J. High-Reliability and High-Precision Braking and Capture Control Technology of Tianwen-1 Probe. Space Sci. Technol. 2024, 4, 125. [Google Scholar] [CrossRef]
- Chen, C.L.; Zhang, Z.F.; Sheng, R.Q.; Yang, M.F. Mission analysis and design of half-ballistic reentry for deep space exploration. J. Deep Space Explor. 2021, 8, 269–275. [Google Scholar]
- Palumbo, R.; Morani, G.; Cicala, M. Reentry trajectory optimization for mission analysis. J. Spacecr. Rocket. 2017, 54, 331–336. [Google Scholar] [CrossRef]
- Wang, Z.; Grant, M.J. Constrained trajectory optimization for planetary entry via sequential convex programming. J. Guid. Control. Dyn. 2017, 40, 2603–2615. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Li, N.; Yu, Y.; Su, Z.; Liu, Y. Time-optimal memetic whale optimization algorithm for hypersonic vehicle reentry trajectory optimization with no-fly zones. Neural Comput. Appl. 2020, 32, 2735–2749. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.L.; Chai, S.; Xia, Y. Trajectory planning for hypersonic reentry vehicle satisfying deterministic and probabilistic constraints. Acta Astronaut. 2020, 177, 30–38. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, Z.; Song, Y.; Jiang, F. Real-time optimal control for irregular asteroid landings using deep neural networks. Acta Astronaut. 2020, 170, 66–79. [Google Scholar] [CrossRef]
- D’Ambrosio, A.; Furfaro, R. Learning fuel-optimal trajectories for space applications via Pontryagin neural networks. Aerospace 2024, 11, 228. [Google Scholar] [CrossRef]
- Yang, H.; Hu, J.; Bai, X.; Li, S. Review of Trajectory Design and Optimization for Jovian System Exploration. Space Sci. Technol. 2023, 3, 0036. [Google Scholar] [CrossRef]
- Jung, O.; Seong, J.; Jung, Y.; Bang, H. Recurrent neural network model to predict re-entry trajectories of uncontrolled space objects. Adv. Space Res. 2021, 68, 2515–2529. [Google Scholar] [CrossRef]
- Dai, P.; Feng, D.; Feng, W.; Cui, J.; Zhang, L. Entry trajectory optimization for hypersonic vehicles based on convex programming and neural network. Aerosp. Sci. Technol. 2023, 137, 108259. [Google Scholar] [CrossRef]
- Wenbo, M.; Qi, L.; Junhong, L.; Jingyun, Z.; Xiaoli, C. Thermal environment and aeroheating mechanism of protuberances on mars entry capsule. Space Sci. Technol. 2021, 2021, 9754068. [Google Scholar] [CrossRef]
- Han, H.; Dang, Z. Orbital Blocking Game Near Earth–Moon L 1 Libration Point. Space Sci. Technol. 2023, 3, 0102. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, H. Initial guess and correction of DRO for earth-moon system in the ephemeris. In Proceedings of the Chinese Congress of Theoretical and Applied Mechanics 2021, Chengdu, China, 1–5 June 2021. [Google Scholar]
- Li, Q.; Rao, W.; Cheng, X.; Wei, H.; Wang, C.; Dong, J. Aerodynamic design, analysis, and validation techniques for the Tianwen-1 entry module. Astrodynamics 2022, 6, 39–52. [Google Scholar] [CrossRef]
- Xie, Y.; Lei, Y.; Guo, J.; Meng, B. Spacecraft Dynamics and Control; Springer: Singapore, 2022. [Google Scholar]
- Ramanan, R.V. Integrated algorithm for lunar transfer trajectories using a pseudostate technique. J. Guid. Control Dyn. 2002, 25, 946–952. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Zhou, L. Trajectory Design for Lunar Spacecraft Emergency Return from Lunar Parking Orbit. Master’s Thesis, National University of Defense Technology, Changsha, China, 2020. [Google Scholar]



| Parameter | Range | Unit | Grid Ize |
|---|---|---|---|
| Re-entry velocity magnitude Vk | [8400, 12,200] | m/s | 200 |
| Re-entry trajectory angle γ | [−13, −11] | deg | 0.1 |
| Re-entry velocity azimuth angle χ | [−180, 180] | deg | 0.5 |
| Area of the parachute | 3 | m2 | |
| Parachute deployment velocity | 0.8 | Mach |
| Parameter | Value | Unit |
|---|---|---|
| Mission epoch | 1 January 2027 | UTC |
| Lunar DRO amplitude | 60,000 | km |
| Lunar DRO resonance | 2 | \ |
| Maximal lunar DRO waiting time | 60 | day |
| Maximal lunar DRO return time | 15 | day |
| Number of transfer impulse maneuver | 2 | \ |
| Desired landing site longitude | 112 | deg |
| Desired landing site latitude | 41 | deg |
| Maneuver | Time | vx (km/s) | vy (km/s) | vz (km/s) | ΔV (km/s) |
|---|---|---|---|---|---|
| 1 | 6-01-2027 23:17:57 | 0.6935 | −0.0094 | 0.0402 | 0.0078 |
| 2 | 7-01-2027 04:53:12 | 0.6819 | 0.0271 | 0.0584 | 0.6969 |
| Re-entry | 13-01-2027 15:32:02 | −4.3360 | 5.8589 | −8.1595 | 0.3082 |
| Parameter | Value | Unit |
|---|---|---|
| Actual landing point longitude | 112.0516 | deg |
| Actual landing point latitude | 41.0119 | deg |
| Landing point distance error | 5.8872 | km |
| Parameter | Value | Unit |
|---|---|---|
| Re-entry point altitude | 193 | km |
| Re-entry point velocity | 10.8145 | km/s |
| Re-entry velocity azimuth | 159.6731 | degrees |
| Re-entry flight path angle | −11.6403 | degrees |
| Maximum load factor | 45.9883 | g |
| Maximum dynamic | 0.0393 | Mpa |
| Maximum heat flux density | 7.3188 | MW/m2 |
| Stationary point heat | 177.6560 | MJ/m2 |
| Parachute deployment height | 23.7884 | km |
| Parachute deployment velocity | 0.8000 | Mach |
| Flight range | 544.6832 | km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Ding, B.; Yang, B.; Xie, R.; Guo, Z.; Sha, J.; Li, S. Design of Entire-Flight Pinpoint Return Trajectory for Lunar DRO via Deep Neural Network. Aerospace 2024, 11, 566. https://doi.org/10.3390/aerospace11070566
Huang X, Ding B, Yang B, Xie R, Guo Z, Sha J, Li S. Design of Entire-Flight Pinpoint Return Trajectory for Lunar DRO via Deep Neural Network. Aerospace. 2024; 11(7):566. https://doi.org/10.3390/aerospace11070566
Chicago/Turabian StyleHuang, Xuxing, Baihui Ding, Bin Yang, Renyuan Xie, Zhengyong Guo, Jin Sha, and Shuang Li. 2024. "Design of Entire-Flight Pinpoint Return Trajectory for Lunar DRO via Deep Neural Network" Aerospace 11, no. 7: 566. https://doi.org/10.3390/aerospace11070566
APA StyleHuang, X., Ding, B., Yang, B., Xie, R., Guo, Z., Sha, J., & Li, S. (2024). Design of Entire-Flight Pinpoint Return Trajectory for Lunar DRO via Deep Neural Network. Aerospace, 11(7), 566. https://doi.org/10.3390/aerospace11070566







