Abstract
The coupling action of gas flow with propellant burning surface regression is the critical process in solid rocket motor (SRM), which has an important effect on the unsteady combustion, erosive burning, dynamic combustion and pressure fluctuation of propellants. The immersed boundary method (IBM) is used to deal with the dynamic boundary of the flow field caused by the burning surface regression, and the face offsetting method (FOM) is applied to track the regression of the burning surface. The combination of these two methods can realize the coupling simulation of gas flow and burning surface regression. In this paper, the mathematical model of the immersed boundary method for all the flow field boundaries and the coupling method of gas flow with the propellant burning surface regression are given. And the implementation method of the immersed boundary method for all boundary conditions in the non-viscous flow field is given. The internal flow fields of the motor with the end-slotted and end-burning propellant and another motor with the perforated cylindrical propellant, considering the erosive burning, are simulated. The numerical results show that IBM, combined with FOM, has effectively realized the simulation of gas flow coupled with the burning surface regression.
1. Introduction
Solid rocket motors are widely used in missile weapons and launch vehicles. The thrust is the key performance parameter of a solid rocket motor, which is closely related to the gas flow field in the motor. The burning surface of solid propellant is constantly regressing, and it may change the burning surface area and lead to a change in gas production rate. Also, the position and shape of the boundary of the internal flow field are altered. Therefore, the regression of the combustion surface profoundly affects the gas flow in the motor. On the other hand, the pressure, the flow rate and the temperature of gas flow affect the propellant burning rate, and, thus, this has a strong influence on burning surface regression. Hence, the gas flow and burning surface regression are coupled to each other. The key to solving this coupling problem is to deal with the moving boundary of the flow field and track the regression of the burning surface. The body-fitted grid is adopted, and the dynamic grid method is used to deal with the flow field moving boundary in most of the simulations of the internal flow field [1,2,3,4,5,6,7,8,9]. The dynamic grid method can be divided into the layering method, smoothing method and remeshing method. The layering method is generally only used for a simple tubular propellant. However, the end face, the inner hole surface, and the outer circumferential surface of the tubular propellant cannot regress at the same time; otherwise, the grid would intersect with each other. That means it cannot work out the situation mentioned in the reference [7] where the burning surface of the propellant is convex to the fluid domain. For the complex shape propellant, the remeshing method should be applied, as it enables the regeneration of global or local meshes. Grid regeneration is a complicated and laborious process. Wang et al. [10,11,12] used the body-fitted mesh and treated the propellant grain as the porous medium, so it is unnecessary to apply the dynamic mesh method to deal with the movement of the burning surface boundary. The immersed boundary method [13,14] is another type of mesh method. It is different from the body-fitted mesh method and usually uses a Cartesian mesh to discretize the fluid domain. Because the immersed boundary method does not require the boundary of the flow field to fit with the edge or surface of the grid element, then it is more suitable for simulating the flow field with complex shape boundaries and moving boundaries. Tran [15,16], Hirose [17], Lin [18,19] and Yuan [20] used the immersed boundary method to deal with the moving burning surface boundary in the flow field without the grid reconstruction in order to achieve a higher efficiency. At present, the application of the immersed boundary method in the motor internal flow field mainly focuses on the simple axisymmetric two-dimensional flow field. In the three-dimensional flow field, it is difficult to solve the complicated interface tracking problem caused by the burning surface regression, so the immersed boundary method is mainly applied to the flow field simulation when the combustion surface remains fixed.
The methods of tracking the interface motion are divided into two categories: the Euler method and the Lagrange method. Euler methods include the level set method (LSM) [21,22,23], the Volume of Fluid (VOF) [24,25], and the minimum distance function (mDF) [26], which implicitly express the curved surface in a higher dimensional space. The advantage lies in its capability to accurately track the deformation and motion of complex interfaces, as well as effectively handle the interface evolution when the topological structure of curved surfaces changes. The disadvantage is that the three-dimensional volume grid is used to store the scalar representing the curved surface, so the calculation amount and memory space are large, and the precision of interface capture is lower than that of the Lagrange method. Lagrange methods include the marker particle method, the front tracking method, the face offsetting method [27] and the dynamic grid method. They can directly track the coordinate position of discrete points or surface elements in the process of interface deformation and movement. The advantage is intuitive and efficient. However, it is hard to deal with the intersection of discrete surface elements or edges, and basically, Lagrange methods cannot handle the changed topological structure during the evolution of curved surfaces. Currently, the most widely used methods for solving the burning surface regression are the minimum distance function method and the level set method [10,11,12,28,29,30,31]. If it is a case of parallel regression, employing the minimum distance function method enables the consideration of both efficiency and accuracy. If it is a case of non-parallel regression, the minimum distance function method is no longer applicable. Most researchers resort to utilizing the level set method and solving partial differential equations. The efficiency of the level set method can potentially be enhanced through certain techniques, but it does not necessarily guarantee an achievement up to the efficiency of the Lagrangian method.
In order to establish an efficient and reliable numerical simulation method for the three-dimensional internal flow field of the solid rocket motor, the immersed boundary method and face offsetting method are investigated in this paper. The following sections are as follows: In Section 2, the governing equation and the discrete method of Euler flow are given. In Section 3, the immersed boundary method for all the boundaries in the motor is presented. In Section 4, the face offsetting method for simulating burning surface regression is introduced. In Section 5, the coupling method of gas flow and burning surface regression is given. In Section 6, the verification and analysis of numerical examples are presented. The summary and conclusion are given in Section 7.
2. Governing Equations and Discrete Methods of Euler Flow
The numerical simulation of the flow field in solid rocket motors has been involved in turbulence, gas–solid multiphase flow, chemical reaction, heat and mass transfer, burning surface regression, etc. In this paper, the immersed boundary method is introduced to investigate the coupling problem of gas flow and burning surface regression, which focuses on the non-viscous flow simulation. Due to the high Reynolds number of the flow field in solid rocket motors, the net pressure acting on the fluid is much larger than the viscous stress and Reynolds stress [32], then the inviscid flow model is basically suitable for the simulation of the flow field in the motor. In addition to non-viscosity, the flow in the motor also adopts the following simplified assumptions [11,33]:
- (1)
- The combustion of propellant is completed instantaneously on the burning surface, without considering the physical and chemical reaction processes such as the phase transition and combustion. The newly generated gas is injected into the combustion chamber along the local burning surface, and it is evenly mixed with the main gas stream after injection. Moreover, there is no chemical reaction during the flow process. The chemical composition and thermodynamic parameters of the newly generated gas are exactly the same as those of the main gas stream.
- (2)
- The gas in the motor is a pure gas phase and an ideal gas with a constant specific heat capacity, and the friction between the gas and the channel surface is ignored.
- (3)
- The gas flow in the motor is adiabatic, and there is no heat and work exchange with the external environment.
- (4)
- The influence of gravity and other forces on the gas flow is ignored.
The vector form of the three-dimensional Euler flow governing equation is
where U is the conserved variable of the flow field, and F, G and H are the convective fluxes in the x, y and z directions of the three Cartesian coordinates. Their specific expressions are as follows:
where u, v and w are the flow velocity in the direction of three Cartesian coordinates, respectively. The relationship between E and p is
The governing equation of three-dimensional inviscid flow consists of two components: the time derivative term and the space derivative term. After dimensional splitting Equation (1), three extended one-dimensional flow equations are obtained:
They are abbreviated as
The governing equation retains the time derivative term, and the spatial discretization is carried out to obtain the following semi-discretization format:
where , and are the numerical fluxes in the x, y and z directions. The algebraic terms are moved to the right of the equation to get the following form:
The R(U) of the corresponding Formulas (11), (12) and (13) are
The numerical flux is constructed using the HLLC format [34,35]. HLLC is an improvement of the HLL format (the approximate Riemann solver proposed by Harten Lax and van Leer) [36], both of which are Godunov types. And the numerical flux is calculated by an approximate Riemann solver. HLLC is capable of capturing flow phenomena such as shock waves, expansion waves, and contact discontinuity, and it is suitable for complex transonic flow fields in solid rocket motors. In this paper, the numerical flux calculation method of HLLC given by Batten et al. [37] is applied. The MUSCL (Monotone Upstream-centered Schemes for Conservation laws) method proposed by van Leer, combined with the min-mod limiter, is used to calculate the left and right values of variables on the boundary of grid cells [35].
For the semi-discrete Equation (14) after the space discretization, the second-order Runge–Kutta method with TVD property is used to solve the following:
In order to ensure the time accuracy of the second order, the following methods are given for carrying out the dimensional splitting advance:
For each extended one-dimensional governing equation, the second-order Runge–Kutta method described above is adopted in time advance.
The time step is determined according to CFL conditions, and it is calculated as follows:
where c is the speed of sound. And the CFL value is 0.9 in this paper.
3. Application of Immersed Boundary Method
The virtual element method [38,39,40,41,42,43,44,45,46,47] is adopted in the immersed boundary method based on a Cartesian grid. The grid element is arranged outside the boundary of the flow field in the virtual element method. According to the boundary condition and the value of the nearby flow field, the specific values are assigned as the difference format template of the flow field grid element around the boundary. Usually, with the help of the mirror point of the virtual point about the boundary, the value of the virtual point is solved by interpolation, as shown in Figure 1. Black points are the center of fluid cells or boundary-fluid cells, green points are ghost cell centers, red points are wall points, and blue points are image points. The black points in the circle are the stencils of inverse distance interpolation for the ip in the same circle. The determination of the solution domain, the generation of surface mesh, the generation of volume mesh, and the determination of the virtual unit for the flow field can be referred to [19]. The boundary types of the flow field are the sliding wall boundary (the inner wall of both the combustion chamber and nozzle), the pressure outlet boundary (the nozzle outlet), the mass flow inlet boundary (the burning surface of propellant grain) and the rotational periodic boundary (the oxy cross-section and oxz cross-section). All boundaries are handled by the immersed boundary method, and the key is to solve the flow field variables on the virtual unit. The virtual cell is taken as the template point in grid cells around the flow field boundary to solve the numerical flux at the cell boundary. The solution method of flow field variables corresponding to virtual units of each boundary is given in the following.
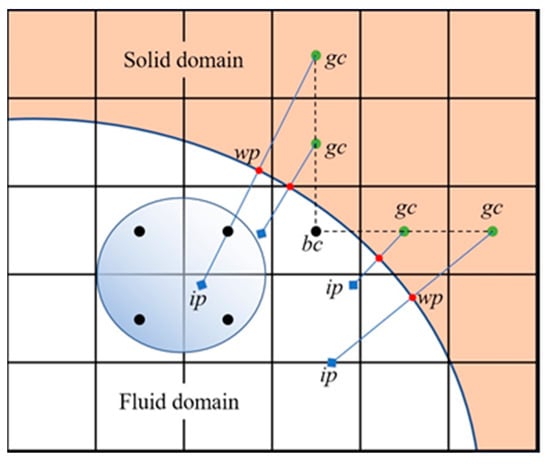
Figure 1.
Schematic diagram of virtual unit method.
3.1. Slip Wall
Using the mirror method, the values of the GC point in the center of the virtual unit are obtained by the linear interpolation of the mirror point IP and the boundary point wp. The calculation formulas are as follows:
In the formula, subscripts n, τ1 and τ2 represent the normal and two tangential directions of the wall at the wp point. According to the characteristic analysis of the flow governing equation, the four variables (, , and ) of slip wall boundary point wp are obtained by interpolating the flow field variables inside the flow field using the numerical boundary condition. The remaining variable,, is obtained using physical boundary condition (no slip condition: ). The IP point is not in the center of the grid cell, and the value of its flow field variable is solved by the interpolation of surrounding flow field points. The interpolation function uniformly uses the inverse distance-weighted average interpolation function, namely Equation (27) or (28).
In the formula, represents any physical quantity, r is the distance from the interpolation template point to the interpolated point, the subscript i is the label of the interpolation template point, and m is the total number of interpolation template points.
3.2. Mass Flow Inlet
For the burning surface of the propellant grain, it is assumed that combustion is completed instantaneously on the burning surface, and the physicochemical reaction processes such as phase transition and combustion are not considered, and then the burning surface is regarded as the mass flow inlet. The gas injection velocity is usually subsonic, so there is one numerical boundary condition and four physical boundary conditions for the mass flow inlet in three-dimensional space. The fluid pressure at the boundary can be interpolated from the internal flow field, and the remaining four physical quantities can be calculated as follows [19]:
where is the mass flow rate, and its calculation formula is in [18]. After the variable values of the flow field on the boundary are determined, the values of the virtual unit center are solved by the mirror method expressed by Equations (22)~(26).
3.3. Pressure Outlet
In most of the working conditions of the rocket motor, the gas flows out of the nozzle outlet at supersonic speed, and the flow outside the outlet does not affect the inside. Therefore, the flow field variable of the virtual grid unit corresponding to the nozzle outlet boundary is no longer solved by linear interpolation using the mirror method, and it is directly equal to the value on the outlet boundary. The calculation formula is as follows:
, , and are interpolated by the value inside the flow field. When it is a case of the subsonic outflow, is equal to the atmospheric pressure. When it is a case of supersonic outflow, is interpolated by the value inside the flow field.
3.4. Rotational Periodic Boundary
The virtual unit value corresponding to the rotational periodic boundary is solved without calculating the value of the w point. In the three-dimensional flow fields studied in this paper, the x-axis is taken as the rotation axis, and the periodic angle is . The fluid field is located in the positive half region of the y direction and in the negative half region of the z direction. Assuming that the coordinate of the virtual unit center corresponding to the oxz cross-section boundary is (x,y,z), and the mapping point (xro,yro,zro) in the fluid domain is obtained after a rotation around the x-axis:
The original variables of the flow field at point are obtained by using the inverse distance-weighted interpolation function and can be expressed as
Then, the velocity vectors in the y and z directions at are rotated by to obtain the original variables on the virtual cell:
Similarly, the flow field variable of the virtual unit center corresponding to the oxy-plane boundary can be achieved by changing the rotation angle to .
4. Application of Face Offsetting Method
The face offsetting method was first proposed by Jiao [27,48]. When using the surface offsetting method to solve the interface motion, the three-dimensional surface is discretized into a triangular surface grid. The surface offsetting method does not change the topology of the surface mesh, and the new position of the mesh vertex is the intersection position of its associated triangle after updating. The associated triangle of the vertex refers to the triangle with that point as a vertex. The face offsetting method determines the advective motion displacement of the vertex and then corrects it to obtain the displacement of the wave motion. The vertex v of a triangular mesh reaches the point p after the interface wave motion, and the local coordinate system is established with point v as the origin. The position vector of p is p, and the normal vector of the plane passing through point p is n, so the equation of the plane is , where . Assuming the point v has m number of associated triangles, the coordinates of point p satisfy the following linear equations of m rows:
where N is a m × 3 coefficient matrix composed of triangular normal vectors, and a is an m-dimensional vector. Each row represents a plane equation of the offset-associated triangle. The vertices in a surface grid usually have more than three associated triangles. That means more than three planes intersect, so the above equations are usually overdetermined. When all the associated triangles become coplanar or distributed in two planes (the vertices fall on the ridges of the interface), the above equations are underdetermined. Jiao generalized the intersection point and introduced the concept of “least square intersection point” to define the intersection point as the point with the smallest sum of distances from the plane where all the associated triangles are located; thus, the problem of overdetermination and underdetermination of the intersection point equations can be solved. The least-square intersection point satisfies the following linear equations:
where and is a 3 × 3 matrix. And . is the m × m diagonal weight coefficient matrix, and the diagonal element wii of each row in the matrix is the area or top angle of the i-th associated triangle. The vector space, formed by the eigenvectors of relatively large eigenvalues of A, is defined as the main space of A. And the vector space, formed by the eigenvectors of smaller eigenvalues of A, is defined as the null space of A. The eigenvalue analysis method is used to solve the system of equations, and the local coordinate d of point p is obtained by the linear combination of eigenvectors in the main space, whose expression is as follows:
In the formula, k is the number of relatively large eigenvalues, that is, the number of basis vectors in the main space, and the smooth point is 1, the ridge point is 2, and the corner point is 3. is the eigenvector of A. Since the above system of equations is defined in the local coordinate system with point v as the coordinate origin, d is the displacement of point v in the interface motion, and the unit vector of d is called the offset direction.
After the advective displacement is determined, the direction of vertex movement is maintained, and the moving distance is corrected to obtain the wave displacement vector. The following formula is used to calculate the wave movement distance:
In the formula, is the vertex moving distance, and the calculation formula of and is
In the formula, represents the area or vertex angle of the associated triangle, represents the distance between the vertex before moving and the associated triangle after moving and represents the angle between the vertex moving direction vector and the normal vector of the face element.
After the interface moves, the surface discrete mesh could stretch or shrink, which may cause the local surface mesh quality to decline. Then, it becomes necessary to smooth the mesh so that the mesh size distribution tends to be uniform. The surface mesh smoothing should maintain the discrete accuracy and geometric features of the surface as much as possible. That means the distance between the vertices of the smoothed mesh and the original surface should be kept as close as possible, and the original sharp corners and ridges should be retained. The face offsetting method can easily achieve this goal by simply moving the vertices in the null space of their matrix A to realize the mesh smoothness. The formula for vertex smoothing displacement is
where t is the displacement vector of vertex in the null space; T is the 3 × (3-k) matrix whose column vectors are the basis vectors of null space of A; k is the number of relatively large eigenvalues; 3-k represents the number of basis vectors of the null space; m is the number of vertex associated triangles; ci is the centroid vector of the i-th associated triangle, which takes the vertex v as its origin; wi is the weight coefficient, equal to the area or vertex angle of the triangle and wi can also be 1.
In order to avoid the intersection of surface meshes in motion, the way to determine the time step of the face offsetting method is given in reference [27]. The combustion surface of the propellant grain is the discrete triangular surface mesh, and the regression of the burning surface is realized by moving the triangle. The moving speed of the triangle is equal to the burning rate at its centroid. The position of the mesh vertex after moving, namely the triangle vertex, is determined according to the intersection position of its associated triangle after moving.
5. Coupling Calculation Method
In the solid rocket motor, the gas flow rate is as high as 103 magnitude, while the burning face regression speed is not greater than 10−2 magnitude. Therefore, the difference between the two orders of magnitude is 105, and the time scale of gas flow is far less than that of the burning face regression. Therefore, the coupling between them can be simplified as a weak coupling [8], and the two processes can be solved separately and alternately along the time advance. In the actual simulation calculation, it is found that the distance of burning face regression in a flow time step is about one ten-thousandth of the side length of the grid cell. Therefore, it can be assumed that the combustion surface remains fixed in several flow time steps to reduce the frequency of the combustion surface moving solution so as to greatly reduce the time proportion of the combustion surface moving solution relative to the flow solution. The step diagram of the coupling solution is shown in Figure 2, where tf is the time step of the gas flow solution, tr is the time step of the burning face regression solution, rb is the propellant burning rate, and p is the fluid pressure. In the coupling advance solution, the moving distance of the combustion surface is accumulated (when it remains fixed) until the cumulative distance reaches a given value dr, which is called the space step of combustion surface movement. Then, the combustion surface moves distance dr at one time, and the grid cell type, virtual unit and mirror point are updated. Moreover, the accumulated moving distance is cleared to zero. In each time step of the flow solution, the pressure of the flow field is transferred to the propellant burning surface, and the burning rate of propellant is solved according to this pressure, and then the burning rate is transferred to the burning surface boundary of the flow field, and the mass flow rate is solved according to this burning rate.
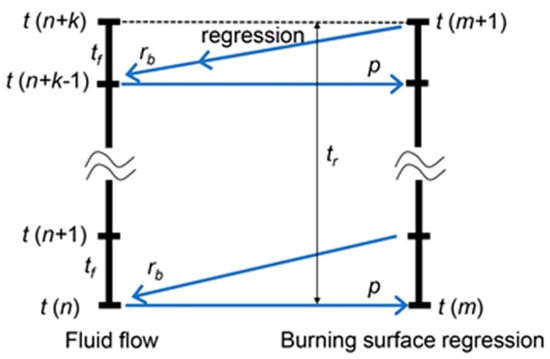
Figure 2.
Schematic diagram of coupling solution steps.
In Figure 2, k is the number of flow-solving time steps when the burning surface remains fixed, and obviously, tr = k × tf. When the value of dr is set too large, the accuracy of the simulation result will decrease. A shift in the type of grid cell is another factor that limits the size of dr. The virtual cell method typically classifies the volume grid units of the solution domain as fluid grid units (FG), solid grid units (SG), boundary fluid grid units (BFG) and boundary solid grid units (BSG) [18,19]. When dr is greater than half of the side length of the grid cell, the cell type may leapfrog. For example, the solid grid cell (SG) could skip the boundary solid grid cell (BSG) and transform directly into the boundary fluid grid cell (BFG). The newly emerged BFG needs to interpolate the values of flow field variables from the surrounding grid cells. In such cases, the grid cells around the BFG were originally BSG, and they now transform into the fluid grid cells (FG); the flow field variable values of these FGS must first be obtained by interpolation. For the newly emerged BFG and FG, it is a laborious operation to ensure the order of obtaining the values of flow field variables, and it is not conducive to parallel computation. Interpolating the flow field variables obtained by interpolation to the flow field variables of another grid cell may lead to reduced accuracy and robustness. Therefore, it is necessary to limit the size of dr to avoid the occurrence of leapfrog transformation of grid cell types. The size of dr is set to 0.4 times the side length of a grid cell so that only three cell-type transitions can occur: SG to BSG, BSG to BFG, and BFG to FG. The newly added BFG is interpolated by the inverse distance weighted average function to obtain the flow field variable value.
6. Numerical Results and Discussion
6.1. Numerical Simulation and Result Analysis of Three-Dimensional Internal Flow Field of Motor with End-Slotted and End-Burning Propellant
6.1.1. Quasi-Static Flow
The quasi-static flow within a solid rocket motor refers to the flow while the combustion surface remains fixed. The quasi-static flow in the motor is calculated to verify the ability of the immersed boundary method to deal with all kinds of boundaries in the three-dimensional flow. The geometric model of the motor is shown in Figure 3, and the main dimensions are shown in Figure 4, where the unit of length is a millimeter. The end-slotted and end-burning propellant is commonly used in single-chamber dual-thrust solid rocket motors [49]. The initial boundary values of propellant parameters and flow field are shown in Table 1. According to the axisymmetric geometric characteristics of the flow field, a quarter of the flow field is taken as the calculated object. The shape of end-slotted and end-burning propellant is complex, the inner flow field has a large number of burning surface boundaries and the burning surface boundaries are both convex and concave. According to the calculation results of axisymmetric two-dimensional flow obtained by the immersed boundary method in reference [18], three sets of grids are used to calculate a three-dimensional flow field. The first one is a uniform grid, and the side length of each direction of a grid cell is 1 mm. The second one is also a uniform grid, and the side length of each direction of the grid unit is 0.5 mm. The third one is a local refinement grid; the side length of the mesh cell near the nozzle border is 0.25 mm, so the side length of the rest of the mesh cell is 0.5 mm, and the side length of each direction is equal. For the stable flow field calculated by the third grid, the pressure distribution in the nozzle region is shown in Figure 5, and the Mach number distribution in the combustion chamber is shown in Figure 6. The cloud map distribution characteristics on the periodic plane oxy and oxz are the same as those of the axisymmetric 2D flow field [18]. In Figure 7, the flow lines on the periodic plane are shown, which start from the burning surface, extend along the wall, and flow towards the outlet. In the nozzle area, the flow line is distributed against the wall, which reflects the “non-penetrating” characteristic of the boundary condition of the sliding wall. In the combustion chamber area, the flow line emanates vertically from the combustion surface and extends downstream, reflecting the Taylor–Culick flow characteristics. These distribution characteristics of the flow field and flow line prove that the immersed boundary method can deal with the corresponding boundary conditions effectively. Table 2 lists the equilibrium pressure calculated by the axisymmetric 2D model [18] and the 3D model simulation. The equilibrium pressure calculated by the 3D model is slightly larger than that of the axisymmetric 2D model, and the difference between the two models would decrease with the reduction of the grid scale. When the mesh cell near the nozzle boundary is refined to 0.25 mm, the equilibrium pressure difference is 0.8%, which proves that the calculation result of the three-dimensional immersed boundary method is accurate and reasonable.

Figure 3.
Schematic structure of motor with end-slotted and end-burning propellant.
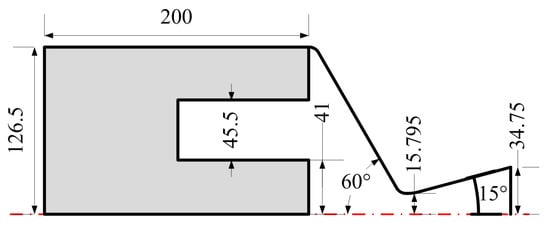
Figure 4.
Main dimensions of motor with end-slotted and end-burning propellant.

Table 1.
Propellant parameters and initial flow field conditions of motor with end-slotted and end-burning propellant.
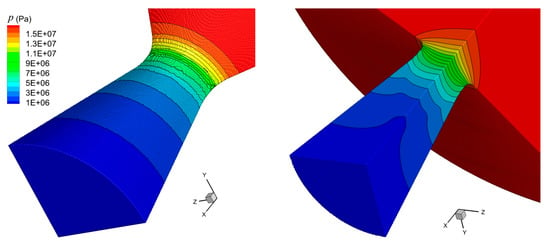
Figure 5.
Pressure distribution in nozzle area.
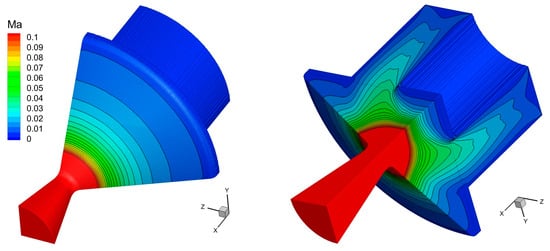
Figure 6.
Mach number distribution of the combustion chamber.
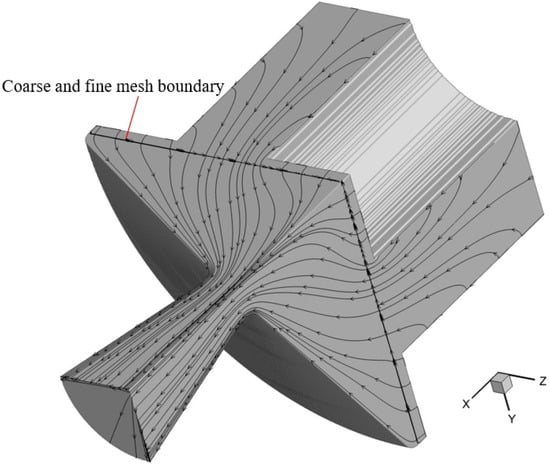
Figure 7.
Flow lines in the periodic plane.

Table 2.
Equilibrium pressure calculated by different-sized grids.
6.1.2. Transient Flow Coupled with Burning Surface Regression
The initial values of the 3D transient flow field of the motor with end-slotted and end-burning propellant are listed in Table 1. The gas pressure distribution in the combustion chamber is uniform and also satisfies the geometric combustion law, which means the burning surface is assumed to be parallel regressed. In the axisymmetric 2D model [18], the simplified assumption is that the movement of the burning surface is interfacial advective motion, and the groove bottom surface of the propellant is always perpendicular to the adjacent cylindrical surface, just like the right angle connection, as shown in the left side of Figure 8. It is more reasonable to assume that the burning surface regression is the interfacial wave motion. In the regression process, a transitional curved surface would be generated between the groove bottom surface and the adjacent cylindrical surface, just as the round connection, as shown on the right side of Figure 8. In the three-dimensional model, the burning surface is regressed according to the wave motion, and the face offsetting method is used to simulate burning surface regression. When the end face of the end-slotted and end-burning propellant is burning, the radial size decreases gradually until it is zero, and the mesh on the end-burning surface is compressed violently. Because the original face offsetting method cannot remove the surface mesh cells, the mesh would go wrong when compressed by distance. The straightest way to handle this process is to perform a mesh cell merge. Jiao [27] changed the geometric features of the vertex at the junction of the conical surface of the propellant and the cylindrical surface of the shell wall from a ridge point to a smooth point. As the mesh is stretched on the cylindrical surface and is compressed on the conical surface, the vertex of the mesh at the junction moves towards the cylindrical surface in the smoothing process. The Jiao method is hard to implement because after the vertex of the junction is transferred to the cylindrical surface, the new vertex has to be determined and, after the mesh of the junction is smoothed, the boundary becomes blurred; moreover, the vertex of the junction is difficult to be determined. Therefore, instead of the Jiao method, another method is proposed to deal with the vertex of the junction in this paper. The vertex of the burning surface mesh that reaches the shell wall is set as a static point. That means not only the radial velocity but also the axial velocity is set to zero. Under such circumstances, the vertex on the conical surface would automatically stay on the cylindrical surface, which is equivalent to the mesh point on the compressed conical surface being transferred to the expanding cylindrical surface. For the convenience of subsequent description, this method is named the surface interface vertex transfer method, which is more efficient than the mesh merging method. The surface interface vertex transfer method is used to move the mesh vertex of the outside end-burning surface to the cylindrical surface of the shell wall, and the small triangular mesh of the inside-end burning surface is removed by the mesh merging method. Because the end surface of the propellant is a plane, the surface mesh merging on the end face almost does not affect the surface dispersion accuracy. In order to reduce the calculation time, the fluid domain mesh adopts a relatively sparse uniform grid, and the side length of the mesh cells is 1 mm. The whole process of burning surface regression would last about 1.17 s, and the number of fluid domain grids increases from 930,000 to 2.19 million. The calculation time is about 43 days using 56 cores on a dual-channel AMD EPYC 7452 computer (AMD, Beijing, China).
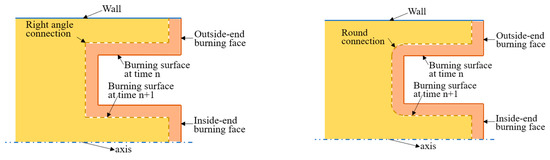
Figure 8.
Comparison of advective motion (left) and wave motion (right) on burning surface.
Figure 9 shows the triangular surface grid and Cartesian body grid of the nozzle region at time 0.244 s. The grid on the left of green dashed lines in the surface grid is originally on the outside end surface of the propellant, but as the burning surface regresses to the shell wall of the combustion chamber, it has a different axial mesh size from the original shell wall grid on the right of green dashed line because the grids at the two places are set to not participate in their own smoothing process during the grid smoothing process. The mesh unit size of the original shell wall is protected to ensure the small size requirement of the surface grid unit at the nozzle throat. Since the local flow field boundary is stationary, the Cartesian body grid of the nozzle region remains unchanged during the burning surface regression process. The above analysis shows that the surface interface vertex transfer method is effective.

Figure 9.
Surface grid (left) and body grid (right) of the nozzle region at 0.244 s.
Figure 10 shows the evolution process of the surface grid and body grid in the combustion chamber and nozzle inlet area. It is clearly observed that the transitional curved surfaces between the groove bottom plane and the cylindrical surfaces (inner and outer) continue to grow. Figure 11 shows the evolution process in the distribution of pressure and Mach number on the flow field periodic surface and outer circumferential surface during the burning surface regression. The contour lines of pressure and Mach number are smooth and symmetrical about the central axis. At the moment of 1.167 s in the later period, as shown in the last two figures of Figure 11, the groove at the rear of the propellant burns to the end, the two circumferential surfaces disappear and only the bottom end surface and transitional surface are left. Then, the total burning surface area decreases sharply, the flow field changes from the original quasi-steady state to the obvious unsteady state and the Mach number distribution in the combustion chamber is different from that in the earlier period, which becomes chaotic. Figure 12 shows the change curve of average pressure in the combustion chamber with the regressing distance of the burning surface. As the wave interface motion model is used to describe the burning surface regression in the three-dimensional model, the groove bottom surface and the two circumferential surfaces no longer remain vertical during the regressing process but form a transitional arc, and the total area of the burning surface keeps decreasing. Therefore, different from the calculation results of the axisymmetric two-dimensional model using the interface convection motion model, no horizontal plateau appears in the pressure curve after the equilibrium pressure. The maximum pressure in the whole regressing process of the burning surface is 17.72 MPa when the regressing distance is about 3.3 mm, and it is very close to the peak equilibrium pressure (17.88 MPa) of initial quasi-static flow on the combustion surface, reflecting the accuracy of transient calculation results. In Figure 12, the local magnification map, corresponding to the regressing distance of 10~15 mm, reveals that one period of pressure fluctuation is about 1 mm, which is exactly the side length of the body grid unit. Therefore, the same conclusion [18] is obtained with the immersed boundary method in the axisymmetric two-dimensional flow simulation calculation, and the transformation of the grid unit type causes a small pressure fluctuation at low frequency during the implementation of the immersed boundary method. The pressure fluctuations are further analyzed, and the pressure curve with the regression distance between 2 mm and 16 mm is enlarged, as shown in Figure 13. The horizontal coordinate interval of the red vertical line is about 1 mm, and the interval of the green vertical line is about 1.6 mm, which is approximately equal to the fluctuation period of the burning surface area caused by the vertex transfer of the end burning surface grid to the shell wall, as shown in Figure 14. The amplitude of both pressure fluctuations is within 1% of the mean value. The above results show that the immersed boundary method and face offsetting method in this paper can be applied to achieve the transient simulation of the internal flow field in the whole process of the groove combustion of end-slotted and end-burning propellant. The calculation results of the flow field are reasonable, and the feasibility of the simulation calculation of the gas flow coupling with burning surface regression is verified when the two methods are combined.
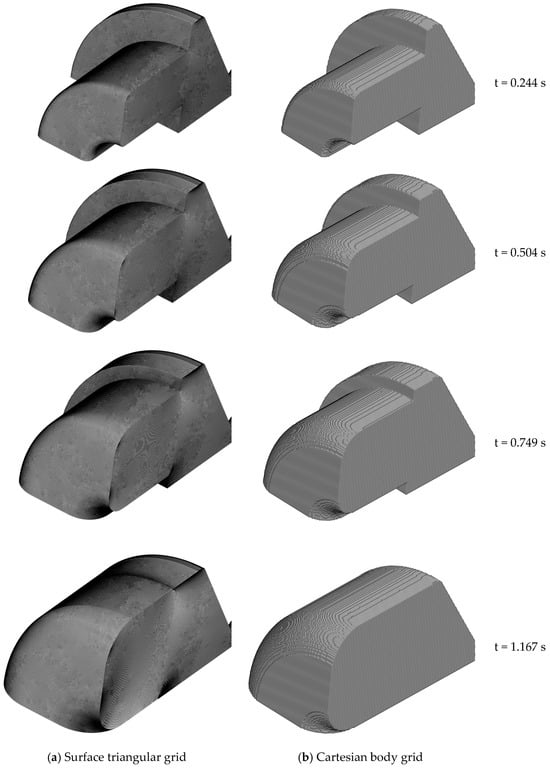
Figure 10.
Evolution of the grid in the combustion chamber and nozzle inlet area.
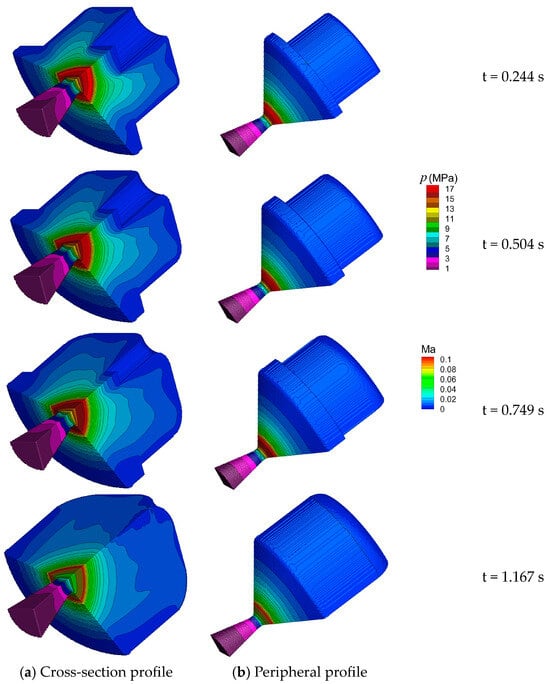
Figure 11.
Evolution of Mach number (combustion chamber and nozzle inlet) and pressure (nozzle throat and outlet).
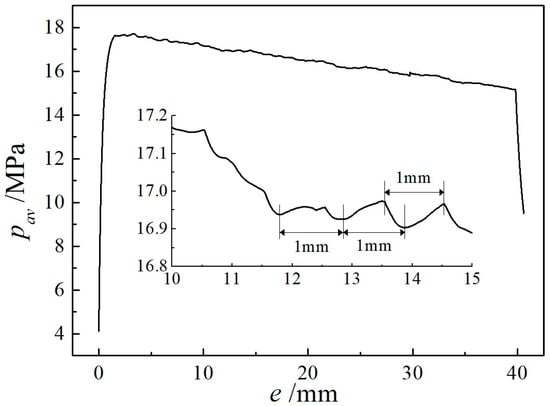
Figure 12.
Change curve of average pressure with the regressing distance of burning surface.
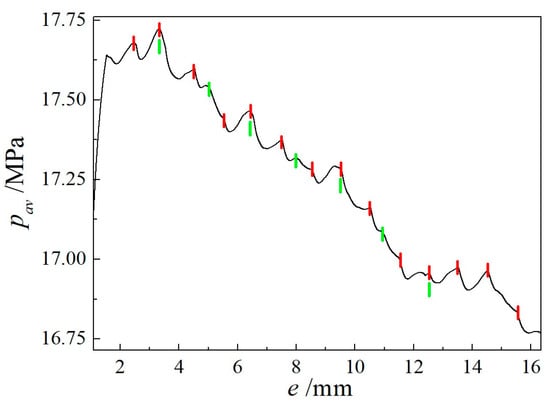
Figure 13.
Local magnification of average pressure curve.
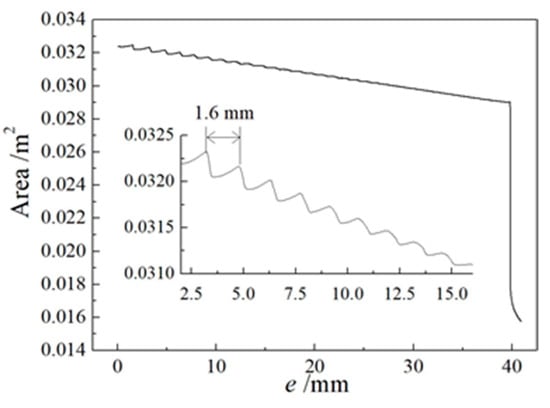
Figure 14.
Change curve of burning surface area with regressing distance.
6.2. Numerical Simulation and Experimental Verification of Three-Dimensional Internal Flow Field of Erosive Burning Motor
Hasegawa [50] has carried out a series of experiments and simulation studies on the erosion-burning rate of aluminum-containing composite propellant. In this paper, a motor example is selected for simulation calculation, and the experimental result in the reference is compared to verify the proposed immersed boundary method. The propellant is tubular, and the length is 1.260 m, and the inner hole diameter is 0.060 m. Both ends are covered with a certain material, and the outer cylindrical surface is fitted to the shell wall; thus, only the inner cylindrical surface can be burned and regressed. The motor is installed with an embedded nozzle, which can reduce the adhesion and accumulation of aluminum and aluminum oxide particles in the nozzle throat. The throat diameter is 0.034 m. The physical property parameters of the propellant and the initial value conditions of the flow field calculation are listed in Table 3.

Table 3.
Propellant parameters and initial value conditions of the erosive burning motor.
Lin [18] uses the immersed boundary method to simulate the non-parallel burning surface regression coupled with the gas flow in the axisymmetric two-dimensional space, and the simulation calculation is extended to the three-dimensional space in this paper. According to the axisymmetric geometric characteristics of the flow field, a quarter region is taken as the calculation object along the circumferential direction, and the fluid domain is shown in Figure 15. The distribution of the burning rate on the burning surface is no longer uniform due to the erosion burning. After the burning surface is discretized into the triangular grid, the moving speed of each triangle is determined by the flow state corresponding to the center of mass position of the triangular unit. The equation for calculating the moving velocity rbe at the center of mass is the erosive burning rate formula in the reference [18].
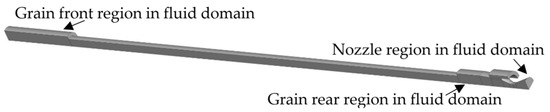
Figure 15.
Fluid domain of erosive burning motor.
In order to shorten the calculation time, a sparse Cartesian body grid is used, but the grid of the nozzle area is refined. Considering the large length-diameter ratio of the motor, the x-direction (axial) size of the grid unit is set to four times that of the y and z directions. The body grid near the nozzle inlet is shown in Figure 16. The size of the mesh cell in the nozzle area is 2 mm × 0.5 mm × 0.5 mm, and the other areas are 4 mm × 1 mm × 1 mm. The whole process of burning surface regression lasts about 2.17 s, and the number of mesh cells in the fluid domain increases from 660,000 to 830,000. The calculation time is about 42 days using 32 cores on a dual-channel Intel Xeon Platinum 8375 C computer (Intel, Shanghai, China).

Figure 16.
Nozzle area body grid.
Figure 17 shows the change curve of pressure at the front of the combustion chamber over time. Compared with the calculation results [18] of the axisymmetric two-dimensional method and the experimental results [50], the accuracy of calculation results is reduced due to the application of large mesh size in the three-dimensional method. However, the overall change trend is consistent, and the pressure curve moves up about 0.3 MPa overall, indicating that the three-dimensional calculation results are reasonable and reliable. Compared with 2D, the 3D pressure curve is smoother and has no obvious burrs because the 3D flow field calculation results do not capture the vortex movement in the combustion chamber. Figure 18 shows the evolution of the surface grid of the fluid domain in the front and rear regions of propellant in the transient flow field. At 2.173 s, the front of the propellant is not completely burned out, and there is still a certain distance between the burning surface and the shell wall of the combustion chamber. The rear end of the propellant has been burned out, and the burning surface is the same height as the shell wall. Figure 19 shows the evolution of the body grid of the fluid domain in the front and back regions of propellant in the transient flow field. At 1.087 s, there are five body grid unit heights in the front region and only three body grid unit heights in the back region. Figure 20 shows the shadow pattern of the burning surface area from the view direction along the negative Z-axis. The lower boundary of the shaded area is the central axis, and the upper boundary is the Y-axis boundary of the burning surface. The size factor of the Y- and Z-axes is 21 times that of the X-axis. In the figure, the upper boundary of the burning surface gradually changes from a horizontal shape to an expanding shape tilted to the upper right, and the axial length decreases greatly in the later moment because the rear region of the propellant burns out first. The results, shown in Figure 18, Figure 19 and Figure 20, present that the immersed boundary method and face offsetting method effectively realize the simulation of non-parallel burning surface regression coupled with the gas flow considering the erosive burning in the solid rocket motor.
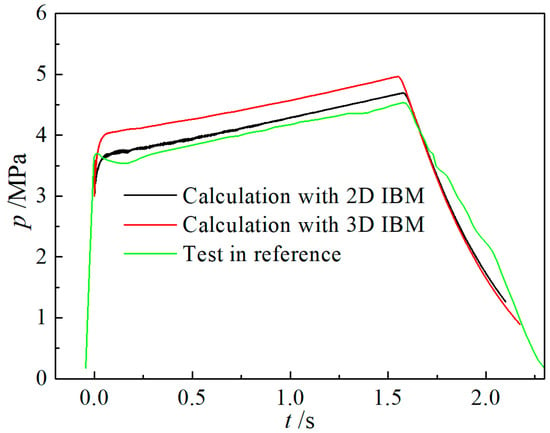
Figure 17.
Pressure–time curve at the front of combustion chamber.

Figure 18.
Evolution of the triangular surface grid in the front and rear regions of propellant.

Figure 19.
Evolution of the Cartesian body grid in the front and rear regions of propellant.
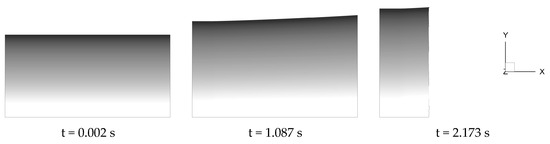
Figure 20.
Shadow pattern of burning surface area.
Figure 21 and Figure 22 show the Mach number cloud image of the combustion chamber and the nozzle pressure cloud image, respectively. In Figure 21, the size factor of the Y- and Z-axes is two times that of the X-axis. The Mach number distribution in the combustion chamber is consistent with the Taylor–Culick flow characteristics, but it is not the complete symmetry of the central axis, especially at the initial moment of 0.002 s. That indicates the mesh size is too large, and the accuracy of calculation results is not enough; thus, the mesh needs to be further refined. In Figure 22, the pressure distribution in the nozzle is basically symmetric about the central axis, and the distribution pattern is consistent with the flow characteristics of the Laval nozzle.
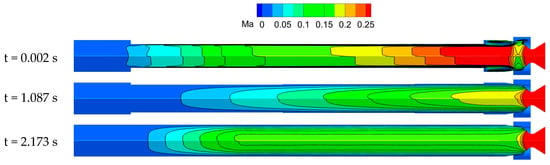
Figure 21.
Evolution of Mach number cloud image of combustion chamber.
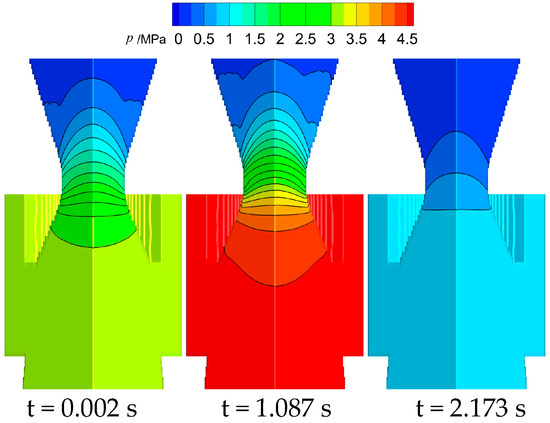
Figure 22.
Evolution of nozzle pressure cloud map.
7. Conclusions
In this paper, the extended application of the immersed boundary method in the numerical simulation of the flow field in solid rocket motors is presented, and the implementation method of the immersed boundary method for all boundary conditions in the non-viscous flow field is given. And the coupling method of gas flow and burning surface regression is investigated. Combined with the face offsetting method, the three-dimensional quasi-static flow field is simulated when the burning surface remains fixed, and the transient flow field is calculated when the burning surface is regressed. According to the calculation results of the flow field, the following conclusions are obtained:
- (1)
- The immersed boundary method and face offsetting method are combined to simulate the three-dimensional internal flow field in the motor in the case of the parallel burning surface regression with the erosive burning. The coupling problem of gas flow with non-parallel burning surface regression with erosive burning is solved. By comparing and analyzing the calculation results of the axisymmetric two-dimensional model and the experimental results in the reference, the rationality of the result obtained by the three-dimensional immersed boundary method coupled with the face offsetting method is verified.
- (2)
- For the end-burning propellant, the intersection point between the propellant end surface and the shell wall is set to remain fixed so that the nearby surface grid can remain smooth during the movement. Although the combustion surface area fluctuation can result in the same frequency fluctuation of combustion chamber pressure, the amplitude of fluctuation is small; moreover, the frequency is low and can be identified. Generally, it does not interfere with the pressure fluctuation caused by vortex shedding.
- (3)
- The simulation result of three-dimensional gas flow coupled with the burning surface regression is reasonable and reliable, but the accuracy of the result is slightly low due to the large grid size. The follow-up work focuses on the distributed and parallel improvement of the existing calculation program so as to achieve the application of a fine enough grid for more accurate results.
Author Contributions
Conceptualization, D.S., Q.L. and R.T.; methodology, D.S. and Q.L.; software, D.S.; validation, D.S. and Q.L.; formal analysis, Q.L.; investigation, Q.L.; resources, D.S. and Q.L.; data curation, Q.L. and R.T.; writing—original draft preparation, D.S.; writing—review and editing, Q.L. and R.T.; visualization, H.W.; supervision, H.W. and R.T.; project administration, R.T.; funding acquisition, H.W. and R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Guoy, D.; Wilmarth, T.; Alexander, P.J.; Jiao, X.; Campbell, M.; Shaffer, E.; Fiedler, R.; Cochran, W. Parallel mesh adaptation for highly evolving geometries with application to solid propellant rockets. In Proceedings of the 16th International Meshing Roundtable; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- He, Z.; Gao, Y.; Gu, X.; Wang, G. The Study of Dynamic Grids Application to Calculate the Inner Flow Field of Solid Rocket Motor. J. Proj. Rocket. Missiles Guid. 2008, 28, 164–166. (In Chinese) [Google Scholar]
- Tang, B. Numerical Simulation of Erosive Burning Unsteady Process in Solid Rocket Motor. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2014. (In Chinese). [Google Scholar]
- Song, D.; Zhou, C. Numerical simulation of Transient Internal Flowfields of Solid Rocket Motor. J. Proj. Rocket. Missiles Guid. 2010, 30, 147–149. (In Chinese) [Google Scholar]
- Wei, T. Study on Combustion Chamber Flow Field of Solid Fuel Ramjet. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2012. (In Chinese). [Google Scholar]
- Su, T. Analysis and Numerical Simulation of a Solid Rocket Booster Flow Field. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2016. (In Chinese). [Google Scholar]
- Gueyffier, D.; Roux, F.X.; Fabignon, Y.; Chaineray, G.; Lupoglazoff, N.; Vuillot, F.; Hijlkema, J.; Alauzet, F. Accurate Computation of Grain Burning Coupled with Flow Simulation in Rocket Chamber. J. Propuls. Power 2015, 31, 1761–1776. [Google Scholar] [CrossRef]
- Li, Q.; He, G.Q.; Liu, P.J.; Li, J. Coupled simulation of fluid flow and propellant burning surface regression in a solid rocket motor. Comput. Fluids 2014, 93, 146–152. [Google Scholar] [CrossRef]
- Zhou, W.; Xie, F.; Li, S. Coupled Simulation of Internal Flow Field and Burning Surface Regression in a Single-Pulse Solid Attitude Control Motor. J. Propuls. Technol. 2019, 40, 107–114. (In Chinese) [Google Scholar]
- Han, W. Simulation of the Transient Internal Flow of SRM with the Grain Surface Regression Based on Level-Set Method. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2016. (In Chinese). [Google Scholar]
- Wang, G.; Li, D.; Han, W.; Zhang, Y. Simulation of Transient Internal Flow Field of Solid Rocket Motor Based on Level-set Method. Acta Armament. 2017, 38, 1520–1531. (In Chinese) [Google Scholar]
- Zhang, Y. Simulation of Working Process of SRM with Complex Grain Based on Porous Media Model. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2018. (In Chinese). [Google Scholar]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Sotiropoulos, F.; Yang, X. Immersed boundary methods for simulating fluid–structure interaction. Prog. Aerosp. Sci. 2014, 65, 1–21. [Google Scholar] [CrossRef]
- Tran, P.H.; Plourde, F. Computing compressible internal flows by means of an Immersed Boundary Method. Comput. Fluids 2014, 97, 21–30. [Google Scholar] [CrossRef]
- Tran, P.H.; Plourde, F. Application of immersed boundary technique in SRM simulations: Toward new insights. In Proceedings of the AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Hirose, T.; Ogawa, S.; Sasaki, D.; Fukushima, Y.; Obayashi, S. Application of Immersed Boundary Method with Wall Injection for Solid Rocket Motor Internal Flow. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Lin, Q.; Jiang, K.; Wang, H.; Wang, J. Application of immersed boundary method to the simulation of transient flow in solid rocket motors. Aerosp. Sci. Technol. 2021, 119, 107228. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Jiang, K.; Wang, H. Application of immersed boundary method to the simulation of three-dimensional flow in solid rocket motors. AIP Adv. 2023, 13, 065016. [Google Scholar]
- Yuan, C. Numerical Simulation of SRM Grain Regression and Flow Field Based on Immersed Boundary Method. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2018. (In Chinese). [Google Scholar]
- Osher, S.; Sethian, J. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamic Implicit Surfaces; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Sethian, J. Level Set Methods and Fast Marching Methods; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Puckett, E.G.; Almgren, A.S.; Bell, J.B.; Marcus, D.L.; Rider, W.J. A High-Order Projection Method for Tracking Fluid Interfaces in Variable Density Incompressible Flows. J. Comput. Phys. 1997, 130, 269–282. [Google Scholar] [CrossRef]
- Rudman, M. Volume-tracking methods for interfacial flow calculations. Int. J. Numer. Methods Fluids 1997, 24, 671–691. [Google Scholar] [CrossRef]
- Willcox, M.A.; Brewster, M.Q.; Tang, K.C.; Stewart, D.C. Solid Propellant Grain Design and Burnback Simulation Using a Minimum Distance Function. J. Propuls. Power 2007, 23, 465–475. [Google Scholar] [CrossRef]
- Jiao, X. Face offsetting: A unified approach for explicit moving interfaces. J. Comput. Phys. 2007, 220, 612–625. [Google Scholar] [CrossRef]
- Qin, F. Algorithm Research on Burning Surface of Complex Charge for Solid Rocket Motor. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2003. (In Chinese). [Google Scholar]
- Wei, R.; Bao, F.; Liu, Y.; Hui, W. Combined Acceleration Methods for Solid Rocket Motor Grain Burnback Simulation Based on the Level Set Method. Int. J. Aerosp. Eng. 2018, 2018, 4827810. [Google Scholar]
- Oh, S.H.; Lee, H.J.; Roh, T.S. Development of a hybrid method in a 3-D numerical burn-back analysis for solid propellant grains. Aerosp. Sci. Technol. 2020, 106, 106103. [Google Scholar] [CrossRef]
- Ren, P.; Wang, H.; Zhou, G.; Li, J.; Cai, Q.; Yu, J.; Yuan, Y. Solid rocket motor propellant grain burnback simulation based on fast minimum distance function calculation and improved marching tetrahedron method. Chin. J. Aeronaut. 2021, 34, 208–224. [Google Scholar] [CrossRef]
- Dunlap, R.; Hermsen, R.W.; Willouchby, P.G. Flowfield in the Combustion Chamber of a Solid Propellant Rocket Motor. AIAA J. 1974, 12, 1440–1442. [Google Scholar] [CrossRef]
- Wu, X.; Chen, J.; Wang, D. Principles of Solid Rocket Engines; Ordnance Industry Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Harten, A.; Lax, P.D.; Van Leer, B. On upstream differencing and Godunov-type scheme for hyperbolic conservation laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Batten, P.; Leschziner, M.A.; Goldberg, U.C. Average-state Jacobians and implicit methods for compressible viscous and turbulent flows. J. Comput. Phys. 1997, 137, 38–78. [Google Scholar] [CrossRef]
- Ghias, R.; Mittal, R.; Dong, H. A sharp interface immersed boundary method for compressible viscous flows. J. Comput. Phys. 2007, 225, 528–553. [Google Scholar] [CrossRef]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Dadone, A.; Grossman, B. Ghost-Cell Method for Inviscid Two-Dimensional Flows on Cartesian Grids. Comput. Fluids 2007, 36, 1513–1528. [Google Scholar] [CrossRef]
- Matsumura, Y.; Jackson, T.L. Numerical simulation of fluid flow through random packs of cylinders using immersed boundary method. Phys. Fluids 2014, 26, 043602. [Google Scholar] [CrossRef]
- Xiao, W.; Mao, C.; Jin, T.; Luo, K.; Fan, J. Fully resolved simulation of a shockwave interacting with randomly clustered particles via a ghost-cell immersed boundary method. Phys. Fluids 2020, 32, 066105. [Google Scholar] [CrossRef]
- Mortimer, F.; Fairweather, M. Assessment of behavioral modification techniques through immersed boundary method simulation of binary particle interactions in isotropic turbulence. Comput. Fluid 2021, 33, 073307. [Google Scholar] [CrossRef]
- Cai, S.G.; Mozaffari, S.; Jacob, J.; Sagaut, P. Application of immersed boundary based turbulence wall modeling to the Ahmed body aerodynamics. Phys. Fluids 2022, 34, 095106. [Google Scholar] [CrossRef]
- Li, C.; Bale, R.; Wang, W.; Tsubokura, M. A sharp interface immersed boundary method for thin-walled geometries in viscous compressible flows. Int. J. Mech. Sci. 2023, 253, 108401. [Google Scholar] [CrossRef]
- Wang, X.; Deiterding, R.; Liang, J.; Cai, X.; Zhao, W. A second-order-accurate immersed boundary ghost-cell method with hybrid reconstruction for compressible flow simulations. Comput. Fluids 2022, 237, 105314. [Google Scholar] [CrossRef]
- Choung, H.; Saravanan, V.; Lee, S.; Cho, H. Nonlinear weighting process in ghost-cell immersed boundary methods for compressible flow. J. Comput. Phys. 2021, 433, 110198. [Google Scholar] [CrossRef]
- Jiao, X. Volume and Feature Preservation in Surface Mesh Optimization. In Proceedings of the 15th International Meshing Roundtable; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Song, Y. Study on Burning Law of Single Chamber Dual Thrust of Grain for Solid Rocket Motor. Master’s Thesis, Shenyang Ligong University, Shenyang, China, 2017. (In Chinese). [Google Scholar]
- Hasegawa, H.; Tokudome, S.I.; Hanzawa, M.; Kohno, M. Erosive Burning of Aluminized Composite Propellants: X-ray Absorption Measurement, Correlation, and Application. J. Propuls. Power 2006, 22, 975–983. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).