A Time Series Prediction-Based Method for Rotating Machinery Detection and Severity Assessment

Abstract

Monitoring the condition of rotating machinery is critical in aerospace applications like aircraft engines and helicopter rotors. Faults in these components can lead to catastrophic outcomes, making early detection essential. This paper proposes a novel approach using vibration signals and time series prediction methods for fault detection in rotating aerospace machinery. By extracting relevant features from vibration signals and using prediction models, fault severity can be effectively quantified. Our experimental results show that the proposed method has potential in early fault detection and is applicable to various types of bearing faults and the different statuses of these faults under complex running conditions, achieving very good generalization ability.

1. Introduction

Monitoring the health of rotating machinery is crucial in ensuring the reliability of aerospace systems. Among the components of rotating machinery, rolling bearings are particularly critical, especially in aerospace applications like aircraft engines and helicopter rotors. Effective diagnosis of bearing faults is vital in reducing maintenance costs and enhancing safety within aerospace systems.

Modern aerospace machinery operates under extreme conditions for long periods, making it susceptible to component failure, which poses significant safety risks and can lead to catastrophic outcomes. Vigilance over the health of rotating equipment in aerospace is therefore essential. In recent years, fault diagnosis technology for rotating machinery has developed rapidly. Researchers have conducted many investigations on the condition assessment and diagnosis of rotating machinery faults based on vibration signals [1,2,3,4].

Based on previous research, fault severity assessment techniques can be broadly categorized into signal processing-based methods and learning-based methods [5]. Traditional signal processing techniques involve extracting features from signals obtained from various sources that are related to fault severity estimation and bearing wear assessment. This is achieved by analyzing specific frequencies or calculating indicators that characterize the faults. Well-known methods in this category include Fourier transform, Hilbert transform [6], wavelet transform [7], empirical mode decomposition [8], and related methods.

Since its inception, deep learning has achieved remarkable success in numerous domains and has found extensive applications in engine fault diagnosis. Deep learning methods for fault diagnosis in rotating machinery can be broadly classified into three categories.

The first category focuses on the detection of defect locations or types, with defect classification as the primary objective. This area has produced very promising results. Notable achievements include CNN-LSTM (Convolutional Neural Network-Long Short-Term Memory) with 99.6% accuracy [9], SDAE (Stacked Denoising Auto-encoder) with 99.83% accuracy [10], and EDAE (Ensemble Deep Autoencoder) with 99.15% accuracy [11], among others.

The second category involves the computation of a degradation indicator that quantifies the health of the machine and facilitates the assessment of fault severity. Regression models are often used for this purpose. For example, Shen et al. [12] used a support vector regression (SVR) model to quantitatively estimate fault sizes. It is also possible to treat different levels of defect severity as distinct categories, using classifiers to accomplish the task. Lei et al. [13] used Wavelet Neural Networks (WNNs) as a severity classifier, with input features selected from the most sensitive Intrinsic Mode Function (IMF) obtained via Empirical Mode Decomposition (EMD). The selection criteria were based on the mean and standard deviation of the kurtosis values for data samples of each IMF.

The third category is a hybrid method, and the above two categories of methods were used together. For example, Smith et al. [14] used a correlation-based algorithm to cluster data into separate groups, upon which Principal Component Analysis (PCA) was applied. Faults are detected by calculating Hotelling’s T² statistic, and potential sources of faults are localized by analyzing PCA loadings, which trace the variables contributing most significantly to the T² values. Chang et al. [15] proposed a multi-fault diagnosis method using the Extreme Gradient Boosting (XGBoost) classifier. It identifies up to 20 different fault types based on vibration signals from the Flight Data Recorder (FDR). Additionally, they utilized a health indicator (HI) assessment model, combined with hyperparameter optimization and random search algorithms, to accurately predict the Remaining Useful Life (RUL) of the landing gear.

This study argues that in real-world operational contexts, the severity of mechanical faults inherently exhibits continuous variation, ranging from mild to severe. A significant portion of the existing research in this area has mainly employed methods dedicated to classification. Such classification methods may have certain limitations when deployed in practice. Therefore, this paper attempts to propose an AI-driven approach to establish a degradation metric for rotating machinery failure, with a particular focus on engine vibration signals. The method has good generalizability while maintaining continuity, making it more suitable for practical applications.

This paper is structured as follows: Section 1 introduces the context and current research landscape related to fault detection and estimation in rotating machines. Section 2 elucidates fundamental concepts, including time and frequency domain features, LSTM networks, and the Dynamic Time Warping algorithm. In Section 3, a novel fault detection approach is proposed. Section 4 presents the experimental validation of the proposed method using simulated vibration signals, coupled with a comprehensive analysis of the results. Finally, in Section 5, conclusions are drawn based on the insights gained from the results of the study.

2. Theoretical Fundamental

This section provides an insight into the techniques used in the proposed diagnostic approach.

2.1. Feature Extraction

As bearing failures progress, the mechanical system experiences an increase in vibration intensity, which is manifested in vibration signals. To prevent machine downtime and ensure optimum production efficiency, the challenge is to monitor the severity of the fault in real time to enable timely intervention based on fault trends. It is therefore essential to extract sensitive features that accurately reflect the current condition of the bearing. This step plays a crucial role in subsequent procedures.

In fault diagnosis, it is crucial to utilize the complete information available from vibration signals and filter out the optimal features during the subsequent information processing steps. Therefore, when conducting feature extraction, the extracted features should encompass all commonly used characteristics in signal analysis. In this paper, a range of common features across time, frequency, and statistical domains, as listed in

Table 1. Time domain features [12,16].

Feature	Definition	Domain	Feature	Definition	Domain
RMS	$X_{rms}={\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i^2}\right)}^{\frac{1}{2}}$	Time	CF	$X_{cf}=\max (|x_i|)/X_{rms}$	Time
SRA	$X_{sra}={\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N\sqrt{\left|x_i\right|}}\right)}^2$	Time	IF	$X_{if}=\frac{\max (|x_i|)}{\frac{1}{N}{\displaystyle \sum _{i=1}^N|}{x}_i|}$	Time
KV	$X_{kv}=\frac{1}{N}{\left({\displaystyle \sum _{i=1}^N\frac{x_i-\overline{x}}{\sigma }}\right)}^4$	Time	MF	$X_{mf}=\max (|x_i|)/X_{sra}$	Time
SV	$X_{sv}=\frac{1}{N}{\left({\displaystyle \sum _{i=1}^N\frac{x_i-\overline{x}}{\sigma }}\right)}^3$	Time	SF	$X_{sf}=\frac{X_{rms}}{\frac{1}{N}{\displaystyle \sum _{i=1}^N|}{x}_i|}$	Time
PPV	$X_{ppv}=\max (x_i)-\min (x_i)$	Time	KF	$X_{kf}=\frac{X_{kv}}{{\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i^2}\right)}^2}$	Time
FC	$X_{fc}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{f}_i}$	Frequency	RVF	$X_{rvf}={\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N{(f_i-X_{fc})}^2}\right)}^{\frac{1}{2}}$	Frequency
RMSF	$X_{rmsf}={\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N{f}_i^2}\right)}^{\frac{1}{2}}$	Frequency	Mean	$\overline{x}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i}$	Statistical
Var	$S=\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-\overline{x})}^2}$	Statistical	Std	$\sigma =\sqrt{S}$	Statistical
Max	$\max (x_i)$	Statistical	Min	$\min (x_i)$	Statistical

, were utilized. These features are defined in references [12,16]. Specific features include the root mean square (RMS), square root of amplitude (SRA), kurtosis value (KV), skewness value (SV), peak-to-peak value (PPV), crest factor (CF), impulse factor (IF), margin factor (MF), shape factor (SF), kurtosis factor (KF), frequency center (FC), RMS frequency (RMSF), root variance frequency (RVF), mean, variance, standard deviation, maximum, and minimum.

2.2. Dynamic Time Warping

Dynamic Time Warping (DTW) [17] is a non-linear warping technique that uses dynamic programming to perform time warping and compute distance measures. By establishing a matching path between data points within two correlated time series of arbitrary length, the algorithm assesses the similarity of these sequences. DTW excels at handling time shifts between sequences and demonstrates notable fault tolerance and robustness. Therefore, it has been used as an application in the feature selection phase of rotating bearing fault detection. Experimental results indicate that DTW can improve the accuracy of fault diagnosis while minimizing the number of features, thereby improving the efficiency and effectiveness of fault diagnosis [18].

Assume that the corresponding lengths of the two time series $X=\{x_1,x_2,\dots ,x_n\}$ and $Y=\{y_1,y_2,\dots ,y_m\}$ are $n$ and $m$, respectively. The core principle of DTW revolves around finding an optimal alignment path between $X$ and $Y$. DTW aims to discover an alignment path $P$ that minimizes the total distance between corresponding elements in $X$ and $Y$. To construct $P$, we define a set of conditions: the path starts at the first elements of both sequences $(i_1,j_1)=(1,1)$, ends at the last elements $(i_k,j_k)=(n,m)$, and adheres to monotonically increasing indices, where $i_1\le i_2\le \dots \le i_k$ and $j_1\le j_2\le \dots \le j_k$. The objective is to find the alignment path that satisfies these conditions while minimizing the accumulated cost along the path.

To compute the DTW distance between sequences X and Y, the algorithm employs a dynamic programming approach. It constructs a matrix $D$ with dimensions $n\times m$, initialized with infinity values. The elements $D\left[i\right]\left[j\right]$ represent the cumulatived cost up to the $(i,j)$ element in the alignment path. The computation involves pairwise comparison elements $(x_i,y_j)$ in the sequences and updating the matrix $D$ based on the following formula:

$$D\left[i\right]\left[j\right]=\cos \mathrm{t}(x_i,y_j)+\mathit{min}\{D[i-1]\left[j\right],D\left[i\right][j-1],D[i-1][j-1]\}$$

(1)

Once the matrix is complete, the DTW distance is calculated as $D\left[n\right]\left[m\right]$, which is the optimal cumulative cost of the alignment path.

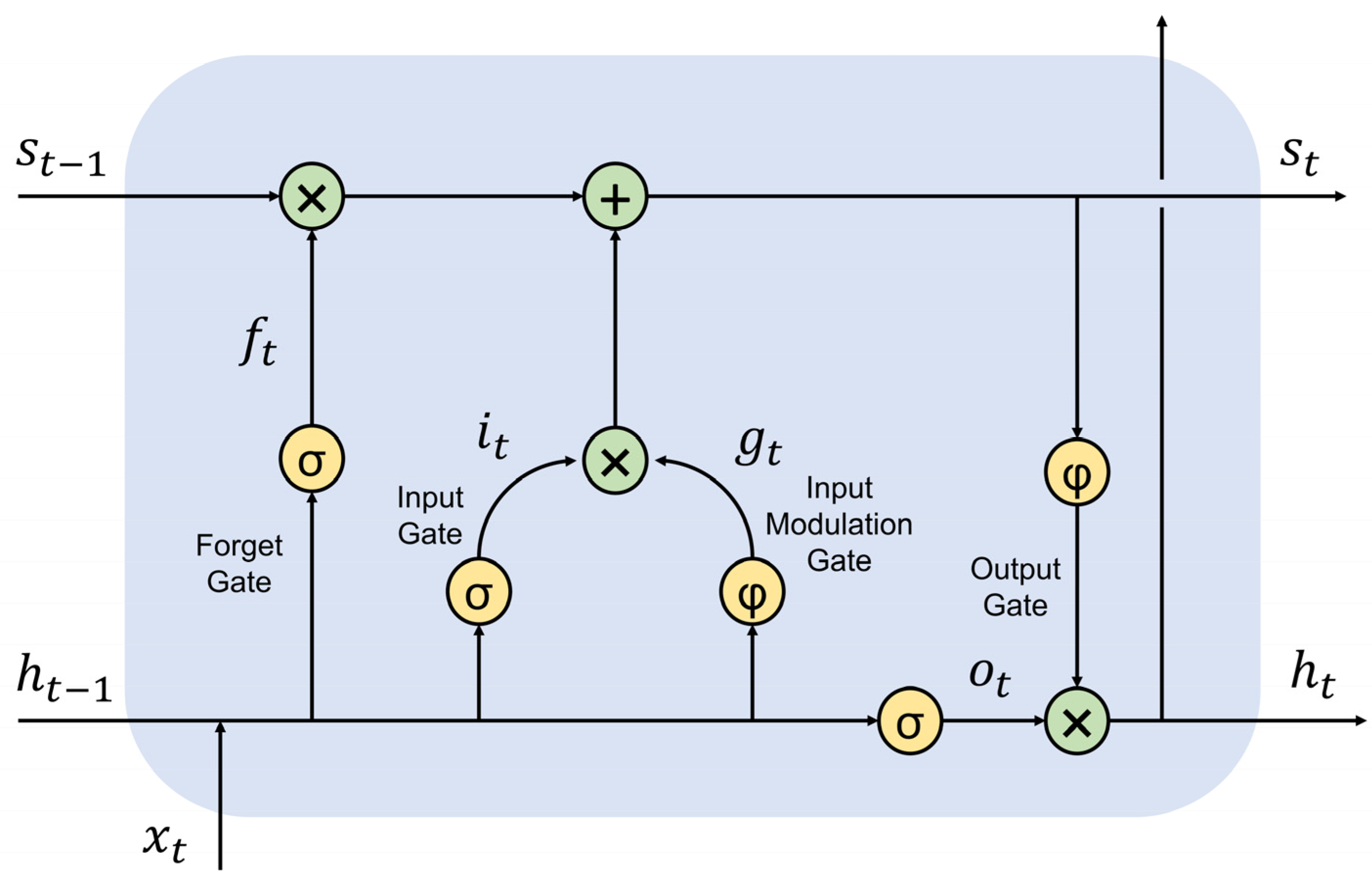
2.3. Long Short-Term Memory

Long Short-Term Memory (LSTM) has demonstrated significant success in the field of speech and images. Engineers extract the acoustic features (mel-frequency cepstral coefficients and log-filterbank energy) of speech and feed them into the LSTM network for natural language modeling [19]. Given this, we fed a specific order of multi-domain features into the LSTM model instead of raw signals for fault diagnosis.

This architecture was introduced by Hochreiter and Schmidhuber in 1997 [20]. The LSTM has demonstrated superior classification and regression capabilities over conventional RNNs on time series datasets, including speech and natural language processing datasets. LSTM contains a memory cell that replaces the role of hidden RNN units. This memory cell contains four gates: the forgetting gate (which determines the extent to which information from the previous cell state is retained), the input gate (which determines whether new information is incorporated into the cell), the input modulation gate (which regulates the amount of information to be written into the cell), and the output gate (which manages the amount of information to be extracted from the cell) [21]. LSTM skillfully maintains error propagation during back-propagation across time and layers

Figure 1 shows a typical LSTM cell, where σ (sigmoid) represents the gate activation function and φ (tanh) represents the input or output node activation. The LSTM model shown in Figure 1 is described by Equation (2).

$$\left\{\begin{array}{l}{f}_t=\sigma (w_{fx}{x}_t+w_{fh}{h}_{t-1}+b_f)\\ i_t=\sigma (w_{ix}{x}_t+w_{ih}{h}_{t-1}+b_i)\\ g_t=\varphi (w_{gx}{x}_t+w_{gh}{h}_{t-1}+b_g)\\ o_t=\sigma (w_{ox}{x}_t+w_{oh}{h}_{t-1}+b_o)\\ s_t=g_t{i}_t+s_{t-1}{f}_t\\ h_t=\varphi \left(s_t\right)o_t\end{array}\right.$$

(2)

where, $w_{gx},w_{ix},w_{fx}$ and $w_{ox}$ are the weights at time $t$ between the input layer and the hidden layer, $w_{gh},w_{ih},w_{fh}$ and $w_{oh}$ are the weights at time $t$ and $t-1$ between the hidden layers, $b_g,b_i,b_f$ and $b_o$ are the biases of the gates, $h_{t-1}$ is the value of the hidden layer at time $t-1$, $f_t,g_t,i_t$ and $o_t$ are the output values of the forget gate, input modulation gate, input gate, output gate, respectively, and $s_t$ and $s_{t-1}$ are the current state at time $t$ and $t-1$, respectively.

2.4. Modified Z-Score

In the study conducted on the application of neural network methods for signal analysis, the imperative of outlier identification and rectification was paramount to ensure analytical robustness and the integrity of the results. The adoption of the modified Z-score method, as explained in [22], provided a rigorous framework for this purpose. Departing from conventional norms, this method uses the median and the mean absolute deviation (MAD) as its basic estimators, which makes it more suitable for outlier detection in small samples with pseudo-normal distribution data. The formulation of the modified Z-score is mathematically expressed as:

$$M_i=\frac{0.6745(x_i-\tilde{x})}{\mathrm{M}\mathrm{A}\mathrm{D}}$$

(3)

where $\tilde{x}$ denotes the median of the dataset and $\mathrm{M}\mathrm{A}\mathrm{D}=median\left\{\right|x_i-\tilde{x}\left|\right\}$. Iglewicz and Hoaglin (1993) suggested that observations are labeled outliers when $M_i>3.5$ through the simulation based on pseudo-normal observations for sample sizes of 10, 20, and 40 [22].

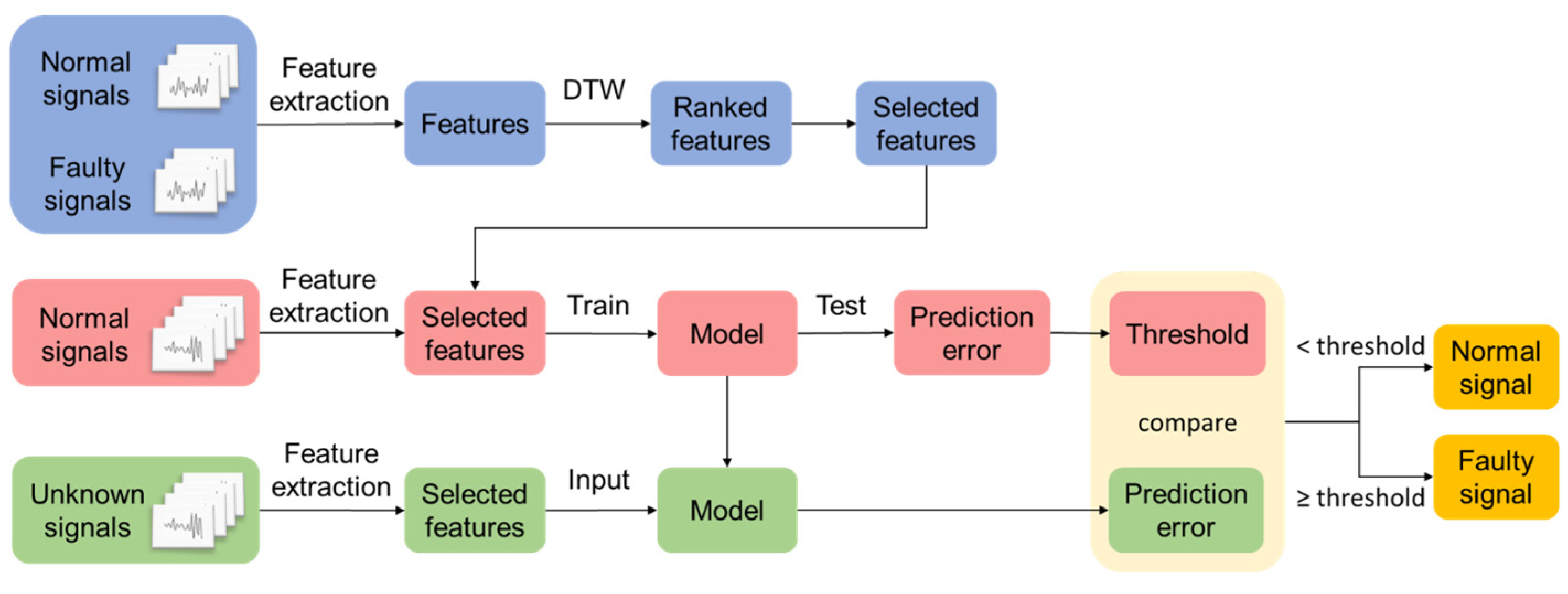
3. Proposed Method

The fault detection method proposed in this paper is rooted in a core concept: the vibration signals of normally operating machines inherently possess a regular pattern. Based on this characteristic, we can establish a time series prediction model based on signals under normal conditions. When unknown signals align with the predictions of the model, we have reason to believe that these signals also originate from the normal operating state of the machine. Conversely, if the unknown signals significantly deviate from the model’s predictions, this serves as a clear indicator that the machine may have encountered some kind of fault.

The delineation of the proposed bearing fault severity detection method is illustrated in Figure 2.

We wanted to build a time series prediction model to learn the regularity of normal vibration signals. In principle, this model could be any regression model. Due to the powerful multi-input and multi-output capabilities of LSTM, we chose LSTM as our prediction model in this study. The main hypothesis of this work is that higher discriminative power of the fault detection system can be achieved if as much information as possible is extracted from the signal and a subsequent feature selection reduces the final number of features to a reasonable amount and uses these feature sequences for training.

The input signals to the algorithm are denoised, and the exact method of denoising does not matter for the purposes of this paper. All input signals mentioned later will be denoised and will not be specified.

To construct the feature time series, the signal is first converted into multiple samples using a sliding window. Let the original signal be represented by $\{x_1,x_2,...,x_N\}$, where $x_i$ is a vector of dimension $channel$. This is represented as a 2D array of shape $(N,channel)$ in the program. The goal is to transform it into multiple signal segments, with each segment calculating a feature vector.

A sliding window of length $L$ is used to sequentially extract segments from the original signal. To obtain as many samples as possible, the step size of the window is set to 1. Thus, a maximum of $N-L+1$ signal segments can be extracted from the original signal, and the number of segments to be extracted is marked as $piece$. Each signal segment is of length $L$, with the kth sample (signal segment) represented as $\{x_k,x_{k+1},...,x_{k+L-1}\}$, which in the program is a 2D array of size $(L,channel)$. All signal segments together form a 3D array of size $(piece,L,channel)$.

For the multiple signal segments obtained, each being a matrix with length $L$ and dimension $channel$ ($L$ rows by $channel$ columns), a feature value can be calculated from each column of each signal segment so that a signal segment is transformed into a feature vector. Multiple signal segments are then transformed into multiple feature vectors, which are sequentially concatenated to form a high-dimensional feature time series.

As mentioned in Section 2.1, we consider 18 features (listed in Table 1) from the field of signal analysis. It is important to note that the feature calculation formulas mentioned in the paper are only applicable to one-dimensional signals. However, real signal acquisition involves multiple measurement points, with the data from each measurement point constituting a signal channel. Therefore, in practical processing, features should be extracted separately for each channel of the signal. The final feature time series will have dimensions equal to the product of the number of original signal channels and the number of features.

For the input signal, after it is converted into multiple signal segments using a sliding window, each channel of each signal segment can calculate $18\times channel$ features, i.e., each signal segment matrix produces a feature vector with dimensions of $18\times channel$. Thus, each original signal ($N$ rows by $channel$ columns) is transformed into a feature time series ($piece$ rows by $18\times channel$ columns).

If all $18$ dimensions of the feature time series are considered, the dimensionality of the data becomes too high, making it difficult for the model to converge. Therefore, it is reasonable to select a subset of features for use. Our subsequent experiments also showed that the use of filtered features accelerated the convergence speed of model training. Since the goal is to reflect the presence of faults through prediction accuracy, the appropriate features should show significant differences between the feature time series generated by normal signals and those generated by fault signals. Assuming that we have normal signals and some known “reference fault signals” from faulty machines, we extracted all possible features from both normal and fault signals and calculated the similarity for each corresponding feature one by one. The feature with the lowest similarity is the appropriate feature.

Similarity selection uses the Dynamic Time Warping (DTW) algorithm to calculate the DTW score for each column between two feature matrices. It is worth noting that for a given feature (such as the mean), since a sequence is calculated on each channel (assuming there are three channels, there would be chn1_Mean, chn2_Mean, and chn3_Mean), each channel will have a corresponding DTW score. We take the sum of the scores from each channel as the final score for that feature.

Sorting the features in descending order of score gives the order in which the features should be used. In general, selecting the first feature is sufficient to discriminate between normal and erroneous signals.

It should be pointed out that using the DTW score to measure similarity and determine the most suitable features is a relative standard, not an absolute one. It identifies which features are more or less suitable compared to others. If multiple features exhibit high DTW scores, they are all considered appropriate, and the choice should then be based on which feature contributes to better model convergence. Conversely, if all features show low DTW scores, this indicates that the normal and fault signals are very similar in their data representations, suggesting that our method may not be applicable in such scenarios. However, such cases are exceptionally rare.

Assuming that only one feature that has the highest DTW score is selected, the next step is to construct a feature sequence sample of normal signals for the sequence prediction model to learn the temporal information of this feature sample. Here, LSTM is used as the sequence prediction model.

Again, a sliding window is applied to extract feature sequence sample matrices from the feature matrix of normal signals to train the LSTM model. The LSTM model aims to predict the values of the next $p$ points (feature vectors) based on the previous $m$ points (feature vectors) in the sequence. Therefore, the length of the sliding window, marked as $fL$, is set to $fL=m+p$. The sliding step size remains at 1. The training dataset must contain at least $fpiece$ samples; therefore, the length of the feature time series, $piece$, must be greater than or equal to $fL+fpiece-1$.

Each feature sequence sample is a matrix of $fL$ rows by $channel$ columns (if two features are selected, it would be $channel\times 2$ columns), with the first $m$ rows by $channel$ columns as input and the subsequent $p$ rows by $channel$ columns as output for that sample. Training is performed with a total of $fpiece$ samples.

After training is complete, the feature sequence samples of normal signals used for training are fed into the model, yielding a set of normal MAEs that represent the distribution of MAE generated by normal signals after prediction. The same method is applied to other normal signals and the MAEs obtained should conform to this distribution. The MAEs generated by abnormal signals do not conform to this distribution, i.e., the MAEs of abnormal signals are considered outliers compared to the normal MAEs.

The modified Z-score is widely regarded as an efficient method for outlier detection, particularly when it comes to handling non-normal data distributions [22]. Experiments indicate that the normal MAEs follow a non-normal distribution, making the modified Z-score suitable for our method. However, our goal is not to identify outliers within a data set but rather to determine whether a set of unknown MAEs fits the distribution of another set of MAEs. Therefore, we need to adapt the modified Z-score method by calculating a threshold determined by the normal MAEs. By comparing the unknown MAEs to this threshold, we can determine whether they are outliers.

The original definition of the modified Z-score has already been described in Section 2.4. A feasible criterion for being classified as an outlier is $\left|M_i\right|=\left|\frac{0.6745(x_i-\tilde{x})}{MAD}\right|>3.5$, which is equivalent to $\left|x_i-\tilde{x}\right|>\frac{3.5MAD}{0.6745}$, where $x_i$ is the unknown MAE to be judged and $\tilde{x}$ is the median of the normal MAEs. Considering that only an excessively large unknown MAE is deemed a fault, it can be asserted that $x_i>\tilde{x}$. Therefore, the threshold given by the modified Z-score is:

$$\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}=\tilde{x}+\frac{3.5MAD}{0.6745}$$

where $\tilde{x}$ is the median of the normal MAEs and MAD is the median absolute deviation of the normal MAEs, calculated as $MAD=\underset{x_i\in \mathrm{normal\; MAE}}{\mathrm{median}}\left\{\right|x_i-\tilde{x}\left|\right\}$.

For the unknown signals to be tested, feature sequences are extracted in the same way as in the training phase and fed into the time series prediction model to obtain the corresponding MAE. In effect, each fault signal is divided into several samples, resulting in a set of MAEs. This set of MAEs is compared to the threshold provided by the modified Z-score. If the average of these MAEs exceeds the threshold, or if the proportion of MAEs exceeding the threshold reaches a certain level (e.g., 50%), then the unknown signal is said to be abnormal. Otherwise, it is considered normal.

For the analysis of run-to-failure data collected from continuously operating machinery, the initial sampling serves as the reference normal signals. The reference fault signal can be filled with a known fault signal under similar operating conditions. Each sampled signal is diagnosed in the aforementioned manner, and the first sample identified as abnormal is considered the point of failure occurrence, thus determining the result of fault detection.

4. Experiment Validation

This section presents the dataset used in the experiments and validates the effectiveness of the proposed method through experimental evaluations.

4.1. Case Western Reserve University Bearing Data (CWRU)

4.1.1. Description

The bearing fault dataset provided by the Case Western Reserve University (CWRU) Bearing Data Center [23] focuses on the fault diagnosis of engine bearings and provides rich laboratory-level fault diagnosis data by simulating various types of bearing defects, such as inner race defects, outer race defects, and rolling element defects, serving as an important resource in the field of bearing fault analysis.

The data used in this research came from two bearings installed in an engine-driven mechanical system, one at the drive end of the engine and the other at the fan end. In both bearings, three types of defects (outer race, inner race, and ball defects) were introduced using electro-discharge machining with different defect diameters. In the case of the outer ring defects, tests were carried out on both fan and drive end bearings with outer ring defects located at 3 o’clock (directly in the load zone), 6 o’clock (perpendicular to the load zone), and 12 o’clock. Each bearing was tested at four different loads, 0, 1, 2, and 3 hp.

After collecting data with a 16-channel DAT recorder, they were processed in the MATLAB environment, and all data files were saved in MATLAB (.mat) format. Each file includes one or more recordings of DE (Drive-end), FE (Fan-end), and BA (Normal-baseline) acceleration data, collected at sampling frequencies of 12 kHz and 48 kHz. In our experiments, only DE and FE data were used, with them being treated as two channels of a test dataset.

A more detailed description of the experimental setup and the equipment involved can be found on the Case Western Reserve University website [23].

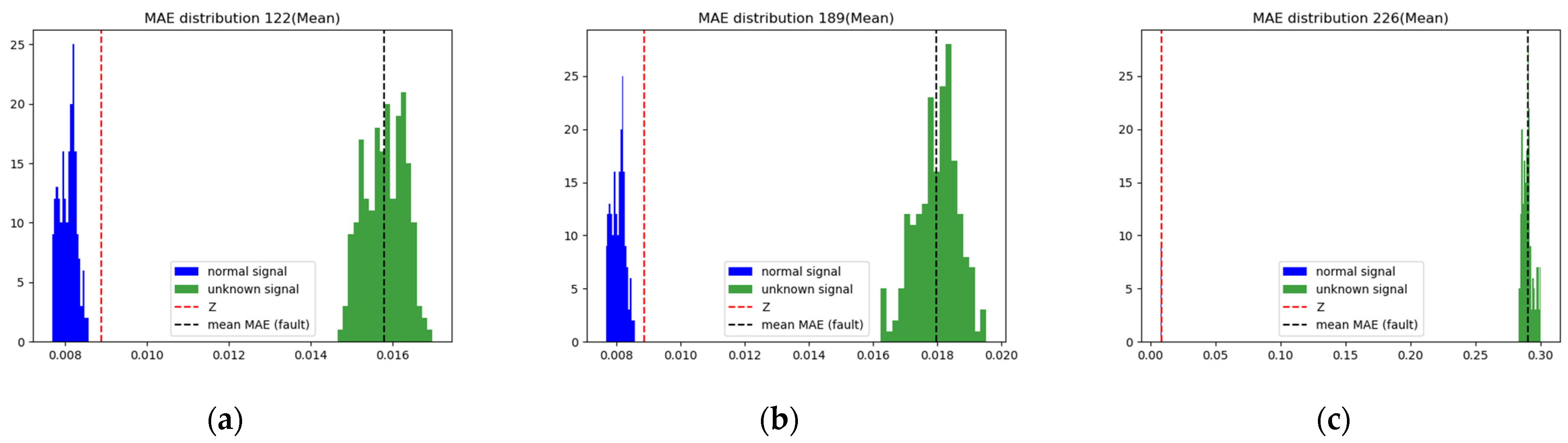
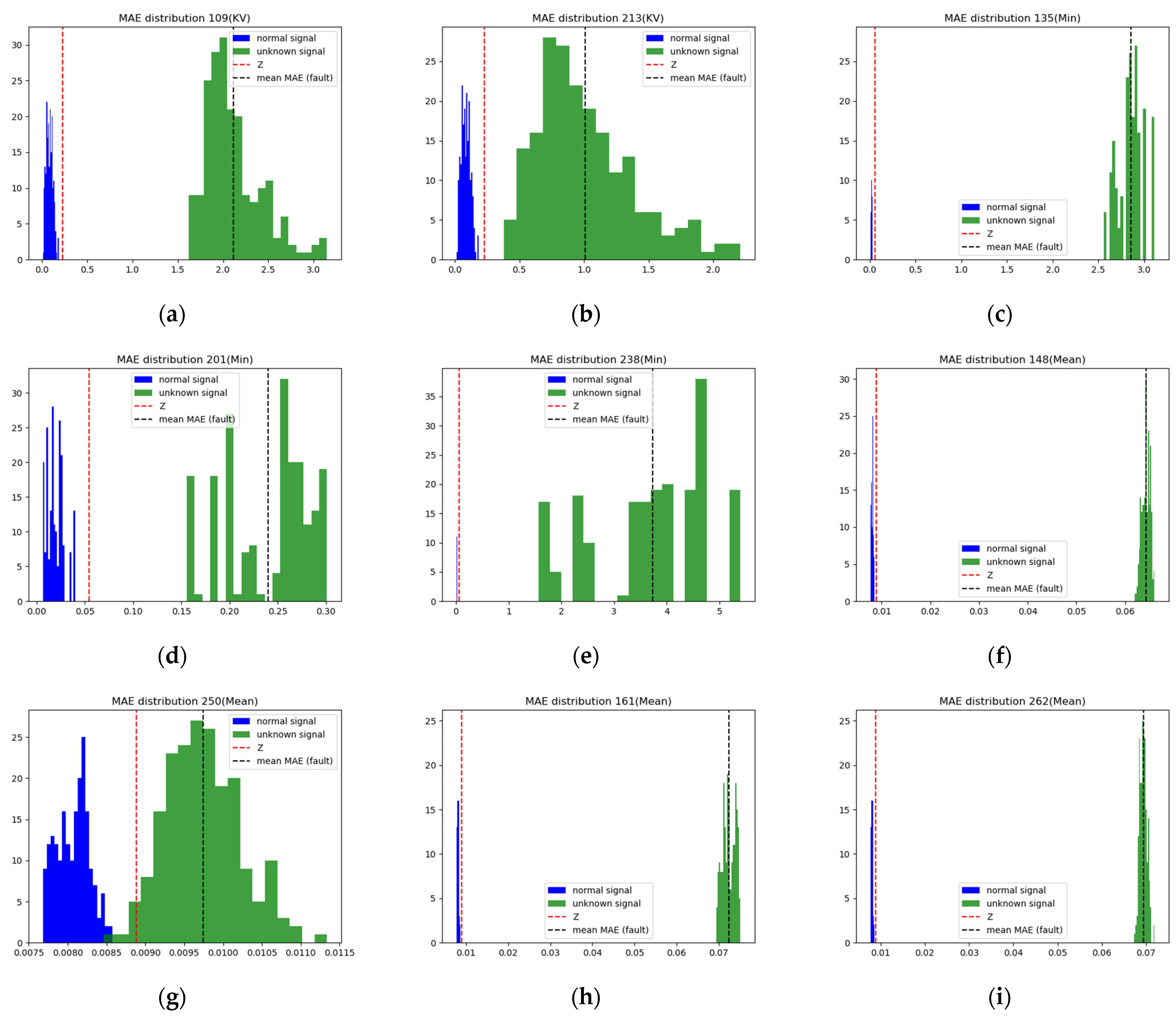
4.1.2. Result

This dataset provides signals under different operating conditions and fault situations, with each signal measured at a constant fault level. In order to verify the effectiveness of the method proposed in this paper in diagnosing faults, the normal signal with a motor load of 0 (approx. motor speed 1797 rpm) numbered 97 and signals numbered 109–262 in different fault situations from the drive side with the same motor load and sampling frequency of 48 k were used, as listed in

Table 2. 48 k drive end bearing fault data.

Fault Diameter	Inner Race	Ball	Outer Race (Position 6:00)	Outer Race (Position 9:00)	Outer Race (Position 12:00)
0.007″	109	122	135	148	161
0.014″	*	189	201	*	*
0.021″	213	226	238	250	262

* No data available for this case

.

The important hyperparameter settings in the algorithm are shown in

Table 3. Hyperparameter setting.

Parameter	Value	Parameter	Value
L	2048	m	100
piece	22,000	p	10
fL	110	fpiece	200

.

Taking signal 97 as the normal signal and 226 as the reference fault signal, feature sequences are extracted separately. The DTW scores are calculated for each column of the feature sequences and ranked in descending order. The higher the ranking, the greater the difference between the feature in the normal and fault signals, making it suitable for further processing. It is important to note that these scores are only indicative and that other factors, such as the convergence of the prediction model, should also be considered when determining the actual features to be used.

The top 10 features are shown in

Table 4. DTW scores of different features.

Feature	DTW Score	Feature	DTW Score
Mean	29.77	Var	17.63
RVF	19.87	KF	17.51
RMSF	19.70	Min	17.31
SRA	18.11	FC	17.09
RMS	17.85	MF	16.99

. Ultimately, the mean value (Mean) would be selected as the feature used in the prediction model. Since 226 represents the highest level of ball failure, this score ranking implies that “Mean” is suitable for use in this method to detect different levels of ball failure, with this score ranking implying that the mean value feature is suitable for detecting different degrees of faults in the algorithm proposed in this paper.

We used the Mean feature sequence extracted from normal signals to train an LSTM as a time series prediction model. After obtaining the model, for each type of fault signal, we also extracted the Mean feature sequence, fed it into the LSTM to obtain the corresponding MAE (Mean Absolute Error), and compared it with the MAE distribution of normal signals and the calculated threshold, plotting the comparison in a histogram as in Figure 3.

In Figure 3, the blue and green sections represent the distributions of the MAE (Mean Absolute Error) for normal and test signals, respectively, as determined by the algorithm. The red dashed line indicates the threshold calculated on the basis of the MAE of normal signals, where MAEs exceeding this threshold are considered anomalies, indicating that the signals from which these MAEs arise are abnormal compared to normal signals. The black dashed line represents the average MAE of the test signals, with values above the threshold used as the criterion for declaring an error.

It can be seen from the graph that the MAE distribution of the signals from each fault level is generally much higher than that of the normal signals and, of course, exceeds the threshold set based on the Z-score. Although only the highest fault level, signal 226, was used during training, signals 122 and 189 are completely unknown to the algorithm, yet it can still accurately detect faults.

The same approach was used for inner ring and outer ring defects in three different orientations, with the results shown in

Table 5. CWRU failure signals test result.

Fault Type	Inner Race	Outer Race (Position 6:00)	Outer Race (Position 9:00)	Outer Race (Position 12:00)
Reference fault signal	213	238	250	262
Best feature	KV	Min	Mean	Mean
DTW score of the best feature	17.67	18.50	17.07	16.11

and Figure 4.

Based on the results of the above experiments, it can be seen that our algorithm can effectively distinguish between normal signals and signals with different degrees of faults. However, it is worth noting that approximately 6% of the Mean Absolute Error (MAE) for the 250th fault signal falls below the threshold. However, considering that the average MAE is above the threshold, it can still be said that the algorithm has detected the fault in this signal.

4.2. Dataset of Intelligent Maintenance Systems (IMS), University of Cincinnati

4.2.1. Description

The bearing fault dataset from the Intelligent Maintenance Systems (IMS) Center at the University of Cincinnati, was collected on an endurance test rig of the University of Cincinnati and released in 2014 [24]. It collects comprehensive data on bearing performance under various operating conditions, which is widely used in bearing fault prediction and health management research. The test rig (shown in Figure 5) has the following characteristics:

• 4 double-row bearings;
• 2000 rpm stationary speed;
• 6000 lbs load applied onto the shaft and bearing by a spring mechanism;
• high-sensitivity Quart ICP accelerometers.

An AC motor, coupled with a rub belt, keeps the rotation speed constant. The four bearings are in the same shaft and are forced lubricated by a circulation system that regulates the flow and temperature.

Three datasets are provided on the downloaded file, composed of numerous files of one second each. Each file is made of 20,480 samples. Although it is mentioned that the sampling frequency is 20 kHz, it is thus believed that it was actually 20.48 kHz. A one-second acquisition is made every 5 (for the first 54 acquisitions) or 10 min, but it is sometimes subjected to a series of interruptions that make the time history not continuous (Figure 6).

The trial was stopped in the conventional way when the build-up of debris on a magnetic plug exceeded a certain level, indicating the possibility of imminent failure. The resulting life was 49,680 min (i.e., 34 days and 12 h), exceeding the bearing’s design life of more than 100 million revolutions. It should be emphasized that this data set is particularly valuable because bearing degradation was allowed to develop naturally and was not artificially induced, as is often carried out to speed up the experimental test.

4.2.2. Results

IMS is a full lifecycle experiment dataset with signals collected from machines operating normally until they stop due to a fault, during which time the fault level gradually increases. With signals from a full lifecycle experiment, it is not possible to make a binary diagnosis of normal or fault as with the CWRU data. Instead, we hoped to calculate the critical point at which the mechanical state deteriorates from normal to fault. The implication is that in real industrial processes when this critical point is reached, the machinery should be shut down for maintenance to prevent more serious damage.

In the IMS dataset experiment, several signal samples are taken during a test, resulting in several segments of vibration signals. The above algorithm is applied to each signal segment in turn, resulting in a corresponding set of MAEs. When the proportion of MAEs above the threshold reaches a certain level, for example, 50% of the sample MAEs above the threshold, the signal segment is considered abnormal. The acquisition time of this signal segment is then identified as the critical point of failure. To demonstrate the reliability of our algorithm, our experimental results will be compared with existing studies on the IMS dataset.

Gousseau et al. [25] utilized the dataset provided by the Center for Intelligent Maintenance Systems (IMS) at the University of Cincinnati, using a comprehensive suite of signal processing techniques such as time-domain analysis, spectral analysis, blind deconvolution, spectral coherence, and envelope spectrum for in-depth diagnostics and prognosis of vibrations in rolling element bearings. Their analysis successfully diagnosed inner race damage in bearing 3 and ball damage in bearing 4 within dataset 1, as well as outer race damage in bearing 1 in dataset 2, while bearing 3 failed to reveal the expected fault characteristics. For dataset 1’s bearing 3, time–frequency analysis detected damage from 33.8 days, envelope spectrum analysis detected it slightly earlier at 32 days and spectral coherence analysis detected it earliest at 29.2 days. For dataset 1’s bearing 4, time–frequency analysis detected damage at 18 days, envelope spectrum analysis showed signs of damage at 25 days, and spectral correlation analysis confirmed the presence of damage at 23 days. In test 2, all methods (time–frequency analysis, envelope spectrum, and spectral correlation) accurately diagnosed damage to the outer ring of bearing 1 at 3.5 days.

Research by Sacerdoti and colleagues [26] involved the use of the first test data from the IMS dataset to evaluate various signal-processing techniques for detecting and locating bearing faults. By comparing the kurtosis values of the diagnostic techniques, they found that Cepstrum Pre-Whitening (CPW) and Improved Envelope Spectrum (IES) performed best in locating and identifying faults. Fault detection focused on bearings 3 and 4, with an inner race fault in bearing 3 detected between the 33rd and 34th day of the experiment while rolling element and outer race faults in bearing 4 were detected from the 26th day.

In order to compare the results with the two aforementioned studies, our experiment uses only dataset 1, excluding bearings 1 and 2, which had no faults, and focusing only on the data from the four channels corresponding to bearings 3 and 4 (as perforemed in [22]).

Table 6. Comparison of bearing fault detection methods.

Study	Bearing 3	Bearing 4
[25]	Time–frequency analysis: 33.8 days (11/23) Envelope spectrum analysis: 32 days (11/22) Spectral coherence analysis: 29.2 days (11/19)	Time–frequency analysis: 18 days (11/8) Envelope spectrum analysis: 25 days (11/15) Spectral coherence analysis: 23 days (11/13)
[26]	Last part of the 33rd day (11/23) and the 34th day (11/24)	From the 26th (11/16) day until the end

presents a comparison of the fault detection results for bearings 3 and 4 from the literature [25,26].

Considering that the machine is certainly normal at the start of operation and that the fault level increases during operation, the signals obtained from the first few samples are considered normal signals, and the signal from the last sample is used as a reference fault signal for validation. Given the long duration of the experiment and the large amount of data, considering only the first normal signal could lead to overfitting. Therefore, during feature selection, the first four signal segments are all considered normal signals, with DTW scores calculated and summed for each. The hyperparameter $fpiece$ is set to 100, with other settings consistent with Section 4.2.1 of the CWRU data experiment.

The results of the experiment are shown in Figure 7.

When more than 50% of the MAE calculated for a signal segment exceeds the threshold based on the Z-score, it is considered that a fault has occurred. Using the method proposed in this paper, the fault occurrence date for bearing 3 was determined to be 22 November, corresponding to the 32nd day after the start of the experiment, and the fault occurrence date for bearing 4 was determined to be 14 November, corresponding to the 24th day after the start of the experiment. 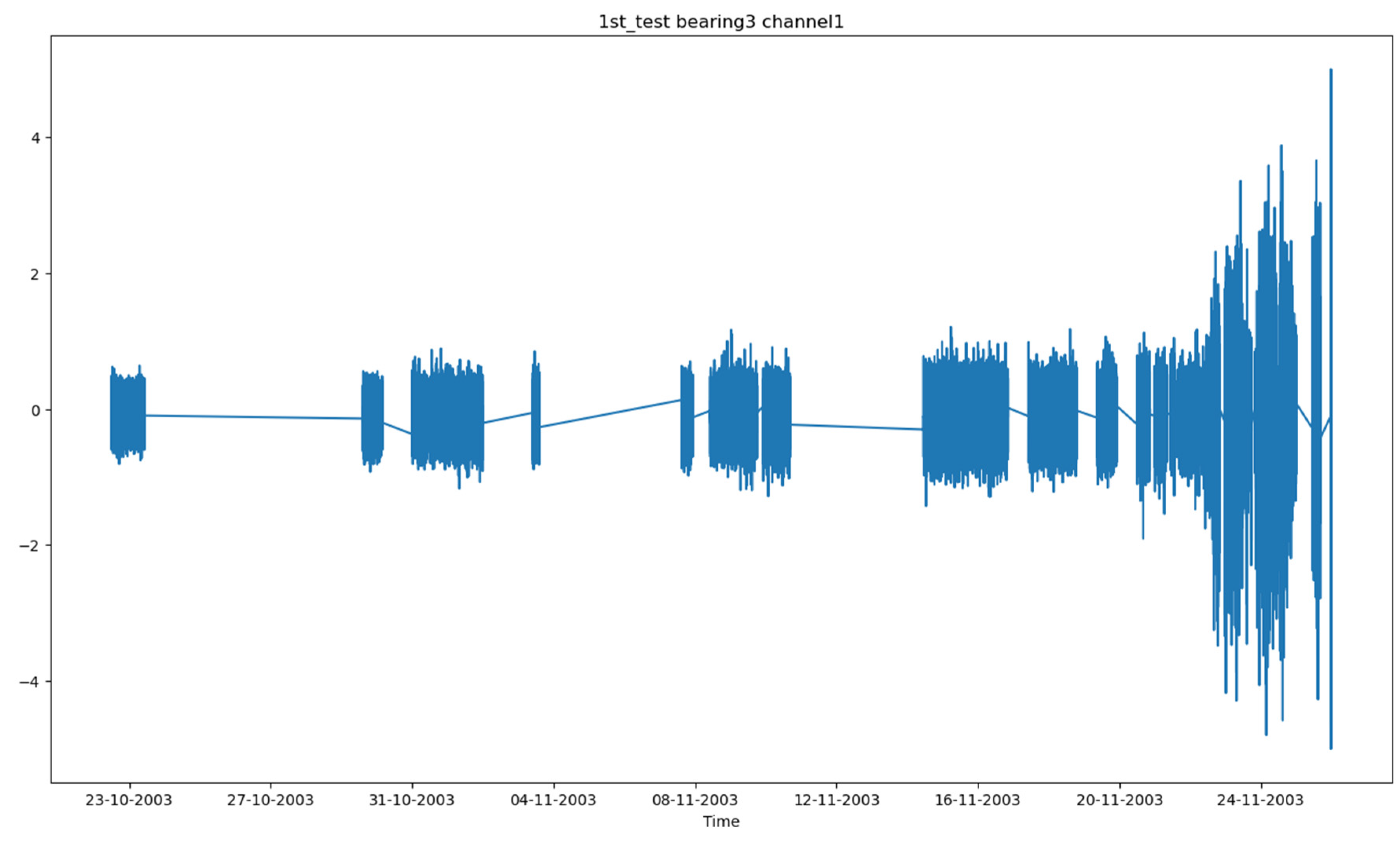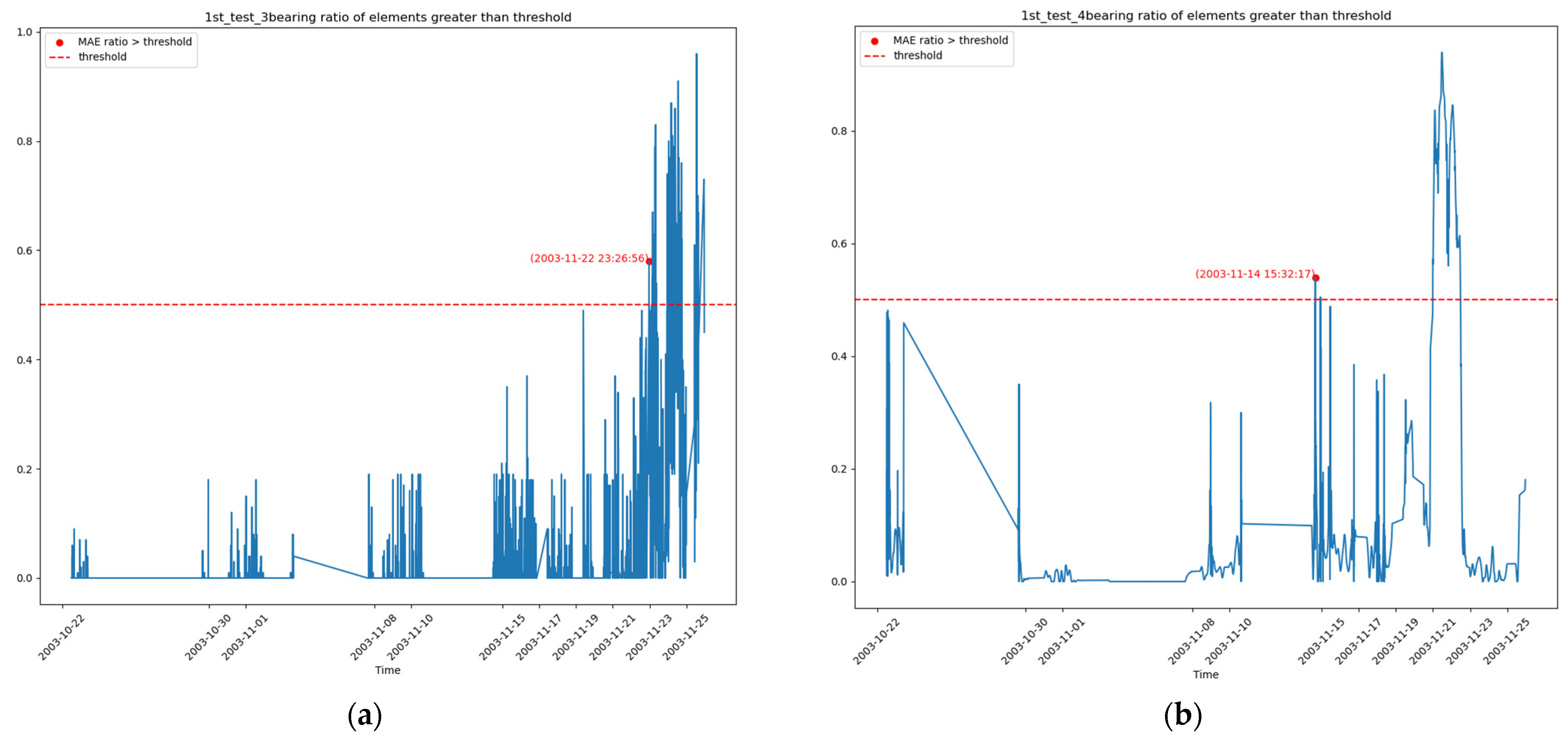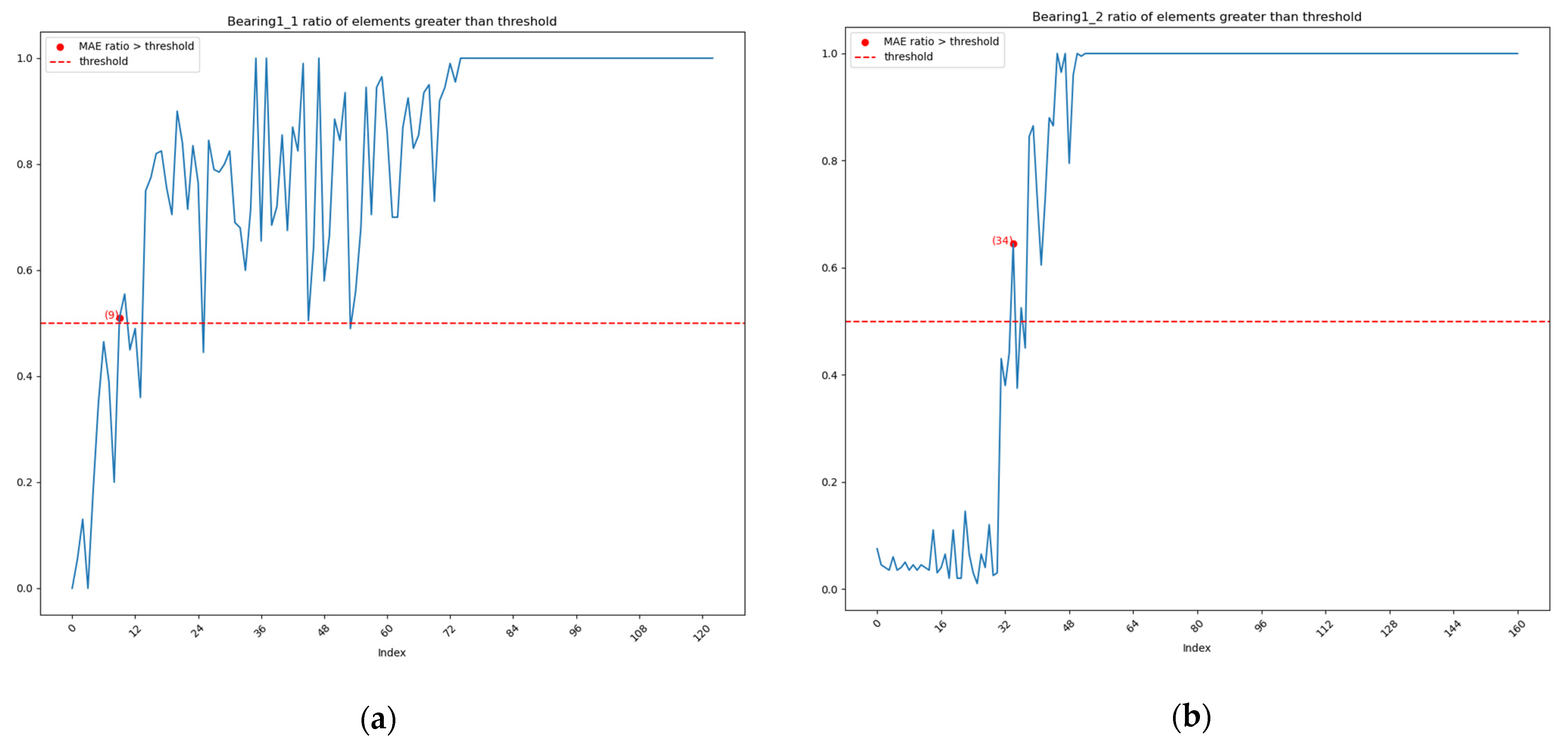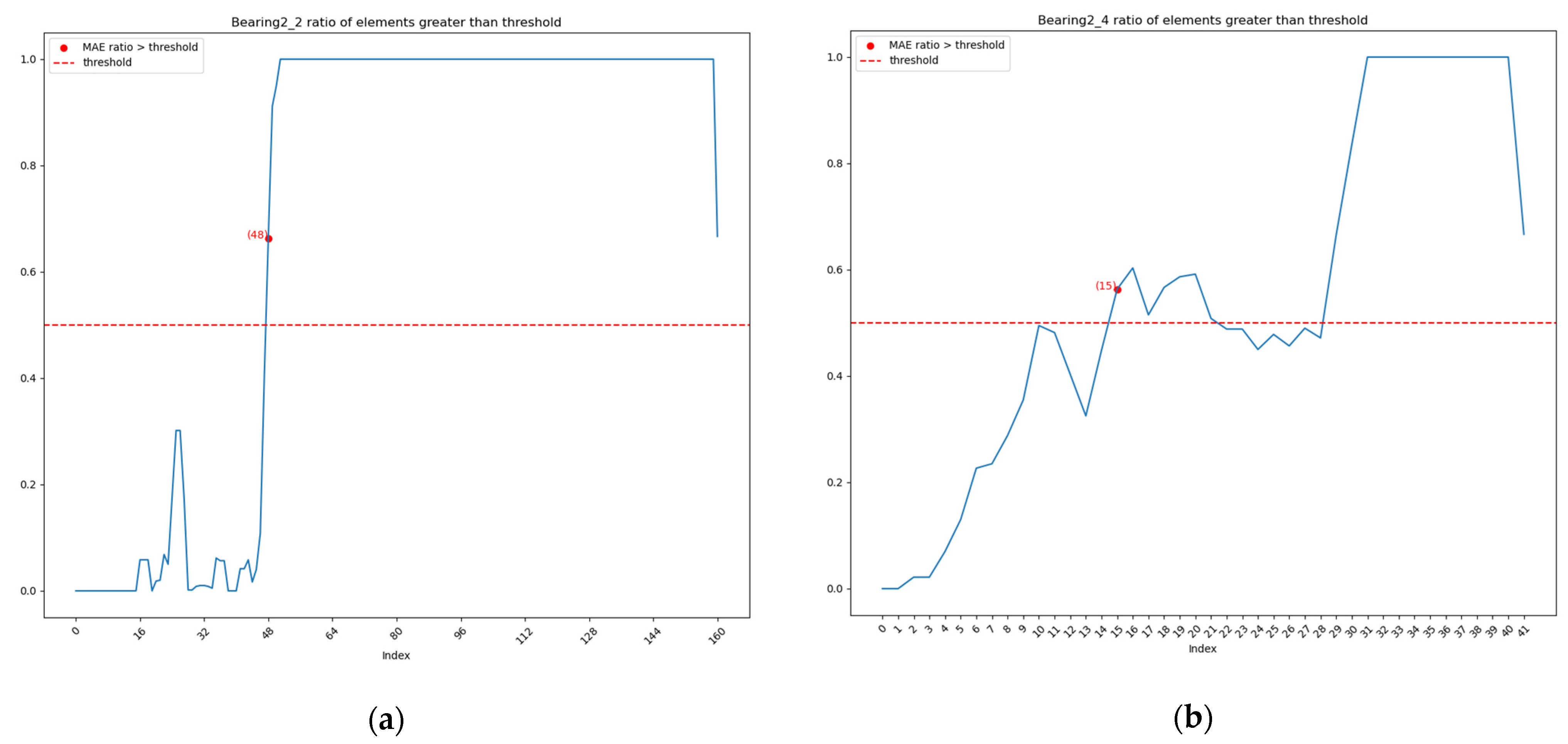These results are 1 to 2 days earlier than those reported in the literature [26] and shorter than a day different from the envelope spectrum analysis results in [25], demonstrating that the method proposed in this paper can indeed effectively detect faults.

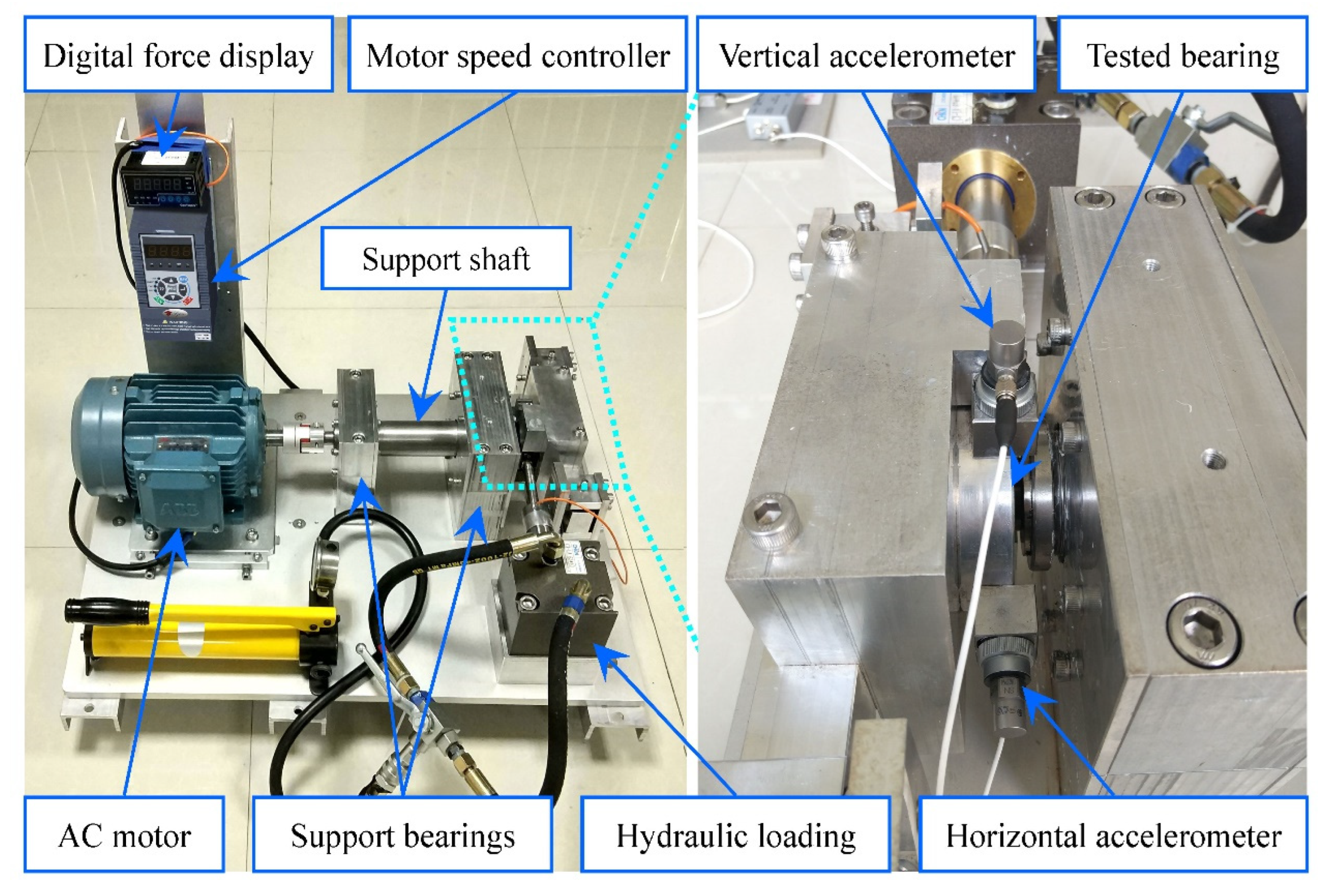
4.3. Xi’an Jiaotong University Bearing Fault Dataset (XJTU-SY)

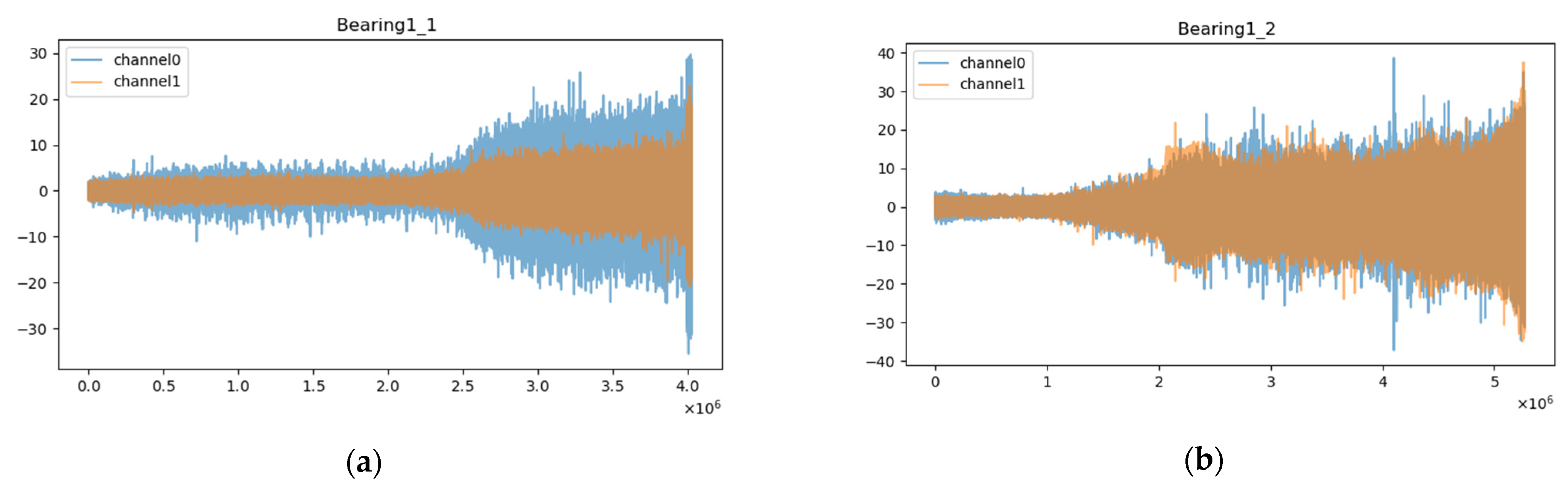
4.3.1. Description

The XJTU-SY dataset, provided by the Institute of Design Science and Basic Component of Xi’an Jiaotong University (XJTU) and Changxing Sumyoung Technology Co., Ltd. (SY), Changxing, China [27], is a bearing fault dataset containing complete run-to-failure data of 15 rolling element bearings. The XJTU-SY bearing dataset was obtained by conducting many accelerated degradation experiments, which is designed to provide more detailed and comprehensive fault mode analysis data to advance fault diagnosis technologies [28].

The bearing testbed includes several key components as shown in Figure 8. This test rig is designed to perform the accelerated degradation tests of rolling element bearings under different operating conditions (i.e., different radial forces and speeds). The radial force is generated by the hydraulic loading system and applied to the housing of the tested bearings, and the speed is set and maintained by the speed controller of the AC induction motor.

The dataset used in this study was based on bearings. The relevant parameters of these bearings are given in

Table 7. LDK UER204 bearing parameters [27].

Parameter	Value	Parameter	Value
Inner race diameter (mm)	29.30	Ball diameter (mm)	7.92
Outer race diameter (mm)	39.80	Number of balls	8
Bearing median diameter (mm)	34.55	Contact angle (°)	0
Basic rated dynamic load (N)	12,820	Basic rated static load (N)	6.65

. To comprehensively evaluate their performance, the experiments were structured around three different operating conditions, as shown in

Table 8. Bearing accelerated life test conditions [27].

Number	1	2	3
Rotational Speed	2100	2250	2400
Radial Force	12	11	10

. For each operating condition, several sets of vibration signals were meticulously collected throughout the life of the bearings. Throughout the experiments, two unidirectional accelerometers were attached to the test bearings using magnetic mounts to ensure secure attachment in both horizontal and vertical orientations. A portable dynamic signal acquisition system was used to record the vibration signals. The sampling frequency was carefully set at 25.6 kHz with a 1 min sampling interval. Each individual sampling session lasted 1.28 s. A detailed interpretation of the dataset can be found in [27].

To obtain a complete time series, the data from each sample are concatenated, resulting in run-to-failure vibration signals. The first two signals are shown in Figure 9. The label Bearing 1_2 means that the data are from the second test in working condition 1, and so on.

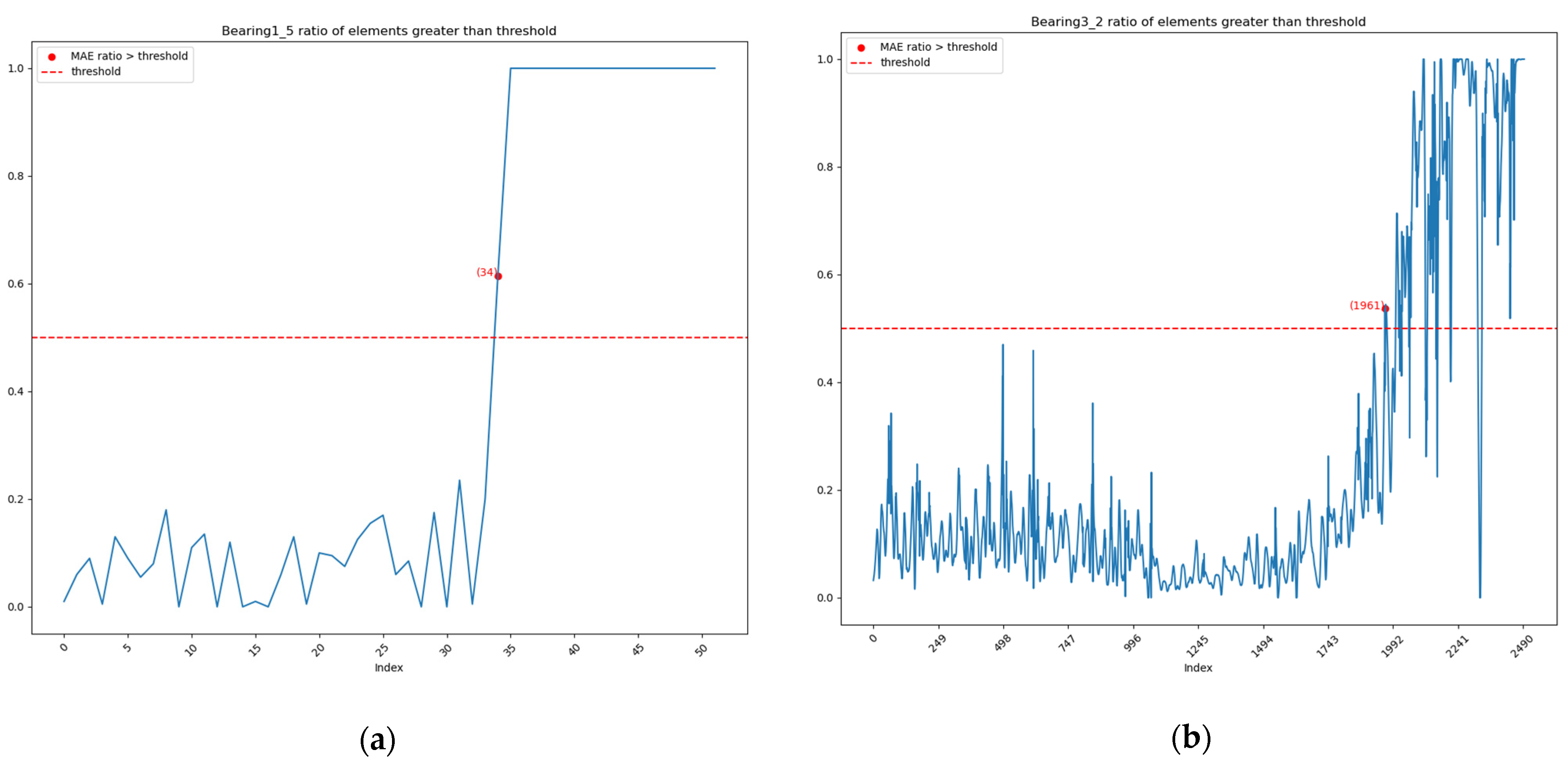
4.3.2. Results

XJTU-SY is another open-source dataset that covers the entire life of the experimental data. The experimental methodology used for the XJTU-SY dataset is exactly the same as that used for the IMS dataset. Three experiments are considered:

(1) Using the data from the first three experiments under operating condition 1 and given that these experiments had the same type of failure, the data from the third experiment (Bearing1_3) are used for feature selection, while the other two experiments are used for testing.

After computation, the most suitable feature was found to be Min with a DTW score of 7.98. The experimental results for Bearing1_1 and Bearing1_2 are shown in Figure 10.

From the graph, it can be seen that Bearing1_1 showed abnormalities as early as the 9th sampling, with the severity of the abnormalities fluctuating initially. By the 73rd sampling, the proportion of abnormal MAE reached 1, at which point it can be considered a complete failure. Bearing1_2 showed abnormalities by the 14th sampling and quickly progressed to complete failure.

(2) Using the data from three outer ring failure experiments under Operating Condition 2, namely Bearing2_2, Bearing2_4, and Bearing2_5, feature selection was performed on Bearing2_5, while the other two were used for testing.

After calculation, the most suitable feature was found to be Meanf with a DTW value of 8.33. The experimental results for Bearing2_2 and Bearing2_4 are shown in Figure 11.

The graph shows that Bearing2_2 showed abnormalities by the 48th sampling, whereas Bearing2_4 showed abnormalities by the 15th sampling and quickly progressed to complete failure.

(3) We used Bearing1_3 (with an outer ring defect) for feature selection and Bearing1_5 (with both inner and outer ring defects) for testing and used Bearing3_3 (with an inner ring defect) for feature selection and Bearing3_2 (with inner ring, rolling element, cage and outer ring defects) for testing. The purpose of this experiment is to demonstrate that the algorithm proposed in this paper remains effective for data with mixed defect types.

The selected features and the results of anomaly detection on the test data are shown in Figure 12.

Bearing1_5 is considered to have developed a fault at the 34th sampling; Bearing3_2 first showed an abnormal MAE ratio near 50% at the 497th sampling, which could be considered a false alarm from the perspective of the whole experiment. This is because the abnormal MAE ratio remained relatively low for a long time after the 1120th sampling and did not rise to 50% until the 1961st sampling.

4.4. Results Analysis

Validation using three different datasets shows that the algorithm proposed in this paper can effectively detect anomalies in vibration signals and has the following advantages:

(1)

Experiments on the CWRU dataset show that the method can perform fault detection tasks with a small number of samples. Although it uses only 0.021 inch diameter defect data for training, it can detect 0.007 and 0.014 inch diameter defects. This feature is particularly suited to real-world industrial environments. In many practical application scenarios, the acquisition of a large amount of labeled data is often costly and time-consuming. Therefore, an algorithm that can effectively use a limited number of samples for accurate detection is of significant practical value. In addition, this method is versatile and can detect a variety of defects, including inner ring defects, outer ring defects, and rolling element defects, all using the same approach.

(2)

Experiments on the IMS dataset demonstrate that this method can be used to monitor the health of rotating machinery and provide timely warnings when the machine exhibits abnormalities. Compared to existing work, our method does not use complex signal analysis techniques, nor does it require manual identification of characteristic lines in spectrograms, yet it detects faults at times similar to or earlier than existing methods. This suggests that the method is more suitable for unsupervised scenarios.

(3)

The experiments conducted on the XJTU-SY dataset confirm the conclusions of the previous two experiments. In experiments (1) and (2) on the XJTU-SY dataset, the data used for testing and the data used for feature selection were not the same, which once again demonstrates that this method can perform defect detection tasks with a small number of samples. Furthermore, despite the different operating conditions in (1) and (2), the method proposed in this paper was able to detect the occurrence of faults, demonstrating its universality. Experiment three (3) shows that this method remains effective even when the fault mode of the unknown signal is a mixture of several faults.

5. Conclusions

This paper presents a novel method for fault detection based on engine vibration signals. The method involves extracting time and frequency domain features from normal signals to build an LSTM time series prediction model. Prediction accuracy is used as a continuous indicator for unknown signals to indicate the presence of faults and the effectiveness of the method is validated by experiment.

The method for rotating machinery fault detection and severity assessment presented in this study offers significant implications for aerospace applications. By providing sensitive and early detection of faults, this method can be effectively applied to rotating machines such as aircraft engines and helicopter rotors. Its robustness and early-warning capabilities will enhance aerospace equipment’s reliability, particularly given the challenging environments.

The advantages of this method are as follows:

(1)

Overcoming the limitations of traditional strategies that categorize fault severity in a discrete manner, this method uses a continuous indicator to indicate fault severity. As a result, it provides greater flexibility in setting thresholds to differentiate defects.

(2)

Thanks to a well-structured algorithmic framework, this method is highly scalable and adaptable. In the feature selection phase, in addition to the 18 features preset in this paper, other new features can be included. In addition to the DTW algorithm used in this paper, other similarity measurement algorithms can be used. During the training phase, other time series prediction models can be used instead of the LSTM network used in this paper. Furthermore, algorithms other than Z-score can be used for outlier detection.

(3)

Only a small amount of fault data were used during training (particularly in the feature selection process), yet the method can still effectively detect faults in unknown signals. Given that fault data collection in real-world engineering environments can be challenging, and typically only a small amount of fault data can be obtained, this method is expected to perform well in real-world production scenarios with limited samples.

The limitations of this work include:

(1)

Training the deep learning model requires a large number of feature time series samples, and obtaining these feature samples requires slicing of the original signals. Therefore, implementing this method requires a sufficient amount of original data, and it may consume significant memory resources during computation.

(2)

Manual feature selection is an insufficient approach for many applications. If features could be extracted adaptively using neural network methods, it would save time and resources while increasing generality.

(3)

The process of feature selection and thresholding lacks standardized criteria and relies on the subjective decisions of researchers. There is a need for more general and robust methods for adaptive decision-making.