3.1. Constraints on Establishing Dynamic Links
In the previous section, three fixed links were established. Now, it is necessary to commence the construction of dynamic temporary links. As we can see in
Figure 6, the red dashed lines in the following diagram represent the dynamic temporary links under discussion.
Based on the current number of lasers equipped on Starlink satellites, it is stipulated that each satellite can only connect to four other satellites with its available lasers. Presently, each satellite can utilize one of these lasers for establishing a dynamic link at any given time; if a laser is connected to another satellite at a particular moment, both satellites cannot connect to any other satellite at that same instant. Thus, the problem can be abstracted into a two-by-two pairing issue between satellites at every moment.
Given the numerous potential connections around each satellite at any given time, the following constraints are necessary to identify the most suitable connections:
The link duration should be maximized to minimize the additional overhead caused by the frequent re-establishment of links.
The link distance must not be excessively large, since smaller distances reduce the signal transmission latency.
Angular velocities between satellites should not exceed maximum thresholds, as frequent angular velocity changes would incur extra energy consumption for altitude adjustments.
Topological changes (re-linking events) should be minimized; ideally, multiple satellites should switch links synchronously. Note that the link duration evaluations should occur after all other constraints are met, i.e., selecting satellites that satisfy all previous conditions before assessing the link duration.
Specifically, to enhance the flexibility of dynamic links and enable interconnection among satellites crossing orbits, it is imperative first to avoid connecting to satellites on adjacent or identical orbits during the selection process for each satellite’s potential connections. Moreover, to achieve a lower latency, reliance solely on “mutual visibility” between satellites for determining connectivity is insufficient, especially when satellites are in close spatial proximity. Therefore, when defining dynamic link connections, it is mandated that the connection distance be less than the maximum distance found in the fixed links. Through an analysis of the fixed links, the longest distance between neighboring orbit satellites over a complete orbital period in the network was found to be 1620.06 km. Consequently, when constraining the relative distance of the dynamic links, satellites within a distance of less than 1620.06 km must be selected to meet the inter-satellite distance constraint.
Additionally, the establishment of dynamic links also necessitates limiting the relative angular velocity to an acceptable maximum. Using the existing Formulas (4) and (5), the elevation angle and azimuth angle between any two satellites can be calculated. From the simulation in the previous section, it is observed that elevation angle variations are generally small and unlikely to exceed limits, especially when satellites are close. Hence, the primary focus is on the azimuth angle. Given its significant variation, based on the previous section’s findings, it is crucial to ensure that the azimuthal angular velocity does not exceed 0.5°/s.
To improve computational efficiency, it is possible to perform azimuth angular velocity filtering on the satellites after completing the orbit and distance filtering. In order to achieve optimal satellite pairing, a satellite state connectivity matrix
can be established based on the constraints outlined in this section.
In order to facilitate the implementation and administration of dynamic link formation, it is essential to document at each discrete time interval the set of satellites with which every individual satellite is capable of establishing a dynamic temporary link.
The matrix is symmetric and initialized with zeros, signifying no initial connections between satellites. Non-zero elements in denote the duration during which corresponding satellites can maintain a connection, subject to specified constraints. If a satellite fails to meet these constraints, the corresponding element in is set to zero. Once the entire orbital cycle’s matrix is constructed, the optimization process involves determining the best matching satellite for each satellite combination at the current time.
3.2. Greedy Algorithm for Dynamic Link Establishment
In the realm of dynamic link problems, ensuring stable and enduring connections is paramount for satellite communication systems. Traditional greedy algorithms [
12] tend to exhibit local optimization, often resulting in inadequate connection durations and, at times, failure to meet communication demands. Greedy algorithms iteratively select satellite combinations based solely on their immediate connection durations, neglecting opportunities for global optimization.
We use
as the matrix for finding the optimal links for each satellite, employing the greedy algorithm approach to search for the optimal link configuration. In
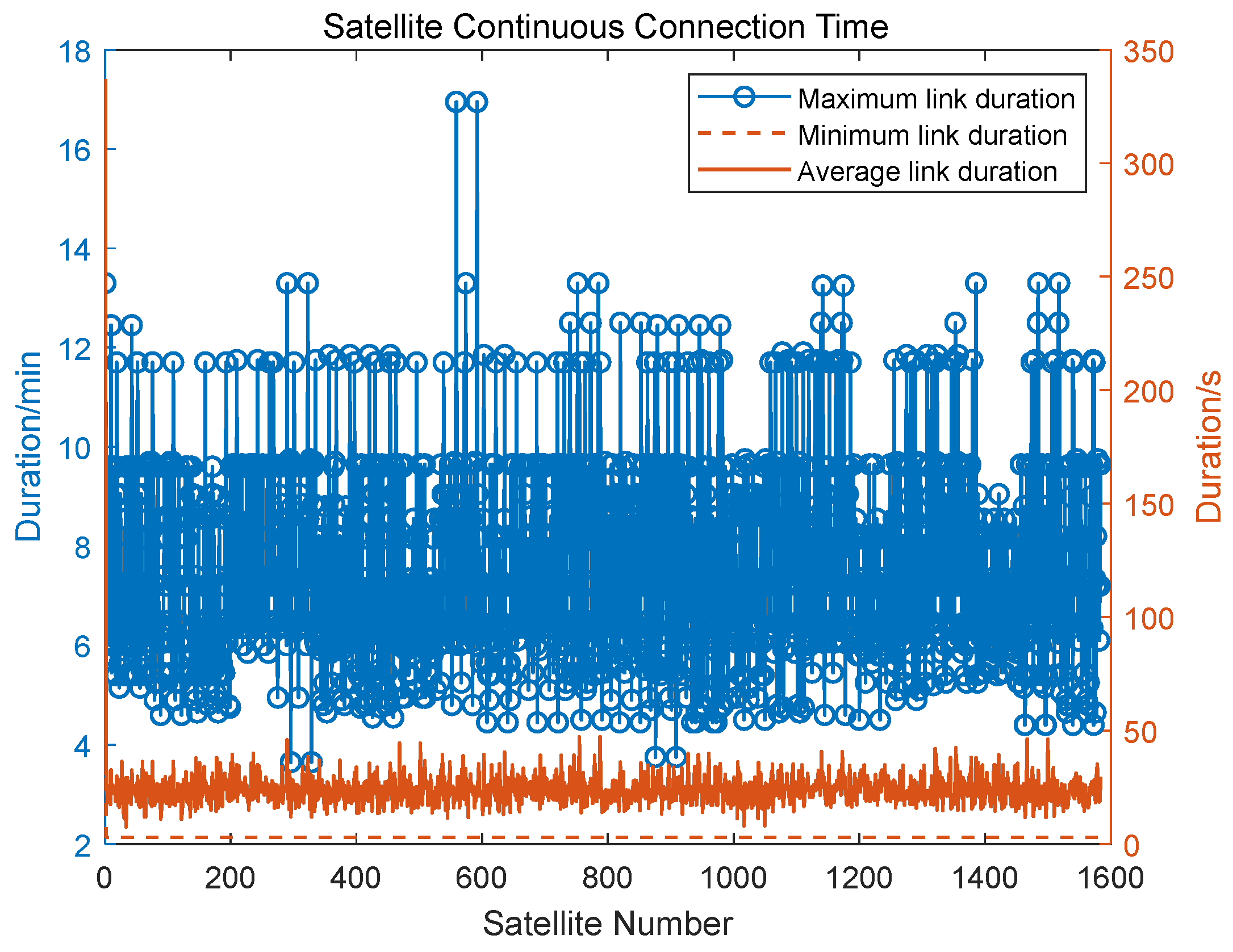
Figure 7, the greedy algorithm is applied to optimize the link durations for each satellite within an orbital cycle. The blue curve illustrates the maximum link duration. Following computation, the greedy algorithm yields an average maximum link duration of 450.74 s (approximately 7.51 min), with an average link duration of 23.96 s. However, the average minimum link duration is merely 3.0852 s, posing potential challenges in establishing stable connections.
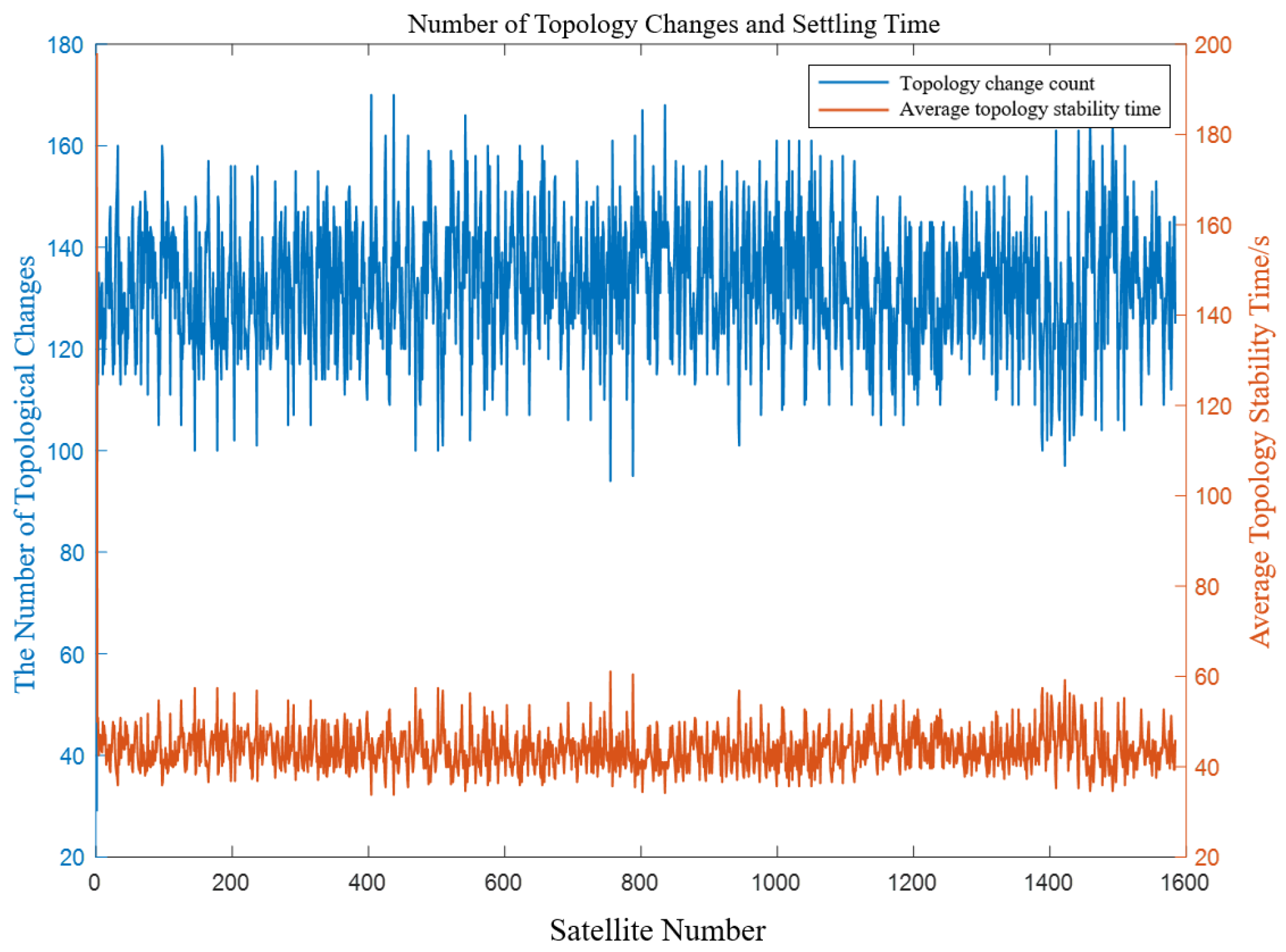
The localized optimization strategy often leads to inadequate connection durations, as depicted in the variations in the satellite topology over the orbital period shown in
Figure 8.
The average number of topological transformations per satellite is approximately 132, and the average stable time for each satellite can be determined using Equation (8), as follows:
According to the orange line in
Figure 8, the average satellite stabilization time is 43.86 s, derived through qualitative calculations for comparison with the mean link duration discussed earlier. Notably, the mean link duration is shorter than the average satellite stabilization time, indicating that most of the satellites exhibit shorter link persistence times. Consequently, the satellite matching obtained via the greedy algorithm tends to result in shorter average durations of unconnected dynamic links, suggesting poorer overall link connectivity on average.
Following this, a cross-sectional analysis was conducted by simulating the number of satellites with unconnected dynamic links per time slot using the greedy algorithm, as depicted in
Figure 9. Throughout a satellite’s orbit period, a substantial number of satellites remain unconnected at any given moment. With a total constellation size of 1584 satellites, the simulation results reveal that the number of satellites in unconnected dynamic links determined by the greedy algorithm ranges from a maximum of 1416 to a minimum of 88, indicating an excessive number of satellites remaining unconnected.
Subsequently, a longitudinal comparison was conducted focusing on simulating the duration within each satellite’s orbital period during which dynamic links remain unconnected, with only permanent fixed links being engaged.
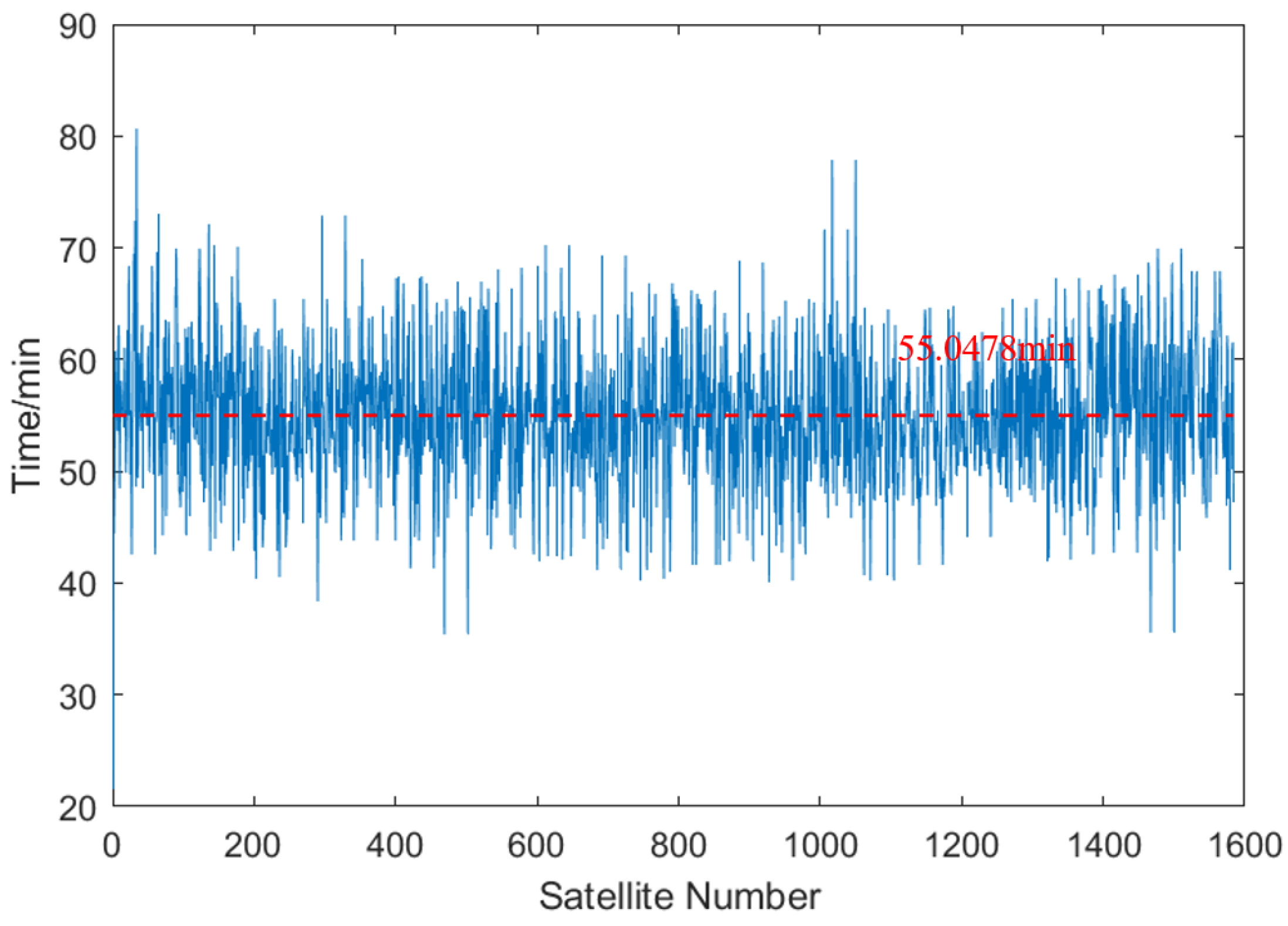
Figure 10 demonstrates that the average total unconnected time for satellites calculated using the greedy algorithm is 55.05 min. It should be noted that the orbital period for each satellite is merely approximately 95 min.
Comparison between
Figure 9 and
Figure 10 reveals that the greedy algorithm often produces satellite dynamic link configurations that are suboptimal. Satellites frequently rely on fixed links instead of establishing dynamic links, which undermines our goal of enhancing the link flexibility and reducing the latency. This issue stems from earlier connection selections that limit subsequent satellites from finding compatible partners for connections. The lack of global optimization in the greedy algorithm exacerbates this problem, causing some of the satellites to struggle to identify suitable counterparts. Additionally, frequent topology changes introduce instability into the communication system.
While the greedy algorithm excels in computational efficiency for maximizing link duration times, it results in shorter average minimum link durations and more frequent switching events. This may hinder certain satellites from establishing effective links, impacting the overall system performance. The shorter link durations increase the number of satellites not connected through dynamic links, prolonging their average duration of unconnectedness [
15,
16,
17]. This makes forming links more challenging, restricting the network capacity and affecting the system performance and stability.
3.3. Optimization Matching Algorithm for Dynamic Links
This section introduces an optimization matching algorithm based on general graphs in graph theory, aimed at addressing the shortcomings of traditional greedy algorithms in terms of the connection duration and numbers of topology changes [
16,
17,
18,
19,
20,
21,
22,
23].
Inter-satellite links are bidirectional, thus the topology of satellites within the constellation at time t can be represented using undirected graphs according to the definition in graph theory, as follows:
where
represents the set of vertices, representing the collection of satellite nodes within the constellation at time
t;
represents the set of edges, representing the collection of inter-satellite communication links that can be established at time
t. For ease of subsequent discussion,
V and
E are used in the article to denote the sets of vertices and edges within each time slot [
21].
In the previous section, we identified the establishment of dynamic links as analogous to a maximum weight-matching problem in graph-matching algorithms within computer science. While the Hungarian algorithm for bipartite graph maximum weight matching is a common approach for solving such problems, it is challenging in our scenario to partition all of the satellites in the constellation into two sets where no internal connections exist among the satellites within each set. Therefore, we propose employing a general graph maximum weight-matching algorithm instead. However, traditional algorithms like Edmonds’ Blossom Algorithm tend to result in frequent link switching [
11]. To address this issue, this paper introduces an improved algorithm—the general graph maximum weight-matching algorithm with an elite retention strategy. Next, we will proceed to outline the description of this enhanced algorithmic process.
We define an alternating path as starting from an unmatched satellite and traversing connections according to matrix A, alternating between unmatched and matched edges. An augmenting path is an alternating path that terminates at an unmatched satellite. Reversing the matching or non-matching status of the entire path yields a new matching result.
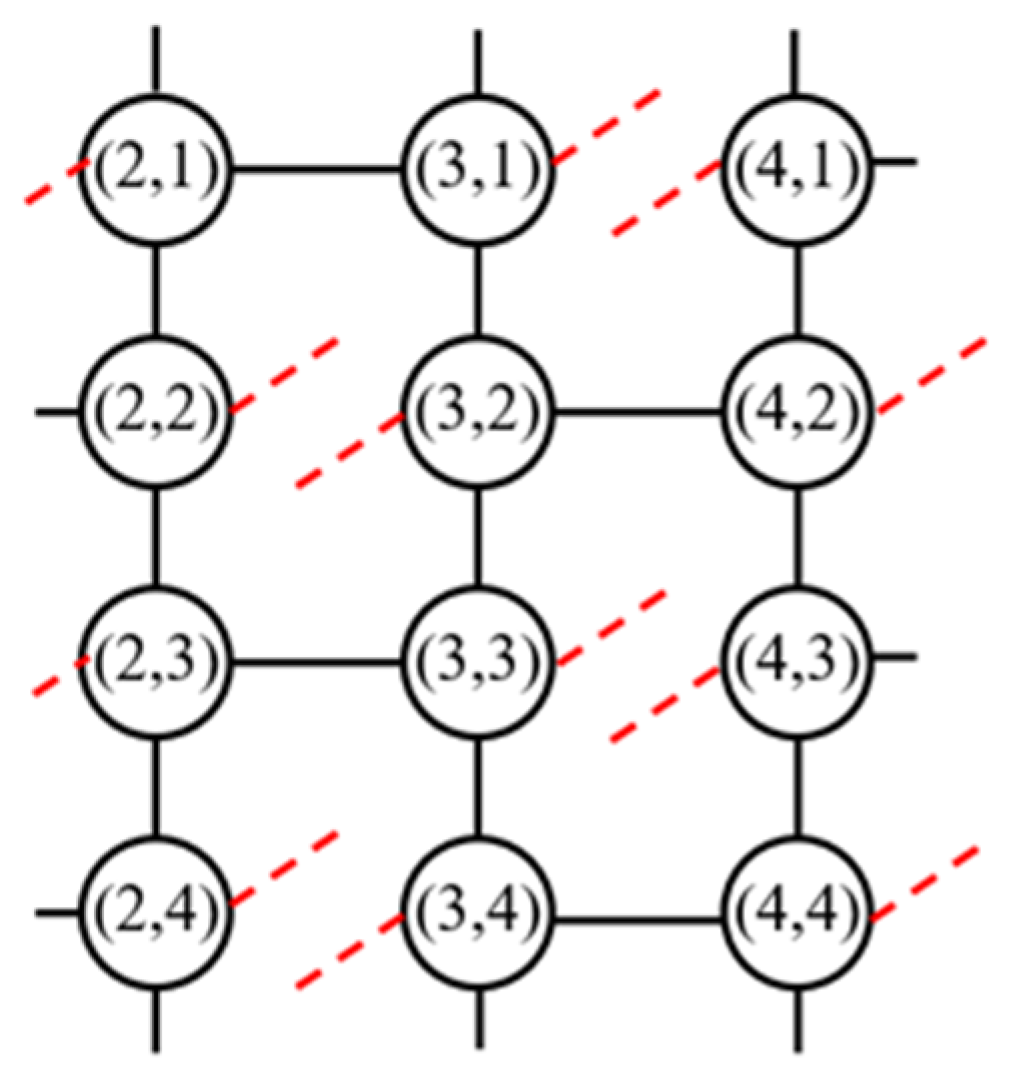
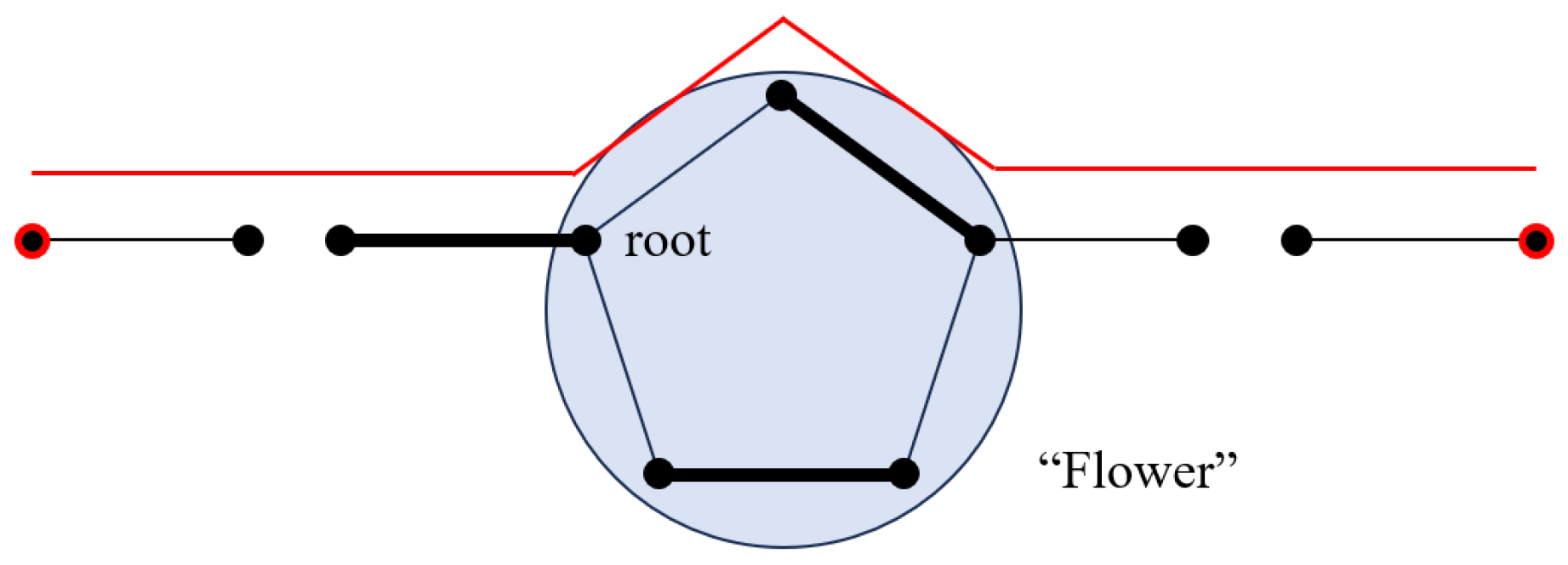
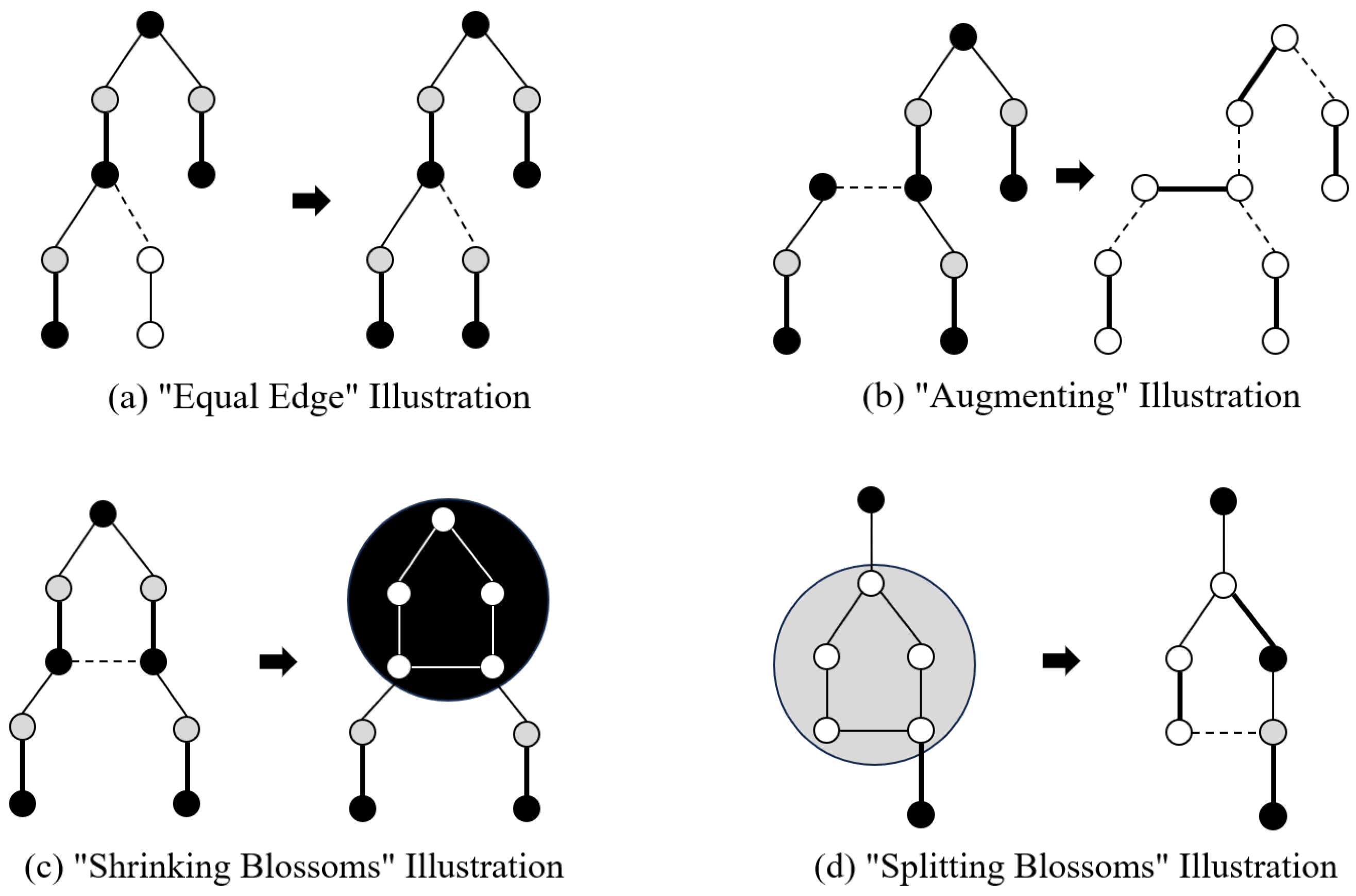
In the context of maximum matching in general graphs, there exist odd cycles, which are cycles of odd length. As depicted in
Figure 11, such “odd cycles” are commonly referred to as a “flower” or “blossom”.
In graph theory, a “blossom” is a special type of graph structure consisting of a group of an odd number of nodes, each pair of which are connected, forming a cycle, denoted as B, where |B| is odd and |B| ≥ three.
This ring is interconnected with other nodes, referred to as “petals,” thus creating a distinctive graphical structure. Every point on the odd cycle that possesses an outgoing unmatched edge has the potential to serve as an edge in an augmenting path, where reversing the state of edges within a flower according to the definition of an augmenting path would disrupt the matching pattern inside of the flower. However, as evident from
Figure 9, any non-matching edge emanating from any point within a flower can be part of an alternating path originating from the root node; hence, all satellite nodes within a flower can effectively be regarded as a single entity concerning the entire path. Consequently, upon encountering a flower, one can perform a contraction operation that condenses it into a single even-pointed vertex, which then behaves as a single node extending outwardly along the alternating tree until conditions are met for decompressing the flower back into its points. It is noteworthy that there always exists a unique point within the cycle that connects two non-matching edges, and this point serves as the root (or receptacle) of the flower. Therefore, in practical implementation, it suffices to record merely the position of the receptacle for each flower to represent the entire configuration. This encapsulates the approach to resolving issues arising from odd cycles.
In the case of considering the maximum weight matching, let
represent whether to select edge e as the matching edge between two satellite nodes, where
indicates selecting the edge, otherwise
. Let
, defining
, and
, representing the set of edges in set
S. Let
denote the set of edges connected to satellite node
v,
w(
e) be the edge weight, and O represent all of the blossoms. Assign a weight value to each satellite node, denoted as
for node
u, and when encountering a blossom, let the weight be
. For all of the edges (
u,
v), in the context of maximum weight matching, all matching edges must be “equal edges (Grow)”, meaning that the sum of the weight of the satellite nodes
u and
v’s weights should equal the weight of edge (
u,
v), as shown in Equation (10):
In this case, the edge label
. Then, solving the maximum weight-matching problem can be expressed as the following linear programming problem:
Thereby transforming the problem into its dual form via primal–dual, as follows:
It can be observed that it is desirable to maximize
, but, in many cases, it is challenging to satisfy this condition. Hence, the objective is to maximize this while minimizing it whenever the former is not satisfied. According to the complementary slackness condition, it follows that, for the selected edge e, it must imply
, i.e.,
Similarly, for the selected blossom B, we have the following:
Therefore, as the augmenting paths formed by the “equal edges” continuously expand, the resulting maximum weight matching still satisfies the “equal edge” condition for all of the matches. The algorithm consists of the following four important steps: 1. using the “equal edges” to find the alternating trees; 2. finding the augmenting paths and expanding the matches by the reversing node states; 3. shrinking the blossoms; 4. splitting the blossoms. This is illustrated in
Figure 12.
During the expansion process, if encountering issues with no “equal edge” augmentation, refer to the solution method outlined in reference [
7]. Use
and
to represent satellite node u as an odd and even vertex on the alternating tree, corresponding to the gray and black points in
Figure 12, respectively. Use
to denote satellite node u not on any alternating tree, corresponding to the white points in
Figure 12. Similarly, for blossom B, use
,
, and
to represent the even blossom, odd blossom, and blossom not on any alternating tree, respectively. Suppose there are currently n alternating trees
. Then, let us define the following:
Let
, then let
If
occurs, to prevent
, it is necessary to split the blossom. During the blossom-splitting process, alternating paths within the blossom need to be retained, and the remaining satellite nodes not included in the alternating paths are designated as white. During the algorithm initialization, all of the top labels of satellite nodes
u are set to the following:
For all matched points u, is required; points with top labels of zero will become unmatched points.
The above describes the solution method for the maximum weight-matching problem in a general graph. As mentioned earlier, through the previously calculated , we have already determined whether the satellites are subject to the connectable constraints at each time moment.
The matrix itself is constructed based on the persistence duration of the satellites, serving as the weights for the subsequent matching processes. As time progresses, the persistence duration of the satellites gradually decreases, leading to a reduction in the weights within the matrix. Consequently, during the next round of matching, satellites with diminished durations may receive less priority due to their relatively smaller weights, resulting in frequent switching phenomena. To mitigate this issue, we introduce the “elite retention strategy” borrowed from genetic algorithms to address the problem of frequent switches caused by diminishing weights.
Before each matching operation at any given time, we first examine whether pairs of satellites that were previously connected in various connection strategies exist. If such pairs are found, they are designated as “elite” pairs. For these elite pairs, their corresponding weights are not calculated based on the current moment’s values but are instead adjusted to reflect their initial maximum weight when the connection was first established. Consequently, even as the persistence duration of the satellites decreases, the weights of these elite pairs remain at a high level, effectively mitigating the issue of frequent switches.
Through this enhancement, we can more effectively manage satellite matching problems at each time instant, thereby improving the stability and efficiency of the system. A flowchart illustrating this method is presented in
Figure 13.
This improvement offers a more reliable solution for optimizing satellite communication systems, enabling them to better cope with the challenges brought about by time-varying conditions, thereby enhancing the overall performance of the systems.
3.4. Simulation Analysis
The simulation commenced at 04:00:00 UTCG on 29 January 2024 and concluded at 05:35:39 UTCG on 29 January 2024. The simulation time step was set to 3 s.
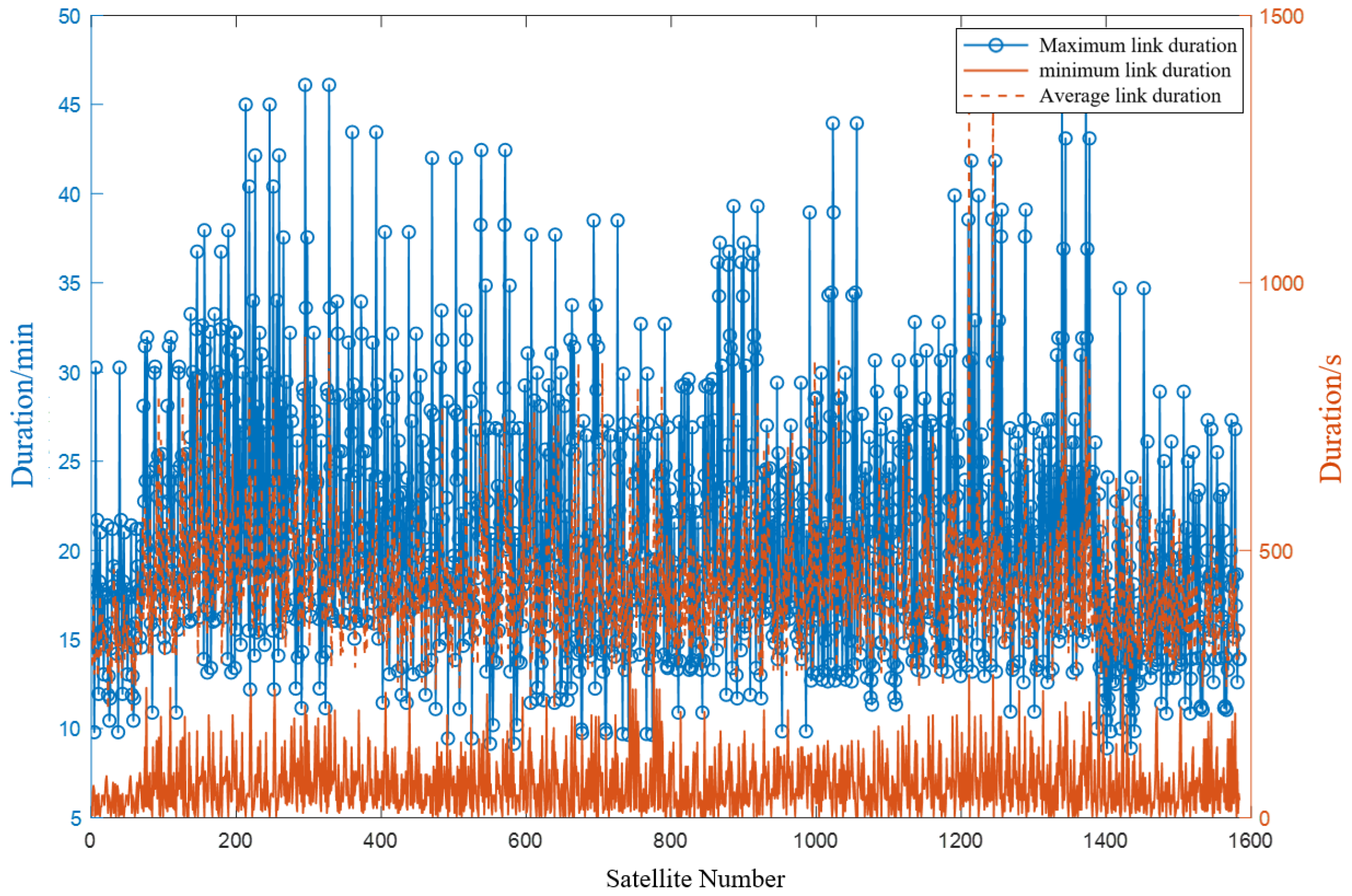
Initially, based on the general graph maximum weight-matching algorithm, the solution was derived to calculate the continuous connection duration for each satellite.
According to the graphical representation shown in
Figure 14, the average maximum link duration computed by the maximum weighted matching algorithm for general graphs is 1870.4 s (approximately 31.17 min), whereas the average minimum link duration is 11.92 s, and the overall average link duration stands at 216.00 s. The minimum link duration determines the frequency of link switches, and while comparing with the results from the greedy algorithm, it is evident that the solution provided by the maximum weighted matching algorithm significantly improves upon it, yet an average link duration of 11.92 s remains excessively short for normal link switching operations. Subsequently, we proceed to solve for the number of topological changes, as shown in
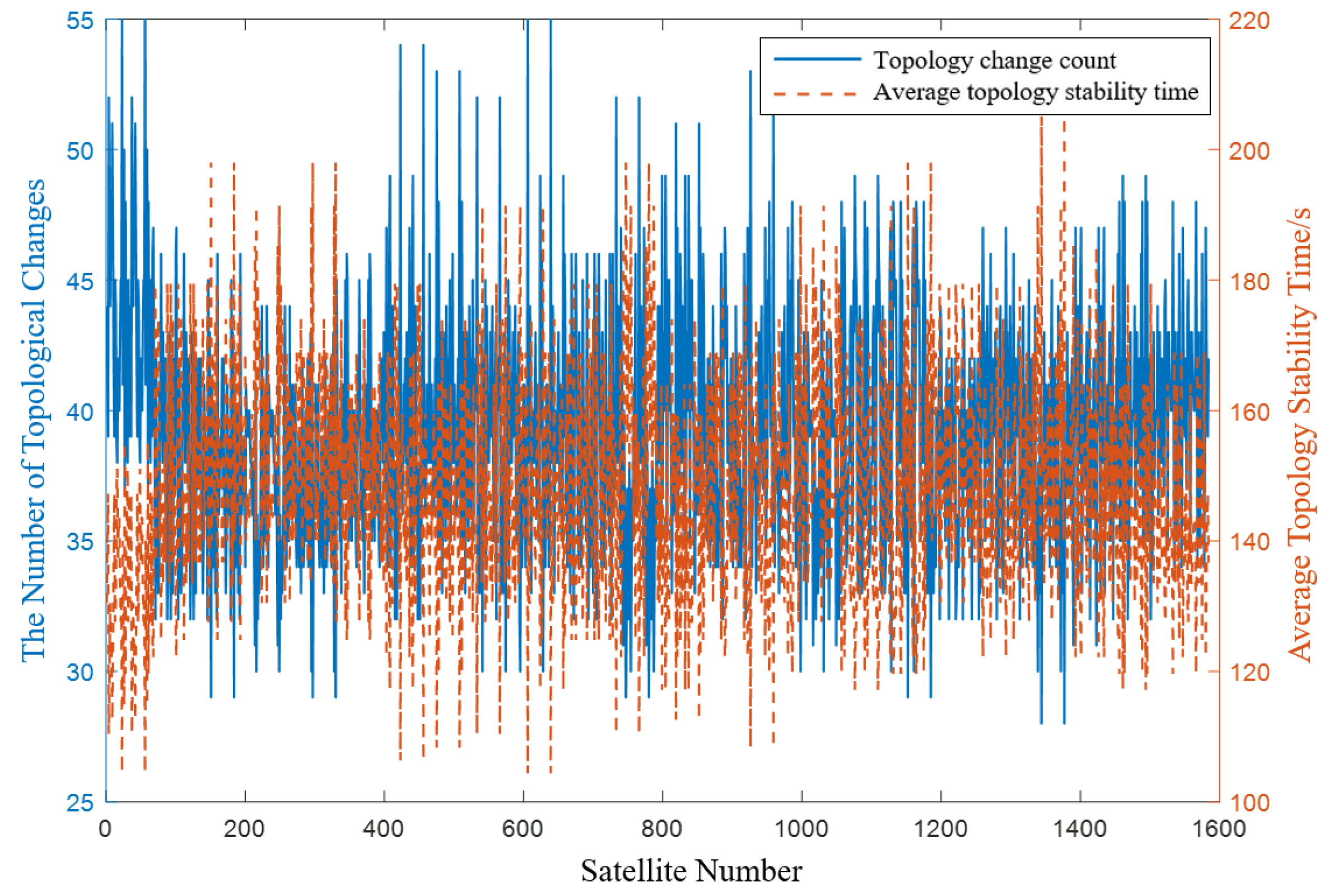
Figure 15.
After calculating an average of 250 topological changes, we determined the average topological stability time to be approximately 23.0678 s using Formula (8). Comparing this with the previously found average link duration of 216.00 s, we observe a significant difference, indicating that satellite connections typically last much longer. This suggests that the maximum weighted matching algorithm for general graphs tends to result in longer durations of unconnected dynamic links for satellites. Moving forward, we analyze a variant of this algorithm incorporating an elite retention strategy and present the resulting satellite connection durations in
Figure 16.
Upon processing the data, the application of the elite retention strategy within the maximum weighted matching algorithm for general graphs resulted in an average maximum link duration of 1252.8 s (approximately 20.88 min), with an average minimum link duration of 62.69 s and an overall average link duration of 429.0628 s. In comparison with the outcomes of the conventional maximum weighted matching algorithm for general graphs, the improved version notably enhances the minimum average duration, which now falls within a reasonable range for low-Earth-orbit satellite connections. Consequently, this modification contributes to enhanced system performance.
We conducted a qualitative analysis of the number of topological changes and average link duration under the elite retention variant of the maximum weighted matching algorithm for general graphs, as shown in
Figure 17.
The average number of topological changes in the maximum weighted matching algorithm for general graphs employing an elite retention strategy was computed to be 39 occurrences. This represents a significant improvement over both the greedy algorithm and the standard maximum weighted matching algorithm, highlighting the advanced nature of the improved algorithm. Subsequently, a comprehensive horizontal and vertical comparative analysis of the data from both algorithms will be conducted.
In the horizontal comparison, we focus on the performance of two algorithms in each time slice. By counting the number of satellites without dynamic links in each time slice, we can assess the immediate efficiency of the algorithms.
Figure 18 presents the count of satellites without dynamic links in each time slot, determined by the general graph maximum weight-matching algorithm and the same algorithm incorporating an elite retention strategy. The blue line represents the general graph maximum weight-matching algorithm, showing significant performance variability across different time intervals. These fluctuations may reflect changes in the spatial configuration of the satellites and variations in the resource availability. In certain time slots, the blue line indicates a noticeable increase in the number of satellites without dynamic links, suggesting a lower resource allocation efficiency during these periods.
In contrast, the red line represents the algorithm augmented with the elite retention strategy. The red line demonstrates that this algorithm maintains a consistently lower and relatively stable number of satellites without dynamic links throughout most time intervals. This indicates that the elite retention strategy effectively reduces satellite disconnections and significantly enhances the resource allocation efficiency and stability. Regardless of high- or low-resource-demand periods, the red line consistently exhibits superior performance, showing that this strategy is more flexible and effective in handling varying conditions. The vertical comparison focuses on the overall performance of the algorithms throughout an entire orbital period. By calculating the total time each satellite is without dynamic links during the orbital period, we can evaluate the long-term efficiency of the algorithms.
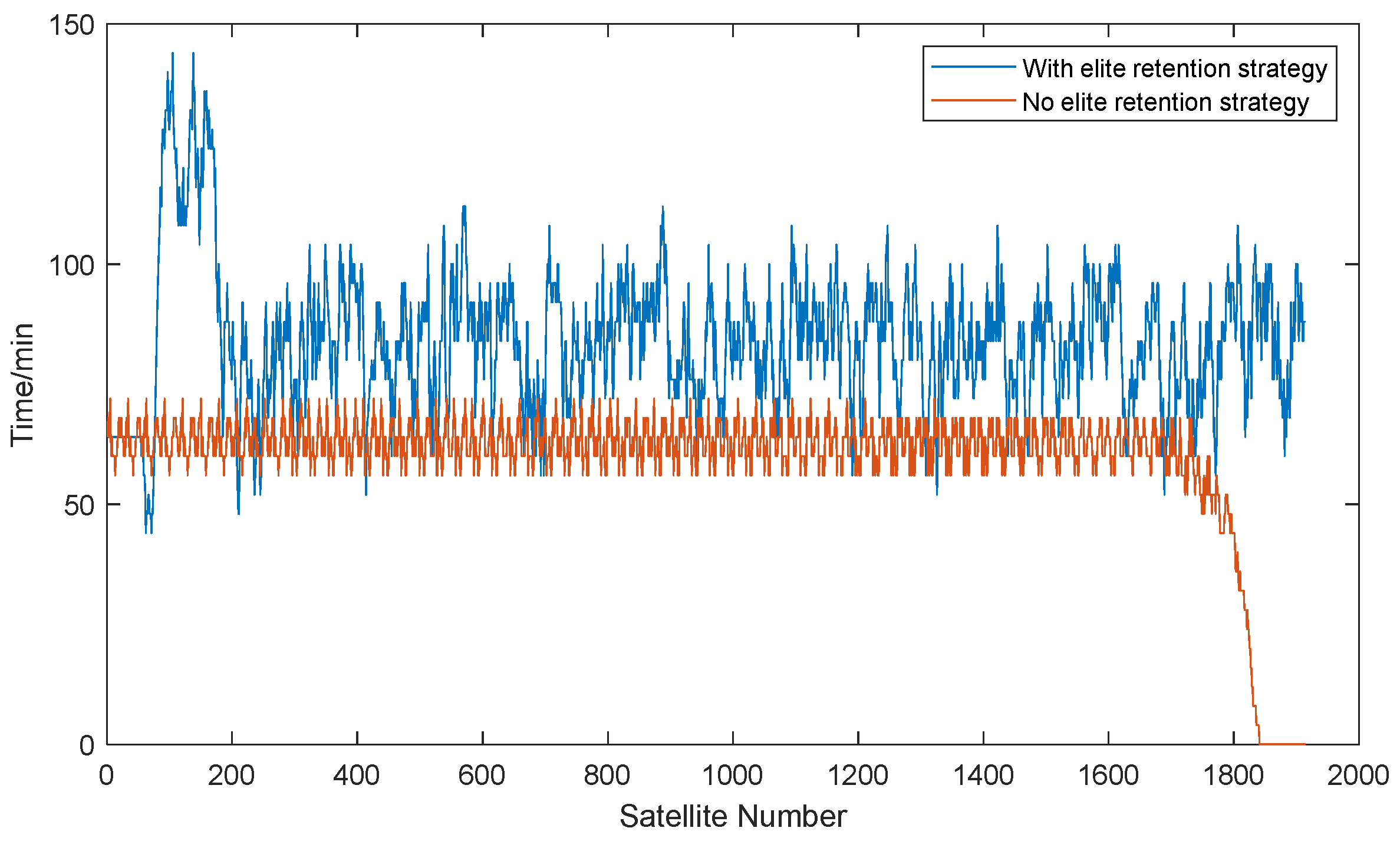
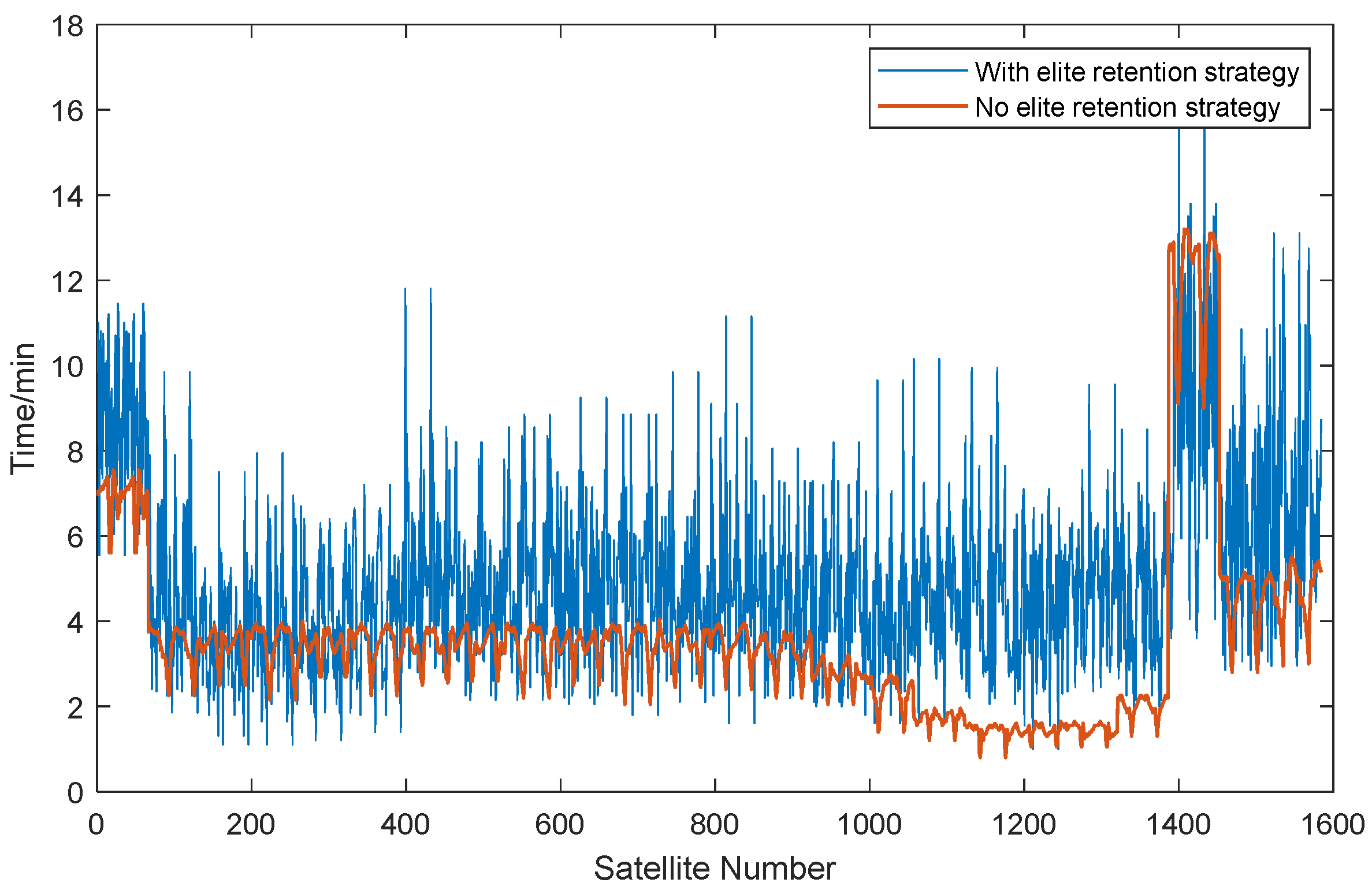
Figure 19 is a graph showing the total time for each satellite without dynamic links calculated by the general graph maximum weight-matching algorithm and the total time for each satellite without dynamic links calculated by the general graph maximum weight-matching algorithm with an elite retention strategy. The blue line in this picture shows that the average total time without dynamic links for the general graph maximum weight-matching algorithm is 3.5773 min within the orbital period, which, although improved, still has room for enhancement. In contrast, the red line in this picture indicates that the algorithm with the elite retention strategy reduces this time to 5.0804 min, further optimizing the connection efficiency.
Data computations show that, on average, each satellite lacks dynamic links for 5.0804 min when employing the maximum weighted matching algorithm for general graphs with an elite retention strategy. Subsequently, a summary of the outcomes for the three algorithms under consideration is presented in
Table 3.
Comparing the results of the greedy algorithm, the general graph maximum weight-matching algorithm, and the general graph maximum weight-matching algorithm with the elite retention strategy, we can draw the following conclusions: Firstly, in terms of average maximum link duration, the greedy algorithm yields the shortest duration. This is because the greedy algorithm only considers the current satellite being traversed, which can lead to subsequent satellites being unable to connect with those that could potentially yield longer connections. In contrast, the general graph maximum weight-matching algorithm may encounter scenarios where most satellites have relatively short remaining connection times with other satellites, while a few have significantly longer periods, causing these satellites to remain connected until the end. However, the general graph maximum weight-matching algorithm with the elite retention strategy ensures that each satellite connects to others in its best possible state, which might slightly reduce the maximum connection time but still outperforms the greedy algorithm.
In terms of the average minimum link duration, the performance improves progressively from the greedy algorithm to the general graph maximum weight-matching algorithm, and further to the one with the elite retention strategy, with durations extending accordingly. The latter significantly outperforms the former two, being 20 times better than the greedy algorithm and 6 times better than the standard general graph maximum weight-matching algorithm, demonstrating the superiority of this strategy. Additionally, the algorithm with the elite retention strategy exhibits the longest average link duration, being 20 times that of the greedy algorithm and 2 times that of the standard general graph maximum weight-matching algorithm. Moreover, it performs best in terms of the average number of topological changes, showing fewer changes compared to the standard algorithm, which requires optimal matching at all times, potentially leading to premature disconnections and an increased frequency of topological changes.
In summary, although in some cases the standard general graph maximum weight-matching algorithm surpasses the version with the elite retention strategy, when the latter performs better, its superiority is far more pronounced, sometimes demonstrating an order-of-magnitude improvement in effectiveness, thus proving its superiority in dynamic link matching. Therefore, the elite retention strategy remains a proven effective and applicable method for dynamic link matching.
The above content compares the algorithms [
24,
25]. Next, this study validates the superior performance of the satellite-to-satellite topology structure established by the proposed algorithm in terms of its configuration compared to the traditional Manhattan configuration. Taking the communication delay between Los Angeles, United States, and Xiamen, China, as an example, only the propagation delay (not the transmission delay) is considered, and the Dijkstra algorithm is used to calculate the shortest path. Due to space limitations, this paper does not present the specific implementation of the Dijkstra algorithm, but directly presents the propagation delay results based on this algorithm for the Los Angeles–Xiamen route.
Table 4 lists the latitude and longitude data for Los Angeles and Xiamen.
Before calculating the communication delay, it is essential to determine the satellite connections directly above the coordinates of both cities at each moment. In this study, the proximity principle is adopted, assuming that, at each moment, both Xiamen and Los Angeles establish connections with the nearest satellite directly above them. The dynamic links obtained using the general graph maximum weight-matching algorithm proposed in this research, which incorporates an elite retention strategy, serve as the configuration for the “3 + 1” topology scheme. This configuration is then compared to the traditional Manhattan configuration, which does not utilize dynamic links. The simulation results are shown in the figure below.
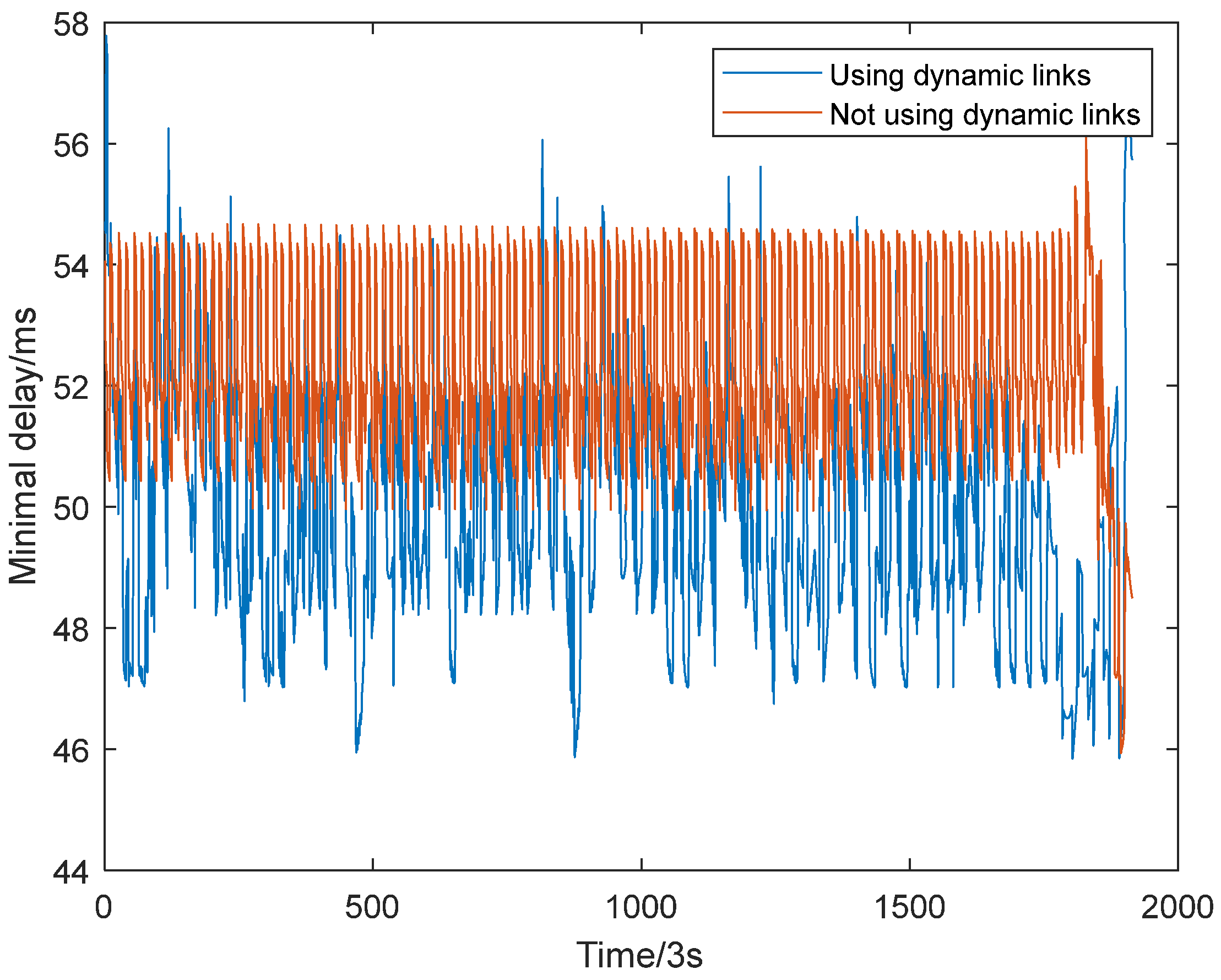
From
Figure 20, it is evident that, in most cases, the latency of the Manhattan configuration without dynamic links is higher than that of the ‘3 + 1’ topology with dynamic links. Through the quantitative analysis of the simulation results, we found that, within a complete orbital cycle, the average minimum latency for the ‘3 + 1’ topology with dynamic links is 49.8839 ms, with a standard deviation of 1.9694 ms. In contrast, the average latency for the Manhattan configuration without dynamic links is 52.2685 ms, with a standard deviation of 1.5634 ms. These results indicate that dynamic link topologies effectively reduce the information propagation delay. This is because dynamic links ensure that each satellite establishes connections with the nearest satellites, considering both cross-orbit and satellite number distances. As a result, the overall propagation delay in the network is reduced compared to the traditional Manhattan configuration. Regarding the standard deviation, the larger value observed after introducing dynamic links reflects their inherent instability, as they require real-time link switching based on current conditions.
Furthermore, the introduction of dynamic links brings additional potential advantages. For instance, it enhances the network robustness by allowing the system to swiftly switch to alternative links even if certain links fail, thereby maintaining continuous communication. Additionally, dynamic links can adjust link configurations based on real-time traffic and network conditions, optimizing the resource utilization and overall efficiency. Therefore, from the perspective of configuration-based simulation results, the ‘3 + 1’ topology with dynamic links significantly outperforms the Manhattan configuration without dynamic links in reducing communication latency. The introduction of dynamic links not only reduces information propagation delay but also enhances the network robustness and efficiency, particularly when considering cross-orbit and closely spaced satellites.
In summary, the general graph maximum weight-matching algorithm with an elite retention strategy exhibits significant advantages when applied to dynamic link matching. It effectively enhances the performance and stability of satellite networks. Notably, this strategy not only demonstrates theoretical superiority but also provides more reliable and efficient communication services in practical applications. Future research could further explore the potential application of this strategy in different types and scales of satellite networks, as well as how to optimize the algorithm to adapt to increasingly complex network environments and communication requirements