A Smart Wing Model: From Design to Testing in a Wind Tunnel with a Turbulence Generator

Abstract

The paper concerns the technology of the design, realization, and testing of a flexible smart wing in a wind tunnel equipped with a turbulence generator. The system of smart wing, described in detail, consists mainly of: a physical model of the wing with an aileron; an electric servomotor of broadband with a connecting rod-crank mechanism for converting the rectilinear motion of the servoactuator into the aileron deflection; two transducers: an encoder for measuring the deflection of the control aileron and an accelerometer mounted on the wing to measure its bending and torsional vibrations; a procedure for determining the mathematical model of the wing by experimental identification; a turbulence generator in the wind tunnel; implemented ${\mathscr{H}}_{\infty }$ and LQG algorithms for active control of vibrations. The attenuation experimentally obtained for the aeroelastic vibrations of the wing, but also for those accentuated by the turbulence, reaches values of up to 50%.

1. Introduction

1.1. Directions for Aircraft Wing Vibrations Attenuation and Flight Envelope Expansion

The tendency of modern aviation is to create lighter and more flexible aircraft to accomplish the new regulations regarding green technology (https://www.tandemaerodays19-20.eu/, accessed on 17 June 2024). These specific requirements come at some cost: the stability of the flexible structures, as in the case of an airplane wing, is strongly influenced by becoming more vulnerable to the action of forces. As a response to these potentially destabilizing issues, solutions to mitigate the vibrations induced by turbulence and to expand the flight envelope across the limit of flutter occurrence, as an indirect consequence, are in the attention of the engineering community.

A main debating point present on the agenda of major aeronautical forums, see the aforementioned Tandem AERO days 19–20 Congress, is represented by the more and more accentuated climatic changes that put pressure in the aerospace industry [1]. Rising temperatures, especially in the tropopause area where jet streams meet, the destruction of the ozone layer, and the odd changes in weather patterns affect aircraft infrastructure and performance, leading to flight cancellations, delayed or rerouted flights, increased fuel consumption, and high costs dedicated to aircraft maintenance. For example, hundreds of millions of dollars per year were spent only in the USA due to this issue [2,3,4]. The worrying effect that accompanies climate change is the increased occurrence of areas with atmospheric turbulence, especially of Clear-Air Turbulence (CAT) [5,6]. This is the most dangerous type of turbulence, both for passengers and cabin crew, as well as for the aircraft, because it is found in areas without clouds, areas that do not announce such an atmospheric phenomenon, which is an element of surprise for pilots. They are generally present at very high altitudes in the tropopause region, where jet streams are encountered and most civil aircraft fly [2]. Accidents, not necessarily catastrophic but causing severe panic and even injuries to passengers and cabin crew, caused by the unexpected entry of the plane into CAT, are more and more common in civil aviation. In fact, no less than 91 CAT events were recorded between 1 April 2018 and 25 June 2021 [7].

Recent efforts are focused on the discovery of atmospheric patterns through which CAT areas can be identified. Unfortunately, at present, this problem is still unresolved, as CAT cannot be identified by using LIDAR or other known methods [8,9]. However, there are some promising results after a long research for over 50 years (see [10]). Note that in the literature there are some references regarding actions to prevent the injuries of passengers and cabin crew and less related to the technical part of counteracting the effects induced by the strong vibrations produced by the turbulence; see also [11,12].

Another significant benefit related to vibration attenuation is that the presence of an active control system allows the calculation of an increased flight envelope right from the design phase, which means an increased aircraft performance, whether it is commercial or military.

A phenomenon that can produce strong vibrations with everything that comes from here, even catastrophes, is the flutter, usually that of control surfaces. It consists of self-sustaining, unstable oscillations whose amplitude grows strongly in a short time, accumulating energy in the structure. Beyond a threshold, the vibrations can no longer be dampened, the amplitude increases rapidly, and fluid energy is accumulated in the structure, leading to extremely violent reactions such as the breaking down of some aircraft parts or severe injuries to the pilot. The unpredictable, nonlinear, and chaotic character of the flutter makes the study of this phenomenon a complex and difficult process to approach. This unstable vibration has been carefully studied since the origins of aviation, but the causes are neither fully identified nor fully controlled; see [13]. For the history of the flutter phenomenon, see [14,15].

The authors would like to mention, based on their own experience in the field, the risk of triggering the flutter if the impedance (also called dynamic stiffness) of the hydraulic servomechanism in the flight control chain has negative damping [16,17,18,19]. On 24 November 1977, an IAR 93 Eagle aircraft crashed due to tail flutter (see [20]). The negative evaluation of the aeroservoelastic compatibility of the hydraulic servomechanism BU-51MS retrieved from aircraft MIG 21 out of use had already been expressed in an internal report [21], but it was ignored by the decision makers, given the lack of specific requirements about impedance in the Aviation Publication (AvP) 970 dated 1959. (As an irony of fate, the express requirement on the impedance function of the servomechanisms from the primary flight controls was introduced a few years later in the updated version of that Regulation). The consequence of the catastrophe was to replace the initial hydraulic servomechanisms of the flight controls, which were improperly designed from an aeroservoelastic point of view, with hydraulic servomechanisms manufactured in collaboration with Dowty Group [22].

It should be added that the weakness of the BU-51MS servomechanism configuration was not repeated in the case of the Romanian SMHR servomechanism that equips the ailerons of the IAR 99 Hawk aircraft, according to [23]. The lesson of IAR 93 was well learned.

There is a huge bibliography related to the active control of the flutter and vibrations of the aircraft in general, the influence of servoactuators, the gust loads and gust load alleviation, the active control techniques, the programs and tests in wind tunnels etc. [24,25,26,27]. A comprehensive presentation of the state-of-the art and technology maturation needs in the field of aircraft active flutter suppression is given in detail in the paper [28]. It should be noted that just a few of the 703 references concern vibration attenuation. Instead, most of the 126 references in [29] concern active vibration suppression of plate-like structures, representative of aerospace structures, with piezoelectric actuators.

Another phenomenon that can cause catastrophes is the phenomenon of pilot-induced-oscillations (PIO) in the closed loop with the aircraft controls. PIO is homologated as factual if there is at least one measurable state of the aircraft that is 180° out of phase with at least one measurable pilot control input [30].

This paper presents the results of a complex project that was aimed at achieving a demonstrator test in the Subsonic INCAS wind tunnel (WT) [31,32] for active vibration control. The controlled system, tested in WT in a turbulent environment by a turbulence generator (TG), is an elastic smart wing with aileron (Figure 1). A smart system incorporates functions of sensing, actuation, and control in order to describe and analyze a situation and make decisions based on the available data in a predictive or adaptive manner [33]. A fine distinction must be made between a smart system and an artificial intelligence-based system, or simply, an intelligent system, which must contain one or more of the following techniques: artificial neural networks, fuzzy logic, and genetic algorithms. For applications in aviation systems, see [34,35].

The control exercised by means of the aileron is executed with a broadband electric servo actuator. The approach is quite different from those existing in the literature. Thus, paper [24] is the one that introduces a series of control-active applications in which a piezoelectric V-stack actuator is used. Active control, thought of as positive position feedback, is applied to a rigid wing supported on springs, simulating the pitch and plunge degrees of freedom of the wing system. In the paper [36], the control law is given by the same positive position feedback, a totally atypical approach compared to the mainstream in control that has become prevalent since the mid-80s and that is based on the already classical package MATLAB (Version 10.4) (R2018a) Control Toolbox of the LQG robust control generations. In last few years, the scene has begun to be dominated by artificial intelligence techniques. The approach for increasing the flutter speed presented in [37] is similar to that in [36] by using the same type of actuator and positive position feedback and obtaining a 20% increase in the flutter speed.

There is a long dispute in the field of active control between the supporters of piezoelectric actuators and the supporters of electric actuators. This is also the case with aircraft flight controls, with fans of hydraulic servomechanisms and those who vote for green aviation and all-electric aircraft, with electromechanical servomechanisms.

In order to be able to evaluate the arguments a bit, let us say that, on the one hand, we have the actual benefits of using piezoelectric actuators for aeroelastic vibration attenuation: increased control bandwidth, mechanical simplicity, lack of control lag, and the nonintrusive nature of flat piezoelectric actuators. However, their major drawback is the additional heavy, bulky, and expensive hardware required to power piezoelectrics, that is, amplifiers of the order of hundreds of volts. On the other hand, the usage of electrical actuators, such as DC motors, will bring together multiple benefits, such as their lightweight, the fact that they can be easily integrated into a system, and the necessity of less power than any smart materials, such as piezoelectric actuators.

In the present paper, it is shown how a competitive bandwidth with that of a piezoactuator is obtained by adding an internal feedback loop PD (Proportional-Derivative) to a coil linear actuator.

Figure 1. Up: left: elastic smart wing with aileron and encapsulated electric actuator and accelerometer; middle: turbulence generator (TG) mounted in the wind tunnel and right: flutter test in WT; down: layout and TG dimensions; right: hybrid model for the study of turbulent flow: Stress-Blended Eddy Simulations [38].

Figure 1. Up: left: elastic smart wing with aileron and encapsulated electric actuator and accelerometer; middle: turbulence generator (TG) mounted in the wind tunnel and right: flutter test in WT; down: layout and TG dimensions; right: hybrid model for the study of turbulent flow: Stress-Blended Eddy Simulations [38].

1.2. Motivation of the Research

There were several reasons for writing this paper, as follows:

• Airlines frequently report turbulence during flights, with or without injuries to passengers, cabin crew, or damage to aircraft.
• Costs of maintenance, fuel, infrastructure, cancellation, and rerouting of the flight increase as turbulence often occurs.
• The complex problem of turbulence remains an unresolved issue and still brings challenges in the field of scientific research [39].
• Lack of method for identifying CAT leads to the development of ways to combat the effects induced by turbulence by controlling and reducing vibrations.
• The desire of the aeronautical companies is to make long-distance flights in the shortest possible time, which can be achieved by increasing the flight envelope inclusively through vibration control.
• In general, the design of aviation wind tunnels was based on the outdated idea that aircraft usually fly at altitudes of kilometers where the degree of turbulence is very low, which is true only if the phenomenon of CAT is ignored.
• Also, the paper is based on results obtained over time in projects and comes as a development of those results [40,41,42].
• The goal assumed in the project was to apply simple and efficient solutions, both in terms of hardware and software.

1.3. Contributions

• Elaboration of a complex procedure for active vibration control of an elastic model of the wing with aileron in the presence of turbulence generated in the wind tunnel, based on a methodology of simple experimental identification of the open loop system in the frequency domain
• Designing an elastic physical wing model displaying a given set of basic natural (modal) frequencies
• Designing an electric servo actuator consisting of a moving coil linear actuator and a crank-type mechanism
• Developing an algorithm for tuning the PD internal feedback loop of a servo actuator to increase the bandwidth
• Designing a passive turbulence generator in the wind tunnel, with the important property that the achieved degree of turbulence does not depend on the value of the air speed V upstream of the generator
• Developing a procedure for system mathematical model identification
• Reaching a vibration reduction of about 18 dB on the basic 5 Hz modal frequency for both control laws LQG and ${\mathscr{H}}_{\infty }$, meaning a competitive performance with other achievements described in the literature of the field.

The paper is organized as follows: Section 2 describes in detail the hardware components of the smart wing system: the physical model of the wing with aileron, the synthesis of the electric servo actuator with increased bandwidth, the transducer system, the synthesis of the turbulence generator, and the LQG and ${\mathscr{H}}_{\infty }$ active vibration control laws. Section 3 presents a software-type component of the smart wing in subsonic WT, namely the procedure for determining the mathematical model of the wing by experimental identification. Section 4 reviews the active control laws LQG and ${\mathscr{H}}_{\infty }$. Section 5 details the results of the active control tests. Section 6 ends the work with some concluding remarks.

2. Smart Wing System with Active Control

The smart wing system described in this paper consists of (1) a physical model of a wing with aileron, (2) an electric broadband servoactuator with a connecting rod-crank mechanism (CR-CM) for converting the rectilinear motion of the servoactuator into aileron deflection, (3) two transducers: an encoder for measuring the deflection angle of the aileron, and a wing-mounted accelerometer so as to capture the bending and torsional vibrations, (4) a Turbulence Generator (TG) in the wind tunnel (WT) required to test the proposed procedure, Figure 1, right, (5) a procedure for determining the mathematical model of the wing by experimental identification, and (6) LQG and ${\mathscr{H}}_{\infty }$ with static weights active control laws of vibrations.

In the following, an essential description of the elements composing the smart wing system is given. Section 3 and Section 4 are reserved for elements (5) and (6).

(1) The wing physical model has a special design in view of obtaining a realistic elastic wing that, in principle can reproduce a set of vibration modes of an aircraft wing in the preliminary, conception phase. This goal can be achieved relatively simply through a trial-and-error procedure, including ANSYS analysis applied to the geometry of the wing model. This approach differs radically from those widespread in the literature, where the model is represented by a rigid wing supported on two springs to simulate the first two vibration modes of bending and torsion [43]. Thereby, the wing is composed of a longeron, Figure 2, covered by an aerodynamic layer (profile NACA 0012). The longeron is a 1 mm-thick rectangular tube of aluminium (1200 × 120 × 25 mm³), provided with notches to control its stiffness. At one end of the wing there is the aileron, and at the other end there is a flange whose role is to fix the wing in the WT.

The elements defining the aerodynamic surface were accomplished from woodchips or resin ROHACELL 71S. One design requirement was to ensure the occurrence of flutter for the uncontrolled system in INCAS subsonic WT [32]. The tests performed in WT established that the flutter speed was 41 m/s and the flutter frequency was 5.8 Hz [41]. Thus, the flutter speed of 41 m/s and the flutter frequency of 5.8 Hz were experimentally measured, as the effect can be seen in Figure 1 (see also work [41]). These values were not intended as actual values for a specific aircraft. The purpose of the flutter tests was to develop an active vibration control methodology. Therefore, firstly, we had to prove that flutter was actually a risk in our field of vibration damping tests, and secondly, we had to prove that we could, under an actively controlled regime, rise above this speed with the tests. In another context of interpretation, it is well known that flutter is an aeroelastic phenomenon, and its appearance is proof that the wing is elastic, therefore realistic. Flutter cannot, in principle, appear on a rigid wing, as many vibration-damped models in the literature take into account. The tests reported in the paper show that vibration damping is convincingly illustrated, and these vibrations are simultaneously aeroelastic and turbulent.

The modal frequencies of the wing model, measured in the laboratory, were 5.1 Hz (bending), 17.4 Hz (torsion), 23.14 Hz, 41.85 Hz, and 49.41 Hz. In a previous stage, instead of the electric actuator, a piezoelectric actuator was used for tests. With some minimal details different from the current smart wing, the results from

Table 1. Natural frequencies determined by CATIA and measured, respectively, see Figure 2.

Mode Number	Longeron Frequency [Hz] CATIA Model	Wing Frequency [Hz] CATIA Model	Wing Frequency [Hz] Experimental Tests
1	13.59	6.23	5.93
2	43.42	10.21	11.70
3	44.12	20.83	22.73
4	59.14	26.32	-
5	78.91	29.83	-

were obtained.

(2) The electric broadband servoactuator consists of (a) a moving coil linear actuator NCC05-18-060-2PBS connected with (b) an atypical rod-crank mechanism converting the linear motion of the actuator into an incomplete rotational movement of the aileron hinge of about 20 degrees in both directions (in short, a connecting rod-crank mechanism, CR-CM, Figure 3), and (c) an internal PD (Proportional-Derivative) feedback loop (Figure 4) to transform the actuator into an angular displacement tracking actuator.

The connecting rod-crank mechanism. For proper operation, the CR-CM meets several essential conditions: symmetry of movement and efforts in both directions of movement; minimal clearances to avoid discontinuity of movement when changing direction; minimal wear during operation. The disadvantages of a classic CR-CM are eliminated by an atypical constructive solution, as follows: With reference to Figure 3, to reduce the overall size of the assembly and maintain the linearity of the movement, firstly, the connecting rod 1 (Figure 3) does not have a plane-parallel movement as in classic cases, but only a translational back-and-forth motion. Secondly, given the fact that, through mounting, the connecting rod 1 is stiffened with the actuator CR-CM at the opposite end of the actuator 4, it is replaced by a slider that gives the crank 2 a rotational movement in both directions. Pair 1–2 supports high contact pressures, being built on radial bearing rollers; therefore, if a cambered airfoil is used instead of the NACA0012, the load asymmetry on the aileron will not pose problems to the CR-CM and the smart wing system.

Fourthly, the crank 2, integral with the flange shaft 5, in turn transmits the movement to the wing, without the existence of other joints and supports other than those strictly necessary for the operation of the assembly.

Fifthly, for the slider, in order to avoid backlash and ensure its reliability and sustainability, a constructive solution was adopted in which the parts in contact on the connecting rod and crank elements are bearing rollers (Figure 3, middle and Figure 3) down, of current execution, specially intended for intensively demanded rotating joints and which ensure minimal functional clearances.

In order to avoid clearances and ensure the reliability and sustainability of the crank guideway, the solution from Figure 3 down left was adopted. The contact parts on the CR-CM elements are bearing rollers, of current manufacturing, specially designed for the highly demanded rotating joints and which ensure minimum functional clearances. In the adopted solution, the bearing rollers are used for linear motion. Two identical rollers were used, pressed into the base material of the crank (drive part). By the correct execution of the holes in this part and the observance of the distance “D” between the axles, the desired distance between the rollers is ensured. This distance must coincide with the diameter of the roller “d” (Figure 3, middle right), provided to be pressed in the connecting rod element, the driving element. The pair of rollers is chosen from the series production of the bearing manufacturers. The axles of these two linear bearings allow relative movement; the contact point “K” between the driving roller and the driven rollers, not being fixed, is able to move along the rollers 1 (Figure 3 middle right). Thus, the oscillation radius of the crank “R” is modified (Figure 3 down), which is necessary for the operation of the mechanism.

The internal Proportional-Derivative (PD) feedback loop. A simplified scheme for calculating CR-CM dynamics is shown in Figure 5. Note that point C slides in the OD direction and rotates around point O in the plane $\left(\mathrm{X},\mathrm{Y}\right).$ By $F_A$ and $F_R$ were noted the active force, called also electromagnetic force, and the resistance force, respectively. The two forces act on the aileron by means of a lever OC of variable length. As seen in Figure 5, the perpendicular distance from the line of action of the force to the pivot is b, $b=0.02615 \mathrm{m},$ as the mechanism was designed. The active force $F_A$ is developed by the linear actuator and is expressed as

$$F_A=K_{M}i$$

(1)

where $K_M$ is the constant force of the actuator, $K_M=27.8 \mathrm{N}/\mathrm{A},$ and $i$ represents the intensity of the electric current in the actuator coil

$$i=K_a\tilde{u}$$

(2)

with $\tilde{u}$ the electrical voltage applied to the voltage-current amplifier (VCA) considered here as a control variable and $K_a=1$ is the amplification factor established in the design. VCA is included in the block diagram of the controlled system, CS, Figure 4. It follows from (1) and (2) that

$$F_A=K_a{K}_M\tilde{u}.$$

(3)

$F_R$ is the resistance force consisting of inertia force and viscous friction force. This force is associated with the rectilinear motion of a moving coil linear actuator and is expressed as

$$F_R=m\ddot{x}+f_1\dot{x}$$

(4)

where $m$ is the mass of the movable actuator assembly, $m=0.12 \mathrm{kg}$ and $f_1$ is a conventional viscous friction coefficient. The resistance moment associated with the rotational movement of the aileron around the hinge shaft, $M_{R\mathrm{\delta }}$, is given by

$$M_{R\mathrm{\delta }}=\tilde{I}\ddot{\mathrm{\delta }}+f_2\dot{\mathrm{\delta }}+k\mathrm{\delta }$$

(5)

with $\tilde{I}$ the moment of inertia of the aileron, $f_2$ the viscous friction coefficient (of mechanical and aerodynamic nature), and $k$ the modulus of elasticity of the elastic aerodynamic force. The equation of the dynamic equilibrium of the moments with respect to the hinge axle is

$$F_{A}b-F_{R}b-M_{R\mathrm{\delta }}=0$$

(6)

or, taking into account (3)–(5)

$$b\left[K_a{K}_{M}u-m\ddot{x}-f_1\dot{x}\right]-\tilde{I}\ddot{\mathrm{\delta }}-f_2\dot{\mathrm{\delta }}-k\mathrm{\delta }=0.$$

(7)

Consider the kinematic equation in the usual hypothesis of small angles $\mathrm{\delta },$

$$x=b\mathrm{\delta }.$$

(8)

Therefore,

$$\dot{x}=b\dot{\mathrm{\delta }}, \ddot{x}=b\ddot{\mathrm{\delta }}$$

(9)

and substituting in (7), it results in

$$\left(\tilde{I}+b^{2}m\right)\ddot{\mathrm{\delta }}=-k\mathrm{\delta }-\left(f_2+b^2{f}_1\right)\dot{\mathrm{\delta }}+b{K}_a{K}_{M}u.$$

(10)

By defining the state variables $x_1:=\mathrm{\delta }$, $x_2:=\dot{\mathrm{\delta }}$ and noting

$$F:=f_2+b^2{f}_1, I:=\tilde{I}+b^{2}m,$$

(11)

system (10) is rewritten in the form of a system of first-order differential equation

$$\left[\begin{array}{l}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -\frac{k}{I }& -\frac{F}{I}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ \frac{b{K}_a{K}_M}{I}\end{array}\right]\tilde{u}.$$

(12)

From (12), the open loop transfer function from $\tilde{u}$ to $x_1=\mathrm{\delta }$ is obtained (Figure 4)

$$H_{\mathrm{\delta }\tilde{u}}(s)=\frac{b{K}_a{K}_M}{I{s}^2+Fs+k}:=\frac{K}{I{s}^2+Fs+k}.$$

(13)

A suitable internal PD loop is required to increase the servoactuator bandwidth (Figure 4).

The servoactuator has the following closed loop transfer function from ${\mathrm{\delta }}_c:=u$ to $\mathrm{\delta }$

$$H_{\mathrm{\delta }u}(s)=\frac{K_{P}K/I}{s^2+\left(F+K_{D}K\right)s/I+\left(k+K_{P}K\right)/I}:=\frac{K_{P}K/I}{s^2+2\mathrm{\zeta }{\mathrm{\omega }}_{n}s+{\mathrm{\omega }}_n^2}.$$

(14)

The determination of the parameters $(K_P,K_D)$ follows an analytical-experimental identification. In the first step, the initial estimated values $k_1,I_1,F_1$ are considered. The choice of poles $s_{1,2}=-\mathrm{\zeta }{\mathrm{\omega }}_0\pm i{\mathrm{\omega }}_0\sqrt{1-{\mathrm{\zeta }}^2}$ takes into account the achievement of a bandwidth of at least 30 Hz. This is equivalent to imposing values ${\mathrm{\omega }}_n=2\mathrm{\pi }\times 30 \mathrm{rad}/\mathrm{s}$ and $\mathrm{\zeta }=1/\sqrt{2},$ which leads to the identification of intermediate values for $(K_{P,1},K_{D,1}).$ For a better understanding, if $k=0$ and $\mathrm{\zeta }=1/\sqrt{2},$ the attenuation in the closed loop (14), at the frequency $\mathrm{\omega }={\mathrm{\omega }}_n,$ is exactly 3 dB, which corresponds to the definition of the bandwidth. In a subsequent step, the control law of the internal loop of the servoactuator is implemented with these intermediate values $(K_{P,1},K_{D,1})$, in order to control the wing system in WT. The system is excited by a chirp signal ${\mathrm{\delta }}_c\left(t\right)$, i.e., a sinusoidal signal with a constant amplitude (corresponding to an expected angular aileron displacement of 2 degrees) and a frequency that is linearly variable in time in the range of interest of the frequencies $\left(0.1 Hz ÷ 60 Hz\right)$. The deflection angle of the aileron $\mathrm{\delta }\left(t\right)$ provided by an encoder is recorded. Then, the experimental transfer function $H_{\mathrm{\delta }{\mathrm{\delta }}_c;\mathbf{exp}}\left(\mathrm{i}\mathrm{\omega }\right)$ will be a result of the Fast Fourier Transform (FFT) of the two experimental time signals $\mathrm{\delta }\left(t\right)$ and ${\mathrm{\delta }}_c\left(t\right)$. The next step is to get, based on MATLAB System Identification Toolbox functions, a convenient approximation of this response $H_{\mathrm{\delta }{\mathrm{\delta }}_c;\mathbf{exp}}\left(\mathrm{i}\mathrm{\omega }\right)$ by a rational transfer function (i.e., a ratio of two polynomials in the complex variable $s=\mathrm{i}\mathrm{\omega }$) $H_{{\mathrm{\delta }}_{c}y;\mathbf{idt}}\left(\mathrm{i}\mathrm{\omega }\right)$, in other words, to obtain $H_{{\mathrm{\delta }}_{c}y;\mathbf{idt}}\left(\mathrm{i}\mathrm{\omega }\right)\cong H_{{\mathrm{\delta }}_{c}y;\exp }\left(\mathrm{i}\mathrm{\omega }\right)$. Then, the relation (14) is reformulated in this way

$$H_{\mathrm{\delta }{\mathrm{\delta }}_c}(s)=\frac{K_{P,1}K/I}{s^2+\left(F+K_{D,1}K\right)s/I+\left(k+K_{P,1}K\right)/I}:=H_{\mathrm{\delta }u,\mathrm{idt}}(s)=\frac{b_0}{s^2+a_{1}s+a_0}$$

(15)

and, as a result, three algebraic equations are obtained, with the solutions $k_2,I_2,F_2.$ These values are substituted in the equations

$$\left(F_2+K_D{K}_2\right)/I_2=2\mathrm{\zeta }{\mathrm{\omega }}_n;\left(k_2+K_{P}K\right)/I_2={\mathrm{\omega }}_n^2.$$

(16)

from which are deduced the values of the second iteration $(K_{P,2},K_{D,2})$. Starting with these values, the parameters $(K_P,K_D)$ will be experimentally tuned through a “trial and error” procedure. The following iterations can be continued by repeating the previous steps. After 3 iterations, the desired values of the PD controller gains are obtained: $K_P=12.786,$ $K_D=0.069$. The diagram of the tuning algorithm of the PD controller of the servoactuator is given in Figure 6.

The successful synthesis of a high-performance servoactuator for vibration attenuation, whose signal bandwidth is over 30 Hz, is attested by Figure 7 and by the vibration attenuation results described below in Section 5. In fact, the frequency characteristic recorded online in WT denotes a 3 dB bandwidth of about 36.6 Hz. Therefore, an indirect but essential condition, required by Shannon’s sampling theorem, is met: the bandwidth is at least twice as large as the second modal frequency of the wing, identified experimentally. This is because only the first two modal frequencies, about 5 Hz (bending) and 17 Hz (torsion), are subject to active control, as shown in the following sections of the paper.

(3) The two used transducers are a Winkel MOT 13 encoder (Megatron Elektronik GmbH & Co. KG, München, Germany) and a capacitive accelerometer 4394-S (Brüel & Kjær, DK-2830, Virum, Denmark).

(4) Turbulence generator (TG). The aviation WTs are specially built so as to ensure the lowest possible degree of turbulence, which is relevant for aerospace tests. However, for certain aerospace applications, or even for some civil engineering applications, certain degrees of turbulence intensity are required. It was established that the optimal solution in terms of cost-quality for increasing the degree of turbulence in WT is to introduce a passive grid upstream of the experiment chamber with a square mesh (M) with dimensions of 0.15 m × 0.15 m and a distance between neighboring meshes of 0.05 m. A degree of turbulence (the ratio of the standard deviation of fluctuating wind velocity to the mean wind speed) of 8% obtained with TG designed and manufactured by INCAS, located 30 cm from the physical wing model, represents a high turbulence case, causing abrupt variations in altitude and attitude for the airplane in that field and panic and injuries for passengers [44].

Using relations (38) from [45], the degree of turbulence I is calculated, which is, as can be seen, independent of the velocity from infinity upstream U₀, thus:

$$\begin{array}{l}I=\frac{\mathit{u}}{U_0}=\frac{\sqrt{\left(u_1^2+u_2^2+u_2^2\right)/3}}{U_0}=\\ \sqrt{\frac{1}{3\times 21\times {\left(\frac{X}{M\times 1.27}-3.5\right)}^{1.25}}+\frac{2}{3\times 20\times {\left(\frac{X}{M\times 1.27}-3.5\right)}^{1.25}}}=\\ =\frac{1}{3}\sqrt{\frac{31}{70}}\frac{1}{{\left(\frac{X}{M\times 1.27}-3.5\right)}^{1.25}}.\end{array}$$

(17)

Taking into account the fact that the grid and the WT in [45] are not identical to those from INCAS, a correction factor of 1/4.63 was introduced to obtain the same degree of turbulence at the distances X = 3 m and M = 0.15 m.

Therefore, for the INCAS grid, the relationship is recommended

$$I=\frac{u^{\prime }}{U_0}=\frac{1}{3}\sqrt{\frac{31}{70}}\frac{1}{{\left(\frac{X}{M\times 1.27}-3.5\right)}^{0.625}}\frac{1}{4.63}.$$

(18)

With this relationship, the following results are obtained: see

Table 2. The evolution of the turbulence intensity depending on the distance to the grid.

X (m)	1	1.5	2	2.5	3	3.5	4	4.5	5
I	0.0338	0.019	0.0142	0.0116	0.01	0.0089	0.008	0.0073	0.0068

.

The evolution of the turbulence intensity depending on the distance to the grid, as well as the graph in Figure 8, is described in percentages.

3. Tests on the Smart Wing in Subsonic WT for Mathematical Model Identification

In the case of a classical control law synthesis, two problems must be solved: that of the mathematical modeling and that of compatibility between the mathematical methodology used for control law synthesis and the obtained mathematical model [46,47]. The conventional approach follows an analytical path, e.g., [48], or a numerical one by using the finite element method (FEM) [49]. As will be seen below, herein will be avoided the determination of a structural mathematical model, respectively, of the matrices M, C, K (mass, damping and stiffness matrices) by an online (in process) identification, considered much safer than any analytical or FEM approach, even more in this particular case of the wing having such an atypical longeron.

The identification procedure takes place in the mounting set-up shown in Figure 1 right, at various air speeds, and is sequentially carried out as follows:

(a)

A chirp signal ${\mathrm{\delta }}_c\left(t\right)$ (Figure 4) is applied to the actuator; the signal has constant amplitude (corresponding to an expected angular aileron displacement, for example, 2 degrees, 4 degrees, etc.) and a linearly variable frequency in time in the band [0 Hz; 60 Hz], which sufficiently covers the interest field of the first two modal frequencies of the wing.

(b)

The signal $y\left(t\right)$ (Figure 4), corresponding to wing displacement in the normal direction on the wing, and provided by the accelerometer, is recorded by integrating the acceleration twice; the accelerometer is mounted on the wing (Figure 2) so as to react simultaneously to the bending and torsional movements corresponding to the first two modes of vibration.

(c)

The experimental frequency response, defined by the $\arctan \left(\mathrm{Im}\left(H_{{\mathrm{y}\mathsf{\delta }}_{\mathrm{c}},\mathbf{exp}}\left(\mathrm{i}{\mathrm{\omega }}_j\right)/\mathrm{Re}\left(H_{y{\mathrm{\delta }}_c,\mathbf{exp}}\left(\mathrm{i}{\mathrm{\omega }}_j\right)\right)\right)\right)$ − phase-$\left|H_{y{\mathrm{\delta }}_c,\mathbf{exp}}\left(\mathrm{i}{\mathrm{\omega }}_j\right)\right|$ − attenuation-frequency characteristics, and frequency characteristics, $j=1,\dots ,M$, $\mathrm{i}=\sqrt{-1},$ associated with the transfer function $H_{y{\mathrm{\delta }}_c;\exp }\left(\mathrm{i}\mathrm{\omega }\right)$ is estimated; the latter is obtained by comparing (dividing) the Fast Fourier Transform (FFT) of the two experimental time signals $y\left(t\right)$ and ${\mathrm{\delta }}_c\left(t\right)$; therefore $H_{y{\mathrm{\delta }}_c;\exp }\left(\mathrm{i}\mathrm{\omega }\right)$ consists of a sequence of complex numbers, of length M, indexed with values of the circular frequencies ${\mathrm{\omega }}_j$.

(d)

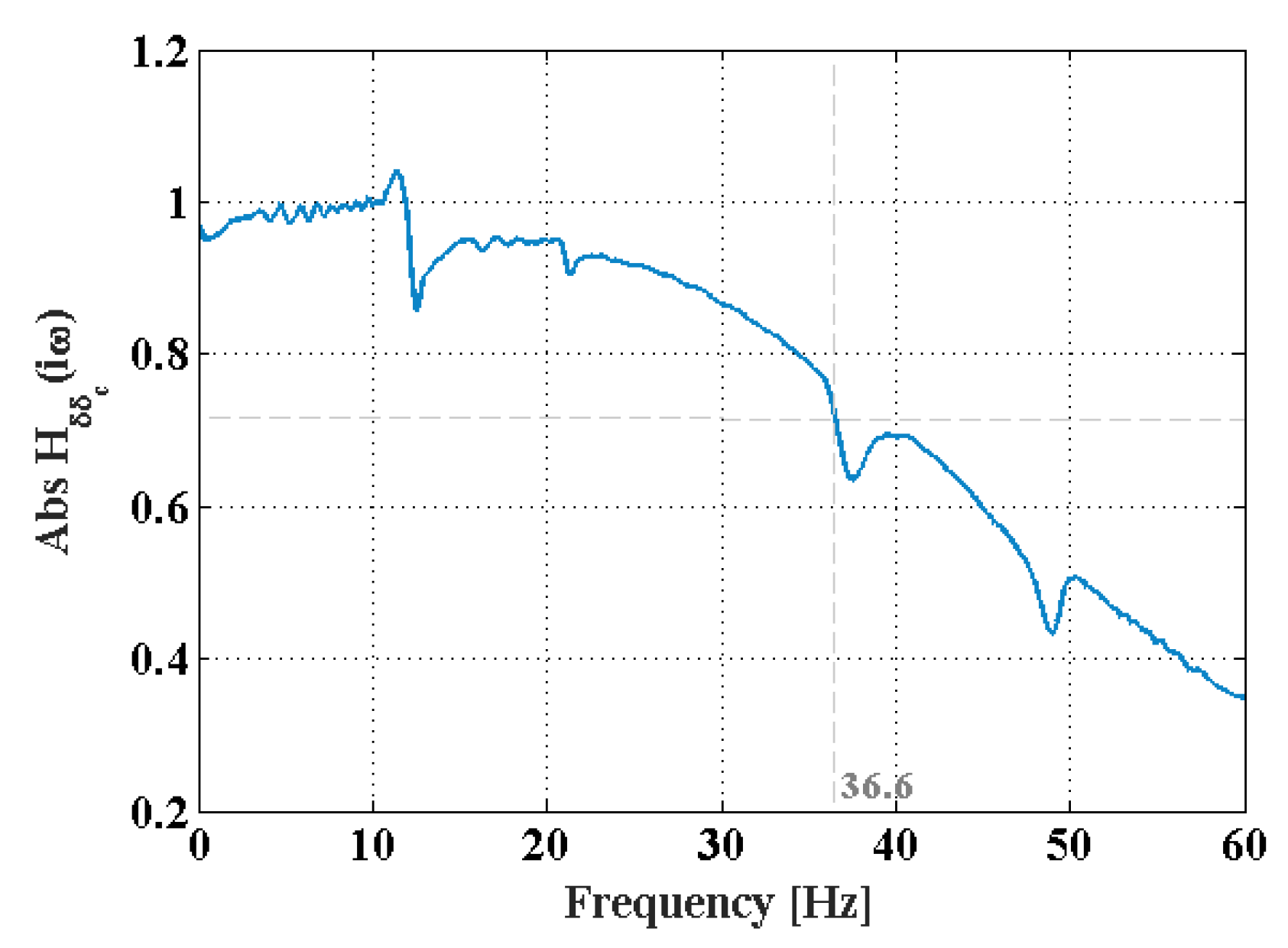
A convenient approximation of this response by rational transfer functions is sought (i.e., a ratio of two polynomials in the complex variable $s=\mathrm{i}\mathrm{\omega }$), $H_{y{\mathrm{\delta }}_c;\mathbf{idt}}\left(\mathrm{i}\mathrm{\omega }\right)\cong H_{y{\mathrm{\delta }}_c;\exp }\left(\mathrm{i}\mathrm{\omega }\right)$; for this purpose, functions from the MATLAB System Identification Toolbox are available. For the air speed in WT of 25 m/s, the experimental $H_{y{\mathrm{\delta }}_c;\exp }\left(\mathrm{i}\mathrm{\omega }\right)$ and identified $H_{y{\mathrm{\delta }}_c;\mathrm{idt}}\left(\mathrm{i}\mathrm{\omega }\right)$ transfer functions are represented in the graphs in Figure 9. $H_{{\mathrm{\delta }}_{c}y;\mathrm{idt}}\left(\mathrm{i}\mathrm{\omega }\right)$ is obtained with an accuracy of estimation of 81.58% (see Figure 10) and is given analytically below as a rational expression of two polynomials, with two zeros and two pairs of complex-conjugated poles ($u:={\mathrm{\delta }}_c$, see Figure 4). The estimation accuracy of over 80% of the transfer function.

$$H_{yu}(s)=\frac{611.7s^2-4.986\times {10}^{4}s-2.533\times {10}^6}{s^4+94s^3+1.327\times {10}^4{s}^2+1.286\times {10}^{5}s+1.232\times {10}^7}$$

(19)

It proved to be excellent during the online vibration dampening process in the wind tunnel.

(e)

The identification of the frequency domain is followed by converting the transfer function (19) into the state space system $\left(\tilde{\mathit{A}},{\tilde{\mathit{B}}}_2,{\tilde{\mathit{C}}}_2,0\right)$; for this purpose, the MATLAB function tf2ss is used

$$\dot{x}=\tilde{\mathit{A}}x+{\tilde{\mathit{B}}}_{2}u,y={\tilde{\mathit{C}}}_{2}x+0u.$$

(20)

Since the interest is the active control of vibration modes, the initial matrices $\tilde{\mathit{A}}$ and ${\tilde{\mathit{B}}}_2$ are subjected to an intermediary state transformation in order to be brought to a „modal form” to highlight the first modal (angular) frequencies ${\mathrm{\omega }}_i$ and dampings ${\mathrm{\zeta }}_i$, $i=1,2$ of each mode of $\tilde{\mathit{A}}$

$$\begin{array}{l}{\mathit{B}}_2=\left[\begin{array}{c}-2.29\\ 2.29\\ -301.18\\ 912.86\end{array}\right],\mathit{A}=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ -{\mathrm{\omega }}_1^2& 0& -2{\mathrm{\zeta }}_1{\mathrm{\omega }}_1& 0\\ 0& -{\mathrm{\omega }}_2^2& 0& -2{\mathrm{\zeta }}_2{\mathrm{\omega }}_2\end{array}\right]\\ \mathit{A}=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ -1024.93& 0& -2.92& 0\\ 0& -11975.1& 0& -91.08\end{array}\right],{\mathit{C}}_2={\left[\begin{array}{c}1\\ 1\\ 0\\ 0\end{array}\right]}^{\mathrm{T}}.\end{array}$$

(21)

The two modal frequencies are 5.1052 Hz (bending mode) and 17.4168 Hz (torsion mode), and the damping factors are 0.0455 and 0.4162, respectively; these values derive from poles −1.459 ± 32.044i, −45.542 ± 99.506i of $H_{yu}(s)$. The synthesis of the control laws starts from with triplets $\left(\mathit{A},{\mathit{B}}_2,{\mathit{C}}_2\right)$ corresponding to WT air speeds $V_1=15 \mathrm{m}/\mathrm{s},$ $V_2=20 \mathrm{m}/\mathrm{s},$ $V_3=25 \mathrm{m}/\mathrm{s},$ $V_3=30 \mathrm{m}/\mathrm{s},$ and so on.

4. Brief Presentation of Active Control Laws

Two control laws, LQG (Linear Quadratic Gaussian) and ${\mathscr{H}}_{\infty }$ will be implemented with the purpose of having reciprocal comparison for vibration attenuation performance.

4.1. Standard LQG Control Synthesis

The stochastic framework of the LQG problem requires the formal presence of a white Gaussian noise component on the right sides of Equation (20). This is because the stochastic content of the turbulence phenomenon is already well known [50]. Therefore, the following system is used as a basis for the control law synthesis of a LQG standard optimal problem (which has its origin in the works of R. E. Kalman from 1960 [51,52])

$$\dot{\mathit{x}}(t)=\mathit{A}\mathit{x}(t)+{\mathit{B}}_{1}w(t)+{\mathit{B}}_{2}u(t),z(t)={\mathit{C}}_1\mathit{x}(t),y(t)={\mathit{C}}_2\mathit{x}(t)+\mathrm{\eta }(t).$$

(22)

A Gaussian component ${\mathit{B}}_{1}w\left(t\right)$ representing the disturbance introduced as aerodynamic turbulence is considered and ${\mathit{B}}_1$ is entered as equal with ${\mathit{B}}_2$. These equations herein characterize a SISO (Single-Input-Single Output) system $w\left(t\right)\to z\left(t\right)$. $\mathit{x}(t)$ is the state vector, $z(t)$ is the quality output, $y(t)$ is the measured output, and $u(t)$ is the control input. $w(t)$ and $\mathrm{\eta }(t)$ are white Gaussian noises on state and measured output, respectively. The role of control LQG is to diminish the influence of the unknown input disturbance $w\left(t\right)$ on the quality output $z\left(t\right)$. The state vector is given by the displacements and velocities of the two modes highlighted in (21)

$$\mathit{x}\left(t\right)={(x_1,x_2,{\dot{x}}_1,{\dot{x}}_2)}^{\mathrm{T}}$$

(23)

(by ${(\cdot )}^{\mathrm{T}}$ is noted the transposed matrix of $(\cdot )$).

The statement of LQG control synthesis: find the control law $u(t)$ that stabilizes the system (18) and minimizes the cost function

$$\begin{array}{l}{J}_{LQG}=\underset{T\to \infty }{\lim }\mathbf{E}\left\{{\displaystyle {\int }_0^T\left[\begin{array}{cc}{z}^{\mathrm{T}}(t)& u\left(t\right)\end{array}\right]\left[\begin{array}{cc}{Q}_J& 0\\ 0& R_J\end{array}\right]\left[\begin{array}{c}z(t)\\ u(t)\end{array}\right]}dt\right\}=\\ \underset{T\to \infty }{\lim }\mathbf{E}\left\{{\displaystyle {\int }_0^T\left[\begin{array}{cc}{\mathit{x}}^{\mathrm{T}}(t)& u(t)\end{array}\right]\left[\begin{array}{cc}\mathit{Q}& 0\\ 0& R_J\end{array}\right]\left[\begin{array}{c}\mathit{x}(t)\\ u(t)\end{array}\right]}dt\right\},\mathit{Q}:={\mathit{C}}_1^{\mathrm{T}}{Q}_J{\mathit{C}}_1.\end{array}$$

(24)

E is the expectation operator [53]. $Q_J$ and $R_J$ are weights on the cost function, which is thought to be a trade-off between the quality output $z(t)$ and control $u(t)$ achieved by manipulating these weights. For example, the decrease of the weight $R_J$ has as a consequence the increase of the control variable $u(t)$ and, implicitly, the decrease of the quality output variable $z(t)$, which represents, after all, the essential objective of active control, that of diminishing as much as possible the influence of the disturbance $w$ in the system. Unfortunately, $u’\mathrm{s}$ growth is physically limited by saturation, and the latter, if it appears, is accompanied by a dangerous behavior of the entire system, called windup [54]. The solution to the LQG problem is given by a controller and a state-estimator, e.g., a Kalman filter providing an estimate of the internal state of the system from measurements. The state estimator is described by

$$\dot{\widehat{x}}(t)=\mathit{A}\widehat{\mathit{x}}(t)+{\mathit{B}}_{2}u(t)+{\mathit{K}}_f\left(y(t)-{\mathit{C}}_2\widehat{\mathit{x}}(t)\right)$$

(25)

and the controller is given by

$$u(t)=-{\mathit{K}}_R\widehat{\mathit{x}}(t)$$

(26)

The two gains ${\mathit{K}}_f$ and ${\mathit{K}}_R$ are obtained by first solving the decoupled algebraic Riccati equations

$${\mathit{A}}^{\mathrm{T}}\mathit{P}+\mathit{P}\mathit{A}-\mathit{P}{\mathit{B}}_2{R}_J^{-1}{\mathit{B}}_2^{\mathrm{T}}\mathit{P}+\mathit{Q}=0,\mathit{A}\mathit{S}+\mathit{S}{\mathit{A}}^{\mathrm{T}}-\mathit{S}{\mathit{C}}_2^{\mathrm{T}}{Q}_{\mathrm{\eta }}^{-1}{\mathit{C}}_2\mathit{S}+{\mathit{B}}_1{Q}_w{\mathit{B}}_1^{\mathrm{T}}=0$$

(27)

$${\mathit{K}}_R={\mathit{R}}^{-1}{\mathit{B}}_2^{\mathrm{T}}\mathit{P}, {\mathit{K}}_f=\mathit{S}{\mathit{C}}_2^{\mathrm{T}}{Q}_{\mathrm{\eta }}^{-1}.$$

(28)

The noise matrices ${\mathit{Q}}_w$ and $Q_{\mathrm{\eta }}$ are described by the relation

$$\mathbf{E}\left\{\left[\begin{array}{c}w(t)\\ \mathrm{\eta }(t)\end{array}\right]\left[\begin{array}{cc}w(t)& \mathrm{\eta }(t)\end{array}\right]\right\}=\left[\begin{array}{cc}{Q}_w& 0\\ 0& Q_{\mathrm{\eta }}\end{array}\right]\mathrm{\delta }(t-\mathrm{\tau })$$

(29)

which characterizes the independence of the two noises $w\left(t\right)$ and $\mathrm{\eta }\left(t\right).$ $\mathrm{\delta }(t-\mathrm{\tau })$ is the Dirac distribution. Substituting the controller (26) in the first Equation (22) and in (25), we obtain the closed-loop system.

$$\begin{array}{c}\dot{\mathit{x}}(t)=\mathit{A}\mathit{x}(t)+{\mathit{B}}_{1}w(t)-{\mathit{B}}_2{\mathit{K}}_R\widehat{\mathit{x}}(t)\\ \dot{\widehat{x}}(t)={\mathit{K}}_f{\mathit{C}}_2\mathit{x}(t)+{\mathit{K}}_f\mathrm{\eta }(t)+\left(\mathit{A}-{\mathit{B}}_2{\mathit{K}}_R-{\mathit{K}}_f{\mathit{C}}_2\right)\widehat{\mathit{x}}(t).\end{array}$$

(30)

The LQG optimal compensator, with input $y\left(t\right)$ and output $u\left(t\right),$ is

$$\begin{array}{c}\dot{\widehat{x}}(t)={\widehat{\mathit{A}}}_{cp}\widehat{\mathit{x}}(t)+{\widehat{\mathit{B}}}_{cp}y(t);\hspace{1em}u\left(t\right)={\widehat{\mathit{C}}}_{cp}\widehat{\mathit{x}}(t)\\ {\widehat{\mathit{A}}}_{cp}=\mathit{A}-{\mathit{B}}_2{\mathit{K}}_R-{\mathit{K}}_f{\mathit{C}}_2; {\widehat{\mathit{B}}}_{cp}={\mathit{K}}_f; {\widehat{\mathit{C}}}_{cp}=-{\mathit{K}}_R.\end{array}$$

(31)

Essentially, the solution to the LQG problem is ensured by the conditions of stabilizability of the pair $\left(\mathit{A},{\mathit{B}}_2\right)$ and detectability of the pair $\left(\mathit{A},{\mathit{C}}_2\right)$ [53]. The fulfillment of these conditions is verified in Section 5, before proceeding to the synthesis of the compensator (31).

It is worth noting that almost all reference books and papers give an endless variation of “technical conditions” for solving the LQG problem, considered equivalent to the ${\mathscr{H}}_{\infty }$ problem (see, for example, [55], Chapter 14, where three more conditions appear that “can be relaxed”), so that the proverb “many men, many minds” is once again true.

4.2. ${\mathscr{H}}_{\infty }$ Synthesis

A simplified version of output feedback ${\mathscr{H}}_{\infty }$ control concerns the system [55]

$$\begin{array}{c}\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+{\mathit{B}}_1\mathit{w}\left(t\right)+{\mathit{B}}_{2}u\left(t\right),\mathit{z}\left(t\right)={\mathit{C}}_1\mathit{x}\left(t\right)+{\mathit{D}}_{12}u\left(t\right),y\left(t\right)={\mathit{C}}_2\mathit{x}\left(t\right)+{\mathit{D}}_{21}\mathit{w}\left(t\right)\\ \dot{\stackrel{⌢}{x}}\left(t\right)=\stackrel{⌢}{\mathit{A}}\stackrel{⌢}{x}\left(t\right)+\stackrel{⌢}{\mathit{B}}y\left(t\right),u\left(t\right)=\stackrel{⌢}{\mathit{C}}\stackrel{⌢}{x}\left(t\right).\end{array}$$

(32)

The top dynamic system (the first three equations) is the plant (the controlled system) $\mathit{G}\left(s\right),$ and the bottom one is the compensator $\mathit{K}\left(s\right),$ in standard notations, $s$ is the Laplace variable. Equations in the time domain (32) are seen as realizations of transfer matrices $\mathit{G}\left(s\right)$ and $\mathit{K}\left(s\right).$ Herein $\mathit{x}\in {ℝ}^4$ is the state vector, $\mathit{z}\in {ℝ}^3$ represents the quality output, which includes the control variable $u,$ $\mathit{z}={\left[\begin{array}{ccc}{x}_1& x_1& u\end{array}\right]}^{\mathrm{T}},$ $\mathit{w}={\left[w,\mathrm{\eta }\right]}^{\mathrm{T}}\in {ℝ}^2$ are the exogenous disturbances on state $\mathit{x}$ and on the measured output $y,$ respectively, $y\in {ℝ}^1$ is the measured output.

There are thousands of papers, workshops, sessions at conferences, MATLAB toolboxes, and numerous books since the theoretical foundations of the ${\mathscr{H}}_{\infty }$ topic were laid by G. Zames [56,57]. We try to present, in what is essential, a formulation and a solution to the suboptimal problem ${\mathscr{H}}_{\infty }$ as approached in this paper.

Obviously, the compensator must have the sine qua non property that it internally stabilizes the system. The ensemble $\left(\mathit{G},\mathit{K}\right)$ (we give up the writing of the variable) is called internally stable if the origin $\left(\mathit{x},\stackrel{⌢}{\mathit{x}}\right):=\left(\mathbf{0},\mathbf{0}\right)$ is asymptotically stable; in other words, the closed loop spectrum of the system $\left(\mathit{x},\stackrel{⌢}{\mathit{x}}\right)$, defined by the eigenvalues of the closed loop matrix ${\mathit{A}}_e$ of the extended system

$$\begin{array}{c}{\dot{\mathit{x}}}_e\left(t\right)={\mathit{A}}_e{\mathit{x}}_e\left(t)+{\mathit{B}}_e\mathit{w}\right(t)\\ \mathit{z}\left(t\right)={\mathit{C}}_e{\mathit{x}}_e\left(t)+{\mathit{D}}_e\mathit{w}\right(t)\\ {\mathit{x}}_e\left(t\right)={\left[{\mathit{x}}^{\mathrm{T}}\left(t\right),{\stackrel{⌢}{\mathit{x}}}^{\mathrm{T}}\left(t\right)\right]}^{\mathrm{T}}\end{array}$$

(33)

must be located in the left open half-plane. There is also the matrix ${\mathit{T}}_{\mathit{z}\mathit{w}}:={\mathit{G}}_{11}+{\mathit{G}}_{12}\mathit{K}{\left(\mathit{I}-{\mathit{G}}_{22}\mathit{K}\right)}^{-1}{\mathit{G}}_{21}$ (the calculation of this matrix involves the partitioning of the matrix $\mathit{G}\left(s\right)$ into four blocks; the notation was simplified by giving up the writing of the Laplace variable $s$) which characterizes the stability and magnitude of the transfer input $\mathit{w}$$\to$output $\mathit{z}$. This matrix has the set of poles included in the set of eigenvalues of the matrix ${\mathit{A}}_e$. Therefore, internal stability guarantees input-output stability, with the reciprocal not being true without some additional assumptions. These are given next:

(i)

The pairs $(\mathit{A},{\mathit{B}}_1)$, $({\mathit{C}}_1,\mathit{A},)$ are stabilizable, respectively, detectable.

(ii)

The pairs $(\mathit{A},{\mathit{B}}_2)$, $({\mathit{C}}_2,\mathit{A},)$ are stabilizable, respectively, detectable.

(iii)

${\mathit{D}}_{12}^{\mathrm{T}}\left[\begin{array}{cc}{\mathit{C}}_1& {\mathit{D}}_{12}\end{array}\right]=\left[\begin{array}{cc}\mathit{O}& \mathit{I}\end{array}\right], \left[\begin{array}{c}{\mathit{B}}_1\\ {\mathit{D}}_{21}\end{array}\right]{\mathit{D}}_{21}^{\mathrm{T}}=\left[\begin{array}{c}\mathit{O}\\ \mathit{I}\end{array}\right]$.

Remark 1 [55].

Assumption (ii) is necessary and sufficient for a controlled system $\mathit{G}$ to be internally stabilizable, but is not needed to prove the equivalence of internal and input-output stabilities. This equivalence does not occur if the controlled system $\mathit{G}$ or compensator $\mathit{K}$ is not stabilizable and detectable.

Internal stability is a concept stronger than input-output stability (more precisely, bounded input-bounded output stability). Indeed, some internal modes of system response may not be seen in the input-output transfer function. In the case of the linear feedback system, internal stability is ensured if the characteristic closed-loop polynomial is stable and if any pol-zero simplifications appearing in the KG loop take place only in the left open half-plane.

Proposition 1 (Corollary 16.3, [55]).

Suppose that assumptions (i) and (iii) hold. Then a controller $\mathit{K}$ is an internally stabilizing compensator if and only if the system is input-output stable (in other words, if ${\mathit{T}}_{zw}$ has all the poles in the left open half-plane.

Remark 2.

We have preferred here to refer to the assumptions in Proposition 1, much simpler to verify than those in Lemma 16.1 [55], which provide the same necessary and sufficient condition given in Proposition 1.

Proposition 2 (Lemma 16.1, [55]).

Suppose that the realizations for $\mathit{G}$ and $\mathit{K}$ are both stabilizable and detectable. Then the feedback connection ${\mathit{T}}_{zw}$ of the realizations for $\mathit{G}$ and $\mathit{K}$ is (a) detectable if $\left[\begin{array}{cc}\mathit{A}-\mathrm{\lambda }\mathit{I}& {\mathit{B}}_2\\ {\mathit{C}}_1& {\mathit{D}}_{12}\end{array}\right]$ has full column rank for all $\mathrm{Re}\mathrm{\lambda }\ge 0;$ (b) stabilizable if $\left[\begin{array}{cc}\mathit{A}-\mathrm{\lambda }\mathit{I}& {\mathit{B}}_1\\ {\mathit{C}}_2& {\mathit{D}}_{21}\end{array}\right]$ has full row rank, for all $\mathrm{Re}\mathrm{\lambda }\ge 0$. Moreover, if (a) and (b) hold, then $K$ is an internally stabilizing compensator if and only if the system is input-output stable.

Optimal ${\mathscr{H}}_{\infty }$ control synthesis: find all compensators $\mathit{K}$ that internally stabilizes the system (32) and such that infinite norm ${\Vert {\mathit{T}}_{\mathit{z}\mathit{w}}(s)\Vert }_{\infty }$ of the transfer function ${\mathit{T}}_{\mathit{z}\mathit{w}}(s)$ is minimized.

Suboptimal ${\mathscr{H}}_{\infty }$ control synthesis: given $\mathrm{\gamma }>0,$ find all compensators $\mathit{K}$ that stabilize internally the system, if there are any, such that ${\Vert {\mathit{T}}_{\mathit{z}\mathit{w}}(s)\Vert }_{\infty }:=\underset{\mathrm{\omega }\in ℝ}{\sup }\overline{\mathrm{\sigma }}\left[{\mathit{T}}_{\mathit{z}\mathit{w}}(j\mathrm{\omega })\right]<\mathrm{\gamma }$.

The first problem is extremely difficult and has no unique solution [55]. We now present the solution of the suboptimal problem, using as a reference Theorem 16.4 [55].

The problem of suboptimal synthesis will be approached for System (32) (first three equations), for which assumptions (i)–(iii) are true.

Proposition 3.

If assumptions (i)–(iii) are true and the realization of $\mathit{K}\left(s\right)$ is stabilizable and detectable, then it is true the equivalence of internal and input-output stabilities.

Proof. 

According to Proposition 2, it is enough to show that the matrices $\left[\begin{array}{cc}\mathit{A}-\mathrm{\lambda }\mathit{I}& {\mathit{B}}_2\\ {\mathit{C}}_1& {\mathit{D}}_{12}\end{array}\right]$, $\left[\begin{array}{cc}\mathit{A}-\mathrm{\lambda }\mathit{I}& {\mathit{B}}_1\\ {\mathit{C}}_2& {\mathit{D}}_{21}\end{array}\right]$ are full column rank, and full row rank, respectively, for all $\mathrm{Re}\mathrm{\lambda }\ge 0$. We assume the opposite for the first matrix. Then there is a $\mathrm{\lambda }\in C$ with $\mathrm{Re}\mathrm{\lambda }\ge 0$ and ${\left[\begin{array}{cc}{\mathit{x}}^{\mathrm{T}}& u\end{array}\right]}^{\mathrm{T}}\ne 0$ such that $\left[\begin{array}{cc}\mathit{A}-\mathrm{\lambda }\mathit{I}& {\mathit{B}}_2\\ {\mathit{C}}_1& {\mathit{D}}_{12}\end{array}\right]$$\left[\begin{array}{c}\mathit{x}\\ u\end{array}\right]$ = 0, or, otherwise written, $\mathit{A}\mathit{x}+{\mathit{B}}_{2}u=\mathrm{\lambda }\mathit{x}, {\mathit{C}}_1\mathit{x}+{\mathit{D}}_{\mathit{12}}u=0$. It immediately follows that $D_{12}^{\mathrm{T}}\left({\mathit{C}}_1\mathit{x}+{\mathit{D}}_{12}u\right)=0$, hence, with assumption (iii) it results that $u=0$; $\mathit{A}\mathit{x}+{\mathit{B}}_{2}u=\mathrm{\lambda }\mathit{x}, {\mathit{C}}_1\mathit{x}+{\mathit{D}}_{12}u=0$ is rewritten $\left[\begin{array}{c}\mathit{A}-\mathrm{\lambda }\mathit{I}\\ {\mathit{C}}_1\end{array}\right]\mathit{x}=0,$ therefore, according to assumption (i), $\mathit{x}=0,$ which together with $u=0$ involves $\left[\begin{array}{cc}{\mathit{x}}^{\mathrm{T}}& u\end{array}\right]=0$, which is absurd. Similarly, it is shown that $\left[\begin{array}{cc}\mathit{A}-\mathrm{\lambda }\mathit{I}& {\mathit{B}}_1\\ {\mathit{C}}_2& {\mathit{D}}_{21}\end{array}\right]$ is full row rank, for all $\mathrm{Re}\mathrm{\lambda }\ge 0$. □

The demonstration also shows that in assumption (iii) values other than the identity matrix $\mathit{I}$ do not affect the validity of Proposition 1.

Proposition 4 (Theorem 16.4 [55]).

There exists a compensator $\mathit{K}$ that internally stabilizes the system (32) and so that ${\Vert {\mathit{T}}_{\mathit{z}\mathit{w}}(s)\Vert }_{\infty }<\mathrm{\gamma }$ if and only if the spectral radius $\mathrm{\rho }\left(\mathit{X},\mathit{Y}\right)<{\mathrm{\gamma }}^2$ where $\mathit{X},\mathit{Y}$ are the semi-positively defined solutions (if any) of the Riccati equations

$$\begin{array}{l}{\mathit{A}}^{\mathrm{T}}\mathit{X}+\mathit{X}\mathit{A}-\mathit{X}\left({\mathit{B}}_2{\mathit{B}}_2^{\mathrm{T}}-{\mathrm{\gamma }}^{-2}{\mathit{B}}_1{\mathit{B}}_1^{\mathrm{T}}\right)\mathit{X}+{\mathit{C}}_1^{\mathrm{T}}{\mathit{C}}_1=0\\ \mathit{A}\mathit{Y}+\mathit{Y}{\mathit{A}}^{\mathrm{T}}-\mathit{Y}\left({\mathit{C}}_2^{\mathrm{T}}{\mathit{C}}_2-{\mathrm{\gamma }}^{-2}{\mathit{C}}_1^{\mathrm{T}}{\mathit{C}}_1\right)\mathit{Y}+{\mathit{B}}_1{\mathit{B}}_1^{\mathrm{T}}=0.\end{array}$$

(34)

When these conditions hold, one such compensator is

$$\begin{array}{l}\dot{\stackrel{⌢}{\mathit{x}}}\left(t\right)={\stackrel{⌢}{\mathit{A}}}_{cp}\stackrel{⌢}{x}\left(t\right)+{\stackrel{⌢}{\mathit{B}}}_{cp}y\left(t\right), u\left(t\right)={\stackrel{⌢}{\mathit{C}}}_{cp}\stackrel{⌢}{x}\left(t\right)\\ {\stackrel{⌢}{\mathit{A}}}_{cp}:=\mathit{A}+{\mathrm{\gamma }}^{-2}{\mathit{B}}_1{\mathit{B}}_1^{\mathrm{T}}\mathit{X}-{\mathit{B}}_2{\mathit{B}}_2^{\mathrm{T}}\mathit{X}-{\left(\mathit{I}-{\mathrm{\gamma }}^{-2}\mathit{Y}\mathit{X}\right)}^{-1}\mathit{Y}{\mathit{C}}_2^{\mathrm{T}}{C}_2,\\ {\stackrel{⌢}{\mathit{B}}}_{cp}:={\left(\mathit{I}-{\mathrm{\gamma }}^{-2}\mathit{Y}\mathit{X}\right)}^{-1}\mathit{Y}{\mathit{C}}_2^{\mathrm{T}}, {\stackrel{⌢}{\mathit{C}}}_{cp}:=-{\mathit{B}}_2^{\mathrm{T}}\mathit{X}\end{array}$$

(35)

with$\mathit{X},\mathit{Y}$solutions of algebraic Riccati Equation (34).

The Equation (35) or the System (32) characterizes a MIMO (Multi-Input-Multi-Output) system $\mathit{w}\to \mathit{z}$.

Remark 3.

It is risky to determine a priori which is the best solution to a given problem. Often, the best solution does not actually exist, as shown in [18,46,47]. As an example, we refer to a multitude of control laws applied to solve an active control problem. It turned out that all methods of control synthesis, LQG, $\mathrm{LQG}/\mathrm{LTR},$ preview control, receding horizon, ${\mathscr{H}}_{\infty },$ robust ${\mathscr{H}}_{\infty },$ sliding mode, backstepping, neural control, fuzzy logical control, neuro-fuzzy control etc., were competitive in giving substantially similar results.

A justification for the optimal ${\mathscr{H}}_{\infty }$ control resides in the min-max nature of the problem, with the argument that minimizing the “peak” of the transfer $\mathit{w}\to \mathit{z}$ necessarily renders the magnitude of ${\mathit{T}}_{\mathit{z}\mathit{w}}$ small at all frequencies. Otherwise stated, minimizing the ${\mathscr{H}}_{\infty }$-norm of a transfer function is equivalent to minimizing the energy in the output signal due to the inputs with the worst possible frequency distribution. This improvement of the “worst-case scenario” has a direct correspondent in the active vibration control problem and seems particularly attractive for light structures with embedded piezoelectric actuators.

Remark 4.

In the problem ${\mathscr{H}}_{\infty },$ unlike the LQG problem, the variables $\mathit{w}$ and $\mathit{z}$ are vectors by concatenation: $\mathit{w}$ concatenates the disturbances on input and output, and $\mathit{z}$ concatenates an actual output of quality and control variable $u.$

5. Results of Active Control Tests

The experimental setup for smart wing active control in WT is shown in Figure 11. The user interface runs on the PC-type computer (1), from which the start and stop of the experiment are commanded and the signals from the sensors are monitored. The control algorithms PD, LQG, and ${\mathscr{H}}_{\infty }$ are implemented in the same LabVIEW project, which is compiled and downloaded on a real time computing system type PXI-1082 (2). The PXI system is equipped with a PXI-6225 data acquisition board (3) with analog and digital input channels. A voltage source (5) supplies the driver (6) of the linear motor (7), which drives the wing aileron (10), with the mechanical system CR-CM, which converts the linear motion into rotational motion. A capacitive accelerometer (8) measures the acceleration of the wing. A signal conditioner/load amplifier (9) takes the signal from the accelerometer and converts it into a voltage signal proportional to the displacement of the wing. To measure the deflection angle of the aileron, a Winkel MOT 13 encoder (7) connected to the connector board (4) of the acquisition board (3) is used, which feeds the angular transducer (7).

The mathematical model of the LQG control law described in Section 4 must be completed with the numerical values of the key parameters, which are the weights in the Riccati equations. The numerical simulations outlined values for these weights, which were thus established online: $Q_{\mathrm{\eta }}=0.000001,$ $Q_w=5,$ $Q_J=1,$ $R_J=0.1$. The influence matrix ${\mathit{B}}_1$ of the perturbation is chosen ${\mathit{B}}_1={\mathit{B}}_2$. The quality output selection matrix is ${\mathit{C}}_1=\left[\begin{array}{cccc}1& 0& 0& 0\end{array}\right],$ as active vibration control focuses on bending modal displacement $x_1:=q_1,$ and the matrix ${\mathit{C}}_2=\left[\begin{array}{cccc}1& 1& 0& 0\end{array}\right]$ indicates that the accelerometer collects information about both modal displacements $x_1, x_2.$

Unlike the case of the LQG mathematical model, the ${\mathscr{H}}_{\infty }$ mathematical model (32) will be structured by introducing static weights, as illustrated in the block diagram in Figure 12 (see also [58]), with the benefit of manipulating vibration attenuation performance and increasing the robustness of the system [59]. The quality output $\mathit{z}={\left[\begin{array}{ccc}{x}_1& x_2& u\end{array}\right]}^{\mathrm{T}}$ is replaced by the weighted quality output $\mathit{e}={\left[\begin{array}{ccc}{e}_1& e_2& e_3\end{array}\right]}^{\mathrm{T}}:={\left[\begin{array}{ccc}{W}_{z_1}{z}_1& W_{z_2}{z}_2& W_{u}u\end{array}\right]}^{\mathrm{T}};$ the disturbance $\mathit{w}={\left[\begin{array}{cc}w& \mathrm{\eta }\end{array}\right]}^{\mathrm{T}}$ is replaced by the weighted (by software) disturbance $\tilde{\mathit{w}}={\left[\begin{array}{cc}\tilde{w}& \tilde{\mathrm{\eta }}\end{array}\right]}^{\mathrm{T}}:={\left[\begin{array}{cc}{W}_{x}w& W_{\mathrm{\eta }}\mathrm{\eta }\end{array}\right]}^{\mathrm{T}}$. The equations of the controlled system in (32) are rewritten as follows:

$$\begin{array}{c}\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+{\tilde{\mathit{B}}}_1\mathit{w}\left(t\right)+{\mathit{B}}_{2}u\left(t\right),\mathit{e}\left(t\right)={\tilde{\mathit{C}}}_1\mathit{x}\left(t\right)+{\tilde{\mathit{D}}}_{12}u\left(t\right),y\left(t\right)={\mathit{C}}_2\mathit{x}\left(t\right)+{\tilde{\mathit{D}}}_{21}\mathit{w}\left(t\right)\\ {\tilde{\mathit{B}}}_1=\left[\begin{array}{cc}{b}_1& 0\\ b_2& 0\\ b_3& 0\\ b_4& 0\end{array}\right]\left[\begin{array}{cc}{W}_x& 0\\ 0& W_{\mathrm{\eta }}\end{array}\right],{\tilde{\mathit{D}}}_{21}=\left[\begin{array}{cc}0& W_{\mathrm{\eta }}\end{array}\right]\\ {\tilde{\mathit{C}}}_1=\left[\begin{array}{cccc}{W}_{z_1}& 0& 0& 0\\ 0& W_{z_2}& 0& 0\\ 0& 0& 0& 0\end{array}\right],{\tilde{\mathit{D}}}_{12}=\left[\begin{array}{c}0\\ 0\\ W_u\end{array}\right],{\mathit{C}}_2:=\left[\begin{array}{cccc}1& 1& 0& 0\end{array}\right]\end{array}$$

(36)

where $b_i,i=1,\dots ,4$ are the entries in the matrix ${\mathit{B}}_2$. Again, the numerical simulations outlined values for these weights, which were then established online:$W_{z_1}=0.5; \hspace{1em}{W}_{z_2}=0$ and $W_u=0.3$ are weights on the quality output (first mode displacement, second mode displacement, and control), $W_x=3$ and $W_{\mathrm{\eta }}=0.01$ are weights on the state perturbation and on the output perturbation, respectively. These weights characterize the compensator called „strong” below. With $W_{\mathrm{\eta }}=\mathrm{0.01}$ and $W_u=1.2$ we have a so called “standard” compensator. Decreasing further $W_u$ to $W_u=0.1$, we have the compensator called “superstrong” with accentuated vibration attenuation properties, as a result of increased control. The names “standard”, “strong”, and “superstrong” are given in correlation with the maneuvers performed on the weights but are perfectly proven, as will be seen, by the experimental results.

Before proceeding to the synthesis of the compensator ${\mathscr{H}}_{\infty }$ for the system governed by the matrix quartet (21), the fulfilment of the conditions from the Proposition 1 and the Proposition 2 is verified making replacements ${\mathit{B}}_1\to {\tilde{\mathit{B}}}_1,$ ${\mathit{C}}_1\to {\tilde{\mathit{C}}}_1,$ ${\mathit{D}}_{12}\to {\tilde{\mathit{D}}}_{12},$ ${\mathit{D}}_{21}\to {\tilde{\mathit{D}}}_{21}.$ As shown in Remark 2, in condition (iii) in the first equality instead of $\mathit{I}$ we obtain $W_u^2$ and in the second $b_4{W}_x{W}_{\mathrm{\eta }}$.

As “smart”, a wing system can only be a feedback system in which information about the output behavior $y\left(t\right)$ is taken with the sampling frequency ${\mathrm{\nu }}_s={\mathrm{\tau }}^{-1},$ where $\mathrm{\tau }$ is the sample time, i.e., a scalar interval between samples; in the project, $\mathrm{\tau }$ was taken at 0.001 s. The retrieved information on $y\left(t\right)$ is processed, generating the control variable $u\left(t\right)$, in accordance with the assumed control law, ${\mathscr{H}}_{\infty }$ or LQG. Note that the structure of the control law $u\left(t\right)$ has been synthesized off line, in continuous time, and that it must be implemented in discrete time at times $n\mathrm{\tau }$. Therefore, the displacement information $y\left(n\mathrm{\tau }\right)$ is received from the accelerometer (Figure 11), it is calculated based on this information, the control, $u\left(n\mathrm{\tau }\right),$ which will be applied at times $\left(n+1\right)\mathrm{\tau }$, remains constant throughout the interval $\left[\left(n+1\right)\mathrm{\tau },\left(n+2\right)\mathrm{\tau }\right]$. This is the so-called zero-order hold discretization. We add that discretization is also intuitively justified by the low value of $\mathrm{\tau }$.

To exemplify discretization in the case of the law (31), the calculations start with the general solution of the second equation in (32)

$$\widehat{x}(t)=e^{{\widehat{\mathit{A}}}_{cp}\left(t-t_0\right)}\widehat{\mathit{x}}(t_0)+{\displaystyle {\int }_{t_0}^t{e}^{{\widehat{\mathit{A}}}_{cp}\left(t-s\right)}}{\widehat{\mathit{B}}}_{cp}y\left(s\right)ds.$$

(37)

Substituting $t_0=n\mathrm{\tau }, t=\left(n+1\right)\mathrm{\tau }$ and taking into account the choice of zero-order hold $y\left(t\right)=y\left(n\mathrm{\tau }\right), \mathrm{for} t\in \left[n\mathrm{\tau },\left(n+1\right)\mathrm{\tau }\right]$ yields

$$\widehat{x}\left[\left(n+1\right)\mathrm{\tau }\right]=e^{{\widehat{\mathit{A}}}_{cp}\mathrm{\tau }}\widehat{\mathit{x}}(n\mathrm{\tau })+{\displaystyle {\int }_{n\mathrm{\tau }}^{\left(n+1\right)\mathrm{\tau }}{e}^{{\widehat{\mathit{A}}}_{cp}\left[\left(n+1\right)\mathrm{\tau }-s\right]}}{\widehat{\mathit{B}}}_{cp}dsy\left(n\mathrm{\tau }\right).$$

(38)

Changing in integral the Laplace variable s by $S=\left(n+1\right)\mathrm{\tau }-s,$ discrete LQG compensator equation results

$$\begin{array}{l} \widehat{x}\left[\left(n+1\right)\mathrm{\tau }\right]=e^{{\widehat{\mathit{A}}}_{cp}\mathrm{\tau }}\widehat{\mathit{x}}(n\mathrm{\tau })+{\displaystyle {\int }_0^{\mathrm{\tau }}{e}^{{\widehat{\mathit{A}}}_{cp}\mathrm{\tau }}}{\widehat{\mathit{B}}}_{cp}dSy\left(n\mathrm{\tau }\right)={\widehat{\mathit{A}}}_{cp,D}\widehat{\mathit{x}}(n\mathrm{\tau })+{\widehat{\mathit{B}}}_{cp,D}y\left(n\mathrm{\tau }\right)\\ {\widehat{\mathit{A}}}_{cp,D}:=e^{{\widehat{\mathit{A}}}_{cp}\mathrm{\tau }},{\widehat{\mathit{B}}}_{cp,D}:={\widehat{\mathit{A}}}_{cp}^{-1}\left(e^{{\widehat{\mathit{A}}}_{cp}\mathrm{\tau }}-I_4\right){\widehat{\mathit{B}}}_{cp},u\left[\left(n+1\right)\mathrm{\tau }\right]={\widehat{\mathit{C}}}_{cp}\widehat{\mathit{x}}\left[\left(n+1\right)\mathrm{\tau }\right]\end{array}$$

(39)

We take as a starting point the matrix quartet (21). All the data is now gathered to numerically write the discrete LQR compensator matrices

$$\begin{array}{l}{\widehat{\mathit{A}}}_{cp,D}=\left[\begin{array}{cccc}-0.0488& -0.0586& -0.00003& -0.00004\\ 0.0484& 0.0581& 0.00003& 0.00004\\ -1.6021& -1.5811& 0.0085& -0.0011\\ -4.0657& -4.1820& -0.0023& 0.0063\end{array}\right]\\ {\widehat{\mathit{B}}}_{cp,D}=\left[\begin{array}{c}5.8799\\ -4.8346\\ 158.6613\\ 408.0732\end{array}\right],{\mathit{C}}_{cp}=\left[\begin{array}{cccc}1.8145& -0.00& 0.0725& -0.00\end{array}\right].\end{array}$$

(40)

Proceeding similarly for the discrete ${\mathscr{H}}_{\infty }$ compensator, the matrices are obtained.

$$\begin{array}{l}{\stackrel{⌢}{\mathit{A}}}_{cp,D}=\left[\begin{array}{cccc}0.7212& -0.0233& -0.0056& -0.00001\\ 0.3040& 0.9850& 0.0079& -0.0009\\ -30.2510& 0.8736& -0.2353& 0.0004\\ 78.8723& -14.3941& 2.0692& 0.9059\end{array}\right]\\ {\stackrel{⌢}{\mathit{B}}}_{cp,D}=\left[\begin{array}{c}0.0004\\ 0.0002\\ -0.0163\\ 0.0554\end{array}\right];{\stackrel{⌢}{\mathit{C}}}_{cp,D}=\left[\begin{array}{cccc}74616.25& -0.00& 1792.40& -0.00\end{array}\right].\end{array}$$

(41)

Relevant results for the performance of vibration active control are summarized by the graphs in Figure 13, Figure 14 and Figure 15. In Figure 13, the simulation of mathematical models with the two laws, LQG and ${\mathscr{H}}_{\infty },$ attests, at V = 25 m/s, a reduction of about 18 dB at the basic modal frequency of 5 Hz for both laws compared to the uncontrolled vibration regime (UC). In literature, for an experiment carried out also in a wind tunnel, a reduction of about 6 dB of the modal frequency 7 Hz is shown in [60,61]. The attenuation of $y$ displacement in WT is illustrated in the time domain, in pure air, Figure 14, top, and in turbulent regime, Figure 14, middle. By superposing the graphs, one can see the efficiency of the control. Figure 14, down, highlights the efficiency of the electric broadband servo actuator: the movement of the aileron $\mathrm{\delta }$ follows the control $u$ very well for the experiment in WT. Figure 15 shows the net faster extinction of the transient vibration at rest, at the suspension of the excitation, when the active control is present.

Next, the AC (Active Control) versus UC (UnControlled) results are presented quantitatively in

Table 3. Pure air, V = 25 m/s.

Control Law	#	UC	AC	Attenuation
${\mathscr{H}}_{\infty }$ Normal (−37.04%)	1	0.096	0.052	−45.83%
	2	0.085	0.061	−28.24%
LQG (−41.49%)	1	0.061	0.045	−26.23%
	2	0.085	0.044	−48.24%
	3	0.080	0.040	−50.00%

,

Table 4. Turbulence, V = 25 m/s.

Control Law	#	UC	AC	Attenuation
${\mathscr{H}}_{\infty }$ Strong (−24.61%)	1	0.642	0.537	−16.36%
	2	0.746	0.524	−29.76%
	3	0.722	0.522	−27.70%
${\mathscr{H}}_{\infty }$ super-strong (−36.04%)	1	0.815	0.447	−45.15%
	2	0.749	0.498	−33.51%
	3	0.662	0.467	−29.46%
LQG (−26.75%)	1	0.784	0.558	−28.83%
	2	0.635	0.529	−16.69%
	3	0.726	0.447	−34.71%

and

Table 5. Attenuation, comparison, pure air.

Control Law	V = 25 m/s	V = 33 m/s
${\mathscr{H}}_{\infty }$ robust	−37.04%	−30.16%

. The vibration attenuation coefficients are calculated with the relation

$$C_{ij}=\frac{\mathrm{std}\left(A{C}_j\right)-\mathrm{std}\left(U{C}_i\right)}{\mathrm{std}\left(U{C}_i\right)}$$

(42)

in which the standard deviation (in mm) is noted with std. For a motion signal recorded by the accelerometer as in Figure 14, with random evolution, the quantification given by the relation (42) is used naturally.

Table 3 and Table 4 show a comparison of vibration attenuation at 25 m/s from a double perspective: pure air versus turbulence and ${\mathscr{H}}_{\infty }$ versus LQG regimes. It was specified in the synthesis that the introduced static weights, according to the block diagram in Figure 12, allow a choice regarding the relaxation or intensification of the control variable, with consequences for the relaxation or intensification of the vibration attenuation. In this context, the regimes marked “strong” and “superstrong” were also launched in the process. Table 5 shows a comparison regarding the vibration attenuation in pure air at two air velocities by applying a ${\mathscr{H}}_{\infty }$ control law. The percentage attenuations in Table 3, Table 4 and Table 5 can be interpreted as attenuation values in dB. For example, an attenuation of −45.83% would mean a vibration attenuation of about 33 dB.

6. Concluding Remarks

There are several particularities of this paper that deserve to be emphasized. An elastic wing model has been designed and used, whose resonant frequencies can in principle be achieved in a predetermined sequence, starting from the geometry of the longeron. The result of active vibration control proves to be more relevant than in the case of a rigid wing supported on two springs that simulates only two resonant frequencies. Although the mathematical model of the wing system included only two modes, no harmful, spillover type high-frequency oscillating phenomena were observed in the WT, neither in the absence nor in the presence of air turbulence. Spillover is an instability of a closed-loop system caused by the observation or excitation of unmodeled dynamics by sensors or actuators; see [62]. A second aspect is to highlight the effect of turbulence generated in the WT. The level of vibration in the absence of GT is relatively low, as shown by the comparison of Table 3 and Table 4. In the presence of disturbances, the level of (controlled) oscillations increases by an order of magnitude.

It is known that applying active control to the wing reduces the load on the wing and, implicitly, reduces the bending moments of the wing. Consequently, the designer can extend the wing span or reduce the structural weight of the wing. Increasing the span for a given wing area improves the aerodynamic efficiency of the wing; that is, it increases the lift-to-drag ratio. In addition, more importantly, the active control of vibrations prevents the appearance of flutter, eventually leading to the expansion of the flight envelope.

The use of weights, even only static ones, in the ${\mathscr{H}}_{\infty }$ synthesis can ensure the robustness of the system and gives the possibility to manipulate these weights in order to obtain a more severe reduction of the vibrations, as shown in Table 4 and Table 5. In fact, the problem of static weights in the ${\mathscr{H}}_{\infty }$ model can be treated in terms of robustness, with the variables newly introduced on the diagram in Figure 11 being called fictitious inputs and outputs [18,63,64,65,66].