A Joint Surface Contact Stiffness Model Considering Micro-Asperity Interaction
Abstract
1. Introduction
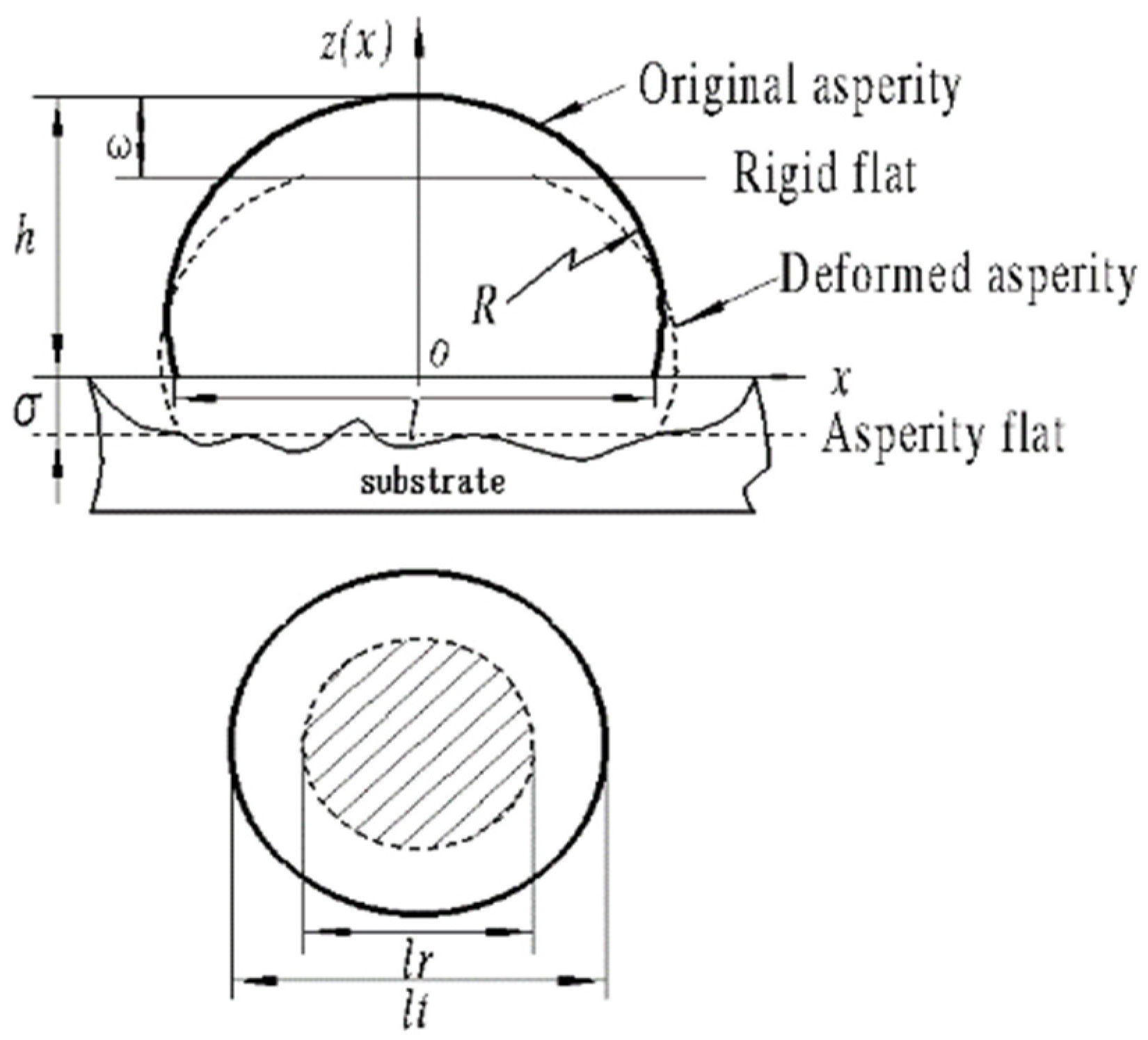
2. Single Micro-Asperity Body Deformation Mechanism
2.1. Elastic Deformation Regime
2.2. Elastoplastic Deformation Regime
2.3. Plastic Deformation Stage
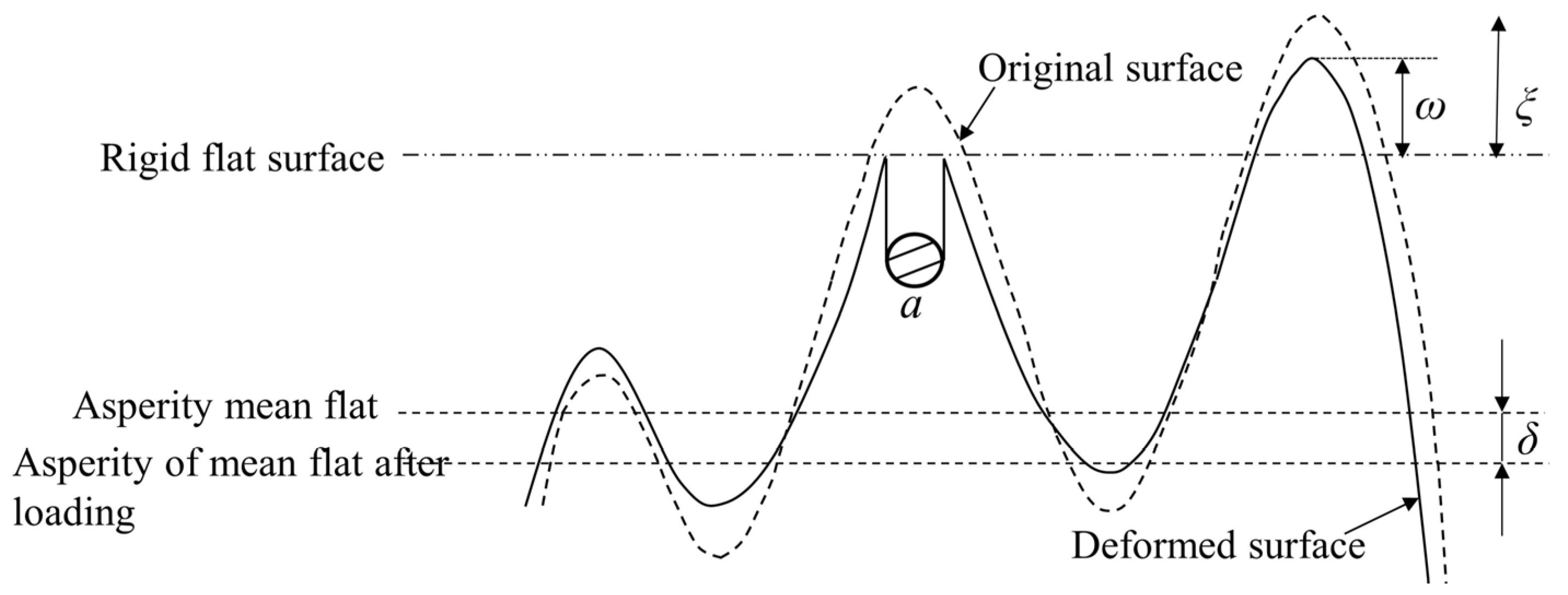
3. Contact Stiffness Affected by Micro-Asperities Interactions
3.1. Micro-Asperity Deformation
3.2. Micro-Asperity Contact Stiffness
4. The Contact Characteristics of the Interface
4.1. Normal Contact Load on the Contact Interface
4.2. The Normal Contact Stiffness of the Contact Interface
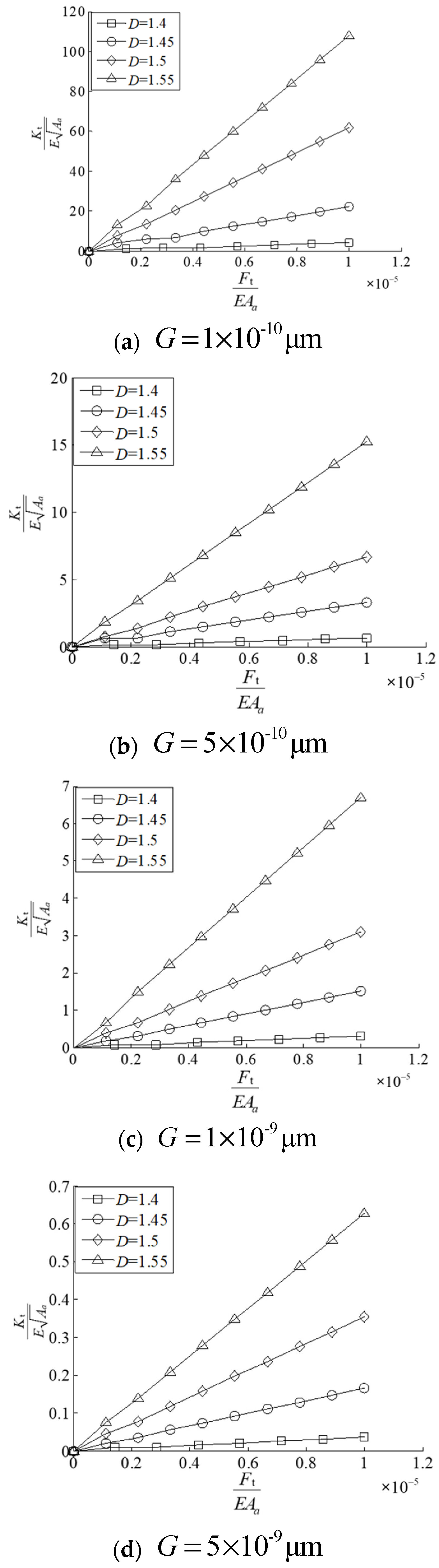
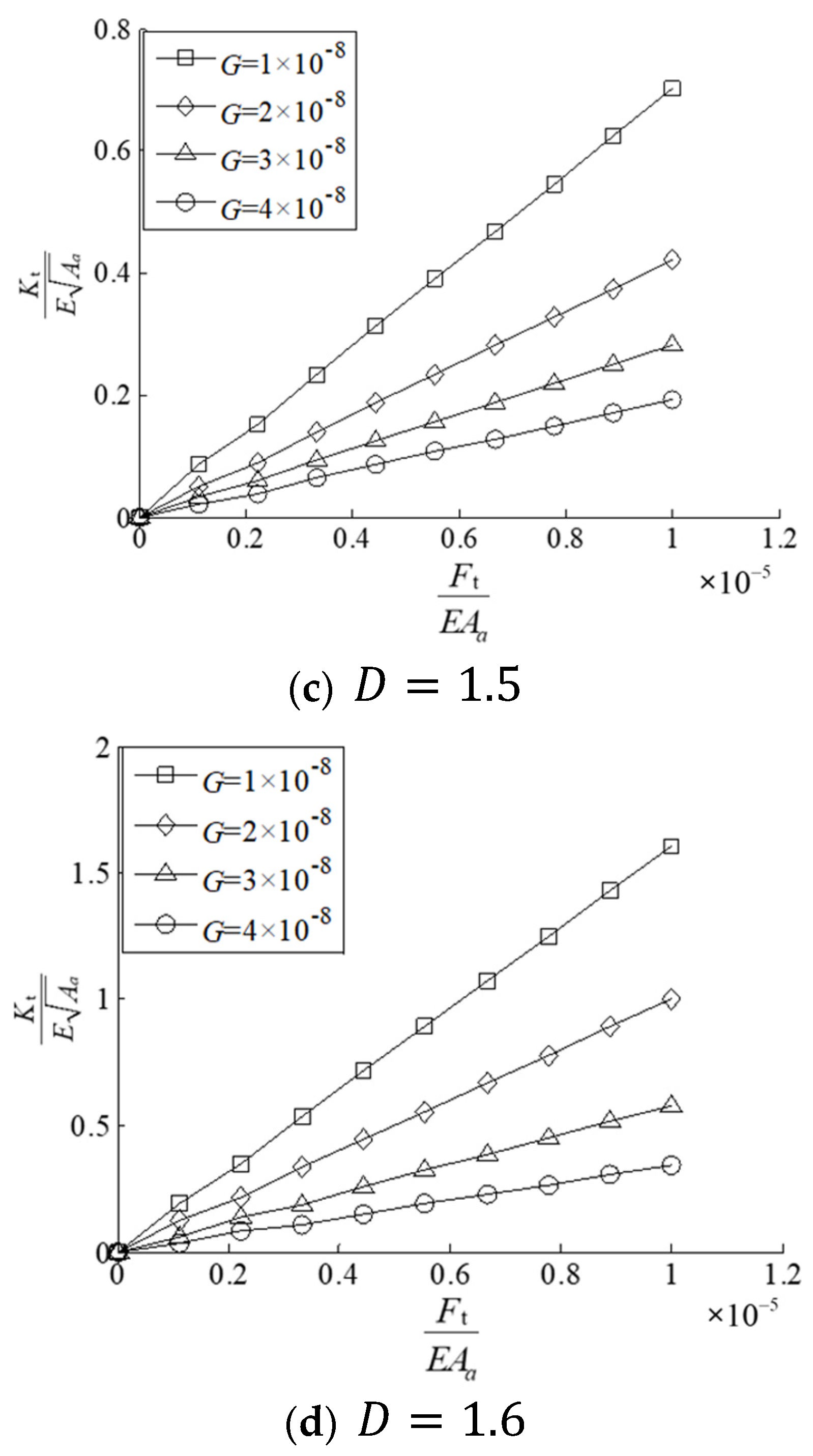
5. Simulation and Result Analysis of the Normal Stiffness Model for the Contact Interface
5.1. Model Simulation
5.2. Model Validation
6. Conclusions
- (1)
- The introduction of the K-E elastoplastic contact theory has led to the development of a comprehensive contact stiffness model, considering the impact of micro-asperity interactions throughout the entire deformation process, including elasticity, first elastoplasticity, second elastoplasticity, and complete plastic deformation.
- (2)
- The influence of fractal parameters on contact stiffness was analyzed. Specifically, the increase in fractal dimension D and decrease in scale parameter G will weaken the interaction among asperities, reducing deformation and increasing contact stiffness. In other words, smoother machined surfaces exhibit higher contact stiffness.
- (3)
- Considering the interaction of micro-asperities will lead to an overall increase in the total deformation, resulting in lower stiffness values calculated using the model proposed in this paper.
- (4)
- With the consideration of asperity interaction, the established fractal contact model is suitable for fixed joint interfaces, such as bolted joint structures, but not for moveable interfaces.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Liu, Y.; Zhou, P. Assembly Success Rate Calculation Method for Aero-Engine Based on Improved Taguchi Method. J. Propuls. Technol. 2018, 39, 653–659. [Google Scholar]
- Xie, S.; Ai, Y.; Zhao, D. Study on Contact Stiffness of Three-dimensional Rough Surface Based on Stochastic Process. Surf. Technol. 2022, 51, 326–334. (In Chinese) [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. 1966, 295, 300–319. [Google Scholar]
- Liu, Y.; Xia, T.; Chen, Z. The Development of Statistical Contact Model for Rough Surface. Tribology 2020, 40, 395–406. [Google Scholar]
- Ren, Y.; Beards, C.F. Identification of’ Effective’ Linear Joints Using Coupling and Joint Identification Techniques. J. Vib. Acoust. 1998, 120, 331. [Google Scholar] [CrossRef]
- Tian, H.; Zhong, X.; Zhao, C. One Loading Model of Joint Interface Considering Elastoplastic and Variation of Hardness with Surface Depth. J. Mech. Eng. 2015, 51, 90–104. [Google Scholar] [CrossRef][Green Version]
- Aeroengine Design Manual Editorial Board. Aeroengine Design Manual; Aviation Industry Press: Beijing, China, 2001; Volume 18, pp. 15–19. [Google Scholar]
- Zhai, C.; Gan, Y.; Hanaor, D.; Proust, G.; Retraint, D. The Role of Surface Structure in Normal Contact Stiffness. Exp. Mech. 2015, 56, 359–368. [Google Scholar] [CrossRef]
- Shi, J.P.; Ma, K.; Liu, Z.Q. Normal Contact Stiffness on Unit Area of a Mechanical Joint Surface Considering Perfectly Elastic Elliptical Asperities. J. Tribol. 2012, 134, 031402. [Google Scholar] [CrossRef]
- Shi, J.; Cao, X.; Hu, Y.; Zhu, H. Statistical Analysis of Tangential Contact Stiffness of Joint Surfaces. Arch. Appl. Mech. 2015, 85, 1997–2008. [Google Scholar] [CrossRef]
- Li, L.; Cai, A.; Ruan, X. Statistical Models of Mechanical Joint Interface Considering Elastic-plastic Deformation. China Sci. 2016, 11, 459–463. [Google Scholar]
- Zhang, W.; Zhang, X.; Wen, S. A Normal Contact Stiffness Model of Joint Surfaces Considering Interaction of Deformations of Substrate and Asperity. J. Xi’an Jiaotong Univ. 2020, 54, 115–121. [Google Scholar]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Ding, X.; Yan, R.; Jia, Y. Construction and Analysis of Fractal Contact Mechanics Model for Rough Surface Based on Base Length. Tribology 2014, 34, 341–347. [Google Scholar]
- Wang, Q.; Zhang, L.; Chen, B. A Deterministic Contact Model Considering the Interaction Between Asperities. J. Xi’an Jiaotong Univ. 2018, 52, 91–97. [Google Scholar]
- Shi, J.; Liu, J.; Ding, X.; Yang, Z.; Gong, H. On the Multi-scale Contact Behavior of Metal Rough Surface Based on Deterministic Model. J. Mech. Eng. 2017, 53, 111–120. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L.; Du, B. Re-definition of Asperity-peak for Deterministic Contact Model on Rough Surfaces. J. Xi’an Jiaotong Univ. 2016, 50, 115–120. [Google Scholar]
- He, L.; Zhu, J. Proposal and Development of Rough Surface Contact Fractal Model. Tribology 1996, 88–97. (In Chinese) [Google Scholar]
- Zhang, X.; Huang, Y.; Han, Y. Fractal Model of the Normal Contact Stiffness of Machine Joint Surfaces Based on the Fractal Contact Theory. China Mech. Eng. 2000, 11, 727–729. [Google Scholar]
- Wen, S.; Zhang, X.; Wu, M. Fractal Model and Simulation of Normal Contact Stiffness of Joint Interfaces and its Simulation. Trans. Chin. Soc. Agric. Mach. 2009, 40, 197–202. [Google Scholar]
- Yang, H.; Fu, W.; Wang, W.; Yang, S.; Li, P.; Wang, W. Calculation Model of the Normal Contact Stiffness of Joints Based on the Fractal Geometry and Contact Theory. J. Mech. Eng. 2013, 49, 102–107. [Google Scholar] [CrossRef]
- Li, X.; Liang, Y.; Zhao, G.; Ju, X.; Yang, H. Fractal Model for Normal Stiffness of Joint Surface Considering Friction Factors and its Simulation. J. Vib. Meas. Diagn. 2013, 33, 210–213+336. [Google Scholar]
- Li, X.-P.; Ju, X.; Zhao, G.-H.; Liang, Y.-M.; Wen, B.-C. Fractal Prediction Model for Tangential Contact Stiffness of Joint Surface Considering Friction Factors and its Simulation Analysis. Tribology 2013, 33, 463–468. [Google Scholar]
- Wang, R.; Zhu, L.; Zhu, C. Investigation of Contact Stiffness Model for Joint Surfaces Based on Domain Expansion Factor and Asperity Interaction. J. Mech. Eng. 2018, 54, 88–95. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, Y. On the normal contact stiffness and contact resonance frequency of rough surface contact based on asperity micro-contact statistical models. Eur. J. Mech.-A/Solids 2019, 75, 450–460. [Google Scholar] [CrossRef]
- Kang, H.; Li, Z.M.; Liu, T.; Zhao, G.; Jing, J.; Yuan, W. A novel multi-scale model for contact behavior analysis of rough surfaces with the statistical approach. Int. J. Mech. Sci. 2021, 212, 106808. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Jin, S.; Zhang, J. A multi-scale model of real contact area for linear guideway based on the fractal theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 5796–5813. [Google Scholar] [CrossRef]
- Sun, X.; Meng, C.; Duan, T. Fractal model of thermal contact conductance of two spherical joint surfaces considering friction coefficient. Ind. Lubr. Tribol. 2022, 74, 93–101. [Google Scholar] [CrossRef]
- Pan, W.; Sun, Y.; Li, X.; Song, H.; Guo, J. Contact mechanics modeling of fractal surface with complex multi-stage actual loading deformation. Appl. Math Modell. 2024, 128, 58–81. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Wu, S. Two-dimensional contact of asperities to multi-stage contact between curved fractal surfaces based on attitude angle. Tribol. Int. 2023, 189, 108989. [Google Scholar] [CrossRef]
- Li, Y.H.; Shen, F.; Güler, M.A.; Ke, L.L. A rough surface electrical contact model considering the interaction between asperities. Tribol. Int. 2023, 190, 109044. [Google Scholar] [CrossRef]
- Shen, F.; Li, Y.H.; Ke, L.L. On the size distribution of truncation areas for fractal surfaces. Int. J. Mech. Sci. 2023, 237, 107789. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, Q. Closure Deformation Model for Rock Joints Considering Asperity Interaction. Chin. J. Geotech. Eng. 2015, 37, 853–859. [Google Scholar]
- Majumdar, A.; Bhushan, B. Fractal Model of Elastic-plastic Contact Between Rough Surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An Asperity Microcontact Model Incorporating the Transition from Elastic Deformation to Fully Plastic Flow. J. Tribol. 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Raous, M.; Jean, M.; Moreau, J.J. Contact Mechanics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kogut, L.; Etsion, I. Elastic-plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Yun, R.; Ding, B. New Fractal Contact Model Considered Multi-Scale Levels. J. Mech. Eng. 2019, 55, 80–89. [Google Scholar] [CrossRef]
- Zhou, H.; Long, X.; Meng, G.; Liu, X. A Stiffness Model for Bolted Joints Considering Asperity Interactions of Rough Surface Contact. J. Tribol. 2021, 144, 011501. [Google Scholar] [CrossRef]
- Morag, Y.; Etsion, I. Resolving the Contradiction of Asperities Plastic to Elastic Mode Transition in Current Contact Models of Fractal Rough Surfaces. Wear 2007, 262, 624–629. [Google Scholar] [CrossRef]
- Zhang, X.L.; Chen, Y.H.; Wen, S.H.; Lan, G.S.; Ding, H.Q.; Wang, N.S.; Zhang, Z.Y. The Model of Normal Contact Stiffness of Joint Interfaces Incorporation Elastoplastic Deformation Mechanism. J. Vib. Eng. 2015, 28, 91–99. [Google Scholar]
- Tian, X.; Wang, W.; Fu, W.; Gao, Z.; Lou, L.; Wu, J.; Li, P. Contact Stiffness Model of Mechanical Joint Surfaces Considering the Asperity Interaction. J. Mech. Eng. 2017, 53, 149–159. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Zhu, H. A Contact Stiffness Model of Machined Plane Joint Based on Fractal Theory. J. Tribol. 2010, 132, 011401. [Google Scholar] [CrossRef]


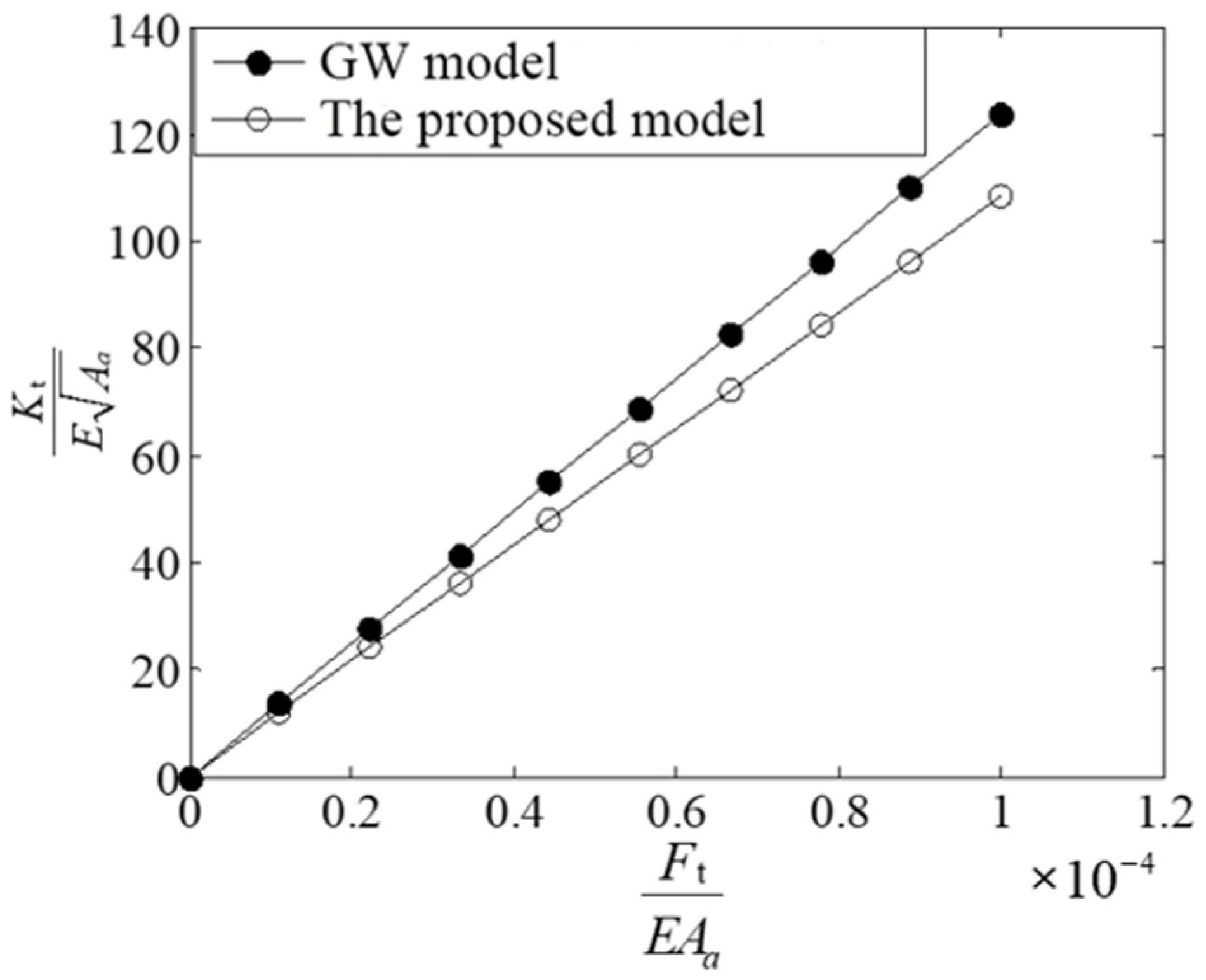
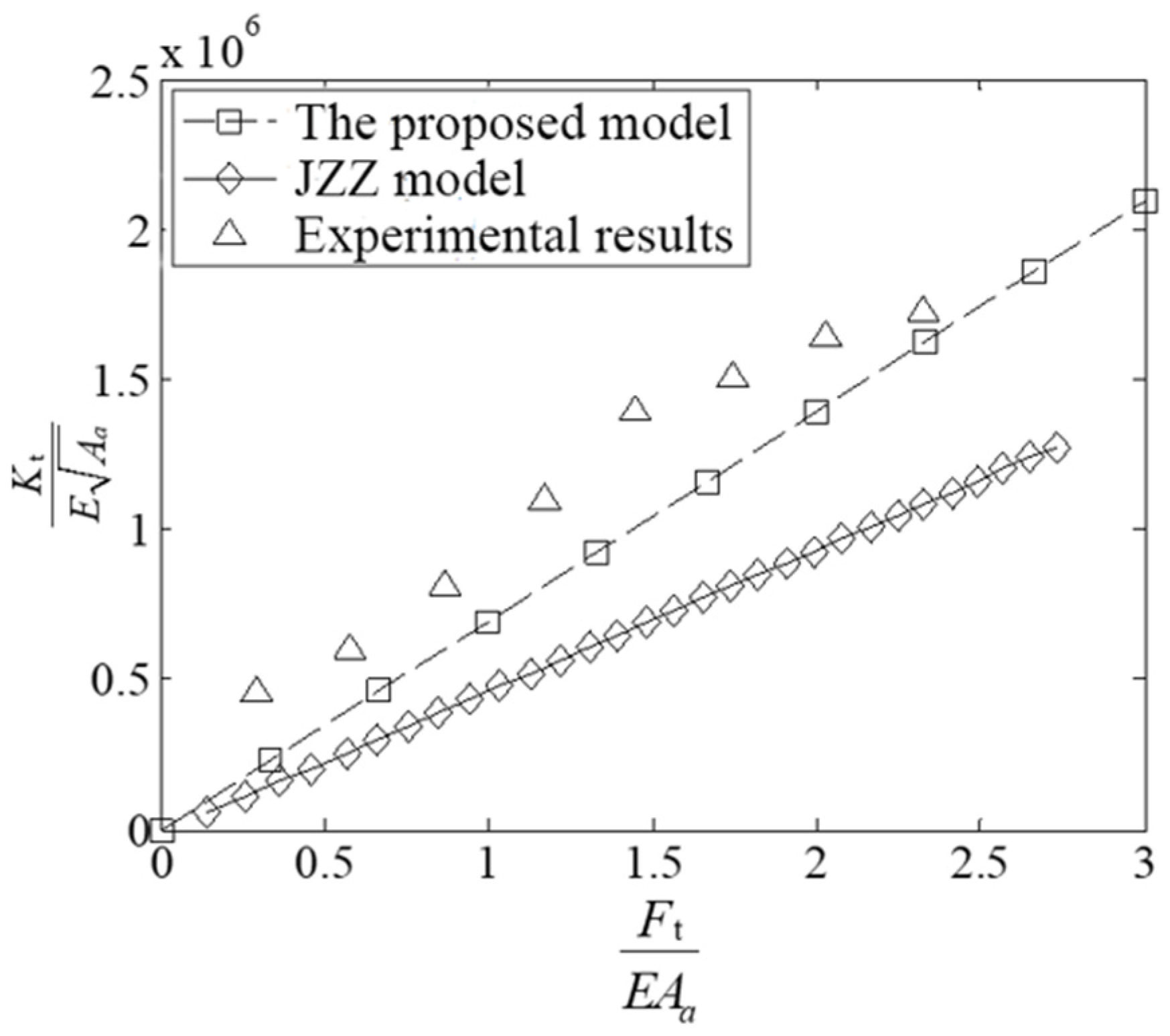

| Parameter | Value |
|---|---|
| Fractal dimension | 1.4058 |
| Characteristic Parameters/m | 2.2826 × 10−10 |
| Stiffness | 220.0000 |
| Hardness/GPa | 100.0000 |
| Poisson’s ratio | 0.2500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Qu, J.; Liu, Y. A Joint Surface Contact Stiffness Model Considering Micro-Asperity Interaction. Aerospace 2024, 11, 472. https://doi.org/10.3390/aerospace11060472
Xia T, Qu J, Liu Y. A Joint Surface Contact Stiffness Model Considering Micro-Asperity Interaction. Aerospace. 2024; 11(6):472. https://doi.org/10.3390/aerospace11060472
Chicago/Turabian StyleXia, Tian, Jie Qu, and Yong Liu. 2024. "A Joint Surface Contact Stiffness Model Considering Micro-Asperity Interaction" Aerospace 11, no. 6: 472. https://doi.org/10.3390/aerospace11060472
APA StyleXia, T., Qu, J., & Liu, Y. (2024). A Joint Surface Contact Stiffness Model Considering Micro-Asperity Interaction. Aerospace, 11(6), 472. https://doi.org/10.3390/aerospace11060472






