Abstract
Flight delay identification is an important way to coordinate the operation time of airport ground service providers and improve the efficiency of airport operations. By analyzing the flight turnaround operation process, considering the randomness and synchronization of the turnaround process, and using Colored Petri Nets and Python (4.0.1), we explore the correlation between various links in the flight turnaround process and the take-off delay at the next station. This paper is committed to improving the service performance of airports and airlines, dynamically predicting flight delays, and providing guidance for avoiding excessive time in the actual operation of bad combinations. The results show that there are six kinds of bad combinations in the departure slip-out link, which is the most likely to affect the transit time. The maximum lifting degree in the bad combination is 2.043, and the maximum average delay time in the bad combination is 22.5 min. When the combination of passenger boarding and departure slip-out time is too long, it has a great positive correlation with delay. When the other links are in a state of being able to pass the station on time, the departure time and baggage loading and unloading are the two links that most affect the flight delay value.
1. Introduction
With the rapid development of civil aviation, higher requirements have been put forward for the operation and management level. The increase in the number of flights in and out of airports has increased the pressure on turnaround flight support, which has led to a lack of airport operation efficiency and business coordination ability. As of 2023, the total number of civil aviation airports in China has reached 259, with a total capacity of 1.56 billion passengers. There are 20 airports with a passenger throughput of more than 20 million passengers. Those responsible for ensuring the punctual departure of large-scale flights are facing increasing pressure. With the continuous development and improvement of the existing operation control system, predicting flight departure times can coordinate the operation time of the airport ground service and improve the operation level of the airport.
Flight delay is affected by many factors. It is very difficult to accurately predict flight departure times. The research results have distinct characteristics of airport data samples, and the analysis results have low portability. At present, the A-CDM (Airport-Collaborative Decision-Making) system, which has been widely used in airports, is a prediction model based on empirical statistics. It has the function of predicting the target take-off time and the target roll-off time. Many researchers are now making improvements on this basis, and the most commonly used methods are as follows.
In recent years, scholars have used more intelligent methods to optimize this prediction process, using machine learning algorithms such as Support Vector Machine [1], Random Forest [1,2], Colored Petri Net [3,4], Bayesian network [5,6,7,8,9], and Long Short-Term Memory neural network [10,11] to make predictions. Deep learning algorithms such as the Gated Recurrent Unit (GRU) model [12] and Convolutional Long Short-Term Memory network [13,14] are used to predict flight delays. The factors affecting the prediction process are shown in Table 1.

Table 1.
Factors Affecting Flight Turnaround Process.
This paper mainly focuses on the study of flight delays for scene factors. Xu Tao [18] constructed a cascade BP neural network model and used four nodes in the middle to predict the rollback time. The accuracy of the model prediction is much higher than that of the empirical statistical prediction model. Xing [3] proposed a quantitative description model of flight ground support service based on the colored time Petri net and used the Monte Carlo method to estimate the time. Later [19] established a Gaussian probability model of flight ground support vehicle arrival time and a flight ground support time prediction model based on a deep neural network. The results show that the prediction accuracy of this method is 3–5% higher than that of traditional BP neural networks and Bayesian networks. However, the deep neural network method cannot perceive the microscopic evolution of the guaranteed process. Wang [20] predicted each support link and constructed a dynamic prediction method of the ground support process based on the traditional Bayesian network combined with Gaussian kernel probability density estimation. The verification method is better than the deep neural network. The process outlined in the above research is relatively simple, and the interaction between the links is greatly neglected. Considering the interdependence of priority tasks, Sánchez [21] conducted a detailed time assessment of different disturbances that may affect the turnaround time. His research not only examines the performance of detail prediction but also explores the interaction in the steps and the influence of delays in different links on the total guarantee time. It reduces the spread of delays, enhances the robustness of the turnover operation process, and concludes with recommendations for optimizing the service time of the station.
To solve the problem of flight delays, many scholars consider a certain link as a fixed required time while optimizing the support process to minimize time or cost, ignoring the impact of the uncertainty of task time on the total support time. The uncertainty of tasks is reflected in various aspects, such as unpredictable emergency support services [22], inability to determine the start time of work tasks, uncertainty in work time, and differences between vehicles. Xu [23] used logarithmic normal distribution to fit the operating time of various airport support vehicles based on historical data of a domestic airport, evaluated the volatility of each operating time, and designed algorithms to improve the adaptability of vehicle scheduling to uncertain operating times. Zhu [24] also analyzed the uncertainty factors present in the scene and changed the originally fixed fitness value of the scheduling scheme to have a certain degree of randomness in the genetic algorithm to meet the uncertainty of task time consumption. Yao [25] designed a vehicle capability difference allocation method that not only considers the difference in working capabilities between vehicles, but also easily copes with the changes in dispatch plans caused by service time windows or changes in working hours (such as aircraft delays).
At present, the research on predicting flight departure time is relatively complete and the technology is mature. There is much research on the factors affecting flight delays, but there are few studies considering various influencing factors. The ability to dynamically observe flights and improve business collaboration is insufficient. By improving the ability to identify departure flight delays, solving the problem of insufficient business collaboration capabilities, and improving the efficiency of airport operations, this study clarifies that bad combinations of links have a great impact on stopover times. It also realizes a quantitative description of the impact value of bad combinations on flight stopover time. According to this description, the occurrence of bad combinations does not necessarily lead to flight delays. Finally, we find sufficient conditions for flight delays.
2. The Turnaround Process Description and Research Process
The flight turnaround operation process refers to a series of ground operations in the flight area between the landing of the aircraft and the take-off for the next flight task. It includes a series of ground service tasks for passengers, luggage, and aircraft, providing the resources and ground services required for the aircraft to perform the next flight normally, which are usually carried out in parallel or in sequence. In this paper, commonly used aircraft such as the A330, B747, and others with seat capacities of 251–500 are taken as the research objects. The turnaround process can be roughly used as shown in Figure 1 and Table 2.
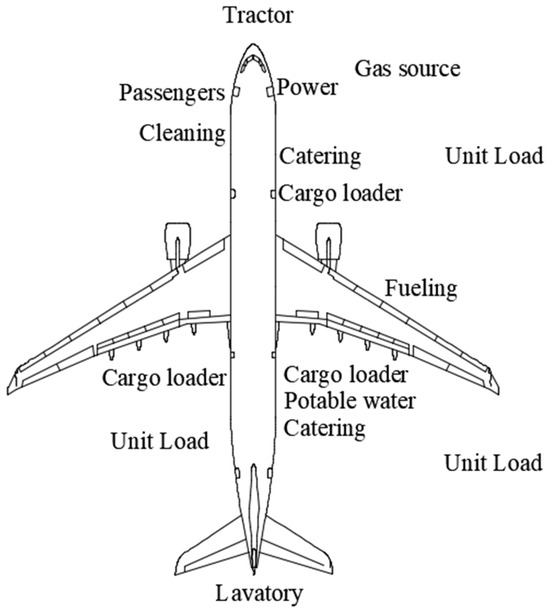
Figure 1.
A330 door configuration, equipment arrangement.

Table 2.
Aircraft turnaround operation process and operation project.
It is assumed that flight delays depend on the flight turnaround time and are not affected by the spread of previous flight delays. Taking the operation data of a hub international airport in China in 2023 as an example, the operation is divided into 12 links, as shown in Table 3. According to the airport level and the airport’s daily normal operations, a delay is recorded when the actual departure time (ATD) is later than the planned departure time (STD) by 30 min. This is expressed as TDelay = ATD-STD-30.

Table 3.
Flight turnaround link.
3. The Correlation Analysis of the Influence of the Turnaround Operation Process on the Actual Turnaround Time
Firstly, the data need to be preprocessed, and the feature elements (K-means) are classified according to the time standard. Based on the prior frequent pattern Apriori algorithm, the influence value of each prior frequent item on the actual turnaround time of the flight is obtained. The existing research mostly uses the three indicators of support (Equation (1)), confidence (Equation (2)) and lift (Equation (3)) in the Apriori algorithm to measure the degree of influence.
Among them, support is used to measure the co-occurrence frequency of item set X and item set Y in the total item set. Confidence represents the ratio of the probability of occurrence of X and Y to the probability of occurrence of X. The minimum support is set to supmin = 0.30, and the minimum confidence is set to conmin = 0.80. Only using the two indicators of support and confidence is an easy way to produce a reverse correlation, and it is also necessary to use the promotion degree to reflect the promotion relationship between the former and the latter. When the promotion degree is greater than 1, it is proved that the former has a positive impact on the latter. Generally, the greater the promotion degree, the higher the positive impact. Select the rules with a large degree of improvement in the influencing factors (former) and flight delays (latter) in the effective rules. Observe the position and role of the influencing factors in the process, and select one or more nodes as the key node moments or feature elements (K-means); that is, the project time is classified according to different value ranges. The results are shown in Table 4, and the results of the correlation analysis are shown in Figure 2 and Table 5.

Table 4.
Classification results of feature elements.
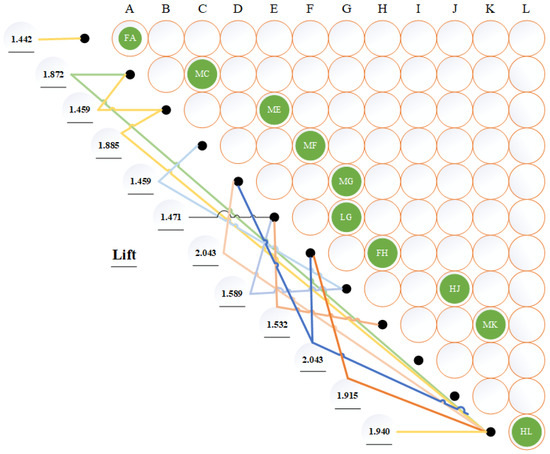
Figure 2.
Association analysis conforming to valid rules.

Table 5.
Association analysis that conforms to valid rules.
From the point of view of the number of combinations of single links, we find that there are 6 kinds of bad combinations when the L link takes more than 16 min. The bad combinations are the most likely to affect the station time. When the G link takes more than 20 min, there are 5 kinds of bad combinations. When the time of the C link is more than 30 min, or the time of the E link is more than 15 min, or the time of the H link is more than 0 min, or the time of the J link is more than 76 min, there are two bad combinations. When the A link takes more than 4 min, or the F link takes more than 14 min, or the K link takes more than 4 min, there is one bad combination. There is no bad combination in links B, D, and I.
From the point of view of the lifting degree value, the lifting degree reaches 2.043 when the G link takes more than 20 min and the L link takes more than 16 min, regardless of whether the H link takes more than 0 min or not. This is the most influential combination. The lifting degree reaches 1.940 when the L link takes more than 16 min. The lifting degree reaches 1.915 while the H link takes more than 0 min. The lifting degree reaches 1.885 when the E link takes more than 15 min. The lifting degree reaches 1.872 when the C link takes more than 20 min. When the G link takes more than 29 min, it is matched with the J link for more than 76 min, with an increase of 1.589, and the K link takes more than 4 min, with an increase of 1.532. The lifting degree reaches 1.471 when the G link takes more than 29 min. The lifting degree reaches 1.459 when the time of the C link is more than 20 min and the time of the E link is more than 15 min. The lifting degree reaches 1.459 when the F link takes more than 14 min and the J link takes more than 76 min. The lifting degree reaches 1.442 when the A link takes more than 4 min.
This method is used to infer whether the flight is delayed according to the matching of the conditional characteristics of the flight. By avoiding the occurrence of bad combinations, the influence value of each bad combination is studied, which provides the guiding significance for the real flight to take off on time.
4. The Influence of Bad Combination on the Actual Turnaround Time
The information available to the system for dynamically deciding whether a flight will be delayed is incomplete. Thus, in addition to avoiding the above situation, how to predict the specific delay value in the historical data information field is particularly important. According to the content of Table 2, the following Colored Petri Network (Figure 3) is constructed, and tested to be in line with the logic of the flight turnaround process. The network can quantitatively analyze the average value of the impact of delays in each link on the turnaround time.
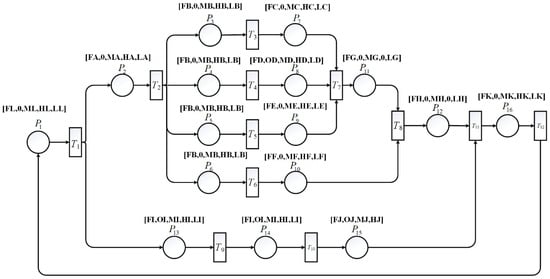
Figure 3.
CPN diagram of flight turnaround operation process.
4.1. Colored Petri Network (CPN)
The systems that can be described by Petri nets are those composed of discrete time. There is a certain interdependence between events, which is reflected by the state of the system. In a certain state of the system, some events may occur, and the occurrence of events will change the state of the system. The process of continuous occurrence of events and changing state is the operation of the system. The basic Petri net is composed of places, transitions, directed arcs, tokens, and other elements. Places are represented by P (circle) meaning state elements. Transitions are represented by T (rectangle), meaning event elements. Directed arcs represent flow relationships. Tokens are represented by black dots, meaning the movement or state of resources.
A CPN is used to classify the tokens in the Petri net with different colors. In order to realize the folding and simplification of the network system and to better understand the concept of color and classification, we establish a simple CPN model (Figure 3).
4.2. Measure the Impact of Bad Combinations on the Results
Through the Python tool simulation verification, combined with the Monte Carlo algorithm, based on the results of Section 3, it is confirmed that the average impact value of each association combination that conforms to the effective rules on delays is shown in Figure 3. In the statistical data, a total of 49% of flights take off on time, so the flight data within the 49% quantile are used as non-delay data.
In Figure 4, F, O, M, H, and L, respectively, represent the first letter in Table 4. Each circle in the figure represents a link, and the numbers outside the circle represent the influence value, measured in minutes. According to Figure 4 and the simulation results, when LC and LL are combined, the impact value is the largest, and the average delay time is 22.5 min. Additionally, when LG and HJ match, MF and HJ match, HF and HJ match, LF and HJ match, and LG, LH, and LL match, the average delay value is 18.5 min. When LA appears, the average delay value is 16.5 min. When LC and HL match, the average delay value is 16 min. By observing the data and network structure, 38% of the flight cargo doors are closed later than the cabin doors. Therefore, it is recommended to cooperate with the passenger service department when the baggage operation is completed and strive to complete the operation when the passenger boarding is completed. Figure 4 also proves that the occurrence of bad combinations does not necessarily lead to flight delays. Therefore, the threshold of flight delays caused by single link time is studied.
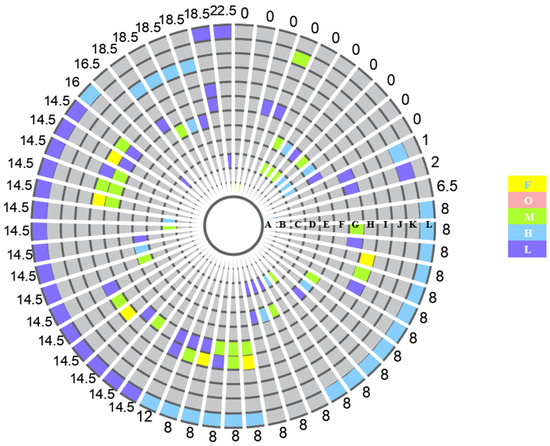
Figure 4.
The average impact of association combinations that conform to valid rules on delays.
4.3. Threshold Analysis of the Impact of Flight Turnaround on Delay
From the above research results, it is known that the occurrence of a single or multiple links with a large correlation with delay does not necessarily lead to flight delays. However, when the value of a link exceeds a certain range, it will inevitably lead to flight delays. The analysis results and the probability values of occurrence are shown in Figure 5 and Figure 6.
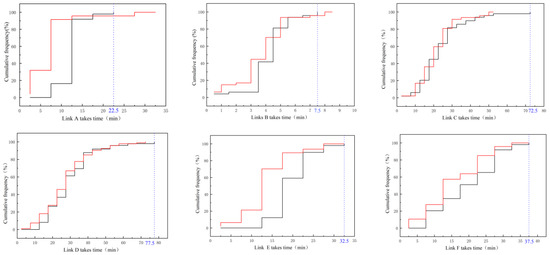
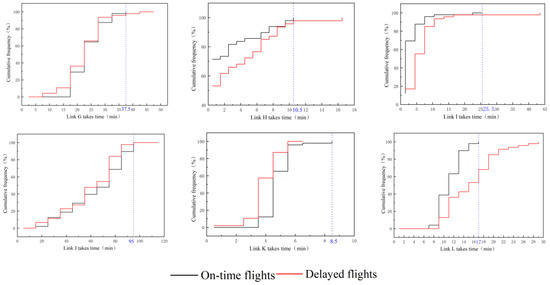
Figure 5.
Cumulative experience probability distribution diagram of each link.
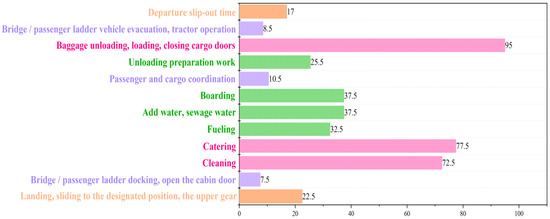
Figure 6.
The boundaries of delays caused by the operation of each link.
Taking link A as an example, when the link takes more than 22.5 min, the flight must be in a state of delay. When the B link exceeds 8.5 min, the flight will definitely be delayed. When the G link takes more than 37.5 min, the flight will definitely be delayed. From the point of view of the influence of a single link, not all links that take too much time lead to flight delays. The link times for C, D, E, F, and K have no obvious relationship with flight delays.
5. Conclusions
Based on the background of today’s increasingly busy airports, this paper is committed to improving the service performance of airports and airlines. It studies the relationship between the many links of flight turnaround and flight take-off delays, and provides guidance for avoiding excessive delays due to bad combinations in actual operations. At the same time, the degree to which bad situations influence delays is checked by simulation.
The correlation analysis is based on the prior frequency of the item set. It is concluded that when the combination of passenger boarding and departure times is too long, it has a great positive correlation with the lift. It is recommended to avoid the occurrence of bad combinations in practical operations. Quantitative analysis shows that when other links are in the state of being able to pass the station on time, the average influence value of the link with too long-time combination on the delay is obtained. It is concluded that the two links, “Departure slip-out time” and “Baggage unloading, loading, closing cargo doors”, have the most effect on the flight delay value. When single or multiple links with a large correlation with the delay appear, it does not necessarily lead to flight delays, but when a certain link exceeds the corresponding threshold, a delay will definitely occur.
Author Contributions
Conceptualization, Q.D. and Y.C.; Methodology, Q.D. and Y.C.; Software, X.H.; Writing—original draft preparation, B.C.; Writing—review and editing, L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Technologies Research and Development Program of China, grant number 2021YFB1600500-2021YFB1600502.
Data Availability Statement
Data available on request due to restrictions. The data presented in this study are available on request from the corresponding author. The data are not publicly available due to according to the relevant requirements and agreements of the scientific research project on which the article is based, the data not provided in the manuscript will not be disclosed.
Conflicts of Interest
No conflicts of interest exist in the submission of this manuscript, and the manuscript is approved by all authors for publication. On behalf of my co-authors, we would like to declare that the work described was original research that has not been published previously and is not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.
References
- Pavel, S.; Rokas, Š.; Olga, K. Prediction of Flight Time Deviation for Lithuanian Airports Using Supervised Machine Learning Model. Comput. Intell. Neurosci. 2020, 2020, 8878681. [Google Scholar]
- Guo, Z.; Yu, B.; Hao, M.; Wang, W.; Jiang, Y.; Zong, F. A novel hybrid method for flight departure delay prediction using Random Forest Regression and Maximal Information Coefficient. Aerosp. Sci. Technol. 2021, 116, 106822. [Google Scholar] [CrossRef]
- Xing, Z.W.; Wei, Z.Q.; Luo, Q. Flight support service process modeling method based on colored time Petri net. Syst. Eng. Electron. 2018, 40, 1064–1069. [Google Scholar]
- Zhang, S.Q.; Ma, C.T.; Zhu, J.N.; Mei, Y.C. Research on the Method for Improving Time Elasticity of Apron Operation Scheduling Based on Time Delay Petri Net. Fire Control Command. Control 2021, 46, 103–107+112. [Google Scholar]
- Xing, Z.W.; Tang, Y.X.; Luo, Q. Dynamic estimation about service time of flight support based on Bayesian network. J. Comput. Appl. 2017, 37, 299–304. [Google Scholar]
- Tang, Y.X. The Estimation about Flight Support Service Time of Hub Airport. Master’s Thesis, Civil Aviation University of China, Tianjin, China, 2017. [Google Scholar]
- Cao, W.D.; He, G.G. Bayesian networks analysis for sequence flight delay and propagation. J. Comput. Appl. 2009, 29, 606–610. [Google Scholar] [CrossRef]
- Cao, W.D.; Lin, X.Y. Flight turnaround time analysis and delay prediction based on Bayesian network. Comput. Eng. Des. 2011, 32, 1770–1772+1776. [Google Scholar]
- Wu, W.W.; Meng, T.T.; Zhang, H.Y. Flight Plan Optimization Based on Airport Delay Prediction. J. Transp. Syst. Eng. Inf. Technol. 2016, 16, 189–195. [Google Scholar]
- Xu, T.; Ding, Y.; Lu, M. Flight off block time prediction based on cascaded BP neural network. Comput. Appl. Softw. 2019, 36, 226–232. [Google Scholar]
- Kim, S.; Park, E. Prediction of flight departure delays caused by weather conditions adopting data-driven approaches. J. Big Data 2024, 11, 11. [Google Scholar] [CrossRef]
- Zhou, H.; Li, W.; Jiang, Z.; Cai, F.; Xue, Y. Flight Departure Time Prediction Based on Deep Learning. Aerospace 2022, 9, 394. [Google Scholar] [CrossRef]
- Qu, J.Y.; Wu, S.X.; Zhang, J.J. Flight Delay Propagation Prediction Based on Deep Learning. Mathematics 2023, 11, 494. [Google Scholar] [CrossRef]
- Ai, Y.; Pan, W.; Yang, C.; Wu, D.; Tang, J. A deep learning approach to predict the spatial and temporal distribution of flight delay in network. J. Intell. Fuzzy Syst. 2019, 37, 6029–6037. [Google Scholar] [CrossRef]
- Ding, J.L.; Zhao, J.T.; Cao, W.D. Dynamic Estimation About Turnaround Time of Flight Based on Bayesian Network. J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 517–524. [Google Scholar]
- Fricke, H.; Schultz, M. Delay Impacts onto Turnaround Performance-Optimal Time Buffering for Minimizing Delay Propagation. In Proceedings of the USA/Europe Air Traffic Management Research and Development Seminar, Napa, CA, USA, 29 June–2 July 2009. [Google Scholar]
- He, X.; Sun, Q.; Yang, D.Y. Research on key influencing factors of airport ground support service efficiency. Aeronaut. Comput. Tech. 2021, 51, 23–26+31. [Google Scholar]
- Xu, T.; Zhao, C.X.; Lu, M. Flight off-block time prediction based on factor analysis. Comput. Eng. Des. 2017, 38, 3011–3017. [Google Scholar]
- Xing, Z.; Biao, L.; Hui, Z.; Qian, L. Research on flight ground service time prediction based on deep neural network. J. Syst. Simul. 2020, 32, 678–686. [Google Scholar]
- Wang, L.W.; Li, B.; Xing, Z.W.; Liu, H.; Luo, Q. Dynamic prediction of ground support process for transit flight. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1095–1104. [Google Scholar]
- Sánchez, N.J.; Eroles, P.A.M. Causal analysis of aircraft turnaround time for process reliability evaluation and disruptions’ identification. Transp. B Transp. Dyn. 2018, 6, 115–128. [Google Scholar]
- Wang, J.; Guo, H.; Bakker, M.; Tsui, K.L. An integrated approach for surgery scheduling under uncertainty. Comput. Ind. Eng. 2018, 118, 1706924. [Google Scholar] [CrossRef]
- Xu, C.; Shao, Q. Optimization of airport ground service support equipment scheduling under uncertain operation time. Sci. Technol. Eng. 2018, 18, 372–378. [Google Scholar]
- Zhu, X.P.; Xu, H.Y.; Wang, S.J. Scheduling of serv-ice vehicles for aircraft turnaround under uncertain task duration. J. Nanjing Univ. Aeronaut. Astronaut. 2019, 51, 749–755. [Google Scholar]
- Yao, Y.; Zhu, J.F.; Bang, M.G. An optimization scheduling algorithm for flight turnaround ground service. Inf. Control 2007, 36, 486–492+500. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).