Instrument to Study Plume Surface Interactions (PSI) on the Lunar Surface: Science Motivation, Requirements, Instrument Overview, and Test Plans
Abstract
1. Introduction
1.1. Overview of PSI and Its Importance
1.2. Past Missions
2. Development of Instrument Requirements—Method and Results
2.1. Particle Flux and Time Duration
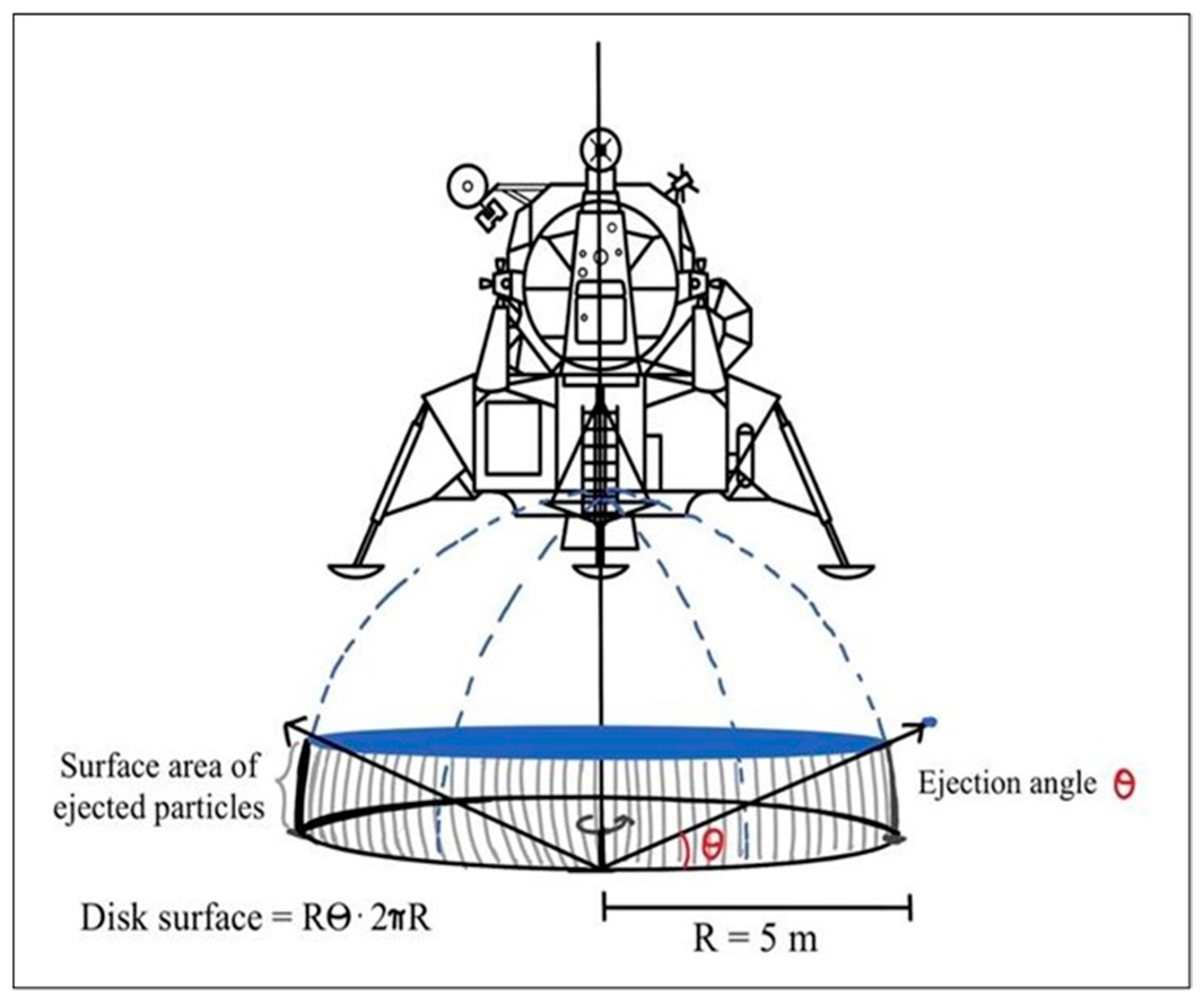
2.2. Scaling for Landers of Various Sizes
- Plume gas density: [ρ] = M/L3
- Plume gas velocity: [v] = L/T
- Plume gas kinematic viscosity: [µ] = L2/T
- Plume gas nozzle exit diameter: [D] = L
- Lander altitude above the lunar surface at which PSI starts: [h] = L
- Particle diameter: [d] = L
- Particle mass: [mp] = M
- Lander thrust force: [F] = M·L/T2
- Lander descent velocity: [w] = L/T
- Celestial body’s gravitational acceleration: [g] = L/T2
- Regolith bulk density: [ρb] = M/L3
- Regolith cohesion (pressure): [C] = M/(L·T2)
- Speed of sound in the regolith: [c] = L/T
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
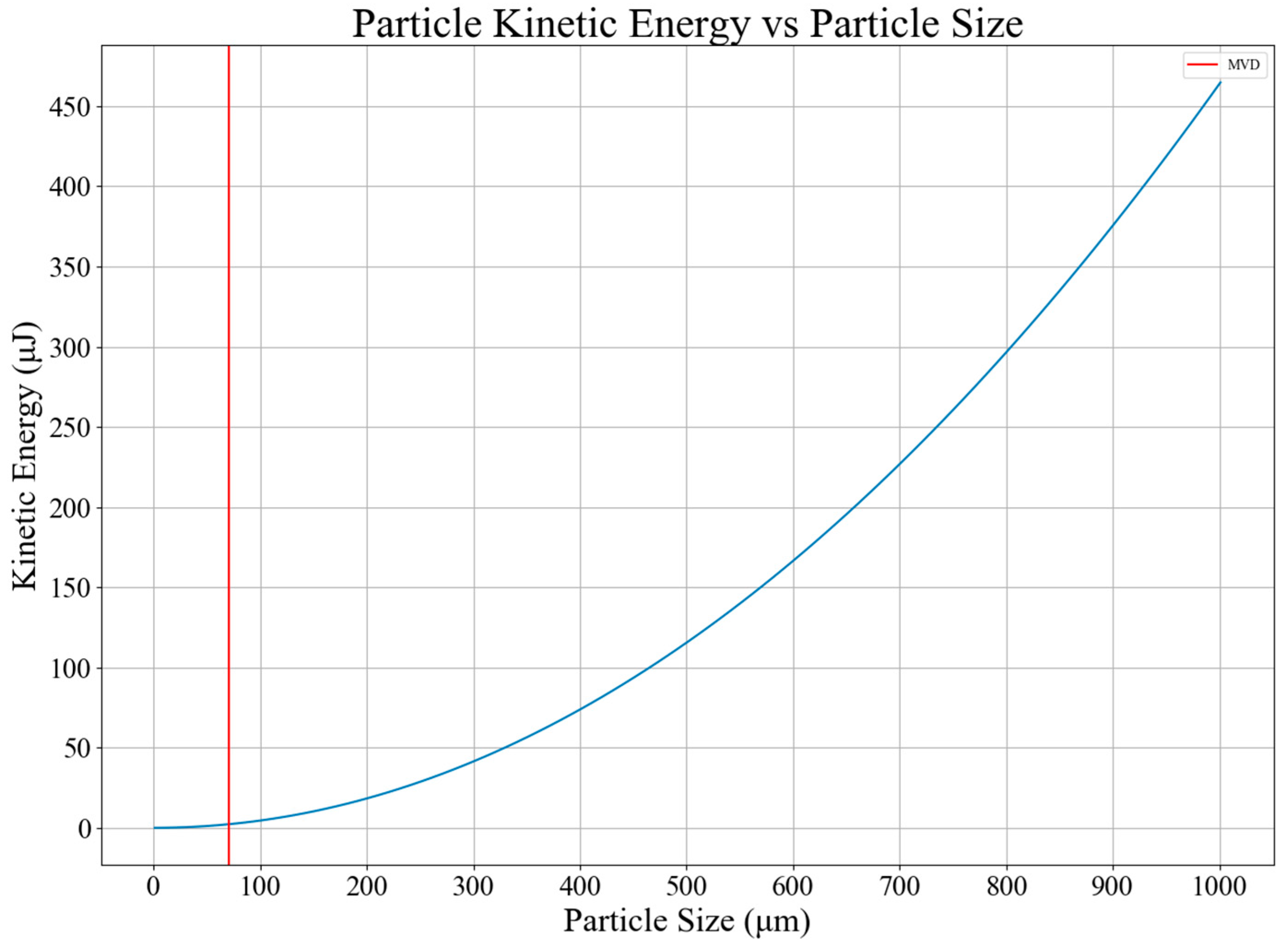
2.3. Velocity and Energy Range
2.4. Measurement Frequency and Environmental Conditions
2.5. Requirements
3. Particle Impact Event (PIE) Sensor
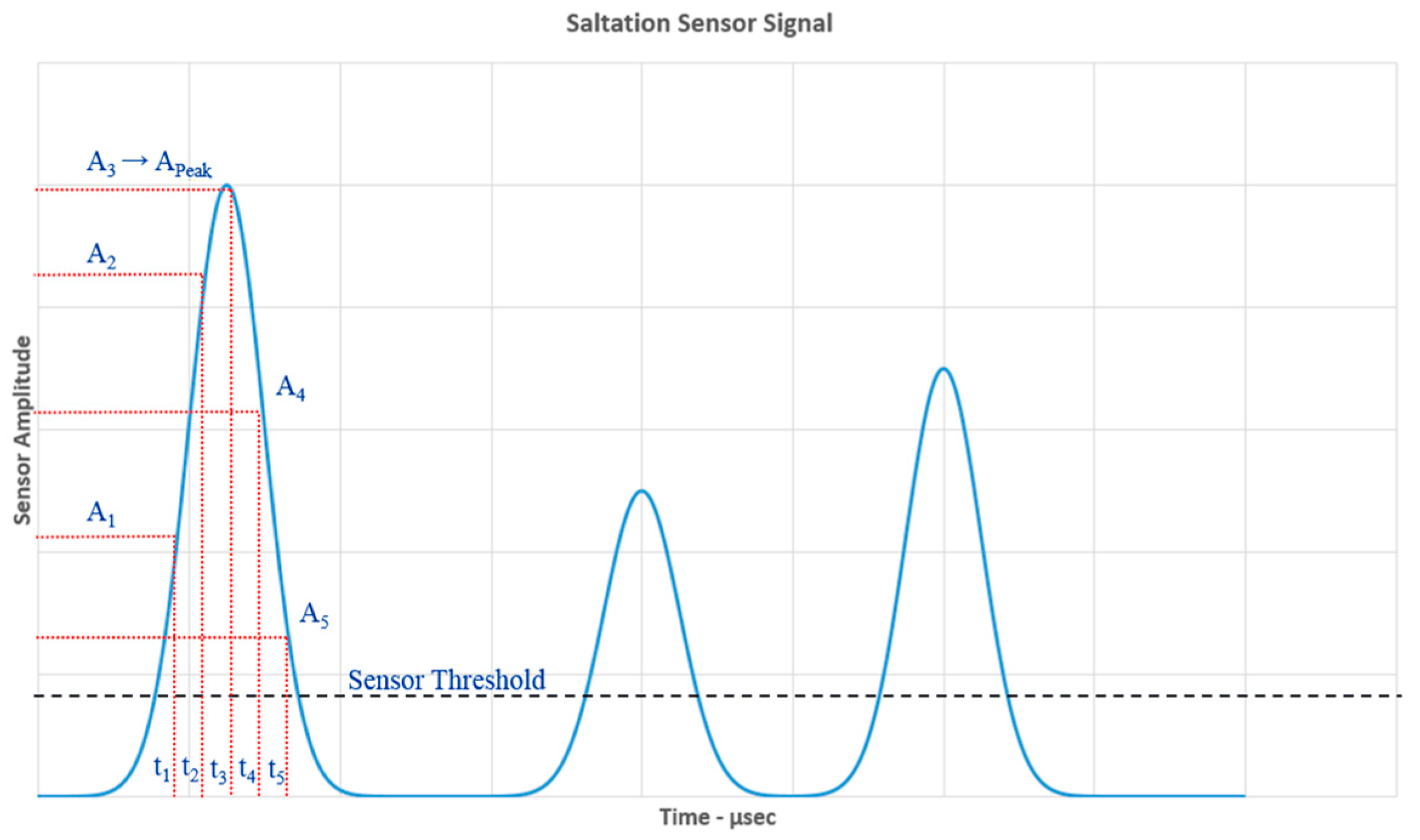
3.1. Particle Impact Event (PIE) Sensor Heritage—Saltation Sensor
3.2. Current PIE Sensor Design
3.3. Testing
- Drop tower calibration testing: functional controlled laboratory testing using simulant particles that will be dropped to produce similar energies to PSI on the Moon. This test will verify if the instrument meets the PSI energy range requirements.
- Impact flux calibration testing: functional controlled test used to measure impact counts to verify the instrument meets the PSI flux measurement requirements.
- Thermal testing: environmental testing to ensure the sensor can withstand the thermal conditions during launch, flight, and landing sequences.
- Pressure testing: environmental testing to ensure operability in lunar pressure conditions during lunar lander descent and landing.
- EMI and EMS testing:
- ○
- Electromagnetic susceptibility (EMS) testing to ensure sensor electronics operate as intended for expected electromagnetic radiation conditions at the lunar south pole and the in-transit space environment.
- ○
- Electromagnetic interference (EMI) testing to ensure that the sensor electronics do not negatively interfere with lunar lander electronics or communications.
- Shock and vibration testing: testing to ensure the instrument can measure particle impacts without interference from the shock and vibrations during launch and descent.
- Dust exposure test: although the instrument can measure the lunar regolith particles as they impact the sensor it is important that the overall instrument can withstand constant dust exposure during landing, so the instrument does not degrade during measurements.
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mehta, M. Rocket Plume Interactions for NASA Landing Systems. NASA-DLR Technical Interchange Meeting on Powered Descent and Plume-Surface Interaction Environments. 2019. Available online: https://ntrs.nasa.gov/api/citations/20200000979/downloads/20200000979.pdf (accessed on 29 March 2024).
- Li, S.; Jiang, X.; Tao, T. Guidance Summary and Assessment of the Chang’e-3 Powered Descent and Landing. J. Spacecr. Rocket. 2016, 53, 258–277. [Google Scholar] [CrossRef]
- Metzger, P.; Dove, A.; Conroy, M.; Gloria, J.; O’Reilly, A.; St John, A. Ejecta Sheet Tracking, Opacity and Regolith Maturity (Ejecta Storm): An Instrument for Lunar Landing Plume Effects and Dust Dynamics. In Proceedings of the 52nd Lunar and Planetary Science Conference, Woodlands, TX, USA, 15–19 March 2021. no. 2548. [Google Scholar]
- Tyrrell, O.K.; Thompson, R.J.; Danehy, P.M.; Dupuis, C.J.; Munk, M.M.; Nguyen, C.P.; Maddock, R.W.; Fahringer, T.W.; Krolick, W.C.; Weaver, A.; et al. Design of a lunar plume-surface interaction measurement system. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA; Virtual, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022; p. 1693. [Google Scholar] [CrossRef]
- Peale, R.E.; Hathnagoda, D.; Kelley, C.; Fredricksen, C.J.; Walker, C.; Posada, C.; Zorovich, J.; Cariker, C.; Dhakal, N.; Gonzalez, J.; et al. Laser particle sizer for lunar plume-surface interaction studies. In Laser Radar Technology and Applications XXVIII; Turner, M.D., Kamerman, G.W., Magruder, L.A., Eds.; SPIE: Orlando, FL, USA, 2023; pp. 67–74. [Google Scholar] [CrossRef]
- Langton, A.G.; Mantovani, J.G.; Kemmerer, B.W.; Atkins, A.R.; Batcheldor, D.P. A Millimeter Wave Doppler Radar to Measure Plume Surface Interactions Ejecta Velocities. In Proceedings of the ASCEND 2022, Las Vegas, NV, USA; Online, 24–26 October 2022; American Institute of Aeronautics and Astronautics: Reston VA, USA, 2022; p. 4282. [Google Scholar] [CrossRef]
- Metzger, P.T.; Smith, J.; Lane, J.E. Phenomenology of soil erosion due to rocket exhaust on the Moon and the Mauna Kea lunar test site. J. Geophys. Res. 2011, 116, E06005. [Google Scholar] [CrossRef]
- Metzger, P.T.; Mantovani, J.G. The Damage to Lunar Orbiting Spacecraft Caused by the Ejecta of Lunar Landers. arXiv 2023, arXiv:2305.12234. [Google Scholar] [CrossRef]
- Apollo 12 Landing from PDI to Touchdown. 2014. [Online Video]. Available online: https://www.youtube.com/watch?v=kFSa6vUix70 (accessed on 29 March 2024).
- Korzun, A.M.; Eberhart, C.J.; West, J.; Liever, P.; Weaver, A.; Mantovani, J.; Langton, A.; Kemmerer, B.; Atkins, A.; Rubio, J.S.; et al. Design of a Subscale, Inert Gas Test for Plume-Surface Interactions in a Reduced Pressure Environment. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA; Virtual, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston VA, USA, 2022. [Google Scholar] [CrossRef]
- McDivitt, J. Apollo 15 Mission Report; Technical Report; NASA Manned Spacecraft Center: Houston, TX, USA, 1971.
- Taylor, T.J. Apollo Experience Report: Thermal Protection from Engine-Plume Environments. NASA Technical Note (TN) 19720018272. 1972. Available online: https://ntrs.nasa.gov/api/citations/19720018272/downloads/19720018272.pdf (accessed on 1 January 2024).
- Immer, C.; Metzger, P.; Hintze, P.E.; Nick, A.; Horan, R. Apollo 12 Lunar Module exhaust plume impingement on Lunar Surveyor III. Icarus 2011, 211, 1089–1102. [Google Scholar] [CrossRef]
- Liever, P.A.; Gale, M.P.; Mehta, R.S.; Weaver, A.B.; West, J.S.; Westra, D.G. Gas-Particle Flow Simulations for Martian and Lunar Lander Plume-Surface Interaction Prediction. In Proceedings of the Earth and Space, Virtual, 19–23 April 2021; American Society of Civil Engineers: Reston, WV, USA, 2021; pp. 84–98. [Google Scholar] [CrossRef]
- NASA. Apollo 12 Technical Air-to-Ground Voice Transcription; NASA Manned Space Center: Houston, TX, USA, 1969.
- NASA Manned Space Center. Apollo 17 Technical Debriefing; Rep. MSC-7631; NASA Manned Space Center: Houston, TX, USA, 1973.
- Immer, C.; Lane, J.; Metzger, P.; Clements, S. Apollo video photogrammetry estimation of plume impingement effects. Icarus 2011, 214, 46–52. [Google Scholar] [CrossRef]
- Lane, J.E.; Metzger, P.T.; Carlson, J.W. Lunar Dust Particles Blown by Lander Engine Exhaust in Rarefied and Compressible Flow. arXiv 2021, arXiv:2104.06332. [Google Scholar] [CrossRef]
- Wang, T.-S.; Canabal, F.; Knox, K.S.; Hawkins, R.F. Base Heating Environment During Ground Testing of a Lunar Lander Demonstrator. J. Thermophys. Heat Transf. 2020, 34, 826–835. [Google Scholar] [CrossRef]
- Qiao, L.; Hess, M.; Xu, L.; Wöhler, C.; Head, J.W.; Chen, J.; Wang, Y.; Bugiolacchi, R.; Xiao, A.; Zhang, F.; et al. Extensive Lunar Surface Disturbance at the Chang’e-5 Mission Landing Site: Implications for Future Lunar Base Design and Construction. J. Geophys. Res. Planets 2023, 128, e2022JE007730. [Google Scholar] [CrossRef]
- Kaydash, V.; Shkuratov, Y.; Korokhin, V.; Videen, G. Photometric anomalies in the Apollo landing sites as seen from the Lunar Reconnaissance Orbiter. Icarus 2011, 211, 89–96. [Google Scholar] [CrossRef]
- Johnson, K.J.; Eckman, E.M.; Swank, A.J.; Zemba, M.J. RF Metrology of Lunar Highlands Regolith Simulant NU-LHT-2M. In Proceedings of the 28th Ka and Broadband Communications Conference (Ka), Bradford, UK, 23–26 October 2023. [Google Scholar]
- Carrier, D.W. The Four Things You Need to Know about the Geotechnical Properties of Lunar Soil; Lunar Geotechnical Institute: Lakeland, FL, USA, 2005. [Google Scholar]
- Carrier, W.D. Particle Size Distribution of Lunar Soil. J. Geotech. Geoenviron. Eng. 2003, 129, 956–959. [Google Scholar] [CrossRef]
- Getchius, J.; Renshaw, D.; Posada, D.; Henderson, T.; Hong, L.; Ge, S.; Molina, G. Hazard Detection and Avoidance for the Nova-C Lander. arXiv 2022, arXiv:2204.00660. [Google Scholar] [CrossRef]
- Roberts, B.C. Cross-Program Design Specification for Natural Environments (DSNE) Revision G; NASA: Washington, DC, USA, 2019.
- NASA Manned Space Center. Apollo 11 Technical Air-to-Ground Voice Transcription; NASA Manned Space Center: Houston, TX, USA, 1969.
- Morris, A.B.; Goldstein, D.B.; Varghese, P.L.; Trafton, L.M. Approach for Modeling Rocket Plume Impingement and Dust Dispersal on the Moon. J. Spacecr. Rockets 2015, 52, 362–374. [Google Scholar] [CrossRef]
- Mehta, M. Plume-Surface Interactions Due to Spacecraft Landings and the Discovery of Water on Mars. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2010. Available online: https://deepblue.lib.umich.edu/handle/2027.42/78975 (accessed on 30 March 2024).
- Teramoto, K.; Yano, H. Measurements of Sound Speed in Granular Materials Simulated Regolith. In Proceedings of the 36th Annual Lunar and Planetary Science Conference, League City, TX, USA, 14–18 March 2005; p. 1856. [Google Scholar]
- Mitchell, J.K.; Houston, W.N.; Scott, R.F.; Costes, N.C.; Carrier, D.W.; Bromwell, L.G. Mechanical properties of lunar soil—Density, porosity, cohesion, and angle of internal friction. In Proceedings of the Lunar Science Conference, Houston, TX, USA, 10–13 January 1972; Legacy CDMS. p. 3235. [Google Scholar]
- Hutton, R.E. Mars Surface Soil Erosion Study—Technical Report. NTRS-NASA Technical Report Server, Pasadena, CA, Technical Report 0934-6001-R000. 1968. Available online: https://ntrs.nasa.gov/api/citations/19690015515/downloads/19690015515.pdf (accessed on 30 November 2023).
- Fontes, D.; Mantovani, J.G.; Metzger, P. Numerical estimations of lunar regolith trajectories and damage potential due to rocket plumes. Acta Astronaut. 2022, 195, 169–182. [Google Scholar] [CrossRef]
- Kim, Y.-B.; Jeong, H.-J.; Park, S.-M.; Lim, J.H.; Lee, H.-H. Prediction and Validation of Landing Stability of a Lunar Lander by a Classification Map Based on Touchdown Landing Dynamics’ Simulation Considering Soft Ground. Aerospace 2021, 8, 380. [Google Scholar] [CrossRef]
- Cannon, K.M.; Dreyer, C.B.; Sowers, G.F.; Schmit, J.; Nguyen, T.; Sanny, K.; Schertz, J. Working with lunar surface materials: Review and analysis of dust mitigation and regolith conveyance technologies. Acta Astronaut. 2022, 196, 259–274. [Google Scholar] [CrossRef]
- NASA. Classifications and Requirements for Testing Systems and Hardware to be Exposed to Dust in Planetary Environments. 2021. Available online: https://ntrs.nasa.gov/api/citations/20210019714/downloads/2021-08-21%20NASA-STD-1008-Approved.pdf (accessed on 30 November 2023).
- Rennó, N.O.; Backhus, R.; Cooper, C.; Flatico, J.M.; Fischer, E.; Greer, L.C.; Krasowski, M.J.; Kremic, T.; Martínez, G.M.; Prokop, N.F.; et al. A Simple Instrument Suite for Characterizing Habitability and Weathering: The Modern Aqueous Habitat Reconnaissance Suite (MAHRS). Astrobiology 2019, 19, 849–866. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y. (Ed.) The Dynamics and Modelling of Saltation. In Physics and Modelling of Wind Erosion. Atmospheric and Oceanographic Sciences Library; Springer: Dordrecht, The Netherlands, 2009; Volume 37, pp. 149–210. [Google Scholar] [CrossRef]
- Greer, L.C.; Krasowski, M.J. A Saltation Sensor for the Martian Aqueous Habitat Reconnaissance Suite (MAHRS); NASA Glenn Research Center: Cleveland, OH, USA, 31 May 2021.






| NASA’s Artemis Plan Recommendations |
| |||||
| CLPS PSI Suite Project Goals | Goal 1: Develop capability to quantify PSI effects in the lunar environment. | Goal 2: Mature concepts to measure the fundamental PSI process of ejecta dynamics, plume physics, and erosion physics. | Goal 3: Support scientists and engineers developing dust transport modeling. | Goal 4: Advance PSI science to inform commercial providers of Human Landing Systems (HLS) and Commercial Lunar Payload Services (CLPS) landers of the potential risks to their vehicles during landing. | ||
| Particle Impact Event Sensor | Science Requirements | Instrument Requirements | Strategy | Mission Requirements | ||
| Observables | Physical parameters measured | Accuracy and precision | Sampling rate | |||
| Objectives: Measure the effects of ejecta dynamics and erosion physics during PSI. Determine the potential damage caused by PSI. Determine the potential contamination inflicted by PSI on landing sites. | The flux of PSI ejecta. The kinetic energy of PSI ejecta impacts. | Particle impact counts as Gaussian-shaped pulses. | Flux ranging from 0 to 10,000 particles/m2s and kinetic energy of ejecta 0.1 nJ–400 µJ (1 µm < d < 1 mm; 10 m/s < v < 1 km/s) with uncertainty 10%. | 300 kHz | Measure the particle impact counts using piezoelectric material that has excellent sensitivity to energy impacts. Apply the Gaussian-shaped pulses to a threshold and measure the number of impacts to determine flux. Measure the kinetic energy proportional to the area under the impact pulses. | Survive and operate during landing in the lunar south pole environment. Accommodate a suite of instruments on the lander, preferably on the struts with minimal obstruction to the lander. Provide power for the instrument to operate during terminal phase of landing. |
| # | Nondimensional Parameter | Small-Scale Lander (D = 0.24 m) | Apollo Large-Scale Lander (D = 1.62 m) |
|---|---|---|---|
| 1 | 0.04 | 0.05 | |
| 2 | Re | 25 × 105 | 2.0 × 105 |
| 3 | Fr | ~4000 | ~2000 |
| 4 | τ | ~40,000 | ~50,000 |
| 5 | β | 1.0 × 1012 | 1.4 × 1013 |
| 6 | 1600 | 2700 | |
| 7 | δ | 11 × 1010 | 1 × 1010 |
| 8 | f | 0.46 | 0.46 |
| 9 | Ma | ~16 | ~20 |
| 10 | σ | 2.5 × 108 | 3.5 × 109 |
| PIE Sensor Requirements for Lunar Plume Surface Interaction(s) Measurement | |
|---|---|
| 1.0 | The instrument shall measure lunar regolith ejecta particle flux ranging from 1 to 10,000 particles/m2·s with 10% uncertainty. |
| 2.0 | The instrument shall measure the kinetic energy ranging from 0.1 nJ to 400 μJ of lunar ejecta impactors (10 m/s < v < 1000 m/s; 1 μm < d < 1 mm) with 10% uncertainty. |
| 3.0 | The instrument shall be capable of capturing measurements at 300 kHz for the entirety of the PSI process. |
| 4.0 | The instrument should meet the measurement requirements even when exposed to spacecraft vibrations. |
| 5.0 | The instrument shall be capable of operating with any combination of other PSI instruments. |
| 6.0 | Instrument subsystems that are externally mounted onto the lunar lander shall be compatible with a non-operating environment consistent with launch and travel conditions. |
| 7.0 | Instrument subsystems that are externally mounted onto the lunar lander shall meet operational and measurement requirements even while exposed to regolith impacts. |
| 8.0 | Instrument subsystems shall be compatible with an operating pressure and temperature environment consistent with landing conditions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bueno, A.; Krasowski, M.J.; Prokop, N.; Greer, L.C.; Adams, C.M.; Rennó, N.O. Instrument to Study Plume Surface Interactions (PSI) on the Lunar Surface: Science Motivation, Requirements, Instrument Overview, and Test Plans. Aerospace 2024, 11, 439. https://doi.org/10.3390/aerospace11060439
Bueno A, Krasowski MJ, Prokop N, Greer LC, Adams CM, Rennó NO. Instrument to Study Plume Surface Interactions (PSI) on the Lunar Surface: Science Motivation, Requirements, Instrument Overview, and Test Plans. Aerospace. 2024; 11(6):439. https://doi.org/10.3390/aerospace11060439
Chicago/Turabian StyleBueno, Ariana, Michael J. Krasowski, Norman Prokop, Lawrence C. Greer, Christina M. Adams, and Nilton O. Rennó. 2024. "Instrument to Study Plume Surface Interactions (PSI) on the Lunar Surface: Science Motivation, Requirements, Instrument Overview, and Test Plans" Aerospace 11, no. 6: 439. https://doi.org/10.3390/aerospace11060439
APA StyleBueno, A., Krasowski, M. J., Prokop, N., Greer, L. C., Adams, C. M., & Rennó, N. O. (2024). Instrument to Study Plume Surface Interactions (PSI) on the Lunar Surface: Science Motivation, Requirements, Instrument Overview, and Test Plans. Aerospace, 11(6), 439. https://doi.org/10.3390/aerospace11060439






