Abstract
In the field of civil aviation, the nose landing gear is a critical component that is prone to damage during taxiing. With the advent of new technologies such as towing taxi-out and hub motors, the nose landing gear faces increasingly complex operational environments, thereby imposing higher performance demands. Ensuring the structural safety of the nose landing gear is fundamental for the successful application of these technologies. However, current research on aircraft nose landing gear under these new conditions is somewhat lacking, particularly in terms of reliable analysis models for real-world scenarios. This study focuses on a typical Class C aircraft, specifically the B-727 model, for which a finite element model of the nose landing gear is developed. Modal testing of the aircraft’s nose landing gear is conducted using the impact hammer method, and the results are compared with those from the simulations. The experimental data indicate that the error range for the first seven natural frequencies is between 0.23% and 9.27%, confirming the high accuracy of the developed landing gear model. Furthermore, with towing taxi-out as the primary scenario, a dynamic model of the aircraft towing system is established, and an analysis on the structural strength and topological optimization of the nose landing gear under various conditions, including high speeds and heavy loads, is performed. The results show that the developed model can effectively support the analysis and prediction of the mechanical behavior of the nose landing gear. Under high-speed, heavy-load conditions, the nose landing gear experiences significantly increased loads, with the maximum deformation primarily occurring at the lower section of the shock strut’s outer cylinder. However, no damage occurred. Additionally, under these conditions, an optimized structural design for the landing gear was identified, which, while ensuring structural strength, achieves a 22.32% reduction in the mass of the outer cylinder, also ensuring safety in towing taxi-out conditions.
1. Introduction
An aircraft’s nose landing gear is a key component that bears significant loads, and plays multiple critical roles during ground taxiing, including directional control, shock absorption, and braking deceleration. Because the nose landing gear has lower structural strength than the main landing gear, it is more susceptible to structural damage [1] during taxiing. Therefore, the structural integrity of the nose landing gear directly impacts the aircraft’s takeoff and landing performance, serving as a vital safeguard for flight safety.
Considering that aircraft inherently lack a reverse function, an aircraft’s departure process usually involves being towed by a tug using a tow bar or wheel-lift mechanism connected to the nose landing gear. This towing is performed at low speeds (not exceeding 10 km/h) and moves the aircraft to an open area (illustrated in Figure 1 as the red dashed area). Subsequently, the crew initiates engine-powered taxiing to join the takeoff queue, waiting at the runway end for flight clearance (shown in Figure 1 as the red solid line area). This pre-flight preparation phase, accounting for 10–30% of flight time [2], increases the risk [3,4,5] of aircraft damage and personnel accidents because of the need for coordination among multiple departments [6]. Additionally, a prolonged ground operation of the aircraft engines during this phase can lead to issues [7] such as foreign object damage, high fuel consumption, noise pollution, and excessive engine depreciation. Collectively, these issues signify that the traditional aircraft ground taxiing method has become a critical bottleneck constraining airport operational safety, economic efficiency, and environmental sustainability.
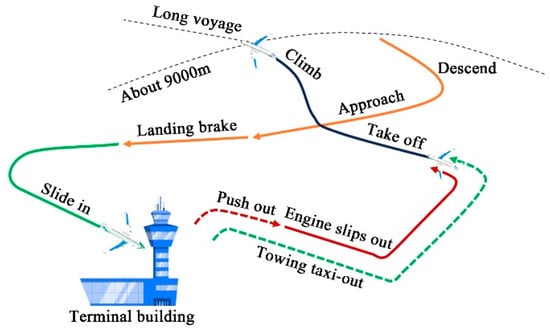
Figure 1.
Schematic diagram of aircraft taxiing during departure.
With the growing global emphasis on energy conservation and reduced emissions, the civil aviation industry has introduced technologies such as onboard-driven autonomous taxiing [8] systems and towing taxi-out departure modes [9,10,11,12]. These innovations not only challenge the traditional aircraft ground operation methods, but also impose new demands [13] on the structure and performance of the landing gear. The former involves installing a wheel hub electric drive system [14] on the aircraft’s nose or main landing gear, which is powered by an electric motor and supplied by an Auxiliary Power Unit (APU), with the pilot controlling the aircraft’s speed and direction. However, retrofitting this system requires modifications to the aircraft’s landing gear and complex certification through the Supplementary Type Certificate process, along with substantial R&D investment. The system also faces limitations introduced by the APU’s power supply capacity, motor size, and landing gear structure [15], failing to fundamentally resolve the inefficiencies of taxiing. Conversely, the latter method uses a towless aircraft tug for taxiing, with the tug providing power and control for the tug–aircraft towing system. This significantly enhances the efficiency, safety, and fuel economy of aircraft towing taxi-out [16], without the need for modifications to the aircraft structure, wiring, or engine start-up. As a result, major research institutions [17,18,19,20,21] such as NASA, the University of Nottingham, and Airbus are studying this efficient and safe intelligent aircraft taxiing mode, which is enabled by wireless technology, as a key approach for achieving next-generation ground operation control efficiency and safety in aviation.
Current research on the structural response of landing gear under towing conditions is mainly focused on low-speed towed taxi-out. A contact force model between the tow bar and landing gear has been established [22], enabling analyses of how the load on the nose gear’s drag strut changes with respect to the contact gap. The findings indicate that, under low-speed towing conditions below 7 km/h, the drag strut of a Boeing 737-800 generally does not fail from excessive compressive stress. However, in abnormal conditions, shear pin fractures [23] can occur as a result of overload impacts in the towing system’s gaps. Additionally, based on strain gauge measurements, methods have been proposed for static and fatigue testing of the nose landing gear’s outer cylinder suspension joint during towing taxi-out [24], focusing on structurally weak links or heavily loaded key parts of the landing gear.
During aircraft taxiing to overcome ground resistance and achieve high-speed movement, the nose landing gear structure is subjected to a maximum towing load equivalent to 15% of the Maximum Ramp Weight (MRW), while simultaneously experiencing approximately 15% [9] of the MRW in the vertical direction. These factors significantly affect the lateral load-carrying performance of the landing gear. Although no researchers have yet analyzed the structural vibration and strength of the landing gear under these compressive stresses during towing taxi-out, several studies have been conducted in other structural fields. For instance, Li et al. [25] researched aircraft structures operating in various environmental conditions, and evaluated the impact of in-plane thermal loads on lateral vibration performance. Similarly, Kharaghani [26] and others have proposed a higher-order shear deformation theory to evaluate the ultimate bending strength of composite materials under compressive stress.
Given the prevalence of Category C aircraft (including the A-320 family and B-737 family, as well as B-727, MD-82, and other models) in the civil aviation transport market, this study selects the B-727 as the primary research subject. A finite element analysis model of the nose landing gear’s shock-absorbing strut has been established, and its accuracy verified through modal testing [27,28]. Based on this model, a kinematic model of aircraft towing taxi-out has been constructed, providing a theoretical basis for studying the mechanics of towing taxi-out and optimizing the landing gear.
2. Model Verification
2.1. Modal Theory
The nose landing gear of an aircraft experiences different external loads when it is stationary on the ground, autonomously taxiing, and being towed. These variations affect the overall structural stiffness, resulting in different natural frequencies and mode shapes. Considering the different initial conditions of the structure, the analysis is as follows:
In a modal analysis, when external load effects are not considered, the dynamic control equation can be represented as
where
- represents the mass matrix;
- represents the damping matrix;
- represents the stiffness matrix;
- represents the nodal acceleration vector;
- represents the nodal velocity vector;
- represents the nodal displacement vector.
When considering the influence of external loads, the equation can be represented as
where
- represents the force vector.
If prestressing, damping effects, and similar influences can be neglected, the equation becomes
When simple harmonic motion occurs, the equation is represented as
where
- represents the i-th mode natural frequency of the structure;
- represents the i-th mode shape of the structure.
In the case of statically loaded structures with prestressing, it is first necessary to conduct a linear static analysis to obtain the stiffness matrix . Subsequently, a prestressed modal analysis can be performed, and the equation is represented as
2.2. Finite Element Modeling
As a typical Class C aircraft, the B-727 reflects the characteristics of mainstream aircraft models in terms of landing gear layout and structure. In this study, a specific B-727-200F model aircraft’s nose landing gear was surveyed within an airport, as shown in Figure 2. The survey mainly included components such as shock absorbers, drag struts, torsion arms, actuators, landing gear transfer valves, and wheels, are shown in Figure 2a,b.

Figure 2.
Physical representation of B-727 aircraft and nose landing gear.
A modal analysis is used to study the vibrational behavior of structures. The modes reflect the macroscopic vibrational characteristics of objects or structures. Removing surface cables from the nose landing gear and simplifying the mass of local structures relative to the main landing gear body has relatively little effect, so the use of simplified models for the analysis has only a minor impact on the results. An equivalent geometric model of the main structure of the nose landing gear was established, in which the structure had been geometrically cleaned and the faces had been repaired.
The shock absorbers and lower drag struts of the landing gear used for testing were designed as integrated components. The overall structural analysis mainly considers the landing gear’s own weight, the pressure from the upper drag strut on the lower drag strut, the support force of the actuator on the upper drag arm, the pressure from the aircraft’s weight on the shock absorber rear axle, the pressure from the torsion arms and transfer valve on the shock absorbers, the support force from the wheels and axles on the structure, and the support force from the jack on the jack platform, as shown in Figure 3.
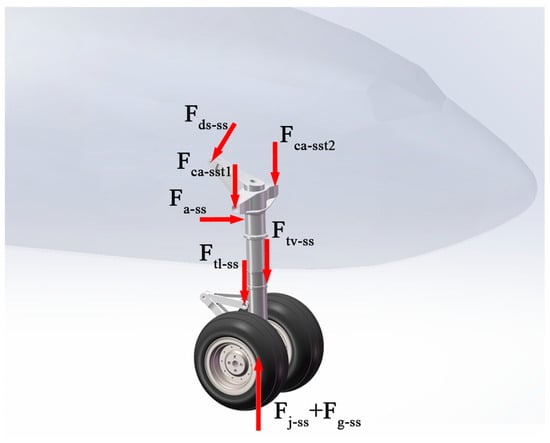
Figure 3.
Force analysis diagram of nose landing gear.
The overall structure is modeled using solid elements, primarily hexahedral elements, with the occasional use of tetrahedral elements in specific areas. The material used is 300 M steel, as shown in Figure 4.
Figure 4.
Finite element model of nose landing gear.
The first 12 mode shapes were calculated and the effective masses in the X-, Y-, and Z-directions were obtained. The effective masses in all directions are real values, and the cumulative effective mass fractions are shown in Figure 5.
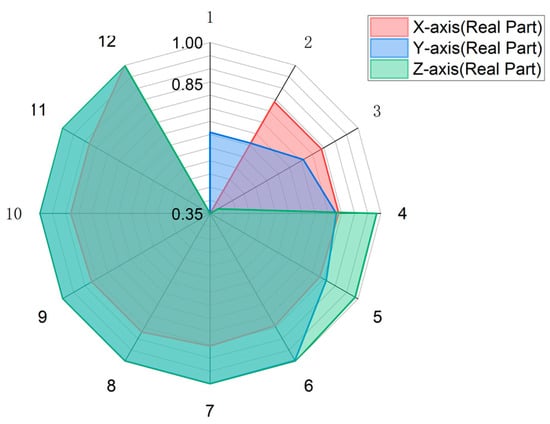
Figure 5.
Accumulated effective mass fraction plots in X-, Y-, and Z-directions for first 12 modes.
The cumulative effective mass fraction is calculated as the sum of the equivalent mass from the first mode to the respective mode divided by the total equivalent mass. A higher value indicates that a greater portion of the excitation force is distributed among the various modal shapes, meaning that the analysis results more accurately reflect the actual vibration situation. The cumulative effective mass fraction in the X-direction exceeds 0.85 after the seventh mode; for the Y- and Z-directions, this occurs after the fifth and fourth mode, respectively. Therefore, analyzing the first seven modes satisfies the requirements for analyzing the vibration characteristics of the landing gear. The first seven modal shapes are shown in Figure 6.

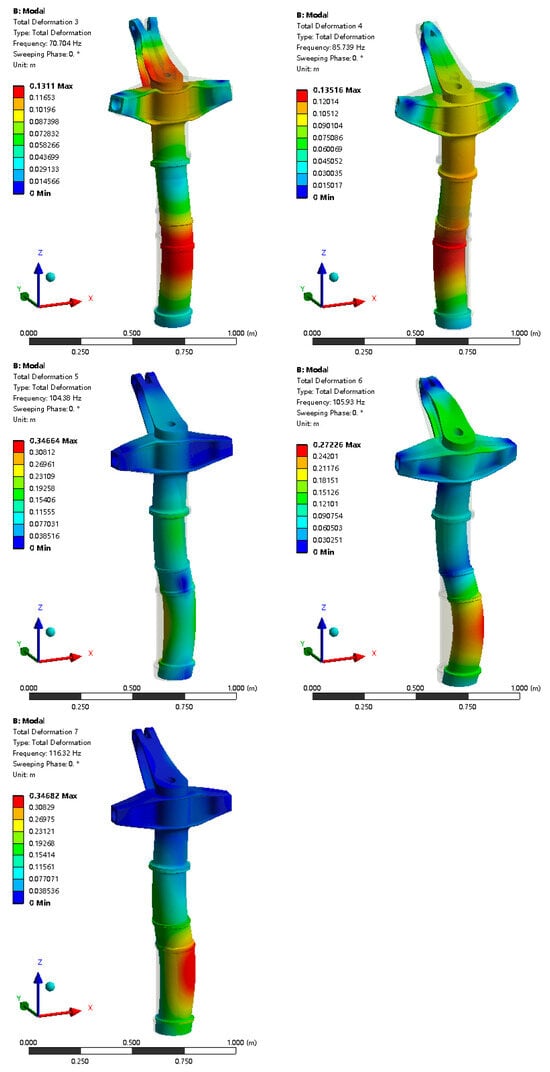
Figure 6.
Numerical mode shape diagrams for first seven modes.
Considering the mode shape diagrams for the first seven modes, along with the information from the solution analysis regarding modal mass ratios and effective mass parameters in each direction, we derived the corresponding mode shapes for each mode (see Table 1).

Table 1.
Analysis of the First Seven Modes of the Nose Landing Gear.
As indicated in Table 1, the first four modal states of the nose landing gear exhibit bending vibration, while the latter three exhibit torsional vibration. The middle and lower sections of the shock-absorbing strut have relatively lower structural strength and are more prone to resonance, whereas the drag strut has higher structural strength and is less likely to resonate.
2.3. Modal Testing
Modal testing was conducted using a Single Input Multiple Output (SIMO) approach. Accelerometers were positioned at intervals of 100 mm along both the nose and side surfaces of the landing gear, perpendicular to the ground direction. Because the landing gear was installed on an aircraft and multiple points on the structural surface were not conducive to sensor placement, slight adjustments were made to the positions of these points where necessary. The resulting sensor placement diagrams for both directions are shown in Figure 7.
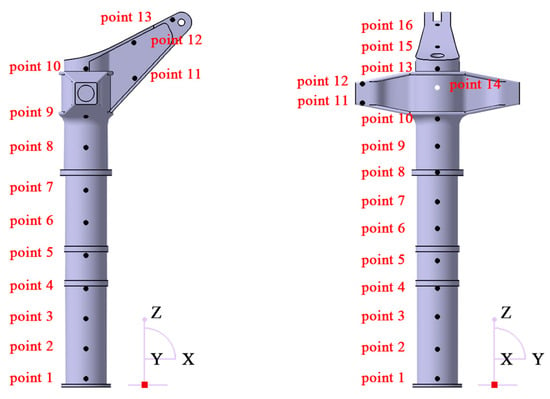
Figure 7.
Modal testing measurement point diagram.
According to the sensor placement diagram, two simplified structural models were created in the modal analysis software. These are shown in Figure 8.
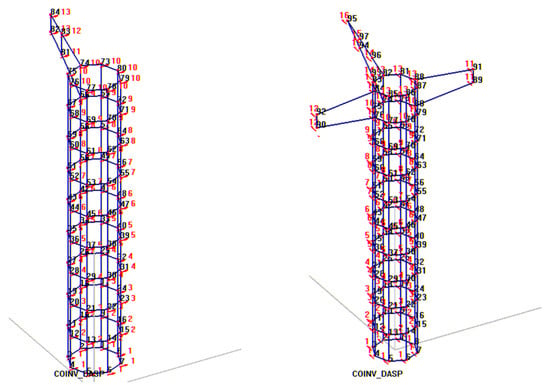
Figure 8.
Structural simplification diagrams created in modal analysis software.
The hammer test method is a common modal testing approach, characterized by its strong adaptability to complex structures, high efficiency in obtaining modal parameters, low cost, independence from external excitation sources, and minimal structural damage. To reduce the impact of the test on the aircraft and landing gear structure, the hammer test method was employed. A medium-sized force hammer was selected in Figure 9, and a signal acquisition instrument and hammer circuit were connected according to the point layout. Point 6 was used as the excitation point. The hammer struck alternately three times in succession and three times intermittently to complete one vibration data collection. The data quality was analyzed using modal analysis software to determine whether adjustments to the instruments or additional data collection was necessary. The test site is a busy airport apron, and the vibration signal collection was affected by the takeoff and landing of planes at the airport, often resulting in prolonged, irregular low-frequency signals. Although the validity of the hammer test response can be judged by analyzing the frequency response function curves, it is challenging to prevent the environment from influencing the test results, particularly for low-frequency data.

Figure 9.
Modal testing of nose landing gear.
As illustrated in Figure 10a,b, the data from the two directions were imported into the modal analysis software Data Acquisition & Signal Processing V11 (DASP V11) using the Fast Fourier Transform (FFT) method. The output frequency response functions facilitated the generation of modal identification state diagrams for both directions. The modal identification state diagrams were obtained directly by employing the Eigensystem Realization Algorithm (ERA) included in the software. Figure 10c,d were thus produced. By integrating the modal stability corresponding to each frequency, the first four modes and the first three modes were, respectively, selected for the two directions.
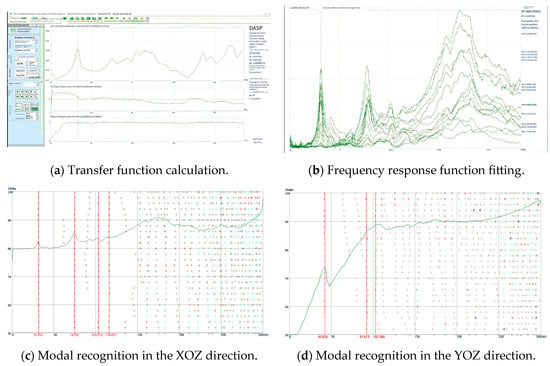
Figure 10.
Modal recognition state chart.
The first seven modes were sorted in ascending order of their corresponding natural frequencies (see Table 2).

Table 2.
Natural Frequencies of the First Seven Modes of the Nose Landing Gear.
2.4. Comparative Analysis
In the numerical modal analysis and experimental modal analysis of the first seven modes of the constructed nose landing gear model, the maximum error of 9.27% in the natural frequencies occurs for the second mode. The minimum error of 0.23% occurs for the seventh mode. Overall, the errors are relatively small, indicating good similarity between the landing gear model and the physical structure. Therefore, this landing gear model can be used as a reliable model for the analysis and prediction of its mechanical behavior, as shown in Figure 11.
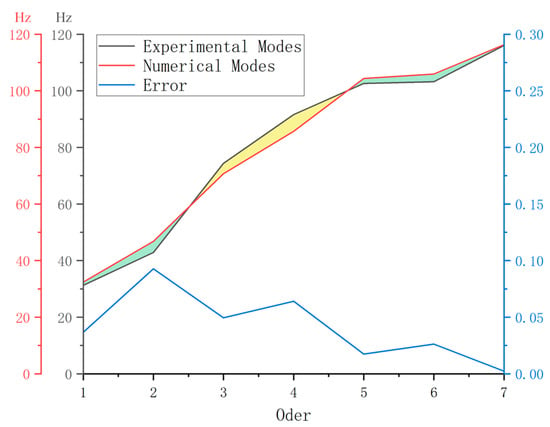
Figure 11.
Comparison of natural frequencies between numerical and experimental modal analyses.
The structural mass () of the landing gear was computed in the software. Additionally, a static analysis was performed by applying pressure at the rear axle of the shock strut, with the lower end of the fixed landing gear in place. The static load was calculated as
where represents the vertical stiffness coefficient of the nose landing gear, represents the vertical displacement of the structural node during the static analysis, and represents the static load on the structure, as shown in Figure 12.
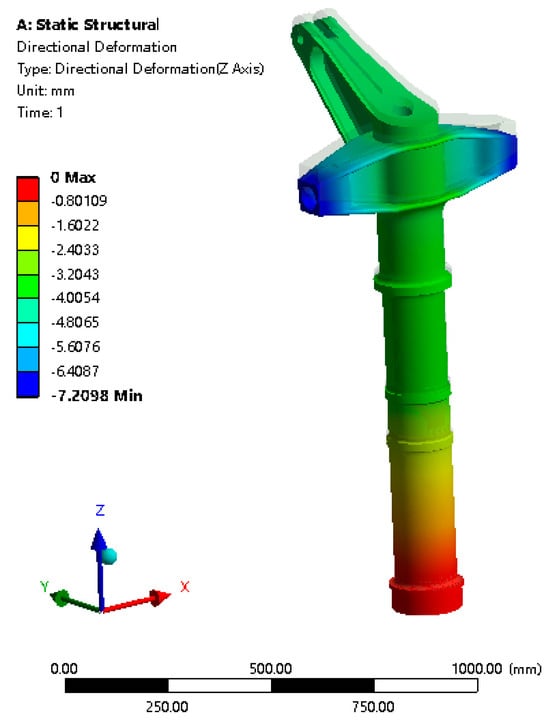
Figure 12.
Vertical deformation diagram for landing gear static analysis.
3. Dynamic Simulations
3.1. Dynamic Modeling
During the aircraft taxiing process, the nose landing gear structure is subjected to a maximum towing load equivalent to 15% of the MRW and approximately 15% of the MRW in the vertical direction. The resulting compressive stresses can significantly impact the lateral load-carrying performance of the landing gear. Taking the WeiHai GuangTai AM210 tow-bar-less aircraft tow tractor as an example, the nose landing gear of the aircraft was connected to the tow tractor’s wheel mechanism to form a towing system, as shown in Figure 13.

Figure 13.
Tow-bar-less towing for B-727.
In the numerical analysis process, this paper primarily investigates whether the strength of the B-727 nose landing gear is sufficient for aircraft taxiing conditions. Earlier, the mass and stiffness of the nose landing gear were obtained through a finite element model. To reduce the impact of uncertainties introduced by factors such as the wheel mechanism, tires, and tow tractor in the entire system, a partial simplification [27] was applied to the fuselage, nose landing gear, and tow tractor. The nose landing gear was simplified as a model consisting of a spring and a mass block, and the tow tractor tire was simplified as a model with a spring and a damper. The simplified model is shown in Figure 14.
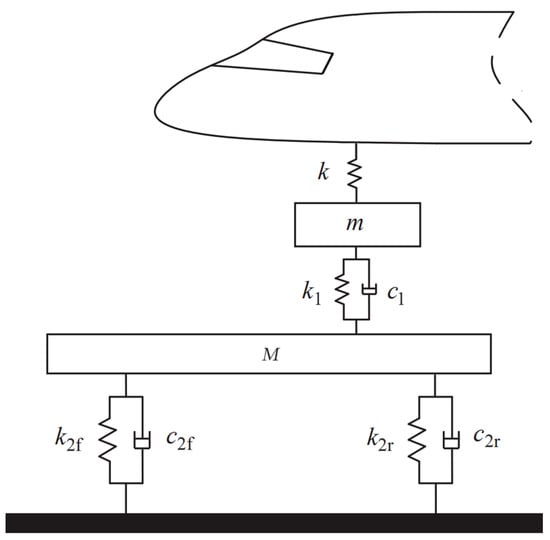
Figure 14.
Aircraft towing system dynamic model.

Table 3.
Aircraft and Tow Tractor Parameters.
The irregularities in the runway surface formed under the combined influence of environmental factors and loads is known as pavement roughness. The pavement of the airport used in this study is relatively smooth, and so Grade A pavement was chosen as the tire input for aircraft taxiing conditions. By simulating the roughness of Grade A pavement using computer modeling, a geometric model of the runway was created in three-dimensional modeling software, providing a relatively accurate representation of the airport pavement.
The geometric model of the aircraft towing system was established and imported into the ADAMS View 2020 software package to build the dynamic model of the towing system [30], as shown in Figure 15.
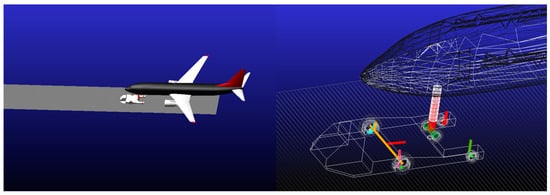
Figure 15.
Modeling aircraft towing taxi-out dynamics in ADAMS software.
3.2. Simulation Results
The towing operations of the aircraft towing taxi-out system are categorized into three speeds: high (greater than 25.93 km/h), medium (11.11–25.93 km/h), and low (less than 11.11 km/h). Using the same 2 km long Grade A runway, simulations were conducted for medium- and high-speed taxiing at towing speeds of 54 km/h and 36 km/h, respectively. These simulations were performed under both empty and fully loaded aircraft conditions, with aircraft masses of 44,330 kg and 78,100 kg, respectively. The vertical forces on the nose landing gear were obtained as a function of the aircraft taxiing distance, as shown in Figure 16.
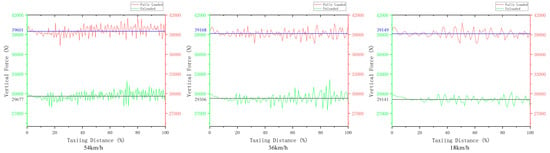
Figure 16.
Variation of vertical forces on nose landing gear with different towing speeds and loads.
Under empty and fully loaded conditions, there are significant differences in the vertical forces on the nose landing gear, with the maximum force occurring during the 54 km/h fully loaded taxiing process. To further investigate the mechanical performance of the structure, ANSYS Workbench was used to analyze the deformations of the landing gear under each condition, as shown in Figure 17.

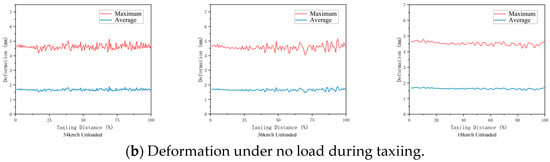
Figure 17.
Deformation of nose landing gear shock absorbers with different towing speeds and loads.
As shown in Figure 17, the maximum deformation of the landing gear occurs during the fully loaded condition at 54 km/h during towing operations.
Finite element analysis results indicate that, under extreme conditions, the maximum deformation of the structure occurs in the middle–lower section of the structure, near the towing point. The maximum deformation reaches 6.2102 mm and the average deformation is 2.2672 mm. These deformations do not have destructive effects on the structure,as shown in Figure 18.
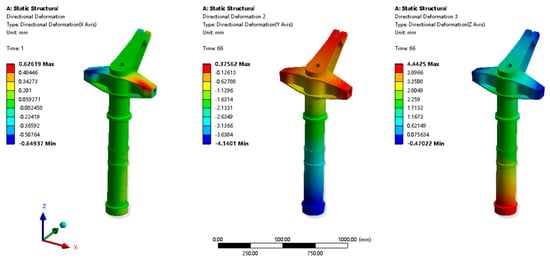
Figure 18.
Maximum deformation of landing gear during full-load towing at 54 km/h.
4. Structure Optimization
4.1. Topological Optimization
Topological optimization is a type of structural optimization widely utilized in the structural design of the aerospace industry [31,32,33,34]. This method iteratively determines the optimal distribution of materials within a specified design area using the finite element method, based on given load conditions and constraints. It optimizes the paths for force transmission while significantly reducing the structural mass. Globally, existing nose landing gear can handle the current aircraft takeoff and landing environments. However, the design of the nose landing gear in service today did not consider complex conditions such as towing taxi-out at the outset. Introducing structural topology into the landing gear model constructed in this paper can lead to a landing gear design more suited for the towing taxi-out mode. This provides a reference for future improvements to landing gear design following the widespread application of the towing taxi-out mode.
In the geometric modeling software CATIA P3 V5-6R2019, without affecting the setting of boundary conditions, the space is filled according to the geometric model of the outer cylinder of the landing gear’s vibration-damping strut, resulting in the geometric model ready for topology as shown in Figure 19a. In ANSYS Workbench, finite element analysis settings corresponding to the towing taxi-out mode are added to the model awaiting topology, and the topology optimization region is selected, as shown in Figure 19b.
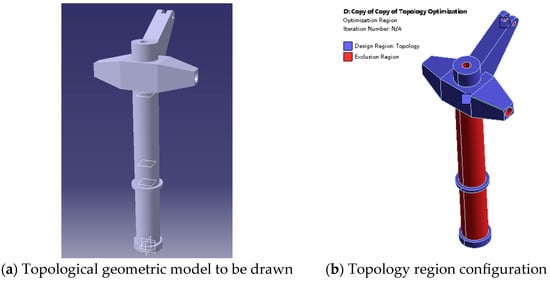
Figure 19.
Topological geometric model and finite element model.
The topology was conducted with the optimization objectives of retaining 60%, 70%, and 80% of the mass of the model awaiting topology, resulting in the outcomes shown in Figure 20 and Figure 21.
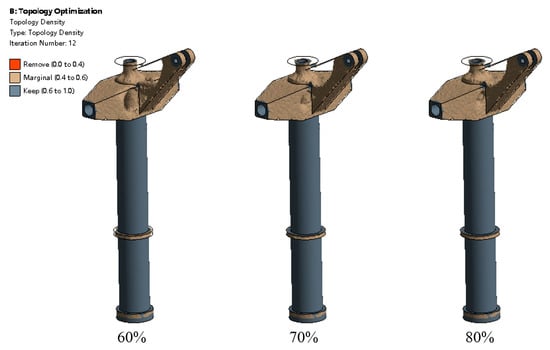
Figure 20.
Topological results with different optimization objectives.

Figure 21.
Topological results with 75% retained mass.
The topology results reveal that in response to the optimization of the upper segment of the outer cylinder and the lower resistance arm of the vibration-damping strut, the optimization characteristics include preserving the shape of the upper segment’s tubing and optimizing the connection between the lower resistance arm and the upper segment of the vibration-damping strut’s outer cylinder. As shown in Figure 22, for the topology model that retains 75% of the mass, exporting and performing surface repairs and other geometric clean-up operations are conducted. In the geometric modeling software, a model suitable for a finite element analysis is reconstructed.
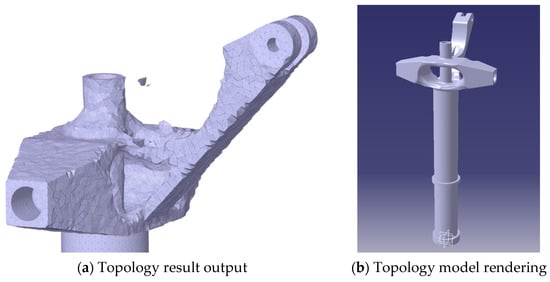
Figure 22.
Topological model reconstruction.
According to Equation (6), the optimized parameters are solved in the finite element analysis software, the dynamic modeling model is revised, and the reanalysis of the dynamics simulation part of this paper is completed.
4.2. Result Analysis
After calculation, the mass of the outer cylinder of the vibration-damping strut after topology optimization is reduced by 37.83 kg, which is a 22.32% reduction compared to the original structure. The maximum deformation occurs in the lower segment of the vibration-damping strut, at 8.419 mm, an increase of 35.4–37.4%. The minimum deformation occurs at the ear shaft of the vibration-damping strut, at 0.037 mm, an increase of 401.3–467.5%. The average deformation of the structure ranges between 1.560 and 2.123 mm, a reduction of 5.0–5.7%, and all deformations did not lead to structural failure.
The optimized landing gear has been noticeably reduced in weight. Although the maximum and minimum deformations have significantly increased, the average deformation has been reduced through the optimization of the force transfer path, thereby enhancing the overall strength of the structure and achieving a good optimization effect, as shown in Figure 23.

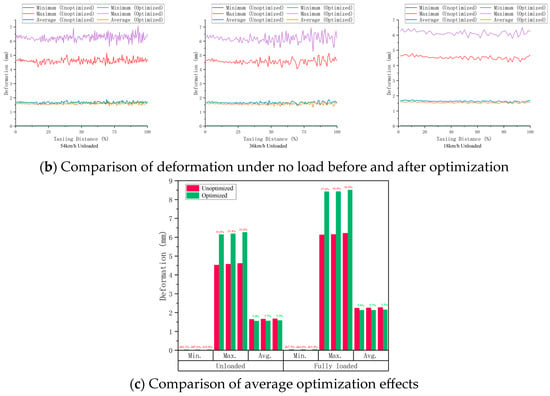
Figure 23.
Comparison of effects before and after optimization of nose landing gear shock absorber.
5. Conclusions
This study successfully established a mechanical model of the nose landing gear of a B-727 aircraft and validated the accuracy of the model through modal testing. This model was used to simulate the force and deformation of the landing gear under towing taxi-out conditions, and topological optimization was carried out, yielding the following specific conclusions:
1. Modal Testing and Error Analysis: The mechanical model of the aircraft’s nose landing gear established in this study achieved a cumulative effective mass fraction of 85% for the first seven numerical modal orders. Comparisons with actual experimental data showed that the error between the simulation results and the experimental data for the first seven orders of vibration frequency was less than 10%, with the experimental modal vibration frequency ranging from 31.252 to 116.057 Hz for the first seven orders. The discrepancies between the experiments and simulations may have been caused by the entire modal test being conducted in a busy airport, where low-frequency vibrations from aircraft takeoffs and landings interfered with data collection, particularly affecting low-frequency modal data. Indeed, the second order showed relatively large errors, possibly the result of airport environmental influences. Other causes of discrepancies include errors in the geometric model of the landing gear during surveying, including simplifications of the internal structure because of the inability to observe it, and errors arising from the modal recognition algorithms used in the modal analysis software, which may not accurately identify all modes.
2. Model Reliability: The landing gear mechanical model established in this study has been verified through modal testing to be highly reliable, effectively supporting the analysis and prediction of the mechanical behavior of the aircraft’s nose landing gear.
3. Relationship Between Force and Deformation: During medium- and high-speed towing taxi-out, a greater towing speed results in a greater average vertical force on the landing gear. Similarly, a greater aircraft weight produces a greater average vertical force on the landing gear. The maximum force and deformation of the landing gear occurred under towing at 54 km/h, with the maximum deformation being 8.284 mm and the average deformation being 2.897 mm.
4. Nose Landing Gear Safety Assessment: Under the same surface conditions, the nose landing gear of the aircraft showed the greatest deformation under high-speed, full-load conditions. Despite this, there was no structural damage to the nose landing gear, and its mechanical performance satisfied the strength requirements. The maximum deformation primarily occurred in the middle and lower sections of the shock strut, near the towing point. Therefore, if optimizing the landing gear structure, priority should be given to strengthening the stiffness of the middle and lower sections of the shock strut to enhance the overall stability and durability of the structure.
5. Topology Optimization Analysis: Through the structural topology of vibration-damping struts, this study primarily conducted structural optimization on the upper segment of the outer cylinder and the lower resistance arm of the vibration-damping struts. By ensuring safety within prescribed limits, the weight of the outer cylinder of the vibration-damping struts was reduced by 22.32%. The maximum deformation of the structure increased by 35.4–37.4%, while the average deformation decreased by 5.0–5.7%. This optimization scheme maintains the basic mechanical performance of the structure and demonstrates a good optimization effect.
Author Contributions
Conceptualization, Q.L.; Methodology, Q.L.; Software, C.Y.; Investigation, Y.B.; Data curation, C.Y.; Writing—original draft, Q.L.; Writing—review & editing, J.Q.; Funding acquisition, J.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Jiahao Qin, study on the lateral instability mechanism and multi-stage stabilization control of high-speed heavy-duty aircraft traction system, 52102446.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Chang Yang was employed by the company China Automotive Technology and Research Center Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Tang, Y.D. Design and Optimization of Landing Gear Structure for New Large Passenger Aircraft. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2021. [Google Scholar]
- Zhang, H.; Jiao, Z.X.; Shang, Y.X.; Liu, X.C.; Qi, P.Y.; Wu, S. Ground maneuver for front-wheel drive aircraft via deep reinforcement learning. Chin. J. Aeronaut. 2021, 34, 166–176. [Google Scholar] [CrossRef]
- Boeing Commercial Airplanes. Statistical Summary of Commercial Jet Airplane Accidents. Worldwide Operations 2008. Available online: https://www.boeing.com/content/dam/boeing/boeingdotcom/company/about_bca/pdf/statsum.pdf (accessed on 13 May 2024).
- ASN Wikibase Occurrence # 224818. [EB/OL]. Available online: https://aviation-safety.net/wikibase/224818 (accessed on 23 January 2020).
- Liu, C.X. Research on Ground Towing Safety of Aircraft. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- MH/T 3011.3-2006; Civil Aircraft Maintenance Ground Safety Part 3: Towing of Civil Aircraft. Civil Aviation Administration of China: Beijing, China, 2006.
- Hein, K.; Baumann, S. Acoustical comparison of conventional taxiing and dispatch towing-Taxibot’s contribution to ground noise abatement. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences (ICAS), Daejeon, Republic of Korea, 25–30 September 2016. [Google Scholar]
- Tao, J.F.; Guo, J.X.; Liu, C.L. A review of powered wheel for aircraft. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016. [Google Scholar]
- Sun, Y.K.; Zhang, W.; Yang, X.W.; Liu, J.H.; Zhu, H.J.; Liu, Y.X.; Qin, J.H. Overview of Aircraft Towing and Taxiing Techniques. J. Traffic Transp. Eng. 2023, 23, 23–43. [Google Scholar]
- MH 5001-2021; Technical Standards for Flight Areas of Civil Airports. Civil Aviation Press of China: Beijing, China, 2021. (In Chinese)
- Wollenheit, R.; Mühlhausen, T. Operational and environmental assessment of electric taxi based on fast-time simulation. Transp. Res. Rec. 2013, 2336, 36–42. [Google Scholar] [CrossRef]
- Re, F. Viability and state of the art of environmentally friendly aircraft taxiing systems. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012; pp. 1–6. [Google Scholar]
- Available online: http://www.airbus.com/support/maintenance-engineering/technical-data/aircraft-characteristics/ (accessed on 5 November 2010).
- Galea, M.; Xu, Z.; Hamiti, T.; Gerada, C.; Pickering, S. Development of an aircraft wheel actuator for green taxiing. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), IEEE, Berlin, Germany, 2–5 September 2014. [Google Scholar]
- Raminosoa, T.; Hamiti, T.; Galea, M.; Gerada, C. Feasibility and electromagnetic design of direct drive wheel actuator for green taxiing. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, IEEE, Phoenix, AZ, USA, 17–22 September 2011. [Google Scholar]
- Airbus MoU with IAI to Explore Eco-Efficient “Engines-off” Taxiing [EB/OL]. Available online: https://www.airbus.com/newsroom/press-releases/en/2009/06/airbus-mou-with-iai-to-explore-eco-efficient-apos-engines-off-apos-taxiing.html (accessed on 13 February 2015).
- Lukic, M.; Hebala, A.; Giangrande, P.; Klumpner, C.; Nuzzo, S.; Chen, G.; Gerada, C.; Eastwick, C.; Galea, M. State of the art of electric taxiing systems. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), IEEE, Nottingham, UK, 7–9 November 2018. [Google Scholar]
- Postorino, M.N.; Mantecchini, L.; Paganelli, F. Improving taxi-out operations at city airports to reduce CO2 emissions. Transp. Policy 2019, 80, 167–176. [Google Scholar] [CrossRef]
- Coetzee, E.; Krauskopf, B.; Lowenberg, M. Analysis of medium-speed runway exit maneuvers. J. Aircr. 2011, 48, 1553–1564. [Google Scholar] [CrossRef]
- Dzikus, N.M.; Wollenheit, R.; Schaefer, M.; Gollnick, V. The benefit of innovative taxi concepts: The impact of airport size, fleet mix and traffic growth. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar]
- Tabares, D.A.; Mora-Camino, F. Aircraft ground operations: Steps towards automation. CEAS Aeronaut. J. 2019, 10, 965–974. [Google Scholar] [CrossRef]
- Chen, S.W.; Liu, H.; Liu, H.; Li, F.H.; Zhang, H. Analysis of Aircraft Ground Towing Load with Contact Collision. J. Harbin Eng. Univ. 2017, 38, 1794–1799. [Google Scholar]
- Liang, Q.X.L.; Hu, B.T.; Wang, Z. Static Strength Test Design of Aircraft Nose Landing Gear Based on Vertical Self-Balanced Loading. Test Technol. Test. Mach. 2023, 63, 40–42. [Google Scholar]
- Li, Z.P.; Wu, B.; Wang, X.M.; Lv, W.; Fan, Q.B. A Fatigue Test Method for Aircraft Nose Landing Gear Outer Cylinder Suspension Street Towing Takeoff. Chinese Patent CN108163225A, 29 November 2017. [Google Scholar]
- Li, Y.M.; Li, X.Y.; Chai, Y.J.; Yang, X.W. Dynamic Response Analysis of Front Landing Gear under New Towing Slipway Mode for Aircraft. Acta Aeronaut. Astronaut. Sin. 2022, 43, 214–227. [Google Scholar]
- Kharghani, N.; Guedes Soares, C. Analytical and experimental study of the ultimate strength of delaminated composite laminates under compressive loading. Compos. Struct. 2019, 228, 111355. [Google Scholar] [CrossRef]
- Caputo, F.; De Luca, A.; Greco, A.; Maietta, S.; Marro, A.; Apicella, A. Investigation on the static and dynamic structural behaviors of a regional aircraft main landing gear by a new numerical methodology. Frat. Ed Integrità Strutt. 2018, 12, 191–204. [Google Scholar] [CrossRef]
- Zhu, H.J.; Lv, X.; Zhang, B.Z. Research on the Smoothness of the Traction System of a Cableless Aircraft Considering Flexible Frame. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 1458–1467. [Google Scholar]
- Zhang, Y.; Jin, Z.R.; Jia, W.T.; Liu, X.C.; Xu, Y. Random Response and Reliability Analysis of Aircraft Landing Gear under Uneven Runway Excitation. J. Vib. Eng. 2024, 37, 497–504. [Google Scholar]
- Qin, J.H.; Liu, J.W.; Lin, Q.W.; Zhang, W. Research on Instability and “Jack-Knifing” of Civil Aircraft Towing Taxi-Out System. Appl. Sci. 2023, 13, 3636. [Google Scholar] [CrossRef]
- Munk, D.J.; Auld, D.J.; Steven, G.P.; Vio, G.A. On the benefits of applying topology optimization to structural design of aircraft components. Struct. Multidiscip. Optim. 2019, 60, 1245–1266. [Google Scholar] [CrossRef]
- Xue, C.J.; Dai, J.H.; Wei, T.; Liu, B.; Deng, Y.Q.; Ma, J. Structural optimization of a nose landing gear considering its fatigue life. J. Aircr. 2012, 49, 225–236. [Google Scholar] [CrossRef]
- Deng, Y. Application of shape optimization in landing-gear structural design of small aircraft. Mech. Eng. 2008, 30, 47–51. [Google Scholar]
- Yang, G.; He, P.; Wang, Y.; Liu, C. Structural Optimization of the Lower Door of the Main Landing Gear of an Aircraft. J. Phys. Conf. Ser. 2023, 2557, 012019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).