A High Step-Down SiC-Based T-Type LLC Resonant Converter for Spacecraft Power Processing Unit
Abstract
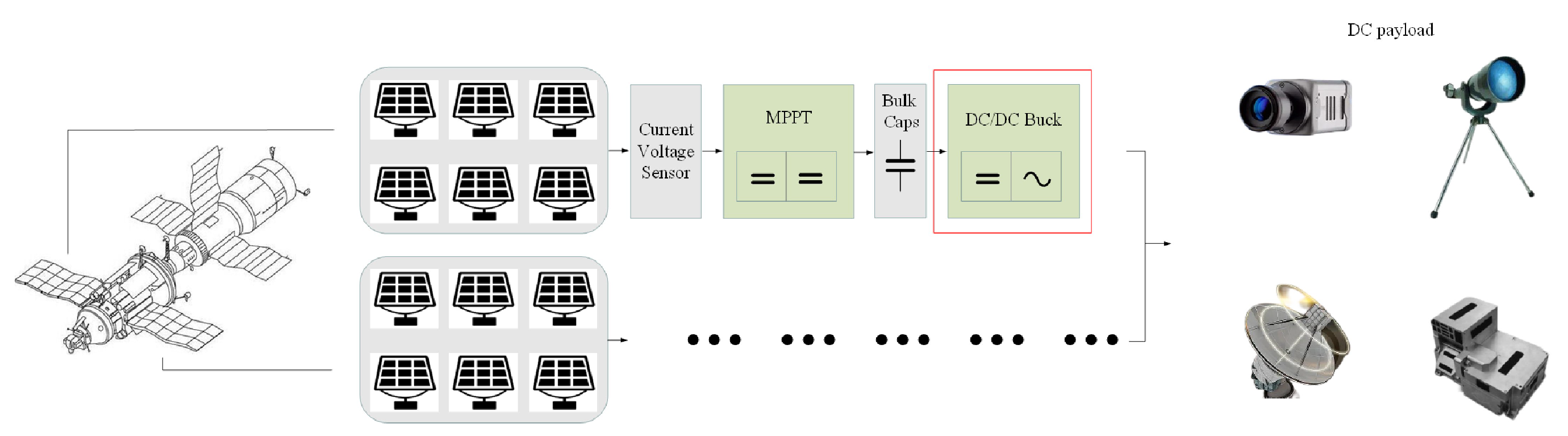
1. Introduction
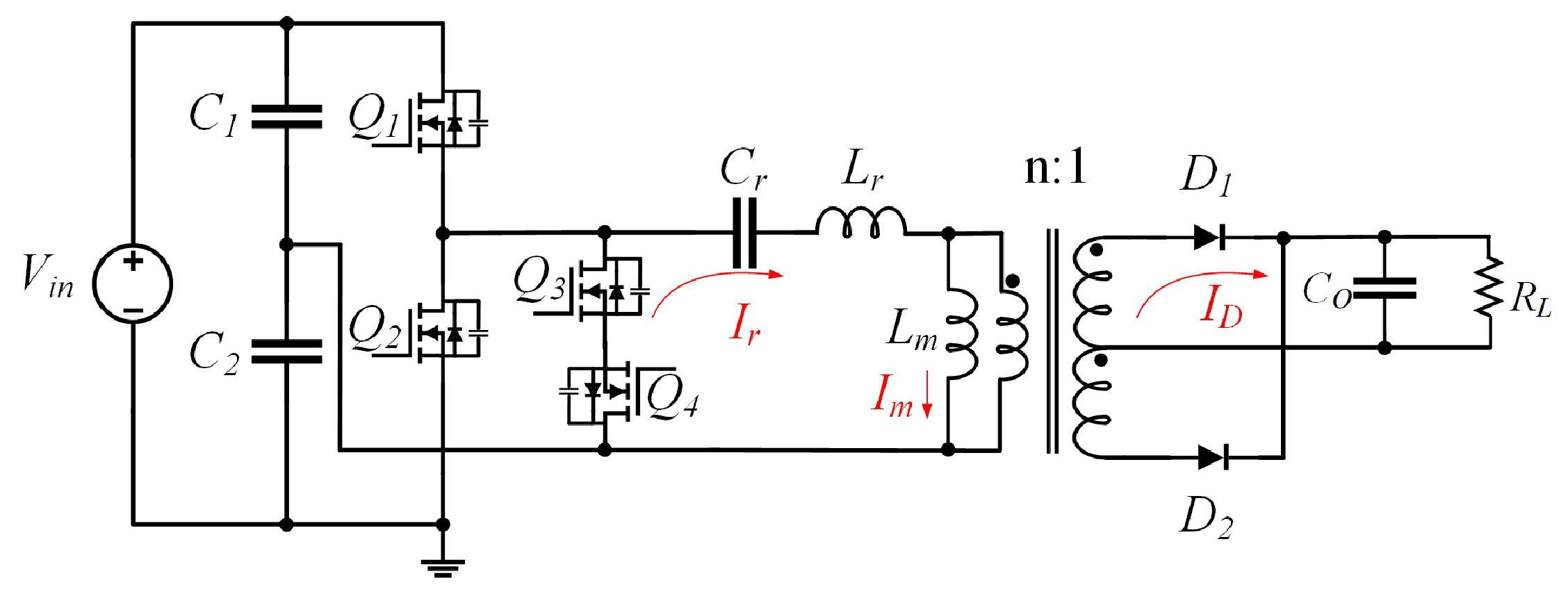
2. The Topology and Operation Modes
2.1. The Topology
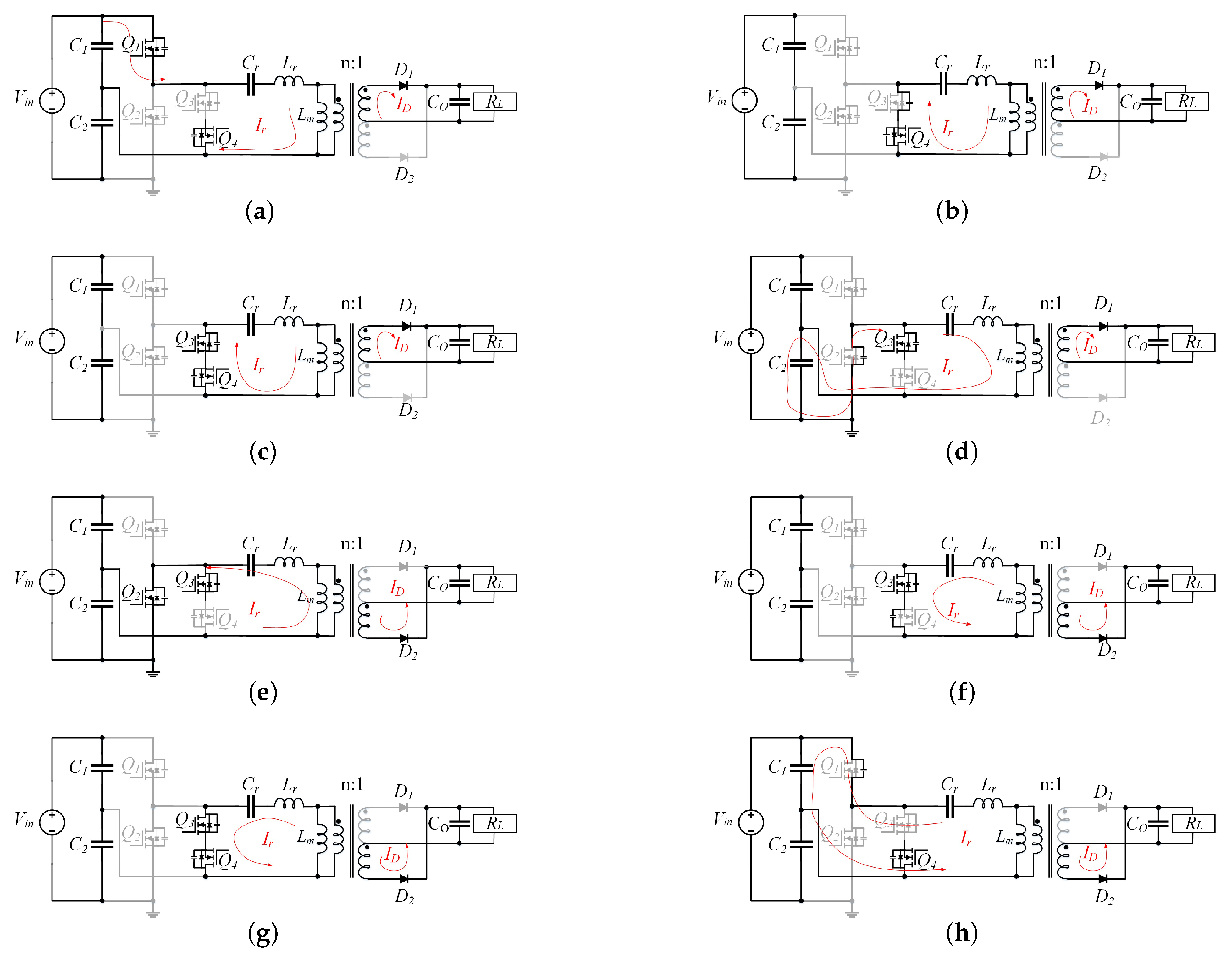
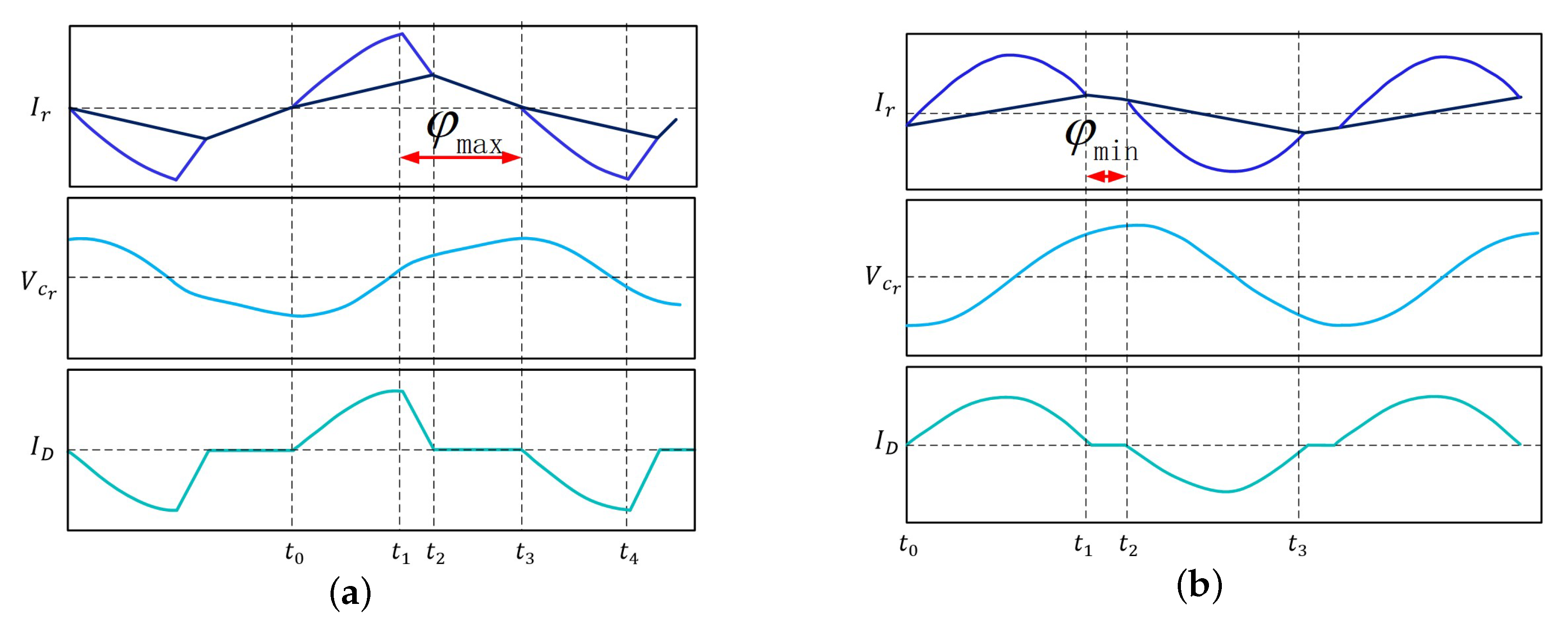
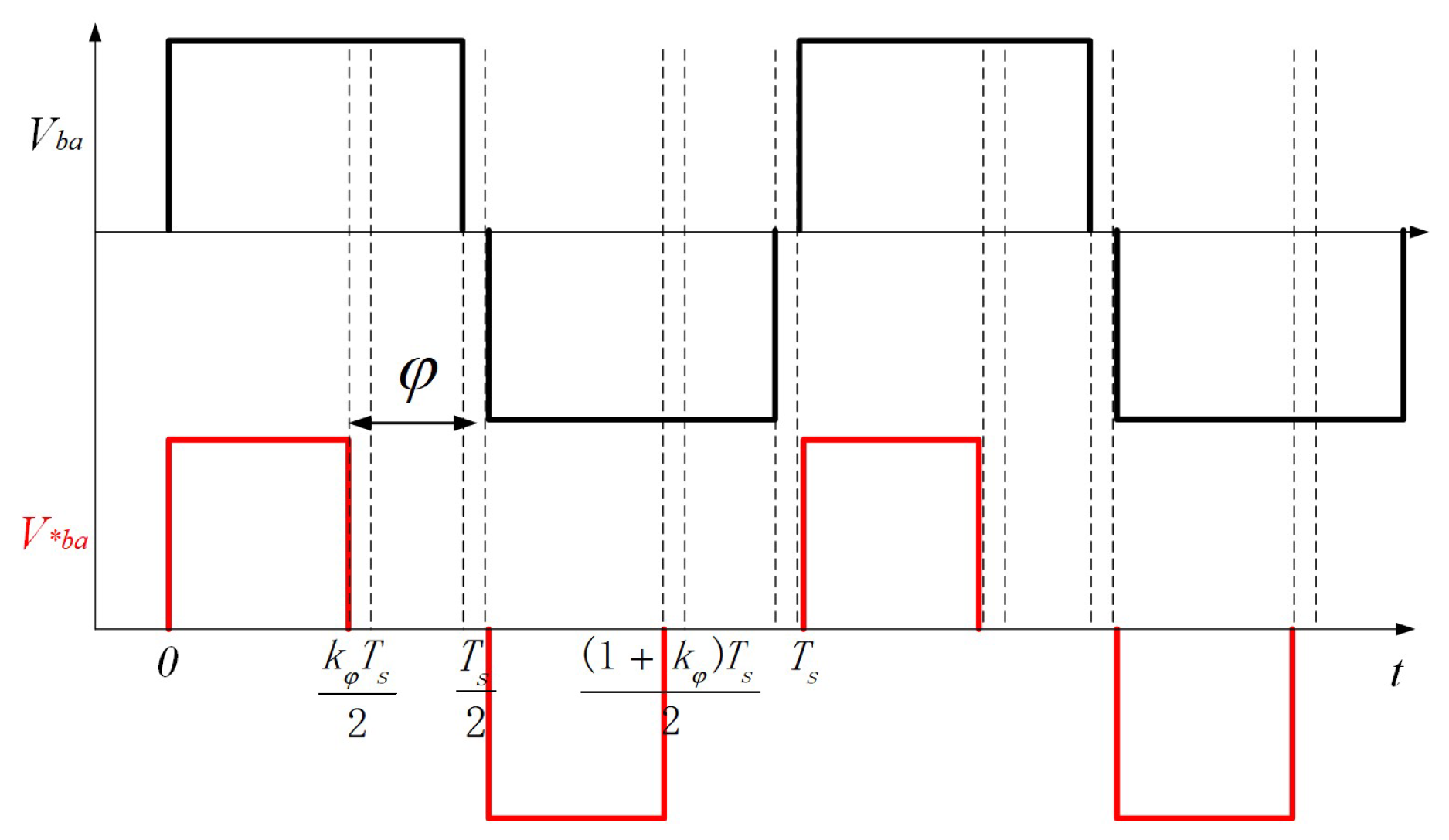
2.2. The Operation Modes
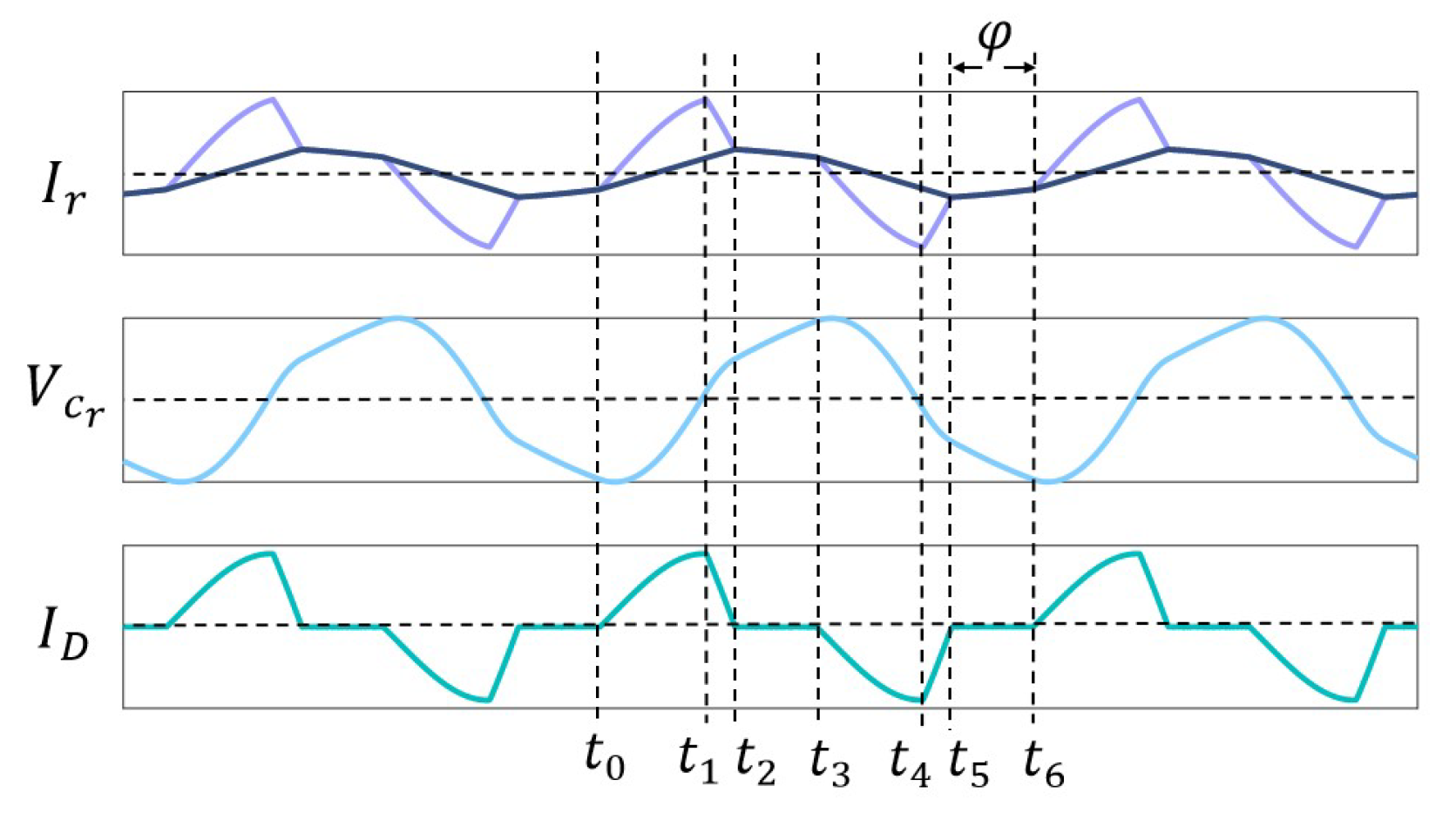
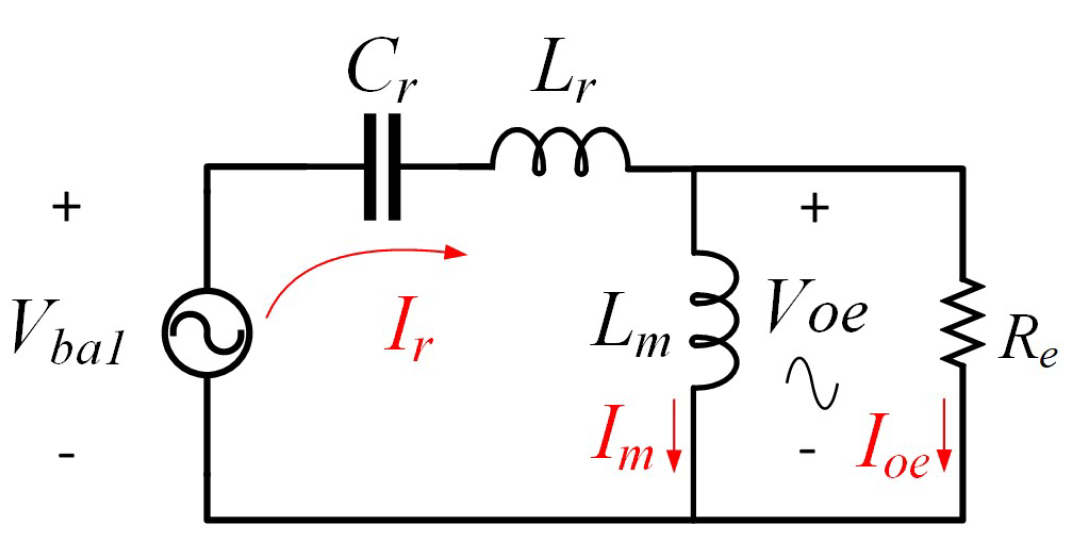
2.3. The Time-Domain Analysis of Mode 2
3. The Design Algorithm
3.1. Basic Parameters Used in Derivations
3.2. Boundary Conditions
3.2.1. Boundary Conditions for Soft Switching
3.2.2. Boundary Conditions between Mode 1 and Mode 2
3.3. Resonant Elements
3.4. Dead Times
3.5. VFAPS Design Procedure
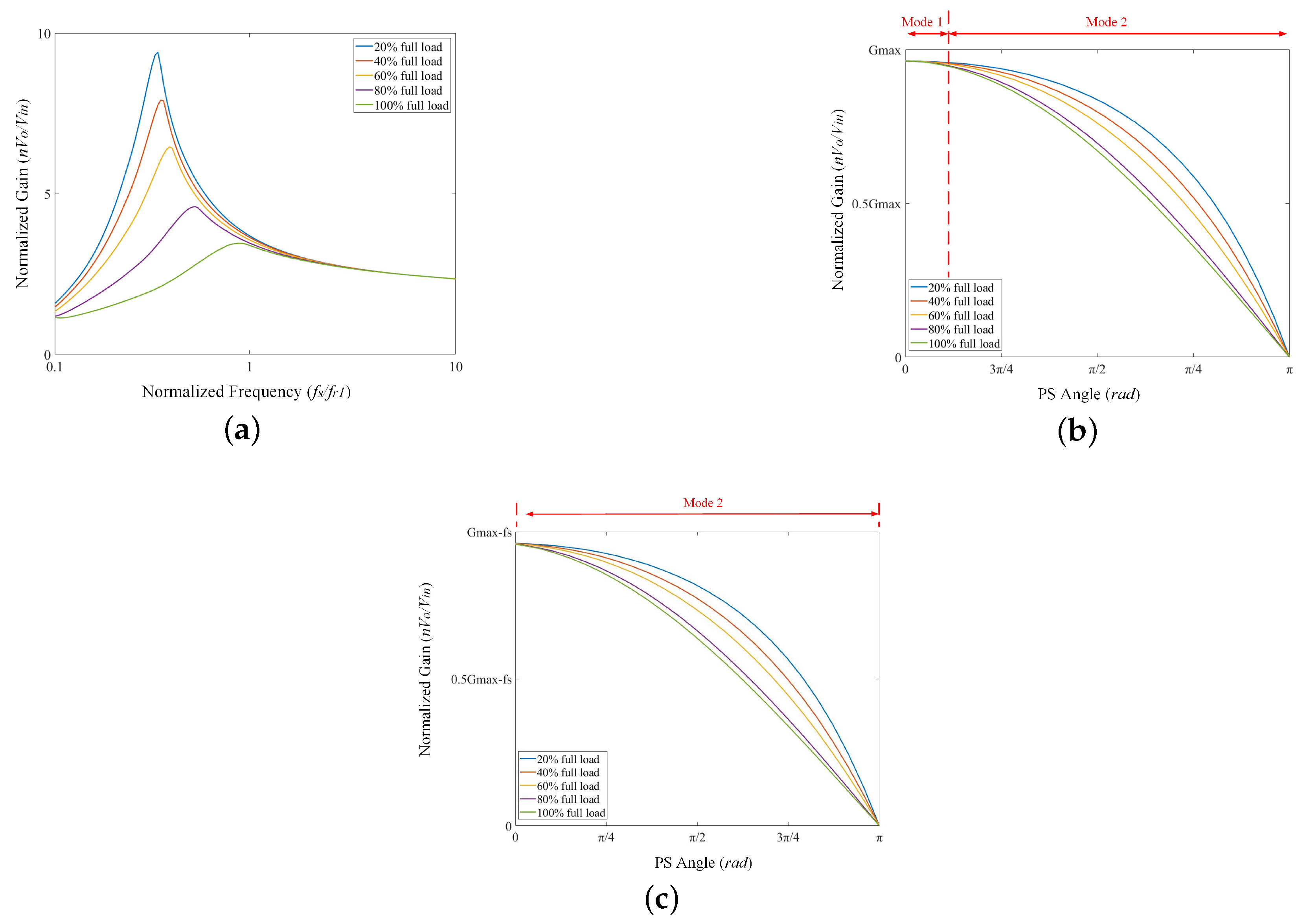
3.6. The Simulation of Voltage Gain
4. Experimental Verification
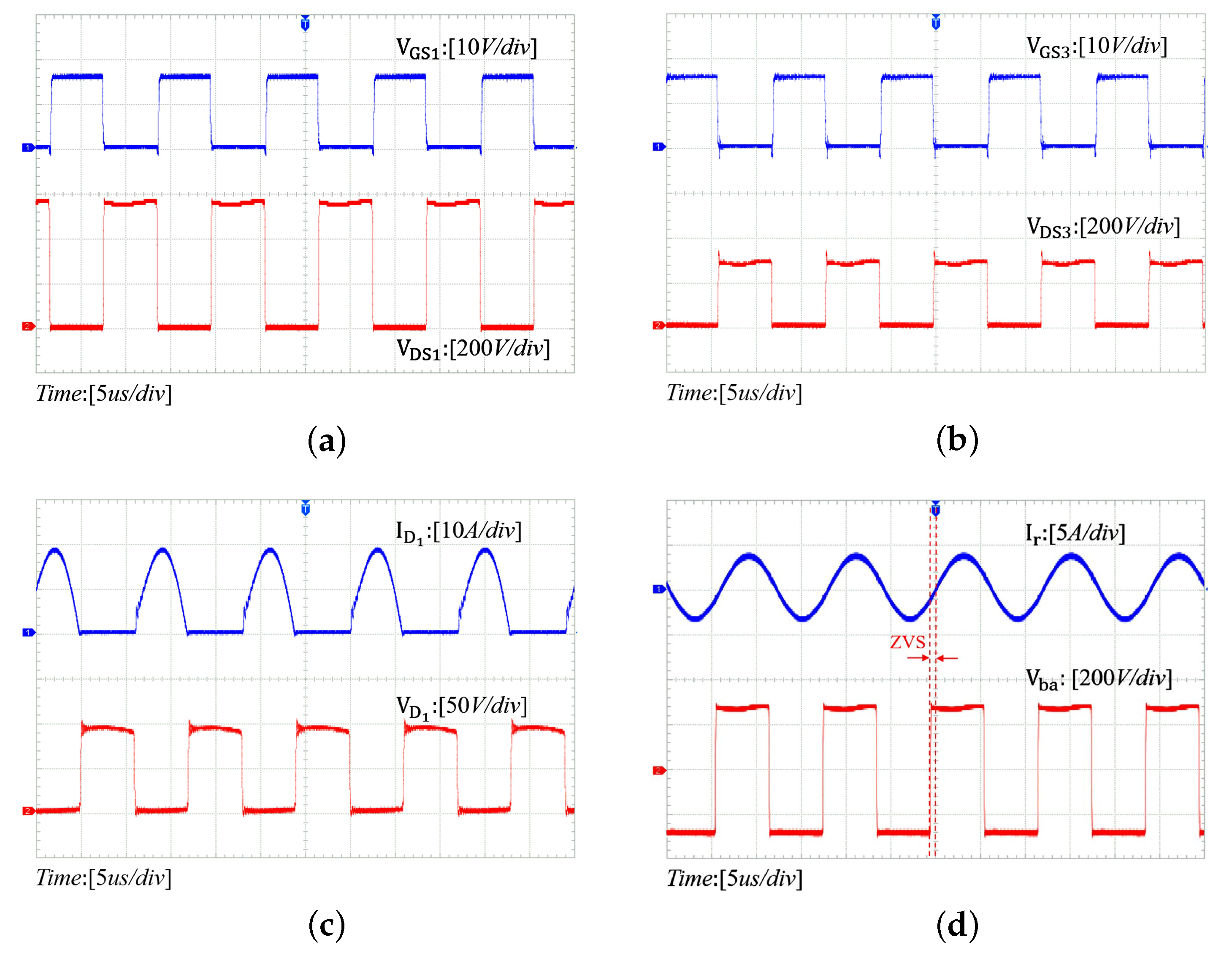
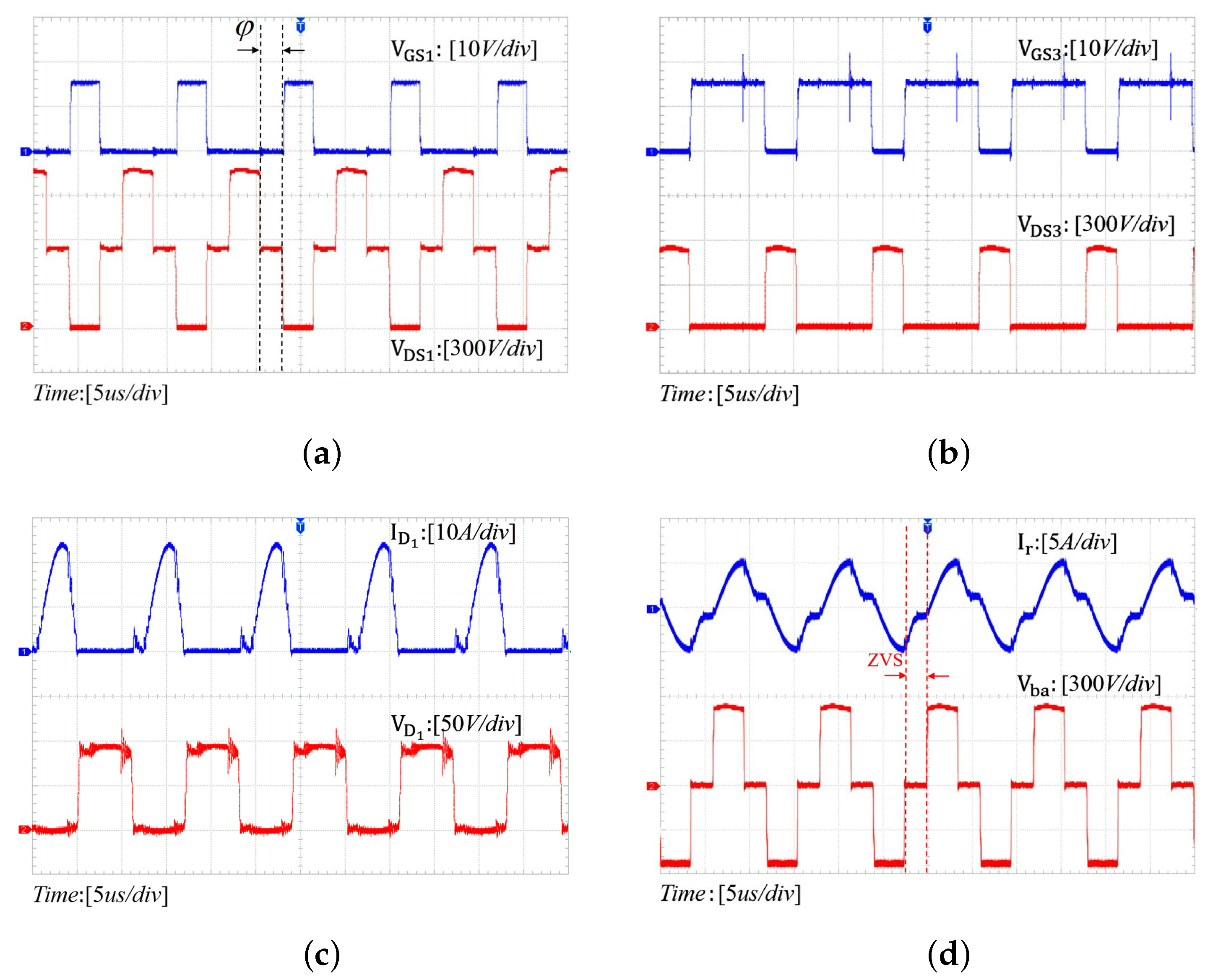
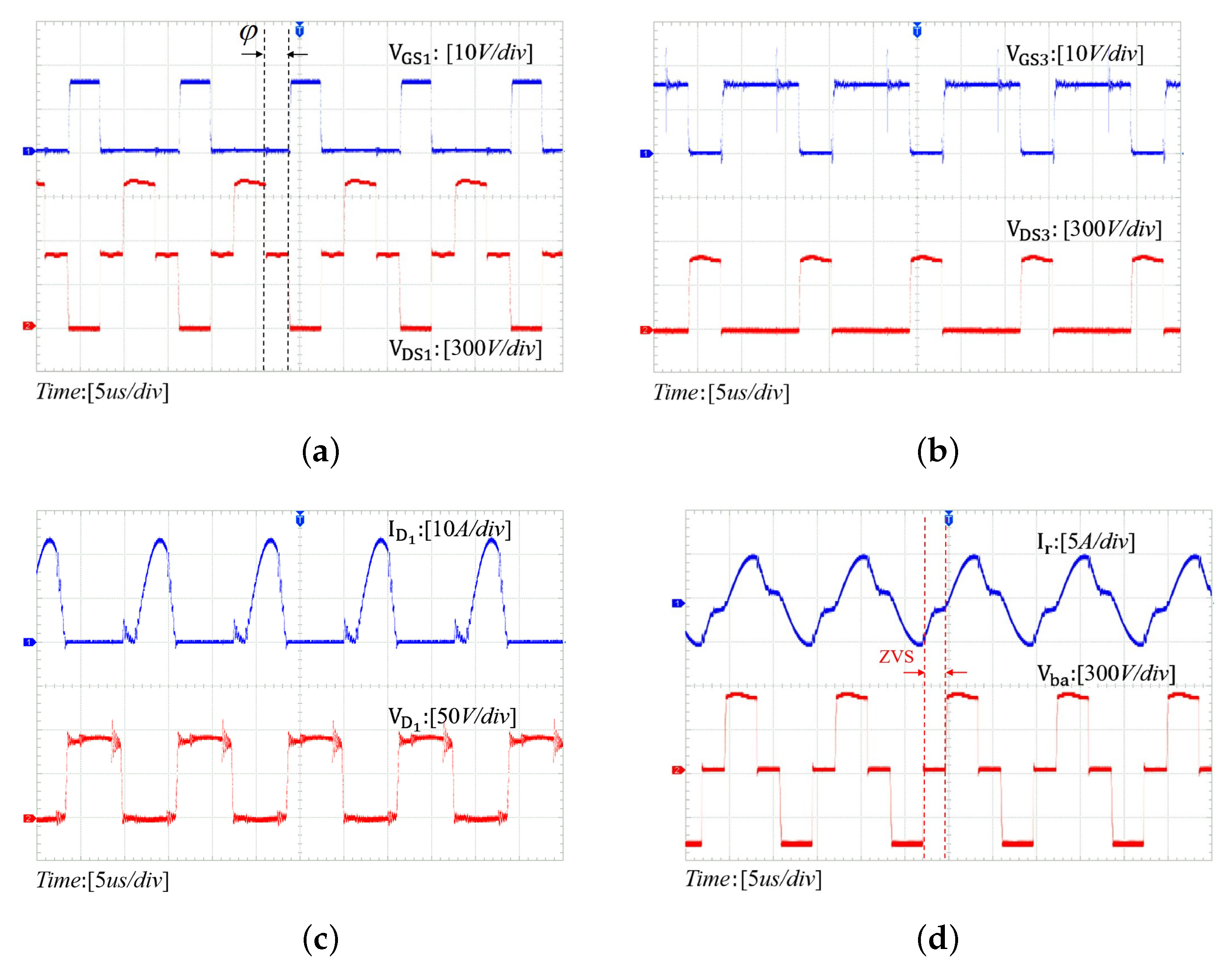
4.1. Prototype
4.2. Steady-State Waveforms
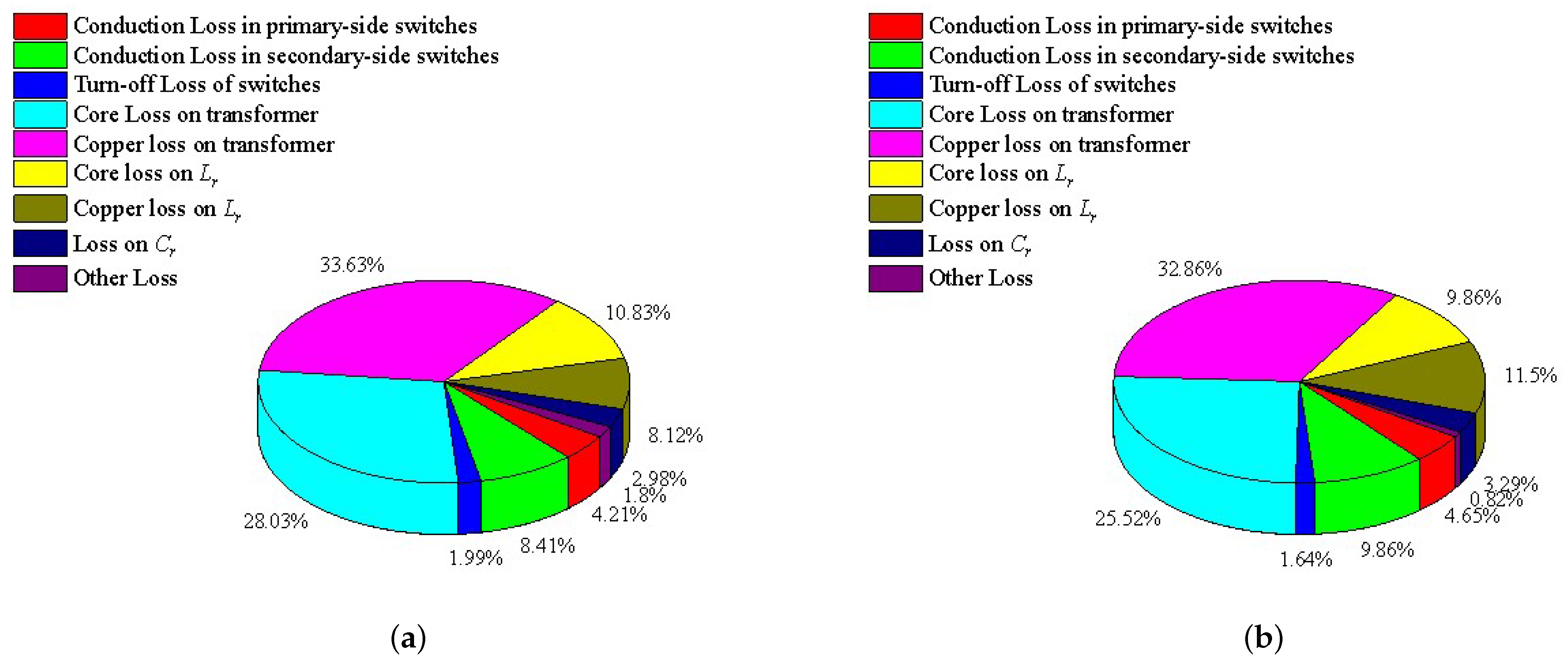
4.3. The Conversion Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Zhang, D.; Duan, J.; Li, J. Design and research of high voltage power conversion system for space solar power station. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Fang, M.; Zhang, D.; Qi, X. A novel power processing unit (PPU) system architecture based on HFAC bus for electric propulsion spacecraft. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5381–5391. [Google Scholar] [CrossRef]
- Osuga, H.; Kurokawa, F. Power Processing Unit for the next generation satellite. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–8. [Google Scholar]
- Carr, G.A.; Iannello, C.J.; Chen, Y.; Hunter, D.J.; Del Castillo, L.; Bradley, A.T.; Stell, C.; Mojarradi, M.M. Extreme environment capable, modular and scalable power processing unit for solar electric propulsion. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–9. [Google Scholar]
- Huang, X.; Lan, J.; Chen, N.; Fang, T.; Ruan, X.; He, X. A novel two-stage DC/DC converter applied to power processing unit for astronautical ion propulsion system. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 343–348. [Google Scholar]
- Hassanzadeh, N.; Yazdani, F.; Haghbin, S.; Thiringer, T. Design of a 50 kw phase-shifted full-bridge converter used for fast charging applications. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Bonten, R.W.T.; Schellekens, J.M.; Vermulst, B.J.D.; Clermonts, F.M.; Huisman, H. Improved Dynamic Behavior for the Series-Resonant Converter Using Bidirectional Charge Control. IEEE Trans. Power Electron. 2022, 37, 11607–11619. [Google Scholar] [CrossRef]
- Kim, J.W.; Barbosa, P. PWM-controlled series resonant converter for universal electric vehicle charger. IEEE Trans. Power Electron. 2021, 36, 13578–13588. [Google Scholar] [CrossRef]
- Saha, T.; Wang, H.; Riar, B.; Zane, R. Analysis and Design of a Parallel Resonant Converter for Constant Current Input to Constant Voltage Output DC-DC Converter Over Wide Load Range. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018. [Google Scholar]
- Vakacharla, V.R.; Rathore, A.K. Isolated Soft Switching Current Fed LCC-T Resonant DC–DC Converter for PV/Fuel Cell Applications. IEEE Trans. Ind. Electron. 2019, 66, 6947–6958. [Google Scholar] [CrossRef]
- Vakacharla, V.R.; Rathore, A.; Singh, R.; Mishra, S. Fixed-Frequency Current-Fed LCL Series Resonant Soft-Switching Converter with Capacitive Doubler. IEEE Trans. Ind. Appl. 2021, 57, 6611–6621. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z. A PWM LLC Type Resonant Converter Adapted to Wide Output Range in PEV Charging Applications. IEEE Trans. Power Electron. 2017, 33, 3791–3801. [Google Scholar] [CrossRef]
- Colak, K.; Asa, E.; Czarkowski, D. A comparison analysis of CLL and LLC resonant converter for multi-phase applications. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Patil, U.; Nagendrappa, H. Analysis and Design of a Three Phase Interleaved CLL Resonant Converter with Fixed Frequency Modified PWM Control. In Proceedings of the 2021 IEEE 6th International Conference on Computing, Communication and Automation (ICCCA), Arad, Romania, 17–19 December 2021; pp. 144–149. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, H.; Hu, Z.; Liu, Y.; Liu, X.; Afsharian, J.; Yang, Z. LCLC Converter with Optimal Capacitor Utilization for Hold Up Mode Operation. IEEE Trans. Power Electron. 2018, 34, 2385–2396. [Google Scholar] [CrossRef]
- Yin, S.; Xin, X.; Wang, R.; Dong, M.; Lin, J.; Gu, Y.; Li, H. A 1-MHz GaN-Based LCLC Resonant Step-Up Converter with Air-Core Transformer for Satellite Electric Propulsion Application. IEEE Trans. Ind. Electron. 2022, 69, 11035–11045. [Google Scholar] [CrossRef]
- Wen, H.; Jiao, D.; Lai, J.S.; Strydom, J.; Lu, B. A MHz LCLCL Resonant Converter Based Single-Stage Soft-Switching Isolated Inverter with Variable Frequency Modulation. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 848–854. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zhang, H.; Shi, Y. A Dual Coupling LCC-LCC Topology Based WPT System for Wireless Slip Ring. In Proceedings of the 2023 IEEE 2nd International Conference on Electrical Engineering, Big Data and Algorithms (EEBDA), Changchun, China, 24–26 February 2023; pp. 1333–1336. [Google Scholar] [CrossRef]
- Rodríguez, G.N.; Martínez, M.A.; Zajc, A.; Zajc, F.; Cabanuz, J.T.; Zajc, F.; Hortal, R.R.; Cervera, P.A. Isolated DC/DC Converter for RF generator of a Power Propulsion Unit: Topology Comparison Based on GaN Semiconductors. In Proceedings of the 2023 13th European Space Power Conference (ESPC), Elche, Spain, 2–6 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Jie, X.; Qing, K.; Xuan, Z.; Feng, L. Application prospect of SiC power semiconductor devices in spacecraft power systems. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 185–190. [Google Scholar]
- Piñero, L.R.; Scheidegger, R.J.; Aulsio, M.V.; Birchenough, A.G. High input voltage discharge supply for high power hall thrusters using silicon carbide devices. In Proceedings of the International Electric Propulsion Conference (IEPC2013), Washington, DC, USA, 6–10 October 2013. number NASA/TM-2014-216607. [Google Scholar]
- Fu, D.; Lee, F.C.; Qiu, Y.; Wang, F. A novel high-power-density three-level LCC resonant converter with constant-power-factor-control for charging applications. IEEE Trans. Power Electron. 2008, 23, 2411–2420. [Google Scholar] [CrossRef]
- Choudhury, A.; Pillay, P. Space Vector Based Capacitor Voltage Balancing for a Three-Level NPC Traction Inverter Drive. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1276–1286. [Google Scholar] [CrossRef]
- Narimani, M.; Wu, B.; Cheng, G.; Zargari, N. A new nested neutral point clamped (NNPC) converter for medium-voltage (MV) power conversion. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 2372–2377. [Google Scholar] [CrossRef]
- Khoshkbar Sadigh, A.; Abarzadeh, M.; Corzine, K.A.; Dargahi, V. A New Breed of Optimized Symmetrical and Asymmetrical Cascaded Multilevel Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1160–1170. [Google Scholar] [CrossRef]
- Belkhode, S.; Rao, P.; Shukla, A.; Doolla, S. Comparative Evaluation of Silicon and Silicon-Carbide Device-Based MMC and NPC Converter for Medium-Voltage Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 856–867. [Google Scholar] [CrossRef]
- Sun, Z.; Peng, F.; Magne, P.; Emadi, A. A Phase Shifted Full Bridge Converter with ZCS Synchronous Rectifier for Auxiliary Power Units. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2945–2951. [Google Scholar]
- Yu, M.; Sha, D.; Guo, Z.; Liao, X. Hybrid PS Full Bridge and LLC Half Bridge DC/DC Converter for Low-Voltage and High-Current Output Applications. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1088–1094. [Google Scholar]
- Kalayci, K.; Demirel, O.; Arifoglu, U.; Hizarci, H. Analysis of Three-Level T-Type LLC Resonant Isolated Bidirectional DC–DC Converter Under Three-Degrees-of-Freedom Modulation. IEEE Access 2023, 11, 60605–60625. [Google Scholar] [CrossRef]
- Huang, H. Designing an LLC resonant half-bridge power converter. In Proceedings of the 2010 Texas Instruments Power Supply Design Seminar, SEM1900, Topic; Texas Instruments Incorporated Dallas: Dallas, TX, USA, 2010; Volume 3, pp. 2010–2011. Available online: https://www.ti.com.cn/cn/lit/pdf/ssztch0 (accessed on 1 May 2024).
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]





| Topology | Advantage | Disadvantage |
|---|---|---|
| NPC | Simple structure; Low voltage stress; Good dynamic response; Low EMI. | Extra conduction loss for freewheeling diodes; Uneven distributed losses. |
| ANPC | Simple structure; Low voltage stress; Good dynamic response; Low EMI; Improved Efficiency comparing to NPC. | High cost; More complex modulation scheme comparing to NPC. |
| NNPC | Less components comparing to NPC. | Can not be applied to higher levels. |
| CHB | Modular structure; High reliability; fault-tolerant features. | Isolated DC links. |
| MMC | Modular structure; High reliabilty; More balanced loss distribution and less harmonics comparing to NPC. | More bulky capacitances comparing to NPC; Precharging process. |
| FB | Low current stress comparing to NPC; Low conduction loss comparing to NPC. | High cost; High voltage stress; High insulation and high withstand voltage for transformer; High rated voltage for passive components; Worse EMI comparing to NPC. |
| T-type | Low voltage stress for switches on auxiliary leg comparing to NPC; Low conduction loss comparing to NPC; Low turn-off current for switches on auxiliary leg; No floating capacitances; Low EMI. | High voltage stress for main switches. |
| Parameters | Value/Type |
|---|---|
| Input voltage () | 650∼950 V |
| Resonant inductor () | 110 H |
| Resonant capacitor () | 0.025 cuF |
| Turns ratio of transformer (n) | 6 |
| magnetizing inductor () | 450.4 H |
| Filter capacitor () | 470 F |
| Resonant frequency of , ( | 83 kHz |
| Resonant frequency of , , ( | 41 kHz |
| MOSFETs (, ) | C2M0080120D |
| MOSFETs (, ) | SCT3060AL |
| Rectifiers (, ) | MUR6060P |
| Conditions | kHz = 0 | kHz = | kHz = | kHz = |
|---|---|---|---|---|
| Reverse Recovery Loss (W) | 0.07 | 0.09 | 0.09 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Li, H. A High Step-Down SiC-Based T-Type LLC Resonant Converter for Spacecraft Power Processing Unit. Aerospace 2024, 11, 396. https://doi.org/10.3390/aerospace11050396
Ma W, Li H. A High Step-Down SiC-Based T-Type LLC Resonant Converter for Spacecraft Power Processing Unit. Aerospace. 2024; 11(5):396. https://doi.org/10.3390/aerospace11050396
Chicago/Turabian StyleMa, Wenjie, and Hui Li. 2024. "A High Step-Down SiC-Based T-Type LLC Resonant Converter for Spacecraft Power Processing Unit" Aerospace 11, no. 5: 396. https://doi.org/10.3390/aerospace11050396
APA StyleMa, W., & Li, H. (2024). A High Step-Down SiC-Based T-Type LLC Resonant Converter for Spacecraft Power Processing Unit. Aerospace, 11(5), 396. https://doi.org/10.3390/aerospace11050396






