Redundant Space Manipulator Autonomous Guidance for In-Orbit Servicing via Deep Reinforcement Learning

Abstract

The application of space robotic manipulators and heightened autonomy for In-Orbit Servicing (IOS) represents a paramount pursuit for leading space agencies, given the substantial threat posed by space debris to operational satellites and forthcoming space endeavors. This work presents a guidance algorithm based on Deep Reinforcement Learning (DRL) to solve for space manipulator path planning during the motion-synchronization phase with the mission target. The goal is the trajectory generation and control of a spacecraft equipped with a 7-Degrees of Freedom (7-DoF) robotic manipulator, such that its end effector remains stationary with respect to the target point of capture. The Proximal Policy Optimization (PPO) DRL algorithm is used to optimize the manipulator’s guidance law, and the autonomous agent generates the desired joint rates of the robotic arm, which are then integrated and passed to a model-based feedback linearization controller. The agent is first trained to optimize its guidance policy and then tested extensively to validate the results against a simulated environment representing the motion synchronization scenario of an IOS mission.

1. Introduction

The recent surging interest in advancing technologies and methodologies for IOS of satellites and space systems is motivated by the continuous expansion of space exploration and utilization, demanding efficient and dependable approaches to repairing, refueling, and repositioning space assets. Spaceborne robotic systems are a key technology potentially unlocking the ability to perform these tasks, and their accurate handling and control is an essential aspect of IOS missions. The aforementioned activities are carried out either on a cooperative or an uncooperative target, and it is the latter scenario that is driving the current research field. The inherent uncertainties associated with the interaction with uncooperative targets necessitate a high degree of motion control autonomy, reactivity, and adaptability to the surrounding environment. The rapid progress in the field of Artificial Intelligence is promising substantial enhancements in the capabilities of autonomous Guidance, Navigation, and Control (GNC) within these systems. Reinforcement Learning (RL), above all, seems like a promising tool to solve complex decision making problems, formulated as Markov Decision Processes (MDPs). The fusion of neural networks’ generalization abilities with Reinforcement Learning methods has given rise to DRL, which is extensively employed in solving planning problems, for its capacity to handle high-dimensional state and action spaces, as well as its ability to cope with Partially Observable Markov Decision Processes (POMDPs).

DRL has been recently adopted to generate the trajectory to fly around a target object, for its autonomous shape reconstruction, in [1,2]. Other applications of RL and, more specifically, meta-RL were applied in [3] to enhance the guidance and control of endo-atmospheric missiles, in [4] for 6-Degrees of Freedom (6-DoF) planetary landing applications, and in [5] for the autonomous generation of asteroid close-proximity guidance.

Regarding the application of RL to aid in Space Robot guidance and control, such methodology is currently considered one of the most promising research directions [6], but the present literature is still quite scarce. Indeed, further research efforts in the short term will be required to unlock its full potential. In [7], a motion planning strategy for a 7-Degrees of Freedom (7-DoF) space manipulator was implemented, and some of the concepts detailed in that work are also applied here, specifically in the context of the reward function. Multi-target trajectory planning is presented in [8], while control of a free-floating Space Robot through RL is tackled in [9].

This work originates from the recent applications of DRL for GNC problems in the space field, which have demonstrated the possibility of training highly autonomous agents, capable of executing complex objectives even in environments that they have not been strictly trained in. With regards to more classic Space Robot control approaches, there are currently many difficulties that hinder the use of redundant manipulators in space while being able to exploit their full potential, such as the ill-posed inverse kinematics, and complexities in the implementation of trajectory constraints. While optimization-based approaches have been developed to achieve such goals, they are often unfit for real-time implementation on space-rated hardware. To this extent, the ability to achieve such objectives with an autonomous DRL agent, requiring little to no real-time optimization, could be highly beneficial for robotics technologies in space but requires large research efforts before becoming a viable alternative. Given the novelty of such approaches, this work aimed to take a step forward in the application of DRL for the trajectory planning of a redundant space manipulator in a challenging and dynamic IOS mission environment. The obtained results demonstrate the enhanced autonomy and reactivity provided by the application of DRL in the context of the motion-synchronization phase of a hypothetical IOS mission and prove that the proposed method has the potential to be extended to a wider set of spaceborne scenarios.

2. Problem Statement

In robotic IOS missions, a key phase involves motion synchronization. The main operations performed during a robotic IOS mission are reported in a block diagram in Figure 1:

During this phase, the chaser spacecraft fine-tunes its relative position and orientation until its end effector remains stationary relative to the target capture point. Achieving the correct relative state at the end of this closing phase is critical for the subsequent tasks of grasping and making contact. Figure 2 illustrates the problem at hand.

The end effector of the space manipulator shall effectively track a specified grasping point on the tumbling target and follow its motion, in preparation for the subsequent activities. A generic shape for the target is selected, without loss of generality, and it is designed as a cylinder with two appendages representing solar panels. The chaser, instead, is a 6-Degrees of Freedom (6-DoF) spacecraft equipped with a 7-Degrees of Freedom (7-DoF) redundant manipulator.

The DRL agent—that is, the PPO—performs the guidance and control tasks, receiving the input data from the navigation block. The work operates under the assumption of having prior knowledge of the state variables describing the scenario at every time instant and omits the inclusion of a physical navigation block responsible for estimating these state parameters since it is outside the scope of this study.

Consequently, the state variables are presumed to be available and are directly input into the guidance and control blocks. These blocks then generate control actions, which are subsequently applied to the system. The system, in turn, integrates the equations of motion for both the chaser and the target and provides the scenario for the next simulation step, effectively closing the feedback loop.

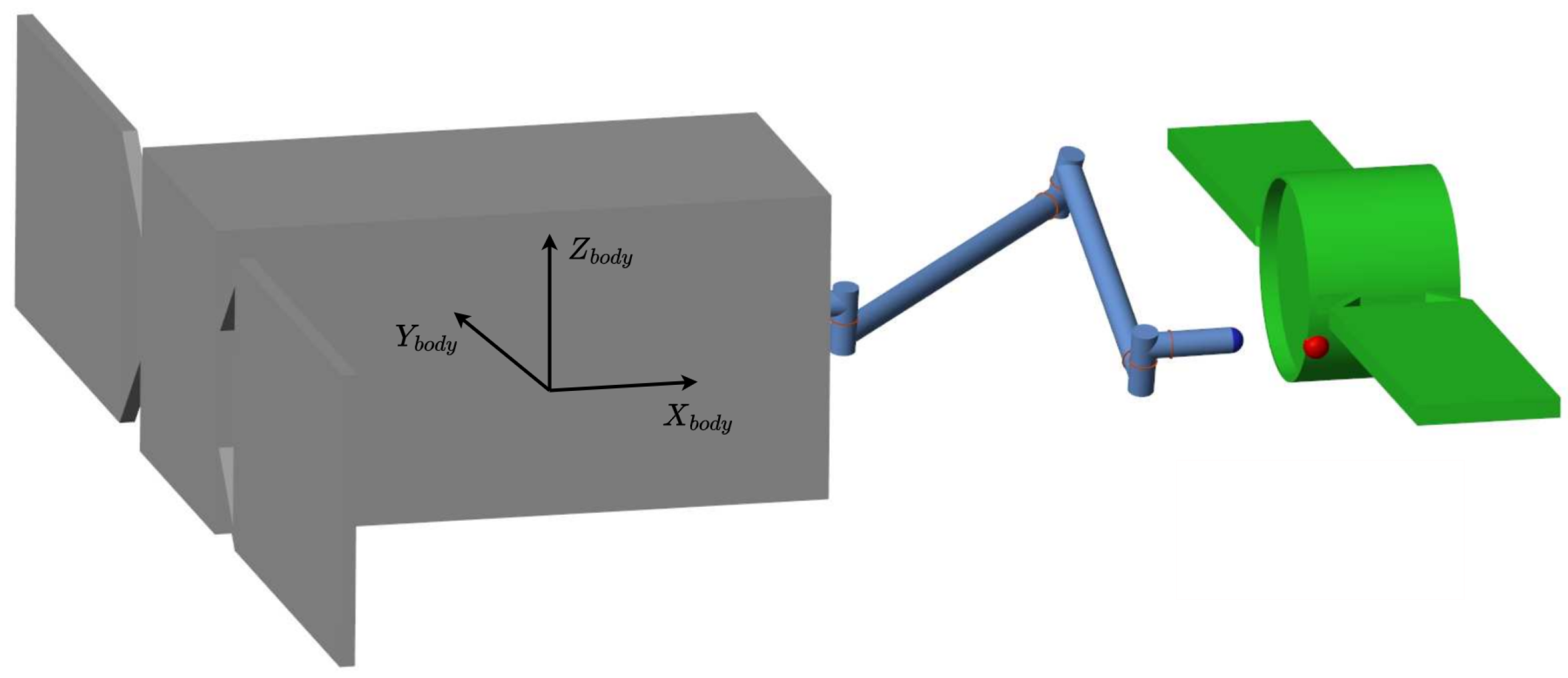
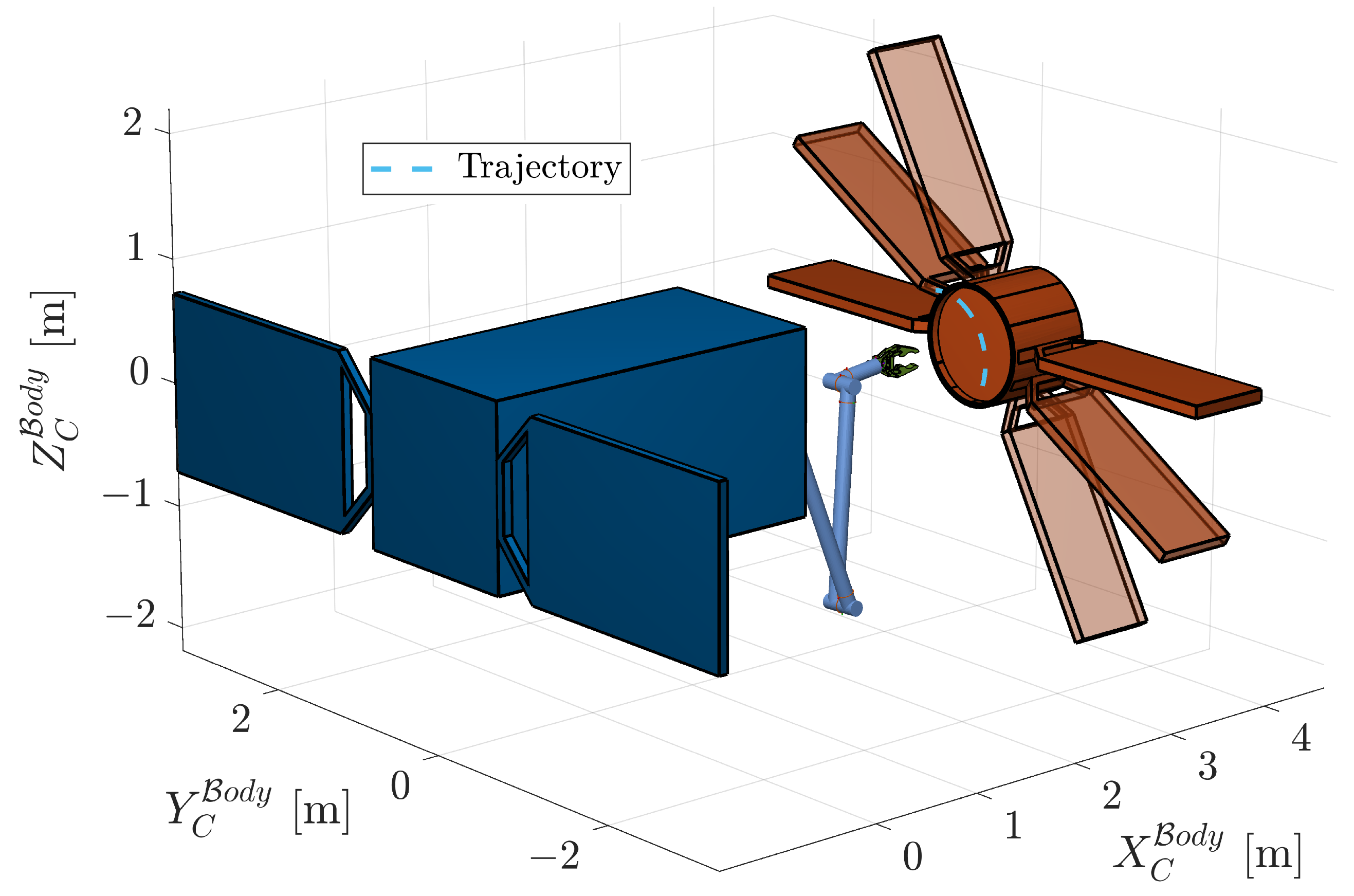
2.1. Space Manipulator Dynamics

This section provides a concise introduction to the equations of motion for a space manipulator with N DoF. It is important to note that in the scope of this study the multi-body system is described as free-flying, signifying that the spacecraft is actively controlled in both translation and rotation, in contrast to the free-floating scenario [10]. By employing the direct path approach, the spacecraft’s center of mass is utilized as the representative point for translational motion, enabling the derivation of the system’s kinematics and dynamics [11]. This approach results in more streamlined equations. Using a Newton–Euler formulation, the equations of motion of the space manipulator system are computed, and they are reported in Equation (1) [11]:

$$\mathit{H}\left(\mathit{q}\right)\ddot{\mathit{q}}+\mathit{C}(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}=\mathit{\tau }$$

(1)

$\mathit{H}\in {\mathbb{R}}^{(6+N)\times (6+N)}$ is the symmetric, positive-definite Generalized Inertia Matrix (GIM), $\mathit{C}\in {\mathbb{R}}^{(6+N)\times (6+N)}$ is the Convective Inertia Matrix (CIM), containing the nonlinear contributions, the Coriolis, and the centrifugal forces, and $\mathit{\tau }\in {\mathbb{R}}^{(6+N)}$ is the vector of generalized forces in the joint space. The parameter $\mathit{q}$ entails the selected generalized variables, which compose the space manipulator state and are reported in Equation (2):

$$\mathit{q}={[{\mathit{r}}_0,{\mathit{R}}_0,{\mathit{q}}_m]}^{\top }={[{\mathit{q}}_0,{\mathit{q}}_m]}^{\top }$$

(2)

where ${\mathit{r}}_0$ is the position vector of the base spacecraft in the inertial frame, ${\mathit{R}}_0$ is the orientation of the base spacecraft with respect to the inertial frame, employing a quaternion representation, ${\mathit{q}}_m$ contains the joint angles of the robotic arm, and ${\mathit{q}}_0$ is an auxiliary variable used to collect the state of the base (${\mathit{r}}_0,{\mathit{R}}_0$) in a single vector.

The kinematic and dynamic properties of the system were determined using the MATLAB R2023a library SPART (SPAce Robotics Toolkit) [11], a software package designed for modeling and controlling mobile-base robotic multi-body systems with efficient and recursive algorithms, taking advantage of the kinematic tree topology of the system. Additionally, for solving the equations of motion, a model of the space manipulator was constructed using the Simulink Simscape Multi-body library. The implemented simulator captures some of the main characteristics typical of multi-body systems in space, such as the high degree of dynamic coupling between the base and the manipulator. To limit the computational complexity of the model, considering the large number of simulations required to train the autonomous agents, flexibility effects in the joints and the links of the manipulator were not considered. Especially when employing large manipulators, flexibility effects are expected to produce non-negligible deviations from the rigid body model that has been implemented, but such aspects were omitted from this work as its scope was to evaluate the possibility of using DRL as a guidance strategy for space manipulators. In the future, once a strong baseline guidance architecture has been determined, an insightful extension to the work contained here would be to evaluate whether the agent provides any benefits in overcoming flexibility effects.

2.2. Target Dynamics

As the target is positioned at the origin of the LVLH (Local-Vertical, Local-Horizontal) reference frame, its translational motion can be disregarded, focusing instead on the rotational dynamics, which are modeled using Euler equations in orthogonal principal axes of inertia coordinates, as in Equation (3):

$$\mathit{I}{\dot{\mathit{\omega }}}_{\mathit{T}}+{\mathit{\omega }}_T\times \left(\mathit{I}{\mathit{\omega }}_T\right)=\mathit{M}$$

(3)

$\mathit{I}$ is the target’s inertia matrix, ${\mathit{\omega }}_T$ is its angular velocity vector, and $\mathit{M}$ is the vector of applied torque, assumed to be null in this work. Once again, the equations of motion of the target were solved through a Simulink Simscape Multi-body model of the target.

3. Reinforcement Learning Guidance

RL is a widely utilized tool for tackling Markov Decision Processess (MDPs). When combined with Neural Networks for function approximation, it becomes a potent method for addressing complex problems characterized by high dimensionality and partial observability [12]. A cutting-edge DRL algorithm designed for problems with continuous state and action spaces—that is, the PPO [13]—was investigated, for the robotic manipulator’s guidance optimization.

3.1. Proximal Policy Optimization

The PPO is a state-of-the-art on-policy, model-free DRL algorithm belonging to the family of policy gradient methods. With respect to its predecessor, Trust Region Policy Optimization (TRPO) [14], the PPO provides a simpler implementation with higher sample efficiency [13], which makes for faster training without compromising reliability. As for its performance on complex, high-dimensional, and partially observable continuous control problems, the PPO outperforms many of its competitors in various benchmarks and provides high training stability. The PPO is based on the Actor–Critic framework [15], where the Actor represents the decision-making logic of the agent (i.e., the policy $\pi$), and the Critic evaluates the actions of the Actor in the environment. Both Actor and Critic are approximated through Deep Neural Networks (DNNs) parametrized through variables $\theta$, which are updated throughout the training process. The Actor–Critic approach is briefly described:

• An agent is initially situated at a state s and perceives its environment through observations o.
• Based on o, the Actor autonomously decides the action a to take and applies it in the environment to move to a new state $s^{\prime }$.
• Depending on the definition of the reward $R(a_k,s_k)$, the Critic evaluates the action that has been taken and guides the parameter updates of the Actor through a stochastic gradient descent on a loss function.

The optimal policy in an infinite-horizon problem is found through Equation (4), and provides the agent with the maximum reward when applied in the environment:

$${\pi }^{*}=\underset{\pi }{\mathrm{argmax}}{E}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^{k}R(a_k,s_k)\right]$$

(4)

where the discount factor $\gamma \in [0,1]$ introduces a decay of rewards obtained distantly in time and measures whether the agent seeks short-term or cumulative rewards, and $R(a_k,s_k)$ is the reward function.

Compared to the loss function in TRPO, the PPO’s clipped surrogate objective (Equations (5) and (6)) has the advantage of limiting the policy’s parameter updates by clipping the loss function, providing increased training stability:

$$p_k\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_k\right|s_k)}{{\pi }_{{\theta }_{old}}\left(a_k\right|s_k)}}$$

(5)

$$L^{CLIP}\left(\theta \right)=E_k\left[min(p_k\left(\theta \right),clip(p_k\left(\theta \right),1-\epsilon ,1+\epsilon ))\right]A_k$$

(6)

where $A_k$ (Equation (7)) is the advantage function at timestep k, and where $\epsilon$ is the hyperparameter defining the clipping range. The entropy loss term $S\left({\pi }_{\theta }\right)s_k$, weighted by a hyperparameter w, is added to Equation (6) to promote agent exploration, and it encourages the Actor to try a variety of different actions, without becoming too greedy towards the ones it thinks are best. Finally, the advantage function $A(s_k,a_k)$ (Equation (7)) measures how advantageous taking an action a at timestep k is, instead of simply running the current policy ${\pi }_{\theta }$. The Critic’s job is to approximate the value function $V\left(s_k\right)$, which represents the cumulative sum of discounted rewards if only the current policy were run until the end of the episode:

$$A(s_k,a_k)=\left[\sum _{j=k}^T{\gamma }^{j-k}R(a_k,s_k)\right]-V\left(s_k\right)$$

(7)

3.2. GNC Implementation and Environment

This work presents a novel Artificial Intelligence (AI)-based autonomous guidance law for a 7-Degrees of Freedom (7-DoF) redundant manipulator mounted on a Space Robot (SR), used to achieve simultaneous end effector positioning and attitude alignment with respect to a desired state, as well as its tracking. As defined in [12], the environment in the DRL framework corresponds to everything outside the agent’s control; hence, everything outside the manipulator’s guidance system is taken as part of the environment, including the remainder of the SR and the target. A simplified scheme of the SR’s GNC system is reported in Figure 3:

The SR’s control system is implemented through a coupled, nonlinear model-based feedback linearization controller, where the resulting system is controlled through two Proportional-Derivative (PD) regulators, for the base and manipulator, respectively. The base is kept at the desired synchronized state with respect to the target, while the manipulator is commanded by the DRL agent. The coupled control law is provided in Equation (8), but being part of the DRL environment, it could be substituted with a more performant control approach with little to no retraining:

$$\mathit{\tau }=\left\{\begin{array}{c}{\mathit{\tau }}_0\\ {\mathit{\tau }}_m\end{array}\right\}=\mathit{H}\left\{\begin{array}{c}PD({\mathit{q}}_0^{*}-{\mathit{q}}_0)\\ PD({\mathit{q}}_m^{*}-{\mathit{q}}_m)\end{array}\right\}+\mathit{C}\dot{\mathit{q}}$$

(8)

where $\mathit{H}$ and $\mathit{C}$ are, respectively, the system’s 13 × 13 GIM and CIM [11], and $\mathit{q}={[{\mathit{q}}_0,{\mathit{q}}_m]}^{\top }$ is the Space Robot’s state collecting the 6-DoF of the base and the 7-DoF of the manipulator. The scalar gains of the two PDs are set as in

Table 1. PD gains for the Space Robot base and manipulator.

DoF	Proportional Gain 1	Derivative Gain 1
Base	0.4	0.3
Manipulator	2.5	1.25

¹ PD gains are the same for all base DoF and all manipulator DoF, respectively.

, and were tuned through trial-and-error before the training process, such that the manipulator’s joints effectively converged to the desired values produced by the agent. In any case, the controller was not found to limit the agent’s performance, and the control errors converged to zero within the first seconds of the simulation.

3.3. Action Space and Observation Space

The agent’s policy, which represents the Actor of the PPO implementation and provides the autonomous guidance of the manipulator, receives 32 observations $\mathit{o}$ (Equation (9)), and outputs seven actions $\mathit{a}$ (Equation (10)):

$$\mathit{o}={[{\mathit{q}}_m,{\dot{\mathit{q}}}_m,\tilde{\mathit{r}},\mathit{D}\tilde{\mathit{C}}\mathit{M},\tilde{\mathit{v}},\tilde{\mathit{\omega }}]}^{\top }$$

(9)

The terms in Equation (9) correspond to the current joint angles and joint rates of the manipulator (${\mathit{q}}_m,{\dot{\mathit{q}}}_m$) and the errors between the current and desired end effector states ($\tilde{\mathit{r}},\mathit{D}\tilde{\mathit{C}}\mathit{M},\tilde{\mathit{v}},\tilde{\mathit{\omega }}$), retrieved through kinematics and rotated in the SR’s body frame. The observation vector is normalized before providing it to the guidance for better convergence of the PPO [8]. The main benefit of using the agent only to provide manipulator guidance is that kinematic information is sufficient in the observations, which decreases the complexity of the policy and eases convergence of the algorithm.

$$\mathit{a}={\dot{\mathit{q}}}_m^{*}={[{\dot{\varphi }}_1,{\dot{\varphi }}_2,{\dot{\varphi }}_3,{\dot{\varphi }}_4,{\dot{\varphi }}_5,{\dot{\varphi }}_6,{\dot{\varphi }}_7]}^{\top }$$

(10)

The seven actions $\mathit{a}$ produced by the agent correspond to the desired joint rates of the manipulator, and are integrated (Figure 3), such that both the desired joint angles and rates (${\mathit{q}}_m^{*},{\dot{\mathit{q}}}_m^{*}$) can be provided to the manipulator’s PD controller [16].

3.4. Reward

Providing the agent with rewards and penalties is the sole mechanism that incentivizes the manipulator’s guidance system to increase its performance. Adequate reward function design is critical as it directly impacts the convergence of the policy towards the optimal one, as well as the overall attainable performance. Since training on a sparse reward with high-dimensional state and action spaces is extremely difficult, reward shaping has been introduced through the definition of an Artificial Potential Field (APF) (Equation (11)), expanding upon [7]:

$$U_k=-\tilde{r}+{\displaystyle \frac{10}{1+{\tilde{r}}_{ax}}}+{\displaystyle \frac{10}{1+{\tilde{r}}_{tx}}}+{\displaystyle \frac{10}{1+\tilde{\theta }}}$$

(11)

where $\tilde{r}$ is the magnitude of the error between the desired and current positions of the end effector, ${\tilde{r}}_{ax}$ and ${\tilde{r}}_{tx}$ are the projections of $\tilde{r}$ parallel and transverse to the X-axis of the SR’s body frame (Figure 2), and $\tilde{\theta }$ is the scalar error angle between the desired and current attitude of the end effector, in axis–angle representation. The reward is given as a function of the end effector’s potential variation ($\mathsf{\Delta }U$) between timesteps (Equations (12) and (13)):

$$\begin{array}{c}\mathsf{\Delta }U=U_k-U_{k-1}\end{array}$$

(12)

$$\begin{array}{c}{R}_k=\left\{\begin{array}{cc}\mathsf{\Delta }U\hfill & \mathrm{if}\mathsf{\Delta }U\ge 0\hfill \\ 1.5\mathsf{\Delta }U\hfill & \mathrm{if}\mathsf{\Delta }U<0\hfill \end{array}\right.\end{array}$$

(13)

where the $1.5\times$ multiplier discourages the end effector from moving along equipotential surfaces. A bonus sparse reward of $+0.01$ is provided while ${\tilde{r}}_{ax}$, ${\tilde{r}}_{tx}$, and $\tilde{\theta }$ are simultaneously below a desired threshold.

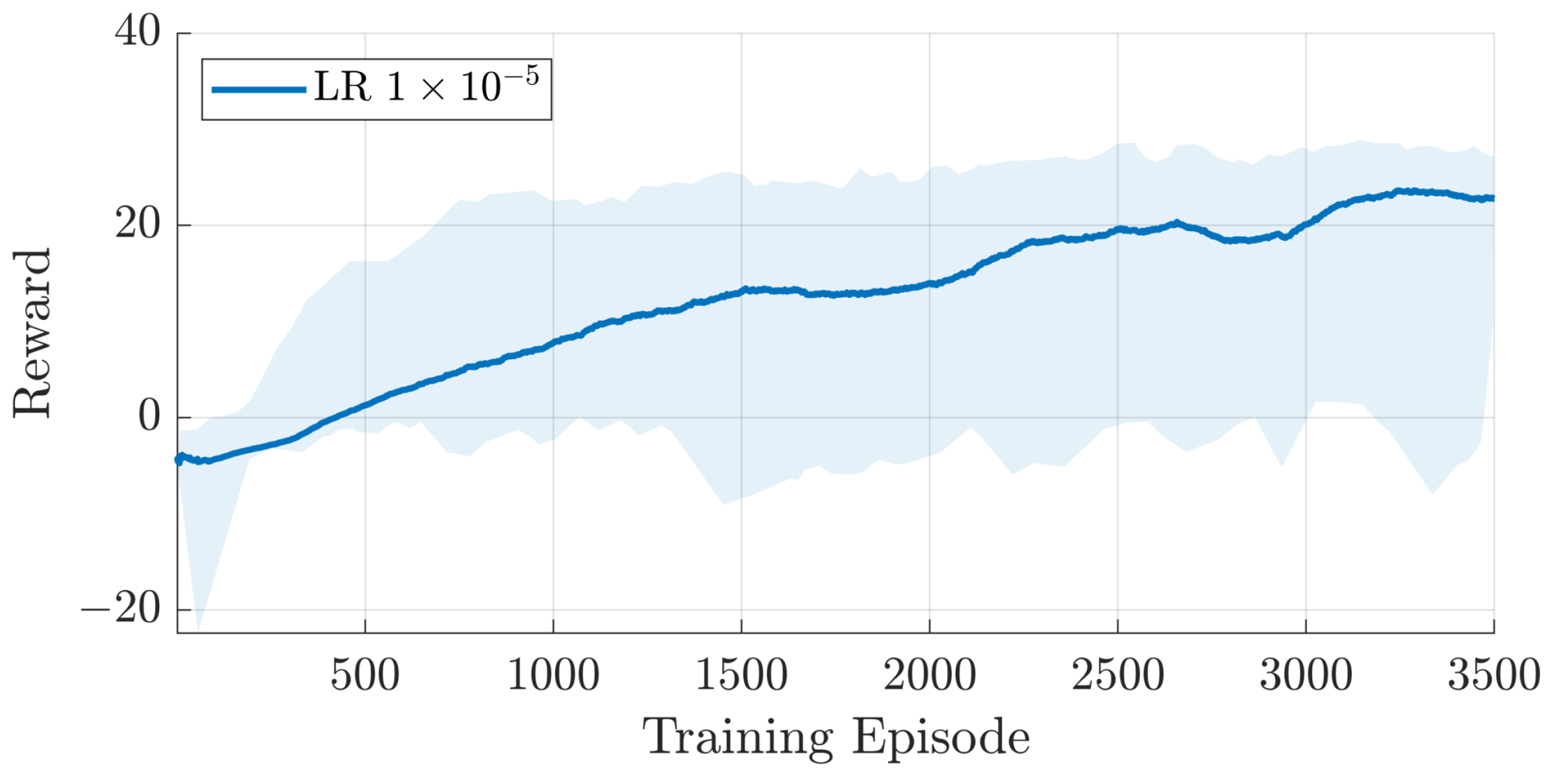
4. Training and Results

Before proceeding with training, the initial conditions and the DRL hyperparameters were introduced. The scenario was that of a target spacecraft tumbling around its major inertia axis. The SR’s state was kept synchronized with that of the target, such that they spun together and any relative motion between the desired end effector state and the SR was minimized. The SR was positioned along the angular momentum (${\mathit{L}}_T$) of the target at a nominal distance of 5 m, and its angular velocity was set as in Equation (14) for synchronization purposes:

$${\mathit{\omega }}_0={[{\mathit{\omega }}_T·{\widehat{\mathit{L}}}_T,0,0]}^{\top }$$

(14)

The nominal initial manipulator state was found in Equation (15), and it was selected to point the end effector in the direction of the target at the start of each episode:

$$\begin{array}{ccc}\hfill {\mathit{q}}_m={[0,285,0,210,0,75,0]}^{\top }\mathrm{deg}& \hfill & \hfill {\dot{\mathit{q}}}_m={[0,0,0,0,0,0,0]}^{\top }\mathrm{deg}/\mathrm{s}\end{array}$$

(15)

To increase the robustness of the agent, and to show that it could adapt to conditions that it had not strictly been trained on, the nominal initial conditions of the target object and the SR were randomized at the start of each simulation, according to the following list:

• Target’s major-axis spin rate ${\mathit{\omega }}_T\in [-3,3]$ deg/s.
• Each initial manipulator joint angle is perturbed by a random value $\delta {\varphi }_i\in [-15,15]$ deg.
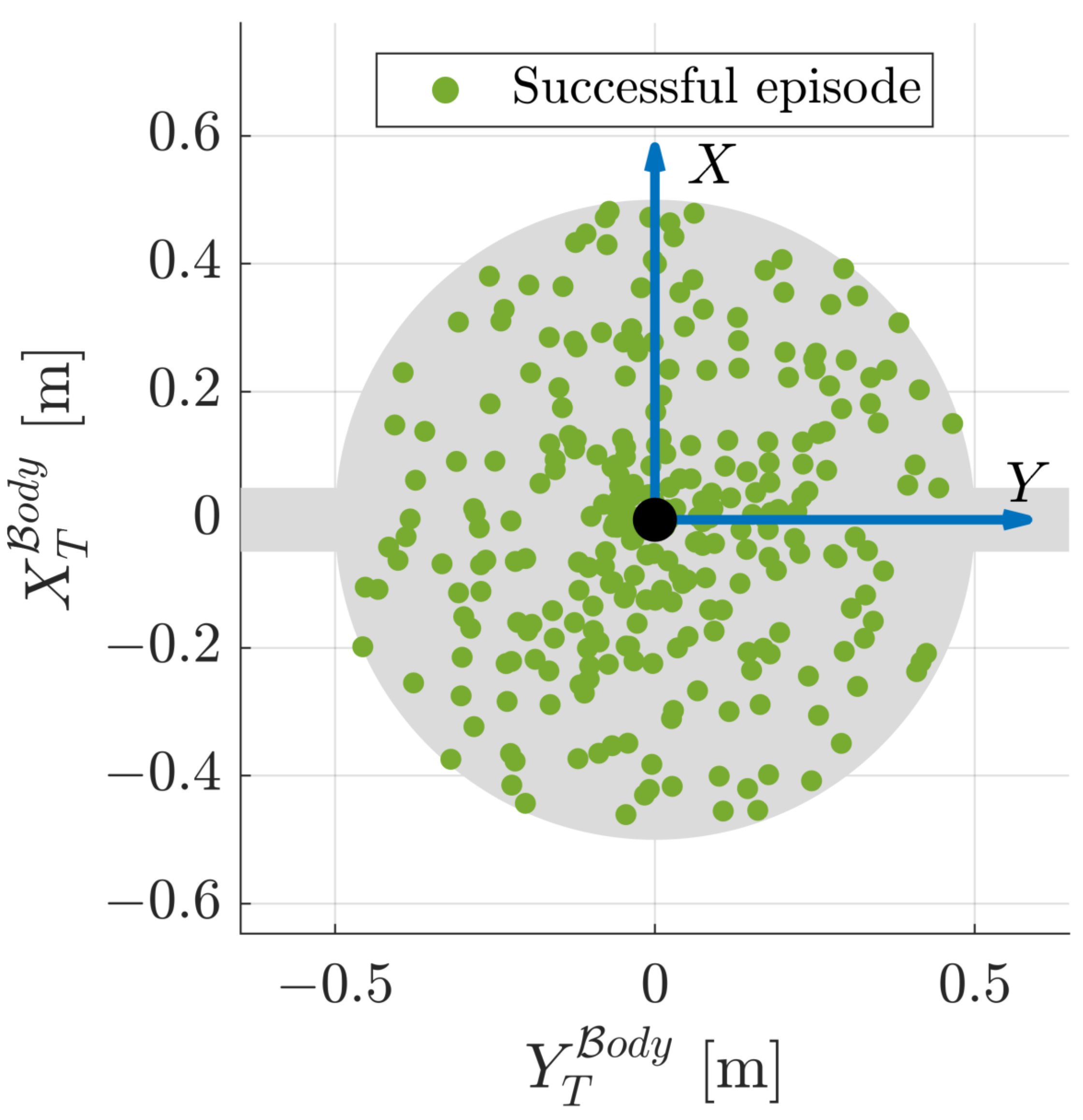
• Desired end effector state is randomized on the whole SR-facing side of the target, both in terms of position and attitude.
• Distance between SR and target is perturbed by a random value $\delta d\in [-25,25]$ cm.

Simulations were only terminated if the manipulator’s configuration became singular, to prevent the DRL algorithm from breaking down due to mathematical issues. With regards to the PPO hyperparameters, the sample time of the agent was set to $0.3$ s as a trade-off between the computational expense, convergence, and reactivity of the SR. The Actor and Critic were represented through two Feedforward Neural Networks (FNNs), with the hyperparameters in

Table 2. Actor and Critic Networks hyperparameters.

Layers	Actor Neurons	Critic Neurons
Input	32	32
1st hidden	300	300
2nd hidden	300	300
3rd hidden	300	300
Output	14	1
Learning Rate	1 × 10−5	1 × 10−5
Activation	$tanh$	$tanh$

.

A stochastic policy was used to increase agent exploration [9]; hence, the Actor’s 14 outputs (Table 2) represent, respectively, the mean and standard deviation of each desired joint velocity. The remainder of the PPO hyperparameters were selected among typical values: the clipping factor $\epsilon =0.2$, the discount factor $\gamma =0.99$, the entropy loss weight $w=0.01$, the mini-batch size was 128, and the training epochs were 4. The agent was trained for 3500 episodes, each of 420 s duration, for a total of 4.9 M timesteps (see Figure 4).

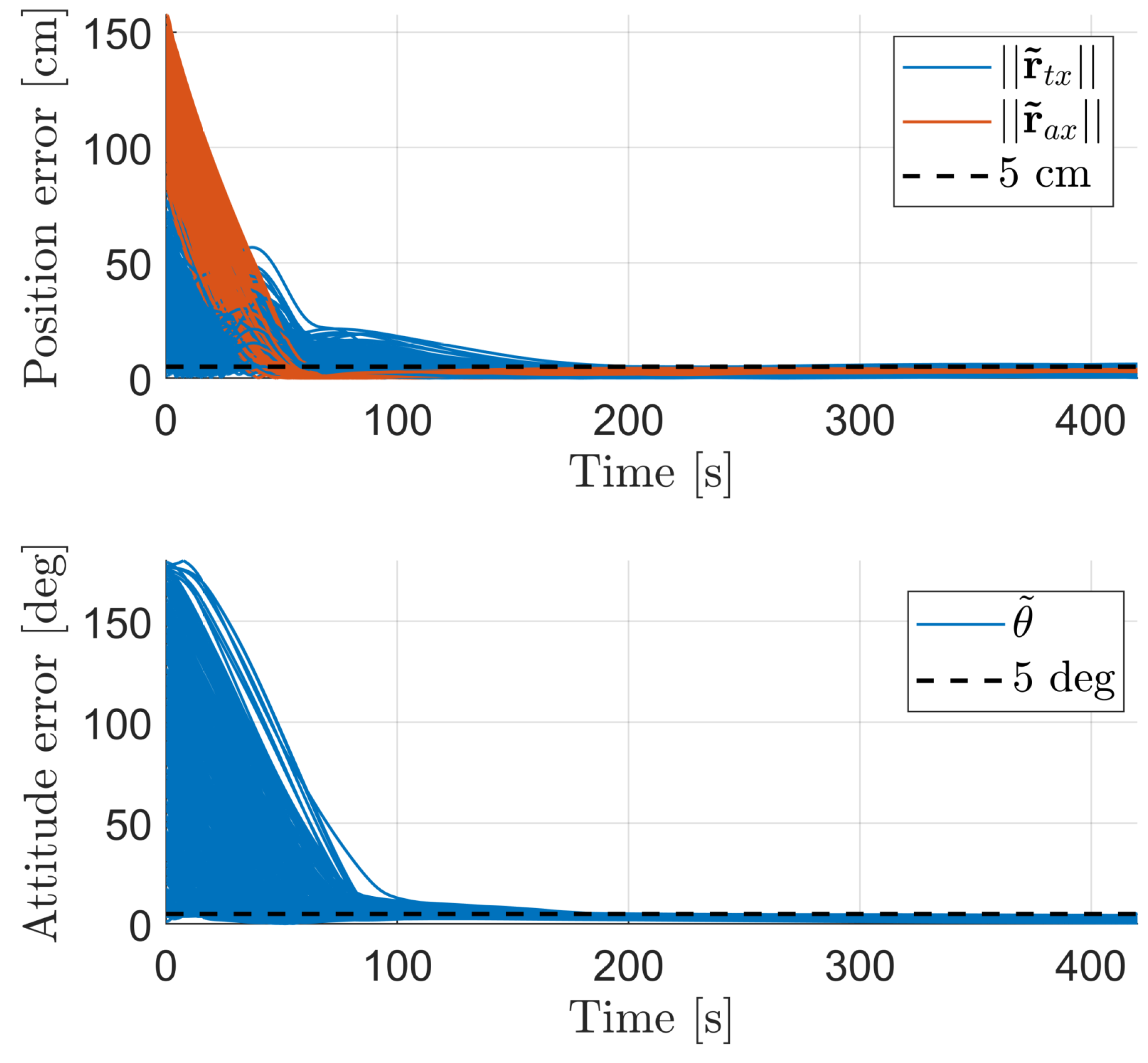
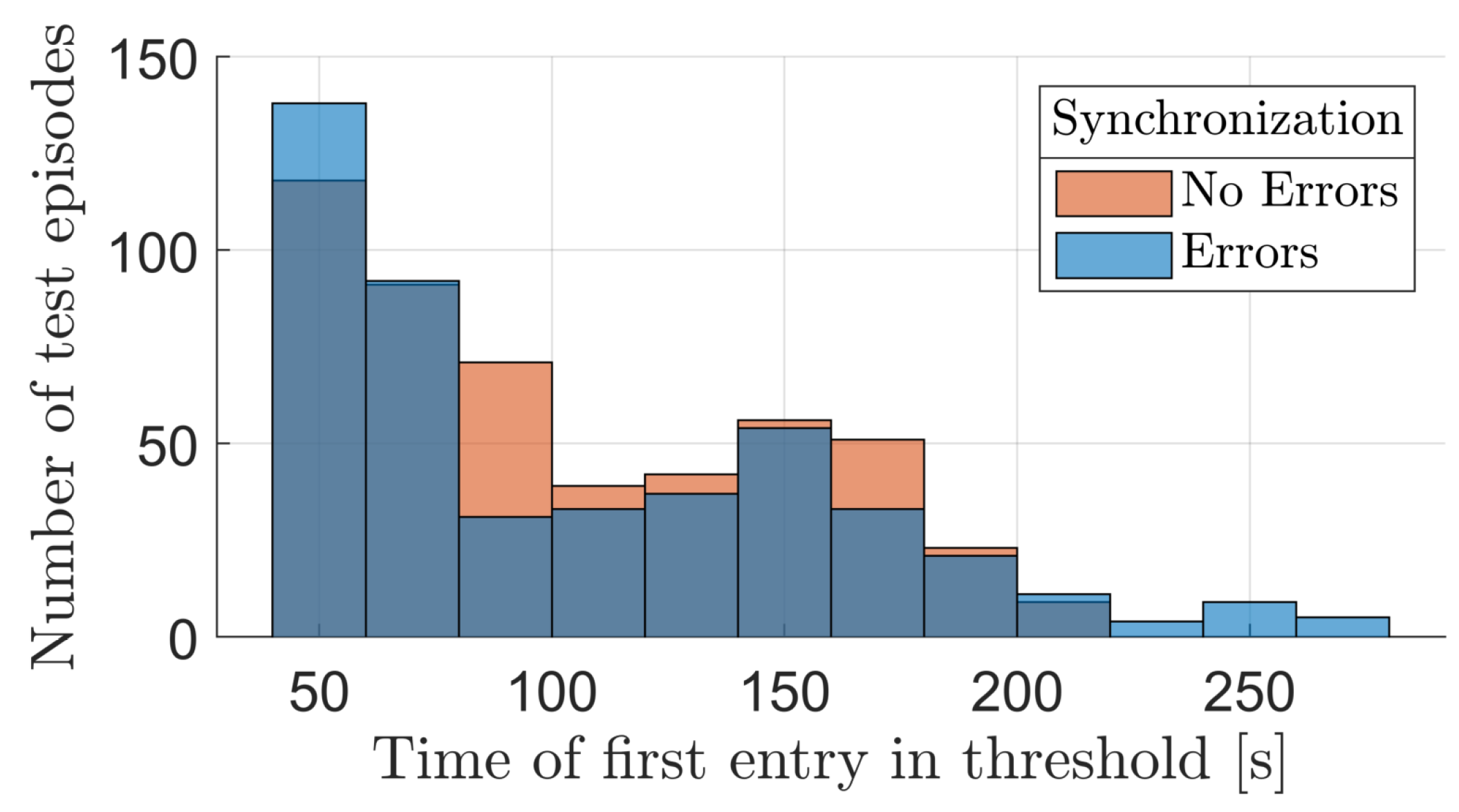
4.1. Agent Performance

The agent’s success in a simulation was defined as its ability to keep the end effector within a selected tolerance from the desired state, in terms of both position and orientation, consecutively for at least $t_{min}=30$ s. This differs with respect to what is currently done in the majority of the literature, where, once the end effector enters the selected threshold for the first time, the episode is considered successful and the simulation is terminated. In such a highly dynamic scenario, the latter approach does not prove that the end effector’s state can remain synchronized with that of the grasping position, and would artificially increase the agent’s performance in the environment.

The minimum error thresholds that guaranteed the 100% success rate of the agent, and that represented its performance baseline, were ${\tilde{r}}_{ax},{\tilde{r}}_{tx}<5$ cm, and $\tilde{\theta }<5$ deg. These results were confirmed through the Monte Carlo analysis in Figure 5 and Figure 6, which show that regardless of the grasping point’s location in the target’s body frame the agent could successfully synchronize the manipulator’s end effector with the desired state, for consecutive periods that were much higher than $t_{min}$.

Through a deeper analysis of Figure 6, the average time that the end effector took to successfully converge to the desired state was found to be 103 s, and, in any case, no episodes took longer than 219 s to accomplish the objective, which was approximately half of the complete episode duration. These values were driven by the randomized initial configuration between the manipulator and grasping point and increased proportionally to the range of motion that needed to be carried out by the robotic arm. Additionally, the average consecutive time that the end effector stayed within the selected error tolerances was 312 s, corresponding to 74% of the total episode duration. This confirms that once the end effector converges to the desired state, it does not manifest largely oscillatory behavior.

Building on the few studies found in the literature, this work demonstrates that the proposed AI-based robotic arm guidance strategy, when applied to a 7-Degrees of Freedom (DoF) redundant manipulator that has a randomized positioning and attitude alignment goal for extended periods of time, reliably provides performance in the order of centimeters and degrees. These results show an improvement on what is currently found in the literature: in [17], the guidance of a 7-Degrees of Freedom (DoF) manipulator was trained to achieve an end effector positioning goal, whereas its attitude was neglected; in [7], a 7-Degrees of Freedom (DoF) manipulator was trained to accomplish both a positioning and attitude alignment objective, but only the first 6 of 7 joints were controlled, since the end effector was symmetrical around the last joint’s rotation axis.

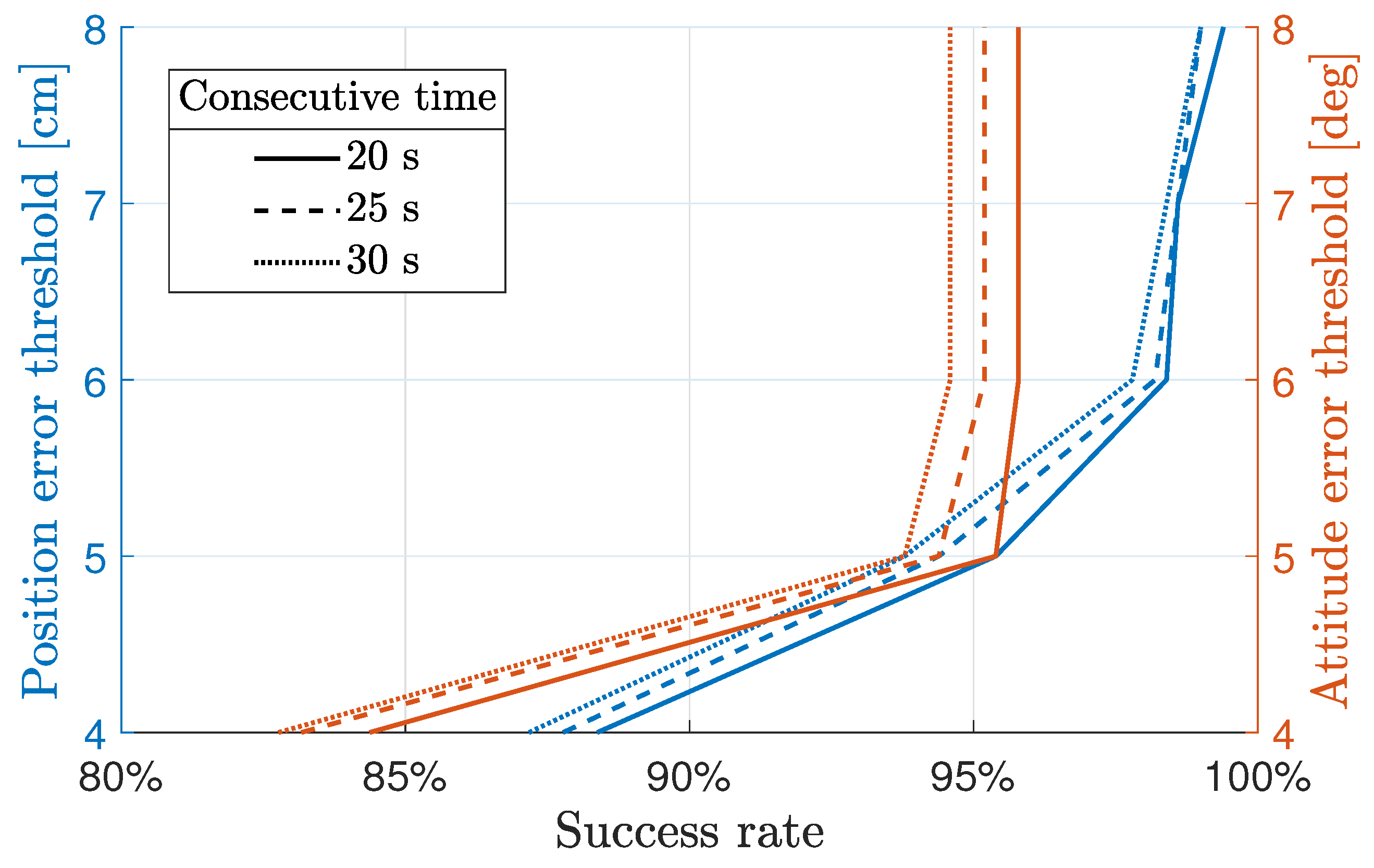
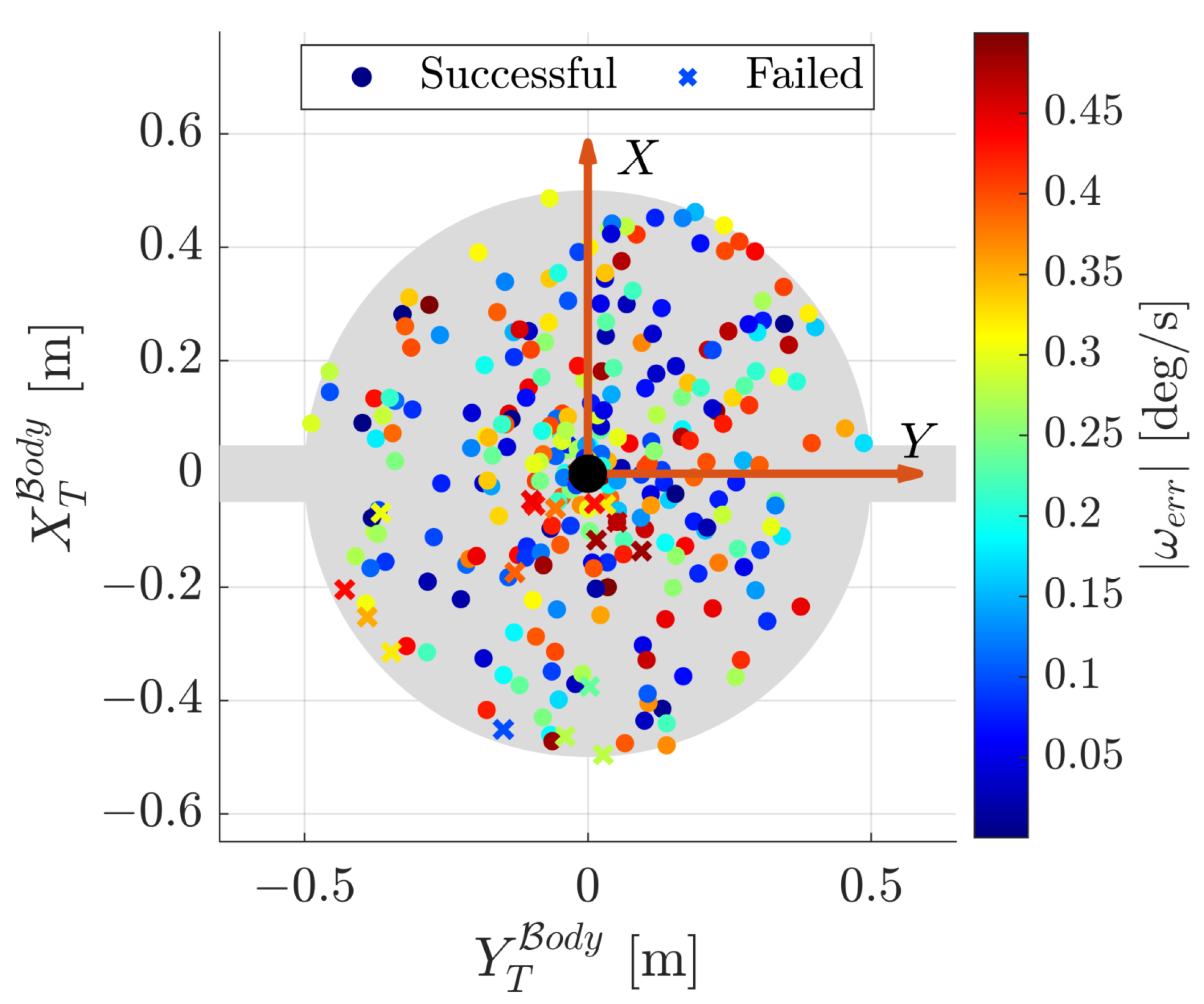
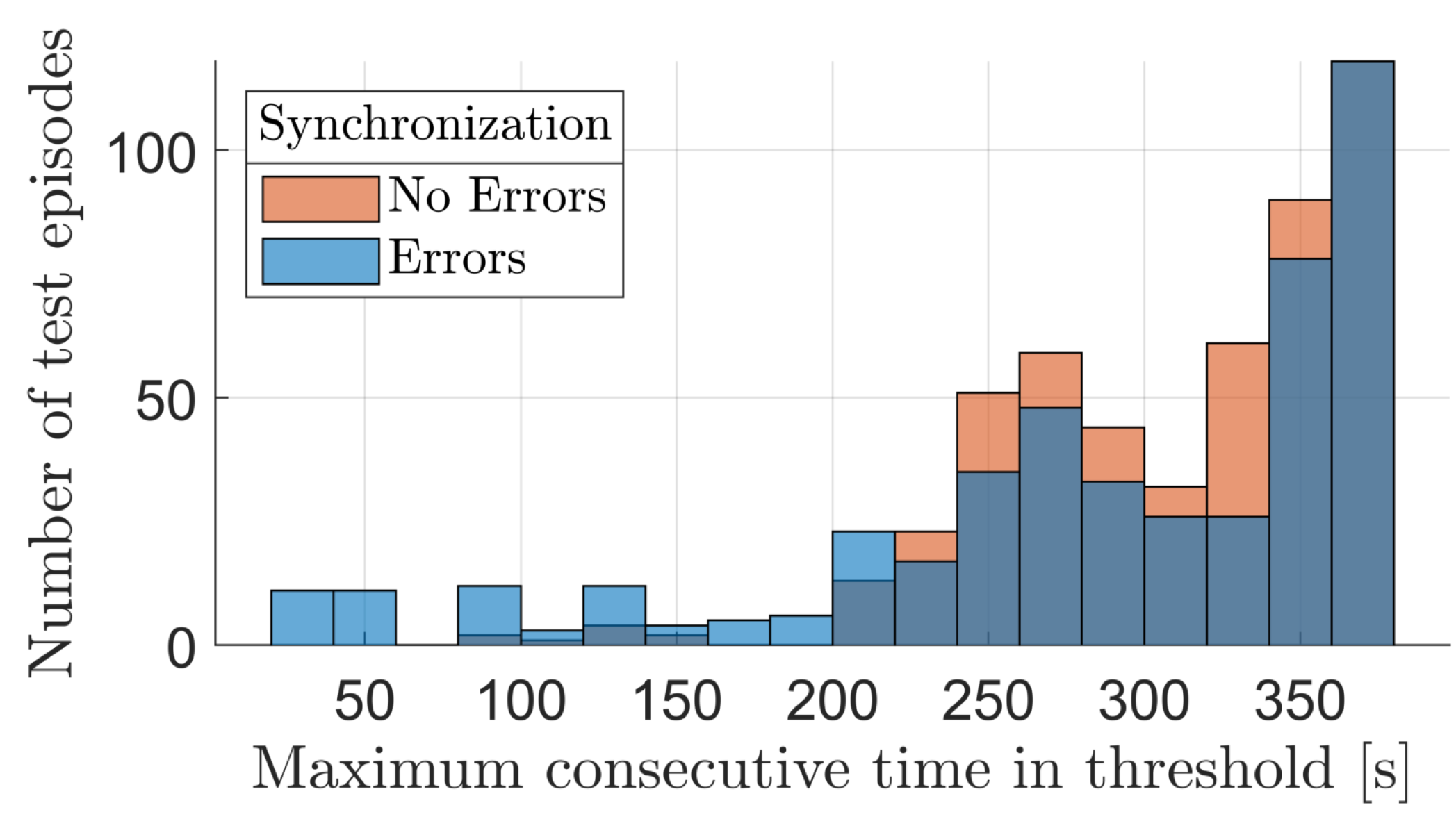
4.2. Agent Robustness

The need for highly reactive, adaptive, and autonomous systems anticipated for future close-proximity operations has been one of the driving factors towards the introduction of AI-based methods into spacecraft GNC. Despite being new, the recent applications of DRL in the space field have emerged as promising strategies for the generation of highly adaptive agents that can handle unforeseen conditions that they have not strictly been trained on, with significant increases toward mission robustness. These capabilities have been shown to be intrinsic to the use of Deep Neural Networks, and, if achieved, would provide many benefits supporting the addition of AI into classic GNC systems. To give some preliminary insight into why using such approaches could be advantageous, the agent’s limits and generalization capabilities were stressed in two scenarios that it had not been trained to handle.

To this extent, errors in the spin rate synchronization around the target’s rotation axis were added, to see whether the agent could adapt to this new scenario without further training. The difference from the previous case, in which the grasping point was static with respect to the SR, was that the end effector now needed to track a moving point and synchronize its motion with it, maintaining a constant attitude. The maximum spin rate error between the base of the SR and the target was taken from the COMRADE study [18], where the requirement for the angular rate control error was set to $\left|\right|{\mathit{\omega }}_0-{\mathit{\omega }}_T\left|\right|<0.5$ deg/s. Hence, the SR’s angular velocity was perturbed each episode by a random value ${\omega }_{err}\in [-0.5,0.5]$ deg/s, as in Equation (16). An overview of this new scenario is provided in Figure 7.

$${\mathit{\omega }}_0={[{\mathit{\omega }}_T·{\widehat{\mathit{L}}}_T+{\omega }_{err},0,0]}^{\top }$$

(16)

A Monte Carlo analysis was conducted to evaluate the agent’s performance over 500 testing episodes. In these conditions that the agent had never experienced during training, the success rate, defined in the same way as in the previous section, dropped to $94\%$. These results show that despite a small decrease in performance the agent was robust against errors in the attitude synchronization and was capable of tracking a moving position in time. Referring to Figure 8, it can be seen that the episode failures do not show a correlation to ${\omega }_{err}$ since many episodes were successful even when the synchronization error between the SR and the target was high in magnitude. Instead, the failures of the agent were more tied to the initial configuration between the manipulator and grasping point and were located primarily in the third quadrant.

For a more thorough comparison of the agent’s behavior with and without errors in the SR’s base attitude synchronization, the distribution of two performance indicators is reported in Figure 9 and Figure 10: the first figure shows how the time of the end effector’s first successful entry in the thresholds was distributed among episodes, whereas the second figure shows the distribution of the maximum consecutive time that the end effector remained inside the threshold, in each episode. Overall, even when the agent was subjected to a new environment that it had not been trained in, its behavior was quite similar to that which it demonstrated in nominal conditions. The main difference was found in terms of outliers in the distributions, which recurred more often when synchronization errors were present. Despite this similarity in results, better and more robust performance could be obtained by directly training the agent to handle the more complex environment, where possible.

To better understand how and why the episodes were failing, a sensitivity analysis on the definition of episode success was carried out. The end effector’s error thresholds ${\tilde{r}}_{ax},{\tilde{r}}_{tx}<5$ cm and $\tilde{\theta }<5$ deg, which needed to be guaranteed consecutively for at least $t_{min}=30$ s, were selected arbitrarily, and in real scenarios would be heavily mission-dependent. Figure 11 shows the variation of the success rate over 500 episodes, when these values were changed, in two distinct cases:

• The curves associated to the left axis show how the success rate varied in function of the thresholds on ${\tilde{r}}_{ax}$, ${\tilde{r}}_{tx}$, and $t_{min}$ while keeping the one on $\tilde{\theta }$ fixed.
• The curves associated with the right axis show how the success rate varied in function of the thresholds on $\tilde{\theta }$ and $t_{min}$ while keeping the ones on ${\tilde{r}}_{ax}$ and ${\tilde{r}}_{tx}$ fixed:

Figure 11. Success sensitivity to thresholds.

Figure 11. Success sensitivity to thresholds.

From Figure 11, it can be seen that in both analyses, varying $t_{min}$ had negligible effects on the success rate, which is explained by the fact that in the majority of cases the agent could keep the end effector’s errors low for consecutive periods much longer than $t_{min}$. By increasing the threshold on $\tilde{\theta }$ from its baseline value of 5 deg, the success rate remained unchanged, signifying that the end effector’s attitude was not the main factor limiting performance. Differently, by increasing the end effector’s positioning thresholds, the success rate started to increase, making this value act as the main bottleneck in the obtained performance.

These results were determined by a combination of different effects: firstly, the simple PD controller that was used to control the system after feedback linearization could not guarantee null steady-state errors, which was a first factor impacting the convergence of the end effector towards its final desired state; secondly, the agent’s sample time of 0.3 s, coupled with the integration of the Actor’s outputs, may also have reduced the agent’s maximum performance, especially once the end effector errors had been reduced below the baseline threshold values.

A final test was conducted to further stress the agent’s generalization capabilities when applied to a target that was larger than the one used during training. Specifically, the agent was trained to correctly position and align the end effector in front of a target of 50 cm radius, and was instead asked to complete the same randomized objective, but on a target of 150 cm radius. The agent’s performance was evaluated over 500 testing episodes, and its success rate is shown in Figure 12.

The results show that as the goal position of the end effector moved outside the area where it had been trained, the performance dropped significantly. Despite this, it was found that no episodes fell below a radius of 64.5 cm, which shows that the agent could adapt to a condition that it had not experienced during training, and achieve the objective on a target that was at most 28% larger than the one used in training. To confirm these results in a statistical sense, 200 additional testing episodes were conducted, randomizing the goal position within a radius of 64.5 cm from the center of the target, and the success rate of the agent remained at 100%.

5. Conclusions

This work proposes a novel autonomous guidance algorithm for the manipulator of a free-flying Space Robot, allowing automatic synchronization of the end effector with a desired state fixed to the uncooperative target spacecraft in a hypothetical IOS mission. The problem was formulated as a Partially Observable Markov Decision Process (POMDP), and solved through the state-of-the-art PPO algorithm. An FNN provided the guidance of the manipulator in real time based on values retrieved through the navigation system, which was not implemented, and its outputs were provided to a model-based feedback linearization controller, which coupled the control laws of the base of the servicer and its manipulator. After the training process, the agent successfully reached a randomized end effector state objective, in a highly randomized environment, with a 100% success rate, keeping its errors in terms of position and attitude below thresholds of 5 cm and 5 deg for lengthy consecutive periods. Without any further training, the same agent was found to be robust against errors in the attitude synchronization between SR and target, and it could also complete the same objective on a target that was at most 28% larger than the one used during training. Future extensions of similar approaches could obtain better results by using more performant control systems that guarantee null steady-state errors, or by decreasing the sample time of the agent. The latter would have to be tuned based on the frequency of the values provided by the navigation filters.

Despite the literature on this topic being new and with many shortcomings, the results produced in this work convey that DRL should be investigated further, as a prospective solution to an even wider set of robotic IOS scenarios.

Further Developments

The outcomes obtained in this study show great potential and emphasize a few of the advantages that implementing a DRL-driven space manipulator guidance system could offer in upcoming Orbital Robotics Missions. These advantages include enhanced autonomy, reactivity, and robustness of the system for off-nominal scenarios. However, the practical application of such techniques in real missions remains distant, requiring further research and development efforts. Several directions for enhancing the agent’s performance beyond the current state are suggested as potential extensions to this work. The main focus should be on increasing the achievable accuracy of the end effector’s positioning and attitude alignment, which is currently in the order of (5 cm, 5 deg) for a 7-Degrees of Freedom (DoF) manipulator that needs to concurrently track a desired full state, randomized in each simulation.

• A possible strategy is to develop new reward functions to train the agent, that inherently take into account the end effector’s position and attitude. Indeed, the majority of reward functions found in the literature only consider the positioning component and are unfit to achieve goals similar to those set in this work. Detailed analyses on alternative reward functions is a topic often overlooked, but could be one of the main strategies to improve the convergence properties of the DRL algorithm and the manipulator’s performance at end effector level.
• Another approach to increasing the agent’s performance and robustness would be to focus on the neural network architectures themselves, to see which ones provide the greatest benefits to the manipulator’s guidance. For example, Recurrent Neural Networks (RNN) have been demonstrated to provide increased robustness against autonomous DRL agents [1,2] when subject to environments with large domain gaps with respect to training, and their evaluation could provide insightful extensions to this work.
• Finally, methods are being explored in the literature to ease policy convergence during optimization, which is often hindered by a difficult selection and the tuning of the reward function and hyperparameters, especially in environments with large observation spaces. Among these is the use of offline data to pre-train the neural networks, which has been shown [19] to provide considerable benefits to the subsequent online optimization process, achieved through agent–environment interactions. Considering the current computational limitations of space-rated hardware, running complete agent training in space is unrealistic, and deploying agents that have been pre-trained on the ground seems to be one of the most promising approaches. To this extent, many research lines are emerging within the so-called Sim2Real DRL transfer [20,21], which are aimed at finding ways to limit the discrepancies between the performances of agents tested both in a simulated environment and the real world.