Abstract
This paper presents the second stage of a tandem fixed-wing unmanned aerial vehicle (UAV) aerodynamic development. In the initial stage, the UAV was optimized by analyzing its characteristics only in symmetrical flight conditions. Posted requirements were that both wings should produce relevant positive lift, the initial stall must occur on the front wing first, the center of pressure should be close to the center of gravity, and longitudinal static stability should be in the optimum range. Computational fluid dynamic (CFD) analyses were performed, where the applied calculation model was derived from the authors’ previous successful projects. The eighth version TW V8 has satisfied all longitudinal requirements. Lateral-directional CFD analyses of V8 showed that the ratio of the lateral and directional stability at the nominal cruising regime was optimal, but both lateral and directional static stabilities were too high. On further development versions, the lower vertical tail was eliminated, a negative dihedral was implemented on the front wing, and four inverted blended winglets were added. Version TW V14 has largely improved lateral and directional stability characteristics, while their optimum ratio at the cruising regime was preserved. Longitudinal characteristics were also well preserved. Maximum lift coefficient and lift-to-drag ratio were increased, compared to the V8.
1. Introduction
Nowadays, remote and/or automatic controlled unmanned aerial vehicles have replaced piloted aircraft in many roles. They have also become involved in missions and flight profiles that would be either too risky for men flying an aircraft, or manned aircraft would not be able to perform them for various reasons, mostly due to the human factor. The authors of this paper have recently been involved in the research project of a multipurpose UAV [1], with the intended weight and speed of an advanced ultralight aircraft, but smaller in size. It was supposed to be applicable for various duties, such as terrain mapping and photo reconnaissance, ground traffic observation and control, and agricultural applications. It should also be capable of carrying customized stores, equipment, and payloads for a variety of other applications.
Insights in a vast number of available references such as [2,3,4,5,6,7,8,9] support the decision of the authors of this paper to finally adopt the tandem wing (TW) configuration for the new UAV. Namely, in the case of classical concepts, the horizontal tail most often generates negative lift in order to provide proper trim in cruising flight. Because of that, the wing has to generate positive lift both to support the weight of the aircraft and to compensate for the negative lift of the tail. In the case of tandem wing configurations, both front and rear wings provide positive lift and carry the airplane’s weight, while enabling trim at the same time. So tandem wing configurations do not require a horizontal tail. This contributes to a proportional increase in their aerodynamic efficiency, compared to the classical concepts with the tail. More detailed explanations considering other aspects of the decision to adopt the tandem wing concept can be found in [1]. With an estimated maximum mass of 400 kg and fuselage length of 3.8 m, it was supposed to be powered by four electric motors mounted on the front and the rear wing, powering four tractor-type propellers. Two cruising flight regimes were considered: the nominal regime implied fast cruise—low-level flight (FC/LL) at the speed of 250 km/h and theoretically, for calculation purposes, at sea level (zero altitudes); the second—economical (EC) cruising regime assumed flight at speeds that would correspond to the maximum lift-to-drag ratio, at low and medium altitudes. Calculations have shown that the speed that would correspond to the EC regime is of the order of 160 km/h at sea level. The envelope defined by the speed range 160–250 km/h and by the altitude range 0–5000 m was considered sufficient for most of the possible multipurpose applications.
The initial UAV’s configuration TW V1 had the front and the rear wings of the same size. Optimization of this configuration, performed considering longitudinal analyses for the symmetrical flow conditions is described in detail in [1]. It led to a completely different TW V8 geometry (Figure 1).
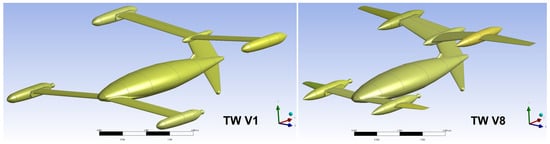
Figure 1.
Starting and final aerodynamic configurations obtained during the initial aerodynamic design stage, by longitudinal analyses [1].
The TW V8 has fulfilled all the design requirements posted during the longitudinal analyses, which can be summarized as follows:
- In the FC/LL flight, both V8 wings generate the same amount of lift, while in the EC flight regime, the front wing produces about 70% of the lift generated by the rear wing. In that sense, the V8 geometry, which has a noticeably smaller front wing than V1, is still a tandem wing, and not a canard configuration.
- The center of pressure (CP) of the V8 is very close to its center of gravity (CG), which has been estimated at 1.7 m from the fuselage nose, requiring very small trim forces at all flight regimes, except at negative angles of attack which are not expected in operational use. This CG position has been, to a first approximation, assumed to be the same for all considered TW modifications.
- At the FC/LL regime, the V8’s longitudinal static stability of 9.5% is small to moderate (corresponding jet trainer aircraft [10]), enabling sufficiently high longitudinal maneuverability for terrain avoidance at low altitudes. At the EC regime, it is 20.8% (corresponding to the business jets category [10]), enabling inherently more stable cruising flight, with lower actuator power consumption.
- Up to the maximum operational fuselage angle of attack = 10°, the front wing wake passes below the rear wing, preserving its efficiency at all flight regimes. (Fuselage angle of attack is used as the reference for this UAV, because front and rear wing incidence angles are different, and so their nominal angles of attack are different as well. In the case of classical concepts, the wing angle of attack α is most often taken as the longitudinal angular reference).
- Initial flow separation (stall) on V8 occurs first on the front wing, at an angle of attack of = 7°, while on the rear wing, it happens at = 10°. This generates a natural stall recovery tendency, without the influence of flight controls. The eventual opposite tendency (rear wing stalls first) would most probably lead to an irrecoverable deep stall.
During all CFD analyses and modifications leading from TW V1 to TW V8 configuration, lateral-directional issues were considered only by the authors’ previous project experiences, without any actual numerical verifications. This practically meant that sizing of the lower and the upper vertical tails and dihedral angles of the front and the rear wing were estimated and assigned to enable efficient oncoming modifications that would lead to equally good lateral-directional results, but without degrading already well-established longitudinal characteristics. CFD analyses that lead to presently latest modification TW V14 are described in the following chapters. Lateral-directional calculations of the V8 have shown that the ratio of its lateral-directional stability derivatives at the nominal FC/LL cruising regime was optimal. On the other hand, their actual derivative values were beyond their optimum range limits, showing that V8 was too stable in both the lateral and directional sense. High static stability implies low maneuverability and vice versa. In the case of this UAV, very high stability would require a higher actuator workload and power consumption to perform assigned maneuvers, than if those two stabilities were within their optimum ranges. Also, if they were small and below their optimums, higher actuator workload and power consumption would be necessary to sustain cruising flight. Following step-by-step modifications were carefully introduced to define the trends, or gradients of how certain aerodynamic geometry modifications were affecting these two derivatives.
The latest present outcome TW V14 has preserved the optimal lateral-directional stability derivatives ratio of the V8, but with lateral and directional stability characteristics substantially improved. All V8’s well-established longitudinal flying characteristics were preserved, while maximum lift coefficient and lift-to-drag ratios were even slightly increased. Further optimization of V14’s blended inverted winglets, as well as the evaluation of the control surface sizing and their influence on the longitudinal and lateral-directional performances, will be analyzed within the next design steps.
2. Computational Methods
From the very beginning of this TW UAV project [1] it was clear that the application of analytical calculation tools for the optimization of quite an unconventional UAV configuration, although this should be the first step in aerodynamic design, might be problematic considering the reliability and accuracy of the results, and possibly misleading at the key stages of the project development. The application of wind tunnel tests for the preliminary analyses was also excluded as an option. Namely, a possibly large number of required modifications could easily stop the work due to the exceeded budget, which was limited to the professor/doctoral students’ research project level. This turned out to be a true estimate, because, to the present state, TW has evolved through 14 development versions (several sub-versions were not taken into official account). Because of that, the decision was made to start the aerodynamic optimization of the TW V1 using viscous CFD analyses in ANSYS Fluent software [11,12,13].
To enable full compatibility of the results during the entire TW’s aerodynamic project development, it was mandatory to apply the same calculation procedure settings used in longitudinal analyses for its lateral-directional optimizations as well. For the consistency of this manuscript, some important issues of the calculation algorithm described in [1] are briefly repeated here. In longitudinal analyses with implied symmetrical flow conditions, it is a common practice to perform all analyses using half, instead of full models, with the symmetry condition assigned at the plane of symmetry. This way, results obtained for one-half of the aircraft geometry and control volume are simply mirrored on the other side. For TW V1 to V8 calculations, unstructured half-model meshes were generated, with the number of elements ranging from 1,600,000 to 2,000,000 elements, depending on the actual version (Figure 2—above). Initial half-model calculations were performed both with lower and higher mesh element numbers, in order to conduct the mesh independence study. Twice a higher number of mesh elements did not provide any relevant changes in obtained aerodynamic coefficients in the sense of practical engineering applications, while the CPU time had noticeably increased. As mentioned in [1], the above-stated domain was finally adopted as an optimal compromise between the expected quality of the results and the number of iterations and CPU time required to achieve stable convergence. For the asymmetrical lateral-directional calculations, full models had to be used, whereas for TW V8 to V14 unstructured meshes of about 3,000,000 elements were generated, the same settings as for the half-model calculations were used (Figure 2—below).

Figure 2.
Half-model mesh used for the TW V8 analyses, and full-model mesh, generated for the TW V14 CFD calculations.
The computational model in Fluent was established based on the authors’ previous relevant projects and works where, to mention a few, CFD results were compared: with the other relevant computational and design tools within a light piston-engined trainer aircraft development [14,15]; with available wind tunnel test data for a supersonic fighter jet [16]; with data obtained in flight tests of a jet trainer aircraft [17], etc. All calculations were performed using RANS (Reynolds-averaged Navier–Stokes) equations with k-ω SST turbulent model [11,12,18], providing stable convergence of the solutions. The Reverse Cuthill–McKee method [13] was used for the initial reordering of the mesh, and Full Multi–Grid (FMG) solution initialization at 4 levels [12,13] was applied, while the convergence was controlled by the Courant number optimization.
In these TW analyses, usual forms of aerodynamic coefficient equations for single-wing aircraft [10,19] had to be customized for tandem wing calculations. The reference area for a single-wing aircraft is its projected aerodynamic planform area (including its fictive portion under the fuselage, i.e., is its imaginary extension to the plane of symmetry which physically does not exist) S, while for TW is denoted as and represents the sum of the front and rear wing aerodynamic areas:
The mean aerodynamic chord or MAC is used as the reference length in calculations of the pitching moment coefficient; for TW analyses, it was obtained by area averaging of the front and rear wing’s MAC values:
The same applies to the wing span b, used as the reference length in calculations of the rolling and yawing moment coefficients:
Using notations: L—for the lift force, D—for the drag force, Y—for the side force, Lroll—for the rolling moment about CG, M—for the pitching moment about CG, and N—for the yawing moment about CG, their aerodynamic coefficients were calculated as follows:
where in Equations (4)–(9), represents dynamic pressure for the given analyses, m2, m, and m.
Initial verifications of the full model calculation algorithm were carried out as follows: (a) by comparing the results for TW V8 lift, drag, and pitching moment coefficients obtained within longitudinal analysis with those obtained by the half model [1] (Table 1) and, (b) by comparing calculated values of six aerodynamic coefficients obtained by the full model at sideslip angles = ± 5° and = ± 10° (Table 2 and Figure 3).

Table 1.
Comparison of the lift, drag, and pitching moment coefficients obtained by half and full calculation models.

Table 2.
Comparison of the six aerodynamic coefficients at two (±) sideslip angles.
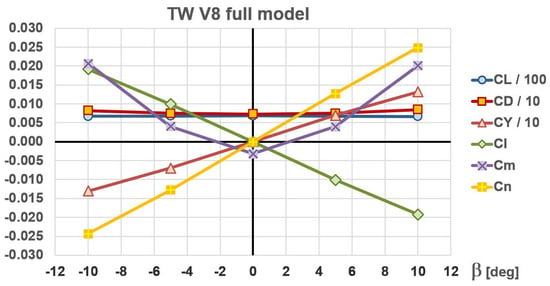
Figure 3.
One of the verification steps of the applied computational model—comparison of six aerodynamic coefficients for the same positive and negative sideslip angles.
For all calculations, the fuselage angle of attack = 5°, which corresponds to the TW V8’s maximum lift-to-drag ratio has been selected, although any other within the operational range would lead to quite similar conclusions. From Table 1, it is obvious that relative differences between the and the values obtained by the two models (0.02% and 0.11%, respectively) are negligible. The TW V8 pitching moment coefficient at this angle of attack is ≈ 0, while calculated values are very small and very close to this value, thus determination of their relative difference was not performed.
Theoretically speaking, absolute values of aerodynamic coefficients at sideslip angles of = ±5° and of = ±10° and the same angle of attack should be exactly the same, with the same or opposite sign, depending on the actual coefficient. Due to the inevitable numerical errors, this is not possible. In this particular case, Figure 3 and Table 2 indicate that their relative differences are very small, with 7 out of 12 being under 1%, while the two largest are of the order of 3%, which is, based on the authors’ previous experiences, acceptable for practical engineering applications.
Prior to any operational optimization analyses, such verifications should always be carried out when switching from half-model to full-model calculations. In some cases, relative differences presented in Table 1 and Table 2 can be noticeably larger, and often indicate that some of the assigned calculation options, and/or mesh generation algorithm settings should be revised.
3. Lateral-Directional Optimization and Results
3.1. Lateral-Directional Analyses of the TW V8
After the calculation model verifications described in the previous chapter, the full model algorithm was applied for the TW V8 lateral-directional analyses. Results obtained for moment coefficients and are presented in Figure 4a.

Figure 4.
Lateral-directional analyses of the TW V8: (a) roll and yaw coefficients; (b) roll and yaw derivatives and their optimum range envelopes; (c) ratios of the two derivatives for different fuselage angles of attack.
For all lateral-directional analyses, the sideslip angle = +5° was selected, which by convention is positive when the free stream flow comes in from the right-wing direction [20,21]). As shown in Table 2 and Figure 3, dependances and for TW V8 are linear functions in the whole = ±10° domain. In order to obtain the lateral static stability derivative (or dihedral effect), and the directional static stability derivative , verification calculations for angles = −5°, = +10° and = +10° were considered unnecessary. This way, derivatives were calculated as and . Taking into account conclusions from Table 2, and , and calculated lateral stability derivative has unit [1/°]. Accordingly, , etc. An aircraft is laterally statically stable when and directionally statically stable when [20,21]. From Figure 4b it is obvious that TW V8 is both laterally and directionally stable. In order to quantify these derivatives, boundaries or range of their recommended optimum values had to be adopted.
It is known that the contemporary computerized control systems on modern advanced aircraft and UAVs, with powerful and superfast actuators can easily provide precise guiding and control of both too stable and unstable flying vehicles. On the other hand, on manned aircraft without computer-guided controls, stability and control characteristics must be very carefully examined and adjusted, depending on the aircraft’s category and purpose. The logic applied in [1], within the TW’s longitudinal optimization process, was based on the requirement that this UAV should possess inherent (natural) longitudinal static stability like a hand-flown manned aircraft. This would provide lower workload and power consumption of the actuators and flight control system, and thus enable longer flight endurance and range. The same reasoning was applied in lateral-directional optimizations.
For TW V8’s nominal (FC/LL) cruising, Mach number M = 0.2 (corresponding to V = 250 km/h at H = 0 m), and for the derivative, the recommended range in reference [20] is between ≈0.001 [1/°] (“suggested goal values”) and ≈0.002 [1/°] (“NASA TN D-423”). On the other hand, in [21], the upper limit is the same, but the lower limit is relaxed to about 0.0005 [1/°]. The authors have decided to adopt [1/°] as the optimum range for TW directional static stability evaluations.
For the derivative, no recommended range is explicitly provided, since it changes as a function of the lift coefficient [20] (and accordingly, angle of attack). As a rule of thumb, both previously mentioned references suggest that for a selected relevant flight regime, the optimum ratio between the lateral and directional static stability derivatives should be . Based on this recommendation, the range [1/°] for TW’s lateral stability was formally established. Keeping in mind that inevitably increases towards higher negative values with the increase of , the derivative is expected to be within this range predominantly in the vicinity of the nominal FC/LL cruising regime.
These values were used in Figure 4b as horizontal boundaries, while angles of attack ≈ 0° (nominal cruise) and = 5° (economical cruise) as vertical, defining the optimum zones of interest for and . Unfortunately, both of these derivatives were way above their optimum zones by absolute values, meaning that V8 was both laterally and directionally too stable. The “good news” was that their ratio at the nominal cruise regime was almost exactly optimal , as shown in Figure 4c. That was quite irrelevant, because it was obvious that V8 had to be subjected to further geometry modifications in order to improve its lateral-directional aerodynamic characteristics, by which the optimal ratio at the FC/LL regime could likely be lost.
3.2. Lateral-Directional Optimization Steps
In the modern engineering world, many successful technical optimizations have been accomplished using genetic algorithms (GAs), and recently artificial intelligence (AI), and this applies to the aviation industry as well. These contemporary methods can efficiently provide convergence for very complex multiple degrees of freedom problems, but they are most often very time and resource demanding. An opposite extreme to them is trial and error methods where, for example, due to the insufficient understanding of certain physical phenomena, blind attempts are repeated until the final satisfactory solution is obtained (or not). Historically speaking, this approach has initially contributed to the growth of general scientific knowledge, where instead of guessing, dozens of optimization methods and approaches have been developed, with precisely controlled convergence of the solutions.
In [1] and in this paper, a kind of “manual” gradient method was implemented in TW optimizations. Well-understanding the general influence of important aircraft geometry parameters (such as lifting surface area, distance from CG, dihedral angle, etc.) on certain aerodynamic parameters, after initial calculations, relevant geometry was altered and changes in coefficients/derivatives, flow patterns, CP, etc., were observed. Knowing their desired optimums, geometry variations were revised (interpolated or extrapolated), and calculations were repeated. The five posted quantitative and qualitative requirements within the longitudinal TW optimizations [1], briefly described in the introduction of this manuscript, were fully satisfied reasonably quickly, within 8+2 geometry modifications, finishing with the TW V8 version. Such optimization technique requires caution, but also experience and solid background knowledge and understanding of the investigated aerodynamic phenomena, or otherwise, the gradient method can easily turn to a trial-and-error approach, with unpredictable outcomes. Also, the authors of this paper strongly believe that here presented gradient method can provide a very useful knowledge database for higher-level optimizations using advanced AI methodology.
All TW lateral-directional modifications were supposed to be carried out in a way to preserve well-established longitudinal characteristics of the V8. In that sense, the front and the rear wing positions, areas, spans, taper ratios [1], front wing incidence +5° and rear wing incidence +1°, both without twist, as well as the NACA 652-415 [22] wing airfoil, had to remain unchanged. As in the case of the V8 analyses, lateral and directional calculations were performed for the sideslip angle = +5°. The maximum operational angle of attack used in lateral-directional calculations was up to = 9° (in symmetrical cases it was = 10°), because asymmetric flow due to sideslip triggered local separation effects earlier. Geometry modifications TW V9–V14 are shown in Figure 5, Figure 6 and Figure 7, their moment coefficients and in Figure 8, derivatives and in Figure 9, and their ratios in Figure 10.
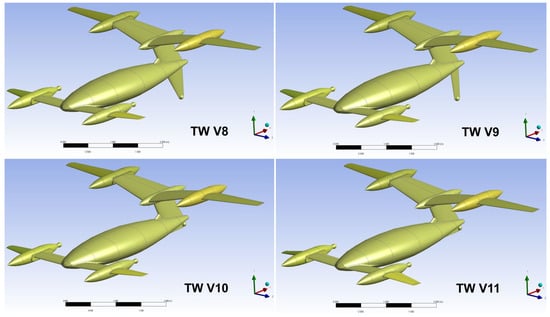
Figure 5.
Starting TW V8 configuration for lateral-directional optimizations, and the first three optimization models without winglets. TW V9—lower vertical tail area was halved, with span preserved; TW V10—lower vertical tail was removed; TW V11—anhedral angle was applied on outer segments of the front wing.
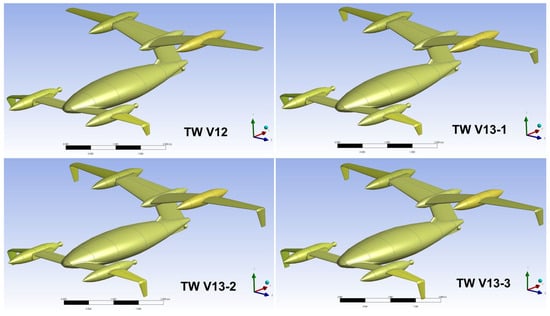
Figure 6.
Consecutive four lateral-directional optimization models with inverted winglets. TW V12—inverted winglets were added to the front wing only, to investigate their basic influence; TW V13-1, V13-2, and V13-3—winglets were added to the rear wing as well; front and rear winglet spans (vertical lengths) were varied.

Figure 7.
Finally adopted winglet spans on configuration TW V14.

Figure 8.
Comparison of roll and yaw aerodynamic coefficients.
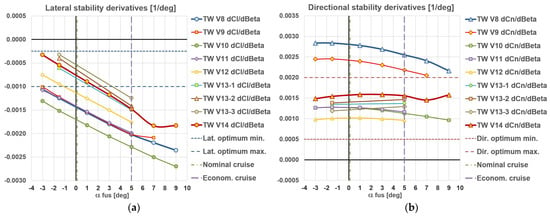
Figure 9.
Comparison of (a) roll, and (b) yaw derivatives.

Figure 10.
Roll/yaw stability ratios.
The evolution of each of the new TW versions developed during lateral-directional analyses is explained consecutively:
- In TW V9 modification, the influence of the lower vertical tail was investigated. Positioned under the CG, it generates destabilizing influence laterally and stabilizing influence directionally (unlike the upper vertical tail, whose influence is stabilizing both in the lateral and directional sense). In V9, the span of the lower vertical tail was preserved, but the aerodynamic area was approximately halved, keeping the same tip chord (Figure 5). Due to this modification, the yawing moment coefficient was noticeably reduced, but the rolling moment coefficient practically remained the same (Figure 8). This meant that its aerodynamic area dominantly influences directional stability, while its span dominantly affects the dihedral effect, i.e., with preserved span the lateral stability has not changed, although the tail area was decreased (and V10 has further expanded these conclusions). The same trend could be seen—considering the lateral and directional static stabilities, the has not changed, while is smaller, but still outside the optimum range (Figure 9). The ratio at the nominal FC/LL regime was increased to a higher negative value, about ≈−0.58 (Figure 10).
- The lower vertical tail on TW V10 was reduced to the form of a small ventral fin (Figure 5), but intentionally, it was not completely eliminated. Ventral fin sizing is often used for “fine tuning” the directional stability at the final design stages. By this, was additionally reduced, and this time, was positioned right in the middle of the optimum range. As expected, both and have increased towards higher negative values, which was an undesired but inevitable consequence of this modification. The stability ratio has drastically diverged from the optimum value, to ≈ −1.35. The aim for all oncoming geometry variations was to decrease the dihedral effect while keeping directional stability within the optimum.
- One of the ways to reduce lateral static stability is to apply anhedral (negative dihedral angle) to the wings, and this led to the TW V11. In the case of this UAV, the application of anhedral angle to the rear wing brought the risk of immersing it inside the front wing’s wake at higher angles of attack. So, the decision was made to apply anhedral only to the outer segments of the front wing. An anhedral angle of = −10° was implemented, estimated as the highest value that would still not affect the lifting capabilities of these wing segments. Through this modification, was kept within the desired boundaries, and was brought back to the values of V8 and V9, while the stability ratio was reduced to = −1.1, yet still far from the optimum.
- Another way, applicable to this UAV, to reduce the dihedral effect was to add inverted (tips pointing down) winglets to the wings (winglets pointing upwards would increase the dihedral effect). The expected side effect was that they should hopefully improve the UAV’s lifting characteristics to a certain extent as well. For the initial investigation purposes considering their basic influence, version TW V12 had winglets added only to the front wing (Figure 6). A very small chord plane blending radius of 0.03 m was used, with a span of 0.2 m below the blending zone and taper ratio of 0.5, cant angle of −90° with respect to the horizontal plane, no incidence, and with the wing airfoil preserved all the way to the tip. This design provided that the effective planform area of the front wing was negligibly altered. Additional winglet optimizations, such as the application of alternative airfoil, incidence angle, blending radius, taper, type (elliptical...), etc., were left for future design stages. The outcome was very promising—lateral stability derivative has entered the optimum zone for the first time at negative , with remaining within the desired domain, but with lower values (as expected—the influence of vertical lifting surfaces in front of the CG).
- The following three modifications TW V13-1, V13-2, and V13-3 had winglets on the rear wings as well. They were generated by the same algorithm used for the front winglets on V12. The only parameter that was altered on these three versions was the front and rear winglet vertical span: on V13-1, the front span was the same as on V12 and the rear was 0.25 m; on V13-2, the front span was 0.3 m and the rear 0.35 m; on V13-3, the front span was 0.35 m and the rear 0.3 m. For all three versions, derivatives were within the desired domain, while lateral stability derivatives were progressively decreasing by absolute value from one version to the next. Figure 9 shows that extensions of this derivative for V13-2 and 13-3 to = −3° vicinity would put them in the region below the minimum limit for lateral static stability, i.e., it would be too low. The angle of attack = −3° corresponds to a near-zero lift angle, which in practice, is encountered in a very steep, almost vertical dive. Although for this TW UAV, such a flight profile is not considered usual and standard, and it might be necessary for emergency situations, when sudden descent would be mandatory for whatever reasons. In such cases, too low lateral stability would not be acceptable, and so versions V13-2 and 13-3 were excluded from further investigations. The V13-1 remained under consideration, with a small disadvantage in that its stability ratio was slightly above the optimum −0.5 (≈ −0.6).
- After a simple interpolation work, version V13-4 was designed with a front winglet vertical span of 0.2 m and a rear winglet vertical span of 0.35 m. Its directional static stability was of the order ≈ 0.0016 and thus it was well within the range. Lateral static stability at = −3° was ≈ −0.000326, so it was within the assigned range and it remained within it up to = 2°. Also, its stability ratio was optimal . Because of that, version TW V13-4 was adopted as the final within this optimization process and was renamed to TW V14 (Figure 7). It will be further discussed and analyzed in the following chapter.
4. Discussion
For the clarity of the discussions, in Figure 11a,b, static stability derivatives and their ratios were extracted and shown only for the starting version TW V8 and the finally adopted V14 for here presented analyses. Actual numerical quantifications given at the end of the previous chapter indicate that all the assigned goals of the lateral-directional optimizations have been reached. Once again, being a function of the lift coefficient, lateral derivative increases with the angle of attack, while directional changes very little. Because of that, textbooks suggest only the optimum range for the while as mentioned before, authors of this paper have formally prescribed optimums using the −0.5 rule for the . We do not imply that it should or could stay within it in the entire operational range, but expectantly in the vicinity of the nominal cruising flight regime. Figure 11a shows that it has been satisfied for the V14.

Figure 11.
Comparisons between the TW V8 and TW V14: (a) roll and yaw derivatives and their optimum range definitions; (b) ratios of the two derivatives for different fuselage angles of attack.
The ratio is optimal for TW V14 at the nominal FC/LL regime, while at the economical EC, it is (Figure 11b). In order to discuss the second value, a small digression will be made. Reference [20] states that the optimum lateral-directional stability ratio of −0.5 can increase to about −1.0 in the transonic speed domain, which is considered tolerable (due to the influence of compressibility effects, lift curve slope increases as M = 1 is approached; remark by authors of this paper). Although here, the analyzed TW UAV is not aimed to fly even near the transonic regime, this statement by Raymer [20] can indirectly be transferred to formally establish another rule of thumb, that can be adopted as an acceptable range for this ratio in operational use; too large static stabilities are not desirable as well. The mentioned value at the EC regime fits within this range.
From the diagrams in Figure 11, it is obvious that the V8 shows a rather uniform trend of variations of , and with increase. For the V14, those trends are also quite uniform, but after = 7°, a lateral-directional “stall” occurs, categorized by increase and drop.
To provide a qualitative insight into this phenomenon, flow field visualizations based on the eddy viscosity distributions have been made, and they are presented in Figure 12, Figure 13 and Figure 14. At = 5°, the asymmetric flow due to the β = 5° shows no visible difference between the V8 and V14 flow field patterns. At = 7° on V8, a separation vortex on the inner side of the front-left engine nacelle is noticeable, together with a small vortex on the outer edge of the front-right nacelle. On the V14, the front-left nacelle vortex is a bit stronger, while the front-right nacelle vortex is hardly visible. A crucial difference can be observed in Figure 14, where at = 9° on V8, four separation vortices appear on both sides of the front engine nacelles. At the same angle of attack, on the V14′s outer right nacelle, the vortex has almost vanished, while the left outer vortex has moved from the left nacelle to the front left winglet. This has degraded its efficiency, causing a slight increase in directional stability (its destabilizing contribution is downgraded), and stagnation in the dihedral effect, in spite of the increase from 7° to 9° (see Figure 11).

Figure 12.
Eddy viscosity distributions over and behind the two models, at the fuselage angle of attack α fus = 5° and sideslip angle β = 5°.

Figure 13.
Eddy viscosity distributions over and behind the two models, at the fuselage angle of attack α fus = 7° and sideslip angle β = 5°.
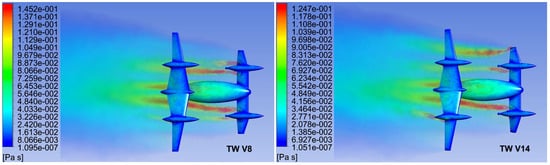
Figure 14.
Eddy viscosity distributions over and behind the two models, at the fuselage angle of attack α fus = 9° and sideslip angle β = 5°.
All the abovementioned statements and conclusions have been drawn from flow patterns carefully observed on a UHD monitor. Their conversion to journal pictures came at a price, that some of the phenomena might not have been properly captured and clearly visible when scaled. It should also be emphasized that primary decisions about the UAV design progress and steps were derived dominantly from the quantitative results, as those shown in diagrams in Figure 8, Figure 9 and Figure 10. Qualitative analyses based on flow pattern examinations, on the other hand, were mostly used to provide guidelines about possible problem sources and hints of what the next most efficient modification could or should be.
The next very important step was the assessment of applied lateral-directional optimization on the possible degradation of the V8’s well-established longitudinal characteristics. For that purpose, their longitudinal aerodynamic characteristics were summarized in Table 3 and Table 4. The lift , drag , and pitching moment coefficients, as well as lift-to-drag ratios, were presented as functions of the fuselage angle of attack. The following column shows variations of the center of pressure distance from the fuselage nose with , next to the estimated position of the center of gravity , which is the same for all aerodynamic analyses of this UAV. In the next three columns, separate contributions of the front and rear wing, as well as other structural components (fuselage and four engine nacelles) to the global lift are presented.

Table 3.
Summary of the longitudinal aerodynamic characteristics for the V8.

Table 4.
Summary of the longitudinal aerodynamic characteristics for the V14.
The most important aspects of V14 evaluation will be addressed in the same order as in the Introduction chapter of this manuscript:
- At the FC/LL regime, the front wing of the V8 was generating 40%, the rear wing 39%, and other structural components 21% of the total TW configuration lift. At the same cruising regime, the front wing of the V14 generates 41%, the rear wing 39%, and other structural components 20% of the total TW configuration lift. At EC regime, the front wing of the V8 was generating 33%, the rear wing 45%, and other structural components 22% of the configuration lift. At this regime, the front wing of the V14 generates 33%, the rear wing 46%, and other structural components 21% of the total lift. Partial lift contributions have obviously remained the same, and thus the V14 is also a tandem wing configuration, and not a canard.
- Positions of the V14s’ center of pressure compared to the V8 have changed negligibly, from 1.578 m to 1.574 m at the FC/LL regime, and from 1.712 m to 1.724 m at the EC regime (Figure 15).
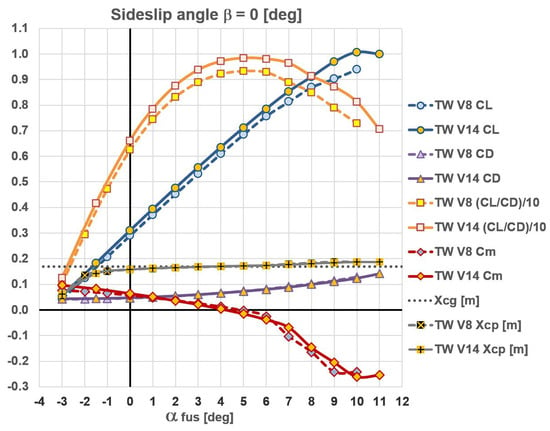 Figure 15. Comparisons of lift, drag, and moment coefficients and lift-to-drag ratios show improvements in TW V14 aerodynamic characteristics in symmetric flight conditions as well.
Figure 15. Comparisons of lift, drag, and moment coefficients and lift-to-drag ratios show improvements in TW V14 aerodynamic characteristics in symmetric flight conditions as well. - Longitudinal static stability (its quantification was described in detail in [1]) has increased from 9.5% on V8 to 14.3% on V14 at the nominal, and from 20.8% to 24.6% in the economical cruising flight. This 4% increase can readily be attributed to the influence of winglets, which have improved the lifting characteristics of both wings. Their vertical span sizing, which came out from the lateral-directional optimizations, provided larger winglets on the rear wing. They obviously generate proportionally larger moment/lift contributions of the rear wing at both cruising regimes. Longitudinal static stability increase of the order of 4% does not degrade any of the established aerodynamic design goals; on the other hand, its eventual hypothetic 4% decrease would certainly require additional attention considering the FC/LL flight.
- Up to the maximum operational fuselage angle of attack = 10°, the V14′s front wing wake passes below the rear wing preserving its efficiency at all flight regimes, as was the case with the V8.
- Initial flow separation on V14 occurs first on the front wing, at an angle of attack of = 7°, while on the rear wing, it happens at = 10°, exactly as it was the case with the V8 version (Figure 16). This has preserved the V8′s natural stall recovery tendency. More detailed observations considering stall analyses and the behavior of this UAV can be found in [1].
 Figure 16. In both configurations, the initial stall occurs on the front wing first.
Figure 16. In both configurations, the initial stall occurs on the front wing first.
From previous discussions, it is obvious that the optimization steps presented in this paper have brought the TW V14 lateral-directional static stability to the desired values, without affecting previously established V8’s good longitudinal aerodynamics.
Furthermore, due to the introduction of winglets, some of V14’s aerodynamic characteristics have been improved compared to the V8 version: maximum operational lift coefficient at = 10° is 7.2% higher; maximum lift-to-drag ratio at = 5° is also 5.4% higher; at FC/LL regime, ratio has increased by 5.8%, while the corresponding V8 and V14 drag coefficients are practically the same in previous three cases (data derived from in Table 3 and Table 4).
Yet another indirect consequence of here presented optimizations due to the application of winglets is that flow patterns at moderate and high angles of attack are categorized by noticeably lower vorticity levels on V14 than on the V8 version, (Figure 17 provides an obvious example), contributing to the increase of its global aerodynamic efficiency.

Figure 17.
The TW V8 [1] and TW V14: flow patterns represented by eddy viscosity, at the angle of attack α fus = 10° and no sideslip (isometric and side views).
At this point, it is obvious that all obtained results and trends derived from here applied manual gradient optimizations contribute to the gradual and progressive build-up of a base of knowledge necessary for the automation and high-level optimization at the final UAV design stages, that could be based on the contemporary AI approaches.
5. Conclusions
Lateral-directional aerodynamic optimizations described in this manuscript are a part of the second development stage of a multipurpose tandem wing unmanned aerial vehicle. The first stage—longitudinal aerodynamic optimizations were successfully accomplished satisfying all posted qualitative/quantitative goals. The outcome was a version denoted as TW V8. They were all confined to the symmetric flight case analyses, without control surface deflections. Optimizations presented in this paper were performed by analyzing the asymmetric flow influence due to sideslip on the rolling and yawing moments, static lateral and directional stabilities, and their mutual ratios within a range of operational angles of attack, using V8 configuration as the starting point.
Both longitudinal and lateral-directional UAV optimizations were carried out using ANSYS Fluent software. Viscous CFD analyses were performed using RANS equations with the k-ω SST turbulent model and a number of carefully selected additional settings, based on the authors’ experiences from previous successful works and projects. Lateral-directional optimization steps that lead to the present highest UAV development version TW V14 could be summarized as follows:
- Asymmetric aerodynamic analyses of the TW V8 showed that both lateral and directional static stabilities were too high, beyond the established optimum domain boundaries. Although their mutual ratio was optimal, the V8′s geometry modifications were mandatory.
- The first two new modifications V9 and V10 were used to quantify the influence of the lower vertical tail. By reducing its immense size to a rudimentary ventral fin, the UAV’s directional static stability was substantially decreased and placed within the optimums. The inevitable outcome was a noticeable increase in lateral stability, compared to the V8. In the next V11 version, its front wing outer segments were tilted to the anhedral angle of −10°. This brought lateral stability back to the level of V8, while its newly established directional stability was not much affected. Adding anhedral to the rear wing segments was not considered, because that could possibly immerse them in the front wing’s wake at higher angles of attack. So other solutions for too high lateral static stability had to be found.
- A promising option was foreseen in the application of winglets. Although they are not used on single-wing airplanes as lateral-directional optimization devices, but primarily to improve the wing’s lift-to-drag efficiency, some successful canard-configured airplanes use them both as winglets and vertical tails. Since the dihedral effect had to be decreased, both front and rear wing winglets on the following versions were inverted, with their tips pointing downwards. This orientation was not expected to degrade their additional contribution—improvement of lift-to-drag efficiency of both TW wings, and this assumption turned out to be true. With the aim to preserve established longitudinal characteristics, a small blending radius and cant angle of −90° degrees with respect to the horizontal plane were implemented. By this, effective planform areas of both wings were negligibly altered.
- In order to perform initial investigations, on V12, modification winglets were added only to the front wing. The following versions V13-1, V13-2, and V13-3 had winglets on both wings, their vertical spans were varied, and their influence on lateral and directional derivatives was quantified. As in previous longitudinal optimizations, using a simple “manual” gradient approach, the optimum spans for front and rear winglets were interpolated. This way, the final TW V14 version that has fully satisfied posted lateral-directional goals was obtained, including the requirement that their mutual ratio of −0.5 at the nominal cruising flight regime was optimal.
- Finally, longitudinal analyses of V14 were carried out, assuming symmetrical flow conditions. Results were compared with those obtained for V8 during the first design stage. The conclusion was that none of the well-established longitudinal aerodynamic characteristics of the V8 version was degraded. Furthermore, owing to the application of winglets, some were actually improved: the maximum lift coefficient was increased by some 7%, the maximum lift-to-drag ratio that corresponds to the economical cruise was more than 5% higher, while the value of this parameter at the nominal cruising regime was almost 6% larger. Although defined by single-digit numbers, in the aerodynamic sense these improvements are quite relevant.
Further design steps within the aerodynamic optimization of here presented tandem wing UAV will involve the following: (a) analyses of the control surfaces efficiencies and UAV maneuverability both in the longitudinal and lateral-directional sense; (b) angular velocity influence on derivatives; (c) propeller influence on UAV’s stability and control; (d) optimizations based on the dynamic responses, etc. All so far obtained and the expected oncoming results and approaches based on here presented gradient optimization methodology, will be used to establish a comprehensive knowledge database for the artificial intelligence optimizations, planned for the last aerodynamic design stage of this tandem wing UAV. This step of automation will be very important, because the manual gradient method could sometimes lead to several near-optimal configurations based on this study’s design variables. In such cases, manual optimization might not be a time-efficient decision-making tool, concerning the selection of the best solution. In that sense, implementation of the artificial intelligence will provide much more efficient sensitivity analyses for different design variables, which can reduce both computational and overall design time.
Finally, as a very important part of the conclusion, it should be emphasized that here presented UAV is a completely novel design, not based on or derived from any of the existing unmanned aerial vehicles.
Author Contributions
Conceptualization, I.K., A.S. and O.K.; methodology, I.K., A.S., O.K., D.I. and D.T.; validation, I.K., A.S., O.K. and D.I.; formal analysis, I.K., A.S., O.K., D.I. and D.T.; investigation, I.K., A.S., O.K., D.I. and D.T.; supervision, I.K. and A.S.; writing—original draft preparation, I.K., A.S. and O.K.; supervision, I.K. and A.S.; project administration, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research work is supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia through contract No. 451-03-47/2023-01/200105 from 3rd February 2023.
Data Availability Statement
Additional data may be made available by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kostić, I.; Tanović, D.; Kostić, O.; Abubaker, A.A.I.; Simonović, A. Initial development of tandem wing UAV aerodynamic configuration. Aircr. Eng. Aerosp. Technol. 2023, 95, 431–441. [Google Scholar] [CrossRef]
- Minardo, A. The Tandem Wing: Theory, Experiments, and Practical Realisations, Corso di Laurea Magistrale in Ingegneria Aeronautica, Politecnico di Milano, Italy. 2014. Available online: https://www.politesi.polimi.it/bitstream/10589/93619/1/2014_07_Minardo.pdf (accessed on 11 March 2024).
- Gao, L.; Li, C.; Jin, H.; Zhu, Y.; Zhao, J.; Cai, H. Aerodynamic characteristics of a novel catapult launched morphing tandem- wing unmanned aerial vehicle. Adv. Mech. Eng. 2017, 9, 1687814017692290. [Google Scholar] [CrossRef]
- Cipolla, V.; Dine, A.; Viti, A.; Binante, V. MDAO and Aeroelastic Analyses of Small Solar-Powered UAVs with Box-Wing and Tandem-Wing Architectures. Aerospace 2023, 10, 105. [Google Scholar] [CrossRef]
- Rosid, N.H.; Lukmen, I.E.; Fadlillah, A.M.; Moelyadi, M.A. Aerodynamic Characteristics of Tube-Launched Tandem Wing Unmanned Aerial Vehicle. In Proceedings of the 5th International Seminar of Aerospace Science and Technology, Medan, Indonesia, 27–29 September 2017; Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1005/1/012015/pdf (accessed on 11 March 2024).
- Gao, L.; Zhu, Y.; Liu, Y.; Zhang, J.; Liu, B.; Zhao, J. Analysis and Control for the Mode Transition of Tandem-Wing Aircraft with Variable Sweep. Aerospace 2022, 9, 463. [Google Scholar] [CrossRef]
- Singh, D.; Antoniadis, F.A.; Tsoutsanis, P.; Shin, H.-S.; Tsourdos, A.; Mathekga, S.; Jenkins, W.K. A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight. Aerospace 2018, 5, 66. [Google Scholar] [CrossRef]
- BarbosaOLD5, J.; Goncalves, J.; Gamboa, P. Experimental investigation of the aerodynamic characteristics of a “K” tandem configuration. In Research Bulletin/Warsaw University of Technology; Institute of Aeronautics and Applied Mechanics: Warsaw, Poland, 1998; pp. 75–80. [Google Scholar]
- Zhang, Q.; Xue, R.; Li, H. Aerodynamic Exploration for Tandem Wings with Smooth or Corrugated Surfaces at Low Reynolds Number. Aerospace 2023, 10, 427. [Google Scholar] [CrossRef]
- Roskam, J. Airplane Flight Dynamics and Automatic Flight Controls—Part I; DARcorporation: Lawrence, KS, USA, 2001. [Google Scholar]
- ANSYS Fluent 14.0. Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- ANSYS Fluent 14.0. User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- ANSYS Fluent 14.0. Tutorial Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Kostić, I.; Kostić, O. Several Approaches in Contemporary Light Aircraft Aerodynamic Design. In Proceedings of the Invited Presentation at the 3rd International Forum on Aerospace and Aeronautics AEROFORUM 2023, San Diego, CA, USA, 11–13 December 2023. [Google Scholar]
- Kostić, I.; Stefanović, Z.; Kostić, O. Aerodynamic analysis of a light aircraft at different design stages. FME Trans. 2014, 42, 94–105. [Google Scholar] [CrossRef]
- Šobot, J.; Kostić, I.; Kostić, O. Comparative Aerodynamic Analysis of F-16C Jet fighter at Subsonic and Supersonic Speeds Using Panel and Viscous CFD Methods. In Proceedings of the 9th International Scientific Conference on Defensive Technologies OTEH 2020, Belgrade, Serbia, 15–16 October 2020. [Google Scholar]
- Šobot, J.; Kostić, I.; Kostić, O. CFD Evaluation of Transonic Flow Analysis Around Jet Trainer Aircraft. In Proceedings of the 7th International Congress of Serbian Society of Mechanics, Sremski Karlovci, Serbia, 24–26 June 2019; Available online: https://www.researchgate.net/publication/369692974 (accessed on 11 March 2024).
- Wilcox, D.C. Turbulence Modelling for CFD; DCW Industries, Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Bertin, J.J.; Cummings, R.M. Aerodynamics for Engineers; Pearson: Prentice-Hall, NJ, USA, 2008. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 3rd ed.; AIAA Education Series: Sylmar, CA, USA, 1999. [Google Scholar]
- Perkins, C.D.; Hage, R.E. Airplane Performance, Stability and Control; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1960. [Google Scholar]
- Abbott, I.H.; Doenhoff, A.E. Theory of Wing Sections, Including a Summary of Airfoil Data; Dover Publications, Inc.: Mineola, NY, USA, 1959. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).