Research on the Zooming Method for Determining the Flow, Heat Transfer, and Infrared Radiation of an Air-Breathing Hypersonic Vehicle Powered by a Scramjet
Abstract
1. Introduction
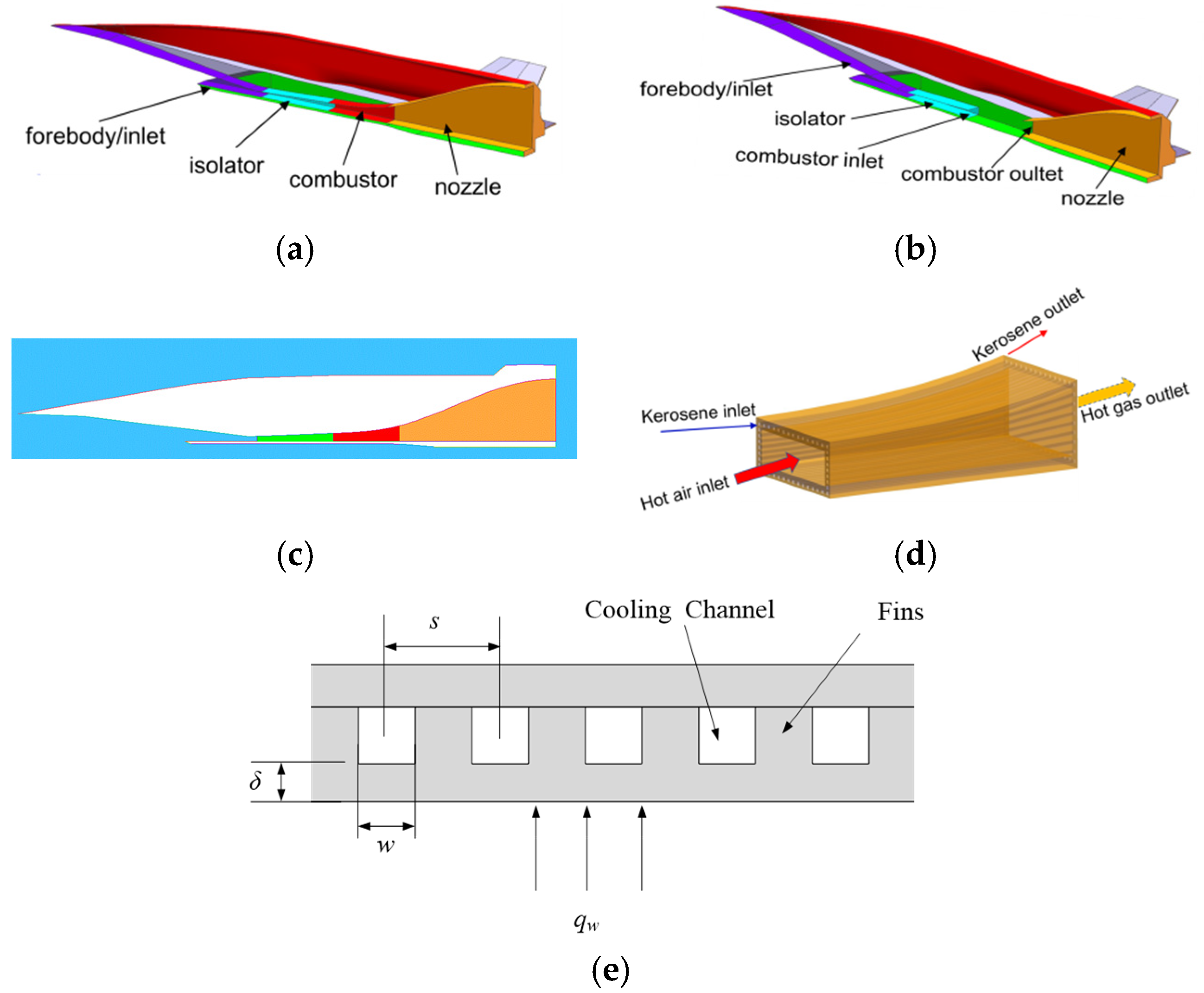
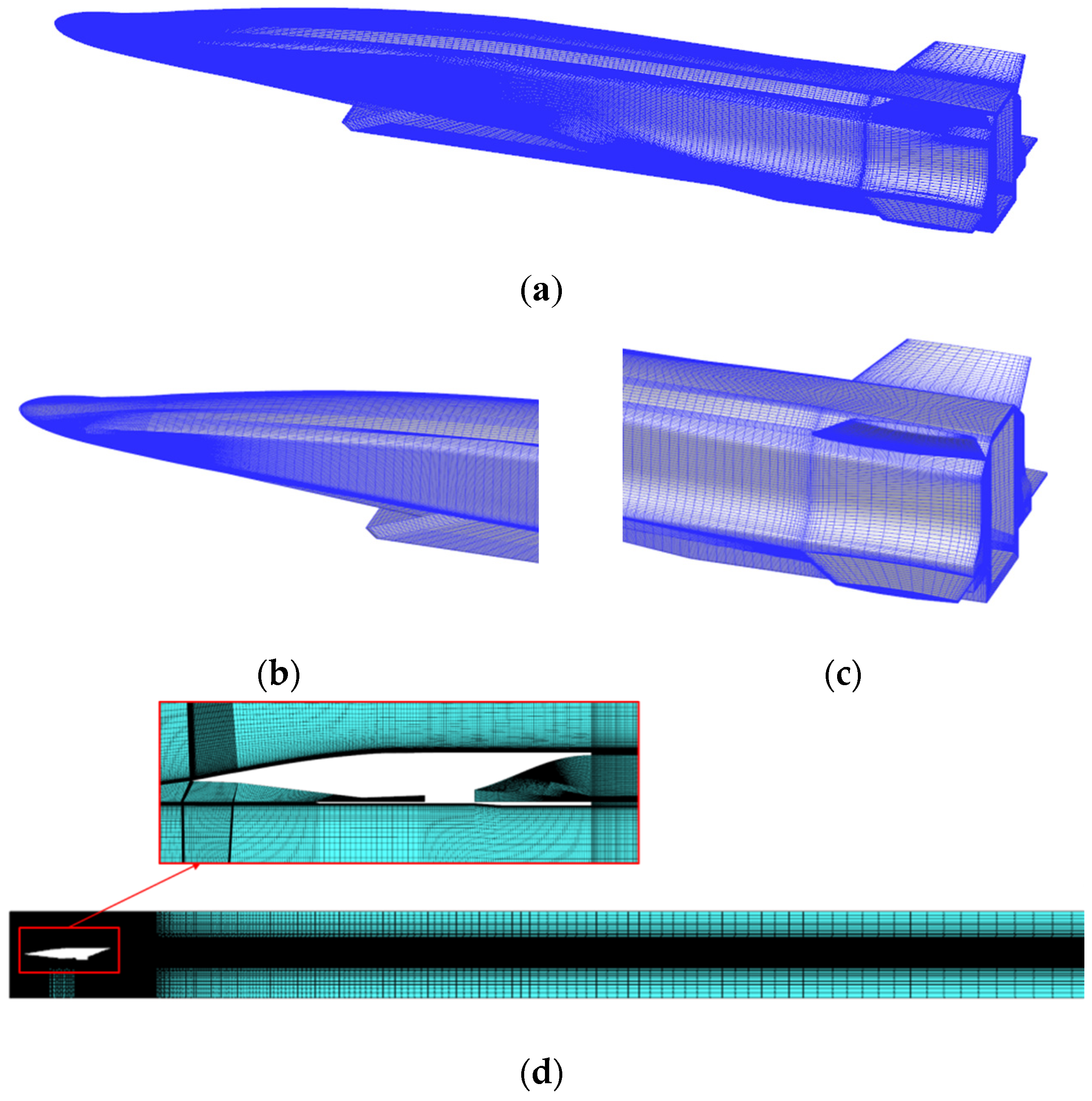
2. Air-Breathing Hypersonic Vehicle Model
3. Zooming Strategy for Calculating the Infrared Radiation of an Air-Breathing Hypersonic Vehicle
- (1)
- (2)
- Carry out the two-dimensional numerical simulation of the flow field on the symmetry plane of the hypersonic vehicle (Figure 1c) to obtain the pressure, temperature, velocity, and other parameters of the air at the outlet of the isolator and the static pressure at the outlet of the combustion chamber, and use these as the inlet boundary condition and the outlet boundary condition of the quasi-one-dimensional calculation for the combustion chamber, respectively.
- (3)
- Perform the quasi-one-dimensional calculation for the combustion chamber (as shown in Figure 1d) and extract the total temperature, total pressure, and static pressure of the air outlet for the combustion chamber as the boundary conditions of the nozzle inlet for the three-dimensional numerical simulation.
- (4)
- Perform the three-dimensional numerical simulation on the internal and external flow fields for the hypersonic vehicle without a combustion chamber (as shown in Figure 1b). Combine the quasi-one-dimensional calculation results to obtain the internal and external flow fields of the entire calculation domain for the air-breathing hypersonic vehicle.
- (5)
- Perform the infrared radiation simulation for the air-breathing hypersonic vehicle at different azimuth angles.
4. Quasi-One-Dimensional Calculation Method for the Flow and Heat Transfer in a Combustion Chamber with Regenerative Cooling
4.1. Governing Equations
4.2. Parameter Models for Solving Quasi-One-Dimensional Governing Equations
- (1)
- The heat-added term dQ/dx and mass-added term dm/dx.
- (2)
- Friction coefficient.
- (3)
- The aerodynamic-heating heat flux qaero.
- (4)
- The radiation heat flux.
- (5)
- A convective heat-transfer model of the cooling channel based on a straight rectangular fin.
4.3. Quasi-One-Dimensional Calculation of Boundary Conditions
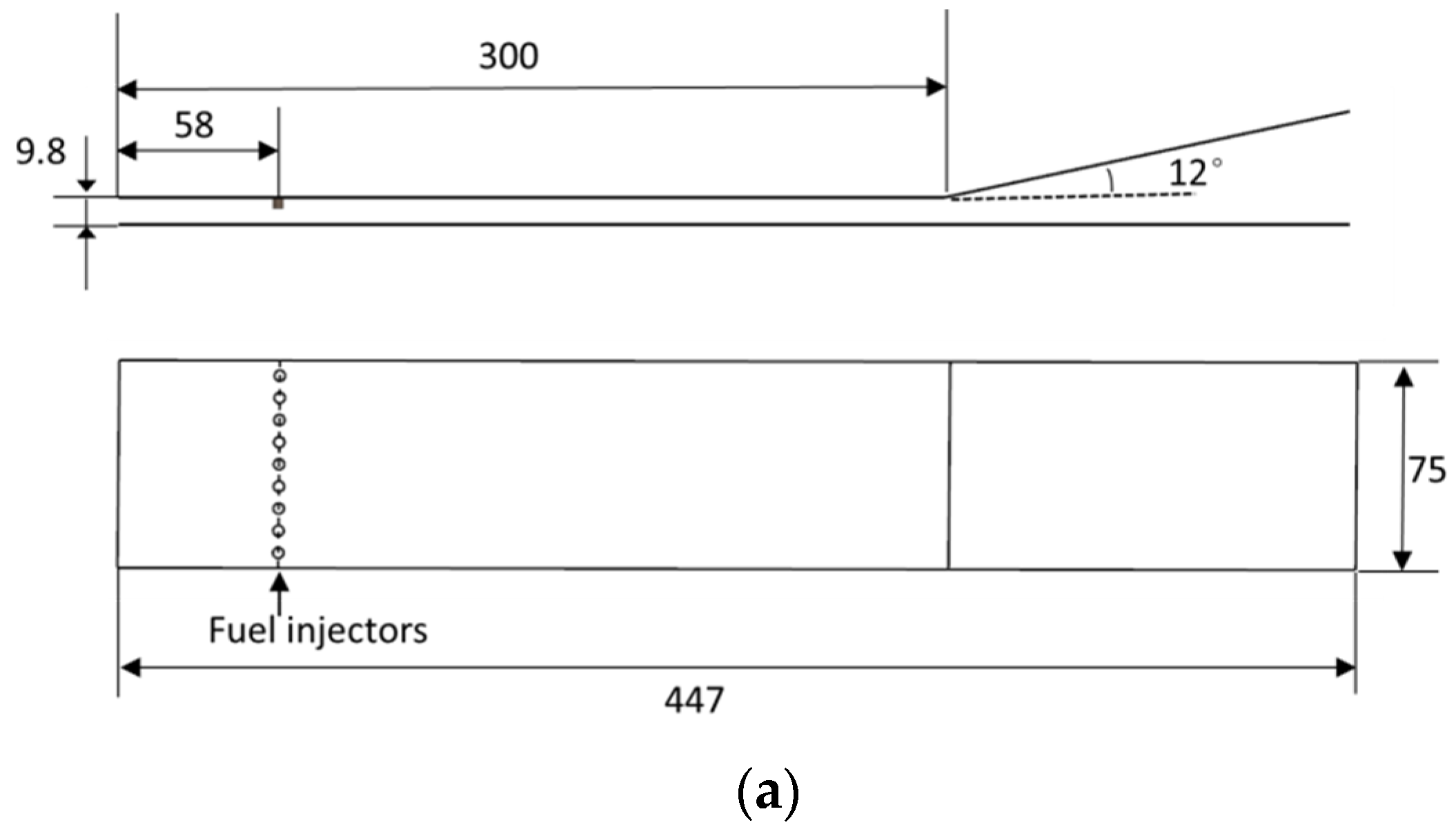
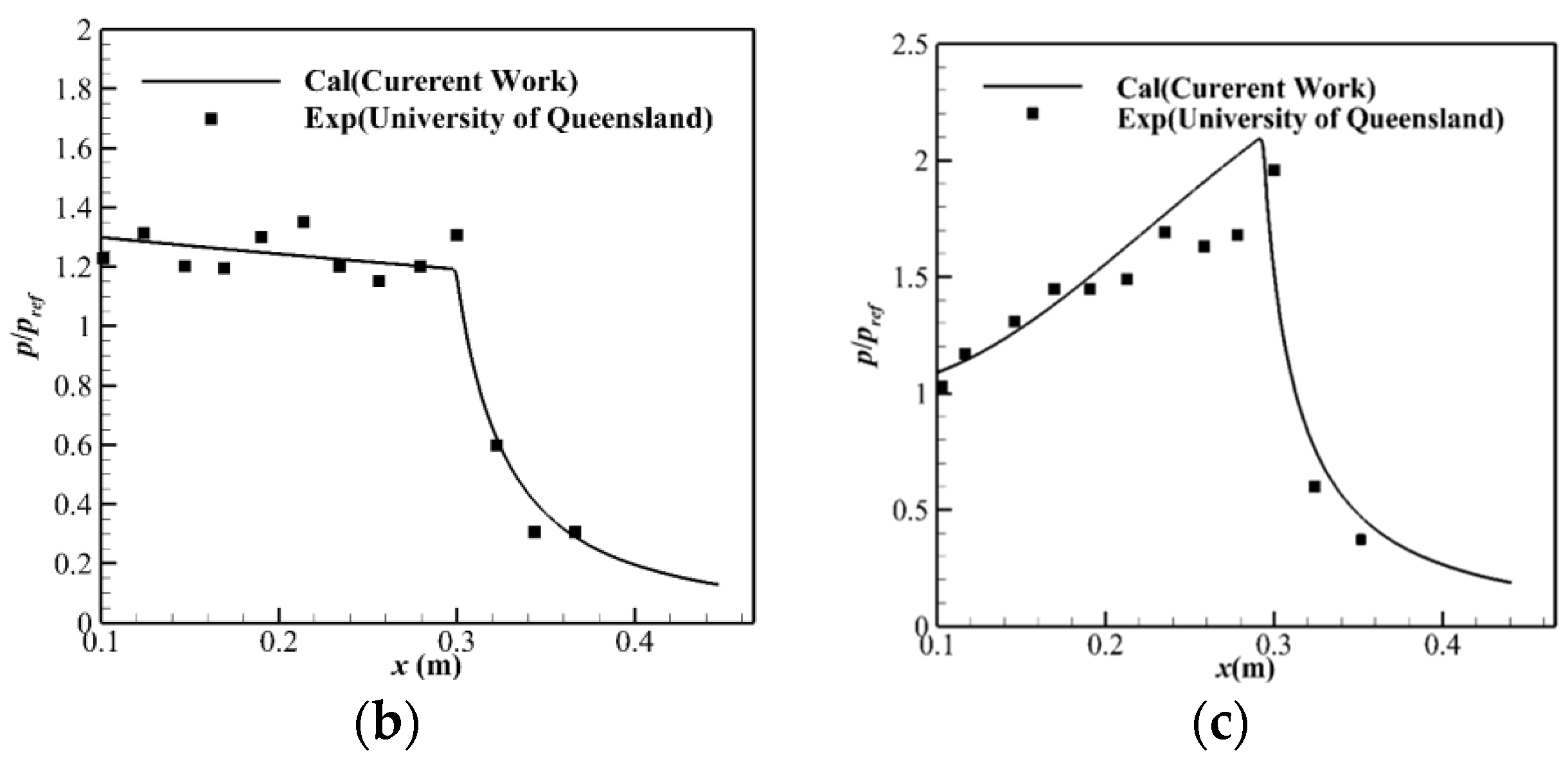
4.4. Validation of the Quasi-One-Dimensional Calculation Method in the Scramjet Combustor
5. Methodology for Calculating the Three-Dimensional Flow Field and Heat Transfer in an Air-Breathing Hypersonic Vehicle without a Combustor
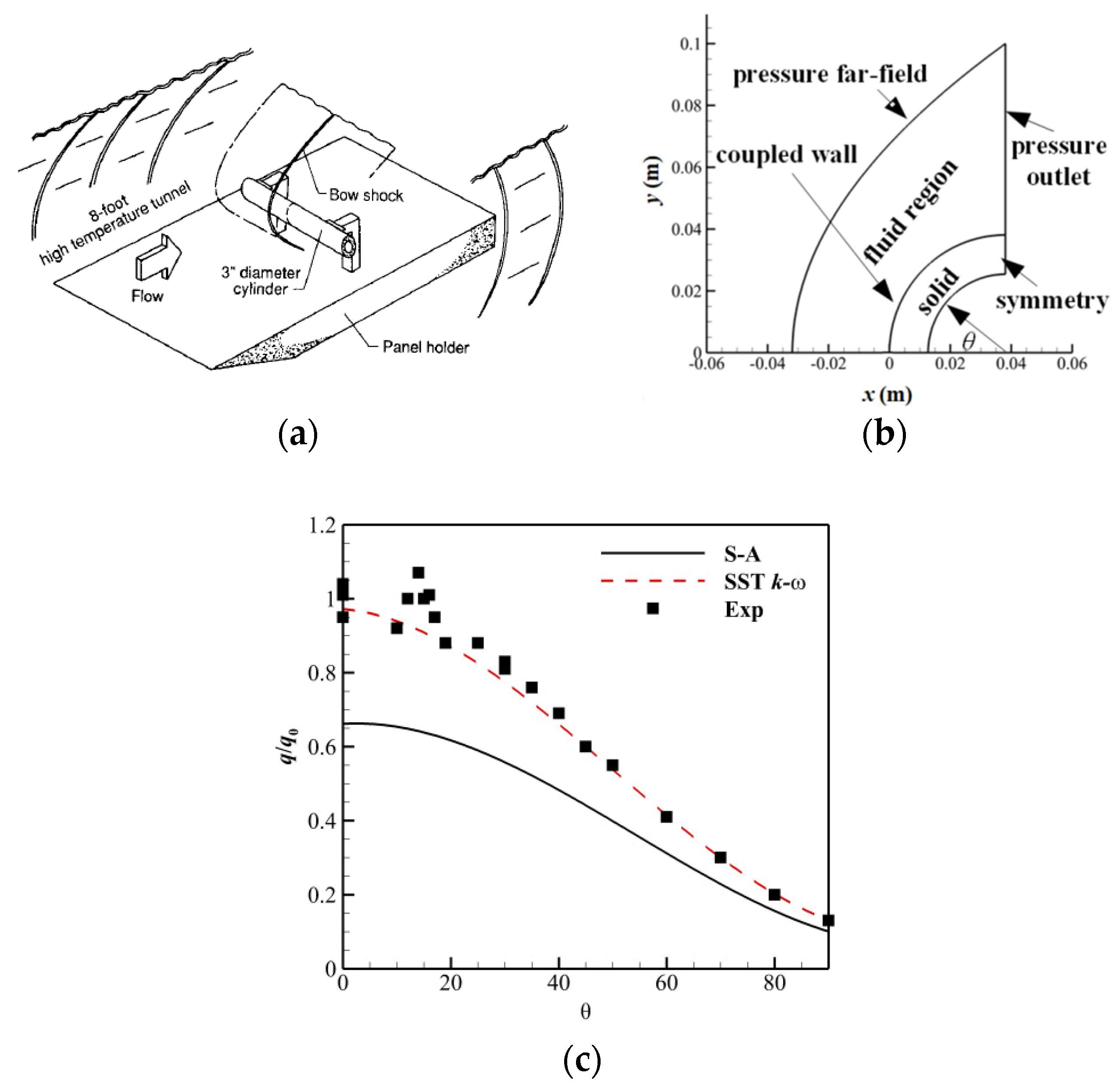
5.1. Boundary Conditions
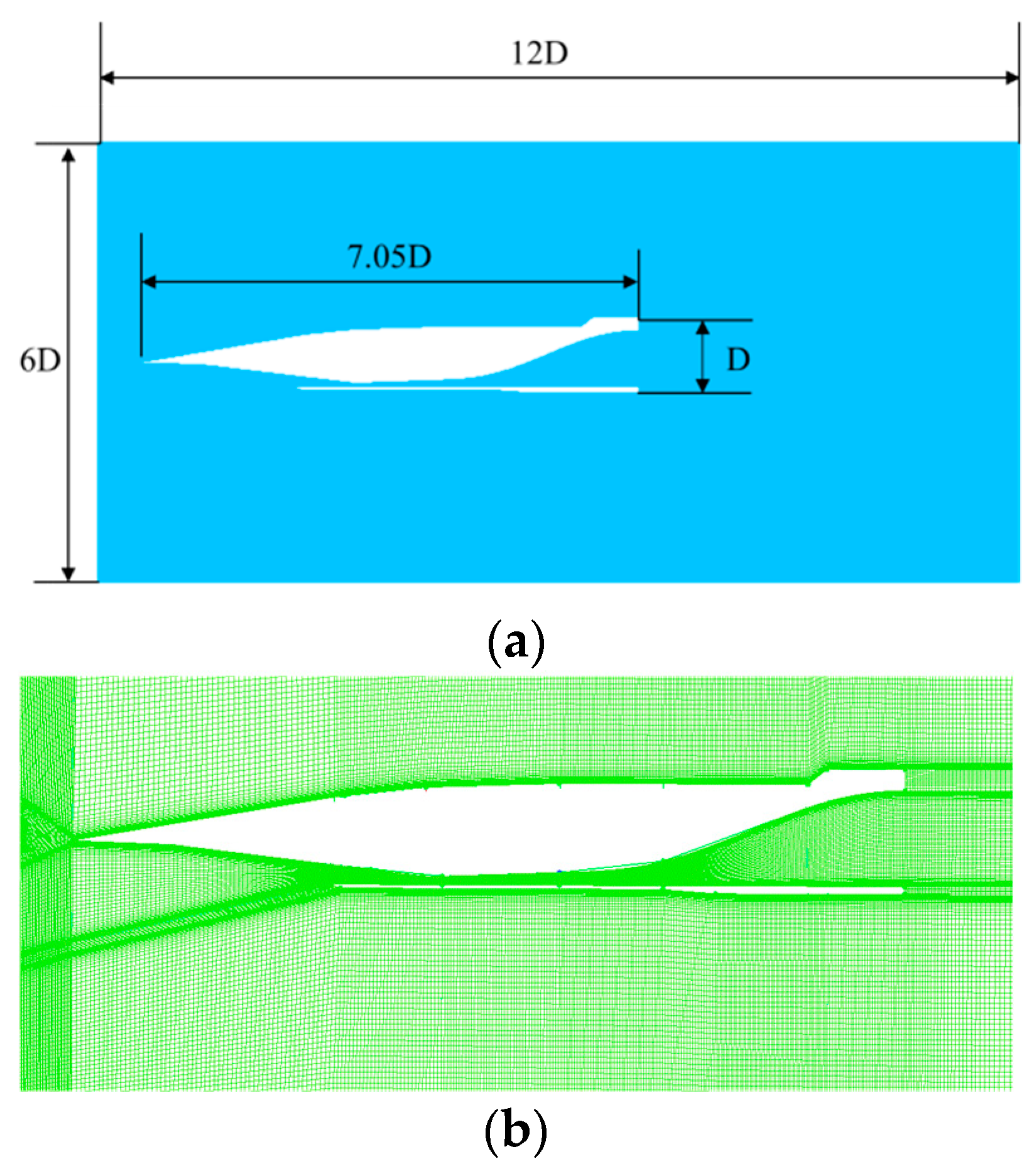
5.2. Grid Division
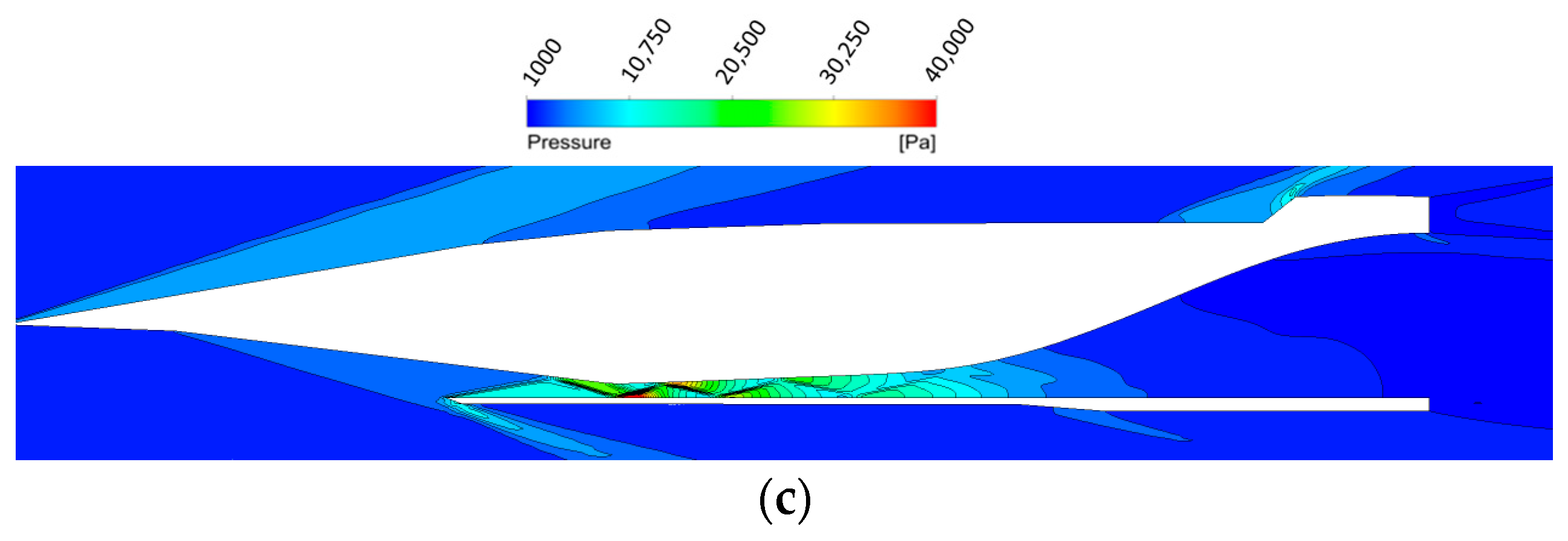
5.3. Validation of the CFD Method for Aerodynamic Heating
6. Numerical Calculation Method for Infrared Radiation
6.1. The Basic Equations for Infrared Radiation Calculation
- (1)
- Radiation-transfer equation expressed using the radiation radiance.
- (2)
- Radiation-irradiance equation on the detector surface.
- (3)
- Radiation-intensity equation of the target.
6.2. Solution Method
6.3. Validation of the IR Calculation Method
7. Results and Discussion
7.1. Flow-Field Distribution in the Combustion Chamber Based on the Quasi-One-Dimensional Calculation Method
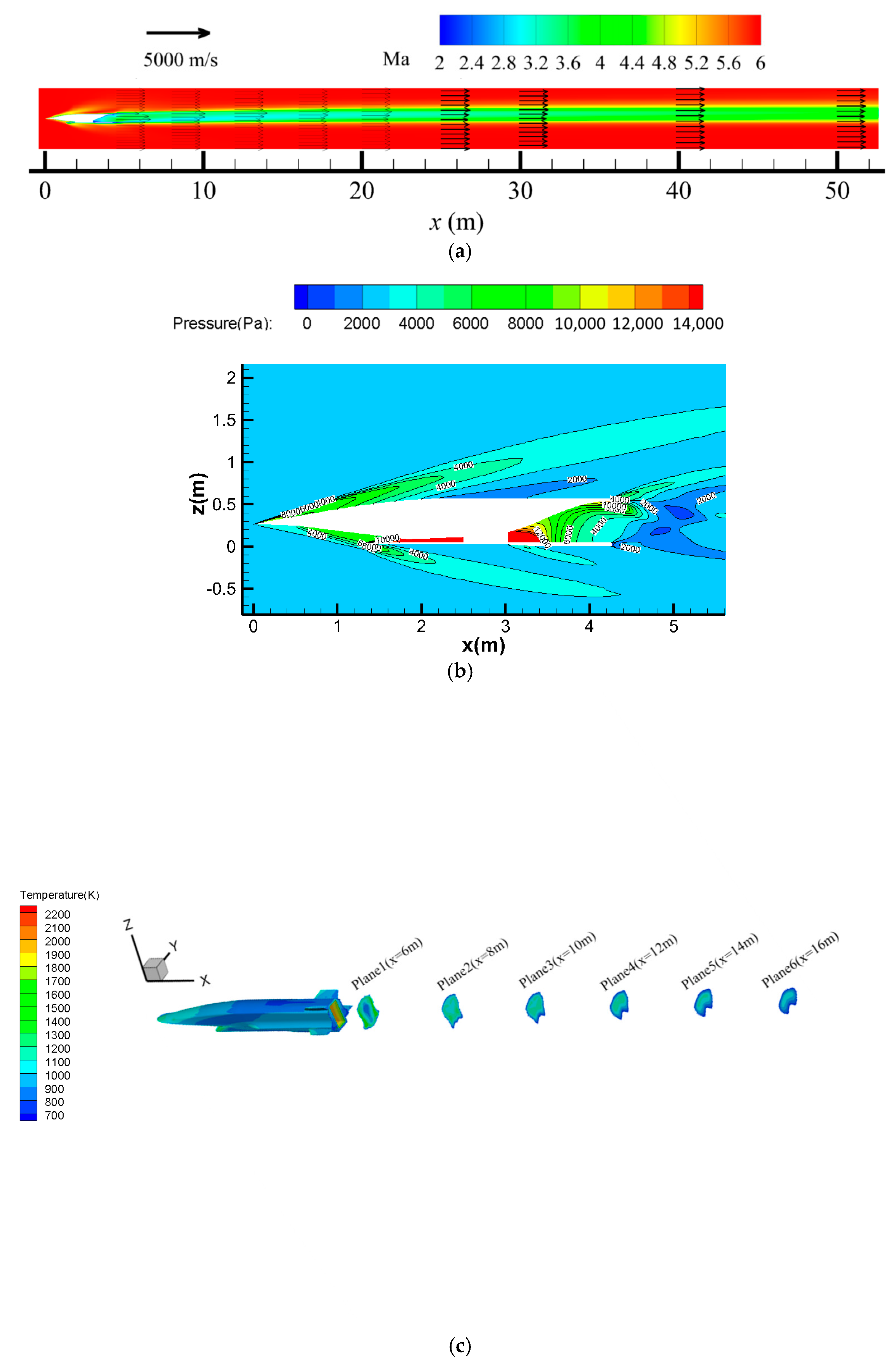
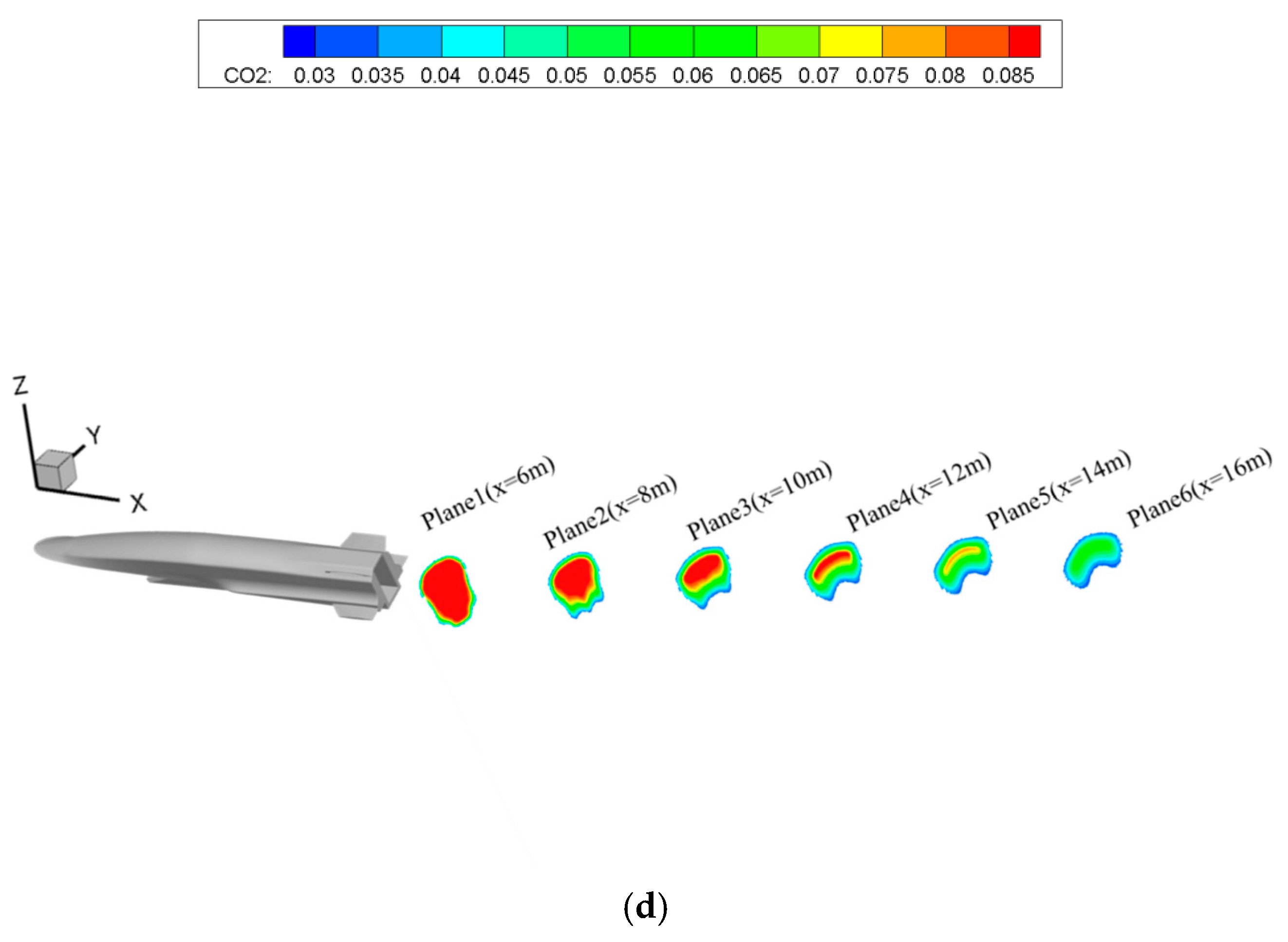
7.2. Three-Dimensional Flow-Field Distribution in the Air-Breathing Hypersonic Vehicle
7.3. The Integrated Radiation Intensity of the Air-Breathing Hypersonic Vehicle
8. Conclusions
- (1)
- Under the flight condition of Ma = 6, the gas temperature and wall heat flux of the scramjet combustion chamber first increased and then decreased along the flow direction. In the middle of the combustion chamber (x = 0.25 m), the wall heat flux of the gas was the largest. The Mach number of the gas decreased rapidly along the flow direction and then increased slowly, while the static-pressure distribution of the gas was opposite to the variation trend of the Mach number.
- (2)
- The Mach number of the plume of the scramjet-powered hypersonic vehicle was smaller than that of the free flow, which could be ascribed to the higher temperature of the plume. However, the velocity of the plume was marginally higher than that of the free flow. This observation suggests that the scramjet engine is capable of producing positive thrust under the flight condition of Mach 6. Under the flight condition of Ma = 6, the average wall temperature of the skin was 850 K, and the average wall temperature of the nozzle was 2102 K.
- (3)
- Under the flight condition of Ma = 6, with the increase in the azimuth angle, the integrated radiation intensity of the scramjet-powered hypersonic vehicle increased slowly at first before increasing rapidly and then decreasing gradually in the 1–3 μm band. In the 3–5 μm band, with the increase in azimuth angle, the integrated radiation intensity showed the characteristics of a pear-shaped distribution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blankson, I.M. Air-Breathing Hypersonic Cruise: Prospects for Mach 4–7 Waverider Aircraft. J. Eng. Gas Turbines Power 1994, 116, 104–115. [Google Scholar] [CrossRef]
- Tang, C.S. Research on integrated optimization design of hypersonic cruise vehicle. Aerosp. Sci. Technol. 2008, 12, 567–572. [Google Scholar]
- Jiang, Z.L.; Zhang, Z.J.; Liu, Y.F. Criteria for hypersonic airbreathing propulsion and its experimental verification. Chin. J. Aeronaut. 2021, 34, 94–104. [Google Scholar] [CrossRef]
- Wang, Y.H.; Wang, Q. Experiment of the thermo-radiation characteristic of infrared window of hypersonic vehicles. Infrared Laser Eng. 2015, 44, 1716–1720. [Google Scholar]
- Horvath, T.J.; Cagle, M.F. Remote observations of reentering spacecraft including the space shuttle orbiter. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–15. [Google Scholar]
- Schwartz, R.; Horvath, T.J.; Propp, T. Scientifically Calibrated In-Flight Imagery (SCIFLI) Mission Operations for the SpaceX CRS-4 Airborne Infrared Imaging. In Proceedings of the AIAA SPACE Astronautics Forum and Exposition, Orlando, FL, USA, 12–14 September 2017; p. 5209. [Google Scholar]
- Kennedy, K.; Walker, B. Tactical missile exhaust plume at angle of attack. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar]
- Mu, L.; Ma, Y.; He, Z.H.; Dong, S.K. Radiation characteristics simulation of non-equilibrium flow field around the hypersonic blunted cone. J. Eng. Thermophys. 2012, 33, 1958–1962. [Google Scholar]
- Levin, D.A.; Candler, G.V.; Limbaugh, C.C. Multispectral shock-layer radiance from a hypersonic slender body. J. Thermophys. Heat Transf. 2000, 14, 237–243. [Google Scholar] [CrossRef]
- Niu, Q.L.; Yuan, Z.C.; Chen, B.; Dong, S.K. Infrared radiation characteristics of a hypersonic vehicle under time-varying angles of attack. Chin. J. Aeronaut. 2019, 32, 861–874. [Google Scholar] [CrossRef]
- Niu, Q.L.; Yang, S.; He, Z.H.; Dong, S.K. Numerical study of infrared radiation characteristics of a boost-gliding aircraft with reaction control systems. Infrared Phys. Technol. 2018, 92, 417–428. [Google Scholar] [CrossRef]
- Niu, Q.L.; Yang, X.; Chen, B.; He, Z.H.; Dong, S.K. Infrared radiation characteristics and detectability analysis of point source based on high-speed sliding. Infrared Laser Eng. 2018, 47, 160–167. [Google Scholar]
- Yang, X.; Niu, Q.L.; He, Z.H.; Dong, S.K. Analysis of infrared radiation characteristics and detectability of HTV-2 like hypersonic gliding aircrafts. Acta Opt. Sin. 2017, 37, 45–54. [Google Scholar]
- Shen, W.B.; Huang, Y. Mixing and transient combustion processes of scramjet combustor with transverse injector and hypermixer. Case Stud. Therm. Eng. 2021, 26, 101104. [Google Scholar] [CrossRef]
- Gugulothu, S.K.; Nutakki, P.K. Dynamic fluid flow characteristics in the hydrogen-fuelled scramjet combustor with transverse fuel injection. Case Stud. Therm. Eng. 2019, 14, 100448. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chen, Q. Numerical evaluation of shock wave effects on turbulent mixing layers in a scramjet combustor. Case Stud. Therm. Eng. 2021, 25, 100893. [Google Scholar] [CrossRef]
- Kummitha, O.R.; Pandey, K.M.; Gupta, R. Cfd analysis of a scramjet combustor with cavity based flame holders. Acta Astronaut. 2018, 144, 244–253. [Google Scholar] [CrossRef]
- O’Brien, T.F.; Lewis, M.J.; Starkey, R.P. Quasi-one-dimensional high-speed engine model with finite-rate chemistry. J. Propuls. Power 2001, 17, 1366–1374. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Yang, Q.C.; Xu, X. One dimensional method for calculation of dual mode scramjet combustor core flow area. J. Propuls. Technol. 2018, 8, 1803–1809. [Google Scholar]
- Wang, L.; Xing, J.W.; Zheng, Z.H. One dimensional evaluation of the scramjet flow path performance. J. Propuls. Technol. 2008, 29, 641–645. [Google Scholar]
- Doolan, C.J.; Boyce, R.R. A Quasi-one-dimensional mixing and combustion code for trajectory optimisation and design studies. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar]
- Jiang, J.; Chu, M.; Xu, X. A Quasi-one-dimensional method for prediction of dual mode scramjet combustor performance. J. Propuls. Technol. 2013, 7, 803–808. [Google Scholar]
- Follen, G.; auBuchon, M. Numerical Zooming between a NPSS Engine System Simulation and a One-Dimensional High Compressor Analysis Code; NASA/TM-2000-209913; NASA: Washington, DC, USA, 2000. [Google Scholar]
- Lytle, J.K. The Numerical Propulsion System Simulation: An Overview; NASA TM-2000-209915; NASA: Washington, DC, USA, 2000. [Google Scholar]
- Micka, D.; Torrez, S.; Driscoll, J. Heat release distribution in a dual-mode scramjet combustor -measurements and modeling. In Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, 19–22 October 2009; pp. 1–19. [Google Scholar]
- Yuan, H.C.; Liang, D.W.; Guo, R.W. Predicting method for the performance of constant area isolator under back pressure. J. Aerosp. Power 2009, 11, 2421–2428. [Google Scholar]
- Zheng, L.M.; Sun, B. 2D thermal environment numerical simulation of scramjets. J. Aerosp. Power 2007, 22, 823–828. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer; Osborne McGraw-Hill: Sebastopol, CA, USA, 1973. [Google Scholar]
- Chilton, T.H.; Colburn, A.P. Mass transfer (absorption) coefficients: Prediction from data on heat transfer and fluid friction. Ind. Eng. Chem. 1934, 26, 1183–1187. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; Herbert, M.V. Heat transfer processes in gas-turbine combustion chambers. Proc. Inst. Mech. Eng. 1961, 175, 641–668. [Google Scholar] [CrossRef]
- Zhang, F.; Fan, X.; Yu, G. Heat transfer of aviation kerosene supercritical conditions. J. Thermophys. Heat Transf. 2009, 23, 543–550. [Google Scholar] [CrossRef]
- Nie, Y.; Le, G.G.; Ma, D.W. Numerical investigation on properties of angle of attack (AOA) for the X-51A Vehicle. In Proceedings of the 4th International Conference on Mechanical Engineering and Mechanics, Suzhou, China, 10–12 August 2011; pp. 540–544. [Google Scholar]
- Smart, M.K.; Hass, N.E.; Paull, A. Flight data analysis of the HyShot 2 scramjet flight experiment. AIAA J. 2006, 44, 2366–2375. [Google Scholar] [CrossRef]
- Wang, X.D.; Song, W.Y. Effects of fuel injection scheme on the mixing and combustion efficiency of a scramjet combustor. Chin. J. Aeronaut. 2004, 25, 556–559. [Google Scholar]
- Allan, R.W. Experiment study of shock wave interference heating on cylindrical leading edge at Mach 6 and 8. In Proceedings of the AIAA 22nd Thermophysics Conference, Honolulu, HI, USA, 8–10 June 1987. [Google Scholar]
- Yong, S.; Zhang, J.Z. Numerical investigation of flow mixture enhancement and infrared radiation shield by lobed forced mixer. Appl. Therm. Eng. 2009, 29, 3687–3695. [Google Scholar]
- Collins, D.G.; Blattner, W.G.; Wells, M.B. Backward Monte Carlo calculations of the polarization characteristics of the radiation emerging from spherical-shell atmospheres. Appled Opt. 1972, 11, 2684–2696. [Google Scholar] [CrossRef]
- Liu, J.; Ji, H.H. Investigation on infrared signature of axisymmetric vectoring exhaust system with infrared suppressions. J. Thermophys. Heat Transf. 2018, 32, 627–636. [Google Scholar] [CrossRef]




| Ma | Height (m) | Pressure (Pa) | Temperature (K) |
|---|---|---|---|
| 6 | 24,858 | 2607 | 221 |
| Inlet Mach Number | Inlet Static Temperature (K) | Inlet Static Pressure (Pa) | Outlet Static Pressure (Pa) |
|---|---|---|---|
| 3.35 | 593 | 19,689 | 25,435 |
| Flight Ma | Static Pressure of Isolator Outlet (Pa) | Total Temperature of Nozzle Inlet (K) | Static Pressure of Nozzle Inlet (Pa) | Mach Number of Nozzle Inlet |
|---|---|---|---|---|
| 6 | 19,689 | 2818 | 33,502 | 1.92 |
| Component | Pressure Drag (N) | Viscous Drag (N) | Net Drag (N) |
|---|---|---|---|
| skin | 1030 | 565 | 1595 |
| fin | 276 | 59 | 335 |
| isolator | −114 | 138 | 24 |
| forebody | 154 | 84 | 238 |
| combustor | −123 | 59 | -64 |
| inlet | 133 | 114 | 247 |
| nozzle | −670 | 225 | -445 |
| total drag | 1930 | ||
| total trust | 2003 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Shi, X.; Ji, H.; Hu, J. Research on the Zooming Method for Determining the Flow, Heat Transfer, and Infrared Radiation of an Air-Breathing Hypersonic Vehicle Powered by a Scramjet. Aerospace 2024, 11, 212. https://doi.org/10.3390/aerospace11030212
Wei X, Shi X, Ji H, Hu J. Research on the Zooming Method for Determining the Flow, Heat Transfer, and Infrared Radiation of an Air-Breathing Hypersonic Vehicle Powered by a Scramjet. Aerospace. 2024; 11(3):212. https://doi.org/10.3390/aerospace11030212
Chicago/Turabian StyleWei, Xin, Xiaojuan Shi, Honghu Ji, and Jinlong Hu. 2024. "Research on the Zooming Method for Determining the Flow, Heat Transfer, and Infrared Radiation of an Air-Breathing Hypersonic Vehicle Powered by a Scramjet" Aerospace 11, no. 3: 212. https://doi.org/10.3390/aerospace11030212
APA StyleWei, X., Shi, X., Ji, H., & Hu, J. (2024). Research on the Zooming Method for Determining the Flow, Heat Transfer, and Infrared Radiation of an Air-Breathing Hypersonic Vehicle Powered by a Scramjet. Aerospace, 11(3), 212. https://doi.org/10.3390/aerospace11030212






