Rivet Structural Design and Process Optimization for the Double-Sided Countersunk Riveting of Composite Wedge Structures

Abstract

Within the double-sided countersunk riveting process of aircraft wings with a composite wedge structure, riveting consistency is poor, and composite damage is severe, which seriously affects the performance and reliability of the aircraft structure. This paper used the principal stress method to establish a stress model of countersunk riveting, and, based on the analysis of the stress on the structure during the pressure-riveting process, a composite structure rivet was designed. A finite element simulation model of the double-sided countersunk riveting of composite wedge structures’ composite rivets was established. The influences of the structure and the matching parameters of composite rivets on both the plastic flow of pressure riveting and the compressive stress of the structure during the pressure-riveting process were analyzed. The structural parameters and riveting process of composite rivets were optimized. The results show that the composite rivet structure could significantly reduce the contact-compressive stress at the riveting joint by more than 20%, thereby reducing the damage caused by the riveting to the composite material. For 4 mm rivets, an aperture of 4.04~4.06 mm can achieve precise relative interference riveting at 0.6% to 1.0%. Employing a 2.6 mm rivet elongation can exactly fill the countersunk hole of the wedge.

1. Introduction

In the aerospace manufacturing industry, composite materials such as carbon fiber-reinforced polymers (CFRPs) have rapidly been applied to the main load-bearing structures of aerospace products due to their excellent strength, toughness, and fatigue resistance. The corresponding structural component connections are crucial in aircraft assembly, with rivets being the most widely used mechanical connection due to their light weight, high strength, and excellent fit, and this connection’s workload has reached more than 20 percent of the entire aircraft assembly manufacturing industry [1]. However, these mechanical joints inevitably come with disadvantages associated with the presence of connection holes, such as stress concentration around the fastening holes during riveting as well as the resulting composite material damage, such as microcracks and delamination, which pose significant risks to the aircraft structure and to flight safety. On the other hand, the current demands for aircraft performance continue to increase, requiring consideration of structural smoothness and aerodynamics. Many structures adopt wedge-shaped, double-buried riveting [2]. Compared to flat and protruding riveting forms, the deformation mechanism of inclined-buried riveting is more complex, and there has been less corresponding research. During the riveting process, the composite skin is vulnerable to impact damage, the shape of the pier head is irregular, and the rivet rod is inclined [3]. These issues have negative impacts on the strength of the riveted connection. Thus, it is crucial to develop methods to suppress the damage caused by riveting to composite material structures and to enhance the quality of riveted connections. This has become an urgent problem in the current design of aviation assembly technology.

In recent years, scholars, both domestically and internationally, have conducted extensive research on improving riveting quality and damage control. Research by Cheng Hui [4] and others has shown that effectively suppressing material failures and delamination damage and enhancing the assembly quality of aerospace composite structures relies on achieving precise interference fit connections. Li Wen Chao [5] has established an interference fit riveting model for flat conical head rivets, simulating the dynamic riveting process with interference fit for individual rivets. By analyzing the influence of interference fit on the strength of riveted joints, reasonable process parameters are obtained for interference fit rivet holes. Ziqian An [6] studied the effect of bushing on joint fatigue performance, establishing models for rivet specimens with and without bushing under the same interference fit. Comparative analyses indicate that bushing can improve the stress distribution at hole edges, reduce wear between the rivet shank and the hole wall during assembly and loading, and enhance the load-bearing efficiency of laminate panel rivet holes. Siwei Tao [7] investigated the influence of rivet bushing on fatigue life, and demonstrated its beneficial effect on the fatigue life of structures. Seung Jo Kim [8] and others have simulated the entire riveting process of countersunk riveting lap joints, studying the effects of void and washer dimensions in composite overlap. Numerical simulations have demonstrated that damage-controlling riveting techniques for composite laminate panels can be developed by utilizing the gaps between the shaft and the hole wall and selecting suitable washer dimensions. Cheraghi [9] studied the effects of dimensional parameter changes on the quality of riveted joints during the riveting process. It has been proven that the incorrect selection of, or changes in, parameters such as rivet protrusion and hole diameter can lead to excessive stress concentration, crack initiation, and the inappropriate deformation of rivet heads, directly affecting the quality of riveting.

In the above research, the plastic deformation process of pressure riveting, the influence of different process parameters on riveting quality, and the effects of additional rivet structures on the damage control of composite materials are described and discussed. However, the relevant research results have certain limitations for adaptation, as they mainly concentrate on the plane riveting and convex form of the pier head. On the other hand, the rivet structure-improvement process is combined with parameter optimization, while the overall average interference amount and the interference–uniformity index of riveted joints are considered, and research on the stress, deformation principle, and hole–wall action mechanism in the riveting process is relatively scarce [10]. In general, research into damage control within composite materials in connection assembly systems is still in its infancy.

Given the above research, this paper establishes a force model of the pressure-riveting deformation of a buried head, and a new type of structural connector has been designed based on the analysis of the effects of stress on the structure during the pressure-riveting process. Then, the ultra-high-strength aluminum alloy 7075, with high strength and hardness, good wear resistance, and corrosion resistance, was selected as the new material for the rivet, and the solid solution treatment was used to increase the plasticity while ensuring the connection strength. After that, the multi-objective matching optimization design was developed by combining the rivet material–structure–process parameters. At the same time, the precision and uniformity indexes of the interference amount after riveting were introduced to analyze the internal quality of the riveting. Based on the actual working conditions, a precision process parameter standard suitable for the double-sided buried head riveting of the composite wedge structure was explored, which is a breakthrough in the field of improving riveting quality.

2. Structural Design and Optimization

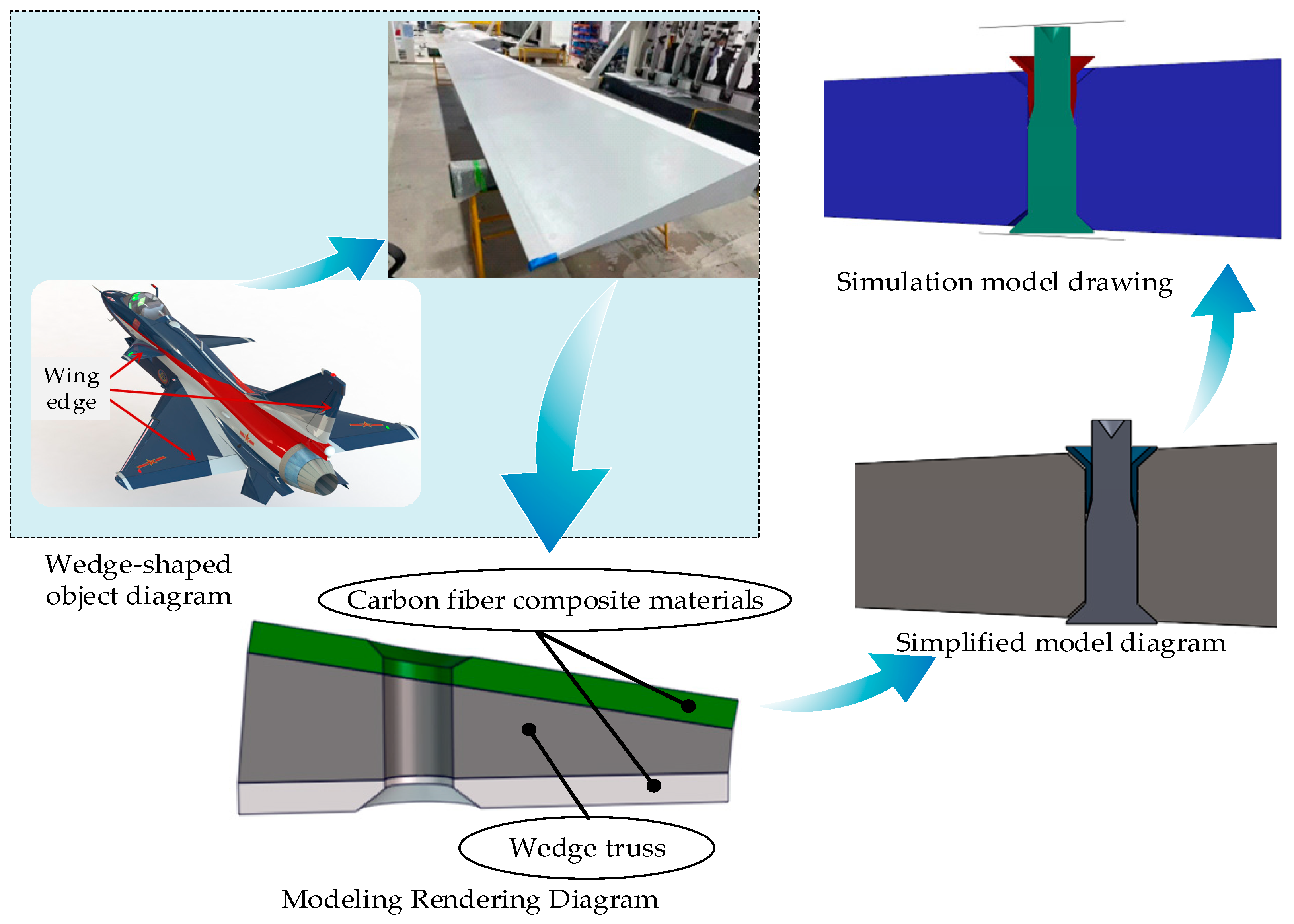
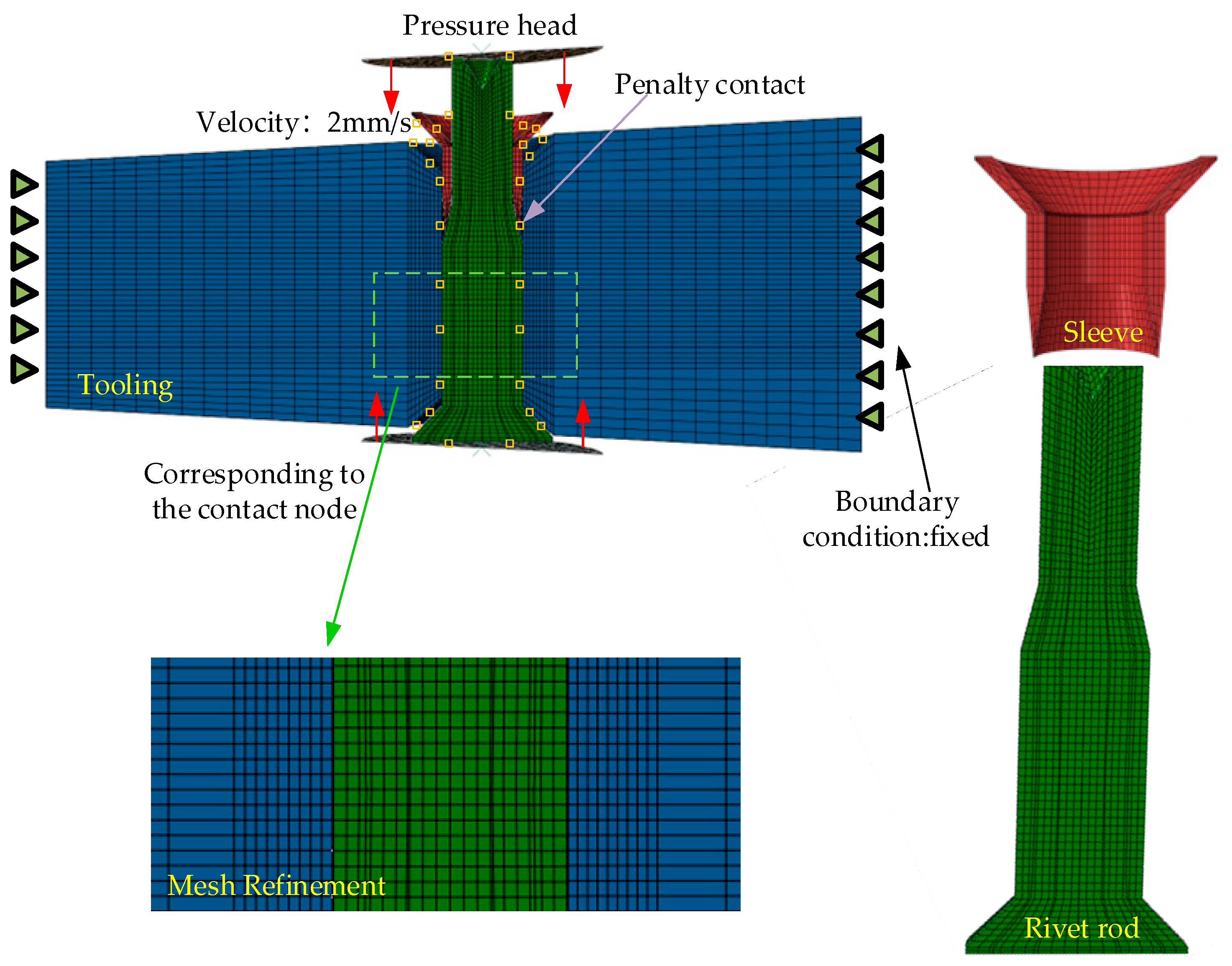
2.1. Analysis of Plastic Forming of Countersunk Pressure Riveting

After summarizing the above issues and the current state of research, this paper proposes a composite rivet with a sleeve and rivet rod matching connection, further optimizing its parameters. To more appropriately analyze the plastic flow of the material during the riveting process and to optimize the structure, in this paper, through metal plastic forming, material mechanics, and other mechanical theories, the principal stress method was used to combine the stress balance equation and the plastic condition to analyze the riveting-deformation process and the force mechanism. Because the angle of the wedge is tiny, it can be ignored in the force analysis; therefore, the following deformation mechanism analysis was undertaken according to the plane [11].

In the process of pressure riveting, the rivet is gradually upset and filled with a countersunk hole by the extrusion of the indenter. Locating the rivet rod in the hole of the wedge belongs to the upsetting method of closed constraint. After filling the gap, the rivet hole begins to be squeezed, so the radial displacement of the inner wall of the rivet hole is induced, and the interference fit is formed. The rivet of the extended part of the wedge is not subject to any constraints, so its deformation process is very similar to free upsetting [12]. It can be seen that these two parts of the rivet rod have specific differences in their modes of deformation and upsetting, so the plastic flow–deformation process of riveting was analyzed separately.

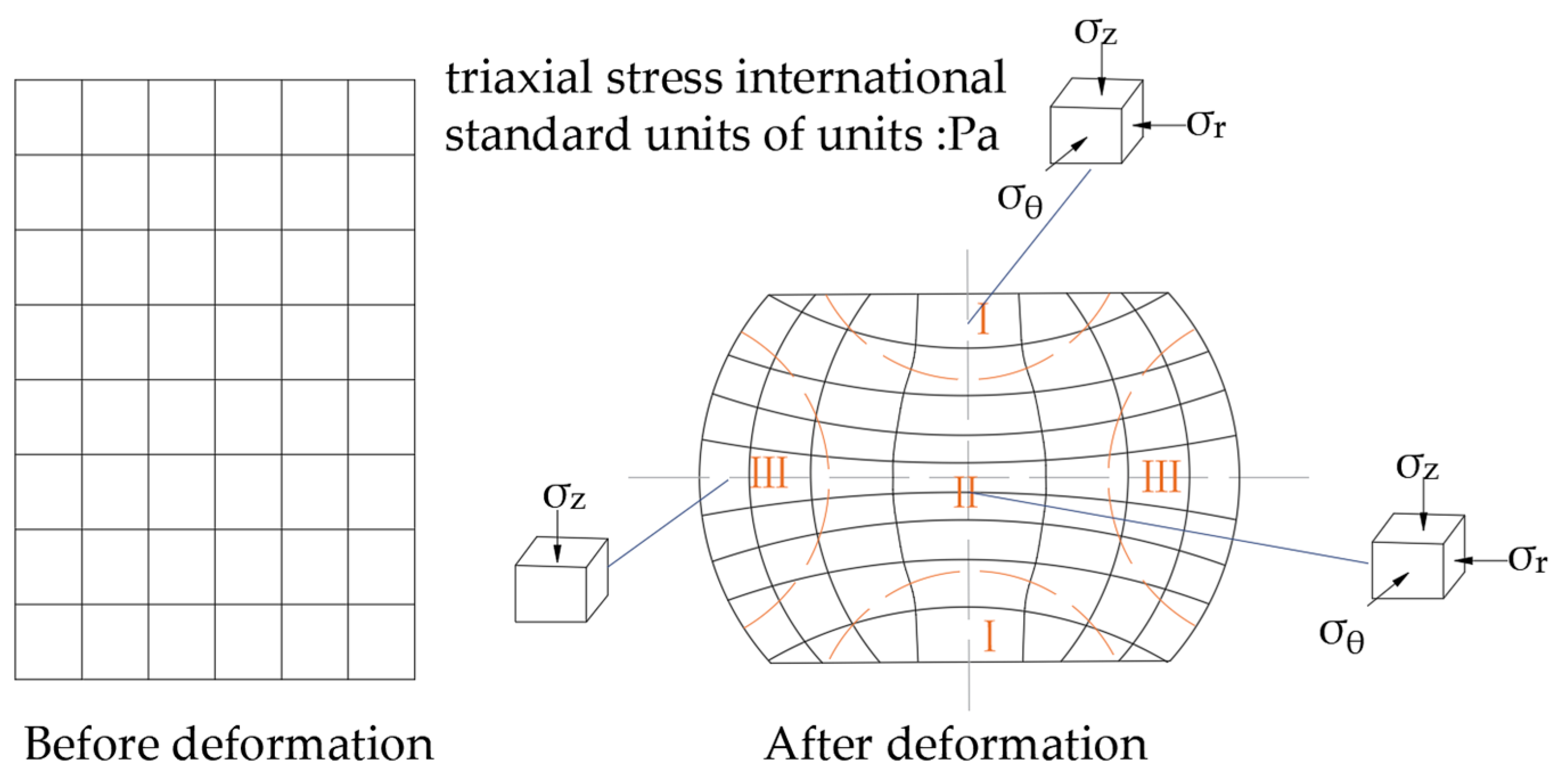
First, upsetting is an unstable plastic flow process applied to the metal material of a rivet elongation part, and the internal deformation is relatively complex. To facilitate the analysis, the deformation area is roughly divided into three regions according to the deformation situation, as shown in Figure 1: The metal material in deformation area I is subjected to three-dimensional compressive stress, and the deformation is difficult, causing stagnant deformation area. Area II is far away from the surface, and the frictional resistance of this part is small, so the compressive stress in the horizontal direction is also tiny, and the unit body mainly produces compression deformation under the action of axial force. Under this action, the radial direction undergoes a significant expansion, and this contributes to the large deformation area. The combined effect of this deformation leads to the overall drum shape; the outer side of deformation zone III is not constrained and is less affected by the end face. The stress state is similar to axial unidirectional compression ${\sigma }_z$. However, due to the large deformation of zone II, the internal metal places radial compressive stress on zone III when it flows outward, so that the metal element in this area is subjected to tangential tensile stress. The closer to the outer surface of the cylinder, the greater the tangential tensile stress.

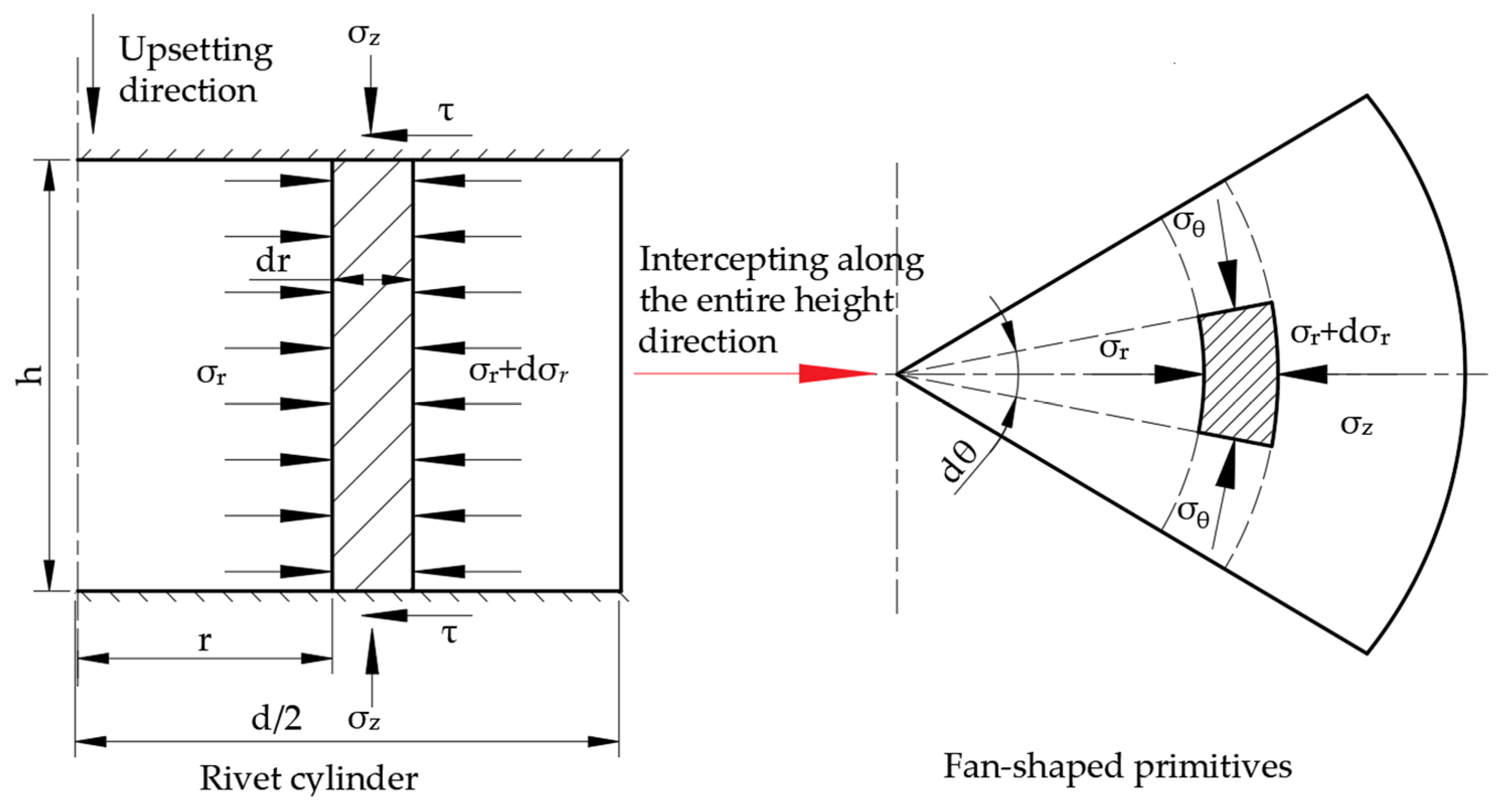
For double-sided pressure riveting, the metal material begins to contact the countersunk element in a large area after free upsetting, and the pier head gradually becomes conical. The riveting process at this time is equivalent to the filling of the forging part with conical die holes to form a boss. This problem is often calculated by the axisymmetric analysis of extrusion deformation force, as shown in Figure 2. The stress analysis is carried out by taking the element block along the metal flow direction.

The column element body force balance equation, omitting the high-order micro, is as follows:

$$2{\sigma }_{z}r\tan \alpha \mathrm{d}z-2\tau r\mathrm{d}z-r^2\mathrm{d}{\sigma }_z-2r{\sigma }_{\theta }\tan \alpha \mathrm{d}z=0$$

(1)

It is known from the horizontal static equilibrium relationship that

$${\sigma }_{\theta }={\sigma }_r+\tau \tan \alpha$$

(2)

When the countersunk hole is riveted, both ${\sigma }_r$ and ${\sigma }_z$ show compressive stress, and the extrusion ${\sigma }_r$ on both sides is more significant than ${\sigma }_z$, so the simplified plastic condition is:

$${\sigma }_r-{\sigma }_z={\sigma }_{\mathrm{s}}$$

(3)

The formulas are combined as:

$$\mathrm{d}{\sigma }_z=-\frac{2[\tau (1+{\tan }^2\alpha )+{\sigma }_{\mathrm{s}}\tan \alpha ]}{r}\mathrm{d}z$$

(4)

From the geometric relationship in Figure 2, we know that

$$r=r_b-z\tan \alpha$$

(5)

We can substitute this into Equation (4) and integrate it to obtain:

$${\sigma }_z=K_1\ln (r_b-z\tan \alpha )+C$$

(6)

where $K_1=\frac{2[\tau (1+{\tan }^2\alpha )+{\sigma }_s\tan \alpha ]}{\tan \alpha }$.

From the boundary condition $z=z_e$, ${\sigma }_z=0$, the obtained integral constant is: $C=-K_1\ln (r_b-z_e\tan \alpha )$ We can substitute this into the above formula to derive:

$${\sigma }_z=K_1\ln \frac{(r_b-z\tan \alpha )}{(r_b-z_e\tan \alpha )}$$

(7)

When $z=0$, ${\sigma }_z$ is the unit pressure when the upsetting of the rivet occurs at the $z_e$ point:

$$p=K_1\ln \frac{r_b}{(r_b-z_e\tan \alpha )}$$

(8)

$$F=p\pi r_b^2=\pi r_b^2{K}_1\ln \frac{r_b}{(r_b-z_e\tan \alpha )}$$

(9)

The principal stress method is used to infer the deformation force and stress distribution of the rivet rod inside the hole wall. We set the cylindrical coordinate system $\left(r,\theta ,z\right)$, and let the coordinate origin be at the center of the rivet rod. The Z-axis coincides with the axis of the rivet rod. The riveting problem is simplified into an axisymmetric problem. A fan-shaped unit body with a thickness of $dr$ and a central angle of $d\theta$ is intercepted at r from the center of the rivet hole along the height direction of the rivet, as shown in the shadow area in Figure 3. The analysis of the force of this part of the unit uses the principle of metal plastic deformation mechanics.

The radial compressive stress ${\sigma }_r$ and $d{\sigma }_r$, as well as the tangential compressive stress ${\sigma }_{\theta }$, are distributed along the horizontal direction of the element. In the process of riveting, ${\sigma }_z$ and ${\sigma }_r$ are the principal stresses. The two are assumed to be the principal stresses, and the frictional shear stress on the contact surface is supposed to be $\tau$. The stress of the element is projected horizontally, and the force balance equation is:

$${\sigma }_{\mathrm{r}}\mathrm{rd}\theta \mathrm{h}+2{\sigma }_{\theta }\sin \frac{\mathrm{d}\theta }{2}\mathrm{hdr}-2\tau \mathrm{rd}\theta \mathrm{dr}-({\sigma }_{\mathrm{r}}+\mathrm{d}{\sigma }_{\mathrm{r}})(\mathrm{r}+\mathrm{dr})\mathrm{hd}\theta$$

(10)

where $d\theta$ is a trace. We can apply a mathematical limit theory to infer that

$$\sin \frac{\mathrm{d}\theta }{2}\approx \mathrm{d}\theta$$

(11)

Substituting Equation (11) into Equation (10) and omitting the second-order higher-order term, we obtain:

$${\sigma }_{\theta }\mathrm{hdr}-\mathrm{rhd}{\sigma }_{\mathrm{r}}-{\sigma }_{\mathrm{r}}\mathrm{hdr}-2\tau \mathrm{rdr}=0$$

(12)

In the upsetting deformation of the rivet, there is ${\sigma }_{\theta }={\sigma }_r$. We substitute this into the above formula to obtain:

$$\mathrm{d}{\sigma }_{\mathrm{r}}=-\frac{2\tau }{\mathrm{h}}\mathrm{dr}$$

(13)

By introducing the plastic condition and ignoring the influence of friction shear stress on the yield criterion, the Mises yield criterion ${\sigma }_z-{\sigma }_r={\sigma }_s$ (${\sigma }_s$ is the yield stress of the material).

After the differential $d{\sigma }_z=\mathrm{d}{\sigma }_r$ is obtained, we can bring it into Equation (13) to get:

$$\mathrm{d}{\sigma }_z=-\frac{2\tau }{\mathrm{h}}\mathrm{dr}$$

(14)

Due to the flow of the metal unit, there is friction, and the Coulomb friction condition is introduced, where $\tau =\mu {\sigma }_z$. We then bring this into Equation (14) to get:

$$\frac{d{\sigma }_z}{{\sigma }_z}=-\frac{2\mu }{h}dr$$

(15)

Integrate Equation (15) to get:

$${\sigma }_z=C{e}^{-\frac{2\mu }{h}r}$$

(16)

By analyzing the upsetting process, we can easily infer that in the initial upsetting stage of the rivet rod, due to the gap between the rivet holes, the boundary of the rivet rod is not constrained. At this time, when $r=d/2$, ${\sigma }_r=0$, and so ${\sigma }_z={\sigma }_s$ can be inferred from the yield criterion, and the integral constant is obtained as $c={\sigma }_s{e}^{\mu d/h}$.

So, the principal stress is obtained:

$${\sigma }_z={\sigma }_s{e}^{\frac{\mu }{h}(d-2r)}$$

(17)

$${\sigma }_r={\sigma }_z-{\sigma }_s={\sigma }_s{e}^{\frac{\mu }{h}(d-2r)}-{\sigma }_s$$

(18)

The unit flow pressure in rivet deformation is

$$p=\frac{F}{A}=\frac{\iint {\sigma }_z\mathrm{d}A}{A}=\frac{4}{\pi d^2}{\int }_0^{\frac{d}{2}}{\sigma }_z\mathrm{d}A=\frac{4}{\pi d^2}{\int }_0^{\frac{d}{2}}{\sigma }_s{\mathrm{e}}^{\frac{2\mu }{h}\left(\frac{d}{2}-r\right)}2\pi r\mathrm{d}r=\frac{2h^2}{\mu d^2}{\sigma }_s[{\mathrm{e}}^{\frac{\mu d}{h}}-1)-\frac{\mu d}{h}]$$

(19)

where $A$ is the cross-sectional area of the rivet rod, $A=\pi d^2/4$.

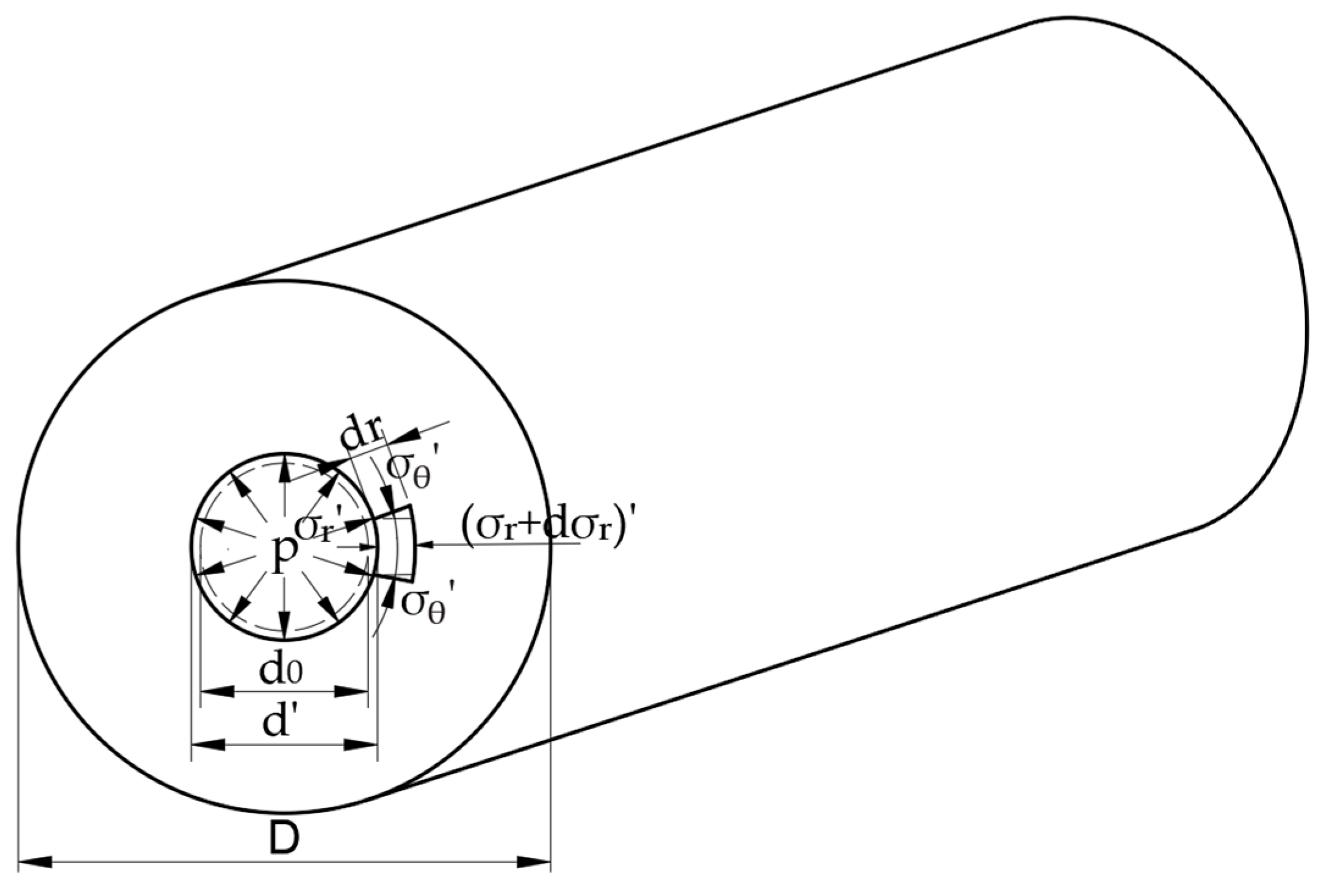
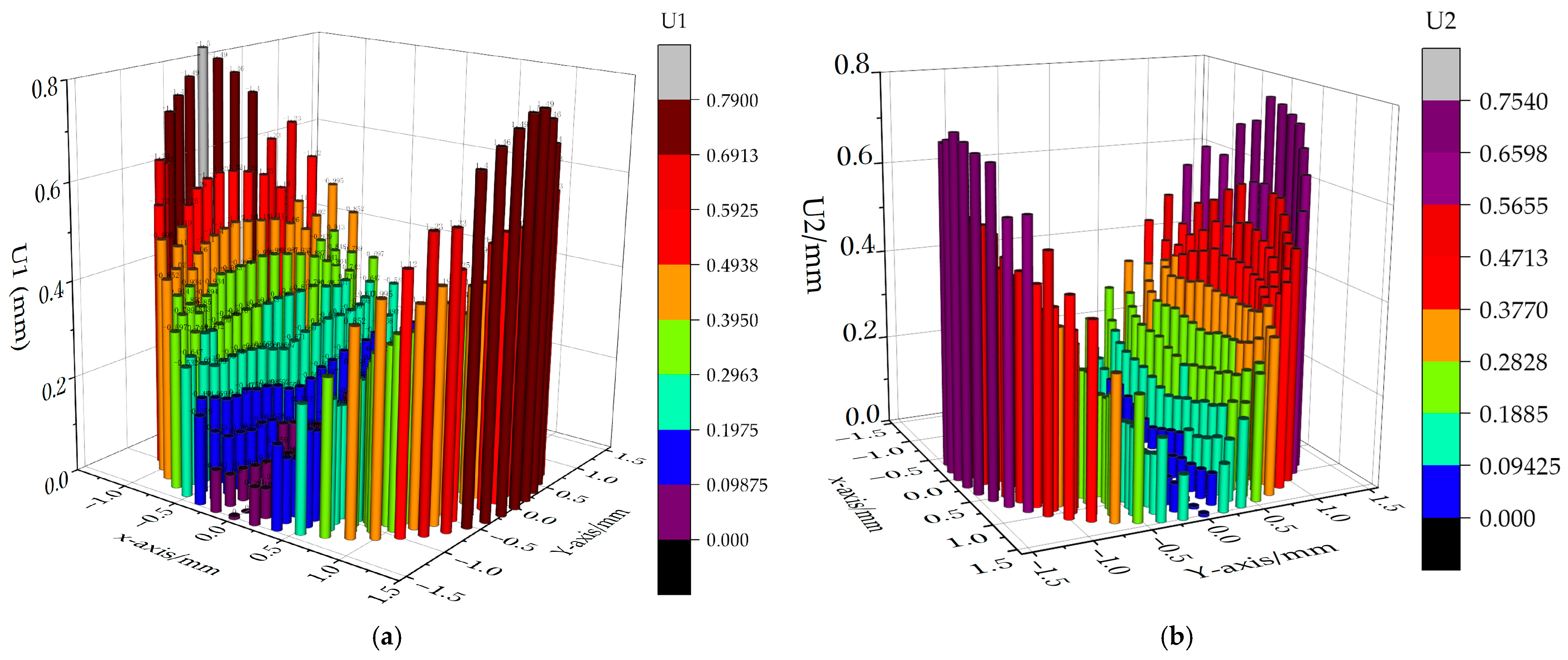
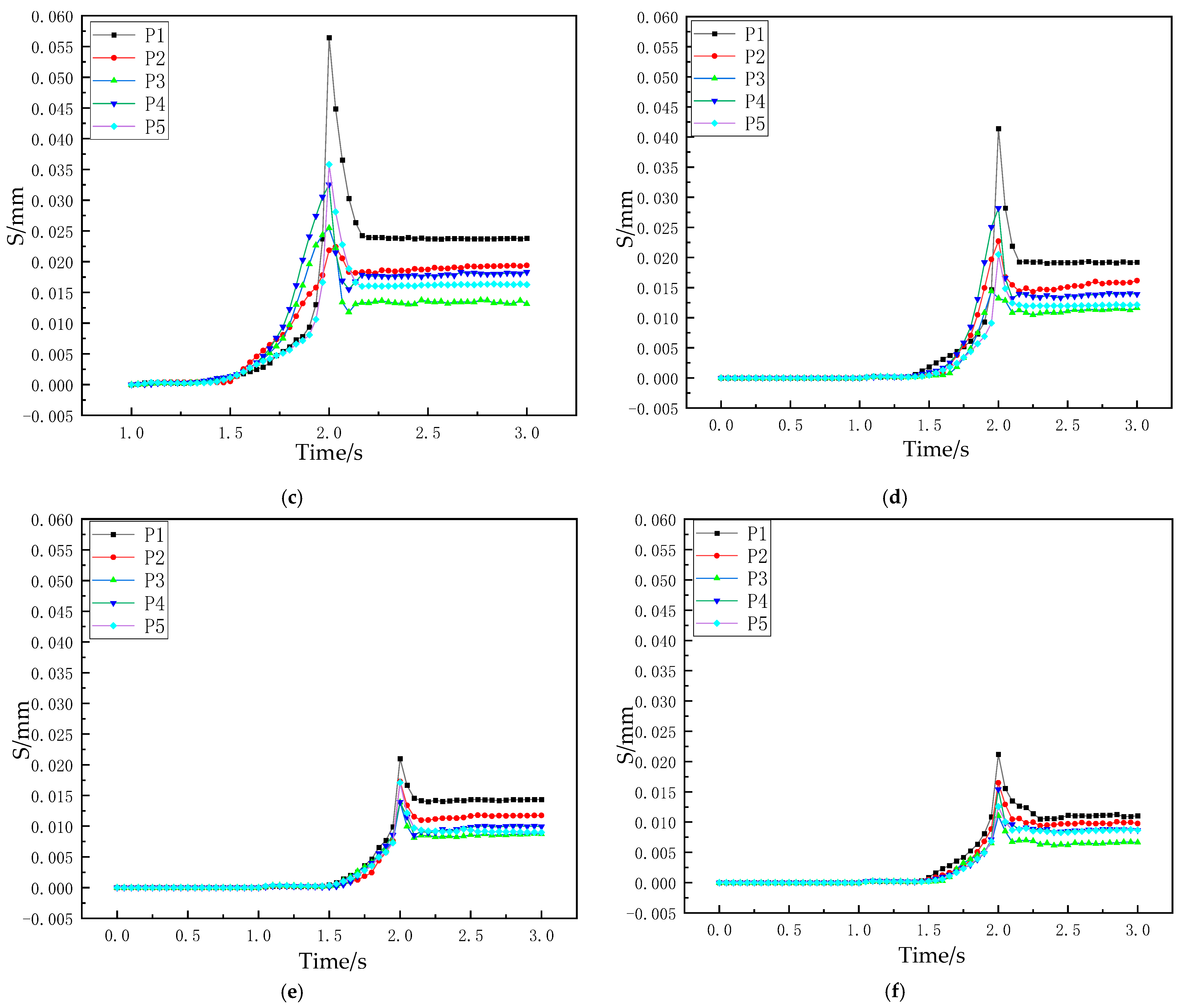
When the rivet is upset and comes into contact with the hole wall, the hole wall will be squeezed as the upsetting is continued, so internal pressure will be generated in the hole to form an interference fit, resulting in residual stress. After the riveting is completed, the edge element of the hole wall is taken as the research object, as shown in Figure 4. At this time, the magnitude of the interference $∆=d^{\prime }-d_0$.

Then, $r=d^{\prime }/2$ is brought into Equation (19), and the stress in the hole wall at the contact surface between the rivet rod and the rivet hole can be obtained as:

$${{\sigma }_r}^{\prime }={\sigma }_s{e}^{\frac{\mu }{h}(d^{\prime }-d_0)}-{\sigma }_s={\sigma }_s{e}^{\frac{\mu }{h}\Delta }-{\sigma }_s$$

(20)

where $d_0$ is the initial aperture of the hole wall and $d^{\prime }$ is the final hole diameter of the hole wall after riveting.

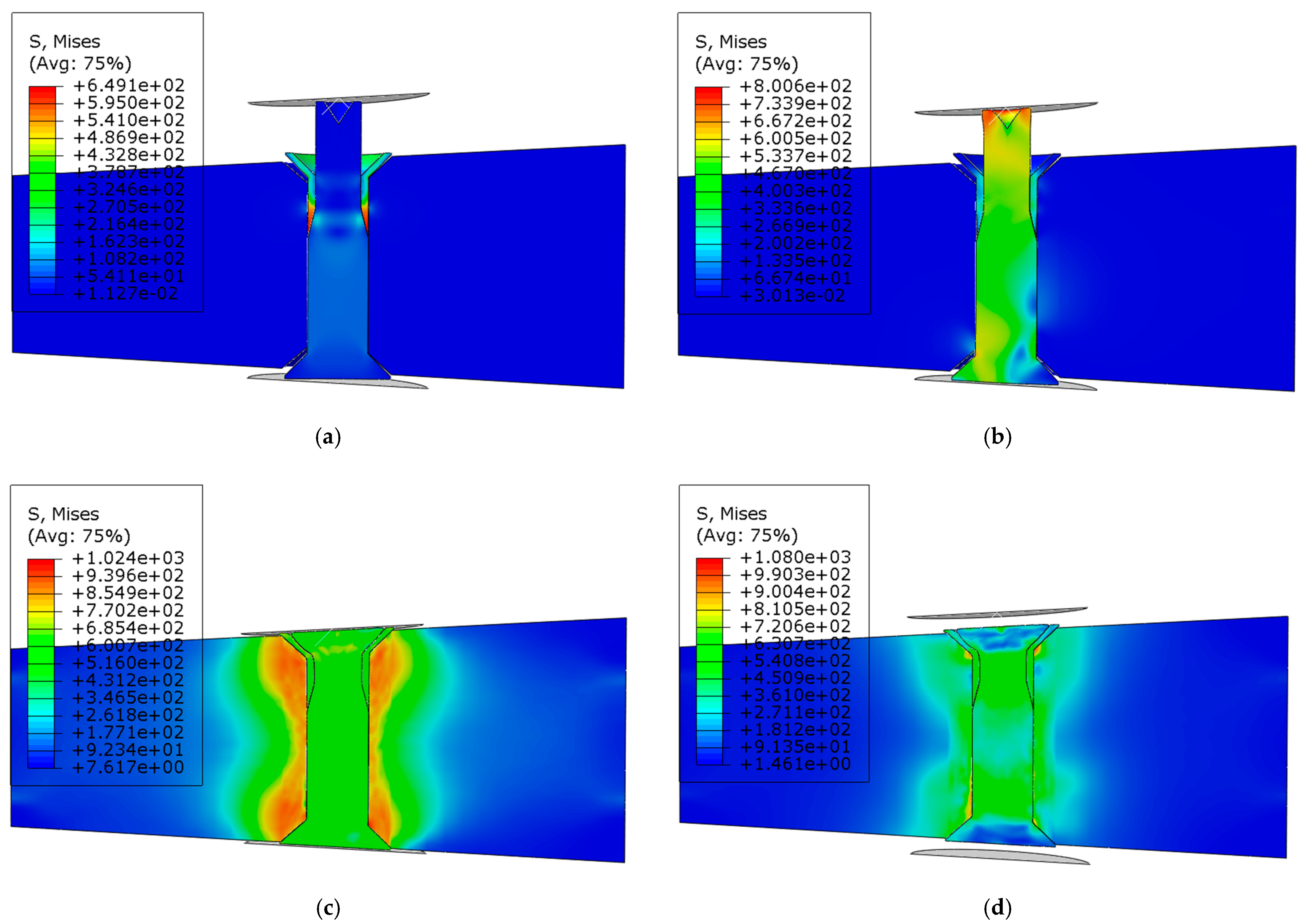
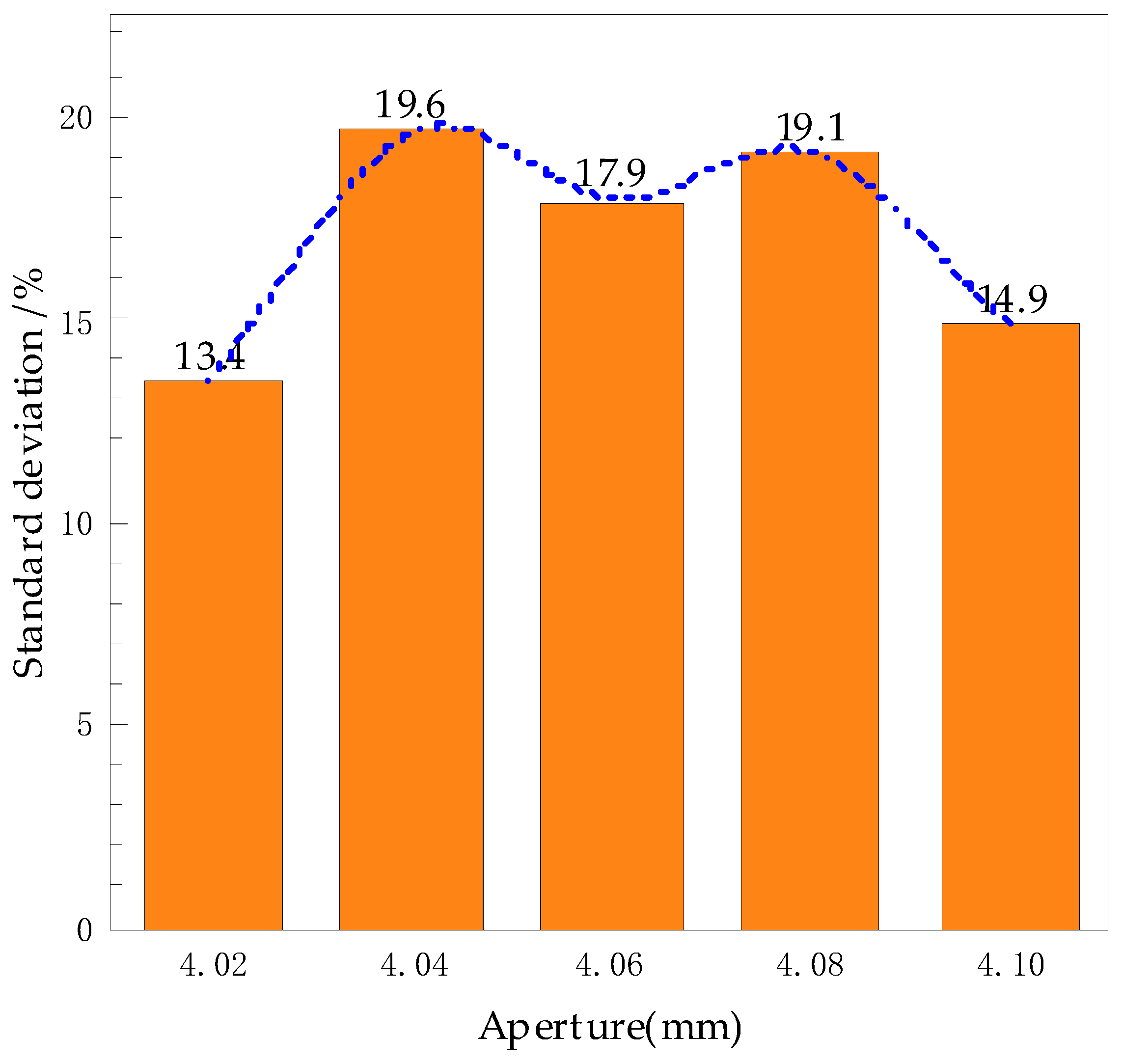
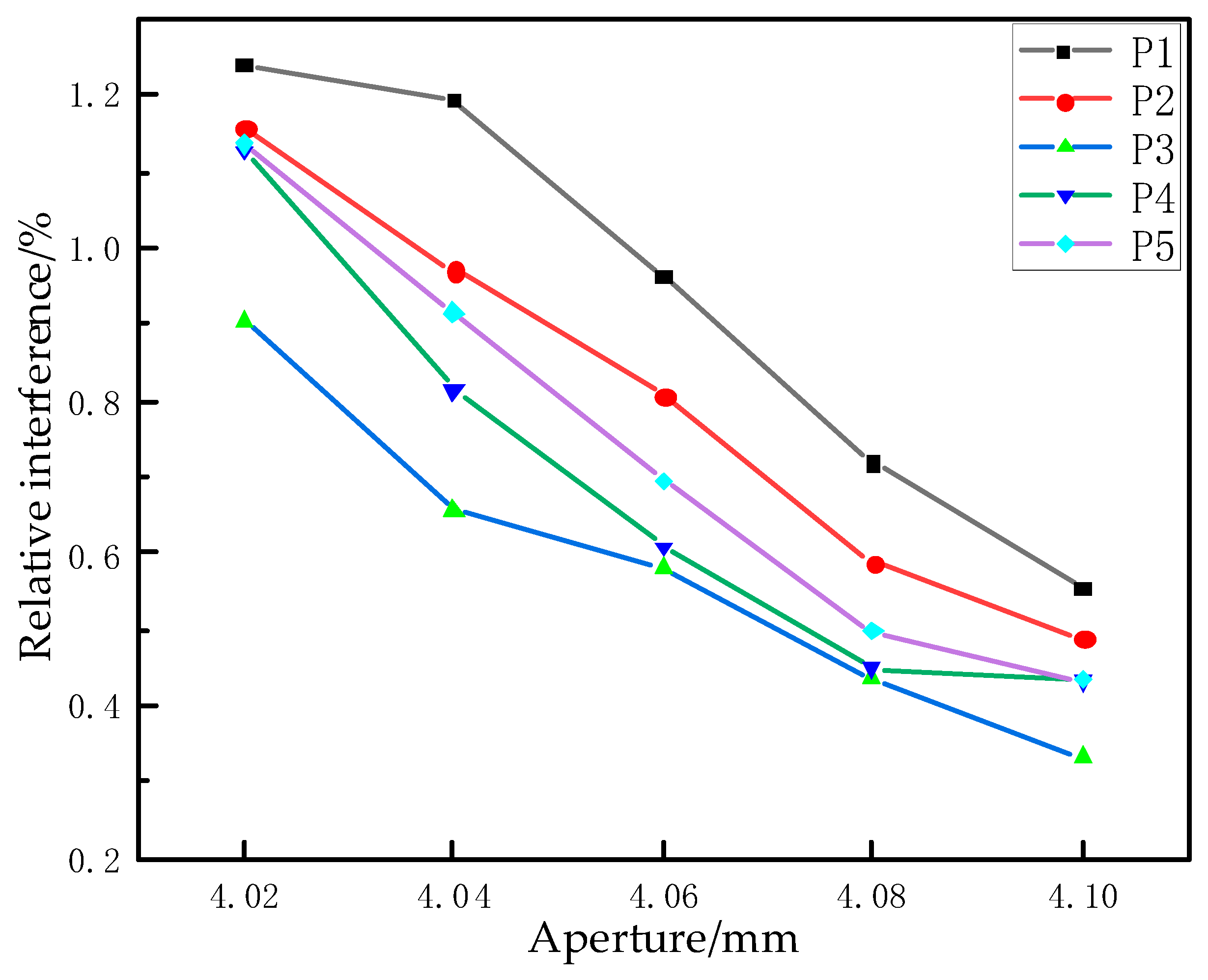
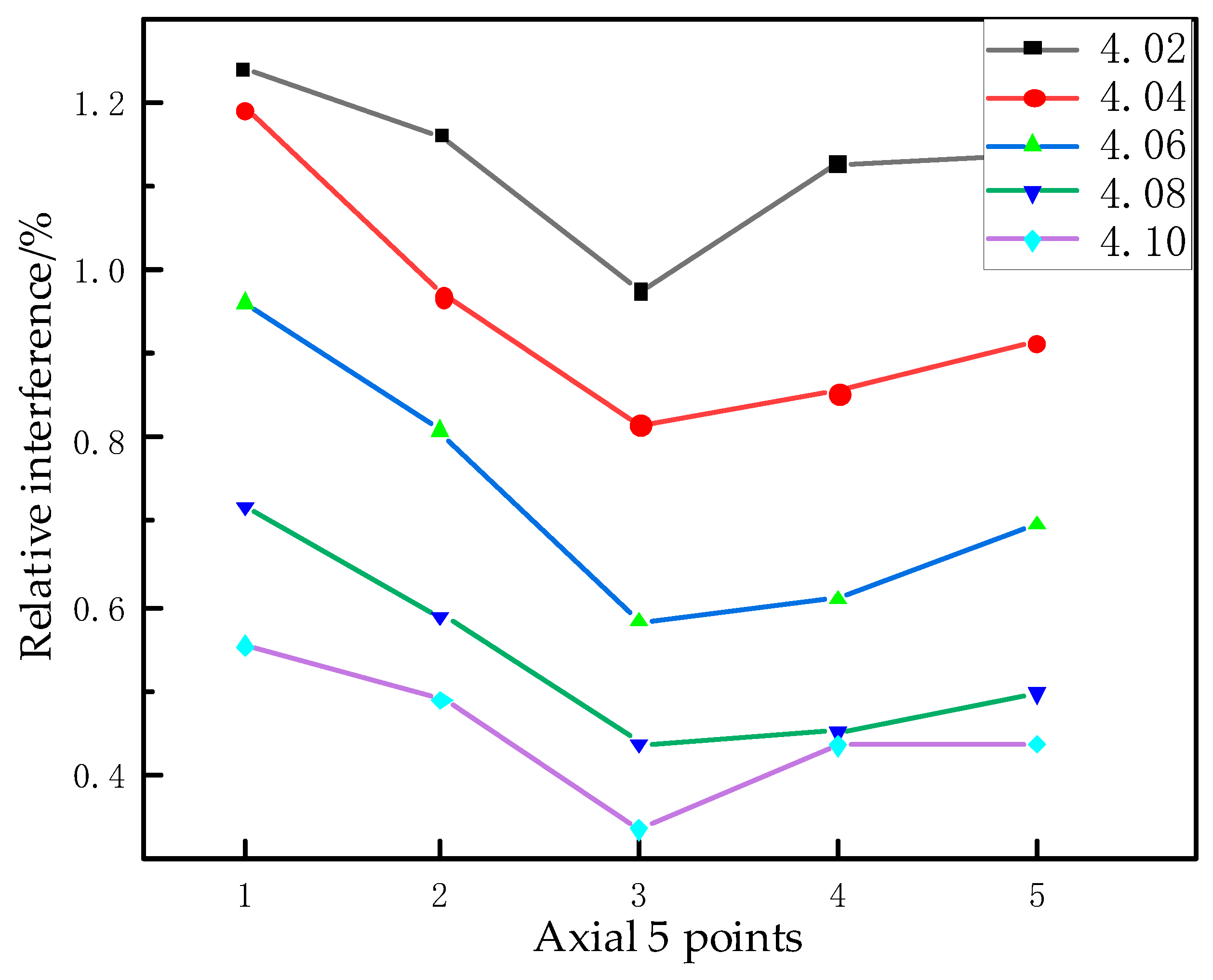
It can be seen from the above expressions that the unit flow pressure is directly related to the diameter and height of the countersunk hole and the elongation of the rivet. In addition, the interference amount of the riveting hole wall determines the size and distribution of the radial residual stress, which is of great significance for the quality control of riveting. Therefore, in this paper, when studying the influence of pressure riveting countersunk deformation on riveting damage and quality, the size of the pier head rivet head, the elongation of the rivet, the surface quality of the pier head, the interference of the hole wall and the residual stress are selected for subsequent analysis to study the riveting situation.

2.2. Rivet Structure Design

According to the above research contents, this paper designs a new type of structural connector: a composite rivet. The composite rivet structural design is divided into a rivet rod and sleeve. The sleeve is pre-assembled into the rivet rod to avoid direct contact between the deformation of the rivet rod and the composite material, and to reduce the extrusion degree of the rivet rod’s expansion to the composite material, which can buffer the stress concentration and material delamination damage at the connecting hole caused by the plastic deformation of the rivet [13]. Thus, the composite material is protected, and the structure is shown in Figure 5.

During pre-assembly, the base shaft interference fit is used to assemble the rivet and sleeve to ensure a stable connection between the rivet rod and the sleeve. Here, the H8/u6 interference fit is used. The operator can pre-assemble this manually and ensure the composite rivet does not loosen. At the mid-joint overlap, a wedge-shaped tightening fit is employed, with an effective expansion stroke of 0.8 mm, guaranteeing an excellent wedging effect at the joint and enhancing the connection strength of the structure. This structure was introduced in the context of an urgent need for “low-stress, non-damaging” assembly and connection techniques in composite material, wedge-structured, double-sided countersunk riveting. Future research will focus on the plastic flow behavior of the wedge-structured, double-sided countersunk riveting connectors and the interaction mechanisms between hole damage and hole wall interference. This research aims to fill the gaps in the riveting assembly and manufacturing technology used for double-sided countersunk composite wedge structures in the domestic and international realms.

2.3. Analysis and Calculation of Rivet Head Parameters

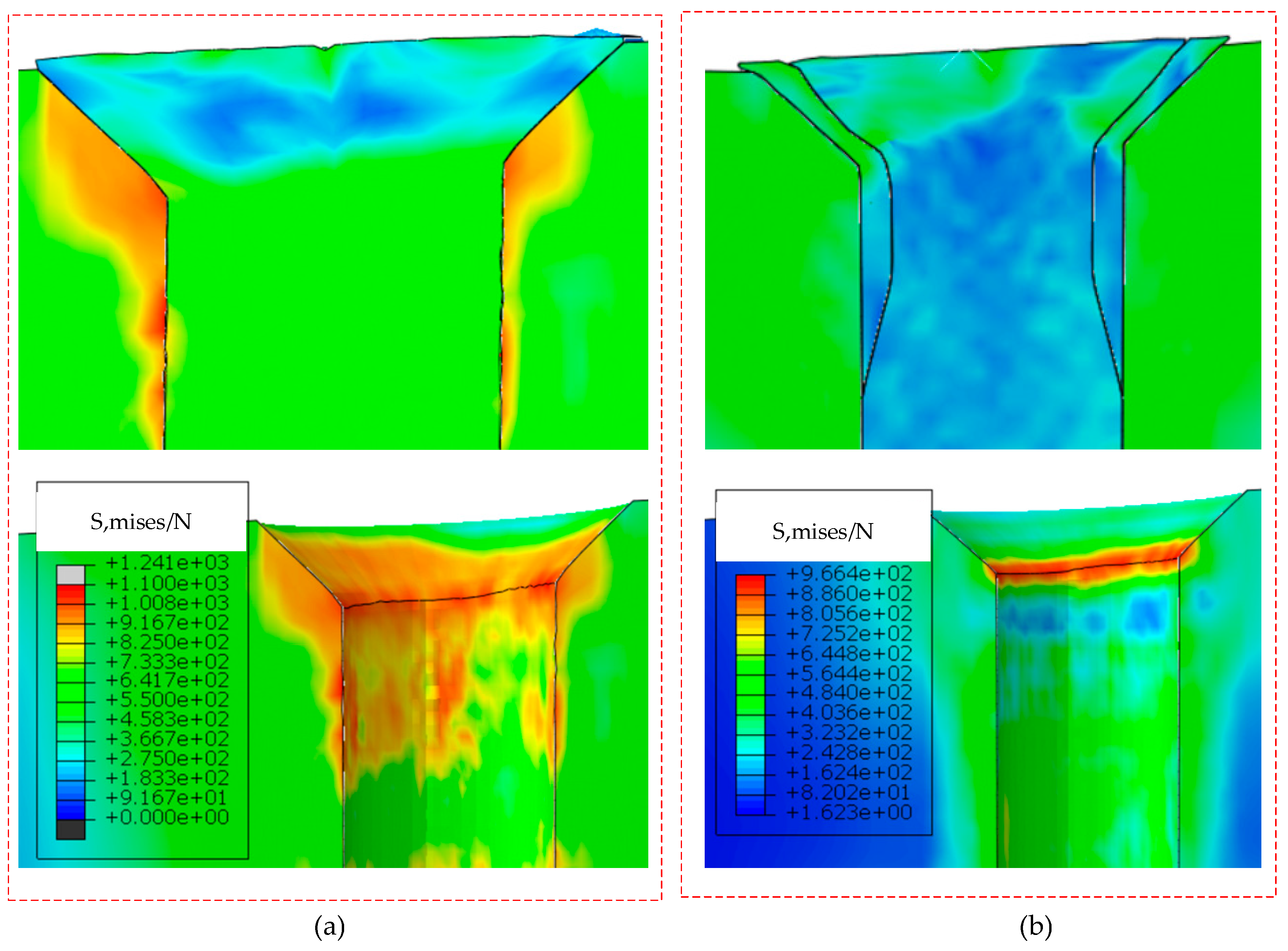
For the countersunk structure, the amount of extrusion is large enough to make the upsetting fill the countersunk. This results in a considerable tangential tensile stress on the outside of the pier head deformation zone III. When the tangential tensile stress exceeds the strength limit of the material or the tangential deformation exceeds the allowable deformation degree of the material, longitudinal cracks will be caused, which directly affects the quality of riveting. Therefore, a vital point of the new structure is the shape parameter of the rivet head. The rivet head is the most crucial part of the plastic flow in the riveting process, and its elongation and shape parameters will directly affect the quality of the riveting surface. Therefore, parameter optimization is essential for improving the overall riveting quality, and reducing the stress distribution of rivet plastic flow on the dimple hole and material damage.

From the deformation principle analysis and mechanical expression of the upsetting process shown in the first section of this chapter, it can be seen that for the flat head rivet, because the middle is solid, considerable unit flow pressure will be induced when the countersunk hole is filled, which will not only direct too much stress to the surface of the composite material and the connecting hole, but also affect the plastic flow of the outer ring material such that the flow deformation effect is very uneven. Therefore, a B-type countersunk head rivet with a conical hole in the rivet head is adopted, and the parameters are optimized on this basis. On the other hand, if the conical diameter is too large, a small pit will be left in the center of the rivet after riveting, which will also affect the surface effect of the riveting. Therefore, the parameter of the conical aperture size of the rivet head needs to be verified by experiment and simulation so as to optimize it.

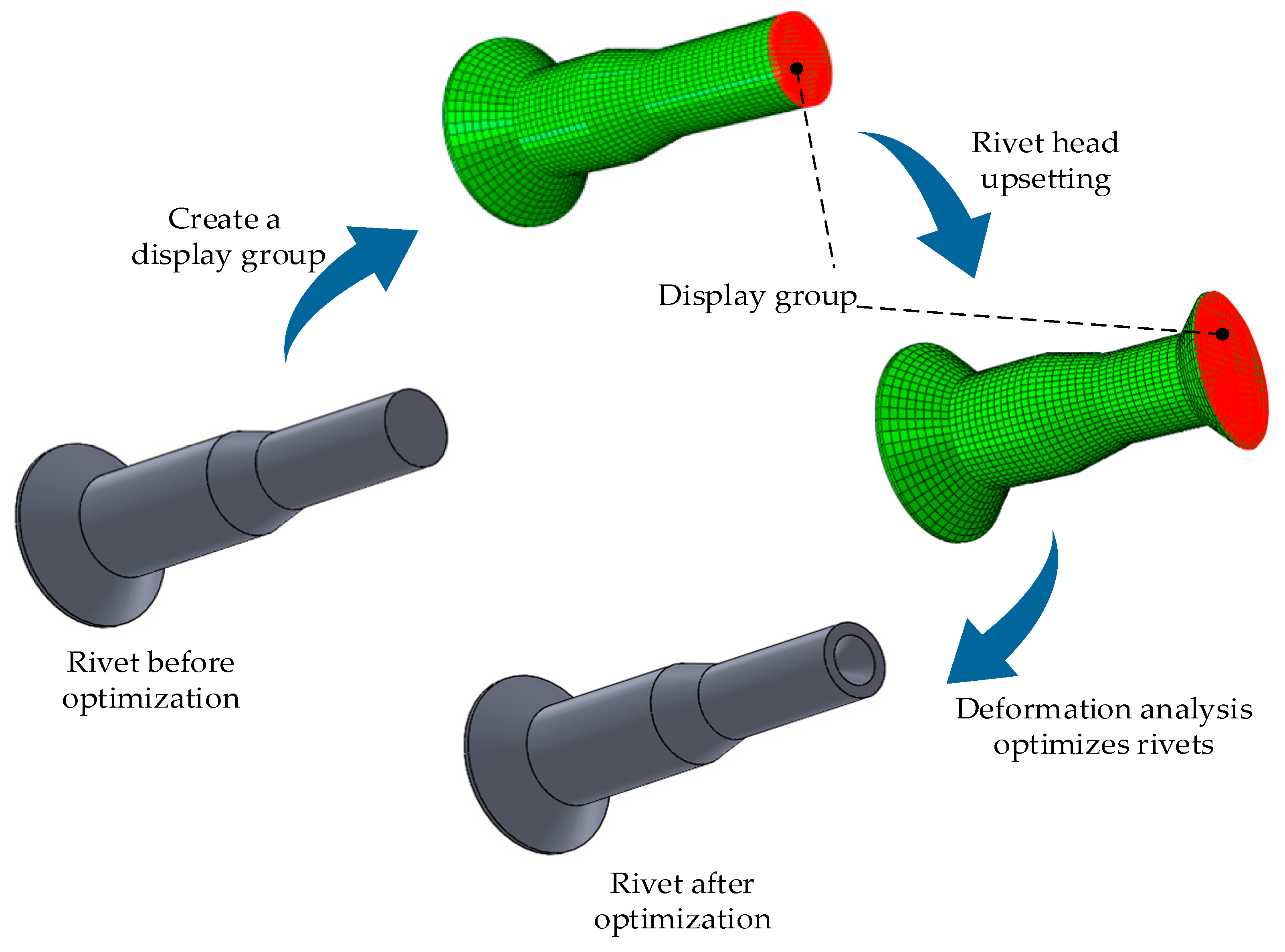
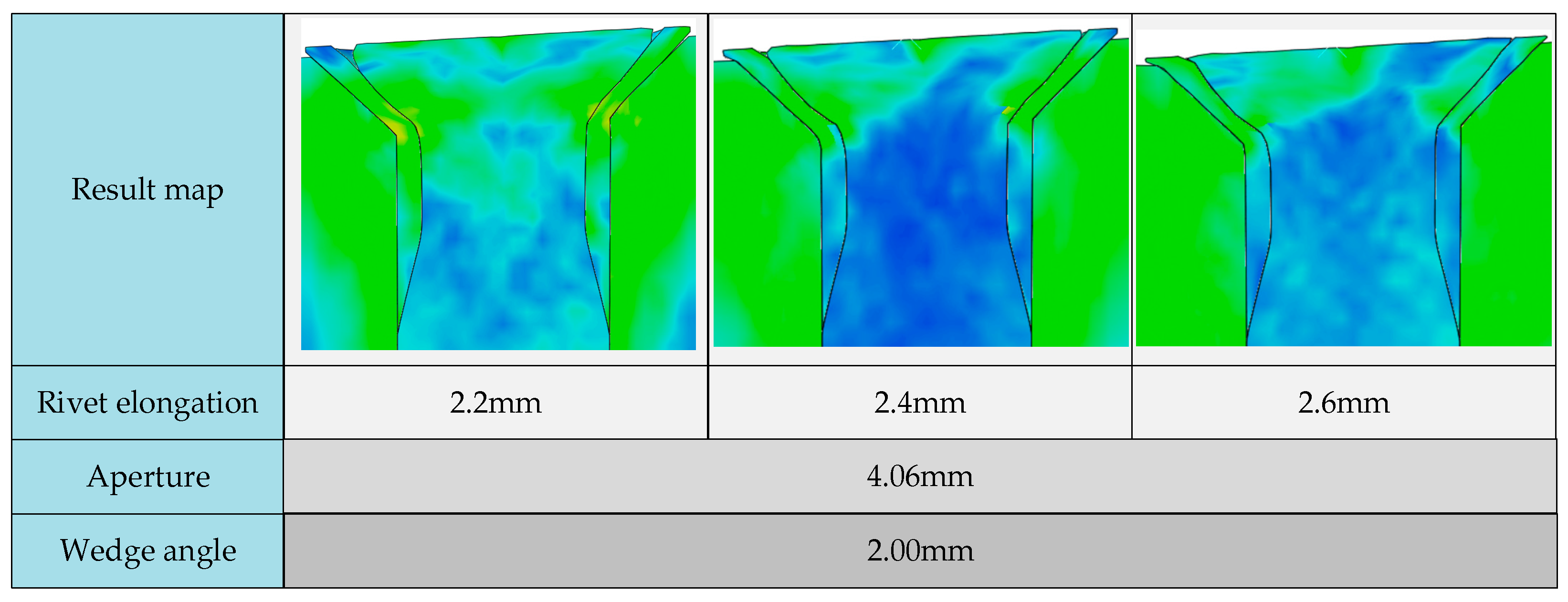
Another critical parameter is rivet elongation. At present, there is no standard stipulation on the length of the rivet in the riveting process of aircraft assembly. In practical work, only the experience of technical personnel can be called upon to judge whether the rivet elongation is appropriate. This leads to the problem whereby there is no theoretical support for the elongation of rivets. If the rivet elongation is too short, the pressing riveting cannot completely fill the sleeve countersunk hole, which affects the locking force of the riveting and the quality of the riveting surface. When the rivet is too long, the volume of the pier head formed after riveting exceeds the cavity volume of the countersunk hole, resulting in the height of the pier head exceeding the surface of the composite material. Continuing riveting will cause the excess part to squeeze the aircraft flap composite material and cause damage. Standardizing the amount of rivet head elongation is important, as it can reduce these problems and shorten the operation time.

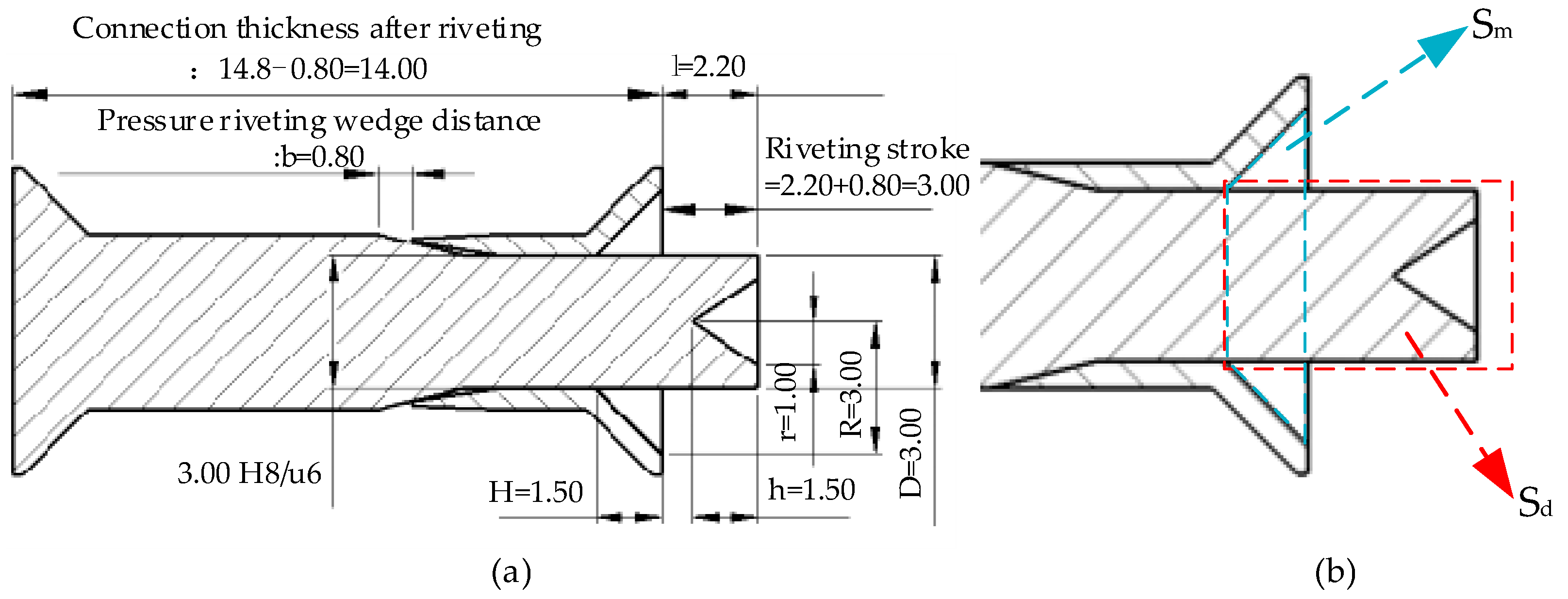
Figure 6a,b is a detailed schematic diagram of each size parameter after matching the rivet rod and sleeve. These size parameters are based on the rivet parameters used in the flaps of an existing aircraft model combined with the new rivet structure in this paper. According to the size initially determined by experience when the riveting thickness is 14 mm, the mathematical relationship between the volume filling of the sleeve countersunk and the volume filling of the elongation of the rivet rod is calculated. According to the principle of constant volume, the best elongation can be theoretically obtained to support the subsequent simulation and field tests and thus derive more accurate parameters, such as elongation.

Volume calculation formula:

The volume of the sleeve countersunk hole to be filled is

$$S_m=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi (R^2+r^2+R\cdot r)H$$

(21)

The volume of the rivet filling length part:

$$S_d=\pi {\left(\raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^2(l+b+H)-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi r^2\mathrm{h}$$

(22)

The relationship between the volume difference $V_c$ and the elongation $l$:

$$V_c=S_d-S_m=\pi {\left(\raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^2\left(l+b+H\right)-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi r^2-\mathrm{h}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi (R^2+r^2+R\cdot r)H$$

(23)

When $V_c=0$, that is, the two volumes are equal, the theoretical elongation value of the pier head just filled with the countersunk hole can be obtained. When we place other existing process sizes into Equation (23) and assume $V_c=0$, the theoretical value of the elongation will be approximately 2.2 mm. However, in the actual process, the filling volume will be slightly smaller than the theoretical value due to the effect of extrusion hardening. Based on the theoretical value, the elongation is gradually increased and tested in groups to determine the most accurate elongation.

3. Simulation and Result Analysis

3.1. Simulation Model Establishment

This paper used ABAQUS/Explicit finite element software to simulate and analyze the riveting process, as it is good at dealing with the complex contact between the components and the strong material flow [14]. The flap, aileron, and other structures of a specific type of aircraft are wedge-shaped. To make the degree of interference after riveting more uniform, the symmetrical loading riveting shown in Figure 7 was used [15]. At this time, the rivet’s strain, stress, and deformation during the riveting process were symmetrical to the central axis, and the change of the sandwich structure was also proportional to the central axis. Therefore, only half of the model was established to reduce the calculation scale when simulating a single rivet’s riveting process, and symmetry constraints were available for addition to ABAQUS. In addition, this model is only used to study the forming law of rivets and the influences of different riveting process parameters on riveting quality and interference amount. At this time, rivets are the focus of attention, and composite materials can be simulated as an orthogonal isotropic whole. Therefore, the laminated plate to be connected was simplified as a whole, and the size and distribution of the stress and strain at the countersunk of the upsetting head were taken as a reference to optimize the structure and parameters of the rivets as quickly as possible and save calculation time. Through the above analysis and with reference to the existing process part’s size, a simplified model for the simulation analysis of the riveting process of the wedge part was obtained, as shown in Figure 7 and

Table 1. The composite rivet and the structure to be riveted—geometry size (mm).

Composite Rivet		Wedge Parts to Be Riveted
Name	Dimension	Name	Dimension
Rivet fit diameter	3.0	Hole diameter	4.1
Length of rivet	17.0	Hole depth	14.0
Sleeve aperture	2.95	Diameter of countersunk	7.5
Sleeve countersunk hole	6.0	Height of countersunk	1.5
Tightening trip	0.8	Wedge angle	6°

The diameter of the pre-assembly fit between the rivet rod and the sleeve is called the fit diameter, and the length of the wedge-shaped tightening transition zone is the tightening stroke.

.

In the wing structure design of a specific type of aircraft, the wedge truss materials of the wing include a TC4 titanium alloy for the frame, and the connector is made of an AL-7075 high-strength aluminum alloy rivet. Based on this, the material properties are defined, and the material performance parameters are shown in

Table 2. Material parameters of rivets and wedge parts.

Name	Material	Density (t/mm3)	Elastic Modulus (Mpa)	Poisson Ratio
Rivet	AL-7075-T6	2.81 × 10−9	72,000	0.33
Wedge part	TC-4	4.45 × 10−9	102,040	0.3

.

In the riveting process, the rivet’s plastic flow is enormous. For this reason, to derive the plastic parameters, we adopted the Johnson–Cook material and failure model. The Johnson–Cook material constitutive model is used to simulate the dynamic plastic behavior of rivets in riveting-related research, and good application results are obtained. It is thus proven that the model is suitable for describing the strength limit and failure process of metal materials under considerable strain and high strain rate environments. It combines elasticity and plasticity, and can better predict the deformation behavior of materials under high strain. At the same time, the model is simple in form, and the parameters of each model are independent of each other and require fewer parameters. Therefore, it is widely used in engineering [16,17]. The description of the Johnson–Cook material constitutive model contains three laws of plasticity: yield criterion, flow criterion, and hardening criterion.

Material yield model:

$$\overline{\sigma }=[A+B{(\overline{ℰ})}^n]\left[1+C\ln \frac{{\dot{\epsilon }}^{pl}}{{\dot{\epsilon }}_0}\right](1-{\widehat{\theta }}^m)$$

(24)

where A—initial yield stress; n—hardening exponent; B—hardening constant; m—thermal softening exponent; C—strain rate constant.

A, B, C, n, and m are the five physical constants that are used to define the Johnson–Cook model, and their values are listed in

Table 3. Failure model parameters of AL-7075-T6 rivet material [18].

A	B	C	n	m
546	678	0.024	0.71	1.56

.

Material failure model (damage initiation + damage evolution):

$${\epsilon }_f=\left[D_1+D_{2}exp\left(D_3\left(\frac{{\sigma }_m}{{\sigma }_{eq}}\right)\right)\right]\left[1+D_4\ln ({{\dot{\epsilon }}_p}^{\ast })\right][1+D_5{T}^{\ast }]$$

(25)

Here, D₁, D₂, D₃, D₄, and D₅ are the failure parameters of the material, and the values are listed in

Table 4. The yield model parameters of the AL-7075-T6 rivet material [18].

D1	D2	D3	D4	D5	Displacement of Failure
−0.068	0.451	−0.952	0.036	0.697	0.5

.

The rivets and wedge structure components are meshed in the eight-node hexahedron C3D8R element. The structured meshing technology is used to refine the local grids of the contact parts in the riveting process while ensuring that the nodes between the rivet and the hole wall contact position correspond to each other to improve the calculation accuracy. The upper and lower pressure heads are divided into shell elements, which are rigid body material models. The specific contact relationship between the components is as follows: the contact between the upper and lower pressure head and the rivet, the contact between the composite rivet and the hole wall of the wedge, the contact between the inner sleeve of the composite rivet and the nail rod, and the general contact of the whole set up. Each component is in automatic face-to-face contact. Related sensitivity studies have shown that the friction coefficient value (these three interfaces are between 0 and 0.2) has no significant effect on the results [19]. Due to the complexity and uncertainty of the contact pair in the riveting process, the friction coefficient is set to 0.1. The Newton–Raphson algorithm [20] in ABAQUS solves the plastic deformation. This method is based on the Newton iterative method. The incremental step under each analysis step is iterated many times to make the incremental step converge, and then the convergence solution under the analysis step is obtained. The process divides the external load into a series of load segments, calculates the current stiffness matrix according to the current load increment step value, and calculates the structural internal force matching the current load. In this way, it iterates each load segment until it converges in the load segment. Finally, it repeats all load segments and accumulates the results. The advantage of this method is that it has a high convergence speed. In addition, contact is the penalty condition; the penalty stiffness is set between the nodes within the contact distance detected by ABAQUS. Then, the contact force is iterated to generate strain. The simulation model of the final grid is shown in Figure 8.

The process of pressure riveting is roughly divided into two steps. First, the sleeve and the rivet rod are pre-assembled in the pores of the wedge, and then the pressure riveting force is applied to the rivet head. Based on this process, three analysis steps are taken. In the first analysis step, a displacement load of 0.8 mm is applied to the upper surface of the sleeve so that the sleeve is thoroughly pressed to achieve wedge tightening with the rivet rod and enhance the connection strength of the lap position. The second analysis step is the riveting stage. The corresponding displacement load is set on the upper and lower pressure heads, and the upper and lower pressure heads are riveted synchronously. Then, in the third analysis step, the model is elastically unloaded and restored so that the riveting die is restored to the initial position. The simulation process of each stage is shown in Figure 9.

3.2. Multi-Objective Optimization of Rivet Head

The importance of the conical aperture of the rivet head has been mentioned above. To further optimize the optimal parameters of the conical aperture of the rivet head, a node display group is next created for the rivet head, as shown in Figure 10, and then the node space displacement value of the entire surface is queried. Through the integration of the data, a spatial histogram of the deformation of each unit is obtained, and the deformation of the rivet head in three-dimensional space after riveting and upsetting is restored to visually show the plastic deformation of each part of the rivet head.

The spatial histograms of all nodes on the rivet head along the X and Y axes are U1 and U2, respectively, as shown in Figure 11a,b. The X and Y axes are the actual X–Y plane coordinates of the nodes. The Z-axes for U1 and U2 show the displacement of each unit in the display group along the X-axis and Y-axis, respectively, after the riveting is completed. The displacement of each element of the display group in the X and Y directions is summed by the vector to obtain a complete spatial displacement histogram of the X-Y plane, as shown in Figure 11c, and the compression displacement U3 in the Z-axis direction, as shown in Figure 11d.

It can be seen from Figure 11 that the flow deformation of the rivet head metal material in the X–Y plane is distributed in a stepped shape, and a part of the rivet head is only compressed along the Z-axis without plastic flow along the X–Y plane during the riveting process, otherwise the flow is minimal. This phenomenon is pronounced within 1.0 mm of the center of the rivet head. Therefore, it is most reasonable to use the conical head of the rivet, which can reduce the stress caused by the axial movement of the material in the riveting process and achieve a lightweight effect. The preliminary design of the rivet conical hole has a radius of 1 mm.

Then, the surface quality of the simulation after riveting with different rivet head elongations is analyzed. The rivet hole of the wedge is 4.06 mm, and the diameter of the cone hole of the rivet head is 2.00 mm. Due to the extrusion strengthening of the material during the riveting process, the theoretical elongation value is imprecise, and a further study of the optimal value is needed. According to different elongations, there are three possible optimums, which are 2.2 mm, 2.4 mm, and 2.6 mm. The other dimensions are unchanged. The details of the riveting simulation and the results after the completion are shown in Figure 12. It can be seen that the shape of the pier head is reasonable, and the elongation of 2.6 mm has the best filling effect. Applying this elongation, it can exactly fill the countersunk hole of the wedge structures and also avoid the excessive deformation of the rivet head, which continues to put compressive stresses on the countersunk hole. Therefore, this elongation is selected for the riveting under this working condition, and the obtained riveting surface quality is the best.

Finally, the improved composite rivet and ordinary rivet are compared via a riveting simulation, and the difference in the stress distribution at the connection hole between the two is analyzed. As shown in Figure 13a,b, in addition to the structure, other parameters and materials of the two are consistent, and this ensures that the filling effect and pressure riveting conditions are the same, allowing us to observe the distribution and size of the stress.

After the riveting is completed, the riveting force of the two is first compared, as shown in Figure 14a. Both yield roughly the same displacement–load curve; under this premise, we extract the stress value of the maximum stress area of the two, that is, the junction of the countersunk hole and the nail hole, for one week. The stress curve is shown in Figure 14b, and the stress of each point on the hole wall is much smaller than that of the traditional rivet extrusion stress. The data are integrated and counted to obtain the histogram shown in Figure 14c. The results show that the maximum value of the extrusion stress of the hole wall after riveting the composite rivet is 22% lower than that of the traditional rivet, and the average stress is reduced by 20.8%. Under the action of the sleeve, the direct contact between the material and the specimen during the plastic deformation of the rivet head is avoided, which plays a specific role in stress buffering and stamping protection. This proves that the new structural rivet can effectively reduce the extrusion stress at the joint, and has a very positive effect on material damage control.

3.3. Interference Fit Simulation Analysis

The rivets with interference fit can closely fill the rivet nest and the rivet hole, and expand the rivet hole evenly and appropriately. This can induce pre-compressive stress around the connecting hole, delay the initiation of fatigue cracks, and significantly improve the structure’s bearing capacity [21]. The specific mechanism of action is as follows: A reasonable amount of interference can cause the stress concentration caused by the structure of the hole itself to pass along the axial direction of the rivet rod, improving the stress distribution of the connecting hole, and the interference fit then produces the “support effect” of the rivet rod on the hole wall, which increases the effective contact area between the fastener and the connecting hole. The friction force between the rivet and the hole will prevent the expansion of the deformation of the inner wall of the hole, which can effectively inhibit crack propagation. As a connection method that can significantly reduce stress concentration and improve connection strength and fatigue life, interference fit is widely used in mechanical connections in various aviation structures [22]. At the same time, the degree of interference is greatly affected by the aperture. When the gap between the rivet holes is too large, the riveting will be equivalent to free upsetting, and the interference fit cannot be formed, as a result of which it may cause the rivet to tilt in the hole, affecting the strength of the connector. If the clearance of the rivet hole is too small, it may cause initial damage to the specimen [23], and this will make the rivet installation difficult. Therefore, it is necessary to analyze the interference fit in the riveting process and obtain the precise interference amount for the damage control and strength improvement of the connecting hole.

According to the aerospace industry standard, the primary rivet hole diameter D0 of a solid rivet with a diameter of 4 mm is 4.1 mm; the upper deviation is 0.12, the lower deviation is 0, and the obtained rivet hole diameter range is 4.10~4.22 mm. However, this size range is for ordinary riveting, and it is difficult to derive the interference amount for this. To realize the interference fit, the aperture size must be about half the size of the ordinary fit. Therefore, the aperture range is set to 4.02~4.10, and the five sizes of 4.02, 4.04, 4.06, 4.08, and 4.10 are taken at equal intervals. The other simulation parameters are left the same to establish a model for simulation analysis. The relevant details are shown in

Table 5. Grouping sequence of interference fit.

Peer Group	1	2	3	4	5
Aperture/mm	Φ4.02	Φ4.04	Φ4.06	Φ4.08	Φ4.10
Elongation/mm	2.6
Diameter of rivet head cone hole/mm	2.0

.

The control variable method has been used in the comparative experiment. In addition to the aperture parameters, the other model sizes are set to the same values. The relative interference amount of each measurement point under different rivet hole diameters is as follows. Five points are selected in the axial vertical central region, and the positions of the measuring points are shown in Figure 15a. The software for point tracking can measure each point’s radial displacement S after riveting, indicating the degree of interference in this part. Firstly, a comparison of the curves of the interference displacement of each point in the axial direction with time under different apertures in the riveting process is observed and analyzed, as shown in the rest of Figure 15.

By analyzing the results in the interference diagram, it can be seen that only the sleeve is pressed, and there is no interference in the hole wall in the first stage of riveting (0–1.0 s). In the second stage, pressure riveting begins. In the first half (1.0–1.3 s), a gap emerges between the rivet rod and the hole wall. Although the rivet rod is slowly upset, it does not contact the hole wall, so the interference amount remains at 0. In the second half of the riveting process (1.3–2.0 s), the upsetting of the rivet rod lead sit into contact with the hole wall. With the increase in riveting time and displacement, the interference gradually increases, and the interference reaches its maximum after the riveting is completed. The interference generated by the plastic flow of the rivet rod is partly caused by elastic deformation, so in the subsequent unloading stage (2.0–3.0 s), elastic deformation unloading recovery is enabled, and finally, the radial displacement is stabilized at a specific value, which is the final result of the applied interference. The final interference displacement value shows that the amounts of interference at the five points in the axial direction are relatively uniform. Among them, the amounts of interference of the two points P1 and P2 near the pier head are the largest, followed by P4 and P5 near the rivet tail. In the process of material flow in the rivet rod, the two ends are first squeezed by the wedge and the outer rivet rod of the laminate, and finally transferred to the center of the rivet rod so that the minimum value is distributed in the middle P5 position. To quantitatively characterize the distribution uniformity of the riveting interference along the axial direction of the hole wall, the standard deviation coefficient $V$ of the statistic is introduced to describe the uniformity of the relative interference of the five measurement points [24], as shown in Equation (26):

$$V=\frac{\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(s_i-\overline{s}\right)}^2}}{\overline{s}}$$

(26)

where $V$ is the standard deviation of the sample; $S_i$ is the radial displacement of the i-th measuring point in the axial direction; $\overline{S}$ is the average of all measured values; n is the total number of samples, which is $n=5$ in this paper.

The standard deviation in rivet interference under different apertures is illustrated above. The results are shown in Figure 16. It can be seen that the standard deviation of interference under each aperture does not differ much, and remains within 20%, while the uniformity of rivet interference is improved.

Similarly, for the same hole wall height, along the circumference of a circle of five equally spaced representative points, as shown in Figure 17, the interference displacement will be basically the same for all points. Therefore, for the countersunk pressure riveting of a wedge structure, the symmetrical loading method can achieve basic interference uniformity in all dimensions.

The radial deformation of the aperture is the amount of interference fit riveting. The calculation algorithm generally uses the relative interference $I_r$, which is defined as:

$$I_r=\frac{d\prime -d_0}{d_0}\times 100\%=\frac{2S_i}{d_0}\times 100\%$$

(27)

where S_i represents the radial displacement of each measuring point P_i (i = 1, 2, 3, 4, 5).

After processing the riveting data derived from the finite element analysis, the deformation displacement of the hole edge under different aperture sizes was obtained. The average relative interference amount of riveted parts with varying aperture sizes was calculated according to the distribution of the above five axial points. The results are plotted in Figure 18 and Figure 19 and

Table 6. Average relative interference of hole wall.

Aperture/mm	Φ4.02	Φ4.04	Φ4.06	Φ4.08	Φ4.10
Average relative interference value	1.13	0.95	0.73	0.54	0.45

.

Here, Figure 18 shows the interference pattern of five points along the axial direction of the interference under each aperture, and Figure 19 is the change curve of the interference amount at each position in the axial direction with different apertures. Table 6 shows the average relative interference of the hole wall under each aperture fit. It can be seen from the above chart that the interference amount gradually decreases from both ends of the specimen to the inside of the hole edge. This is because the interference amount is formed by the material flowing radially and squeezing the hole wall under the action of the riveting force. The whole riveting process involves the metal material gradually flowing along the axial direction from both ends to the inside. However, due to the friction force caused by the extrusion between the rivet hole and the rivet, the material flows from both ends to the middle, hindering the rivet’s downward metal flow [25]. The two ends of the deformed rivet rod are large, and the middle is small, but the difference is not significant, and is within the reasonable interference range. To a certain extent, this reduces the problem whereby the interference amount caused by the previous unidirectional riveting is large and small in the shape of a cone, which leads to the initial damage caused by the excessive interference at the end of the pier, and the gap at the bottom seriously affects the fatigue life. In addition, with a smaller aperture of the wedge, due to the smaller clearance between the rivet hole, the plastic flow of the material squeezes the hole wall, and the amount of interference formed will also be more considerable, while the overall average interference of the riveting piece will be more significant. Among these, the amount of interference related to the minimum aperture of 4.02 mm is the largest, reaching 1.13%, and the interference amount gradually decreases with the increase in the aperture.

There is an optimal interference range for the interference of various structural parts made of different materials. The titanium alloy truss structure has enormous strength, and according to the actual riveting process, it is difficult for an interference amount greater than 1% to form, which is also consistent with the simulation results of this paper. According to previous studies [26], the ideal interference range of titanium alloy truss structural parts is 0.6% to 1.0%; at this moment, the riveting quality is good, and the fatigue life is the highest. According to the above chart, in the range of 4.04 mm to 4.06 mm, the overall average relative interference amount and the interference amount of each point are within this range. Therefore, in the actual production process, the rivet hole size range of the titanium alloy wedge truss member is recommended to be 4.04~4.06 mm.

On the other hand, the residual compressive stress and tensile stress are also generated with the interference of the hole wall. The fatigue failure of the specimen is caused by stress concentration at the hole’s edge, and the residual circumferential compressive stress will affect the stress amplitude at the hole’s edge, thus affecting the fatigue performance of the specimen [27].

After unloading, a specific amount of residual stress is formed at the hole’s edge, and the residual stress distribution cloud chart and curve of wedge riveting parts with different apertures were output along the axial path of the hole edge, as shown in Figure 20. It can be seen from the chart that a certain depth of the residual compressive stress layer is formed at the head of the pier of the hole wall of the wedge, which gradually turns into tensile stress wit movement along the axial direction, and the maximum tensile stress area is at the edge of the hole inside the specimen. Comparing the distribution curves yielded by different amounts of interference in the hole wall shows that both have a consistent distribution pattern. The interference near the upper and lower surfaces of the connecting hole is significant, and so the material is extruded and deformed, and the residual compressive stress is also significant. Near the axial center of the hole wall, the rivet undergoes a small extrusion deformation on the hole wall, which is similar to bending deformation, resulting in a tensile stress state at a certain depth along the radial direction of the internal hole, as a result of which residual tensile stress is formed [28,29].

4. Experimental Verification

4.1. Test Specimen

In order to prove the validity of the finite element model simulation results and the accuracy of the selected elongation, the corresponding wedge riveting experiment is carried out below. The other size parameters of the wedge and the rivet are consistent with the simulation parameters, as shown in

Table 7. Important parameters of the test group.

Test Group	1	2	3	4
Elongation/mm	2.20	2.20	2.40	2.60
State	Unpressed riveting	After pressing riveting
Aperture/mm	4.06
Hole depth/mm	14.00

. Before riveting, the tool microscope (with scale, the measurement accuracy is ±0.001 mm) is used to measure the diameter of the hole and the large diameter of the countersunk hole. The diameter and length of the rivet are measured with a micrometer, and the accuracy is 0.001 mm, which ensures the accuracy of the size. The rivets are divided into three groups according to different elongations, which are 2.2 mm, 2.4 mm, and 2.6 mm, respectively; that is, the interval is increased by 0.2 mm, and the unpressed riveting state is divided into four groups for testing. Sequence 1 is the state before the rivet is put into the rivet hole without riveting, and the elongation of sequences 2–4 is 2.2 mm, 2.4 mm, and 2.6 mm, respectively.

4.2. Equipment and Methods

The experimental riveting equipment was the CFXYM-01 mobile cantilever riveting machine produced by Qingdao Qianshao Company located in Qingdao, Shandong Province, China. The riveting machine can adapt to wedge structures under different working conditions by adjusting the angle of the riveting head, which is suitable for riveting wedge-shaped parts. The following Figure 21 and

Table 8. Main performance parameters of the riveting machine.

Name	Numerical Value	Name	Numerical Value
Peak pressure/KN	56	Maximum stroke of riveting/mm	30
Angle of pressure head/°	6	Pressure holding time/s	6
Applicable rivet diameter/mm	Φ2.5~Φ4	indenter velocity/mm/s	2

show a detailed schematic diagram of the structure and work of the riveting head of the experimental equipment, and the parameters set according to the working conditions.

The specific operation methods of the riveting experiment are as follows: (1) The corresponding manual drilling and countersinking of holes are carried out on the wedge parts to be riveted, and a tool microscope (with scale, the measurement accuracy is ±0.001 mm) is used to measure the aperture and the size of the countersunk hole. The diameter of the rivet is measured with a micrometer to ensure the accuracy of the experimental size. (2) According to the angle of the wedge to be riveted, the upper indenter and the lower pad with appropriate angles are adjusted. The angle of the wedge in this experiment is 6°, so the upper and lower angles are adjusted to 3°, respectively, such that the center line of the wedge is kept horizontal and symmetrical riveting is carried out. (3) Place the wedge block to be riveted, adjust the height of the lower block according to the thickness, and test the pressure to determine the movement stroke of the upper indenter. (4) Fix the wedge to be riveted in a specific position of the riveting machine and set the loading speed to 2 mm/s. The maximum peak value of the riveting force is adjusted to 10 KN. (5) After the riveting is completed, the pressure is held for 6 s and then unloaded. We repeated the above steps to perform riveting experiments on the three groups of specimens.

4.3. Results and Analysis

A rivet head is an essential geometric evaluation standard often used to ensure riveting quality, and its results will directly affect the aerodynamic performance of an aircraft [30]. From the results of the field experiment, shown in Figure 22 below, we know that when the elongation adopts the theoretical value of 2.2 mm, due to the extrusion hardening of the material and the expansion of the hole wall, the rivet head material is not able to fill the countersunk, and the pier head contains a gap. With the increase in elongation, the filling effect is improved. When the elongation is 2.6 mm, the rivet head can fill the countersunk hole, and the filling effect is better.

After the riveting experiment is completed, the rivet is cut out, the deformation of the rivet is observed, and the height, diameter, and appearance of the pier head are measured and recorded. In order to assess the consistency of results between the experiment and the simulation, the pier heads obtained by the experiment and the simulation are compared, and the comparison results are shown in Figure 23 and

Table 9. Comparison between simulation values and experimental values.

Category	Pier Head Diameter 1	Pier Head Diameter 2	Pier Head Diameter 3	Mean Values of Diameter	Mean Values of Height
Simulative/mm	6.051	6.205	6.297	6.184	1.511
Test value/mm	5.996	6.113	6.235	6.114	1.508
Error/%	0.9	1.5	0.1	1.1	0.1

. The results show that the experimental value is lower than the simulated value. The main reason is that uneven deformation in the clinching of the inclined plane leads to the formation of a non-standard circle in the riveted pier head. At the same time, it is difficult for the experimental cutting surface of the pier head to pass through the central axis of the rivet completely, so the measured value given in the experimental results will be slightly smaller. On the other hand, there may be differences between the model and the experiment as regards the performance of the wedge structure materials. For example, the riveting contact pair is more complex, as the friction coefficient and the material extrusion strengthening coefficient change and show uncertainty. However, on the whole, the trend of the change curve is consistent. The diameter of the pier head increases slowly with greater elongation, and the growth rate is in good agreement with this trend. The height of the pier head remains stable with the increase in elongation because the displacement of the pressure head determines the riveting stroke. For pressure riveting, as long as the stroke is kept constant, the height of the pier head will also be specific, and this finding is consistent with the conditions of actual production.

Within the actual processing techniques employed by some aviation manufacturing enterprises, it is necessary to finish the structural surface after completing double-sided pressure riveting to improve the flatness and aerodynamic performance of the wing. According to the principle of constant volume, the height of the rivet is increased by 0.2–0.4 mm, which can increase the upsetting height of the rivet head by about 0.1 mm, leaving a margin for subsequent surface processing. Therefore, an appropriate increase of 0.2–0.4 mm based on 2.6 mm elongation can improve the surface flatness of the pier head after finishing. In general, the maximum error in the results for the diameter of the pier head given by the simulation and the experiment is 1.4%, the average error is 1.1%, and the height of the pier head remains basically the same, which proves that the consistency between the simulation and the experiment is high, the accuracy meets the analysis requirements, and the reliability is high.

5. Conclusions

In this paper, the plastic deformation behavior related to the double-sided countersunk pressure riveting of composite wedge structures was studied, and the structure’s stress during the riveting process was analyzed. Through the simulation of the riveting process and the analysis of the riveting test, it was proven that the designed composite rivet and the optimized riveting process could effectively improve the quality of the double-sided countersunk riveting of the composite wedge structure, and reduce the extrusion damage caused by the contact compressive stress of the composite material. These research results can fill the gaps in our theoretical understanding of the riveting process. The main conclusions can be summarized as follows:

(1)

We established a stress model of the deformation caused during the double-sided countersunk pressure-riveting of a wedge structure, as well as the deformation partition of the upsetting process and the stress distribution inside the hole wall, and we also developed design criteria and a parameter optimization method for the new composite rivet;

(2)

A simulation model of the composite pressure riveting of a double-sided countersunk wedge structure was established. The plastic flow behavior and expansion behavior of the rivet during the riveting process were analyzed, and different rivets were compared. The results show that the contact compressive stress at the connecting hole was reduced by more than 20% compared with the ordinary rivet after the composite rivet structure had been applied in riveting;

(3)

During the double-sided countersunk pressure-riveting of a wedge structure, the variations in the distributions of amounts of interference with analysis time under different apertures were obtained. For 4 mm rivets, the aperture size that can endow the optimal connection strength interference was 4.04~4.06 mm. At this time, the relative interference amount was kept within 0.6% to 1.0%, and the standard deviation of the quantity of the interference was within 20%, indicating that the interference uniformity was better;

(4)

The filling quality of the composite rivet increased with the increase in elongation, and the compressive stress of the composite also increased. When the rivet elongation was 2.6 mm, the countersunk pressure riveting filling amount reached its critical value, and the size values of the pier head under experiment and simulation were measured, with results showing that the riveting consistency was good.

In summary, the research results of this paper provide an important reference for the parameter optimization of the double-sided riveting process of composite wedge structures, and the damage control of composite materials. However, the current research also faces problems and challenges, such as those related to the progressive damage analysis of composite materials after riveting, the forms and distribution of damage done to composite materials under extrusion loading, the evaluation and prediction of riveting connection strength and composite damage, and so on. Working on the foundation of this study, we will gradually solve these problems in future research. Finally, a solution inducing “low stress and no damage” during the double-sided buried head riveting of composite wedge structures will be developed based on the composite rivet structure.