Online Deterministic 3D Trajectory Generation for Electric Vertical Take-Off and Landing Aircraft
Abstract
1. Introduction
2. Trajectory Construction: Overview
2.1. On Plane Curves
2.2. On Straight Line Segments
Curvature and Arc Length of the Line Segment
2.3. On Circle Segment
2.3.1. Curvature of the Circle Segment
2.3.2. Arc Length of the Circle Segment
2.4. On Clothoid Segment
2.4.1. Curvature of the Clothoid Segment
2.4.2. Arc Length of the Clothoid Segment
2.4.3. Change in Direction
2.4.4. Clothoid Approximation
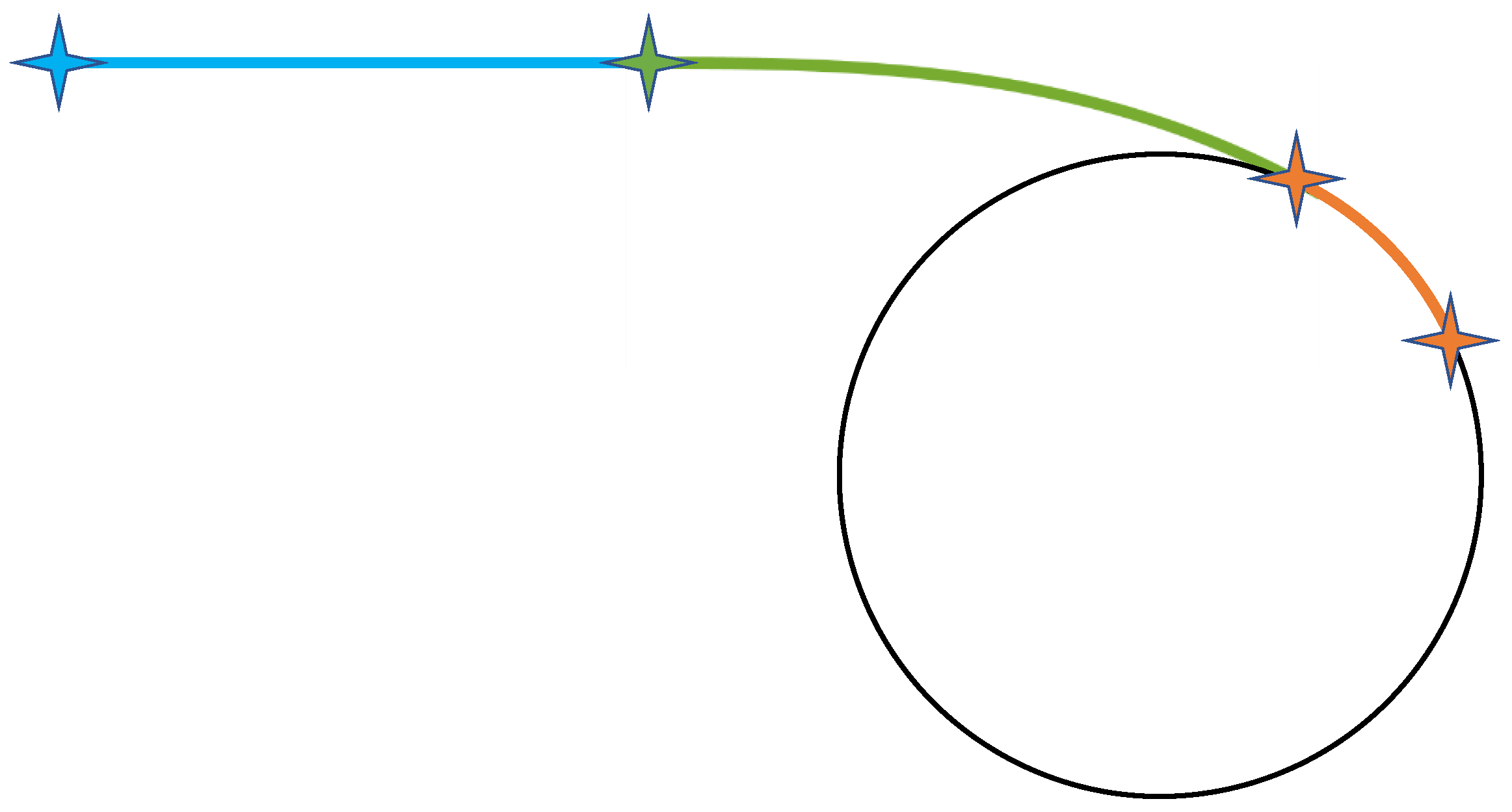
3. Trajectory Construction: Flyby
- Fixed parameters resulting from the flight plan:course angle change between two subsequent legs , kinematic speed ;
- Fixed parameters resulting from the inner loop controller design, the resulting inner loop dynamics and aircraft performance:roll time constant , roll rate command ;
- Trajectory design parameter:desired turn rate .
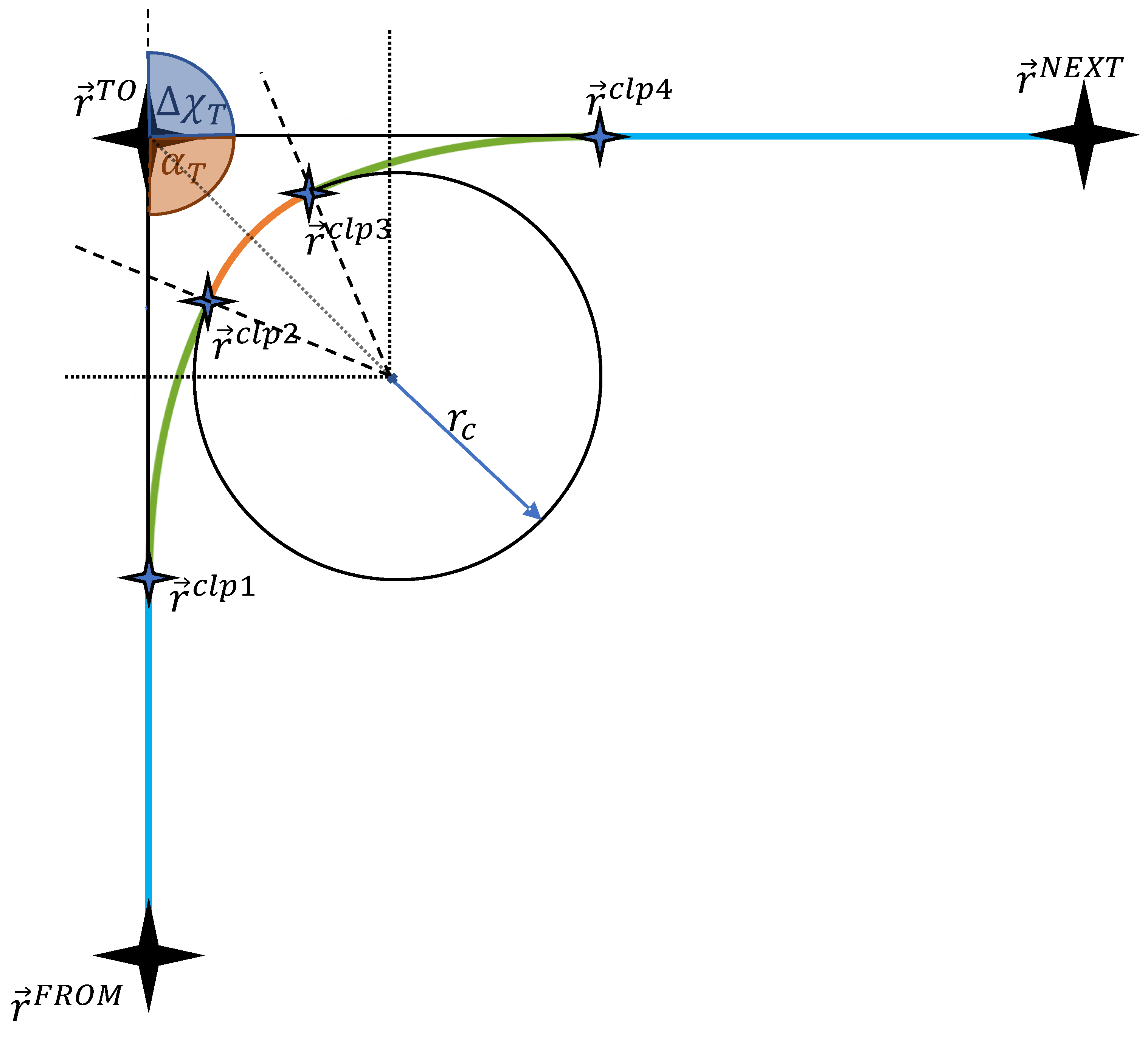
3.1. Horizontal Plane
- 1.
- Straight line: the aircraft is flying in a straight line with a kinematic bank angle .
- 2.
- Circle: The aircraft is performing a turn with a kinematic bank angle as given by Equation (33)where is the kinematic speed, is the desired turn rate, and is the gravitational acceleration.
3.1.1. Turn Distance
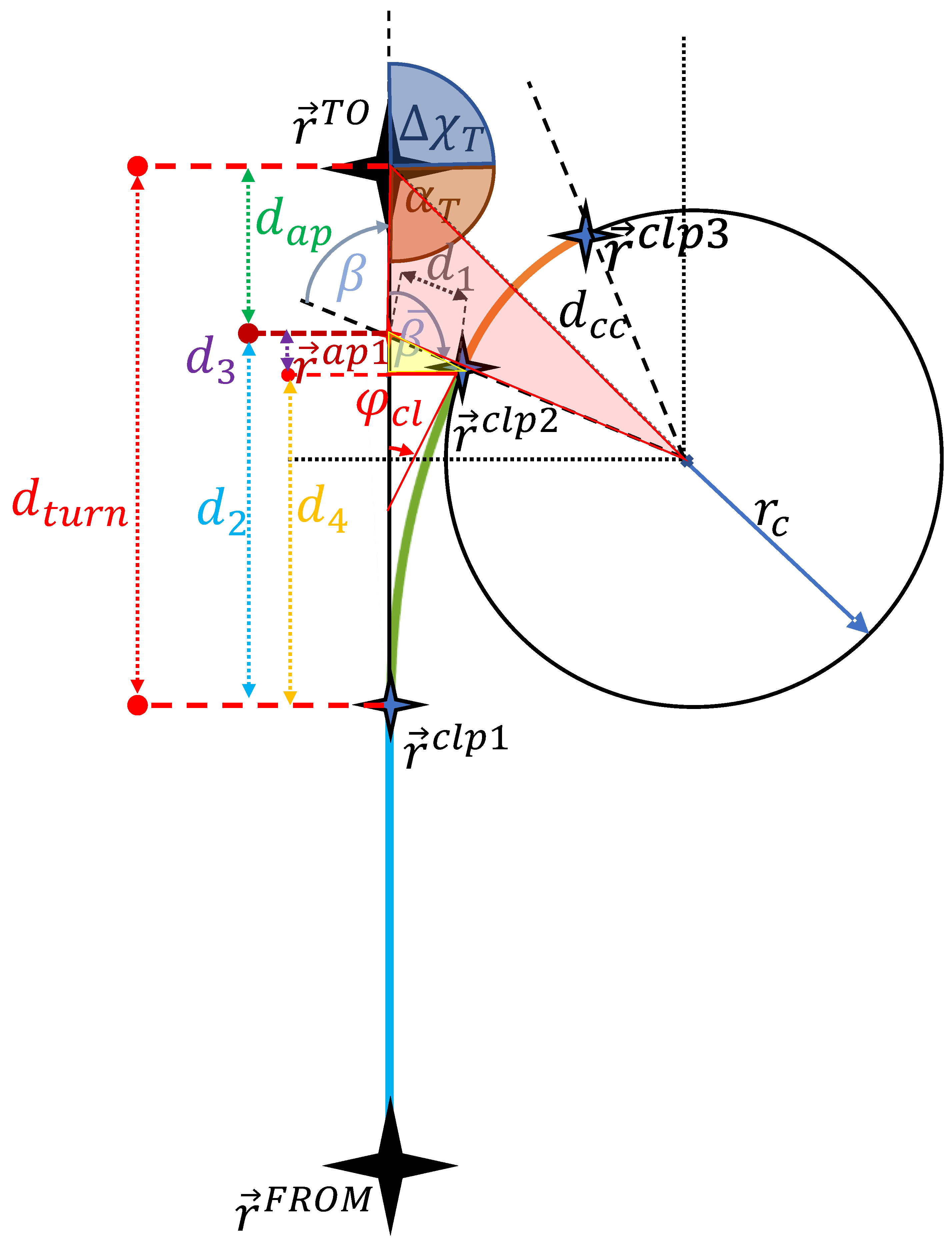
3.1.2. Implementation Considerations
- 1.
- Calculate the maneuver circle using Equation (34), where is defined during design.
- 2.
- Calculate the corresponding bank angle using Equation (33).
- 3.
- Calculate the clothoid transition time using Equation (35), where is the maximum achievable roll rate.
- 4.
- Calculate the clothoid shaping parameter A using Equation (40).
- 5.
- Calculate the clothoid running parameter (dimensionless time) using Equation (37).
- 6.
- Calculate the clothoid displacement using Equation (32).
- 7.
- Calculate the turn distance using Equation (52).
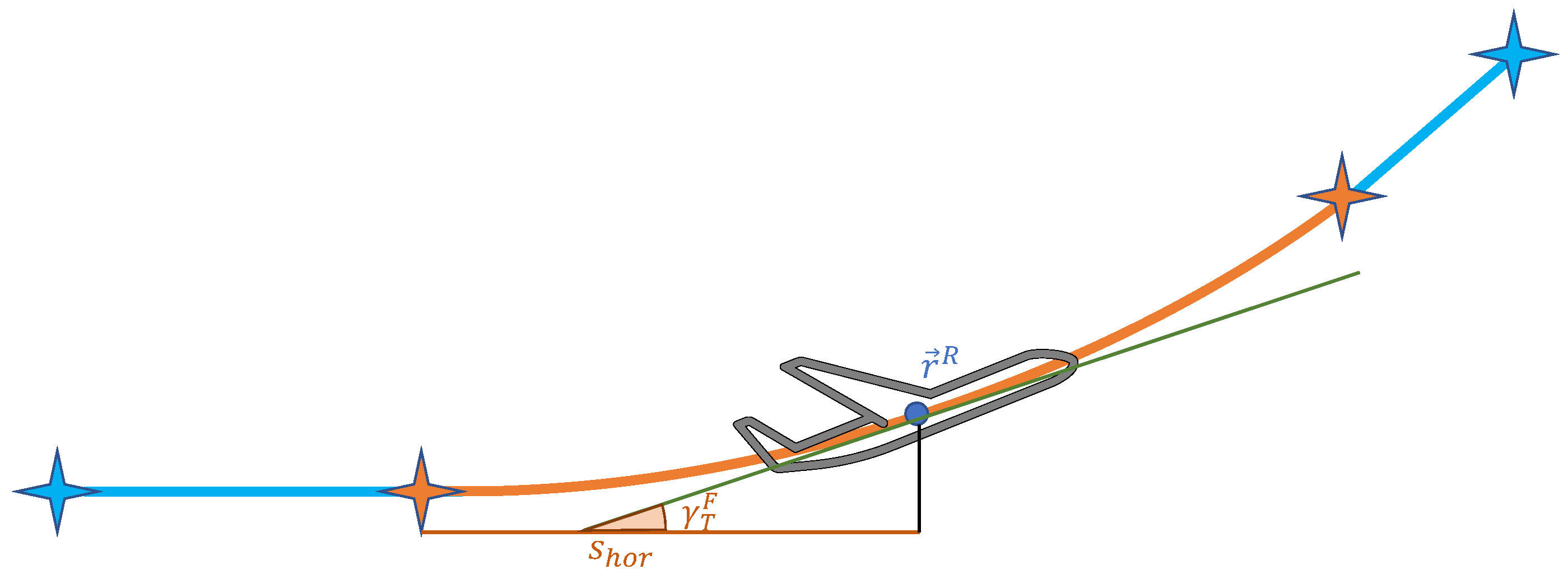
3.2. Vertical Plane
3.2.1. Altitude Polynomial Definition
3.2.2. Polynomial Coefficients
- ;
- ;
- .
4. Trajectory Construction: Flyby Implications for eVTOLs
4.1. Minimum Distance between Waypoints
- Aircraft speed : The slower the aircraft, the less distance we need to turn.
- Desired turn rate : The higher the turn rate, the less distance we need to turn.
4.2. Maximum Angle between Legs
4.2.1. Making the Turn Rate Dynamic
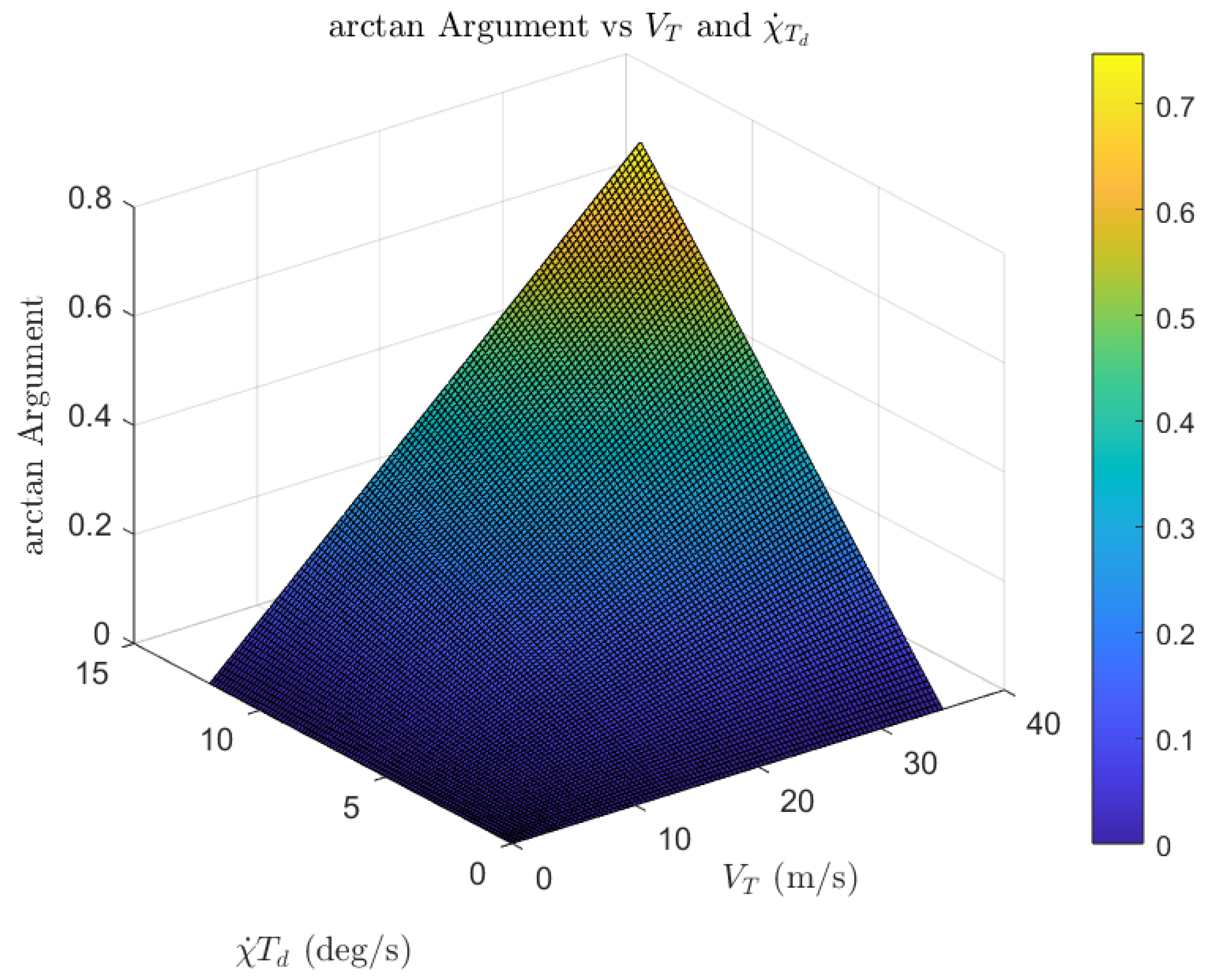
4.2.2. Integrating the Dynamic Turn Rate

5. Consolidation and Results
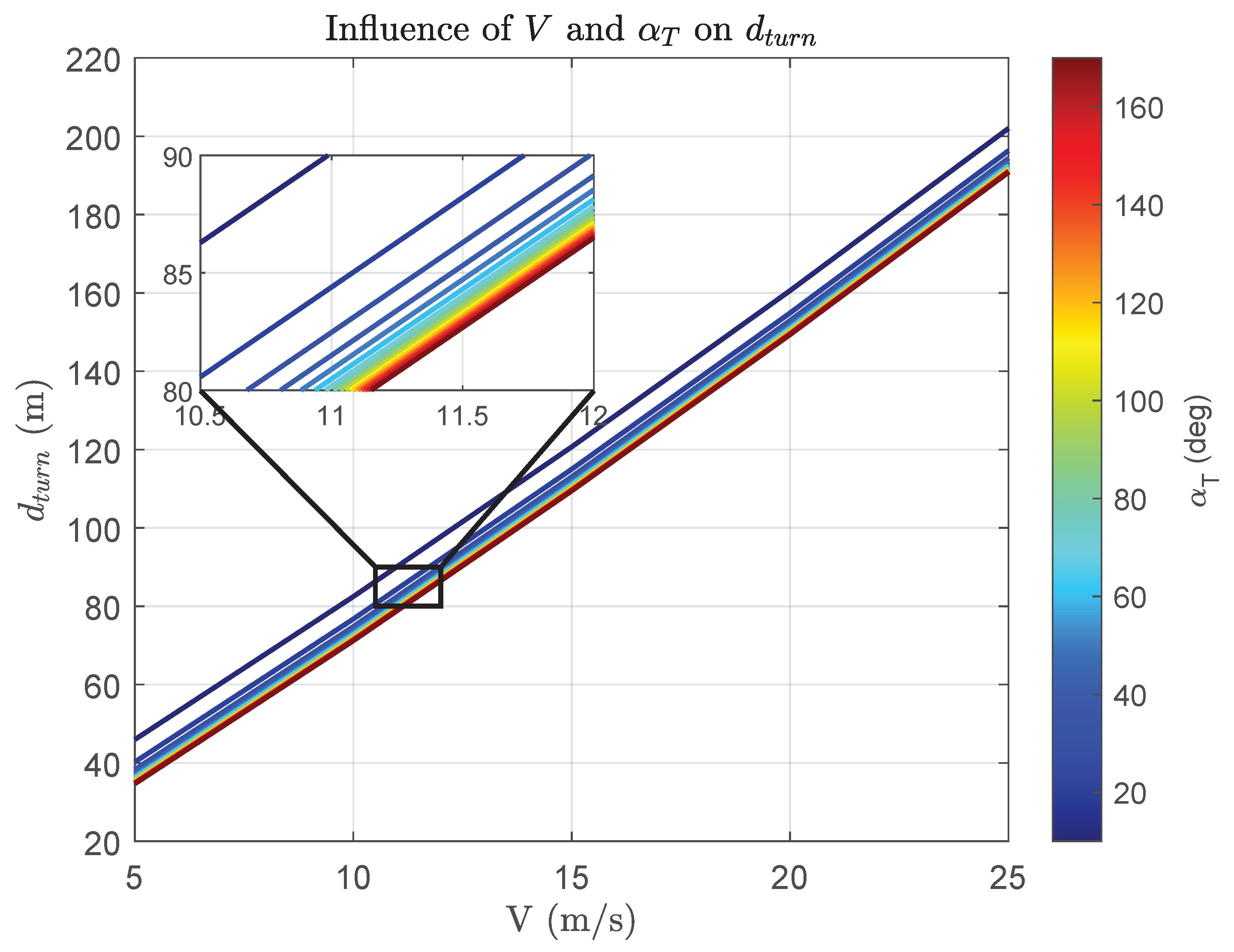
5.1. Turn Distance
- Roll rate command:
- Roll time constant: s
- Design turn rate:
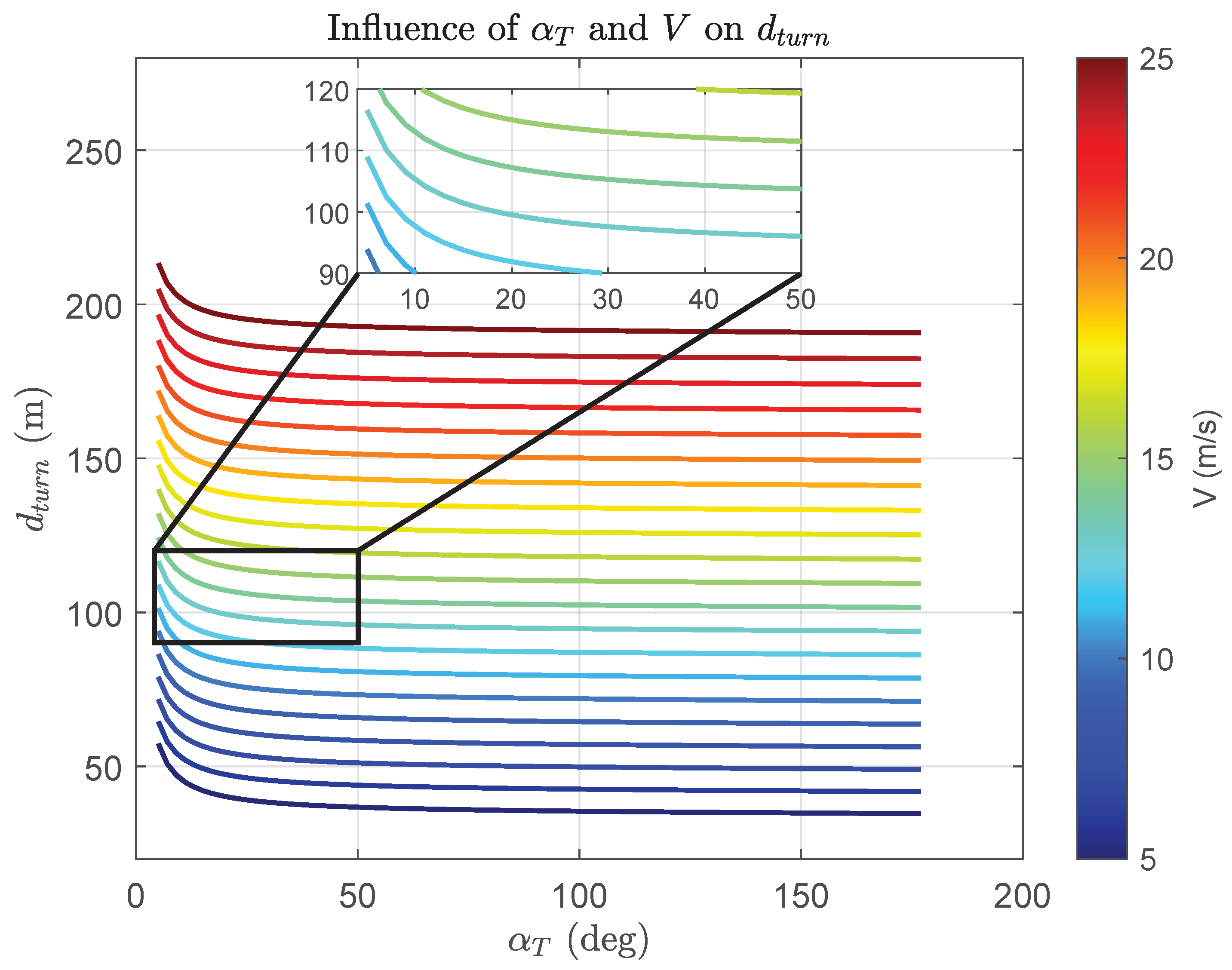

5.2. Maximum Angle between Legs
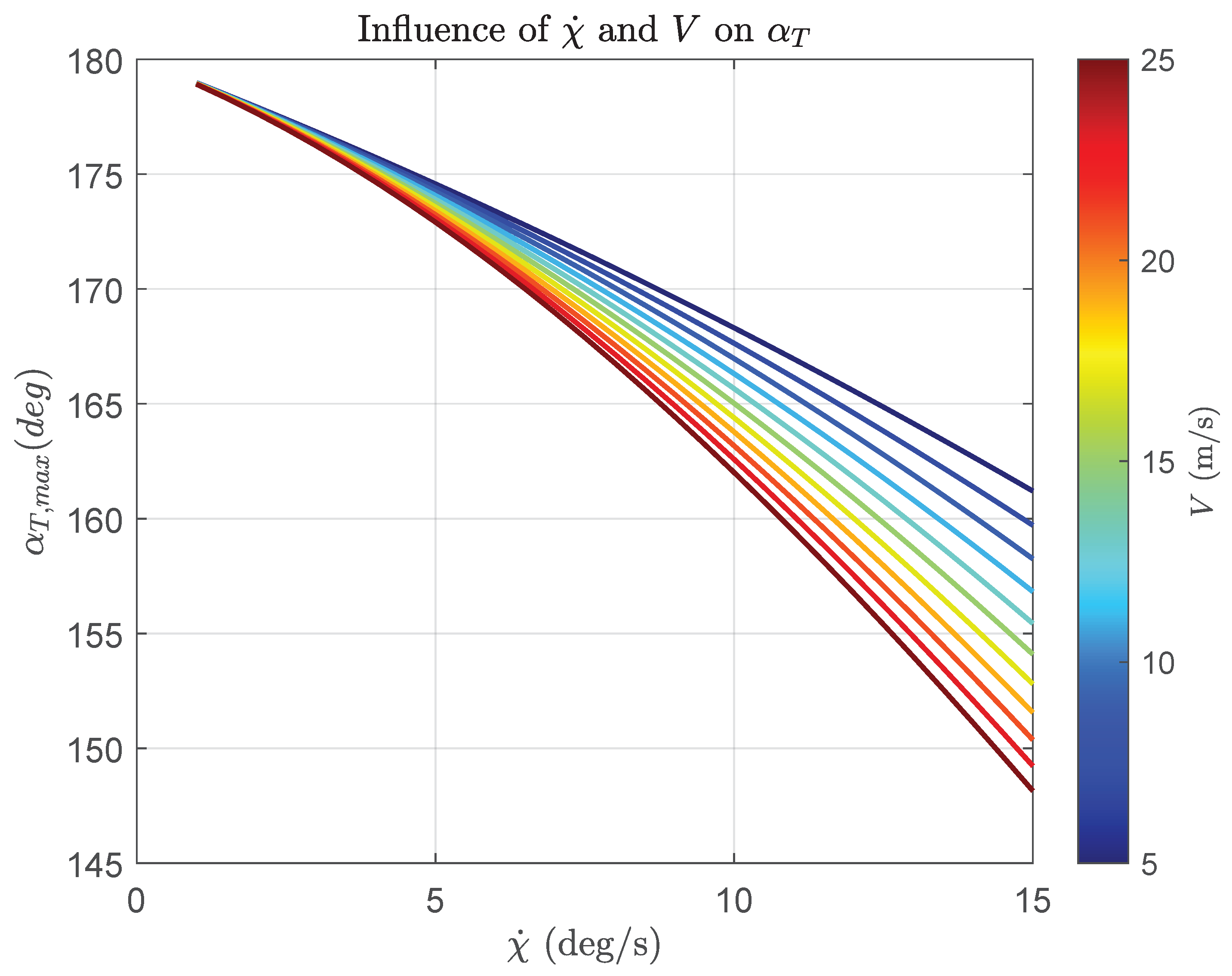

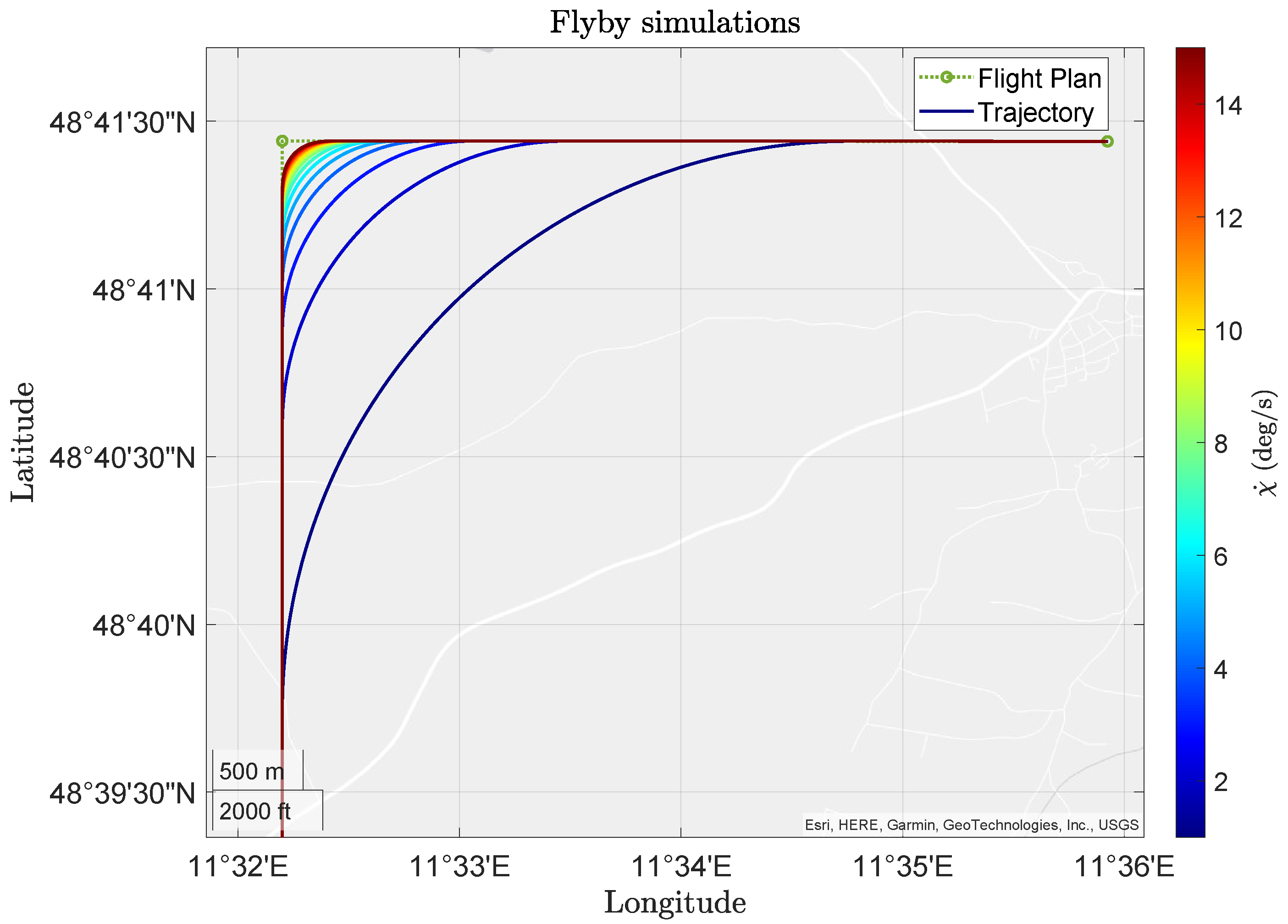
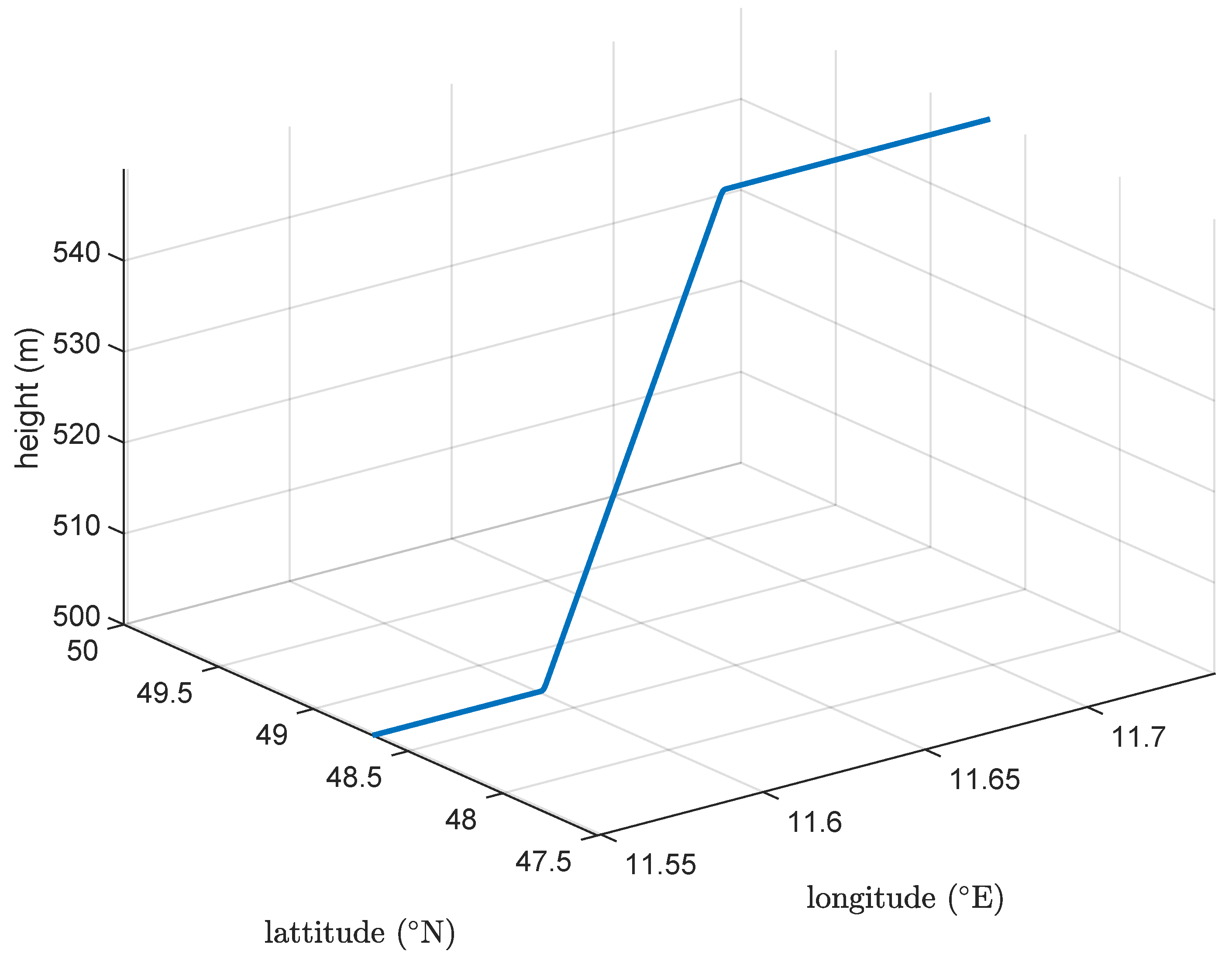
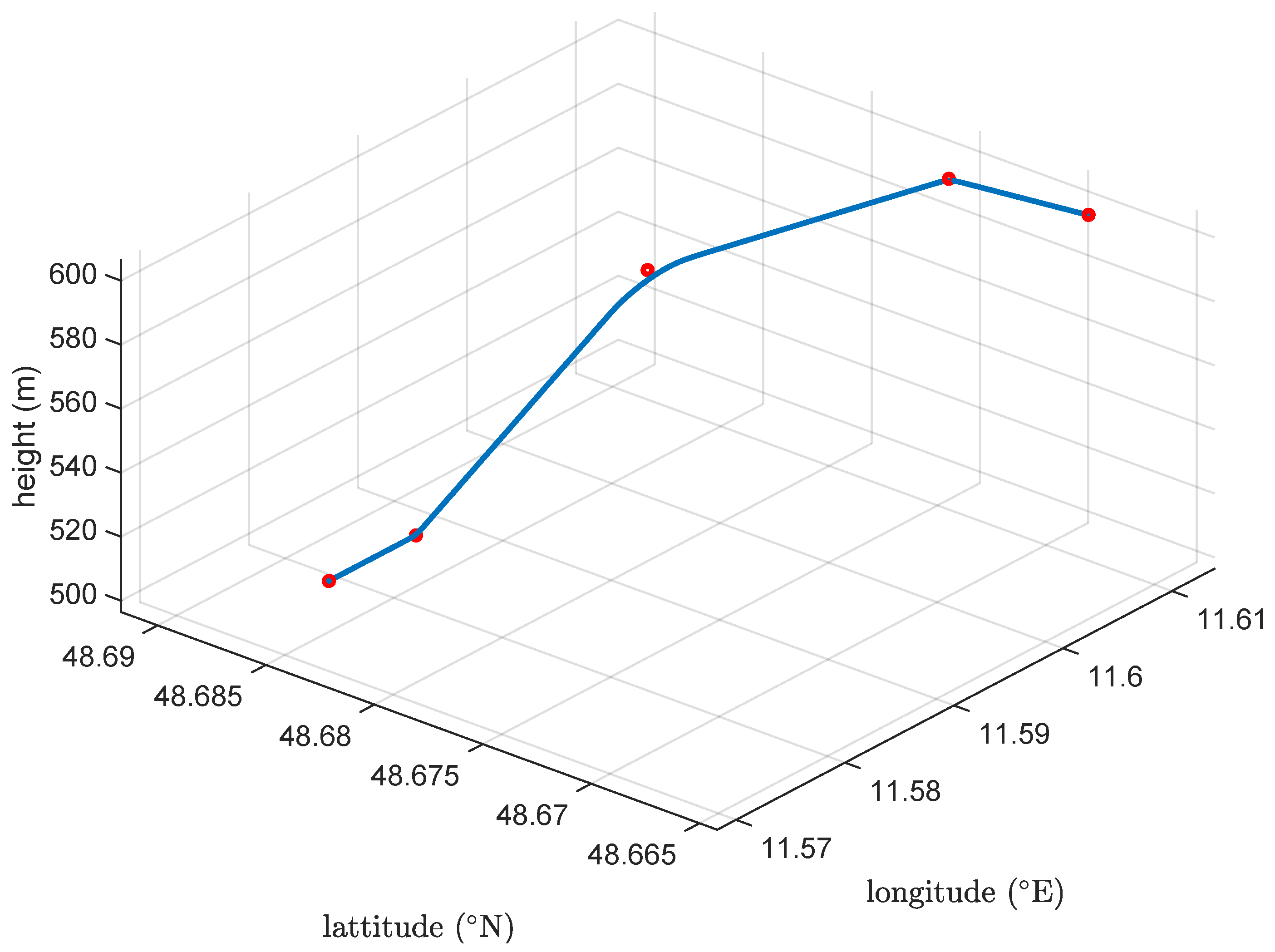
5.3. Simulation Results
5.3.1. Testing Environment Overview
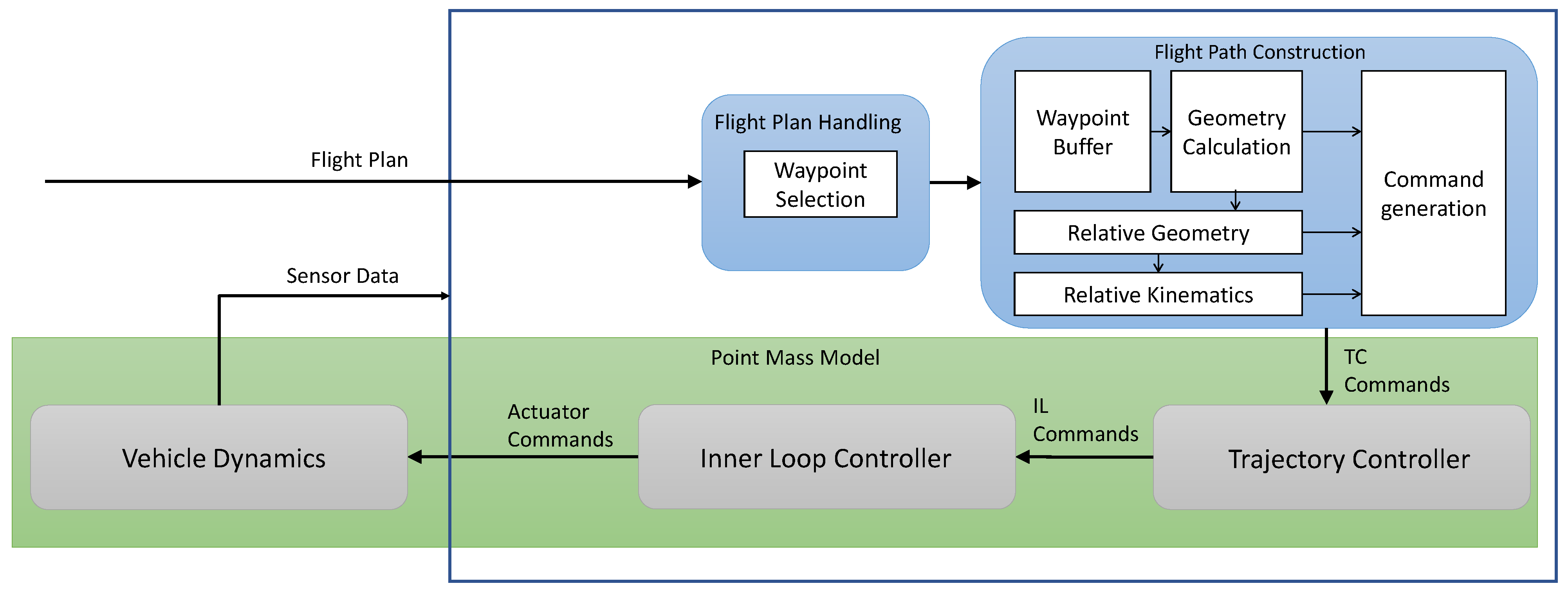
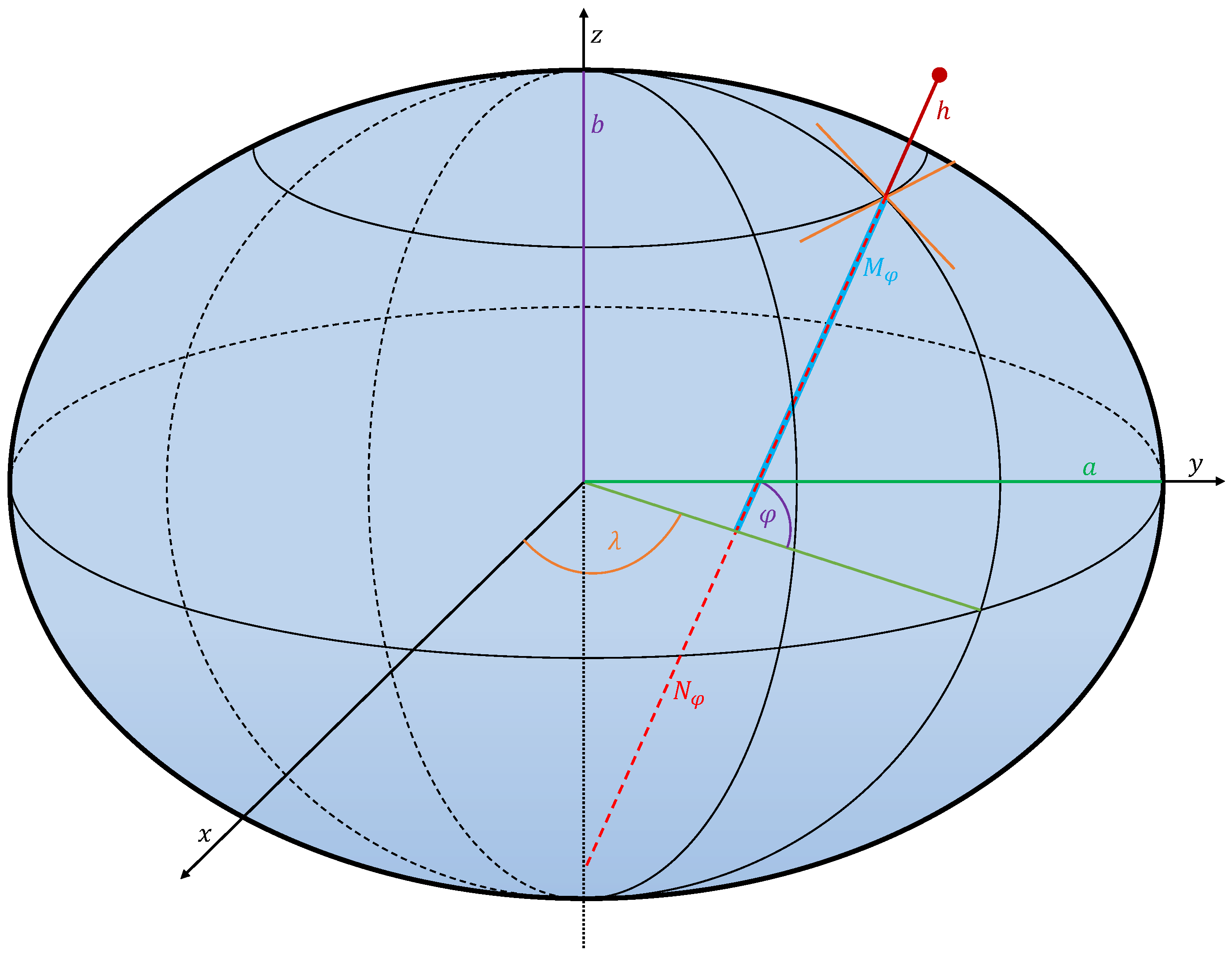
5.3.2. Point Mass Model
- The prime vertical radius of curvature, is:
- The meridian radius of curvature, is:where:
- is the latitude;
- m is the length of the semi-major axis;
- m is the length of the semi-minor axis;
- e is the first eccentricity, calculated as:where the flattening f is:
5.3.3. Results
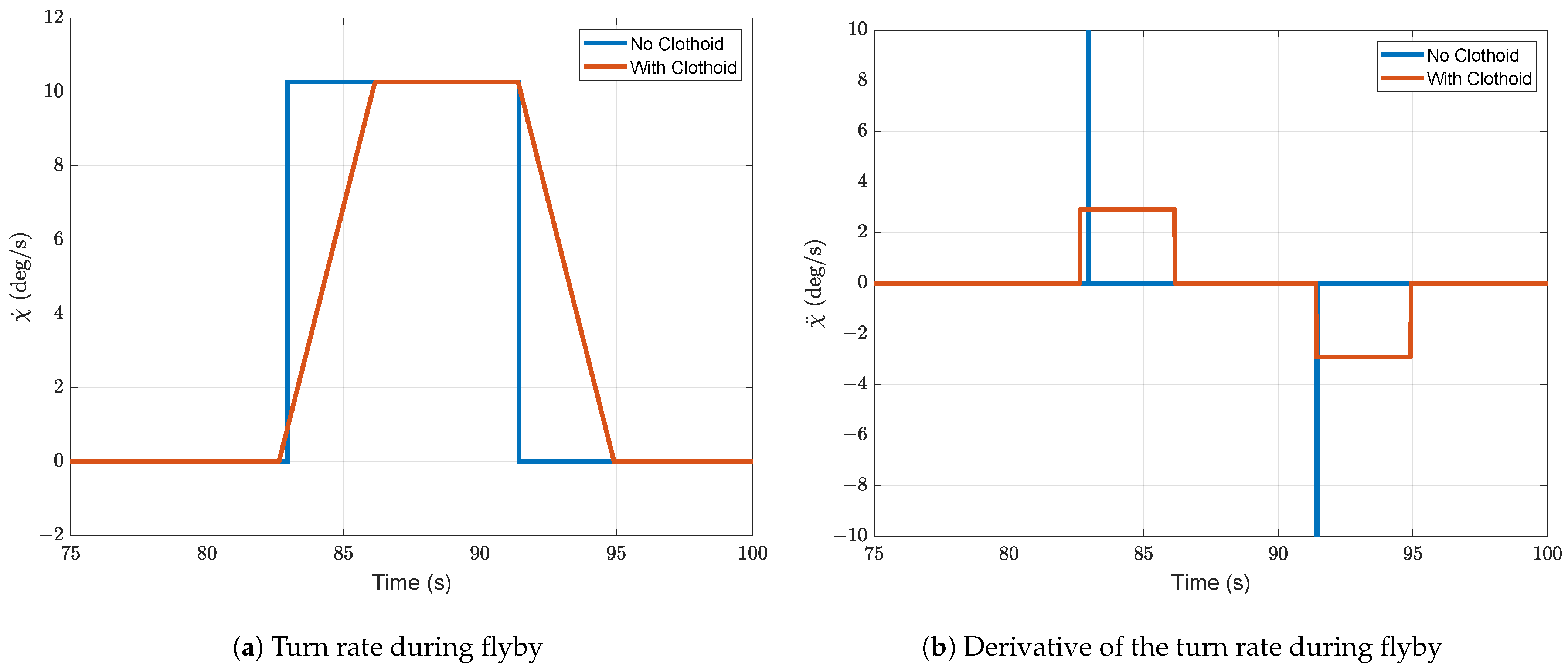
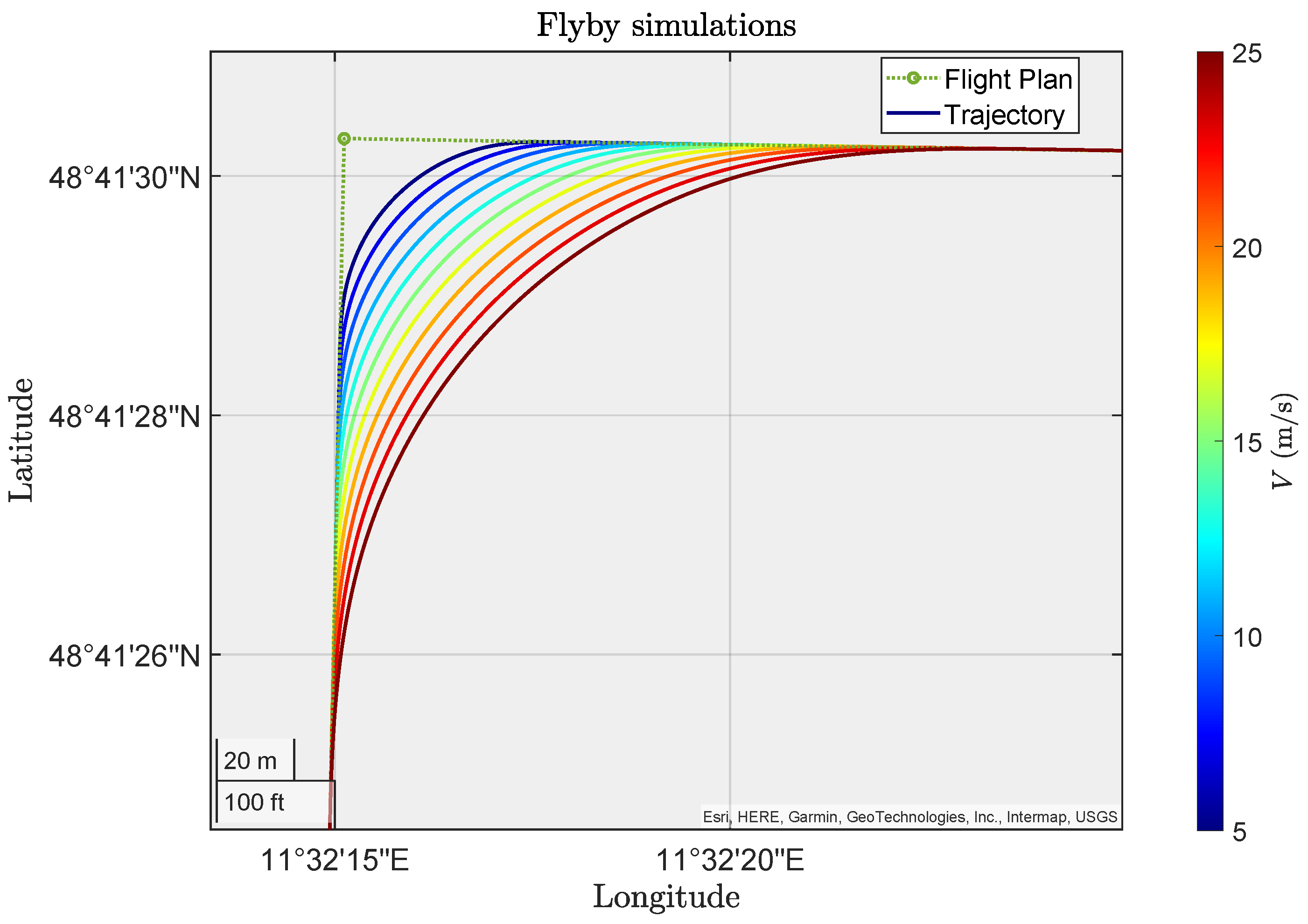

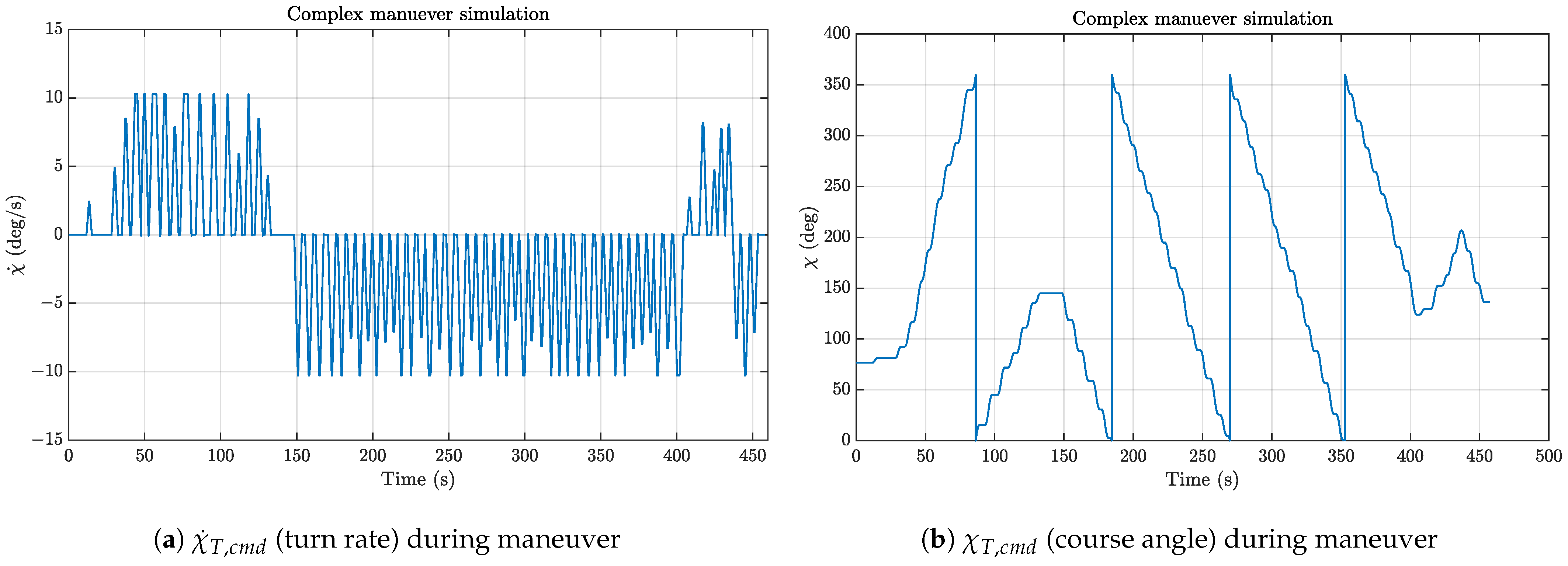
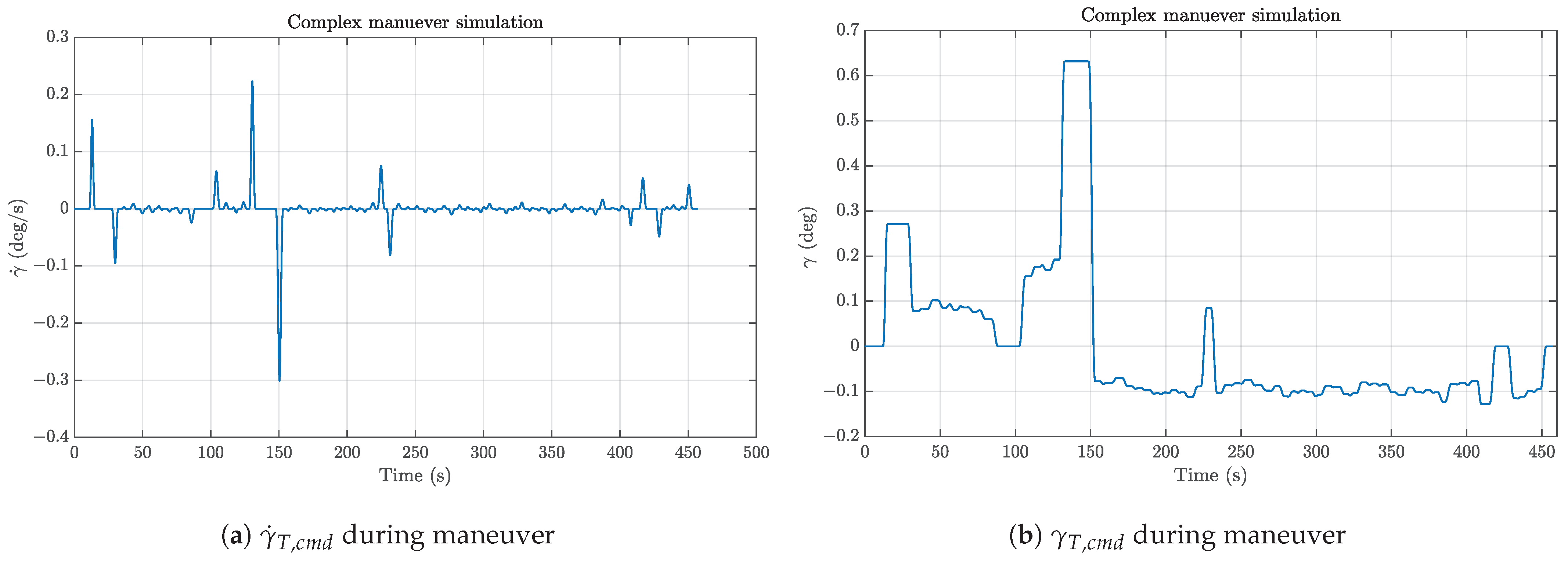
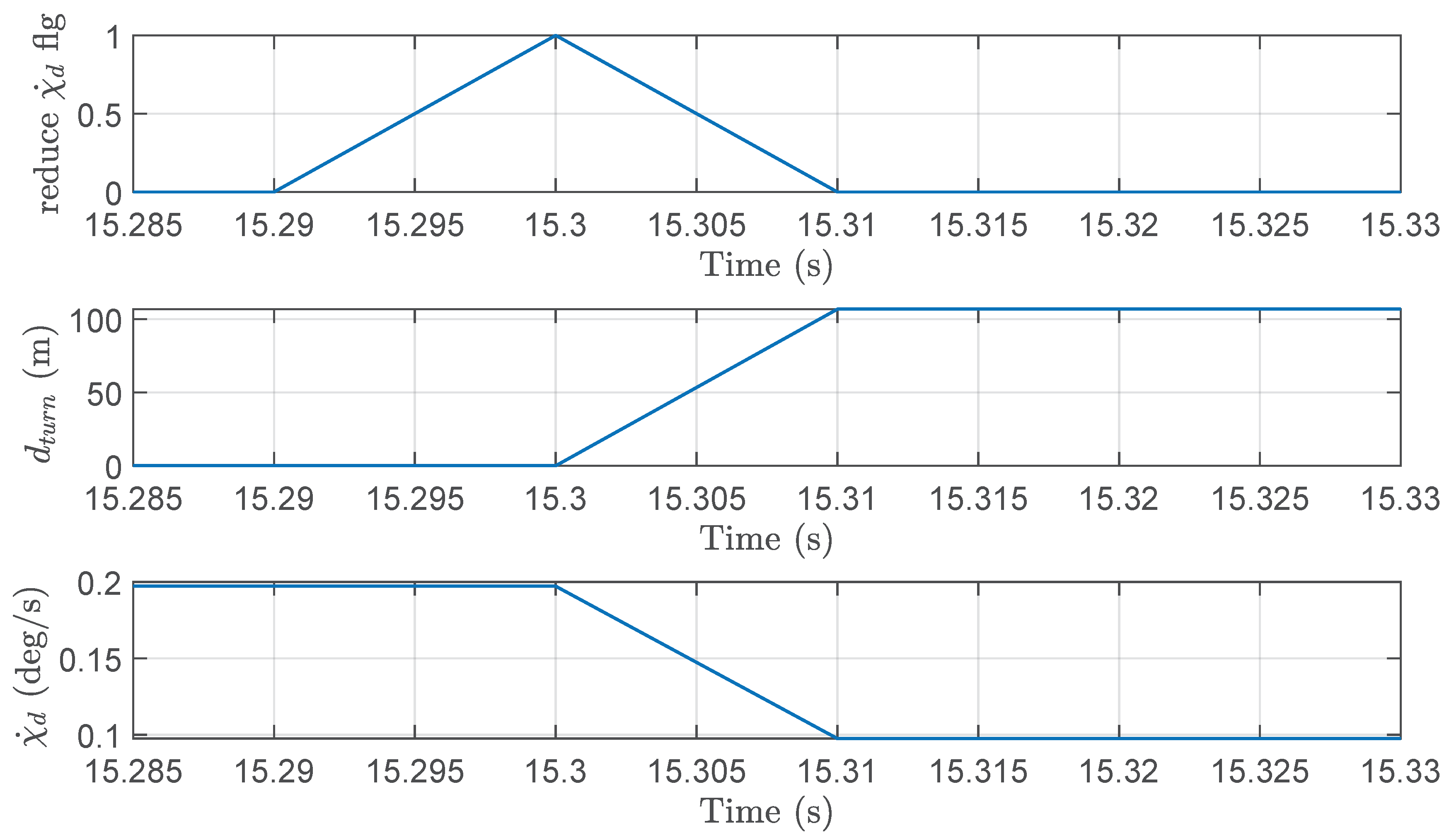
6. Conclusions
7. Recommendations for Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| eVTOL | Electric Vertical Take-Off and Landing |
| RRT | Rapidly exploring Random Tree |
| BLP | Bi-Level Programming |
| UAV | Unmanned Aerial Vehicle |
| TrajGen | Trajectory Generation |
| Symbol | |
| A | Clothoid shaping parameter |
| Coefficient of a polynomial | |
| Curve in a 2D Euclidean space | |
| Line coefficient for approximation of atan | |
| , | x- and y- components of a curve |
| Clothoid point n | |
| subscript | Command |
| Distance from the TO waypoint to the auxiliary point | |
| Distance from the TO waypoint to the center of the maneuver circle | |
| Turn distance | |
| subscript | Desired |
| gravity acceleration | |
| Altitude of a reference point F | |
| Meridian radius of curvature | |
| Prime vertical radius of curvature | |
| p | Roll rate |
| Radius of a maneuver circle | |
| s | Arc length of a curve |
| Distance traveled in the horizontal plane | |
| tangent vector | |
| Unit tangent vector | |
| Roll time constant | |
| Planning speed | |
| Buffer speed used for in the planning speed | |
| Kinematic speed | |
| , | Change in position of induced by a clothoid segment |
| Kinematic bank angle command | |
| Turn rate | |
| Change in course | |
| Angle between two legs in the flight plan | |
| Climb angle of a reference point F | |
| Bandwidth | |
| Running parameter/dimensionless time of a curve | |
| Kinematic course angle of a reference point R | |
| Longitude | |
| Curvature | |
| Angle representing change in direction over an arc length s |
References
- Goerzen, C.; Kong, Z.; Mettler, B. A survey of motion planning algorithms from the perspective of autonomous UAV guidance. J. Intell. Robot. Syst. 2010, 57, 65–100. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Devaurs, D.; Siméon, T.; Cortés, J. Optimal path planning in complex cost spaces with sampling-based algorithms. IEEE Trans. Autom. Sci. Eng. 2015, 13, 415–424. [Google Scholar] [CrossRef]
- LaValle, S.M.; James J Kuffner, J. Randomized Kinodynamic Planning. SageJournals 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, Y.L. Survey on computational-intelligence-based UAV path planning. Knowl.-Based Syst. 2018, 158, 54–64. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Satai, H.A.; Zahra, M.M.A.; Rasool, Z.I.; Abd-Ali, R.S.; Pruncu, C.I. Bézier Curves-Based Optimal Trajectory Design for Multirotor UAVs with Any-Angle Pathfinding Algorithms. Sensors 2021, 21, 2460. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zheng, Z.; Cai, K.Y. Bi-level programming based real-time path planning for unmanned aerial vehicles. Knowl.-Based Syst. 2013, 44, 34–47. [Google Scholar] [CrossRef]
- Bousson, K.; Machado, P.F. 4D trajectory generation and tracking for waypoint-based aerial navigation. WSEAS Trans. Syst. Control 2013, 3, 105–119. [Google Scholar]
- Hentschel, M.; Lecking, D.; Wagner, B. Deterministic path planning and navigation for an autonomous fork lift truck. IFAC Proc. Vol. 2007, 40, 102–107. [Google Scholar] [CrossRef]
- Schneider, V.; Piprek, P.; Schatz, S.P.; Baier, T.; Dörhöfer, C.; Hochstrasser, M.; Gabrys, A.; Karlsson, E.; Krause, C.; Lauffs, P.J.; et al. Online trajectory generation using clothoid segments. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Schneider, V.; Mumm, N.C.; Holzapfel, F. Trajectory generation for an integrated mission management system. In Proceedings of the 2015 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Bali, Indonesia, 3–5 December 2015; pp. 1–7. [Google Scholar]
- Schatz, S.P.; Schneider, V.; Karlsson, E.; Holzapfel, F.; Baier, T.; Dörhöfer, C.; Hochstrasser, M.; Gabrys, A.; Krause, C.; Lauffs, P.J.; et al. Flightplan flight tests of an experimental DA42 general aviation aircraft. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Schneider, V. Trajectory Generation for Integrated Flight Guidance. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2018. [Google Scholar]
- Casey, J. Exploring Curvature; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Walton, D.J.; Meek, D.S. A controlled clothoid spline. Comput. Graph. 2005, 29, 353–363. [Google Scholar] [CrossRef]
- Levien, R. The Euler Spiral: A Mathematical History; Technical Report No. UCB/EECS-2008-111; University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- Sendra, J.R.; Winkler, F. Symbolic parametrization of curves. J. Symb. Comput. 1991, 12, 607–631. [Google Scholar] [CrossRef]
- Peterson, J.W. Arc Length Parameterization of Spline Curves. J. Comput. Aided Des. 2006. Available online: http://www.saccade.com/writing/graphics/RE-PARAM.PDF (accessed on 10 December 2023).
- Morvan, J.M.; Morvan, J. Generalized Curvatures; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Alexander, D.C.; Koeberlein, G.M. Elementary Geometry for College Students; Cengage Learning: Singapore, 2014. [Google Scholar]
- Herman, E.; Strang, G. Calculus Volume 2; OpenStax: Houston, TX, USA, 2016. [Google Scholar]
- Farouki, R.T.; Pelosi, F.; Sampoli, M.L. Approximation of monotone clothoid segments by degree 7 Pythagorean–hodograph curves. J. Comput. Appl. Math. 2021, 382, 113110. [Google Scholar] [CrossRef]
- Sandoval-Hernandez, M.; Vazquez-Leal, H.; Hernandez-Martinez, L.; Filobello-Nino, U.; Jimenez-Fernandez, V.; Herrera-May, A.; Castaneda-Sheissa, R.; Ambrosio-Lazaro, R.; Diaz-Arango, G. Approximation of Fresnel integrals with applications to diffraction problems. Math. Probl. Eng. 2018, 2018, 4031793. [Google Scholar] [CrossRef]
- Abramson, J. Precalculus 2e; OpenStax: Houston, TX, USA, 2021. [Google Scholar]
- Euclid. Euclid’s Elements; 300 BC; Printed by Erhard Ratdolt; Green Lion Press: Santa Fe, Mexico, 1482. [Google Scholar]
- Heimsch, D.; Söpper, M.; Speckmaier, M.; Mbikayi, Z.; Kellringer, S.; Holzapfel, F. Development and Implementation of a Safety Gateway for a Medical Evacuation eVTOL Aircraft. In Proceedings of the 2024 AIAA AVIATION Forum, Las Vegas, NV, USA, 29 July–3 August 2024. [Google Scholar]
- McLain, T.; Beard, R.W.; Owen, M. Implementing dubins airplane paths on fixed-wing uavs. In Handbook of Unmanned Aerial Vehicles; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lugo-Cárdenas, I.; Flores, G.; Salazar, S.; Lozano, R. Dubins path generation for a fixed wing UAV. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 339–346. [Google Scholar]
- Sabetghadam, B.; Cunha, R.; Pascoal, A. Real-time trajectory generation for multiple drones using bézier curves. IFAC-PapersOnLine 2020, 53, 9276–9281. [Google Scholar] [CrossRef]
- Petit, P.J.; Wartmann, J.; Fragnière, B.; Greiser, S. Waypoint based online trajectory generation and following control for the ACT/FHS. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0918. [Google Scholar]
- Dmitriev, K.; Zafar, S.A.; Schmiechen, K.; Lai, Y.; Saleab, M.; Nagarajan, P.; Dollinger, D.; Hochstrasser, M.; Holzapfel, F.; Myschik, S. A lean and highly-automated model-based software development process based on do-178c/do-331. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–10. [Google Scholar]
- Piprek, P.; Schneider, V.; Fafard, V.; Schatz, S.P.; Dörhöfer, C.; Lauffs, P.J.; Peter, L.; Holzapfel, F. Enhanced kinematics calculation for an online trajectory generation module. Transp. Res. Procedia 2018, 29, 312–322. [Google Scholar] [CrossRef]
- Vanicek, P.; Krakiwsky, E.J. Geodesy: The Concepts; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Scherer, S.; Speckmaier, M.; Gierszewski, D.; Mishra, C.; Steinert, A.C.; Steffensen, R.; Wulf, S.; Holzapfel, F. AUTOMATIC TAKE-OFF AND LANDING OF A VERY LIGHT ALL ELECTRIC OPTIONALLY PILOTED AIRCRAFT. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences (ICAS), Stockholm, Sweden, 4–9 September 2022. [Google Scholar]
- Scherer, S.; Mishra, C.; Holzapfel, F. Extension of the capabilities of an automatic landing system with procedures motivated by visual-flight-rules. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences (ICAS), Stockholm, Sweden, 4–9 September 2022. [Google Scholar]
- Labakhua, L.; Nunes, U.; Rodrigues, R.; Leite, F.S. Smooth trajectory planning for fully automated passengers vehicles: Spline and clothoid based methods and its simulation. In Proceedings of the Informatics in Control Automation and Robotics: Selected Papers from the International Conference on Informatics in Control Automation and Robotics 2006; Springer: Berlin/Heidelberg, Germany, 2008; pp. 169–182. [Google Scholar]
- Aeronautical Radio, Inc. ARINC 424-20 Navigation System Database; Aeronautical Radio, Inc.: Annapolis, ML, USA, 2011. [Google Scholar]
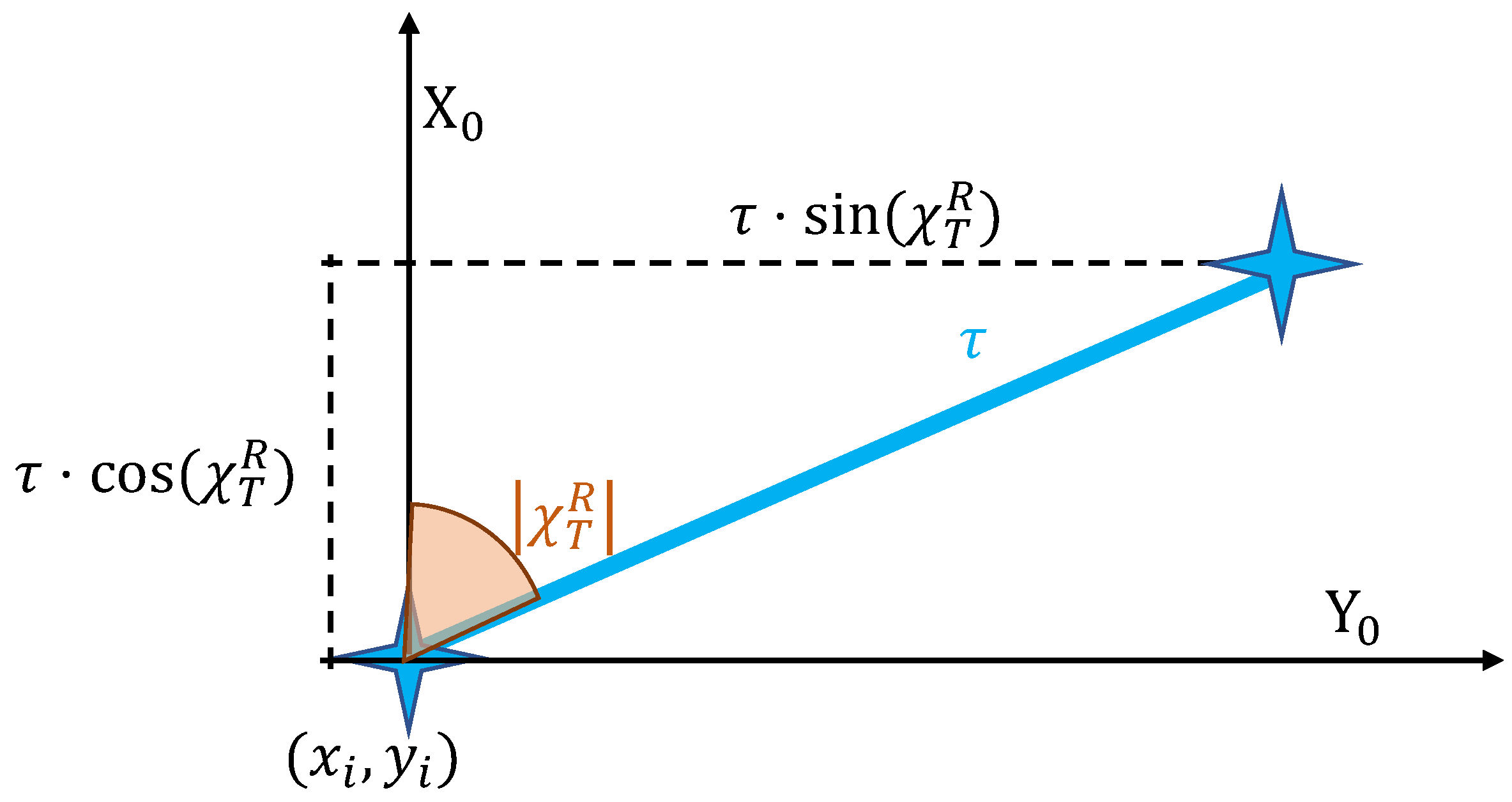









| Condition Parameter | Condition for | Condition for |
|---|---|---|
| 0 | 0 | |
| 0 | 0 | |
| 0 | 0 |
| Coefficient | Expression |
|---|---|
| 0 | |
| 0 | |
| 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mbikayi, Z.; Steinert, A.; Heimsch, D.; Speckmaier, M.; Rudolph, P.; Liu, H.; Holzapfel, F. Online Deterministic 3D Trajectory Generation for Electric Vertical Take-Off and Landing Aircraft. Aerospace 2024, 11, 157. https://doi.org/10.3390/aerospace11020157
Mbikayi Z, Steinert A, Heimsch D, Speckmaier M, Rudolph P, Liu H, Holzapfel F. Online Deterministic 3D Trajectory Generation for Electric Vertical Take-Off and Landing Aircraft. Aerospace. 2024; 11(2):157. https://doi.org/10.3390/aerospace11020157
Chicago/Turabian StyleMbikayi, Zoe, Agnes Steinert, Dominik Heimsch, Moritz Speckmaier, Philippe Rudolph, Hugh Liu, and Florian Holzapfel. 2024. "Online Deterministic 3D Trajectory Generation for Electric Vertical Take-Off and Landing Aircraft" Aerospace 11, no. 2: 157. https://doi.org/10.3390/aerospace11020157
APA StyleMbikayi, Z., Steinert, A., Heimsch, D., Speckmaier, M., Rudolph, P., Liu, H., & Holzapfel, F. (2024). Online Deterministic 3D Trajectory Generation for Electric Vertical Take-Off and Landing Aircraft. Aerospace, 11(2), 157. https://doi.org/10.3390/aerospace11020157








