Abstract
The T-WING project, a CS2-CPW (Clean Sky 2 call for core partner waves) research initiative within FRC IADP (Fast Rotor-Craft Innovative Aircraft Demonstrator Platform), focuses on developing, qualifying and testing the new wing of the Next-Generation Civil Tilt-Rotor (NGCTR). This paper introduces a case study about a methodology for refining the stick-beam model for the NGCTR wing, aligning it with the GFEM (Global Finite Element Model) wing’s dynamic characteristics in terms of modal frequencies and mode shapes. The initial stick-beam model was generated through the static condensation of the GFEM wing. The tuning process was formulated as an optimization problem, adjusting beam properties to minimize the sum of weighted quadratic errors in modal frequencies and Modal Assurance Criterion (MAC) values. Throughout the optimization, the MAC analysis ensured that the target modes were tracked, and, at each iteration, a new set of variable estimates were determined based on the gradient vector and Hessian matrix of the objective function. This methodology effectively fine-tunes the stick-beam model for various mass cases, such as maximum take-off weight (MTOW) and maximum zero-fuel weight (MZFW).
Keywords:
tiltrotor; wing; stick beam; structural dynamics; optimization; structural tuning; modal analysis; MAC 1. Introduction
The T-WING consortium designed and manufactured the wing of the Next-Generation Civil Tiltrotor Technology Demonstrator, shown in Figure 1, to take it to TRL6 through an experimental flight.

Figure 1.
NGCTR-TD.
A tiltrotor is an aircraft that combines the capability to hover, typical of helicopters, with the possibility for cruising flight at high speeds, like propeller-driven aircraft. It represents a concrete possibility to overcome the main limitations of helicopters and propeller aircraft by matching together the peculiarities of both of them [1,2].
Since the improvement of the performance in an aircraft mode is one of the focus points for the future developments of new tiltrotors, non-conventional configurations have to be investigated in order to preserve the performance in a helicopter mode.
The design and architecture of a tiltrotor configuration make it, from a general point of view, a step beyond the state of the art in terms of performance, design, architecture and product supportability. This aspect was confirmed by the US Government Accountability Office, according to which the tiltrotor was identified as a vehicle for the future long-range assault aircraft (FLRAA) [3].
A relevant point for improving the global permeance in both operative modes is related to the structural efficiency that can be achieved only through a radical change in the structural architecture and methodology design approach based on the use of different analysis techniques closely linked to each other. Owing to such a new design approach, it was possible to define a completely new structural architecture like the one presented below.
The present work was performed in the framework of the T-Wing project that aims to qualify the wing structure, shown in Figure 2, which includes the moveable surfaces, encompassing design, manufacturing and ground tests up to flight, in compliance with the technical specifications set by the Work Area Leader Leonardo Helicopters.
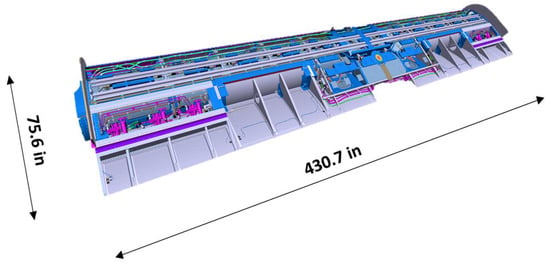
Figure 2.
NGCTR-TD wing.
The main innovations regarding the wing structure concern the highly integrated composite concept [4,5,6] and the presence of two mobile surfaces: one is an external flaperon while the other is a so-called morphing surface, which has the function of reducing the exposed wing area on the wing of the propellers’ slide in a helicopter mode. All of these characteristics lead to a rather compact wing structure since the largest moving surface extends to almost half of the wing chord.
The several requirements to be fulfilled, often in conflict with each other, make the tiltrotor wing one of the most critical airframe subsystems of the entire aircraft. Indeed, like in any airworthy structure, the wing subsystem needs to guarantee the minimum weight requirement while meeting the strength, buckling and stiffness requirements [7].
Another specific concern of tiltrotors is the airframe mode placement [8]: the modes that involve significant movements of the hub center in the rotor disc plane directions (usually caused by the local deformation of the rotor and nacelle supporting structure) shall have their frequency outside of prescribed bands to avoid forced-response oscillations. In addition, the frequency of the lowest elastic airframe mode shall not be lower than a prescribed value to avoid coupling with aeromechanical modes.
The wing design needs to consider the interaction between wing, pylon and rotor systems to achieve aircraft aeroelastic stability [9]. In aircraft mode, wing flexural and torsional stiffness has a fundamental role in pitch-whirl stability.
Indeed, the structural sizing of the wing for the Next-Generation Civil Tiltrotor Technology Demonstrator (NGCTR-TD) requires careful consideration of aeroelastic instabilities, specifically whirl flutter, which is inherent to tiltrotors [10]. Aeroelastic and dynamic analyses play a crucial role in sizing, design and obtaining approval for flight permits. The reliability of the dynamic model of the wing is paramount in this context.
Throughout the design evolution, aeroelastic analyses were initially conducted on a finite element (FE) beam-like model with 1D elements. This model was manually constructed and updated iteratively until the design was finalized. As the design progressed, a coarse FE model consisting of 2D elements (GFEM) was developed. While this GFEM provided a high level of reliability in terms of structural frequencies and mode shapes, it proved computationally burdensome, especially with an increasing number of calculation cases. The time required for a single run with the GFEM model could be more than ten times longer compared to a run with a simpler stick-beam model.
Stick-beam models, commonly employed in civil aircraft design and multidisciplinary design optimizations (MDOs) [11], offer a quicker alternative for dynamic analysis, but at the cost of reduced result fidelity. The accuracy of stick-beam models depends on the evaluation of stiffness properties, including the main structure and the elastic axis of the beam elements. Various methods, such as those outlined in Refs. [11,12,13], have been proposed for stiffness and mass matrix reduction, but they often lack precision in determining the physical distribution of parameters along the real structure.
To address these limitations, Ref. [14] introduces a method incorporating two displacement contributions: the motion of a reference section of the beam and a three-dimensional warping field. Ref. [15] provides a general solution for the cross-section without assuming a redundant displacement field, while, starting from a known wing structure, Ref. [11] reviewed different methodologies to create wing stick-beam models. However, these methods still face challenges in accurately determining the real physical distribution of parameters.
This paper presents a methodology developed to tune the structural stick-beam model of the NGCTR-TD’s green wing (identifying as green wing the standalone wing structure, with no movable surfaces installed and with no system masses). The objective is to achieve a precise match, in terms of mode shapes and modal frequencies, between the original GFEM and the reduced-order stick-beam model. This alignment is essential to enable the use of the stick-beam model in activities such as massive load computation via aeroelastic simulations. While significantly reducing simulation time, the methodology ensures that the reliability and fidelity of the analyses remain comparable to those conducted with the higher-resolution GFEM. Figure 3 illustrates both the GFEM and the stick-beam green-wing models.
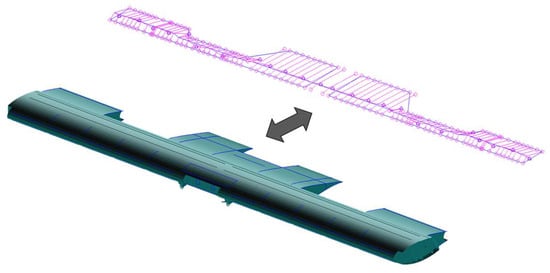
Figure 3.
Green-wing GFEM and stick-beam models.
The tuned green-wing stick-beam model, the output of the tuning process, is then exploited for the dynamic analysis performed to support the vibration tests of the wing and for speeding up the aeroelastic analysis performed with a full model for load computation.
2. Methodology
The primary objective of the developed tuning process, as outlined in the present paper, is to align the behavior of a stick-beam model of the wing with that of the GFEM wing, focusing on eigenfrequencies and mode shapes. This alignment is achieved by adjusting the structural properties of the beams within the stick-beam model. The tuning process is formulated as an optimization problem, starting from an initial guess derived from the output of a static condensation applied to a stick-beam model.
It is noteworthy that the structural mass of the green wing has not been factored into the tuning process. This decision was made due to the adoption of identical distributions of concentrated masses for both the GFEM and the stick-beam green-wing models. This approach simplifies the tuning process, as it ensures consistency in the consideration of mass properties between the two models.
2.1. GFEM Dynamic Model
The GFEM that has been considered as a reference for the tuning of the stick-beam model, shown in Figure 4, is a high-fidelity model of the wing composed mainly of 2D membrane elements (MSC Nastran [16] CQUAD4 elements) used to model the composite parts of the wing as panels, spar webs and ribs and 1D bar elements (MSC Nastran CBAR elements) used to model the spar caps.

Figure 4.
Global FE model of the wing-box. (Left): 3D view; (Bottom Right): top view; (Top Right): bottom view.
In total, 83760 nodes, 73232 CQUAD4 elements and 1923 CBAR elements have been used to model the wing. The fasteners connecting, for example, the wing panels to the spars and the ribs have been modeled using CBUSH elements connected to the components via MPC elements. The average element size considered in the wing FE model is equal to 50 mm. Such a value has been defined according to a convergence mesh study (not reported in this context for the sake of brevity) which aims to evaluate the best ratio between stress distribution detail and computational cost.
The elements used to model the wing do not have any density assigned since the structural mass has been modeled using concentrated masses (MSC Nastran CONM2 elements) which have been connected to the wing-box, as shown in Figure 5, via interpolation elements (MSC Nastran RBE3 elements).

Figure 5.
GFEM mass connection to the wing-box.
Some details of the GFEM wing-box, like the models of the connections between the wing-box and the fuselage or the tip rib of the wing, which represents the connection to the nacelle, are shown in Figure 6.

Figure 6.
Details of the GFEM. (Right): wing to fuselage connection; (Left): tip rib.
The mechanical properties of the adopted materials are reported in Table 1, Table 2, Table 3 and Table 4. The reported material properties are derived from experimental test campaigns, performed by Magnaghi Aeronautica, and they represent the material data adopted for the wing design. Therefore, they include all standard knockdown factors for aeronautical application (statistics, environmental conditions, damage, etc.) [17].

Table 1.
Mechanical properties of fabric CFRP-CYTEC 977-2-42-3KT300D-8H-372-1524.

Table 2.
Mechanical properties of UD CFRP.

Table 3.
Mechanical properties of honeycomb in sandwich structure.

Table 4.
Mechanical properties of Al7050-T7451.
Moreover, several parts, like the nose rib, the leading edge, and the tip and root ribs, are made of aluminum alloy Al7050-T7451 (Table 4).
2.2. Stick-Beam Dynamic Model
The stick-beam model of the wing-box, the object of the tuning process described in the present paper and shown in Figure 7, is composed of 1D beam elements (MSC Nastran CBEAM elements) and rigid elements (MSC Nastran RBE2 elements) distributed along the span in the chord direction for visualization purposes, in order to ease the recognition of the torsional modes clarifying the rotation of the sections of the wing-box. In total, 285 nodes, 82 CBEAM elements and 96 RBE2 elements have been used to model the wing-box.
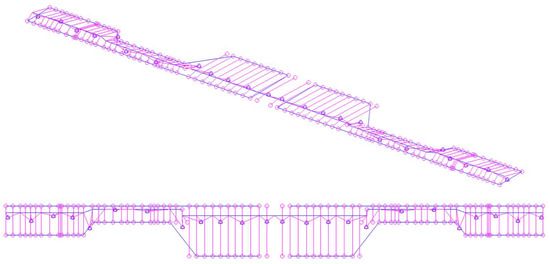
Figure 7.
Stick-beam model of the wing-box. (Top): 3D view; (Bottom): top view.
The stiffness of the different beams has been defined using Nastran PBEAM cards, directly specifying the structural properties of the beam (i.e., area of the beam cross-section A, out-of-plane area moment of inertia I1, in-plane area moment of inertia I2, area product of inertia I12 and polar moment of inertia J).
Coherently with the GFEM wing-box, no density has been defined for the stick-beam elements since the mass has been applied to the structure by means of concentrated masses (same CONM2 elements used for the GFEM) connected to the wing-box via interpolation elements (MSC Nastran RBE3 elements). In Figure 8, it is possible to see the wing concentrated masses, highlighted in green, connected to the wing beams (blue lines) by means of RBE3 elements (pink lines).

Figure 8.
Stick-beam model mass connection to the wing-box beams.
2.3. Structural Tuning as an Optimization Problem
In order to achieve the goal, the tuning process has been set up as an optimization problem where the variables (x ∈ Rn, n is the number of variables) of the problem are the beam structural properties in terms of cross-section area moments of inertia: out-of-plane area moment of inertia I1, in-plane area moment of inertia I2, cross-product I12 and polar moment of inertia J. These properties subsequently drive the stiffness properties of the beams of the model. On the other hand, the objective function (f ∈ R) has been defined as the sum of the weighted quadratic errors of both frequencies and MAC values.
The percent error between the eigenfrequency of the i-th mode (fi) and the target eigenfrequency of the i-th mode (fi*) is computed as shown in Equation (1), while the MAC values are computed as shown in Equation (2), where ϕi is the modal vector of the i-th mode and ϕi* is the target modal vector of the i-th mode.
The definition of the objective function is shown in Equation (3):
where fi is the eigenfrequency of the i-th mode, wi are the error weights, MACi is the MAC value of the i-th mode and qi* is the target eigenfrequency of the i-th mode.
The MAC values are calculated as a function of ϕi and ϕi* (mode shapes of target modes), while the error weights are defined manually by the user and satisfy the constraint shown in Equation (4).
Once the objective function has been minimized, these weights are useful for defining the best trade-off among the errors of the final model (see Ref. [18] for further details and applications).
In this particular case, due to the fact that the objective function f is expressed in a non-explicit formulation (Nastran must be run and frequencies must be read from the result files at each iteration), the calculation of the function f is considered as a black box where only the inputs (x) and output (f) are known. Since gradient-based algorithms work well for continuous variable problems [19] (continuous variable problems are usually smoother and differentiable, meaning that a gradient-based algorithm could be used to find a solution efficiently, i.e., fast and accurately enough even for problems with many variables), a gradient-based solver has been used. The gradient vectors and Hessian matrices of the function f must be calculated numerically: the derivative terms have to be evaluated through finite differences or similar methods at each iteration.
2.4. Tuning Process
Due to the fact that at each iteration the beam structural properties change with respect to the previous one, the structural model is technically different, and the order of the modes could change. For this reason, to preserve the coherency between target modes and current modes of the tuned model, it is necessary to properly track the modes at each iteration using a MAC analysis that permits the identification of the correct modes whose frequency and shape have to be addressed for the computation of the objective function .
The methodology adopted for the tuning process is summarized in Figure 9. The optimization starts with an initial guess of the variables (beam properties contained in the stick-beam model output of a static condensation), re-writes the Nastran model with these variables, runs a modal analysis (Nastran Sol-103) and reads the eigenfrequencies and mode shapes. Finally, it selects frequencies and mode shapes of the modes of interest (target modes) via a MAC analysis and computes the new objective function. In case the iteration does not comply with the convergence criteria, a new guess of the variables is estimated as a function of the gradient and Hessian of the objective function.
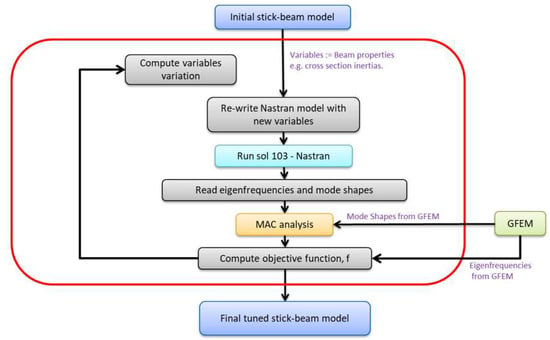
Figure 9.
Tuning methodology flowchart.
Considering the geometry of the stick-beam model (i.e., no sweep, dihedral and incidence angles), bending modes are mainly driven by the out-of-plane area moment of inertia I1, fore–aft modes are mainly driven by the in-plane area moment of inertia I2 and torsion modes are mainly driven by the polar moment of inertia J. Therefore, as shown in Figure 10, the optimization tool has been set up to perform, as a first step, three parallel tunings (1.A, 1.B and 1.C) which help to find a better guess of the variables I1, I2 and J. As a second step, a main tuning (2.Final) is performed, involving all the variables of the problem (I1, I2, J, I12) simultaneously.
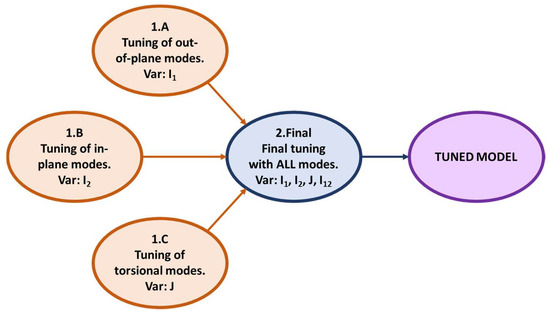
Figure 10.
Logic of the tuning process.
2.5. Target Modes
For the definition of the objective function, only some of the modes of the GFEM green wing are selected as targets, picking only the most important and relevant modes in terms of the dynamic characterization of the wing. The eigenmodes of both the stick-beam green wing and GFEM green wing have been computed considering the models free–free, thus unconstrained.
In fact, a correct representation of the wing dynamics is fundamental for performing aeroelastic analysis with a sufficient level of reliability, with the coupling between the aerodynamics of the wing and the wing’s structural deformation being the key point of this activity. Nevertheless, exploiting the knowledge gained from the studies that have been conducted during the years [20,21,22], it is possible to identify which modes of the wing are the drivers of the aeroelastic behavior and which modes can be neglected. For example, the bending modes and the torsional modes can dangerously couple and generate aeroelastic instabilities like flutter. Furthermore, as the rotors of this machine are installed on the tips of the wing, the fore–aft modes can be drivers of whirl-flutter phenomena since these modes involve a significant movement of the wing tips.
On the other hand, the high-frequency modes (frequency above 120 Hz) can be safely considered negligible in terms of impact on the aeroelastic behavior of the wing: considering the nominal cruise speed of this type of machine and its mean aerodynamic chord, according to the definition of reduced frequency reported in Equation (5) where c is the mean aerodynamic chord and V is the flight speed, these modal frequencies would translate into unreasonably high reduced frequencies, way outside of the range of coupling between the structure and aerodynamics.
In fact, the physical meaning of a very high reduced frequency corresponds to a significant offset between the characteristic frequency of the aerodynamics of the wing and the frequency of the structural vibrations, denying the possibility of coupling between the two of them.
The eight modes that have been pre-selected as target modes are shown in Table 5 together with their modal frequencies and description.

Table 5.
Target mode optimization process.
2.6. Results
The results of the tuning process in terms of frequency percent error and MAC values for each target mode are shown in the following tables. Table 6 reports the results of the initial guess model (output of the static condensation) while Table 7 reports the results of the tuned green wing.

Table 6.
Errors in frequencies and MAC values of the initial guess.

Table 7.
Errors in frequencies and MAC values of the tuned green wing.
A comparison between some mode shapes of the target modes of the GFEM and the tuned stick-beam model is shown in Figure 11, Figure 12, Figure 13 and Figure 14.

Figure 11.
First bending sym. (Left): GFEM. (Right): stick beam.

Figure 12.
First fore–aft sym. (Left): GFEM. (Right): stick beam.

Figure 13.
First bending anti. (Left): GFEM. (Right): stick beam.

Figure 14.
First torsion anti. (Left): GFEM. (Right): stick beam.
The very low frequency percent errors and MAC values of the stick-beam wing model show a very good result in terms of the dynamic representativeness of the GFEM wing. Of course, it was not possible to achieve frequency errors close to 0 and MAC values close to 1 for all the target modes since a trade-off was necessary during the optimization phase in order to provide the best possible results for all the modes, and to increase the results of some modes, it was necessary to penalize some others. Nevertheless, the tuning process was able to provide satisfactory results in terms of the dynamic representation of all the target modes of the GFEM wing.
3. Verification
To validate the developed methodology for tuning the stick-beam green-wing model, three distinct steps have been undertaken. The first step involves assessing the dynamic behavior, considering modal frequencies and mode shapes, through a comparison between the full aircraft model incorporating the target GFEM wing and the aircraft model with the tuned stick-beam wing. The second step includes an aeroelastic check, examining the aeroelastic behavior, specifically through V g diagrams, of the two aforementioned aircraft models. The third and final check comprises a comparison of the static behavior between the GFEM green wing and the tuned stick-beam green wing.
The details of each validation step are elaborated in the following paragraphs.
3.1. Full Model Dynamic Check
The first check that has been performed is based on the comparison between frequencies and MAC values, for the target modes, of the two full aircraft models with the target GFEM wing and the tuned stick-beam wing integrated.
The comparison, in terms of frequencies and MAC values for both full-fuel and zero-fuel mass conditions, is shown in Table 8 and Table 9, respectively.

Table 8.
Full A/C target mode verification—full fuel.

Table 9.
Full A/C target mode verification—zero fuel.
The observed increase in the relative error in frequency, compared to the results presented in the previous section, can be attributed to the absence of consideration for the link between the fuselage and wing during the tuning process of the isolated wing. As a result, a dedicated complete aircraft tuning becomes imperative to enhance these results, especially if the application demands coupled wing–fuselage dynamics. It is acknowledged that the tuned stick-beam model of the isolated wing may exhibit limitations in accurately replicating the complete aircraft’s dynamic behavior due to the exclusion of fuselage interactions. However, it is important to highlight that the validity of the tuned stick-beam model for the isolated wing remains well suited for its intended purpose, which is to faithfully replicate the dynamic behavior of the GFEM wing. This suitability is particularly valuable for conducting component experimental vibration tests. In scenarios where coupled wing–fuselage dynamics are crucial, further tuning efforts involving the complete aircraft model would be necessary to achieve a more comprehensive and accurate representation of the dynamic characteristics.
3.2. Full Model Aeroelastic Check
Flutter calculations have been performed with the full aircraft models with the target GFEM wing and the tuned stick-beam wing integrated.
The calculations have been carried out at Mach number 0.40 at sea level, and all the modes with frequencies smaller than 40 Hz have been considered. The V g diagrams of the GFEM model and the stick-beam model, considering for the plots the target modes only, are shown in Figure 15 and Figure 16, where the blue lines and the red lines represent, respectively, the modal damping and the modal frequency of each mode depending on the flight speed.
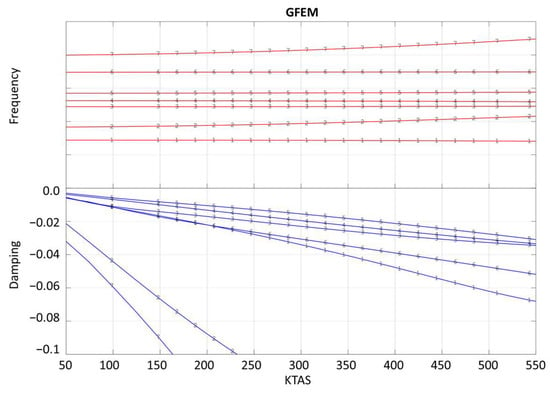
Figure 15.
Frequency and damping vs. speed diagram: GFEM wing.
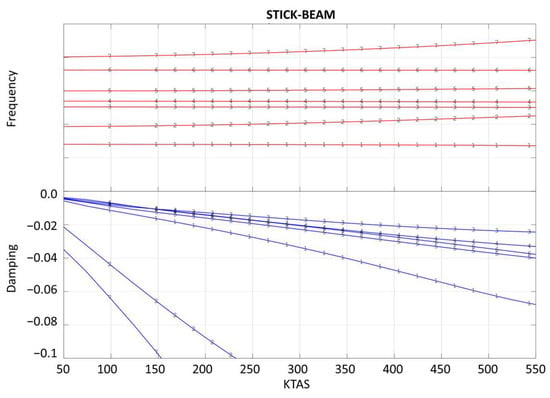
Figure 16.
Frequency and damping vs. speed diagram: stick-beam wing.
The diagrams depict a commendable alignment in terms of frequency and damping variations as the flight speed increases, especially for modes characterized by a small relative frequency error and high MAC values. Consistent with expectations, modes exhibiting a larger relative frequency error and smaller MAC values, such as the fifth mode on the V g diagram, demonstrate less precise matching of frequency and damping variations with respect to the flight speed. This outcome aligns with anticipated results, reinforcing the understanding that modes with greater discrepancies in frequency and lower MAC values may exhibit less accurate alignment in response to changes in flight speed.
3.3. Static Check
For a comprehensive analysis, a static assessment was conducted by comparing the static responses to unitary loads (vertical and horizontal forces applied to the wing tip) among the GFEM wing (referred to as GFEM), the pre-tuning stick-beam wing (referred to as Stick: Initial guess) and the tuned stick-beam wing (referred to as Stick: Tuned). The objective was to evaluate any errors introduced from a static perspective due to the dynamic tuning of the wing.
It is essential to note that the initial guess for the stick-beam model is derived from a static condensation of the GFEM wing, inherently representing the best possible approximation of the static behavior. Consequently, the adjustments made to the beam structural properties by the optimizer, aimed at enhancing the dynamic behavior of the wing, naturally impact its static response.
This static check provides valuable insights into the compromise between dynamic and static performance resulting from the tuning process. While the initial guess stick beam excels in static representation, the tuned stick beam, designed for improved dynamic behavior, may exhibit variations in static response due to the introduced modifications in structural properties. This assessment contributes to a holistic understanding of the trade-offs associated with the dynamic tuning of the wing.
The wing displacements in the vertical direction of the different models caused by a vertical force applied to the wing tip are shown in Figure 17.
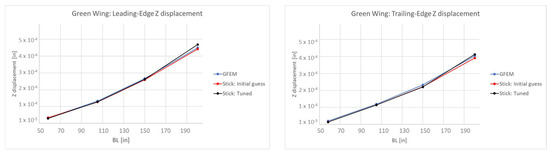
Figure 17.
Vertical displacement on the wing tip. (Left): green-wing leading edge. (Right): green-wing trailing edge.
Table 10 summarizes the percent errors in the vertical displacements of the wing tips of the different models, reporting the percent errors in terms of the difference between the vertical wing tip displacements on the leading edge and trailing edge of the initial guess stick-beam model and tuned-wing stick-beam model with respect to the vertical wing tip displacement of the GFEM wing.

Table 10.
Percent error in wing tip vertical displacement.
The wing displacements in the horizontal direction of the different models caused by a horizontal force applied to the wing tip are shown in Figure 18.
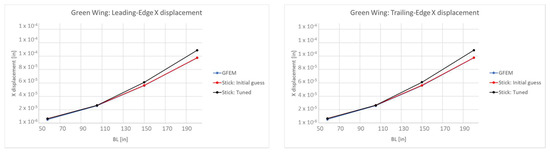
Figure 18.
Horizontal displacement on the wing tip. (Left): green-wing leading edge. (Right): green-wing trailing edge.
Table 11 summarizes the percent errors in the horizontal displacements of the wing tips of the different models, reporting the percent errors in terms of the difference between the horizontal wing tip displacements on the leading edge and trailing edge of the initial guess stick-beam model and tuned-wing stick-beam model with respect to the horizontal wing tip displacement of the GFEM wing.

Table 11.
Percent error in wing tip horizontal displacement.
As expected, the pre-tuning stick-beam green wing outperforms the tuned stick-beam wing from a static standpoint. This outcome is in line with expectations and can be attributed to the fact that the initial guess is derived from a static condensation of the GFEM wing. Consequently, the initial guess stick-beam model provides the most accurate representation of the static behavior of the GFEM wing. The tuning process, focused on aligning the stick-beam model with the dynamic behavior of the GFEM, naturally compromises the static representativeness of the model. It is crucial to reiterate that the primary objective of the optimization process is the enhancement of the dynamic behavior of the model, specifically for dynamic simulations. Therefore, the trade-off involving a reduction in static fidelity is considered an acceptable compromise in pursuit of improved dynamic performance. The tuned stick-beam wing is tailored for dynamic simulations, and any sacrificed static representativeness is deemed reasonable given the targeted application and objectives of the optimization process.
4. Conclusions
This paper introduces a methodology developed to create a tool capable of fine-tuning a stick-beam model with the specific objective of matching predefined modes, both in terms of frequencies and mode shapes, with a more intricate GFEM model. The structural tuning optimization tool was applied to refine the stick-beam model of the green wing of the NGCTR-TD, yielding commendable results in terms of modal frequency matching and MAC values. Notably, percent errors in frequencies ranged between 2% and 5%, while MAC values were consistently high, ranging from 0.96 to 0.99 for most modes. Slightly higher errors were observed only for one very-high-frequency mode. This successful tuning process accurately represents the dynamic behavior of the GFEM wing, enabling the use of the stick-beam green wing to support the dynamic test campaign conducted on the isolated wing.
Subsequently, the tuned stick-beam model of the green wing was integrated into the complete aircraft stick-beam model to evaluate its representativeness from an aeroelastic standpoint, targeting the overall aircraft GFEM behavior. The assessment yielded positive results in terms of matching. However, for a more reliable tuned stick-beam full aeroelastic model, it is essential to perform wing tuning considering the entire aircraft, encompassing the dynamic models of the fuselage and the wing-to-fuselage junction.
Finally, an analysis of the static behavior of the tuned stick-beam dynamic model was conducted to evaluate any deviations introduced from a static perspective during the dynamic tuning of the wing. Given that the initial guess of the stick-beam model is derived from a static condensation of the GFEM wing, it inherently provides the best possible representation of the static behavior. As anticipated, modifications to the beam structural properties introduced by the optimizer, aimed at enhancing the dynamic behavior, naturally incur a penalty in terms of static response. While the dynamically tuned model does not exhibit superior static performance, this compromise is deemed acceptable, given that the optimization process’s primary goal is the improvement of the dynamic behavior for limited application in dynamic simulations.
Author Contributions
Conceptualization, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; methodology, J.B.; software, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; validation, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; formal analysis, J.B.; investigation, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; resources, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; data curation, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; writing—original draft preparation, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; writing—review and editing, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; visualization, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; supervision, J.B., A.C. (Andres Cardozo), N.P., A.C. (Antonio Chiariello) and M.B.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Clean Sky 2 Joint Undertaking under the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement number: 945542—GAM-2020-FRC—H2020-IBA-CS2-GAMS-2019/H2020-IBA-CS2-GAMS-2019 Amendment Reference No. AMD-945542-10.
Data Availability Statement
The authors of this paper are unable to share the raw/processed data used in this study due to legal and proprietary concerns. Readers should however feel free to reach out to the authors for additional information within the constraints that the authors have on sharing of data.
Conflicts of Interest
Author Jacopo Beretta is employed by IBK-INNOVATION. Authors Andres Cardozo and Nicola Paletta have previously been employed by IBK-INNOVATION. All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| AC | Aircraft |
| FE | Finite Element |
| GFEM | Global Finite Element Model |
| LE | Leading Edge |
| MAC | Modal Assurance Criterion |
| MTOW | Maximum Take-Off Weight |
| MZFW | Maximum Zero Fuel Weight |
| NGCTR-TD | Next-Generation Civil Tilt-Rotor Technology Demonstrator |
| TE | Trailing Edge |
| TRL | Technology Readiness Level |
References
- Ward, R. The Long Road to the Tiltrotor. Available online: https://www.ainonline.com/aviation-news/business-aviation/2018-04-06/long-road-tiltrotor (accessed on 15 January 2024).
- Bauranov, A.; Rakas, J. Designing airspace for urban air mobility: A review of concepts and approaches. Prog. Aerosp. Sci. 2021, 125, 100726. [Google Scholar] [CrossRef]
- Roque, A. Sikorsky-Boeing’s FLRAA Bid Was Much Cheaper, but Couldn’t Offset ‘Unacceptable’ Design Metric: GAO, Breaking Defense. Available online: https://breakingdefense.com/2023/04/sikorsky-boeings-flraa-bid-was-much-cheaper-but-couldnt-offset-unacceptable-design-metric-gao/ (accessed on 14 April 2023).
- Waddoups, M.; Jackson, S.; Rogers, C. The Integration of Composite Structures into Aircraft Design. J. Compos. Mater. 1972, 6, 174–190. [Google Scholar] [CrossRef]
- Belardo, M.; Beretta, J.; Marano, A.D.; Diodati, G.; Paletta, N.; Di Palma, L. On the Preliminary Structural Design Strategy of the Wing of the Next-Generation Civil Tiltrotor Technology Demonstrator. Int. J. Aeronaut. Space Sci. 2020, 22, 613–624. [Google Scholar] [CrossRef]
- Belardo, M.; Marano, A.D.; Beretta, J.; Diodati, G.; Graziano, M.; Capasso, M.; Ariola, P.; Orlando, S.; Di Caprio, F.; Paletta, N.; et al. Wing Structure of the Next-Generation Civil Tiltrotor: From Concept to Preliminary Design. Aerospace 2021, 8, 102. [Google Scholar] [CrossRef]
- Wang, Z.; Wan, Z.; Groh, R.M.; Wang, X. Aeroelastic and local buckling optimisation of a variable-angle-tow composite wing-box structure. Compos. Struct. 2020, 258, 113201. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, L.; Qu, X.; Wang, L. Time-varying linear control for tiltrotor aircraft. Chin. J. Aeronaut. 2018, 31, 632–642. [Google Scholar] [CrossRef]
- Yang, C.; Xia, P. Aeroelastic stability of wing/pylon/rotor coupled system for tiltrotor aircraft in forward flight. Sci. China Technol. Sci. 2011, 54, 2708–2715. [Google Scholar] [CrossRef]
- Dong, L.; Li, Q. Whirl Flutter Suppression of Tiltrotor Aircraft Using Actively Controlled Aileron. Aerospace 2022, 9, 795. [Google Scholar] [CrossRef]
- Elsayed, M.S.A.; Sedaghati, R.; Abdo, M. Accurate Stick Model Development for Static Analysis of Complex Aircraft Wing-Box Structures. AIAA J. 2009, 47, 2063–2075. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C. Coupling of Substructures for Dynamic Analysis. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- Giavotto, V.; Borri, M.; Mantegazza, P.; Ghiringhelli, G.; Carmaschi, V.; Maffioli, G.; Mussi, F. Anisotropic beam theory and applications. Comput. Struct. 1983, 16, 403–413. [Google Scholar] [CrossRef]
- Morandini, M.; Chierichetti, M.; Mantegazza, P. Characteristic Behavior of Prismatic Anisotropic Beam via Generalized Eigenvectors. Int. J. Solids Struct. 2010, 47, 1327–1337. [Google Scholar] [CrossRef]
- MSC Nastran Quick reference Guide. Available online: https://help-be.hexagonmi.com/bundle/MSC_Nastran_2022.1_Quick_Reference_Guide/raw/resource/enus/MSC_Nastran_2022.1_Quick_Reference_Guide.pdf (accessed on 12 November 2023).
- Federal Aviation Authority. Airworthiness Advisory Circular No: 20-107B. Change 1. 2010. Compos. Aircr. Struct. 2009, 9, 2009. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentID/99693 (accessed on 24 August 2010).
- Royster, L.A.; Hou, G. Gradient-Based Trade-Off Design for Engineering Applications. Designs 2023, 7, 81. [Google Scholar] [CrossRef]
- Lung, S.F.; Pak, C.G. Structural Model Tuning Capability in an Object-Oriented Multidisciplinary Design, Analysis, and Optimization Tool; NASA/TM-2008-214640; NASA Dryden Flight Research Center: Edwards, CA, USA, 2008. [Google Scholar]
- Goland, M. The Flutter of a Uniform Cantilever Wing. J. Appl. Mech. 1945, 12, A197–A208. [Google Scholar] [CrossRef]
- Striz, A.G.; Venkayya, V.B. Influence of structural and aerodynamic modeling on flutter analysis. J. Aircr. 1994, 31, 1205–1211. [Google Scholar] [CrossRef]
- Heinze, S.; Borglund, D. Robust Flutter Analysis Considering Mode Shape Variations. J. Aircr. 2008, 45, 1070–1075. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).