Air and Structural Loads Analysis of a 5-Ton Class Rotorcraft in a Pull-Up Maneuver Using CFD/CSD Coupled Approach

Abstract

The air and structural loads of a 5-ton class light helicopter (LH) rotor in a 2.24 g pull-up maneuver are investigated using a coupling between the computational structural dynamics (CSD) and computational fluid dynamics (CFD) methods. The LH rotor is characterized by a five-bladed system with elastomeric bearings and inter-bladed dampers. The periodic trim solution along with the converged CFD/CSD delta airloads obtained in steady-level flight (advance ratio of 0.287) are used to perform the transient CSD maneuver analysis. The resulting vehicle attitude angles and velocity profiles of the aircraft are then prescribed in the quasi-static (QS) CFD maneuver analysis. It is demonstrated that the present QS approach provides an effective means for the maneuver loads’ analysis. The important flow behaviors such as BVI (blade–vortex interaction)-induced oscillations and the negative pitching moment peaks met in maneuver flight are captured nicely with the proposed method. Either the vortex trajectories or the surface pressure distributions are examined to identify the sources of the oscillations. A loose CFD/CSD coupling (LC) is used to predict the blade elastic motions, structural moments, and pitch link loads at the specified maneuver revolution of the rotor and also to correlate these with the transient CSD-based predictions. A reasonable correlation is obtained. The LC results show more pronounced 5P (five per revolution) oscillations on the structural response than those of the CSD-based methods.

1. Introduction

Recently, a 5-ton class light helicopter (LH) which is based on the earlier platform of H155B by AH (Airbus Helicopter) [1] has been under development in South Korea. Figure 1 shows the conceptual image of the LH prototype vehicle. The rotor has a five-bladed articulated hub with a radius and chord of 6.3 m and 0.385 m, respectively. The rotor is equipped with an inter-bladed damper along with an elastomeric bearing to accommodate the desired pitch control input. In developing new helicopters, detailed load analyses around the extreme corner points of the flight envelope are needed to ensure the safe operation of the vehicle. For helicopters, the most critical loadings and severe vibration levels are generated during the transient flights such as the high-g pull-up maneuver [2,3,4].

Accurate and reliable predictions of airloads and structural loads in maneuver are challenging because of the highly nonlinear and transient nature of the flight. Among others, three-dimensional transonic effects [5] near the blade tip in the advancing side, reversed flow [6] and dynamic stall (DS) [7] in the retreating side, and blade–vortex interaction (BVI) events [8] in the rear portions of the rotor disk are the major factors of the aeromechanics analysis that should be countered correctly. Highly unsteady air flows and large blade deformations make the analysis more involved and demand the most sophisticated solution technologies such as CFD/CSD coupling to correctly identify the complex phenomena and understand the detailed physics related with the aeroelastic behavior of the vehicle in motion.

In the rotorcraft aeromechanics analysis, CFD/CSD coupling is rooted in Tung et al. [9] where two separate codes (CSD and CFD solvers) are loosely coupled by transferring data per periodic base. This pioneering approach later invokes researchers to revisit and tackle the unsolved rotorcraft aeroelastic problems, particularly with the UH-60A airloads program, as pointed out by Bousman and his associates [10,11], resulting in significant advances in the prediction capability and the level of understanding for many problems in the rotorcraft aeromechanics fields [12,13,14,15,16]. Richez [17] conducted an LC analysis employing ONERA CFD code elsA and Airbus Helicopters CSD code HOST, particularly to investigate the DS mechanism of an isolated 7A rotor in a high-thrust forward flight. The alternative method is a tight coupling (TC) approach where the blade motion (CSD) and airloads (CFD) data are exchanged at every time step, by which the periodicity assumption in the LC algorithm is abandoned for time-accurate response solutions. Some of the representative works on TC approaches are found in [18,19,20,21]. Remarkably, Nygaard et al. [20] applied the TC algorithm successfully for simple longitudinal maneuver problems, combining the periodic trimmed solution by LC and a lagged scheme with the exchange of information between the CSD (RCAS) and CFD (OVERFLOW-D) codes.

Bhagwat et al. [22] extended their earlier work [20] to examine the aerodynamic and structural loads of a UH-60A rotor in a UTTAS pull-up maneuver. The simulation results demonstrated significantly improved correlations with the flight test data as opposed to the CSD-alone method, inevitably consuming heavy computational resources. It is interesting to note that they compared the accuracy of the air and structural loads of the rotor (during the peak maneuver events) between the LC and TC schemes, resulting in no significant deviations between the two methods. In either approach, the measured flight data on the rotor pitch controls and the hub motions are utilized and prescribed for the pull-up maneuver analysis. It should be noted that the TC scheme appears to be more straightforward and rigorous than its LC counterpart. However, a time lag between the CFD and CSD codes for TC cannot be avoided during the data exchange cycles. Furthermore, it is difficult to reach the trim. Rajmohan et al. [23] worked to develop a stable TC method in the analysis of a transient pull-up maneuver of the UH-60A rotor. Either DYMORE (CSD) or GT-Hybrid (CFD) code was employed to enable the coupling analysis. The steady flights demonstrated reasonable converged solutions while confronting a convergence problem in the maneuvering flight region. Battey and Sankar [24] applied the LC algorithm successfully for the evaluation of airloads of the UH-60A rotor in maneuver. It is emphasized that, so far, only limited works on detailed loads and vibration analysis of a rotor in maneuver flight have been found, and hence, there is a need to fill the gap in the literature.

In the present work, a quasi-static (QS) CFD/CSD approach is employed to evaluate the airloads and structural loads of a five-bladed rotorcraft in maneuvering flight. Either the CAMRAD II [25] or KFLOW [26] code which has been extensively studied by the present authors is used to conduct the analysis. It should be noted that the validity of the respective codes and their coupled analyses (LC) has been successfully demonstrated previously while validating the measured data of the HART II [15,27,28] and HART I rotors [16]. A high-g, transient pull-up maneuver condition is chosen for the present investigation. As the measured data on the vehicle attitude angles and flight trajectories of the maneuver profile are not yet available for the present rotorcraft, the flight dynamics simulation results predicted using CAMRAD II with converged CFD/CSD delta airloads are used instead to conduct the maneuver loads’ analysis. The proposed method is applied to predict the airloads, pressure distributions, vortex trajectories, blade motions, structural loads, and pitch link load responses of the rotor, and detailed discussions are made to evaluate the aeromechanics characteristics of the rotor in maneuvering flight.

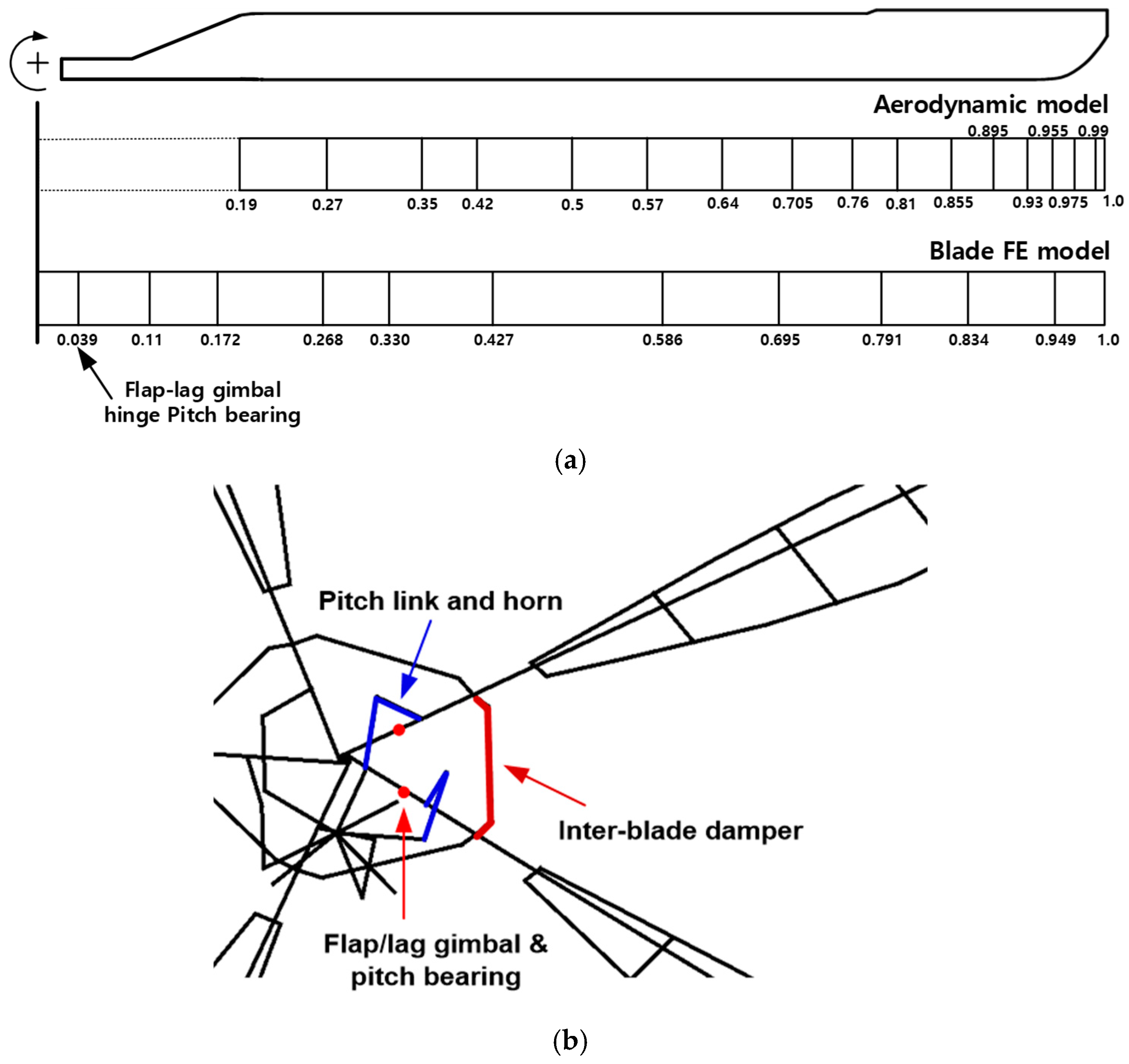
2. LH Rotor Model

2.1. CSD Model

The rotorcraft computational dynamics analysis code CAMRAD II [25] is used to analyze the five-bladed rotor. CAMRAD II is a comprehensive rotorcraft code that is characterized by the multibody dynamics, nonlinear finite elements, and various levels of rotorcraft aerodynamics based on a lifting-line theory using steady two-dimensional airfoil characteristics and the vortex wake. Several different attached-flow unsteady aerodynamics models along with various dynamic-stall models are implemented. The code is built based on multibody dynamics, nonlinear finite elements, and various levels of aerodynamic models. For the structural model, the blades are discretized as a series of beam finite elements. The aerodynamic loads acting on the blades are computed using ONERA-EDLIN unsteady airfoil theory combined with C81 airfoil table look-up. A rolled-up free wake model is employed for the vortex wake representation, and a semi-empirical Beddoes–Leishman model is used for the DS prediction. Similar descriptions of the aerodynamic models implemented in CAMRAD II can also be found in Yeo’s work [29].

Figure 2 shows the aerodynamic and structural models adopted in the present CSD analysis. The airfoil blade region is divided into 16 non-uniform aerodynamic panels with finer segments modeled toward the tip to capture the realistic distribution of airloads over the blade outboard region. For the blade structure, a total of 13 beam finite elements are discretized over the blade span. Each beam element consists of 15 degrees of freedom (DOF) with six rigid and nine elastic motions (three axial, two flap, two lag, and two torsion). The hub model includes pitch horns and their linkage mechanisms along with the lead–lag damper interconnected between the adjacent blades (see Figure 2b).

Table 1. General properties of LH rotor.

Properties	Value
Number of blades	5
Radius, R	6.3 m
Mean chord length, c	0.385 m
Solidity, $\sigma$	0.0972
Lock number, $\gamma$	7.432
Rotational speed, $\Omega$	350 rpm

summarizes the general properties of the present rotor. It is remarked that the rotor has articulated hinges co-located at 0.039R (blade radius) for flap, lag, and torsion motions. In the CSD analysis, a pitch link model is used to accommodate the pitch control input. The measured pitch link stiffness is not available yet and the vehicle is determined to match the first torsion frequency, targeted at higher than 6P (per rotor revolution).

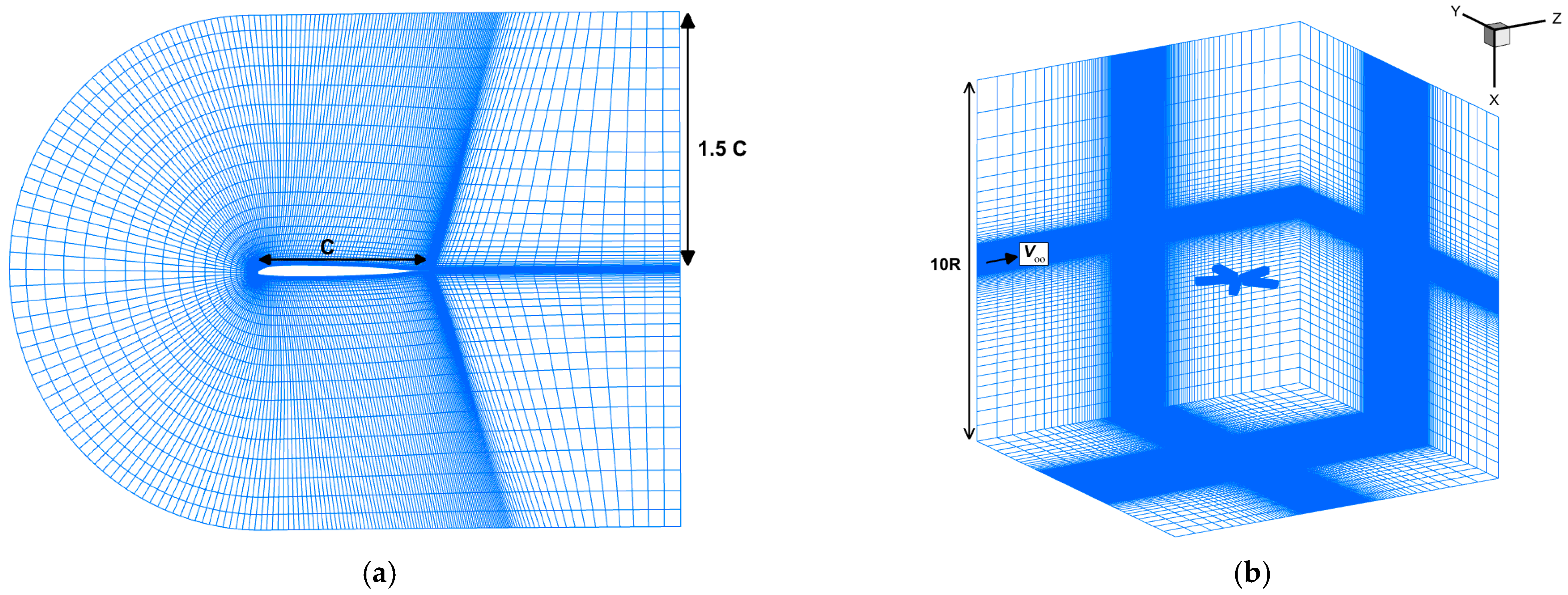
2.2. CFD Model

The 3D compressible RANS (Reynolds-Averaged Navier–Stokes) flow solver KFLOW [15,26] is used for the CFD analysis. KFLOW is a parallelized multiblock structured solver and is capable of computing time-accurate moving body problems by employing a Chimera overlapped grid system. For time-accurate flow simulations, the second-order dual-time stepping scheme combined with a diagonalized alternating-directional implicit method is used to simulate the unsteady flow fields of the rotor. For a spatial discretization, the inviscid fluxes are calculated using the fifth-order weighted essentially non-oscillatory scheme, while the central difference scheme is used for the viscous fluxes [30]. The k-ω Wilcox–Durbin scheme is employed for the turbulence model [31]. The characteristic boundary condition using the Riemann invariant is applied at the far-field boundary, whereas the no-slip condition is enforced at the solid wall of the blades and the body.

A moving overlapped Chimera grid system is constructed for both the rotating blades and the Cartesian off-body background field. The C-H mesh topology grids are formed near the blade surface (Figure 3a). Figure 3b shows the overall computational grid system used for an isolated, five-bladed LH rotor. The blade grids extend 1.5 times a chord length (c) in the normal direction, measured from the blade surface. A fine inner off-body region around the blade grids extends 6c upward, 5c below the blade surface, and 1.5c away from the blade tip. The far field boundary is stretched up to 5R, centered at the rotor hub. Numerical experiments have shown that the cell spacing of 0.1c is appropriate for the off-body background grids for capturing unsteady dynamic-stall effects or blade vortex interaction effects from the preliminary studies [15,16]. The blade grid has dimensions of (49 × 161 × 297) accordingly to the normal, spanwise, and chordwise directions, respectively, which sums up to 2.27 M (million) cells per blade, with the background grid system having dimensions of 161 × 449 × 401 (vertical, lateral, and longitudinal). Overall, the CFD computational grids amounts to a total of 40.0 M cells including the near-body blade grids and the off-body background grids for the present isolated LH rotor model. Two hundred CPU cores (Intel Xeon CPU E5-2640) with ten nodes implemented through the message-passing interface (MPI) are used to execute the CFD computations. The average computation time per one rotor revolution takes about 35,500 s.

3. Maneuver Analysis

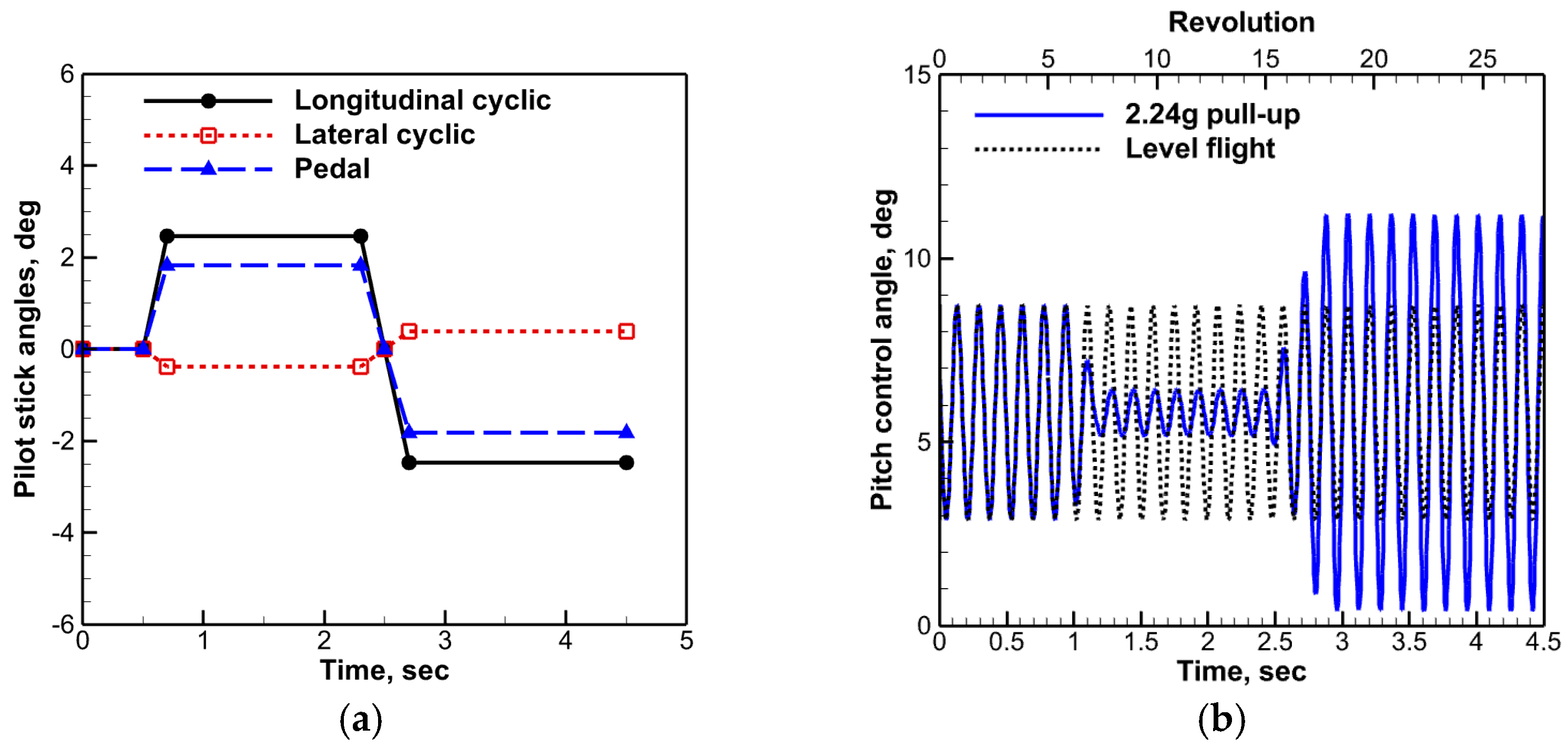
3.1. Pull-Up Maneuver

The LH pull-up maneuver pilot input scenario is presented in Figure 4 where the longitudinal cyclic stick is pulled back to 2.5 degrees to vary the pitch control angles. The longitudinal stick input begins to rise at 0.7 s, reaches the peak value at 0.9 s, stays for a duration of 1.6 s, and then decreases to −2.5 degrees to retrieve back and nose down the attitudes of the vehicle. While manipulating the longitudinal stick to simulate the pull-up maneuver, the lateral cyclic and pedal (tail rotor collective) are also varied for maintaining the roll and yaw balance of the aircraft attitude angle to produce the aircraft pitch-up motion of the pull-up maneuver as closely as possible. The main rotor collective angle is held constant during the pilot input. The time period of 4.5 s elapsed for the pilot input corresponds to approximately 27.8 revolutions of the rotor. The resulting changes in the blade pitch control angles of the first blade of the rotor, due to the pilot stick input for the pull-up maneuver (continuous lines), are illustrated in Figure 4b, as compared with the level flight Inputs (dotted lines). The reference azimuthal angle of the first blade is set as 0 degrees which is positioned at the rear (${\psi }_1=0°$, ${\psi }_1$ is the azimuthal angle of first blade). The pilot stick angles transferred to the blade pitch angles become decreased by about 2 degrees in comparison with those of the level flight condition and drop substantially thereafter. This pilot input schedule (pull-up) appears to be rather drastic and results in deep changes in the vehicle attitude angles, blade loadings, and rotor thrust outcomes.

Figure 5a presents the variation of the effective weight coefficients ($C_w/\sigma$, $C_w$ is the weight coefficient, and $\sigma$ is the rotor solidity, respectively) during the pull-up maneuver depicted as a function of the advance ratios. Even though the aircraft classes are quite different from each other, the UH-60A pull-up maneuver case [22] is presented together for a reference purpose. The McHugh lift boundary which can be used as a limit of the static lift coefficient of the rotor, due to the occurrence of DS events or any unsteady airloads, is inserted in the figure (dotted lines) to identify the level of thrust amplitudes generated during the present pull-up maneuver flight. Since UH-60 airload results are not available to the public, the data are extracted from Bhagwat et al. [22]. It should be mentioned that both rotors indicate crossing well over the McHugh lift boundary for higher thrust values which may lead to severe DS events. The dashed circles indicated in Figure 4b represent the first revolution that goes over the McHugh lift boundary for the present analysis (14 revolutions). Figure 5b shows a comparison of the load factors encountered during the pull-up maneuver between the present and UH-60A flights. The load factor reaches up to a maximum of 2.24 g for the LH rotor during the pull-up maneuver with UH-60A touching 2.1 g, which is slightly higher than that of the UTTAS pull-up maneuver case.

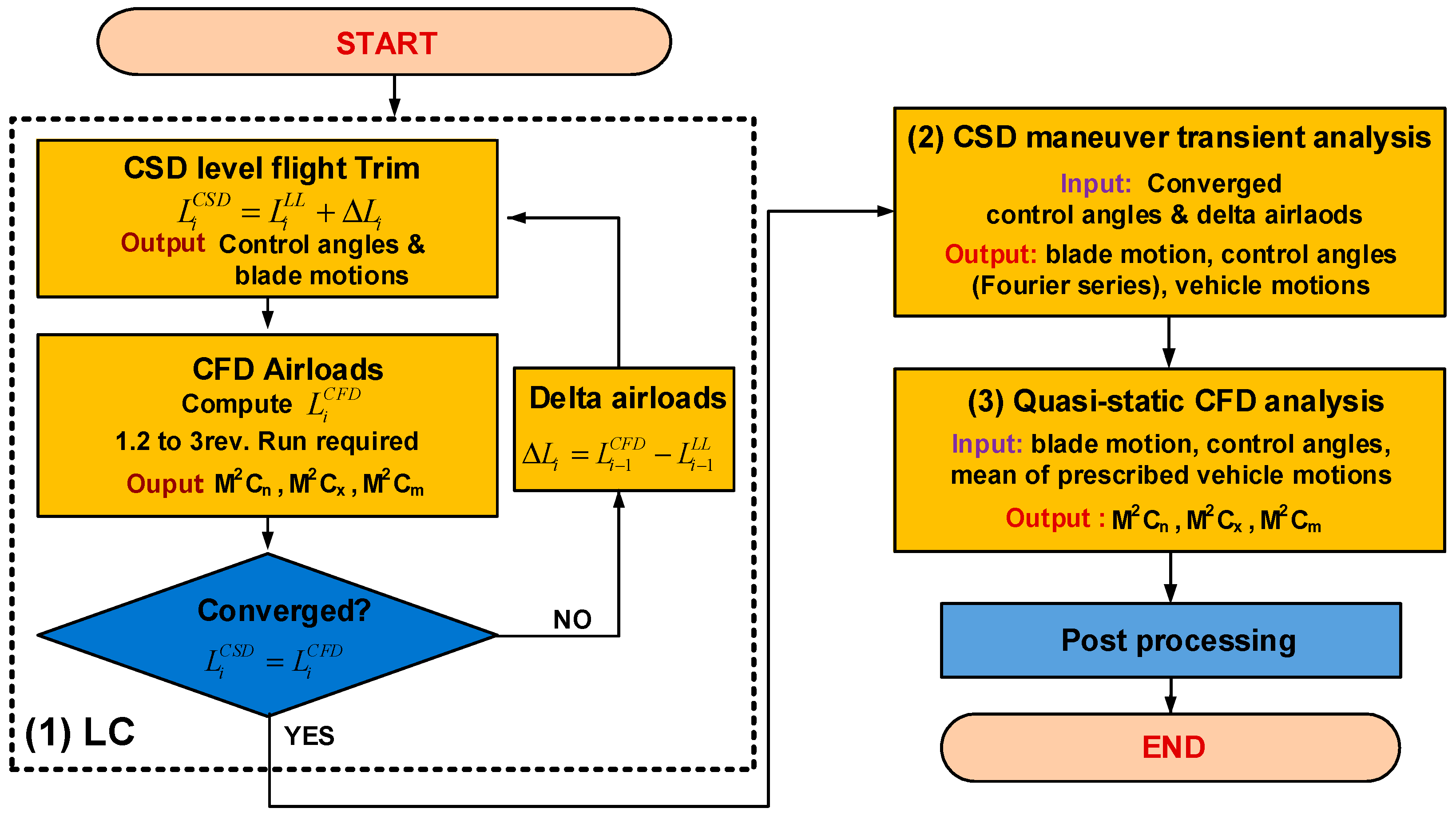
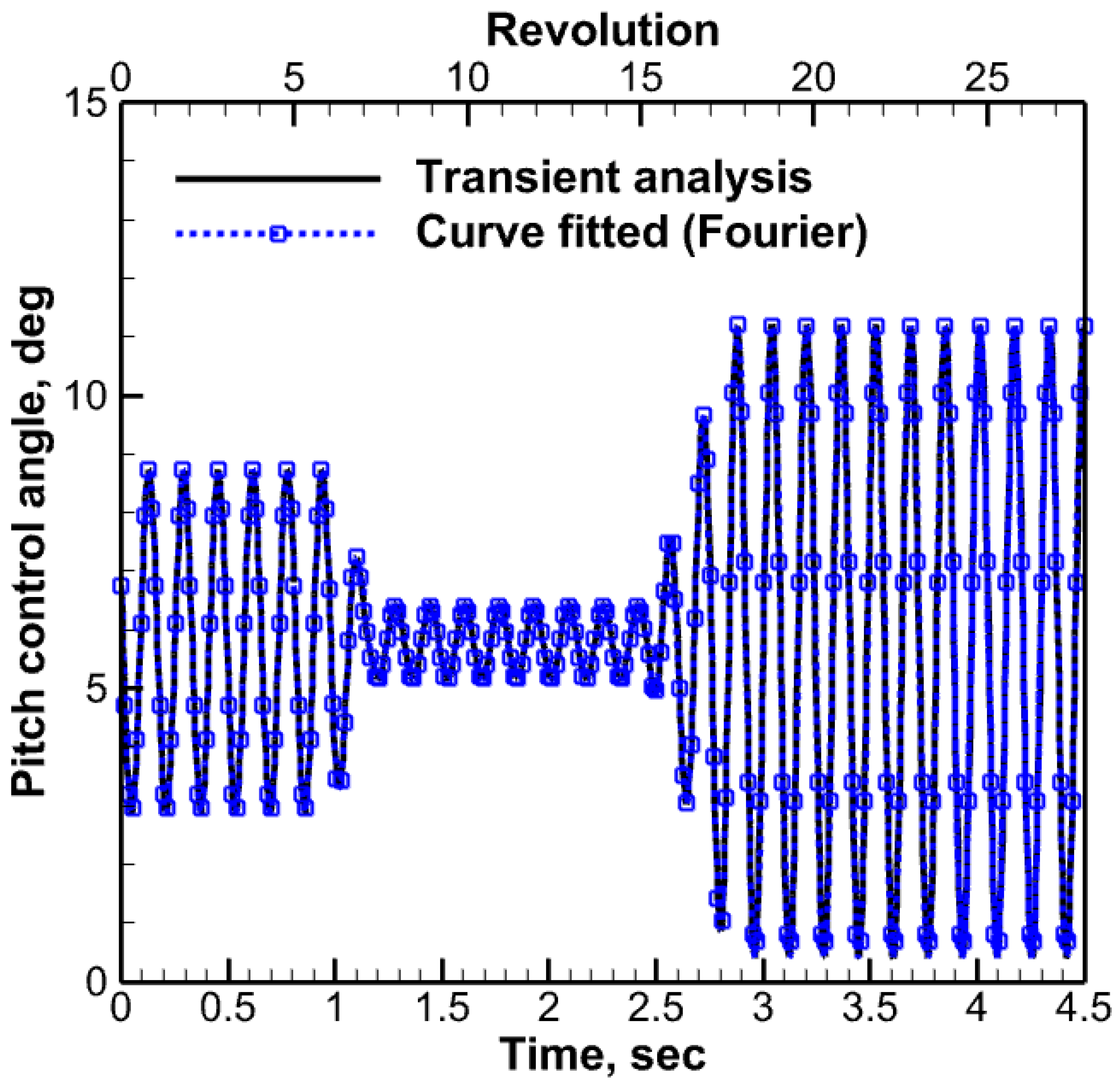
3.2. Maneuver Analysis Methodology

To predict the air and structural loads of a rotor in maneuver, a time-accurate TC scheme may truly be desired since the problem is inherently unsteady. However, considering the observations made by Bhagwat et al. [22] in the prediction of UH-60A maneuver loads, it is assumed in this study that each revolution during the pull-up maneuver can be approximated as a steady state with respect to the prescribed vehicle attitude angles and blade motions, which essentially results in a QS condition. The overall flow diagram of the present QS maneuver analysis is presented in Figure 6. The analysis is composed of three stages: (1) LC in level flight condition; (2) CSD transient analysis for prescribed vehicle motions; (3) QS maneuver analysis at specified instant of time (revolution) for aeromechanic loads of the rotor. To ensure a sufficient convergence, each QS maneuver analysis is marched for three consecutive rotor revolutions. The second stage of the analysis (flight dynamics simulation) is required since no measured flight data on vehicle motions of the present helicopter in maneuver are available so far.

The analysis begins with the LC between the CFD and CSD predictions in steady-level flight condition. The level flight speed μ is set as 0.287, as depicted in Figure 5. The LC run requires about 6 to 8 iteration cycles for transferring data between airloads (CFD) and blade motions (CSD) for a converged solution, as indicated in Figure 7. In this stage, a free flight trim strategy is employed to balance the forces and moments acting on the helicopter with the usage of pilot stick controls and vehicle attitude angles. Figure 7 shows the coupling iteration histories on CSD trim control angles, CFD/CSD delta airloads on section normal forces $M^2{C}_n$ ($M$ and $C_n$ are the Mach number and the section normal force coefficient, respectively), and section pitching moments $M^2{C}_m$ ($C_m$ is the section pitching moment coefficient). Once the convergence is achieved, the final converged delta airloads are saved for later use in the CSD transient maneuver analysis. Next, with the converged trim angles and delta airloads, a separate CSD transient analysis is conducted to find out the time histories of the LH rotor blade motions during the maneuver flight, which include the vehicle attitude angles and freestream velocity components according to the predetermined maneuver input scenario. In the transient analysis, the converged delta airloads obtained from the LC in level flight are added in the CSD analysis to provide additional unsteady airflow components and to improve the solution accuracy of the flight dynamics predictions.

Figure 8 shows the time histories of vehicle attitude angles (Figure 8a) and speed components (Figure 8b) of an LH aircraft predicted using the transient CSD analysis with and without the effect of delta airloads. The effects of incorporating delta airloads in the transient CSD analysis are seen to be substantial as the time (rotor revolutions) marches further, especially on the behavior of aircraft roll motions. From the transient analysis results, the vehicle velocity and angles are averaged for each revolution. Considering the distribution of the delta airloads on the section normal force in Figure 7b, the non-negligible differences captured in the advancing side of the rotor are attributed the large deviations of the roll angles as the time marches on further. Figure 8c shows the schematic of the present pull-up maneuver path, depicted as functions of the rotor revolutions for the QS analysis with the increase in vehicle pitch angles. As depicted in Figure 8c, the present pull-up maneuver study covers up to 19 revolutions, reflecting the roll and yaw balance of the vehicle attitude angles (Figure 8b). In the plot, the control angles required for each revolution are interpolated from the transient analysis results using the Fourier harmonic series. Figure 9 presents the transient CSD predictions of the control angles as well as their curve-fitted results obtained during the pull-up maneuver. It is found that the pitch angle’s changes with time are accurately described as the Fourier series up to 10th harmonics are used. Given the computed vehicle motion data prescribed during the pull-up maneuver, the CFD time marching analysis or LC approach at a specified revolution of interest is readily engaged to perform the desired QS maneuver analysis.

4. Results and Discussion

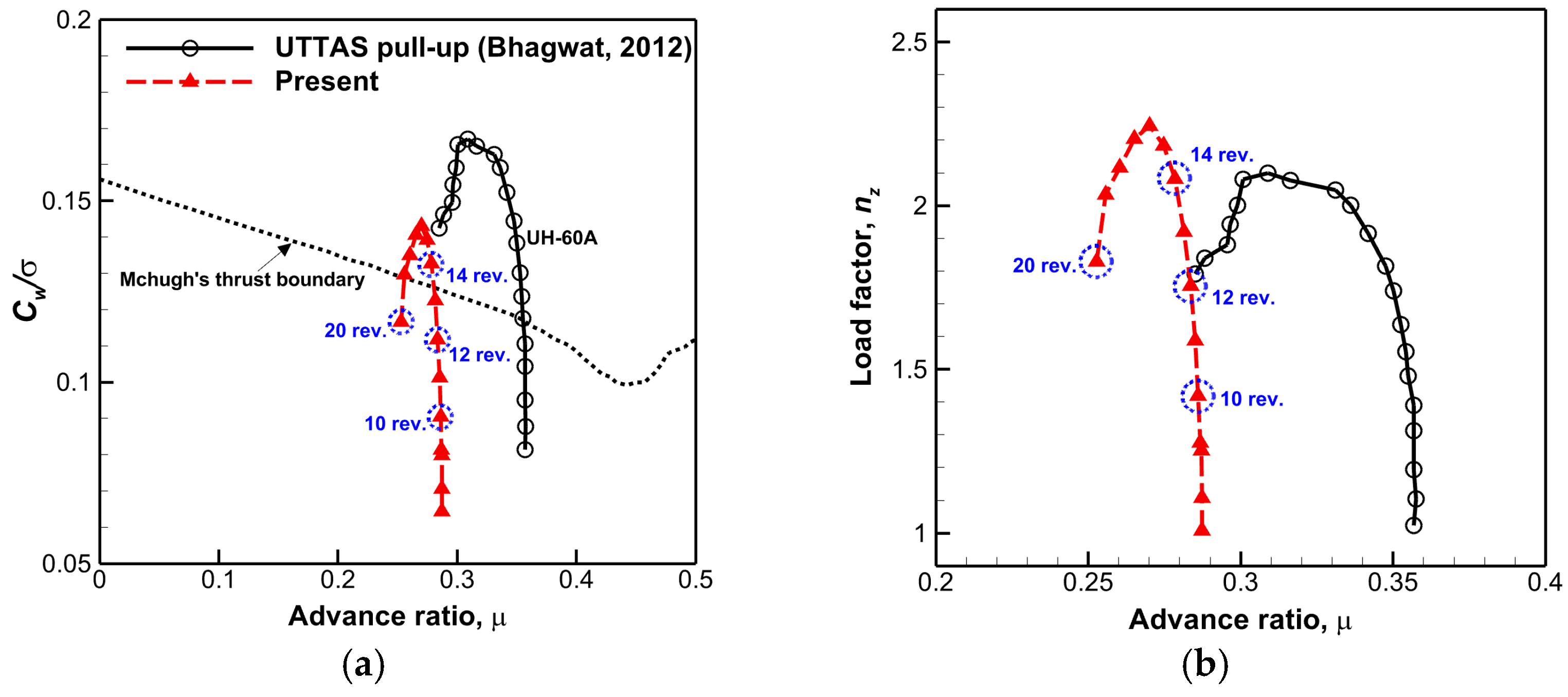
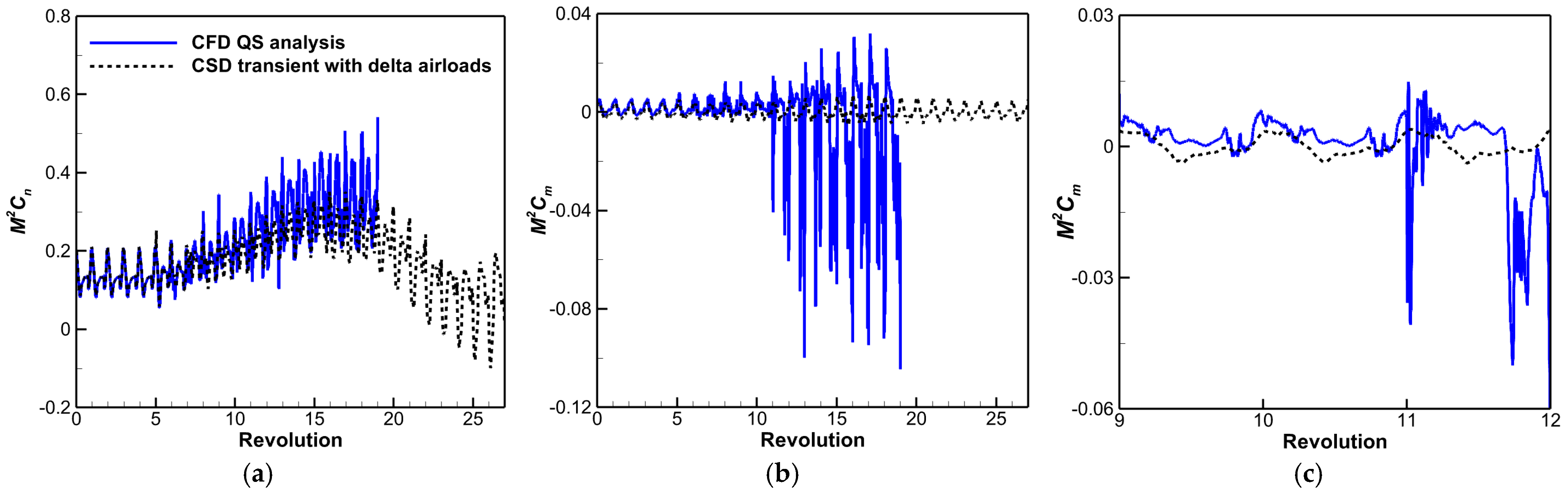
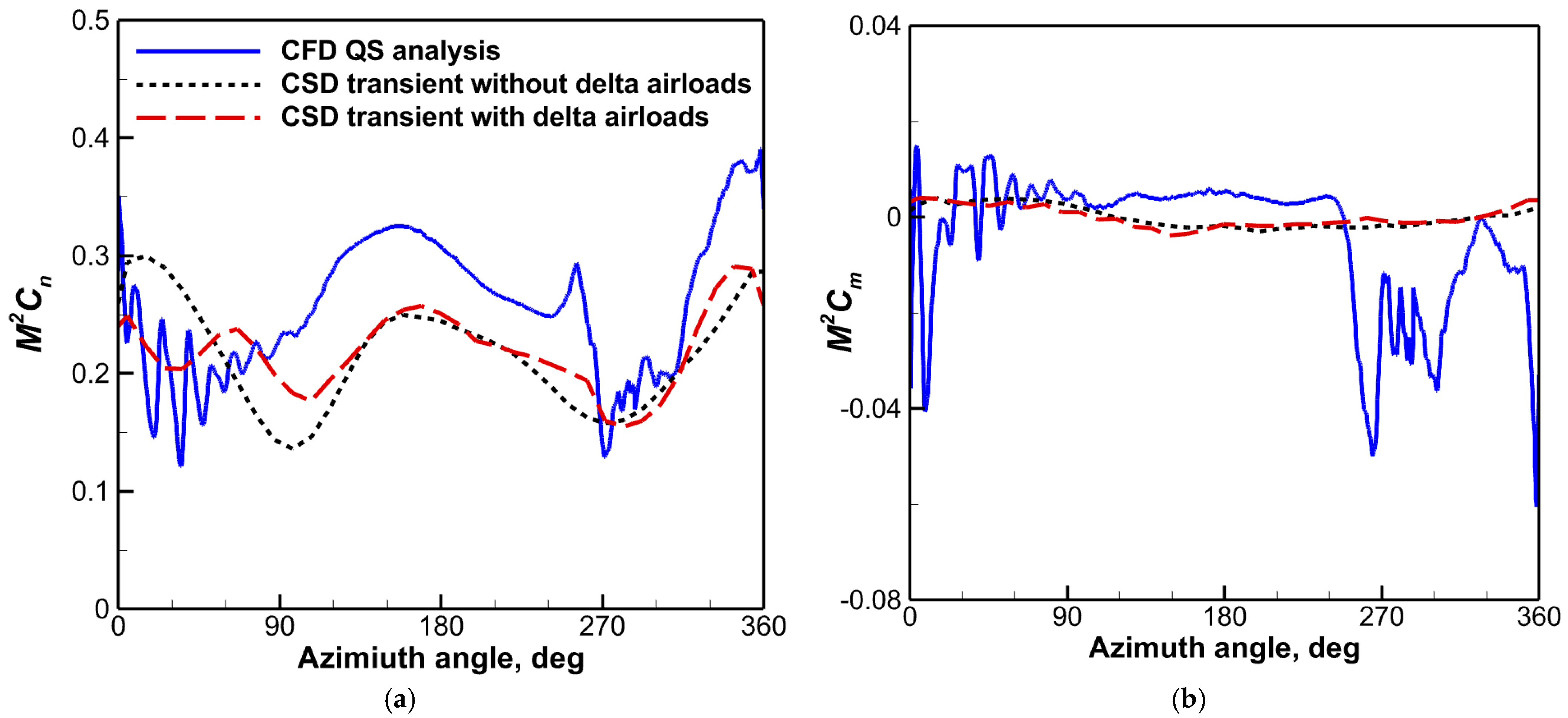
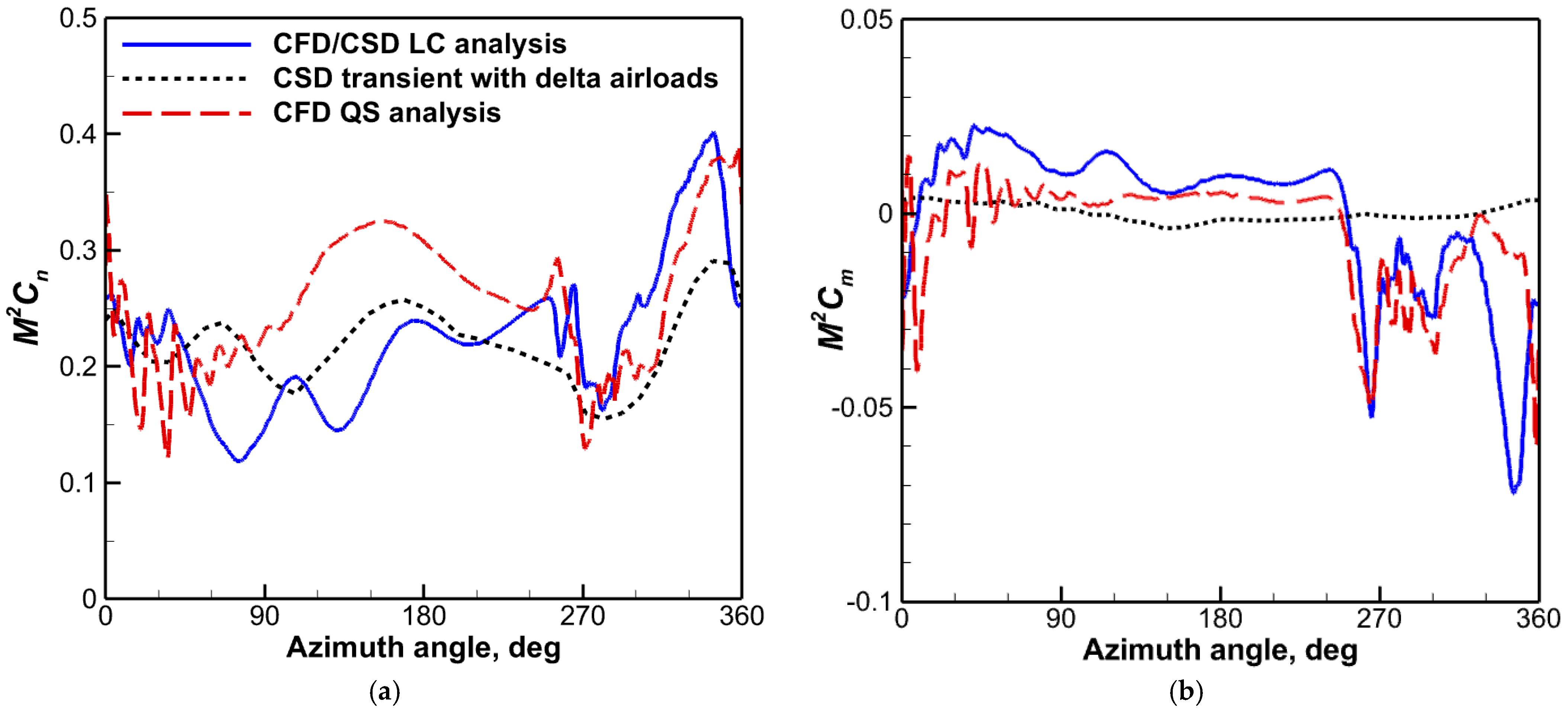
4.1. CFD QS Analysis

A numerical simulation study for the LH rotor in a 2.24 g pull-up condition is carried out using the QS maneuver scheme described in the previous section. Unless otherwise specified, a rolled-up free wake model is employed for the CSD analysis, whereas in CFD computation, the time-accurate, compressible RANS (Reynolds-Averaged Navier–Stokes) flow solver KFLOW [15,26] is used for the present investigation.

Figure 10 shows the time history responses of section normal forces ($M^2{C}_n$) and section pitching moments ($M^2{C}_m$) at 0.833R, respectively, with respect to the rotor revolutions. In the plot, either CFD predictions with prescribed blade motions (solid lines) or CSD transient analysis results with delta airloads (dotted lines) of the rotor are presented as a function of rotor revolutions. Since the pull-up maneuver ends at 19 revolutions, the QS CFD predictions are only shown until 19 rotor revolutions. It is observed in Figure 10 that the two different approaches predict large variations with each other. As the revolutions continue further, the QS CFD analysis results indicate more pronounced peaks with greater harmonic contents than those of the CSD analysis. Specifically, much stronger DS peaks are noticed in section pitching moment signals of the QS CFD analysis. The enlarged view of the section pitching moment signals ranging from 9 to 12 revolutions is presented in Figure 10c for more clarity. The QS CFD results indicate more oscillations on the advancing side, which are presumably caused by BVI events, while two large spikes in the retreating side represent the occurrence of DS events. Meanwhile, in the CSD predictions, no such spikes exist. In the present CSD analysis, the Beddoes–Leishmann DS model is adopted to predict the DS events. It is indicated that the CSD analysis with the embedded DS model is seen to be ineffective in capturing DS peaks. One more thing to remark is that the McHugh lift boundary is crossed at around 13 to 14 revolutions (Figure 5a), whereas the predicted pitching moment results start to capture the peaks at as early as 10 to 11 revolutions. Taking the time-varying unsteady maneuver flight characteristic into account is a source of the earlier prediction of DS, when compared with the McHugh thrust boundary [32] determined using the steady-flight conditions. Overall, the present CFD predictions appear to pick up the fundamental flow characteristics of the rotor encountered during the pull-up maneuver, which is in line with the predictions found by Bhagwat et al. [22].

Figure 11 shows the influence of incorporating the delta airloads in the CSD transient analysis results predicted at 11 to 12 maneuver revolutions, as compared to the QS CFD predictions. The solid line presents the CFD QS analysis results, while the dotted lines and the dashed lines denote the CSD predictions without and with delta airloads, respectively. Both the mean values and the basic waveforms for both CSD predictions show reasonable agreement with each other. The inclusion of the CFD/CSD delta airloads leads to more oscillatory responses due to the addition of unsteady airflow components (from CFD), especially in the section normal force signals. This effect becomes higher in the advancing side signals (BVI) with increasingly greater oscillations near the DS peak region. However, both of the CSD predictions failed to capture the highly oscillatory BVI signals in the first and the fourth quadrants of the rotor disk due to the low-fidelity solutions of the analyses. Despite the advancements in the predicted results, the current observations should only be verified by flight test measurements of the rotor.

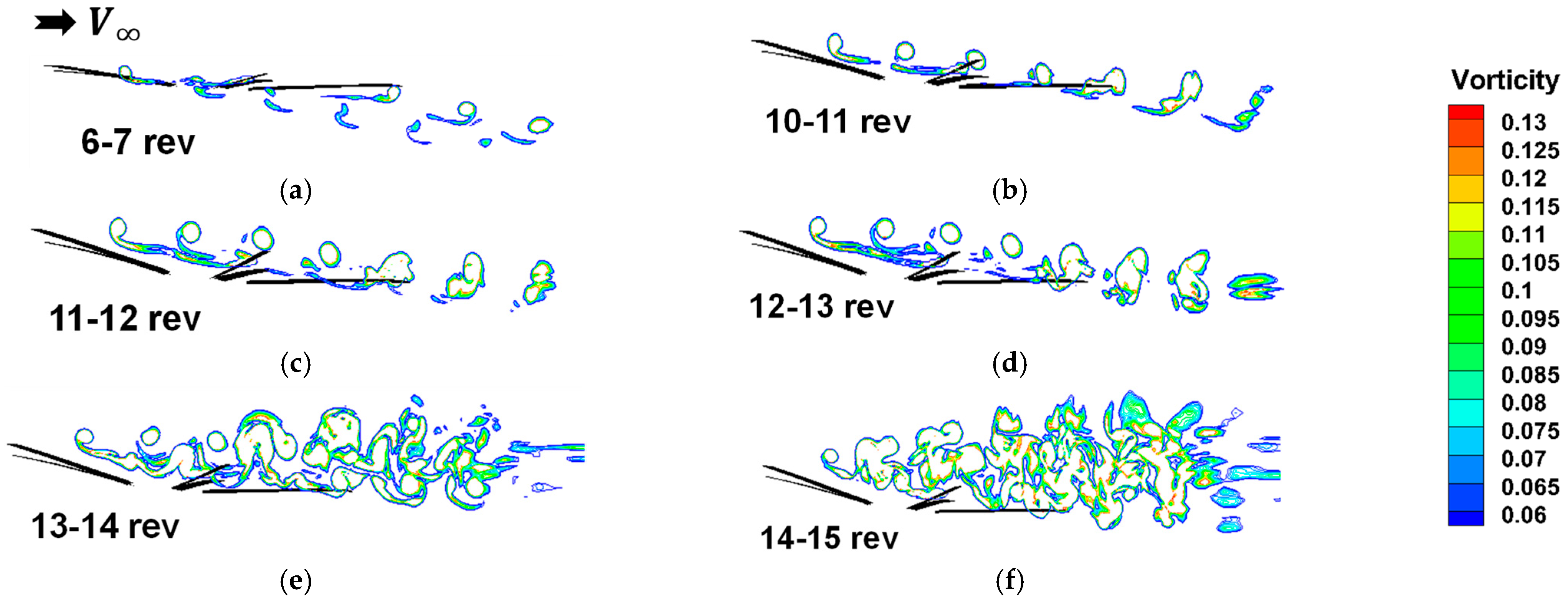
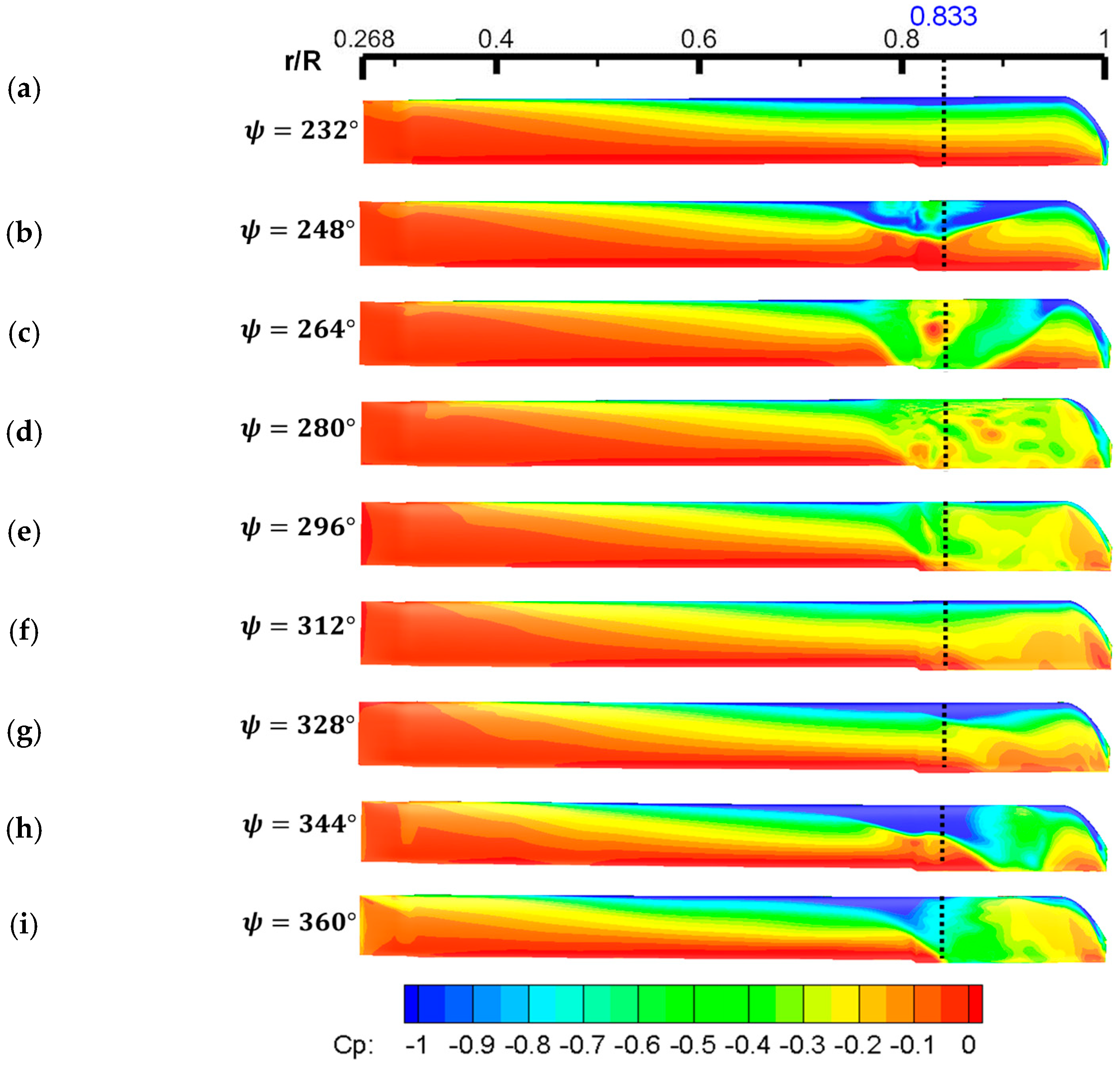
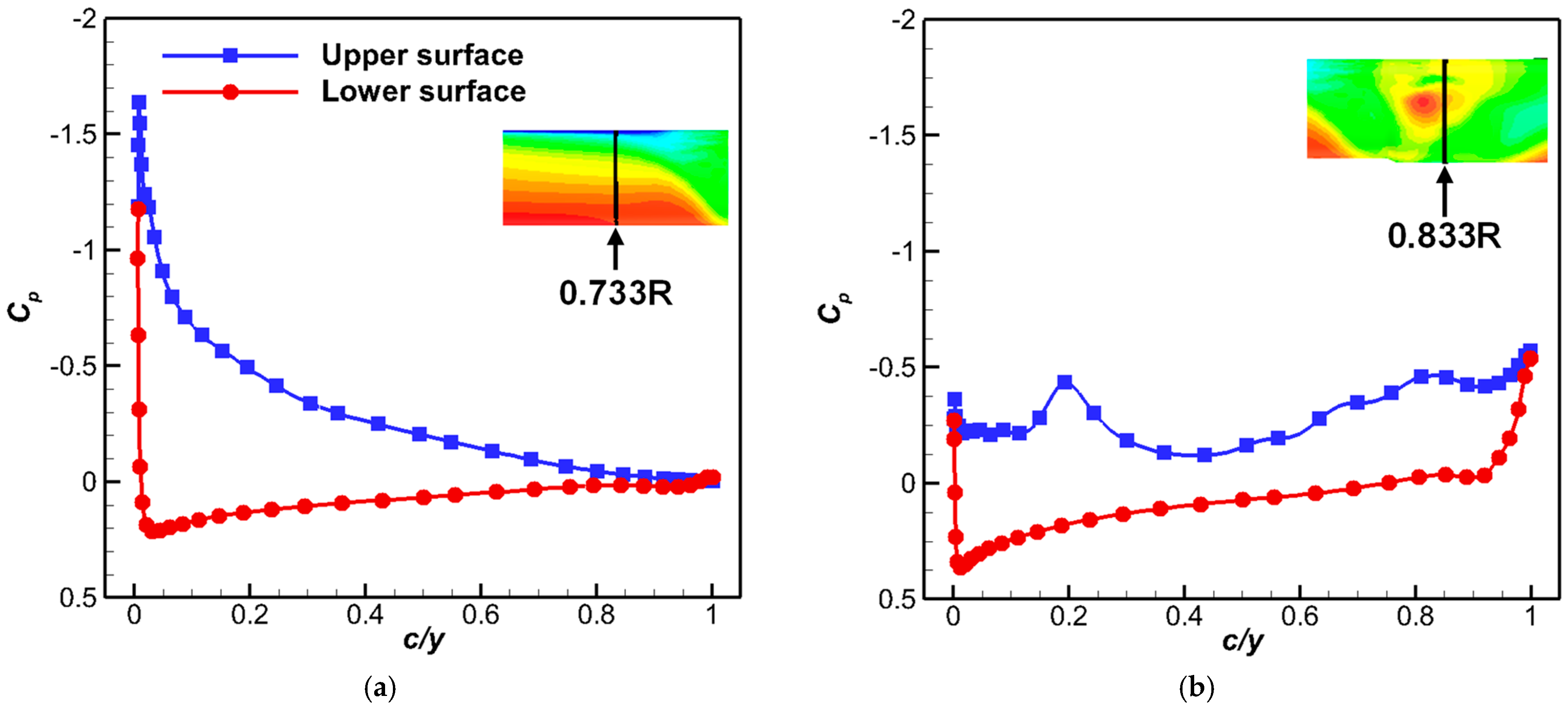
4.2. Vortex Trajectories and Pressure Distributions

Figure 12 shows the Q-criterion plot colored by vorticity to visualize the vortex trajectories of the rotor wake, predicted during the pull-up maneuver where high load factors from 1.59 g to 2.18 g resulted (10 to 15 rotor revolutions) due to the pilot control inputs (Figure 4a). The plots are viewed from the top (Figure 12) as well as the port side positioned at 0.64R of the blade (Figure 13), respectively. In Figure 12 and Figure 13, since the pull-up maneuver starts at five revolutions, the vortex trajectories of six to seven revolutions are also shown for a reference purpose. As expected, the vortices developed in the vicinity of the front edge of the rotor initially (6–7 rev.) convect downward as they travel toward the rear side of the disk. Then, the vortex trajectory slowly shifts upwards over the rotor disk due to the increased pitch-up angles of the vehicle. The side-trajectory view at 11 to 12 revolutions (Figure 13) indicates that most of the vortices formed near the front disk drift up, travel over the rotor disk, and convect downward to interact with the blades positioned rear of the rotor disk. This upshift pattern becomes dominant as the maneuver revolutions proceed further. Comparing this with the top view (Figure 12) clearly indicates some BVI events between the developed tip vortices and the approaching blades, particularly in the first and the fourth quadrants of the rotor disk. These BVI oscillations are clearly captured in the section normal force and pitching moment signals at 83.3% blade radial locations, as can be found in Figure 10 and Figure 11.

To investigate the DS events indicated in the fourth quadrant of the rotor disk at 11 to 12 pull-up maneuver revolutions (Figure 10 and Figure 11), the distribution of the surface pressure coefficient $C_p$ computed over the suction side of the blade is presented in Figure 14 as a function of the rotor azimuth angles. To this end, the predicted CFD pressure coefficients from 232- to 360-degree azimuth angles with the interval of 16 deg. are illustrated in contour format. It is seen that the predicted pressure coefficients vary substantially according to the spanwise and timewise stations of the rotor blade. The pressure gradients at the earlier stages (e.g., ψ = 232 deg.) over the blade’s entire regions are rather smooth and favorable in the prediction of lift. Meanwhile, other positions such as around the azimuth angles of 264 deg. and 360 deg., particularly near the 83.3% blade radial station (dashed lines), large pressure fluctuations are observed, indicating the development of a powerful DS vortex system over a large portion of the blade’s surface. It should be mentioned that these fluctuating pressure regions coincide well with the locations of the pitching moment spikes (near 270 and 360 deg.) as observed in Figure 10 and Figure 11. As expected, the pitching moment peaks are located approximately in the vicinity of the blade where the pressure fluctuations are the largest. It should be remarked that the three-dimensional vortical structures of the DS vortex system are represented with the pressure contour plot, as is indicated in Figure 14. Similar observations were also made by Kan et al. [33].

In Figure 15, the chordwise distribution of the pressure coefficients predicted at the azimuth angle of 264 deg. (case of Figure 14c) is shown at three blade radial locations. The surface pressure distribution contours are also inserted in the upper right corner of the figures for reference purpose. At the station of 0.733R, the suction peak is seen to be developed reasonably close to the leading edge, and the recovery of the pressure toward the trailing edge is smooth enough (i.e., favorable pressure gradient) for claiming the typical attached flow pattern. However, as the blade stations are shifted toward the tip, a sudden drop in the strengths of the suction peak is encountered with significant changes in the pressure distribution over the upper surface of the blade at 0.833R. At the station of 0.833R, some adverse or fluctuations in pressure gradient regions dominate many portions of the blade surface, signifying the development of a strong DS vortex system, as observed in Figure 12 and Figure 13.

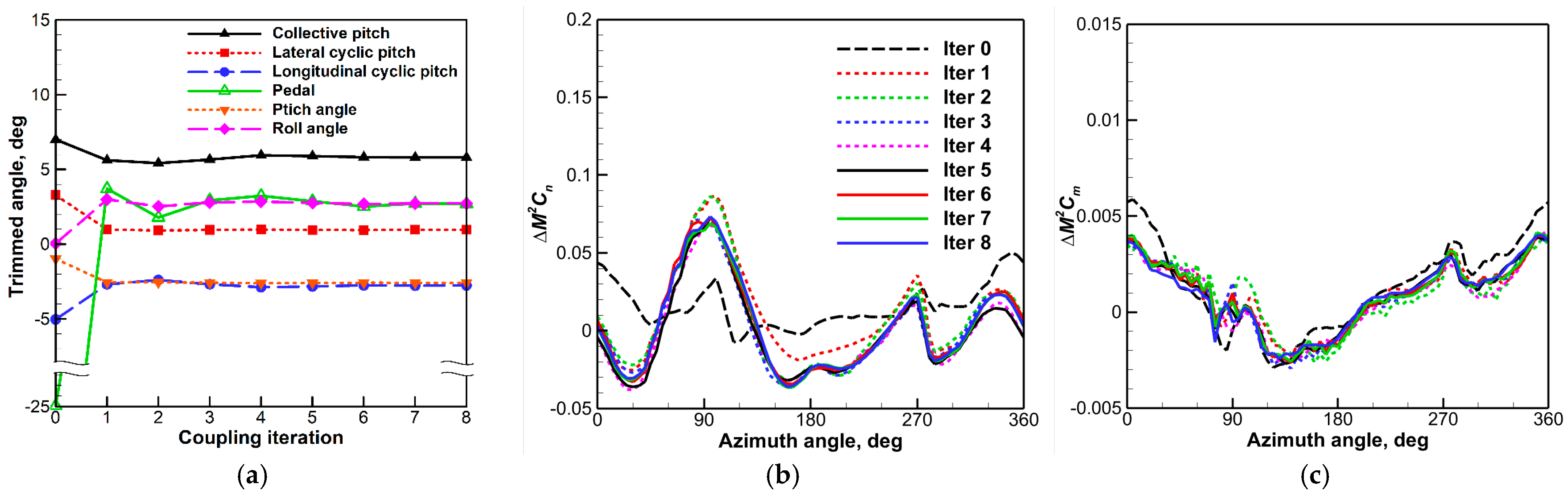
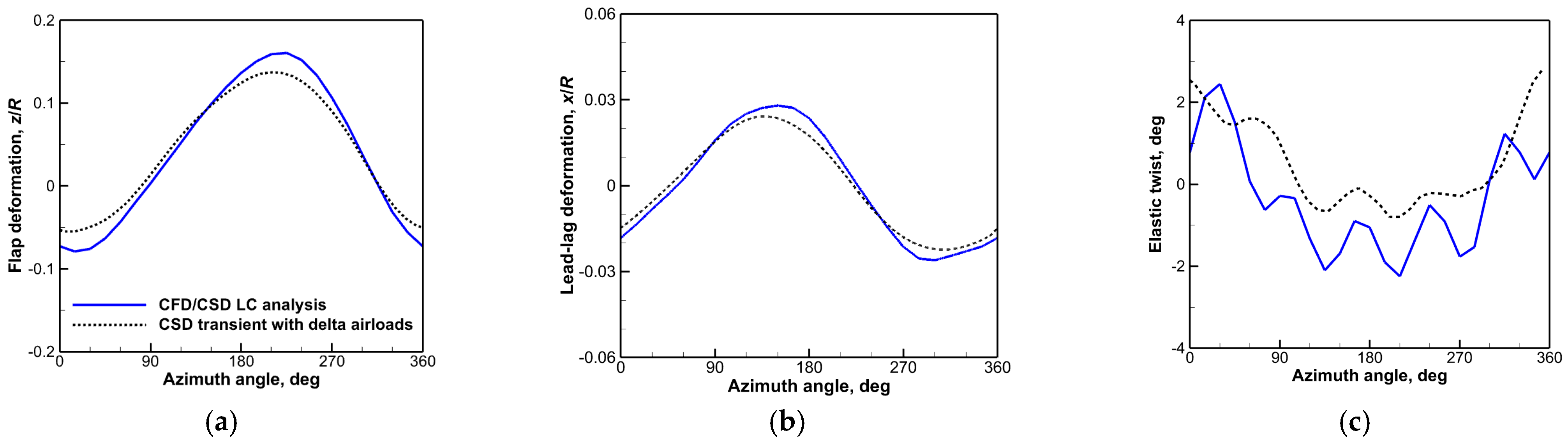
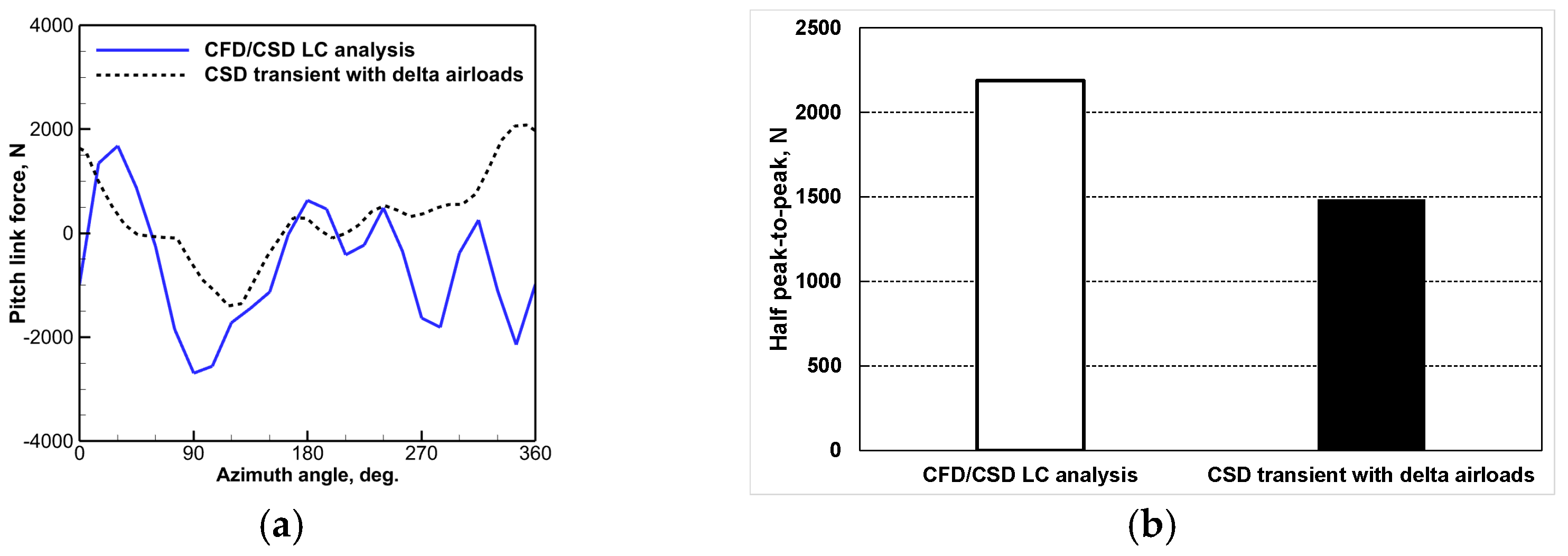
4.3. CFD/CSD LC Approach

Next, the CFD/CSD LC approach is engaged to predict not only airloads but also blade elastic motions, structural loads, and pitch link loads at the specified revolutions of the rotor during the pull-up maneuver flight. For consistency, the time at 11 to 12 revolutions is chosen to evaluate blade loads. For the LC approach, the control trim angles prescribed from the transient analysis are held fixed during the specified rotor revolutions, while the blade deformations and delta airloads are updated for each LC iteration. Figure 16 shows the comparison of the section airload results at 0.833R at 11 to 12 maneuver revolutions. The dashed lines indicate the LC predictions with the solid lines representing the QS analysis results (replica of Figure 11). The CFD/CSD LC predictions show reasonable agreement on the pitching moment signals and BVI oscillatory responses, especially in the first and the fourth quadrants of the rotor disk, as compared with the CFD QS analysis results. The correlation is less satisfactory over the second and the third quadrants between the predicted section normal force signals. It is noted that the DS peaks located near 270 deg. and 360 deg. are clearly captured in both the QS analysis and the LC results, whereas the CSD transient responses miss most of the impulsive signals. Similar behavior is also observed in both the predicted results and flight test data of UH-60A [22,34] which indicate multiple DS peaks in the first, third, and fourth quadrants of the rotor disk. This is remarkable considering the fundamental differences adopted in both approaches (i.e., quasi-static vs. time-varying transient). It is observed in Figure 16 that despite the substantial deviations over the front disk region of the section normal force signals, the prime DS events are captured clearly in the present CFD/CSD LC predictions while showing reasonable agreement with the CFD QS analysis results. The QS approach is based on the averaged responses of vehicle attitudes per the rotor revolution base, which allows fo achieving the trimming with superior computational efficiency. It should be noted that the validity of the present outcomes should be confirmed by a comparison with the flight test data.

In Figure 17, the elastic deformations at the blade tip obtained using CFD/CSD LC analysis (continuous lines) are compared with the predictions by CSD transient analysis with delta airloads (dotted lines). The CFD QS results are not included in Figure 17 due to the lack of the analysis capability of the method. It is also noted that the CFD/CSD delta airloads obtained from the steady-level flight condition are added to the CSD analysis (airloads) to supplement additional unsteady terms into the system and to analyze transience in more realistic manner. It is indicated that the predicted flap displacements show predominant 1P behavior with no significant deviations between the two different methods. For the lead–lag displacement as well, both approaches show close agreement in terms of the magnitudes and phases of their signals. Regarding the elastic twist deformation results, substantial deviations are found. A particularly strong 5P response is captured on the elastic twist results with the CFD/CSD LC approach, possibly due to the lead–lag dampers inter-connected between the blades, whereas much smaller responses are obtained with the CSD approach. Despite the apparent gaps, the phase behavior is shown to be reasonably captured with the simple CSD analysis. Figure 18 shows the comparison of flap bending (FB), lead–lag bending (LB), and torsion moments (TM) calculated at the 13% blade radial station (0.13R) between CSD predictions with delta airloads and CFD/CSD LC results for 11 to 12 maneuver revolutions. Similar to in the case of the elastic torsion results, the 5P harmonic behavior is pronounced for all the blade structural moments (FB, LB, and TM) results, especially with the CFD/CSD LC approach. A possible reason is the mechanism of the inter-bladed lead–lag dampers installed in the LH rotor system. The other dominant harmonic component is 1P, which is typical for structural moment signals. One more thing to point out is that the torsion moments predicted using CFD/CSD LC analysis are much larger than those obtained by the CSD method. This pattern is in line with the earlier observations made for the oscillatory section pitching moment signals presented in Figure 16b, originating from the development of DS events.

Finally, the timewise variation of the pitch link loads predicted using the two different analysis methods is presented in Figure 19a. The waveforms of both the pitch link loads are shown to be dominated by 5P harmonic components, as observed in the aerodynamic pitching moments (Figure 16b) and structural TM (Figure 18c). In Figure 19b, the half peak-to-peak (PP) amplitudes of the pitch link loads estimated using the two methods are presented in bar-chart format. The half PP value of the pitch link force is a crucial measure of the oscillatory load that determines the fatigue life of the moving parts (e.g., pitch link) and also the overall performance and durability of the rotorcraft. As can be seen in Figure 18b, the CSD analysis with delta airloads significantly underpredicts the half PP loads of the pitch link, which are about 32.2% of those predicted by CFD/CSD LC analysis. The large gap between the predicted structural loads of the pitch link is non-negligible, which signifies the importance of appropriate solution methodologies being adopted in the rotor aeromechanics analysis.

5. Conclusions

A QS maneuver analysis has been performed to investigate the air and structural loads of the LH rotor in a 2.24 g pull-up maneuver condition. The QS maneuver load analysis began with the CFD/CSD LC approach in the steady-level flight condition ($\mu =0.287$). The converged delta airloads from the level flight condition were fed into the CSD (CAMRAD II) for a realistic transient maneuver analysis. The resulting changes in the vehicle motion data were prescribed to enable the QS maneuver simulation for the evaluation of airloads and the detailed flow analysis. Finally, the LC analysis was engaged to examine the airloads, blade elastic motions, structural loads, and pitch link loads at specified instants of time during the maneuvering flight:

(1)

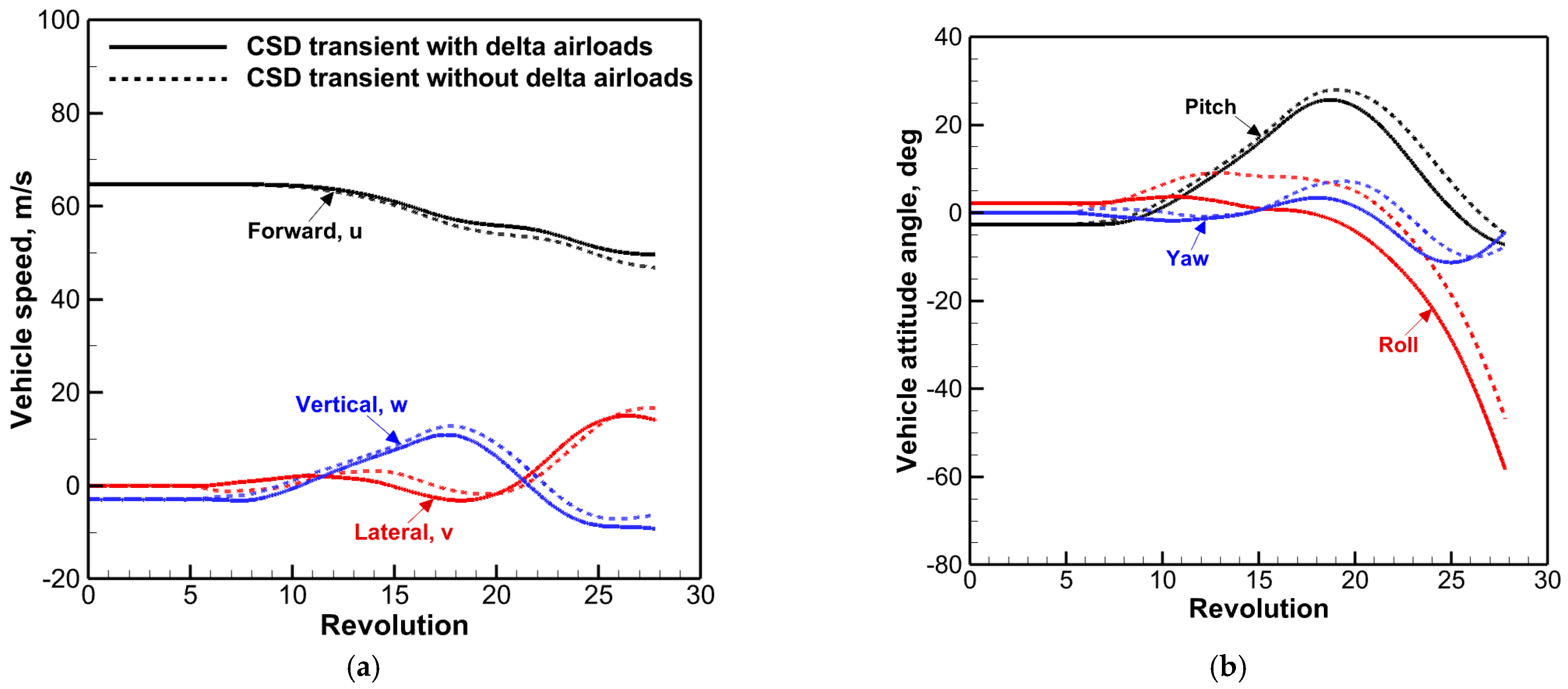
The predicted results by the QS CFD or CFD/CSD LC approach were correlated with the CSD predictions with and without the contribution of delta airloads. Both CFD-based methods were demonstrated to capture the important flow characteristics such as BVI-induced oscillations in the advancing side and the negative DS peaks of the rotor in a pull-up maneuver. The CSD transient results with delta airloads indicated some improvements in the section normal force predictions by picking up more harmonics in the advancing side with a negligible influence on the section pitching moments.

(2)

The sources of violent pitching moment spikes encountered during the DS events in maneuvering flight were identified considering the spanwise surface pressure contours and the chordwise distribution of the pressure coefficients at specified radial stations. The results indicated large pressure fluctuations in both chord and span directions with an adverse pressure gradient over the upper surface induced due to the DS vortex system.

(3)

The combined QS CFD analysis and CFD/CSD LC approach was shown to be effective in performing a detailed maneuver load study. The CFD-based predictions indicated reasonable agreement with the CSD-based results. The dominant 5P responses of elastic twist motions, structural moments, and pitch link loads were captured more clearly by the CFD/CSD LC method. It is suggested to conduct a series of flight tests in the future to confirm and verify the present findings.

The present maneuver analysis is based on the flight dynamics simulation results. The validity and the quantitative assessment of the present observations can be confirmed with the availability of the flight test data. A series of validation studies should be performed in the future.