Four-Dimensional Generalized AMS Optimization Considering Critical Engine Inoperative for an eVTOL
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Motivation and Objective
2. Preliminaries and Definitions
3. Optimization Setup
3.1. Problem Definition
given a fixed RMS , search for an optimal set of effector-related parameters within their constraint limits, to maximize the margin between and .
3.2. Optimization Formulation
- is the total number of vertices on RMS;
- is the margin factor of the RMS vertex;
- is the vector of variables to optimize, with and its lower and upper limits;
- is the vector of additional constraints, e.g., structural or spatial restriction;
- is the upper limits of .
3.3. Optimization to Account for Critical Engine Failure
- is the total number of inputs;
- is the margin factor of the RMS vertex of index i to the AMS given the failure of the input of index j.
3.4. Solving for
3.5. Solving the Optimization
4. Test Implementation
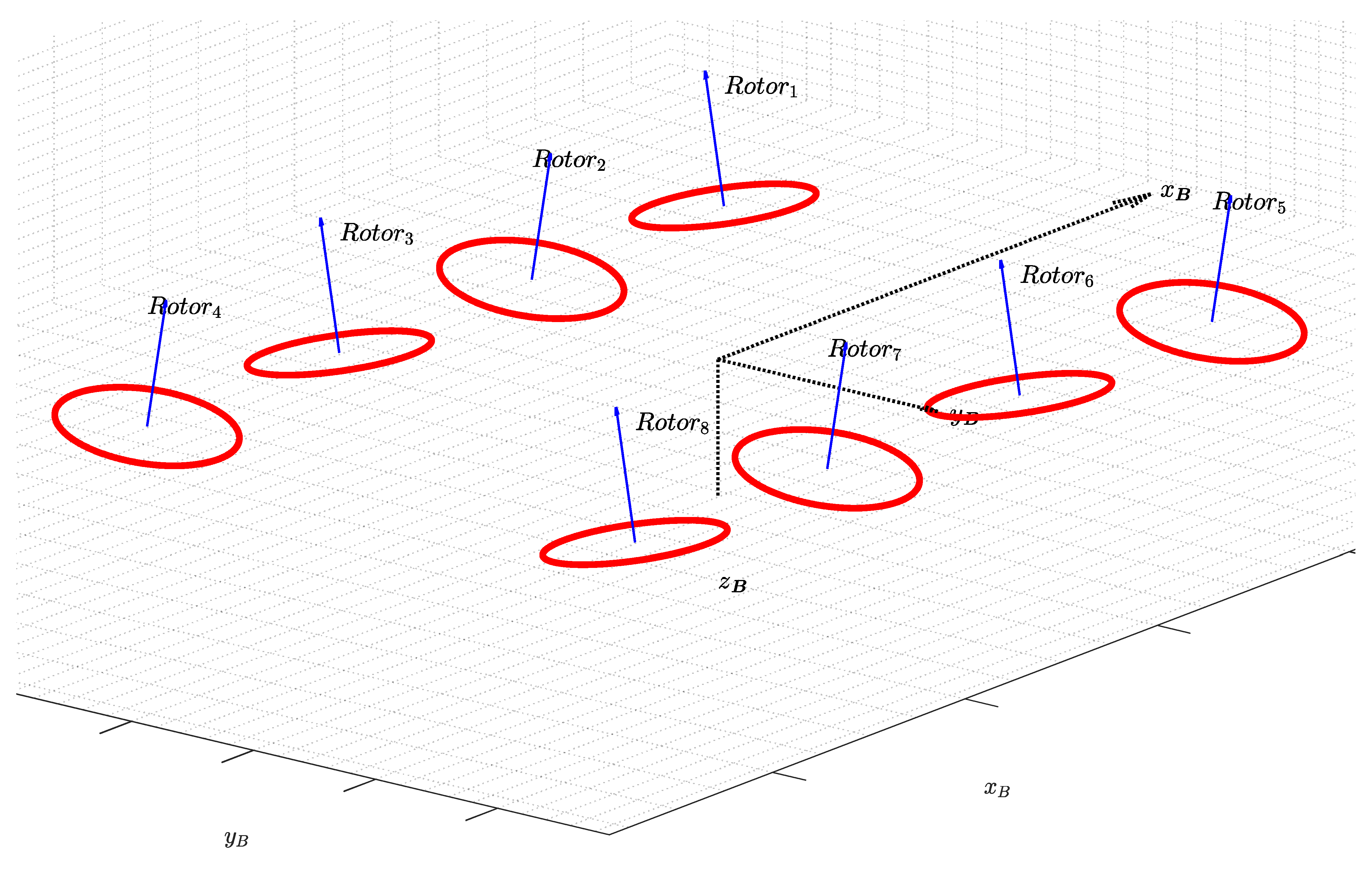
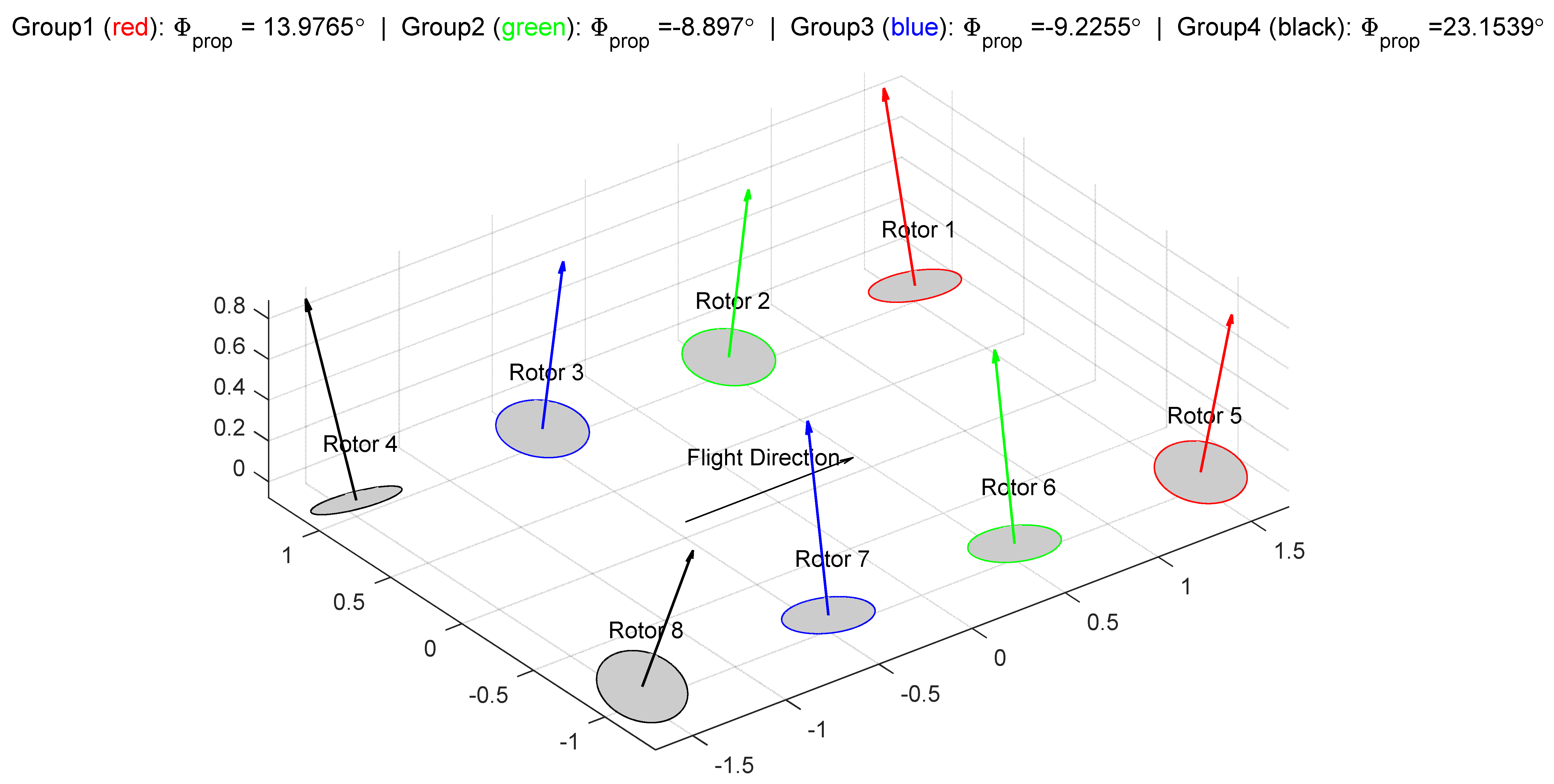
4.1. Airframe Under Consideration
- are the orientations of rotors around the longitudinal axis, positive is defined by the right-hand rule;
- is the generalized moments vector of rotational accelerations and vertical load factor in the body-fixed axis;
- is the effectiveness matrix [29], as a function of ;
- and are the rotational speed of the propellers and their upper limit.
4.2. Assumptions
4.3. Test Setup
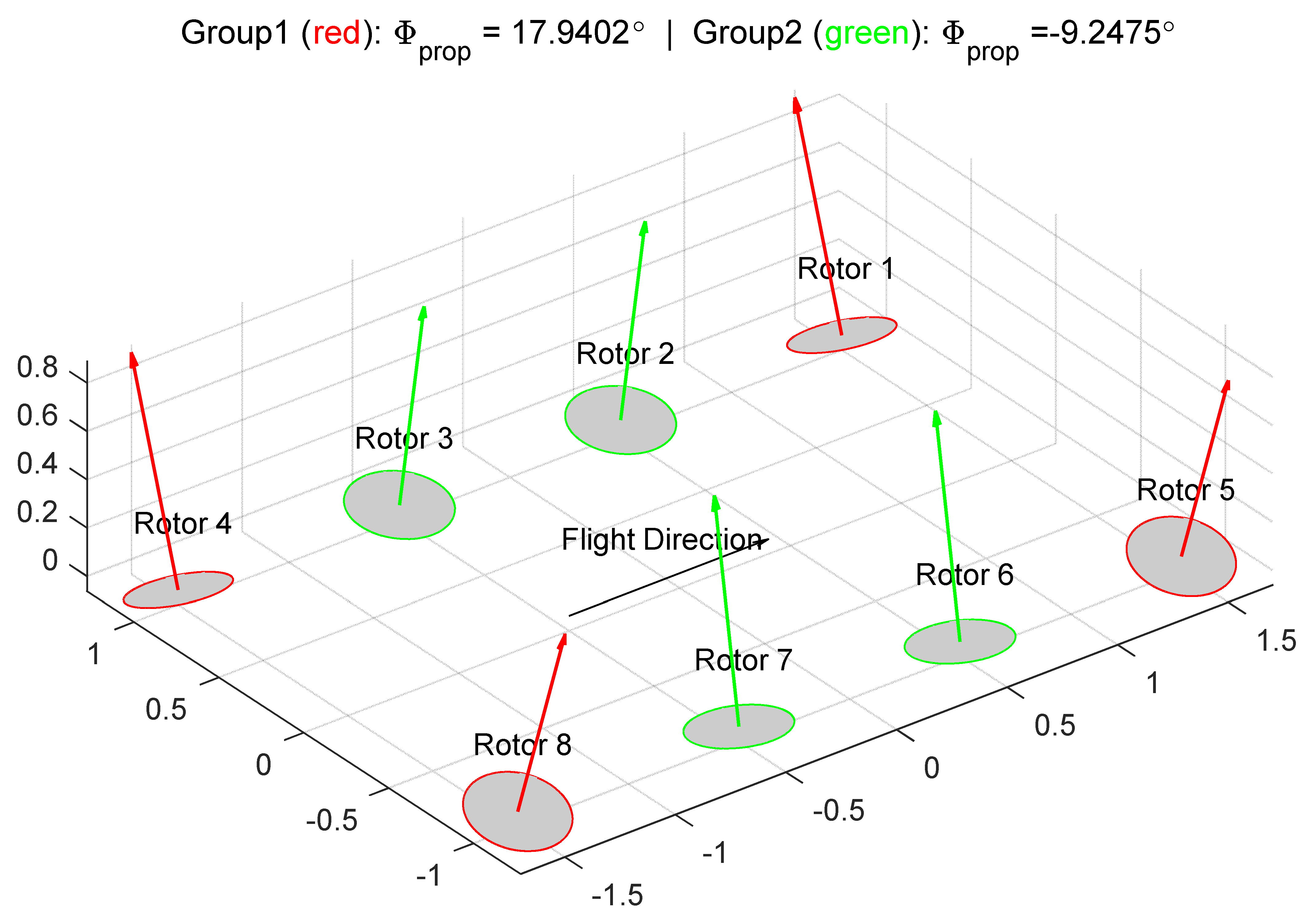
- Two-variable failure-free test as Equation (2), with
- Two-variable failure-free test as Equation (2), with
- Same grouping as Test 1, including critical OEI according to Equation (3);
- Same grouping as Test 2, including critical OEI according to Equation (3).
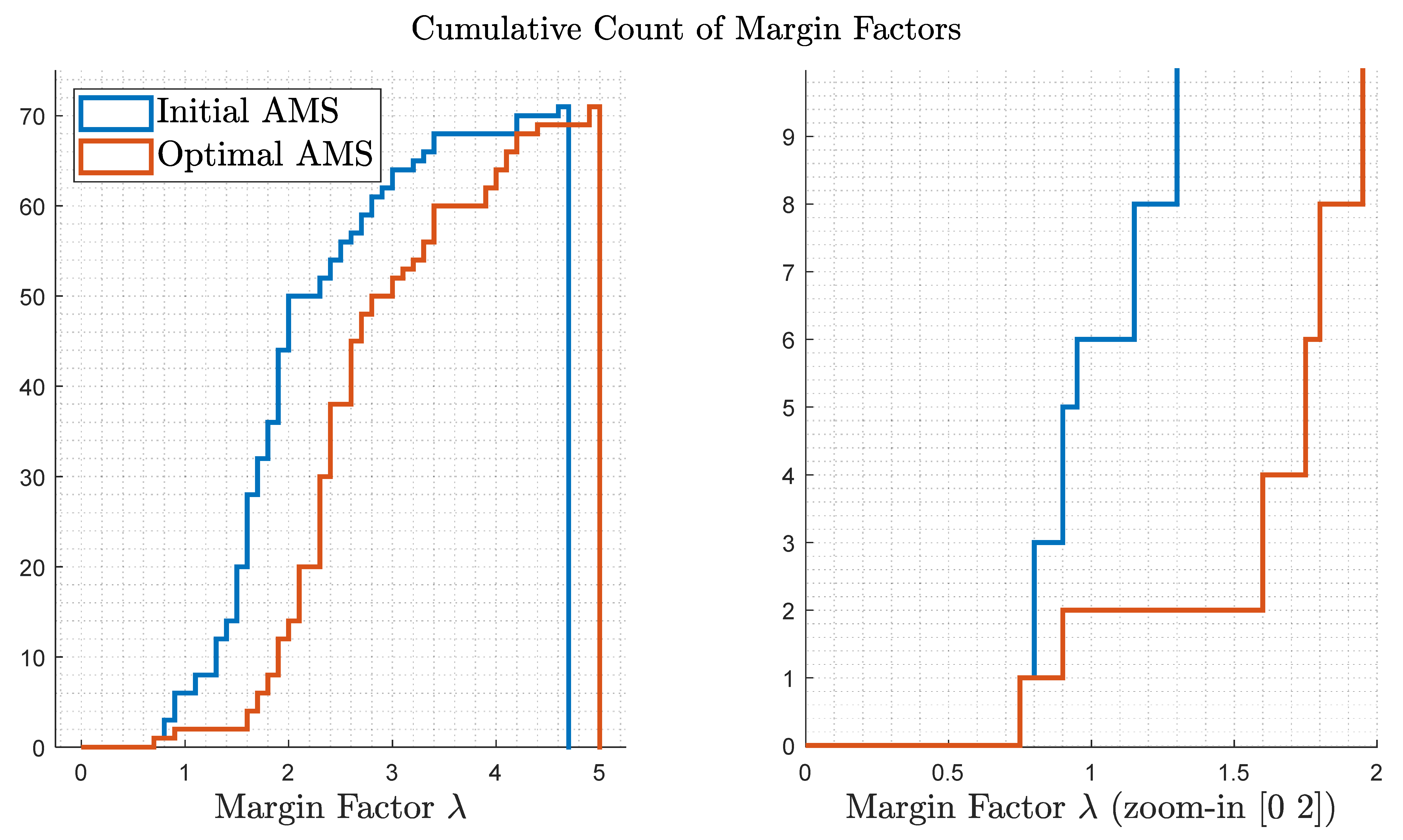
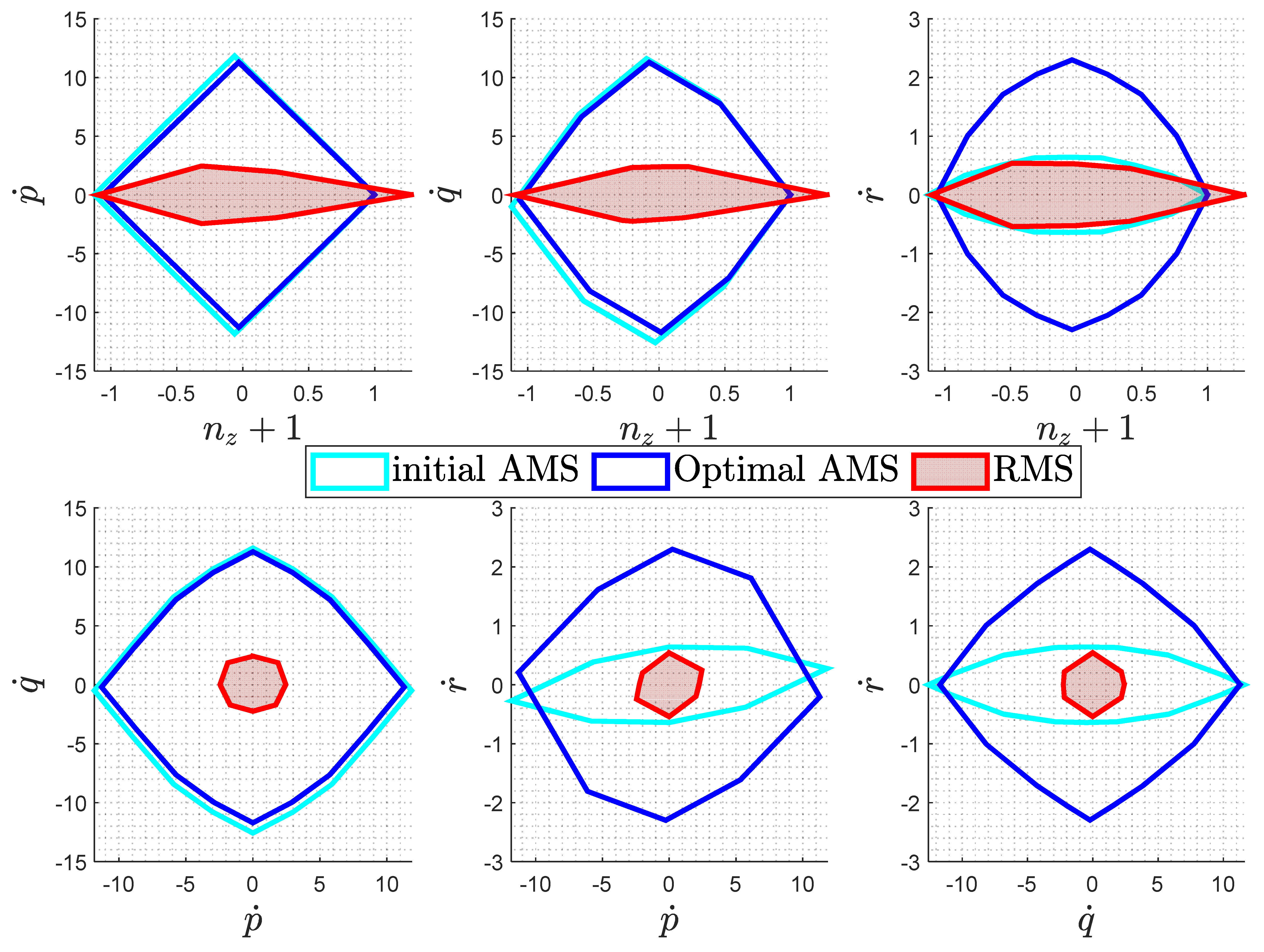
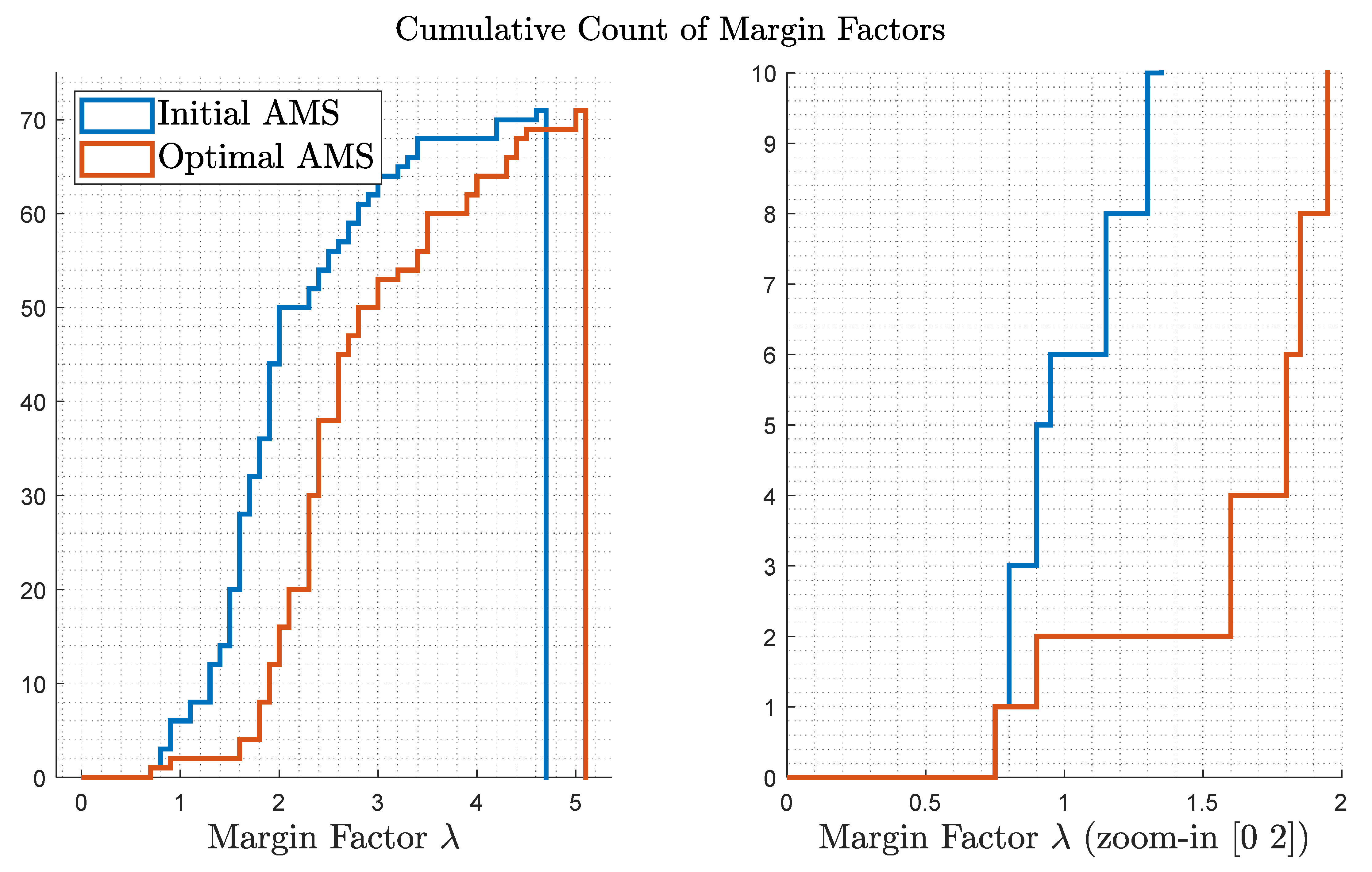
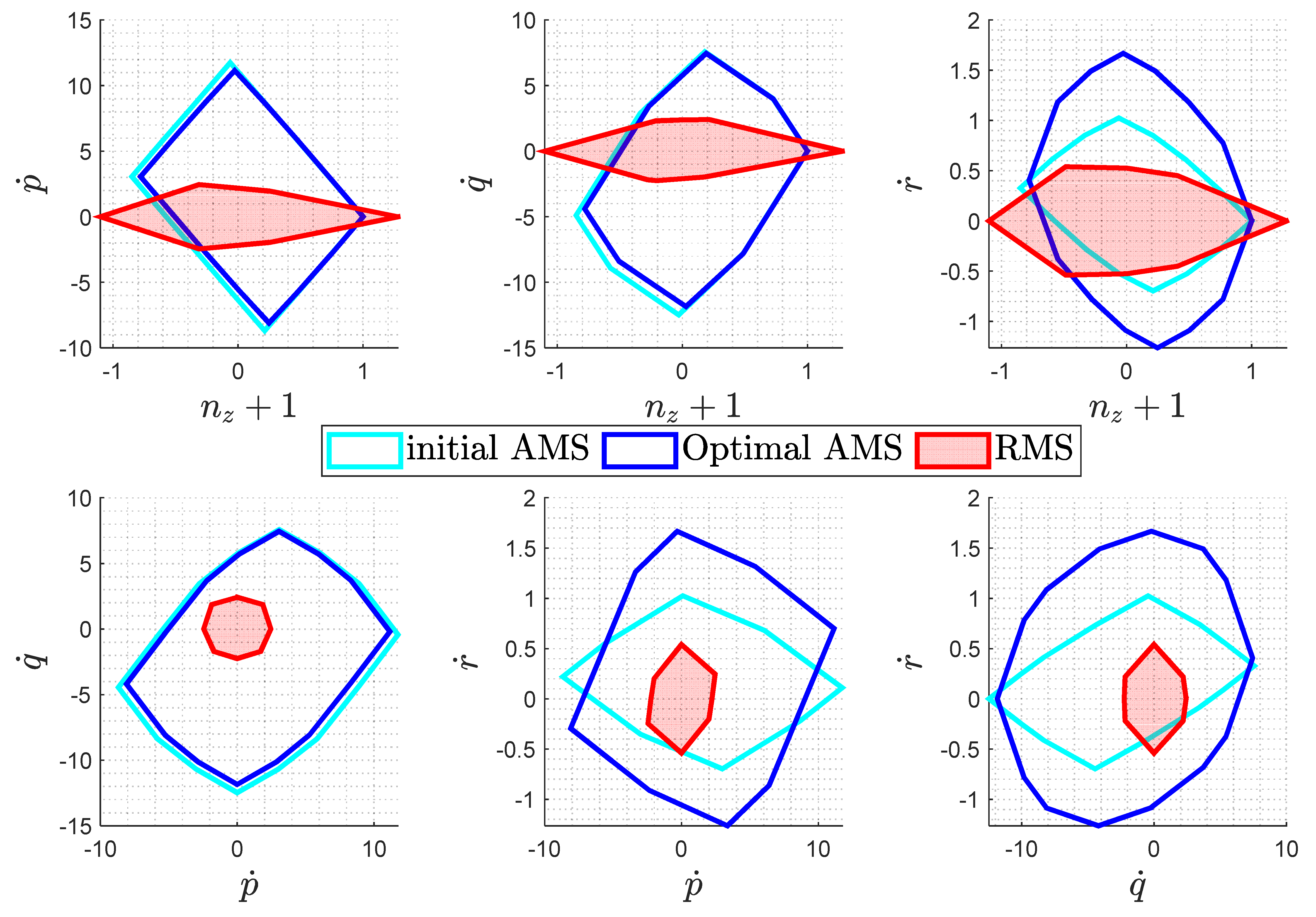
5. Optimization Results
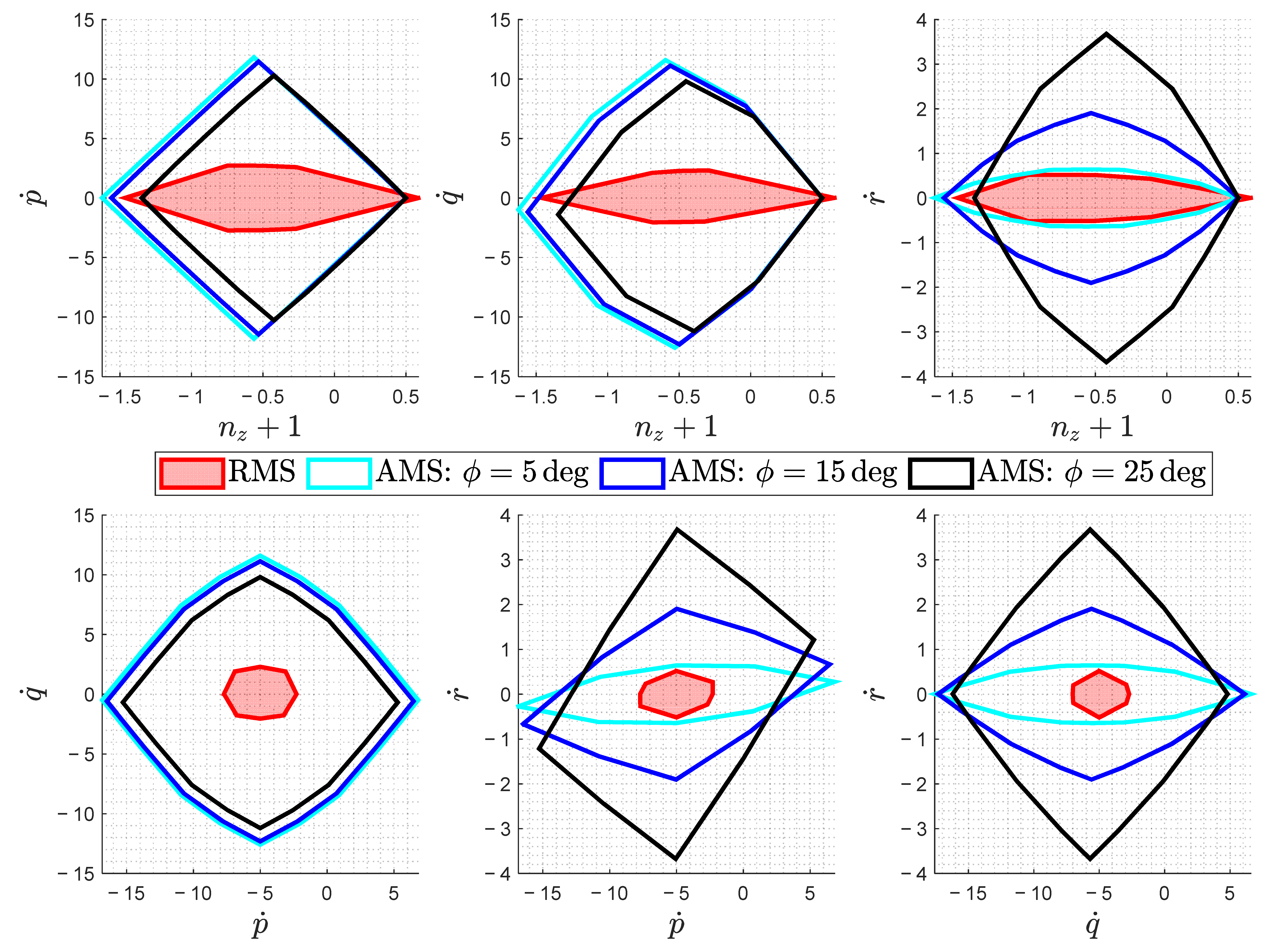
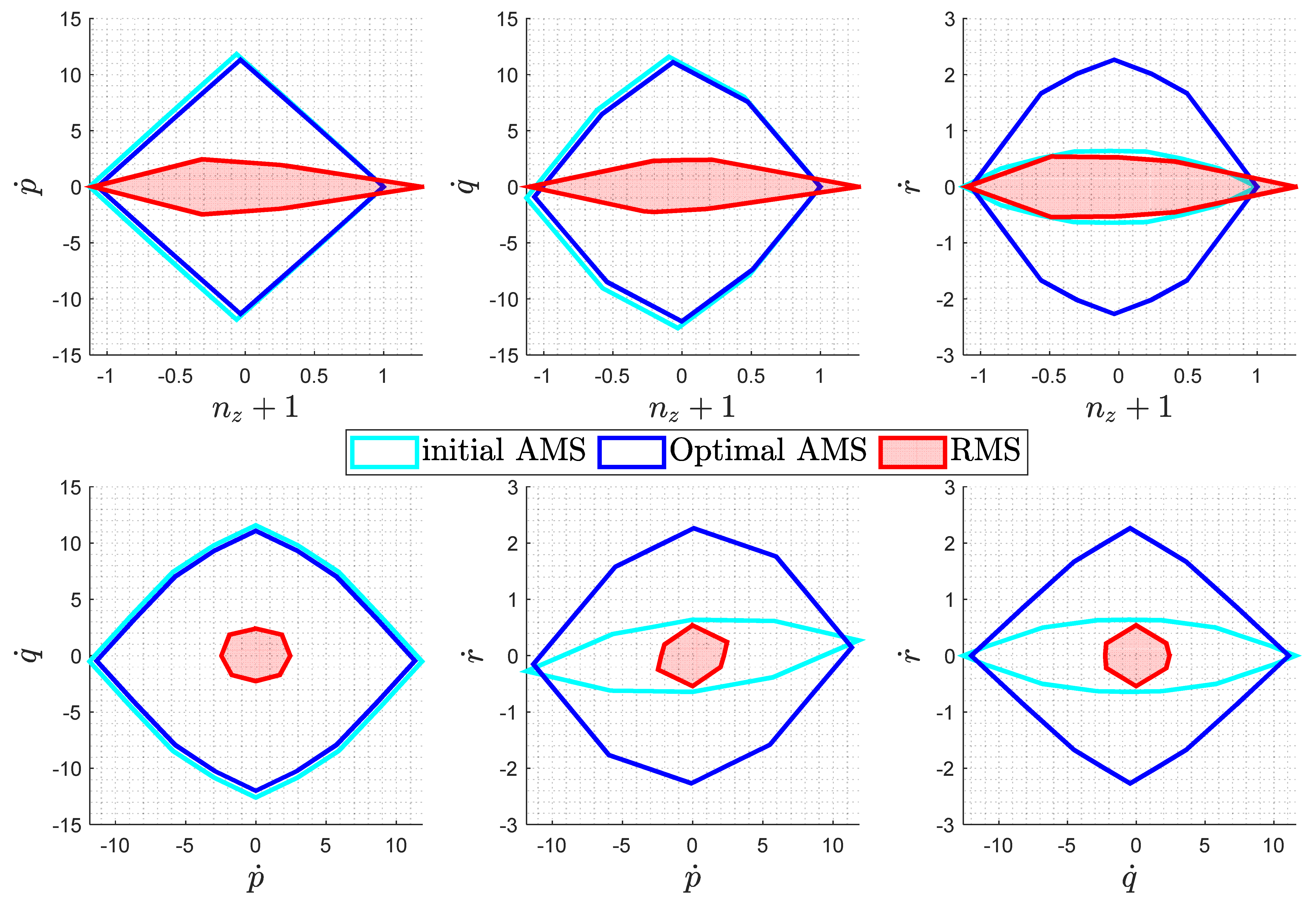
5.1. Optimization Results—Failure-Free Cases
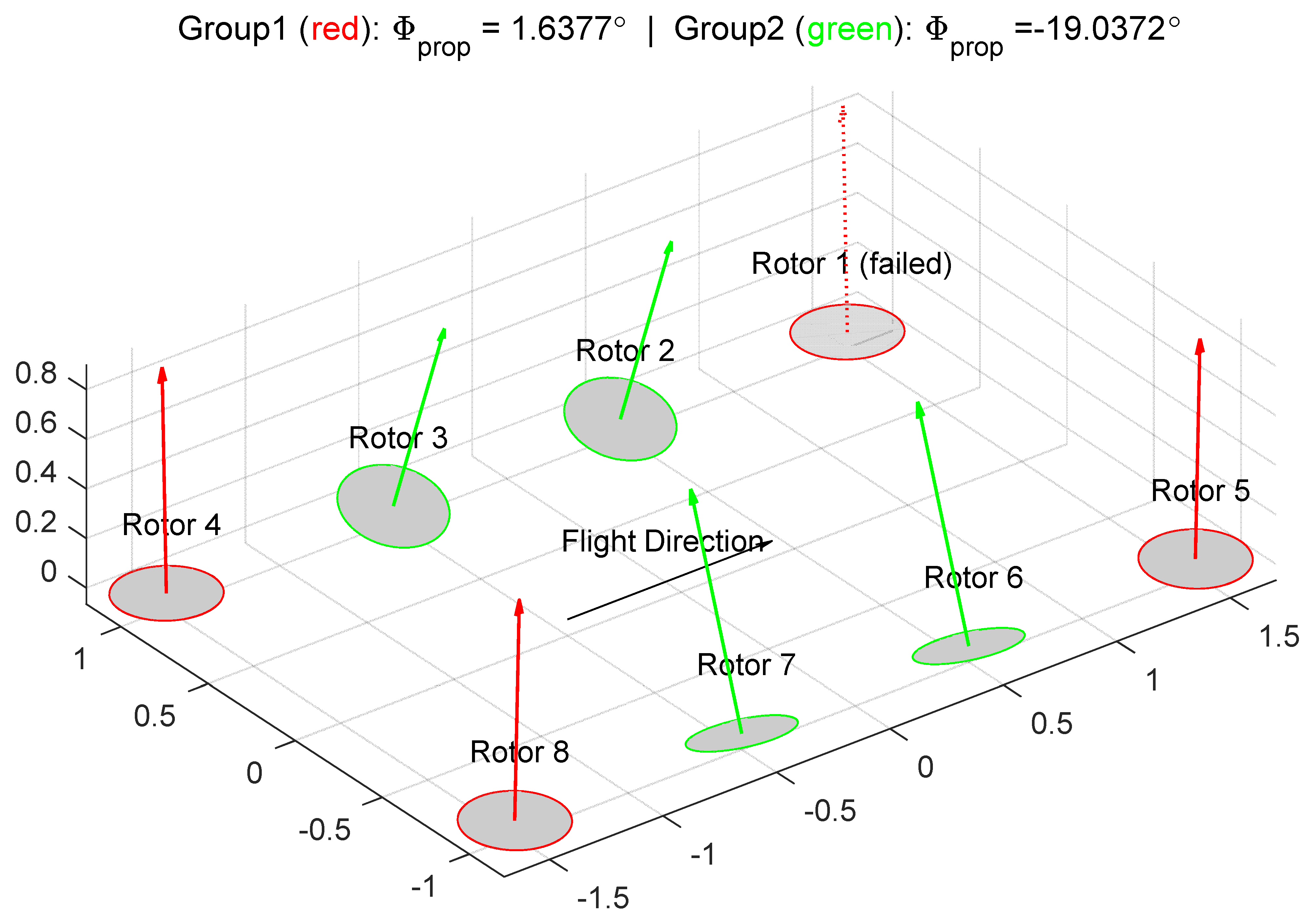
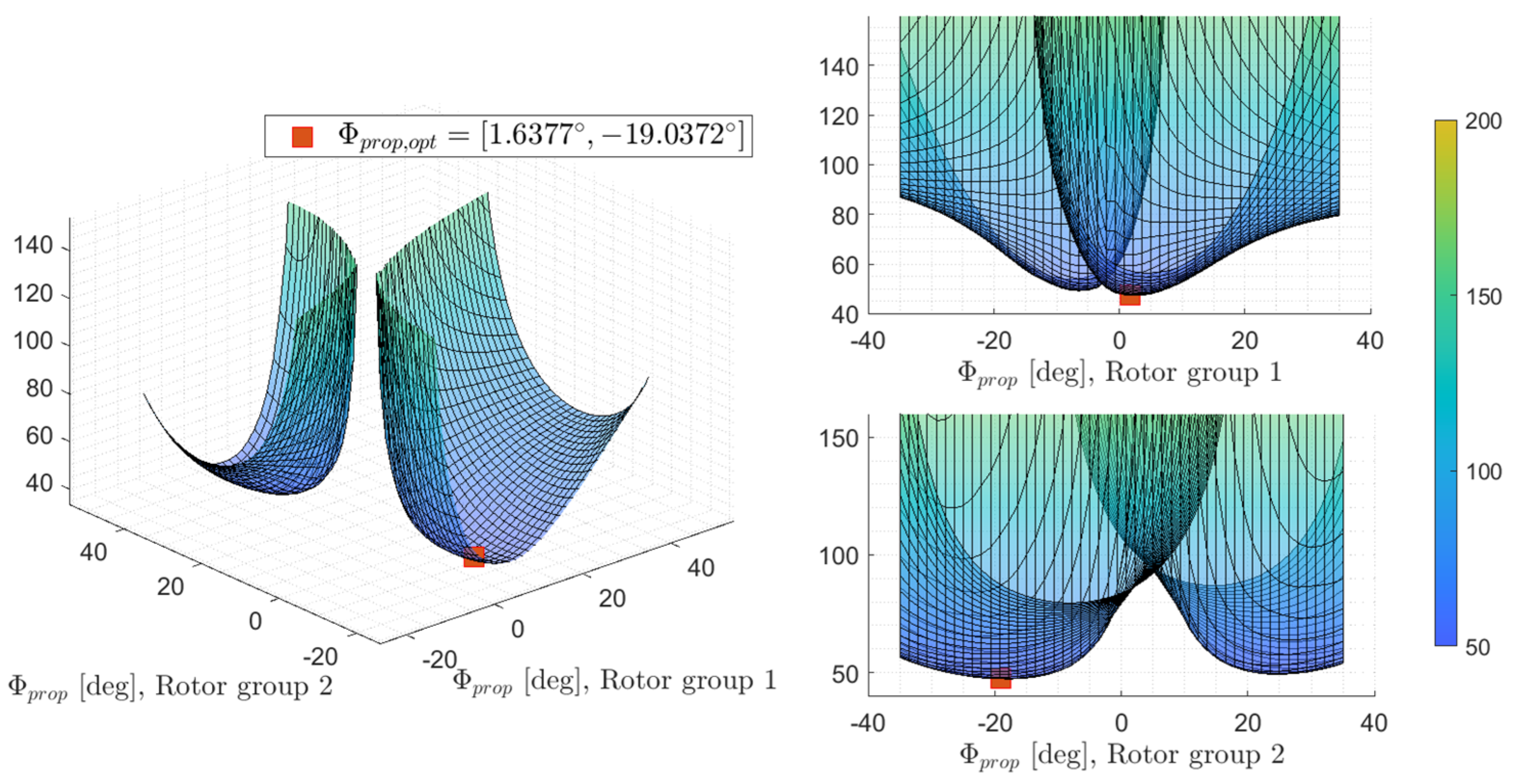
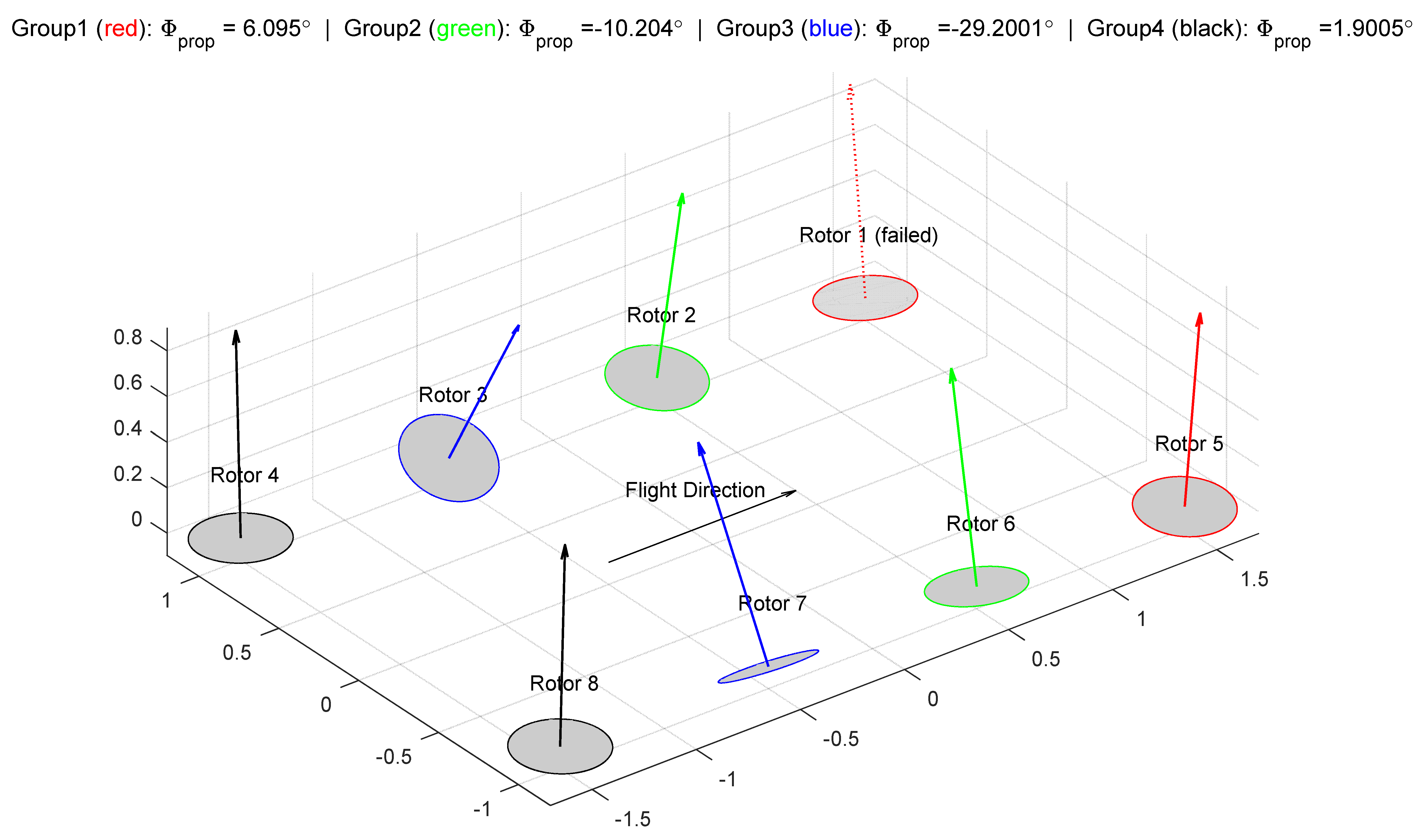
5.2. Optimization Results—Critical Failure Case
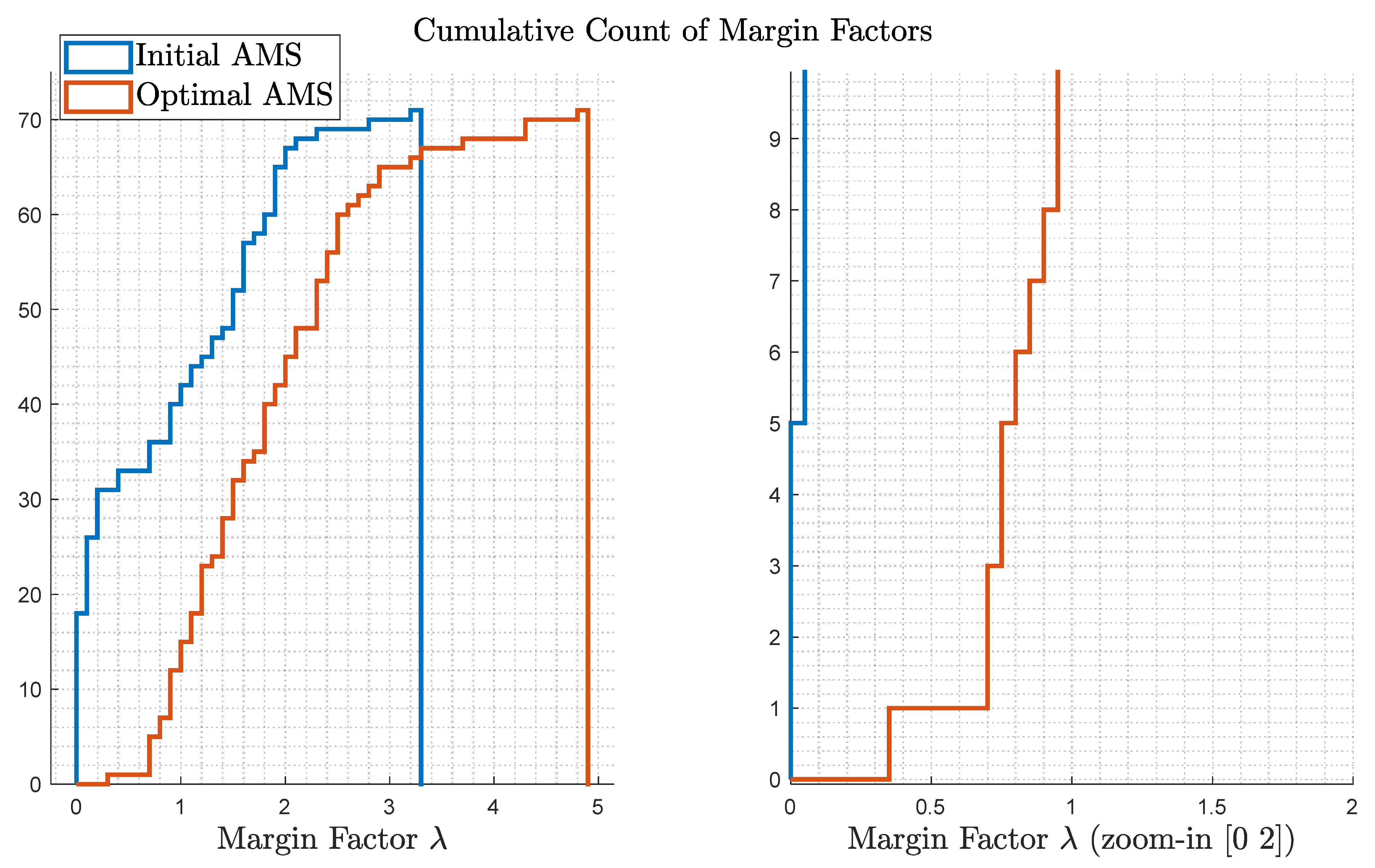
5.3. Validation and Comparison of Optimization Results
6. Closed-Loop Verification
6.1. Closed-Loop Simulation Framework
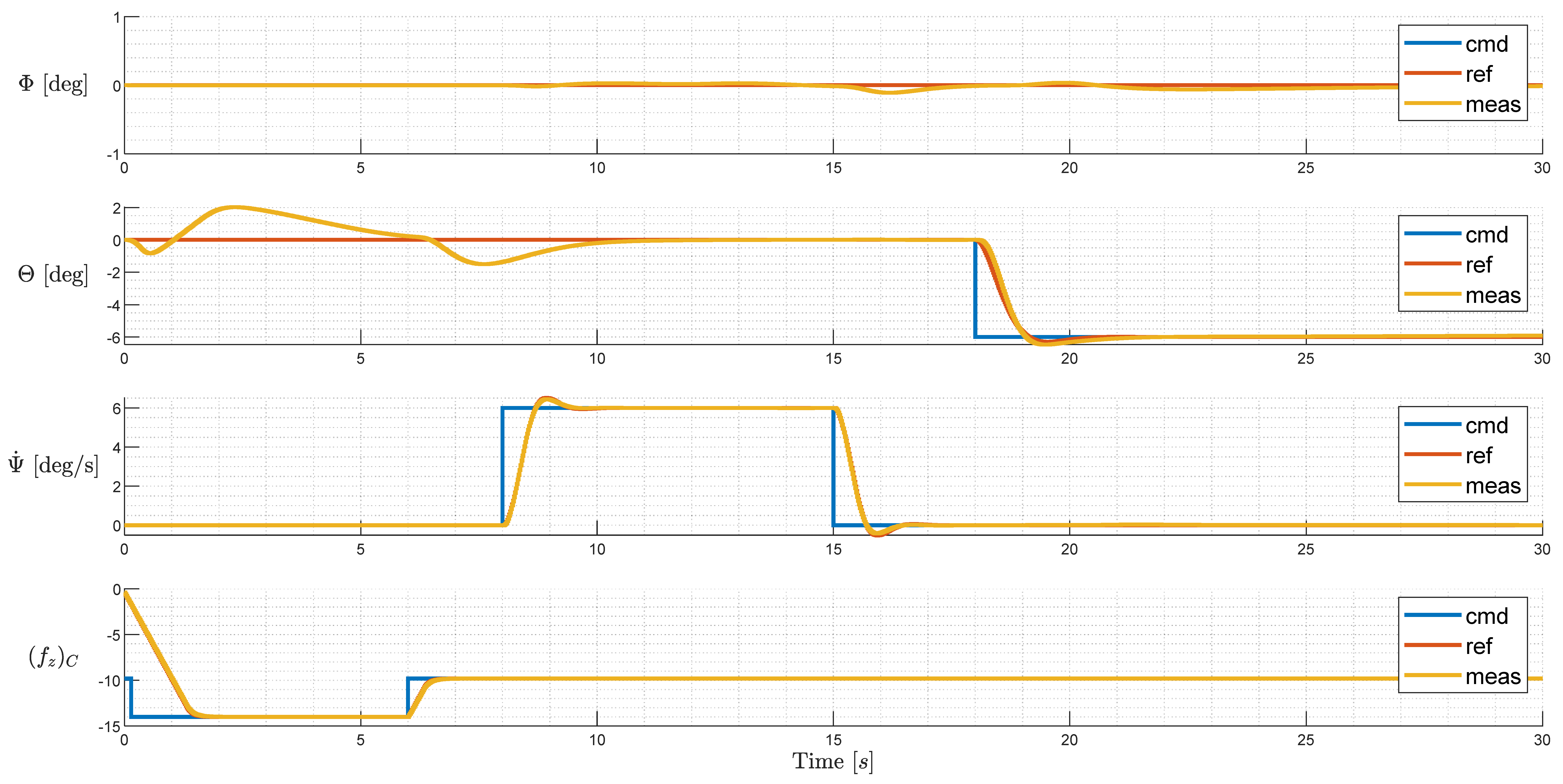
6.2. Initial Configuration: Failure-Free Simulation
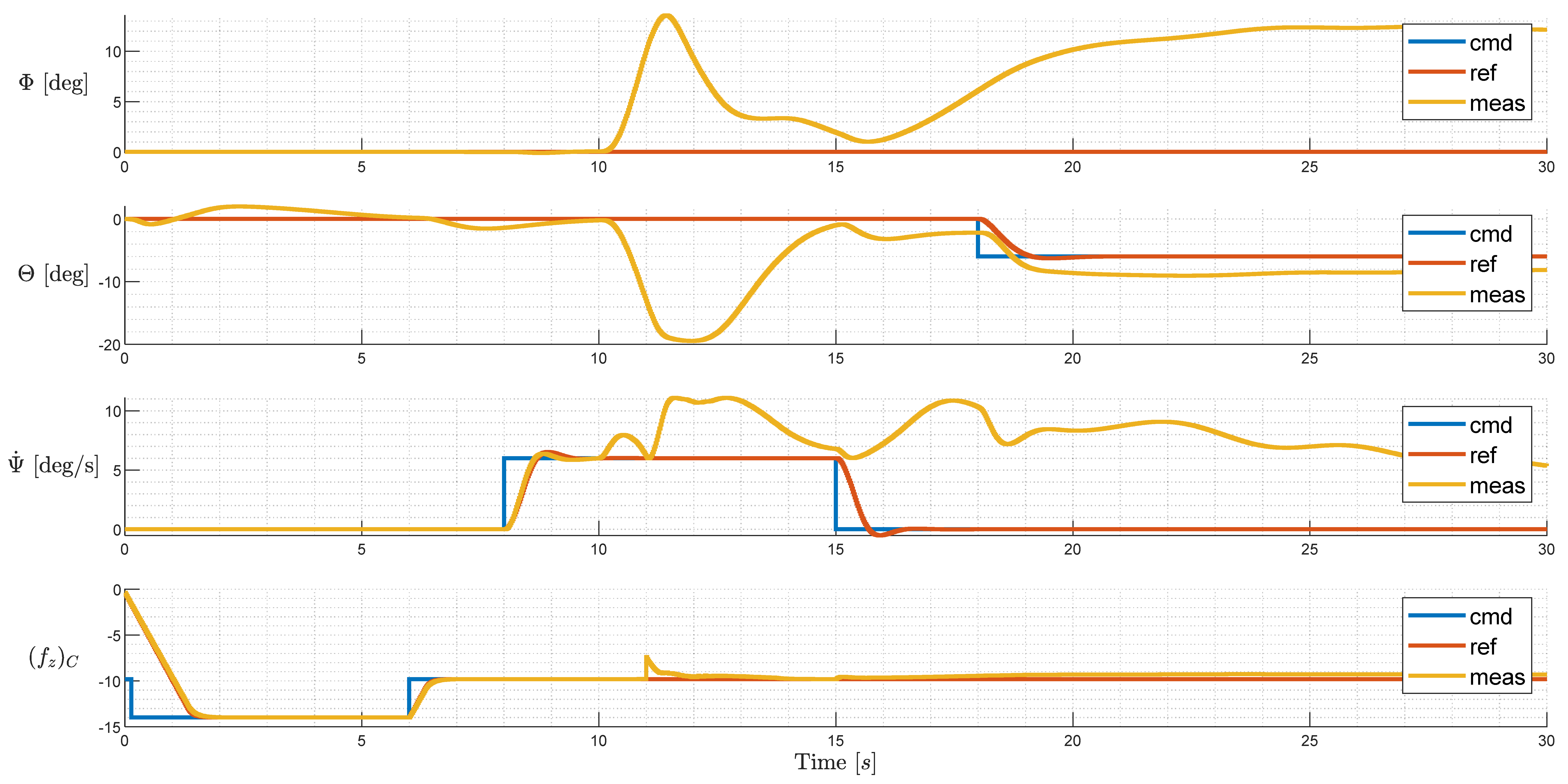
6.3. Initial Configuration: Simulation with Injected Failure
6.4. Failure-Free Optimized Configuration: Simulation with Injected Failure
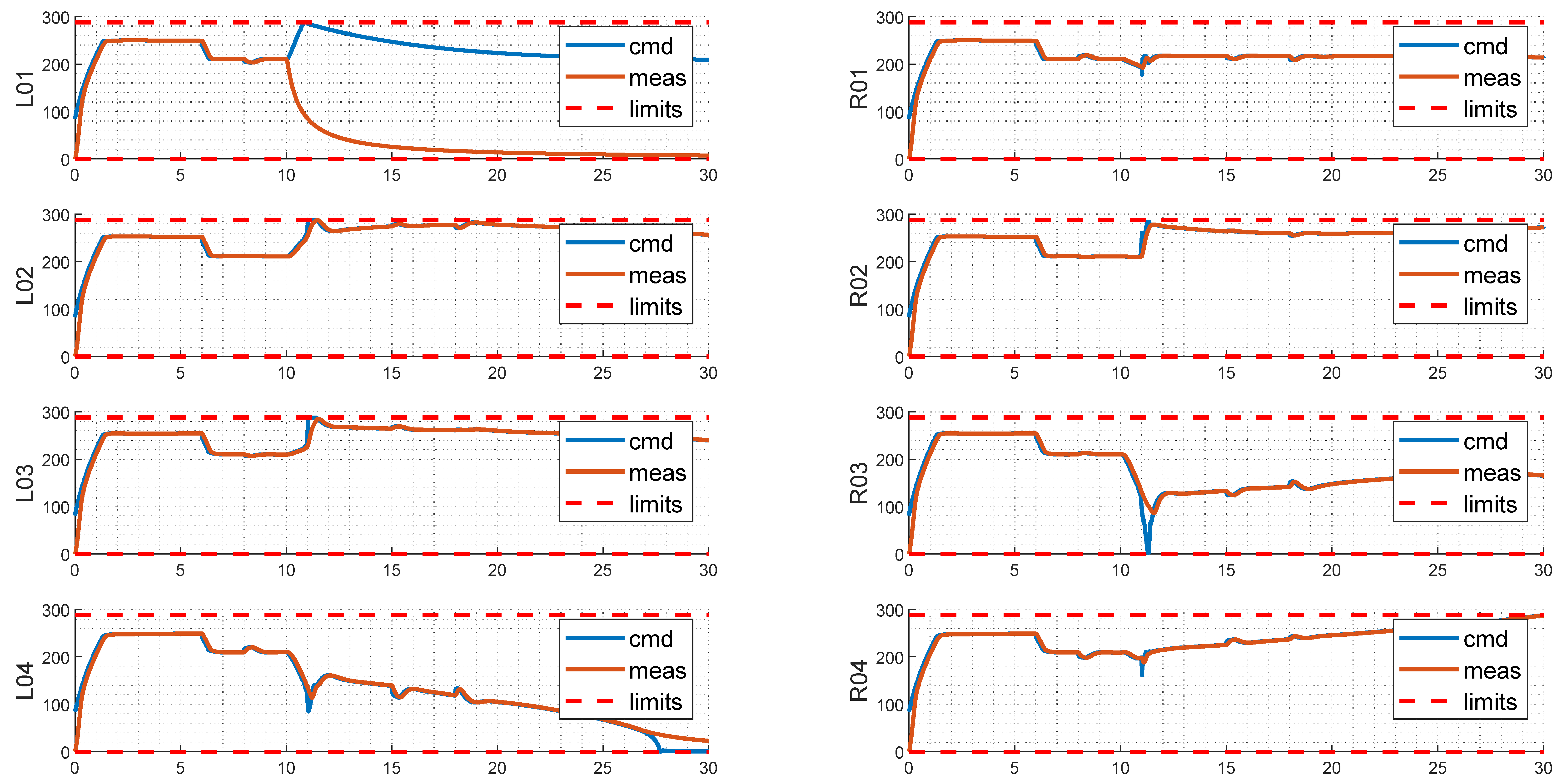
6.5. Critical-Failure-Optimized Layout Simulation with Injected Failure
6.6. Summary of Simulation Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Durham, W.C. Constrained control allocation. J. Guid. Control Dyn. 1993, 16, 717–725. [Google Scholar] [CrossRef]
- Durham, W.C. Constrained control allocation—Three-moment problem. J. Guid. Control Dyn. 1994, 17, 330–336. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I. Control allocation—A Survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef]
- Durham, W.C. Attainable moments for the constrained control allocation problem. J. Guid. Control Dyn. 1994, 17, 1371–1373. [Google Scholar] [CrossRef]
- Varriale, C.; Voskuijl, M.; Veldhuis, L.L. Trim for Maximum Control Authority using the Attainable Moment Set. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. ISBN 9781624105951. [Google Scholar]
- Ma, T.; Wang, X.; Qiao, N.; Zhang, Z.; Fu, J.; Bao, M. A Conceptual Design and Optimization Approach for Distributed Electric Propulsion eVTOL Aircraft Based on Ducted-Fan Wing Unit. Aerospace 2022, 9, 690. [Google Scholar] [CrossRef]
- Suiçmez, E.C. Full Envelope Nonlinear Controller Design for a Novel Electric VTOL(eVTOL) Air-taxi via INDI Approach Combined with CA. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2021. [Google Scholar]
- Moore, K.R.; Ning, A. Distributed Electric Propulsion Effects on Existing Aircraft Through Multidisciplinary Optimization. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018; ISBN 978-1-62410-532-6. [Google Scholar]
- Fard, M.T.; He, J.; Huang, H.; Cao, Y. Aircraft Distributed Electric Propulsion Technologies—A Review. IEEE Trans. Transp. Electrific. 2022, 8, 4067–4090. [Google Scholar] [CrossRef]
- Bacchini, A.; Cestino, E. Electric VTOL Configurations Comparison. Aerospace 2019, 6, 26. [Google Scholar] [CrossRef]
- Akash, A.; Raj, V.S.J.; Sushmitha, R.; Prateek, B.; Aditya, S.; Sreehari, V.M. Design and Analysis of VTOL Operated Intercity Electrical Vehicle for Urban Air Mobility. Electronics 2022, 11, 20. [Google Scholar] [CrossRef]
- Piccinini, R.; Tugnoli, M.; Zanotti, A. Numerical Investigation of the Rotor-Rotor Aerodynamic Interaction for eVTOL Aircraft Configurations. Energies 2020, 13, 5995. [Google Scholar] [CrossRef]
- Tumuluru Ramesh, N.; Pandurangi, P.V. A Flight Performance Based Optimization Model for eVTOL Vehicles. Eng. Arch. 2022, preprint. [Google Scholar]
- Cook, J. A Strip Theory Approach to Dynamic Modeling of eVTOL Aircraft. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–21 January 2021; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar]
- Stokkermans, T.C.A.; Usai, D.; Sinnige, T.; Veldhuis, L.L.M. Aerodynamic Interaction Effects Between Propellers in Typical eVTOL Vehicle Configurations. J. Aircr. 2021, 58, 815–833. [Google Scholar] [CrossRef]
- EASA. Special Condition for Small-Category VTOL-Capable Aircraft. Available online: https://www.easa.europa.eu/en/downloads/139946/en (accessed on 28 October 2024).
- EASA. Means of Compliance with the Special Condition VTOL—MOC SC-VTOL Issue 2. Available online: https://www.easa.europa.eu/en/downloads/127717/en (accessed on 28 October 2024).
- Eric, N.V.; Pierre, T.; Joël, J.; Daniel, A.; Philippe, P.; Carsten, D. Reduction of Vertical Tail Using Differential Thrust: Influence on Flight Control and Certification. In Proceedings of the Advanced Aircraft Efficiency in a Global Air Transport System (AEGATS’18), Toulouse, France, 23–25 October 2018; pp. 1–8. [Google Scholar]
- Van, E.N.; Alazard, D.; Döll, C.; Pastor, P. Co-design of aircraft vertical tail and control laws using distributed electric propulsion. IFAC-PapersOnLine 2019, 52, 514–519. [Google Scholar] [CrossRef]
- Moore, K.R.; Ning, A. Takeoff and Performance Trade-Offs of Retrofit Distributed Electric Propulsion for Urban Transport. J. Aircr. 2019, 56, 1880–1892. [Google Scholar] [CrossRef]
- Pei, J.; Bassett, G.; Grisham, J.; Finch, P.; Toniolo, M.; Miller, L.; Bandu, P. Generic Control Allocation Toolbox for Preliminary Vehicle Design. In Proceedings of the 2018 Modeling and Simulation Technologies Conference, Reston, VA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. ISBN 9781624105517. [Google Scholar]
- Varriale, C.; Voskuijl, M. A trim problem formulation for maximum control authority using the Attainable Moment Set geometry. CEAS Aeronaut J. 2022, 13, 251–266. [Google Scholar] [CrossRef]
- Söpper, M.; Zhang, J.; Holzapfel, F. Required Moment Sets: Enhanced Controllability Analysis for Nonlinear Aircraft Models. (submitted). Appl. Sci. 2021, 11, 3456. [Google Scholar] [CrossRef]
- Zhang, J.; Söpper, M.; Holzapfel, F. Attainable Moment Set Optimization to Support Configuration Design: A Required Moment Set Based Approach. Appl. Sci. 2021, 11, 3685. [Google Scholar] [CrossRef]
- Lu, Z.; Hong, H.; Schweighofer, F.; Holzapfel, F. Controllability Evaluation for VTOL Aircraft in Velocity Envelope: A Distance-Based Metric. J. Guid. Control Dyn. 2024, 47, 1–14. [Google Scholar] [CrossRef]
- MathWorks. MATLAB Version: 9.8.0.1451342 (R2021a); MathWorks: Natick, MA, USA, 2021. [Google Scholar]
- Gupta, G.; Abdallah, S. Propeller Force-Constant Modeling for Multirotor UAVs from Experimental Estimation of Inflow Velocity. Int. J. Aerosp. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- MIT. Performance of Propellers. Available online: https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node86.html (accessed on 28 October 2024).
- Du, G.-X.; Quan, Q.; Yang, B.; Cai, K.-Y. Controllability Analysis for Multirotor Helicopter Rotor Degradation and Failure. J. Guid. Control Dyn. 2015, 38, 978–985. [Google Scholar] [CrossRef]
- Di Francesco, G.; Mattei, M. Modeling and Incremental Nonlinear Dynamic Inversion Control of a Novel Unmanned Tiltrotor. J. Aircr. 2016, 53, 73–86. [Google Scholar] [CrossRef]
- Wang, X.; van Kampen, E.-J.; Chu, Q.; Lu, P. Stability Analysis for Incremental Nonlinear Dynamic Inversion Control. J. Guid. Control Dyn. 2019, 42, 1116–1129. [Google Scholar] [CrossRef]
- Lu, P.; van Kampen, E.-J.; Visser, C.d.; Chu, Q. Aircraft fault-tolerant trajectory control using Incremental Nonlinear Dynamic Inversion. Control Eng. Pract. 2016, 57, 126–141. [Google Scholar] [CrossRef]
- Smeur, E.J.J.; Chu, Q.; Croon, G.C.H.E.d. Adaptive Incremental Nonlinear Dynamic Inversion for Attitude Control of Micro Air Vehicles. J. Guid. Control Dyn. 2016, 39, 450–461. [Google Scholar] [CrossRef]
- Bodson, M. Evaluation of Optimization Methods for Control Allocation. J. Guid. Control Dyn. 2002, 25, 703–711. [Google Scholar] [CrossRef]
- Zhang, J.; Bhardwaj, P.; Raab, S.A.; Saboo, S.; Holzapfel, F. Control Allocation Framework for a Tilt-rotor Vertical Take-off and Landing Transition Aircraft Configuration. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. ISBN 978-1-62410-559-3. [Google Scholar]
- Raab, S.A.; Zhang, J.; Bhardwaj, P.; Holzapfel, F. Proposal of a Unified Control Strategy for Vertical Take-off and Landing Transition Aircraft Configurations. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. ISBN 978-1-62410-559-3. [Google Scholar]
- Bhardwaj, P.; Raab, S.A.; Zhang, J.; Holzapfel, F. Integrated Reference Model for a Tilt-rotor Vertical Take-off and Landing Transition UAV. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Sieberling, S.; Chu, Q.P.; Mulder, J.A. Robust Flight Control Using Incremental Nonlinear Dynamic Inversion and Angular Acceleration Prediction. J. Guid. Control Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]










| Preliminary Design Parameters | Values |
|---|---|
| Take-off Weight | 250 kg |
| Wingspan | 10 m |
| Motor Diameter | 1–2 m |
| Initial Value | Test 1 | Test 2 | Test 3 | Test 4 | |
|---|---|---|---|---|---|
| P1 tilt angle () | −5 | −17.94 | −13.98 | −1.64 | −6.09 |
| P2 tilt angle () | 5 | 9.25 | 8.90 | 19.04 | 10.20 |
| P3 tilt angle () | −5 | 9.25 | 9.23 | 19.04 | 29.20 |
| P4 tilt angle () | 5 | −17.94 | −23.15 | −1.64 | −1.90 |
| Failure-free cost function: | 33.06 | 29.22 | 29.12 | 30.29 | 30.28 |
| Critical failure cost function: | 61.31 | 67.85 | 59.58 | 47.39 | 45.6667 |
| Total force available in the vertical direction (%): | 99.6% | 96.92% | 96.62% | 97.24% | 96.27% |
| Additional force to trim (%): | 0.40% | 3.18% | 3.50% | 2.84% | 3.87% |
| Additional power to trim (%): | 0.6% | 4.8% | 5.3% | 4.3% | 5.9% |
| Initial Unoptimized Config. (Figure 21 and Figure 22) | Non-Failure-Optimized Config. (Figure 23 and Figure 24; Figure 23; Figure 24) | Critical-Failure-Optimized Config. (Figure 23 and Figure 24) | |
|---|---|---|---|
| Continued Safe Flight after Failure (Y/N) | N | Y | Y |
| Max. Attitude Transient after Failure (Degrees) | 20 | 15 | 12 |
| Number of Saturated Rotors (Non-Failed) @t = 30 s | 4 (L02, R02, L04, R04) | 2 (L04, R04) | 0 |
| Difference between Max. and Min. Rotational Speed (Non-Failed) @t = 30 s (Rad/s) | 288 (btw. L04 & R04) | 288 (btw. L04 & R04) | 158 (btw. L03 & R03) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Söpper, M.; Holzapfel, F.; Zhang, S. Four-Dimensional Generalized AMS Optimization Considering Critical Engine Inoperative for an eVTOL. Aerospace 2024, 11, 990. https://doi.org/10.3390/aerospace11120990
Zhang J, Söpper M, Holzapfel F, Zhang S. Four-Dimensional Generalized AMS Optimization Considering Critical Engine Inoperative for an eVTOL. Aerospace. 2024; 11(12):990. https://doi.org/10.3390/aerospace11120990
Chicago/Turabian StyleZhang, Jiannan, Max Söpper, Florian Holzapfel, and Shuguang Zhang. 2024. "Four-Dimensional Generalized AMS Optimization Considering Critical Engine Inoperative for an eVTOL" Aerospace 11, no. 12: 990. https://doi.org/10.3390/aerospace11120990
APA StyleZhang, J., Söpper, M., Holzapfel, F., & Zhang, S. (2024). Four-Dimensional Generalized AMS Optimization Considering Critical Engine Inoperative for an eVTOL. Aerospace, 11(12), 990. https://doi.org/10.3390/aerospace11120990








