Connectivity-Enhanced 3D Deployment Algorithm for Multiple UAVs in Space–Air–Ground Integrated Network
Abstract
1. Introduction
- The 3D deployment problem of multiple UAVs in SAGIN is divided into horizontal and vertical deployment problems. The coverage performance of UAVs under a determined path loss and the optimal deployment elevation angle are both discussed. Considering the limitations in current research, the objective of maximizing GU coverage is formulated as an optimization problem.
- We propose an improved genetic algorithm (IGA) and a height optimization algorithm to determine the optimal horizontal positions and heights of UAVs, respectively. The coverage of UAVs is maximized while ensuring the QoS and load balance for GUs. Additionally, the connectivity of the UAV network is ensured to maintain robustness.
- To ensure the performance of the 3D deployment algorithm, the k-means algorithm is employed to initialize the horizontal positions of multiple UAVs, which are then used as inputs for the improved genetic algorithm (IGA). A strategy based on elitist selection and adaptive crossover mutation is proposed to prevent premature convergence in the standard genetic algorithm (SGA).
- We evaluate the algorithm’s performance in different scenarios to ensure its adaptability. Simulation results show that compared with other deployment schemes, the proposed 3D deployment algorithm achieves higher coverage. Moreover, it significantly enhances the robustness of the UAV network and achieves better load balance performance.
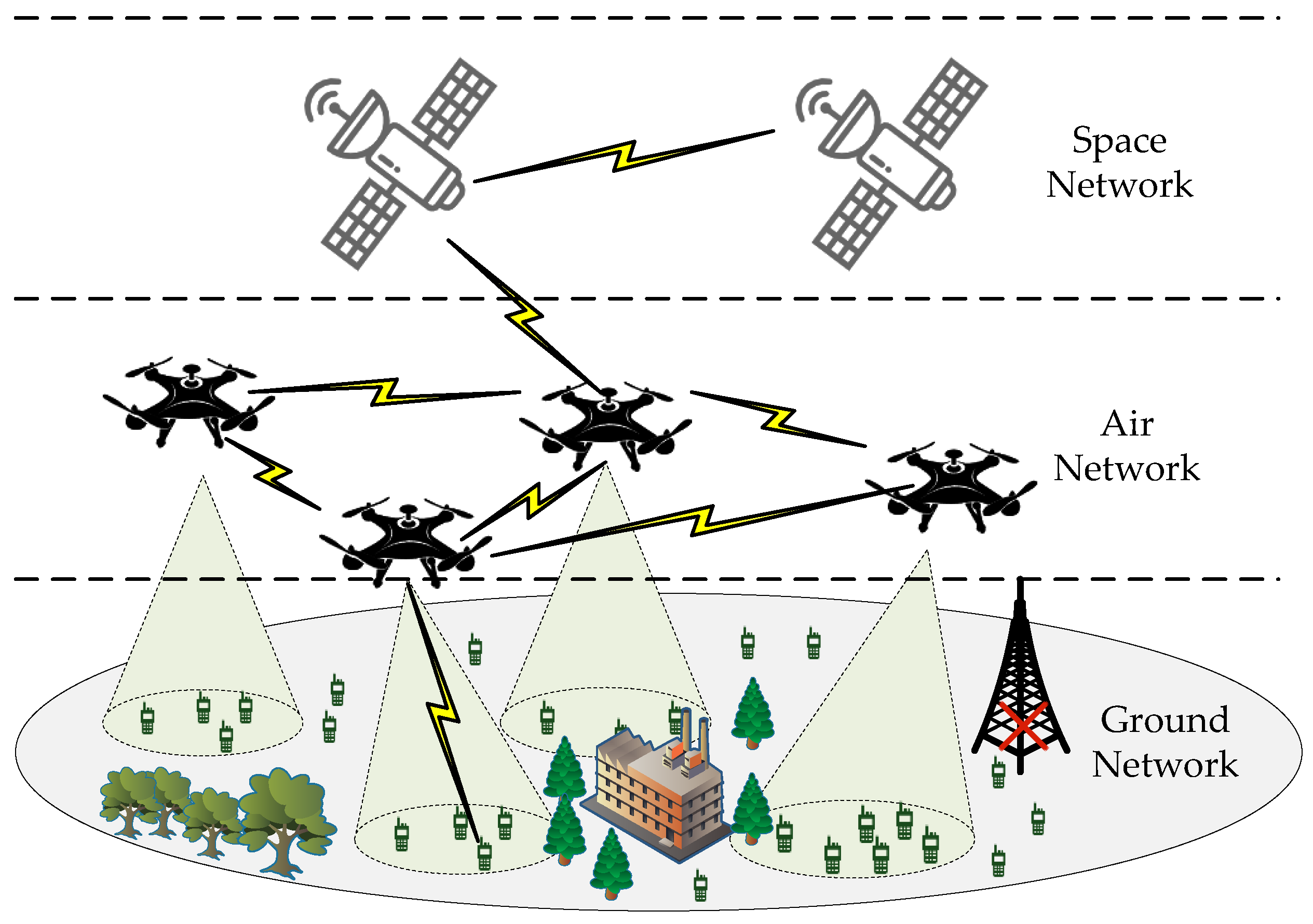
2. System Model and Problem Formulation
2.1. System Model
2.2. Channel Model
2.3. Problem Formulation
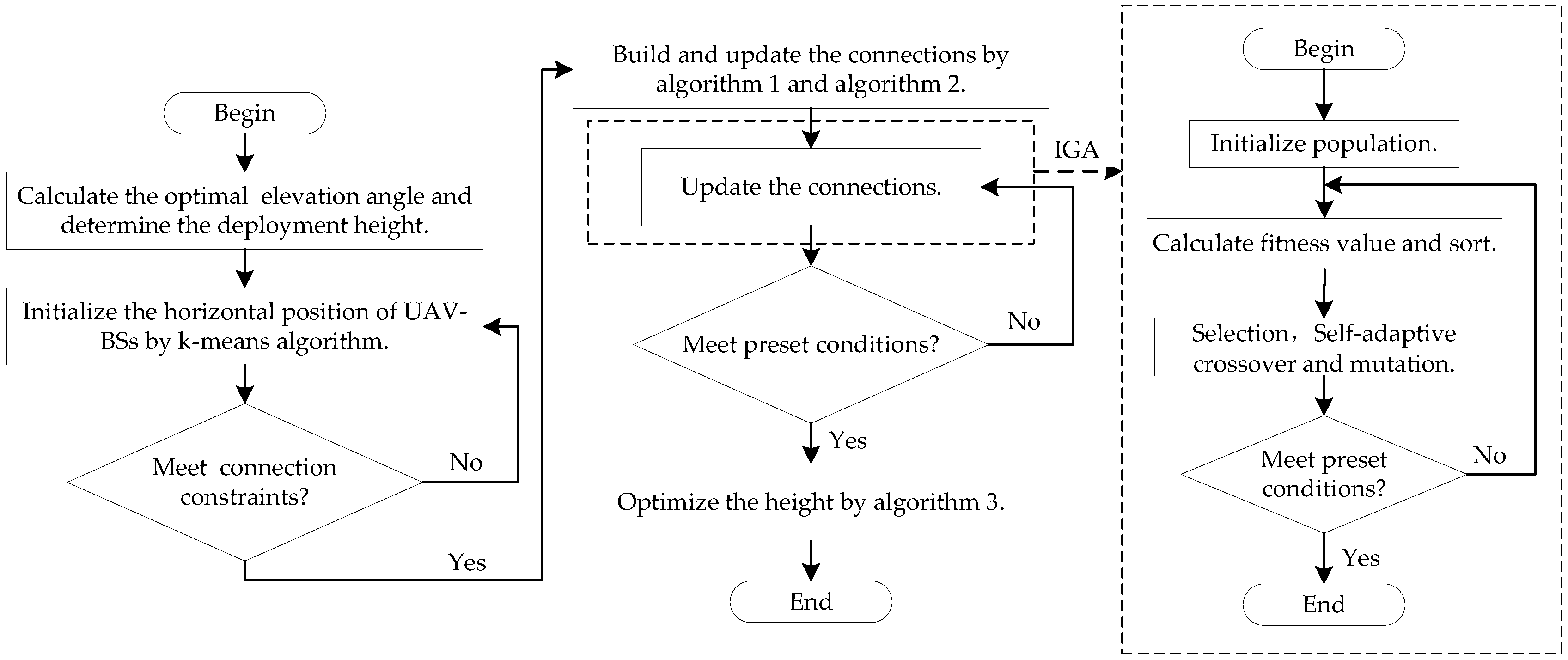
3. Connectivity-Enhanced 3D Deployment Algorithm for UAVs
3.1. Initialization
| Algorithm 1 Establish connections between UAVs. |
|
| Algorithm 2 Establish connections between UAVs and GUs. |
|
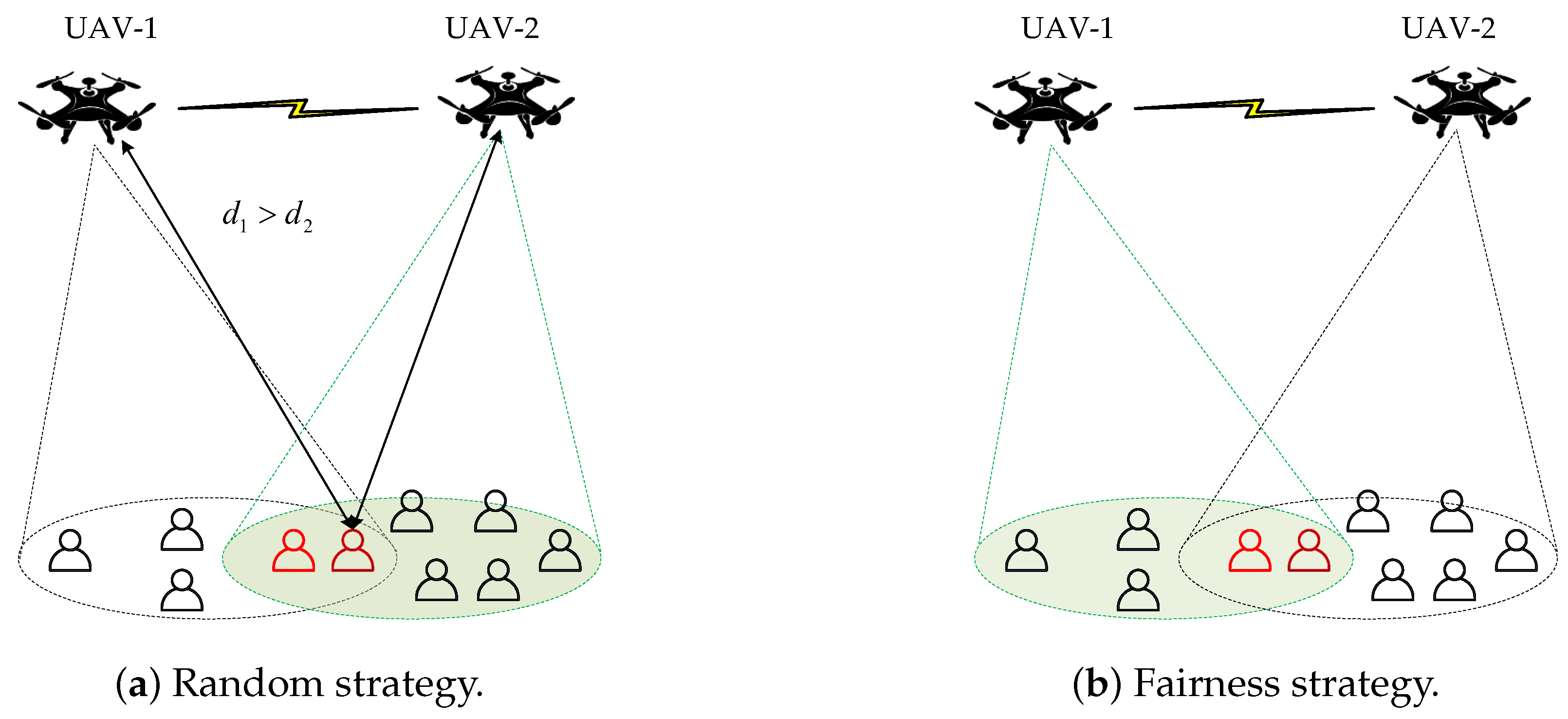
3.2. Horizontal Optimization
3.3. Height Optimization
| Algorithm 3 Height optimization algorithm. |
|
4. Simulation Validations and Discussions
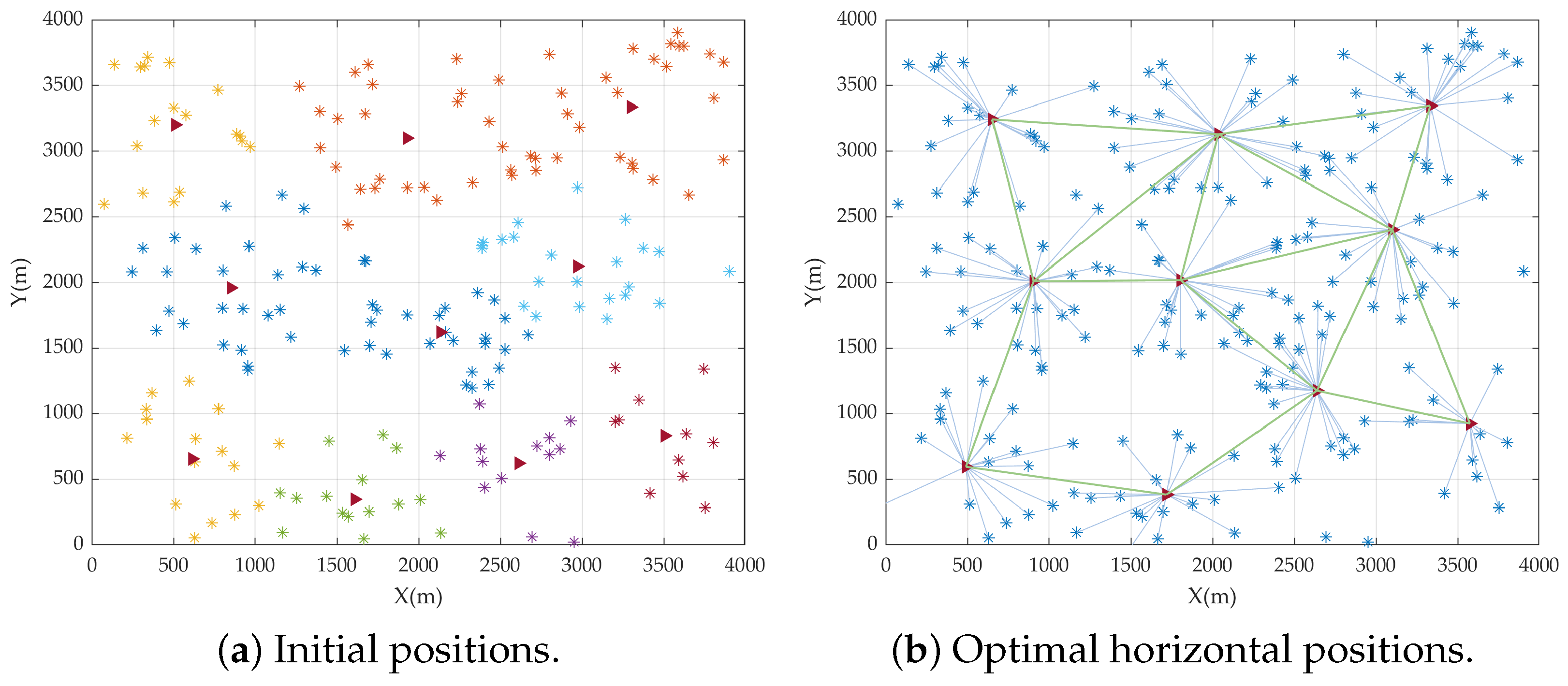
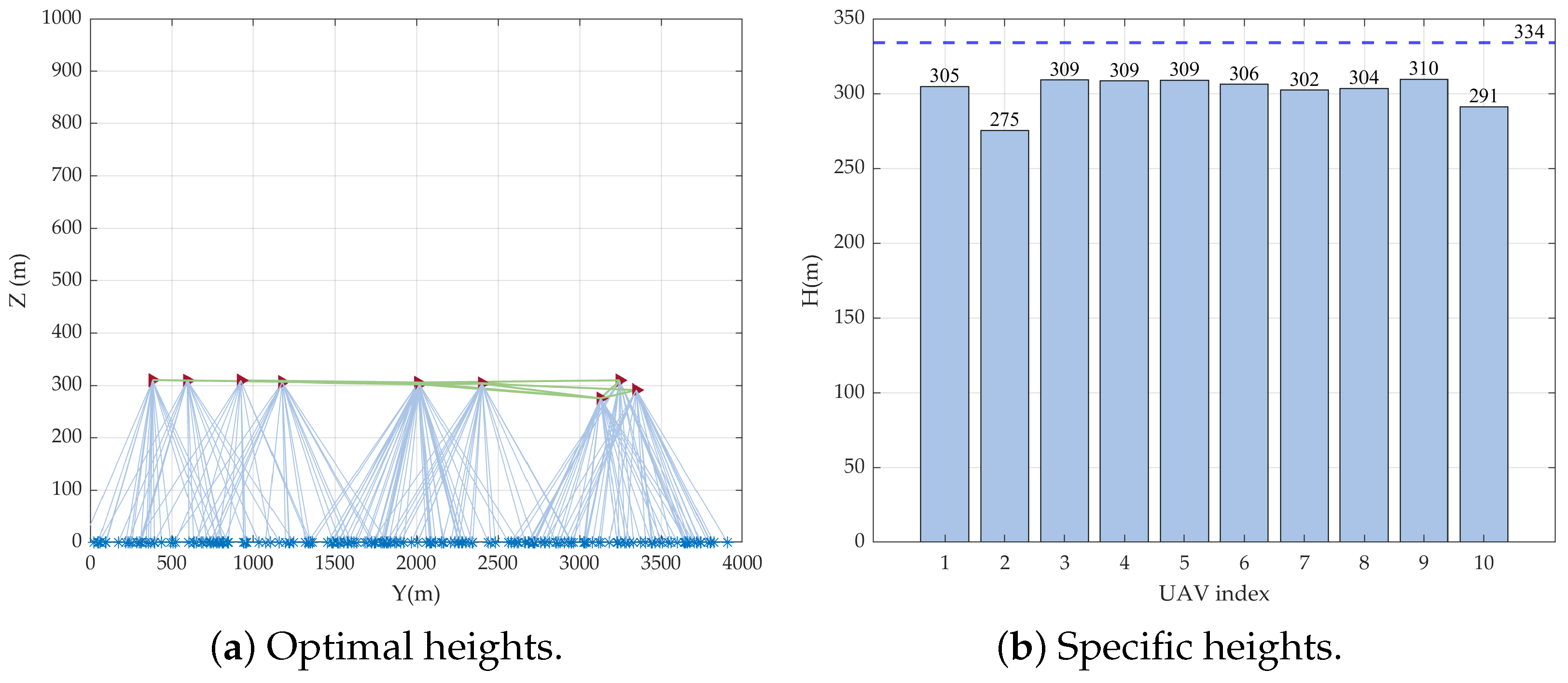
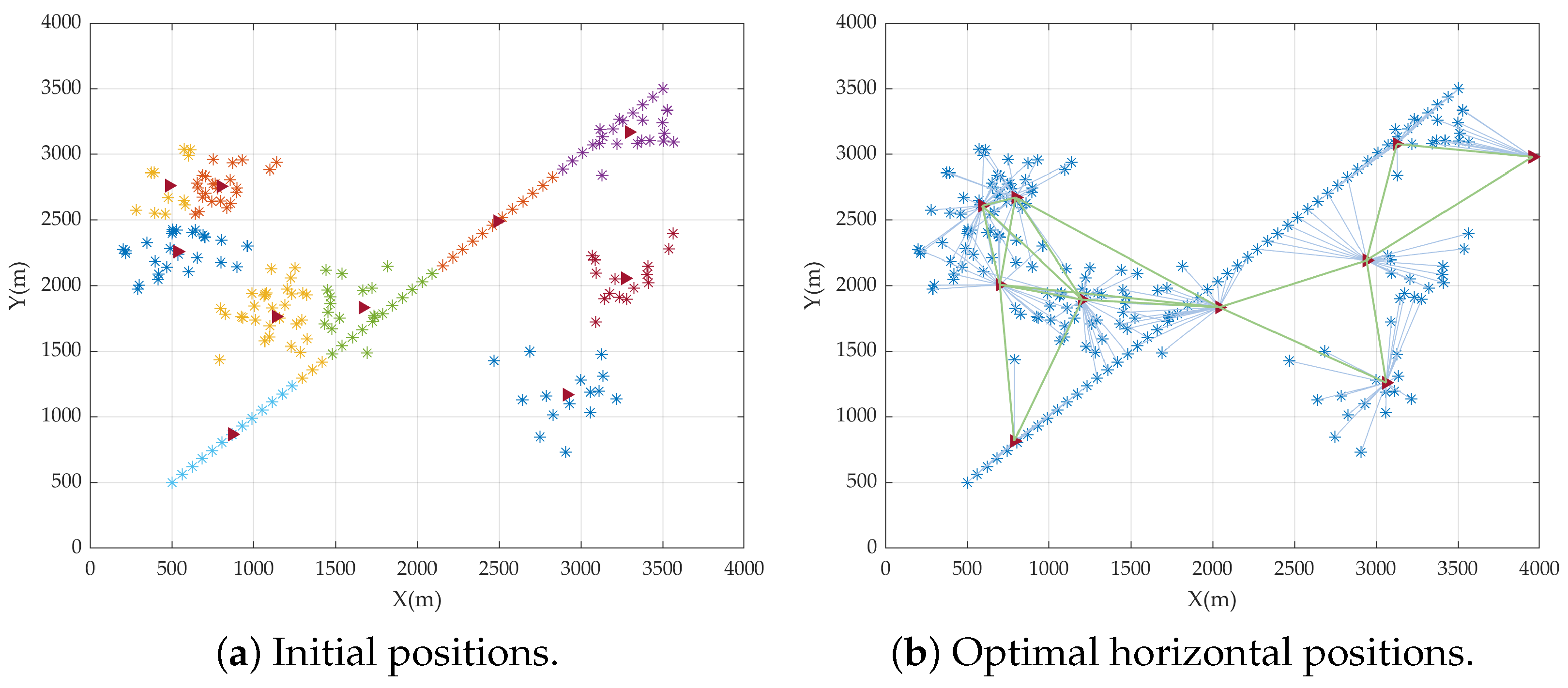
4.1. Deployment Examples
4.2. Performance Metric Statistics
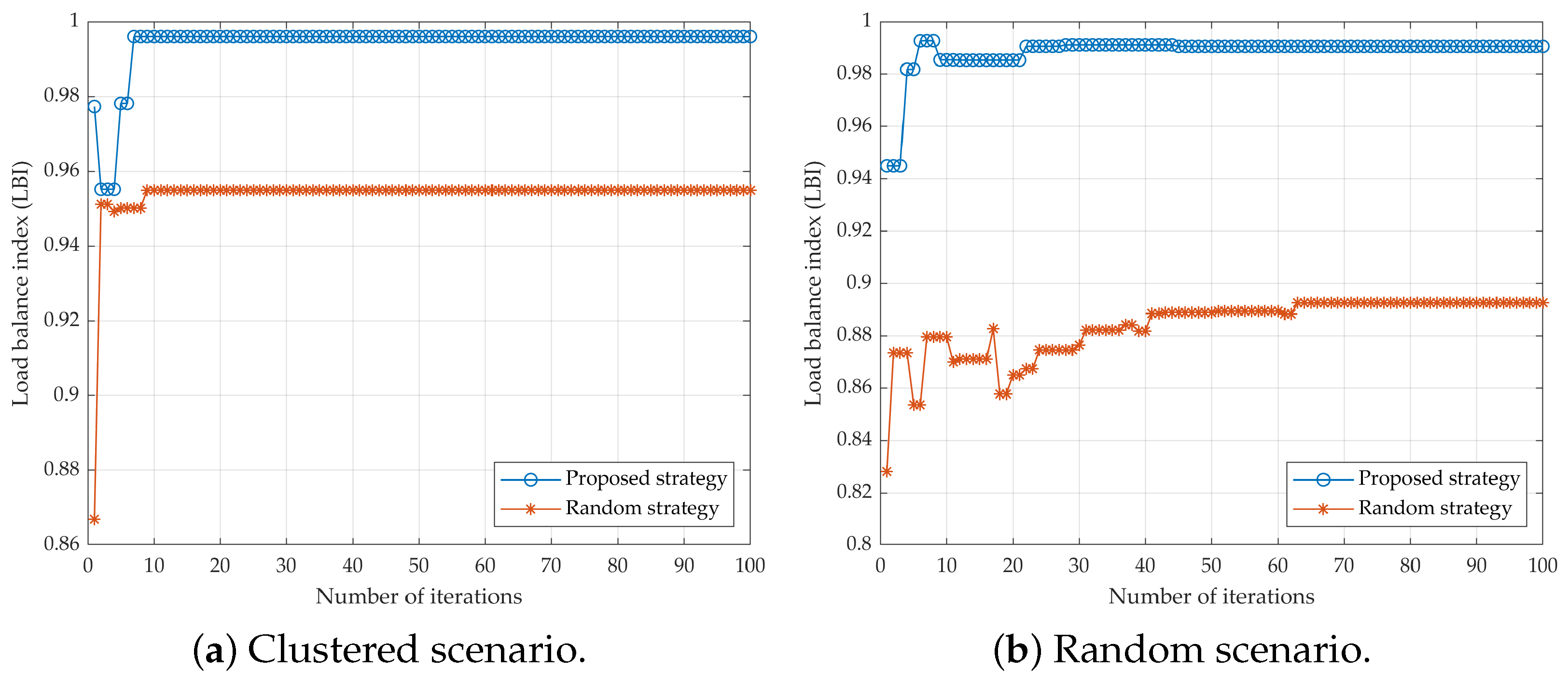
4.2.1. Load Balance
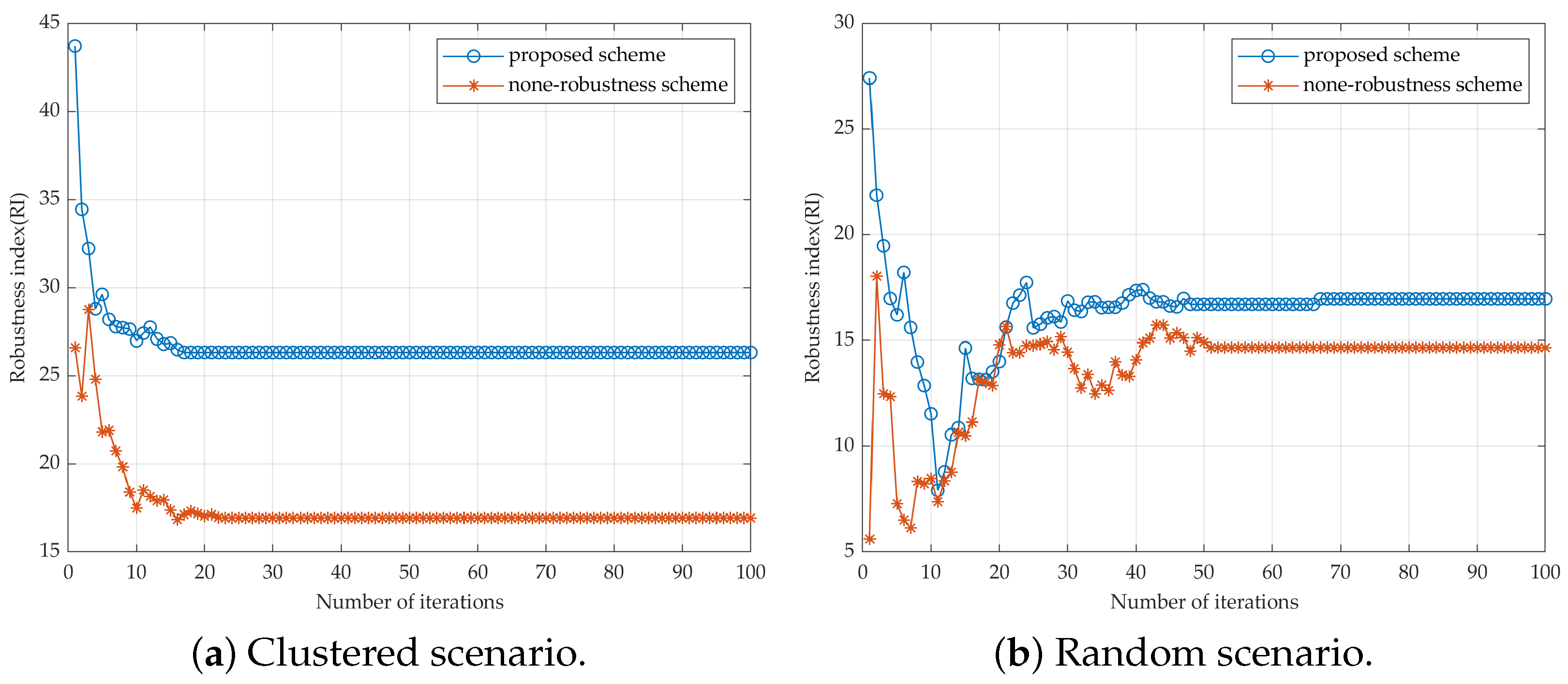
4.2.2. UAV Network Robustness
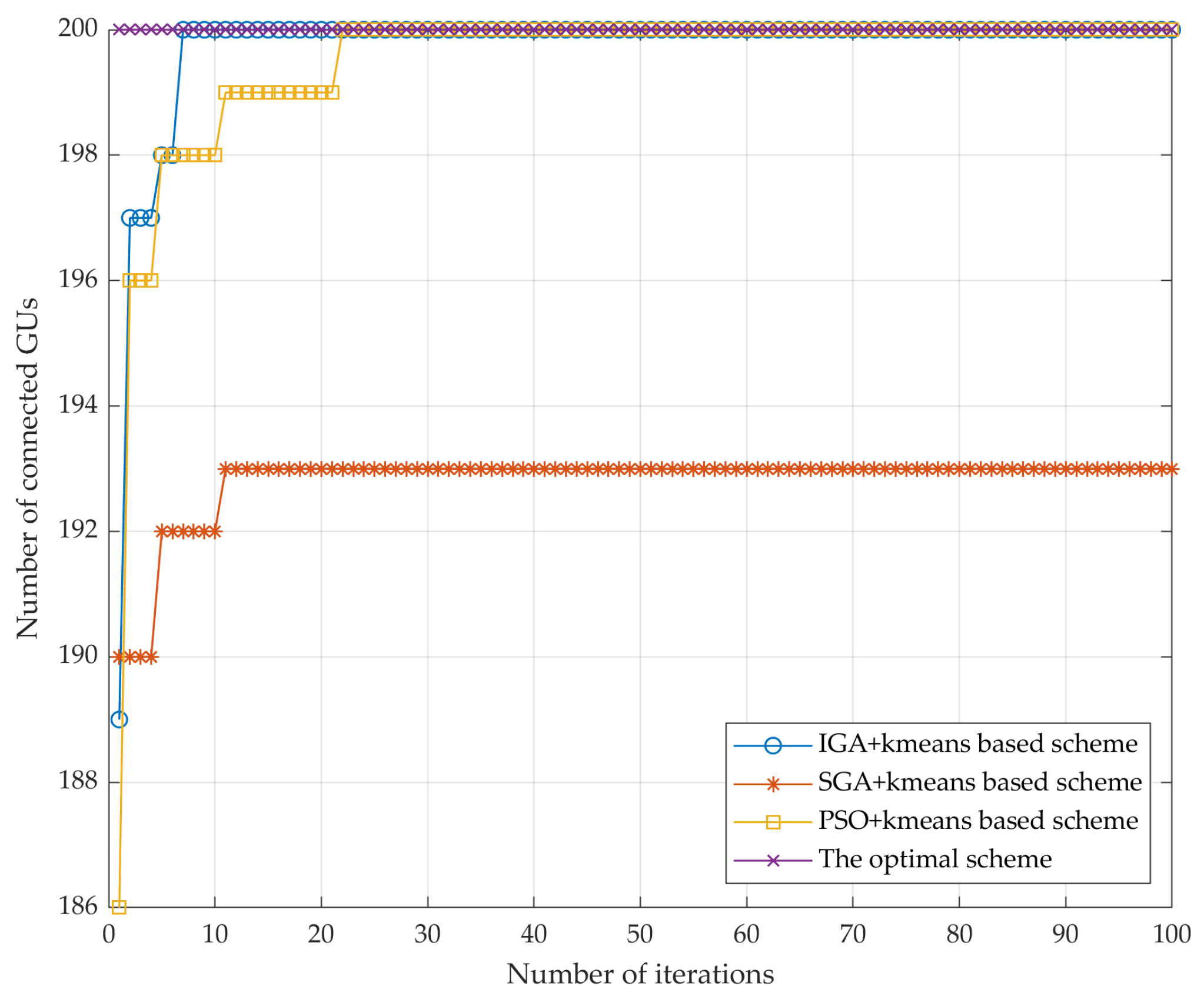
4.2.3. Coverage Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAGIN | space–air–ground integrated network |
| UAV | unmanned aerial vehicle |
| GU | ground user |
| QoS | quality of service |
| LEO | low Earth orbit |
| SGA | standard genetic algorithm |
| IGA | improved genetic algorithm |
| PSO | particle swarm optimization |
| 3D | three dimensional |
| LoS | line of sight |
| NLoS | non-line of sight |
| OFDMA | orthogonal frequency division multiple access |
| A2A | air to air |
| A2G | air to ground |
| FSPL | free-space propagation loss |
| LBI | load balance index |
| RI | robustness index |
References
- Jiang, W.; Han, B.; Habibi, M.A. The road towards 6G: A comprehensive survey. IEEE Open J. Commun. Soc. 2021, 2, 334–366. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, J.; Geng, Y. Space-air-ground integrated network (SAGIN) for 6G: Requirements, architecture and challenges. China Commun. 2022, 2, 90–108. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, H.N.; Wang, Q.; Pandey, O.J.; Fu, Y.; Zhang, N.; Niyato, D.; Lee, C.C. Space-Air-Ground Integrated Networks: Spherical Stochastic Geometry-Based Uplink Connectivity Analysis. IEEE J. Sel. Areas Commun. 2024, 42, 1387–1402. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, G. A survey on UAV-assisted wireless communications: Recent advances and future trends. Comput. Commun. 2023, 208, 44–78. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, H.; Zhou, L.; Wang, Z.; Cao, K.; Wang, J. Joint Resource Scheduling of the Time Slot, Power, and Main Lobe Direction in Directional UAV Ad Hoc Networks: A Multi-Agent Deep Reinforcement Learning Approach. Drones 2024, 8, 478. [Google Scholar] [CrossRef]
- Zhou, L.; Deng, X.; Wang, X.; Li, T.; Yi, L.; Xiong, X.; Tolba, A.; Ning, Z. Data Intelligence for UAV-Assisted Road Inspection in Post-Disaster Scenarios. IEEE Internet Things J. 2024; Early Access. [Google Scholar]
- Lin, Y.; Wang, T.; Wang, S. UAV-assisted emergency communications: An extended multi-armed bandit perspective. IEEE Commun. Lett. 2019, 23, 938–941. [Google Scholar] [CrossRef]
- Hu, Z.; Zeng, F.; Xiao, Z.; Fu, B.; Jiang, H.; Xiong, H.; Zhu, Y.; Alazab, M. Joint resources allocation and 3D trajectory optimization for UAV-enabled space-air-ground integrated networks. IEEE Trans. Veh. Technol. 2023, 72, 14214–14229. [Google Scholar] [CrossRef]
- Karavolos, M.; Tsipi, L.; Bithas, P.S.; Vouyioukas, D.; Mathiopoulos, P.T. Satellite aerial terrestrial hybrid NOMA scheme in 6G networks: An unsupervised learning approach. In Proceedings of the 2022 1st International Conference on 6G Networking (6GNet), Paris, France, 6–8 July 2022; pp. 1–5. [Google Scholar]
- Elnabty, I.A.; Fahmy, Y.; Kafafy, M. A survey on UAV placement optimization for UAV-assisted communication in 5G and beyond networks. Phys. Commun. 2022, 51, 101564. [Google Scholar] [CrossRef]
- Zhou, L.; Mao, H.; Deng, X.; Zhang, J.; Zhao, H.; Wei, J. Real-Time Radio Map Construction and Distribution for UAV-Assisted Mobile Edge Computing Networks. IEEE Internet Things J. 2024, 11, 21337–21346. [Google Scholar] [CrossRef]
- Lai, C.C.; Chen, C.T.; Wang, L.C. On-demand density-aware UAV base station 3D placement for arbitrarily distributed users with guaranteed data rates. IEEE Wirel. Commun. Lett. 2019, 8, 913–916. [Google Scholar] [CrossRef]
- Chen, Y.; Li, N.; Wang, C. A 3D placement of unmanned aerial vehicle base station based on multi-population genetic algorithm for maximizing users with different QoS requirements. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 913–916. [Google Scholar]
- Zhou, F.; Wu, Y.; Hu, R.Q.; Qian, Y. Computation rate maximization in UAV-enabled wireless-powered mobile-edge computing systems. IEEE J. Sel. Areas Commun. 2018, 36, 1927–1941. [Google Scholar] [CrossRef]
- Wu, H.; Wei, Z.; Hou, Y.; Zhang, N.; Tao, X. Cell-edge user offloading via flying UAV in non-uniform heterogeneous cellular networks. IEEE Trans. Wirel. Commun. 2020, 19, 2411–2426. [Google Scholar] [CrossRef]
- Han, S.I. Survey on UAV deployment and trajectory in wireless communication networks: Applications and challenges. Information 2022, 13, 389. [Google Scholar] [CrossRef]
- Liao, Z.; Ma, Y.; Huang, J.; Wang, J. Energy-aware 3D-deployment of UAV for IoV with highway interchange. IEEE Trans. Commun. 2022, 71, 1536–1548. [Google Scholar] [CrossRef]
- Song, M.; Huo, Y.; Liang, Z. Air-to-ground large-scale channel characterization by ray tracing. IEEE Access 2022, 10, 125930–125941. [Google Scholar] [CrossRef]
- Shakoor, S.; Kaleem, Z.; Do, D.T. Joint optimization of UAV 3-D placement and path-loss factor for energy-efficient maximal coverage. IEEE Internet Things J. 2020, 8, 9776–9786. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R. Placement optimization of UAV-mounted mobile base stations. IEEE Commun. Lett. 2016, 21, 604–607. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Zhu, L. 3D deployment of multiple UAV-mounted base stations for UAV communications. IEEE Trans. Commun. 2021, 69, 2473–2488. [Google Scholar] [CrossRef]
- Hayajneh, K.F.; Bani-Hani, K.; Shakhatreh, H. 3D deployment of unmanned aerial vehicle-base station assisting ground-base station. Wirel. Commun. Mob. Comput. 2021, 2021, 2937224. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Wu, W. Deployment algorithms of flying base stations: 5G and beyond with UAVs. IEEE Internet Things J. 2019, 6, 10009–10027. [Google Scholar] [CrossRef]
- Mao, H.; Liu, Y.; Xiao, Z.; Han, Z.; Xia, X.G. Joint resource allocation and 3D deployment for multi-UAV covert communications. IEEE Internet Things J. 2023, 11, 559–572. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Guo, S.; Yuan, D. 3D UAV deployment in multi-UAV networks with statistical user position information. IEEE Commun. Lett. 2022, 26, 1363–1367. [Google Scholar] [CrossRef]
- Zhong, X.; Huo, Y.; Dong, X. QoS-compliant 3-D deployment optimization strategy for UAV base stations. IEEE Syst. J. 2020, 15, 1795–1803. [Google Scholar] [CrossRef]
- Wen, X.; Ruan, Y.; Li, Y. Improved genetic algorithm based 3-D deployment of UAVs. J. Commun. Netw. 2022, 24, 223–231. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Alzenad, M.; El-Keyi, A.; Lagum, F.; Yanikomeroglu, H. 3-D placement of an unmanned aerial vehicle base station (UAV-BS) for energy-efficient maximal coverage. IEEE Wirel. Commun. Lett. 2017, 6, 434–437. [Google Scholar] [CrossRef]
- Lee, W.; Lee, H.; Choi, H.H. Deep Learning-Based Network-Wide Energy Efficiency Optimization in Ultra-Dense Small Cell Networks. IEEE Trans. Veh. Technol. 2023, 72, 8244–8249. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, S.; Feng, T. Trajectory Planning in UAV Emergency Networks with Potential Underlaying D2D Communication Based on K-means. J. Wirel. Commun. Netw. 2021, 356, 260–271. [Google Scholar] [CrossRef]
- Rajabi, M.H.; Toloie, E.A.; Motadel, M.R. A comprehensive review on meta-heuristic algorithms and their classification with novel approach. J. Appl. Res. Ind. Eng. 2021, 8, 63–89. [Google Scholar]
- Vinod Chandra, S.S.; Anand, H.S. Nature inspired meta heuristic algorithms for optimization problems. Computing 2022, 104, 251–269. [Google Scholar]
- Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65–68. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| - | a | 9.61 |
| - | b | 0.43 |
| maximum path loss | 98 dB | |
| crossover probability | 0.3 | |
| mutation probability | 0.1 | |
| number of GUs | N | 200 |
| number of UAVs | M | 10 |
| security distance between UAVs | 100 m | |
| maximum distance between UAVs | 1500 m | |
| minimum deployment height of UAVs | 200 m | |
| maximum deployment height of UAVs | 800 m | |
| carrier frequency of A2G channel | 2G Hz | |
| additional path loss under LoS | 0.1 dB | |
| additional path loss under NLoS | 20 dB | |
| maximum connection capacity per UAV | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Zhou, L.; Liang, S.; Cao, K.; Song, Z. Connectivity-Enhanced 3D Deployment Algorithm for Multiple UAVs in Space–Air–Ground Integrated Network. Aerospace 2024, 11, 969. https://doi.org/10.3390/aerospace11120969
Guo S, Zhou L, Liang S, Cao K, Song Z. Connectivity-Enhanced 3D Deployment Algorithm for Multiple UAVs in Space–Air–Ground Integrated Network. Aerospace. 2024; 11(12):969. https://doi.org/10.3390/aerospace11120969
Chicago/Turabian StyleGuo, Shaoxiong, Li Zhou, Shijie Liang, Kuo Cao, and Zhiqun Song. 2024. "Connectivity-Enhanced 3D Deployment Algorithm for Multiple UAVs in Space–Air–Ground Integrated Network" Aerospace 11, no. 12: 969. https://doi.org/10.3390/aerospace11120969
APA StyleGuo, S., Zhou, L., Liang, S., Cao, K., & Song, Z. (2024). Connectivity-Enhanced 3D Deployment Algorithm for Multiple UAVs in Space–Air–Ground Integrated Network. Aerospace, 11(12), 969. https://doi.org/10.3390/aerospace11120969






