Comparative Analysis of Deep Reinforcement Learning Algorithms for Hover-to-Cruise Transition Maneuvers of a Tilt-Rotor Unmanned Aerial Vehicle
Abstract
1. Introduction
1.1. Emergence of Deep Reinforcement Learning (DRL)
1.2. Trajectory Optimization for Transition Maneuver Between Hover to Cruise
2. Purpose of Study
3. Methodology
4. Modeling and Problem Formulation
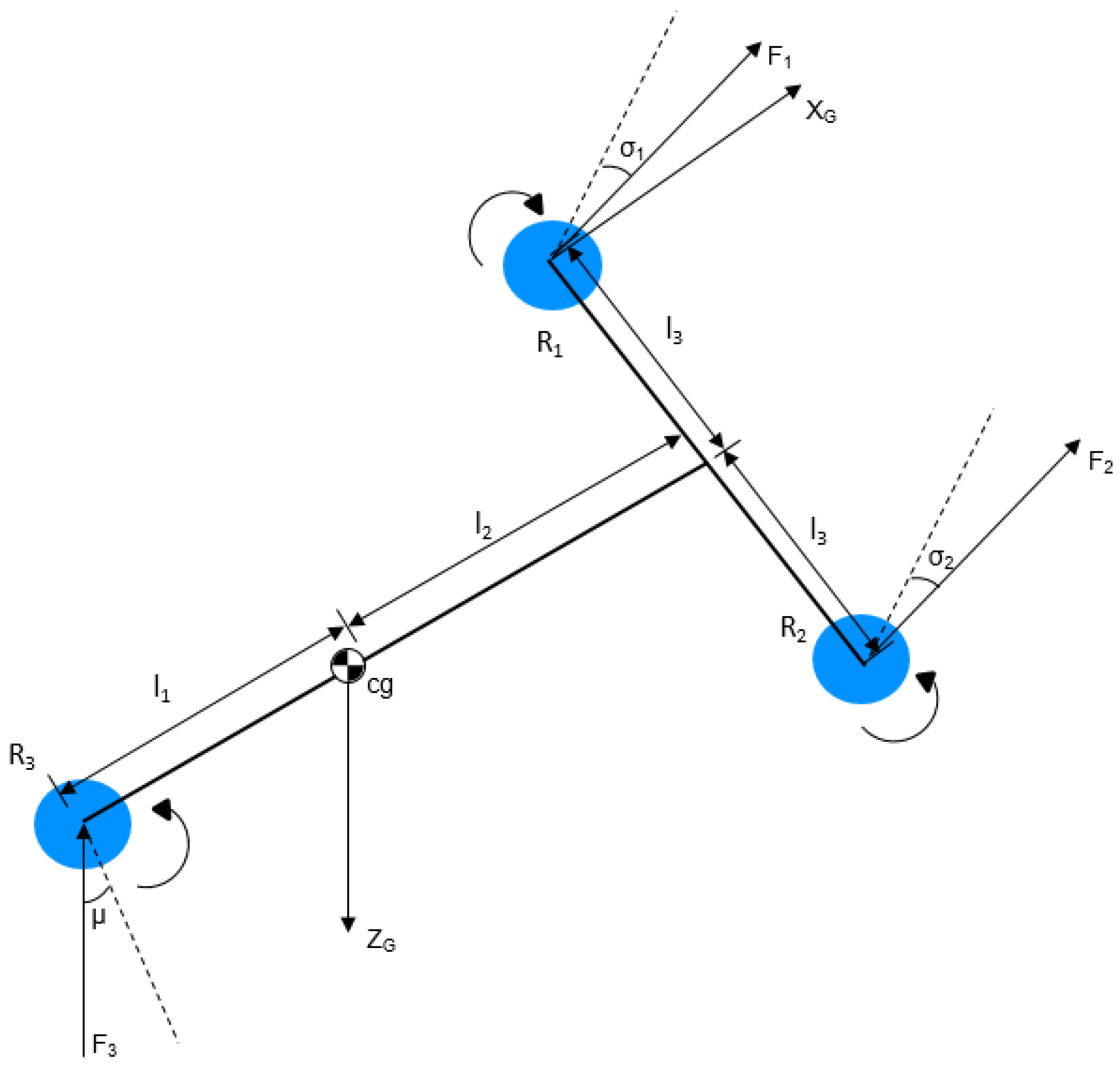
4.1. Description of the Tilt Tri-Rotor UAV
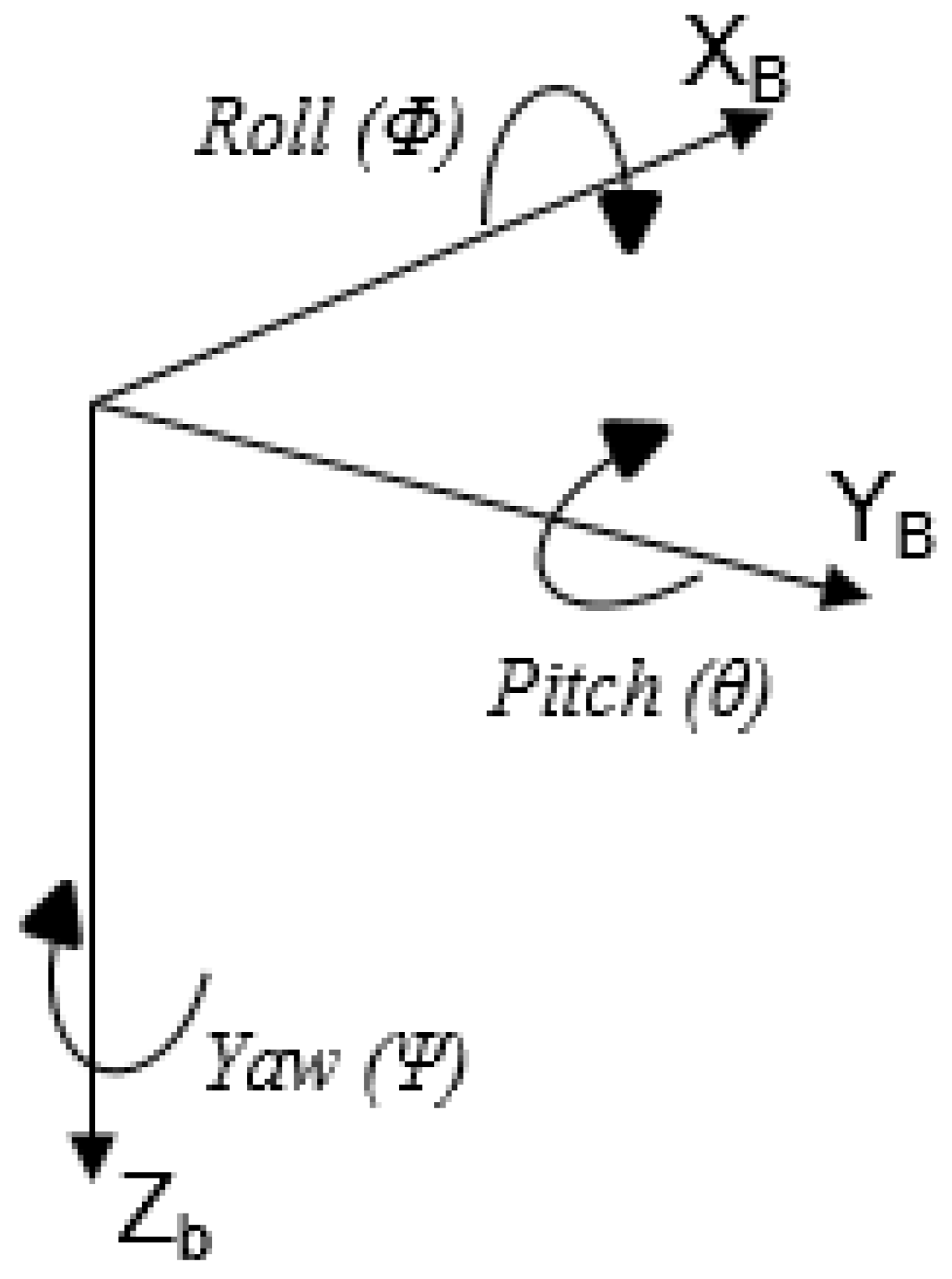
4.2. Coordinate System
4.3. Nonlinear Equations of Motion
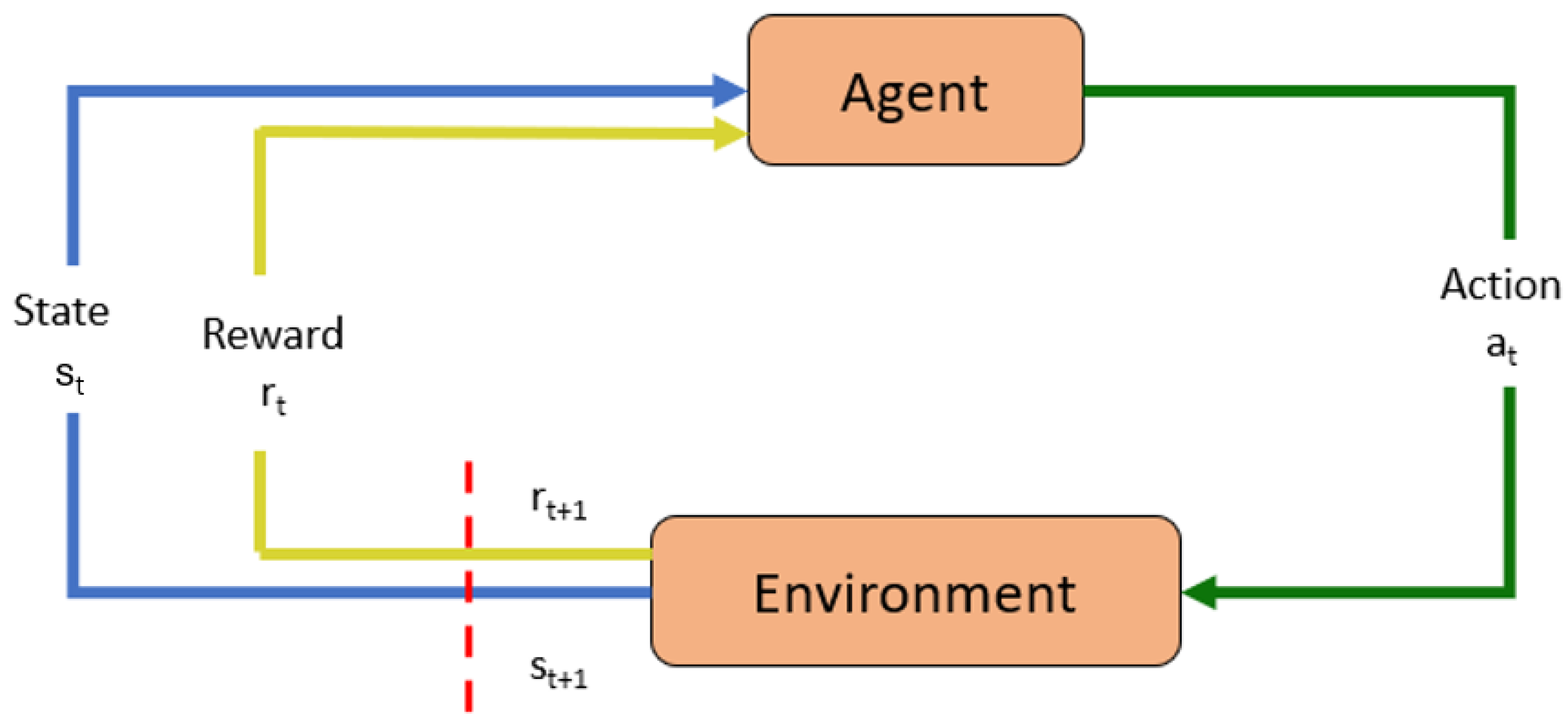
5. Reinforcement-Learning Framework
- A set of states, S, and a distribution of initial states,
- A set of actions, A
- Transition dynamics, T()
- An instantaneous reward function, R()
- A discount factor, ∈ [0, 1]
5.1. Deep-Reinforcement-Learning Algorithms
5.2. Deep Deterministic Policy Gradient (DDPG)
- Actor Network (): Determines the best action, a, for a given state, s.
- Critic Network (): Evaluates action a given the state s.
| Algorithm 1 DDPG (Deep Deterministic Policy Gradient) |
|
5.3. Proximal Policy Optimization (PPO)
| Algorithm 2 PPO (Proximal Policy Optimization) |
|
5.4. Trust Region Policy Optimization (TRPO)
| Algorithm 3 TRPO (Trust Region Policy Optimization) |
|
6. Simulation Environment
7. Training Process
7.1. State Space
7.2. Action Space
7.3. Reward Function
7.4. Reward Function Components
8. Results and Discussion
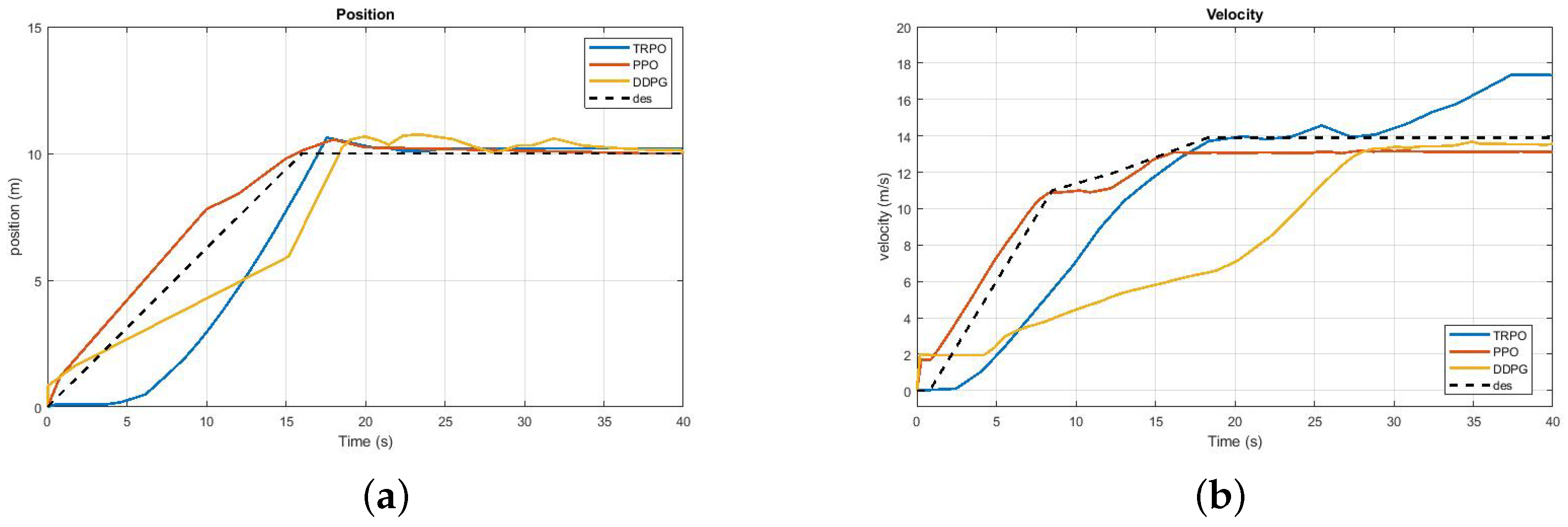
8.1. Trends of Position and Velocity of the UAV
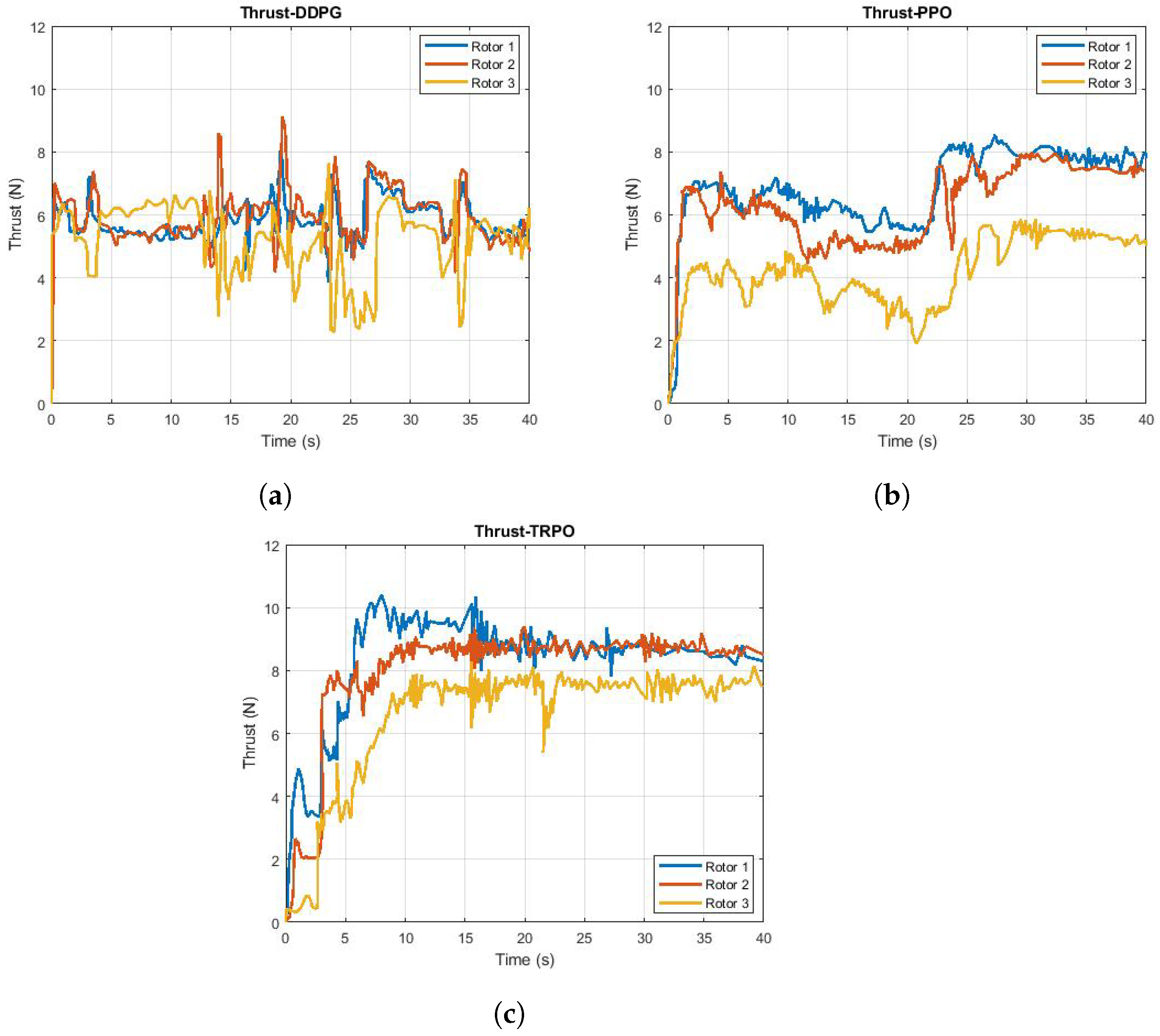
8.2. Control Variable of the UAV
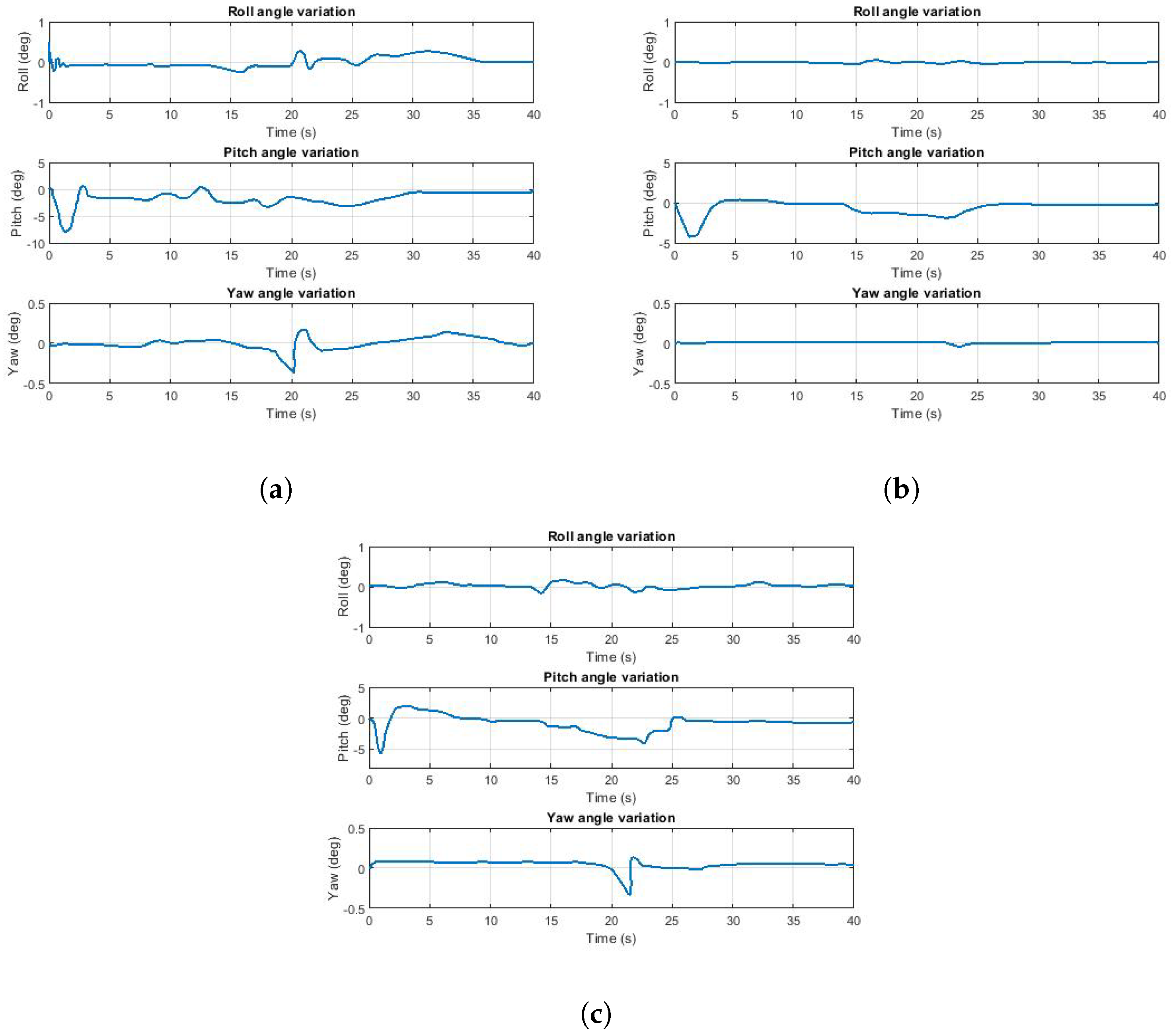
8.3. Trends of Euler Angles of the UAV
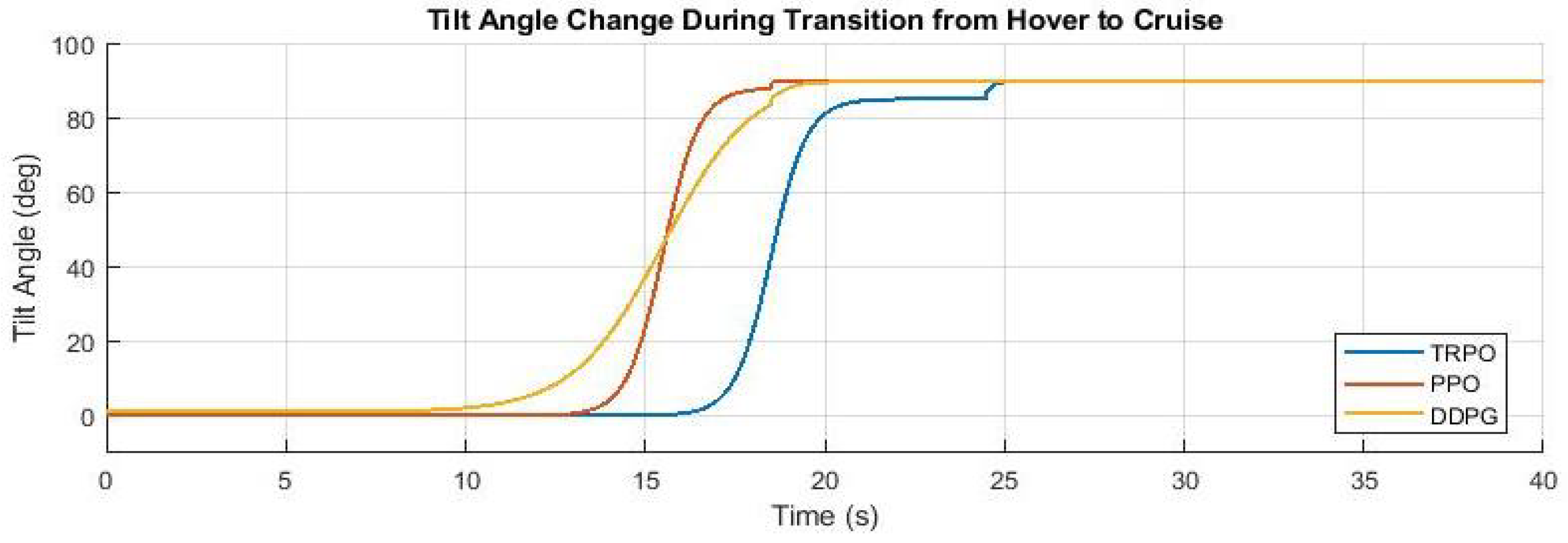
8.4. Variation of the Tilt Angle of Rotors of the UAV
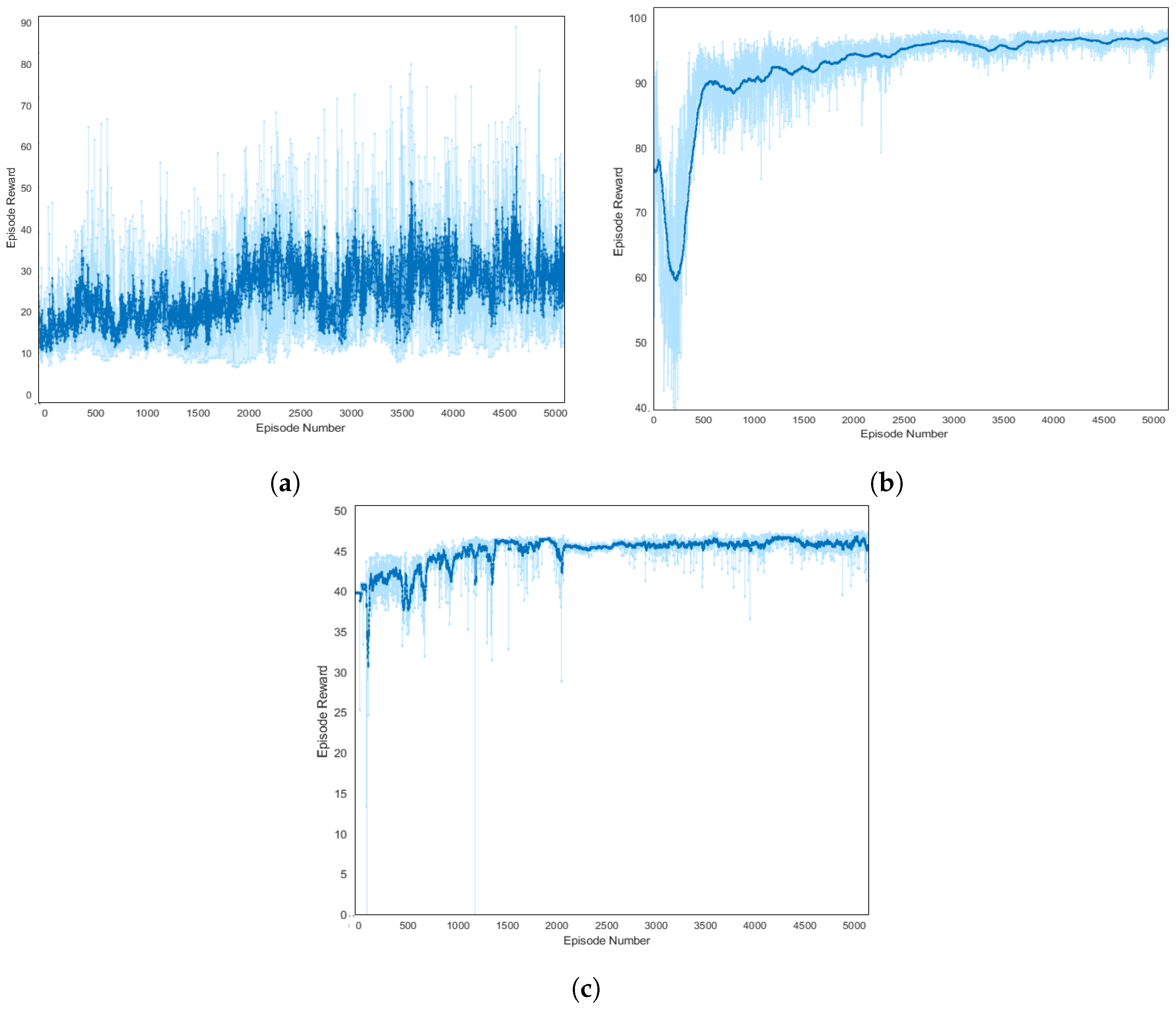
8.5. Learning of Algorithms
8.5.1. Deep Deterministic Policy Gradient (DDPG)
8.5.2. Proximal Policy Optimization (PPO)
8.5.3. Trust Region Policy Optimization (TRPO)
8.6. Reward Generation
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| RL | Reinforcement Learning |
| DDPG | Deep Deterministic Policy Gradient |
| PPO | Proximal Policy Optimization |
| TRPO | Trust Region Policy Optimization |
References
- Ol, M.; Parker, G.; Abate, G.; Evers, J. Flight controls and performance challenges for MAVs in complex environments. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6508. [Google Scholar]
- Sababha, B.H.; Zu’bi, H.M.A.; Rawashdeh, O.A. A rotor-tilt-free tricopter UAV: Design, modelling, and stability control. Int. J. Mechatronics Autom. 2015, 5, 107–113. [Google Scholar] [CrossRef]
- Logan, M.; Vranas, T.; Motter, M.; Shams, Q.; Pollock, D. Technology challenges in small UAV development. In Infotech@ Aerospace; ARC: Arlington, VA, USA, 2005; p. 7089. [Google Scholar]
- Bolkcom, C. V-22 Osprey Tilt-Rotor Aircraft; Library of Congress Washington DC Congressional Research Service: Washington, DC, USA, 2004. [Google Scholar]
- Ozdemir, U.; Aktas, Y.O.; Vuruskan, A.; Dereli, Y.; Tarhan, A.F.; Demirbag, K.; Erdem, A.; Kalaycioglu, G.D.; Ozkol, I.; Inalhan, G. Design of a commercial hybrid VTOL UAV system. J. Intell. Robot. Syst. 2014, 74, 371–393. [Google Scholar] [CrossRef]
- Papachristos, C.; Alexis, K.; Tzes, A. Dual–authority thrust–vectoring of a tri–tiltrotor employing model predictive control. J. Intell. Robot. Syst. 2016, 81, 471–504. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, H. Design of flight control system for a novel tilt-rotor UAV. Complexity 2020, 2020, 4757381. [Google Scholar] [CrossRef]
- Govdeli, Y.; Muzaffar, S.M.B.; Raj, R.; Elhadidi, B.; Kayacan, E. Unsteady aerodynamic modeling and control of pusher and tilt-rotor quadplane configurations. Aerosp. Sci. Technol. 2019, 94, 105421. [Google Scholar] [CrossRef]
- Ningjun, L.; Zhihao, C.; Jiang, Z.; Yingxun, W. Predictor-based model reference adaptive roll and yaw control of a quad-tiltrotor UAV. Chin. J. Aeronaut. 2020, 33, 282–295. [Google Scholar]
- Di Francesco, G.; Mattei, M.; D’Amato, E. Incremental nonlinear dynamic inversion and control allocation for a tilt rotor UAV. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, National Harbor, MD, USA, 13–17 January 2014; p. 0963. [Google Scholar]
- Kong, Z.; Lu, Q. Mathematical modeling and modal switching control of a novel tiltrotor UAV. J. Robot. 2018, 2018. [Google Scholar] [CrossRef]
- Yildiz, Y.; Unel, M.; Demirel, A.E. Adaptive nonlinear hierarchical control of a quad tilt-wing UAV. In Proceedings of the 2015 IEEE European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 3623–3628. [Google Scholar]
- Yoo, C.S.; Ryu, S.D.; Park, B.J.; Kang, Y.S.; Jung, S.B. Actuator controller based on fuzzy sliding mode control of tilt rotor unmanned aerial vehicle. Int. J. Control. Autom. Syst. 2014, 12, 1257–1265. [Google Scholar] [CrossRef]
- Yin, Y.; Niu, H.; Liu, X. Adaptive neural network sliding mode control for quad tilt rotor aircraft. Complexity 2017, 2017, 7104708. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y. Neural network approximation-based nonsingular terminal sliding mode control for trajectory tracking of robotic airships. Aerosp. Sci. Technol. 2016, 54, 192–197. [Google Scholar] [CrossRef]
- Song, Z.; Li, K.; Cai, Z.; Wang, Y.; Liu, N. Modeling and maneuvering control for tricopter based on the back-stepping method. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 889–894. [Google Scholar]
- Crowther, B.; Lanzon, A.; Maya-Gonzalez, M.; Langkamp, D. Kinematic analysis and control design for a nonplanar multirotor vehicle. J. Guid. Control. Dyn. 2011, 34, 1157–1171. [Google Scholar] [CrossRef]
- Lanzon, A.; Freddi, A.; Longhi, S. Flight control of a quadrotor vehicle subsequent to a rotor failure. J. Guid. Control. Dyn. 2014, 37, 580–591. [Google Scholar] [CrossRef]
- Tran, H.K.; Chiou, J.S.; Nam, N.T.; Tuyen, V. Adaptive fuzzy control method for a single tilt tricopter. IEEE Access 2019, 7, 161741–161747. [Google Scholar] [CrossRef]
- Mohamed, M.K.; Lanzon, A. Design and control of novel tri-rotor UAV. In Proceedings of the 2012 IEEE UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 304–309. [Google Scholar]
- Kastelan, D.; Konz, M.; Rudolph, J. Fully actuated tricopter with pilot-supporting control. IFAC-PapersOnLine 2015, 48, 79–84. [Google Scholar] [CrossRef]
- Servais, E.; d’Andréa Novel, B.; Mounier, H. Ground control of a hybrid tricopter. In Proceedings of the 2015 IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 945–950. [Google Scholar]
- Kumar, R.; Sridhar, S.; Cazaurang, F.; Cohen, K.; Kumar, M. Reconfigurable fault-tolerant tilt-rotor quadcopter system. In Proceedings of the Dynamic Systems and Control Conference, Atlanta, GA, USA, 30 September–3 October 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51913, p. V003T37A008. [Google Scholar]
- Kumar, R.; Nemati, A.; Kumar, M.; Sharma, R.; Cohen, K.; Cazaurang, F. Tilting-rotor quadcopter for aggressive flight maneuvers using differential flatness based flight controller. In Proceedings of the Dynamic Systems and Control Conference, Tysons, VA, USA, 11–13 October 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 58295, p. V003T39A006. [Google Scholar]
- Lindqvist, B.; Mansouri, S.S.; Agha-mohammadi, A.a.; Nikolakopoulos, G. Nonlinear MPC for collision avoidance and control of UAVs with dynamic obstacles. IEEE Robot. Autom. Lett. 2020, 5, 6001–6008. [Google Scholar] [CrossRef]
- Wang, Q.; Namiki, A.; Asignacion Jr, A.; Li, Z.; Suzuki, S. Chattering reduction of sliding mode control for quadrotor UAVs based on reinforcement learning. Drones 2023, 7, 420. [Google Scholar] [CrossRef]
- Jiang, B.; Li, B.; Zhou, W.; Lo, L.Y.; Chen, C.K.; Wen, C.Y. Neural network based model predictive control for a quadrotor UAV. Aerospace 2022, 9, 460. [Google Scholar] [CrossRef]
- Raivio, T.; Ehtamo, H.; Hämäläinen, R.P. Aircraft trajectory optimization using nonlinear programming. In System Modelling and Optimization: Proceedings of the Seventeenth IFIP TC7 Conference on System Modelling and Optimization, 1995; Springer: Berlin/Heidelberg, Germany, 1996; pp. 435–441. [Google Scholar]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Control. Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Judd, K.; McLain, T. Spline based path planning for unmanned air vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, QC, Canada, 6–9 August 2001; p. 4238. [Google Scholar]
- Maqsood, A.; Go, T.H. Optimization of transition maneuvers through aerodynamic vectoring. Aerosp. Sci. Technol. 2012, 23, 363–371. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Eisa, S.A.; Taha, H.; Akhtar, S. Optimal morphing–augmented dynamic soaring maneuvers for unmanned air vehicle capable of span and sweep morphologies. Aerosp. Sci. Technol. 2018, 79, 17–36. [Google Scholar] [CrossRef]
- Feroskhan, M.; Go, T.H. Control strategy of sideslip perching maneuver under dynamic stall influence. Aerosp. Sci. Technol. 2018, 72, 150–163. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ma, Z.; Wang, C.; Niu, Y.; Wang, X.; Shen, L. A saliency-based reinforcement learning approach for a UAV to avoid flying obstacles. Robot. Auton. Syst. 2018, 100, 108–118. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Tian, Y.; Sun, C. Reinforcement learning based two-level control framework of UAV swarm for cooperative persistent surveillance in an unknown urban area. Aerosp. Sci. Technol. 2020, 98, 105671. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Fixed-Wing UAVs flocking in continuous spaces: A deep reinforcement learning approach. Robot. Auton. Syst. 2020, 131, 103594. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Tesauro, G. Temporal difference learning and TD-Gammon. Commun. ACM 1995, 38, 58–68. [Google Scholar] [CrossRef]
- Dahl, G.E.; Yu, D.; Deng, L.; Acero, A. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 30–42. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Novati, G.; Mahadevan, L.; Koumoutsakos, P. Deep-Reinforcement-Learning for Gliding and Perching Bodies. arXiv 2018, arXiv:1807.03671. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. Acm Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Wei, E.; Wicke, D.; Luke, S. Hierarchical approaches for reinforcement learning in parameterized action space. In Proceedings of the 2018 AAAI Spring Symposium Series, Palo Alto, CA, USA, 26–28 March 2018. [Google Scholar]
- dos Santos, S.R.; Barros, S.N.; Givigi, C.L.; Nascimento, L. Autonomous construction of multiple structures using learning automata: Description and experimental validation. IEEE Syst. J. 2015, 9, 1376–1387. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning, PMLR, Beijing, China, 22–24 June 2014. [Google Scholar]
- Hausknecht, M.; Stone, P. Deep recurrent q-learning for partially observable mdps. In Proceedings of the 2015 AAAI Fall Symposium Series, Palo Alto, CA, USA, 12–14 November 2015. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Hwangbo, J.; Sa, I.; Siegwart, R.; Hutter, M. Control of a quadrotor with reinforcement learning. IEEE Robot. Autom. Lett. 2017, 2, 2096–2103. [Google Scholar] [CrossRef]
- Heess, N.; TB, D.; Sriram, S.; Lemmon, J.; Merel, J.; Wayne, G.; Tassa, Y.; Erez, T.; Wang, Z.; Eslami, S.; et al. Emergence of locomotion behaviours in rich environments. arXiv 2017, arXiv:1707.02286. [Google Scholar]
- Lopes, G.C.; Ferreira, M.; da Silva Simões, A.; Colombini, E.L. Intelligent control of a quadrotor with proximal policy optimization reinforcement learning. In Proceedings of the 2018 IEEE Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE), Joao Pessoa, Brazil, 6–10 November 2018; pp. 503–508. [Google Scholar]
- Bøhn, E.; Coates, E.M.; Moe, S.; Johansen, T.A. Deep reinforcement learning attitude control of fixed-wing uavs using proximal policy optimization. In Proceedings of the 2019 IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 523–533. [Google Scholar]
- Koch, W.; Mancuso, R.; West, R.; Bestavros, A. Reinforcement learning for UAV attitude control. ACM Trans. Cyber-Phys. Syst. 2019, 3, 1–21. [Google Scholar] [CrossRef]
- Deshpande, A.M.; Kumar, R.; Minai, A.A.; Kumar, M. Developmental reinforcement learning of control policy of a quadcopter UAV with thrust vectoring rotors. In Proceedings of the Dynamic Systems and Control Conference; American Society of Mechanical Engineers: Atlanta, GA, USA, 2020; Volume 84287, p. V002T36A011. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Çakici, F.; Leblebicioğlu, M.K. Control system design of a vertical take-off and landing fixed-wing UAV. IFAC-PapersOnLine 2016, 49, 267–272. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Islam, S.; Dias, J.; Seneviratne, L.; Cai, G. A review on the platform design, dynamic modeling and control of hybrid UAVs. In Proceedings of the 2015 IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 806–815. [Google Scholar]
- Chana, W.F.; Coleman, J.S. World’s first vtol airplane convair/navy xfy-1 pogo. In SAE Transactions; SAE International: Warrendale PA, USA, 1996; pp. 1261–1266. [Google Scholar]
- Smith Jr, K.; Belina, F. Small V/STOL Aircraft Analysis, Volume 1; NASA: Greenbelt, MD, USA, 1974. [Google Scholar]
- Ahn, O.; Kim, J.; Lim, C. Smart UAV research program status update: Achievement of tilt-rotor technology development and vision ahead. In Proceedings of the 27th Congress of International Council of the Aeronautical Sciences, Nice, France, 19–24 September 2010; pp. 2010–2016. [Google Scholar]
- Pines, D.J.; Bohorquez, F. Challenges facing future micro-air-vehicle development. J. Aircr. 2006, 43, 290–305. [Google Scholar] [CrossRef]
- Van Nieuwstadt, M.J.; Murray, R.M. Rapid hover-to-forward-flight transitions for a thrust-vectored aircraft. J. Guid. Control. Dyn. 1998, 21, 93–100. [Google Scholar] [CrossRef]
- Stone, R.H.; Anderson, P.; Hutchison, C.; Tsai, A.; Gibbens, P.; Wong, K. Flight testing of the T-wing tail-sitter unmanned air vehicle. J. Aircr. 2008, 45, 673–685. [Google Scholar] [CrossRef]
- Green, W.E.; Oh, P.Y. A MAV that flies like an airplane and hovers like a helicopter. In Proceedings of the Proceedings, 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 693–698. [Google Scholar]
- Green, W.E.; Oh, P.Y. Autonomous hovering of a fixed-wing micro air vehicle. In Proceedings of the Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 2164–2169. [Google Scholar]
- Green, W.E. A Multimodal Micro Air Vehicle for Autonomous Flight in Near-Earth Environments; Drexel University: Philadelphia, PA, USA, 2007. [Google Scholar]
- Xili, Y.; Yong, F.; Jihong, Z. Transition flight control of two vertical/short takeoff and landing aircraft. J. Guid. Control. Dyn. 2008, 31, 371–385. [Google Scholar] [CrossRef]
- Yanguo, S.; Huanjin, W. Design of flight control system for a small unmanned tilt rotor aircraft. Chin. J. Aeronaut. 2009, 22, 250–256. [Google Scholar] [CrossRef]
- Muraoka, K.; Okada, N.; Kubo, D.; Sato, M. Transition flight of quad tilt wing VTOL UAV. In Proceedings of the 28th Congress of the International Council of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012; pp. 3242–3251. [Google Scholar]
- Mehra, R.; Wasikowski, M.; Prasanth, R.; Bennett, R.; Neckels, D. Model predictive control design for XV-15 tilt rotor flight control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, QC, Canada, 6–9 August 2001; p. 4331. [Google Scholar]
- Hameed, R.; Maqsood, A.; Hashmi, A.; Saeed, M.; Riaz, R. Reinforcement learning-based radar-evasive path planning: A comparative analysis. Aeronaut. J. 2022, 126, 547–564. [Google Scholar] [CrossRef]
- dos Santos, S.R.B.; Nascimento, C.L.; Givigi, S.N. Design of attitude and path tracking controllers for quad-rotor robots using reinforcement learning. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–16. [Google Scholar]
- Wang, C.; Wang, J.; Shen, Y.; Zhang, X. Autonomous navigation of UAVs in large-scale complex environments: A deep reinforcement learning approach. IEEE Trans. Veh. Technol. 2019, 68, 2124–2136. [Google Scholar] [CrossRef]
- Kohl, N.; Stone, P. Policy gradient reinforcement learning for fast quadrupedal locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Proceedings. ICRA’04. 2004. IEEE: New York, NY, USA, 2004; Volume 3, pp. 2619–2624. [Google Scholar]
- Ng, A.Y.; Coates, A.; Diel, M.; Ganapathi, V.; Schulte, J.; Tse, B.; Berger, E.; Liang, E. Autonomous inverted helicopter flight via reinforcement learning. In Experimental Robotics IX; Springer: Berlin/Heidelberg, Germany, 2006; pp. 363–372. [Google Scholar]
- Strehl, A.L.; Li, L.; Wiewiora, E.; Langford, J.; Littman, M.L. PAC model-free reinforcement learning. In Proceedings of the 23rd International Conference on Machine Learning; Association for Computing Machinery: New York, NY, USA, 2006; pp. 881–888. [Google Scholar]
- Wood, C. The flight of albatrosses (a computer simulation). Ibis 1973, 115, 244–256. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Cassandra, A.R. Planning and acting in partially observable stochastic domains. Artif. Intell. 1998, 101, 99–134. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Wierstra, D.; Förster, A.; Peters, J.; Schmidhuber, J. Recurrent policy gradients. Log. J. Igpl 2010, 18, 620–634. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
| Symbol | Description | Value | Unit |
|---|---|---|---|
| m | Mass of tricopter | 1.5 | kg |
| Moment arm | 0.312 | m | |
| Moment arm | 0.213 | m | |
| Moment arm | 0.305 | m | |
| Moment of inertia around x-body axis | 0.0239 | ||
| Moment of inertia around y-body axis | 0.01271 | ||
| Moment of inertia around z-body axis | 0.01273 |
| Weights | Values |
|---|---|
| 0.1 | |
| 0.7 | |
| 0.1 | |
| 0.2 | |
| 0.5 | |
| 0.2 | |
| 0.5 | |
| 0.6 | |
| 0.1 |
| Hyper Parameters | DDPG | PPO | TRPO |
|---|---|---|---|
| Critic Learn Rate | 1 × 10−3 | 1 × 10−4 | - |
| Actor Learn Rate | 1 × 10−4 | 1 × 10−4 | - |
| Value Function Learning Rate | - | - | 1 × 10−3 |
| Sample Time | 0.1 | 0.1 | 0.1 |
| Experience buffer size (N) | 1 × 106 | - | - |
| Discount factor () | 0.99 | 0.997 | 0.99 |
| Mini batch size (M) | 64 | 128 | 128 |
| Target update rate () | 1 × 10−3 | - | - |
| Target network update frequency (steps) | 1000 | - | - |
| KL-divergence limit () | - | 0.01 | 0.01 |
| Clip Factor | - | 0.2 | - |
| Generalised Advantage Estimation () | - | 0.95 | 0.97 |
| Algorithm | Advantages | Disadvantages |
|---|---|---|
| DDPG | - High sample efficiency due to off-policy learning. - Suitable for continuous action spaces. | - Sensitive to hyperparameter tuning. - Prone to instability during training. - Requires careful exploration strategies to avoid local minima. |
| TRPO | - Monotonic policy improvement, ensures stability. - Effective in environments with significant nonlinearity and dynamics. | - High computational cost due to second-order optimization. - Less sample-efficient due to on-policy learning. |
| PPO | - Balances simplicity and performance with clipped objectives. - Computationally efficient. - Relatively robust to hyperparameter choices. | - Still less sample-efficient compared to off-policy methods. - May require extensive tuning to maximize performance. |
| Parameters | DDPG | PPO | TRPO |
|---|---|---|---|
| Average reward | 31.339 | 95.2336 | 46.8981 |
| Episode Q0 | 174.8831 | 93.335 | 99.6194 |
| No. of steps required for convergence | 1600 ± 100 | 2100 ± 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhtar, M.; Maqsood, A. Comparative Analysis of Deep Reinforcement Learning Algorithms for Hover-to-Cruise Transition Maneuvers of a Tilt-Rotor Unmanned Aerial Vehicle. Aerospace 2024, 11, 1040. https://doi.org/10.3390/aerospace11121040
Akhtar M, Maqsood A. Comparative Analysis of Deep Reinforcement Learning Algorithms for Hover-to-Cruise Transition Maneuvers of a Tilt-Rotor Unmanned Aerial Vehicle. Aerospace. 2024; 11(12):1040. https://doi.org/10.3390/aerospace11121040
Chicago/Turabian StyleAkhtar, Mishma, and Adnan Maqsood. 2024. "Comparative Analysis of Deep Reinforcement Learning Algorithms for Hover-to-Cruise Transition Maneuvers of a Tilt-Rotor Unmanned Aerial Vehicle" Aerospace 11, no. 12: 1040. https://doi.org/10.3390/aerospace11121040
APA StyleAkhtar, M., & Maqsood, A. (2024). Comparative Analysis of Deep Reinforcement Learning Algorithms for Hover-to-Cruise Transition Maneuvers of a Tilt-Rotor Unmanned Aerial Vehicle. Aerospace, 11(12), 1040. https://doi.org/10.3390/aerospace11121040





