Mathematical Mechanism of Gini Index Used for Multiple-Impulse Phenomenon Characterization
Abstract
1. Introduction
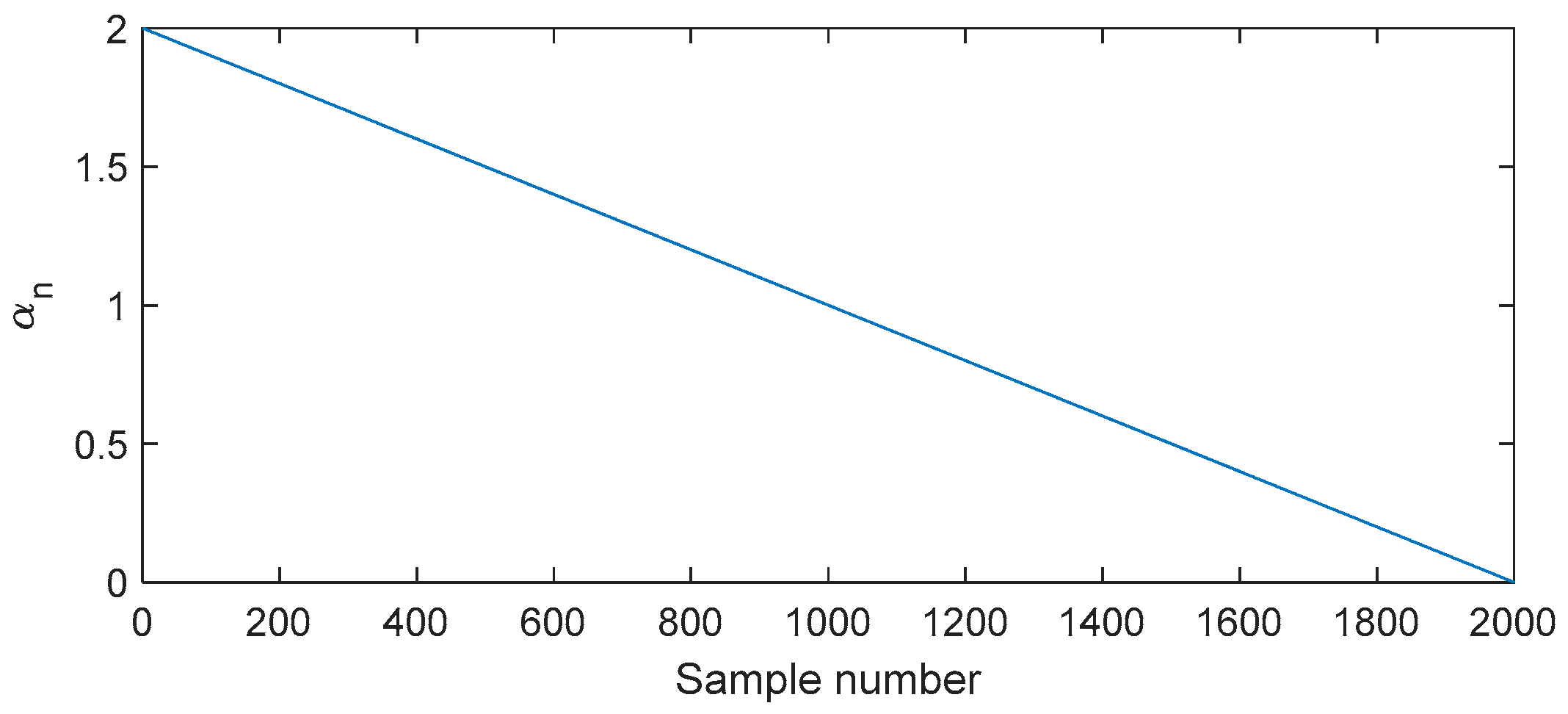
2. Definition of GI
3. GI of Typical Signals
3.1. Constant Signal
3.2. Ideal Series of Cyclical Impulses
3.3. White Noise
3.4. White Noise with Positive Bias
3.5. Cyclic Impulse Series with White Noise
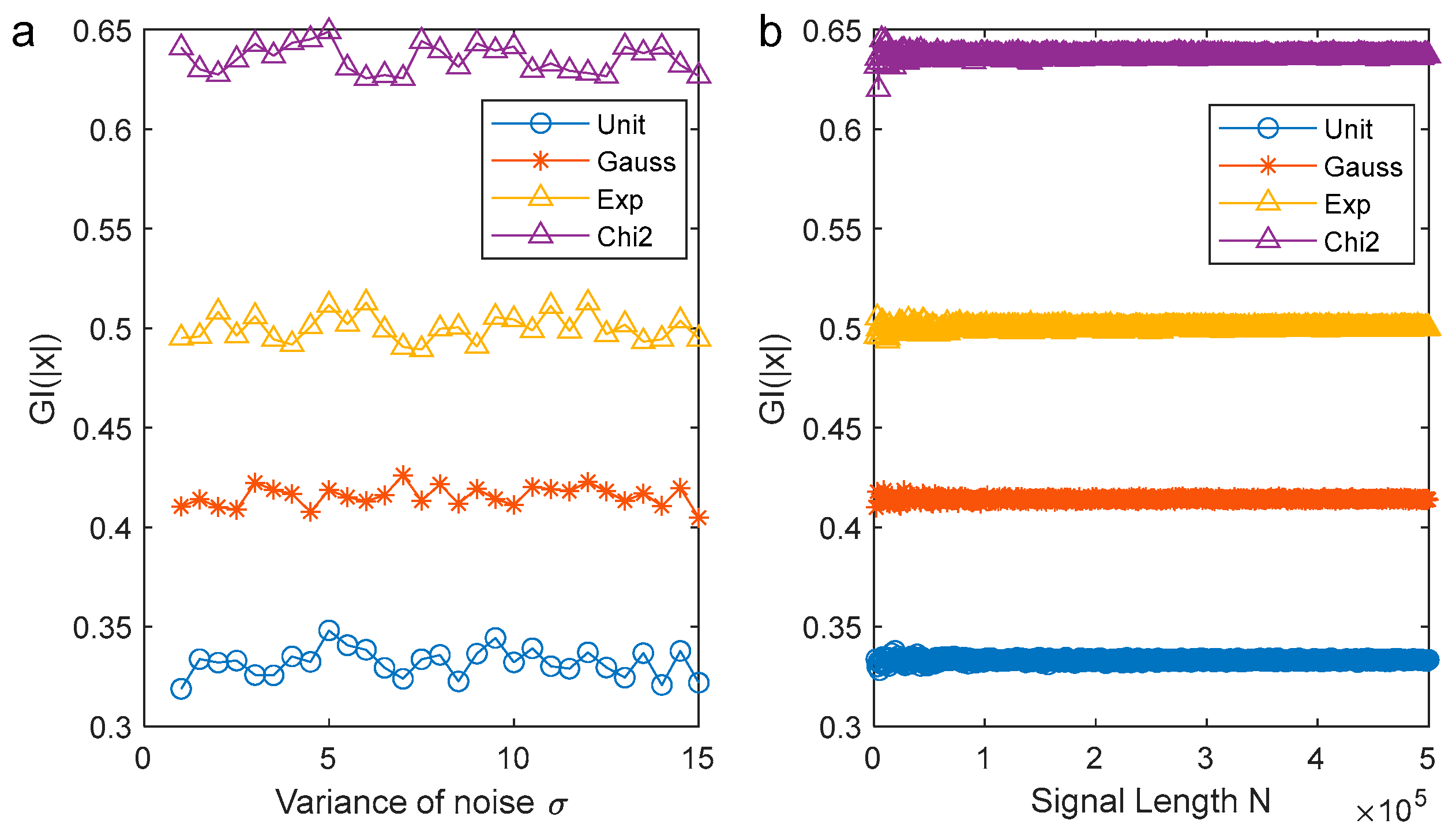
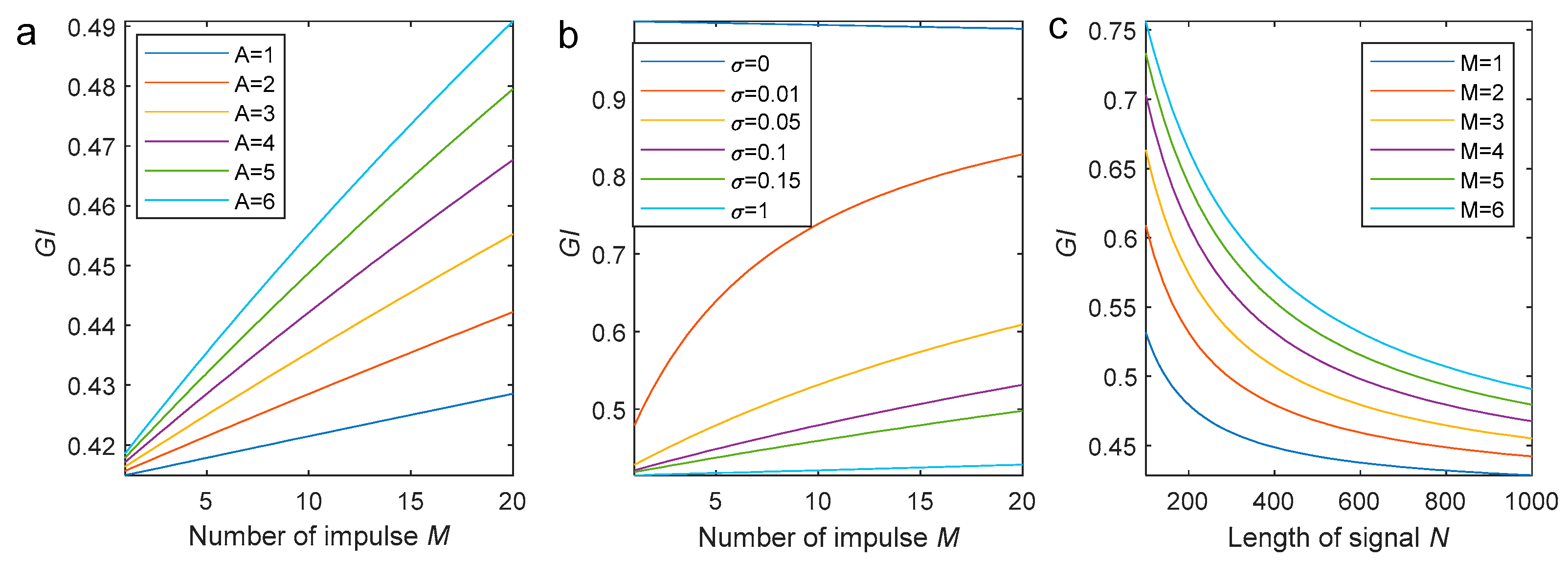
4. Numerical Simulations
5. Applications
5.1. Simulation Analysis
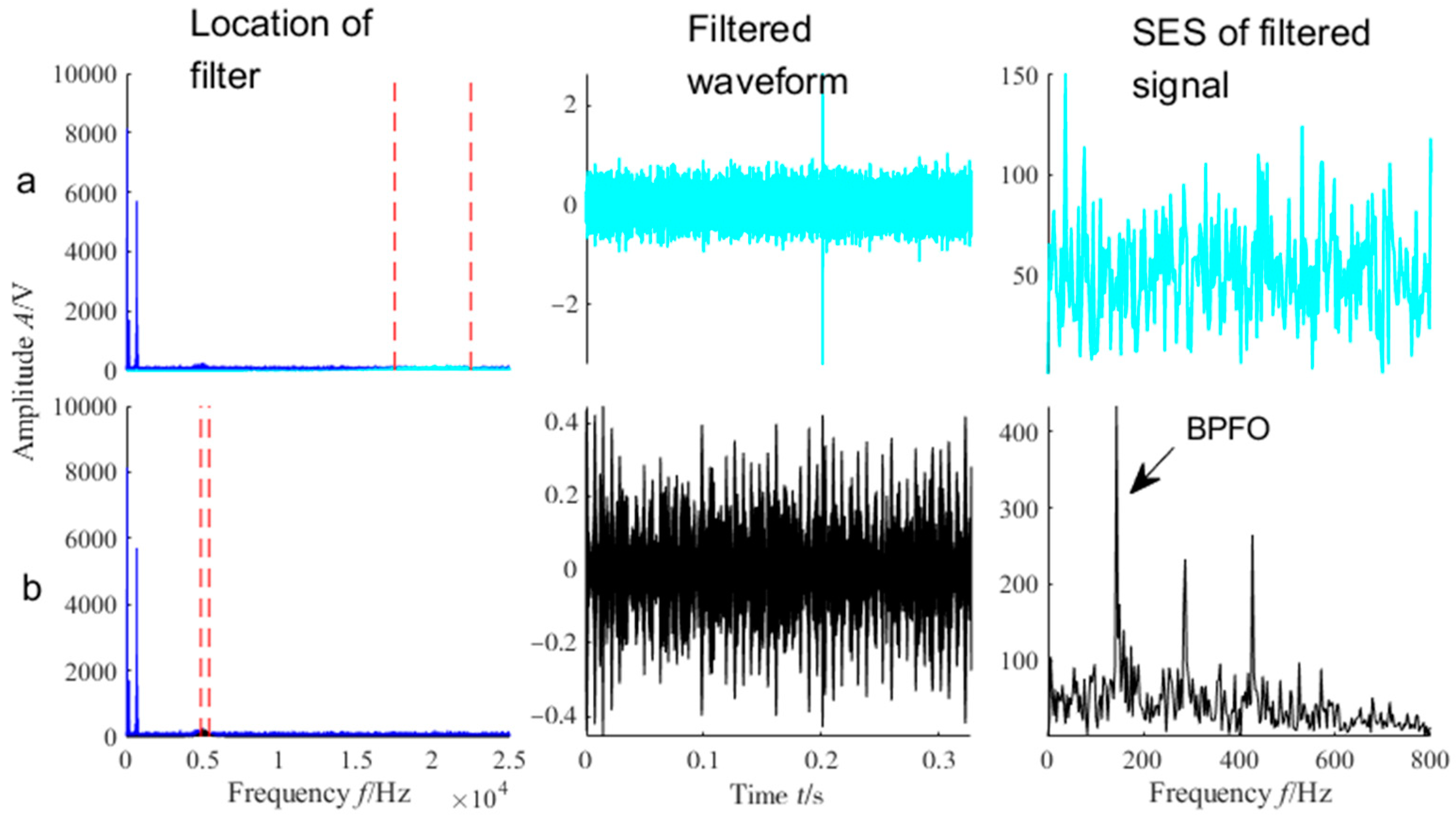
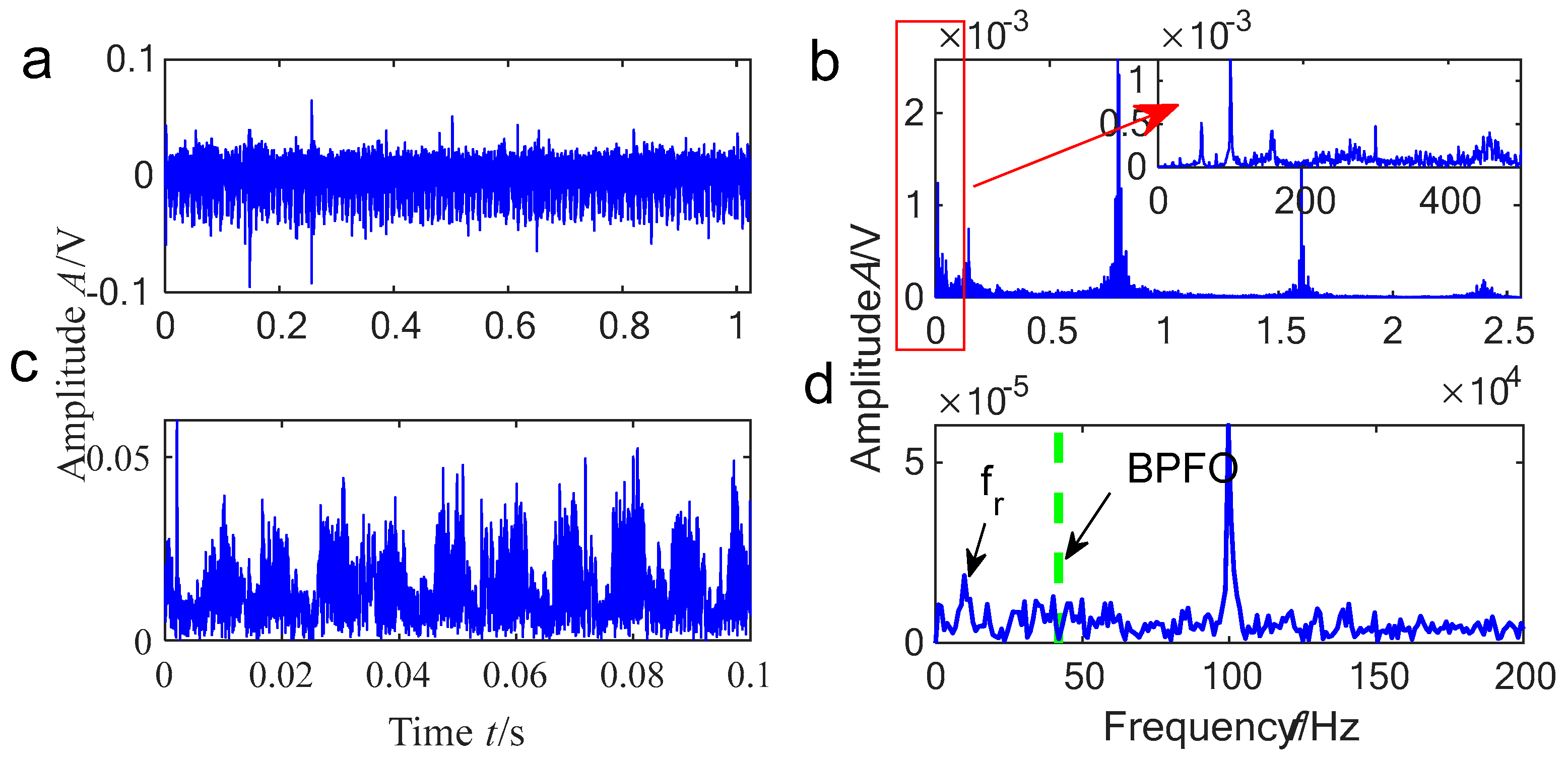
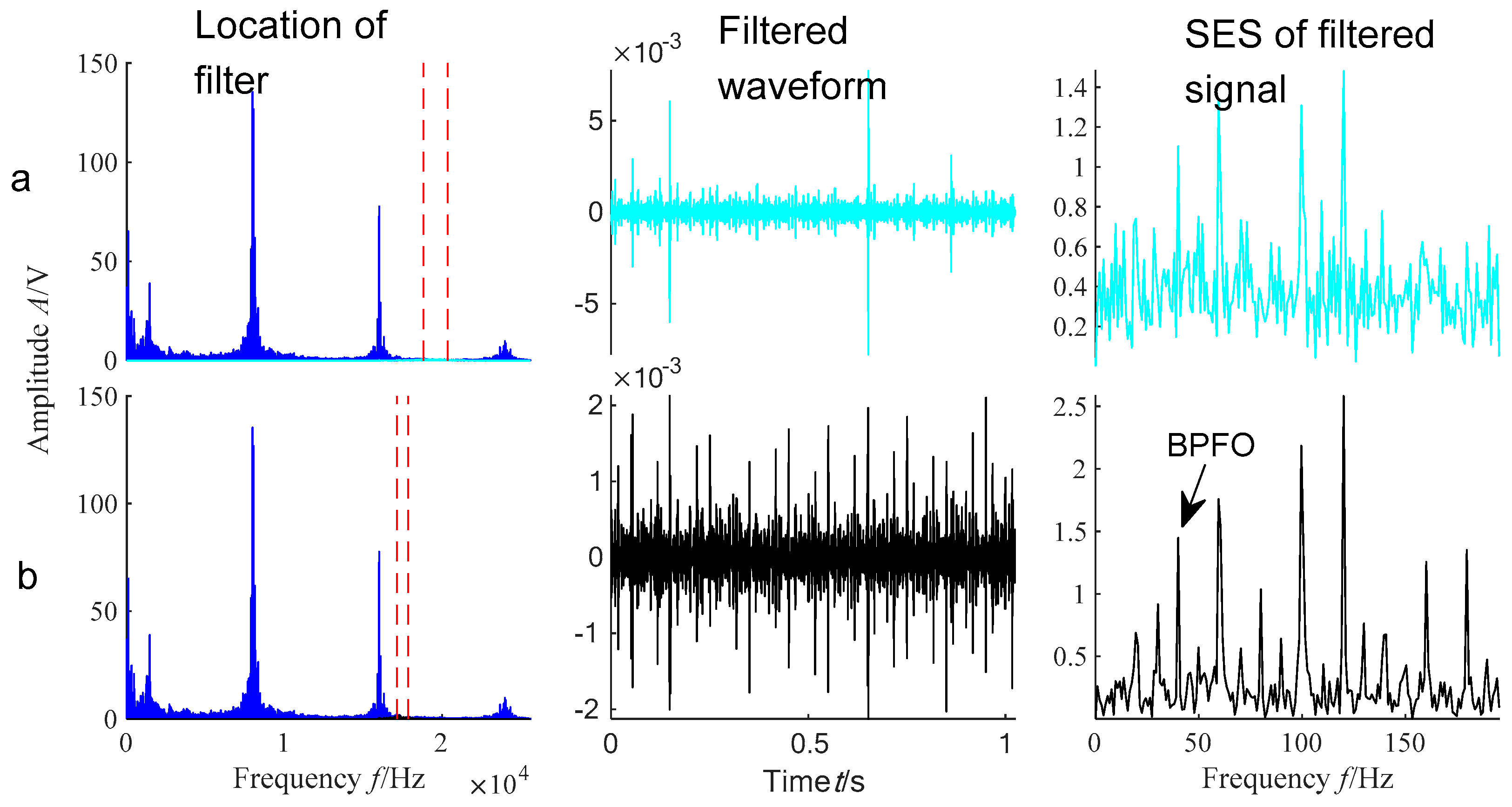
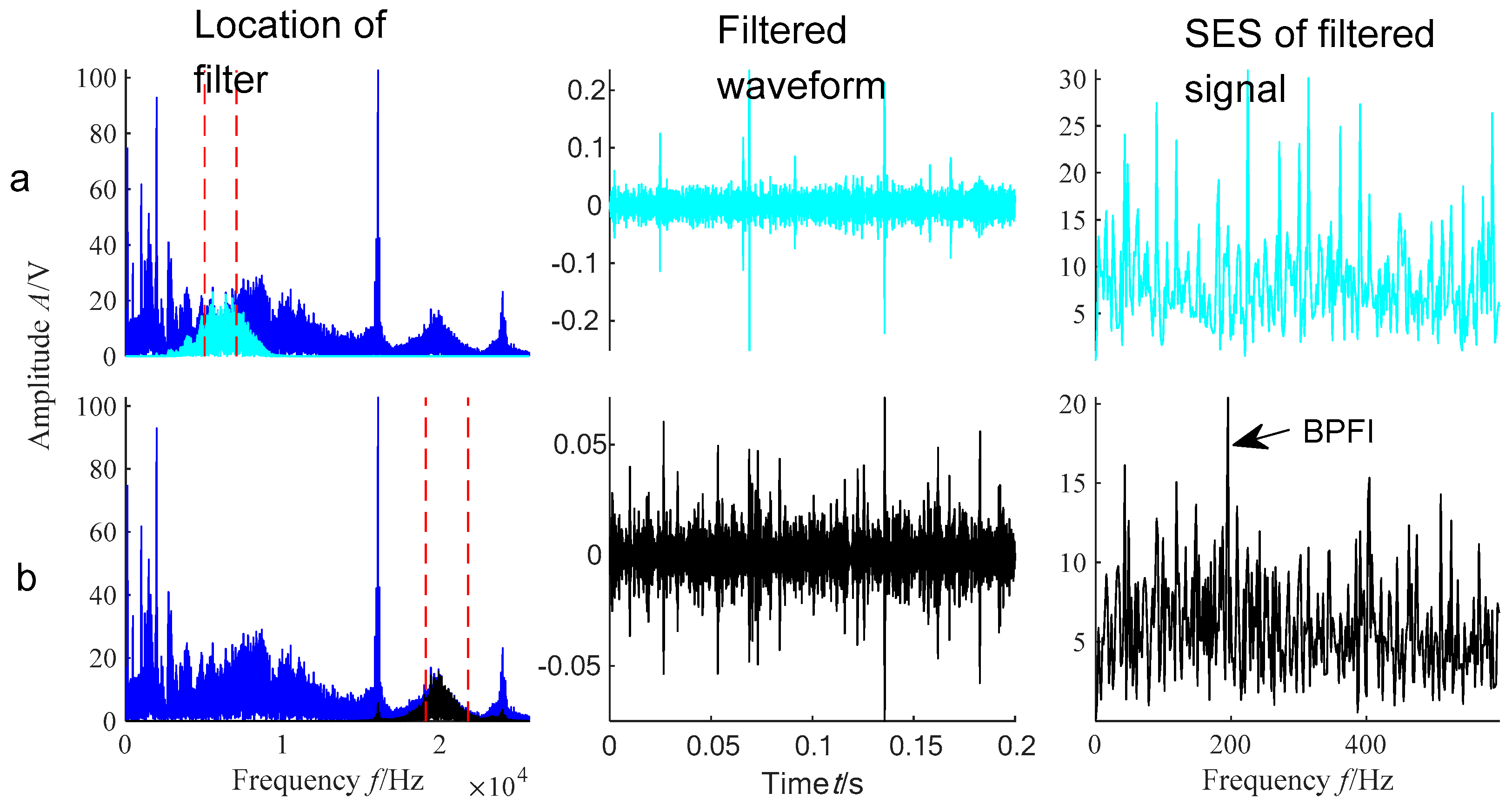
5.2. Experimental Analysis
6. Conclusions
- (1)
- The GI of the constant signal is zero. If there is a large bias in the signal, the bias should be canceled first before the calculation of the GI.
- (2)
- The GI of the ideal cyclical impulse series decreases with the increase in the impulse number.
- (3)
- The distribution of the noise plays an important role in the calculation of the GI. The GI of white noise with normal distribution is around 0.4142.
- (4)
- For the cyclic impulse series affected by white noise, the GI is influenced in a comprehensive manner by the amplitude of the impulse, the number of impulses and the degree of noise. Generally, the GI increases with the increment of the impulse number. The bigger the difference between the amplitude of the impulse and the variance of the white noise, the greater the value of GI is. Therefore, the GI is powerful when it is used for characterizing the impulsive intensity of the multiple-impulse phenomenon.
- (5)
- Both simulation and experimental analyses show that methods based on the maximization of the GI can be used for the extraction of cyclical impulses and are more powerful than those based on the maximization of kurtosis.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Derivation of Equation (6)
Appendix A.2. Derivation of Equation (21)
Appendix A.3. Derivation of Equation (24)
References
- Molero-Simarro, R. Inequality in China revisited. The effect of functional distribution of income on urban top incomes, the urban-rural gap and the Gini index, 1978–2015. China Econ. Rev. 2017, 42, 101–117. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Miao, Y.; Wang, J.; Zhang, B.; Li, H. Practical framework of Gini index in the application of machinery fault feature extraction. Mech. Syst. Signal Process. 2022, 165, 108333. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the Kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Barszcz, T.; Jablonski, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. A new SKRgram based demodulation technique for planet bearing fault detection. J. Sound Vib. 2016, 385, 330–349. [Google Scholar] [CrossRef]
- Nassef, M.G.A.; Hussein, T.M.; Mokhiamar, O. An adaptive variational mode decomposition based on sailfish optimization algorithm and Gini index for fault identification in rolling bearings. Measurement 2021, 173, 108514. [Google Scholar] [CrossRef]
- Hou, B.; Wang, D.; Xia, T.; Xi, L.; Peng, Z.; Tsui, K.-L. Generalized Gini indices: Complementary sparsity measures to Box-Cox sparsity measures for machine condition monitoring. Mech. Syst. Signal Process. 2022, 169, 108751. [Google Scholar] [CrossRef]
- Chen, B.; Cheng, Y.; Zhang, W.; Gu, F. Investigations on improved Gini indices for bearing fault feature characterization and condition monitoring. Mech. Syst. Signal Process. 2022, 176, 109165. [Google Scholar] [CrossRef]
- Wang, D. Some further thoughts about spectral kurtosis, spectral L2/L1 norm, spectral smoothness index and spectral Gini index for characterizing repetitive transients. Mech. Syst. Signal Process. 2018, 108, 360–368. [Google Scholar] [CrossRef]
- Shynk, J.J. Probalility, Random Variables, and Random Processes Theory and Signal Processing Applications; Willey: Hoboken, NY, USA, 2012. [Google Scholar]
- Miao, Y.; Zhao, M.; Hua, J. Research on sparsity indexes for fault diagnosis of rotating machinery. Measurement 2020, 158, 107733. [Google Scholar] [CrossRef]
- Tong, S.; Fu, Z.; Tong, Z.; Cong, F. Gear fault diagnosis using spectral Gini index and segmented energy spectrum. Meas. Sci. Technol. 2024, 35, 116134. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, X. Separation of fault characteristic impulses of flexible thin-wall bearing based on wavelet transform and correlated Gini index. Mech. Syst. Signal Process. 2024, 209, 111118. [Google Scholar] [CrossRef]
- Chen, B.; Song, D.; Cheng, Y.; Huang, B.; Muhamedsalih, Y. IGIgram: An Improved Gini Index-Based Envelope Analysis for Rolling Bearing Fault Diagnosis. J. Dynamics. Monit. Diagn. 2022, 1, 111–124. [Google Scholar] [CrossRef]
- Ming, A.; Zhang, W.; Fu, C.; Yang, Y. L-kurtosis-based optimal wavelet filtering and its application to fault diagnosis of rolling element bearings. J. Vib. Control. 2024, 30, 1594–1603. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, G.; Ming, A.; Zhang, W. Mathematical Mechanism of Gini Index Used for Multiple-Impulse Phenomenon Characterization. Aerospace 2024, 11, 1034. https://doi.org/10.3390/aerospace11121034
Jin G, Ming A, Zhang W. Mathematical Mechanism of Gini Index Used for Multiple-Impulse Phenomenon Characterization. Aerospace. 2024; 11(12):1034. https://doi.org/10.3390/aerospace11121034
Chicago/Turabian StyleJin, Guofeng, Anbo Ming, and Wei Zhang. 2024. "Mathematical Mechanism of Gini Index Used for Multiple-Impulse Phenomenon Characterization" Aerospace 11, no. 12: 1034. https://doi.org/10.3390/aerospace11121034
APA StyleJin, G., Ming, A., & Zhang, W. (2024). Mathematical Mechanism of Gini Index Used for Multiple-Impulse Phenomenon Characterization. Aerospace, 11(12), 1034. https://doi.org/10.3390/aerospace11121034




