Planning and Evaluation of Water-Dropping Strategy for Fixed-Wing Fire Extinguisher Based on Multi-Resolution Modeling
Abstract
1. Introduction
2. Technical Framework
3. Basic Method
3.1. Fire Model
3.2. Water-Dropping Point Scheme Planning Algorithm
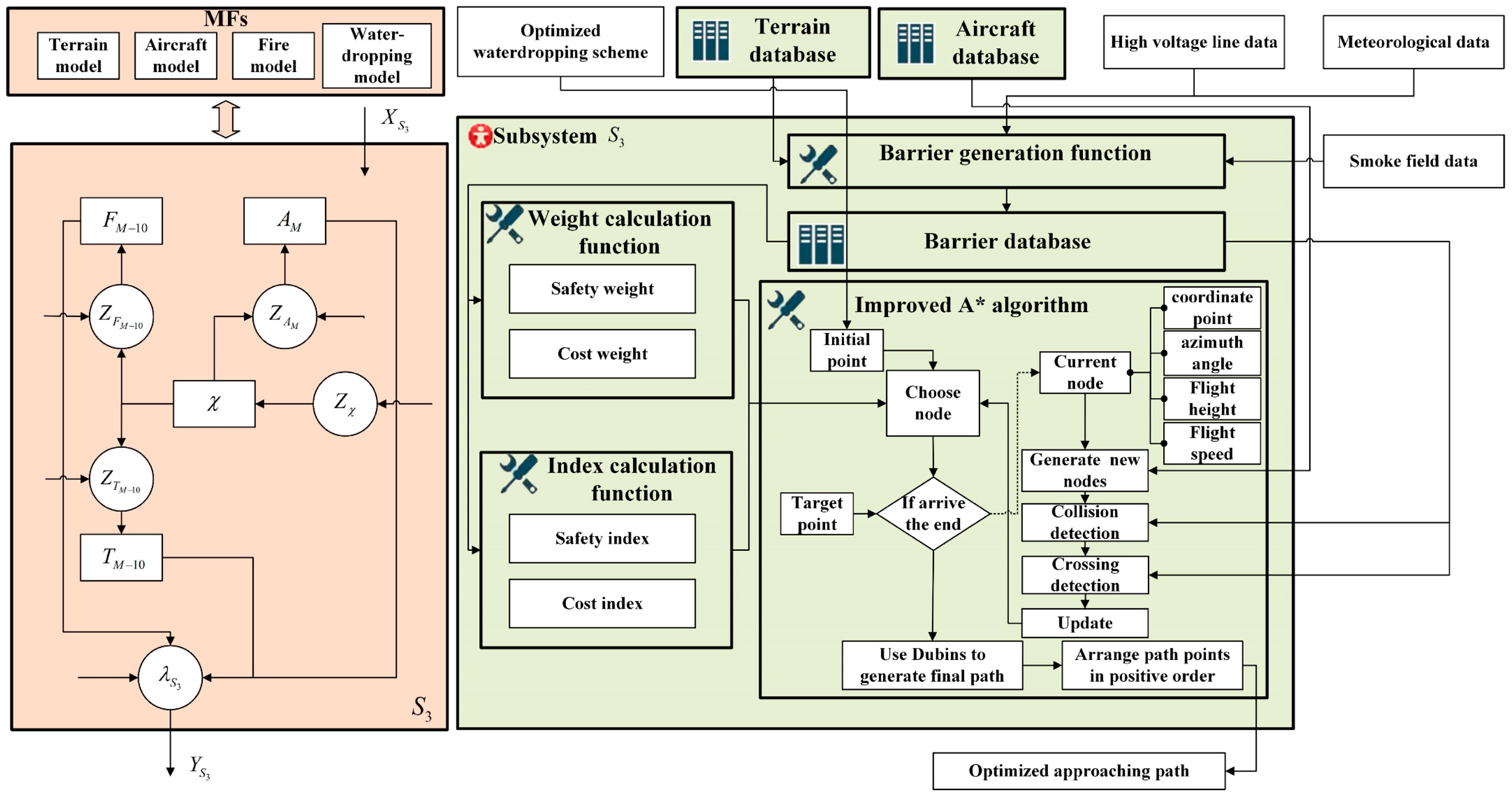
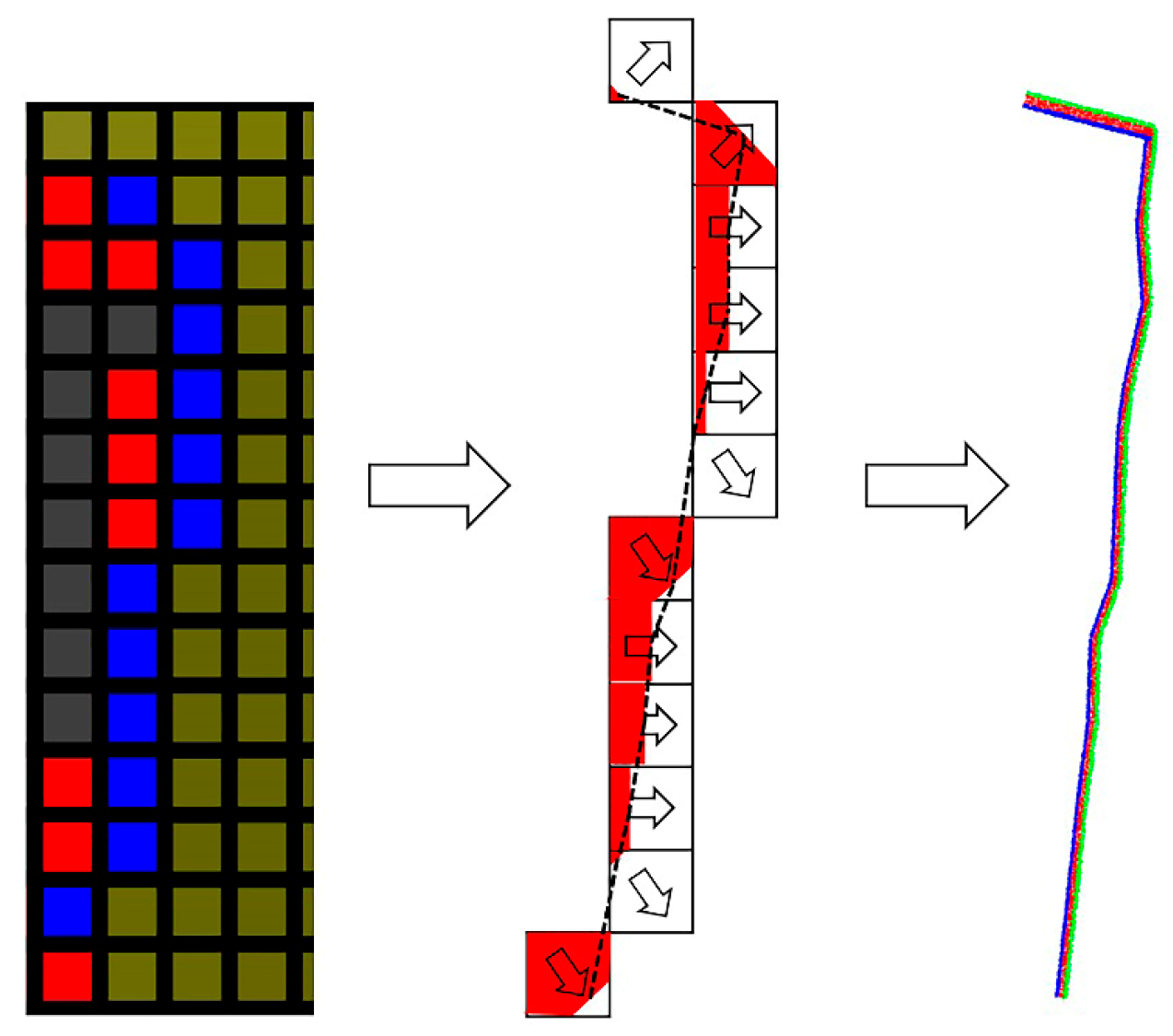
3.3. Approaching Path Planning Algorithm
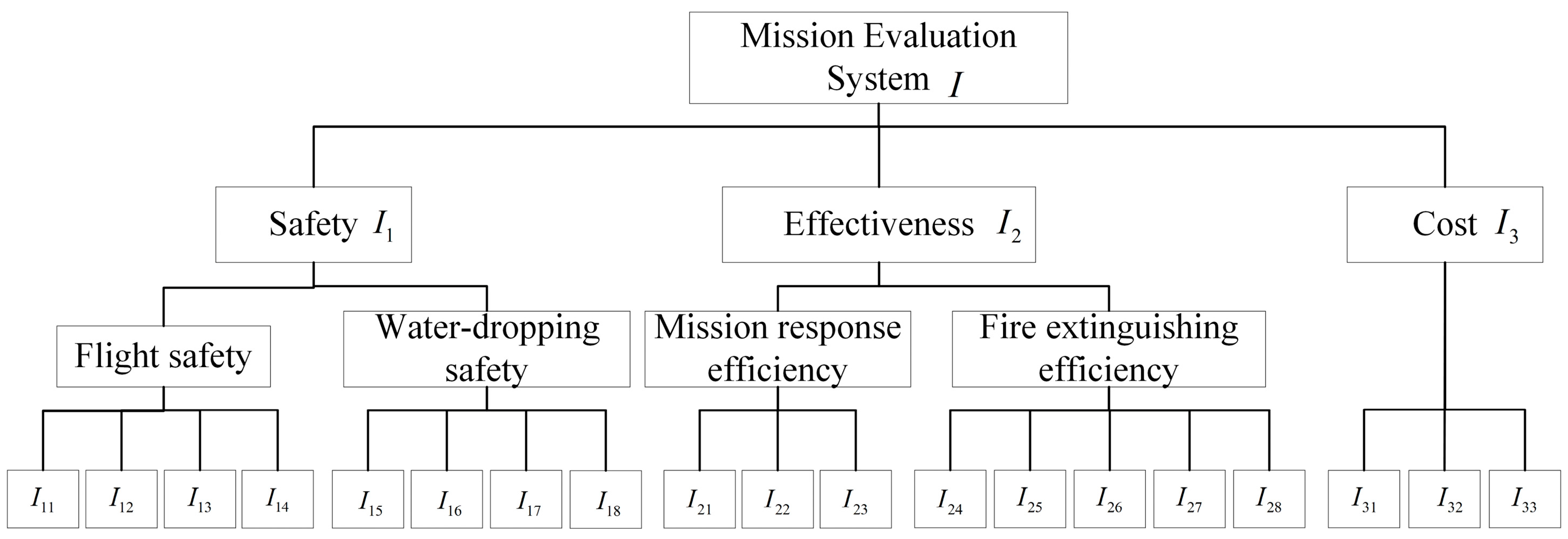
3.4. Complete Mission Effectiveness Evaluation System for Water-Dropping Strategy
4. Results
4.1. Fire Environment
4.2. Water-Dropping Point Scheme Planning
4.3. Path Planning
4.4. Mission Simulation and Evaluation
5. Simulation Experiment
5.1. Case Based Validation
5.2. Performance Comparison of Human-in-Loop Simulation
5.3. Analysis of the Influence of Aircraft Design Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Resolution models for different objects | |||
| High-resolution terrain model | Medium-resolution terrain model | ||
| Low-resolution terrain model | High-resolution fire model | ||
| Medium-resolution fire model | Low-resolution fire model | ||
| High-resolution aircraft model | Medium-resolution aircraft model | ||
| Low-resolution aircraft model | |||
| Fire model | |||
| The component of wind in three directions of ground coordinate system | Side length of square CA | ||
| Fire line spread speed | Reaction intensity | ||
| Heat flux ratio coefficient | Bulk density | ||
| Effective bulk density | Heat of preignition | ||
| Terrain coefficient | Wind coefficient | ||
| Fuel density | Fuel temperature | ||
| Relative fuel moisture | Ambient temperature | ||
| Evaporation temperature | Ignition threshold temperature | ||
| Heat capacity of fuel | Heat capacity of water | ||
| Evaporation latent heat of water | Heat transfer coefficient | ||
| Density of total radiation power | Residual ash density | ||
| Prefactor | Ideal gas constant | ||
| Activation energy | Dirac symbol | ||
| Cellular adjustment coefficient | Base height of the fire source | ||
| Effective plume height | Uplifted height | ||
| Average canopy height | Flame burning height | ||
| Smoke concentration | Cellular point source strength | ||
| Downwind diffusion coefficient | Crosswind diffusion coefficient | ||
| Diffusion coefficient of vertical wind direction | |||
| Water-dropping model (some parameters of fire conform to the above format) | |||
| Outlet section area of the aircraft | Correction coefficient | ||
| Momentum | Maximum coverage level | ||
| Lateral position corresponding to the fixed body coordinate system | Correction coefficient of diffusion | ||
References
- Matta, K. Use of Aviation Technology in Forest Fire Fighting in Slovakia. In Wood & Fire Safety: Proceedings of the 9th International Conference on Wood & Fire Safety 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 386–393. [Google Scholar] [CrossRef]
- Plucinski, M.; McCarthy, G.; Hollis, J.; Gould, J. The effect of aerial suppression on the containment time of Australian wildfires estimated by fire management personnel. Int. J. Wildland Fire 2011, 21, 219–229. [Google Scholar] [CrossRef]
- Burns, K.R.; Burns, M.J. Aviation in Fire Fighting. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 2217. [Google Scholar] [CrossRef]
- Calkin, D.E.; Stonesifer, C.S.; Thompson, M.P.; McHugh, C.W. Large airtanker use and outcomes in suppressing wildland fires in the United States. Int. J. Wildland Fire 2014, 23, 259–271. [Google Scholar] [CrossRef]
- MacPherson, J.I. An Improved Theoretical Model for the Ground Distribution of Water Released from a Fire-Bomber; Aeronautical Report LR 498; National Research Council of Canada: Ottawa, Canada, 1968. [Google Scholar]
- Anderson, W.H. Investigation of Rheological Properties of Aerial-Delivered Fire Retardant Extended Study; Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1974. [Google Scholar]
- Andersen, W.H.; Wong, J.Y. Dynamic Interaction of Fire Retardant Droplets with Fuel, and Correlation with the Rheological Properties of the Retardant: Final Report (7660-02); Shock Hydrodynamics Division, Whittaker Corporation: North Hollywood, CA, USA, 1978. [Google Scholar]
- George, C.W.; Blakely, A.D.; Johnson, G.M. Forest Fire Retardant Research: A Status Report; USDA Forest Service General Technical Report; Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1976. [Google Scholar]
- Blakely, A.D. Static Testing to Evaluate Airtanker Delivery Performance; US Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Washington, DC, USA, 1982. [Google Scholar]
- Swanson, D.H.; Luedecke, A.D.; Helvig, T.N.; Parduhn, F.J. Development of User Guidelines for Selected Retardant Aircraft; U. Intermountain Forest and Range Experiment Station; Government and Aeronautical Products Division: Ogden, UT, USA, 1975. [Google Scholar]
- CarteNav. Available online: https://cartenav.com/aerial-firefighting/ (accessed on 15 February 2023).
- Elbit Systems. Available online: https://elbitsystems.com/pr-new/elbit-systems-successfully-demonstrates-high-altitude-high-precision-aerial-firefighting-solution/ (accessed on 15 February 2023).
- Coulson Aviation. Available online: https://www.coulsonaviationusa.com/fleet (accessed on 14 February 2023).
- Zohdi, T.I. A digital twin framework for machine learning optimization of aerial fire fighting and pilot safety. Comput. Methods Appl. Mech. Eng. 2021, 373, 113446. [Google Scholar] [CrossRef]
- Amorim, J.H. Numerical Modelling of the Aerial Drop of Products for Forest Firefighting; Universidade de Aveiro: Aveiro, Portugal, 2008. [Google Scholar]
- Amorim, J.H. Numerical modelling of the aerial drop of firefighting agents by fixed-wing aircraft. Part I: Model development. Int. J. Wildland Fire 2011, 20, 384–393. [Google Scholar] [CrossRef]
- Amorim, J.H. Numerical modelling of the aerial drop of firefighting agents by fixed-wing aircraft. Part II: Model validation. Int. J. Wildland Fire 2011, 20, 394–406. [Google Scholar] [CrossRef]
- Cigal, N.; Naeem, N.; Ratei, P.; Kilkis, S.; Shiva Prakasha, P.; Nagel, B.; Kurtulus, D.F. Sensitivity analysis of aerial wildfire fighting tactics with heterogeneous fleets using a system of systems simulation framework. In Proceedings of the DLRK 2022, Dresden, Germany, 27–29 September 2022. [Google Scholar]
- Prakasha, P.S.; Nagel, B.; Kilkis, S.; Naeem, N.; Ratei, P. System of systems simulation driven wildfire fighting aircraft design. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021; p. 2455. [Google Scholar] [CrossRef]
- Wang, Y.L.; Cai, Z.Y.; Zhao, H.J. Study of the Algorithm for Dropping Water by Air Tanker. Nanchang Hangkong University, 2012. Available online: https://en.cnki.com.cn/Article_en/CJFDTOTAL-WJSJ201209109.htm (accessed on 1 May 2012).
- Gašparović, G.; Klarin, B.; Grebo, A.; Mladenović, S. New Concept of Firefighting Aerial Support with Autonomous Unmanned Aerial Systems (AUAS). In Proceedings of the 2020 New Trends in Aviation Development (NTAD), Stary Smokovec, Slovakia, 17–18 September 2020; IEEE: New York, NY, USA, 2020; pp. 78–83. [Google Scholar] [CrossRef]
- Çoğay, S.; Seçinti, G. Phoenix: Aerial Monitoring for Fighting Wildfires. Drones 2022, 7, 19. [Google Scholar] [CrossRef]
- Boroujeni, S.P.H.; Razi, A.; Khoshdel, S.; Afghah, F.; Coen, J.L.; O’neill, L.; Fule, P.; Watts, A.; Kokolakis, N.-M.T.; Vamvoudakis, K.G. A comprehensive survey of research towards ai-enabled unmanned aerial systems in pre-, active-, and post-wildfire management. Inf. Fusion 2024, 108, 102369. [Google Scholar] [CrossRef]
- Zhang, H.; Yong, M.P.; Sun, Z.P.; Yan, G.W. Discussion on index system of fire-fighting effectiveness of fire-fighting aircraft. GuangDong Sci. Technol. 2015, 24, 50–52. [Google Scholar]
- Plucinski, M.; Gould, J.; McCarthy, G.; Hollis, J. The Effectiveness and Efficiency of Aerial Firefighting in Australia. 2007. Available online: https://wildfiretoday.com/documents/AustralianStudy-EffectivenessAerialFirefighting.pdf (accessed on 30 June 2007).
- Fidanza, R.; Denante, M. EC225, Water Bombing Helicopter. 2010. Available online: https://dspace-erf.nlr.nl/server/api/core/bitstreams/fb9930fc-2923-4067-9a55-3039f475e940/content (accessed on 31 July 2010).
- Ramírez, Y.P.; Gould, J.; Ferrer, E.P.; Cuchi, E.P.; Plucinski, M. Computing aerial suppression effectiveness by IR monitoring. In Proceedings of the 6th Mediterranean Combustion Symposium, Corsica, France, 7–11 June 2009. [Google Scholar] [CrossRef]
- Kal’avský, P.; Petríček, P.; Kelemen, M.; Rozenberg, R.; Jevčák, J.; Tomaško, R.; Mikula, B. The efficiency of aerial firefighting in varying flying conditions. In Proceedings of the 2019 International Conference on Military Technologies (ICMT), Brno, Czech Republic, 30–31 May 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Plucinski, M.P.; Pastor, E. Criteria and methodology for evaluating aerial wildfire suppression. Int. J. Wildland Fire 2013, 22, 1144–1154. [Google Scholar] [CrossRef]
- Restás, Á. Measuring the Efficiency by Mixing the Costs and the Effectiveness of Extinguishing Materials and Aerial Firefighting. Bratislava Proceedings of the 16th International Conference, Bratislava. 2017. Available online: https://www.sszp.eu/wp-content/uploads/2016_conference_MaZP__p-118__Restas-Measuring-__f4.pdf (accessed on 24 June 2016).
- Restas, A. Examining the Effectiveness of Aerial Firefighting with the Components of Firebreak Requirements and Footprint Geometry—Critics of the Present Practice. Fire 2023, 6, 351. [Google Scholar] [CrossRef]
- Gabbert, B. A 9-Year USFS Aerial Firefighting Study Left Many Questions Unanswered. Wildfire Today, 16 April 2021. Available online: https://wildfiretoday.com/2021/04/16/a-9-year-usfs-aerial-firefighting-study-left-many-questions-unanswered/ (accessed on 16 April 2021).
- Usach, H.; Vila, J.A. Reconfigurable mission plans for RPAS. Aerosp. Sci. Technol. 2020, 96, 105528. [Google Scholar] [CrossRef]
- Peng, G.; Mao, H.; Zhang, H. BMRSS: BOM-based multi-resolution simulation system using components. In Proceedings of the AsiaSim 2013: 13th International Conference on Systems Simulation, Singapore, 6–8 November 2013; Proceedings 13. Springer: Berlin/Heidelberg, Germany, 2013; pp. 485–496. [Google Scholar] [CrossRef]
- Kong, C.Y.; Xing, L.J. Multi-resolution Modeling Framework for Command and Control Simulation in Joint Operations. Command Inf. Syst. Technol. 2013, 4, 9–16. [Google Scholar]
- Borshchev, A. Multi-method modelling: AnyLogic. In Discrete-Event Simulation and System Dynamics for Management Decision Making; Wiley Online Library: New York, NY, USA, 2014; pp. 248–279. [Google Scholar] [CrossRef]
- Ollero, A.; Merino, L. Unmanned aerial vehicles as tools for forest-fire fighting. For. Ecol. Manag. 2006, 234, S263. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Intermountain Forest & Range Experiment Station, Forest Service, US Department of Agriculture: Washington, DC, USA, 1972; Volume 115. [Google Scholar]
- Collin, A.; Bernardin, D.; Sero-Guillaume, O. A physical-based cellular automaton model for forest-fire propagation. Combust. Sci. Technol. 2011, 183, 347–369. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Zhou, Y.; Sun, C. Spread vector induced cellular automata model for real-time crown fire behavior simulation. Environ. Model. Softw. 2018, 108, 14–39. [Google Scholar] [CrossRef]
- Macdonald, R. Theory and objectives of air dispersion modelling. Model. Air Emiss. Compliance 2003, 1–27. [Google Scholar]
- Wang, X.; Liu, H.; Tian, Y.; Chen, Z.; Cai, Z. A fast optimization method of water-dropping scheme for fixed-wing firefighting aircraft. IEEE Access 2021, 9, 120815–120832. [Google Scholar] [CrossRef]
- Legendre, D.; Becker, R.; Alméras, E.; Chassagne, A. Air tanker drop patterns. Int. J. Wildland Fire 2013, 23, 272–280. [Google Scholar] [CrossRef]
- Bridson, R. Fast Poisson disk sampling in arbitrary dimensions. SIGGRAPH Sketches 2007, 10, 1. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, G.; Hu, X.; Xiao, J. Unmanned aerial vehicle route planning method based on a star algorithm. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; IEEE: New York, NY, USA, 2018; pp. 1510–1514. [Google Scholar] [CrossRef]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C.; Rabot, Y.; Martin, O. Lightweight UAV with on-board photogrammetry and single-frequency GPS positioning for metrology applications. ISPRS J. Photogramm. Remote Sens. 2017, 127, 115–126. [Google Scholar] [CrossRef]
- Saaty, T.L. What is the analytic hierarchy process. In Mathematical Models for Decision Support; NATO ASI Series; Mitra, G., Greenberg, H.J., Lootsma, F.A., Rijkaert, M.J., Zimmermann, H.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; Volume 48. [Google Scholar]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Liu, B.H. Research on the Theory and Key Techniques of Multi-Resolution Modeling (MRM); National University of Defense Technology: Changsha, China, 2003. [Google Scholar]
- Chitsaz, H.; LaValle, S.M. Time-optimal paths for a Dubins airplane. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; IEEE: New York, NY, USA, 2007; pp. 2379–2384. [Google Scholar] [CrossRef]
- Legendre, D. Fluid Dynamics of Airtanker Firefighting. Annu. Rev. Fluid Mech. 2024, 56, 577–603. [Google Scholar] [CrossRef]
- Martin, L.; Arbab, Y.; Roberts, L.; Mercer, J.; Walter, C.; McCarty, W.; Sheehe, C. Developing an Unmanned Aircraft System Pilot Kit (UASP-kit) for Wildland Fire UAS Operators. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 4003. [Google Scholar] [CrossRef]






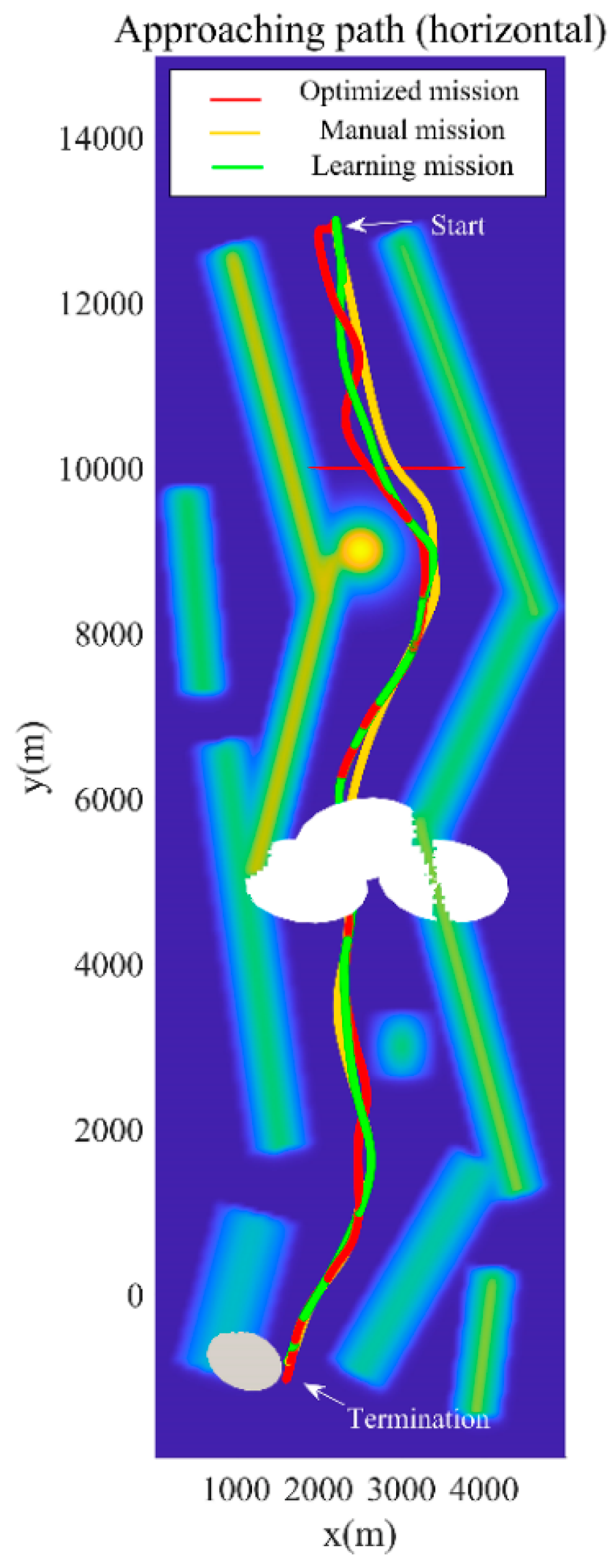
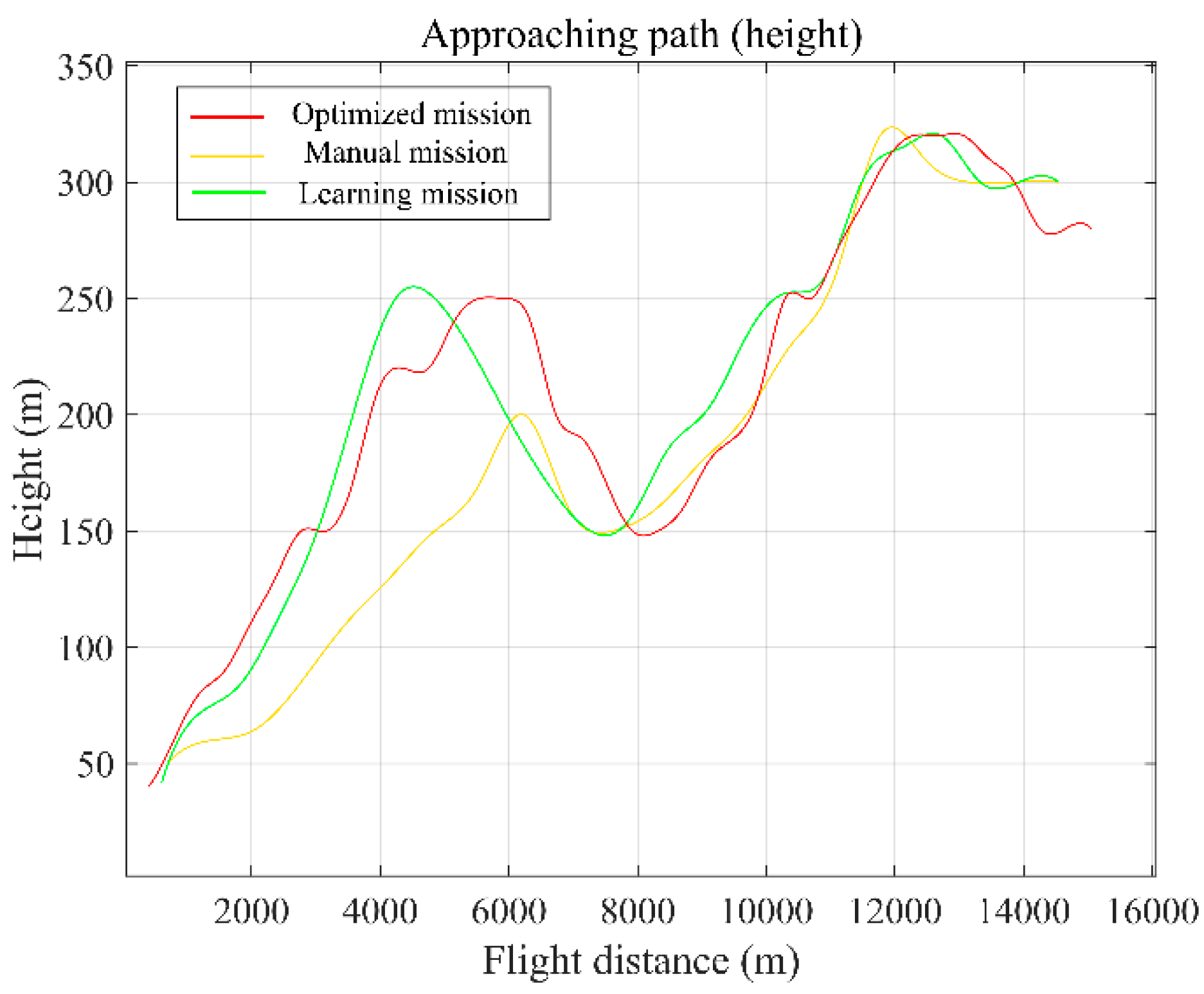
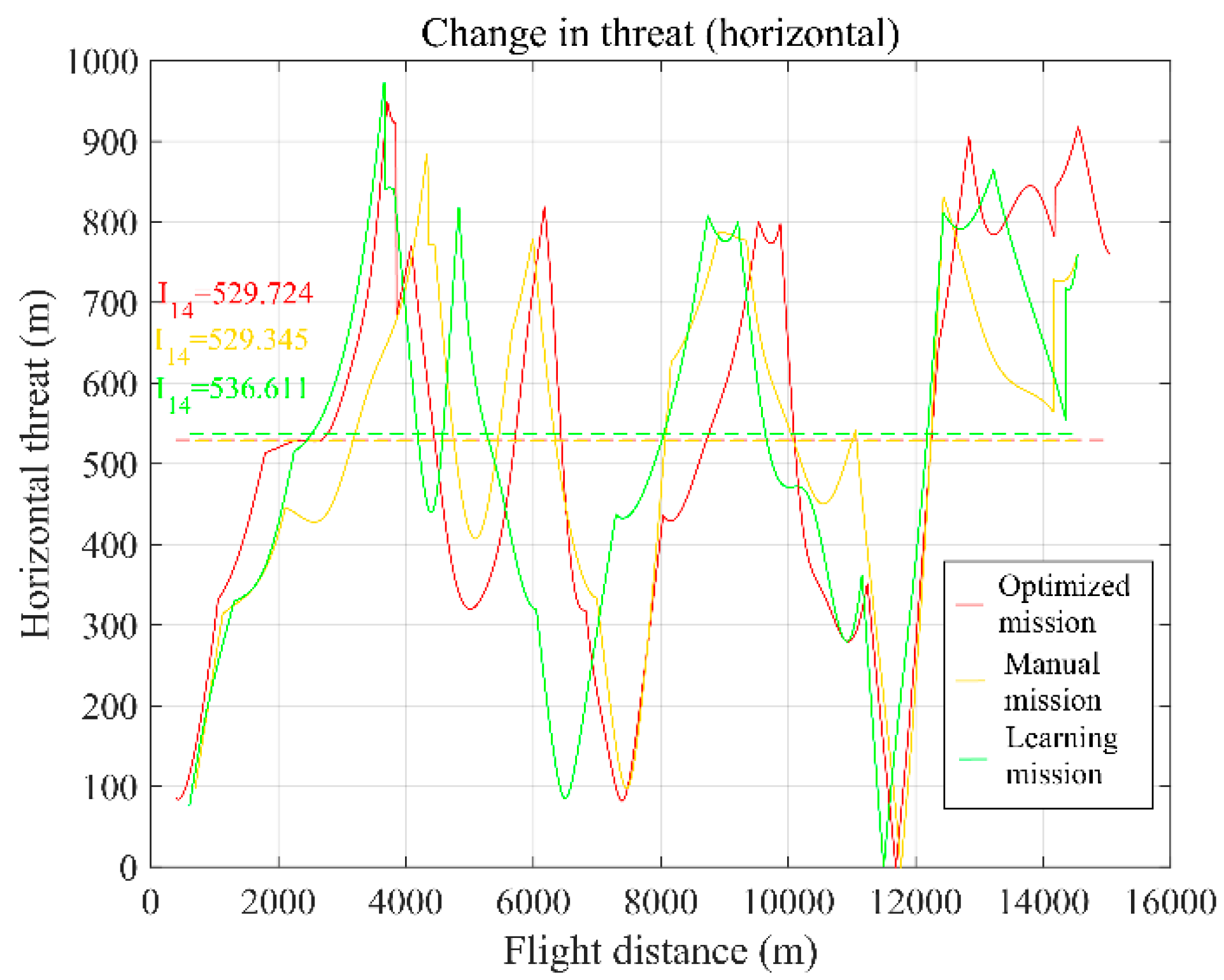

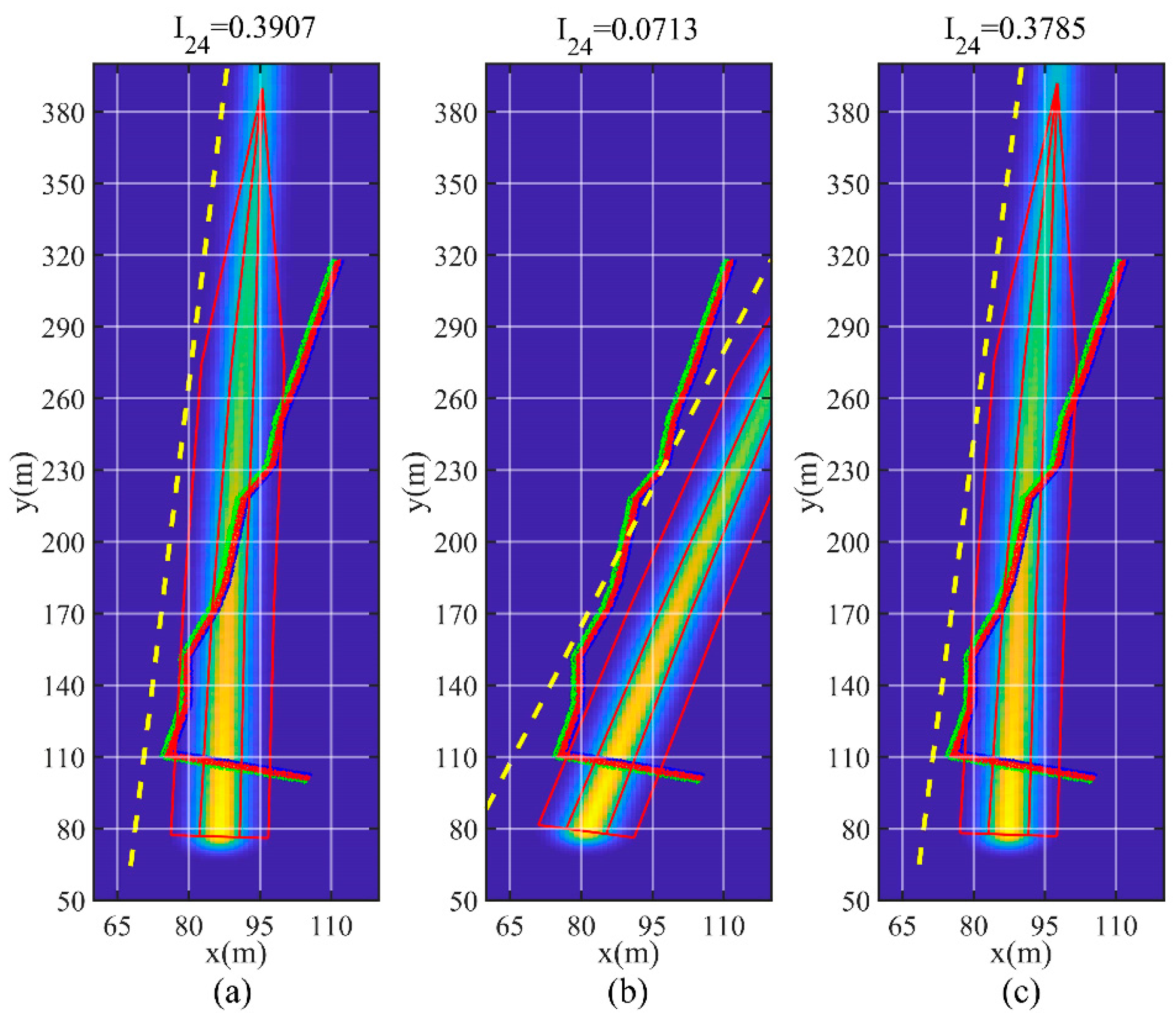
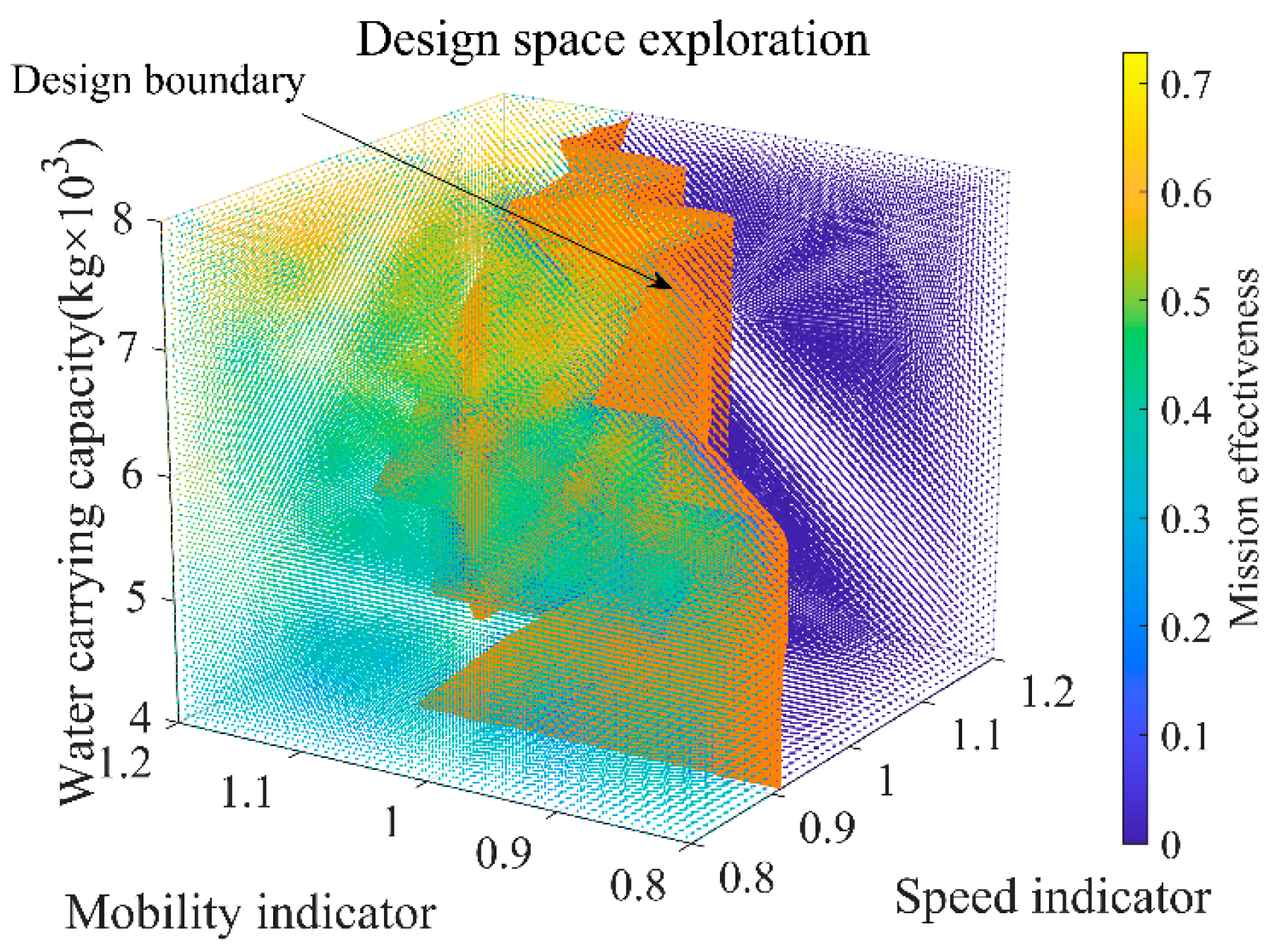
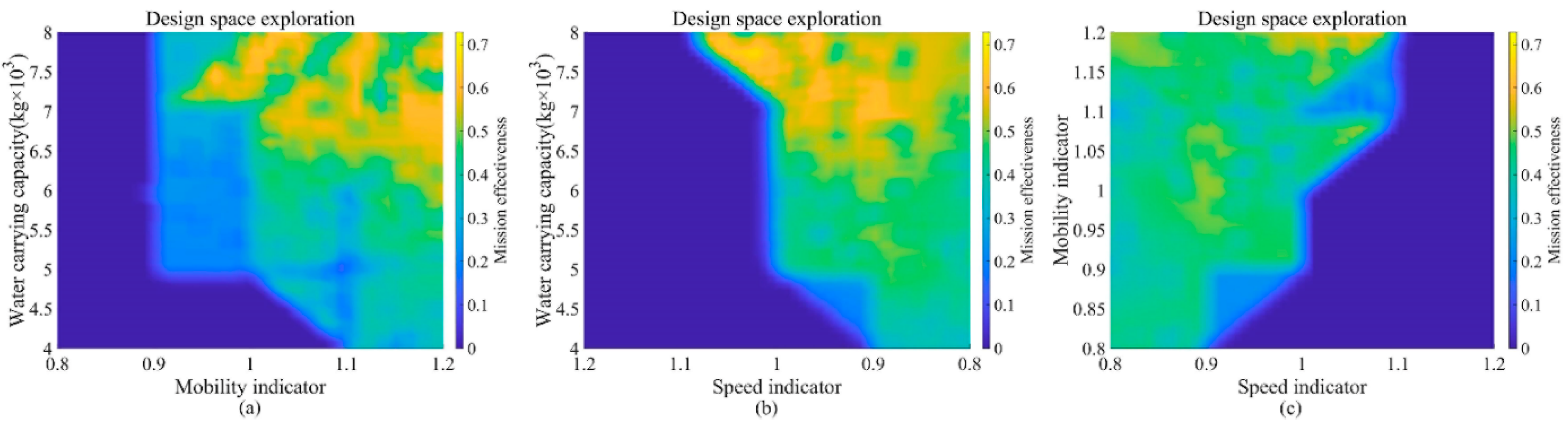
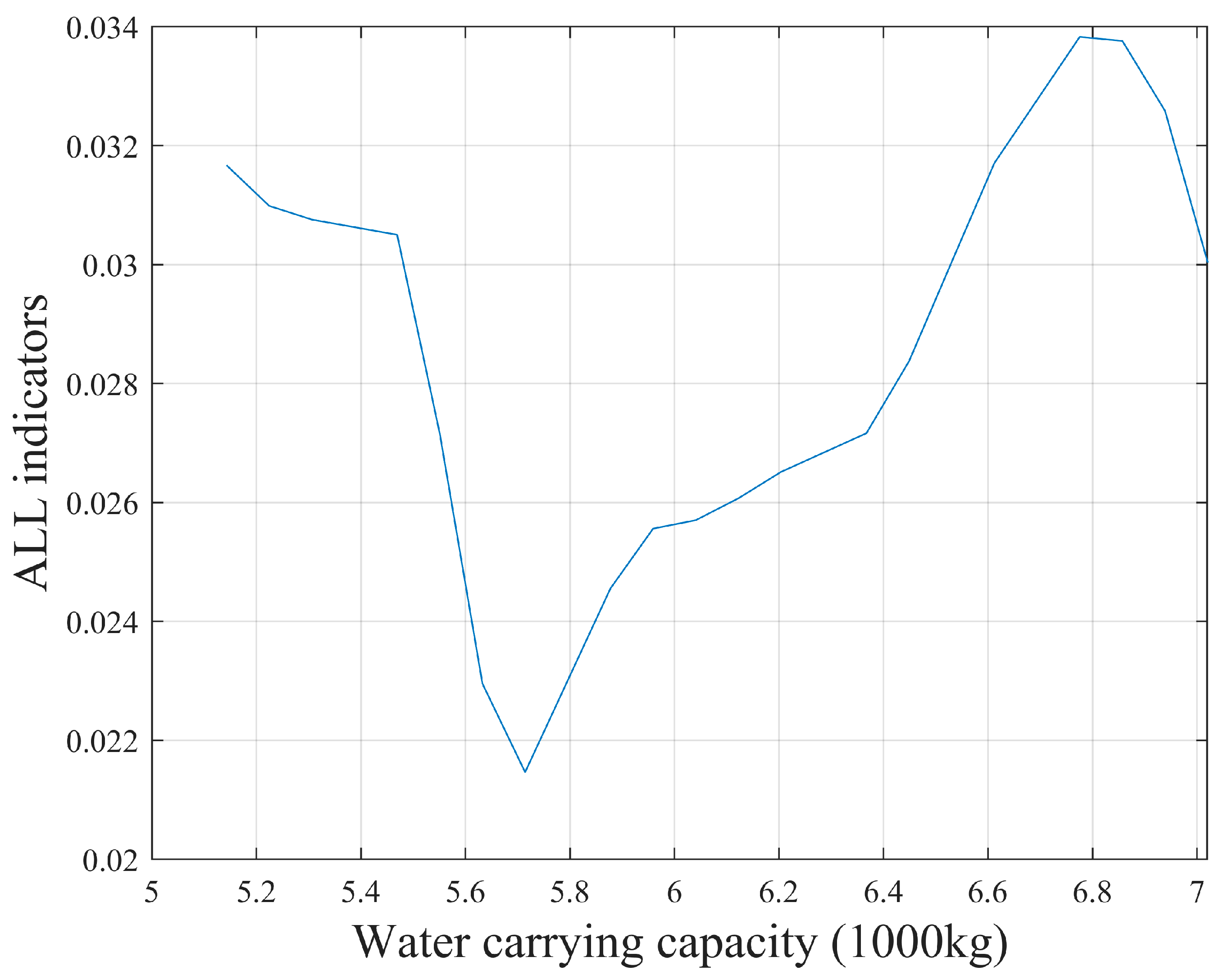
| Environmental Input Information | |||
|---|---|---|---|
| Fire source coordinates | lon: 102.03318 lat: 24.12284 | Fire area optimization range | Width: 2 km length: 3 km |
| Departure airport coordinates | lon: 102.93271 lat: 25.10142 | Water intake point coordinates | lon: 102.89947 lat: 24.56848 |
| Wind | x: 2.5 m/s y: −1.5 m/s z: 0 m/s | ||
| Aircraft input information the amphibious aircraft without specific type | |||
| Aircraft empty weight | 29,300 kg | Fuel quantity | 20,250 L 15,700 kg |
| Max water carrying capacity | 8000 kg | Min turning radius | 600 m |
| Cruising speed | 150 m/s | ||
| Safety Indicators | |||
| 91.95% | 144,600 m | ||
| 203.51 m | 529.72 m | ||
| 38.03 m | 77.25 m | ||
| 27.82 m | 187.61 m | ||
| Effectiveness indicators | |||
| 15 s | 2000 s | ||
| 2965.6 s | 39.07% | ||
| 7712 m2 | 0.778 kg/m2 | ||
| 5496.7 kg/h | 3.6813 kg/L | ||
| Cost indicators | |||
| 362,190 m | 3929.6 s | ||
| 1629.9 L | |||
| Optimized Mission | Manual Mission | Learning Mission | |
|---|---|---|---|
| Mean horizontal threat (m) | 529.724 | 529.345 | 536.611 |
| Mean height threat (m) | 203.507 | 186.736 | 207.612 |
| Effective utilization rate | 0.3907 | 0.0713 | 0.3785 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xue, Y.; Tian, Y.; Liu, H.; Cai, Z. Planning and Evaluation of Water-Dropping Strategy for Fixed-Wing Fire Extinguisher Based on Multi-Resolution Modeling. Aerospace 2024, 11, 929. https://doi.org/10.3390/aerospace11110929
Wang X, Xue Y, Tian Y, Liu H, Cai Z. Planning and Evaluation of Water-Dropping Strategy for Fixed-Wing Fire Extinguisher Based on Multi-Resolution Modeling. Aerospace. 2024; 11(11):929. https://doi.org/10.3390/aerospace11110929
Chicago/Turabian StyleWang, Xiyu, Yuanbo Xue, Yongliang Tian, Hu Liu, and Zhiyong Cai. 2024. "Planning and Evaluation of Water-Dropping Strategy for Fixed-Wing Fire Extinguisher Based on Multi-Resolution Modeling" Aerospace 11, no. 11: 929. https://doi.org/10.3390/aerospace11110929
APA StyleWang, X., Xue, Y., Tian, Y., Liu, H., & Cai, Z. (2024). Planning and Evaluation of Water-Dropping Strategy for Fixed-Wing Fire Extinguisher Based on Multi-Resolution Modeling. Aerospace, 11(11), 929. https://doi.org/10.3390/aerospace11110929






