Three-Dimensional Rapid Orbit Transfer of Diffractive Sail with a Littrow Transmission Grating-Propelled Spacecraft
Abstract
1. Introduction
2. Mathematical Preliminaries and Solar Sail Thrust Model
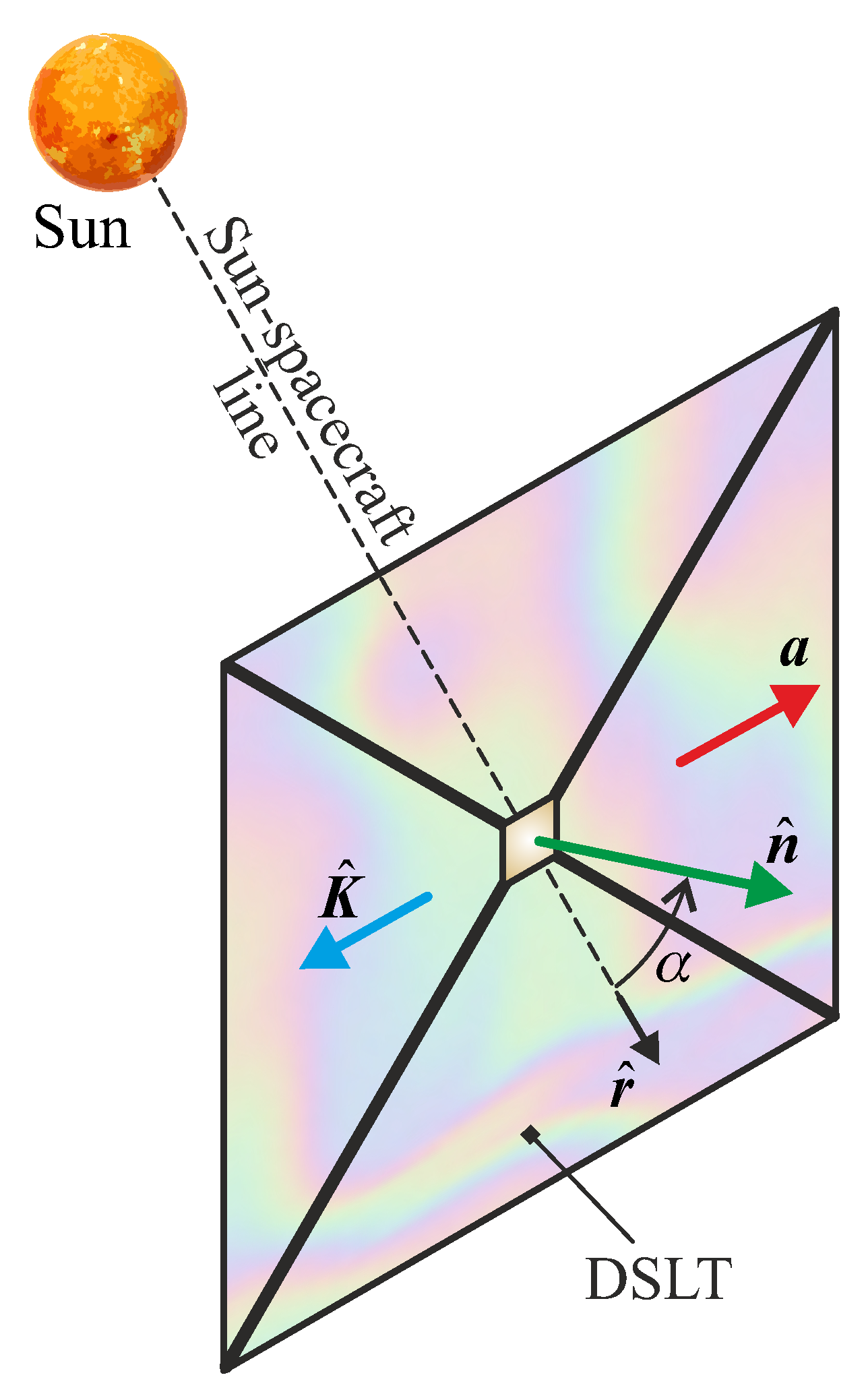
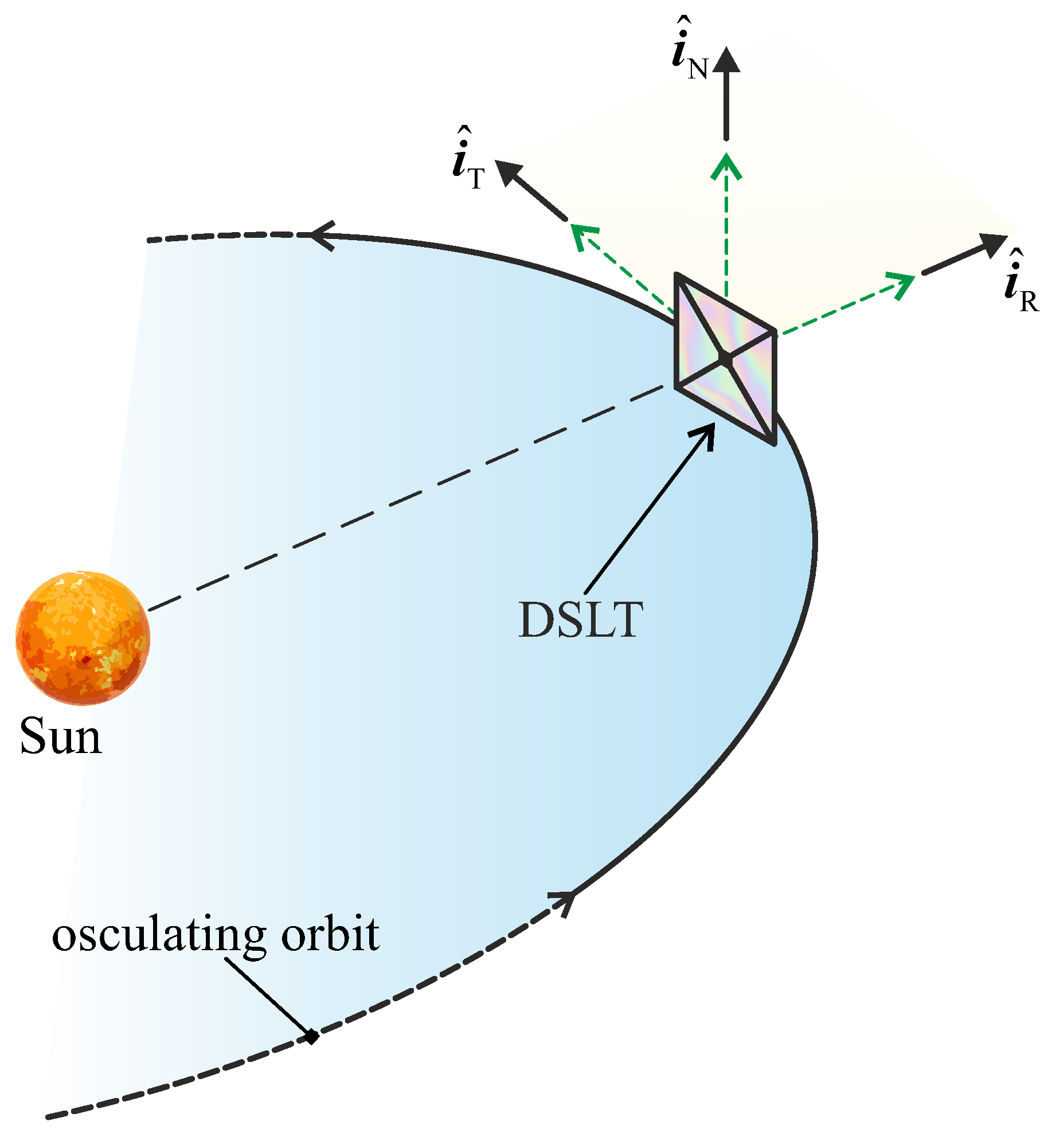
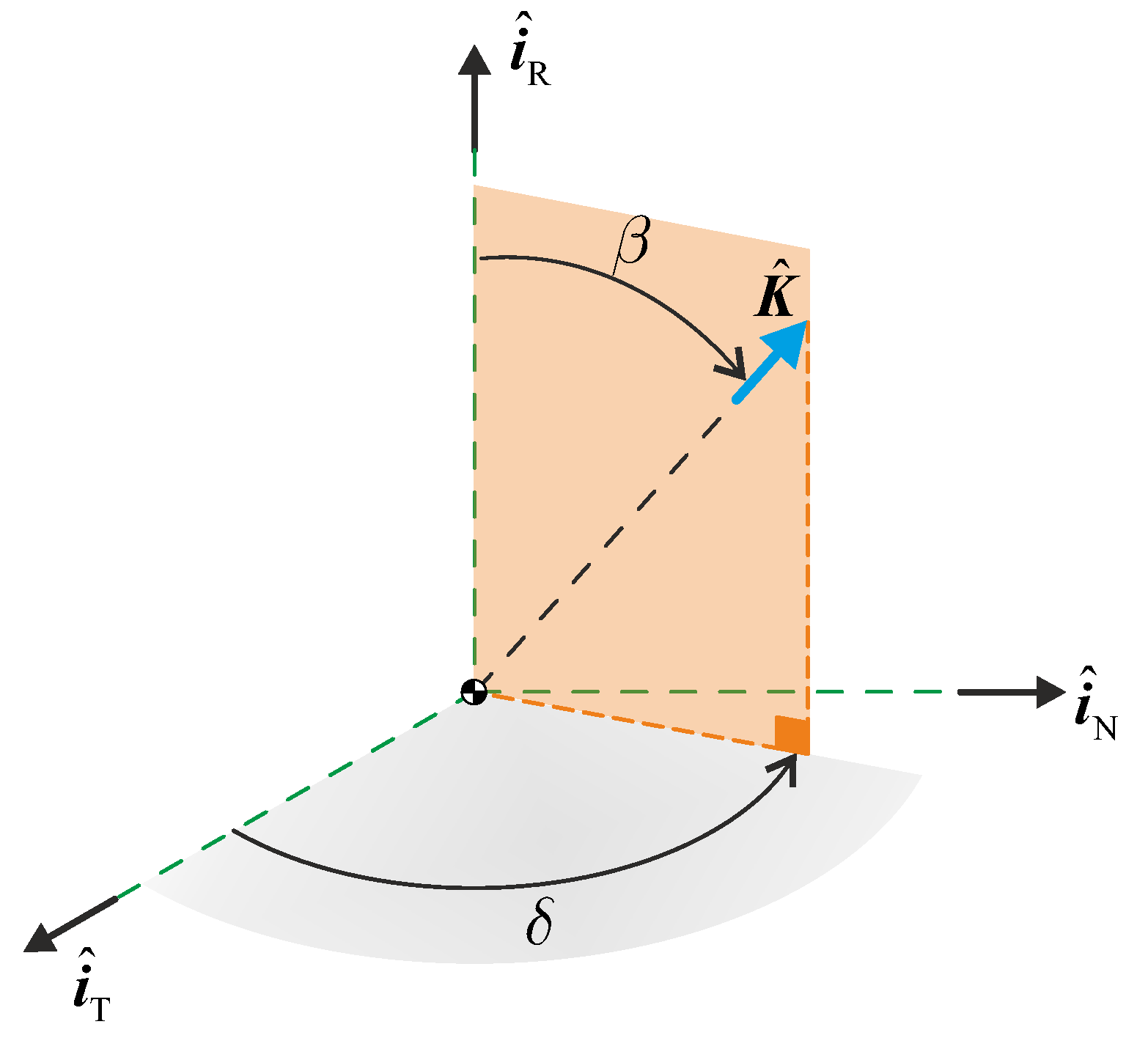
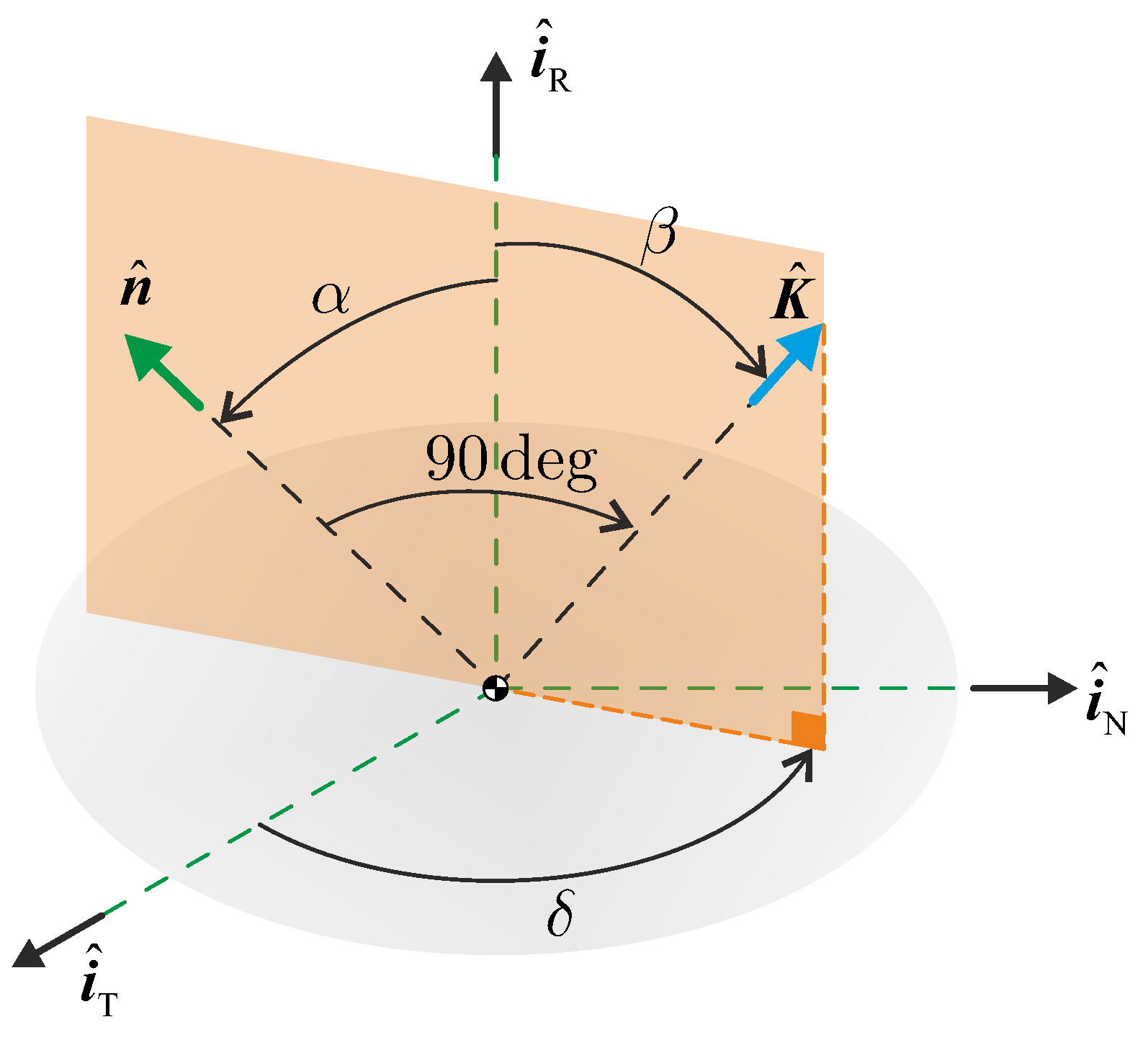
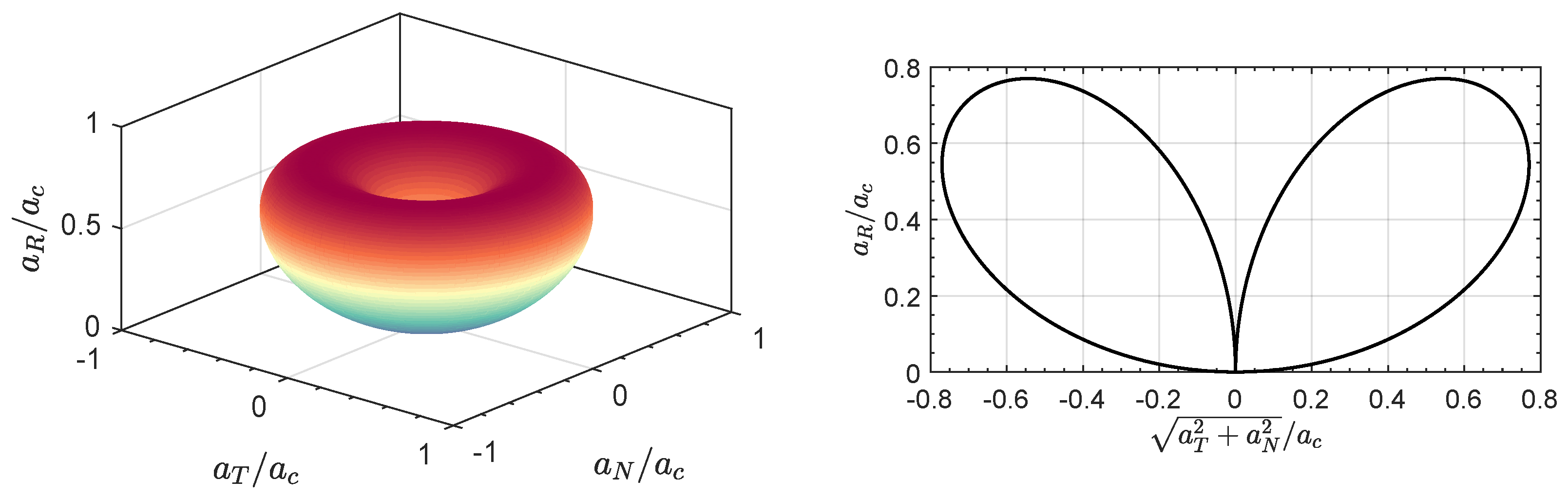
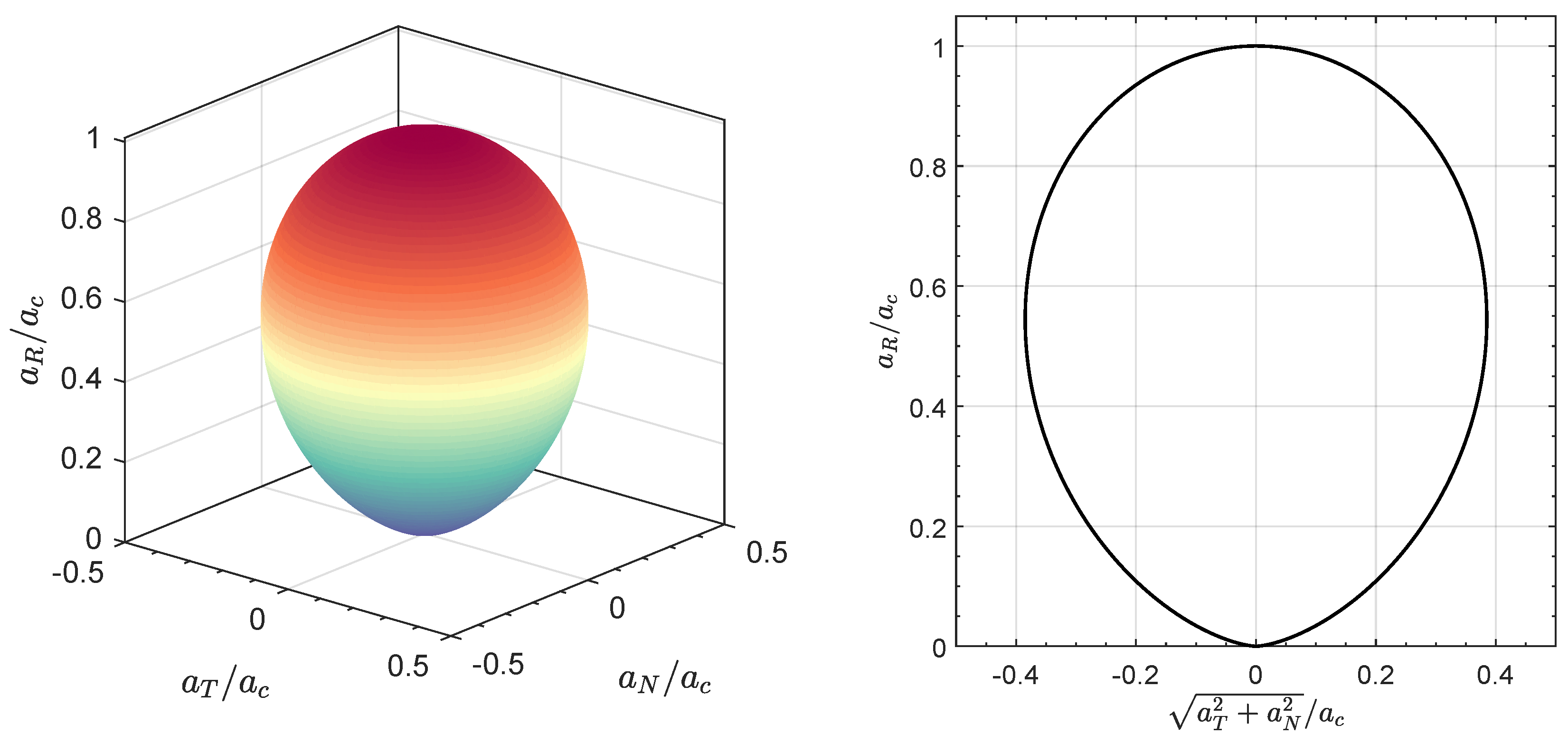
2.1. Simplified DSLT Thrust Model in a Three-Dimensional Heliocentric Scenario
2.2. DSLT-Propelled Spacecraft Dynamics
2.3. Brief Description of the Trajectory Optimization Process
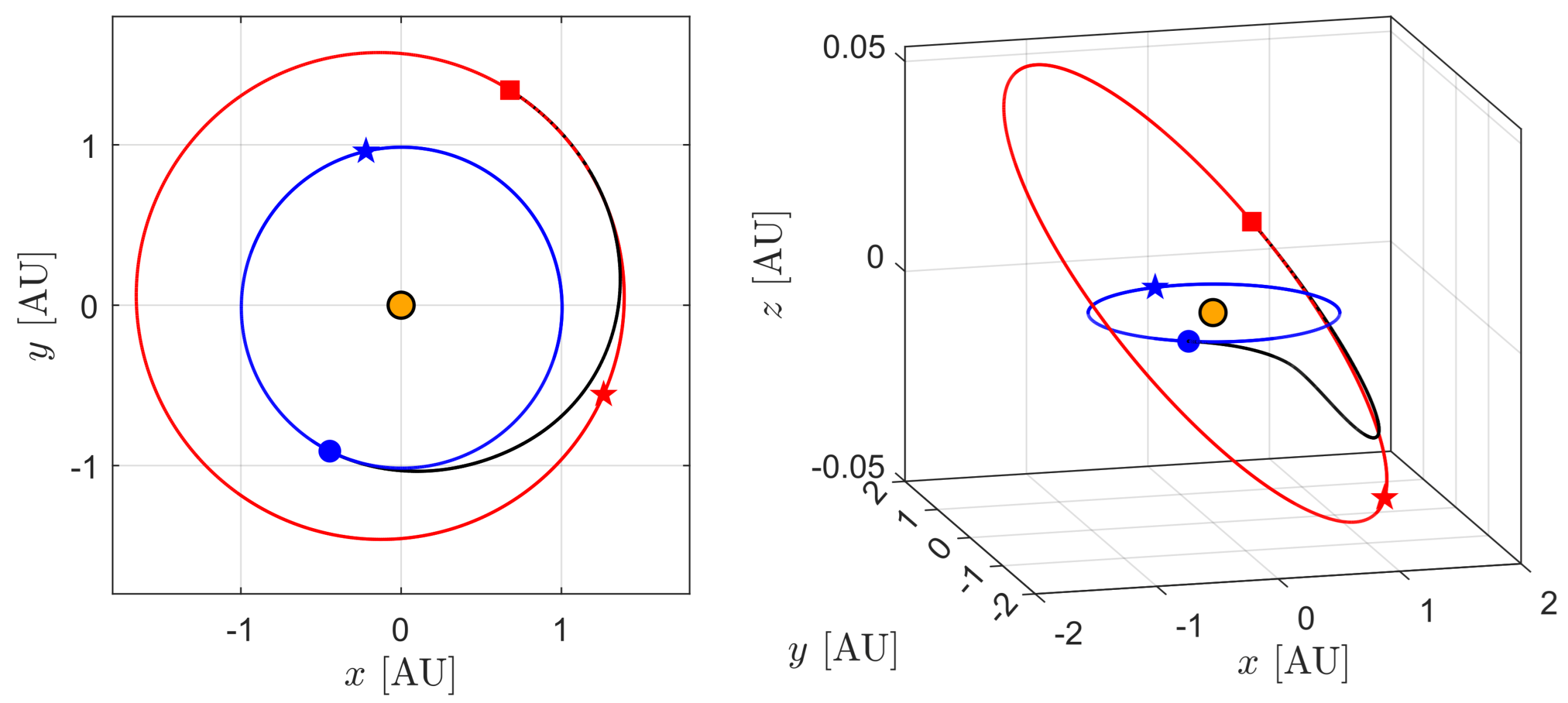
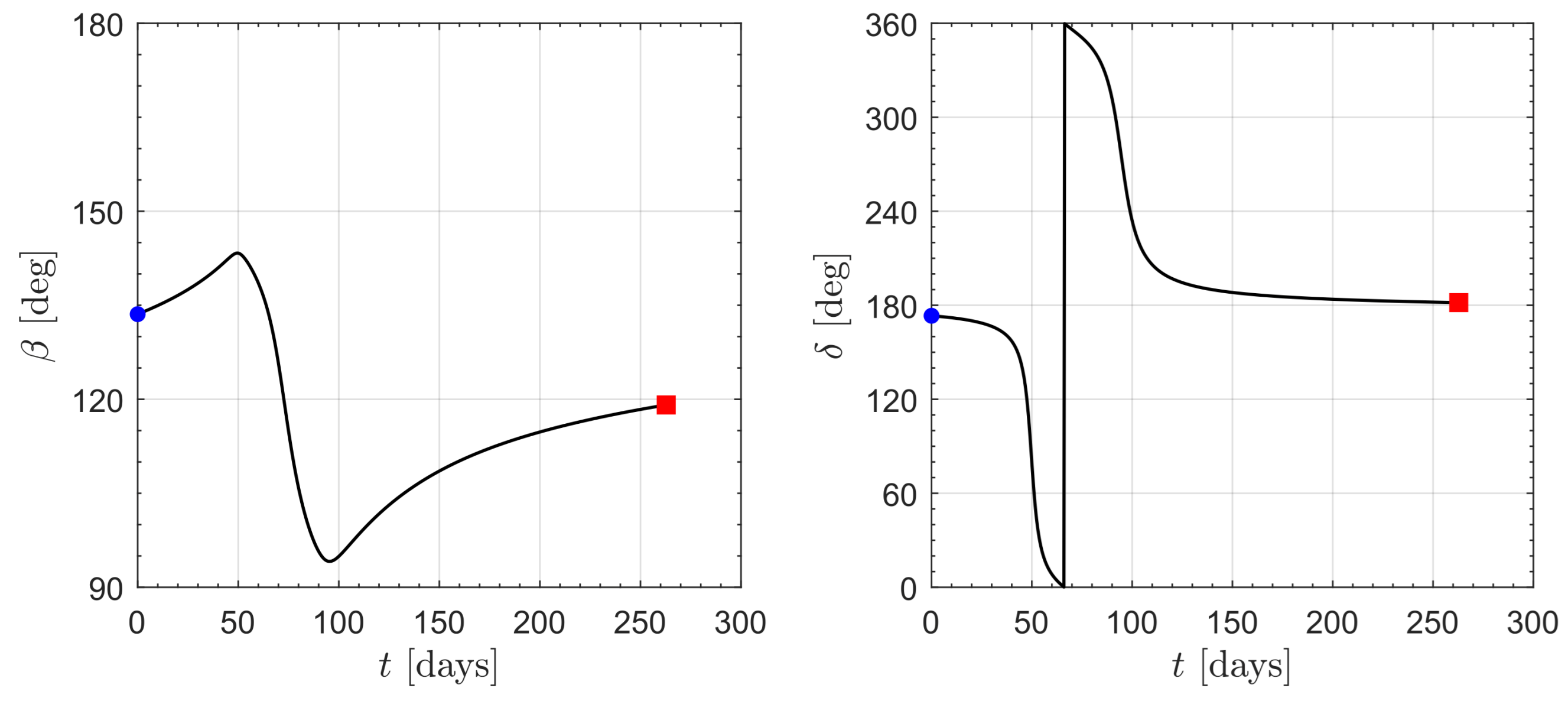
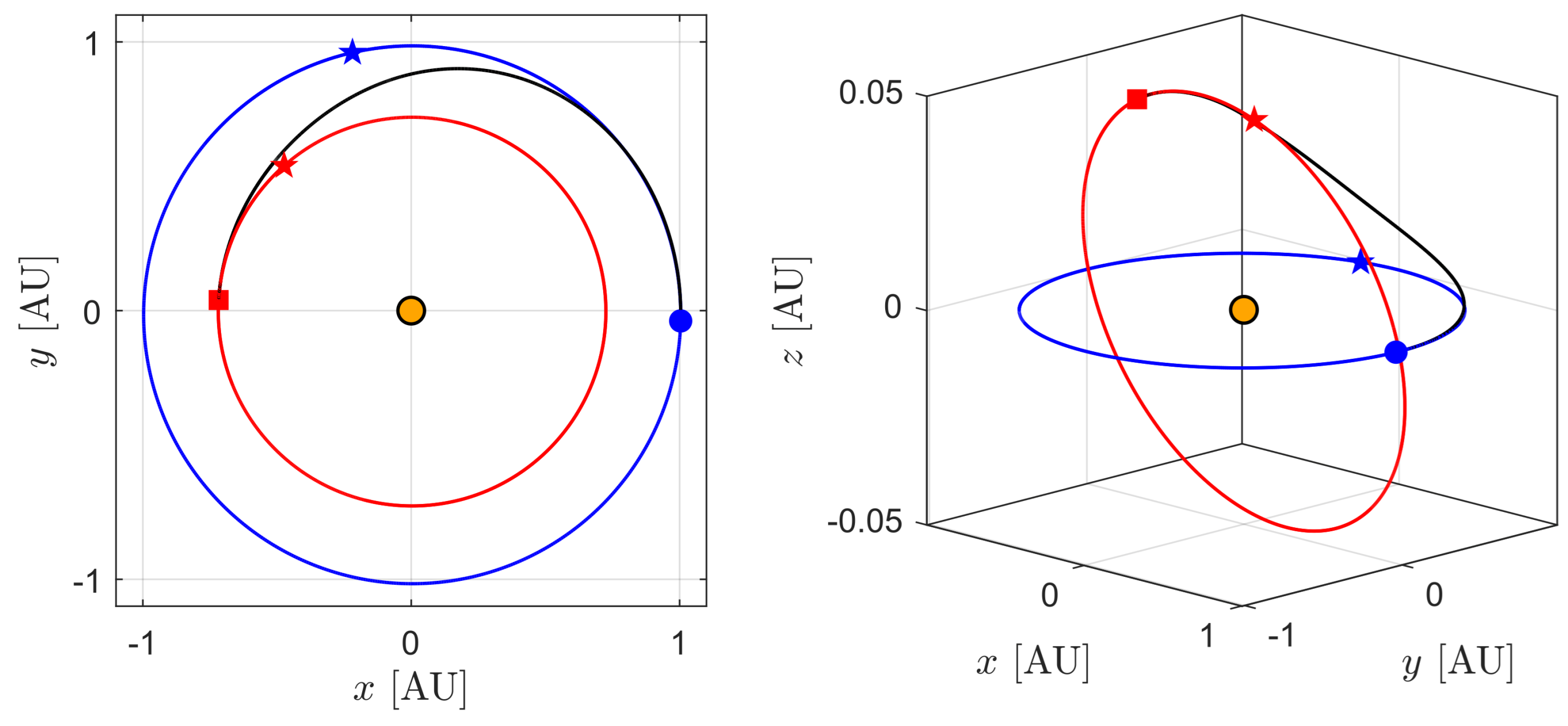
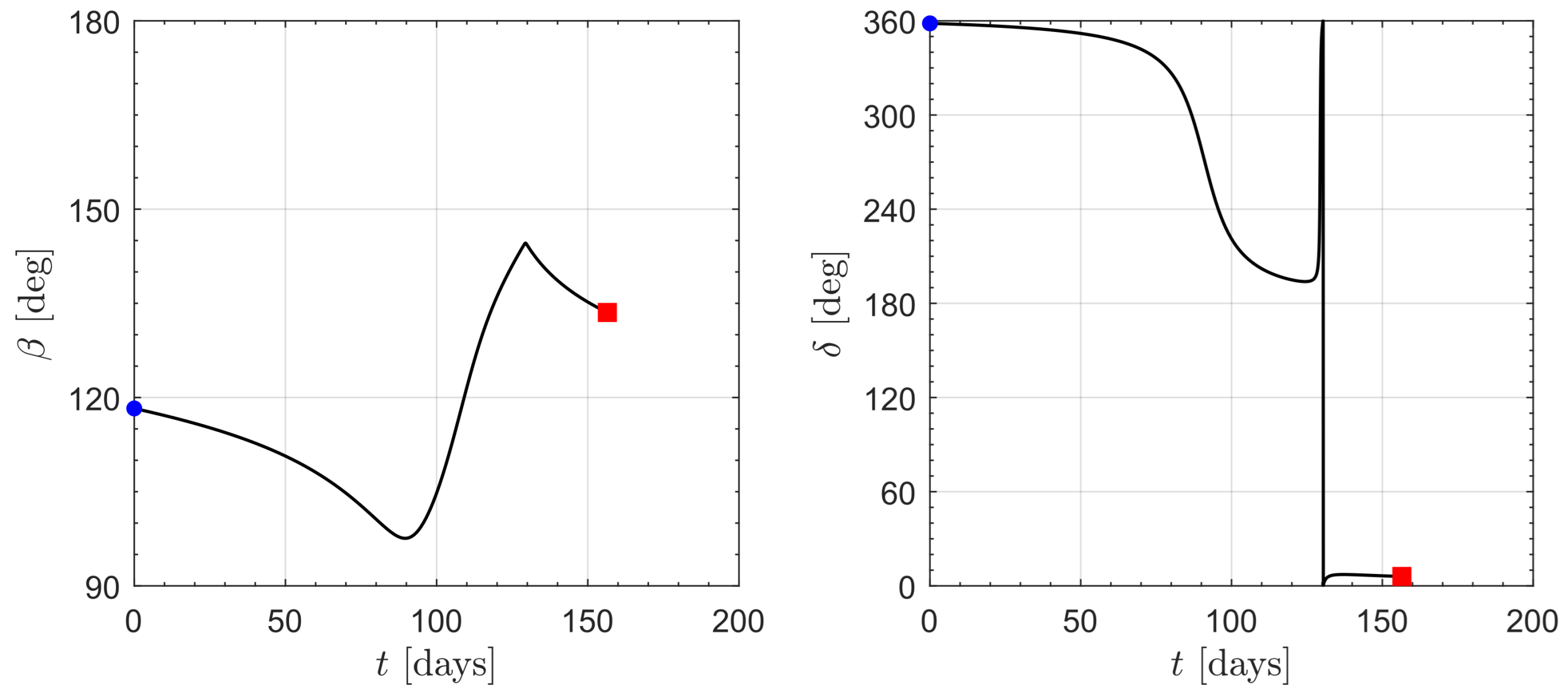
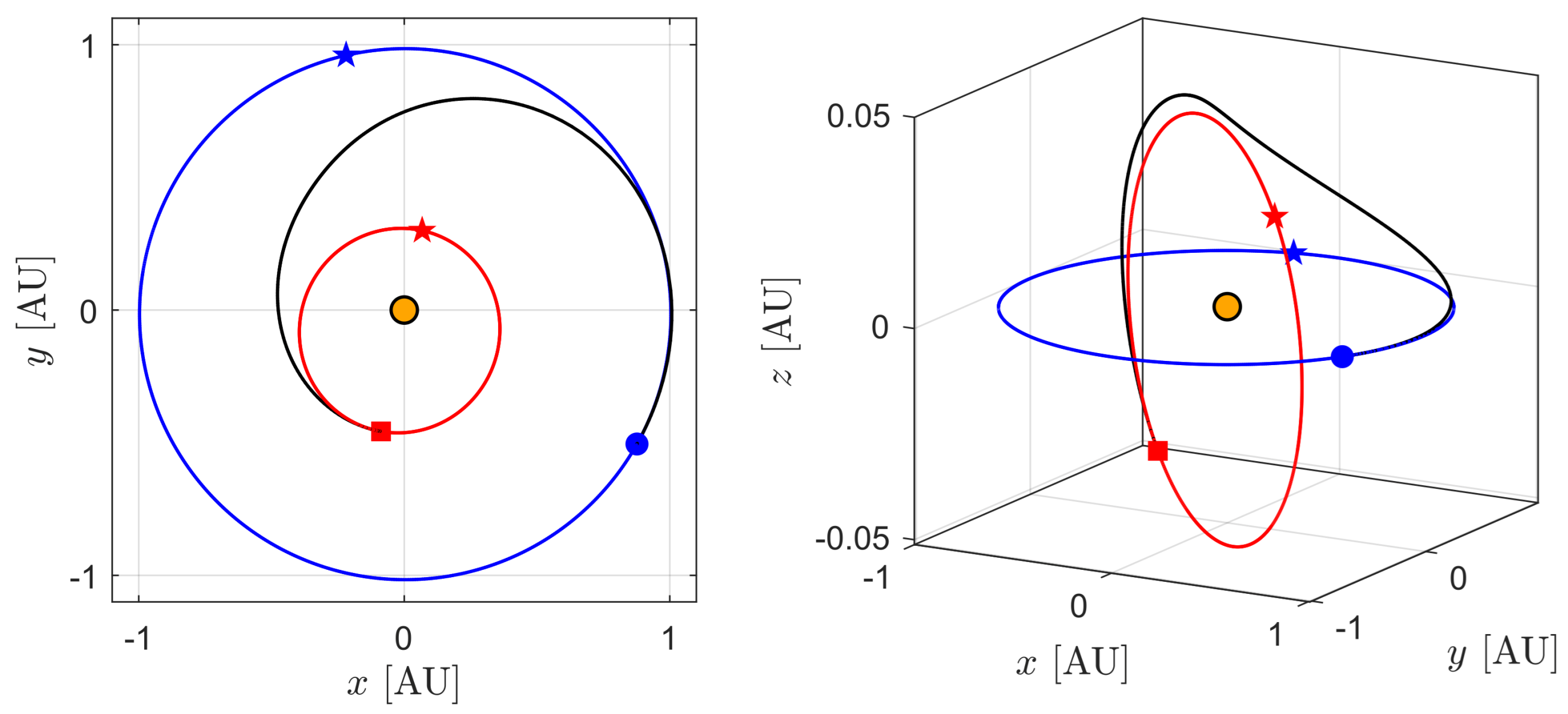
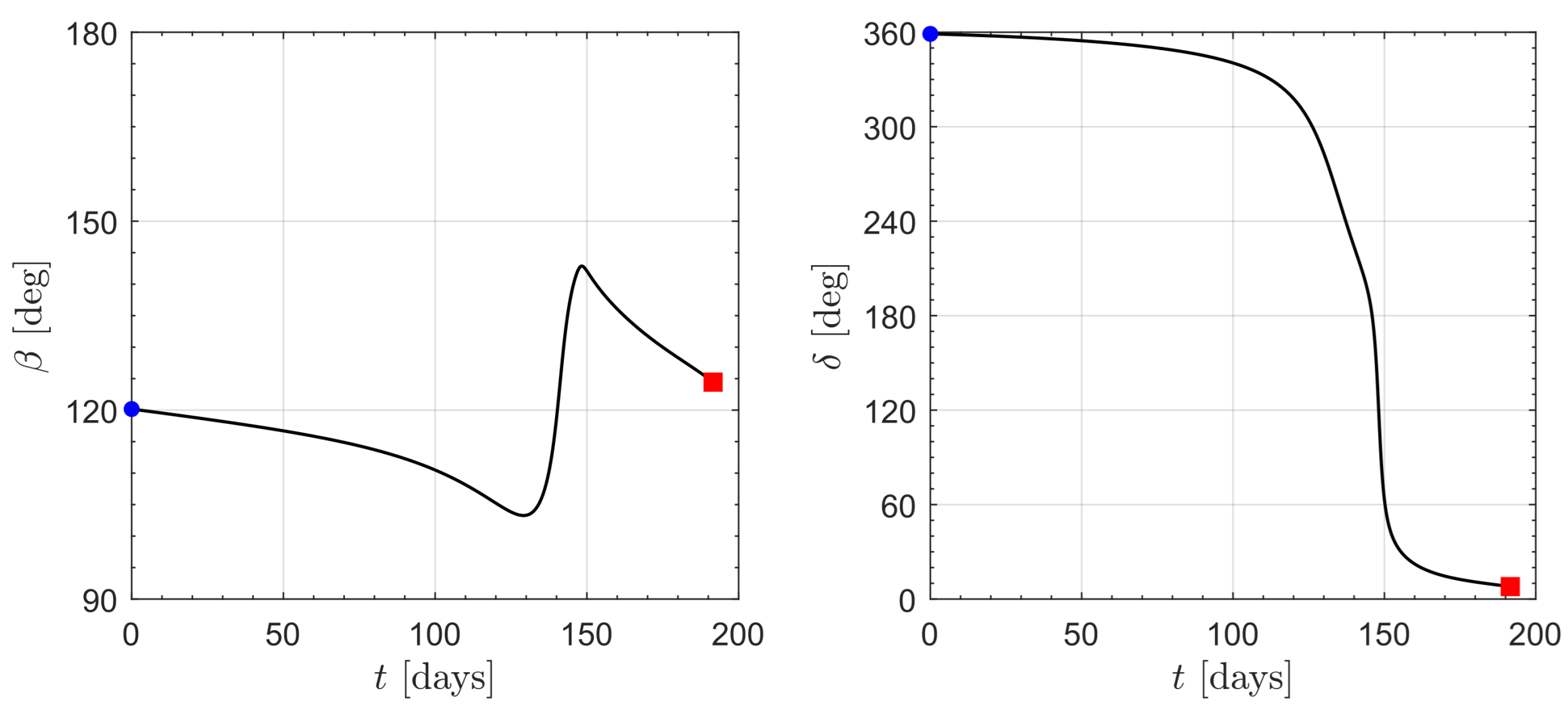
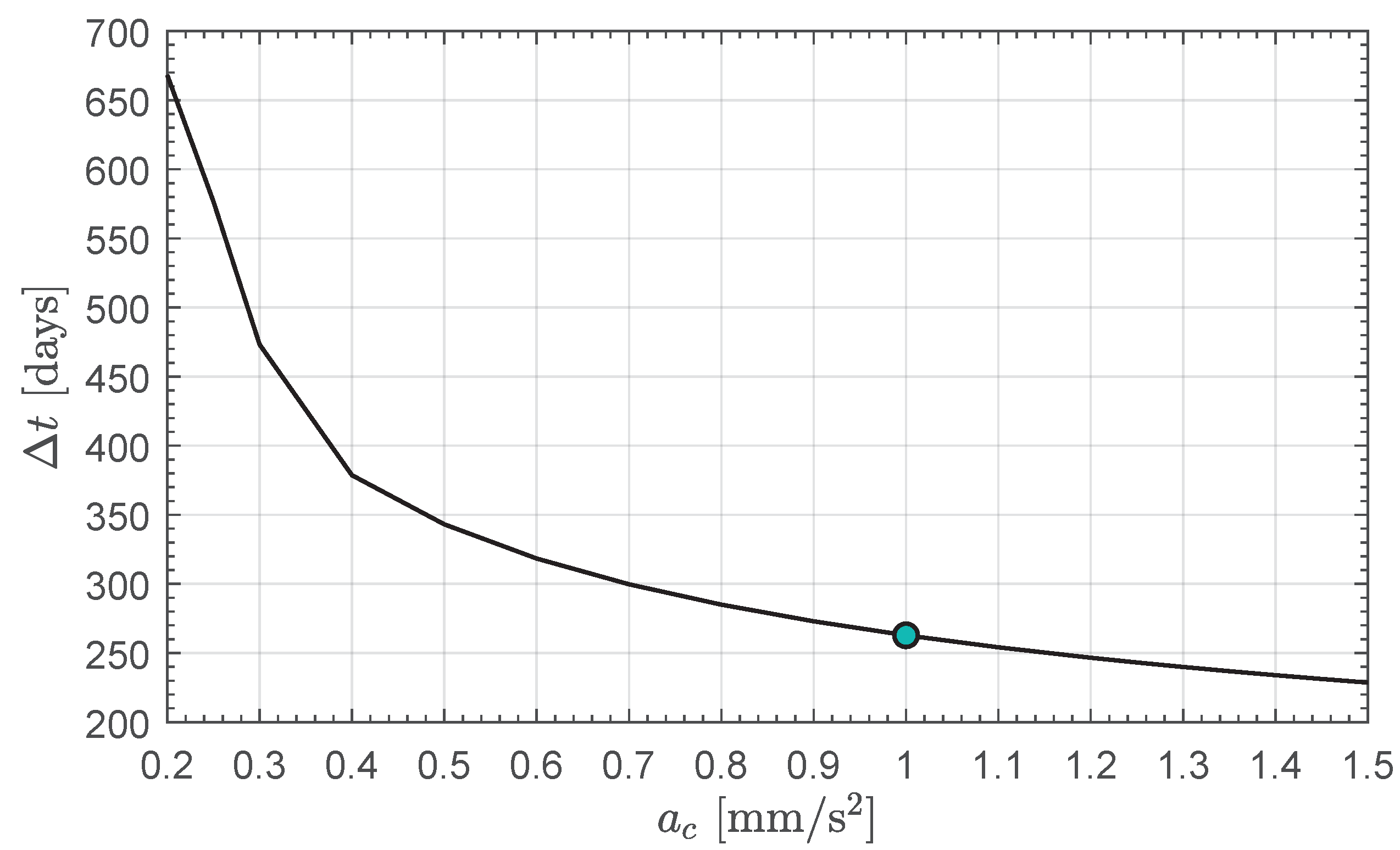
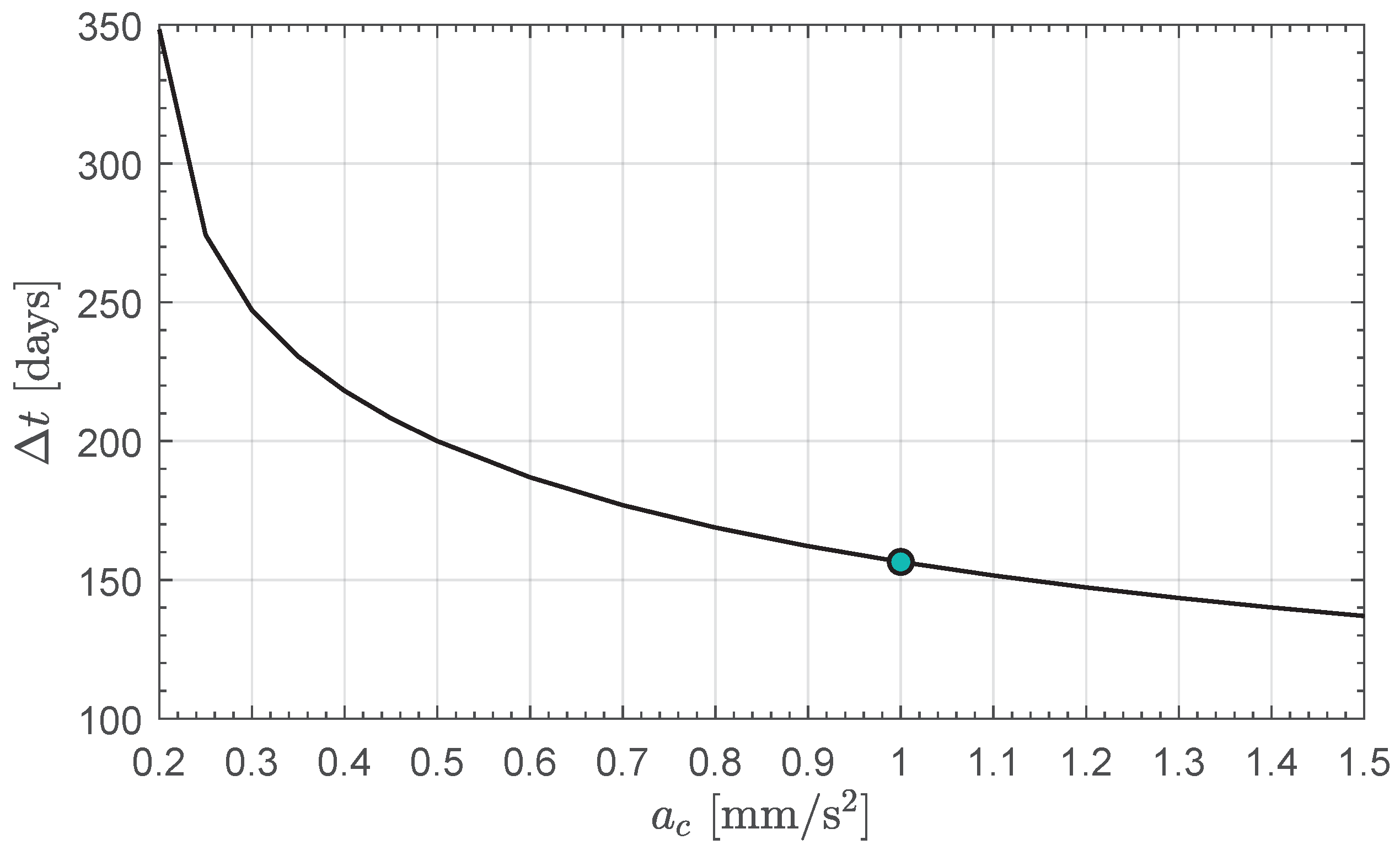
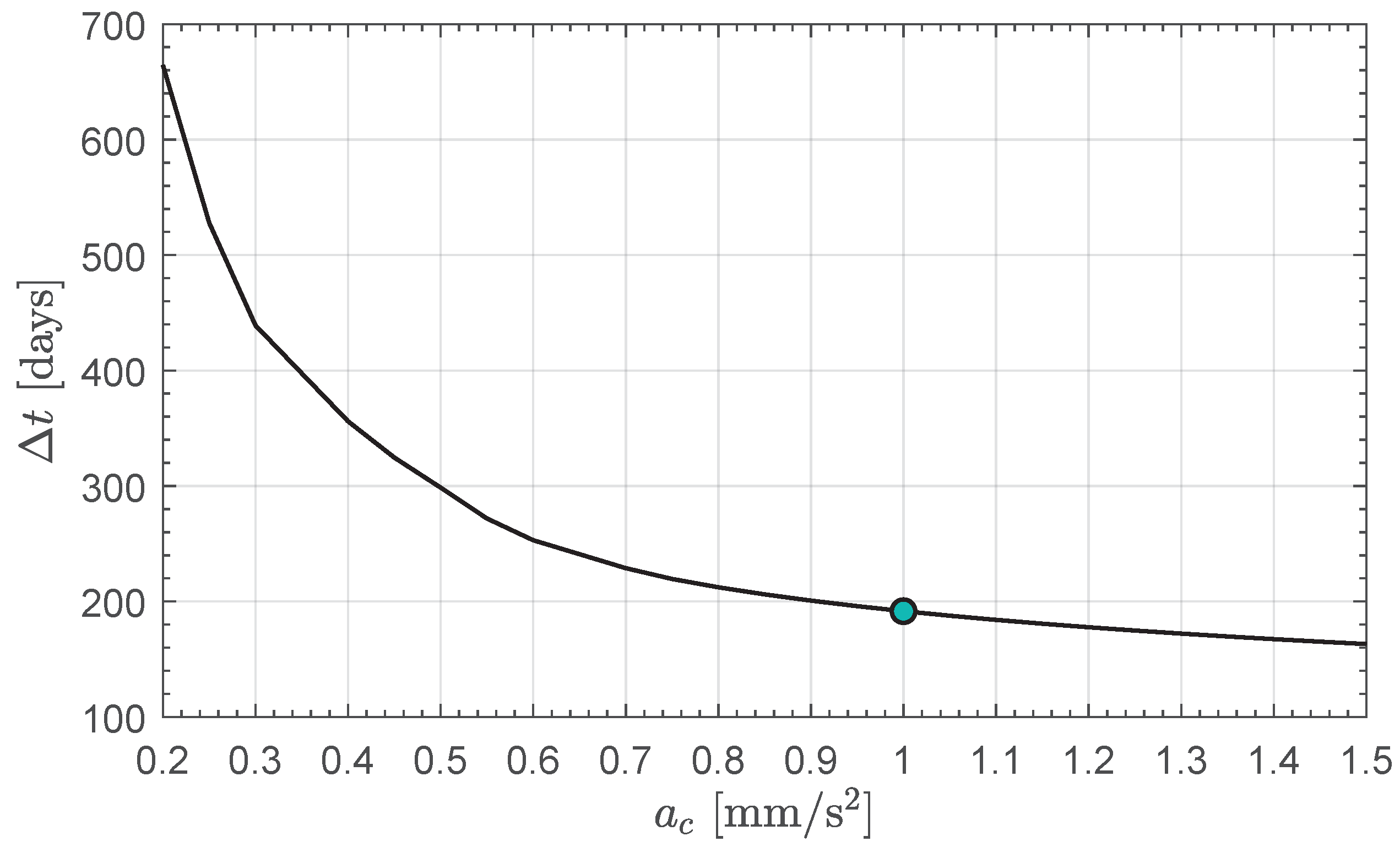
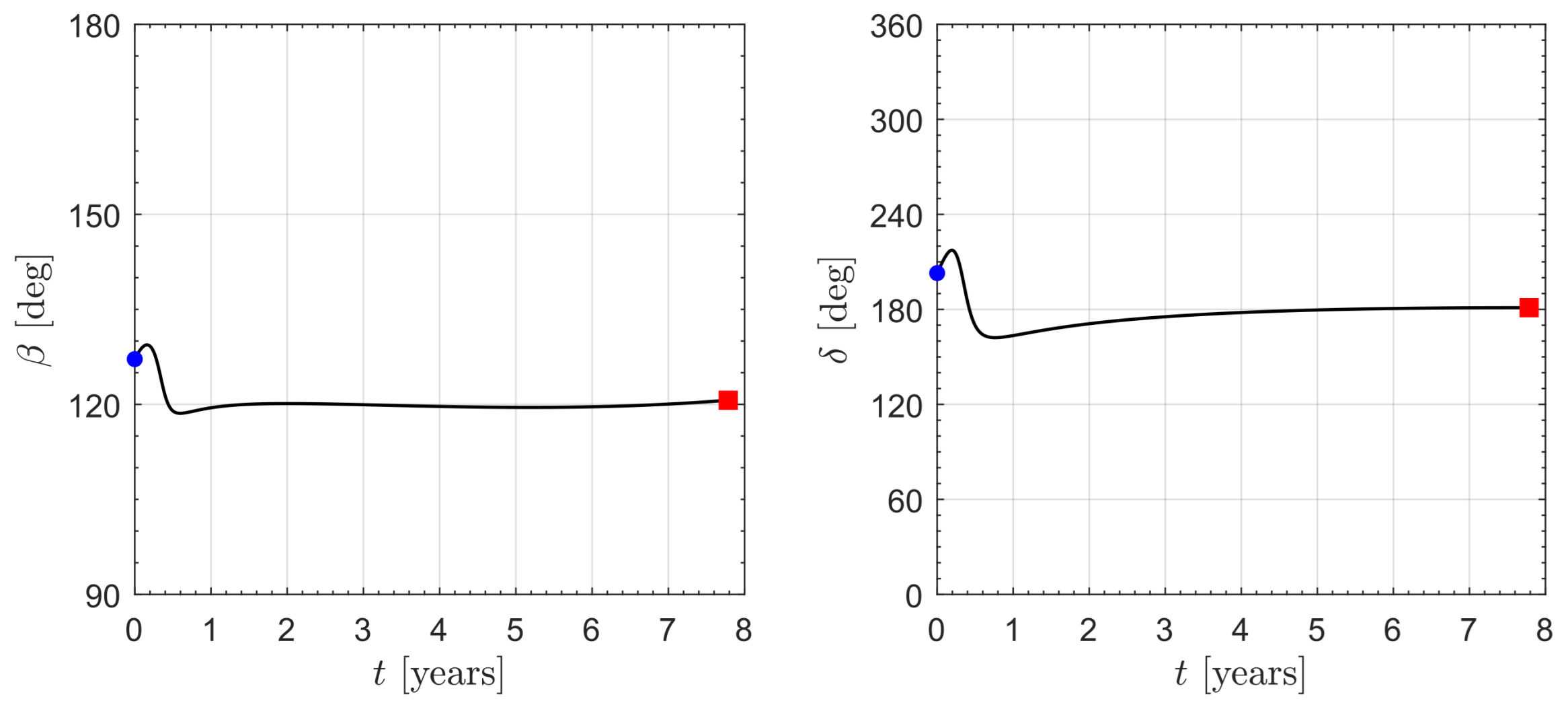
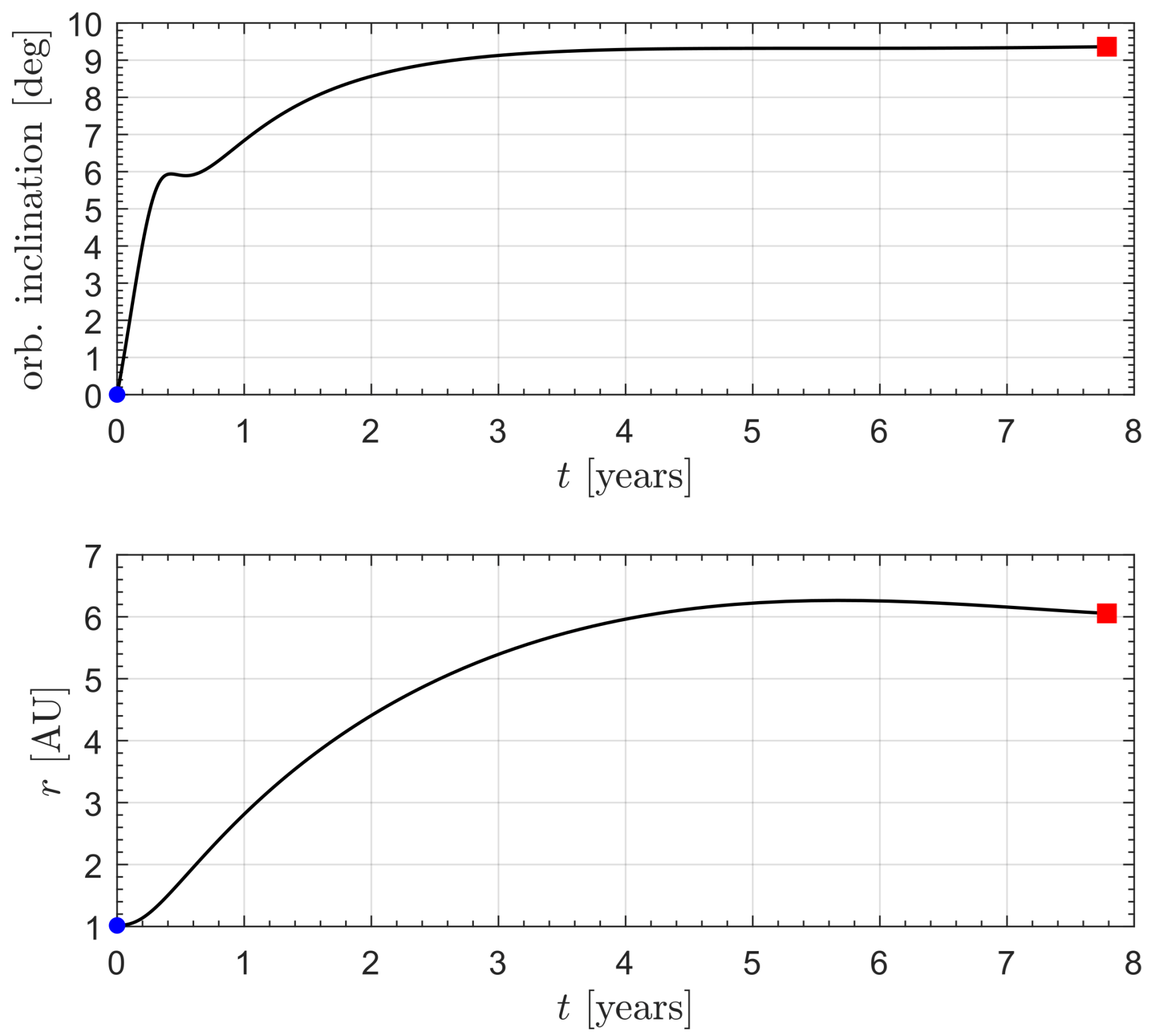
3. Orbital Simulations and Numerical Results
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chandraul, A.; Murari, V.; Kumar, S. A review on dynamic analysis of membrane based space structures. Adv. Space Res. 2024, 74, 740–763. [Google Scholar] [CrossRef]
- Chandra, M.; Kumar, S.; Chattopadhyaya, S.; Chatterjee, S.; Kumar, P. A review on developments of deployable membrane-based reflector antennas. Adv. Space Res. 2021, 68, 3749–3764. [Google Scholar] [CrossRef]
- Rastogi, V.; Upadhyay, S.; Singh, K.S. Self-rigidizable Kapton-SMA conical booms: A comprehensive numerical and experimental study. Adv. Space Res. 2024, 73, 3936–3962. [Google Scholar] [CrossRef]
- Ruggiero, E.J.; Inman, D.J. Gossamer spacecraft: Recent trends in design, analysis, experimentation, and control. J. Spacecr. Rocket. 2006, 43, 10–24. [Google Scholar] [CrossRef]
- Block, J.; Straubel, M.; Wiedemann, M. Ultralight deployable booms for solar sails and other large gossamer structures in space. Acta Astronaut. 2011, 68, 984–992. [Google Scholar] [CrossRef]
- Fernandez, J.M.; Lappas, V.J.; Daton-Lovett, A.J. Completely stripped solar sail concept using bi-stable reeled composite booms. Acta Astronaut. 2011, 69, 78–85. [Google Scholar] [CrossRef]
- Nikolajsen, J.; Kristensen, A.S. Self-deployable drag sail folded nine times. Adv. Space Res. 2021, 68, 4242–4251. [Google Scholar] [CrossRef]
- Fernandez, J.M.; Visagie, L.; Schenk, M.; Stohlman, O.R.; Aglietti, G.S.; Lappas, V.J.; Erb, S. Design and development of a gossamer sail system for deorbiting in low earth orbit. Acta Astronaut. 2014, 103, 204–225. [Google Scholar] [CrossRef]
- Grundmann, J.T.; Bauer, W.; Biele, J.; Boden, R.; Ceriotti, M.; Cordero, F.; Dachwald, B.; Dumont, E.; Grimm, C.D.; Herčík, D.; et al. Capabilities of GOSSAMER-1 derived small spacecraft solar sails carrying MASCOT-derived nanolanders for in-situ surveying of NEAs. Acta Astronaut. 2019, 156, 330–362. [Google Scholar] [CrossRef]
- Dachwald, B. Optimal Solar Sail Trajectories for Missions to the Outer Solar System. J. Guid. Control. Dyn. 2005, 28, 1187–1193. [Google Scholar] [CrossRef]
- Vulpetti, G. Reaching extra-solar-system targets via large post-perihelion lightness-jumping sailcraft. Acta Astronaut. 2011, 68, 636–643. [Google Scholar] [CrossRef]
- Tsuda, Y.; Mori, O.; Funase, R.; Sawada, H.; Yamamoto, T.; Saiki, T.; Endo, T.; Yonekura, K.; Hoshino, H.; Kawaguchi, J. Achievement of IKAROS-Japanese deep space solar sail demonstration mission. Acta Astronaut. 2013, 82, 183–188. [Google Scholar] [CrossRef]
- Mimasu, Y.; Yamaguchi, T.; Nakamiya, M.; Funase, R.; Saiki, T.; Tsuda, Y.; Mori, O.; Kawaguchi, J. Orbit control method for solar sail demonstrator IKAROS via spin rate control. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Girdwood, AL, USA, 31 July–4 August 2012. [Google Scholar]
- Mori, O.; Shirasawa, Y.; Miyazaki, Y.; Sakamoto, H.; Hasome, M.; Okuizumi, N.; Sawada, H.; Furuya, H.; Matunaga, S.; Natori, M.; et al. Deployment and steering dynamics of spinning solar sail “IKAROS”. J. Aerosp. Eng. Sci. Appl. 2012, 4, 79–96. [Google Scholar]
- Funase, R.; Kawaguchi, J.; Mori, O.; Sawada, H.; Tsuda, Y. IKAROS, A solar sail demonstrator and its application to trojan asteroid exploration. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Spencer, D.A.; Johnson, L.; Long, A.C. Solar sailing technology challenges. Aerosp. Sci. Technol. 2019, 93, 105276. [Google Scholar] [CrossRef]
- Lantoine, G.; Cox, A.; Sweetser, T.; Grebow, D.; Whiffen, G.; Garza, D.; Petropoulos, A.; Oguri, K.; Kangas, J.; Kruizinga, G.; et al. Trajectory & maneuver design of the NEA Scout solar sail mission. Acta Astronaut. 2024, 225, 77–98. [Google Scholar] [CrossRef]
- Pezent, J.B.; Sood, R.; Heaton, A. Contingency target assessment, trajectory design, and analysis for NASA’s NEA scout solar sail mission. Adv. Space Res. 2021, 67, 2890–2898. [Google Scholar] [CrossRef]
- Lockett, T.R.; Castillo-Rogez, J.; Johnson, L.; Matus, J.; Lightholder, J.; Marinan, A.; Few, A. Near-Earth Asteroid Scout Flight Mission. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–29. [Google Scholar] [CrossRef]
- Wilkie, W.K.; Fernandez, J.M.; Stohlman, O.R.; Schneider, N.R.; Dean, G.D.; Kang, J.H.; Warren, J.E.; Cook, S.M.; Brown, P.L.; Denkins, T.C.; et al. An overview of the nasa advanced composite solar sail (ACS3) technology demonstration project. In Proceedings of the AIAA Scitech 2021 Forum, Virttual Event, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Mitchell, A.M.; Panicucci, P.; Franzese, V.; Topputo, F.; Linares, R. Improved detection of a Near-Earth Asteroid from an interplanetary CubeSat mission. Acta Astronaut. 2024, 223, 685–692. [Google Scholar] [CrossRef]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer-Praxis Series in Space Science and Technology; Springer: Berlin, Germany, 1999; Chapter 2; pp. 46–54. [Google Scholar] [CrossRef]
- Wright, J.L. Space Sailing; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1992; pp. 223–233. ISBN 978-2881248429. [Google Scholar]
- Firuzi, S.; Song, Y.; Gong, S. Gradient-index solar sail and its optimal orbital control. Aerosp. Sci. Technol. 2021, 119, 107103. [Google Scholar] [CrossRef]
- Firuzi, S.; Gong, S. Refractive sail and its applications in solar sailing. Aerosp. Sci. Technol. 2018, 77, 362–372. [Google Scholar] [CrossRef]
- Swartzlander, G.A., Jr. Radiation pressure on a diffractive sailcraft. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, C25–C30. [Google Scholar] [CrossRef]
- Swartzlander, G.A., Jr. Flying on a rainbow: A solar-driven diffractive sailcraft. JBIS-J. Br. Interplanet. Soc. 2018, 71, 130–132. [Google Scholar]
- Srivastava, P.R.; Swartzlander, G.A., Jr. Optomechanics of a stable diffractive axicon light sail. Eur. Phys. J. Plus 2020, 135, 1–16. [Google Scholar] [CrossRef]
- Dubill, A.L.; Swartzlander, G.A., Jr. Circumnavigating the Sun with diffractive solar sails. Acta Astronaut. 2021, 187, 190–195. [Google Scholar] [CrossRef]
- Chu, Y.; Firuzi, S.; Gong, S. Controllable liquid crystal diffractive sail and its potential applications. Acta Astronaut. 2021, 182, 37–45. [Google Scholar] [CrossRef]
- Lucy Chu, Y.L.; Meem, M.; Srivastava, P.R.; Menon, R.; Swartzlander, G.A., Jr. Parametric control of a diffractive axicon beam rider. Opt. Lett. 2021, 46, 5141–5144. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M.; Niccolai, L. Optimal interplanetary trajectories for Sun-facing ideal diffractive sails. Astrodynamics 2023, 7, 285–299. [Google Scholar] [CrossRef]
- Bassetto, M.; Caruso, A.; Quarta, A.A.; Mengali, G. Optimal steering law of refractive sail. Adv. Space Res. 2021, 67, 2855–2864. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G. Solar sail orbit raising with electro-optically controlled diffractive film. Appl. Sci. 2023, 13, 7078. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Diffractive sail-based displaced orbits for high-latitude environment monitoring. Remote Sens. 2023, 15, 5626. [Google Scholar] [CrossRef]
- Quarta, A.A.; Bassetto, M.; Mengali, G.; Abu Salem, K.; Palaia, G. Optimal guidance laws for diffractive solar sails with Littrow transmission grating. Aerosp. Sci. Technol. 2024, 145, 108860. [Google Scholar] [CrossRef]
- Palmer, C. Diffraction Grating Handbook; MKS Instruments, Inc.: New York, NY, USA, 2020; Chapter 2; pp. 19–38. [Google Scholar]
- Sarid, G.; Volk, K.; Steckloff, J.; Harris, W.; Womack, M.; Woodney, L. 29P/Schwassmann-Wachmann 1, A Centaur in the Gateway to the Jupiter-family Comets. Astrophys. J. Lett. 2019, 883. [Google Scholar] [CrossRef]
- Quarta, A.A.; Abu Salem, K.; Palaia, G. Solar sail transfer trajectory design for comet 29P/Schwassmann-Wachmann 1 rendezvous. Appl. Sci. 2023, 13, 9590. [Google Scholar] [CrossRef]
- McInnes, C.R. Orbits in a Generalized Two-Body Problem. J. Guid. Control. Dyn. 2003, 26, 743–749. [Google Scholar] [CrossRef]
- Dachwald, B.; Seboldt, W.; Macdonald, M.; Mengali, G.; Quarta, A.; McInnes, C.; Rios-Reyes, L.; Scheeres, D.; Wie, B.; Görlich, M.; et al. Potential Solar Sail Degradation Effects on Trajectory and Attitude Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar] [CrossRef]
- Walker, M.J.H.; Ireland, B.; Owens, J. A set of modified equinoctial orbit elements. Celest. Mech. 1985, 36, 409–419. [Google Scholar] [CrossRef]
- Betts, J.T. Very low-thrust trajectory optimization using a direct SQP method. J. Comput. Appl. Math. 2000, 120, 27–40. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control. Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Prussing, J.E. Optimal Spacecraft Trajectories; Oxford University Press: Oxford, UK, 2018; Chapter 4; pp. 32–40. [Google Scholar]
- Prussing, J.E. Spacecraft Trajectory Optimization; Cambridge University Press: Cambridge, UK, 2010; Chapter 2; pp. 16–36. [Google Scholar] [CrossRef]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: Marshalls Creek, PA, USA, 2015; Chapter 2; pp. 127–129. ISBN 9780984357116. [Google Scholar]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Stengel, R.F. Optimal Control and Estimation; Dover Publications, Inc.: Mineola, NY, USA, 1994; pp. 222–254. [Google Scholar]
- Quarta, A.A. Optimal guidance for heliocentric orbit cranking with E-sail-propelled spacecraft. Aerospace 2024, 11, 490. [Google Scholar] [CrossRef]
- Yang, W.Y.; Cao, W.; Kim, J.; Park, K.W.; Park, H.H.; Joung, J.; Ro, J.S.; Hong, C.H.; Im, T. Applied Numerical Methods Using MATLAB®; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; Chapter 6–7; pp. 333–336, 376–378. [Google Scholar]
- Quarta, A.A. Fast initialization of the indirect optimization problem in the solar sail circle-to-circle orbit transfer. Aerosp. Sci. Technol. 2024, 147, 109058. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Shubina, O.; Kleshchonok, V.; Ivanova, O.; Luk’yanyk, I.; Baransky, A. Photometry of comet 29P/Schwassmann–Wachmann 1 in 2012–2019. Icarus 2023, 391, 115340. [Google Scholar] [CrossRef]
- Zhong-Yi, L. Long-term monitoring of comet 29P/Schwassmann–Wachmann from the Lulin Observatory. Publ. Astron. Soc. Jpn. 2023, 75, 462–475. [Google Scholar] [CrossRef]
- Kokhirova, G.; Ivanova, O.; Rakhmatullaeva, F.D.; Buriev, A.; Khamroev, U. Astrometric and photometric observations of comet 29P/Schwassmann-Wachmann 1 at the Sanglokh international astronomical observatory. Planet. Space Sci. 2020, 181, 104794. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarta, A.A. Three-Dimensional Rapid Orbit Transfer of Diffractive Sail with a Littrow Transmission Grating-Propelled Spacecraft. Aerospace 2024, 11, 925. https://doi.org/10.3390/aerospace11110925
Quarta AA. Three-Dimensional Rapid Orbit Transfer of Diffractive Sail with a Littrow Transmission Grating-Propelled Spacecraft. Aerospace. 2024; 11(11):925. https://doi.org/10.3390/aerospace11110925
Chicago/Turabian StyleQuarta, Alessandro A. 2024. "Three-Dimensional Rapid Orbit Transfer of Diffractive Sail with a Littrow Transmission Grating-Propelled Spacecraft" Aerospace 11, no. 11: 925. https://doi.org/10.3390/aerospace11110925
APA StyleQuarta, A. A. (2024). Three-Dimensional Rapid Orbit Transfer of Diffractive Sail with a Littrow Transmission Grating-Propelled Spacecraft. Aerospace, 11(11), 925. https://doi.org/10.3390/aerospace11110925





