Modeling and Transition Flight Control of Distributed Propulsion–Wing VTOL UAV with Induced Wing Configuration

Abstract

The integration of propulsion and wing in distributed propulsion–wing UAVs (DPW UAVs) introduces significant propulsion-aerodynamic coupling, complicating dynamic modeling and flight control. This complexity is heightened by using induced wing surfaces for vertical takeoff and landing, requiring controllers to adapt to configuration changes and disturbances during transition flight. This paper develops a propulsion-aerodynamic coupling model for a medium-sized DPW UAV with induced wings (DPW-IW), enabling real-time aerodynamic performance calculations. Furthermore, a unified flight-control framework is proposed to avoid controller scheduling and switching during flight mode transitions. The proposed control framework employs the time-scale separation principle, divided into an outer loop and an inner loop. The outer loop uses a fuzzy controller to adjust allocation parameters, while the inner loop applies incremental nonlinear dynamic inversion (INDI) and control allocation (INCA) methods, providing robustness to nonlinear changes during flight transitions. Finally, simulations under various conditions demonstrate the controller’s effectiveness in ensuring smooth and robust transitions.

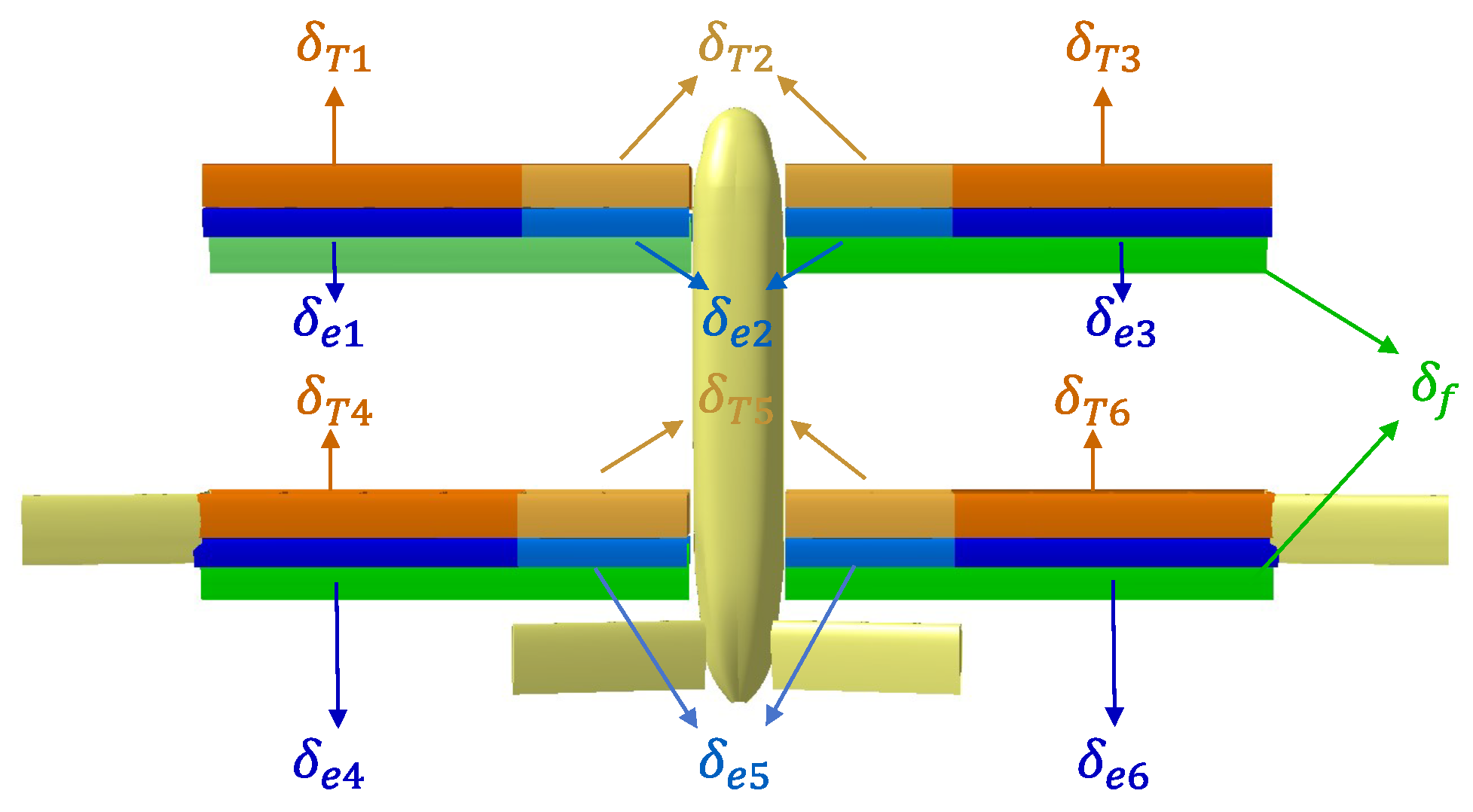
1. Introduction

In recent years, electric propulsion aircraft have gained widespread popularity due to their use of green energy, enabling cleaner and safer flights [1]. With the emergence of urban/intercity air-transportation demands, both NASA [2] and the European Union’s “Clean Sky” program [3] have coincidentally listed distributed electric propulsion vertical takeoff and landing (DEP VTOL) aircraft technology as one of their research directions. Such aircraft typically utilize multiple propellers or ducts as thrust sources, significantly improving propulsive efficiency through propulsion-aerodynamic coupling [4,5,6]. They also utilize thrust vector or distributed propulsion differentials to reduce or eliminate the control surfaces of aircraft, thus increasing flight safety through propulsion redundancy [7,8]. Therefore, compared to traditional electric propulsion VTOL UAVs, DEP VTOL vehicles exhibit higher aerodynamic efficiency, maneuverability, and flight-control robustness.

The existing layout forms of DEP VTOL aircraft can be categorized into three types: forward-wing/aft-wing distributed propulsion, upper-wing/lower-wing distributed propulsion, and distributed propulsion–wing (DPW) configuration [9]. The DPW configuration utilizes a propulsion–wing integrated design, embedding the propulsion units within the wing, thus achieving full integration between distributed propulsion and wing aerodynamic surfaces. This approach greatly facilitates the efficient design of the aircraft.

Additionally, the DPW allows for the placement of the induced wing behind it, facilitating thrust redirection through induced wing deflection [10,11]. Unlike conventional flaps, the induced wing is larger, which not only enables moderate deflection of ducted thrust but also enhances lift during cruise by contributing additional lift. The induced wing thus improves aircraft maneuverability while avoiding the structural complexities associated with propulsion tilting.

However, the distributed propulsion wing with induced wing (DPW-IW) configuration, which integrates induced wing with distributed propulsion wings, engenders pronounced propulsion-aerodynamic coupling [12]. Consequently, the lift and drag of this configuration are concurrently influenced by prevailing freestream conditions, the magnitude of thrust, and the deflection angle of the induced wing. It is difficult to use traditional aircraft modeling methods that only consider changes in lift and drag coefficients with respect to the angle of attack. Additionally, as VTOL aircraft include a hovering mode, developing a unified dynamic model for the entire flight process cannot rely solely on aerodynamic coefficient modeling. Moreover, the coupling characteristic poses formidable challenges to flight control. During transition flight, not only do fluctuations in flight velocity affect the aerodynamic performance of the aircraft, but the propulsion-aerodynamic coupling also introduces additional uncertainties. Coupled with disturbances from the external environment during transition flight, the controller needs to exhibit robustness to achieve a safe and stable flight.

Regarding the dynamic modeling issues of propulsion-aerodynamic coupling, current research primarily focuses on experimental [13,14] and numerical simulation work [15,16,17]. These studies indicate that VTOL aircraft with distributed propulsion wing-induced wing configurations exhibit significant propulsion-aerodynamic coupling effects [18]. Jois [19] conducted quasi-two-dimensional wind tunnel experiments using an aerodynamic propulsion airfoil model, collecting surface pressure data, total lift, drag, and pitching moment performance, as well as individual fan thrust data. Zhao [20] investigated the aerodynamic characteristics of a typical blended wing body (BWB) aircraft equipped with a distributed propulsion system. The study employed experimental and numerical simulation methods to analyze the stall behavior of the aircraft at high angles of attack. However, traditional engineering experience-based aerodynamic analysis methods often struggle to fully capture the coupling characteristics. Numerical simulation methods have limited computational capacity and slow calculation speeds, which cannot meet the real-time solving requirements of dynamic model analysis and flight-control system design. Therefore, it is necessary to research modeling methods for the DEP-IW configuration.

Control methods for vertical takeoff and landing (VTOL) UAVs can be categorized into two types: scheduled control approaches and unified control approaches [21]. Controller switching or scheduling policies need to be designed for scheduled control approaches to blend different controllers [22,23,24]. The limited number of linearization points restricts the controller’s stability region. Additionally, rapid changes in scheduling parameters may affect the stability of the system. Unified control approaches [25,26] are deployed throughout the entire flight envelope using a single controller, often employing adaptive or nonlinear control methods to handle nonlinear dynamics and cover the entire flight envelope. Unified controllers typically employ either nonlinear model predictive control (NMPC) [27] or incremental nonlinear dynamic inversion (INDI) [28]. NMPC transforms the control problem into an optimization problem and calculates the optimal solution in real time. However, NMPC requires significant computational resources [21], leading many researchers to favor the INDI method in practical applications.

The incremental nonlinear dynamic inversion (INDI) method is an improved form of the nonlinear dynamic inversion (NDI) method, which effectively overcomes the drawback of the NDI method relying on accurate system models and has been deployed in various types of aircraft [29,30,31]. INDI utilizes incremental control equations with acceleration as control feedback, enabling compensation for system model uncertainties and external disturbances, and possesses the capability to handle nonlinearity and input non-affine configurations. Zhu [32] extensively discussed INDI control under unknown disturbances, defining attitude rate controllers and velocity controllers based on this method. Zhang [33] employed a unified control methodology and incorporated incremental attitude commands as virtual controls into the control allocation problem to avoid separate controller modes for hover and forward flight. However, this approach still involves a mixture of different algebraic control allocation objectives representing heuristic methods and restricting control authority for various flight modes. Further research by Lombaerts [34] proposed a transitional aircraft with INDI control, where control allocation weights or parameters are arranged based on flight mode.

The INDI control method typically provides virtual control forces and moments, which then need to be computed by control allocation to obtain the actual control inputs for the actuators. Common control allocation methods can be classified into linear control allocation methods and nonlinear control allocation methods [35]. Linear models fail to capture interactions between control effectors and struggle to describe the nonlinear characteristics of individual actuators [36]. For aircraft with DPW-IW configurations, the significant coupling between propulsion and aerodynamic surfaces necessitates a unified consideration of both power and aerodynamic control surfaces. Although nonlinear control allocation methods can effectively account for various nonlinear characteristics of actuators, these methods have high computational requirements and are difficult to run in real time [37].

In the INDI control framework, control allocation must be performed incrementally. To address this, an incremental control allocation (INCA) method is proposed in [37], which takes incremental pseudo-control commands and control effectiveness as inputs to compute the corresponding incremental control inputs. This approach efficiently handles nonlinearities and supports real-time computation due to the linearity of the incremental allocation problem. Consequently, it reduces the dependency of nonlinear flight-control systems on models, making them more robust against model uncertainties. The key to this method lies in its incremental operation, which allows the use of typical linear control allocation algorithms to solve nonlinear control allocation problems. These algorithms are computationally efficient enough to achieve real-time execution. Moreover, unlike most typical control allocation algorithms, INCA utilizes information about the current positions of the actuators. These actuators are dynamically adjusted in small increments to their optimal positions [38,39].

The main contributions of this paper are summarized as follows: (a) A coupled model considering aerodynamic propulsion coupling characteristics, meeting real-time computational requirements for dynamic simulation, and applicable within the entire flight envelope, is proposed in this paper to address the dynamic modeling and control issues of aircraft with DPW-IW configurations. (b) A cascaded control approach has been designed, integrating an incremental nonlinear dynamic inversion (INDI) control method, facilitating seamless transitions between different flight modes. (c) To address the monotonic nonlinear characteristics and coupled nonlinear characteristics of actuators during modal flight, an incremental control allocation method (INCA) is employed, facilitating the incremental acquisition of actuator outputs and enhancing control allocation performance.

This paper is organized as follows: In Section 2, a dynamics model of the aircraft with DPW-IW configuration is developed. It employs a component-based modeling approach to establish unit models for the ducted propulsion system, DPW-IW unit, and aerodynamic surfaces. In Section 3, a unified controller is designed, including an inner-loop controller based on the INDI control method and an outer-loop controller for the velocity control, as well as the development of a multi-level control allocation method. Section 4 presents numeral simulations to verify the proposed flight-control law. It compares the performance of the INDI control method with the PID control method under three conditions: transition flight with no disturbances, transition flight with disturbances in rotational inertia parameters and model parameters, and transition flight under propulsion fault. Finally, the conclusions are summarized in Section 5.

2. Flight Dynamics Model

In this section, the dynamic model of a vertical takeoff and landing unmanned aerial vehicle (VTOL UAV) with a DEP-IW configuration is established. The focus of the dynamic model lies in establishing a coupled model that considers propulsion-aerodynamic coupling characteristics, meets real-time computation requirements for simulation, and is applicable across the entire flight envelope. Therefore, this section first introduces the configuration and control actuators of the UAV in different flight modes. And then derives the overall dynamic model and the dynamic models of each component, and finally validates the model.

2.1. Distributed Propulsion–Wing Vehicle Platform Description

The three-dimensional (3-D) layout of the developed VTOL UAV with the DEP-IW configuration is shown in Figure 1, and the main aircraft parameters are defined in

Table 1. Main Parameters of UAV.

Parameter	Value	Parameter	Value
Wingspan (b/m)	5.2	Mean Aerodynamic Chord (c/m)	0.385
Reference area (s/m2)	2	Mass (m/kg)	100
$I_x$ (kg/m2)	40.56	$I_y$ (kg/m2)	44.46
$I_z$ (kg/m2)	69.68	$I_{xz}$ (kg/m2)	12.35

. The vehicle adopts a tandem-wing layout, with 12 DEP-IW units arranged on each of the front and rear wings. Each unit consists of a duct embedded in the middle of the wing and an induced wing located at the outlet of the duct. The inlet ducts of each unit merge with the upper and lower surfaces of the wing to form a unique configuration of the propulsion wing. Additionally, there is a small winglet on the trailing edge of the rear wing to improve the pitching moment characteristics of the aircraft. In order to simplify the design of the control allocation approach, the 24 units are divided into six groups, with each group containing four units, and they are numbered accordingly as shown in Figure 2.

Figure 1 depicts the changes in aircraft configuration under different flight modes. As shown in Figure 1a, in hover mode, the aircraft maintains a certain pitch angle and achieves thrust-drag balance by deflecting the thrust direction through the deflection of the induced wing. Pitch control is achieved through differential throttle control between the front and rear DEP-IW units, while roll control is achieved through differential control between propulsion units 1 and 3 and units 4 and 6. Although the thrust direction of the inlet fans is not completely vertical upward in hover mode, the change in thrust direction caused by the induced wing surfaces only affects the lift of the aircraft, resulting in minimal additional thrust.

In the cruise mode, the induced wing surfaces do not deflect, thus the thrust direction of the DEP-IW unit also remains unchanged. The aircraft transforms into a conventional fixed-wing UAV with a tandem-wing layout. In this mode, pitch control can utilize both elevator and throttle differential, roll control is achieved through control surfaces, and yaw control is implemented through the differential throttle of wingtip units.

In the most challenging transition flight mode, the UAV smoothly accelerates to cruise speed and completes the transition flight by concurrently reducing the deflection angle of the induced wing to provide greater thrust and decreasing the pitch angle to minimize aircraft drag. Simultaneously, the primary source of lift for the aircraft shifts from deflected thrust to aerodynamic lift. During transition flight, the control logic of the aircraft also gradually changes: pitch control transitions to using both throttle differential and control surface differential, roll control shifts from throttle differential to control surface control, and yaw control gradually transitions from control surface control to throttle differential control. The control logic for different flight phases is summarized in

Table 2. Manipulation allocation.

Channels	Hover Mode	Cruise Mode
Pitch	${\delta }_{T1}$, ${\delta }_{T2}$, ${\delta }_{T3}$, ${\delta }_{T4}$, ${\delta }_{T5}$, ${\delta }_{T6}$	${\delta }_{T1}$, ${\delta }_{T2}$, ${\delta }_{T3}$, ${\delta }_{T4}$, ${\delta }_{T5}$, ${\delta }_{T6}$, ${\delta }_{e1}$, ${\delta }_{e2}$, ${\delta }_{e3}$, ${\delta }_{e4}$, ${\delta }_{e5}$, ${\delta }_{e6}$
Roll	${\delta }_{T1}$, ${\delta }_{T3}$, ${\delta }_{T4}$, ${\delta }_{T6}$	${\delta }_{e1}$, ${\delta }_{e3}$, ${\delta }_{e4}$, ${\delta }_{e6}$
Yaw	${\delta }_{e1}$, ${\delta }_{e3}$, ${\delta }_{e4}$, ${\delta }_{e6}$,	${\delta }_{T1}$, ${\delta }_{T3}$, ${\delta }_{T4}$, ${\delta }_{T6}$

.

2.2. Flight Dynamics

The translational and rotational dynamics equations based on the standard six-degree-of-freedom equations are given as:

$$m(\dot{\mathbf{V}}+\mathit{\omega }\times \mathbf{V})={\mathbf{F}}_b$$

(1)

$$\mathbf{J}\dot{\mathit{\omega }}+\mathit{\omega }\times \left(\mathbf{J}\mathit{\omega }\right)={\mathbf{M}}_b$$

(2)

where $\mathbf{V}={(u,v,w)}^T$ and $\mathit{\omega }={(p,q,r)}^T$ are the velocity vector and angular velocity in the body frame, respectively. $\mathbf{J}$ and m are the aircraft’s mass and moment of inertia, respectively, ${\mathbf{F}}_b={\left(F_x,F_y,F_z\right)}^T$ and ${\mathbf{M}}_b={(L,M,N)}^T$, which represent the force and moment acting on the mass center of the UAV, are given by:

$${\mathbf{F}}_b={\mathbf{E}}_{ba}{\mathbf{F}}_{body}+{\mathbf{E}}_{ba}{\mathbf{F}}_{wt}+\sum _{i=1}^{24}{\mathbf{E}}_{ba}{\mathbf{F}}_{dpw}^i+\mathbf{G}$$

(3)

$${\mathbf{M}}_b={\mathbf{M}}_{body}+{\mathbf{M}}_{wt}+\sum _{i=1}^{24}{\mathbf{M}}_{dpw}^i$$

(4)

where ${\mathbf{F}}_{body}$ and ${\mathbf{M}}_{body}$ are the force and moment generated by the fuselage. ${\mathbf{F}}_{wt}$ and ${\mathbf{M}}_{wt}$ represent the aerodynamic force and moment generated by the winglet, respectively; ${\mathbf{F}}_{dpw}^i$ and ${\mathbf{M}}_{dpw}^i$ denote the force and moment produced by the i-th DEP-IW unit in the wind axis system; ${\mathbf{E}}_{ba}$ represents the coordinate transformation matrix from the wind frame to the body frame. The primary challenge lies in accurately representing the dynamics of propulsion and the aerodynamic forces exerted by distributed propulsion wings throughout the entire flight corridor.

2.3. Component Dynamics Models

The cross-section of the DEP-IW unit is shown in Figure 3a. $V_{\infty },V_p,V_o$ are the freestream velocity, airflow velocity at the propeller axis, and airflow velocity at the inlet duct axis, respectively. ${\alpha }_{\infty }$ is the angle of attack of the freestream. ${\delta }_f$ represents the angle between the chord line of the induced wing and the axis of the inlet duct. And ${\delta }_e$ represents the deflection angle of the upper and lower control surfaces. $A_i,A_p,A_e$ represent the areas of the inlet section, propeller section, and outlet section of the duct, respectively. $r_p,x_e,D_e,c_f$ denotes the radius of the propeller, the distance from the propeller to the outlet of the inlet duct, the diameter of the outlet section of the inlet duct, and the chord length of the induce wing, respectively. $P_{\infty },P_{p1},P_{p2},P_o$ present the freestream pressure, pressure in front of the propeller, pressure behind the propeller, and pressure of the jet flow, respectively. $T_s,T_p$ represent the thrust generated by the shroud and the propeller, respectively. Figure 3b illustrates the sectional flow diagram of the DEP-IW unit. The large stream-tube represents the deflection of the freestream. Within this large tube, there is a smaller tube (indicated by dashed lines), which is composed of the inlet duct flow affected by the induced wing.

2.3.1. Duct Model

When deriving the lift and thrust models for the DPW-IW unit, it is necessary to establish a duct model to obtain the duct thrust and duct jet velocity under different flight conditions. First, consider the flow state when the angle of attack of the freestream is zero (${\alpha }_{\infty }=0$). In this condition, the axial inflow velocity of the duct ($V_a$) is equal to the freestream velocity ($V_{\infty }$). The duct thrust can be represented using the thrust coefficient:

$$T_t=\rho n^2{D}_e^4{C}_T$$

(5)

$$\left\{\begin{array}{cc}\hfill C_T& =K_0+K_1{J}^2+K_{2}J\hfill \\ \hfill J& =V_a/nD\hfill \end{array}\right.$$

(6)

where $T_t$ represents the thrust of the duct, n is the revolution speed, $C_T$ is the thrust coefficient of the airfoil, which is typically fitted as a function of advance ratio based on experimental data or computational fluid dynamics (CFD) results as shown in (6).

To derive the duct jet velocity, a duct thrust model proposed by Werle is employed [40]. The total thrust of the duct is composed of the propeller thrust and the shroud thrust. Alternatively, according to the momentum theorem, the total duct thrust can be expressed as:

$$T_t=\rho A_p{V}_p(V_o-V_a)=T_P+T_s$$

(7)

where $T_P$ denotes the thrust of propeller , and $T_s$ represents the thrust of shroud.

According to Bernoulli’s equation, the relationship between the airflow velocity and pressure can be derived both upstream and downstream of the propeller:

$$\left\{\begin{array}{c}\hfill P_{\infty }+{\displaystyle \frac{1}{2}}\rho V_{\infty }^2=P_{p1}+{\displaystyle \frac{1}{2}}\rho V_p^2\\ \hfill P_o+{\displaystyle \frac{1}{2}}\rho V_o^2=P_{p2}+{\displaystyle \frac{1}{2}}\rho V_p^2\end{array}\right.$$

(8)

The pressure difference between the upstream and downstream of the propeller can be obtained by solving (8) simultaneously:

$$P_{p2}-P_{p1}={\displaystyle \frac{1}{2}}\rho (V_o^2-V_a^2)$$

(9)

Therefore, the thrust generated by the propeller can be expressed as:

$$T_P=A_P(P_{p2}-P_{p1})={\displaystyle \frac{1}{2}}\rho A_p(V_o^2-V_a^2)$$

(10)

To obtain the stream velocity at the propeller, it is necessary to introduce a dimensionless parameter $C_{st}$, representing the ratio of the total thrust generated by the duct to the thrust generated by the propeller. This parameter is defined as the force amplification coefficient, denoted as follows:

$$C_{st}={\displaystyle \frac{T_s+T_p}{T_p}}$$

(11)

By combining (7), (10), and (11), the air velocity at the propeller can be obtained as:

$$V_p={\displaystyle \frac{1}{2}}{C}_{st}(V_o+V_a)$$

(12)

Werle [40] provides the following calculation method for $C_{st}$:

$$C_{st}=u_{ro}(1+\beta f)$$

(13)

where:

$$u_{ro}=a_e{\displaystyle \frac{{(1+\frac{X_e^2}{a_c})}^{\frac{3}{2}}-a_c}{{(1+\frac{X_e^2}{a_c})}^{\frac{3}{2}}-a_e}}$$

(14)

$$\beta ={\displaystyle \frac{a_c-1+X_e{(1+\frac{X_e^2}{a_c})}^{\frac{3}{2}}/\sqrt{1+X_e^2}}{{(1+\frac{X_e^2}{a_c})}^{\frac{3}{2}}-a_c}}$$

(15)

$$f={\displaystyle \frac{V_o-V_a}{V_o+V_a}}$$

(16)

$$a_c={\displaystyle \frac{A_i}{A_p}}, a_e={\displaystyle \frac{A_e}{A_p}}, X_e={\displaystyle \frac{x_e}{r_p}}$$

(17)

In (14) and (15), $u_{ro}$ and $\beta$ contain the geometric parameters of the duct, which are intrinsic properties of the duct. For a given duct, their values are constants, and the parameter f will vary with changes in freestream velocity.

By combining (7), (10), and (13), the simultaneous equations is obtained as:

$$\left\{\begin{array}{c}{T}_t=C_{st}{T}_p\hfill \\ C_{st}=u_{ro}(1+\beta f)\hfill \\ T_p={\displaystyle \frac{1}{2}}\rho A_p(V_o^2-V_a^2)\hfill \end{array}\right.$$

(18)

There are three unknowns in (18): $C_{st}$, $T_p$ and $V_o$. The thrust of the duct ($T_t$) can be obtained by (5). So, the jet velocity can be obtained as:

$$V_o={\displaystyle \frac{{(A^2{V}_a^2+CA+BC)}^{\frac{1}{2}}+B{V}_a}{A+B}}$$

(19)

where:

$$\left\{\begin{array}{c}A=u_{ro}\hfill \\ B=u_{ro}\beta \hfill \\ C=2T_t/\rho A\hfill \end{array}\right.$$

(20)

The above models are derived under the assumption of zero freestream angle of attack. However, when the freestream angle of attack is not zero, Cerny [41] analyzed the aerodynamic efficiency of the duct under different AOA based on experimental and CFD results. It was found that the thrust is mainly influenced by the axial velocity. Since there is no aerodynamic surface blocking in front of the duct, the velocity along the duct axis projection can be used as the axial velocity of the duct as follows:

$$V_a=V_{\infty }cos\left({\alpha }_{\infty }\right)$$

(21)

2.3.2. DPW-IW Unit Aerodynamics Model

As shown in Figure 3b, the unit is simultaneously situated in both the freestream and the duct jet. By superimposing the flow of the two ducts and applying the momentum theorem, the lift and drag of the unit can be determined. The mass flow rate passing through the entire unit can be expressed as:

$$\dot{m}=\rho A_p{V}_p+\rho A_{\infty }{V}_{\infty }-\rho A_o{V}_{\infty }$$

(22)

where the first term represents the mass flow rate in the duct jet, the second term is the mass flow rate in the freestream, and the third term arises because the duct jet flow occupies a portion of the volume of the freestream flow tube, thus subtracting an additional portion of the mass flow rate. It is assumed that the area of the duct flow tube at the wing is contracted to $A_0$, and the duct flow tube does not affect the area of the freestream flow tube.

After the freestream flows over the DEP-IW unit, it will deflect downward by an angle. The jet flow from the duct will also deflect by an angle due to the influence of the induced wing. Therefore, applying the momentum theorem in the lift direction, the lift of the unit can be derived as:

$$L={\gamma }_T\rho A_p{V}_p{V}_{o}sin(\overline{\delta }+{\alpha }_{\infty })+\rho A_{\infty }{V}_{\infty }^{2}sin\epsilon -{\gamma }_T\rho A_o{V}_{\infty }^{2}sin(\overline{\delta }+{\alpha }_{\infty })$$

(23)

where ${\alpha }_{\infty }$ represents the angle of attack of the freestream. ${\gamma }_T$ is the correction factor for duct thrust, tailored for the unit model, and can be assumed to be 1, implying that the deflection angle of the induced wing has minimal impact on the thrust of the duct. $\overline{\delta }$ represents the actual induced deflection angle of the duct flow, and $\epsilon$ is the deflection angle of the freestream tube.

According to Kuhn [42], there exists a certain proportional relationship between the induced angle of the jet flow by the wing and the deflection angle of the wing. This relationship is correlated with the wing chord length, and the tube diameter, and different types of wings have different maximum induced angles for the jet flow. Therefore, the induced angle of the control surface airflow can be expressed as:

$$\left\{\begin{array}{cc}\hfill {\overline{\delta }}_f& ={\eta }_1{\delta }_f+{\eta }_2({\delta }_e-0.5{\delta }_f)+{\delta }_0\hfill \\ \hfill \eta & =f\left({\displaystyle \frac{c_f}{D_e}}\right)\hfill \end{array}\right.$$

(24)

where ${\eta }_1,{\eta }_2$ represent the induced proportion of the airflow, which can be considered a constant value when the diameter of the duct and the chord length of the wing remain unchanged. ${\delta }_0$ is defined as the zero-offset induced angle. When the wing employs an asymmetric airfoil, even when the deflection angle is zero, it still induces an initial angle for the airflow.

Similarly, the thrust generated in the axial direction of the unit can be derived through the momentum theorem as follows:

$$T_c={\gamma }_T\rho A_p{V}_p(V_o-V_{\infty })-A_{\infty }\rho V_{\infty }^2(1-cos\epsilon )-{\gamma }_T\rho A_p{V}_p{V}_o(1-cos({\overline{\delta }}_f+{\alpha }_{\infty }))+{\gamma }_T\rho A_o{V}_{\infty }^2(1-cos({\overline{\delta }}_f+{\alpha }_{\infty }))$$

(25)

The second term in (23) and the second term in (25) represent the lift and drag generated by the deflection of the freestream flow tube. This can be calculated using the momentum theorem. Alternatively, traditional wing aerodynamics models can be employed, using lift coefficient and drag coefficient to represent the aerodynamic forces on the unit, as expressed below:

$$\left\{\begin{array}{cc}\hfill L_{T=0}& ={\displaystyle \frac{1}{2}}\rho V_{\infty }^2{S}_u{C}_L\left({\alpha }_{\infty }\right)\hfill \\ \hfill D_{T=0}& ={\displaystyle \frac{1}{2}}\rho V_{\infty }^2{S}_u{C}_D\left({\alpha }_{\infty }\right)\hfill \end{array}\right.$$

(26)

where $S_u$ is the reference area of unit, $C_L\left({\alpha }_{\infty }\right)$ and $C_D\left({\alpha }_{\infty }\right)$ are the lift coefficient and drag coefficient, respectively. To incorporate the stall characteristics at high angles of attack, the lift model proposed by Beard [43] is employed:

$$C_L\left({\alpha }_{\infty }\right)=(1-\sigma \left({\alpha }_{\infty }\right))[C_{L0}+C_{L{\alpha }_{\infty }}{\alpha }_{\infty }+C_{L_{{\delta }_e}}\left({\delta }_e\right)]+\sigma \left({\alpha }_{\infty }\right)[2\mathrm{sign}\left({\alpha }_{\infty }\right){sin}^2{\alpha }_{\infty }cos{\alpha }_{\infty }]$$

(27)

$$\sigma \left({\alpha }_{\infty }\right)={\displaystyle \frac{1+e^{-M({\alpha }_{\infty }-{\alpha }_0)}+e^{M({\alpha }_{\infty }+{\alpha }_0)}}{(1+e^{-M({\alpha }_{\infty }-{\alpha }_0)})(1+e^{M({\alpha }_{\infty }+{\alpha }_0)})}}$$

(28)

$$C_D\left({\alpha }_{\infty }\right)=C_{D0}+{\displaystyle \frac{{\left(C_{L0}+C_{L\alpha }{\alpha }_{\infty }\right)}^2}{\pi e\mathrm{AR}}}+C_{D_{{\delta }_e}}\left({\delta }_e\right)$$

(29)

where $C_{L{\alpha }_{\infty }}$ is the lift curve slope; $C_{L0}$ and $C_{D0}$ are the lift and drag coefficients at zero AOA, respectively. e is the Oswald factor. M and ${\alpha }_0$ are parameters that need to be given based on calculation results or engineering experience. These parameters describe the characteristics of the blending function (as shown in (28)), where M represents the rate of change in the function, and ${\alpha }_0$ represents the cutoff value of the function.

Combining (7), (21) and (26), the expressions of (23) and (25) can be rewritten as:

$$L={\gamma }_T{T}_{t}sin(\overline{\delta }+{\alpha }_{\infty })+L_{T=0}+{\gamma }_T\rho A_o{V}_{\infty }(V_{o}cos\left({\alpha }_{\infty }\right)-V_{\infty })$$

(30)

$$T={\gamma }_T{T}_{t}cos({\overline{\delta }}_f+{\alpha }_{\infty })-D_{T=0}+{\gamma }_T\rho A_o{V}_{\infty }(V_{o}cos\left({\alpha }_{\infty }\right)cos({\overline{\delta }}_f+{\alpha }_{\infty })-V_o+V_{\infty }-V_{\infty }cos({\overline{\delta }}_f+{\alpha }_{\infty }))$$

(31)

The side force on the aircraft is minimally affected by propulsion and can be expressed as:

$$Y=C_{Y\beta }\beta$$

(32)

The torque generated by the i-th DPW-IW unit can be obtained by taking the cross product of the force generated by the unit and the distance from the point of application of the resultant force to the center of gravity, given as:

$${\mathbf{M}}_{dpw}^i={\mathbf{F}}_{dpw}^i\times {\mathbf{R}}^i$$

(33)

2.3.3. Aerodynamic Model of the Fuselage and Winglets

In addition to the powered wing unit model, the forces on other parts of the aircraft, such as the fuselage and winglet, are primarily aerodynamic. Therefore, their models can be based on the model proposed by Beard [43], with necessary modifications to the parameters within the model. For the sake of brevity and to avoid redundant formulas, the aerodynamic models for the fuselage and winglet are provided in Appendix A.

2.4. Model Validation

The model proposed above is validated with computational fluid dynamics results in this section. The computational domain is divided using a structured grid with approximately 30,000,000 grid points. The flow field is numerically solved using the Reynolds-Averaged Navier–Stokes (RANS) equations, and the turbulence model employed is the $k-\omega$ SST model. The SIMPLE pressure-velocity coupling solver is used, with a second-order upwind scheme for spatial discretization and a first-order implicit scheme for time advancement. Due to the presence of various modes during the flight, the model is verified separately for hover mode, cruise mode, and transition mode.

As shown in Figure 4, in the model verification, the main focus lies on the following quantities: weight (W), total lift (L), total drag (D), total moment (M), forces represented in body frame ($F_x,F_z$), resultant force magnitude ($F_a$), and resultant force direction (${\xi }_T$). In the previous model derivation, thrust is included in the drag, which means that the drag in Figure 4 may be negative. The resultant force magnitude denotes the combined force of lift and drag, while the resultant force direction indicates the angle between the resultant force and either the duct thrust line or the body-axis X-axis. According to the (30) and (31), it can be observed that when the freestream velocity is very low and the duct thrust remains constant, the overall aircraft force will remain essentially unchanged, except for changes in the direction of the resultant force due to variations in the deflection angle of the induced wing. However, during cruise flight, where the duct thrust is relatively small, the aerodynamic characteristics of the entire aircraft will be more similar to those of conventional aircraft. The baseline states for different flight phases are shown in

Table 3. Reference State for Model Validation under Different Conditions.

Flight Mode	${\mathit{\alpha }}_{\mathit{\infty }}{\mathbf{(}}^{\mathbf{\circ }}\mathbf{)}$	${\mathit{T}}_{\mathit{p}}\mathbf{\left(}\mathbf{N}\mathbf{\right)}$	${\mathit{\delta }}_{\mathit{f}}{\mathbf{(}}^{\mathbf{\circ }}\mathbf{)}$	${\mathit{V}}_{\mathit{\infty }}\mathbf{\left(}\mathbf{m}\mathbf{/}\mathbf{s}\mathbf{\right)}$
Hover	45	-	-	0
Transition	20	25	20	20
Transition	20	33.3	20	20
Cruise	0	6.6	0	30

. $T_p$ represents the thrust of the propeller inside the duct.

In hover mode, the model validation results are shown in Figure 5. Figure 5a depicts the resultant force direction under different deflection angles of the induced wing, with the blue solid line representing the model-predicted resultant force direction and the red inverted triangles indicating the calculation results. The result shows that the model predictions are slightly larger than the CFD calculations. Figure 5b illustrates the changes in the magnitude of the resultant force under different rotational speeds, with the blue solid line representing the model predictions and the red inverted triangles showing the calculated results. The figure demonstrates that the model predictions closely match the calculated results.

During the cruise flight phase, the lift-to-drag characteristics of the entire aircraft are similar to those of conventional aircraft. The model validation results in cruise flight mode when the rotor thrust is 6.6 N are shown in Figure 6. Figure 6a shows the variation of the total aircraft lift coefficient and drag coefficient under different angles of attack. It can be seen that the model prediction results are quite accurate, although the predicted drag coefficient values are slightly higher at larger angles of attack. Figure 6b illustrates the variation of the pitching moment coefficient of the vehicle under different angles of attack. It can be observed that the model accurately reflects the trend of the pitching moment with changing angles of attack and exhibits no significant errors.

During the transition flight phase, since the lift and drag coefficients of the entire aircraft include the influence of thrust, the lift coefficient tends to be relatively large. Additionally, when the thrust exceeds the drag, a negative drag coefficient can occur. Figure 7 presents the model validation results for the transition mode under different rotor thrusts. The lift and drag coefficients as functions of the angle of attack during the transition flight phase are shown in Figure 7a. It can be observed that under different propeller thrusts, the model’s predicted lift coefficients are slightly higher, while the predicted drag coefficients are slightly lower. Figure 7b depicts the pitching moment curves. Similar to the cruise flight phase, the model reflects the trend of pitching moment variations under different propeller thrusts. Furthermore, the calculation results indicate that changes in thrust have a minimal impact on the pitching moment, primarily altering the lift and drag characteristics of the entire aircraft.

3. Flight Controller Design

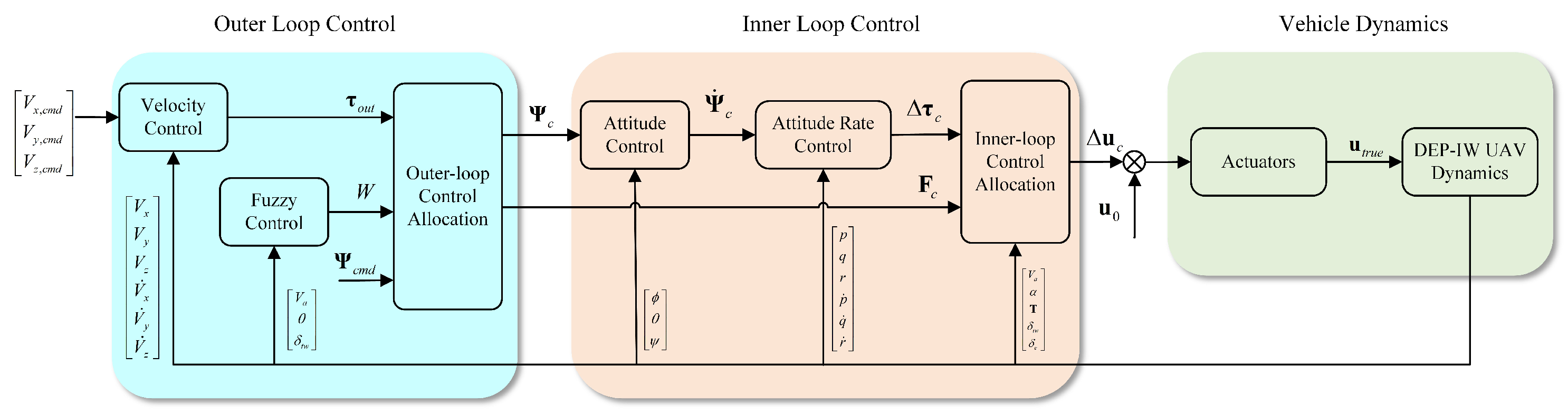
To address the varying control logic and actuator effectiveness characteristics of the DPW-IW VTOL UAVs in different flight modes, a unified flight controller is constructed, eliminating the need for switching between different controllers during the transition flight. The controller divides the UAV control loop into three sub-loops using the time-scale separation method, arranged from fast to slow: angular velocity control loop, attitude control loop, and velocity control loop. These three control loops are cascaded, where the output of the previous level serves as the input to the next level.

As shown in Figure 8, the velocity control loop generates attitude commands (${\mathbf{\Psi }}_c$) and thrust commands (${\mathbf{F}}_c$) based on the speed commands (${[V_{x,cmd},V_{y,cmd},V_{z,cmd}]}^T$) provided by the reference transition trajectory. ${\dot{\mathbf{\Psi }}}_c$ is the angular rate commands and $\Delta {\mathbf{Ø}}_c$ represent the increase moments commands. The validation results of the dynamic model in Section 2.3.2 indicate errors in the estimation of the aircraft’s aerodynamic forces and moments. Additionally, throughout the entire flight process, there are significant external disturbances and variations in airspeed for the aircraft, which greatly affect its aerodynamic characteristics. Therefore, the INDI control approach is utilized in the inner control loop. This method calculates control increments based on the system’s current state relative to the past state over a given increment time, reducing the control system’s dependence on model accuracy.

Simultaneously, as airspeed increases and aircraft configuration changes, the control logic of the vehicle undergoes adjustments, leading to variations in the effectiveness of various control components. To address this, this paper adopts a multi-level control allocation strategy comprising two control allocation schemes for the outer loop and inner loop, respectively. The outer-loop control allocation determines attitude and thrust commands based on the required velocity command. To mitigate the impact of fluctuating actuator effectiveness and nonlinear coupling between different actuators, an incremental control allocation (INCA) method is employed for the inner-loop control allocation. Ultimately, by integrating commands for induced wing surface, torque, and force as inputs to the inner-loop control allocation, the commands for throttle, control surface deflection angle, and induced wing surface deflection angle for each unit duct are derived.

3.1. Inner-Loop Control Law

As shown in Figure 9 The angular velocity loop control serves as the fast control loop and utilizes the INDI control method. Based on (2), the aircraft’s attitude dynamics equation can be written as:

$$\dot{\mathit{\omega }}={\mathbf{J}}^{-1}({\mathbf{M}}_{dpw}+{\mathbf{M}}_e-\mathit{\omega }\times \mathbf{J}\mathit{\omega })$$

(34)

where ${\mathbf{M}}_{dpw}$ represents the control torque generated by the vehicle, and ${\mathbf{M}}_e$ encompasses the torques generated by the aircraft motion and external disturbances.

Traditional nonlinear dynamic inversion (NDI) methods require accurate modeling and estimation of ${\mathbf{M}}_e$ to ensure control precision. The INDI method adopts an incremental control approach, where the control output at the current time is only related to the previous time. Therefore, assuming the aircraft’s flight state at time $t_0$ is $({\mathit{\omega }}_0,{\mathit{\delta }}_0)$, where ${\mathit{\delta }}_0$ represents the control inputs for the DEP-IW, including throttle of the duct and control surface deflection angle, and ${\dot{\mathit{\omega }}}_d$ is the command value for the next time step’s angular acceleration, a Taylor expansion of ${\dot{\mathit{\omega }}}_d$ at point $({\mathit{\omega }}_0,{\mathit{\delta }}_0)$ yields:

$$\begin{array}{cc}\hfill & {\dot{\mathit{\omega }}}_d\approx {\mathbf{J}}^{-1}({\mathbf{M}}_{dpw,0}+{\mathbf{M}}_{e,0}-{\mathit{\omega }}_0\times \mathbf{J}{\omega }_0)+\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial \mathit{\omega }}}{\left[{\mathbf{J}}^{-1}({\mathbf{M}}_{dpw}+{\mathbf{M}}_e-\mathit{\omega }\times \mathbf{J}\mathit{\omega })\right]}_{\omega ={\omega }_0,\delta ={\delta }_0}(\omega -{\omega }_0)\hfill \\ \hfill & +{\displaystyle \frac{\partial }{\partial \delta }}{\left[{\mathbf{J}}^{-\mathbf{1}}({\mathbf{M}}_{\mathbf{dpw}}+{\mathbf{M}}_{\mathbf{e}}-\mathit{\omega }\times \mathbf{J}\mathit{\omega })\right]}_{\omega ={\omega }_0,\delta ={\delta }_0}(\delta -{\delta }_0)\hfill \end{array}$$

(35)

When the control frequency is sufficiently high, the time increment becomes very small. Since the time scales of dynamic responses of state and control variables are different, it can be assumed that within this control period, the change in state is much smaller than the change in control input. Therefore, it can be considered that the change in control input has a much greater impact on the angular acceleration than the angular velocity has on the angular acceleration. Additionally, it can also be assumed that the derivatives of ${\mathbf{M}}_e$ and $(\omega \times J\omega )$ with respect to the control variables are zero. Hence, the above equation can be rewritten as:

$${\dot{\mathit{\omega }}}_d-{\dot{\mathit{\omega }}}_0={\displaystyle \frac{\partial }{\partial \mathit{\delta }}}{\left({\mathbf{J}}^{-1}{\mathbf{M}}_{dpw}\right)}_{\mathit{\omega }={\mathit{\omega }}_0,\mathit{\delta }={\mathit{\delta }}_0}(\mathit{\delta }-{\mathit{\delta }}_0)$$

(36)

where $\mathit{\delta }-{\mathit{\delta }}_0$ represents the increment of the control command, and ${\dot{\mathit{\omega }}}_d-{\dot{\mathit{\omega }}}_0$ represents the increment of the angular acceleration command. From the above equation, it can be seen that the errors in system inertia and control surface effectiveness are reflected in the variations of angular acceleration. Since this is an incremental control method, angular acceleration errors are corrected through feedback in each control cycle, preventing the accumulation of errors. This feature represents the fundamental difference between INDI and the NDI method. The angular accelerations are acquired by differentiating and filtering the angular rates. Define the control effectiveness matrix (${\mathbf{B}}_{dpw}$) and the control increment ($\Delta \delta$) as:

$${\mathbf{B}}_{dpw}={\displaystyle \frac{\partial }{\partial \delta }}{\left({\mathbf{M}}_{dpw}\right)}_{\mathit{\omega }={\mathit{\omega }}_0,\mathit{\delta }={\mathit{\delta }}_0}$$

(37)

$$\Delta \mathit{\delta }=\mathit{\delta }-{\mathit{\delta }}_0$$

(38)

(36) can be rewritten as:

$$\mathbf{J}({\dot{\mathit{\omega }}}_d-{\dot{\mathit{\omega }}}_{\mathbf{0}})={\mathbf{B}}_{dpw}\Delta \mathit{\delta }$$

(39)

The attitude angle control loop aims to generate angular velocity commands for the angular velocity loop control. The desired angular velocity ${\mathit{\omega }}_d$ can be obtained from the following equation:

$${\mathit{\omega }}_d=K_{\Psi }({\Psi }_d-\Psi )$$

(40)

where $K_{\mathbf{\Psi }}$ is the proportional gain.

The desired angular acceleration can be obtained from the following equation:

$${\dot{\mathit{\omega }}}_d=K_{P,\mathit{\omega }}({\mathit{\omega }}_d-\mathit{\omega })+K_{I,\mathit{\omega }}\int ({\mathit{\omega }}_d-\mathit{\omega })dt$$

(41)

$$\left|K_{I,\mathit{\omega }}\int ({\mathit{\omega }}_{\mathbf{d}}-\mathit{\omega })dt\right|\le K_{I,lim}$$

(42)

where the current angular velocity $\mathit{\omega }$ is obtained through online estimation based on the Kalman filtering, and $K_{P,\mathit{\omega }}$ is the proportional coefficient, and $K_{I,\mathit{\omega }}$ is the integral coefficient. $K_{I,lim}$ is the saturation limit of the integrator.

3.2. Outer-Loop Control Law

During the transition flight, it is necessary to control both the flight speed and altitude of the vehicle. Specifically, minimizing the climb implies less energy consumption, allocating all energy toward accelerating the aircraft, resulting in a faster and more efficient acceleration transition process. Additionally, maintaining altitude during transition enables agile unmanned aerial vehicles to operate in more chaotic environments [44].

The outer-loop controller framework is illustrated in Figure 10. During the low-speed flight phase, the horizontal velocity of the vehicle is controlled by adjusting the pitch angle to accelerate or decelerate, while the vertical velocity is directly manipulated by altering the thrust magnitude. Conversely, during the high-speed flight phase, acceleration and deceleration are achieved by varying the thrust magnitude, while changes in vertical velocity or altitude are accomplished by adjusting the aircraft’s pitch angle.

Choose the control states as $V_x$, $V_y$, and $V_z$. The outer-loop control law in different flight phases is given by:

$$\begin{array}{cc}\hfill {\mathbf{\Psi }}_{c,l}& =K_P^{Vxl}(V_{x,cmd}-V_x)+K_I^{Vxl}\int (V_{x,cmd}-V_x)dt\hfill \\ \hfill {\mathbf{\Psi }}_{c,h}& =K_P^{Vzh}(V_{z,cmd}-V_z)+K_I^{Vzh}\int (V_{z,cmd}-V_x)dt\hfill \\ \hfill {\mathbf{\Psi }}_{c,y}& =K_P^{Vy}(V_{y,cmd}-V_y)+K_I^{Vy}\int (V_{y,cmd}-V_y)dt\hfill \\ \hfill {\mathbf{T}}_{c,h}& =K_P^{\dot{V}x}({\dot{V}}_{x,cmd}-{\dot{V}}_x)+K_I^{\dot{V}x}\int ({\dot{V}}_{x,cmd}-{\dot{V}}_x)dt\hfill \\ \hfill {\dot{V}}_{x,cmd}& =K_P^{Vxh}(V_{x,cmd}-V_x)+K_I^{Vxh}\int (V_{x,cmd}-V_x)dt\hfill \\ \hfill {\mathbf{T}}_{c,l}& =K_P^{\dot{V}z}({\dot{V}}_{z,cmd}-{\dot{V}}_z)+K_I^{\dot{V}z}\int ({\dot{V}}_{z,cmd}-{\dot{V}}_z)dt\hfill \\ \hfill {\dot{V}}_{z,cmd}& =K_P^{Vzl}(V_{z,cmd}-V_z)+K_I^{Vzl}\int (V_{z,cmd}-V_z)dt\hfill \end{array}$$

(43)

where the control output ${[{\mathbf{\Psi }}_{c,l},{\mathbf{\Psi }}_{c,h},{\mathbf{\Psi }}_{c,y},{\mathbf{T}}_{c,h},{\mathbf{T}}_{c,l}]}^T$ is the virtual control commands that will be fed directly into the control allocation. And the constants

$$\mathbf{K}={[K_P^{Vxl},K_I^{Vxl},K_P^{Vzh},K_I^{Vzh},K_P^{Vy},K_I^{Vy},K_P^{\dot{V}x},K_I^{\dot{V}x},K_P^{Vxh},K_I^{Vxh},K_P^{\dot{V}z},K_I^{\dot{V}z},K_P^{Vzl},K_I^{Vzl}]}^T$$

(44)

are the PI gains for each control channel.

3.3. Control Allocation

In this section, a two-level hierarchical control allocation method is proposed to allocate separate commands for outer-loop control output and inner-loop virtual commands. The outer-loop control allocates force commands and attitude angle commands based on virtual control input, while the inner-loop control allocation simultaneously allocates torque commands and force commands to manipulate the actuators (such as throttle of the propulsion and the deflection angle of control surfaces).

The implementation of outer-loop control allocation involves adjusting allocation weights to adapt to different flight states. The adjustment of control weights is a common practice for typical VTOL aircraft, such as tiltrotor aircraft and tail-sitter aircraft. For instance, tiltrotor aircraft typically control scheduling based on tilt angle, while tail-sitter aircraft control scheduling based on pitch angle [23]. In contrast to conventional aircraft, the aircraft studied in this paper are influenced by flight speed, pitch angle, and induced wing deflection angle, forming a multi-input single-output system. It is inaccurate to determine flight mode solely based on flight speed. For instance, even with high flight speed, if the aircraft maintains a large pitch angle and induced wing surface deflection, the efficiency of the aircraft’s aerodynamic control surfaces remains low. Therefore, Mamdani fuzzy control [45] is employed to simplify the weight design process. As shown in Figure 11, Gaussian-type membership functions are used in fuzzy control, and outer-loop allocation weight is determined based on flight speed, pitch angle, and induced wing surface deflection. Fuzzy rules can be summarized as follows:

• The higher the flight speed, the greater the weight;
• The smaller the pitch angle, the greater the weight;
• The smaller the induced wing surface deflection, the greater the weight.

The method for defuzzification of output fuzzy quantities adopts the maximum membership average method. The normalization of input variables and fuzzy control rules can be listed in the Appendix B. Then the outer-loop control inputs are calculated by

$$\left\{\begin{array}{cc}\hfill {\mathbf{\Psi }}_c& =(1-{\mathbf{W}}_{\mathbf{FC}}){\mathbf{\Psi }}_{c,l}+{\mathbf{W}}_{\mathbf{FC}}{\mathbf{\Psi }}_{c,h}\hfill \\ \hfill {\mathbf{T}}_c& =(1-{\mathbf{W}}_{\mathbf{FC}}){\mathbf{T}}_{c,l}+{\mathbf{W}}_{\mathbf{FC}}{\mathbf{T}}_{c,h}\hfill \end{array}\right.$$

(45)

where ${\mathbf{W}}_{\mathbf{FC}}$ is the allocation weight, and ${\mathbf{\Psi }}_c$ and ${\mathbf{T}}_c$ denote the attitude command and thrust command, respectively.

Inner-loop control allocation calculates the actuator commands based on the force and moment commands generated by the inner-loop controller. As shown in (37), control allocation requires determining the control allocation matrix based on the control effectiveness matrix. The typical approach involves calculating the control allocation matrices for several representative flight conditions and then using gain scheduling to compute new control allocation matrices during flight. However, this method is not suitable for actuators with nonlinear and coupled characteristics. Therefore, an incremental control allocation method is employed. Based on the current flight and actuator states at each control step, the Jacobian matrix is computed, represented as:

$${\mathbf{B}}_{dpw}={\nabla }_{\delta }{\left({\mathbf{M}}_{dpw}\right)}_{\mathit{\omega }={\mathit{\omega }}_0,\mathit{\delta }={\mathit{\delta }}_0}={\displaystyle \frac{\partial {\left({\mathbf{M}}_{dpw}\right)}_{\mathit{\omega }={\mathit{\omega }}_0,\mathit{\delta }={\mathit{\delta }}_0}}{\partial \mathit{\delta }}}$$

(46)

$$\begin{array}{c}\hfill {\nabla }_{\delta }{\left({\mathbf{M}}_{dpw}\right)}_{\mathit{\omega }={\mathit{\omega }}_0,\mathit{\delta }={\mathit{\delta }}_0}={\left[\begin{array}{cccccc}{\displaystyle \frac{\partial M_{bx}}{\partial T_1}}& \dots & {\displaystyle \frac{\partial M_{bx}}{\partial T_6}}& {\displaystyle \frac{\partial M_{bx}}{\partial {\delta }_{e1}}}& \dots & {\displaystyle \frac{\partial M_{bx}}{\partial {\delta }_{e6}}}\\ {\displaystyle \frac{\partial M_{by}}{\partial T_1}}& \dots & {\displaystyle \frac{\partial M_{by}}{\partial T_6}}& {\displaystyle \frac{\partial M_{by}}{\partial {\delta }_{e1}}}& \dots & {\displaystyle \frac{\partial M_{by}}{\partial {\delta }_{e6}}}\\ {\displaystyle \frac{\partial M_{bz}}{\partial T_1}}& \dots & {\displaystyle \frac{\partial M_{bz}}{\partial T_6}}& {\displaystyle \frac{\partial M_{bz}}{\partial {\delta }_{e1}}}& \dots & {\displaystyle \frac{\partial M_{bz}}{\partial {\delta }_{e6}}}\\ {\displaystyle \frac{\partial F_{bx}}{\partial T_1}}& \dots & {\displaystyle \frac{\partial F_{bz}}{\partial T_6}}& {\displaystyle \frac{\partial F_{bx}}{\partial {\delta }_{e1}}}& \dots & {\displaystyle \frac{\partial F_{bx}}{\partial {\delta }_{e6}}}\\ {\displaystyle \frac{\partial F_{by}}{\partial T_1}}& \dots & {\displaystyle \frac{\partial F_{by}}{\partial T_6}}& {\displaystyle \frac{\partial F_{by}}{\partial {\delta }_{e1}}}& \dots & {\displaystyle \frac{\partial F_{by}}{\partial {\delta }_{e6}}}\\ {\displaystyle \frac{\partial F_{bz}}{\partial T_1}}& \dots & {\displaystyle \frac{\partial F_{bz}}{\partial T_6}}& {\displaystyle \frac{\partial F_{bz}}{\partial {\delta }_{e1}}}& \dots & {\displaystyle \frac{\partial F_{bz}}{\partial {\delta }_{e6}}}\end{array}\right]}_{(6\times 12)}\end{array}$$

(47)

where ${\mathbf{M}}_C={\left[M_{bx}{M}_{by}{M}_{bz}\right]}^T$ and ${\mathbf{F}}_C={\left[F_{bx}{F}_{by}{F}_{bz}\right]}^T$ are moment command and force command, respectively. $T_i$ and ${\delta }_{ei}$ is the throttle and control surface deflection angle of the i-th DEP-IW unit. By substituting (46) into (39), the incremental control inputs for each actuator can be obtained as follows:

$$\Delta \mathit{\delta }={\mathbf{B}}_{dpw}^{+}\mathbf{J}\left({\left[{\mathbf{M}}_c{\mathbf{T}}_c\right]}^T\right)$$

(48)

$${\mathbf{M}}_c={\dot{\mathit{\omega }}}_d-{\dot{\mathit{\omega }}}_{\mathbf{0}}$$

(49)

$${\mathbf{B}}_{dpw}^{+}={\mathbf{B}}_{dpw}^T{\left[{\mathbf{B}}_{dpw}{\mathbf{B}}_{dpw}^T\right]}^{-1}$$

(50)

To simplify the computation of the Jacobian matrix, the model needs to be processed accordingly. In order to obtain the partial derivatives of the overall aircraft forces and moments with respect to each actuator, it is necessary to fit the duct thrust ($T_t$), blending function ($\sigma \left({\alpha }_{\infty }\right)$), and jet velocity ($V_o$) to obtain their functional expressions. Based on these expressions, the real-time Jacobian matrix calculation formulas are derived. The derivation process can be referred to in the Appendix C.

The primary advantage of INCA lies in its ability to compute actuator commands incrementally. As evident from (48), the control allocation problem is linear for given flight and actuator states. Therefore, a straightforward and efficient linear method can be employed to solve it. Furthermore, the fact that only local increments $\Delta \delta$ are determined at each time step implies that the Jacobian determinant can be updated to new actuator positions at each time step. Additionally, this matrix adapts dynamically to actuator changes, enabling it to accommodate nonlinear actuator characteristics and consequently achieve superior control allocation results.

4. Flight Simulation

In this section, the proposed control method is employed to achieve the acceleration/deceleration transition flight. To verify the robustness of the INDI method against unmodeled parameters and external disturbances, it is compared with classical methods. In the inner loop, PID controllers are designed specifically for the hover and cruise modes, with gain scheduling employed to switch controllers during the transition phase. Control allocation weights are also switched along with the controllers rather than using the designed control allocation method. The simulation tests the control algorithm’s effectiveness under three conditions: no disturbances, perturbations in modeling parameters, and propulsion fault.

4.1. Transition Trajectory

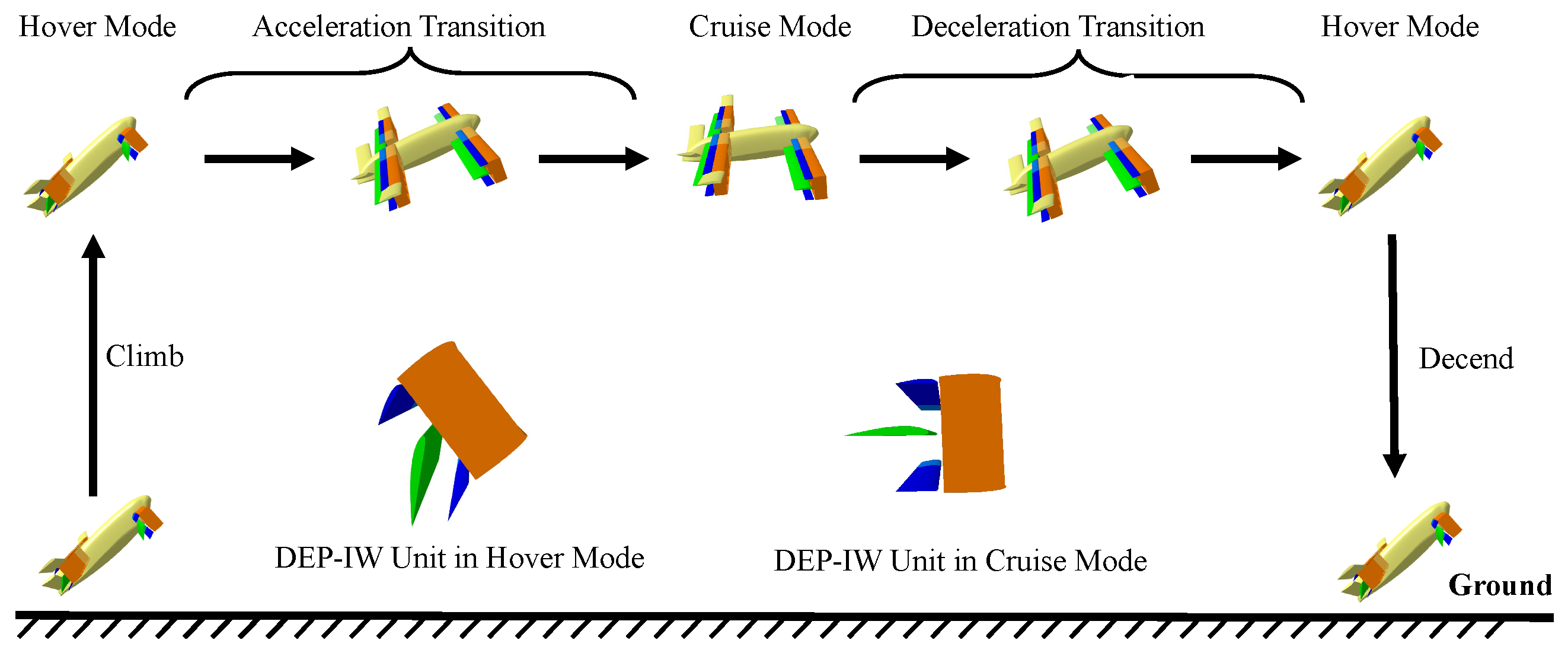
The transition flight trajectory should be designed before starting the flight simulation. Transition flight commands typically include the commands of flight speed, altitude, pitch angle, and tilt angle of the induced wing. The transition trajectory can be generated offline or planned in real time. Since the primary focus of this paper is on the modeling and flight control of the UAV and does not include trajectory planning and generation, a single offline flight trajectory is used consistently in the subsequent simulations for clarity.

As shown in Figure 12, the entire simulation process is as follows: At the start of the simulation, the aircraft’s pitch angle is 45°, the induced wing deflection angle is 45°, and the initial throttle setting is 0.7. And then the aircraft takes off in hover mode and ascends to 20 m before entering the acceleration transition mode. In the acceleration transition mode, the pitch angle is first commanded to ${15}^{\circ }$ to accelerate. When the flight speed exceeds 10 m/s, the pitch angle command is set to $0^{\circ }$, and the induced wing surface deflection angle is reduced from ${45}^{\circ }$ to $0^{\circ }$. When the speed exceeds 25 m/s, the aircraft enters the cruise flight phase. The vehicle transitions into the deceleration mode after 10 s. In the deceleration transition mode, the pitch angle is initially commanded to ${15}^{\circ }$. As the speed decreases to 20 m/s, the pitch angle is further raised to ${45}^{\circ }$, and the induced wing surface is deflected from $0^{\circ }$ to ${45}^{\circ }$. When the speed drops below 5 m/s, the aircraft enters the hover mode and descends for landing.

4.2. Transition Flight Simulation in the Ideal Condition

In ideal conditions, the results of the entire flight simulation process are depicted in Figure 13. For ease of comparison between different control methods, the left side shows the simulation results using the INDI controller, while the right side shows the results using the PID controller. At the beginning of the simulation, the aircraft is in an unbalanced state. To control its horizontal position, adjustments to the pitch angle command are required. During the acceleration transition phase, the pitch angle of the aircraft gradually decreases, and the induced wing surface deflection angle decreases accordingly. Upon entering the cruise flight phase, due to the relatively small angle of attack at this stage, as indicated by the model validation results in Section 2.4, the aircraft experiences a significant pitching moment coefficient. Therefore, the aircraft needs to control the deflection of control surfaces and use differential throttle between the front and rear wing surfaces to balance its pitching moment and achieve stable flight at a constant altitude and speed. In the deceleration transition mode, as the aircraft pitch angle increases, the flight altitude will increase, and consequently, the throttle will gradually decrease. After entering the rotor flight mode, the aircraft gradually descends.

From the simulation results, it can be observed that during the acceleration transition phase, the INDI method achieves faster attitude angle tracking, resulting in minimal altitude variation during flight. Additionally, throttle manipulation exhibits fewer significant fluctuations. During the deceleration transition phase, the INDI method demonstrates more accurate attitude angle tracking compared to the PID method. The PID method, particularly in the early stages of the transition flight phase, exhibits less precise tracking of pitch angle commands, resulting in prolonged deceleration transition flight time.

4.3. Transition Flight Simulation Under Parameter Perturbation

Due to discrepancies in the model, certain characteristic parameters of the aircraft during actual flight may differ from those in the model. Therefore, it is necessary to perform parameter biasing before conducting digital simulations. Specifically, the moment of inertia (J) is increased by $30\%$, the control surface effectiveness ($C_{L_{{\delta }_e}}$) is reduced by $30\%$, and the parameter that represents the influence of the induced wing surface on the duct jet (${\eta }_1$) is increased by $10\%$.

The simulation results are shown in Figure 14. As shown in the figure, it can be observed that the pitch angle required to maintain horizontal equilibrium in the hover state is smaller compared to the simulation under ideal conditions. Comparing the INDI and PID simulation results, it is evident that both methods achieve the specified altitude at $10 \mathrm{s}$. However, in the simulation using the PID controller, the aircraft still has horizontal velocity, and the pitch angle has not yet converged to a stable state. During the acceleration transition phase, the PID method exhibits greater altitude variation, whereas the INDI method’s altitude changes are nearly consistent with those under ideal conditions. During the deceleration transition phase, the INDI method continues to track the attitude commands accurately, while the PID method’s response is slower. Thus, the simulation process demonstrates that the INDI method exhibits better robustness compared to the PID method, effectively adapting to parameter variations.

4.4. Transition Flight Simulation Under Propulsion Fault

Since a distributed propulsion aircraft has multiple propulsion units, the probability of propulsion failure increases significantly. In this simulation, at the 1st second, the duct on the far left of the front propulsion wing experiences a failure, resulting in the inability to generate thrust. The flight simulation results are shown in Figure 15. After the propulsion failure, the attitude of the vehicle changes, and the INDI method quickly adjusts the flight attitude to regain balance. In contrast, the PID method exhibits a relatively slower pitch angle adjustment. During the acceleration phase, the failure of a single duct on the wingtip induces additional roll and yaw moments, causing fluctuations in roll and yaw angles during flight. The simulation results indicate that the INDI method results in smaller changes in roll and yaw angles compared to the PID method. This is because the INDI method employs the INCA (Incremental Nonlinear Dynamic Inversion) control allocation method, which enables more precise force and moment distribution during transition flight, therefore achieving better attitude control of the vehicle.

Furthermore, upon entering the hover state during the deceleration transition, the aircraft’s attitude angles quickly converge under the INDI control method, while the PID method results in significant oscillations.

5. Conclusions

In this paper, a dynamic model for a distributed propulsion wing with induced wing configuration UAV that includes propulsion-aerodynamic coupling effects is established. Beginning with a single ducted fan power model, the calculation method for ducted jet velocity is derived. Using the momentum theorem, a propulsion-aerodynamic coupling model is then formulated for both powered and unpowered states, resulting in a unified dynamic model applicable across the full flight envelope.

A unified control framework is proposed. By comparing the CFD calculation results and model prediction results under different flight conditions, the accuracy of the established model is validated. Based on this model, we design a controller that includes outer-loop speed control and inner-loop attitude control. The attitude control system leverages incremental nonlinear dynamic inversion (INDI), which significantly enhances the robustness of the controller by reducing dependency on an accurate model. Unlike traditional nonlinear dynamic inversion (NDI), INDI requires only an approximate model, allowing it to quickly respond to system disturbances and parameter variations through incremental feedback. This approach provides reliable and adaptive control performance even under uncertain conditions, making it ideal for handling modeling errors and external disturbances. Additionally, a multi-level control allocation scheme is designed, employing an incremental control allocation approach to accommodate changes in actuator control effectiveness and coupling characteristics between actuators under different flight conditions.

Digital simulations are conducted to compare the proposed control method with the PID control method under three conditions: ideal conditions, parameter perturbation, and propulsion failure. The results show that the proposed control method is better at tracking control commands and exhibits greater robustness. Based on the digital simulation results, future work should include flight tests to further validate the proposed control scheme. Additionally, due to the large initial pitch angle of the aircraft, higher landing gear is required. To address this, a ground takeoff method should also be designed. In actual future flights, a smaller initial pitch angle will be considered, with nose lift during takeoff achieved through differential thrust. This approach can reduce the landing gear requirements.