PCA-Kriging-Based Oscillating Jet Actuator Optimization and Wing Separation Flow Control
Abstract
1. Introduction
2. Experimental Setup
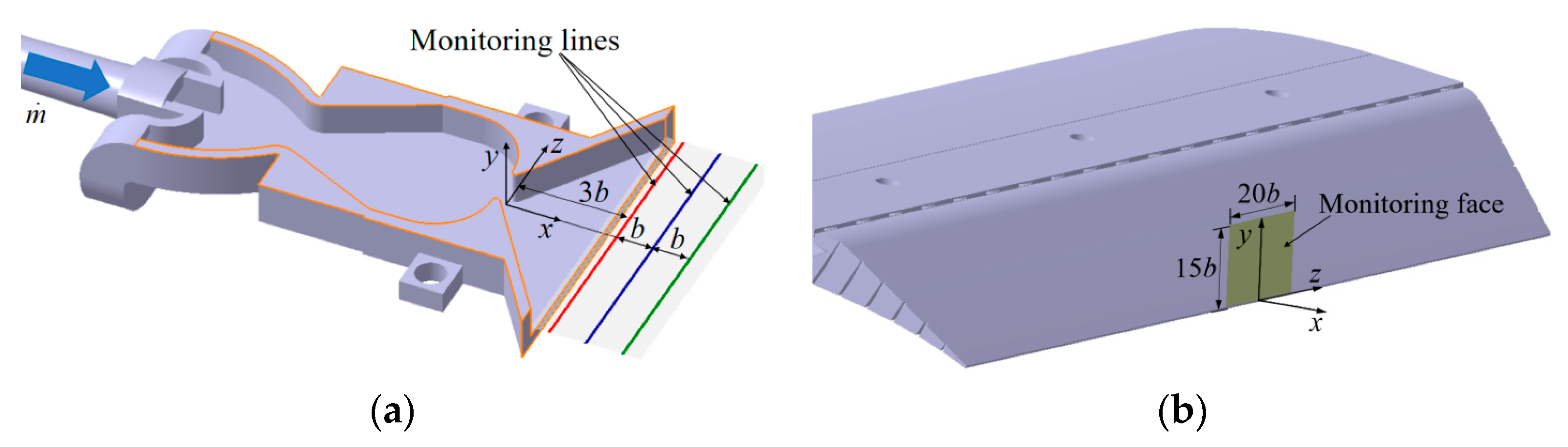
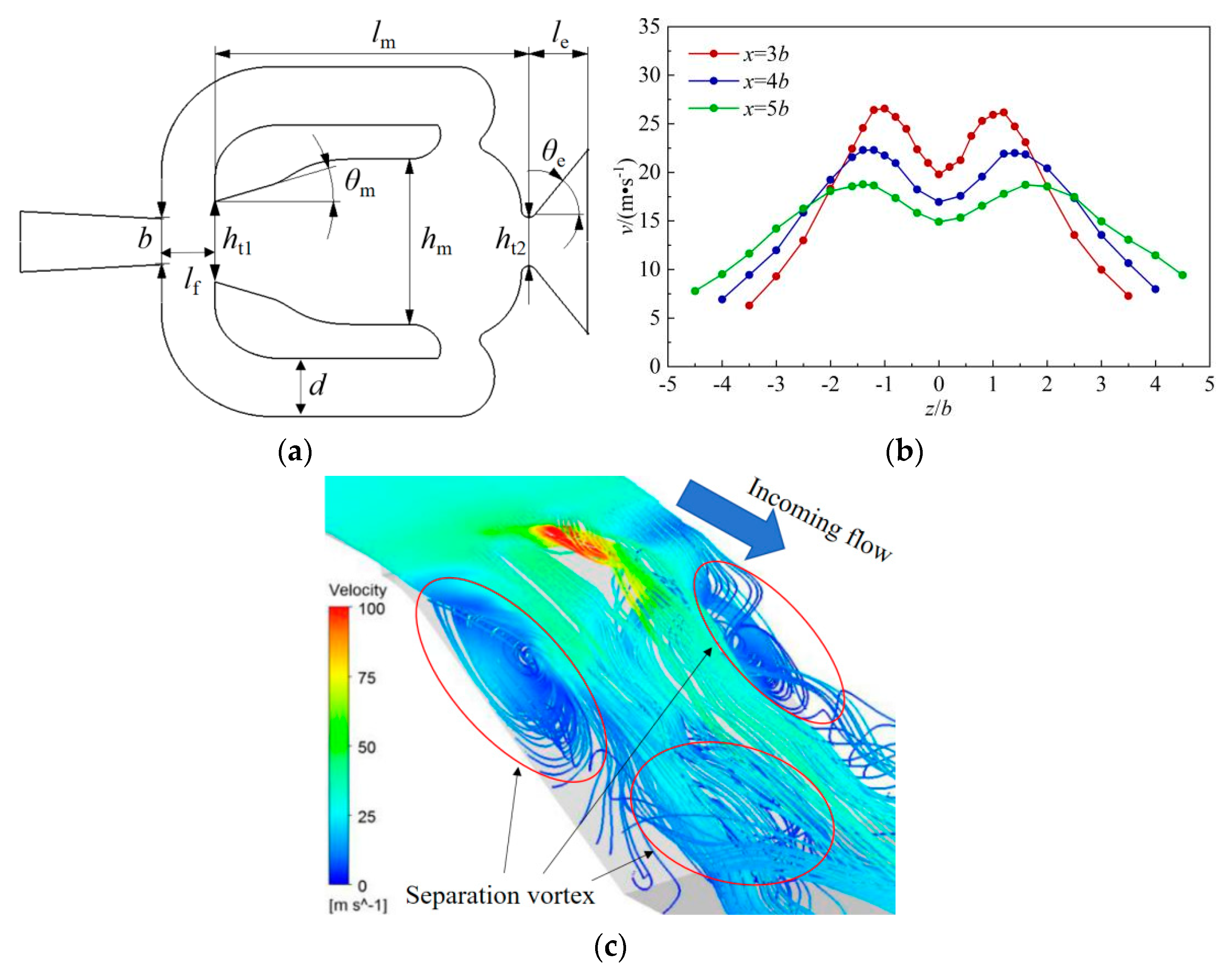
2.1. Oscillating Jet Actuator
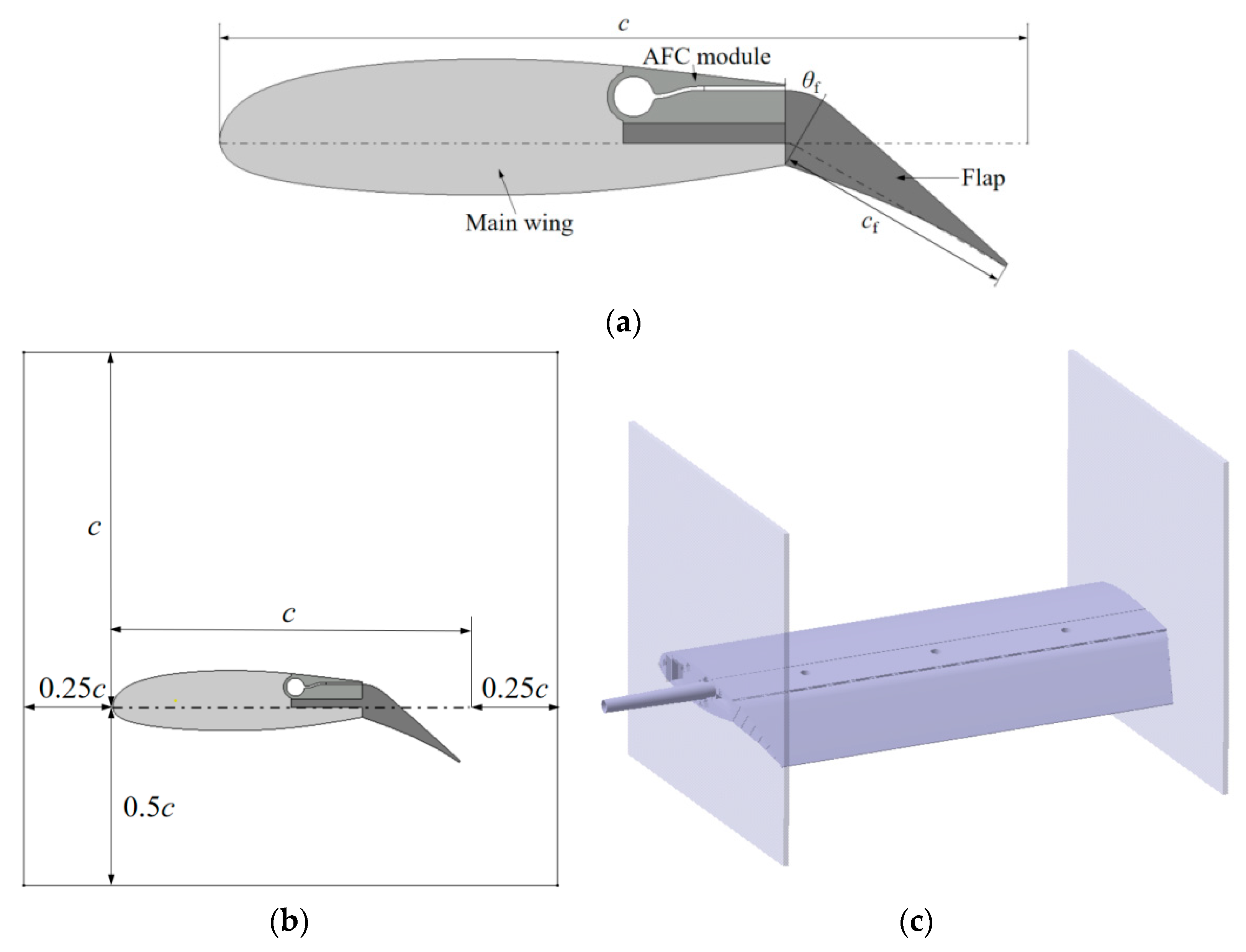
2.2. Wing Model
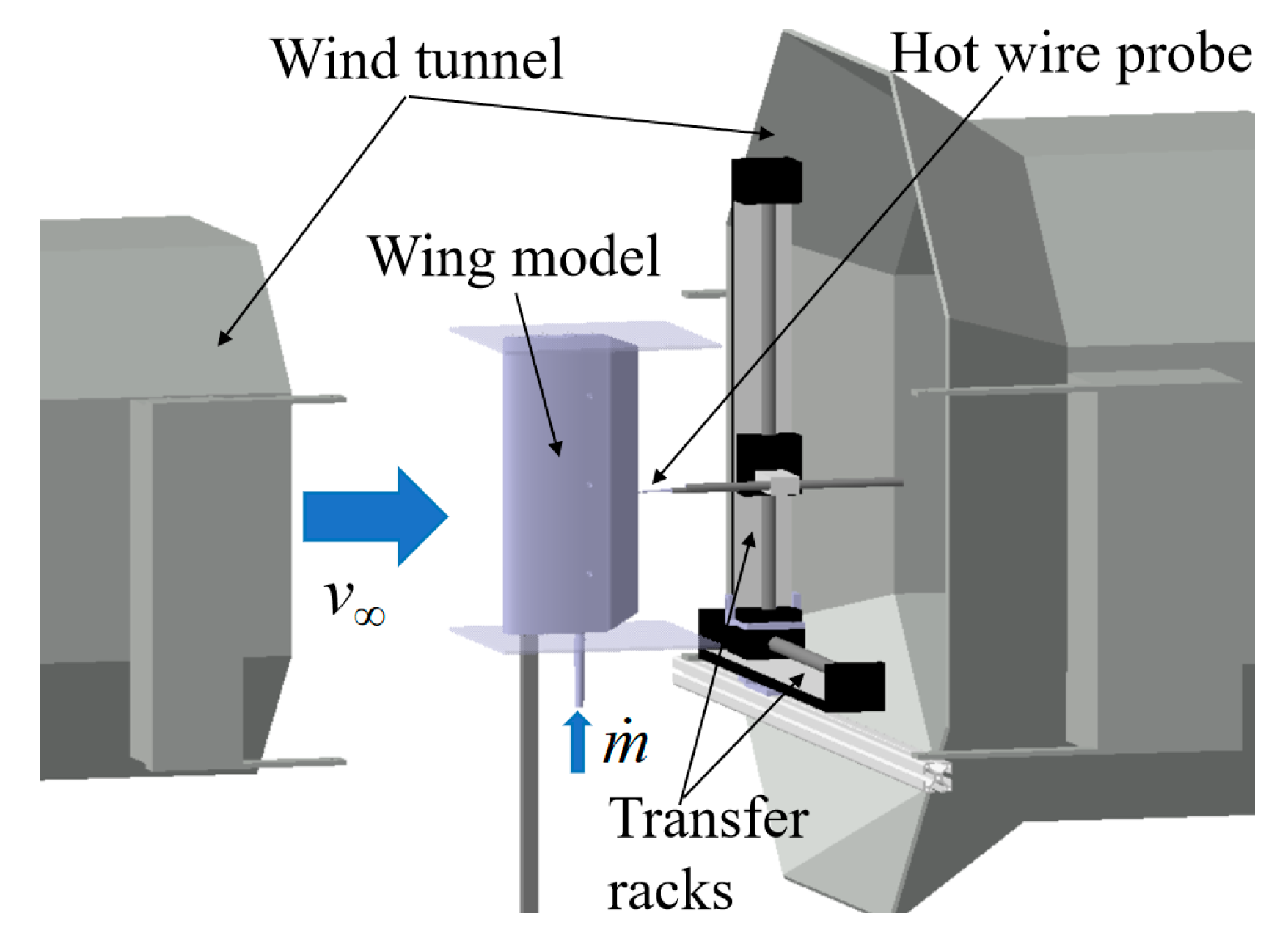
2.3. Experimental Equipment
3. Optimization Methods
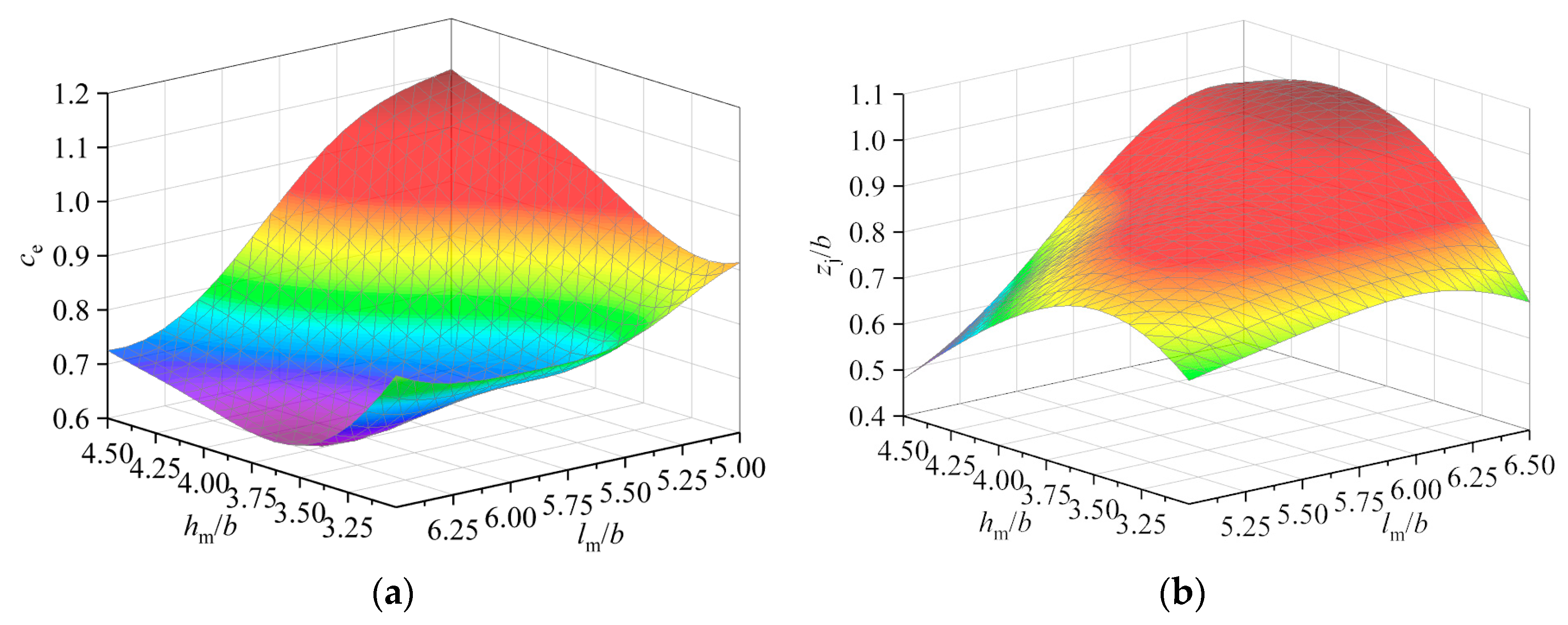
3.1. Optimization Objectives
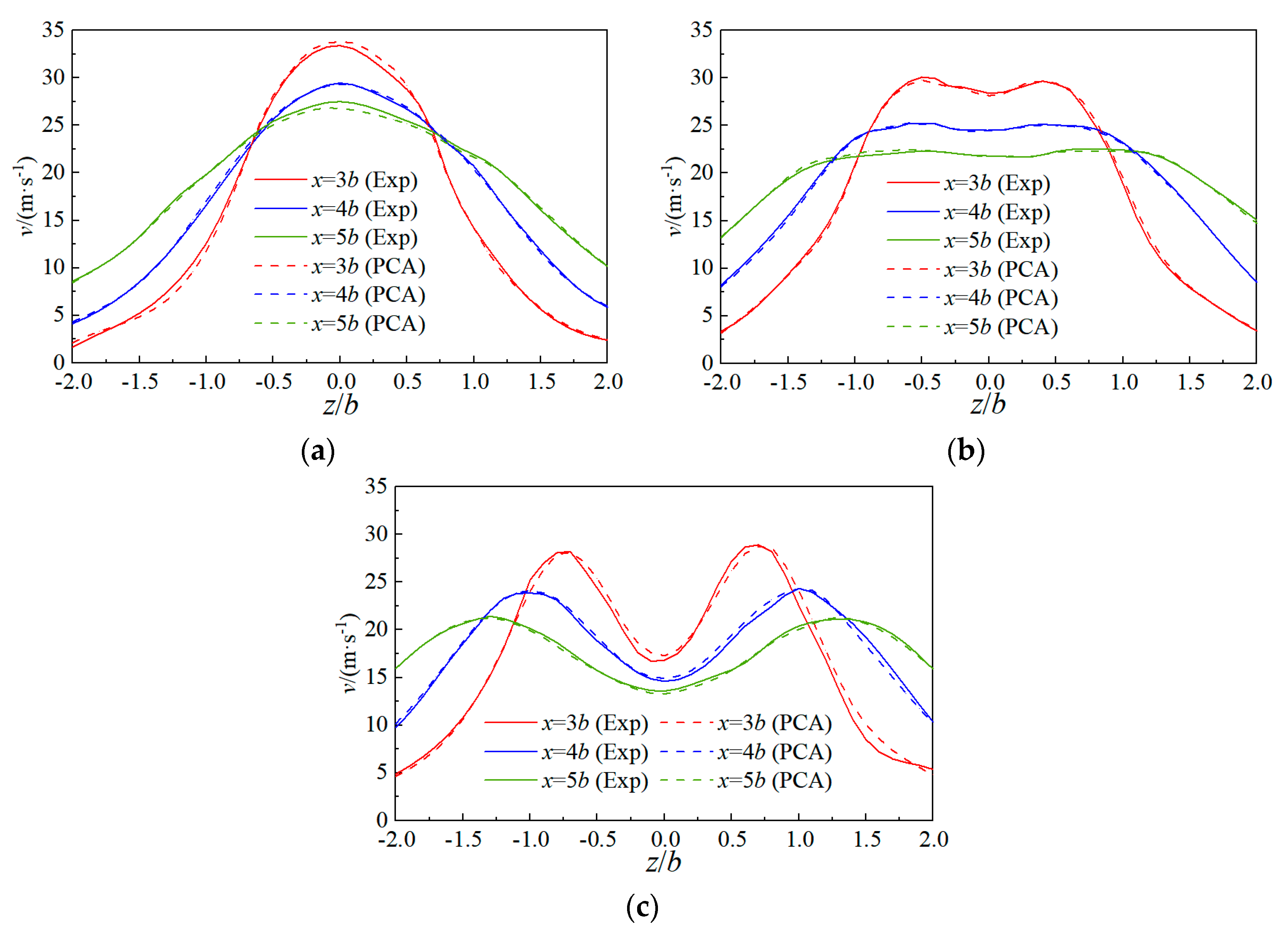
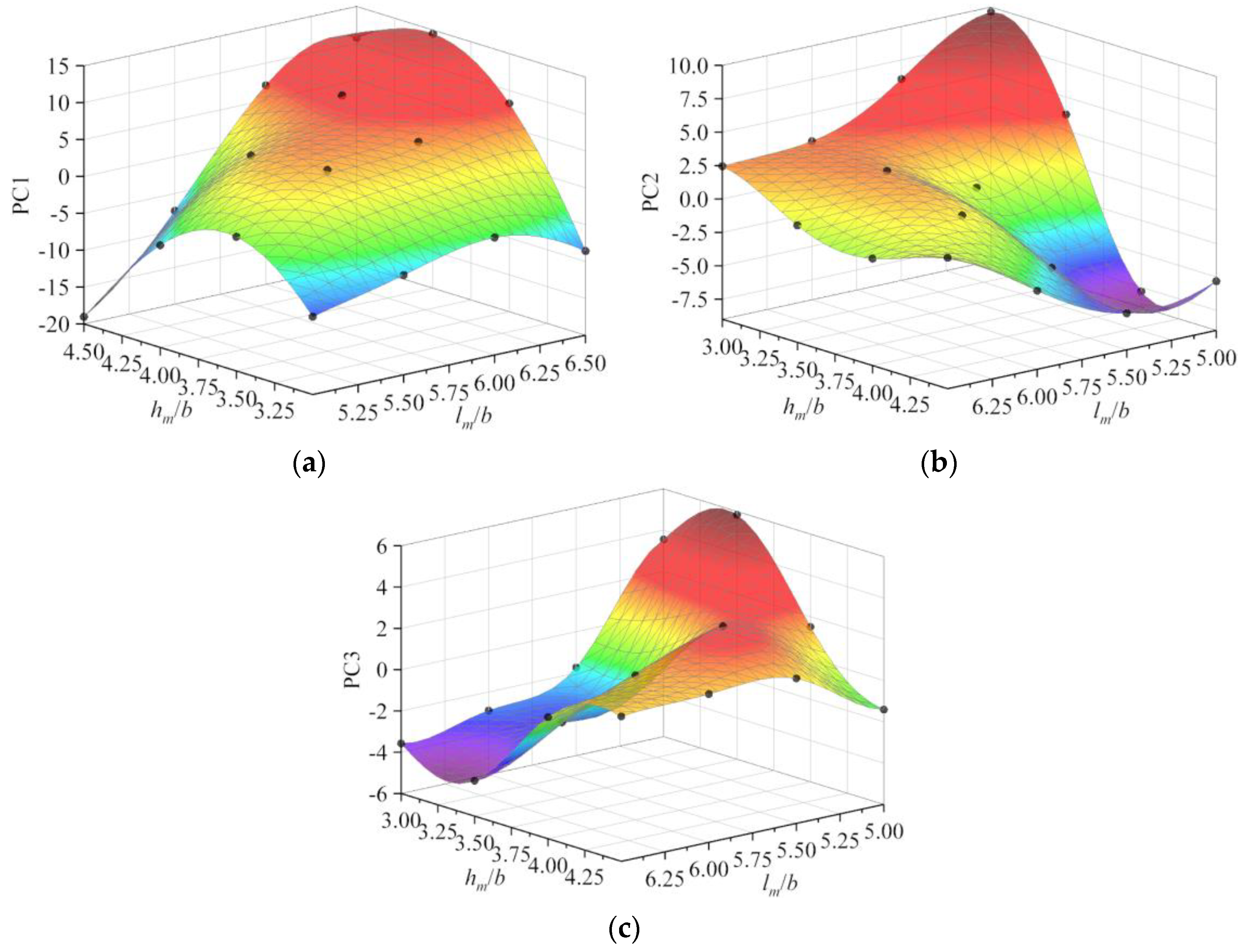
3.2. PCA Methods
3.3. Kriging Surrogate Model
3.4. Multi-Objective Optimization Methods
- Population initialization: Randomly generate the initial population, where each individual represents a solution.
- Evaluation: Calculate the value of the objective function for each individual.
- Non-dominated sorting: Compare all individuals in the population pairwise to determine the set of individuals ps dominated by each individual s (each objective is inferior to the individual s) and the number of individuals ns dominated by s (there is at least one objective exceeding the individual s) and classify the individuals with ns = 0 as the first rank (non-dominated individuals), which are the optimal solutions. Then sort the individuals recursively until they are all assigned to a certain rank.
- Crowding degree calculation: Sort the individuals within each rank separately according to each objective function value, calculate the distances between neighboring individuals, accumulate these distances to obtain the crowding degree of the individual and arrange all individuals within the rank in descending order according to the crowding degree.
- Selection and updating: Perform the binary tournament selection strategy and select the individual with low non-dominance rank and high crowding degree as the parent.
- Genetic operation: Perform the crossover operation on the selected parent individuals to generate new offspring individuals and mutation operation on the offspring individuals to increase the population diversity.
- Merging the population: Combine the newly generated offspring with the best individuals of the previous generation to form a new generation of the population.
- Determining the termination conditions: Determine whether the termination conditions are met, such as reaching the maximum number of iterations, meeting the preset criteria for the quality of the solution or the algorithm converging. If the termination conditions are met, then output the optimal solution set and end the algorithm, otherwise, return to step 2 to continue the iteration.
4. Actuator Optimization Design
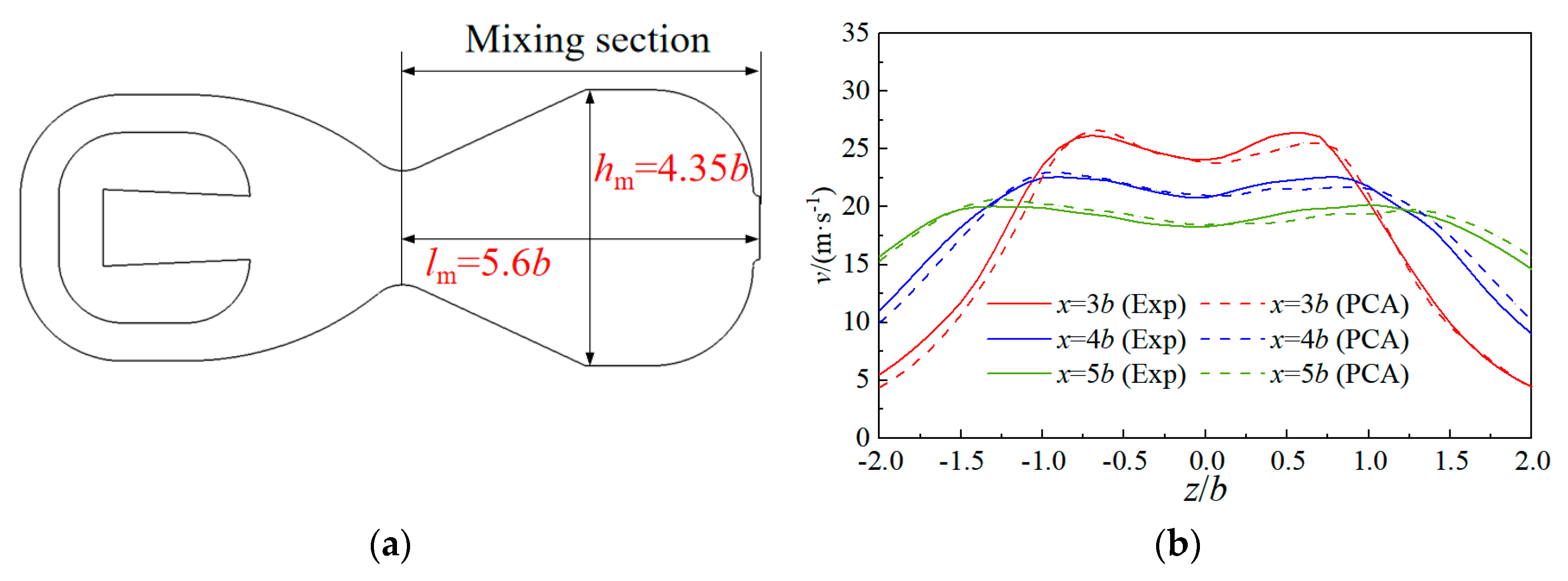
4.1. Optimization Design of Mixing Section
4.2. Optimization Design of Expansion Section
5. Wing Separation Flow Control
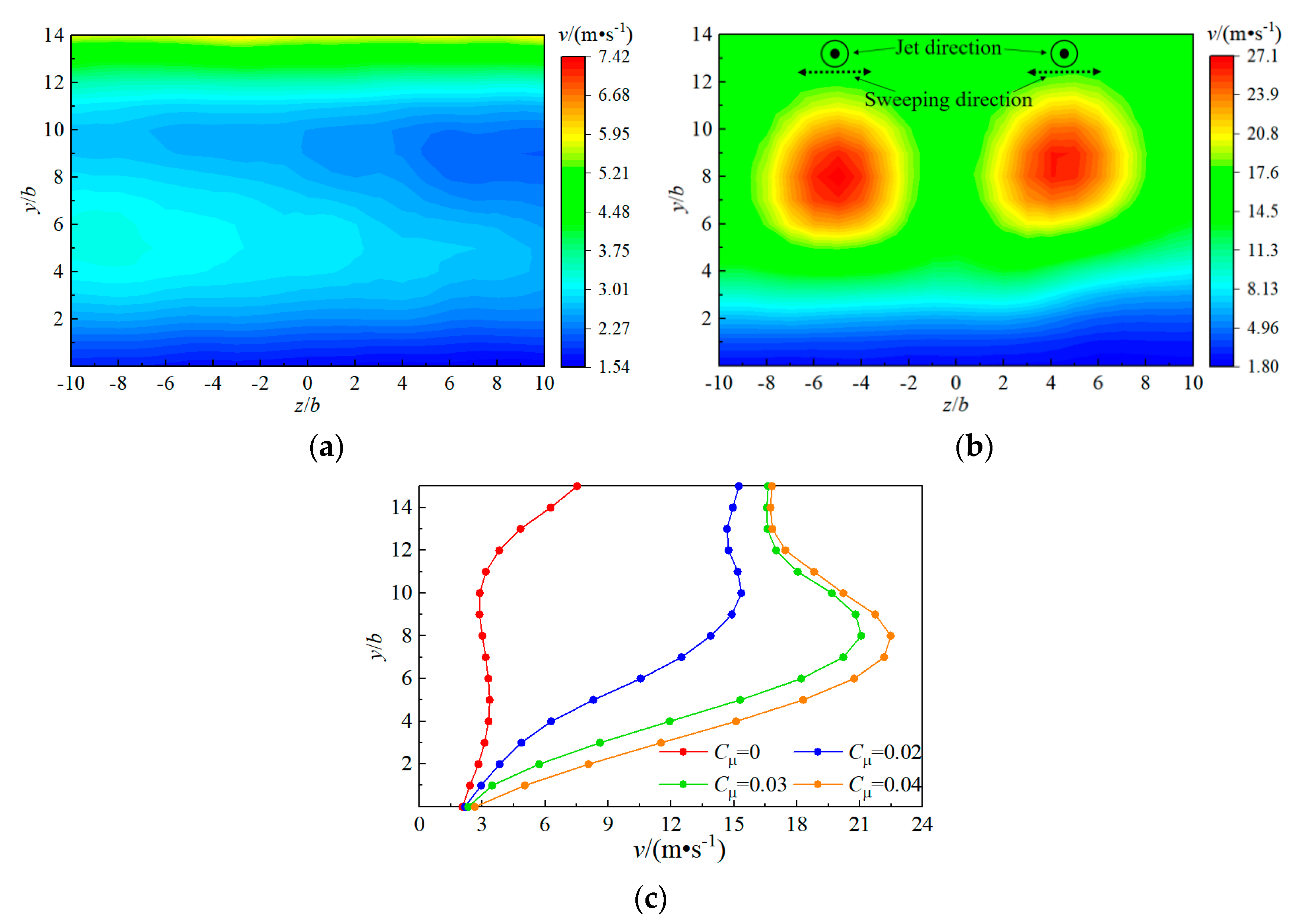
5.1. Effect of Momentum
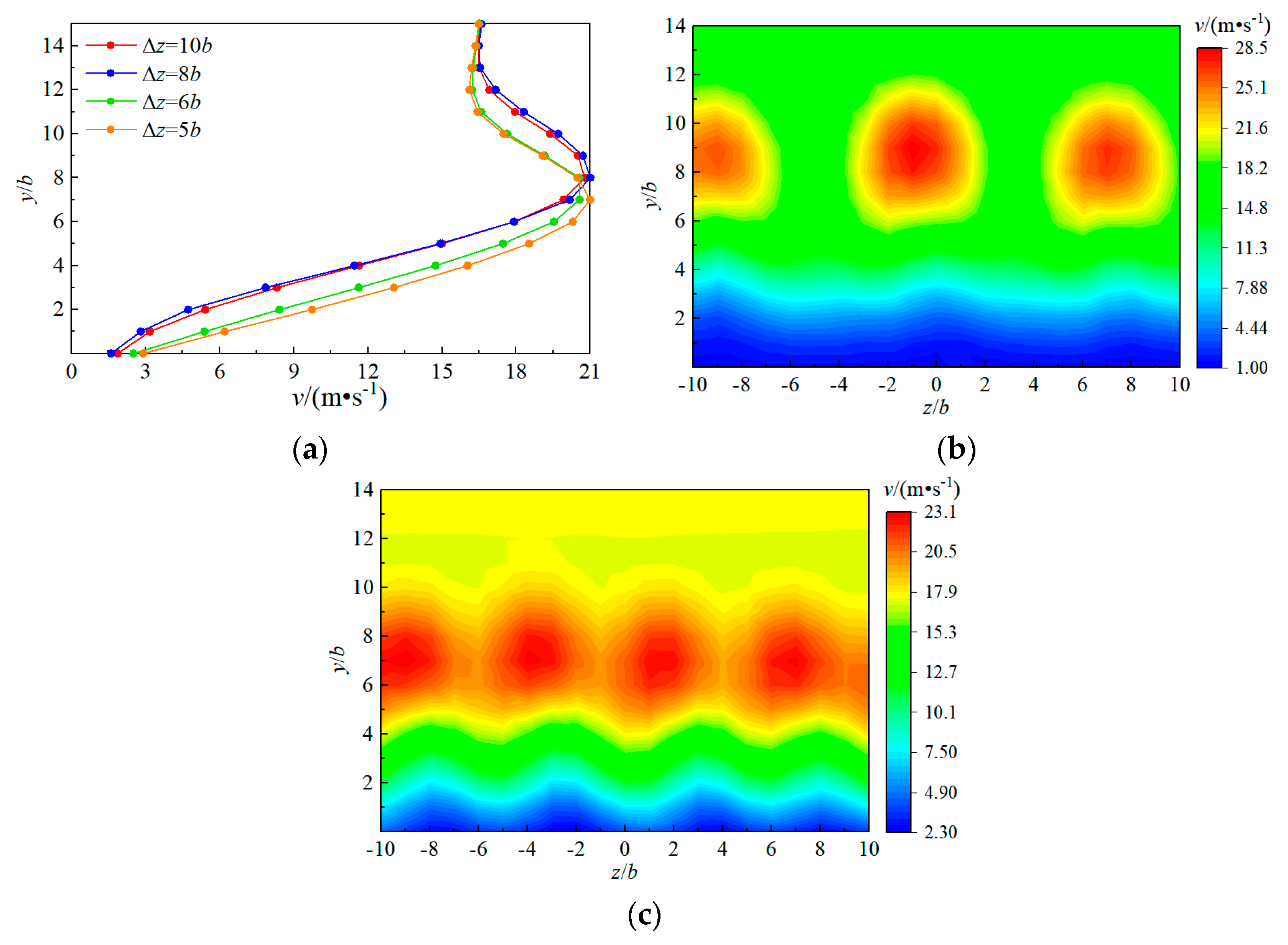
5.2. Effect of Arrangement Distance
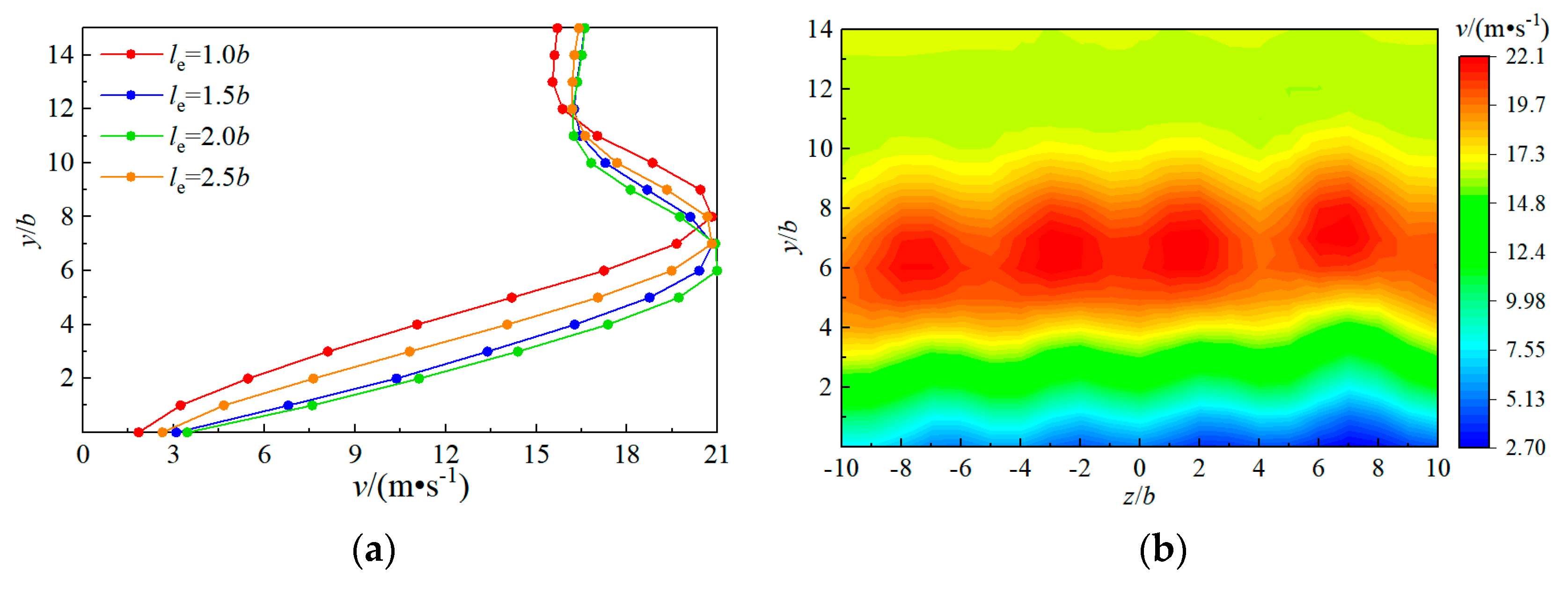
5.3. Effect of the Length of the Expansion Section
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, R.; Bai, J.Q.; Qiu, Y.S.; Gao, G.Z. Effects of Geometrical Parameters of Internal Blown Flap and Its Optimal Design. J. Northwestern Polytech. Univ. 2020, 38, 58–67. [Google Scholar] [CrossRef]
- Zha, G.; Paxton, C.; Conley, C.A. Effect of Injection Slot Size on The Performance of Coflow Jet Airfoil. J. Aircr. 2006, 43, 987–995. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Luo, Z.B.; Yuan, X.X.; Tu, G.H. Review of controlling flow separation over airfoils with periodic excitation. Adv. Mech. 2020, 50, 202007. [Google Scholar]
- Luo, Z.B.; Xia, Z.X.; Deng, X. Research progress of dual synthetic jets and its flow control technology. Acta Aerodyn. Sin. 2017, 35, 252–264. [Google Scholar]
- Sun, F.P.; Lin, R.S.; Haas, M. Air flow control by fluidic diverter for low NOx jet engine combustion. In Proceedings of the 1st Flow Control Conference, Reston, VA, USA, 24–26 June 2002. [Google Scholar] [CrossRef]
- Guyot, D.; Bobusch, B.; Paschereit, C.O. Active combustion control using a fluidic oscillator for asymmetric fuel flow modulation. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Reston, VA, USA, 21–23 July 2008. [Google Scholar] [CrossRef]
- Li, Z.Y.; Liu, Y.D.; Zhou, W.W. Lift augmentation potential of the circulation control wing driven by sweeping jets. AIAA J. 2022, 60, 4677–4698. [Google Scholar] [CrossRef]
- Dandois, J.; Verbeke, C.; Ternoy, F. Performance enhancement of a vertical tail model with sweeping jets. AIAA J. 2020, 58, 5202–5215. [Google Scholar] [CrossRef]
- Kim, S.H. Effects of installation location of fluidic oscillators on aerodynamic performance of an airfoil. Aerosp. Sci. Technol. 2020, 99, 105735. [Google Scholar] [CrossRef]
- Kara, K.; Kim, D.; Morris, P.J. Flow-separation control using sweeping jet actuator. AIAA J. 2018, 56, 4604–4613. [Google Scholar] [CrossRef]
- Koklu, M.; Owens, L.R. Comparison of sweeping jet actuators with different flow-control techniques for flow-separation control. AIAA J. 2017, 55, 848–860. [Google Scholar] [CrossRef]
- Song, J.S. Active flow control in an S-shaped duct at Mach 0.4 using sweeping jet actuators. Exp. Therm. Fluid Sci. 2022, 138, 110699. [Google Scholar] [CrossRef]
- Schmidt, H.J.; Woszidlo, R.; Nayeri, C.N. Drag reduction on a rectangular bluff body with base flaps and fluidic oscillators. Exp. Fluids 2015, 56, 151. [Google Scholar] [CrossRef]
- Veerasamy, D.; Tajik, A.R.; Pastur, L. Effect of base blowing by a large-scale fluidic oscillator on the bistable wake behind a flat-back Ahmed body. Phys. Fluids 2022, 34, 035115. [Google Scholar] [CrossRef]
- Kim, M. Experimental study on heat transfer and flow structures of feedback-free sweeping jet impinging on a flat surface. Int. J. Heat Mass Transf. 2020, 159, 120085. [Google Scholar] [CrossRef]
- Spens, A.; Bons, J.P. Experimental investigation of synchronized sweeping jets for film cooling application. In Proceedings of the AIAA Scitech 2021 Forum, Reston, VA, USA, 11–15 January 2021. [Google Scholar] [CrossRef]
- Zhou, W.W.; Wang, K.C.; Yuan, T.J. Spatiotemporal distributions of sweeping jet film cooling with a compact geometry. Phys. Fluids 2022, 34, 025113. [Google Scholar] [CrossRef]
- Pack, L.G.; Koklu, M. Active flow control using sweeping jet actuators on a semi-span wing model. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Slupski, B.J.; Kara, K. Separated flow control over NACA 0015 airfoil using sweeping jet actuator. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Tewes, P.; Taubert, L.; Wygnanski, I. On the use of sweeping jets to augment the lift of a λ-wing. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef]
- Jones, G.S.; Milholen, W.E.; Chan, D.T. A sweeping jet application on a high Reynolds number semispan supercritical wing configuration. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Spens, A.; Pisano, A.P.; Bons, J.P. Leading-Edge Active Flow Control Enabled by Curved Fluidic Oscillators. AIAA J. 2023, 61, 1675–1686. [Google Scholar] [CrossRef]
- Seele, R.; Graff, E.; Lin, J. Performance Enhancement of a Vertical Tail Model with Sweeping Jet Actuators. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Whalen, E.A.; Lacy, D.S.; Lin, J.C. Performance enhancement of a full-scale vertical tail model equipped with active flow control. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Andino, M.Y.; Lin, J.C.; Washburn, A.E. Flow separation control on a full-scale vertical tail model using sweeping jet actuators. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Vatsa, V.N.; Duda, B.M.; Lin, J.C. Numerical simulation of a simplified high-lift CRM configuration embedded with fluidic actuators. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Lin, J.C.; Pack, L.G.; Hannon, J. Wind tunnel testing of active flow control on the high lift common research model. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Pack, L.G.; Lin, J.C.; Hannon, J. Sweeping jet flow control on the simplified high-lift version of the common research model. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Vatsa, V.N.; Lin, J.C.; Pack, L.G. CFD and experimental data comparisons for conventional and AFC-enabled CRM high-lift configurations (invited). In Proceedings of the AIAA AVIATION 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar] [CrossRef]
- Schloesser, P.; Meyer, M.; Schueller, M. Fluidic actuators for separation control at the engine/wing junction. Aircr. Eng. Aerosp. Technol. 2017, 89, 709–718. [Google Scholar] [CrossRef]
- Ganesh, R.G.; Raghu, S. Cavity Resonance Suppression Using Miniature Fluidic Oscillators. AIAA J. 2004, 42, 2608–2611. [Google Scholar]
- Brayh, C. Cold Weather Fluidic Fan Spray Devices and Method. U.S. Patent 4463904, 7 August 1984. [Google Scholar]
- Stouffer, R.D. Liquid Oscillator Device. U.S. Patent 4508267, 2 April 1985. [Google Scholar]
- Sun, Q.X.; Wang, W.B.; Huang, Y. Key factors affecting the separation control effect of oscillating jets. Acta Aerodyn. Sin. 2023, 41, 56–67. [Google Scholar]
- Jing, Y.U.; Jiang, A.; Liang, L.I.U.; Xiaojun, W.U.; Yewei, G.U.I.; Shenshen, L.I.U. PCA aerodynamic geometry parametrization method. Acta Aeronaut. Et Astronaut. Sin. 2024, 45, 129125. [Google Scholar]
- Bobusch, B.C.; Woszidlo, R.; Bergada, J.M. Experimental study of the internal flow structures inside a fluidic oscillator. Exp. Fluids 2013, 54, 1559. [Google Scholar] [CrossRef]
- Bobusch, B.C.; Woszidlo, R.; Kruger, O. Numerical Investigations on Geometric Parameters Affecting the Oscillation Properties of a Fluidic Oscillator. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]



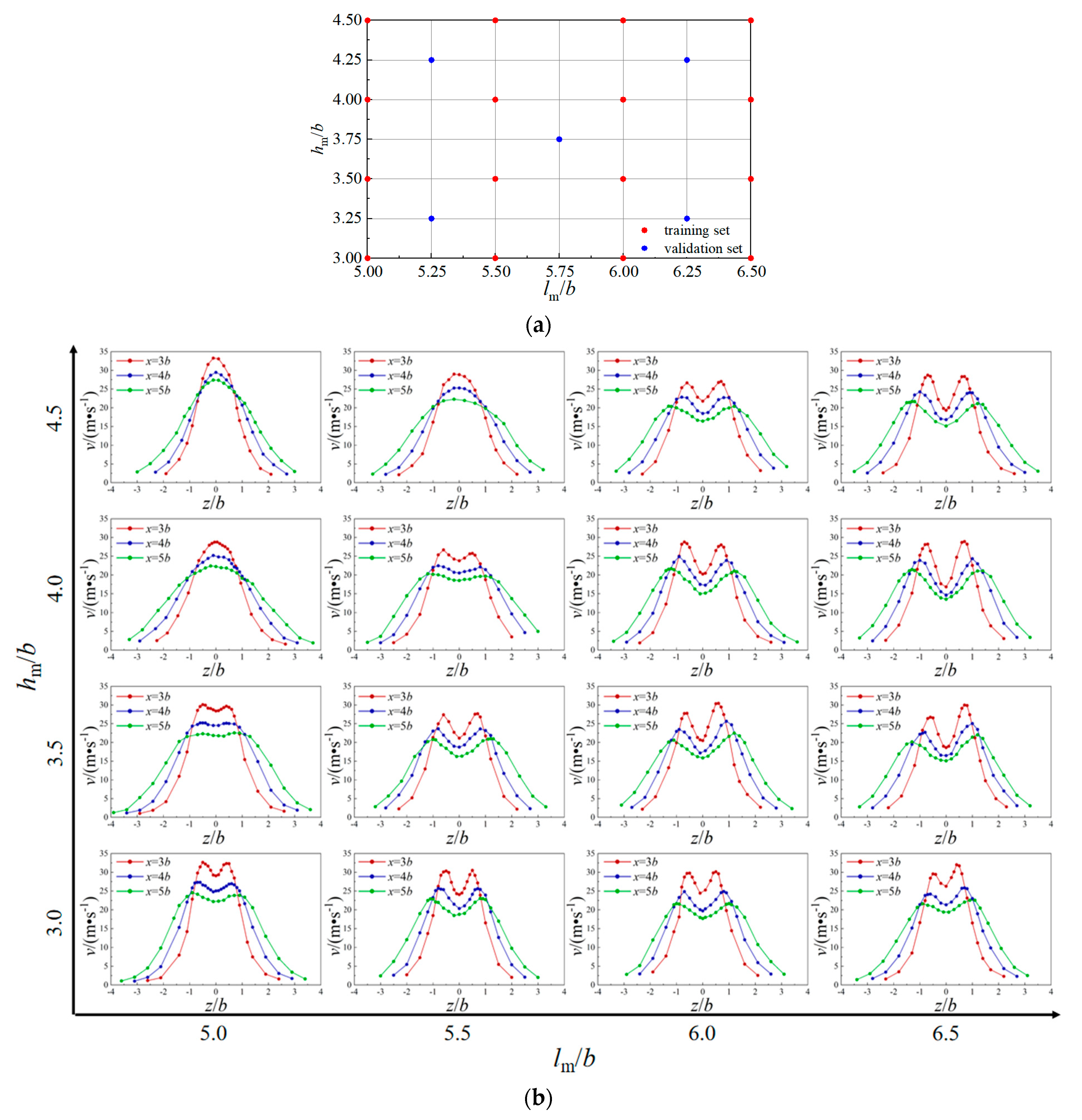
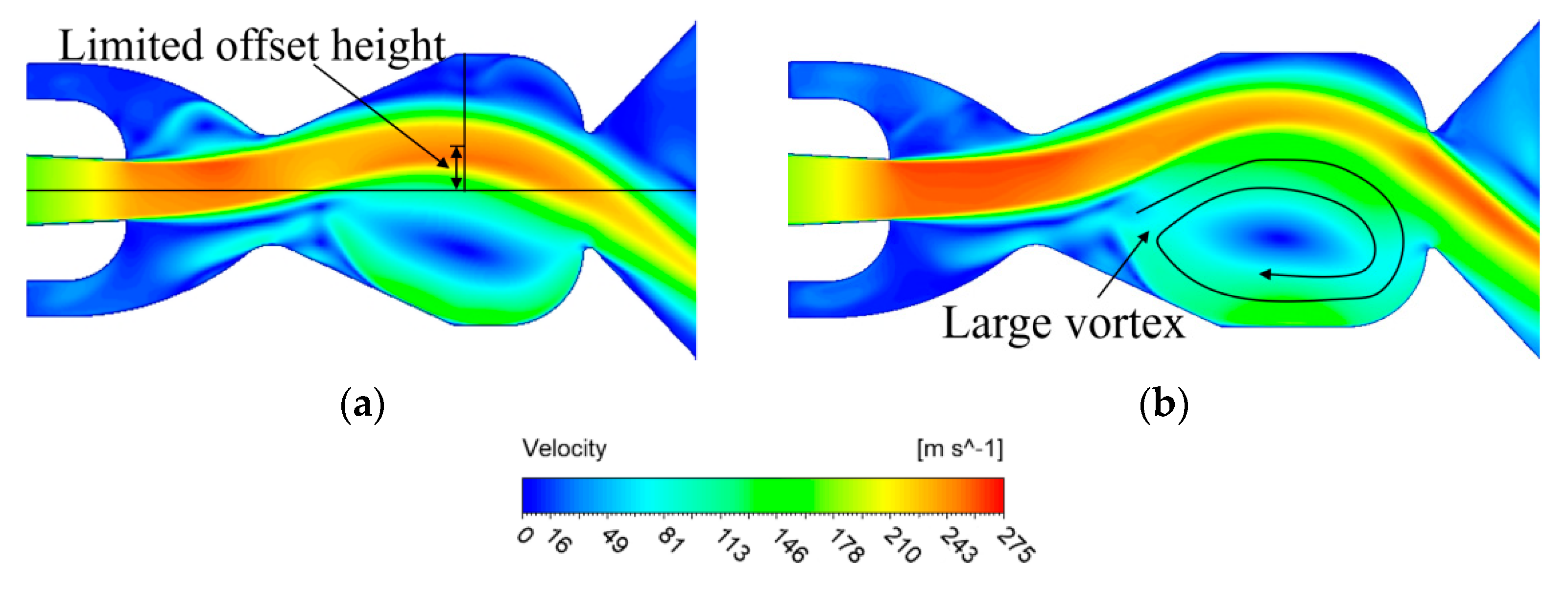
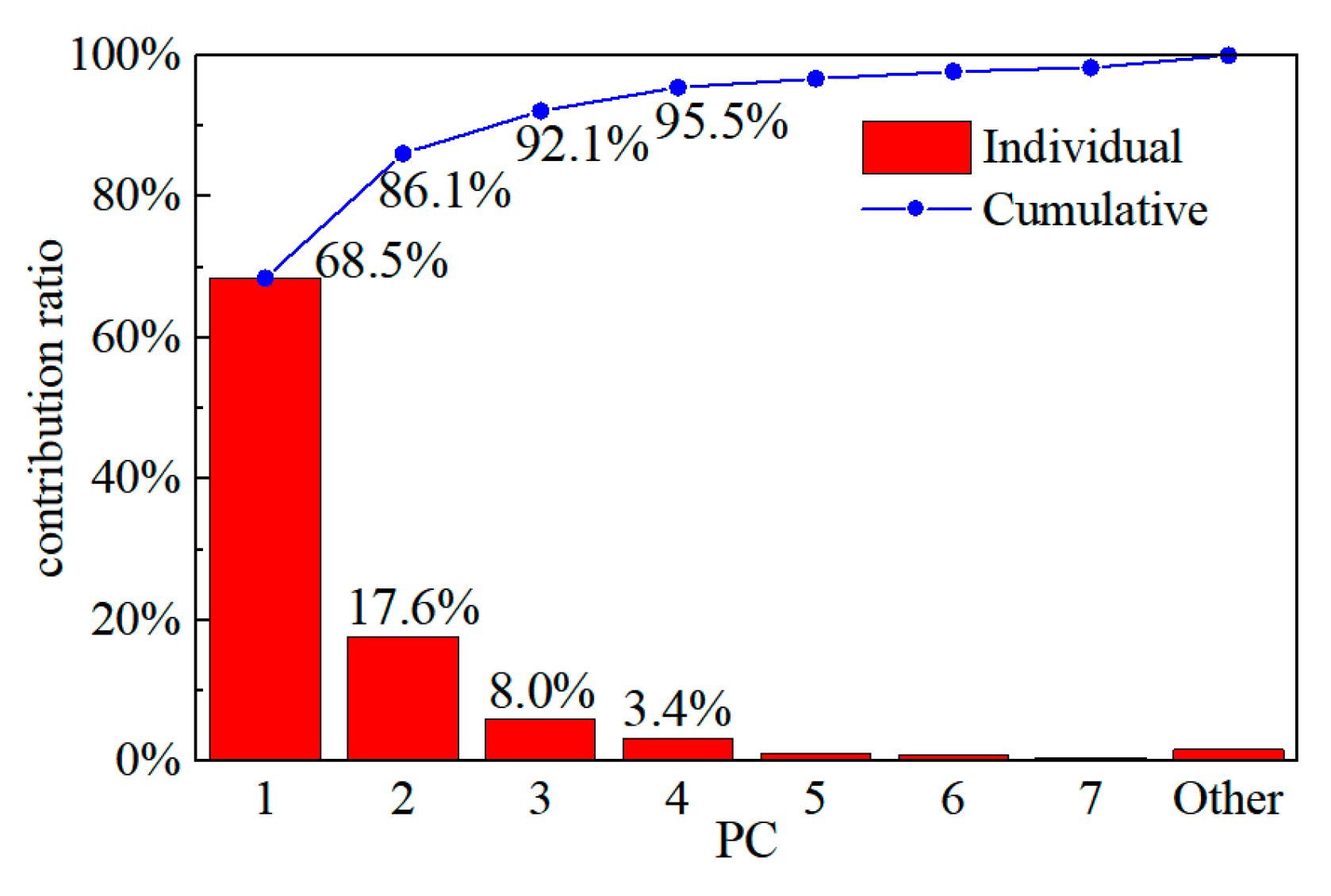

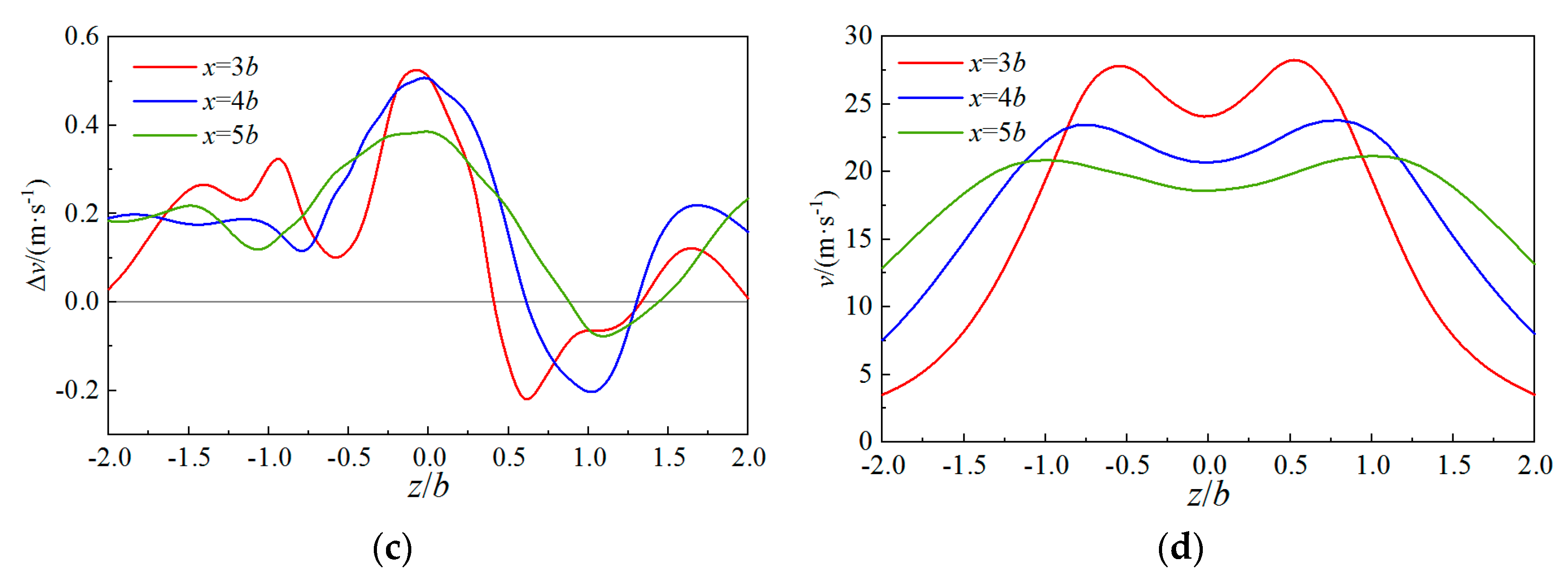

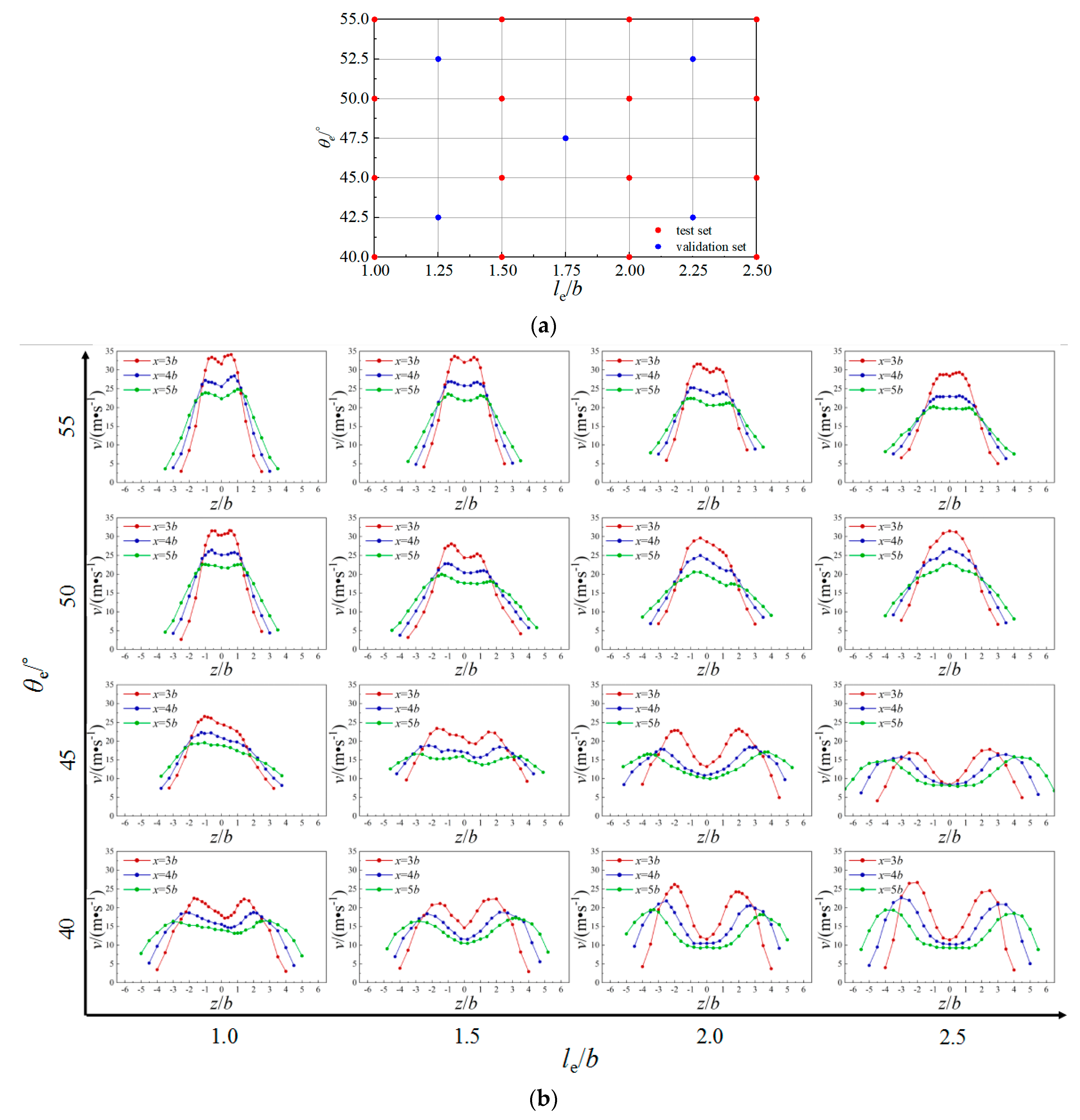
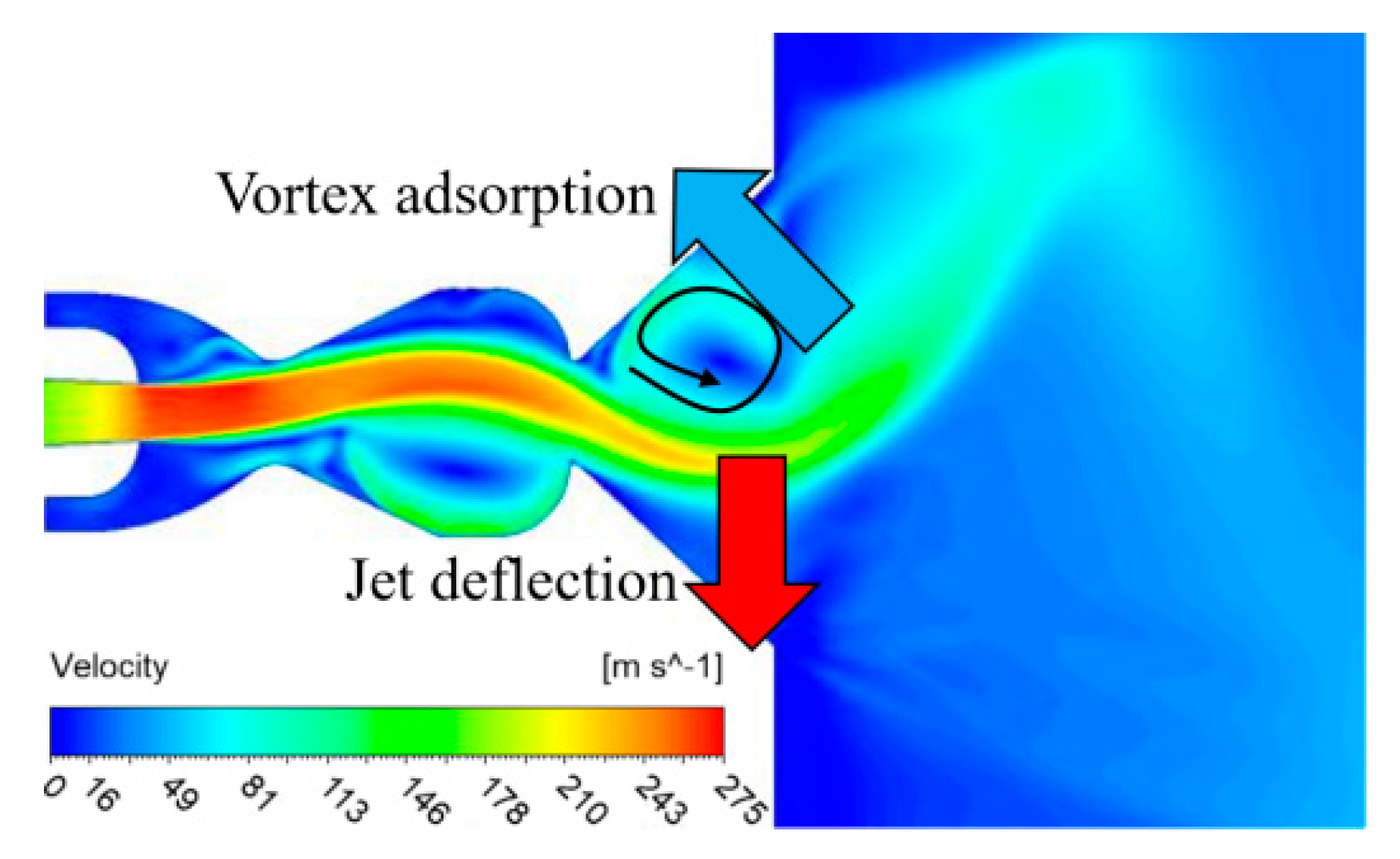
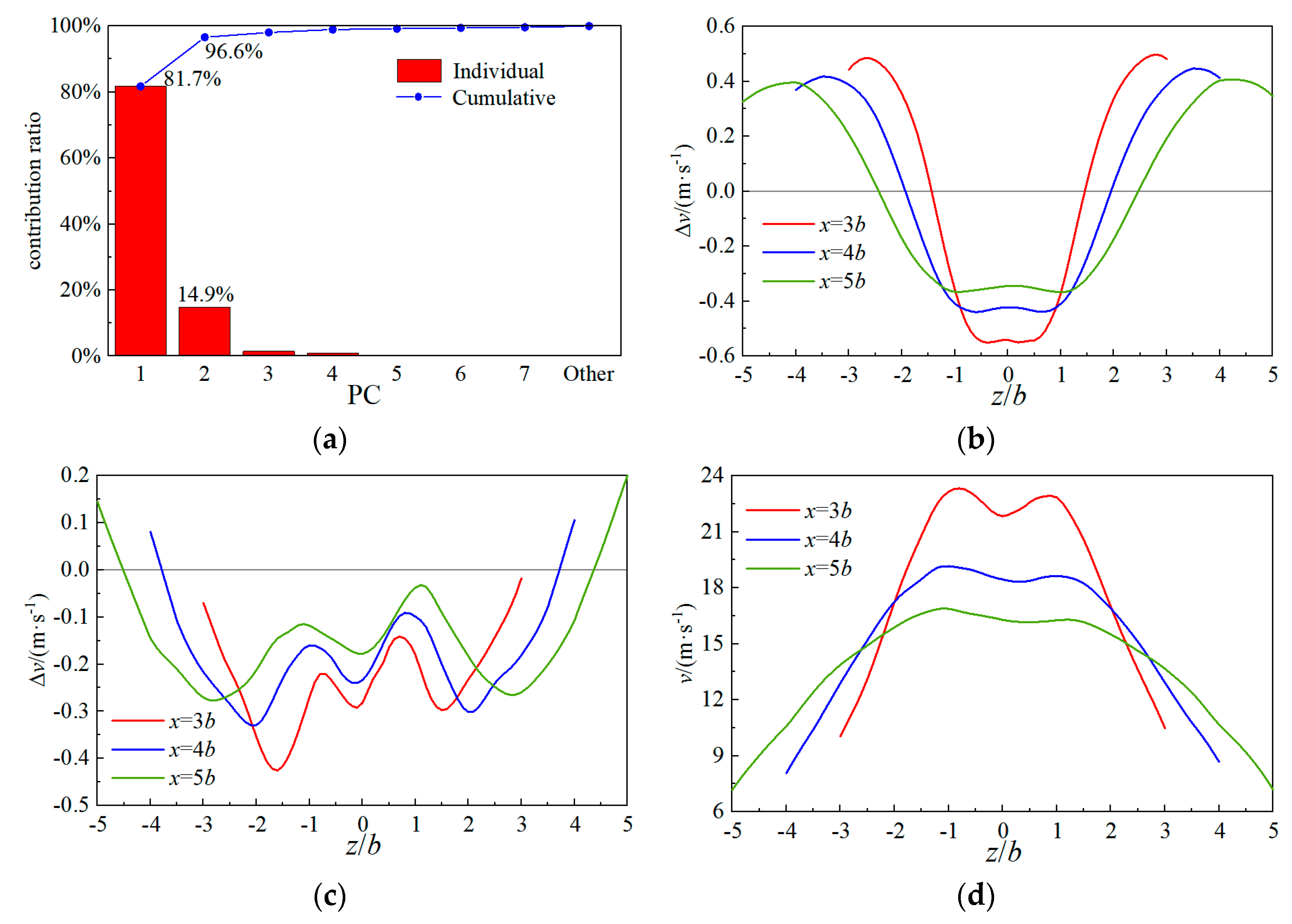

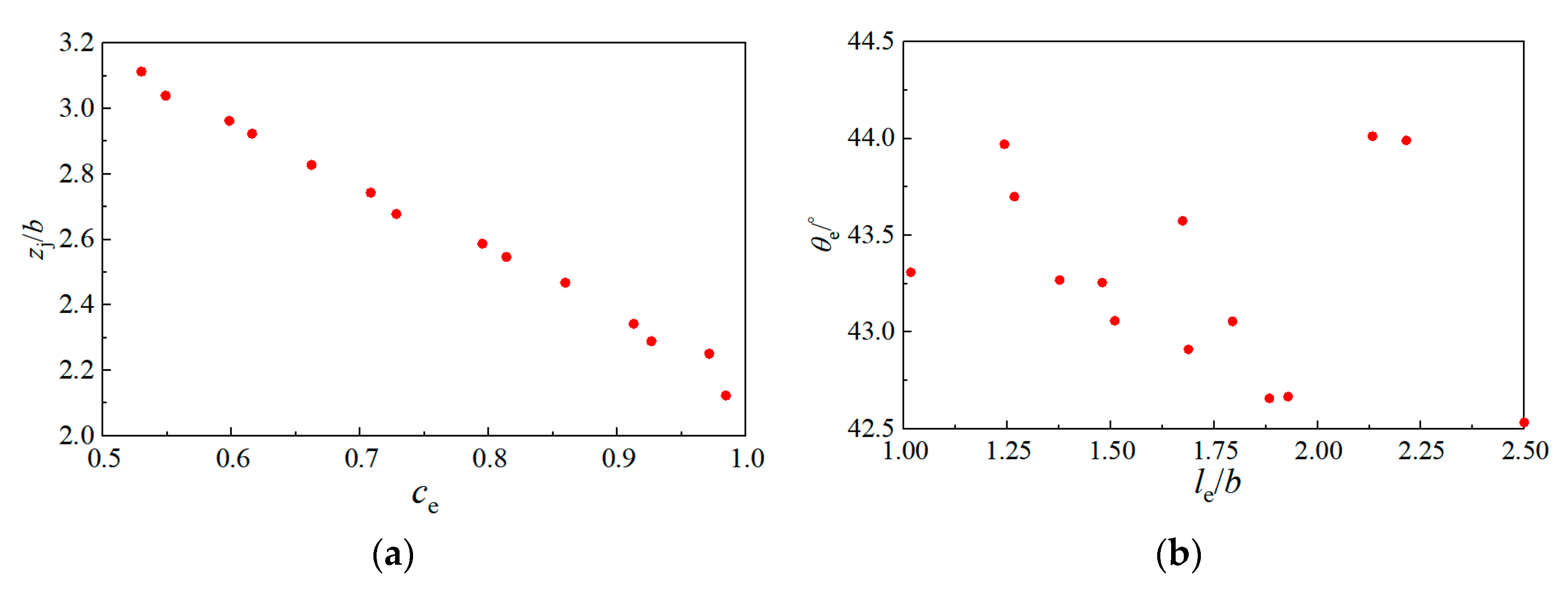

| hm/b | lm/b | ΔPC1 | ΔPC2 | ΔPC3 |
|---|---|---|---|---|
| 3.25 | 5.25 | 6.67% | 3.61% | 3.17% |
| 4.25 | 5.25 | 9.44% | 4.99% | 7.20% |
| 3.75 | 5.75 | 1.36% | 1.02% | 8.87% |
| 3.25 | 6.25 | 8.61% | 4.59% | 3.18% |
| 4.25 | 6.25 | 1.38% | 1.21% | 1.97% |
| θe/° | le/b | ΔPC1 | ΔPC2 |
|---|---|---|---|
| 42.5 | 1.25 | 8.70% | 8.76% |
| 42.5 | 2.25 | 3.03% | 0.22% |
| 47.5 | 1.75 | 1.89% | 3.67% |
| 52.5 | 1.25 | 9.44% | 3.23% |
| 52.5 | 2.25 | 1.44% | 5.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Wang, W.; Pan, J. PCA-Kriging-Based Oscillating Jet Actuator Optimization and Wing Separation Flow Control. Aerospace 2024, 11, 916. https://doi.org/10.3390/aerospace11110916
Sun Q, Wang W, Pan J. PCA-Kriging-Based Oscillating Jet Actuator Optimization and Wing Separation Flow Control. Aerospace. 2024; 11(11):916. https://doi.org/10.3390/aerospace11110916
Chicago/Turabian StyleSun, Qixiang, Wanbo Wang, and Jiaxin Pan. 2024. "PCA-Kriging-Based Oscillating Jet Actuator Optimization and Wing Separation Flow Control" Aerospace 11, no. 11: 916. https://doi.org/10.3390/aerospace11110916
APA StyleSun, Q., Wang, W., & Pan, J. (2024). PCA-Kriging-Based Oscillating Jet Actuator Optimization and Wing Separation Flow Control. Aerospace, 11(11), 916. https://doi.org/10.3390/aerospace11110916





