Flexible Combinatorial-Bids-Based Auction for Cooperative Target Assignment of Unmanned Aerial Vehicles

Abstract

For the cooperative reconnaissance assignment of unmanned aerial vehicles (UAVs) on multiple targets, this paper presents a flexible combinatorial-bids-based auction (FCBA) method that can optimize the number of UAVs for each target. Considering the reconnaissance effectiveness enhancement achieved with cooperative observation and the time-critical characteristic of targets, the multitarget assignment problem is formulated as a nonlinear integer optimization to maximize the cooperative effectiveness. To achieve target assignment without predetermining the number of UAVs for each target, a combinatorial bidding framework is proposed, and an allocation method for rewards and costs among the cooperative UAVs is constructed. Strategies for auction iteration and bid updating are also designed to acquire equilibrium results under the combinatorial bidding mechanism. The simulation results show that the proposed method can generate satisfactory suboptimal results according to the enumerated solutions. A comparison of the results demonstrates that the FCBA can provide comparable optimal results to a genetic algorithm but has better computational efficiency, and the reconnaissance effectiveness can be improved by considering cooperative observation.

1. Introduction

Cooperation among multiple unmanned aerial vehicles (UAVs) is a critical trend given the growing environmental complexities and mission diversities. Target assignment is one of the key technologies in multi-UAV cooperation that is used to improve task effectiveness by managing resources reasonably [1]. Multi-UAV cooperative target assignment is an NP-hard combinatorial optimization problem [2], in which obtaining the optimal solution is computationally expensive. The three current methods for cooperative target assignment mainly include optimization-based methods, market-based methods, and learning-based methods [3].

For optimization-based methods, traditional mathematical programming methods can solve linear-constraint, small-scale problems but are not suitable for assignments with complex constraints. Modern intelligent optimization algorithms, such as the genetic algorithm (GA) [4,5], particle swarm optimization [6,7], ant colony optimization [8], and bee colony optimization [9], have been introduced to solve complex assignment problems. Among them, the GAs can be easily tailored by designing genetic operators to satisfy different assignment constraints. Shima et al. [4] introduced a GA for a cooperative multiple task assignment problem for UAVs and demonstrated that the GA could converge to the near-optimal solution considerably faster than branch and bound (BNB) search method. Wang [5] proposed a modified opposition-based GA for heterogeneous target allocation and demonstrated that the modified GA outperformed ACO in terms of optimality. Although intelligent optimization methods can find the optimal solution, they require large amounts of computational resources.

Machine-learning-based methods have recently been introduced for complex multi-UAV task assignment problems [10,11,12,13,14]. Han et al. [10] used a multiagent deep deterministic policy gradient (MADDPG) framework to perform target assignment and path planning simultaneously. Liu et al. [11] proposed an extensible MADDPG algorithm to improve the robustness and scalability for large UAV swarm sizes. Considering the deterministic DDPG algorithm, in which using a greedy strategy may fall into local optima, [12] introduced a multiagent soft actor–critic framework for multi-UAV task assignment, and the proposed method can support centralized training and decentralized execution. To increase the speed of model training, [13] integrated DRL with a digital twin. To overcome the shortcomings of load balancing and execution efficiency, Wu et al. [14] proposed an improved self-organizing mapping algorithm and introduced an attention mechanism to deal with new UAV tasks and UAV failures. Learning-based methods can provide attractive performance advantages for dynamic assignment problems [15,16] in unknown environments, but they usually rely on large-scale data, which are hard to obtain, and the robustness of these algorithms without effective training may not satisfy the application requirements.

Market-based methods can generate feasible assignment results efficiently for large-scale problems, and they mainly include auction methods and contract net methods. Auction methods can satisfy different task requirements through the design of a benefit model and bidding rules, and many modified versions have been developed to solve different assignment problems. Chandler et al. [17] introduced an iterative auction for multiple task assignments of UAVs to satisfy online computation and task timing constraints. As a single-item auction framework, the optimality of an iterative auction is not satisfactory for targets with strong synergies, and thus Berhault et al. [18] proposed a combinatorial auction, where each bidder can bid on a set or bundle of items. By using a combinatorial auction, a single robot can bid and take charge of several tasks. As the antithesis of the combinatorial auction, Lin et al. [19] considered a single task that required multiple robots to bid together and proposed a combinatorial-bids-based allocation method. To avoid task conflict under local communication, the consensus-based auction algorithm (CBAA) and consensus-based bundle algorithm (CBBA) were proposed [20] to achieve agreement on the winning bid values. Hunt et al. [21] extended the CBBA to the consensus-based grouping algorithm (CBGA) to support tasks that require agents to cooperate in completing individual tasks. Machine learning was also recently integrated into the auction method to improve its performance. Tan et al. [22] proposed a two-stage allocation method where machine learning was used to obtain a parameter to enhance algorithm stability for the dynamic task allocation of UAV swarms.

Although many modified auction methods have been developed for multi-UAV task assignment, these methods, including the existing combinatorial-bids-based method [19], require the number of UAVs to be predefined for each task before starting the auction. And, during the auction, the UAV index under the defined number of UAVs is negotiated, while the number of UAVs assigned to each task is not changed, which cannot ensure the optimality of the assignment. In this paper, we propose a flexible combinatorial-bids-based auction (FCBA) method for cooperative target assignment, where the number of UAVs assigned to each target can be optimized during the auction process. The contributions of our work are listed as follows:

(1)

A modified combinatorial bids-based auction method is proposed to provide flexibility in optimizing the number of UAVs assigned to each target, designing a cost and reward function especially for multi-UAV combinatorial bids.

(2)

A combinatorial optimization model considering the cooperative observation-related task complement probability and a time-sensitive target value is constructed for multi-UAV cooperative reconnaissance assignments.

(3)

Comparison studies were conducted to show that the proposed FCBA has appealing performance in terms of optimality and computational efficiency, and assignments considering cooperative observations could improve the reconnaissance effectiveness.

The rest of this paper is organized as follows: Section 2 formulates the considered target assignment problem as a nonlinear integer optimization problem. Section 3 presents the detailed process of the FCBA and the modified combinatorial bidding mechanism. Section 4 gives the simulation results from tests of the effectiveness and performance of the FCBA. This paper is concluded in Section 5.

2. Problem Formulation

This section formulates the target reconnaissance assignment problem as a nonlinear integer optimization model and provides a method to calculate the reconnaissance effectiveness considering the detection time, detection probability, recognition probability, and cooperative observability.

2.1. Description of Target Assignment for UAVs

Reconnaissance target assignment for UAVs needs to generate reasonable target–UAV match results to maximize the reconnaissance effectiveness with the limited number of UAVs. The study in this paper is conducted under the following assumptions:

(1)

The importance of the target is different, and thus the reconnaissance effectiveness varies with the target.

(2)

The reconnaissance effectiveness of a target decreases with time because the target may have completed or partially completed its tasks as time goes on.

(3)

One UAV can only select one target to reconnoiter, but multiple UAVs can select an identical target area to cooperatively reconnoiter.

(4)

When multiple UAVs cooperatively reconnoiter one target area, the target localization accuracy can be improved through cooperative observation, resulting in improved localization accuracy and detection probability.

According to the taxonomy given in [23], the considered target assignment in this work is an STMR (single-task robots and multi-robot tasks) problem, i.e., each UAV can select one target at most, but a target can be selected by multiple UAVs.

2.2. Optimization Model of Cooperative Target Assignment

It is assumed there are K targets, denoted as T = {T₁, T₂, …, T_K}, and N UAVs, denoted as M = {M₁, M₂, …, M_N}. According to the assumption (3), the target assigned to UAV i is denoted as A_i, and the UAV set which reconnoiters k is denoted as Γ_k, and then we can obtain $A_i\in T,i=1,2,\dots ,N$ and ${\Gamma }_k\subseteq M,k=1,2,\dots ,K$.

The cooperative target reconnaissance assignment problem can be formulated as a nonlinear integer optimization, as shown in Equation (1), where the objective function is to maximize the cooperative reconnaissance effectiveness J, and the target assigned to each UAV $A_i\in T,i=1,2,\dots ,N$ is the design variable.

$$\underset{A_i,i=1,2,\dots ,N}{\max } J={\displaystyle \sum _{k=1}^K[s_k\left(t_k(A_i)\right)\cdot p_k(A_i)]}\hspace{1em} s.t.\hspace{1em} A_i\in T,i=1,2,\dots ,N$$

(1)

where s_k(t_k) is the value of target k at t_k, where t_k denotes the detection time of target k, and p_k is the recognition probability of target k. According to Equation (1), the optimized objective is the sum of the reconnaissance effectiveness on each target, which is decided by the target value s_k and the recognition probability p_k. Each target’s value is considered to decrease with the time; thus, the value at detection time t_k is taken into the calculation. The recognition probability p_k and the detection time t_k of a target is influenced by the assigned UAVs for this target, and the detailed computation methods are given in Section 2.3. Note that according to the design variable A_i, which denotes the target assigned to each UAV, the UAVs assigned to a target Γ_k can be deduced and are employed to calculate the recognition probability and the detection time.

Different from the general target assignment model, the above assignment problem considers the detect-time-depended target value, UAV-status-related target recognition probability and multi-UAV cooperative effects on the detection probability, which makes the model a nonlinear optimization problem, since the detected target value and recognition probability is a complex nonlinear function of the assignment variable.

2.3. Reconnaissance Effectiveness Model

This section provides the calculation model for each part of the reconnaissance effectiveness in Equation (1).

(1)

Time-varying target value

According to assumption (2), which assumes that the targets are time-sensitive, their values are described as a time-varying function in Equation (2):

$$s_k(t_k)=s_{0,k}\cdot e^{-{\lambda }_k{t}_k},k=1,2,\dots ,K$$

(2)

where s_0,k is the initial value of target k, and λ_k is the decay factor of the target value.

(2)

Detection time of the target

The accurate detection time cannot be known before completing the task, so an estimated detection time is used to support the target assignment. If the UAVs work in an environment free of obstacles, such as an open field or high-altitude area, the detection time is estimated according to the guidance trajectory [24]; if the UAVs work in an environment with obstacles, the detection time is estimated according to the collision avoidance path [25,26].

If only one UAV is assigned to target k, the detection time of target k is equal to time t_ik, as per Equation (3), where t_ik is the estimated time that the assigned UAV i finishes detecting target k.

$$t_k=t_{ik}, {\Gamma }_k=\left\{i\right\}$$

(3)

If multiple UAVs are assigned to reconnoiter target k, the detection time is taken as the maximum detection time in the set Γ_k to satisfy the cooperative constraint.

$$t_k=t_{{\mathit{\Gamma }}_{k}k}=\underset{i\in {\Gamma }_k}{\max }(t_{ik})$$

(4)

(3)

Recognition probability of the target

The recognition probability p_ik for a single UAV to reconnoiter target k is defined as:

$$p_{ik}={\overline{p}}_{ik}\cdot {\widehat{p}}_{ik}$$

(5)

where ${\overline{p}}_{ik}$ indicates the detection probability of UAV i to target k, and ${\widehat{p}}_{ik}$ indicates the recognition probability when UAV i detects target k.

The recognition probability of a set of UAVs Γ_k to reconnoiter target k is defined as:

$$p_{{\mathit{\Gamma }}_{k}k}=1-{\displaystyle {\prod }_{i\in {\Gamma }_k}\left(1-{\overline{p}}_{ik}^{\prime }\cdot {\widehat{p}}_{ik}\right)}$$

(6)

where ${\overline{p}}_{ik}^{\prime }$ indicates the detection probability of UAV i against target k, considering cooperation with other UAVs in Γ_k. According to Equation (6), the recognition probability of a target can be increased through cooperative detection. Note that from Equation (6), the detection probability of multiple UAVs reconnoitering a target is not a simple composition of the probability that each UAV can detect the target, but it needs to compute the cooperative effects, which is given as follows in Equation (7).

(4)

Detection Probability Considering Collaborative Observability Enhancement

To detect and localize a target, the UAV has to estimate the relative UAV–target states first. The target state estimation accuracy can be enhanced through the fusion of observation information obtained from other UAVs, so the detection probability can be enhanced. The detection probability of a UAV against a target when considering cooperation with other UAVs is represented as:

$${\overline{p}}_{ik}^{\prime }=1-\left(1-{\overline{p}}_{ik}\right)/{\mu }_{{\Gamma }_{k}k},i\in {\Gamma }_k$$

(7)

where ${\mu }_{{\Gamma }_{k}k}$ represents the reduction factor with cooperative observability enhancement, whose value is related to the observation angle set ${\mathit{\theta }}_{{\mathit{\Gamma }}_{k}k}$, as shown in Equation (8):

$${\mu }_{{\Gamma }_{k}k}={\mu }_{\min }+\mu ({\mathit{\theta }}_{{\mathit{\Gamma }}_{k}k})\cdot ({\mu }_{\max }-{\mu }_{\min })$$

(8)

The observation angle represents the relative UAV–target heading angle. When a set of UAVs cooperatively detect a target, if the relative heading angles of the UAVs reach the optimal configuration [27], the reduction factor can reach its maximum value. On the contrary, if their observation angles are the same, they rarely obtain extra observation information, so the reduction factor will be low. In this work, the maximum and minimum values of the reduction factor were set as 5 and 2, respectively.

3. Flexible Combinatorial-Bids-Based Auction Algorithm

This section proposes the flexible combinatorial-bids-based auction (FCBA) method, which supports multiple UAVs conducting combinatorial bids on the same target. Different with the algorithms outlined in [19,20,21], this work does not need to predefine the number of UAVs assigned to each target, which means that the number of assigned UAVs are also optimized to improve the optimality of target assignment solutions.

3.1. Algorithm Flowchart

The auction algorithm is a kind of free-market-based allocation method, which regards individuals performing tasks as bidders and regards each target as an auction item in a market. Different bidders obtain different benefits from purchasing the auction item. Each bidder places a bid on the item based on its own benefits and capabilities, and the bidder with the highest bid price wins the corresponding auction item. Moreover, each bidder aims to maximize their benefits, which equals the rewards minus the costs. Through iterative auctions, when all bidders are satisfied with the item they win, which means that the individual returns reach the maximum, the auction market will reach equilibrium. The solution to the original allocation problem can be obtained based on the auction results at market equilibrium. For implementation, the auction algorithm can be run in a centralized or decentralized structure. In the centralized way, a UAV or a ground station is selected as the central node, and then it receives the status from all the UAVs and runs the algorithm to generate the assignment. Alternatively, in the decentralized way, each UAV shares its information with all other UAVs, and each UAV can finish the target assignment.

To support multiple UAVs conducting combinatorial bids on the same target in the proposed FCBA, an allocation mechanism of the rewards and costs is constructed, and the auction process and price update method are designed to achieve market equilibrium. The flowchart of the FCBA is shown in Figure 1, and the main steps are as follows.

Step 1: Parameter initialization. Set the prices of all targets and returns of all UAVs as zero, set the bidding target of each UAV as empty, and set i = 0, N_up = 0.

Step 2: Return calculation. For the UAV i, calculate the rewards and costs for each bidding target sequentially, and then obtain the benefits for each bidding target.

Step 3: Bidding target updating. UAV i takes the target with the highest return as its new bidding item. If this item is the same as the item in the last iteration, proceed to Step 4. If not, update the rewards and costs of the bidding item, which will be described in detail in Section 3.3.

Step 4: Bidding status updating. If the current bidding iteration is finished (i = N), proceed to Step 5. If not (i < N), let i = i + 1 and proceed to Step 2 for calculation of the next UAV.

Step 5: Market equilibrium judgment. If any UAV modified its bidding item in this iteration (N_up ≠ 0), set i = 0 and proceed to Step 2 for the next iteration. If not, the auction process ends, and the market reaches equilibrium.

Through the above steps of the FCBA, the optimal target assignment can be obtained by the market equilibrium results. Commonly, the proposed FCBA can generate feasible solutions for the considered target assignment problem, which is solvable since there are no hard constraints such as a task precedence or task window. However, in special cases, there may be several equally optimal solutions, and then the market could jump between the several bidding proposals, thus leading to non-convergence. One method is to add a small randomness to the target value to avoid equally optimal solutions.

3.2. Function of Benefit, Cost, and Reward

To select the optimal item to bid, each UAV needs to compute the benefit R_ik from bidding on different targets according to Equation (9).

$$R_{ik}=a_{ik}-{\rho }_{ik}$$

(9)

where a_ik represents the obtained reward for UAV i by selecting target k, and ρ_ik represents the cost for UAV i to pay out by selecting target k. The method for calculating the reward and cost of a UAV bidding on different kinds of targets is discussed as follows.

(1)

The target has no bidders

If target k has no bidders, the reward a_ik is equal to the whole effectiveness of target k, which is described as per Equation (10).

$$a_{ik}=s_{ik}=s_{0,k}\cdot e^{-{\lambda }_k{t}_{ik}}\cdot p_{ik}$$

(10)

Meanwhile, the lowest price for UAV i to pay is just equal to the current price of the target, shown in Equation (11). Note that the price of a target is initialized as zero but will be updated as its bidder changes after each iteration of the auction, as shown in Equation (19).

$${\rho }_{ik}={\rho }_k$$

(11)

(2)

The target has bidders

If target k has bidders, regard UAV i and the existing bidders as a group Γ_k. The reconnaissance effectiveness on target k by the UAV group Γ_k can be calculated as follows:

$$s_{{\mathit{\Gamma }}_{k}k}=s_{0,k}\cdot e^{-{\lambda }_k{t}_{{\mathit{\Gamma }}_{k}k}}\cdot p_{{\mathit{\Gamma }}_{k}k}$$

(12)

where $p_{{\mathit{\Gamma }}_{k}k}$ denotes the recognition probability of target k by group Γ_k, and $t_{{\mathit{\Gamma }}_{k}k}$ is the detection time of target k by group Γ_k. $p_{{\mathit{\Gamma }}_{k}k}$ and $t_{{\mathit{\Gamma }}_{k}k}$ can be calculated, respectively, using Equations (4) and (6).

Then, the benefit a_ik for each UAV selecting target k can be obtained proportionally based on the effectiveness s_ik when each UAV reconnoiters target k alone, as shown in Equation (13):

$$a_{ik}=s_{{\mathit{\Gamma }}_k^{\prime }k}\cdot s_{ik}/{\displaystyle \sum _{j\in {\mathit{\Gamma }}_k^{\prime }}{s}_{jk}}$$

(13)

Similarly, when the UAVs cooperatively bid on target k as combinatorial bids, the minimum price ρ_ik that UAV i needs to pay can be decided proportionally based on the target price ρ_k, as shown in Equation (14):

$${\rho }_{ik}={\rho }_k\cdot s_{ik}/{\displaystyle \sum _{j\in {\mathit{\Gamma }}_k^{\prime }}{s}_{jk}}$$

(14)

3.3. Bid Price Updating

According to the potential returns in Equation (9) by bidding on different targets, the optimal bidding target is selected for each UAV, and the bid price is calculated to update the market price of the target. The details are given as follows.

The bidding target for UAV i is selected as the target with the highest return, which is regarded as ${\tau }_i\in T$, as shown in Equation (15):

$${\tau }_i=\underset{k=1,2,\dots ,N}{\arg \max }\left(a_{ik}-{\rho }_{ik}\right)$$

(15)

Then, the bid price ${\gamma }_{i{\tau }_i}$ that UAV i submits on the selected target τ_i is calculated as per Equation (16). This bid price is used to improve the target price, and then other UAVs that cannot generate higher returns do not bid on this target. In the equation, the price increment π_i−${\pi }_i^{\prime }$ aims at raising the target price as high as possible to raise the cost for other UAVs bidding on this target under the condition that UAV i can still obtain the highest benefit on target τ_i.

$${\gamma }_{i{\tau }_i}={\rho }_{i{\tau }_i}+({\pi }_i-{\pi }_i^{\prime })$$

(16)

where ${\rho }_{i{\tau }_i}$ is the lowest price decided by Equations (11) and (14), π_i and ${\pi }_i^{\prime }$ denote the highest and second-highest benefit for UAV i to bid on different targets, and their computation methods are shown as per Equations (17) and (18).

$${\pi }_i=\underset{k=1,2,\dots ,N}{\max }\left(a_{ik}-{\rho }_{ik}\right)$$

(17)

$${\pi }_i^{\prime }=\underset{k=1,2,\dots ,N,k\ne {\tau }_i}{\max }\left(a_{ik}-{\rho }_{ik}\right)$$

(18)

After UAV i bids on target τ_i, the current price ${\rho }_{{\tau }_i}$ of target τ_i is updated as per Equation (19), where ${\rho }_{{\tau }_i}$ is initialized as zero and is updated using this equation during the auction process, and π_i and ${\pi }_i^{\prime }$ are given in Equations (17) and (18).

$${\rho }_{{\tau }_i}={\rho }_{{\tau }_i}+({\pi }_i-{\pi }_i^{\prime })$$

(19)

3.4. Bidding Information Updating

During an iteration of the auction process, if any UAV modifies its bidding target or its bidding target τ_i has bidders in the last iteration, the bidding information of related UAVs or targets need to be recomputed as follows.

(1)

The bidding target τ_i of UAV i has other bidders in the last iteration

If there are already other UAVs (j ≠ i) bidding on target τ_i, the rewards and costs of these UAVs need to be recomputed. ${\Gamma }_{{\tau }_i}\subseteq M$ is denoted as the group including UAV i and the UAVs bidding on τ_i in the last iteration, and subset ${\Lambda }_{{\tau }_i}\subseteq {\Gamma }_{{\tau }_i}$ is denoted as the group that will achieve the optimal effectiveness. The optimal subset is decided by enumerating all the possible combinations in the group ${\Gamma }_{{\tau }_i}\subseteq M$.

Based on the cooperative effectiveness $s_{{\mathit{\Lambda }}_{{\tau }_i}{\tau }_i}$ that the group ${\Lambda }_{{\tau }_i}$ can obtain, the rewards for each UAV in ${\Lambda }_{{\tau }_i}$ are calculated in proportion to the effectiveness it can obtain through individual reconnaissance, as shown in Equation (20). Similarly, the total target cost ρ_k can also be proportionally allocated to these UAVs, as shown in Equation (21).

$$a_{j{\tau }_i}=s_{{\mathit{\Lambda }}_{{\tau }_i}{\tau }_i}\cdot s_{j{\tau }_i}/{\displaystyle \sum _{\hspace{1em}j\in {\mathit{\Lambda }}_{{\tau }_i}}{s}_{j{\tau }_i}},j\ne i,j\in {\mathit{\Lambda }}_{{\tau }_i}$$

(20)

$${\rho }_{j{\tau }_i}={\rho }_k\cdot s_{j{\tau }_i}/{\displaystyle \sum _{\hspace{1em}j\in {\mathit{\Lambda }}_{{\tau }_i}}{s}_{j{\tau }_i}},j\ne i,j\in {\mathit{\Lambda }}_{{\tau }_i}$$

(21)

where $a_{j{\tau }_i}$ and ${\rho }_{j{\tau }_i}$ represent the reward and cost for UAV j to cooperatively detect target τ_i. In addition, for the UAVs ($j\notin {\Lambda }_{{\tau }_i}$ and $j\in {\Gamma }_{{\tau }_i}$) that give up on selecting target τ_i, their bidding items are reset to empty, and their rewards and costs are reset to zero.

(2)

UAV i modifies its bidding target in this iteration

If UAV i bid on another target in the last iteration, the price of that target needs to be updated, and the rewards and costs of cooperative UAVs (if they exist) for striking that target need to be recomputed. The detailed strategies are described as follows.

If UAV i bid on target o_i independently before bidding on target τ_i, the price of target o_i needs to be set to zero, i.e., ${\rho }_{o_i}=0$.

If UAV i bid on target o_i cooperatively before bidding on target τ_i, the remaining UAVs who bid on target o_i is set as ${\Lambda }_{o_i}\subseteq M$. The rewards of group ${\Lambda }_{o_i}$ bidding on target o_i are recalculated as $a_{{\Lambda }_{o_i}{o}_i}$. The rewards $a_{{\Lambda }_{o_i}{o}_i}$ are then proportionally allocated to the UAVs in ${\Lambda }_{o_i}$, as shown in Equation (22). Meanwhile, the current price of target o_i is reallocated proportionally to the remaining bidding UAVs, as shown in Equation (23).

$$a_{j{o}_i}=a_{{\mathit{\Lambda }}_{o_i}{o}_i}\cdot s_{j{o}_i}/{\displaystyle \sum _{\hspace{1em}j\in {\mathit{\Lambda }}_{o_i}}{s}_{j{o}_i}},j\in {\Lambda }_{o_i}$$

(22)

$${\rho }_{j{o}_i}={\rho }_{o_i}\cdot s_{j{o}_i}/{\displaystyle \sum _{\hspace{1em}j\in {\mathit{\Lambda }}_{o_i}}{s}_{j{o}_i}},j\in {\Lambda }_{o_i}$$

(23)

where $a_{j{o}_i}$ and ${\rho }_{j{o}_i}$ represent the rewards and costs for each UAV in group ${\Lambda }_{o_i}$.

4. Simulation and Results

This section conducts a numerical simulation to test the effectiveness and performance of the proposed algorithm. The simulation environment used was Matlab (by MathWorks Natick, Massachusetts, US.), and the hardware used was a computer with an Intel Q8200 CPU and 4GB RAM (Lenovo, Beijing, China).

4.1. Verification of Algorithm Effectiveness

To validate the effectiveness of the FCBA algorithm, it was compared with the enumeration method (denoted as EM), which can guarantee optimality. However, due to the computational resource requirement of EM, only small-scale problems were tested.

Two simulation scenarios were designed, and two scenarios added with obstacles were also tested to consider collision avoidance. Case I consisted of six UAVs (M1~M6) and five targets (T1~T5) and case II consisted of eight UAVs (M1~M8) and six targets (T1~T6). The initial positions for UAVs M1 to M8 were (200, 5500)m, (200, 5000)m, (200, 4500)m, (200, 4000)m, (500, 2500)m, (1000, 2000)m, (1500, 1500)m, and (2000, 1000)m, respectively. The initial heading angles of UAVs M1 to M4 were set as 0°, and those of UAVs M5 to M8 were set as 45°. The initial prices of the targets were set as random numbers within [0.5, 1], the target positions were randomly generated within a specific target area, and the decay coefficient of the target value was set as 0.005. The detection probability of an individual UAV was 0.7. On the precondition of detecting the target, the recognition probabilities of the UAVs against targets T1 to T3 were set as 0.5, and those against targets T4~T6 were set as 0.8.

For case I and case II with obstacles, the FCBA algorithm and the enumeration method were used to solve the above assignment problem 100 times, where the target positons and initial prices were randomly generated each time. The obtained assignment results were statistically analyzed, as shown in

Table 1. Assignment results of case I and case II.

Case	Average Optimal Solutions Using EM	Optimal Results Using FCBA
		Average Optimal Solutions	Average Ranks
I without obstacles	1.85	1.82	1.04%
I with obstacles	1.83	1.79	1.20%
II without obstacles	2.50	2.45	0.52%
II with obstacles	2.50	2.45	0.27%
Average	2.17	2.13	0.76%

. From the results shown in Table 1, the average optimal solutions obtained by the FCBA in these two scenarios were only 1.84% lower than those obtained by EM, which is the real optimal solution. In addition, the average results obtained by the FCBA were better than the top 1.20% of all the enumerated results for the two cases with or without obstacle collision. Therefore, the FCBA algorithm can achieve suboptimal but satisfactory assignment results.

Figure 2 and Figure 3 provide an example of the assignment results for case I and case II without obstacles. In the two figures, the curves represent the guidance trajectories of the UAVs, and the sizes of the target circles represent the value of the targets. As shown in Figure 2, the FCBA algorithm assigned M4 and M5 to target T3, allowing it to achieve better cooperative observability and reconnaissance effectiveness compared with assigning two closer UAVs (such as M3 and M4). However, compared to enumeration, the assignment by the FCBA was not the global optimal result, which was obtained by assigning M2 and M5 to target T3, which generated better cooperative observe angles and effectiveness. Moreover, both the FCBA and EM in this test abandoned the distant target T1 with low values. This is because when the detection probabilities are low, cooperatively reconnoitering targets with higher values can achieve better overall effectiveness than individually reconnoitering different targets. The assignment results of case II shown in Figure 3 provide similar conclusions to those of case I, i.e., the high-value targets were assigned to multiple UAVs in order to achieve better cooperative effectiveness, and low-value targets were not assigned to any UAV. According to the simulation results, it can be concluded that the FCBA is an effective cooperative target assignment algorithm that can provide satisfactory results.

Figure 4 and Figure 5 provide an example of the assignment results for case I and case II with obstacles. In the figures, the red circle and rectangle denote the threat area in which the UAVs cannot fly. In this experiment, the A* search algorithm was used for generating the collision avoidance paths. In such obstacle environments, because the detection time of a target is estimated by the collision-free path, targets near to the UAVs in a straight-line distance may not be the most appropriate choice. For example, in Figure 4, the bottom-left target is near to UAV 5 and UAV 6, but this target is located at the back of an obstacle and is not easy to reach, leading to the collision-free flight time being larger than with other targets, and thus no UAVs were assigned to this target. From the two figures, the proposed FCBA could also generate satisfactory assignment results for the environment with obstacles by introducing collision-avoidance path planning.

4.2. Comparison of Algorithm Performances

To further illustrate the performance of the FCBA algorithm, it was compared with a consensus-based auction algorithm (CBAA) [20] and a genetic algorithm (GA) in Matlab [28]. The simulation in case III consisted of 12 UAVs and 10 targets. The UAVs M1 to M8 and targets T1 to T6 were the same as those in case II. The initial heading angles of UAVs M9 to M12 were set as 90°, and their initial positions were (4000, 4000)m, (4500, 400)m, (5000, 400)m, and (5500, 400)m, respectively. The initial prices of targets T7 to T10 were set as random numbers within [0.5, 1], the target positions were randomly generated within a specified target area, and the decay coefficient of the target value was set as 0.005. The detection probability of an individual UAV was set as 0.7. The recognition probabilities of UAVs against targets T7 to T8 were set as 0.5, and those against targets T9 to T10 were set as 0.8.

The FCBA, CBAA, and GA methods were used to solve the above assignment problem in case III a total of 100 times. The statistical results of the assignment results and the time costs are listed in

Table 2. Assignment results of case III.

Statics	FCBA	CBAA	GA
Average of the optimal solution	3.97	3.82	3.92
Average time cost/s	0.19	0.08	6.85
Maximum time cost/s	1.02	0.34	14.42
Minimum time cost/s	0.02	0.06	2.76

, and Figure 6 provides a boxplot of the data.

As shown in Table 2 and Figure 6, the optimal solutions using the FCBA were comparable to those using the GA, and the average value using the FCBA was 1.1% higher than that using the GA. However, the FCBA algorithm had a great advantage in terms of its calculation efficiency compared with the GA. The average time cost of the GA was about 36 times greater than that of the FCBA. As a result, the FCBA algorithm could generate slightly better solutions than the GA while reducing the computation time significantly, which means it could better meet the practical application requirements. On the other hand, compared with the CBAA, the FCBA could generate better solutions with about a 4% higher value, and although the average computation time of the FCBA was over twice of that of the CBAA, the computation time of the FCBA could satisfy the requirement of dynamic assignment since the maximal cost time was about 1 s. From the above simulation results, the proposed FCBA algorithm demonstrated better performance in terms of optimality and satisfied the target assignment requirements in terms of computation time.

4.3. Analysis of Cooperative Observation Effects

To illustrate the effects of cooperative observation on the multi-UAV reconnaissance effectiveness, we compared the target assignment results obtained when considering cooperative observation with those obtained when considering independent observation. Note that target assignment carried out using cooperative observation cannot ensure better results than the assignment results obtained using independent observation because the cooperative observation model increases the complexity of the target assignment, which may lead to the FCBA not being able to generate satisfactory solutions.

The FCBA with cooperative observation (FCBA-CO) and the FCBA with independent observation (FCBA-IO) were, respectively, employed to solve the target assignment problem of case III given in Section 4.2 a total of 100 times.

Figure 7 provides an example of test results obtained by the FCBA-CO and FCBA-IO after running the simulation a total of 100 times. As shown in this figure, target T3 was not assigned by the FCBA-CO, but was assigned by the FCBA-IO. This is because cooperative reconnaissance on a high-value target could deliver better effectiveness using the FCBA-CO, but using the FCBA-IO, the reconnaissance effectiveness enhancement delivered by cooperation was smaller, and reconnoitering more targets was preferred. Moreover, because the observation angles influence the target state estimation accuracy and detection probability, the FCBA-CO preferred to assign UAVs with better cooperative observation angles, such as assigning the UAVs to target T7, while the FCBA-IO preferred to assign UAVs whose arrival time to the target was smaller.

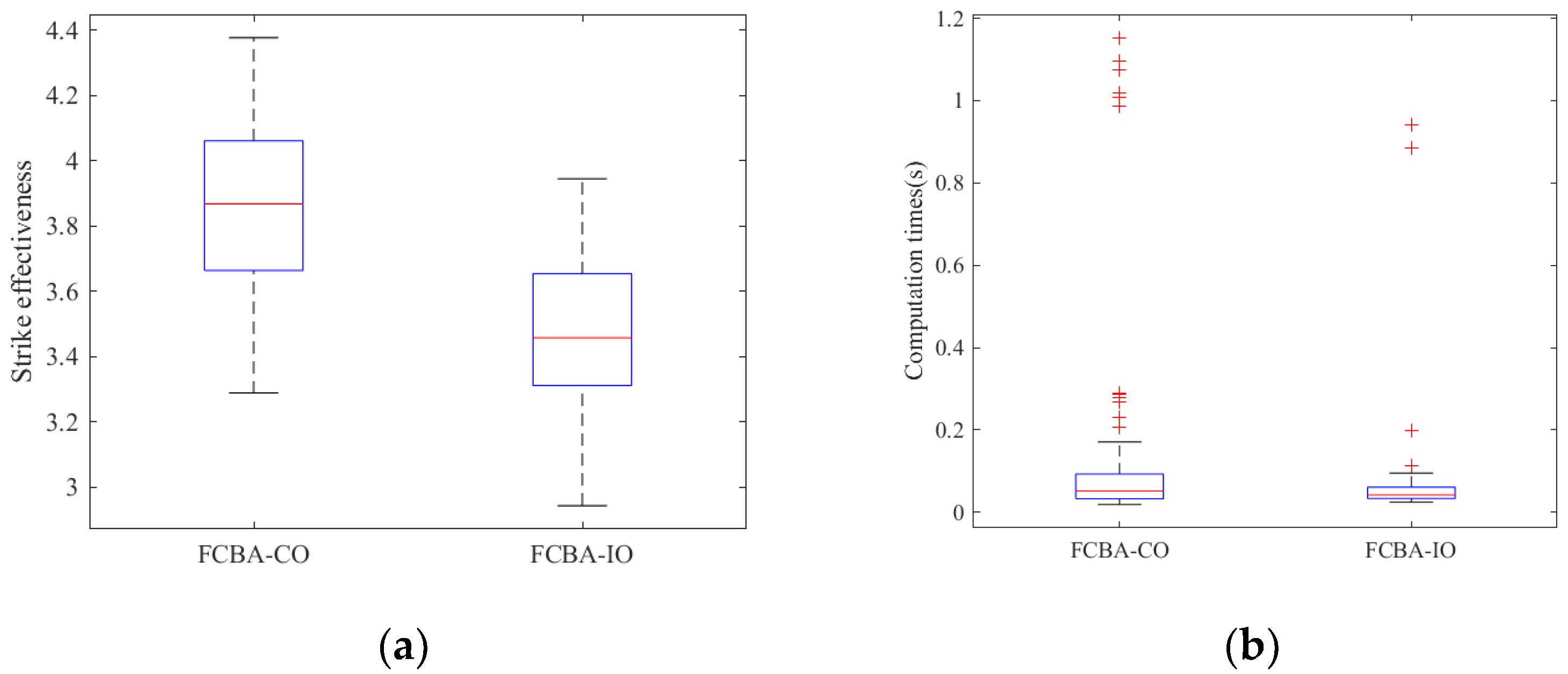
The statistical results obtained using the FCBA-CO and FCBA-IO after running for a total of 100 times are shown in Figure 8. As shown in Figure 8a, the total effectiveness obtained by the FCBA-CO was better than that obtained by the FCBA-IO, and the performance index of effectiveness was improved by about 10% when considering cooperative observation in the target assignment. Figure 8b gives the statistical results of the computation time. From this figure, the average computation time of the FCBA-CO (0.14 s) was about twice the average computation time of the FCBA-IO (0.07 s), which was because the FCBA required extra computation time to estimate the cooperative observation effects. However, the computation efficiency of the FCBA-CO could still satisfy the online assignment requirements, since the maximum computation time was about 1.15 s in the random test computed 100 times and over 90% of the tests were solved within 0.5 s. Thus, using cooperative observation in the target assignment could improve the multi-UAV cooperative effectiveness on the condition that it can still satisfy the computation efficiency needs, although the computation times were increased.

5. Conclusions

This paper proposed a method for solving multi-target cooperative reconnaissance assignment problems considering the relative UAV–target states and the effectiveness of cooperative reconnaissance. First, it described the problem using a nonlinear integer optimization model and then utilized a combinatorial-bids-based auction method to achieve the solution rapidly. Due to the design of the bidding mechanism, a cooperative bidding result that achieves market equilibrium is obtained through bidding, offering, and rewarding. The simulation results show that the proposed algorithm could obtain a satisfactory suboptimal solution efficiently, and utilizing cooperative observation could improve the reconnaissance effectiveness of the target assignment results.