Identification of Critical Nodes for Delay Propagation in Susceptible-Exposed-Infected-Recovered (SEIR) and Genetic Algorithm (GA) Route Networks
Abstract
1. Introduction
2. Route Network Construction
2.1. Route Network Model
2.2. Determination of Route Network Margins
3. Delay Propagation Model for Route Networks
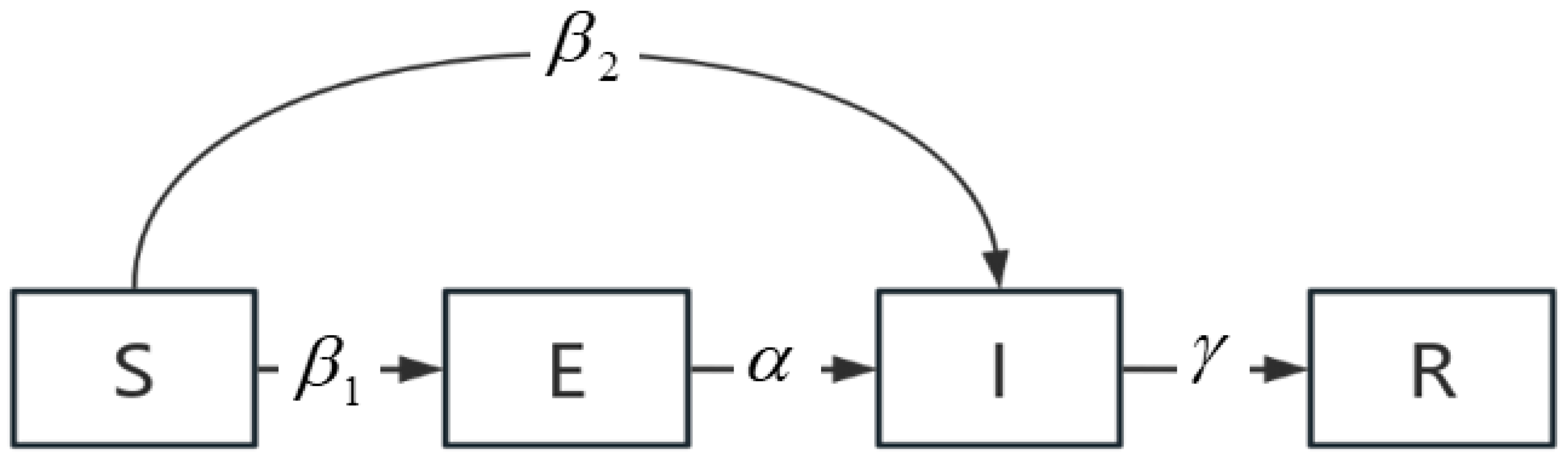
3.1. Suitability of the SEIR Model
3.2. Node Division
3.3. Set the Parameters of the Route Delay Propagation Model
4. Principle and Algorithm of the GA for Identifying the Key Nodes of the Air Route Network
4.1. Principle of GA
4.1.1. Initial Population
4.1.2. Evaluating Fitness Value
4.1.3. Sort and Select
4.1.4. Crossover and Mutation
4.1.5. Save the Best “Fit” Individuals
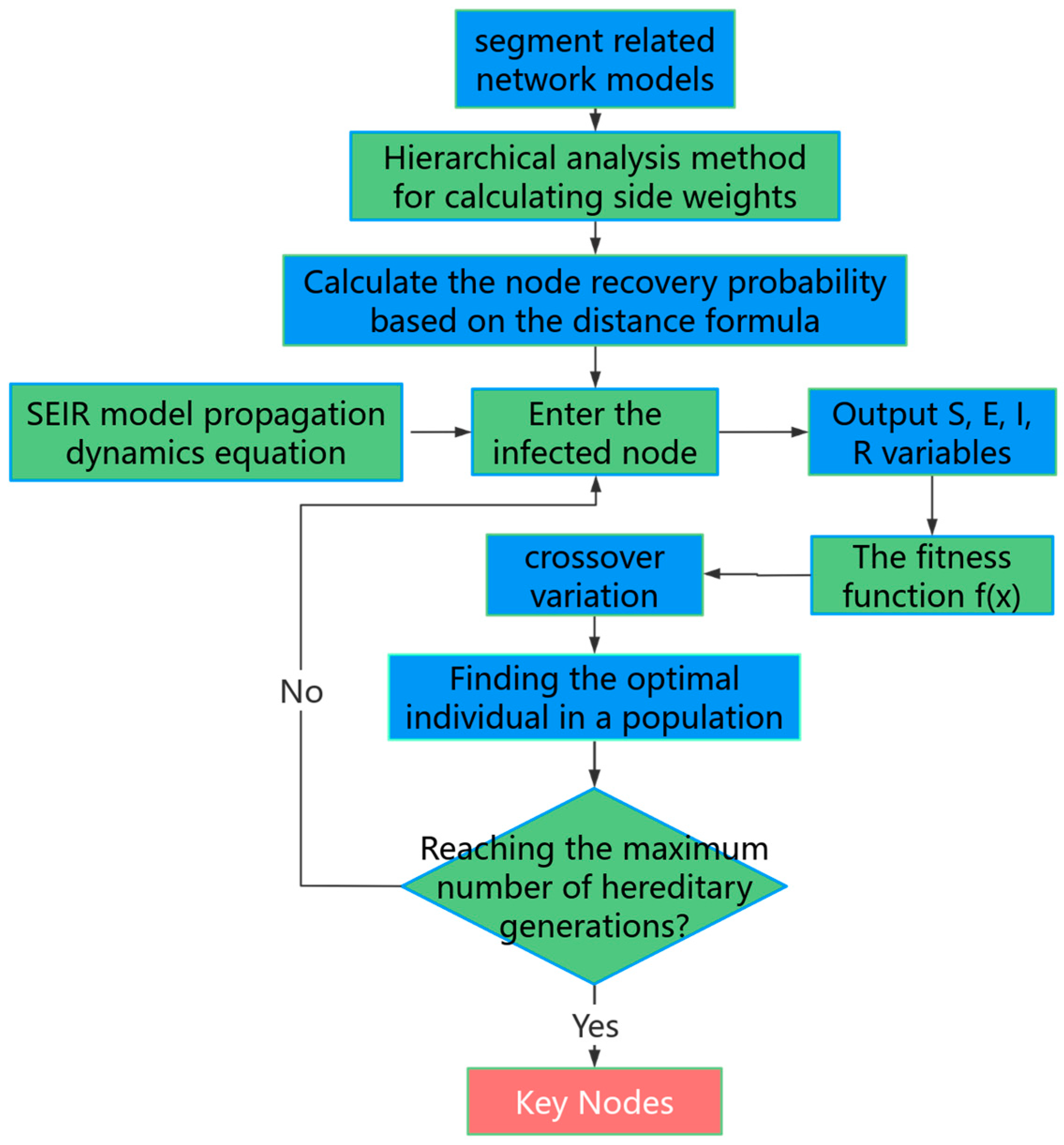
4.2. Overview of the Key Node Identification Methods
4.3. Description of Key Parameters of the Route Delay Propagation Model
4.3.1. Group Size N
4.3.2. Crossing Probabilities
4.3.3. Probability of Variation
4.3.4. Terminating Evolutionary Algebra T of Genetic Operations
5. Experimental Simulation
5.1. Experimental Procedure
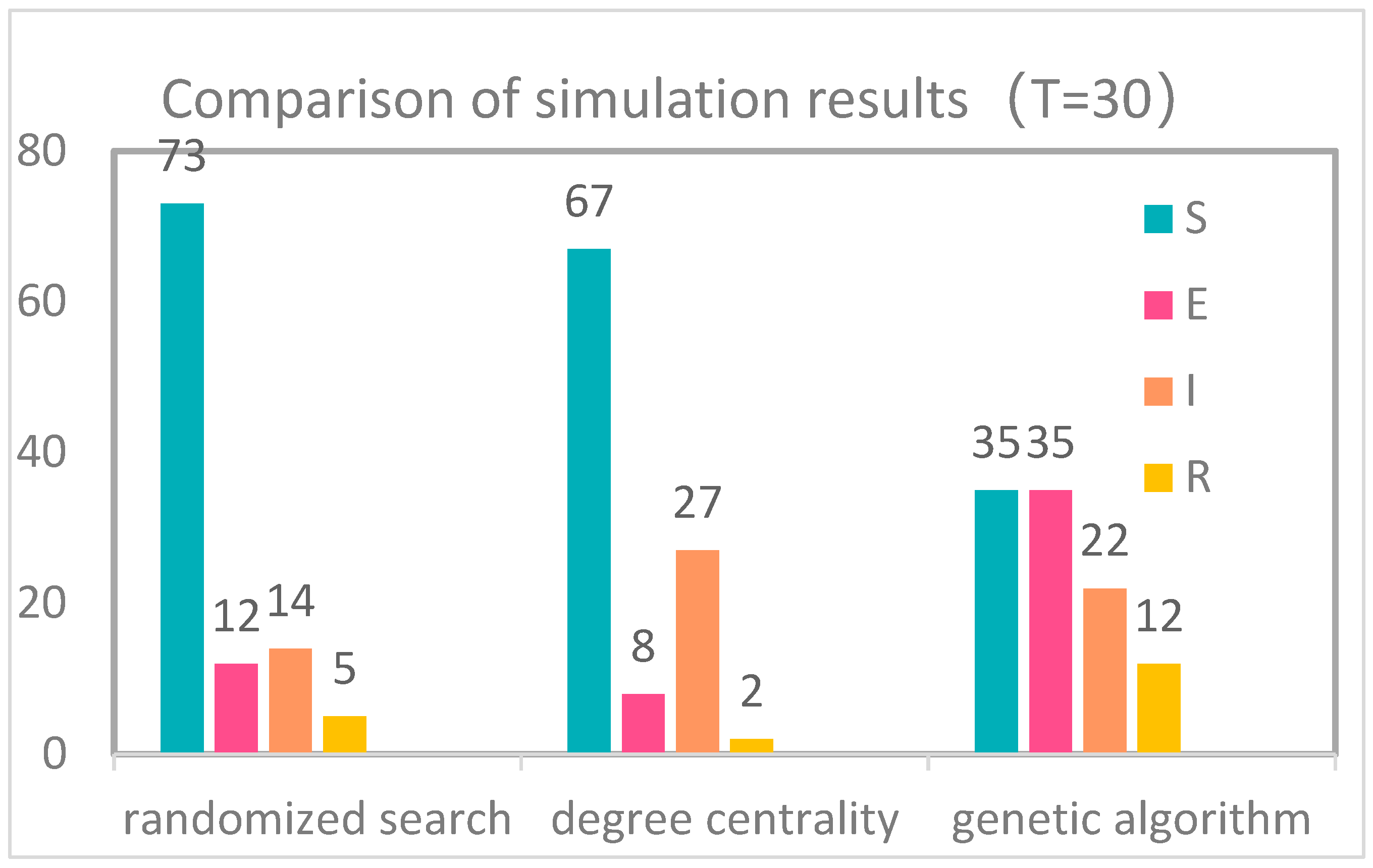
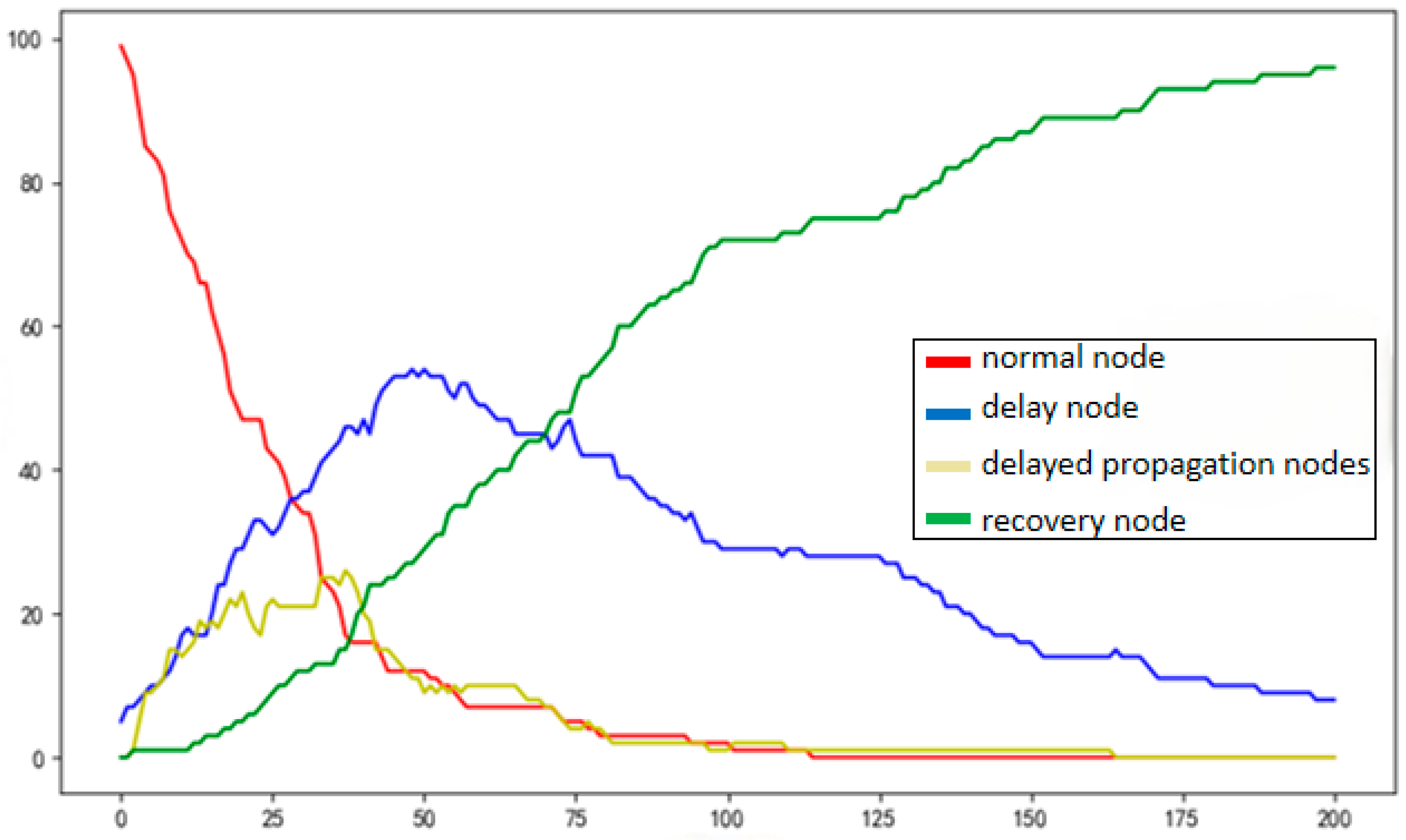
5.2. Simulation Results and the Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iata Economics. International Air Transport Association (IATA). Tech. Rep. 2020. [Google Scholar]
- Bureau of Transportation Statistics. Airline On-Time Performance and Causes of Flight Delays. 5 March 2020. Available online: https://www.transtats.bts.gov/ot_delay/ot_delaycause1.asp (accessed on 15 July 2020).
- Salleh, S.S.; Shukri, A.S.; Othman, N.I.; Saad, N.S.M. Data stories and dashboard development: A case study of an aviation schedule and delay causes. IOP Conf. Ser. Earth Environ. Sci. 2023, 1151, 012049. [Google Scholar] [CrossRef]
- Li, S.; Xie, D.; Zhang, X.; Zhang, Z.; Bai, W. Data-Driven Modeling of Systemic Air Traffic Delay Propagation: An Epidemic Model Approach. J. Adv. Transp. 2020, 2020, 8816615. [Google Scholar] [CrossRef]
- Din, Y.T.; Guo, J.Z.; Xing, X.Q.; Zheng, M.M.; Xia, T.B.; Xi, L.F. Joint optimization strategy of civil aircraft fleet flight assignment and maintenance scheduling. Comput. Integr. Manuf. Syst. 2024, 30, 205–216. [Google Scholar] [CrossRef]
- Qiao, W.H. Thoughts on enhancing the capability of meteorological and extreme weather prediction and early warning service in civil aviation. Civ. Aviat. Adm. 2023, 5, 65–67. [Google Scholar]
- Qi, Y.N.; Wang, X.T.; Wu, Z.Y. Air Traffic-Dependent Network Complexity Prediction Based on ICA-LSTM. Complex Systems and Complexity Science. pp. 1–9. Available online: http://kns.cnki.net/kcms/detail/37.1402.n.20240311.1713.004.html (accessed on 15 May 2024).
- Liu, T.; You, H.L. Research on transportation scheduling optimization based on human-machine collaborative decision-making. Transp. Syst. Eng. Inf. 2024, 24, 136–148. [Google Scholar] [CrossRef]
- He, X.N.; Li, Y.H.; Yang, J. An optimization model of dual hub route network based on competition scenario. J. Beijing Univ. Astronaut. 2022, 50, 2902–2911. [Google Scholar] [CrossRef]
- Yang, W.D.; Huang, Y.N.; Zhang, S.R. RCEP based on multi-layer complex network. Complex Syst. Complex. Sci. 2023, 20, 60–67. [Google Scholar] [CrossRef]
- Du, T.C.; Han, S.C.; Han, Y.X. Analysis of air route network delay propagation. Mod. Comput. 2022, 28, 1–9. [Google Scholar]
- Cheng, Q.; Wang, D.C.; Li, Y.H. Robustness analysis of route network timing under the influence of COVID-19. Comput. Digit. Eng. 2022, 50, 2710–2714+2814. [Google Scholar]
- Cao, L.L.; Yang, H.C. Elegant and pure, and so on. Time-lapse SEQS model analysis under the action of multilayer networks with active nodes. J. TC 2024, 53, 277–283. [Google Scholar]
- Liu, F.F.; Chen, Y.Q.; Xia, H.X. Coupling Model of Competitive Message Transmission and Infectious Disease Spread on Complex Networks. Theory and Practice of System Engineering. pp. 1–20. Available online: http://kns.cnki.net/kcms/detail/11.2267.N.20240515.1026.015.html (accessed on 15 May 2024).
- Zhu, X.F.; Yang, J.H.; Jiang, X. Construction and simulation of symbiotic evolution model of government data with improved SIR model. Mod. Intell. 2020, 40, 122–131. [Google Scholar]
- Wang, Z.; Sun, S.W. Analysis of Viral Transmission Dynamics for the Improved SIR Model. Journal of Tianjin University of Technology. pp. 1–8. Available online: http://kns.cnki.net/kcms/detail/12.1374.N.20240429.1831.044.html (accessed on 15 May 2024).
- Wang, X.L.; Zhu, L.; Zhang, S.T. Time-varying airport network delayed transmission model based on susceptible-sick-susceptible networks. Sci. Technol. Eng. 2019, 19, 414–419. [Google Scholar]
- Dou, Z.L. Kinetic analysis of the Fractional Time Lag SEIR Infectious Disease Model. The Practice and Knowledge of Mathematics. pp. 1–9. Available online: http://kns.cnki.net/kcms/detail/11.2018.O1.20240408.1355.012.html (accessed on 15 May 2024).
- Zhu, F.Q.; Jia, X.Y.; Wei, L.; Li, F.X. A Method for Recognizing the Importance of Hypernetwork Nodes Based on Multi-Indicator Decision Matrix. Complex Systems and Complexity Science. pp. 1–9. Available online: http://kns.cnki.net/kcms/detail/37.1402.N.20240926.1155.008.html (accessed on 27 September 2024).
- Luo, M.Z.; Li, H.X. Risk coupling analysis of old industrial building construction and renovation based on N-K and SNA models. J. Railw. Sci. Eng. 2024, 1–10. [Google Scholar] [CrossRef]
- Li, S.P.; Dong, J.Y.; Liu, J. Link Symbol Prediction for Directed Symbolic Networks Incorporating Node Balance Index. Comput. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Y.; Yang, Z.L. Long-term forecasting of container throughput by introducing logistic Steele growth model. J. Chongqing Jiaotong Univ. 2020, 39, 45–50. [Google Scholar]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Liu, S.Q.; Ma, N.J. Study of peak and peak time in a heterogeneous infectious disease model. J. Shandong Univ. 2023, 58, 1–12. [Google Scholar]
- Zhang, J.; Jian, L.R. Study on the Evolutionary Characteristics of Travel Information Dissemination in the New Media Environment. Complex Systems and Complexity Science. pp. 1–8. Available online: http://kns.cnki.net/kcms/detail/37.1402.N.20240417.1623.002.html (accessed on 14 May 2024).
- Gu, H.S.; Jia, N.; Meng, Z.C.; Chen, P. Evolution and early warning mechanism based on SEIR-SPN. J. Intell. 2024, 43, 146–155. [Google Scholar]






| Index | Method | Influence Degree |
|---|---|---|
| Airline saturation (AS) | The ratio of the route flow to the maximum capacity of the route. | The higher the route saturation, the greater the weight of the network edge, and the more likely it is to affect the corresponding two nodes. |
| Delay rate of flight (DF) | The ratio of the delayed flights to the connecting airport and navigation points on that day. | The higher the delay sorties ratio, the less the impact on the network, and the smaller the weight value. |
| Weather conditions (WC) | Weather conditions on the route on the same day. | The worse the meteorological conditions, the greater the weight of the network connection edge, and the more likely to cause the impact. |
| Military navigation activities (MA) | The ratio of the time of military navigation affecting the operation of the route to the total time of normal operation. | The more military aviation activities, the greater the potential conflict, and the greater the impact on the network delay. |
| Factor i Compared to Factor j | |
| Equal Importance | 1 |
| Marginally Important | 3 |
| More Important | 5 |
| Very Important | 7 |
| Conception | Significance | Mathematical Expression |
|---|---|---|
| Node | Airport and navigation station | Set of points |
| Side | Data | Side set |
| Weight | The passing probability of each route under the influencing factors | of the edges between points i and j |
| Section Number | Name | Distance | Recovery Probability |
|---|---|---|---|
| 1 | AKARA -LAMEN | 48.93015096 | 0.266843177 |
| 2 | KALBA -DYVOR | 155.2191865 | 0.513045005 |
| 3 | HSVOR -POMOK | 69.68911026 | 0.309360889 |
| ... | ... | ... | ... |
| 193 | JNVOR -WFVOR | 171.0139039 | 0.552342289 |
| 194 | LAGAL -LYGVOR | 126.2095388 | 0.440802791 |
| 195 | ATVIM -XZVOR | 34.06497851 | 0.238785375 |
| State | Reason |
|---|---|
| S | The susceptible node refers to the node with no route network delay when the air traffic network is delayed. |
| E | Delay node refers to the node that has experienced route network delay but does not have the transmission ability. |
| I | Delayed transmission node refers to the node that has experienced route network delay and has transmission ability. |
| R | The recovery node is the node where the route network delay has dissipated. |
| Symbol | Significance | Symbol | Significance |
|---|---|---|---|
| S | Predisposing nodes | α | Probability that a delayed node becomes a delayed propagation node |
| E | Airport node (sleeper) | Probability that a susceptible node becomes a delayed node | |
| I | Route crossing point (infected person) | Probability that a susceptible node becomes a delayed propagation node | |
| R | Recovery node | γ | Delayed recovery probability of a node |
| N | Total number of nodes | t | Pacemaker |
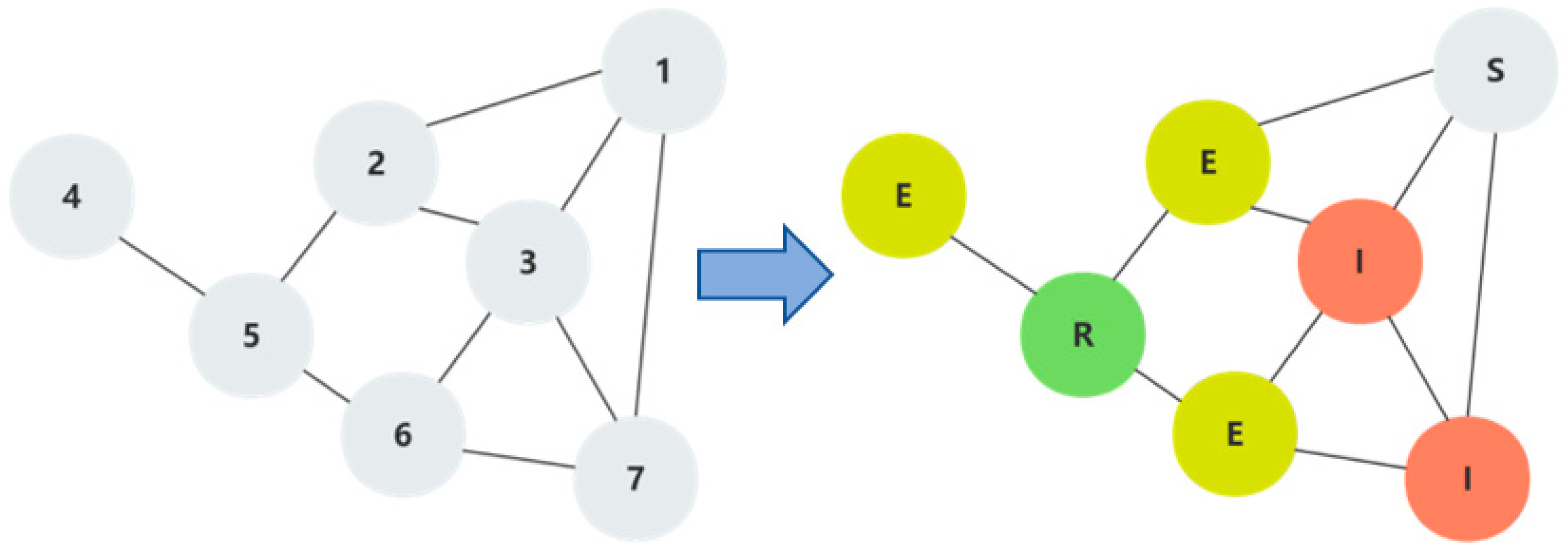
| Node | State | Describe |
|---|---|---|
| 1 | S state | It is associated with node 1 and has a large edge right, but the node is not yet infected and is in a normal state because the airport node has some capacity. |
| 2 | E state | It is currently latent because it is associated with node 3 and is a short distance away, but also has some capacity as an airport node. |
| 3 | I state | For node 3, firstly, there is some relationship with the network nodes connected to the edges, and secondly, node 3 starts with delays and is in the I-state due to saturated routes and a high number of aircraft, as well as the presence of influencing factors such as military aviation activities. |
| 4 | E state | In the case where only node 3 is considered to be infected, the node is in a normal state since only the associated node 5 is a normal node. |
| 5 | R state | Since nodes 2 and 6 are still latent, the node is still in a normal state at this moment. |
| 6 | E state | Since the network side rights are small, it is a navigation point but still latent at the moment. |
| 7 | I state | Due to the close proximity to node 3 and being a navigation point itself without capacity, the node transformed from S-state to I-state immediately after the delay occurred. |
| S | E | I | R | Weighted Sum | |
|---|---|---|---|---|---|
| Random point | 73 | 12 | 14 | 5 | 15.6808 |
| Degree centrality | 67 | 8 | 27 | 2 | 21.2927 |
| GA | 35 | 35 | 22 | 12 | 24.9525 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Wen, X.; Wu, M.; Xie, H. Identification of Critical Nodes for Delay Propagation in Susceptible-Exposed-Infected-Recovered (SEIR) and Genetic Algorithm (GA) Route Networks. Aerospace 2024, 11, 878. https://doi.org/10.3390/aerospace11110878
Zhang M, Wen X, Wu M, Xie H. Identification of Critical Nodes for Delay Propagation in Susceptible-Exposed-Infected-Recovered (SEIR) and Genetic Algorithm (GA) Route Networks. Aerospace. 2024; 11(11):878. https://doi.org/10.3390/aerospace11110878
Chicago/Turabian StyleZhang, Mingyu, Xiangxi Wen, Minggong Wu, and Hanchen Xie. 2024. "Identification of Critical Nodes for Delay Propagation in Susceptible-Exposed-Infected-Recovered (SEIR) and Genetic Algorithm (GA) Route Networks" Aerospace 11, no. 11: 878. https://doi.org/10.3390/aerospace11110878
APA StyleZhang, M., Wen, X., Wu, M., & Xie, H. (2024). Identification of Critical Nodes for Delay Propagation in Susceptible-Exposed-Infected-Recovered (SEIR) and Genetic Algorithm (GA) Route Networks. Aerospace, 11(11), 878. https://doi.org/10.3390/aerospace11110878






