Optimal Selection of Active Jet Parameters for a Ducted Tail Wing Aimed at Improving Aerodynamic Performance
Abstract
1. Introduction
- (1)
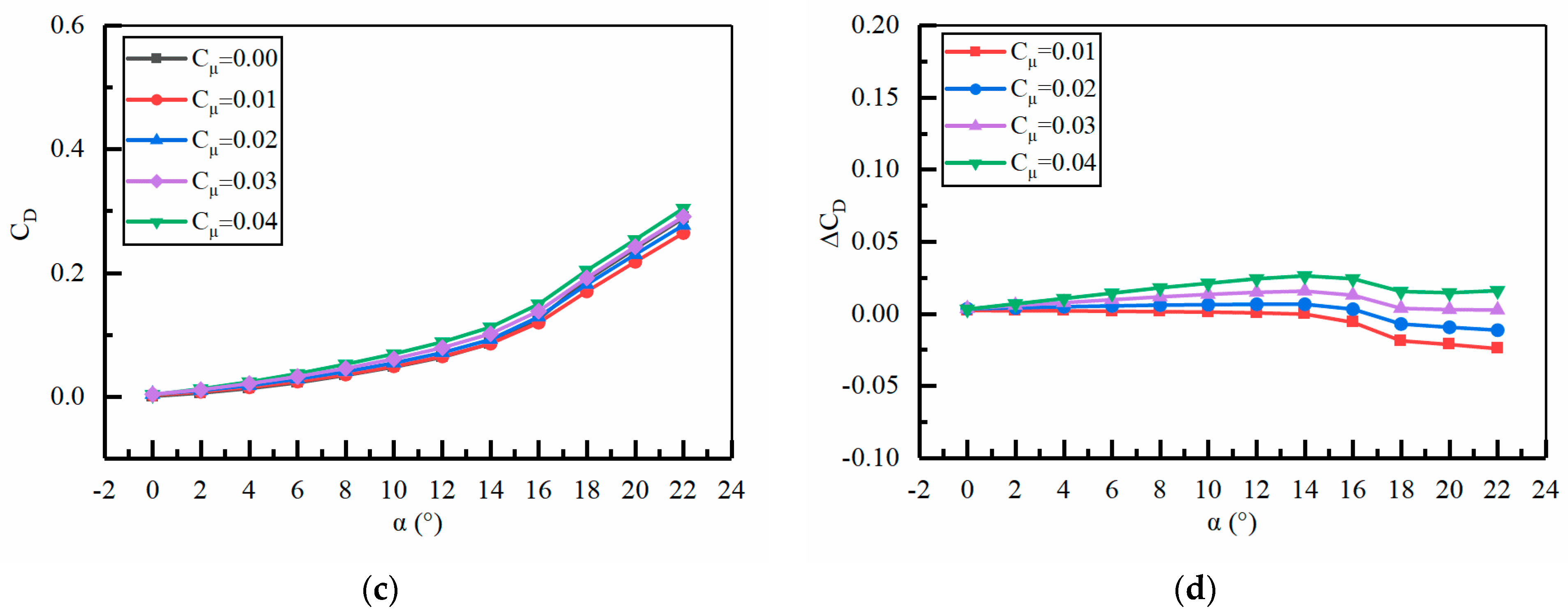
- By studying the effects of parameters such as momentum coefficient, jet hole position, jet hole height, and jet angle on improving the aerodynamic performance of the ducted tail wing, we found that compared with jet hole height and jet angle, momentum coefficient and jet hole position are more effective on improving the aerodynamic performance of the ducted tail wing.
- (2)
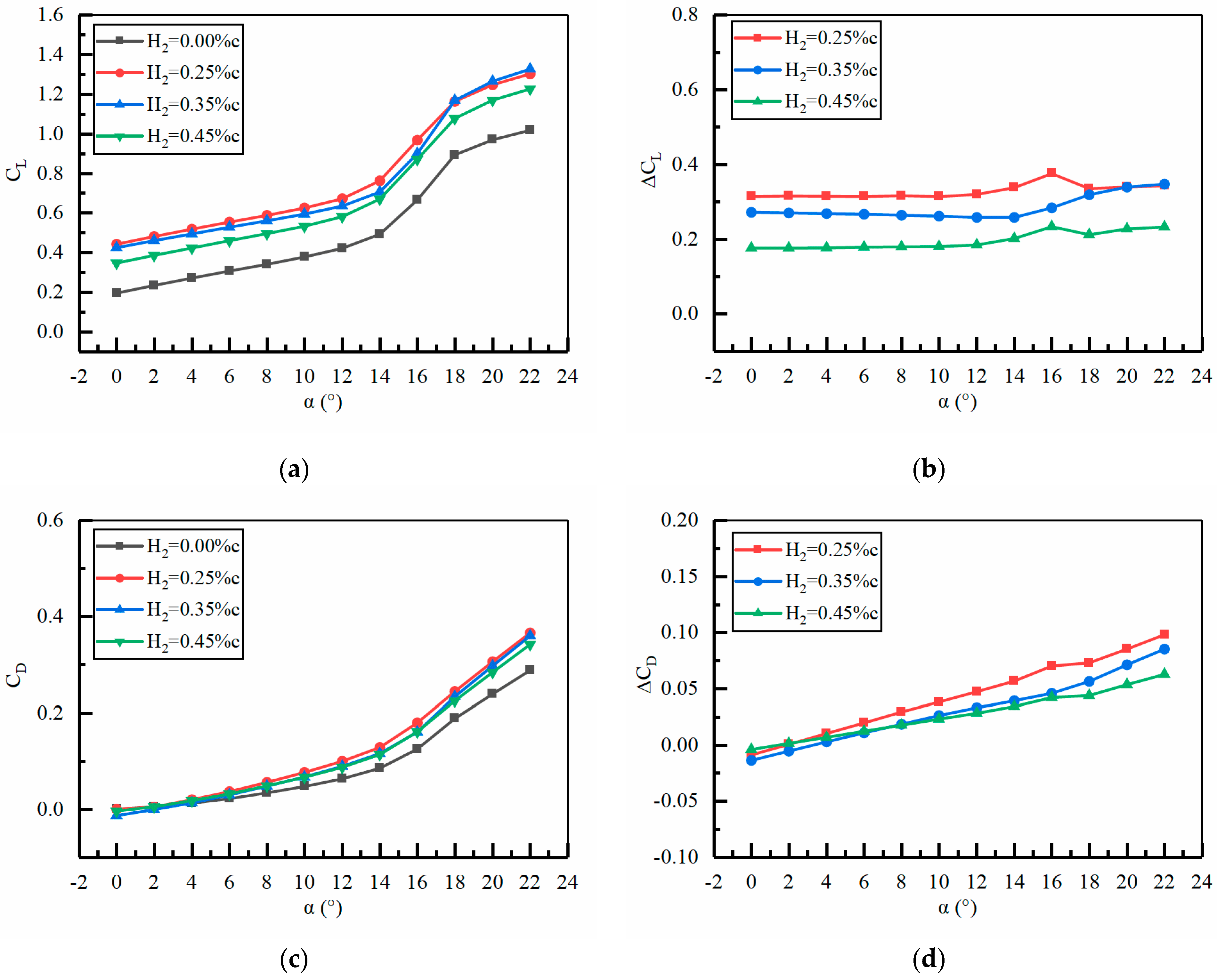
- Under a trailing edge jet, the relatively good jet condition occurs when the jet hole height is equal to 0.25% of the aerodynamic chord length, and the jet angle is equal to 0°. At this time, with the increase of the jet momentum coefficient, the effect of increasing lift of the ducted tail wing is the best.
- (3)
- Finally, a comparative analysis is conducted on the lift and drag characteristics between the ducted tail wing and traditional tail wing, and it is found that the ducted tail wing can generate lift at 0° attack angle and will not stall in the high attack angle range of 12°~22°.
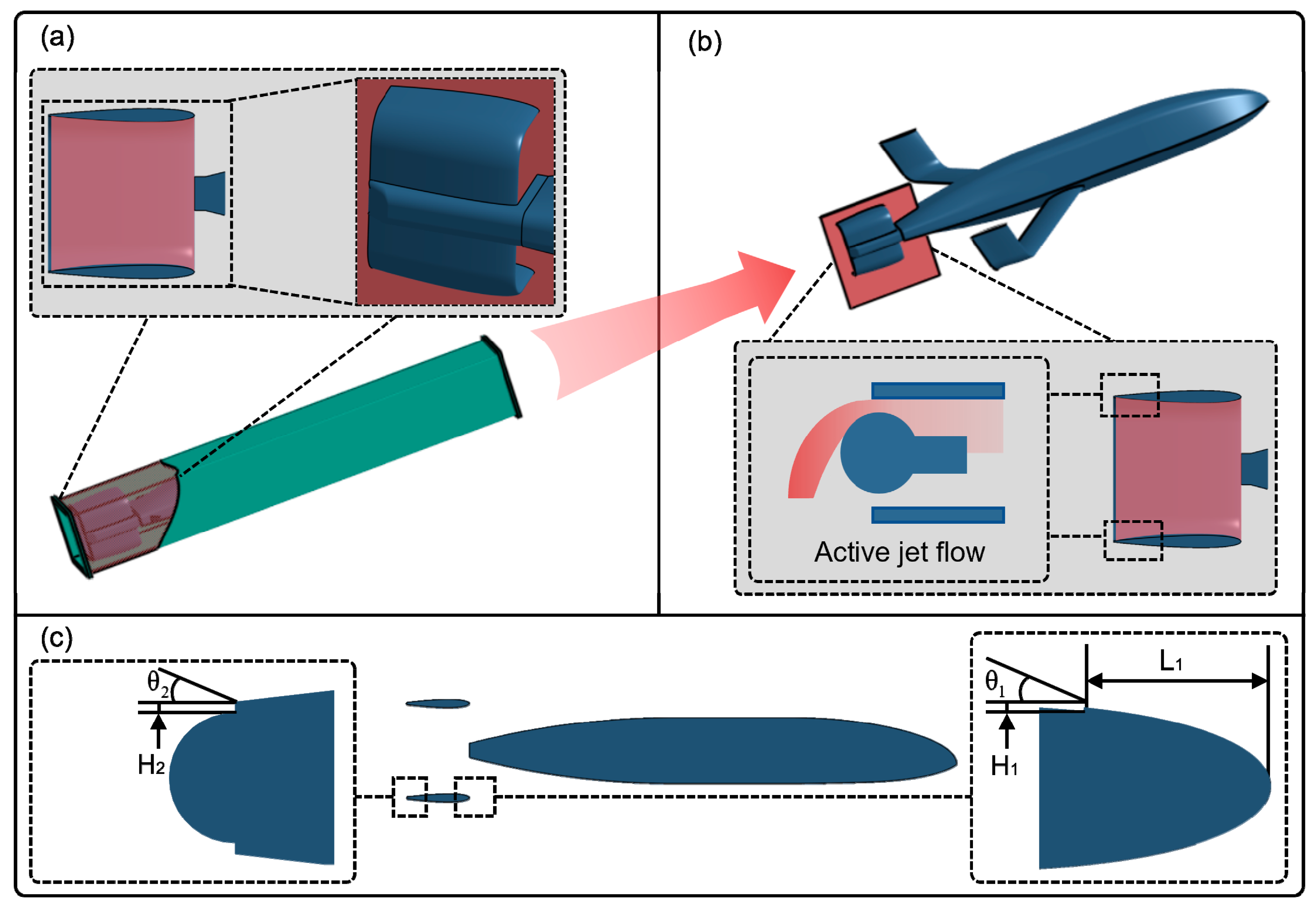
2. Research Object
3. Jet Parameters and Numerical Simulation Methods
3.1. Selection of Active Jet Parameters
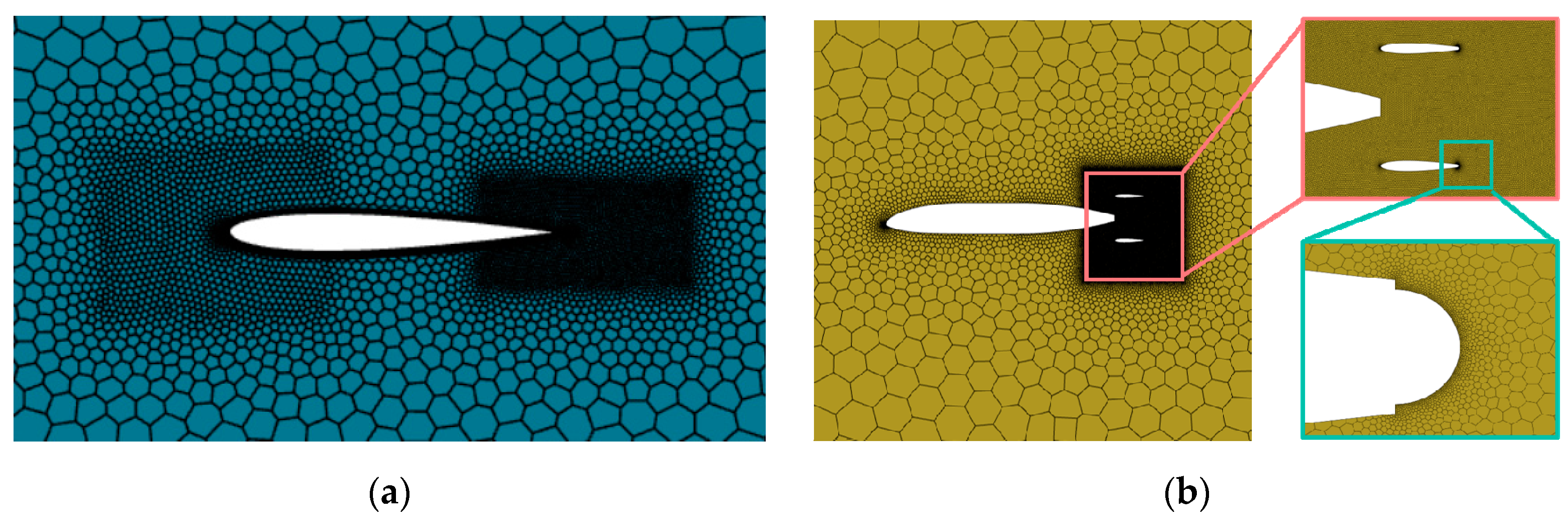
3.2. Simulation Method and Computational Grid Independence
3.2.1. Simulation Method
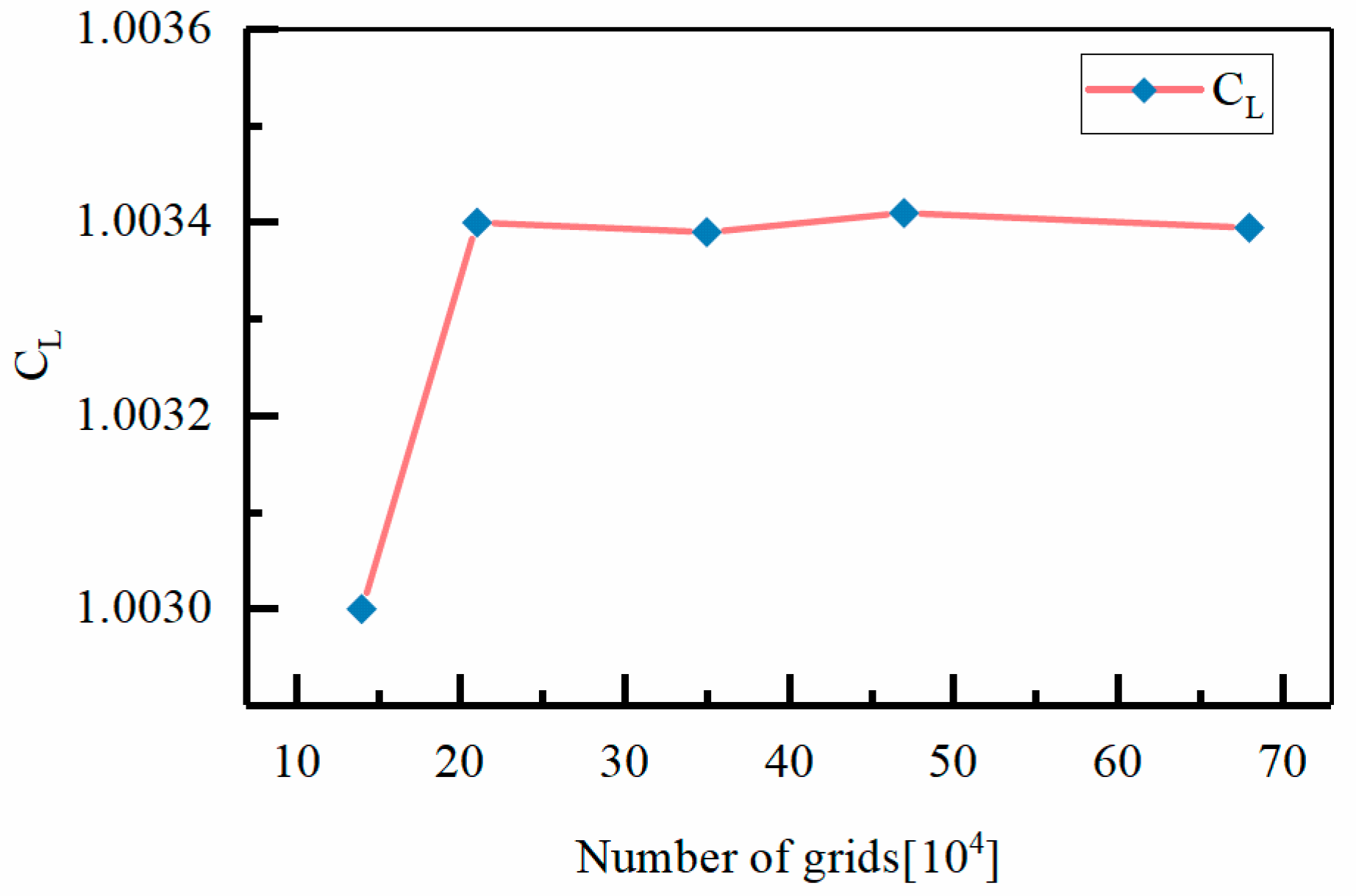
3.2.2. Grid Independence Verification
4. Result Analysis
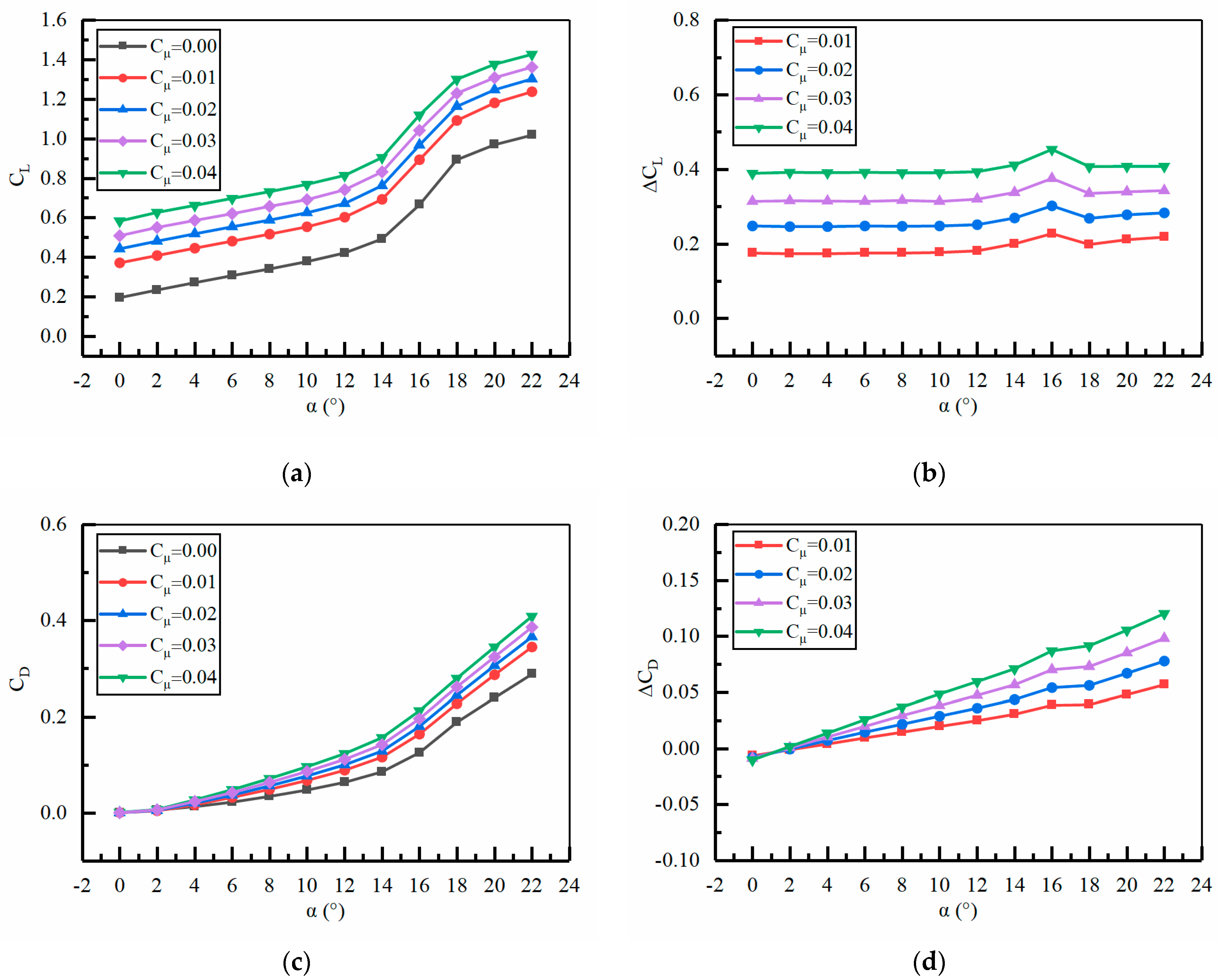
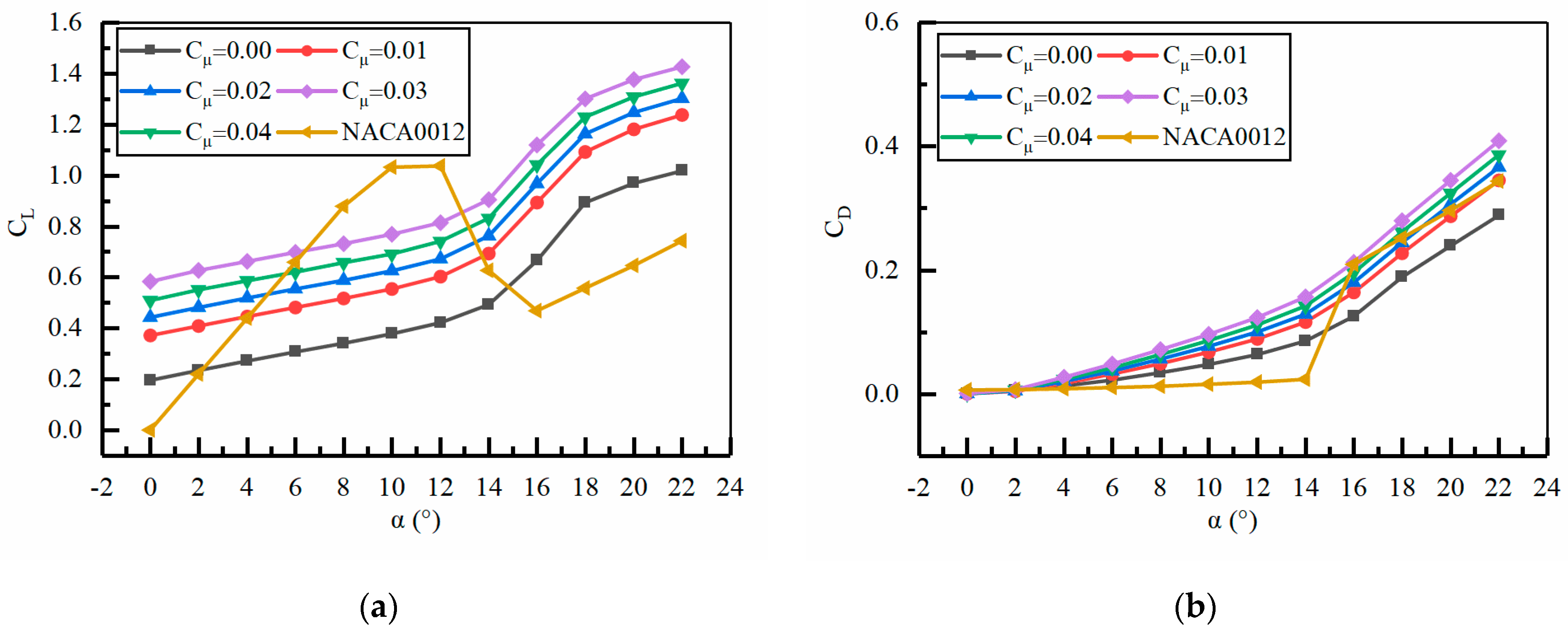
4.1. The Improvement Effect of Momentum Coefficient on Aerodynamic Performance
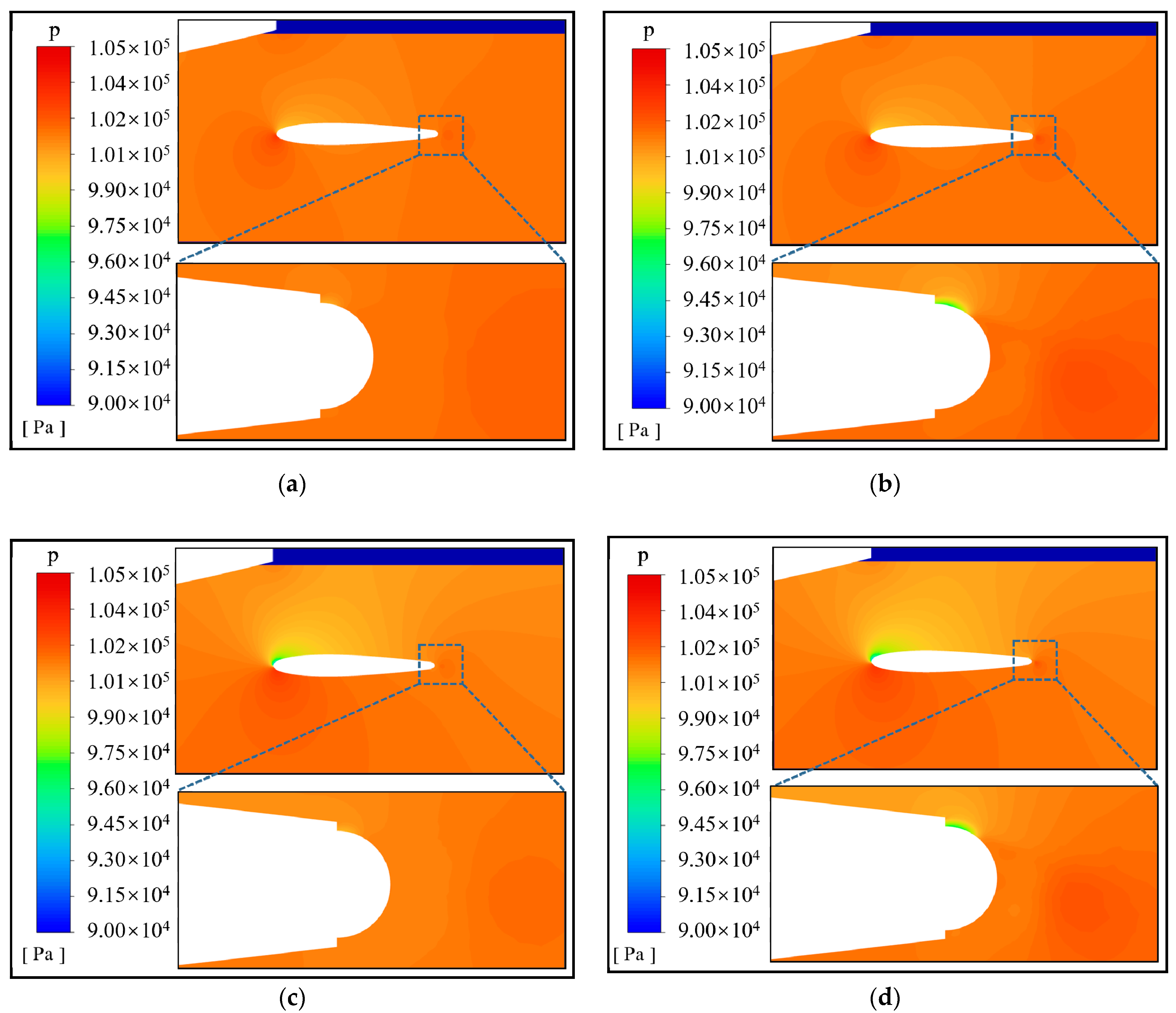
4.2. The Improvement Effect of Jet Hole Height on Aerodynamic Performance
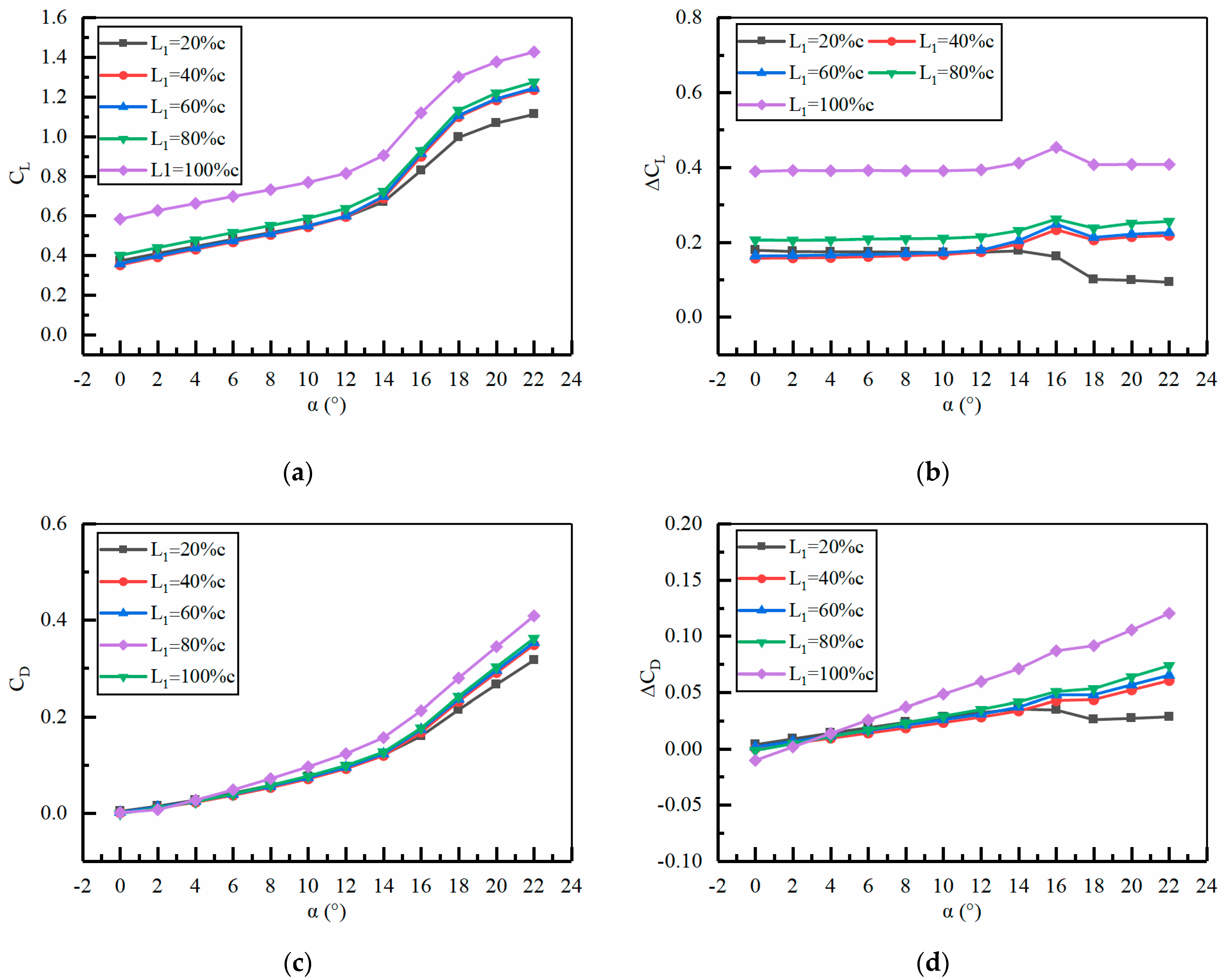
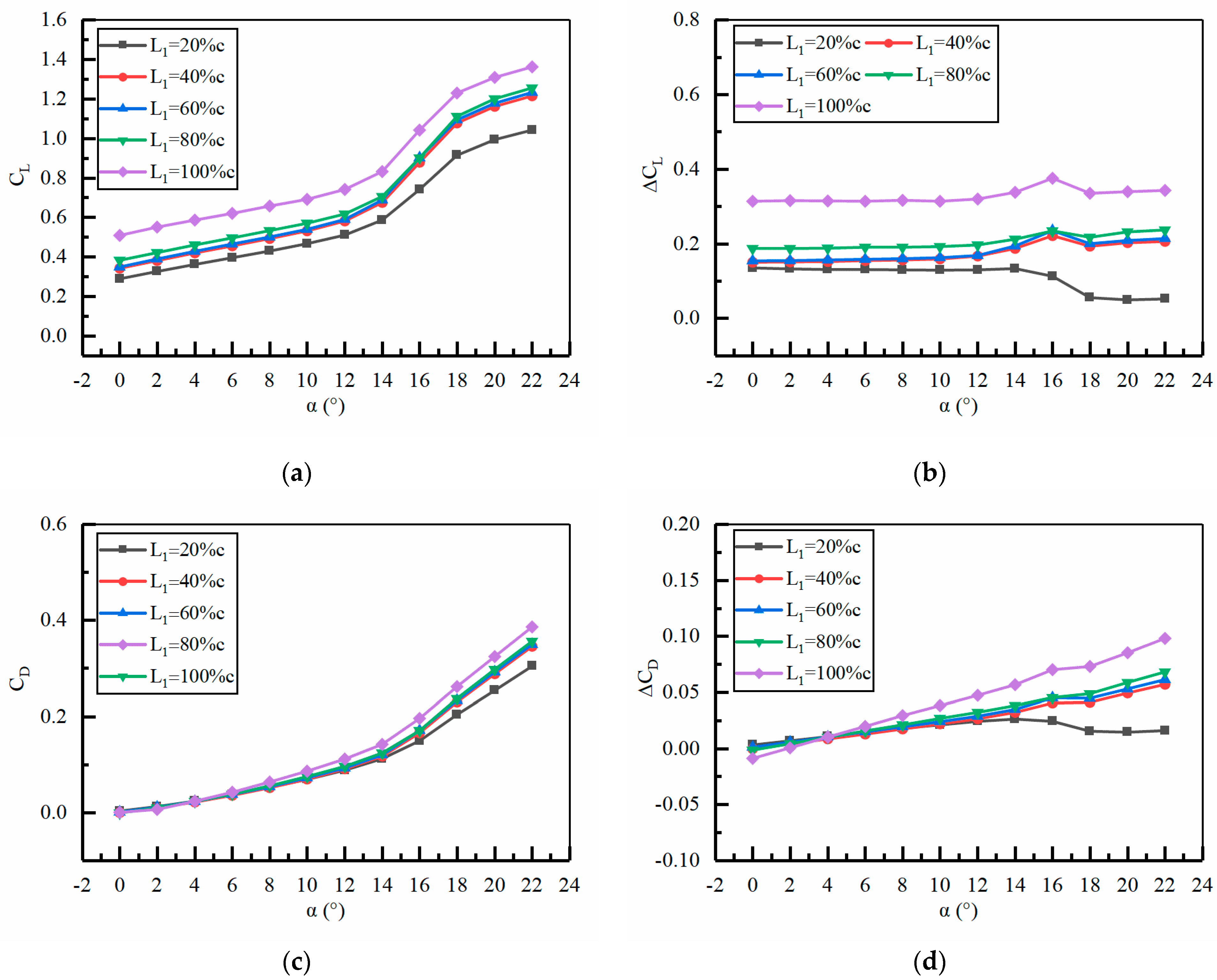
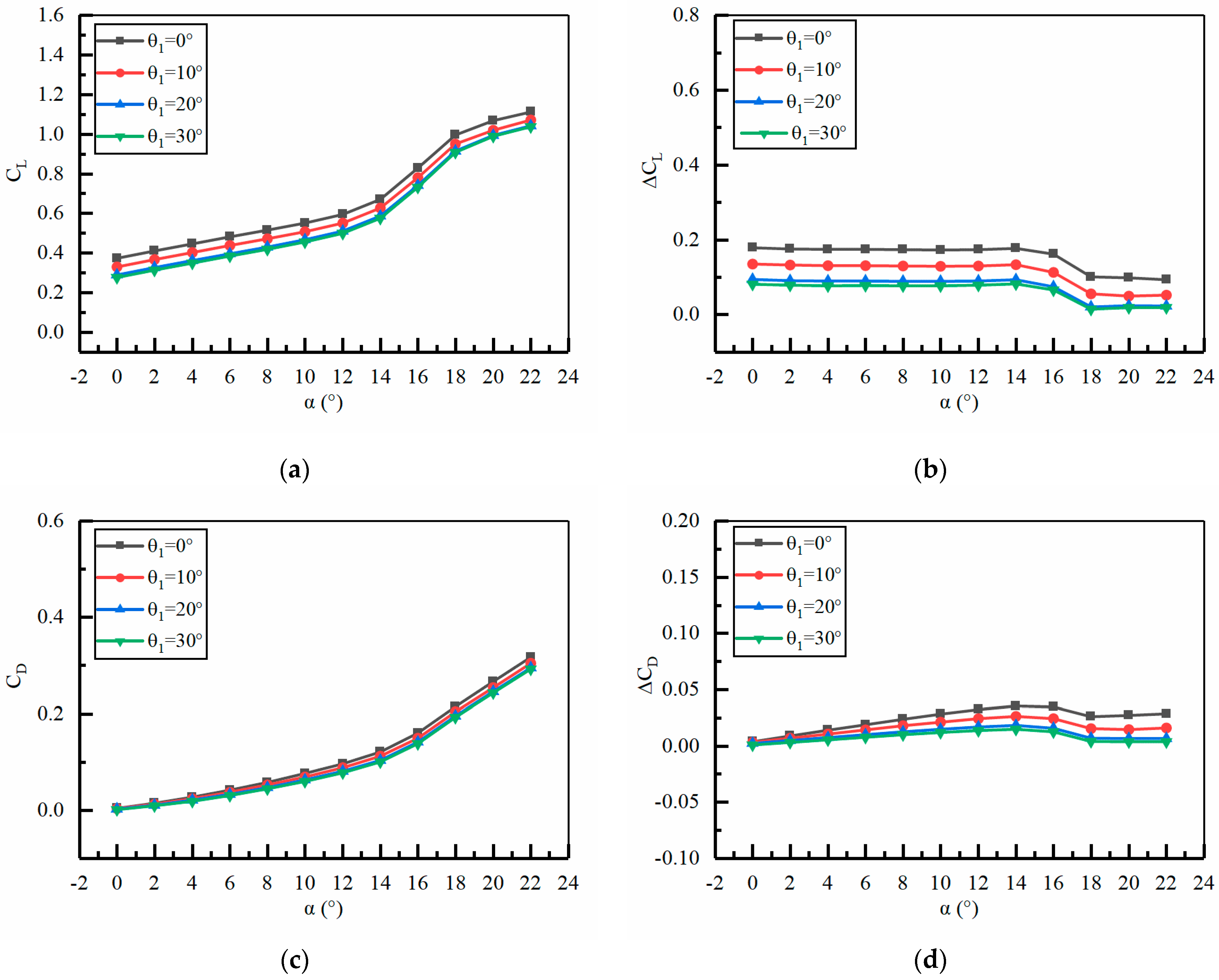
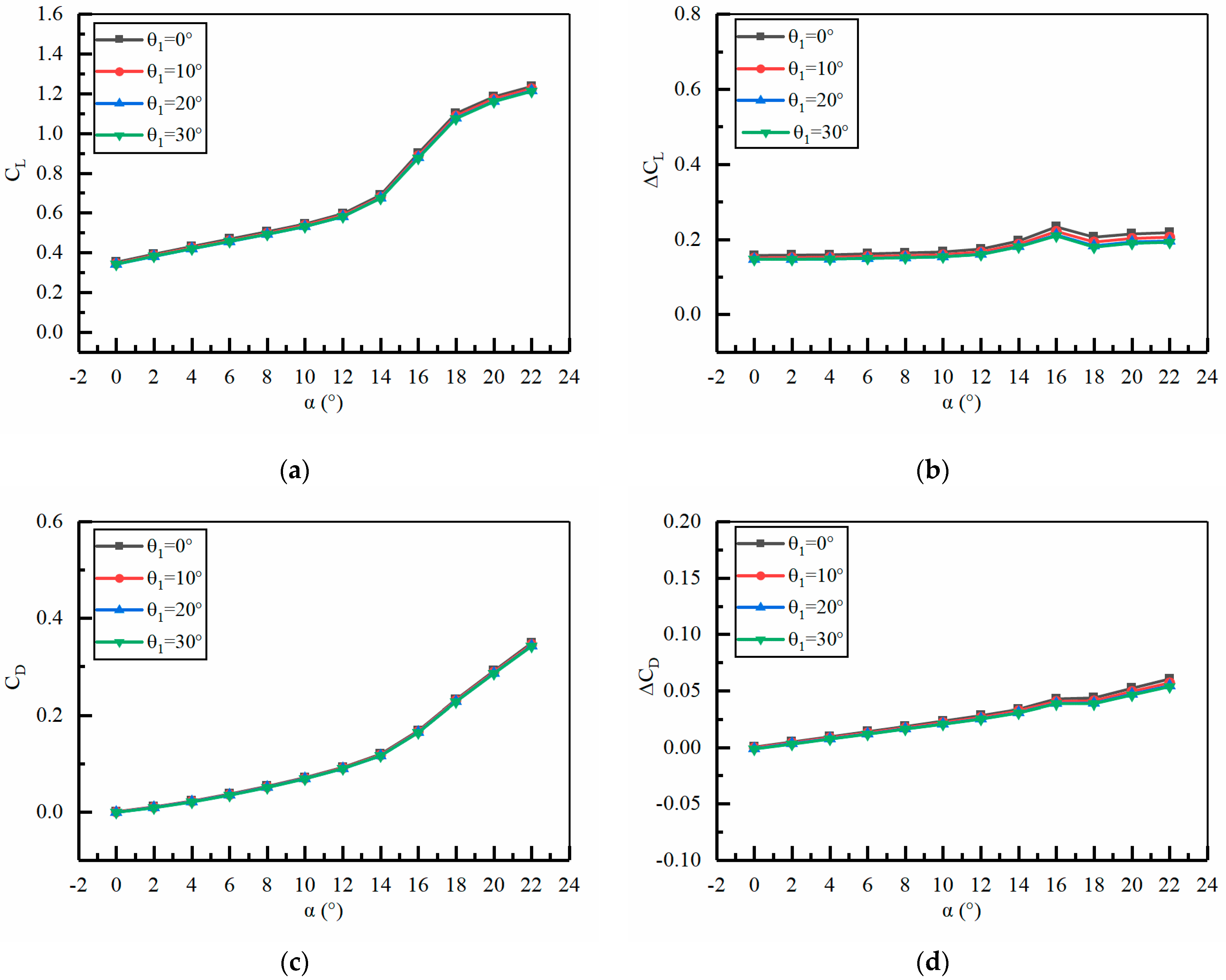
4.3. The Improvement Effect of Jet Hole Position on Aerodynamic Performance
4.4. The Improvement Effect of Jet Angle on Aerodynamic Performance
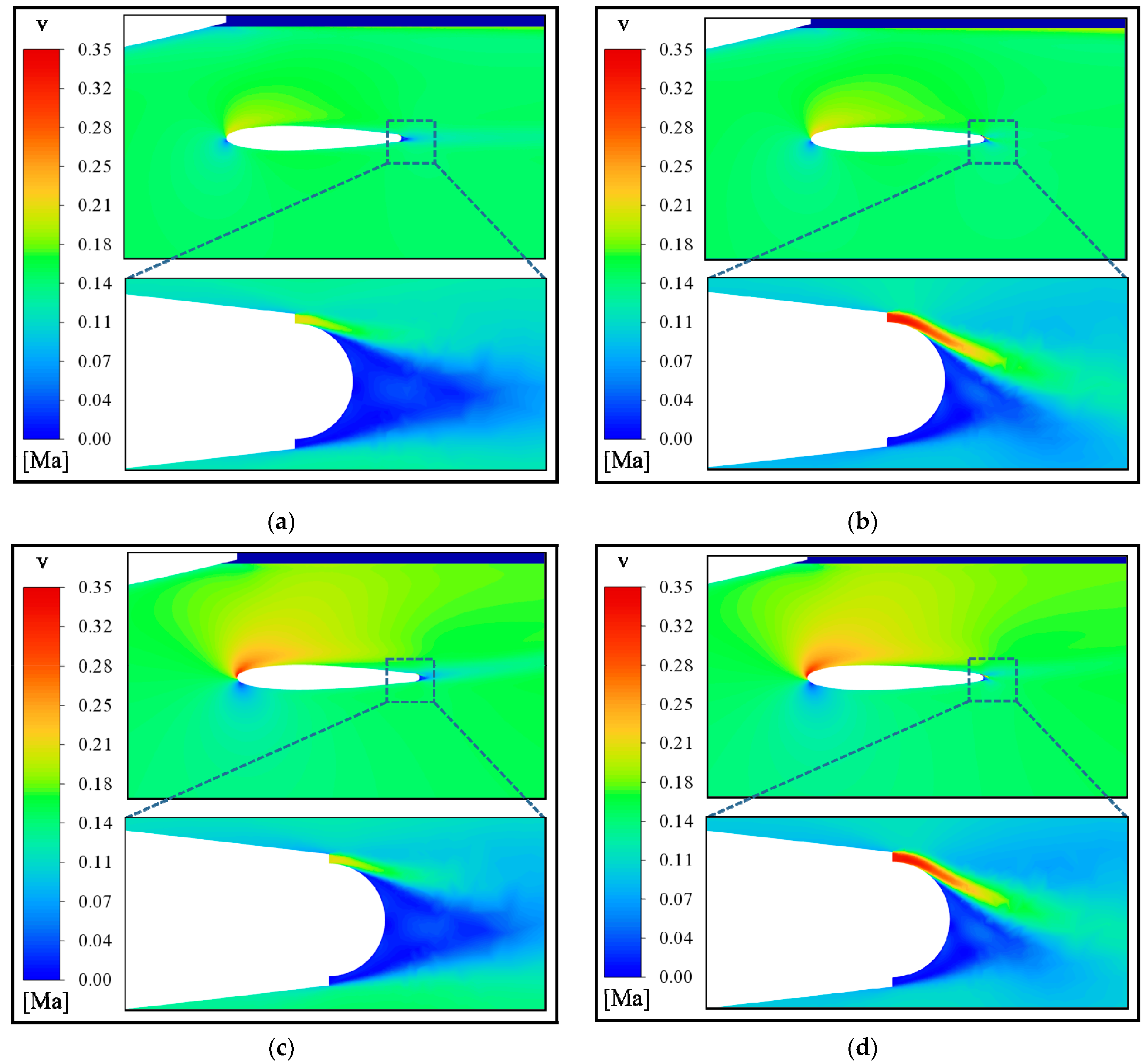
4.5. Advantages and Principle Analysis of the Ducted Tail Wing
5. Conclusions
- (1)
- The improvement effect of jet hole height and jet angle on the aerodynamic performance of ducted tail wing is relatively small. Through comparative analysis, it is found that under the conditions of jet hole height H2 = 0.25%c and jet angle = 0°, it is more conducive to improving the aerodynamic performance of the ducted tail wing.
- (2)
- The momentum coefficient and jet hole position are the main factors affecting the aerodynamic performance of the ducted tail wing. Under the conditions of H2 = 0.25%c, jet angle = 0°, and L1 = 100%c (jet hole located at the trailing edge of the tail wing), the improvement effect of the aerodynamic performance of the tail wing is relatively good as the momentum coefficient increases. At = 0.04, the average of is 0.403; When = 0.03, the average of is 0.329; When = 0.02, the average of is 0.262; When = 0.01, the average of is 0.191. When increases from 0.01 to 0.04, the average growth of can reach 110%.
- (3)
- A comparative analysis is conducted on the aerodynamic performance of ducted tail wings and NACA0012 airfoils. It is found that the ducted tail can generate lift at a 0° angle of attack. In this way, under low angle of attack conditions, the ducted tail can generate control force without jet flow, which can save control energy. Compared with the NACA0012 airfoil, the ducted tail does not stall at angles of attack ≥12° and can provide stable control momentum for the aircraft at high attack angles.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Warsop, C.; Crowther, W.J. Fluidic Flow Control Effectors for Flight Control. AIAA J. 2018, 56, 3808–3824. [Google Scholar] [CrossRef]
- Warsop, C.; Crowther, W. NATO AVT-239 Task Group: Flight Demonstration of Fluidic Flight Controls on the MAGMA Subscale Demonstrator Aircraft. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Jones, G.S.; Joslin, R.D. Applications of Circulation Control Technology; Progress in Astronautics & Aeronautics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. [Google Scholar]
- Englar, R.J. Development of Circulation Control Technology for Powered-Lift STOL Aircraft. 1987. Available online: https://ntrs.nasa.gov/citations/19880008224 (accessed on 17 March 2024).
- Frith, S.; Wood, N. Investigation of Dual Circulation Control Surfaces for Flight Control. In Proceedings of the Aiaa Flow Control Conference, Portland, OR, USA, 28 June–1 July 2015. [Google Scholar]
- Fielding, J.; Lawson, C.; Martins-Pires, R.; Monterzino, G. Design, Build and Flight of The DEMON Demonstrator UAV. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar]
- Hoholis, G.; Steijl, R.; Badcock, K. Circulation Control as a Roll Effector for Unmanned Combat Aerial Vehicles. J. Aircr. 2016, 53, 1875–1889. [Google Scholar] [CrossRef]
- Xu, H.Y.; Qiao, C.L.; Yang, H.Q.; Ye, Z.Y. Active Circulation Control on the Blunt Trailing Edge Wind Turbine Airfoil. AIAA J. 2017, 56, 554–570. [Google Scholar] [CrossRef]
- Xu, H.Y.; Dong, Q.L.; Qiao, C.L.; Ye, Z.Y. Flow Control over the Blunt Trailing Edge of Wind Turbine Airfoils Using Circulation Control. Energies 2018, 11, 619. [Google Scholar] [CrossRef]
- Fu, Z.; Chu, Y.W.; Cai, Y.S.; Xu, H.Y.; Xu, Y. Numerical Investigation of Circulation Control Applied to Flapless Aircraft. Aircr. Eng. Aerosp. Technol. 2020; ahead-of-print. [Google Scholar] [CrossRef]
- Visser, K.D.; Nelson, R.C.; Ng, T.T. A Flow Visualization and Aerodynamic Force Data Evaluation of Spanwise Blowing on Full and Half Span Delta Wings. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. [Google Scholar]
- Amitay, M.; Anders, S.G.; Parekh, D.E.; Washburn, A.E. Active Flow Control on the Stingray Uninhabited Air Vehicle: Transient Behaviour. AIAA J. 2004, 42, 2205–2215. [Google Scholar] [CrossRef]
- Mahmood, G.; Smith, D. Proportional Aerodynamic Control on a UAV Model Using Synthetic Jets. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Englar, R.; Jones, G.; Allan, B.; Lin, J. 2-D Circulation Control Airfoil Benchmark Experiments Intended for CFD Code Validation. In Proceedings of the Aiaa Aerospace Sciences Meeting Including the New Horizons Forum & Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Jones, G.S.; Englar, R.J. Advances in Pneumatic-Controlled High-Lift Systems Through Pulsed Blowing. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Jones, G.S.; Viken, S.A.; Washburn, A.E.; Jenkins, L.N.; Cagle, C.M. An Active Flow Circulation Controlled Flap Concept for General Aviation Aircraft Applications. In Proceedings of the 1st AIAA Flow Control Conference, St. Louis, MI, USA, 24–26 June 2002. [Google Scholar]
- Liu, Y.; Sankar, L.N.; Englar, R.; Ahuja, K.K.; Gaeta, R. Computational Evaluation of the Steady and Pulsed Jet Effects on the Performance of a Circulation Control Wing Section. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2003. [Google Scholar]
- Feng, L.H.; Shi, T.Y.; Liu, Y.G. Lift Enhancement of an Airfoil and an Unmanned Aerial Vehicle by Plasma Gurney Flaps. Aiaa J. 2017, 55, 1622–1632. [Google Scholar] [CrossRef]
- Itsariyapinyo, P.; Sharma, R.N. Large Eddy Simulation of a NACA0015 Circulation Control Airfoil Using Synthetic Jets. Aerosp. Sci. Technol. 2018, 82–83, 545–556. [Google Scholar] [CrossRef]
- Blackwell, J.A. Aerodynamic Characteristics of an 11-Percent-Thick Symmetrical Supercritical Airfoil at Mach Numbers between 0.30 and 0.85. 1969. Available online: https://ntrs.nasa.gov/citations/19830002814 (accessed on 12 March 2024).





| Serial Number | Parameter | Values |
|---|---|---|
| 1 | 0.00/0.01/0.02/0.03/0.04 | |
| 2 | H1 | 0.25%c |
| 3 | H2 | 0.25%c/0.35%c/0.45%c |
| 4 | L1 | 20%c/40%c/60%c/80%c/100%c |
| 5 | 0°/10°/20°/30° | |
| 6 | 0° |
| Model | The Number of Sparse Grids | The Number of Medium Grids | The Number of Fine Grids |
|---|---|---|---|
| NACA0012 tail wing | 1.40 × 105/2.10 × 105 | 3.50 × 105/4.70 × 105 | 6.80 × 105 |
| Jet ducted tail wing | 3.56 × 106 | 7.06 × 106 | 1.50 × 107 |
| Aerodynamic Parameters | The Number of Sparse Grids | The Number of Medium Grids | The Number of Fine Grids |
|---|---|---|---|
| Lift coefficient | 0.8791 | 0.8945 | 0.8963 |
| Drag coefficient | 0.1548 | 0.1887 | 0.1924 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Zheng, H.; Zhou, H.; Huo, S. Optimal Selection of Active Jet Parameters for a Ducted Tail Wing Aimed at Improving Aerodynamic Performance. Aerospace 2024, 11, 851. https://doi.org/10.3390/aerospace11100851
Jia H, Zheng H, Zhou H, Huo S. Optimal Selection of Active Jet Parameters for a Ducted Tail Wing Aimed at Improving Aerodynamic Performance. Aerospace. 2024; 11(10):851. https://doi.org/10.3390/aerospace11100851
Chicago/Turabian StyleJia, Huayu, Huilong Zheng, Hong Zhou, and Shunbo Huo. 2024. "Optimal Selection of Active Jet Parameters for a Ducted Tail Wing Aimed at Improving Aerodynamic Performance" Aerospace 11, no. 10: 851. https://doi.org/10.3390/aerospace11100851
APA StyleJia, H., Zheng, H., Zhou, H., & Huo, S. (2024). Optimal Selection of Active Jet Parameters for a Ducted Tail Wing Aimed at Improving Aerodynamic Performance. Aerospace, 11(10), 851. https://doi.org/10.3390/aerospace11100851





