Research on the Structural Design of a Pressurized Cabin for Civil High-Speed Rotorcraft and the Multi-Dimensional Comprehensive Evaluation Method
Abstract
1. Introduction
2. Introduction to the Structural Configuration of the Pressurized Cabin of the Rotorcraft
2.1. Research Objective
2.2. Structural Program
2.2.1. Structural Configuration Design of the Pressurized Cabin
2.2.2. Selection of Structural Configuration Options for the Pressurized Cabin
3. Finite Element Modeling of Structural Configuration Scheme for Pressurized Cabin
3.1. Selection of Materials for the Pressurized Cabin Model
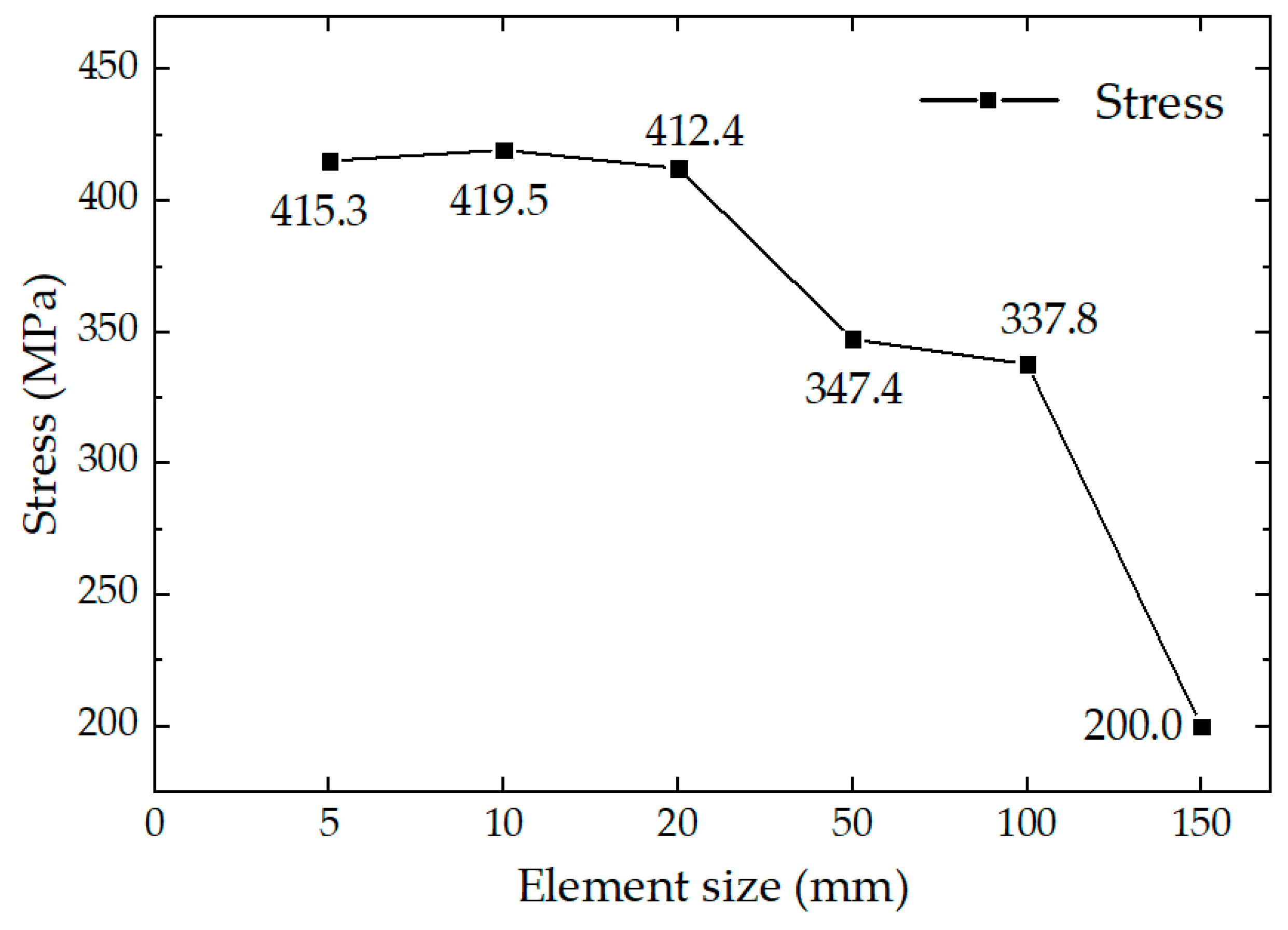
3.2. Mesh Geometry of Pressurized Cabin Structure Configuration
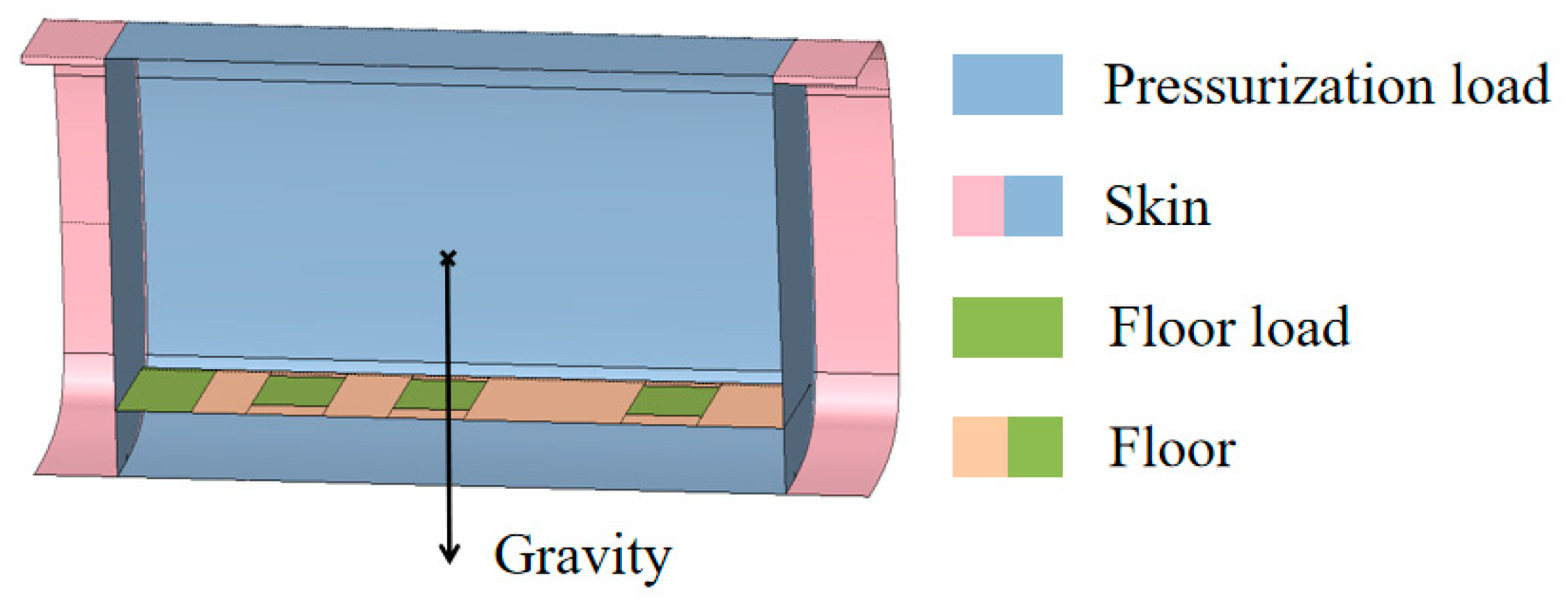
3.3. Load Loading and Boundary Conditions
4. Finite Element Simulation Results of the Structural Configuration Scheme of the Pressurized Compartment
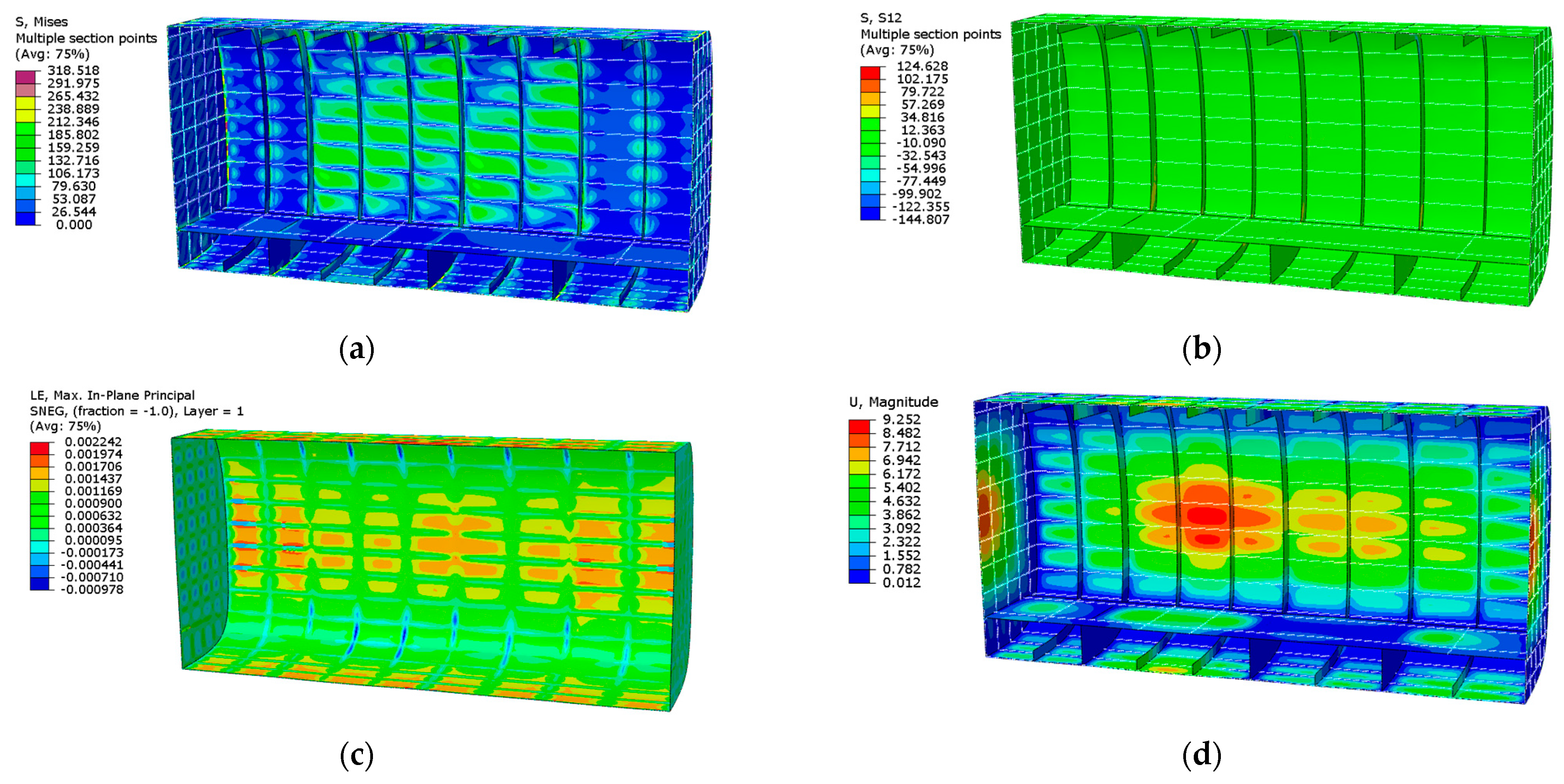
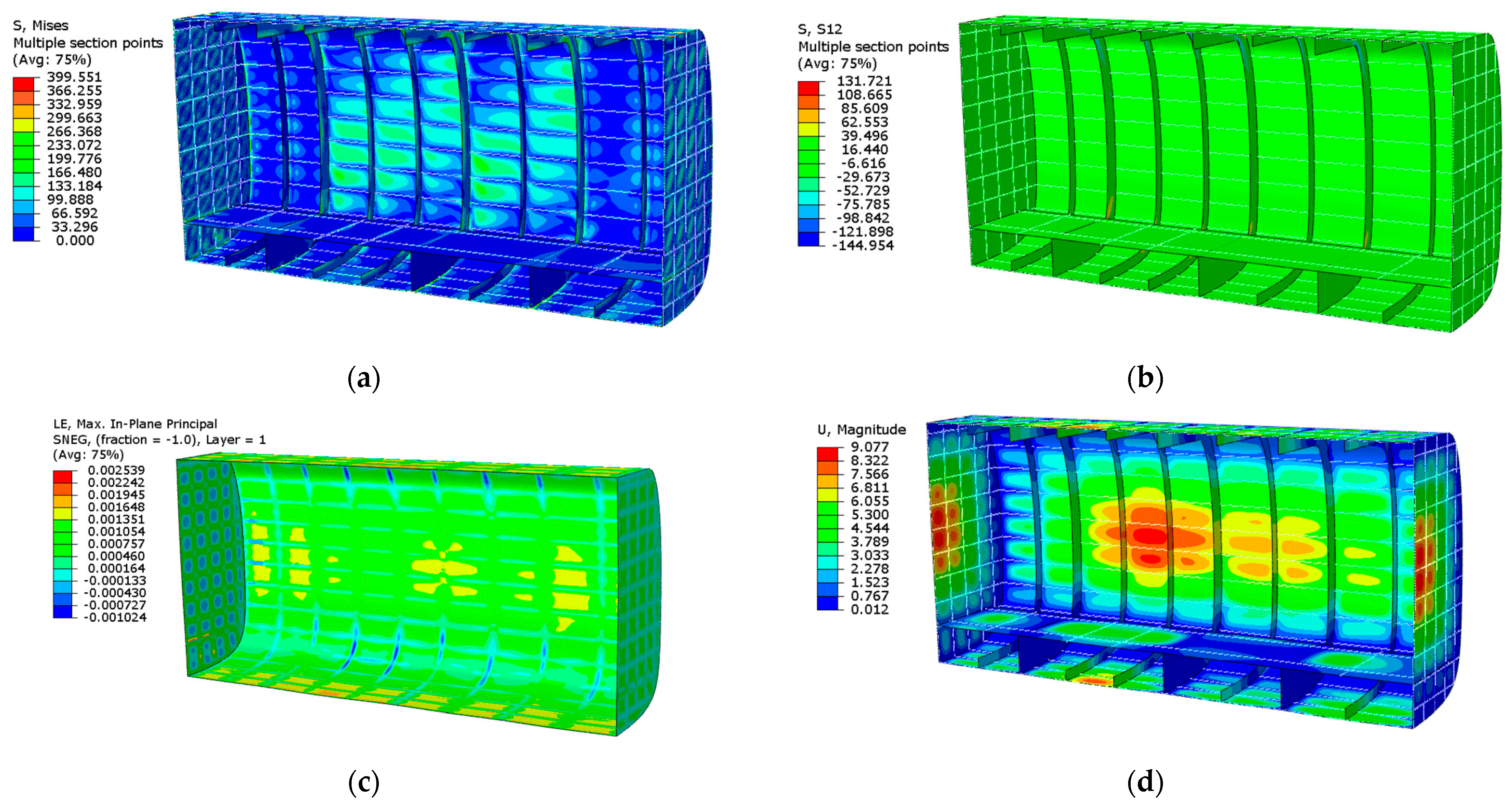
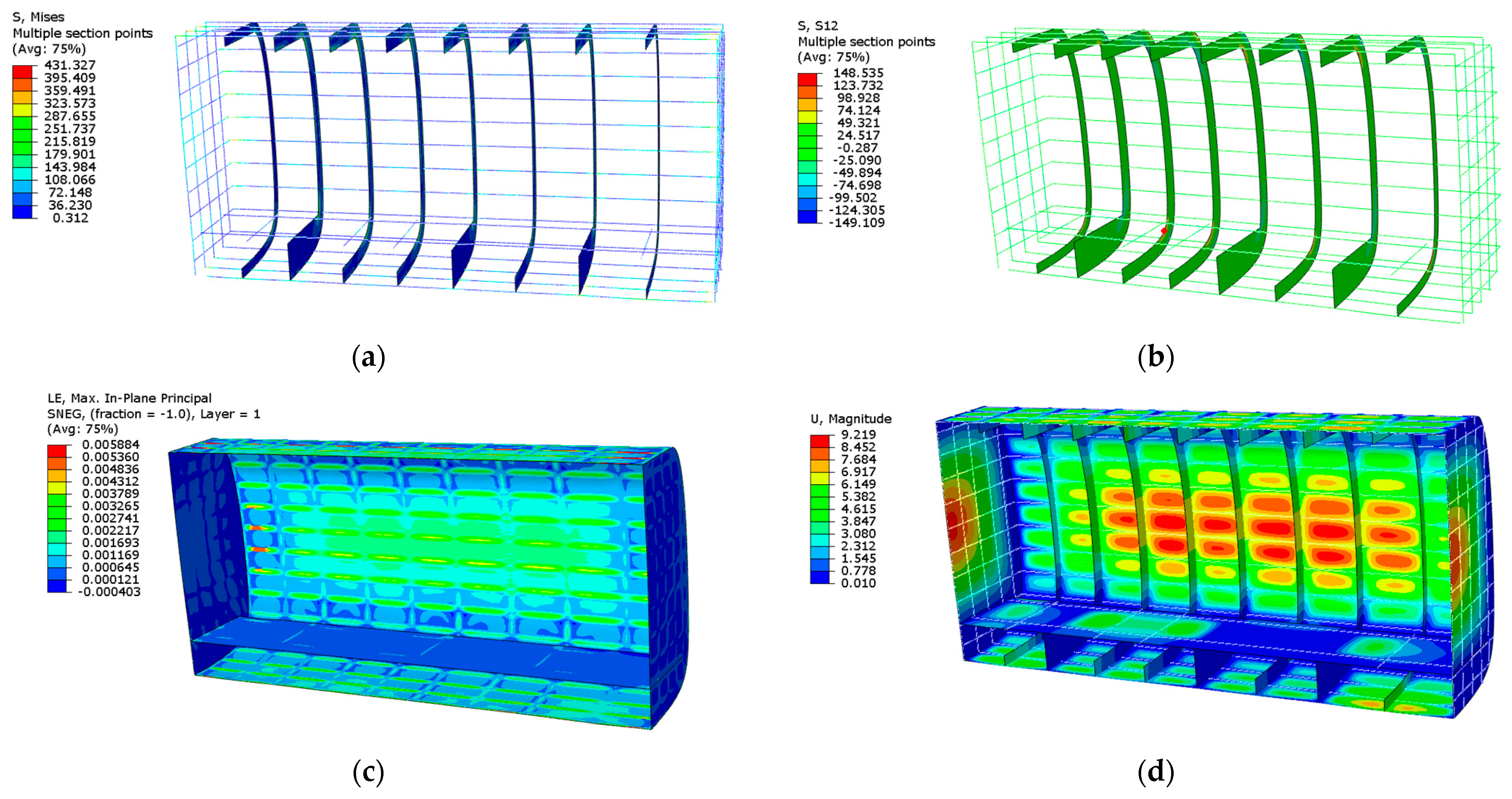
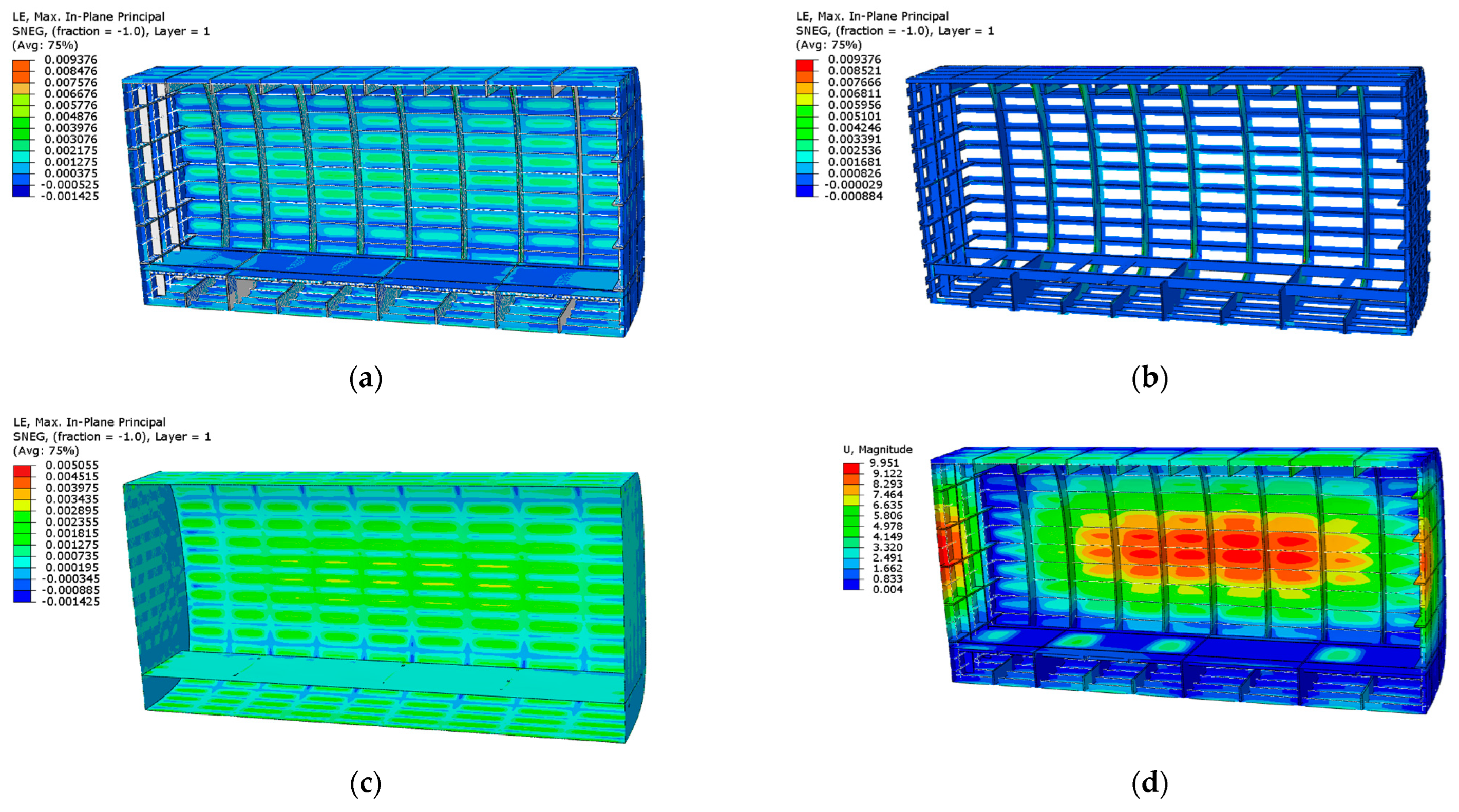
4.1. Finite Element Simulation Results
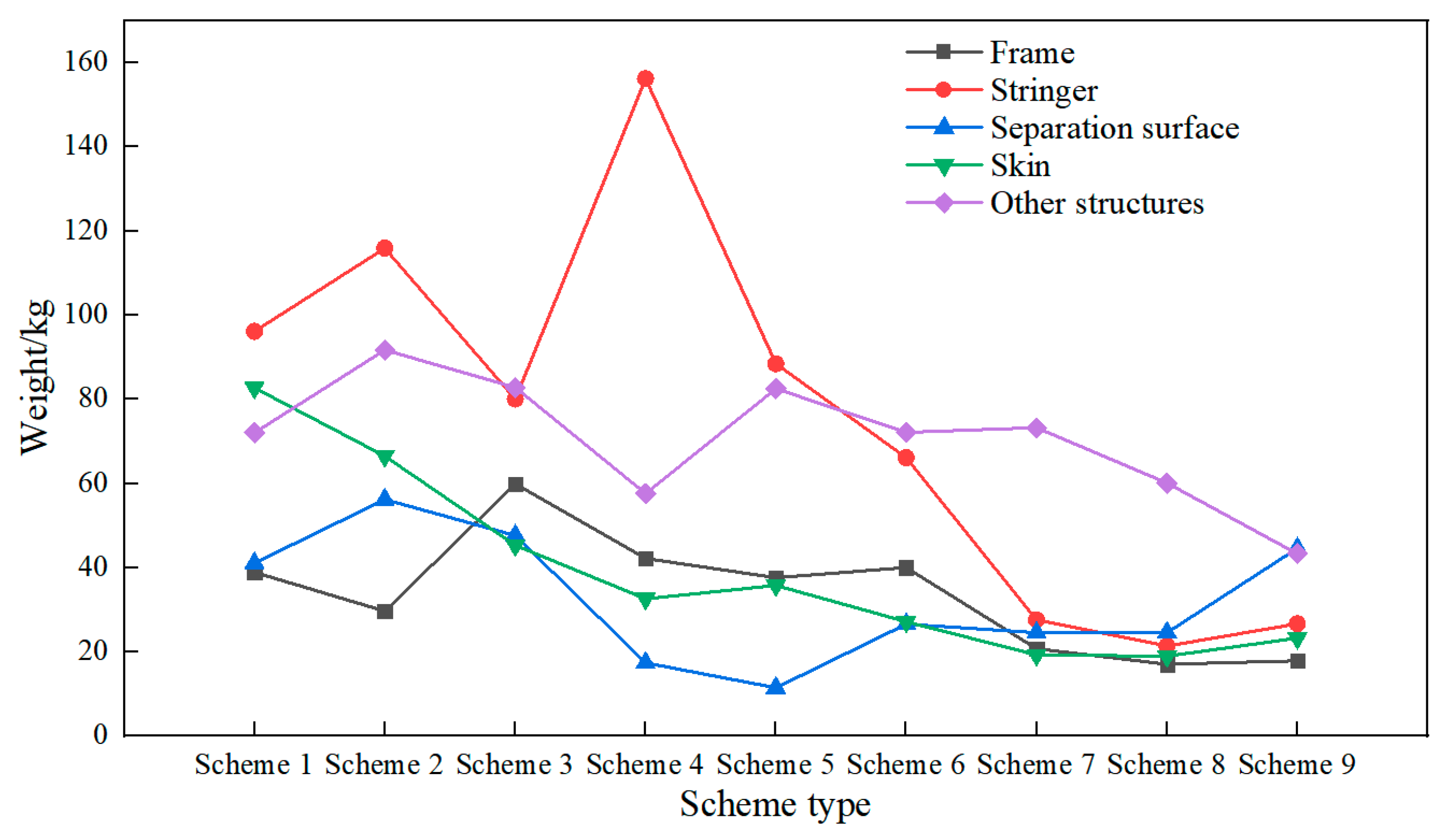
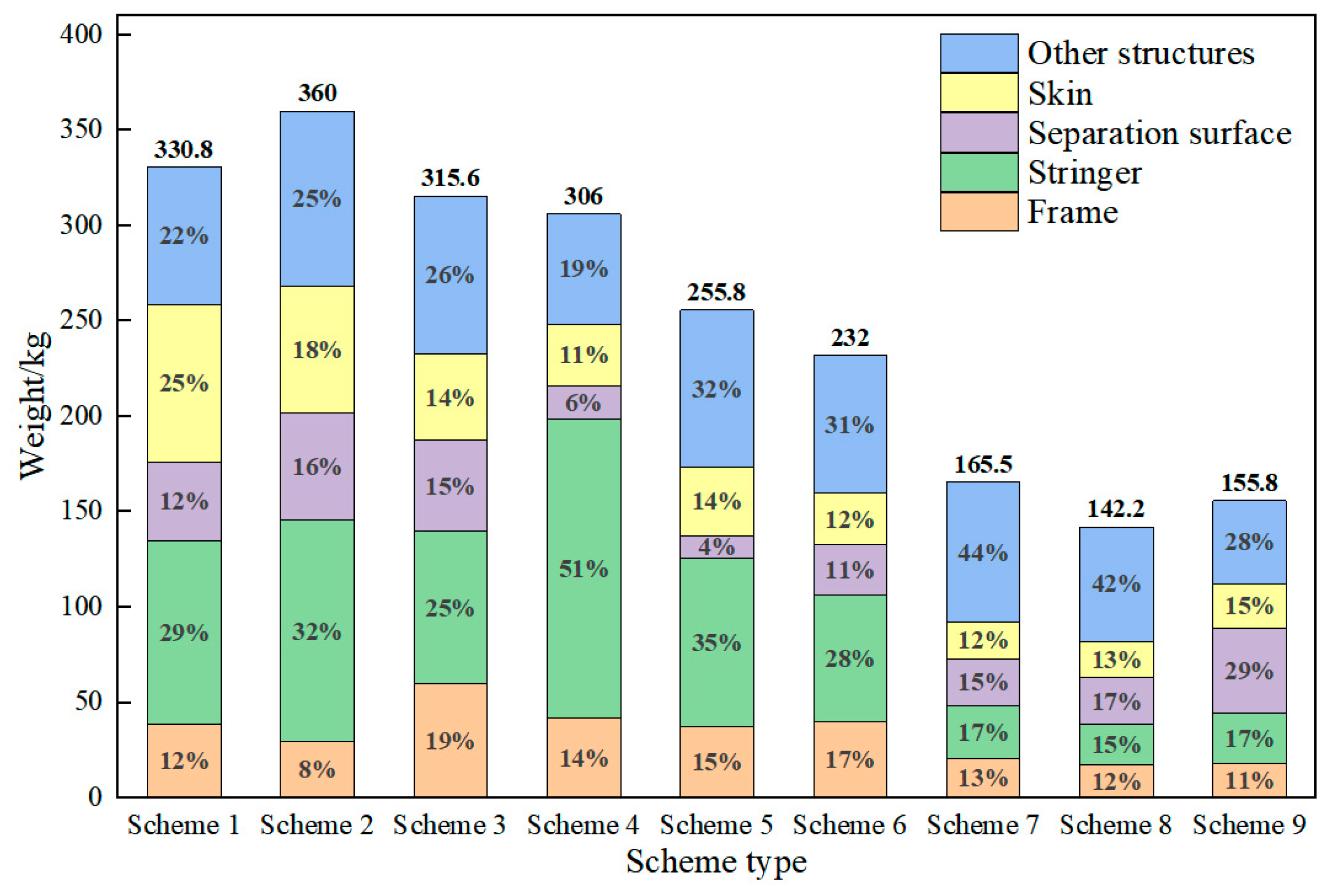
4.2. Analysis of Structural Component Weights
5. Comparative Analysis of Nine Scheme
5.1. The Analytic Hierarchy Process
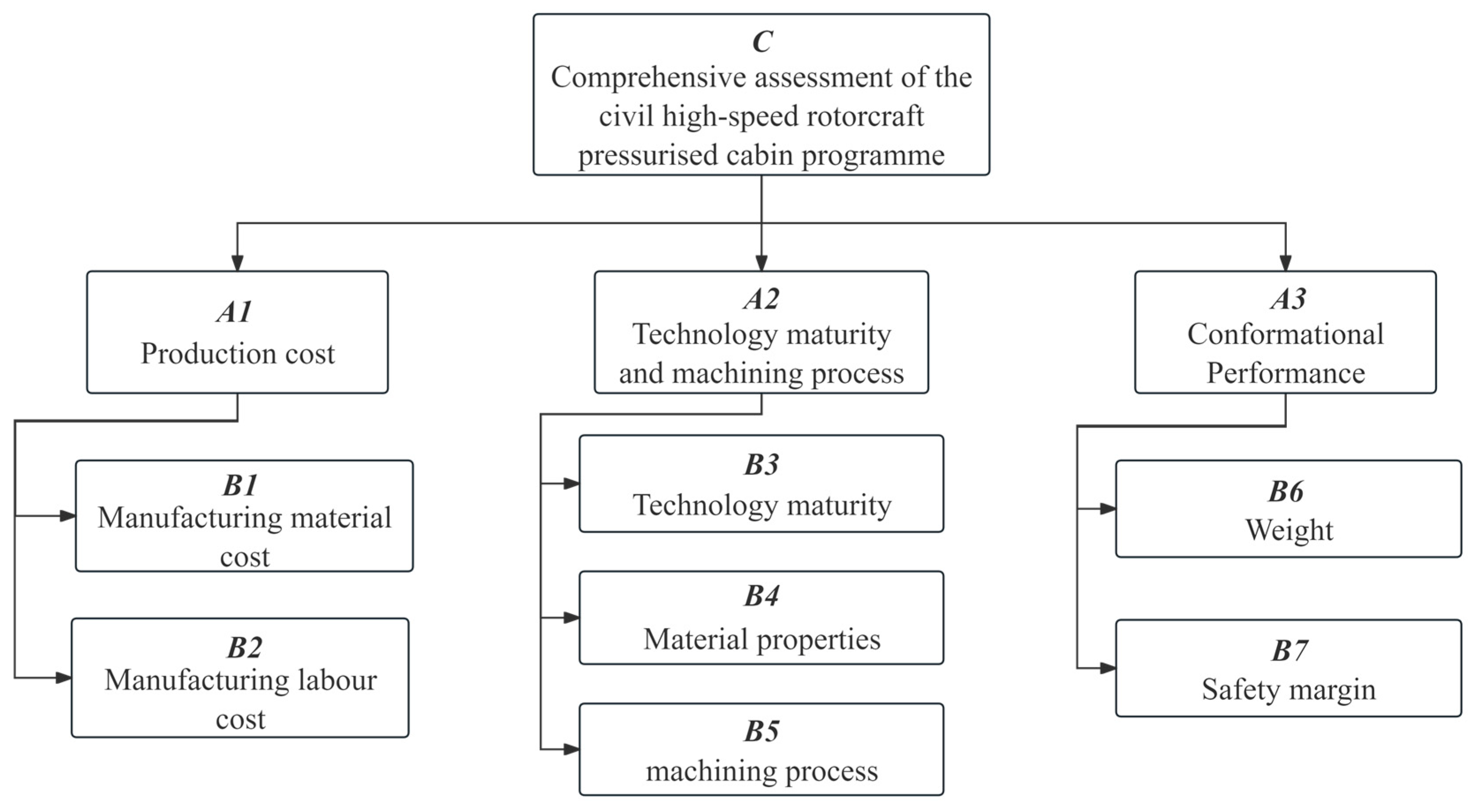
5.1.1. Booster Compartment Structural Configuration Design Indicator Hierarchy
5.1.2. Constructing a Judgment Matrix and Assigning Values
5.1.3. Determining Single-Level Relative Weights and Consistency Checks
5.1.4. Weighting Calculation
5.2. Determination of Mass Function by the Gray Relational Analysis
5.2.1. Production Cost Comparison
5.2.2. Comparison of Technology Maturity and Machining Process
5.2.3. Comparison of Performance of Pressurized Cabin Configurations
5.2.4. Establishment of the Mass Function
5.3. D-S Evidence Theory Deals with Mass Functions
5.4. Multidimensional Comprehensive Evaluation and Analysis Results
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Palmer, M.T.; Rogers, W.H.; Press, H.N.; Latorella, K.A.; Abbott, T.S. A Crew-Centered Flight Deck Design Philosophy for High-Speed Civil Transport (HSCT) Aircraft; NASA: Hampton, VA, USA, 1998.
- Berger, T.; Tischler, M.B.; Horn, J.F. High-Speed Rotorcraft Pitch Axis Response Type Investigation. J. Am. Helicopter Soc. 2023, 68, 32001–32017. [Google Scholar] [CrossRef]
- Zheng, F.; Liu, L.; Chen, Z.; Chen, Y.; Cheng, F. Hybrid multi-objective control allocation strategy for compound high-speed rotorcraft -ScienceDirect. ISA Trans. 2020, 98, 207–226. [Google Scholar] [CrossRef] [PubMed]
- Wu, X. Current Status, Development Trend and Countermeasure for High-Speed Rotorcraft. J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 173–179. [Google Scholar]
- Ramon, E.; Sguazzo, C.; Moreira, P.M.G.P. A review of recent research on bio-based epoxy systems for engineering applications and potentialities in the aviation sector. Aerospace 2018, 5, 110. [Google Scholar] [CrossRef]
- Bachmann, J.; Hidalgo, C.; Bricout, S. Environmental Analysis of Innovative Sustainable Composites with Potential Use in Aviation Sector—A Life Cycle Assessment Review. Sci. China Technol. Sci. 2017, 60, 1301–1317. [Google Scholar] [CrossRef]
- Bozbura, F.T.; Beskese, A. Prioritization of organizational capital measurement indicators using fuzzy AHP. Int. J. Approx. Reason. 2007, 44, 124–147. [Google Scholar] [CrossRef]
- Saaty, T.L. An Exposition of the AHP in Reply to the Paper “Remarks on the Analytic Hierarchy Process”. Manag. Sci. 1990, 36, 259–268. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, H.; Fang, W.; Zhu, C.; Jia, G. Trust Evaluation and Decision Based on D-S Evidence Theory: Early Models and Future Perspectives. IEEE Access 2023, 11, 16032–16041. [Google Scholar] [CrossRef]
- Kuo, T. A review of some modified grey relational analysis models. J. Grey Syst. 2017, 29, 70–77. [Google Scholar]
- Zadeh, L.A. Review of A Mathematical Theory of Evidence. AI Mag. 1984, 5, 235–247. [Google Scholar]
- Yager, R.R. On the aggregation of prioritized belief structures. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 1996, 26, 708–717. [Google Scholar] [CrossRef]
- Inagaki, T. Interdependence between safety-control policy and multiple sensor scheme via Dempster–Shafer theory. IEEE Trans. Reliab. 1991, 40, 182–188. [Google Scholar] [CrossRef]
- Corrado, G.; Ntourmas, G.; Sferza, M.; Traiforos, N.; Arteiro, A.; Brown, L.; Chronopoulos, D.; Daoud, F.; Glock, F.; Ninic, J.; et al. Recent progress, challenges and outlook for multidisciplinary structural optimization of aircraft and aerial vehicles. Prog. Aerosp. Sci. 2022, 135, 100861. [Google Scholar] [CrossRef]
- Li, V.; Velicki, A. Advanced PRSEUS Structural Concept Design and Optimization. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BA, Canada, 10–12 September 2008. [Google Scholar]
- Barile, C.; Casavola, C.; Pappalettere, C. The Influence of Stitching and Unconventional Fibres Orientation on the Tensile Properties of CFRP Laminates. Compos. Part B Eng. 2017, 110, 248–254. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Leong, K.H.; Herszberg, I. A Review of the Effect of Stitching on the In-Plane Mechanical Properties of FibreReinforced Polymer Composites. Compos. Part A Appl. Sci. Manuf. 1997, 28, 979–991. [Google Scholar] [CrossRef]
- Zheng, Y.; Shen, Z.; Cai, C.; Ma, S.; Xing, Y. Influence of Nonmetals Recycled from Waste Printed Circuit Boards on Flexural Properties and Fracture Behavior of Polypropylene Composites. Mater. Des. 2009, 30, 958–963. [Google Scholar] [CrossRef]
- Chung, W.C.; Jang, B.Z.; Chang, T.C.; Hwang, L.R.; Wilcox, R.C. Fracture Behavior in Stitched Multidirectional Composites. Mater. Sci. Eng. A 1989, 112, 157–173. [Google Scholar] [CrossRef]
- Leone, F.A.; Jegley, D.C.; Linton, K.A. Compressive loading and modeling of stitched composite stiffeners. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; p. 2179. [Google Scholar]
- Sanz-Douglass, G.J. Parametric Study of Influence of Stiffener Variables on Postbuckling Response of Frame-Stiffened Composite Panels; San Diego State University: San Diego, CA, USA, 2015. [Google Scholar]
- Przekop, A. Repair Concepts as Design Constraints of a Stiffened Composite PRSEUS Panel. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; AIAA: Reston, VA, USA, 2012. [Google Scholar]
- Ettoumi, S.; Zhang, Y.; Cui, B.; Zhou, J. Failure Initiation analysis of a PRSEUS BWB wing subjected to structural damage. Aerospace 2023, 10, 341. [Google Scholar] [CrossRef]
- Jia, R.S.; Liu, C.; Sun, H.M.; Yan, X.H. A situation assessment method for rock burst based on multi-agent information fusion. Comput. Electr. Eng. 2015, 45, 22–32. [Google Scholar] [CrossRef]
- Sikai, L.; Jun, Y. A satellite-borne SAR target recognition method based on supplementary feature fusion. In Proceedings of the 2018 IEEE 3rd International Conference on Cloud Computing and Big Data Analysis (ICCCBDA), Chengdu, China, 20–22 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 326–330. [Google Scholar]
- Ho, W.; Ma, X. The state-of-the-art integrations and applications of the analytic hierarchy process. Eur. J. Oper. Res. 2018, 267, 399–414. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, H. Intuitionistic Fuzzy Analytic Hierarchy Process. IEEE Trans. Fuzzy Syst. 2014, 22, 749–761. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T. GRA method based on spherical linguistic fuzzy Choquet integral environment and its application in multi-attribute decision-making problems. Math. Sci. 2018, 12, 263–275. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Ishizaka, A.; Labib, A. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 2011, 38, 14336–14345. [Google Scholar] [CrossRef]
- Akkaya, G.; Turanoğlu, B.; Öztaş, S. An integrated fuzzy AHP and fuzzy MOORA approach to the problem of industrial engineering sector choosing. Expert Syst. Appl. 2015, 42, 9565–9573. [Google Scholar] [CrossRef]
- Anand, G.; Alagumurthi, N.; Elansezhian, R.; Palanikumar, K.; Venkateshwaran, N. Investigation of drilling parameters on hybrid polymer composites using grey relational analysis, regression, fuzzy logic, and ANN models: A critical note. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 214. [Google Scholar] [CrossRef]
- Xu, D.L.; Yang, J.B.; Wang, Y.M. The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees. Eur. J. Oper. Res. 2006, 174, 1914–1943. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, R.; Anjum, A.; Wang, J.; Zhang, H.; Ma, M. Intelligent data fusion algorithm based on hybrid delay-aware adaptive clustering in wireless sensor networks. Future Gener. Comput. Syst. 2020, 104, 1–14. [Google Scholar] [CrossRef]
- Mao, Y.; Yang, Y.; Hu, Y. Research into a Multi-Variate Surveillance Data Fusion Processing Algorithm. Sensors 2019, 19, 4975. [Google Scholar] [CrossRef]


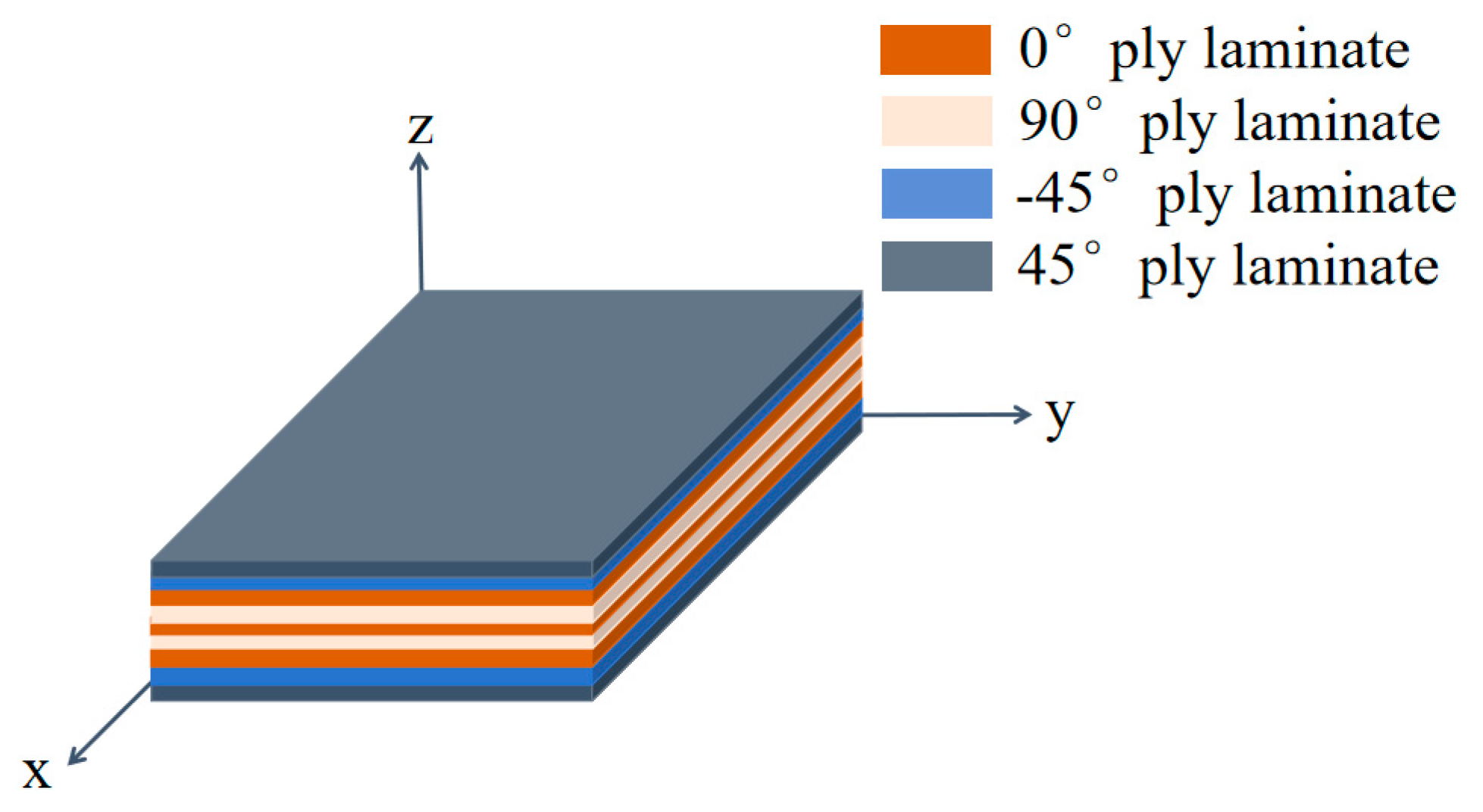
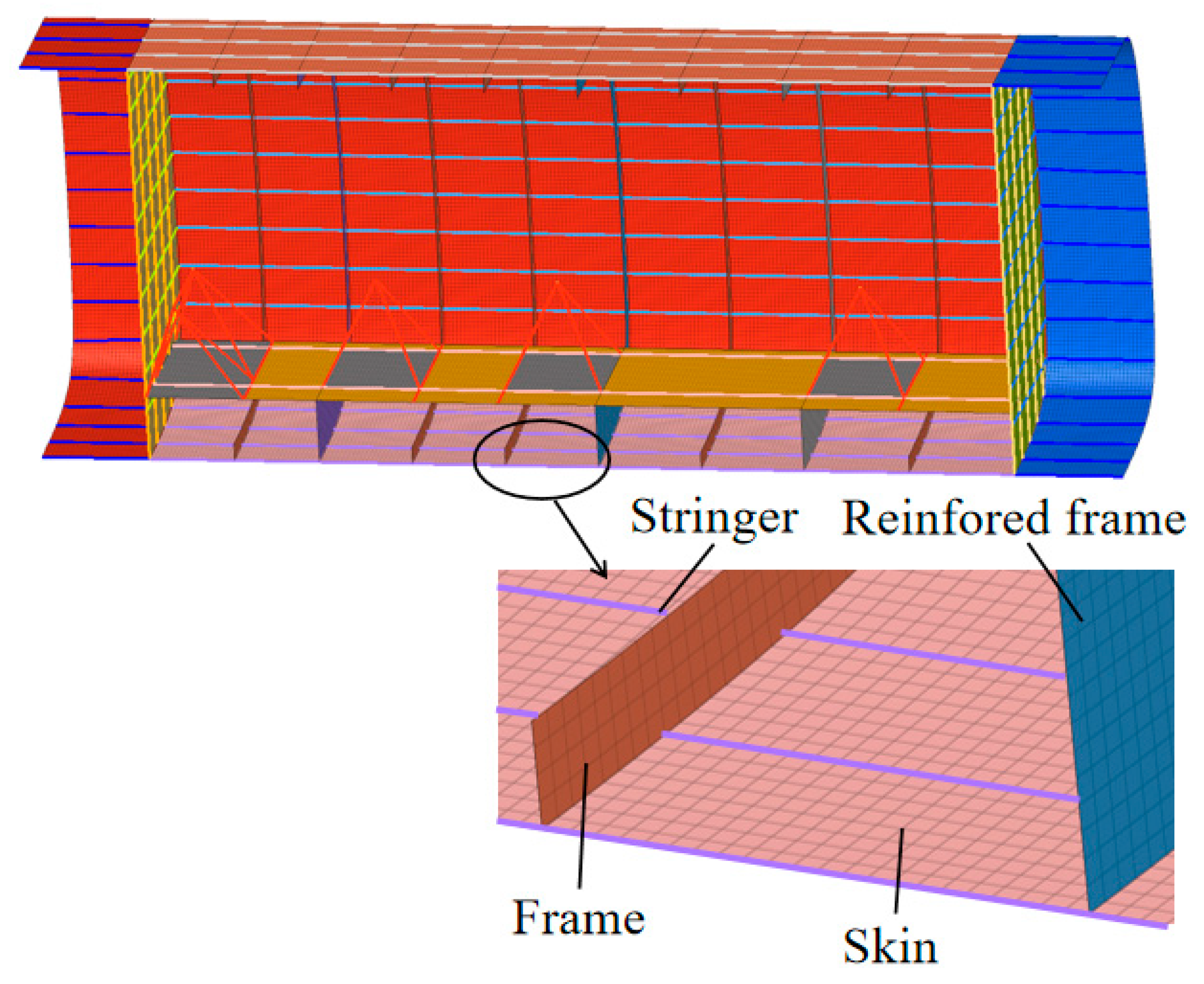
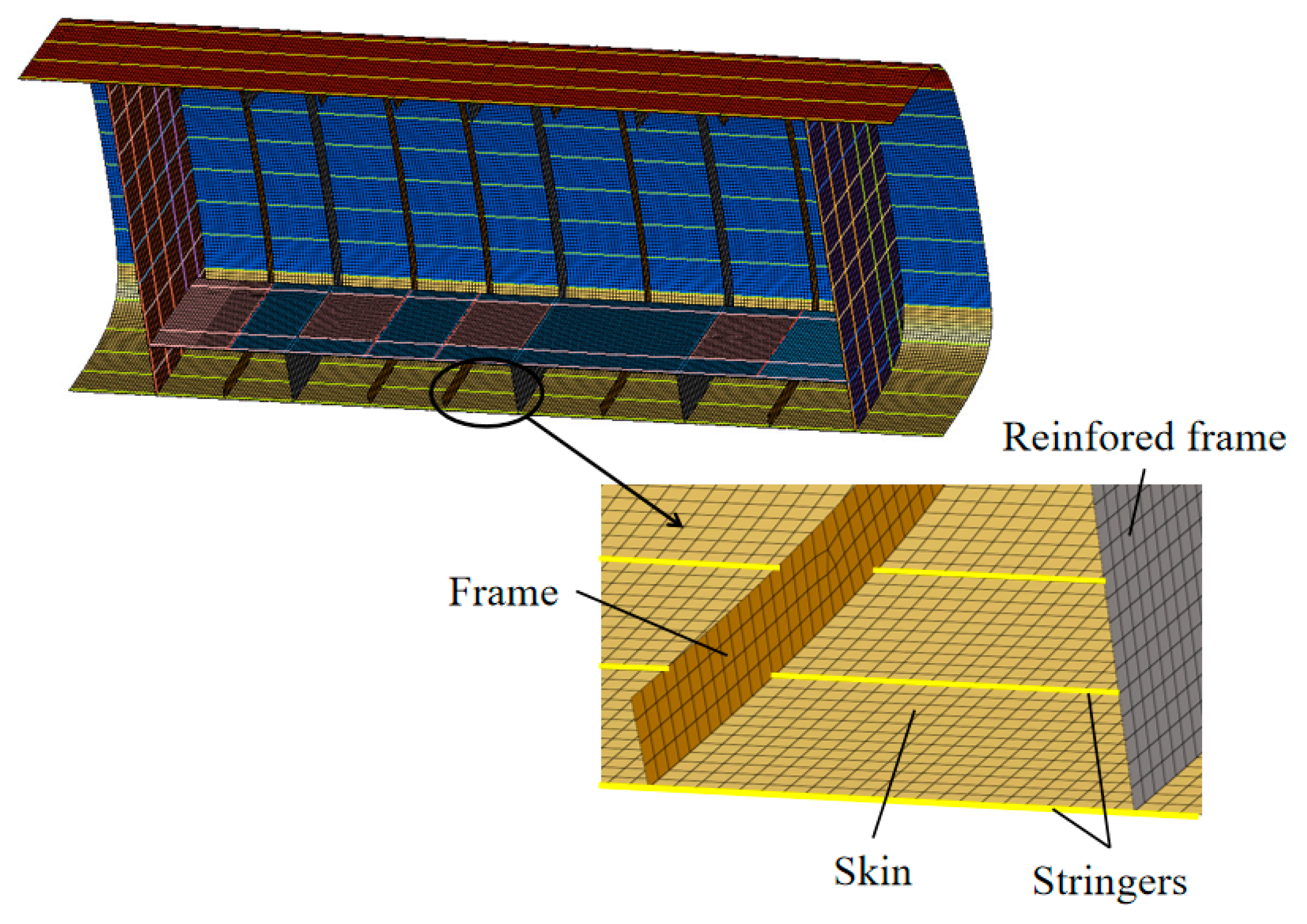
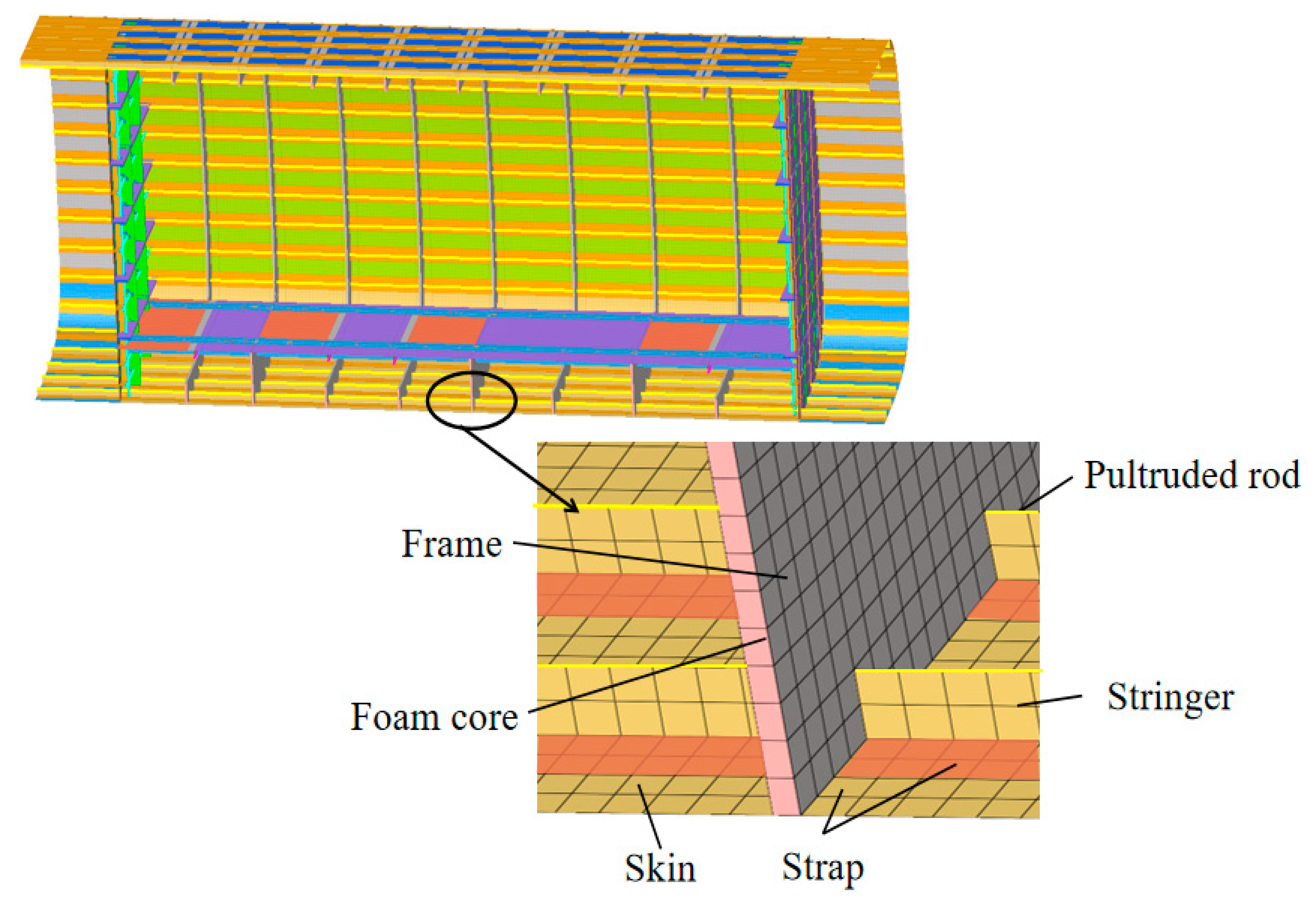
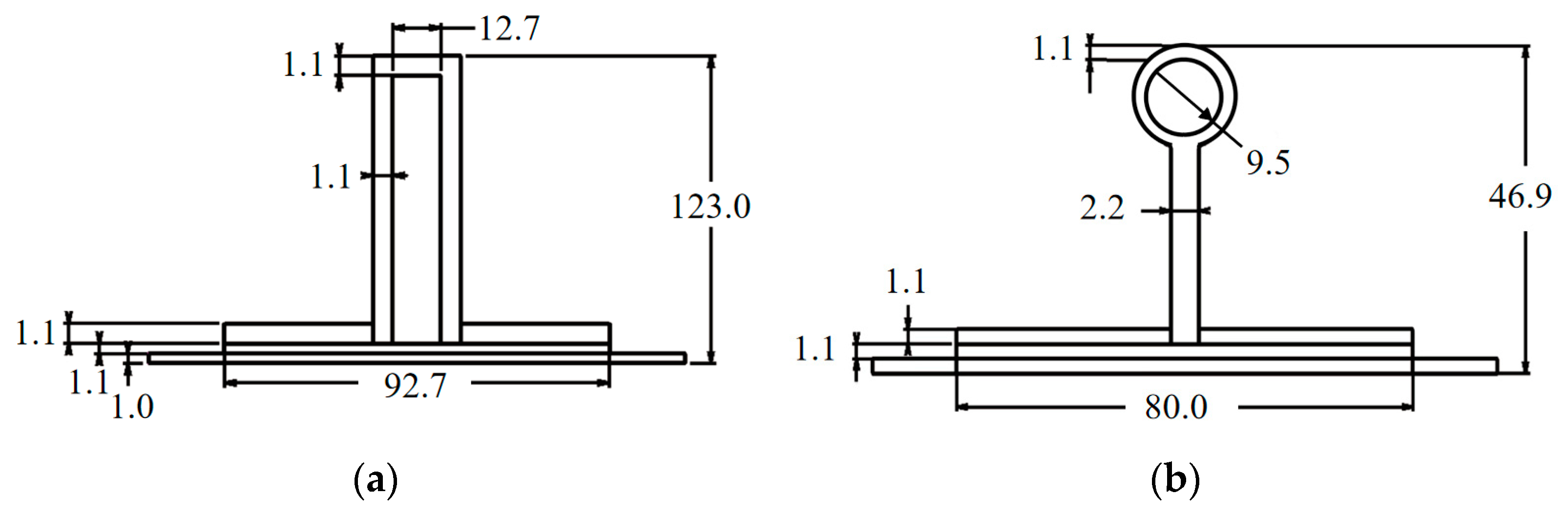







| Scheme | Material Composition |
|---|---|
| Scheme 1: The AL7075-AL7075 scheme | Aluminum alloy AL7075 |
| Scheme 2: The AL7075-AL2024 scheme | Skeleton AL7075/remaining structure AL2024 |
| Scheme 3: The TB6-AL7075 scheme | Skeleton TB6/remaining structure AL7075 |
| Scheme 4: The AL2024-T300 scheme | Skeleton AL2024/remaining structure T300 composite laminate |
| Scheme 5: The AL7075-T300 scheme | Skeleton AL7075/remaining structure T300 composite laminate |
| Scheme 6: The AL7075-T800 scheme | Skeleton AL7075/remaining structure T800 composite laminate |
| Scheme 7: The T800-T300 scheme | Skeleton T800 composite/remaining structure T300 composite (PRSEUS structure) |
| Scheme 8: The T1000-T800 scheme | Skeleton T1000 composite/remaining structure T800 composite (PRSEUS structure) |
| Scheme 9: The T800-T300 scheme | Skeleton T800 composite laminate/remaining structure T300 composite laminate and honeycomb aluminum alloy |
| Material | Young’s Moduli E (GPa) | Poisson’s Ratio | Density (t/m3) |
|---|---|---|---|
| Foam core | 0.1448 | 0.45 | 0.1 |
| Pultruded rod | 126.9325 | 0.3 | 1.6 |
| Aluminum honeycomb | 4.0600 | 0.2 | 0.1 |
| Material | Young’s Moduli E (GPa) | Poisson’s Ratio | Density (t/m3) | Tensile and Yield Strength (MPa) | Shear Strength (MPa) | |
|---|---|---|---|---|---|---|
| AL2024 | 71.0 | 0.334 | 2.9 | 460 | 320 | 285 |
| AL7075 | 71.0 | 0.33 | 2.7 | 524 | 455 | 150 |
| TB6 | 104.0 | 0.33 | 4.6 | 1152 | 893 | 567 |
| Material | Young’s Moduli (GPa) | Poisson’s Ratio | Shear Moduli (GPa) | Density (t/m3) | Allowable Strain () | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | G12 | G23 | G13 | ||||||
| T300 | 181.0 | 10.3 | 103.0 | 0.28 | 0.30 | 0.28 | 7.2 | 7.2 | 3.8 | 1.6 | 3000 |
| T800 | 195.0 | 8.6 | 8.6 | 0.33 | 0.33 | 0.48 | 4.6 | 4.6 | 2.9 | 1.6 | 8000 |
| T1000 | 207.2 | 22.8 | 227.6 | 0.246 | 0.246 | 0.532 | 8.9 | 8.9 | 7.8 | 1.6 | 10,000 |
| Scheme | Component | Lamina | Lamina Thickness | Lay Plate Number | Carbon Fiber Composites |
|---|---|---|---|---|---|
| Scheme 4 | Upper skin | 11 | 0.12 | 1 | T300 |
| Middle part of the skin | 17 | 0.12 | 1 | T300 | |
| Lower skin | 11 | 0.12 | 1 | T300 | |
| Separating surface | 14 | 0.12 | 2 | T300 | |
| Scheme 5 | Skin | 13 | 0.12 | 1 | T300 |
| Separating surface | 19 | 0.12 | 1 | T300 | |
| Scheme 6 | Upper skin | 9 | 0.12 | 1 | T800 |
| Middle section, Lower skin | 11 | 0.12 | 1 | T800 | |
| Separating surface | 11 | 0.12 | 2 | T800 | |
| Floors | 11 | 0.12 | 1 | T800 |
| Scheme | Component | Lamina | Lamina Thickness | Lay Plate Number | Carbon Fiber Composites |
|---|---|---|---|---|---|
| Scheme 7 | Skin | 8 | 0.12 | 1 | T300 |
| Separating surface | 10 | 0.12 | 4 | T300 | |
| Floors | 15 | 0.12 | 1 | T300 | |
| Frame wrapper, tear straps, layer flap | 9 | 0.12 | 1 | T800 | |
| Stringer wrapper, tear straps, layer flap | 9 | 0.12 | 1 | T800 | |
| Stringer | 9 | 0.12 | 2 | T800 | |
| Separation surface wrapper, tear straps, layer flap | 9 | 0.12 | 2 | T800 | |
| Separation surface stringer wrapper, tear straps, layer flap | 9 | 0.12 | 2 | T300 | |
| Separation surface stringer | 9 | 0.12 | 4 | T300 | |
| Floor beam | 9 | 0.12 | 2 | T800 | |
| Floor bottom layer flap, stiffener | 9 | 0.12 | 1 | T800 | |
| Scheme 8 | Skin | 9 | 0.12 | 1 | T800 |
| Separating surface | 14 | 0.12 | 2 | T800 | |
| Floors | 8 | 0.12 | 1 | T800 | |
| Frame wrapper, tear straps, layer flap | 7 | 0.12 | 1 | T1000 | |
| Stringer wrapper, tear straps, layer flap | 7 | 0.12 | 1 | T1000 | |
| Stringer | 7 | 0.12 | 2 | T1000 | |
| Separation surface wrapper, tear straps, layer flap | 9 | 0.12 | 2 | T1000 | |
| Separation surface stringer wrapper, tear straps, layer flap | 9 | 0.12 | 2 | T1000 | |
| Separation surface stringer | 9 | 0.12 | 4 | T1000 | |
| Floor beam | 9 | 0.12 | 2 | T800 | |
| Floor bottom layer flap, stiffener | 9 | 0.12 | 1 | T800 |
| Component | Lamina | Lamina Thickness | Lay Plate Number | Carbon Fiber Composites |
|---|---|---|---|---|
| Skin | 10 | 0.12 | 1 | T300 |
| Separating surface | 14 | 0.12 | 4 | T300 |
| Floors | 8 | 0.12 | 1 | T300 |
| Frame | 14 | 0.12 | 2 | T300 |
| Stringer | 8 | 0.12 | 2 | T800 |
| Stringer layer flap | 8 | 0.12 | 1 | T800 |
| Separation surface stiffener | 13 | 0.12 | 5 | T800 |
| Floor beam | 13 | 0.12 | 1 | T800 |
| Floor stiffener | 13 | 0.12 | 2 | T800 |
| Load Data | Coefficient |
|---|---|
| Pressurized load | |
| Structural gravity | |
| Floor load |
| External Extension Length | Stress | Displacement |
|---|---|---|
| 50 mm | 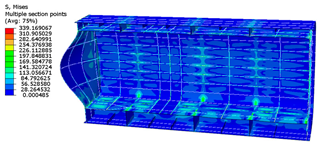 |  |
| 500 mm | 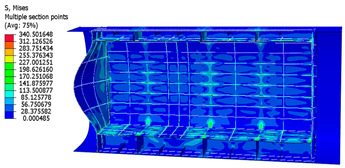 | 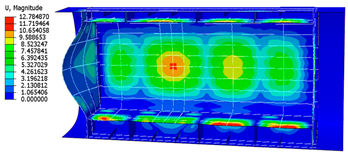 |
| 1000 mm |  | 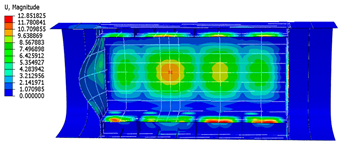 |
| Potential Sources of Risk | Scheme |
|---|---|
| Strength damage (yielding) | 4, 7, 9 |
| Strength damage (shear) | 1, 2, 5, 6 |
| Rigidity failure (displacement) | 3, 8 |
| Scheme | Maximum Displacement (mm) | Weight (kg) | Maximum von Mises Stress (MPa) | Maximum Strain () | ||||
|---|---|---|---|---|---|---|---|---|
| AL7075 | AL2024 | TB6 | T300 | T80 | T1000 | |||
| 1 | 8.937 | 330.8 | 412.4 | / | / | / | / | / |
| 2 | 9.544 | 360.0 | 348.8 | 293.5 | / | / | / | / |
| 3 | 9.985 | 315.6 | 198.9 | / | 822.1 | / | / | / |
| 4 | 9.252 | 306.0 | / | 318.5 | / | / | / | 2242 |
| 5 | 9.077 | 255.8 | 399.6 | / | / | / | / | 2539 |
| 6 | 9.219 | 232.0 | 431.3 | / | / | / | 5884 | / |
| 7 | 9.691 | 165.5 | / | / | / | / | 7294 | 2883 |
| 8 | 9.951 | 142.2 | / | / | / | 9376 | 5055 | / |
| 9 | 9.175 | 155.8 | / | / | / | / | 5240 | 2635 |
| Quantitative Importance | Meaning |
|---|---|
| 1 | Indicator i is equally as important as indicator j |
| 3 | Indicator i is slightly more important than indicator j |
| 5 | Indicator i is significantly more important than indicator j |
| 7 | Indicator i is more strongly important than indicator j |
| 9 | Indicator i is more important than indicator j |
| 2, 4, 6, 8 | Median of the above neighboring judgements |
| reciprocal | If indicator i is aij compared to indicator j, then indicator j compared to indicator i is 1/aij |
| The Order of Judgment Matrix | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 |
| Indicators | B1 | B2 | B3 | B4 | B5 | B6 | B7 |
|---|---|---|---|---|---|---|---|
| Index relative weight | 0.5 | 0.5 | 0.63 | 0.11 | 0.26 | 0.50 | 0.50 |
| Indicators | A1 | A2 | A3 |
|---|---|---|---|
| Index relative weight | 0.25 | 0.25 | 0.50 |
| Target Layer | Tier 1 Indicators and Relative Weights | Tier 2 Indicators and Relative Weights | Weight | Sort |
|---|---|---|---|---|
| Comprehensive assessment of the civil high-speed rotorcraft pressurized cabin scheme | Production cost 0.25 | Manufacturing material cost 0.5 | 0.125 | 4 |
| Manufacturing labor cost 0.50 | 0.125 | 4 | ||
| Reliability and maintainability 0.25 | Technology maturity 0.63 | 0.157 | 3 | |
| Material performance 0.11 | 0.028 | 7 | ||
| Machining process 0.26 | 0.065 | 6 | ||
| Safety 0.50 | Weight 0.50 | 0.250 | 1 | |
| Safety margin 0.50 | 0.250 | 1 |
| Scheme | Probability of Schemes Choice | |
|---|---|---|
| The Cost of Manufacturing Materials | The Cost of Manufacturing Labor | |
| 1 | 0.121 | 0.116 |
| 2 | 0.120 | 0.115 |
| 3 | 0.115 | 0.113 |
| 4 | 0.120 | 0.111 |
| 5 | 0.120 | 0.111 |
| 6 | 0.117 | 0.110 |
| 7 | 0.114 | 0.107 |
| 8 | 0.059 | 0.107 |
| 9 | 0.115 | 0.109 |
| Scheme | Probability of Schemes Choice | ||
|---|---|---|---|
| Technology Maturity | Material Properties | Machining Process | |
| 1 | 0.113 | 0.039 | 0.136 |
| 2 | 0.113 | 0.059 | 0.136 |
| 3 | 0.113 | 0.118 | 0.106 |
| 4 | 0.112 | 0.078 | 0.121 |
| 5 | 0.112 | 0.157 | 0.121 |
| 6 | 0.112 | 0.137 | 0.106 |
| 7 | 0.110 | 0.157 | 0.091 |
| 8 | 0.107 | 0.137 | 0.091 |
| 9 | 0.108 | 0.118 | 0.076 |
| Scheme | Probability of Schemes Choice | |
|---|---|---|
| Weight | Safety Margins | |
| 1 | 0.107 | 0.107 |
| 2 | 0.105 | 0.133 |
| 3 | 0.108 | 0.118 |
| 4 | 0.108 | 0.113 |
| 5 | 0.111 | 0.100 |
| 6 | 0.112 | 0.103 |
| 7 | 0.116 | 0.094 |
| 8 | 0.117 | 0.134 |
| 9 | 0.116 | 0.097 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, T.; Zhou, J.; Cui, B.; Chen, F. Research on the Structural Design of a Pressurized Cabin for Civil High-Speed Rotorcraft and the Multi-Dimensional Comprehensive Evaluation Method. Aerospace 2024, 11, 844. https://doi.org/10.3390/aerospace11100844
Zhang Y, Zhang T, Zhou J, Cui B, Chen F. Research on the Structural Design of a Pressurized Cabin for Civil High-Speed Rotorcraft and the Multi-Dimensional Comprehensive Evaluation Method. Aerospace. 2024; 11(10):844. https://doi.org/10.3390/aerospace11100844
Chicago/Turabian StyleZhang, Yongjie, Tongxin Zhang, Jingpiao Zhou, Bo Cui, and Fangyu Chen. 2024. "Research on the Structural Design of a Pressurized Cabin for Civil High-Speed Rotorcraft and the Multi-Dimensional Comprehensive Evaluation Method" Aerospace 11, no. 10: 844. https://doi.org/10.3390/aerospace11100844
APA StyleZhang, Y., Zhang, T., Zhou, J., Cui, B., & Chen, F. (2024). Research on the Structural Design of a Pressurized Cabin for Civil High-Speed Rotorcraft and the Multi-Dimensional Comprehensive Evaluation Method. Aerospace, 11(10), 844. https://doi.org/10.3390/aerospace11100844






