Investigation of Asymmetric Flow of a Slender Body with Low-Aspect Ratio Fins Having Large Deflection Angles
Abstract
1. Introduction
2. Description of the Wind Tunnel Test Phenomenon
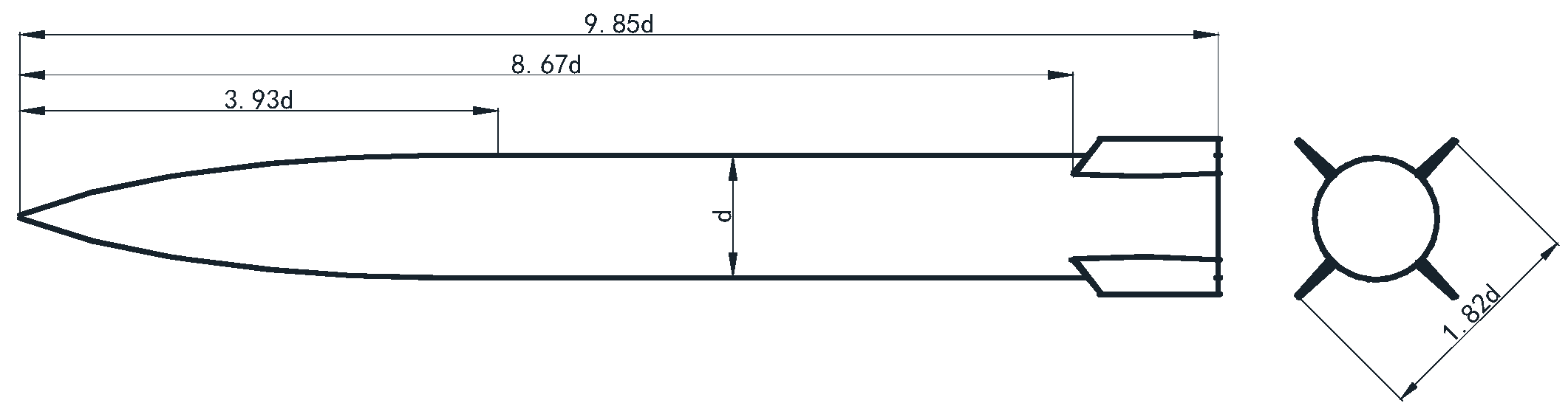
2.1. Test Model
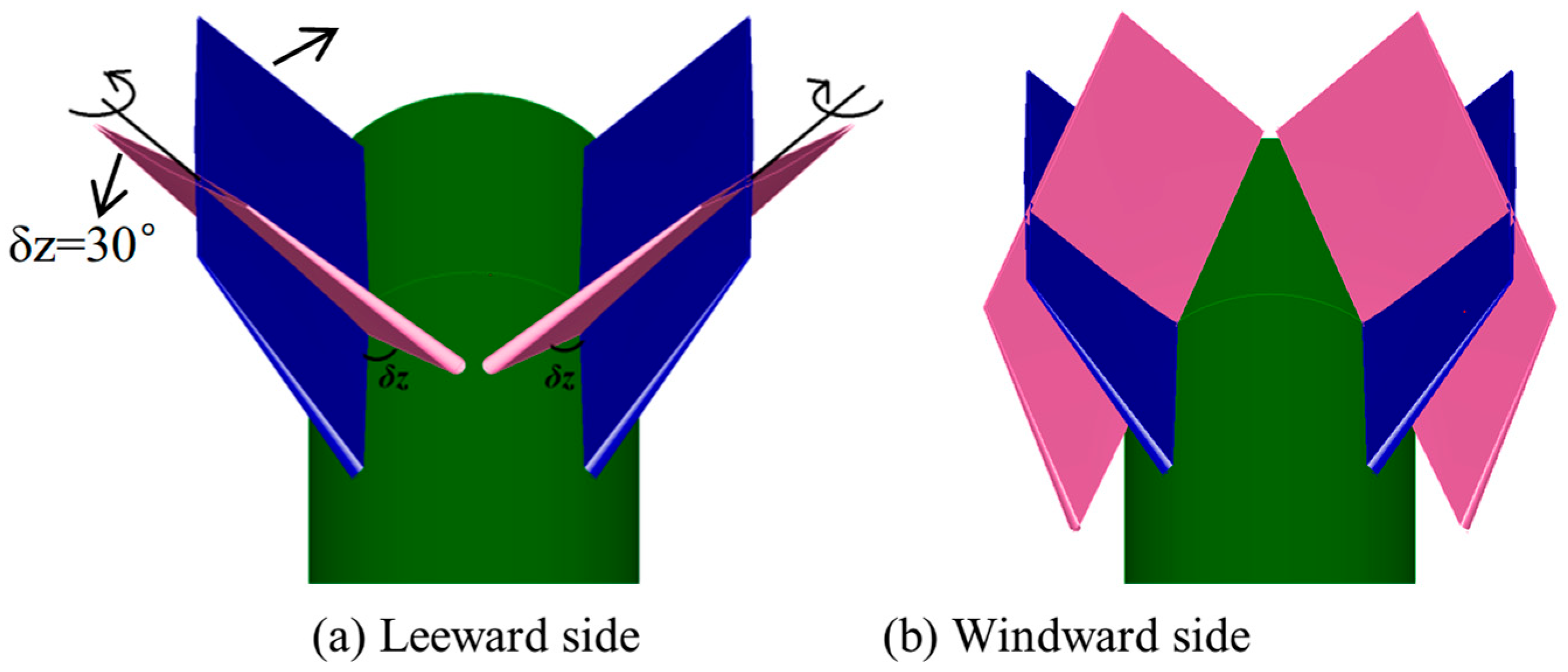
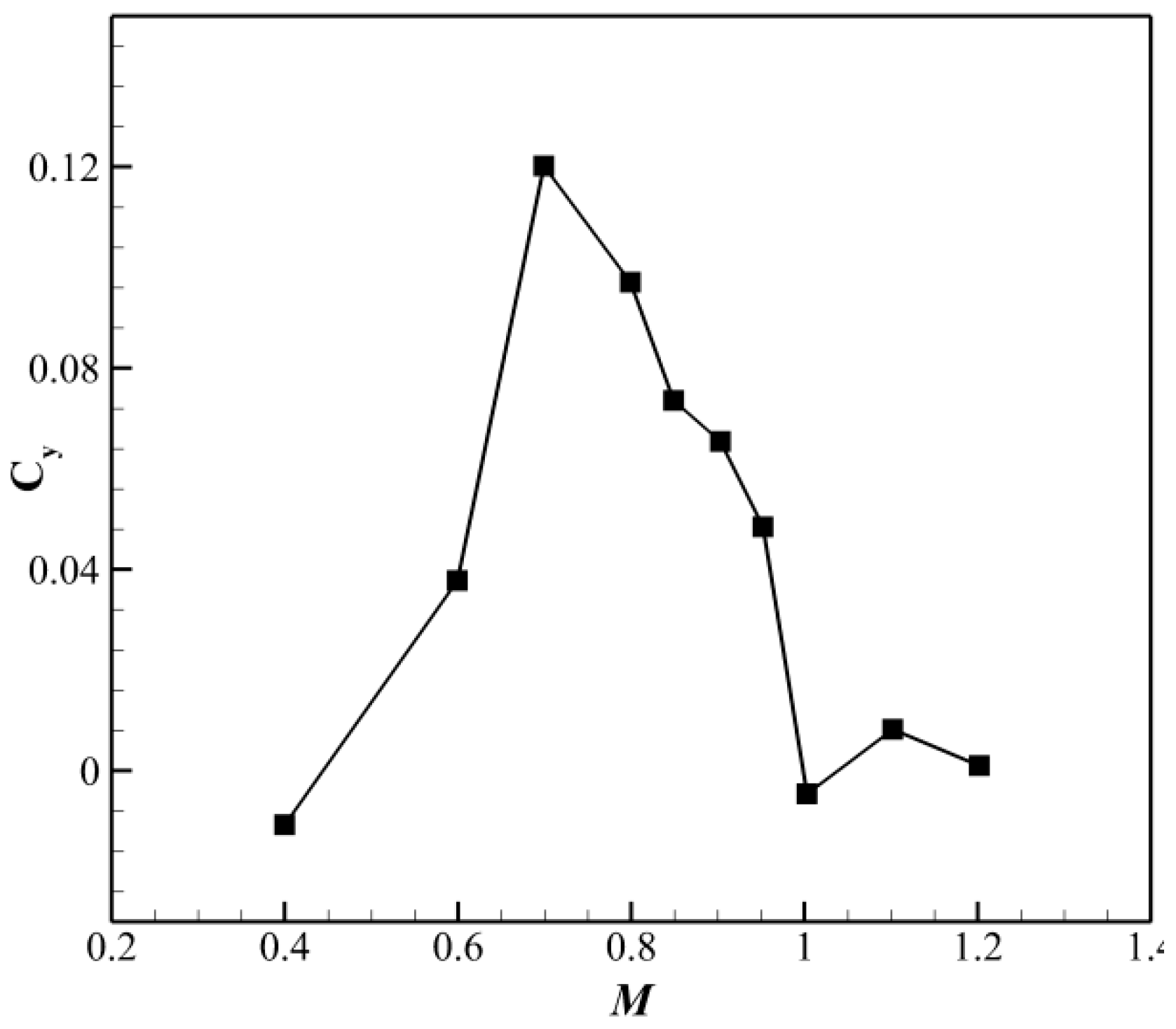
2.2. Description of the Asymmetric Phenomenon
3. The Unsteady Aerodynamic Characteristics of the Pair of Fins under Symmetric Pitching Motions
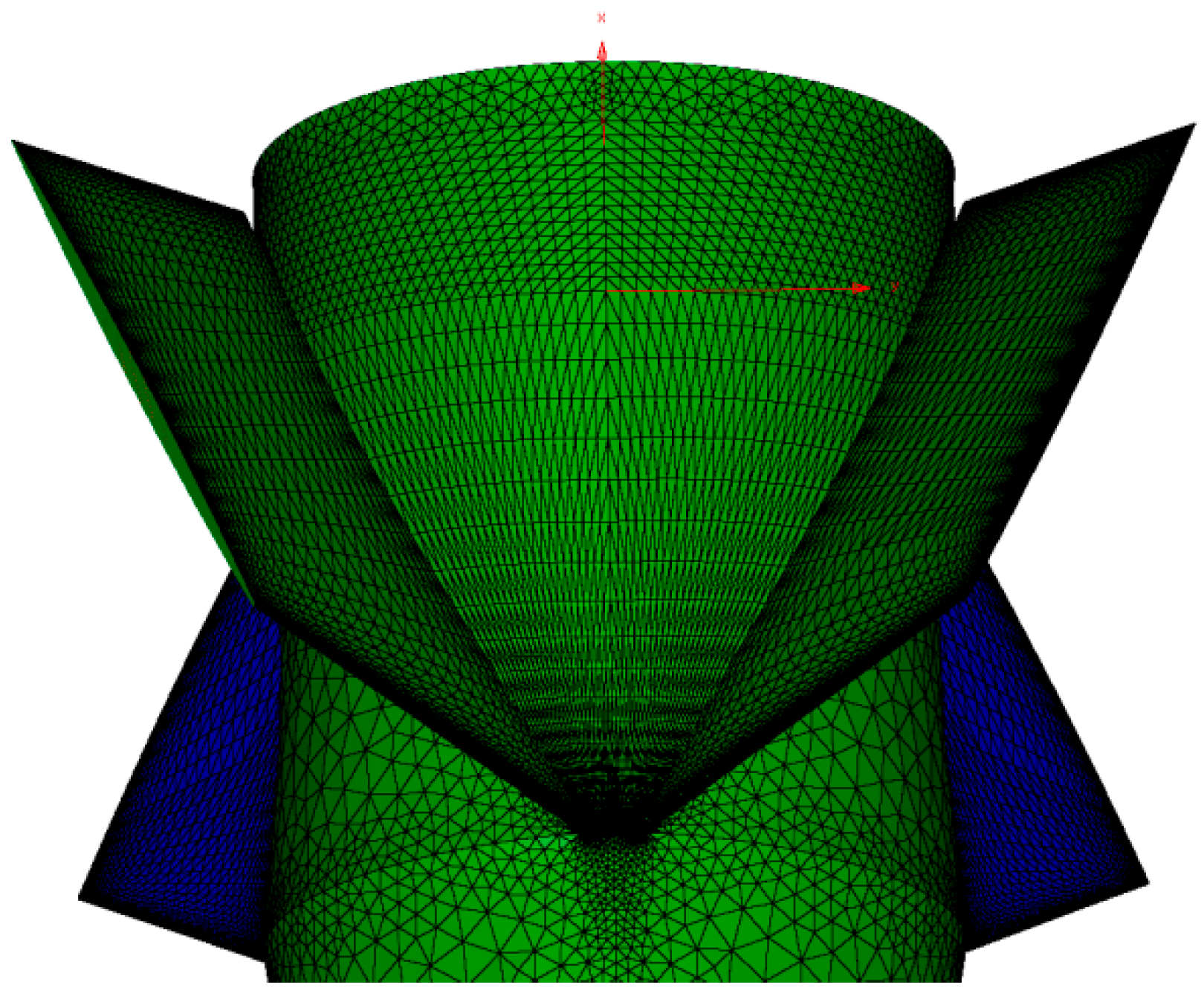
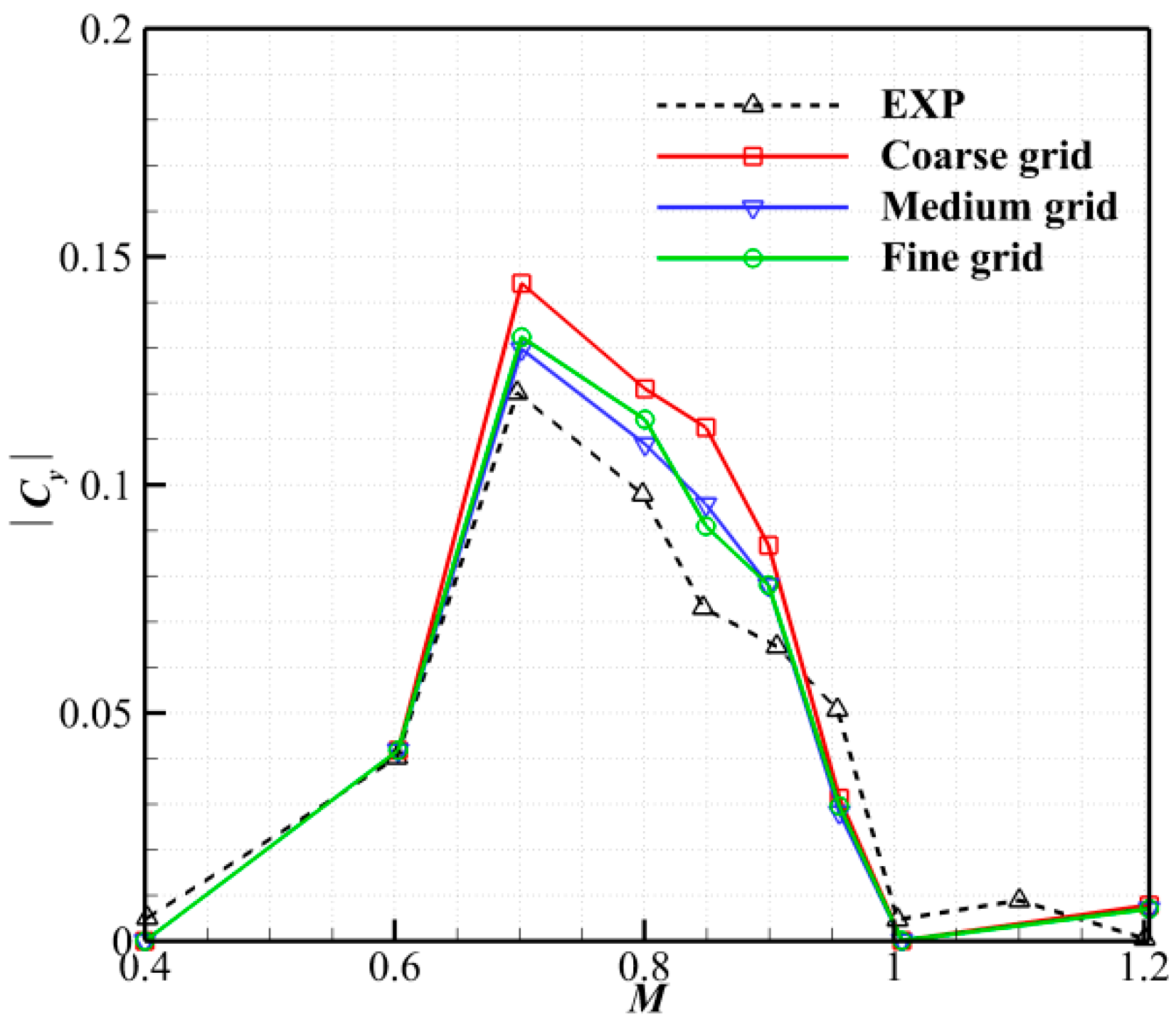
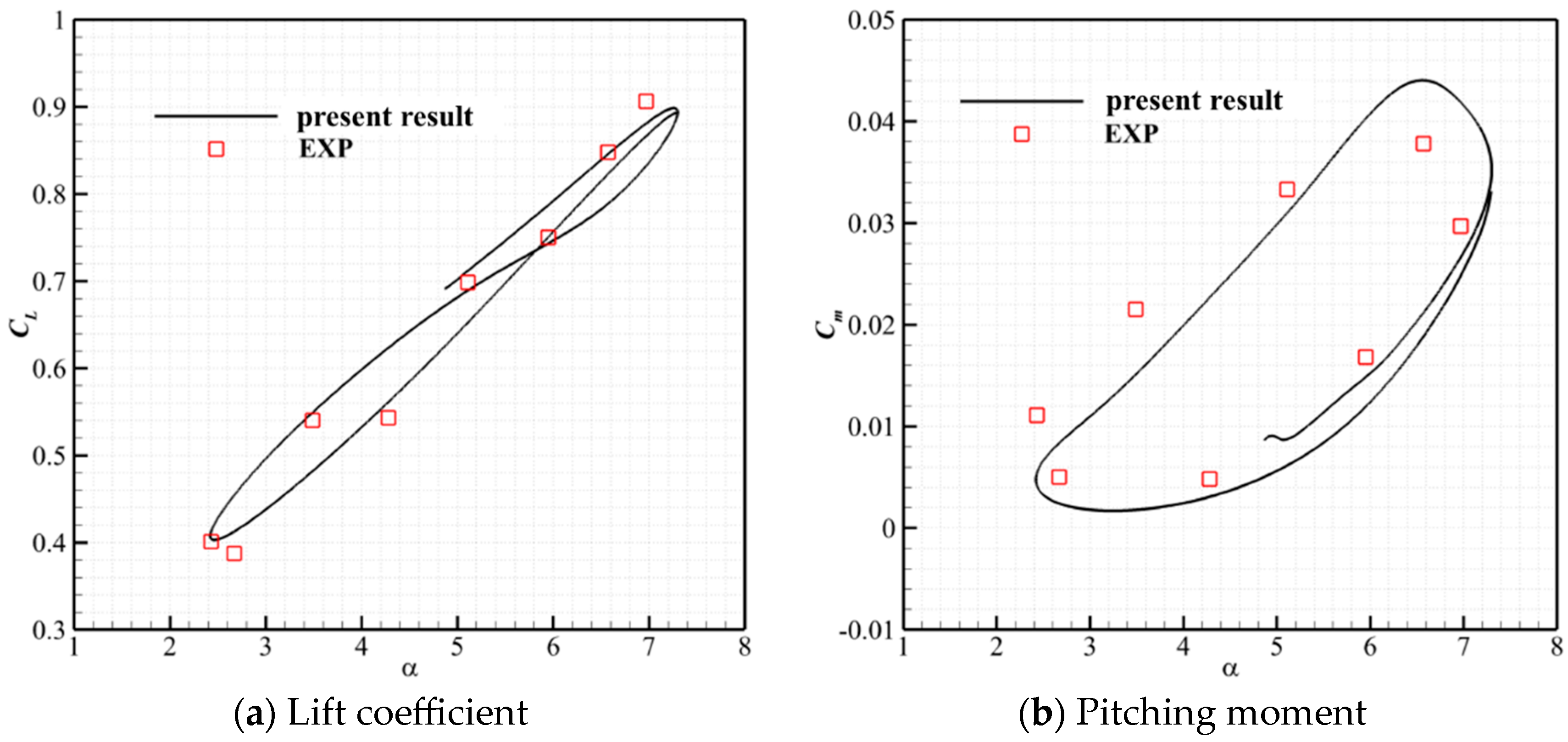
3.1. Numerical Methods and Validation
3.1.1. The Body–Fin Configuration
3.1.2. NACA 0012 Airfoil with Sinusoidal Pitching Motion
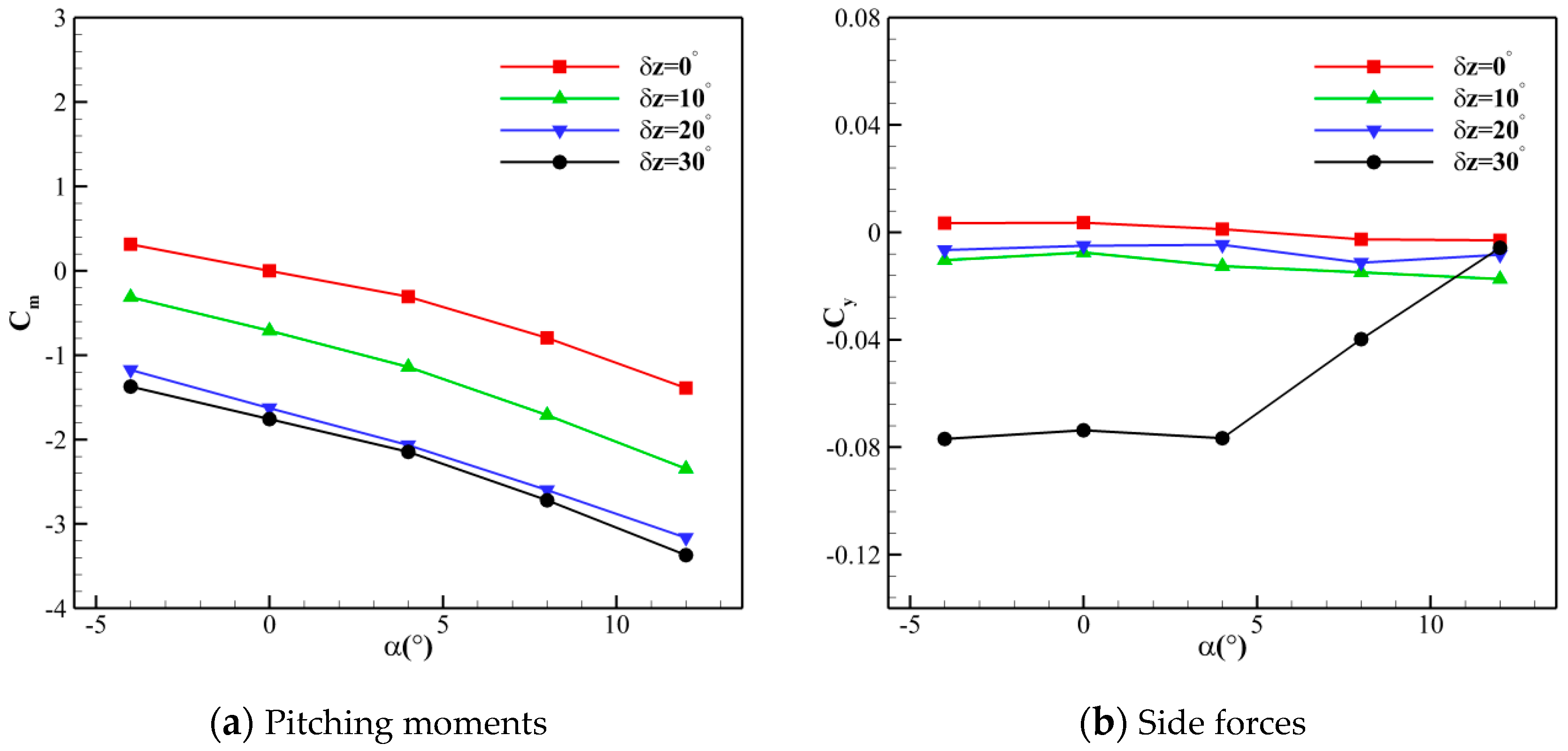
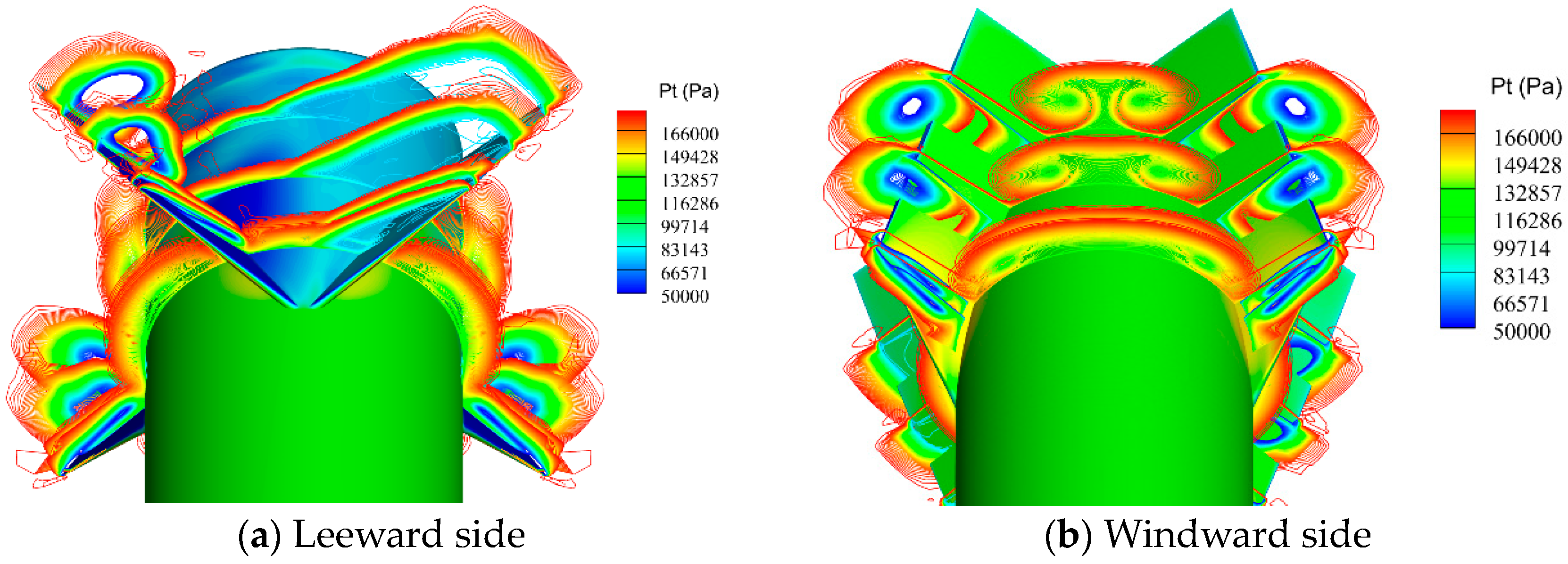
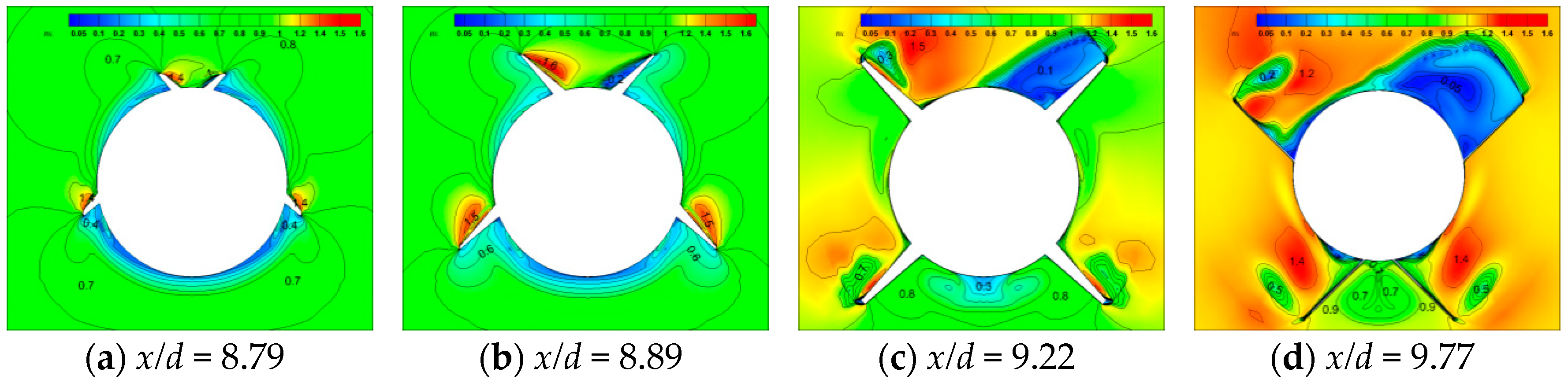
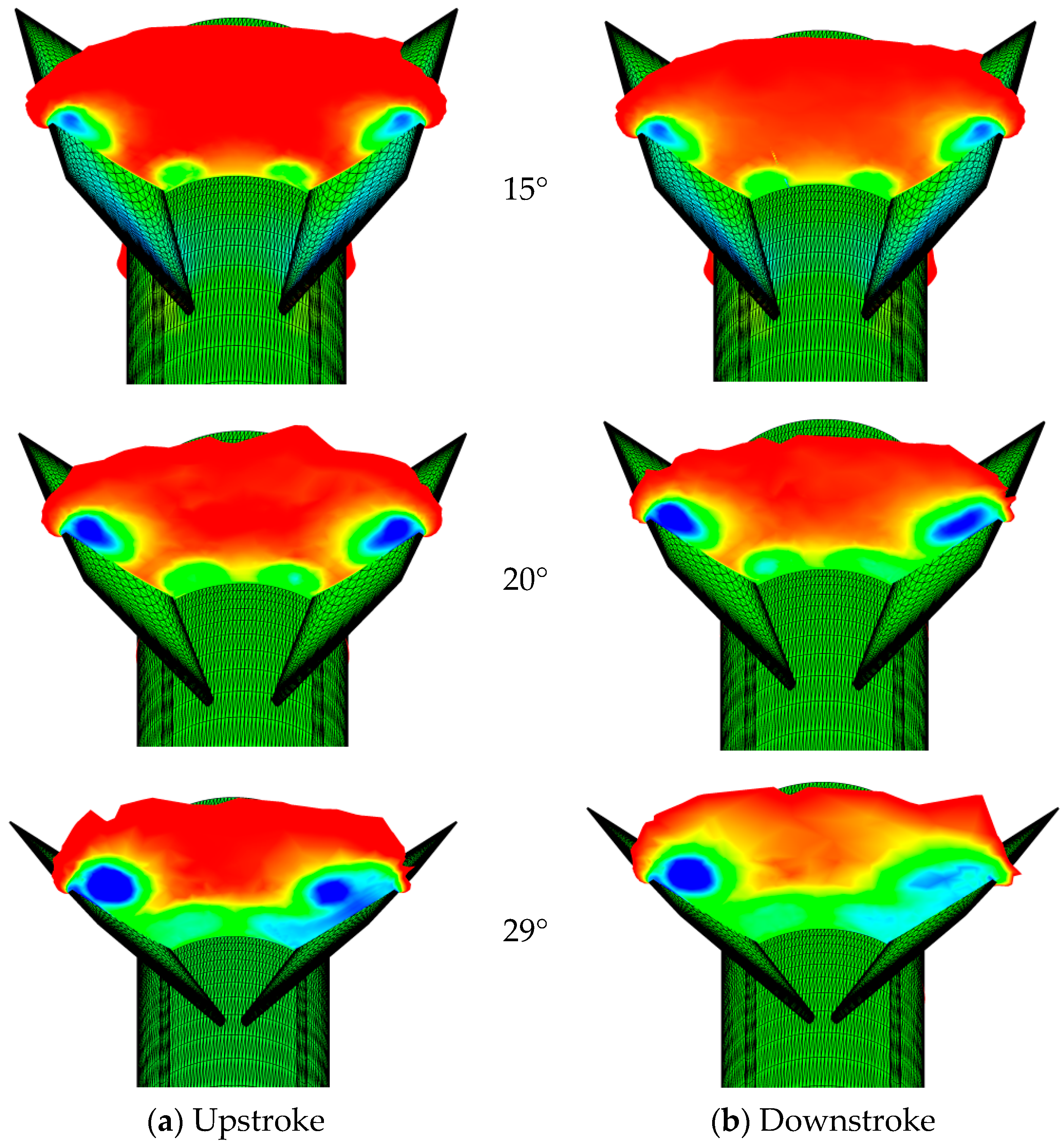
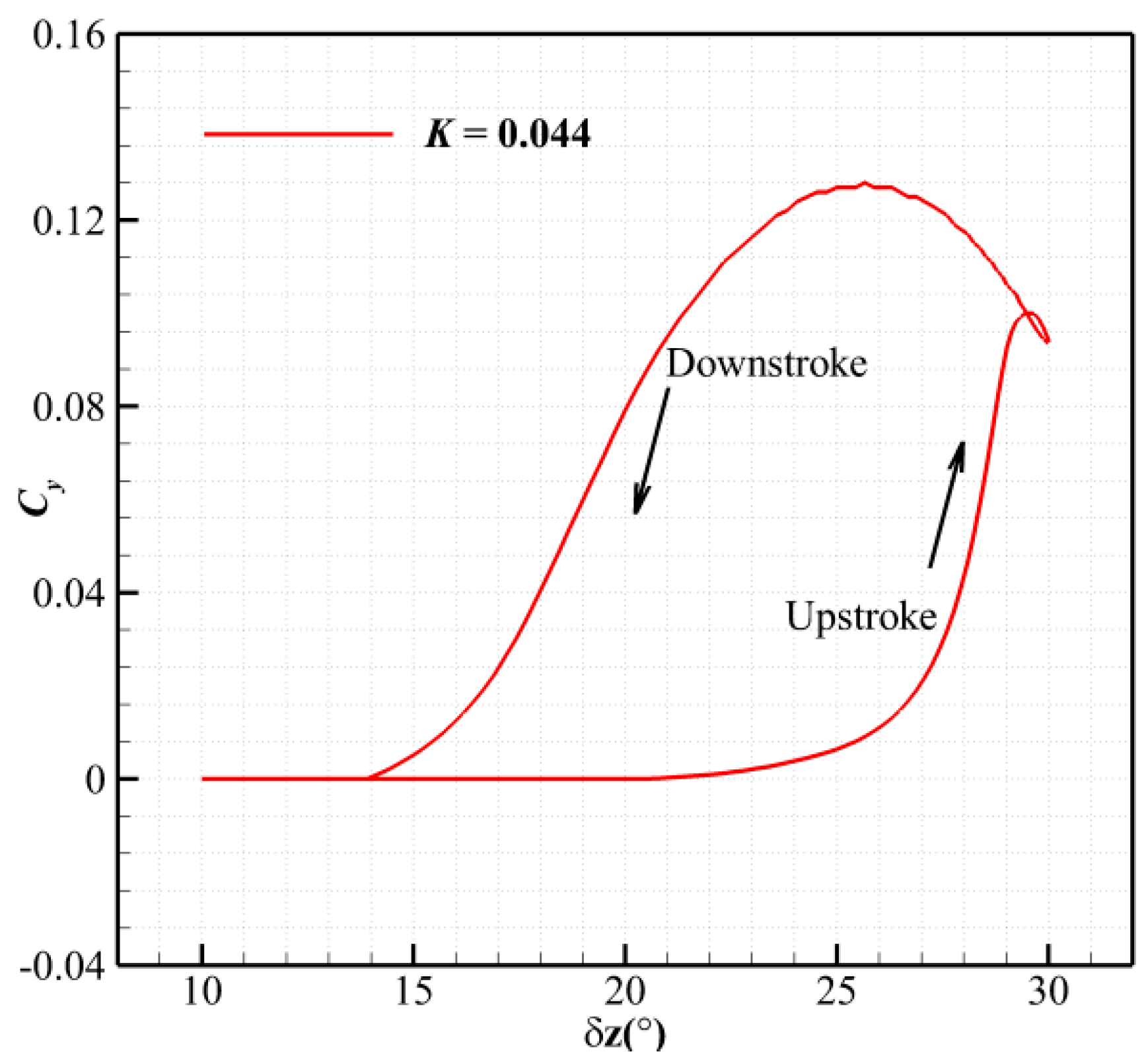
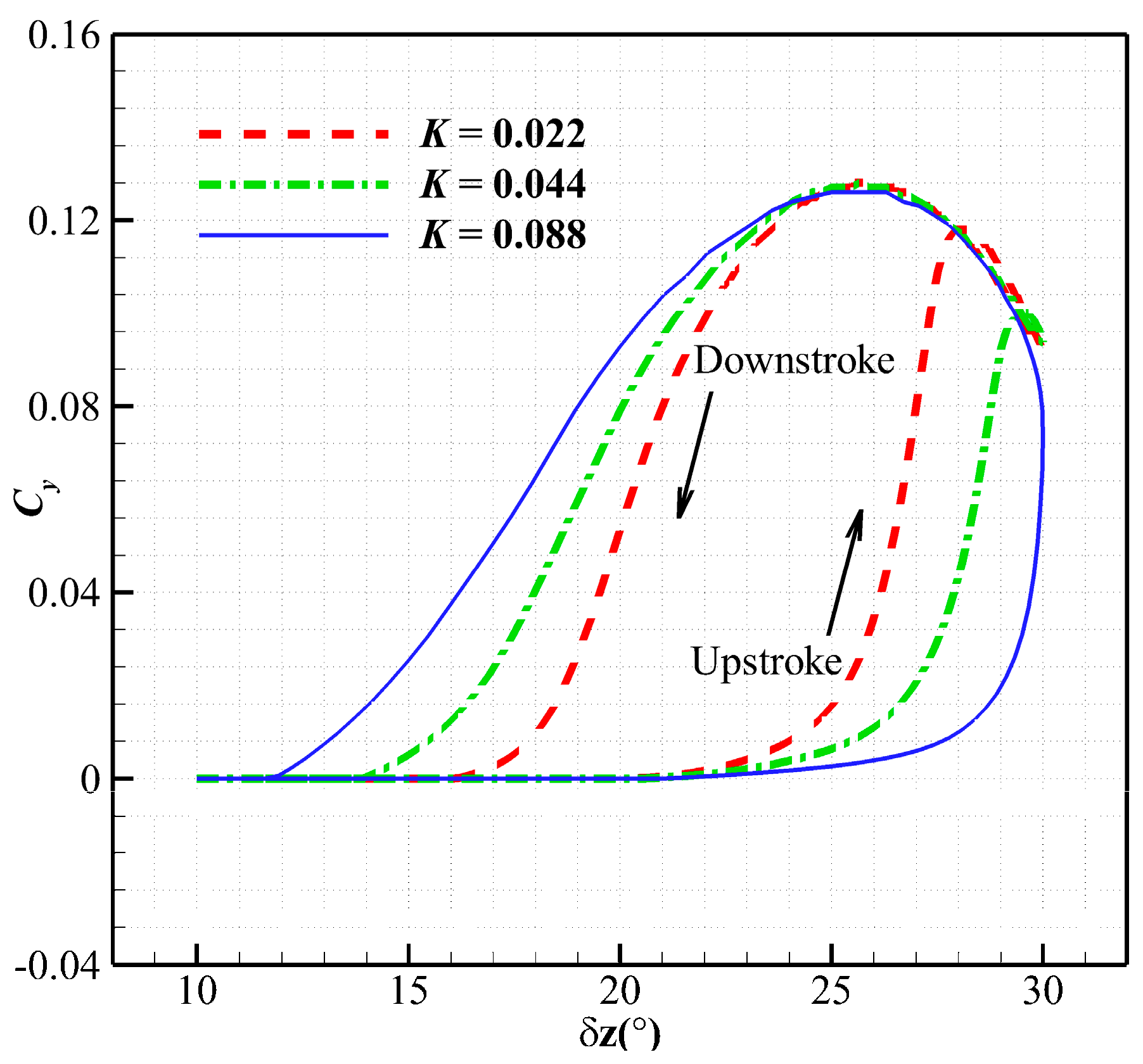
3.2. Results of the Pair of Fins Undergoing Symmetric Deflection Motions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, X.Y.; Tian, W.; Ma, B.F.; Wang, Y.K. Recent progress on the study of asymmetric vortex flow over slender bodies. Acta Mech. Sin. 2008, 24, 475–487. [Google Scholar] [CrossRef]
- Allen, H.J.; Perkins, E.W. Characteristics of Flow over Inclined Bodies of Revolution; NACA RM A50L07; NACA: Kansas City, MO, USA, 1951. [Google Scholar]
- Sampath Kumar, R.K.; Guha, T.K.; Kumar, R. Experimental investigation on the development of asymmetric vortices on a long slender body at high incidence. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019; p. 0844. [Google Scholar]
- Alqadi, I.M.; Eljack, E. Numerical investigation of flow asymmetry around slender body at high angles of attack. In Proceedings of the AIAA SciTech, 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 2083. [Google Scholar]
- Arena, A.S.; Nelson, R.C. The effect of asymmetric vortex wake characteristics on a slender delta wing undergoing wing rock motion. In Proceedings of the 16th Atmospheric Flight Mechanics Conference, AIAA, Boston, MA, USA, 14–16 August 1989. 89-3348-CP. [Google Scholar]
- Stahl, W.H.; Mahmood, M.; Asghar, A. Experimental investigations of the vortex flow on delta wings at high incidence. AIAA J. 1992, 30, 1027–1032. [Google Scholar] [CrossRef]
- Xiao, Z.; Chen, H.; Fu, S. Asymmetrical vortices breakdown of delta wing at high incidence. In Proceedings of the 22nd Applied Aerodynamics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4728. [Google Scholar]
- Obeid, O.; Alqadi, I. Computational study of asymmetric wake-vortex around ogive-cylinder body at high angles of attack. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1829. [Google Scholar]
- Hunt, B.L. Asymmetric vortex forces and wakes on slender bodies. In Proceedings of the 9th Atmospheric Flight Mechanics Conference, AIAA, San Diego, CA, USA, 9–11 August 1982; p. 1336. [Google Scholar]
- Park, M.Y.; Hyung, K.K.; Lee, P.W. Asymmetric vortices around a body in a high angle of attack supersonic flow. J. Korean Phys. Soc. 2009, 55, 2159–2165. [Google Scholar]
- Stephen, E.; Bixler, B.; Turner, J.; McLaughlin, T. Investigation of nose cone enhancement to improve the effectiveness of an articulating nose cone on a subsonic missile. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3165. [Google Scholar]
- Hitzel, S.M.; Osterhuber, R. Enhanced maneuverability of a delta-canard combat aircraft by vortex flow control. J. Aircr. 2018, 55, 1090–1102. [Google Scholar] [CrossRef]
- Stephen, E.; Eastwood, W.O.; McGlon, S.T. Vortex control through forebody strakes and vortex generators on Supersonic Nosecones. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3241. [Google Scholar]
- Bernhardt, J.; Williams, D. Proportional control of asymmetric forebody vortices. AIAA J. 1998, 36, 2087–2093. [Google Scholar] [CrossRef]
- Mahadevan, S.; Rodriguez, J.; Kumar, R. Effect of controlled imperfections on the vortex asymmetry of a conical body. AIAA J. 2018, 56, 3460–3477. [Google Scholar] [CrossRef]
- Fidler, J. Active control of asymmetric vortex effects. J. Aircr. 1979, 18, 54. [Google Scholar]
- Kumar, R.; Viswanath, P.R.; Ramesh, O.N. Nose blowing for side force control on slender cones at high incidence. J. Aircr. 2008, 45, 1156–1166. [Google Scholar] [CrossRef]
- Malcolm, G. Forebody vortex control—A progress review. In Proceedings of the 11th Applied Aerodynamics Conference 1993, American Institute of Aeronautics and Astronautics, Monterey, CA, USA, 9–11 August 1993. [Google Scholar]
- Long, Y.; Li, H.; Meng, X.; Hu, H. Optimized plasma actuation on asymmetric vortex over a slender body. Appl. Phys. Lett. 2018, 112, 014101. [Google Scholar] [CrossRef]
- Keener, E.R.; Chapman, G.T. Onset of aerodynamic side forces at zero sideslip on symmetric forebodies at high angles of attack. In Proceedings of the AIAA Mechanics and Control of Flight Conference, Anaheim, CA, USA, 5–9 August 1974. AIAA Paper 1974-0770. [Google Scholar]
- Kumar, R.; Viswanath, P.R.; Ramesh, O.N. Nose bluntness for side-force control on circular cones at high incidence. J. Aircr. 2005, 42, 1133–1141. [Google Scholar] [CrossRef]
- Lamont, P.J.; Hunt, B.L. Pressure and force distributions on a sharp-nosed circular cylinder at large angles of inclination to a uniform subsonic stream. J. Fluid Mech. 1976, 76, 519–559. [Google Scholar] [CrossRef]
- Keener, E.R.; Chapman, G.T. Similarity in vortex asymmetries over slender bodies and wings. AIAA J. 1977, 15, 1370–1372. [Google Scholar] [CrossRef]
- Woolard, H. Similarity relation for vortex-asymmetry onset on slender pointed forebodies. AIAA J. 1982, 20, 559–561. [Google Scholar] [CrossRef]
- Ericsson, L.E. Sources of high alpha vortex asymmetry at zero sideslip. J. Aircr. 1992, 29, 1086–1090. [Google Scholar] [CrossRef]
- Schiff, L.B.; Degani, D.; Gavali, S. Numerical simulation of vortex unsteadiness on slender bodies of revolution at large incidence. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989; p. 195. [Google Scholar]
- Degani, D.; Schiff, L.B. Numerical simulation of the effect of spatial disturbances on vortex asymmetry. AIAA J. 1991, 29, 344–352. [Google Scholar] [CrossRef]
- Levy, Y. Unsteady vortex shedding behind slender bodies of revolution. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Shi, X.; Li, Y.; Liu, D.; Chang, L.; Yang, K. Asymmetric flow mechanism for small aspect ratio rudders with large deflection angles on rotated missile. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2690–2698. [Google Scholar]
- Gad-El-Hak, M.; Ho, C.M. Aerodynamics of a missile in unsteady flight. In Proceedings of the 24th Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, Reno, NV, USA, 6–9 January 1986. [Google Scholar]
- Gad-El-Hak, M.; Ho, C.M. The pitching delta wing. AIAA J. 1985, 23, 1660–1665. [Google Scholar] [CrossRef]
- Zilliac, G.G.; Degani, D.; Tobak, M. Asymmetric vortices on a slender body of revolution. AIAA J. 1991, 29, 667–675. [Google Scholar] [CrossRef]
- Palacios, F.; Colonno, M.R.; Aranake, A.C.; Campos, A.; Alonso, J.J. SU2: An open-source suite for multiphysics simulation and design. AIAA J. 2016, 54, 828–846. [Google Scholar]
- Landon, R. NACA 0012 Oscillatory and Transient Pitching; Technical report; Aircraft Research Association Ltd.: Beford, UK, 2000. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, L.; Gao, C.; Zhu, J.; Dong, B. Investigation of Asymmetric Flow of a Slender Body with Low-Aspect Ratio Fins Having Large Deflection Angles. Aerospace 2024, 11, 835. https://doi.org/10.3390/aerospace11100835
Li Y, Zhang L, Gao C, Zhu J, Dong B. Investigation of Asymmetric Flow of a Slender Body with Low-Aspect Ratio Fins Having Large Deflection Angles. Aerospace. 2024; 11(10):835. https://doi.org/10.3390/aerospace11100835
Chicago/Turabian StyleLi, Yonghong, Lin Zhang, Chuan Gao, Jilong Zhu, and Bin Dong. 2024. "Investigation of Asymmetric Flow of a Slender Body with Low-Aspect Ratio Fins Having Large Deflection Angles" Aerospace 11, no. 10: 835. https://doi.org/10.3390/aerospace11100835
APA StyleLi, Y., Zhang, L., Gao, C., Zhu, J., & Dong, B. (2024). Investigation of Asymmetric Flow of a Slender Body with Low-Aspect Ratio Fins Having Large Deflection Angles. Aerospace, 11(10), 835. https://doi.org/10.3390/aerospace11100835




