0-D Dynamic Performance Simulation of Hydrogen-Fueled Turboshaft Engine
Abstract
1. Introduction
2. Materials and Methods
2.1. Engine Description
2.2. Fuel Properties and Chemical Equilibrium Calculation
2.3. 0-D Model Assumptions
- The model is 0 dimensional (no spatial dependencies).
- No heat exchanges with the engine structure and external environment (adiabatic processes).
- No pressure losses along the pipes.
- No concentrated pressure losses due to aerodynamic effects.
- Steady-state validation of the model (no transient validation).
- No hardware and components modifications when different fuels were considered.
- Performance comparison in quasi-static working conditions.
- Neat kerosene Jet A-1 and H2 (no fuel blending).
- Simplified combustion model based on the CEA-Run database.
- No changes in the chemical composition of the flow were considered throughout the engine, apart from the combustion chamber.
2.4. Numerical Model
2.5. Thermocouple Dynamic
3. Results and Discussion
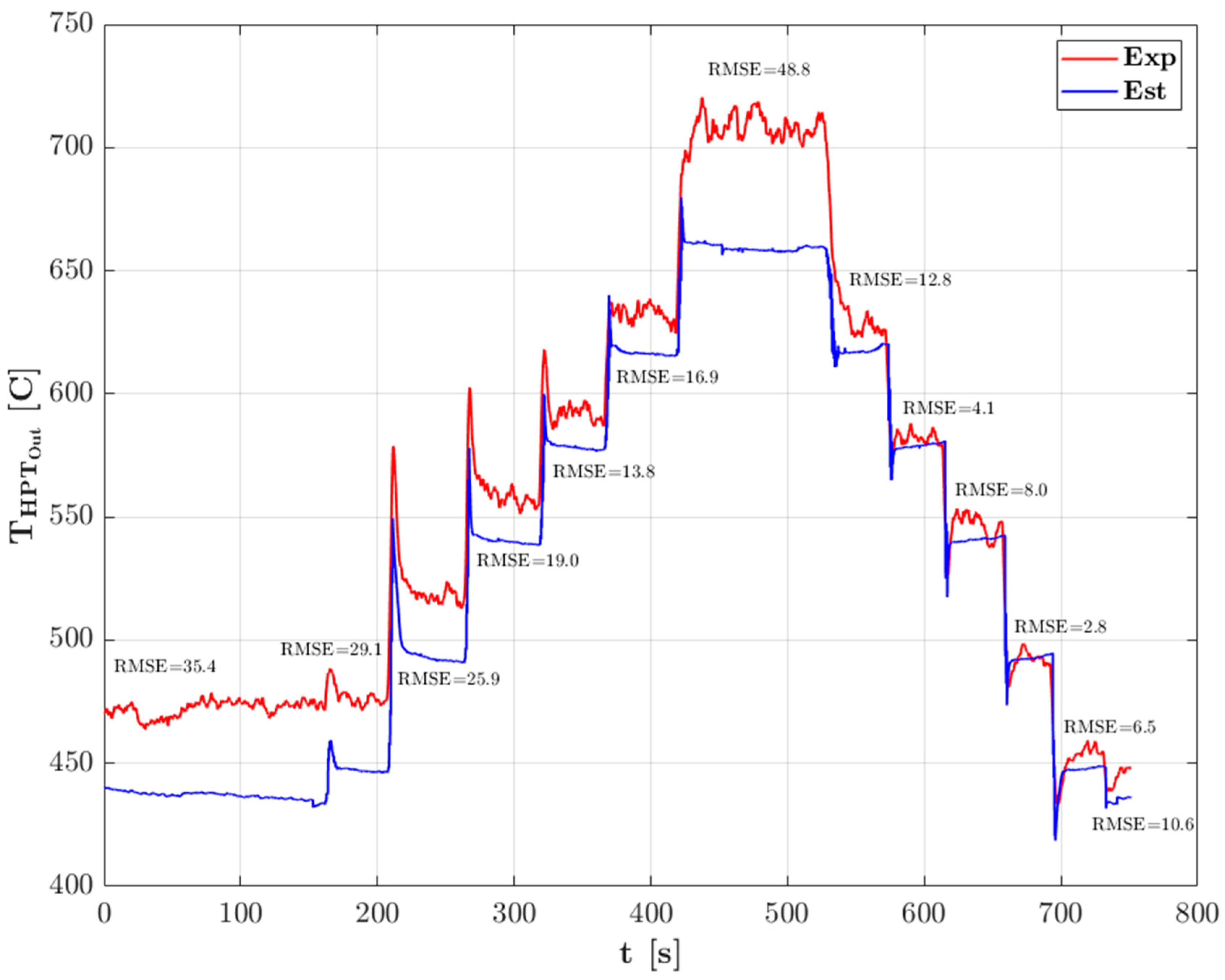
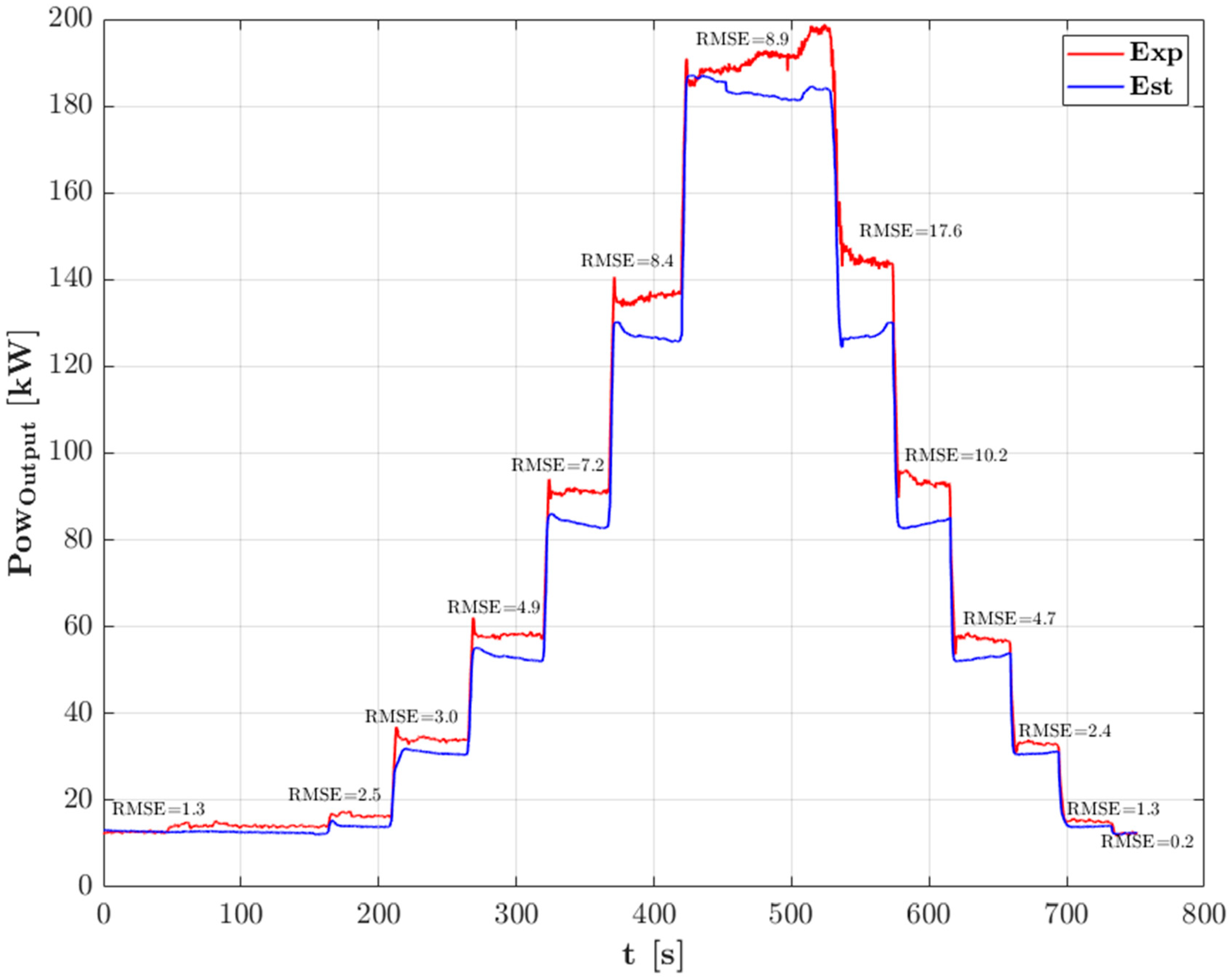
3.1. Model Validation
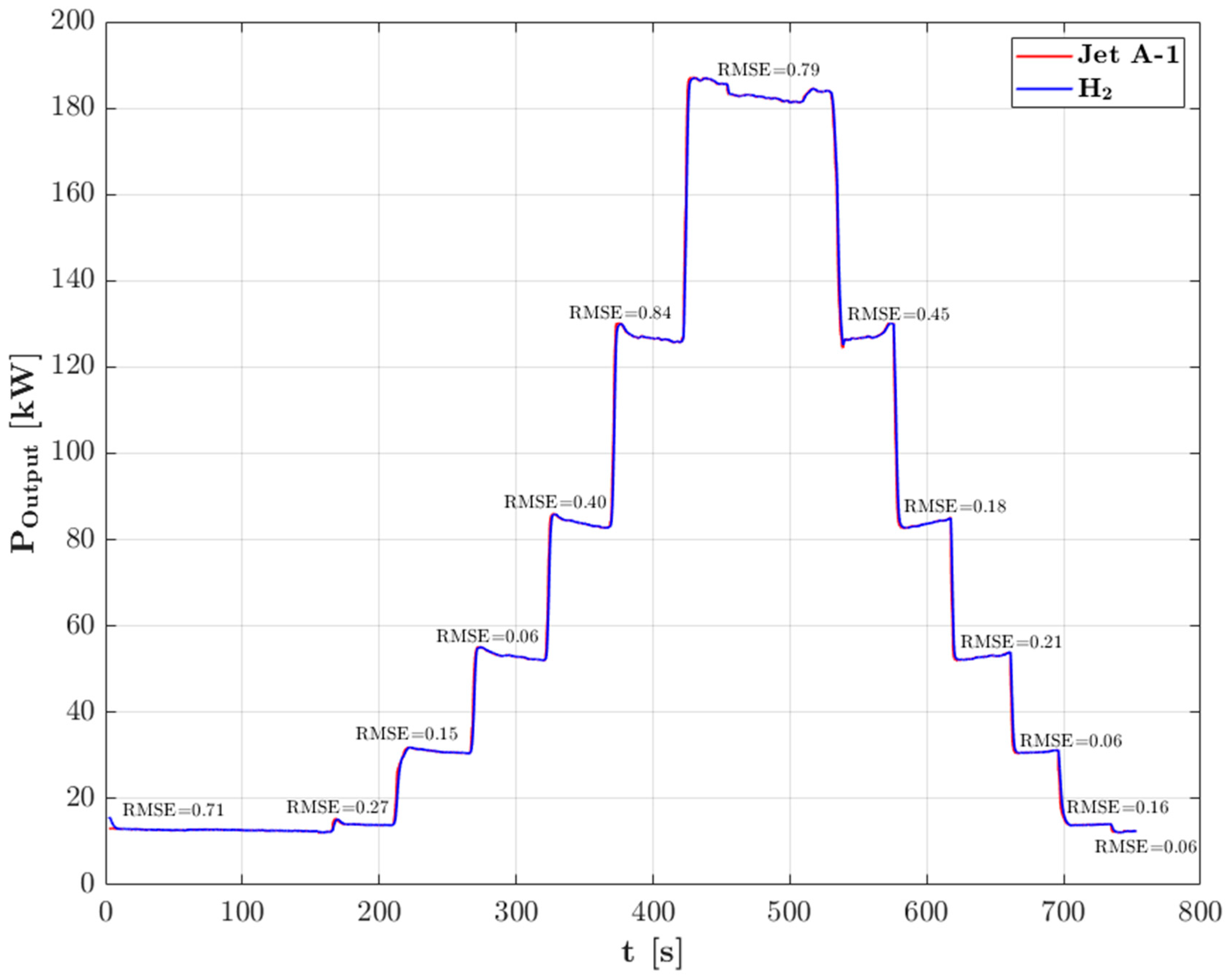
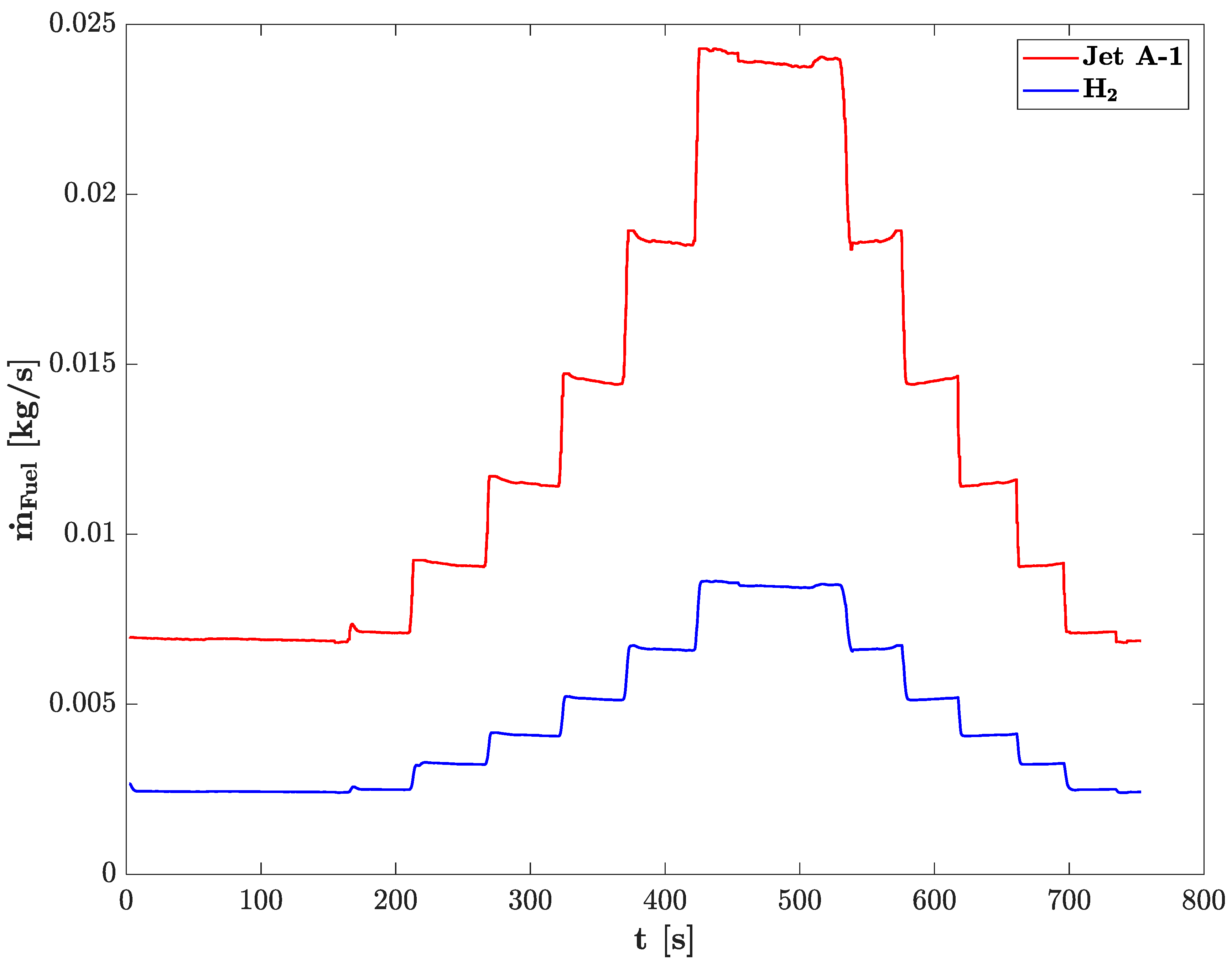
3.2. Performance Comparison between Kerosene Jet A-1 and Hydrogen
- Constant engine power output.
- No hardware modifications.
- Similar environmental conditions.
4. Conclusions
- Due to its much higher LHV, hydrogen reaches the same energy as Jet A-1 with a reduced mass flow rate. Hydrogen revealed a reduction of approximately 64% in fuel flow rate to obtain the same power output as Jet A-1. This condition implies that the fraction of aircraft weight dedicated to fuel could be greatly reduced from an energy standpoint. However, this positive effect cannot be fully exploited with the current generation of hydrogen tanks, which are much heavier compared to traditional aeronautical tanks.
- The similar specific fuel consumption indicates that conventional aircraft could perform similar missions with the same amount of energy stored in the fuel tank system. At ambient conditions, hydrogen is characterized by a mass density five orders of magnitude lower than kerosene, with an LHV only three times higher, requiring pressurized and/or cryogenic tanks to be stored in acceptable volumes. The estimated mass of these tanks compared to Jet A-1 tanks varies significantly in different previous studies, from a maximum increase of 66%. Nonetheless, all studies agree on an increase in the volume of the tank of at least five times.
- Since gaseous hydrogen is CO2-free, the quantity of CO2 present in the combustion of hydrogen is limited to the percentage of CO2 initially present in the air. This result represents the main advantage of hydrogen over conventional fossil fuels in terms of reducing the environmental impact of air traffic.
- Running on hydrogen, the temperature of the engine sections after the CC is lower. At the outlet of the combustion chamber, an average decrease of 2.2% in temperature was observed. Taking into account the thermal and structural limitations of today’s materials, hydrogen would be able to produce more power while reaching the same temperature at the exit of the combustion chamber, either by introducing more fuel or reducing the air intake.
- The decrease in temperature at the inlet of the turbines is partially compensated by the increase in specific heat of the gas (mixture running on hydrogen). The increase in the specific heat (approximately 1.6%) may be related to the higher presence of water vapor in the exhaust flow.
- Running on hydrogen, the dynamic power balance of the GG has been shifted toward different engine conditions, characterized by higher rotational speed, increased air mass flow rate, and an increased compression ratio. Only the LPT has shown lower efficiency at the new operating points (no efficiency variations were recorded for either the compressor or the HPT).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACS | Axial Compressor Stages |
| AD | Average Difference |
| APD | Average Percentage Difference |
| BSFC | Brake Specific Fuel Consumption |
| C | Heat capacity |
| CC | Combustion Chamber |
| CCS | Centrifugal Compressor Stage |
| CEA | Chemical Equilibrium Application |
| CFD | Computational Fluid Dynamic |
| Est | Estimated |
| Exp | Experimental |
| FC | Fuel cell |
| FC-HT | High Temperature FC |
| GG | Gas Generator |
| GGS | Gas Generator Shaft |
| GHG | Green House Gases |
| HPT | High Pressure Turbine |
| HYSYS | HYprotic SYStem |
| IEA | International Energy Agency |
| J | Inertia moment |
| Ker-EBSFC | Kerosene Equivalent Brake Specific Fuel Consumption |
| LHV | Lower Heating Value |
| LPT | Low-Pressure Turbine |
| M | Molar weight |
| MATLAB | MATrix LABoratory |
| MD | Mean Difference |
| MOA | More Electric aircraft |
| MPD | Maximum Percentage Difference |
| MZ | Mixing Zone |
| PID | Proportional Integral Derivative controller |
| N | Rotational speed in RPM |
| NASA | National Aeronautics and Space Administration |
| P | Power |
| PCZ | Primary Combustion Zone |
| PID | Proportional Integral Derivative controller |
| PMD | Percentage Mean Difference |
| R | Specific gas constant |
| RMSE | Root Mean Square Error |
| RPM | Rotations Per Minute |
| S | Surface |
| SAF | Sustainable Aviation Fuels |
| SCZ | Secondary Combustion Zone |
| T | Temperature |
| V | Volume |
| W | Work |
| C | Specific heat |
| cp | Specific heat at constant pressure |
| h | Height |
| k | Coefficient of convective heat exchange |
| Mass flow rate | |
| P | Pressure |
| r | Radius |
| t | Time |
| β | Compression ratio |
| γ | Heat capacity ratio |
| ε | Emissivity |
| λ | Air-fuel ratio |
| ρ | Density |
| η | Thermal/Mechanical efficiency |
| σ | Stefan-Boltzmann constant |
| ω | Rotational speed expressed in rad/s |
References
- Climate Change 2022, Mitigation of Climate Change.pdf. Available online: https://www.ipcc.ch/report/ar6/wg3/downloads/report/IPCC_AR6_WGIII_SummaryForPolicymakers.pdf (accessed on 23 February 2024).
- Climate Change and Sustainable Transport UNECE. Available online: https://unece.org/transport/climate-change-and-sustainable-transport (accessed on 11 March 2024).
- Transforming Our World: The 2030 Agenda for Sustainable Development|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/2030agenda (accessed on 18 March 2024).
- Sustainable Development Goals—European Commission. Available online: https://international-partnerships.ec.europa.eu/policies/sustainable-development-goals_en (accessed on 11 March 2024).
- Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions. The European Green Deal. 2019. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2019%3A640%3AFIN (accessed on 11 March 2024).
- Transport—Energy System. Available online: https://www.iea.org/energy-system/transport (accessed on 18 March 2024).
- Martin, J.; Neumann, A.; Ødegård, A. Renewable hydrogen and synthetic fuels versus fossil fuels for trucking, shipping and aviation: A holistic cost model. Renew. Sustain. Energy Rev. 2023, 186, 113637. [Google Scholar] [CrossRef]
- Ebrie, A.S.; Kim, Y.J. Investigating Market Diffusion of Electric Vehicles with Experimental Design of Agent-Based Modeling Simulation. Systems 2022, 10, 28. [Google Scholar] [CrossRef]
- Su-ungkavatin, P.; Tiruta-Barna, L.; Hamelin, L. Biofuels, electrofuels, electric or hydrogen?: A review of current and emerging sustainable aviation systems. Prog. Energy Combust. Sci. 2023, 96, 101073. [Google Scholar] [CrossRef]
- Tajuddin, M.H.B. The Comparison Study between Aviation Jet A-1 And Super Bio-Jet Fuel (Jatropha Based) Usages on Allison 250 Mockup Gas Turbine Engine. 2013. Available online: https://ir.unikl.edu.my/xmlui/handle/123456789/3912 (accessed on 6 December 2023).
- Almena, A.; Siu, R.; Chong, K.; Thornley, P.; Röder, M. Reducing the environmental impact of international aviation through sustainable aviation fuel with integrated carbon capture and storage. Energy Convers. Manag. 2024, 303, 118186. [Google Scholar] [CrossRef]
- Corchero, G.; Montañés, J.L. An approach to the use of hydrogen for commercial aircraft engines. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2005, 219, 35–44. [Google Scholar] [CrossRef]
- Brewer, G.D. Hydrogen Aircraft Technology; Routledge: London, UK, 2017; ISBN 978-1-351-43979-4. [Google Scholar]
- Adler, E.J.; Martins, J.R.R.A. Hydrogen-powered aircraft: Fundamental concepts, key technologies, and environmental impacts. Prog. Aerosp. Sci. 2023, 141, 100922. [Google Scholar] [CrossRef]
- Tiwari, S.; Pekris, M.J.; Doherty, J.J. A review of liquid hydrogen aircraft and propulsion technologies. Int. J. Hydrogen Energy 2024, 57, 1174–1196. [Google Scholar] [CrossRef]
- Degirmenci, H.; Uludag, A.; Ekici, S.; Karakoc, T.H. Challenges, prospects and potential future orientation of hydrogen aviation and the airport hydrogen supply network: A state-of-art review. Prog. Aerosp. Sci. 2023, 141, 100923. [Google Scholar] [CrossRef]
- Prewitz, M.; Schwärzer, J.; Bardenhagen, A. Potential analysis of hydrogen storage systems in aircraft design. Int. J. Hydrogen Energy 2023, 48, 25538–25548. [Google Scholar] [CrossRef]
- Gimenez, F.R.; Mady, C.E.K.; Henriques, I.B. Assessment of different more-electric and hybrid-electric configurations for long-range multi-engine aircraft. J. Clean. Prod. 2023, 392, 136171. [Google Scholar] [CrossRef]
- Chiara Massaro, M.; Pramotton, S.; Marocco, P.; Monteverde, A.H.A.; Santarelli, M. Optimal design of a hydrogen-powered fuel cell system for aircraft applications. Energy Convers. Manag. 2024, 306, 118266. [Google Scholar] [CrossRef]
- Nicolay, S.; Karpuk, S.; Liu, Y.; Elham, A. Conceptual design and optimization of a general aviation aircraft with fuel cells and hydrogen. Int. J. Hydrogen Energy 2021, 46, 32676–32694. [Google Scholar] [CrossRef]
- Massaro, M.C.; Biga, R.; Kolisnichenko, A.; Marocco, P.; Monteverde, A.H.A.; Santarelli, M. Potential and technical challenges of on-board hydrogen storage technologies coupled with fuel cell systems for aircraft electrification. J. Power Sources 2023, 555, 232397. [Google Scholar] [CrossRef]
- Ringuedé, A.; Hubert, S.; Atwi, L.; Lair, V. Prospects of hydrogen and its derivative as energy vector for electricity production at high temperature: Fuel cells and electrolysers. Curr. Opin. Electrochem. 2023, 42, 101401. [Google Scholar] [CrossRef]
- Haglind, F.; Singh, R. Design of Aero Gas Turbines Using Hydrogen. J. Eng. Gas Turbines Power 2006, 128, 754–764. [Google Scholar] [CrossRef]
- Chiesa, P.; Lozza, G.; Mazzocchi, L. Using Hydrogen as Gas Turbine Fuel. J. Eng. Gas Turbines Power-Trans. ASME 2005, 127, 73–80. [Google Scholar] [CrossRef]
- Adam, A.; He, W.; Fan, Y.; Han, D. Investigation of flow characteristics and mixing of liquid hydrogen within a premixing swirl tube for the turbine engine combustor. Int. J. Hydrogen Energy 2024, 49, 367–383. [Google Scholar] [CrossRef]
- Funke, H.H.-W.; Keinz, J.; Kusterer, K.; Ayed, A.H.; Kazari, M.; Kitajima, J.; Horikawa, A.; Okada, K. Development and Testing of a Low NOx Micromix Combustion Chamber for Industrial Gas Turbines. Int. J. Gas Turbine Propuls. Power Syst. 2017, 9, 27–36. [Google Scholar] [CrossRef]
- Haj Ayed, A.; Kusterer, K.; Funke, H.H.-W.; Keinz, J.; Striegan, C.; Bohn, D. Experimental and numerical investigations of the dry-low-NOx hydrogen micromix combustion chamber of an industrial gas turbine. Propuls. Power Res. 2015, 4, 123–131. [Google Scholar] [CrossRef]
- Aircraft Certification|EASA. Available online: https://www.easa.europa.eu/en/domains/aircraft-products/aircraft-certification (accessed on 24 March 2024).
- Babahammou, H.R.; Merabet, A.; Miles, A. Technical modelling and simulation of integrating hydrogen from solar energy into a gas turbine power plant to reduce emissions. Int. J. Hydrogen Energy 2024, 59, 343–353. [Google Scholar] [CrossRef]
- Balli, O.; Ozbek, E.; Ekici, S.; Midilli, A.; Hikmet Karakoc, T. Thermodynamic comparison of TF33 turbofan engine fueled by hydrogen in benchmark with kerosene. Fuel 2021, 306, 121686. [Google Scholar] [CrossRef]
- Wang, X.; He, A.; Hu, Z. Transient Modeling and Performance Analysis of Hydrogen-Fueled Aero Engines. Processes 2023, 11, 423. [Google Scholar] [CrossRef]
- Paoli, M.D.; Ponti, D.I.F. Validazione Preliminare del Modello Dinamico di un Turboalbero Aeronautico. Master’s Thesis, Università di Bologna, Bologna, Italy, 2014. [Google Scholar]
- M250 Turboshaft. Available online: https://www.rolls-royce.com/products-and-services/civil-aerospace/helicopters/m250-turboshaft.aspx (accessed on 25 March 2024).
- The M250—A Model Engine|Rolls-Royce. Available online: https://www.rolls-royce.com/media/our-stories/discover/2018/the-m250-a-model-engine.aspx (accessed on 27 March 2024).
- Type Certificate Data Sheets (TCDS)|EASA. Available online: https://www.easa.europa.eu/en/document-library/type-certificates (accessed on 17 September 2024).
- 250-C18-Operation-Maintenance-Manual.pdf. Available online: https://pscorp.ph/wp-content/uploads/2019/06/250-C18-Operation-Maintenance-Manual.pdf (accessed on 25 March 2024).
- Chemical and Physical Information. In Toxicological Profile for JP-5, JP-8, and JET A Fuels; Agency for Toxic Substances and Disease Registry (US): Atlanta, GA, USA, 2017. Available online: https://www.ncbi.nlm.nih.gov/books/NBK592027/ (accessed on 30 March 2024).
- Table 1. ASTM Fuel Specification Test Results for Jet A-1. Available online: https://www.researchgate.net/figure/ASTM-FUEL-SPECIFICATION-TEST-RESULTS-FOR-JET-A-1_tbl1_267501767 (accessed on 30 March 2024).
- The Energy Density of Hydrogen: A Unique Property. Demaco Cryogenics. 2024. Available online: https://demaco-cryogenics.com/blog/energy-density-of-hydrogen (accessed on 30 March 2024).
- McBride—Sanford Gordon and Associates Cleveland, Ohio.pdf. Available online: https://ntrs.nasa.gov/api/citations/19950013764/downloads/19950013764.pdf (accessed on 30 March 2024).
- NASA-RP-1311-2.pdf. Available online: https://shepherd.caltech.edu/EDL/PublicResources/sdt/refs/NASA-RP-1311-2.pdf (accessed on 30 March 2024).
- Camporeale, S.M.; Fortunato, B.; Mastrovito, M. A Modular Code for Real Time Dynamic Simulation of Gas Turbines in Simulink. J. Eng. Gas Turbines Power 2002, 128, 506–517. [Google Scholar] [CrossRef]
- Kim, S.-K.; Pilidis, P.; Yin, J. Gas Turbine Dynamic Simulation Using Simulink®; SAE Technical Paper 2000-01–3647; SAE International: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Eastbourn, S.; Roberts, R. Modeling and Simulation of a Dynamic Turbofan Engine Using Simulink. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2023. [Google Scholar] [CrossRef]
- Asgari, H.; Venturini, M.; Chen, X.; Sainudiin, R. Modeling and Simulation of the Transient Behavior of an Industrial Power Plant Gas Turbine. J. Eng. Gas Turbines Power 2014, 136, 061601. [Google Scholar] [CrossRef]
- Roberts, R.A.; Eastbourn, S.M. Modeling Techniques for a Computational Efficient Dynamic Turbofan Engine Model. Int. J. Aerosp. Eng. 2014, 2014, e283479. [Google Scholar] [CrossRef]
- Hashmi, M.B.; Lemma, T.A.; Ahsan, S.; Rahman, S. Transient Behavior in Variable Geometry Industrial Gas Turbines: A Comprehensive Overview of Pertinent Modeling Techniques. Entropy 2021, 23, 250. [Google Scholar] [CrossRef] [PubMed]
- Dixon, S.L. Fluid Mechanics and Thermodynamics of Turbomachinery, 4th ed.; in SI/metric units; Butterworth-Heinemann: Boston, MA, USA, 1998; ISBN 978-0-7506-7059-3. [Google Scholar]
- Venturini, M. Development and Experimental Validation of a Compressor Dynamic Model. J. Turbomach. 2004, 127, 599–608. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. A component map tuning method for performance prediction and diagnostics of gas turbine compressors. Appl. Energy 2014, 135, 572–585. [Google Scholar] [CrossRef]
- Aldi, N.; Morini, M.; Pinelli, M.; Spina, P.R.; Suman, A. Cross Validation of Multistage Compressor Map Generation by Means of Computational Fluid Dynamics and Stage-Stacking Techniques. In Volume 3B: Oil and Gas Applications; Organic Rankine Cycle Power Systems; Supercritical CO2 Power Cycles; Wind Energy; American Society of Mechanical Engineers: Düsseldorf, Germany, 2014; p. V03BT25A009. [Google Scholar] [CrossRef]
- GmbH, G. GasTurb—Smooth C/T. Available online: https://www.gasturb.com/software/smooth-c-t.html (accessed on 17 September 2024).
- Liu, B.; Huang, Q.; Wang, P. Influence of surrounding gas temperature on thermocouple measurement. Case Stud. Therm. Eng. 2020, 19, 100627. [Google Scholar] [CrossRef]
- Manjhi, S.K.; Kumar, R. Performance assessment of K-type, E-type and J-type coaxial thermocouples on the solar light beam for short duration transient measurements. Measurement 2019, 146, 343–355. [Google Scholar] [CrossRef]
- Demsis, A.; Verma, B.; Prabhu, S.V.; Agrawal, A. Heat transfer coefficient of gas flowing in a circular tube under rarefied condition. Int. J. Therm. Sci. 2010, 49, 1994–1999. [Google Scholar] [CrossRef]
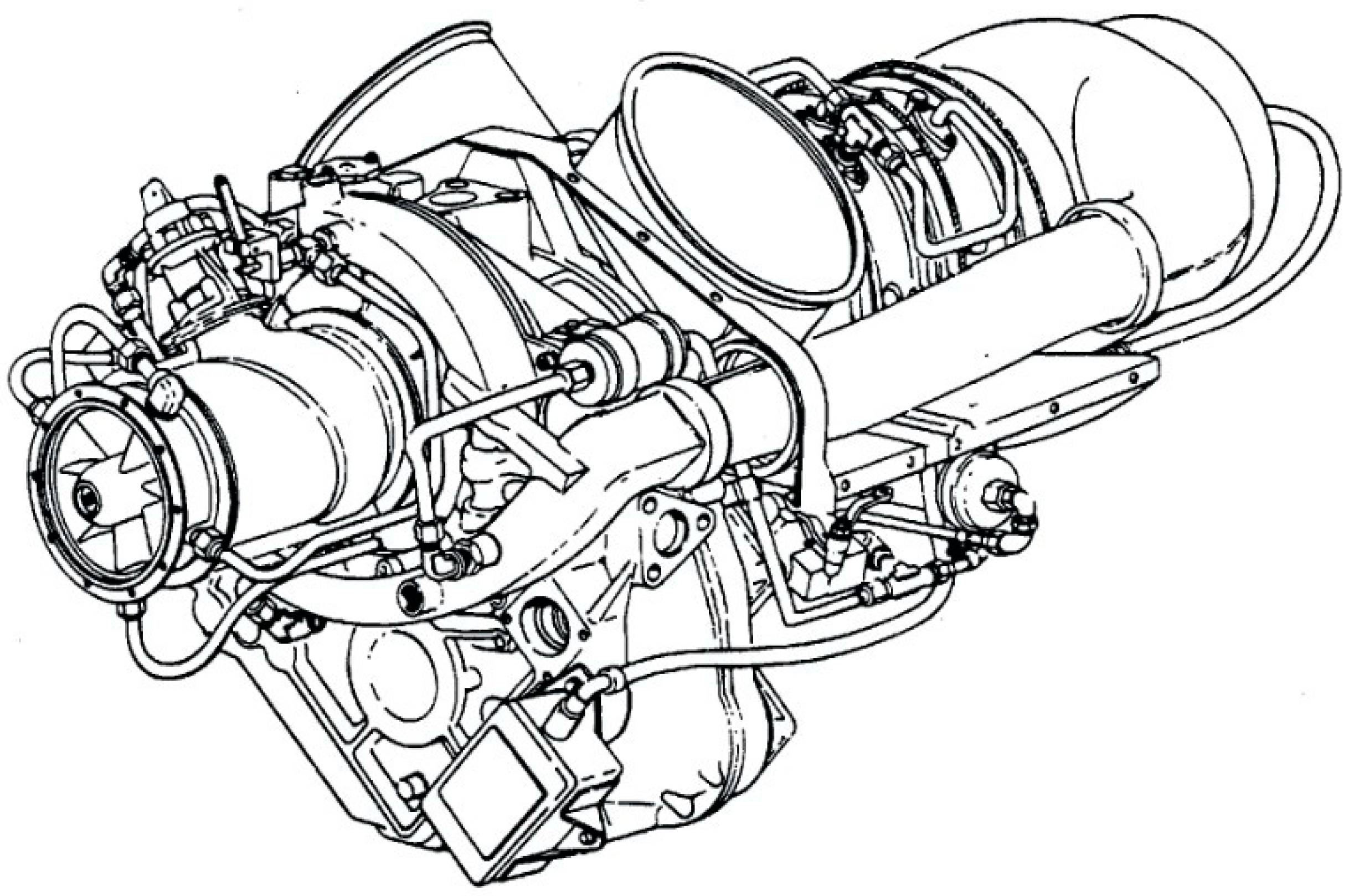
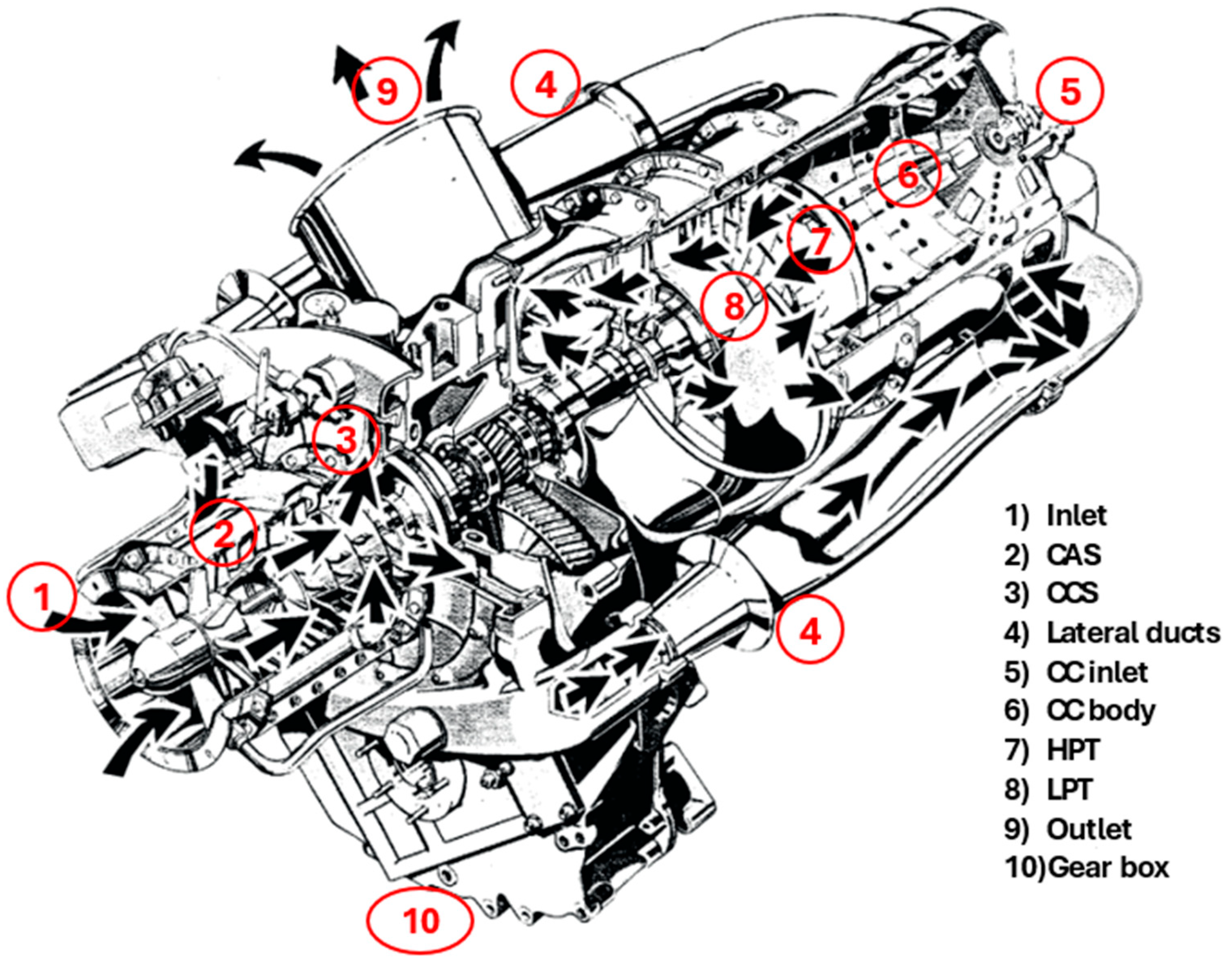
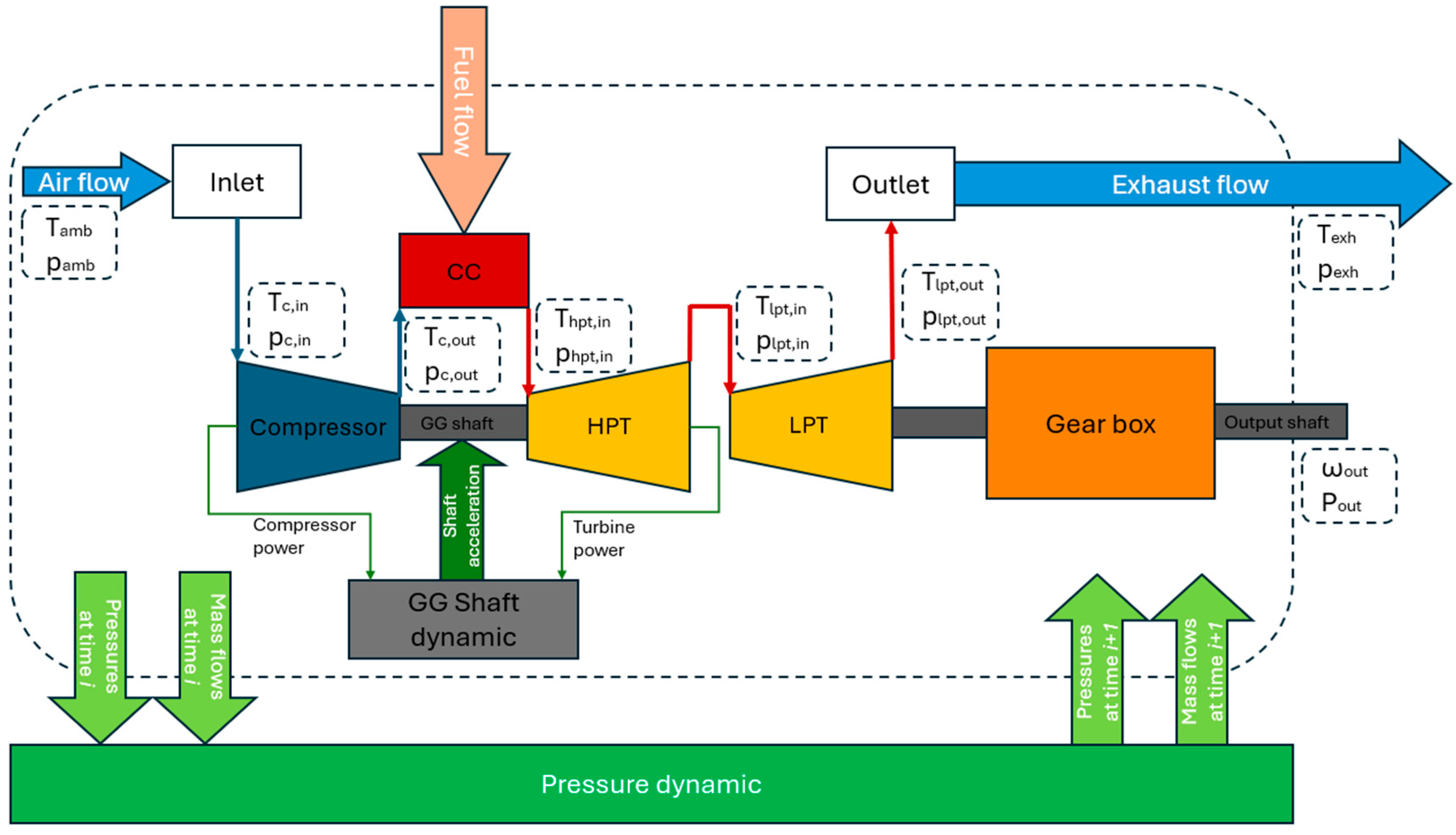
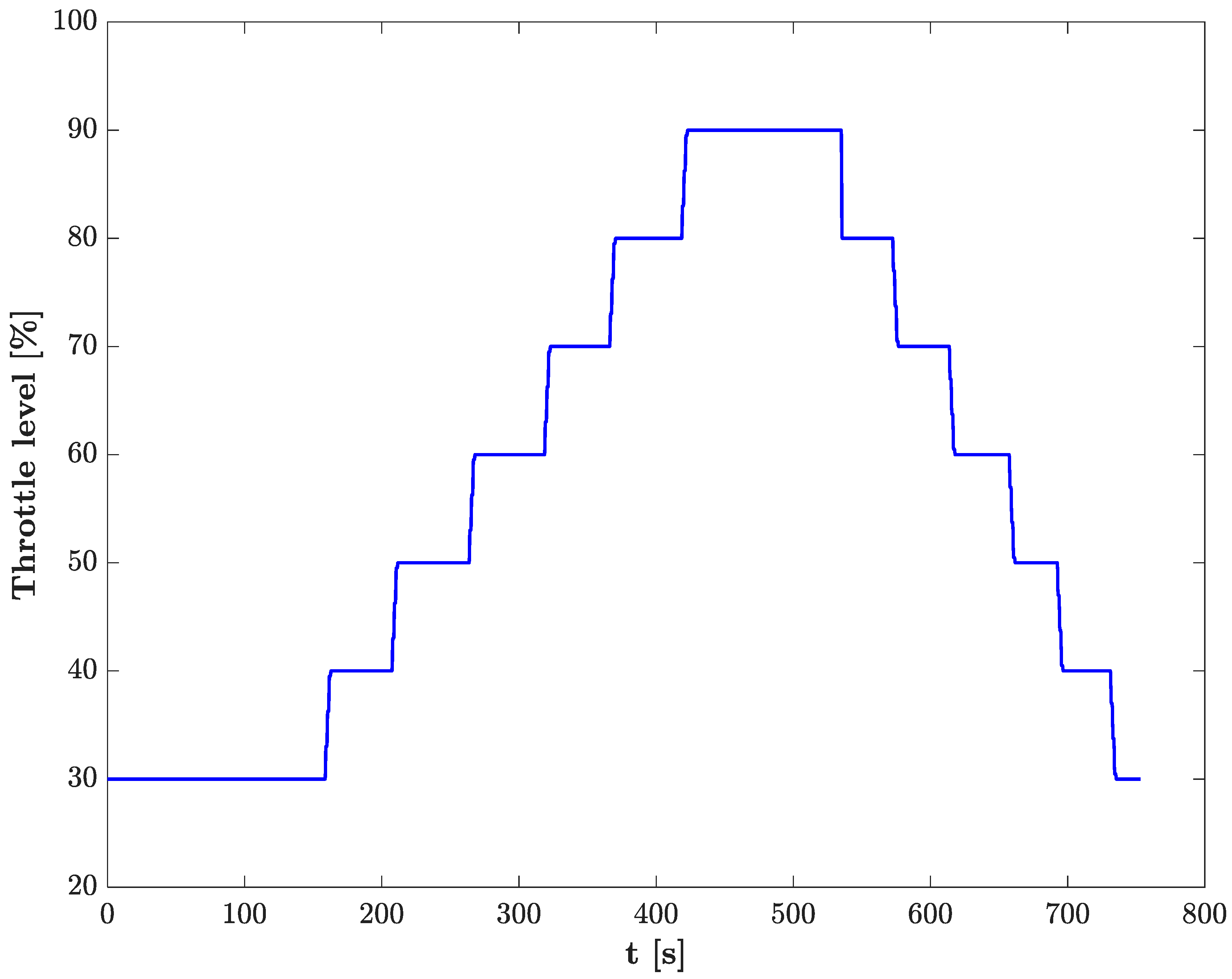
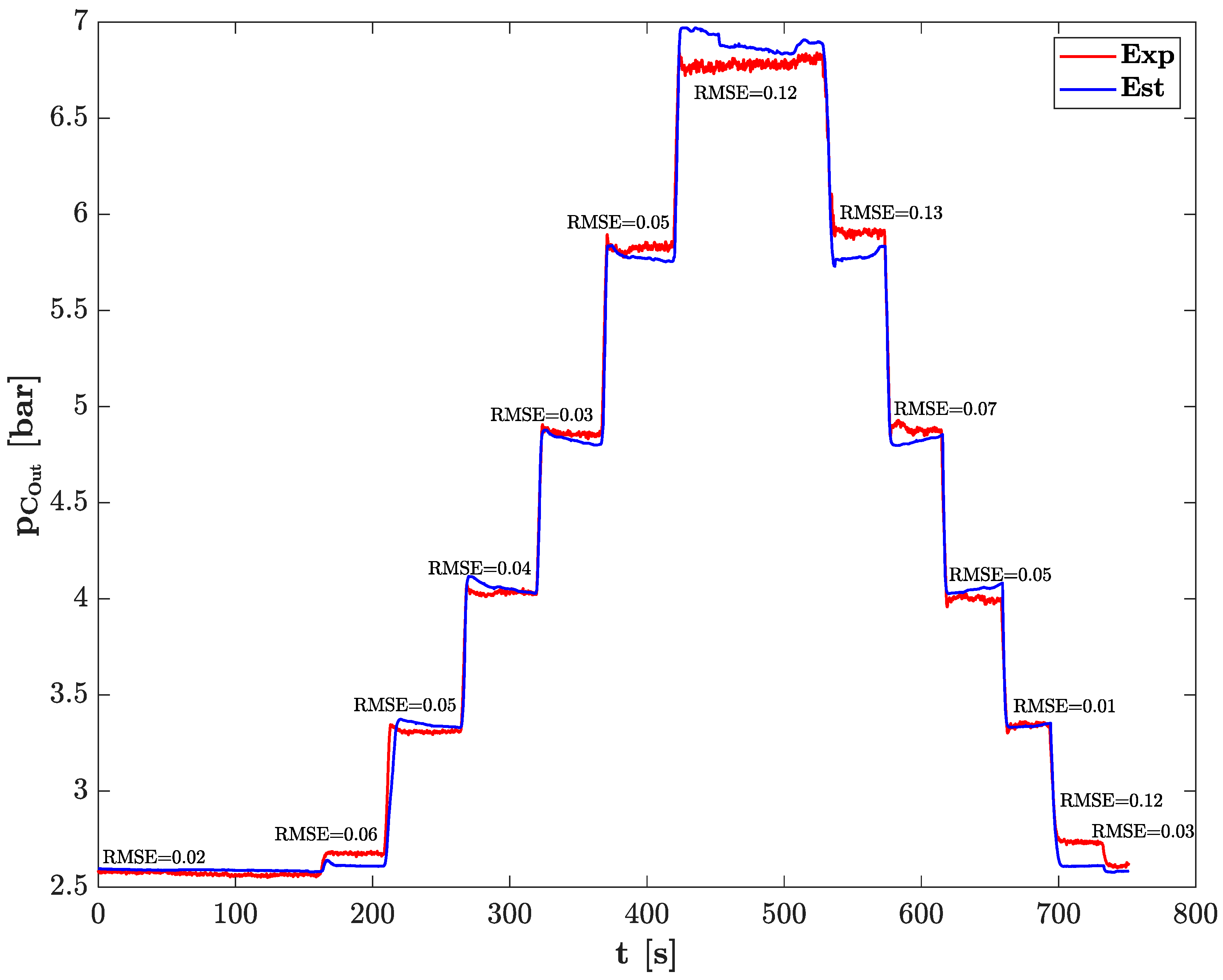
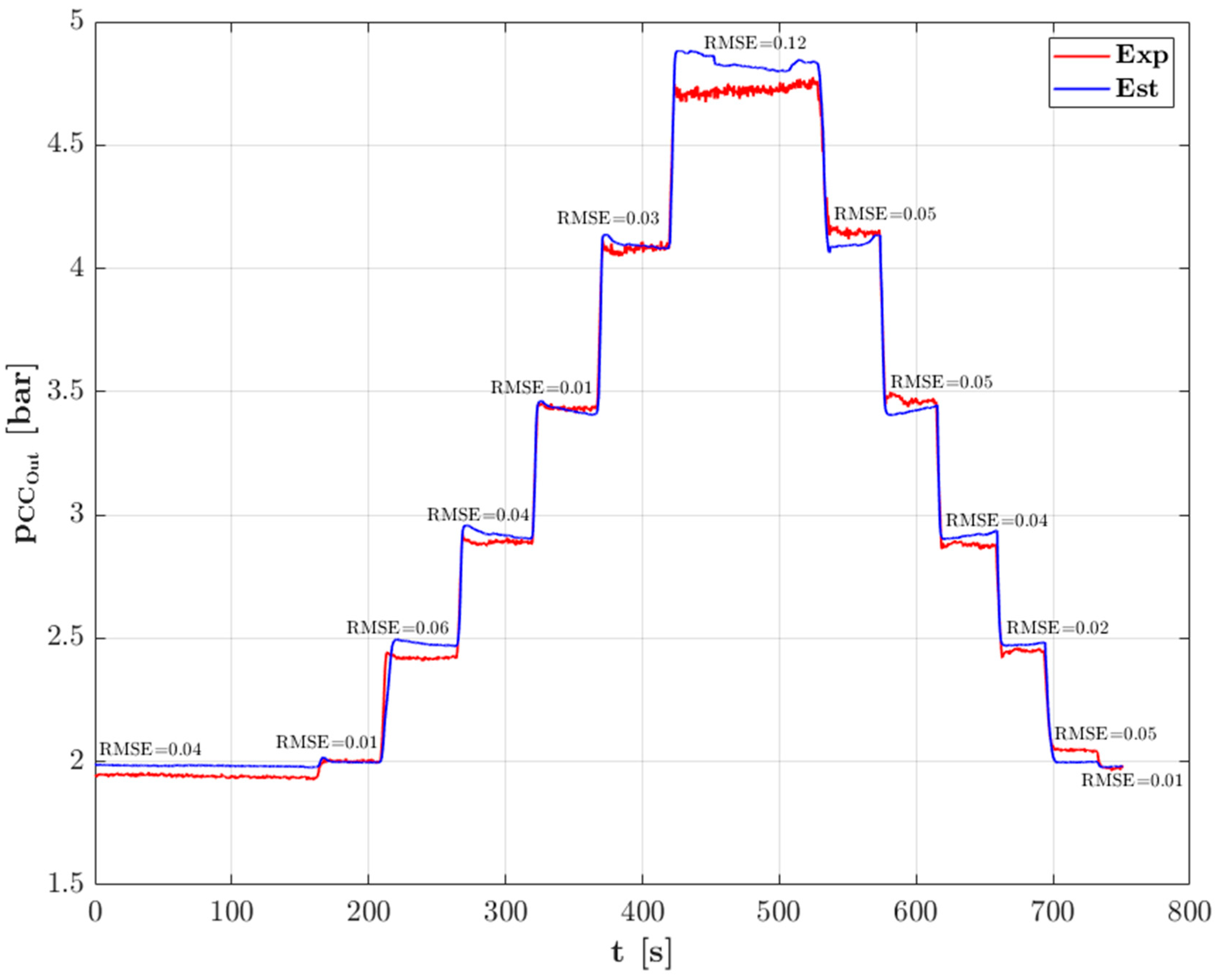

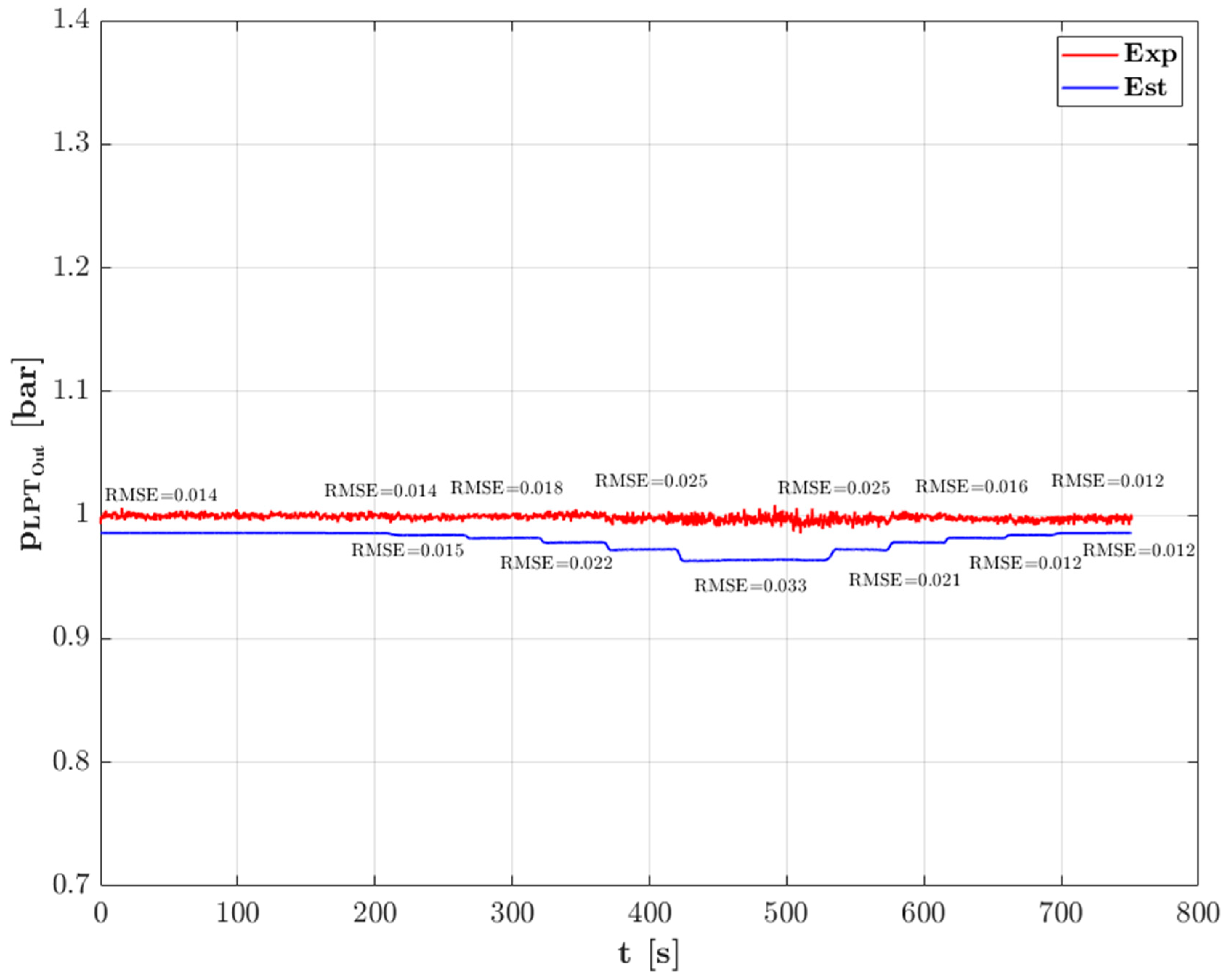
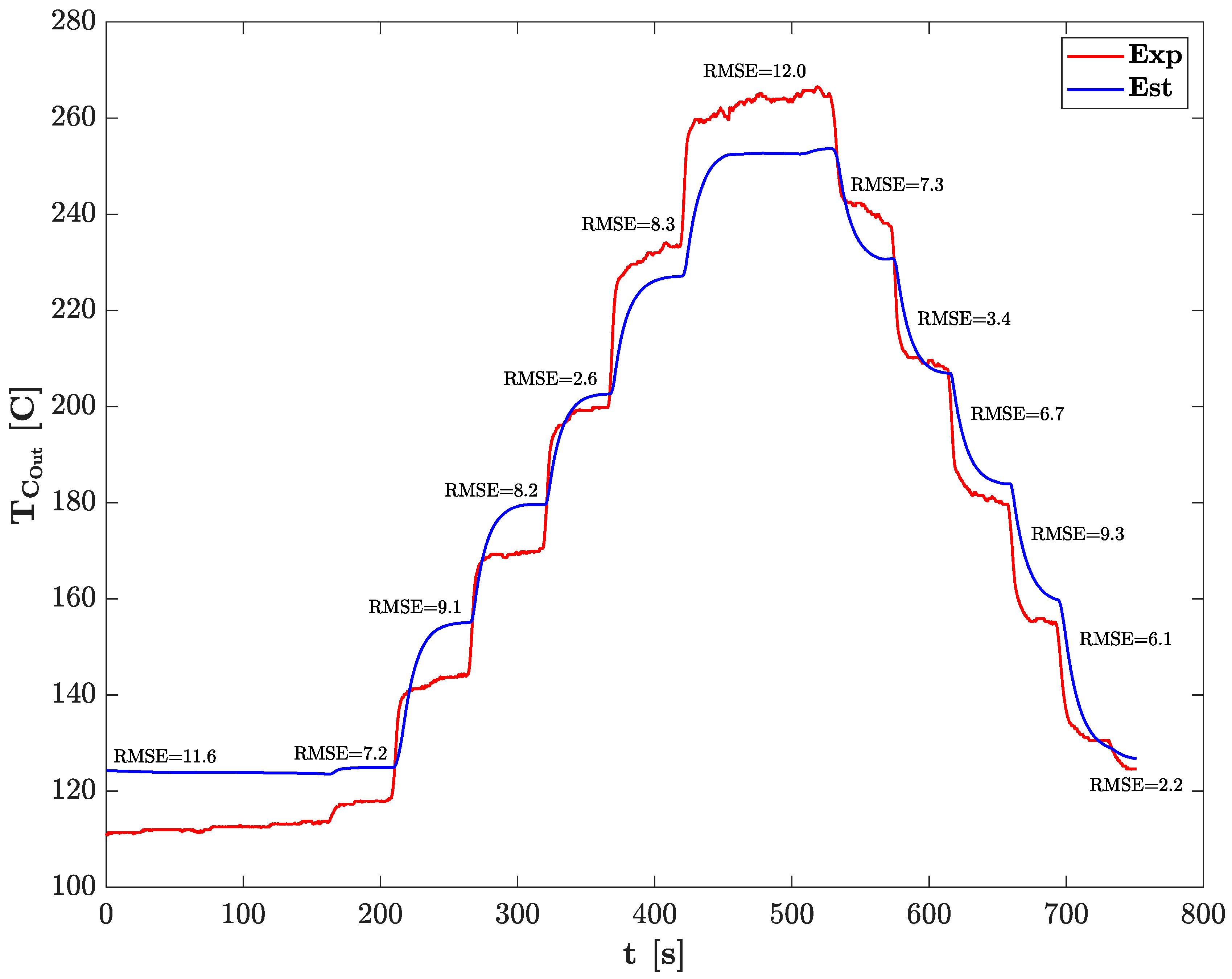


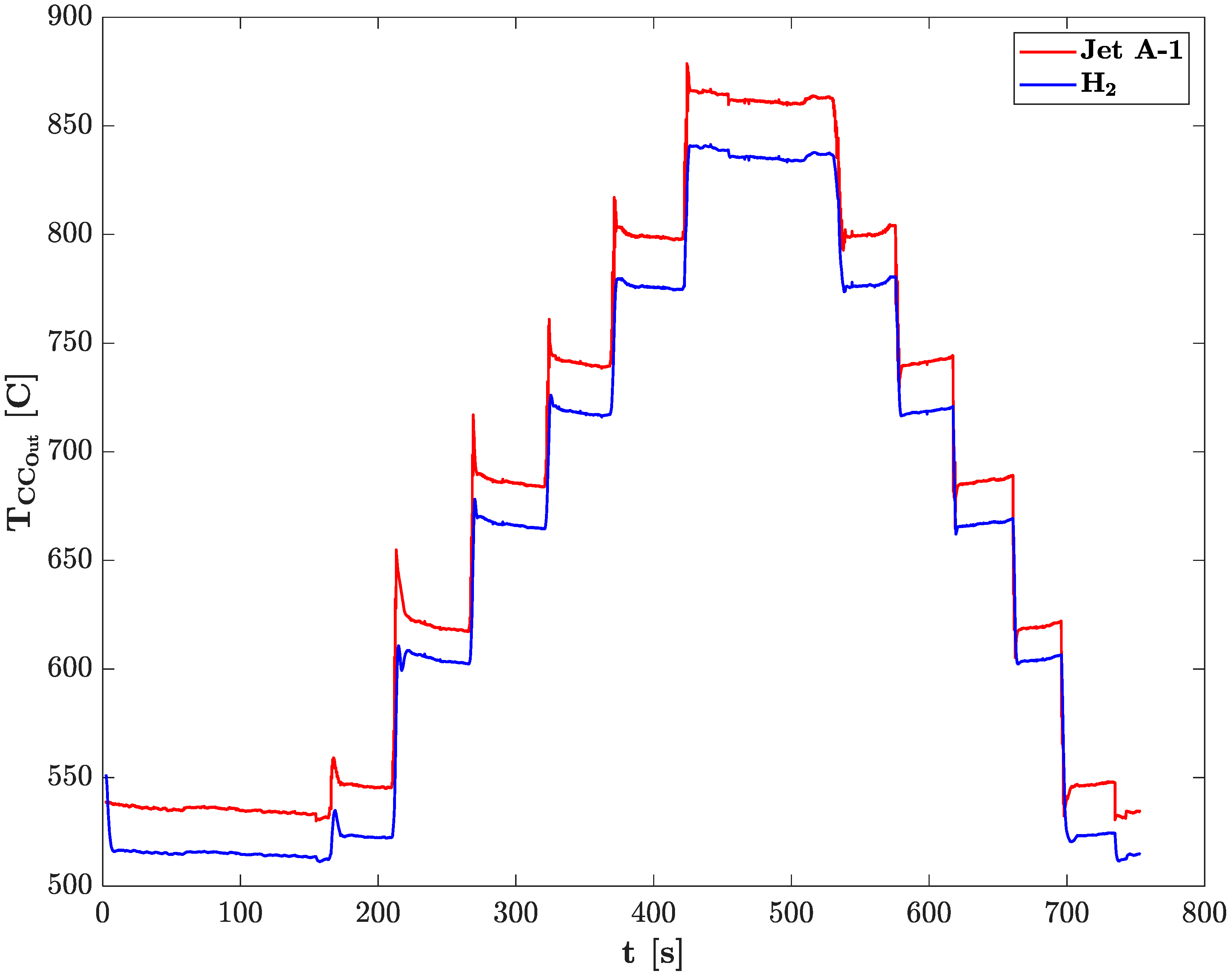
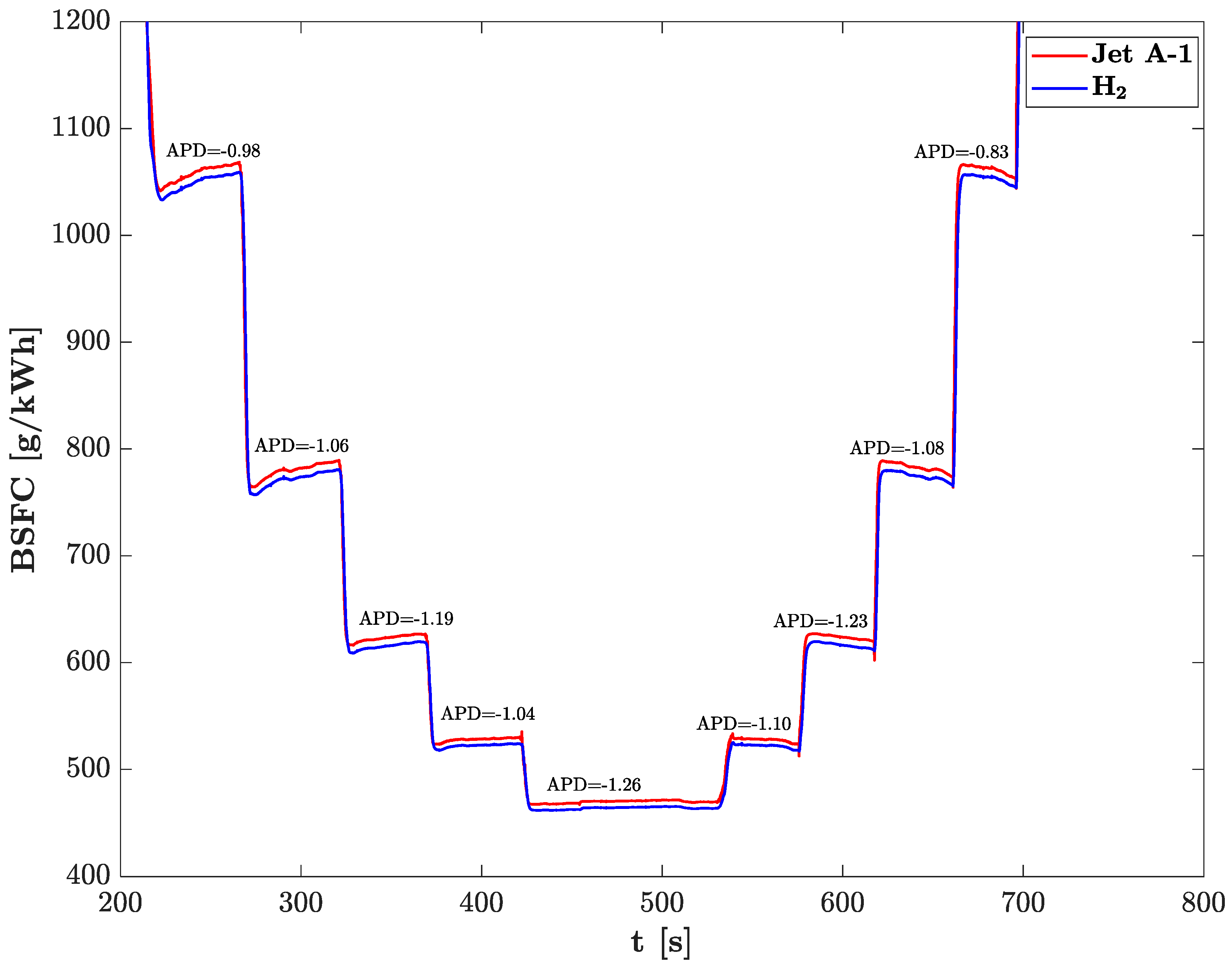
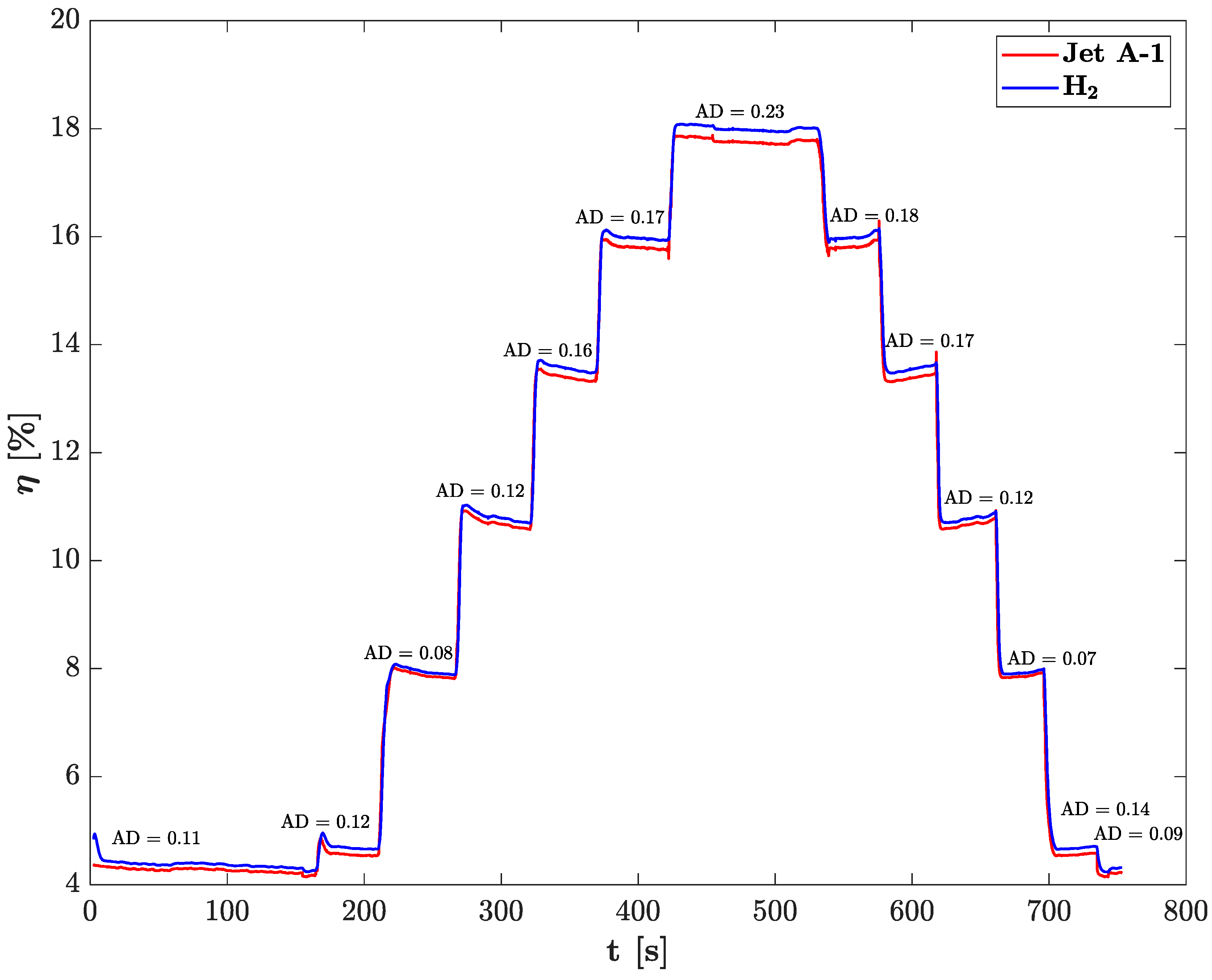
| Engine Parameter | Values |
|---|---|
| Engine Type | Double-shaft turbine engine |
| Compressor Type | 6 axial stages and 1 centrifugal stage |
| Gas generator Turbine Type | 2 axial stages |
| Power Turbine Type | 2 axial stages |
| Combustion Chamber Type | Single Body Three-staged with Reverse Flow |
| Maximum Torque | 338 Nm @ Take-Off |
| Maximum Power | 201 kW @ Maximum Continuous Power at Sea Level |
| Injection System | Single–entry Dual–orifice Type Unit |
| Control System | Hydromechanical |
| Compression ratio | 6.2:1 |
| Gas Generator Shaft Speed at 100% | 51,120 rpm |
| Output Shaft Speed at 100% | 6000 rpm |
| Weight | 64 kg @ Dry |
| Dimensions | 1026 × 483 × 572 mm |
| Fuel | Molar Weight, M [kg*kmol−1] | Lower Heating Value, LHV [kJ*kg−1] | Density [kg*m−3] |
|---|---|---|---|
| Jet A-1 | 167.314 | 43.28 | 802.8 |
| Hydrogen | 2.016 | 119.45 | 0.083 |
[W*m−2*C] | [W*m−2*C] | [W*m−2*K−4] | [-] | [mm] | [mm] | [g/cm3] | [J*g−1*C−1] |
|---|---|---|---|---|---|---|---|
| 500 | 500 | 5.67 × 10−8 | 0.7 | 3.25 | 10.00 | 8.60 | 0.50 |
| External Conditions | Compressor Outlet | GG Shaft | CC Outlet | HPT Outlet | LPT Outlet | Brake | |
|---|---|---|---|---|---|---|---|
| Thermodynamic parameters | p, T | p, T | - | p | p, T | p | - |
| Other parameters | - | - | RPM | - | - | λ | Poutput |
| MPD (%) | APD (%) | |
|---|---|---|
| Air mass flow (kg\s) | +8.0% | +2.3% |
| Total mass flow (kg\s) | +7.1% | +1.5% |
| GGS rotational speed (rpm) | +5.2% | +1.3% |
| β compressor (-) | +8.8% | +2.3% |
| β HPT (-) | +7.5% | +1.8% |
| β LPT (-) | −4.5% | −0.4% |
| Cp after the combustion (J\K*kg) | +3.5% | +1.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magnani, M.; Silvagni, G.; Ravaglioli, V.; Ponti, F. 0-D Dynamic Performance Simulation of Hydrogen-Fueled Turboshaft Engine. Aerospace 2024, 11, 816. https://doi.org/10.3390/aerospace11100816
Magnani M, Silvagni G, Ravaglioli V, Ponti F. 0-D Dynamic Performance Simulation of Hydrogen-Fueled Turboshaft Engine. Aerospace. 2024; 11(10):816. https://doi.org/10.3390/aerospace11100816
Chicago/Turabian StyleMagnani, Mattia, Giacomo Silvagni, Vittorio Ravaglioli, and Fabrizio Ponti. 2024. "0-D Dynamic Performance Simulation of Hydrogen-Fueled Turboshaft Engine" Aerospace 11, no. 10: 816. https://doi.org/10.3390/aerospace11100816
APA StyleMagnani, M., Silvagni, G., Ravaglioli, V., & Ponti, F. (2024). 0-D Dynamic Performance Simulation of Hydrogen-Fueled Turboshaft Engine. Aerospace, 11(10), 816. https://doi.org/10.3390/aerospace11100816









