Resource Allocation Approach of Avionics System in SPO Mode Based on Proximal Policy Optimization
Abstract
1. Introduction
2. System Model and Problem Description
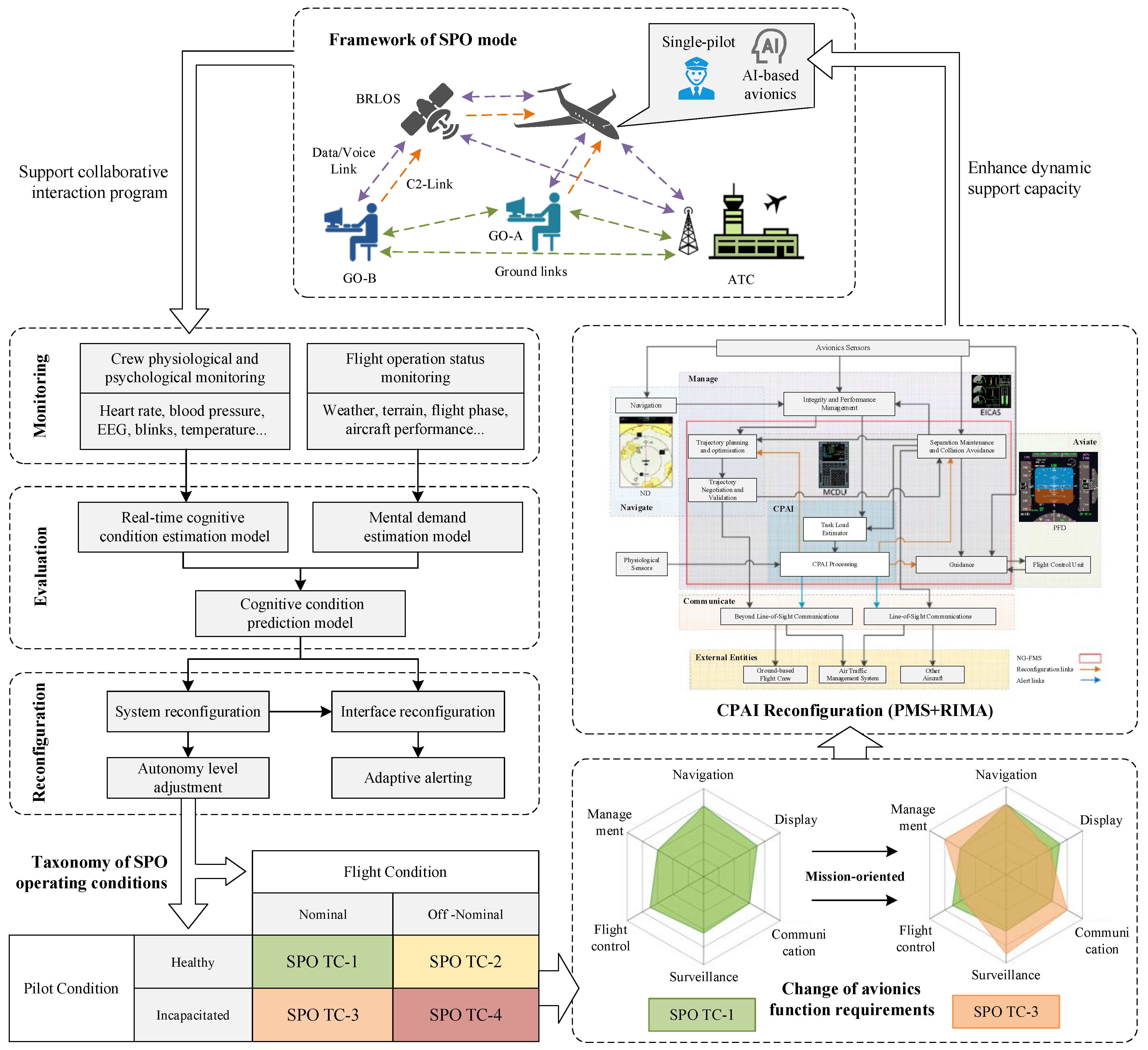
2.1. Resource Allocation Framework for Avionics System in SPO Mode
2.2. Resource Allocation Model for Avionics System in SPO Mode
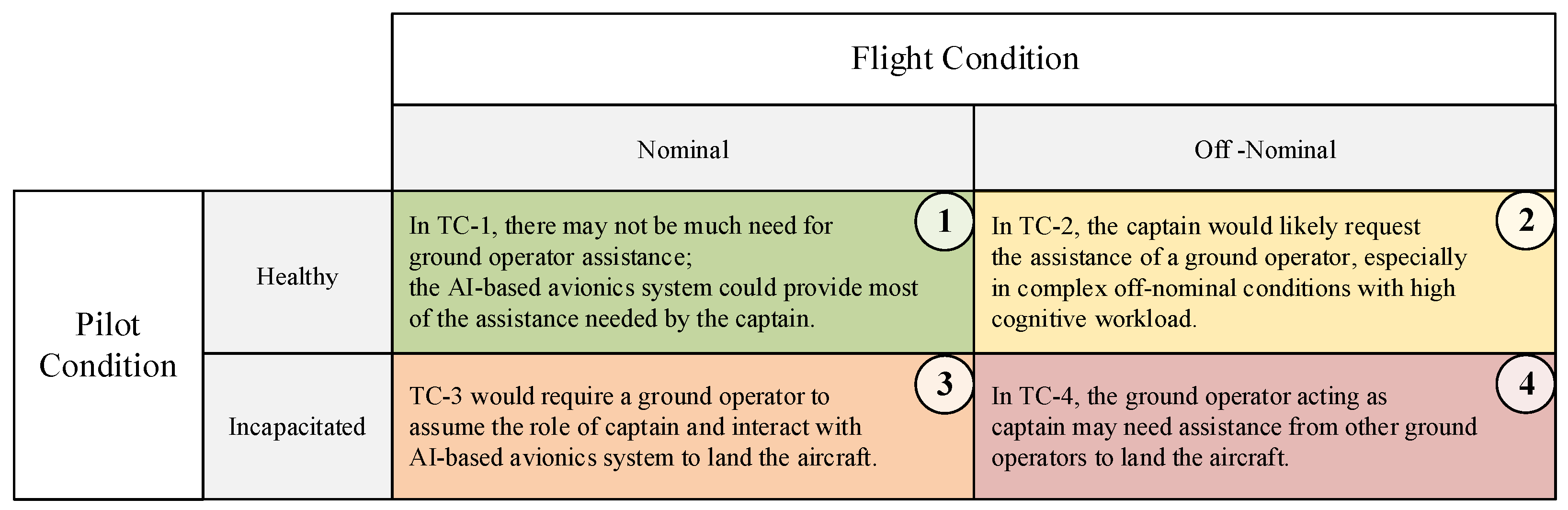
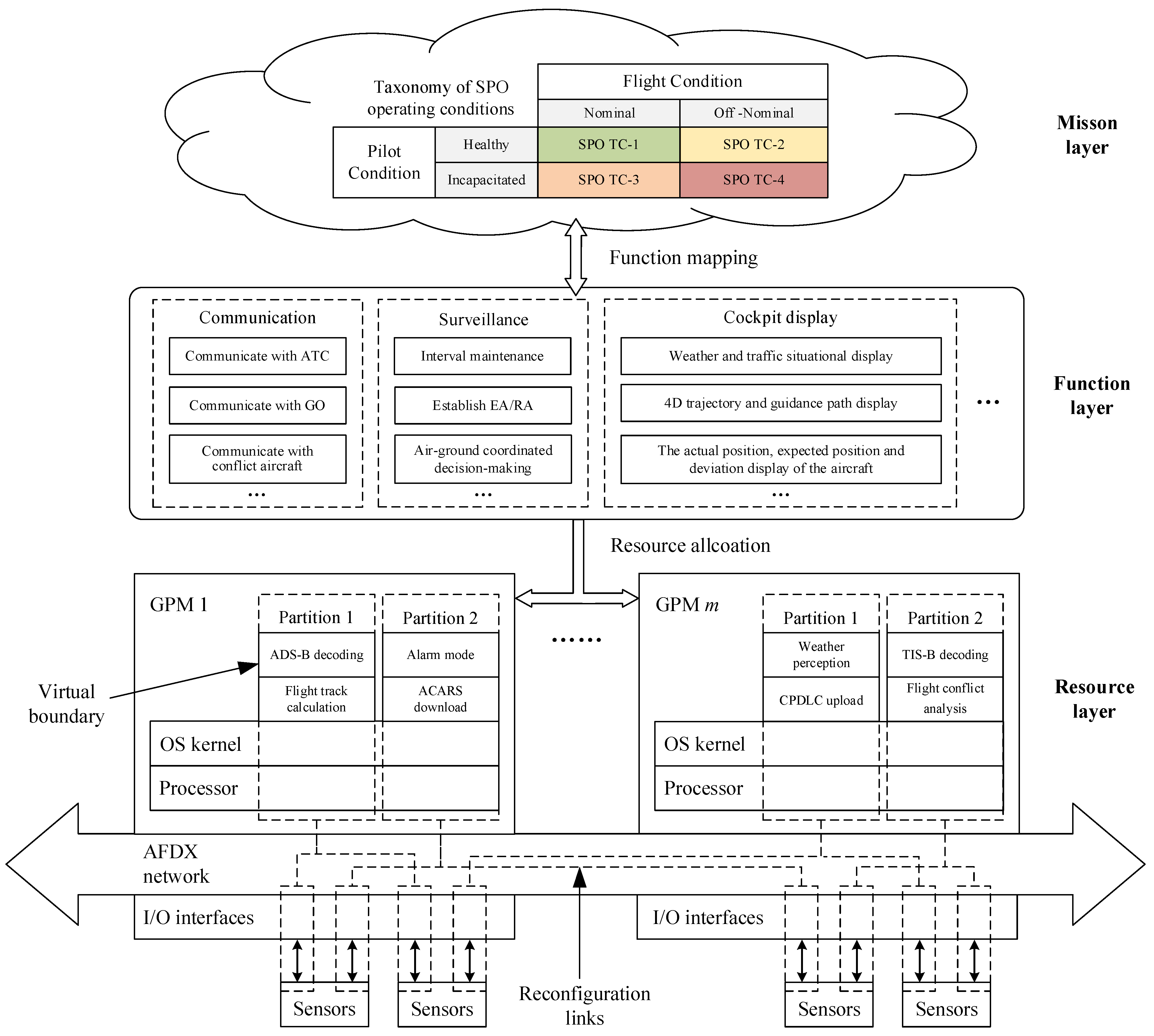
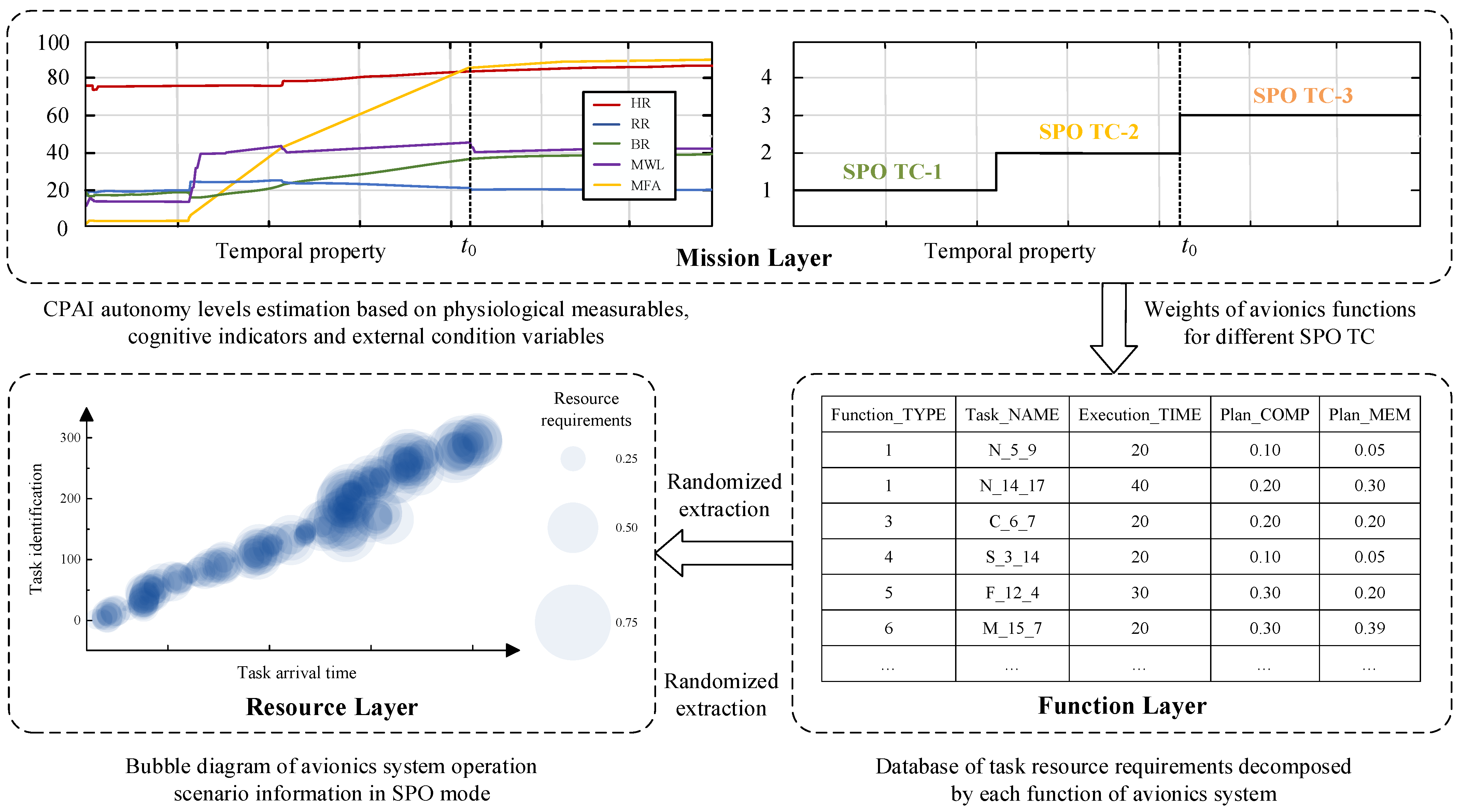
2.2.1. Hierarchical Architecture of Avionics System
- (1)
- Mission layer
- (2)
- Function layer
- (3)
- Resource layer
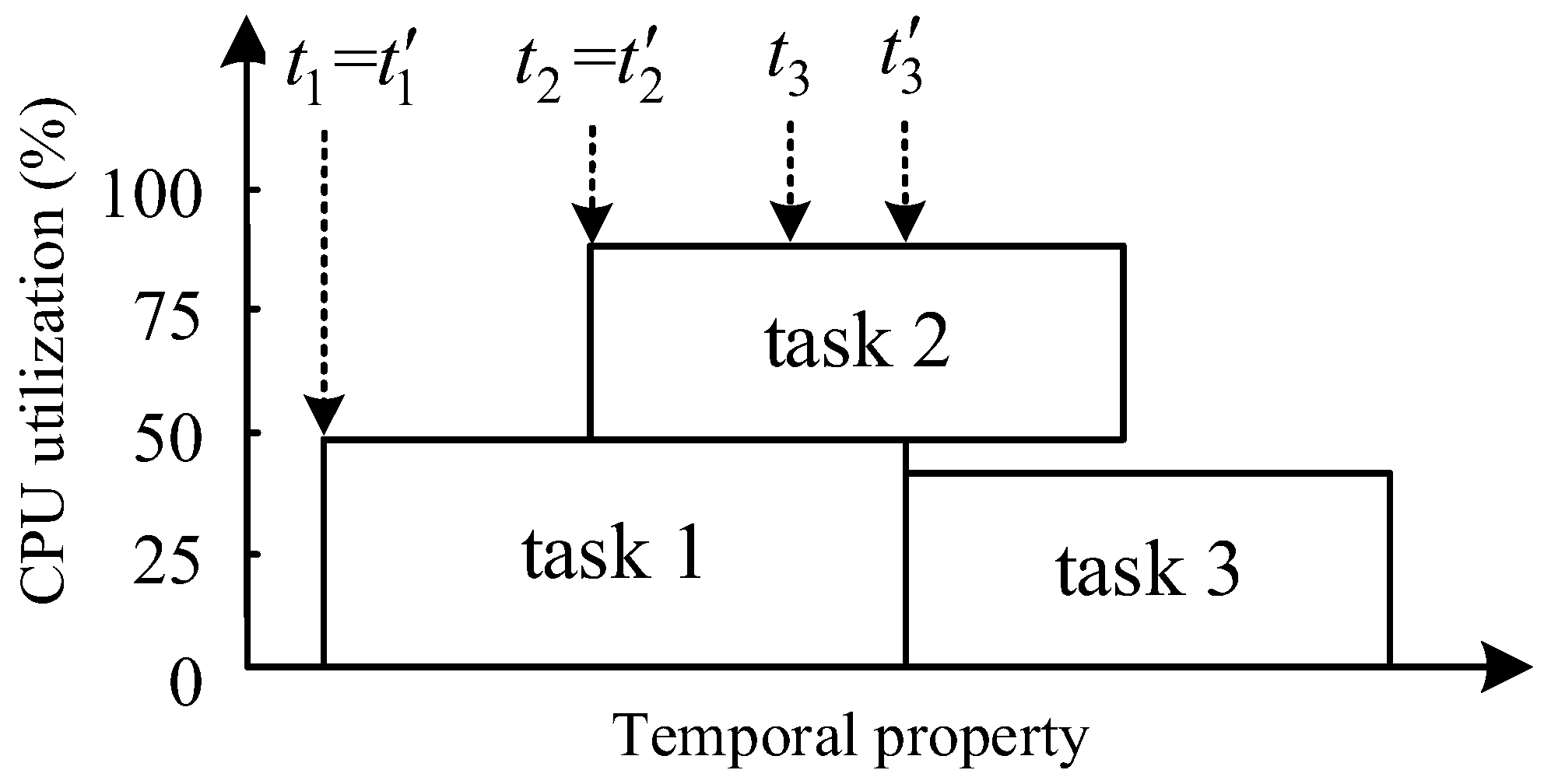
2.2.2. Resource Allocation Mechanism Based on RIMA
2.2.3. Resource Allocation Constraints and Optimization Indicators
- (1)
- Resource allocation constraints
- (2)
- Resource allocation optimization indicators
- (3)
- Objective optimization function
3. Problem Transformation and Algorithm Design
3.1. MDP for Avionics Resource Allocation in SPO Mode
3.1.1. State Space
3.1.2. Action Space
3.1.3. Reward Function
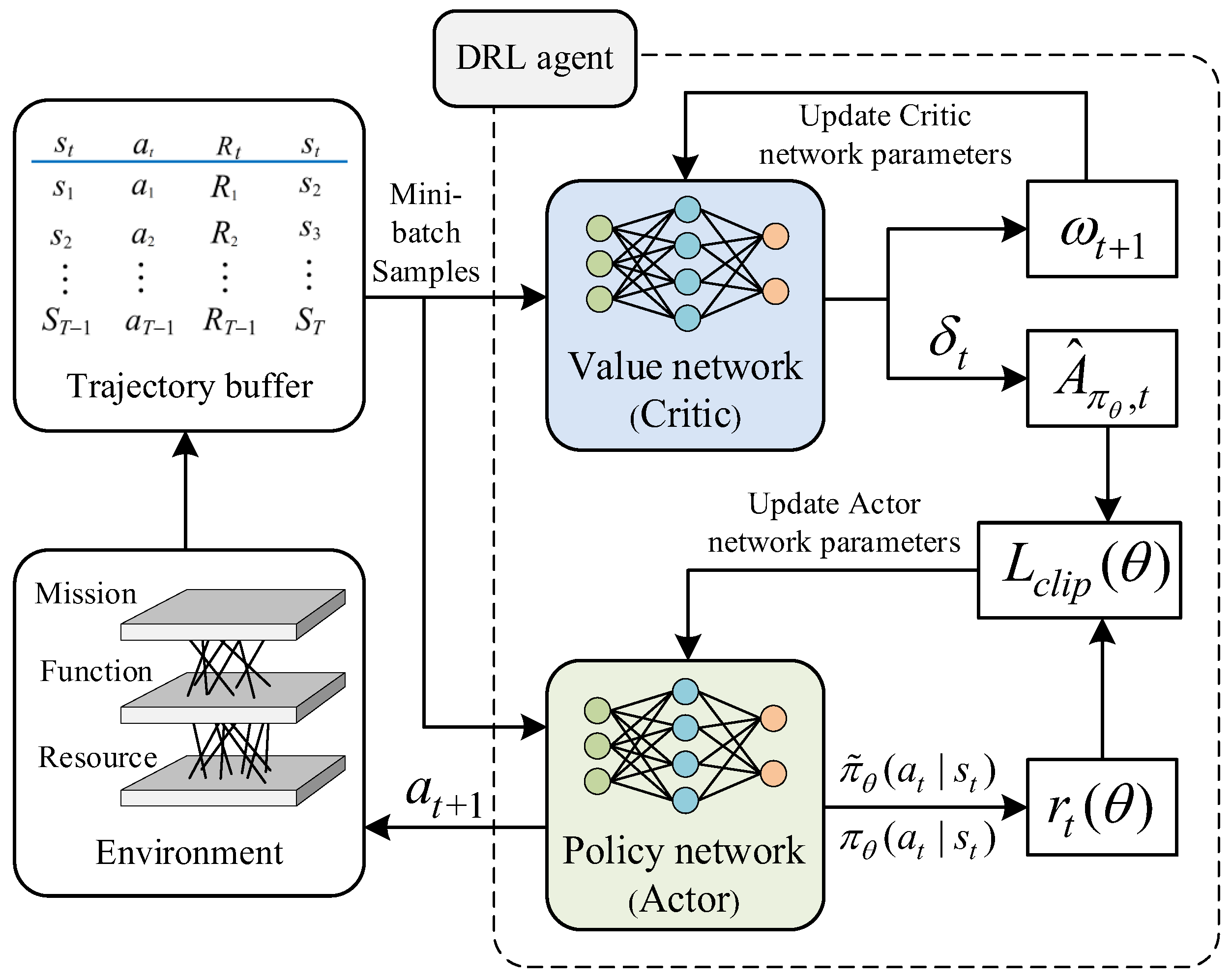
3.2. PPO Algorithm Network Model
3.3. Avionics Resource Allocation Based on the PPO Algorithm
| Algorithm 1. DRL with PPO for avionics resource allocation |
| Input: System parameters, state space, action space, discount factor, learning rate. Run: Initialize the hyperparameter and the network parameter of the PPO algorithm Generate a simulated avionics resource allocation environment for training according to predefined criteria For iteration = 1, 2, …, do Collect trajectory data to replay buffer D For timestep = 1 to T do For task = 1 to K do Observe the state st of the resource allocation environment Run policy to choose an action at based on the observed state The DRL agent receives an immediate reward rt and the next state of the st+1 Input the agent’s state variables into the critic network to estimate the advantage function End for End for Update θ by a gradient method to optimize the loss function Replace the parameters of the actor network End for Output: Resource allocation scheme for avionics system in SPO mode |
4. Simulation Results and Analysis
4.1. Simulation Settings
4.1.1. Experimental Parameters
4.1.2. Operation Scenario Information
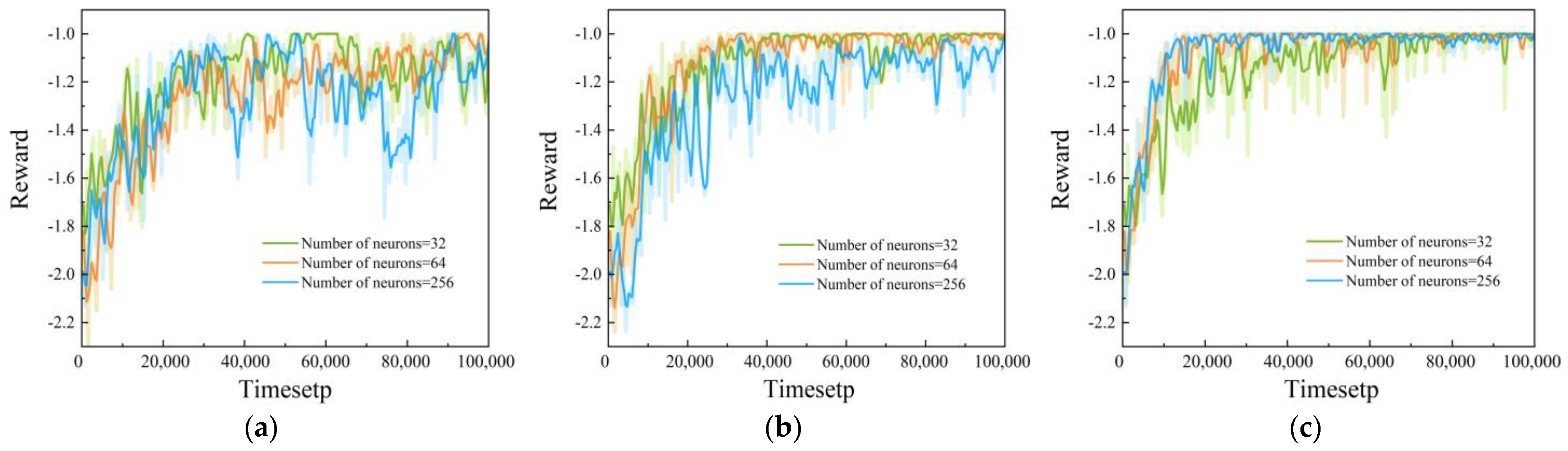
4.1.3. Hyperparameters
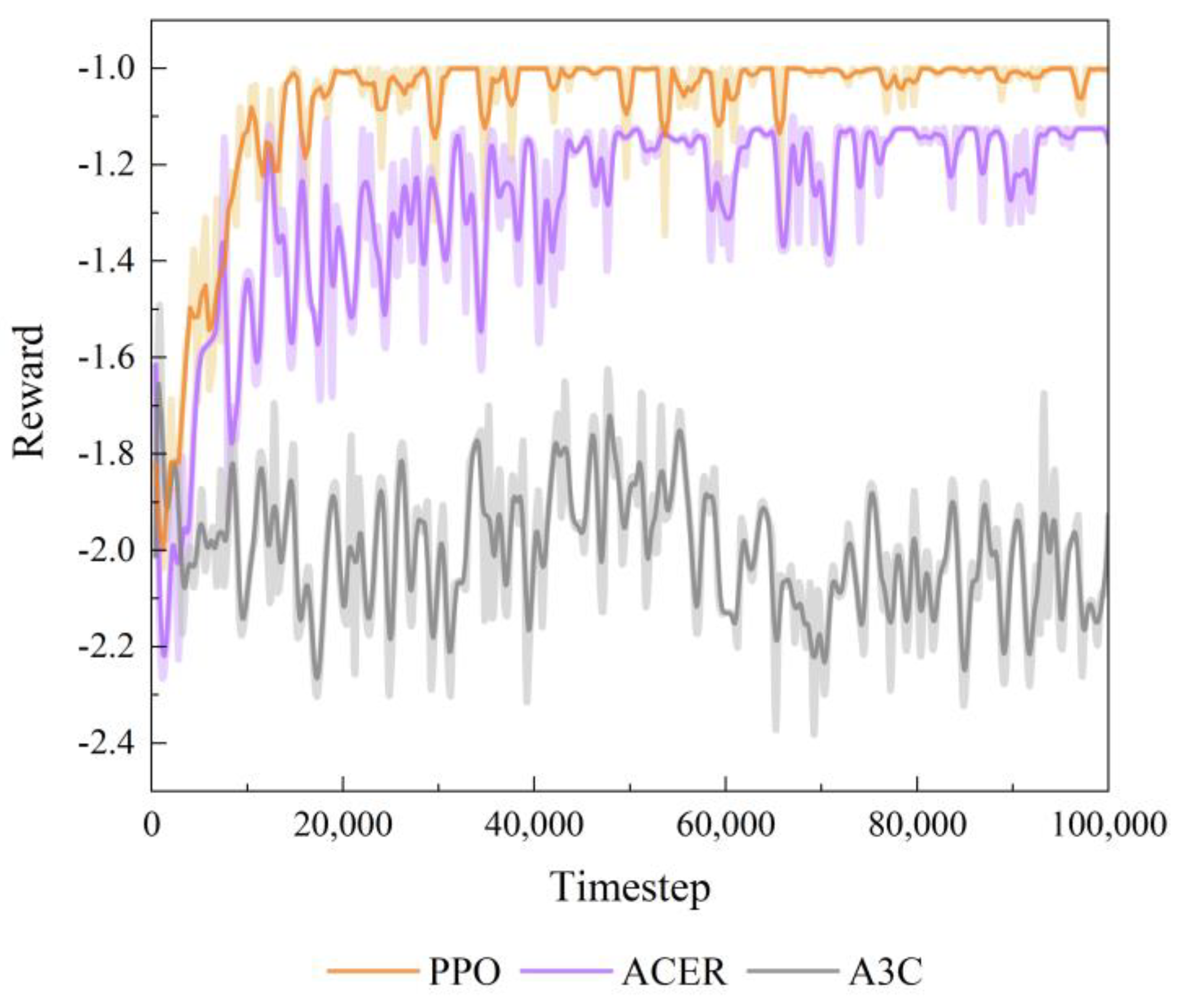
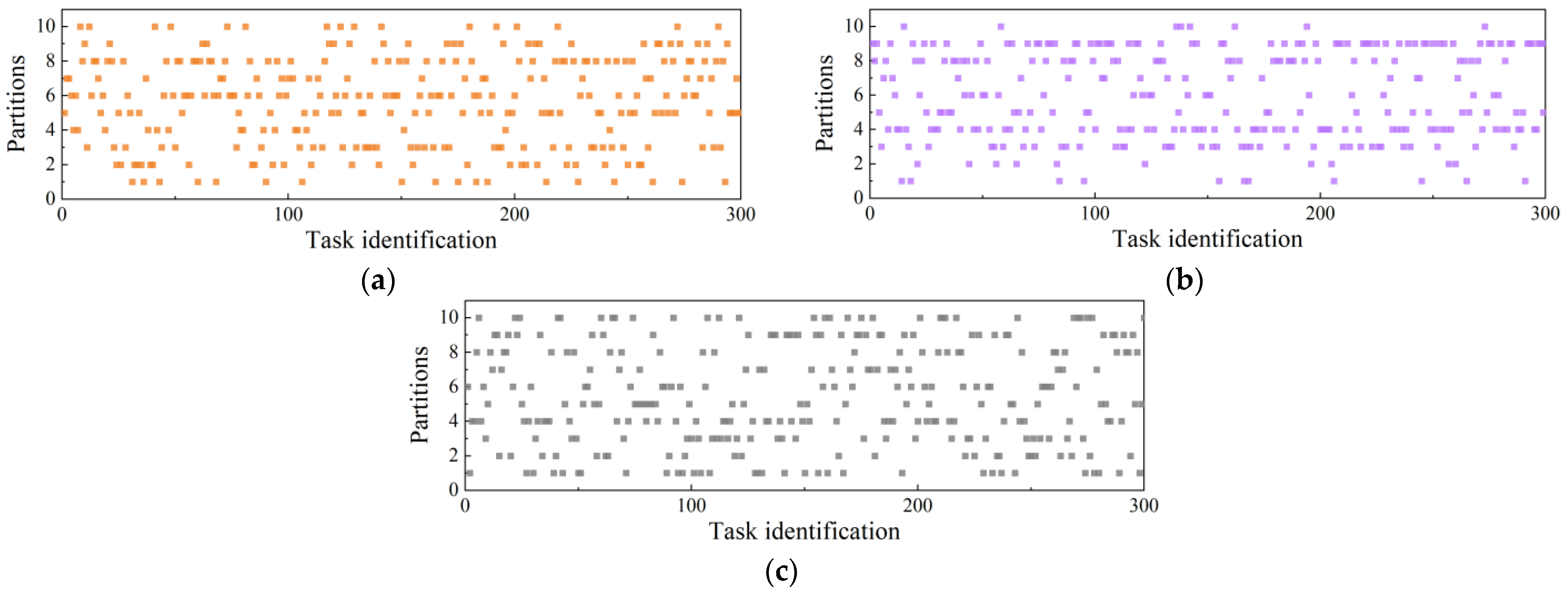
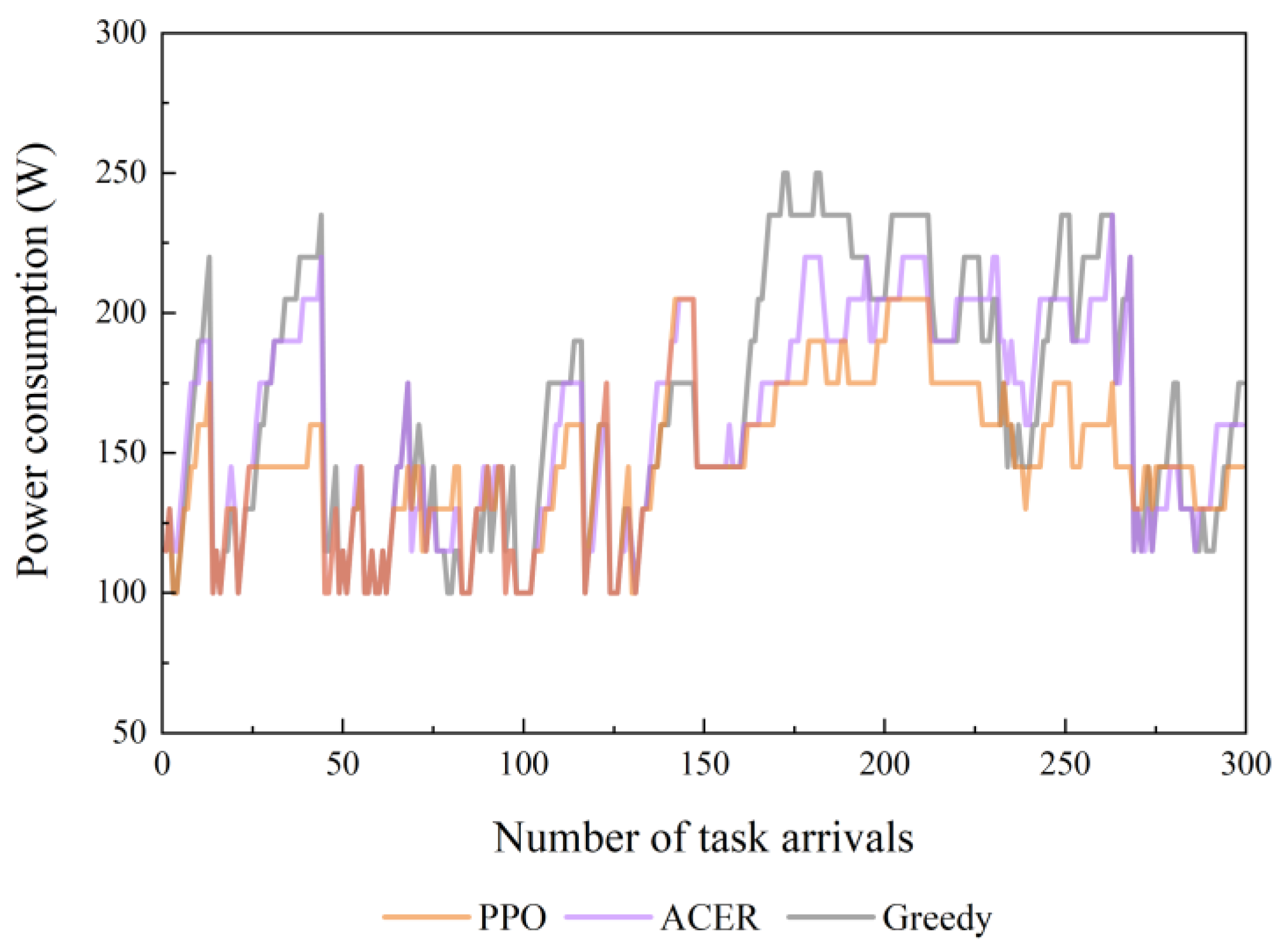
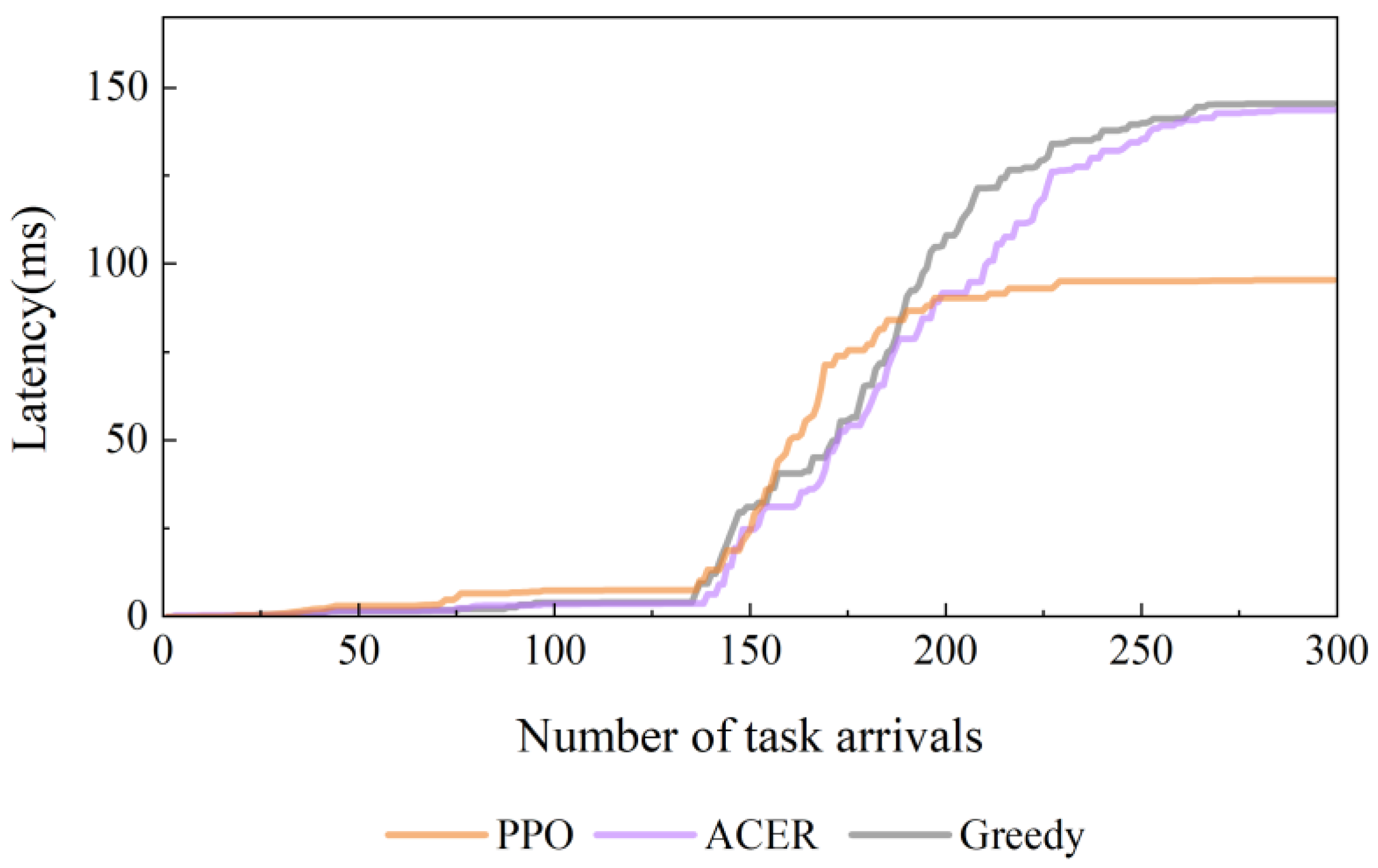
4.2. Simulation Experiments for Different Comparative Methods
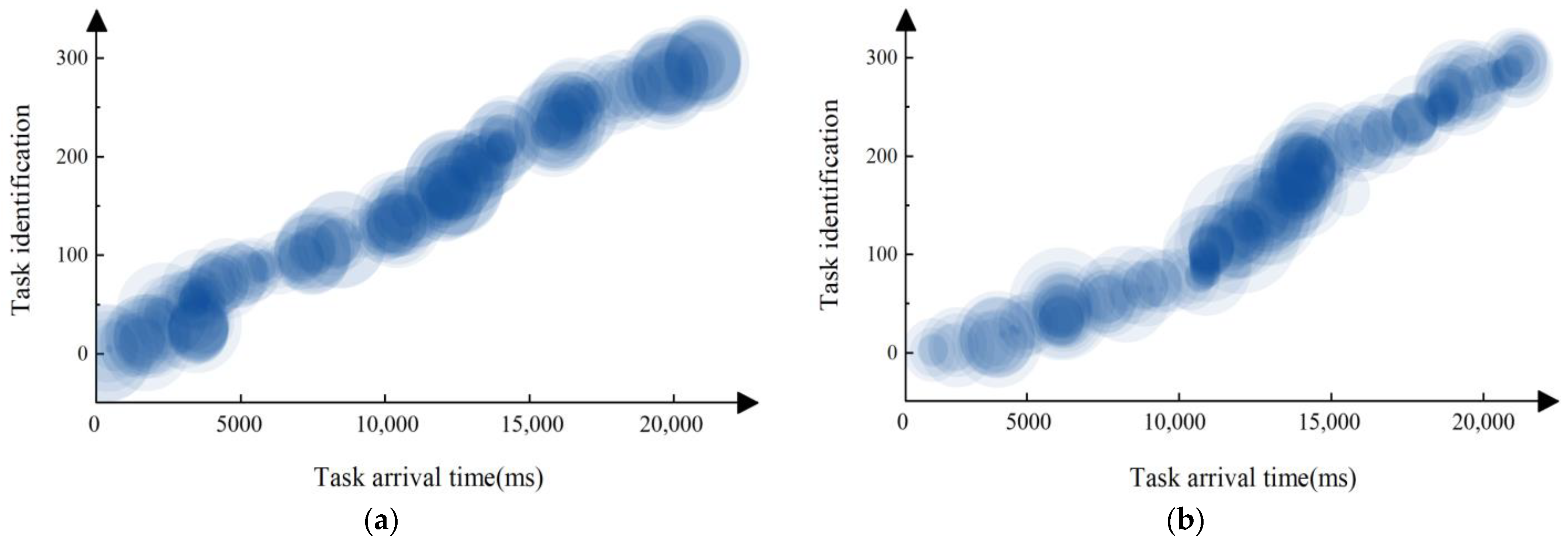
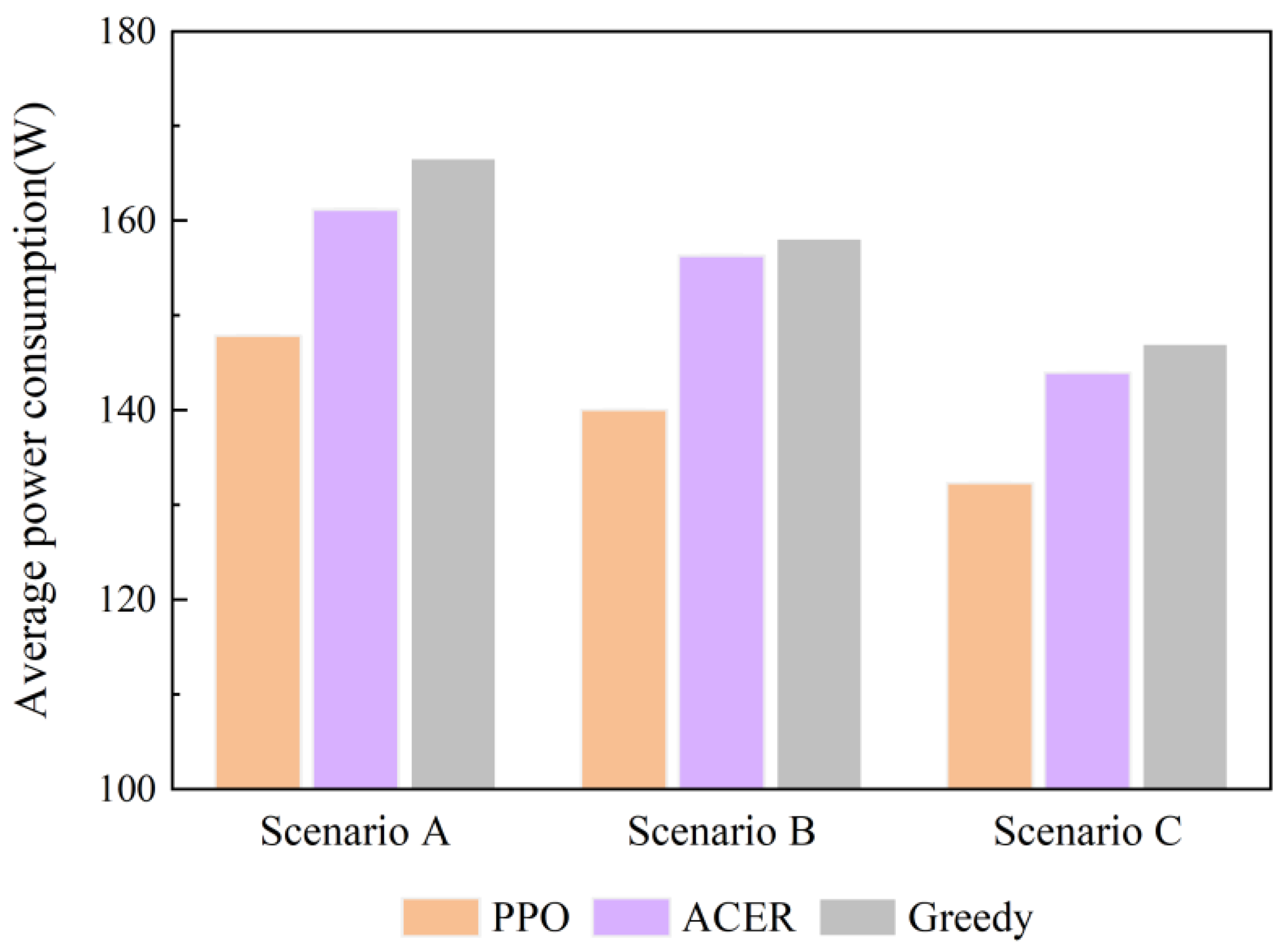
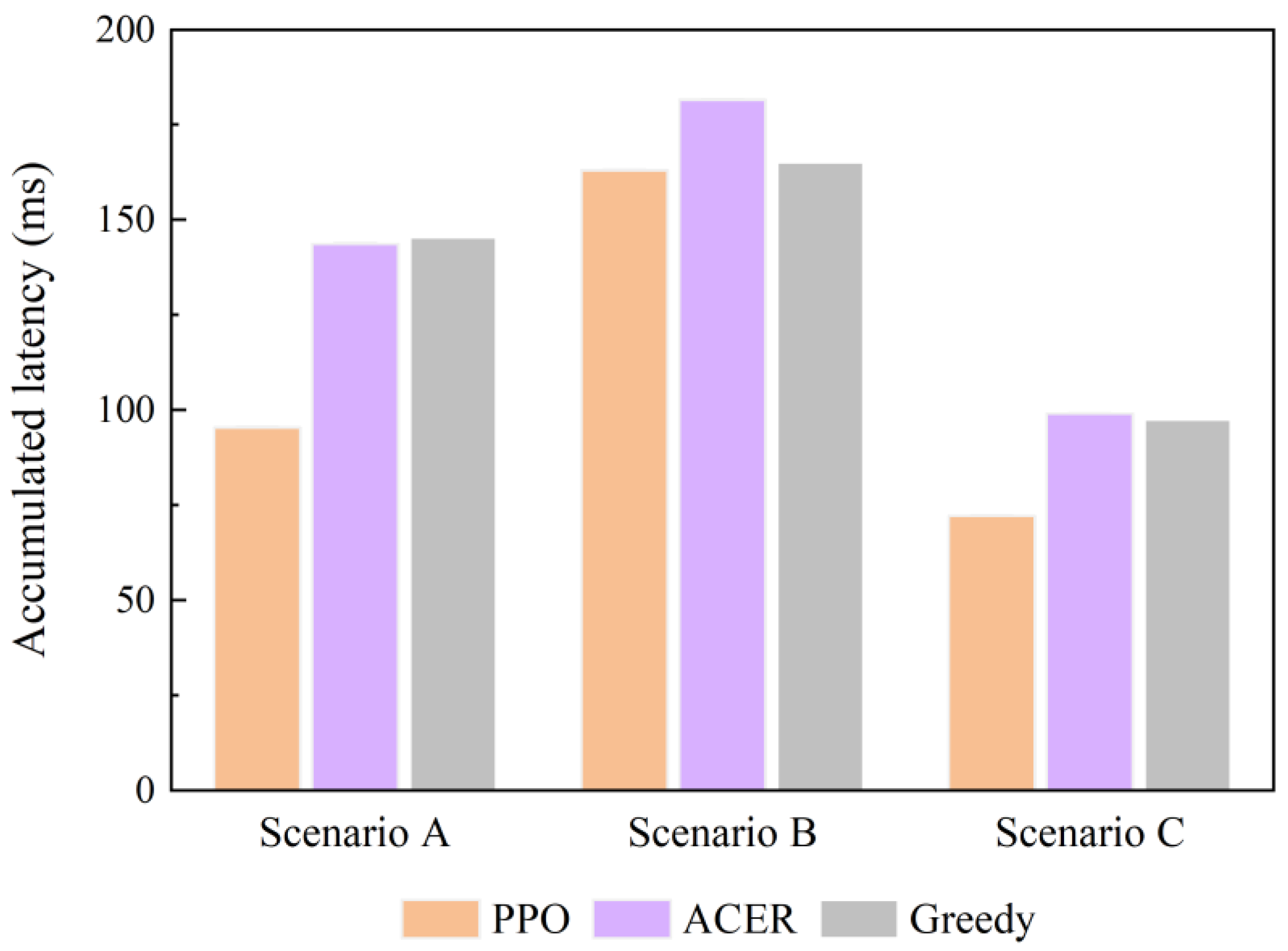
4.3. Simulation Experiments for Different Comparative Operation Scenarios
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPO | Single-Pilot Operations |
| GO | Ground Operators |
| TCO | Two-Crew Operations |
| IMA | Integrated Modular Avionics |
| RIMA | Reconfigurable Integrated Modular Avionics |
| HAT | Human-Autonomy Teaming |
| VPA | Virtual Pilot Assistance |
| V-CoP | Virtual Co-Pilot |
| DRL | Deep Reinforcement Learning |
| PPO | Proximal Policy Optimization |
| TC | Taxonomy Conditions |
| CPAI | Cognitive Pilot-Aircraft Interface |
| GPMs | General Processing Modules |
| FCFS | First-Come-First-Served |
| MDP | Markov Decision Process |
| A3C | Asynchronous Advantage Actor Critic |
| ACER | Actor Critic with Experience Replay |
| TRPO | Trust Region Policy Optimization |
References
- Wang, G.; Li, M.; Wang, M.; Ding, D. A systematic literature review of human-centered design approach in single pilot operations. Chin. J. Aeronaut. 2023, 36, 1–23. [Google Scholar] [CrossRef]
- Gore, B.F.; Wolter, C. A task analytic process to define future concepts in aviation. In Proceedings of the Digital Human Modeling. In Proceedings of the Applications in Health, Safety, Ergonomics and Risk Management: 5th International Conference, Heraklion, Crete, Greece, 22–27 June 2014; pp. 236–246.
- Stanton, N.A.; Harris, D.; Starr, A. The future flight deck: Modelling dual, single and distributed crewing options. Appl. Ergon. 2016, 53, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhong, K.L.; Luo, Y.; Miao, W. Key technology and future development of regional airliner. Acta Aeronaut. Astronaut. Sin. 2023, 44, 156–180. [Google Scholar]
- Bilimoria, K.D.; Johnson, W.W.; Schutte, P.C. Conceptual framework for single pilot operations. In Proceedings of the Proceedings of the international conference on human-computer interaction in aerospace, New York, USA, 30 July–1 August 2014; pp. 1–8.
- Zaeske, W.M.M.; Brust, C.-A.; Lund, A.; Durak, U. Towards Enabling Level 3A AI in Avionic Platforms. In Proceedings of the Software Engineering 2023 Workshops, Paderborn, Germany, 2 February 2023; pp. 189–207. [Google Scholar]
- Gaska, T.; Watkin, C.; Chen, Y. Integrated modular avionics-past, present, and future. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 12–23. [Google Scholar] [CrossRef]
- Lukić, B.; Ahlbrecht, A.; Friedrich, S.; Durak, U. State-of-the-Art Technologies for Integrated Modular Avionics and the Way Ahead. In Proceedings of the IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–10. [Google Scholar]
- Omiecinski, T.; Johnson, D.; Omiecinski, T.; Johnson, D. Autonomous dynamic reconfiguration of integrated avionics systems. In Proceedings of the Guidance, Navigation, and Control Conference, New Orleans, LA, USA, 11–13 August 1997; pp. 1504–1514. [Google Scholar]
- Ziakkas, D.; Pechlivanis, K.; Flores, A. Artificial intelligence (AI) implementation in the design of single pilot operations commercial airplanes. In Proceedings of the 14th International Conference on Applied Human Factors and Ergonomics, San Francisco, CA, USA, 20–24 July 2023; Volume 69, pp. 856–861. [Google Scholar]
- Sprengart, S.M.; Neis, S.M.; Schiefele, J. Role of the human operator in future commercial reduced crew operations. In Proceedings of the IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–10. [Google Scholar]
- Lim, Y.; Bassien-Capsa, V.; Ramasamy, S.; Liu, J.; Sabatini, R. Commercial airline single-pilot operations: System design and pathways to certification. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 4–21. [Google Scholar] [CrossRef]
- Lim, Y.; Gardi, A.; Ramasamy, S.; Sabatini, R. A virtual pilot assistant system for single pilot operations of commercial transport aircraft. In Proceedings of the 17th Australian International Aerospace Congress (AIAC), Melbourne, Australia, 26–28 February 2017; pp. 26–28. [Google Scholar]
- Tokadlı, G.; Dorneich, M.C.; Matessa, M. Development approach of playbook interface for human-autonomy teaming in single pilot operations. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Seattle, WA, USA, 28 October–1 November 2019; Sage: Los Angeles, CAS, USA, 2019; pp. 357–361. [Google Scholar]
- Tokadlı, G.; Dorneich, M.C.; Matessa, M. Evaluation of playbook delegation approach in human-autonomy teaming for single pilot operations. Int. J. Hum.–Comput. Interact. 2021, 37, 703–716. [Google Scholar] [CrossRef]
- Li, F.; Feng, S.; Yan, Y.; Lee, C.-H.; Ong, Y.S. Virtual Co-Pilot: Multimodal Large Language Model-enabled Quick-access Procedures for Single Pilot Operations. arXiv 2024, arXiv:2403.16645. [Google Scholar]
- Montana, D.; Hussain, T.; Vidver, G. A Genetic-Algorithm-Based Reconfigurable Scheduler; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Zhao, C.; Zhang, W.; Dong, F.; Dai, J.; Dong, L. Research on Resource Allocation Method of Integrated Avionics System considering Fault Propagation Risk. Int. J. Aerosp. Eng. 2022, 2022, 8652818. [Google Scholar] [CrossRef]
- Xing, P.P. Dynamic Reconfiguration Strategy and Reliability Model Analysis of Integrated Avionics System. Ph.D. Thesis, Civil Aviation University of China, Tianjin, China, 2020. [Google Scholar]
- Zhang, T.; Chen, J.; Lv, D.; Liu, Y.; Zhang, W.; Ma, C. Automatic Generation of Reconfiguration Blueprints for IMA Systems Using Reinforcement Learning. IEEE Embed. Syst. Lett. 2021, 13, 182–185. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, W.; Dai Ling, C.; Wang, L.; Wei, Q. Integrated Modular Avionics System Reconstruction Method Based on Sequential Game Multi-Agent Reinforcement Learning. Acta Electron. Sin. 2022, 50, 954–966. [Google Scholar]
- Li, D.; Tian, Y.; Zhao, C.; Zou, J. Deep Reinforcement Learning-Based Constrained Optimal Reconfiguration Scheme for Integrated Modular Avionics System. In Proceedings of the 3rd International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Nanjing, China, 21–23 July 2023; pp. 388–391. [Google Scholar]
- Dong, L.; Chen, H.; Chen, X.; Zhao, C. Distributed multi-agent coalition task allocation strategy for single pilot operation mode based on DQN. Acta Aeronaut. Astronaut. Sin. 2023, 44, 180–195. [Google Scholar]
- Neis, S.M.; Klingauf, U.; Schiefele, J. Classification and review of conceptual frameworks for commercial single pilot operations. In Proceedings of the IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–8. [Google Scholar]
- Liu, J.; Gardi, A.; Ramasamy, S.; Lim, Y.; Sabatini, R. Cognitive pilot-aircraft interface for single-pilot operations. Knowl.-Based Syst. 2016, 112, 37–53. [Google Scholar] [CrossRef]
- Yin, J.; Zhu, Z. Flight Autonomy Impact to the Future Avionics Architecture. In Proceedings of the IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–7. [Google Scholar]
- Wang, M.; Luo, Y.; Huang, K.; Zhao, P.; Wang, G. Optimization and verification of single pilot operations model for commercial aircraft based on biclustering method. Chin. J. Aeronaut. 2023, 36, 286–305. [Google Scholar] [CrossRef]
- Tang, M.; Xiahou, T.; Liu, Y. Mission performance analysis of phased-mission systems with cross-phase competing failures. Reliab. Eng. Syst. Saf. 2023, 234, 109174. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, Y.; Wang, M.; Zhong, G.; Xiao, G.; Wang, G. DFCluster: An efficient algorithm to mine maximal differential biclusters for single pilot operations task synthesis safety analysis. Chin. J. Aeronaut. 2022, 35, 400–418. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, J.; Ma, S.; Zong, J.; Shen, J.; Zhu, H. Review of key technologies for avionics systems integration on large passenger aircraft. Acta Aeronaut. Astronaut. Sin. 2024, 45, 253–295. [Google Scholar]
- He, F. Theory and Approach to Avionics System Integrated Scheduling; Tsinghua University Press: Beijing, China, 2017. [Google Scholar]
- Zhao, C.; He, F.; Li, H.; Wang, P. Dynamic reconfiguration method based on effectiveness for advanced fighter avionics system. Acta Aeronaut. Astronaut. Sin. 2020, 41, 355–365. [Google Scholar]
- Wang, P.; Liu, J.; Dong, L.; Zhao, C. Task oriented DIMA dynamic reconfiguration strategy for civil aircraft. Syst. Eng. Electron. 2021, 43, 1618–1627. [Google Scholar]
- Li, J.P.; Wang, Y.; Bai, Y. Design and Implementation for Adaptive Scheduling Strategy of AFDX Virtual Link. Comput. Meas. Control. 2012, 20, 1986–1988. [Google Scholar]
- Li, P.; Xiao, Z.; Wang, X.; Huang, K.; Huang, Y.; Gao, H. EPtask: Deep reinforcement learning based energy-efficient and priority-aware task scheduling for dynamic vehicular edge computing. IEEE Trans. Intell. Veh. 2023, 9, 1830–1846. [Google Scholar] [CrossRef]
- Mnih, V. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar]
- Wang, Z.; Bapst, V.; Heess, N.; Mnih, V.; Munos, R.; Kavukcuoglu, K.; De Freitas, N. Sample efficient actor-critic with experience replay. arXiv 2016, arXiv:1611.01224. [Google Scholar]
- Han, S.-Y.; Liang, T. Reinforcement-learning-based vibration control for a vehicle semi-active suspension system via the PPO approach. Appl. Sci. 2022, 12, 3078. [Google Scholar] [CrossRef]
- Vince, A. A framework for the greedy algorithm. Discret. Appl. Math. 2002, 121, 247–260. [Google Scholar] [CrossRef]
| Experimental Parameters | Value |
|---|---|
| Learning rate α | 1 × 10−4 |
| Discount factor γ | 0.99 |
| Number of total timesteps T | 1 × 105 |
| Number of hidden layers | 2 |
| Number of neurons in each hidden layer | 64 |
| Number of CPMs M | 4 |
| Number of partitions N | 10 |
| 10 W | |
| 25 W | |
| Number of tasks K | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Liu, J.; Sun, Z.; Chen, X.; Wang, P. Resource Allocation Approach of Avionics System in SPO Mode Based on Proximal Policy Optimization. Aerospace 2024, 11, 812. https://doi.org/10.3390/aerospace11100812
Dong L, Liu J, Sun Z, Chen X, Wang P. Resource Allocation Approach of Avionics System in SPO Mode Based on Proximal Policy Optimization. Aerospace. 2024; 11(10):812. https://doi.org/10.3390/aerospace11100812
Chicago/Turabian StyleDong, Lei, Jiachen Liu, Zijing Sun, Xi Chen, and Peng Wang. 2024. "Resource Allocation Approach of Avionics System in SPO Mode Based on Proximal Policy Optimization" Aerospace 11, no. 10: 812. https://doi.org/10.3390/aerospace11100812
APA StyleDong, L., Liu, J., Sun, Z., Chen, X., & Wang, P. (2024). Resource Allocation Approach of Avionics System in SPO Mode Based on Proximal Policy Optimization. Aerospace, 11(10), 812. https://doi.org/10.3390/aerospace11100812






