Physical Modeling of Structure and Dynamics of Concentrated, Tornado-like Vortices (A Review)
Abstract
1. Introduction
- (i)
- Estimation of the probability of a natural disaster occurring in a specific area of space within a certain time period;
- (ii)
- Prediction of the characteristics (structure) of a formed natural disaster;
- (iii)
- Prediction of the changes in characteristics over time (dynamics) along the path of the natural disaster propagation;
- (iv)
- (i)
- Determining the conditions for vortex generation (air temperature values, temperature gradients, etc.);
- (ii)
- Studying their stability (vortex characteristics and their change over time);
- (iii)
- Searching for the possibility to control their parameters (changing of the propagation path, weakening, and destruction).
2. Early Studies of Concentrated, Tornado-like Vortices
- (i)
- The radial Reynolds number , which is defined as
- (ii)
- The swirling parameter S, which is defined as
- (iii)
- The geometric aspect ratio a, which is defined aswhere is the volumetric air flow rate through a unit length of the chamber in the axial direction, is the circulation at the entrance to the lower chamber (to the rotating screen), is the radius of the ascending flow area, and is the depth (height) of the incoming flow.
3. Studies of Wall-Bounded, Stationary, and Concentrated Tornado-like Vortices
4. Studies of Wall-Free, Quasi-Stationary, and Concentrated Tornado-like Vortices
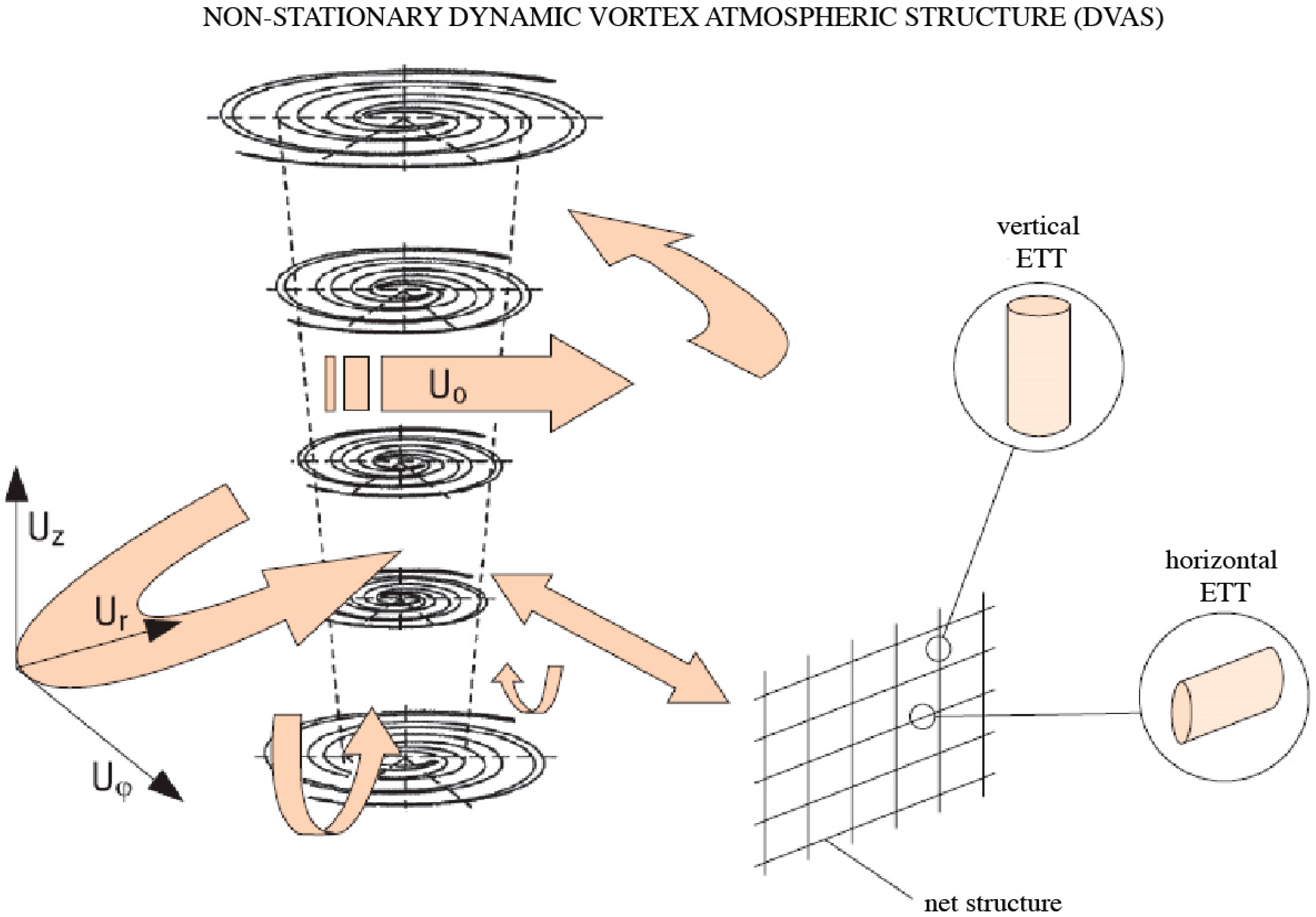
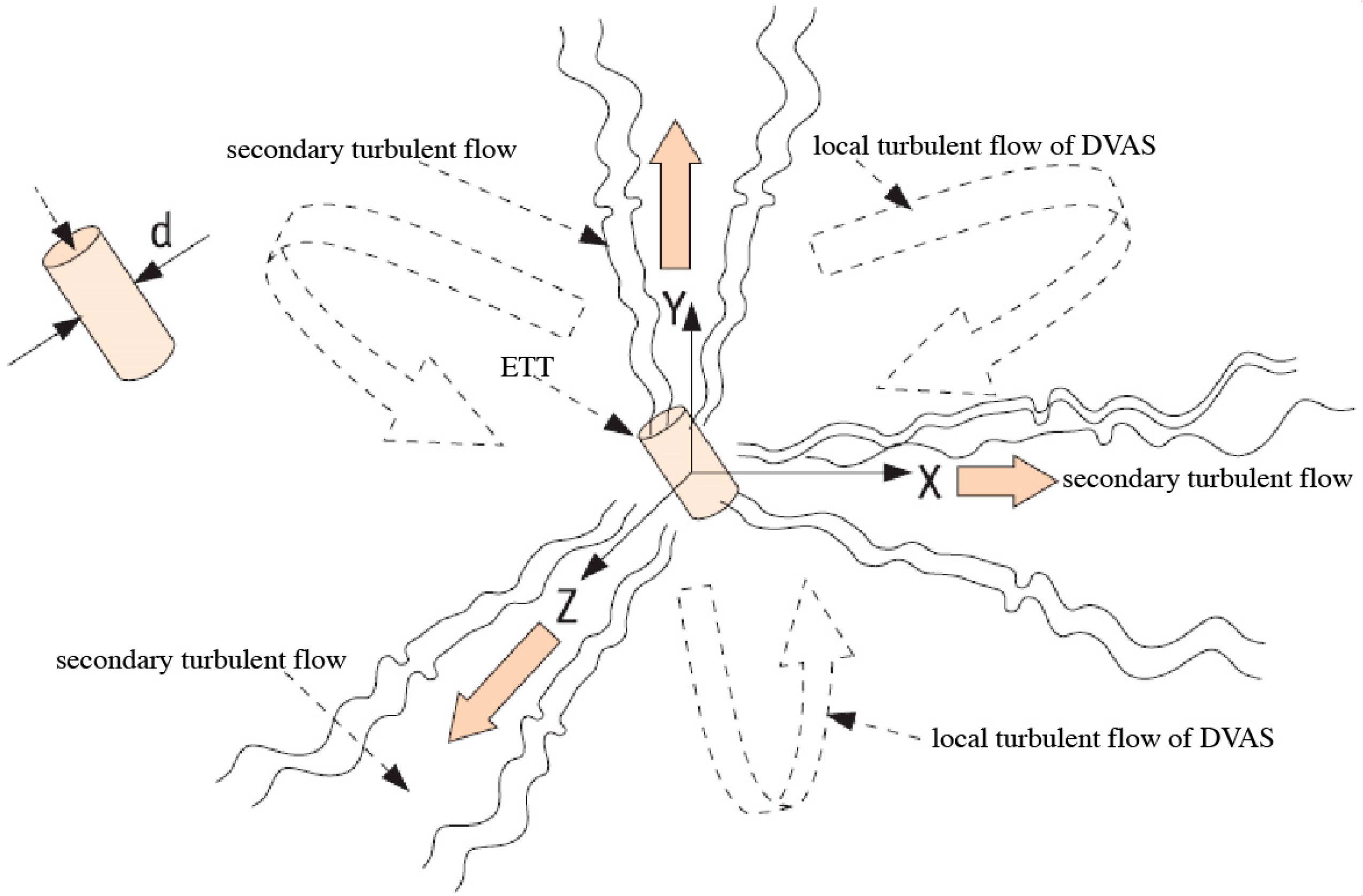
5. Studies of Wall-Free, Non-Stationary, and Concentrated Tornado-like Vortices
- (i)
- The values of temperatures and the heating rates of aluminum sheet (underlying surface) and air, as well as their temperature gradients in the vertical and horizontal directions, leading to a stable (in a statistical sense) generation of wall-free vortices of varying intensity, were found;
- (ii)
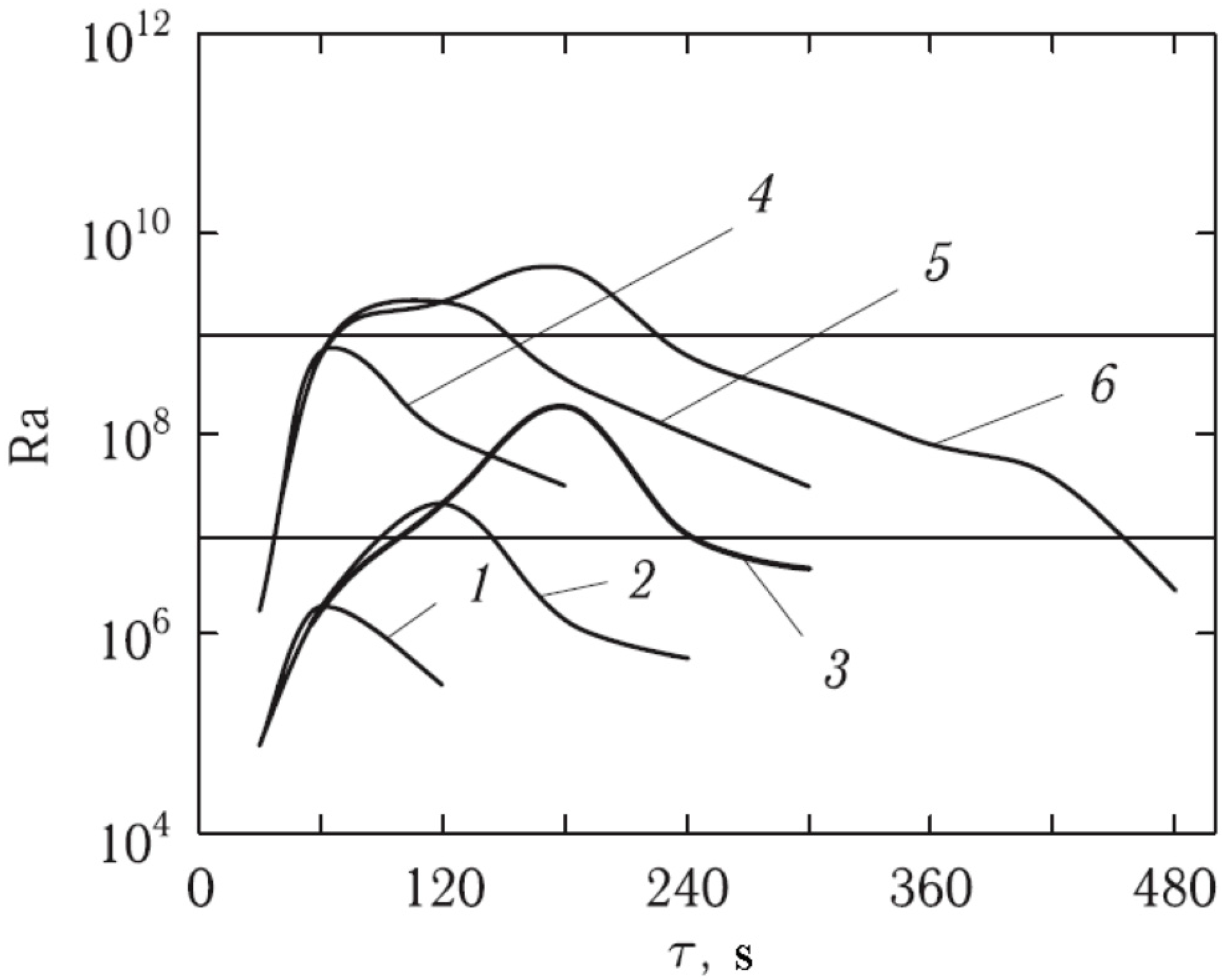
- The ranges of Rayleigh numbers at which the generation of vortices of various intensities occurred were revealed.
6. Conclusions
- (i)
- All the main problems of studies of unsteady atmospheric vortices unlimited by walls (generation conditions, stability studies, the possibility of control) remain out of consideration;
- (ii)
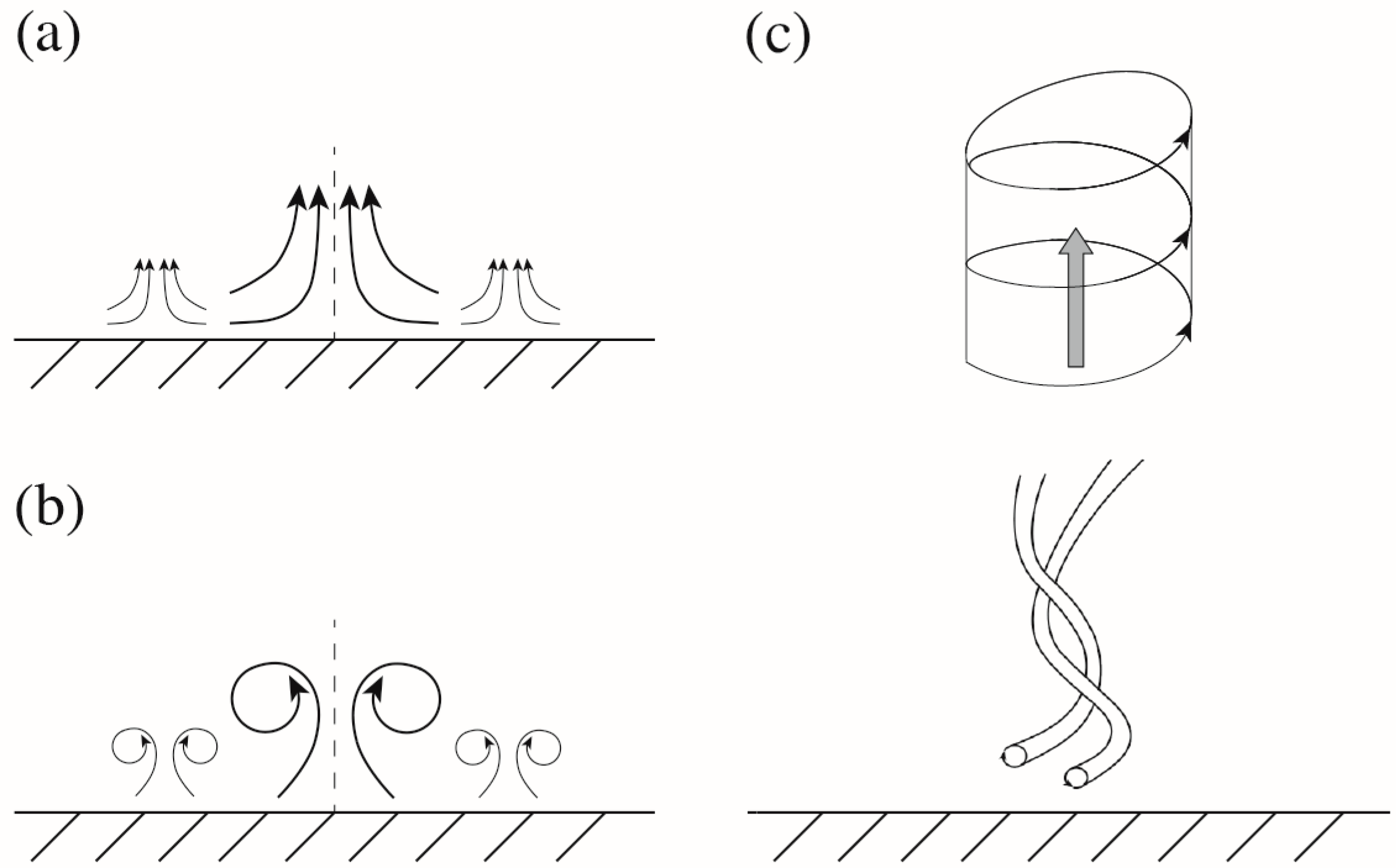
- The impossibility of modeling the two main mechanisms of tornadogenesis, namely the convective instability of the atmosphere at the lower level (“in-and-up mecha-nism”), as well as the occurrence of a supercellular at the upper level («downdraft mechanism»);
- (iii)
- The inability to study important issues related to the two-phase nature of an atmospheric vortex (the presence of water vapor, droplets, solid particles, debris, etc.) and its effect on the vortex generation process, its structure, and its dynamics.
- (i)
- Conducting experiments with higher spatial and temporal resolution in order to study the mechanisms of vortex generation in the surface layer (near the surface);
- (ii)
- Conducting experiments to determine the factors contributing to the stabilization (strengthening) and destabilization (weakening) of the generated vortices;
- (iii)
- Conducting experiments in order to find methods and means of controlling (combating) vortices.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Distance from axis in radial direction, m | |
| Vortex radius, m | |
| Radius of updraft region (radius of entrance to upper chamber), m | |
| Radius of rotating screen (radius of the lower chamber), m | |
| Depth of the inflow layer and the typical vertical dimension, over which the temperature difference is observed, m | |
| Spatial scale, m | |
| Axial velocity at the entrance to upper chamber, m/s | |
| Radial velocity, m/s | |
| Radial velocity at the screen input, m/s | |
| Azimuthal velocity, m/s | |
| Azimuthal velocity at the screen input, m/s | |
| Radial fluctuation velocity, m/s | |
| Axial fluctuation velocity, m/s | |
| Azimuthal fluctuation velocity, m/s | |
| Gravity acceleration, m/s2 | |
| Kinematic viscosity, m2/s | |
| Thermal diffusivity, m2/s | |
| Circulation, m2/s | |
| Volume flow rate per unit axial length through the chamber, m2/s | |
| Time of heating, s | |
| Maximal temperature at the center, K | |
| The temperature difference that causes the convection, K | |
| Coefficient of volumetric expansion, K−1 | |
| Geometric aspect ratio | |
| Swirl ratio | |
| Intensity of turbulent fluctuations (meridian plane) | |
| Intensity of turbulent fluctuations (horizontal plane) | |
| Rayleigh number | |
| Radial Reynolds number | |
| Vortex Reynolds number | |
| Rossby number | |
| Superscripts | |
| Deviation from the mean | |
| Average (over time) value | |
| Subscripts | |
| Maximum value | |
References
- Saffman, P.G. Vortex Dynamics; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Alekseenko, S.; Kuibin, P.; Okulov, V. Theory of Concentrated Vortices: An Introduction; Spinger: Berlin/Heidelberg, Germany, 2007; 506p. [Google Scholar]
- Bluestein, H.B. Severe Convective Storms and Tornadoes: Observations and Dynamics; Spinger Science & Business Media: Berlin/Heidelberg, Germany, 2013; 456p. [Google Scholar]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Tornado; Begell House: New York, NY, USA, 2015; 394p. [Google Scholar]
- Davies-Jones, R.P.; Kessler, E. Tornadoes. In Weather and Climate Modification; Hess, W.N., Ed.; Jon Wiley and Sons: New York, NY, USA, 1974; pp. 552–595. [Google Scholar]
- Lewellen, W.S. Theoretical Models of the Tornado Vortex. In Proceedings of the A Simposium on Tornadoes Assessment of Knowledge and Implications for Man; Hess, W.N., Ed.; Weather and Climate Modification. Texas Tech University: Lubbock, TX, USA, 1976; pp. 107–143. [Google Scholar]
- Shuleikin, V.V. Calculation of Development, Movement, and Attenuation of Tropical Storms and Major Waves Produced by Hurricanes; Gidrometeoizdat: Leningrad, Russia, 1978; 96p. (In Russian) [Google Scholar]
- Rotunno, R. The fluid dynamics of tornadoes. Annu. Rev. Fluid Mech. 2013, 45, 59–84. [Google Scholar] [CrossRef]
- Finley, A.J.; Brun, A.S.; Carlsson, M.; Szydlarski, M.; Hansteen, V.; Shoda, M. Stirring the base of the solar wind: On heat transfer and vortex formation. Astron. Astrophys. 2022, 665, A118. [Google Scholar] [CrossRef]
- Barczynski, K.; Schmieder, B.; Peat, A.W.; Labrosse, N.; Mein, P.; Mein, N. Spectro-imagery of an active tornado-like prominence: Formation and evolution. Astron. Astrophys. 2021, 653, A94. [Google Scholar] [CrossRef]
- Vasheghani Farahani, S.; Ghanbari, E.; Ghaffari, G.; Safari, H. Torsional wave propagation in solar tornadoes. Astron. Astrophys. 2017, 599, A19. [Google Scholar] [CrossRef][Green Version]
- Agee, E.; Taylor, L. Historical analysis of U.S. tornado fatalities (1808–2017): Population, science and technology. Weather. Clim. Soc. 2019, 11, 355–368. [Google Scholar] [CrossRef]
- Anderson-Frey, A.K. Tornado fatalities: An environmental perspective. Weather Forecast. 2019, 34, 1999–2015. [Google Scholar] [CrossRef]
- Alexander, C.R.; Wurman, J. The 30 May 1998 Spencer, South Dakota, storm. Part I: The structural evolution and environment of the tornadoes. Mon. Weather Rev. 2005, 133, 72–96. [Google Scholar] [CrossRef]
- Wurman, J.; Alexander, C.R. The 30 May 1998 Spencer, South Dakota, storm. Part II: Comparison of observed damage and radar-derived winds in the tornadoes. Mon. Weather Rev. 2005, 133, 97–119. [Google Scholar] [CrossRef]
- Kosiba, K.A.; Wurman, J.; Richardson, Y.; Markowski, P.; Robinson, P.; Marquis, J.N. Genesis of the Goshen county, Wyoming, tornado on 5 june 2009 during VORTEX. Mon. Weather Rev. 2013, 141, 1157–1182. [Google Scholar] [CrossRef]
- Trapp, R.J.; Kosiba, K.A.; Marquis, J.N.; Kumjian, M.R.; Nesbitt, S.W.; Wurman, J.; Salio, P.; Grover, M.A.; Robinson, P.; Hence, D.A. Multi-platform and multiple-doppler radar observations of a supercell thunderstorm in South America during RELAMPAGO. Mon. Weather Rev. 2020, 148, 3225–3241. [Google Scholar] [CrossRef]
- Flournoy, M.D.; Coniglio, M.C. Origins of vorticity in a simulated tornadic mesovortex observed during PECAN on 6 July. Mon. Weather Rev. 2019, 147, 107–134. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Lewellen, W.S. Near-surface intensification of tornado vortices. J. Atmos. Sci. 2007, 64, 2176–2194. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Lewellen, W.S. Near-surface vortex intensification through corner flow collapse. J. Atmos. Sci. 2007, 64, 2195–2209. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Evaluation of hydrodynamic instabilities in inertial confinement fusion target in a magnetic field. Probl. At. Sci. Technol. 2013, 4, 103–107. [Google Scholar]
- Romadanov, I.; Smolyakov, A.; Raitses, Y.; Kaganovich, I.; Tian, T.; Ryzhkov, S. Structure of nonlocal gradient-drift instabilities in Hall E×B discharges. Phys. Plasmas 2016, 23, 122111. [Google Scholar] [CrossRef]
- Roberts, B.; Xue, M.; Dawson, D.T. The effect of surface drag strength on mesocyclone intensification and tornadogenesis in idealized supercell simulations. J. Atmos. Sci. 2020, 77, 1699–1721. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. The relative importance of updraft and cold pool characteristics in supercell tornadogenesis using highly idealized simulations. J. Atmos. Sci. 2020, 77, 4089–4107. [Google Scholar] [CrossRef]
- Davies-Jones, R. Invented forces in supercell models. J. Atmos. Sci. 2021, 78, 2927–2939. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Particle-Laden and Droplet-Laden Two-Phase Flows Past Bodies (a Review). Symmetry 2023, 15, 388. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Mathematical modeling of structure and dynamics of concentrated tornado-like vortices: A review. Mathematics 2023, 11, 3293. [Google Scholar] [CrossRef]
- Ying, S.J.; Chang, C.C. Exploratory model study of tornado-like vortex dynamics. J. Atmos. Sci. 1970, 27, 3–14. [Google Scholar] [CrossRef]
- Wan, C.A.; Chang, C.C. Measurement of the velocity field in a simulated tornado-like vortex using a three-dimensional velocity probe. J. Atmos. Sci. 1972, 29, 116–127. [Google Scholar] [CrossRef][Green Version]
- Ward, N.B. The exploration of certain features of tornado dynamics using laboratory model. J. Atmos. Sci. 1972, 29, 1194–1204. [Google Scholar] [CrossRef]
- Jischke, M.C.; Parang, M. Properties of simulated tornado-like vortices. J. Atmos. Sci. 1974, 31, 506–512. [Google Scholar] [CrossRef][Green Version]
- Leslie, F.W. Surface roughness effects on suction vortex formation: A laboratory simulation. J. Atmos. Sci. 1977, 34, 1022–1027. [Google Scholar] [CrossRef][Green Version]
- Lewellen, W.S. A solution for three-dimensional vortex flows with strong circulation. J. Fluid Mech. 1962, 14, 420–432. [Google Scholar] [CrossRef]
- Church, C.R.; Snow, J.T.; Agee, E.M. Tornado vortex simulation at Purdue University. Bull. Am. Meteorol. Soc. 1977, 58, 900–908. [Google Scholar] [CrossRef]
- Baker, G.L.; Church, C.R. Measurements of core radii and peak velocities in modeled atmospheric vortices. J. Atmos. Sci. 1979, 36, 2413–2423. [Google Scholar] [CrossRef][Green Version]
- Church, C.R.; Snow, J.T. The dynamics of natural tornadoes as inferred from laboratory simulations. J. Rech. Atmos. 1979, 12, 111–133. [Google Scholar]
- Snow, J.T.; Church, C.R.; Barnhart, B.J. An investigation of the surface pressure fields beneath simulated tornado cyclones. J. Atmos. Sci. 1980, 37, 1013–1026. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; James, D.L.; Letchford, C.W.; Peterson, C.; Snow, J.T. Development of a prototype tornado simulator for the assessment of fluid-structure interaction. Clemson, S.C., Ed. In Proceedings of the 1st Americas Conference Wind Engineering, Clemson, SC, USA, 4–6 June 2001. [Google Scholar]
- Mishra, A.R.; James, D.L.; Letchford, C.W. Physical simulation of a single-celled tornado-like vortex, Part A: Flow field characterization. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1243–1257. [Google Scholar] [CrossRef]
- Mishra, A.R.; James, D.L.; Letchford, C.W. Physical simulation of a single-celled tornado-like vortex, Part B: Wind loading on a cubical model. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1258–1273. [Google Scholar] [CrossRef]
- Lee, J.J.; Samaras, T.M.; Young, C.R. Pressure measurements at the ground in an F-4 tornado. In Proceedings of the AMS 22nd Conference on Severe Local Storms, Hyannis, MA, USA, 3 October 2004. [Google Scholar]
- Gallus, W.A.; Sarkar, P.; Haan, F.; Le, K.; Kardell, R.; Wurman, J. A translating tornado simulator for engineering tests: Comparison of radar, numerical model, and simulating winds. In Proceedings of the AMS 22nd Conference on Severe Local Storms, Hyannis, MA, USA, 3 October 2004. [Google Scholar]
- Haan, F.L.; Sarkar, P.P.; Gallus, W.A. Design, construction and performance of a large tornado simulator for wind engineering applications. Eng. Struct. 2008, 30, 1146–1159. [Google Scholar] [CrossRef]
- Razavi, A.; Sarkar, P.P. Laboratory investigation of the effects of translation on the near-ground tornado flow field. Wind Struct. 2018, 26, 179–190. [Google Scholar]
- Zhang, W.; Sarkar, P.P. Near-ground tornado-like vortex structure resolved by particle image velocimetry (PIV). Exp. Fluids 2012, 52, 479–493. [Google Scholar] [CrossRef]
- Tari, H.P.; Gurka, R.; Hangan, H. Experimental investigation of tornado-like vortex dynamics with swirl ratio: The mean and turbulent flow fields. J. Wind Eng. Ind. Aerodyn. 2010, 98, 936–944. [Google Scholar] [CrossRef]
- Razavi, A.; Zhang, W.; Sarkar, P.P. Effect of ground roughness on near-surface flow field of a tornado-like vortex. Exp. Fluids 2018, 59, 170. [Google Scholar] [CrossRef]
- Liu, Z.; Ishihara, T. Study of the effects of translation and roughness on tornado-like vortices by large-eddy simulations. J. Wind Eng. Ind. Aerodyn. 2008, 151, 1–24. [Google Scholar] [CrossRef]
- Refan, M.; Hangan, H. Characterization of tornado-like flow fields in a new model scale wind testing chamber. J. Wind Eng. Ind. Aerodyn. 2016, 151, 107–121. [Google Scholar] [CrossRef]
- Refan, M.; Hangan, H. Near surface experimental exploration of tornado vortices. J. Wind Eng. Ind. Aerodyn. 2018, 175, 120–135. [Google Scholar] [CrossRef]
- Ashrafi, A.; Romanic, D.; Kassab, A.; Hangan, H.; Ezami, N. Experimental investigation of large-scale tornado-like vortices. J. Wind Eng. Ind. Aerodyn. 2021, 208, 104449. [Google Scholar] [CrossRef]
- Refan, M.; Hangan, H.; Wurman, J. Reproducing tornadoes in laboratory using proper scaling. J. Wind Eng. Ind. Aerodyn. 2014, 135, 136–148. [Google Scholar] [CrossRef]
- Ashton, R.; Refan, M.; Iungo, J.V.; Hangan, H. Wandering corrections from PIV measurements of tornado-like vortices. J. Wind Eng. Ind. Aerodyn. 2019, 189, 163–172. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Taekin, S.I. The possibility of physical simulation of air tornados under laboratory conditions. High Temp. 2008, 46, 888–891. [Google Scholar] [CrossRef]
- Kurgansky, M.V. A simple model of dry convective helical vortices (with applications to the atmospheric dust devil). Dyn. Atmos. Ocean. 2005, 40, 151–162. [Google Scholar] [CrossRef]
- Balme, M.; Greely, R. Dust devils on Earth and Mars. Rev. Geophys. 2006, 44, RG3003. [Google Scholar] [CrossRef]
- Kurgansky, M.V. Size distriution of dust devils in the atmosphere. Izv. Atmos. Ocean. Phys. 2006, 42, 319–325. [Google Scholar] [CrossRef]
- Kurgansky, M.V.; Montecinos, A.; Villagran, V.; Metzger, S.M. Micrometeorological conditions for dust-devil occurrence in the Atacama Desert. Bound.-Layer Meteorol. 2010, 138, 285–298. [Google Scholar] [CrossRef]
- Kurgansky, M.V.; Lorenz, R.D.; Renno, N.O.; Takemi, T.; Gu, Z.; Wei, W. Dust devil steady-state structure from a fluid dynamics perspective. Space Sci. Rev. 2016, 203, 209–244. [Google Scholar] [CrossRef]
- Kurgansky, M.V. Statistical distribution of atmospheric dust devils on Earth and Mars. Bound.-Layer Meteorol. 2022, 184, 381–400. [Google Scholar] [CrossRef]
- Kurgansky, M.V. Symmetric stability of vertical baroclinic vortices with a warm core. Izv. Atmos. Ocean. Phys. 2023, 59, 211–223. [Google Scholar] [CrossRef]
- Fujita, T.T. Tornadoes around the world. J. Weather. 1973, 26, 56–83. [Google Scholar] [CrossRef]
- Wakimoto, R.; Wilson, J.W. Non-supercell tornadoes. Mon. Weather. Rev. 1989, 117, 1113–1140. [Google Scholar] [CrossRef]
- Greeley, R.; Balme, M.R.; Iversen, J.D.; Metzger, S.; Mickelson, R.; Phoreman, J.; White, B. Martian dust devils: Laboratory simulations of particle threshold. J. Geophys. Res. 2003, 108, 5041. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Greeley, R.; Iversen, J.D.; Balme, M.R.; Eddlemon, E.E. Dust flux within dust devils: Preliminary laboratory simulations. J. Geophys. Res. 2006, 33, L19S09. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Greeley, R. Dust devils in the laboratory: Effects of surface roughness on vortex dynamics. J. Geophys. Res. 2010, 115, E05003. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Greeley, R. Dust devil sediment flux on Earth and Mars: Laboratory simulations. Icarus 2010, 206, 306–318. [Google Scholar] [CrossRef]
- Fizjarrald, D.E. A laboratory simulation of convective vortices. J. Atmos. Sci. 1973, 30, 894–902. [Google Scholar] [CrossRef][Green Version]
- Davies-Jones, R.P. Tornado dynamics. In Thunderstorm Morphology and Dynamics, 2nd ed.; Kessler, E., Ed.; University of Oklahoma Press: Norman, OK, USA, 1986; pp. 197–236. [Google Scholar]
- Brady, R.H.; Szoke, E.J. A case study of non-mesocyclone tornado development in northeast Colorado: Similarities to waterspout formation. Mon. Weather Rev. 1989, 117, 843–856. [Google Scholar] [CrossRef]
- Lewellen, W.S. Tornado vortex theory. In The Tornado: Its Structure, Dynamics, Prediction, and Hazards; Church, C., Burgess, D., Doswell, C., Davies-Jones, R., Eds.; Geophysical Monograph Series; AGU: Washington, DC, USA, 1993; Volume 79, pp. 19–39. [Google Scholar]
- Davies-Jones, R.P.; Trapp, R.J.; Bluestein, H.B. Tornadoes and tornadic storms. In Severe Convective Storms; Doswell, C.A., Ed.; AMS: Boston, MA, USA, 2001; pp. 167–221. [Google Scholar]
- Markowski, P.; Richardson, Y. Mesoscale Meteorology in Midlatitudes; John Wiley and Sons: Hoboken, NJ, USA, 2010; 430p. [Google Scholar]
- Davies-Jones, R. A review of supercell and tornado dynamics. Atmos. Res. 2015, 158, 274–291. [Google Scholar] [CrossRef]
- Davies-Jones, R.; Wood, V.T.; Askelson, M.A. Ray curvature on a flat Earth for computing virtual WSR-88D signatures of simulated supercell storms. Mon. Weather Rev. 2019, 147, 1065–1075. [Google Scholar] [CrossRef]
- Davies-Jones, R.; Markowski, P.M. Circulation around a constrained curve: An alternative analysis tool for diagnosing the origins of tornado rotation in numerical supercell simulations. J. Atmos. Sci. 2021, 78, 2895–2909. [Google Scholar] [CrossRef]
- Davies-Jones, R. Theory of parcel vorticity evolution in supercell-like flows. J. Atmos. Sci. 2022, 79, 1253–1270. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. Transition of near-ground vorticity dynamics during tornadogenesis. J. Atmos. Sci. 2022, 79, 467–483. [Google Scholar] [CrossRef]
- Parker, M.D.; Wicker, L.J. Imported and storm-generated near-ground vertical vorticity in a simulated supercell. J. Atmos. Sci. 2014, 71, 3027–3051. [Google Scholar]
- Dahl, J.M.L. Near-ground rotation in simulated supercells: On the robustness of the baroclinic mechanism. Mon. Weather Rev. 2015, 143, 4929–4942. [Google Scholar] [CrossRef]
- Parker, M.D.; Dahl, J.M.L. Production of near-surface vertical vorticity by idealized downdrafts. Mon. Weather Rev. 2015, 143, 2795–2816. [Google Scholar] [CrossRef]
- Markowski, P.M. An idealized numerical simulation investigation of the effects of surface drag on the development of near-surface vertical vorticity in supercell thunderstorms. J. Atmos. Sci. 2016, 73, 4349–4385. [Google Scholar] [CrossRef]
- Mashiko, W.; Niino, H.; Kato, T. Numerical simulation of tornadogenesis in an outer-rainband minisupercell of Typhoon Shanshan on 17 September. Mon. Weather Rev. 2009, 137, 4238–4260. [Google Scholar]
- Mashiko, W. A numerical study of the 6 May 2012 Tsukuba City supercell tornado. Part II: Mechanisms of tornadogenesis. Mon. Weather Rev. 2016, 144, 3077–3098. [Google Scholar] [CrossRef]
- Roberts, B.; Xue, M.; Schenkman, A.D.; Dawson, D.T. The role of surface drag in tornadogenesis within an idealized supercell simulation. J. Atmos. Sci. 2016, 73, 3371–3395. [Google Scholar] [CrossRef]
- Rotunno, R.; Markowski, P.M.; Bryan, G.H. “Near ground” vertical vorticity in supercell thunderstorm models. J. Atmos. Sci. 2017, 74, 1757–1766. [Google Scholar] [CrossRef]
- Yokota, S.; Niino, H.; Seko, H.; Kunii, M.; Yamauchi, H. Important factors for tornadogenesis as revealed by high-resolution ensemble forecasts of the Tsukuba supercell tornado of 6 May 2012 in Japan. Mon. Weather Rev. 2018, 146, 1109–1132. [Google Scholar] [CrossRef]
- Tao, T.; Tamura, T. Numerical study of the 6 May 2012 Tsukuba supercell tornado: Vorticity sources responsible for tornadogenesis. Mon. Weather Rev. 2020, 148, 1205–1228. [Google Scholar] [CrossRef]
- Boyer, C.H.; Dahl, J.M.L. The mechanisms responsible for large near-surface vertical vorticity within simulated supercells and quasi-linear storms. Mon. Weather Rev. 2020, 148, 4281–4297. [Google Scholar] [CrossRef]
- Markowski, P.M.; Richardson, Y.P. The influence of environmental low-level shear and cold pools on tornadogenesis: Insights from idealized simulations. J. Atmos. Sci. 2014, 71, 243–275. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Gorbachev, M.A. Experimental study of wall-free non-stationary vortices generation due to air unstable stratification. Int. J. Heat Mass Transf. 2012, 55, 6567–6572. [Google Scholar] [CrossRef]
- Navarro, M.C.; Herrero, H. Vortex generation by a convective instability in a cylindrical annulus non-homogeneously heated. Phys. Rev. E 2011, 240, 1181–1188. [Google Scholar] [CrossRef]
- Castano, D.; Navarro, M.C.; Herrero, H. Evolution of secondary whirls in thermoconvective vortices: Strengthening, weakening, and disappearance in the route to chaos. Phys. Rev. E 2016, 93, 013117. [Google Scholar] [CrossRef]
- Castano, D.; Navarro, M.C.; Herrero, H. Secondary whirls in thermoconvective vortices developed in a cylindrical annulus locally heated from below. Commun. Nonlinear Sci. Numer. Simulat. 2015, 28, 201–209. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. The parameters of unstable stratification of air leading to generation of free vortexes. High Temp. 2010, 48, 251–255. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Taekin, S.I.; Kopeitsev, V.N. The generation of free concentrated air vortexes under laboratory conditions. High Temp. 2009, 47, 78–82. [Google Scholar] [CrossRef]
- Gu, Z.; Zhao, Y.; Li, Y.; Yu, Y.; Feng, X. Numerical simulation of dust lifting within dust devils—Simulation of an intense vortex. J. Atmos. Sci. 2006, 63, 2630–2641. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Gong, B.; Lewellen, W.S. Effect of finescale debris on near-surface tornado dynamics. J. Atmos. Sci. 2008, 65, 3247–3262. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Zaichik, L.I. The effect of a fine divided impurity on the turbulence intensity of a carrier flow in a pipe. High Temp. 1998, 36, 983–986. [Google Scholar]
- Zaichik, L.I.; Varaksin, A.Y. Effect of the wake behind large particles on the turbulence intensity of carrier flow. High Temp. 1999, 37, 655–658. [Google Scholar]
- Lebedeva, N.A.; Osiptsov, A.N. Structure of inertial-admixture accumulation zones in a tornado-like flow. Fluid Dyn. 2009, 44, 68–79. [Google Scholar] [CrossRef]
- Maruyama, T. Simulation of flying debris using a numerically generated tornado-like vortex. J. Wind Eng. Ind. Aerodyn. 2011, 99, 249–256. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Vortex flows with particles and droplets (a review). Symmetry 2022, 14, 2016. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Turbulence in two-phase flows with macro-, micro- and nanoparticles: A review. Symmetry 2022, 14, 2433. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Balme, M.R.; Esposito, F.; Kelling, T.; Klose, M.; Kok, J.F.; Marticorena, B.; Merrison, J.; Patel, M.; Wurm, G. particle lifting processes in dust devils. Space Sci. Rev. 2016, 203, 347–376. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. The possibilities of visualization in the case of simulation of air tornados. High Temp. 2010, 48, 588–592. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Protasov, M.V.; Teplitskii, Y.S. About choice of particle parameters for visualization and diagnostics of free concentrated air vortices. High Temp. 2014, 52, 554–559. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Gorbachev, M.A. Physical simulation of air tornados: Some dimensionless parameters. High Temp. 2011, 49, 310–313. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Controlling the behavior of air tornados. High Temp. 2009, 47, 836–842. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. The possibility of influencing vortex atmospheric formations. High Temp. 2010, 48, 411–415. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Computational and Experimental Modeling in Magnetoplasma Aerodynamics and High-Speed Gas and Plasma Flows (A Review). Aerospace 2023, 10, 662. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review). Mathematics 2023, 11, 3290. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Effect of net structures on wall-free non-stationary air heat vortices. Int. J. Heat Mass Transf. 2013, 64, 817–828. [Google Scholar] [CrossRef]
- Bulychev, N.A. Obtaining Nanosized Materials in Plasma Discharge and Ultrasonic Cavitation. High Temp. 2022, 60 (Suppl. 1), S98–S126. [Google Scholar] [CrossRef]
- Azarova, O.A.; Kravchenko, O.V. The Use of Spatially Multi-Component Plasma Structures and Combined Energy Deposition for High-Speed Flow Control: A Selective Review. Energies 2024, 17, 1632. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Development of a Method for Solving Elliptic Differential Equations Based on a Nonlinear Compact-Polynomial Scheme. J. Comput. Appl. Math. 2024, 451, 116098. [Google Scholar] [CrossRef]
- Bizyaev, I.A.; Mamaev, I.S. Qualitative Analysis of the Dynamics of a Balanced Circular Foil and a Vortex. Regul. Chaotic Dyn. 2021, 26, 658–674. [Google Scholar] [CrossRef]
- Bulychev, N.A.; Ioni, Y.V.; Dimitrieva, S.E.; Chebotarev, S.N.; Rabinsky, L.N. Plasma-Chemical Synthesis of Nanosized Bactericidal Particles under the Action of Ultrasonic Cavitation. High Temp. 2022, 60 (Suppl. S2), S263–S266. [Google Scholar] [CrossRef]
- Bizyaev, I.A.; Mamaev, I.S. Dynamics of a Circular Foil and Two Pairs of Point Vortices: New Relative Equilibria and a Generalization of Helmholtz Leapfrogging. Symmetry 2023, 15, 698. [Google Scholar] [CrossRef]
- Youvan, D.C. Vortex Dynamics in Nonequilibrium Thermodynamic Systems: A Multidisciplinary Approach. 2024; preprint. [Google Scholar] [CrossRef]
- Lillek, S.; Barfuß, C.; Sattelmayer, T. Experimental study of the interaction of water sprays with swirling premixed natural gas flames. J. Eng. Gas Turbines Power 2017, 139, 021506. [Google Scholar] [CrossRef]
- Minakov, A.V.; Kuznetsov, V.A.; Anufriev, I.S.; Kopyev, E.P. Numerical analysis of a pre-chamber vortex burner with a steam blast atomizer. Fuel 2022, 323, 124375. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, J.; Wang, J.; Mao, Y. Time-frequency analysis of the vortex motion in a cylindrical cyclone separator. Chem. Eng. J. 2019, 373, 1120–1131. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S.; Ligus, G. Experimental and numerical investigation on the performance of square cyclones with different vortex finder configurations. Sep. Purif. Technol. 2020, 239, 116588. [Google Scholar] [CrossRef]
- Brar, L.S.; Wasilewski, M. Investigating the effects of temperature on the performance of novel cyclone separators using large-eddy simulation. Powder Techol. 2023, 416, 118213. [Google Scholar] [CrossRef]



| No. | Author(s) | Vortex Type | Ascending Flow Creation | Circulation Creation | Advantages |
|---|---|---|---|---|---|
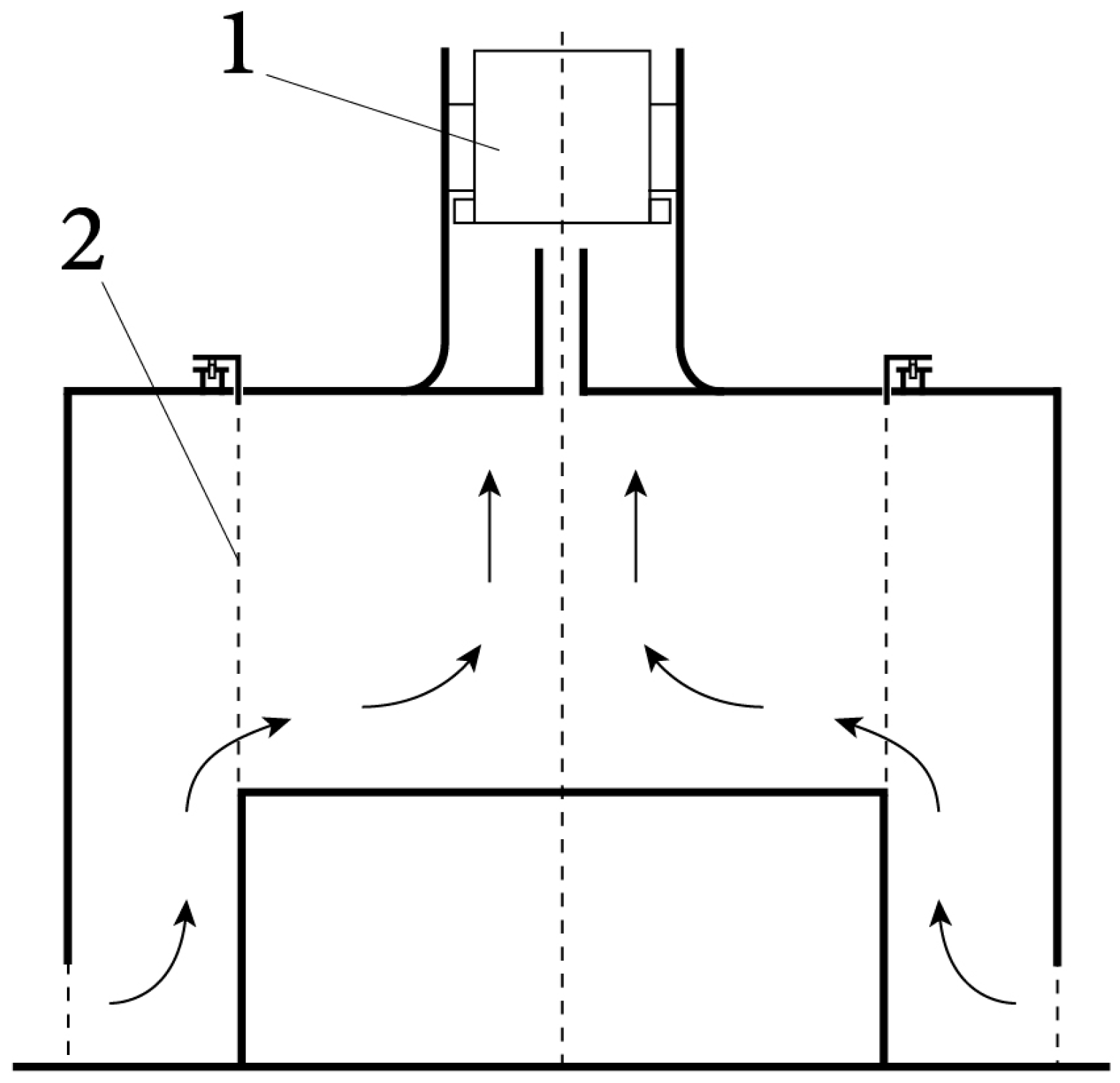
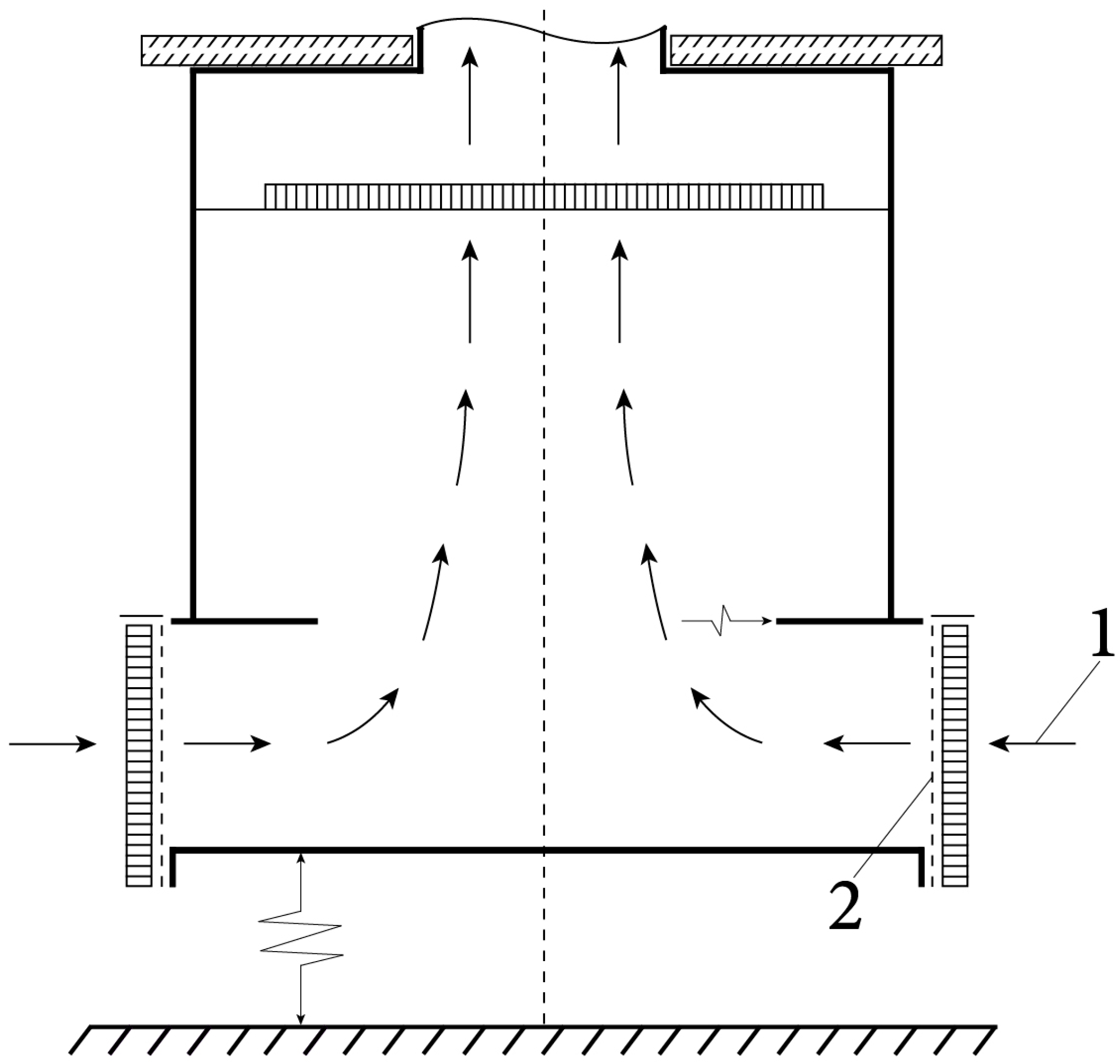
| 1 | Wan and Chang (1972) [29] | Wall-bounded, stationary vortex | Top-mounted fan | Rotating mesh screen | Independent velocity and circulation control |
| 2 | Ward (1972) [30] | Wall-bounded, stationary vortex | Fan | Rotating screen with guide vanes | Suppression of fan circulation by mesh structure |
| 3 | Church et al. (1977) [34] | Wall-bounded, stationary vortex | Incoming flow | Rotating ring and screen | Adjustment of geometric and working parameters |
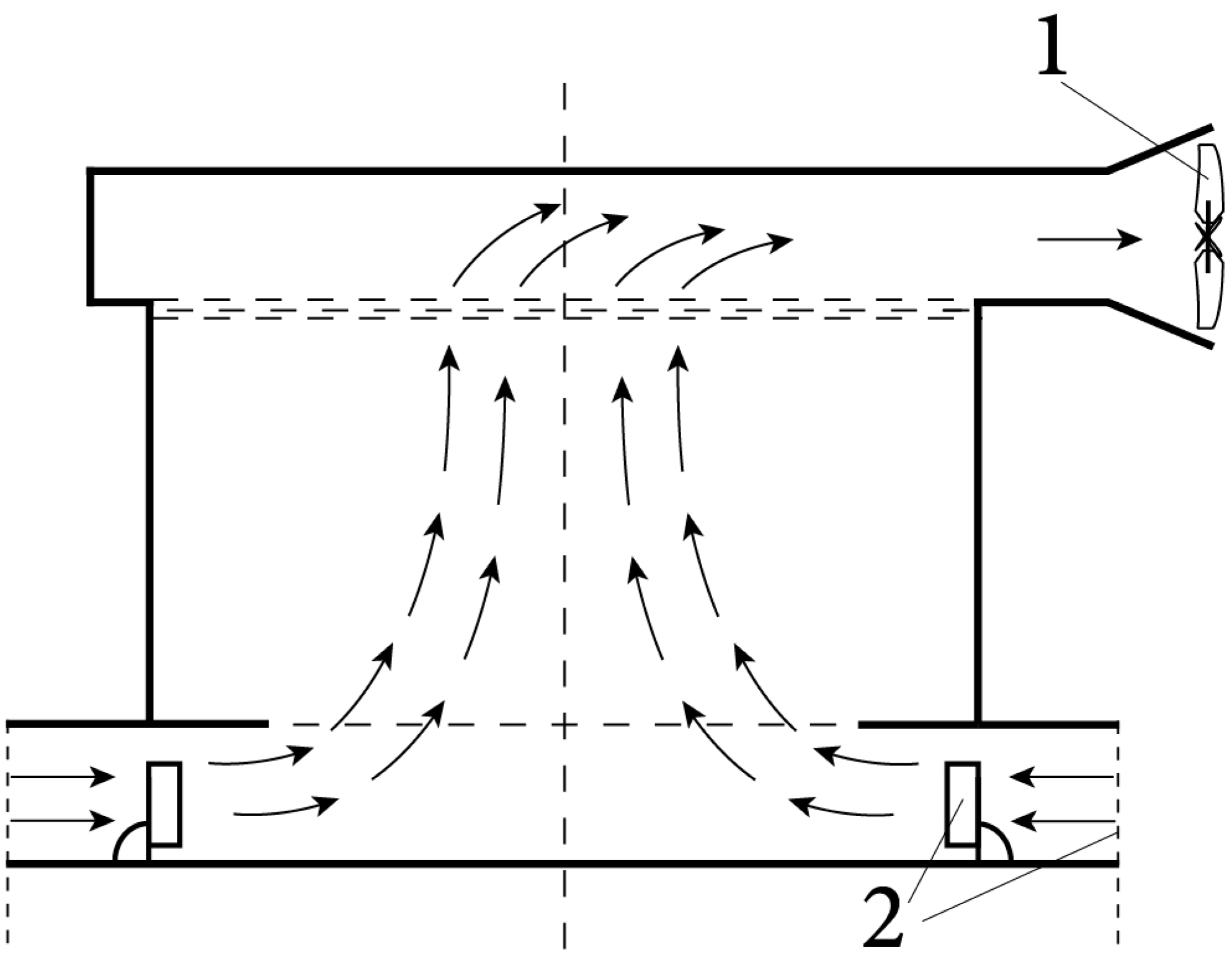
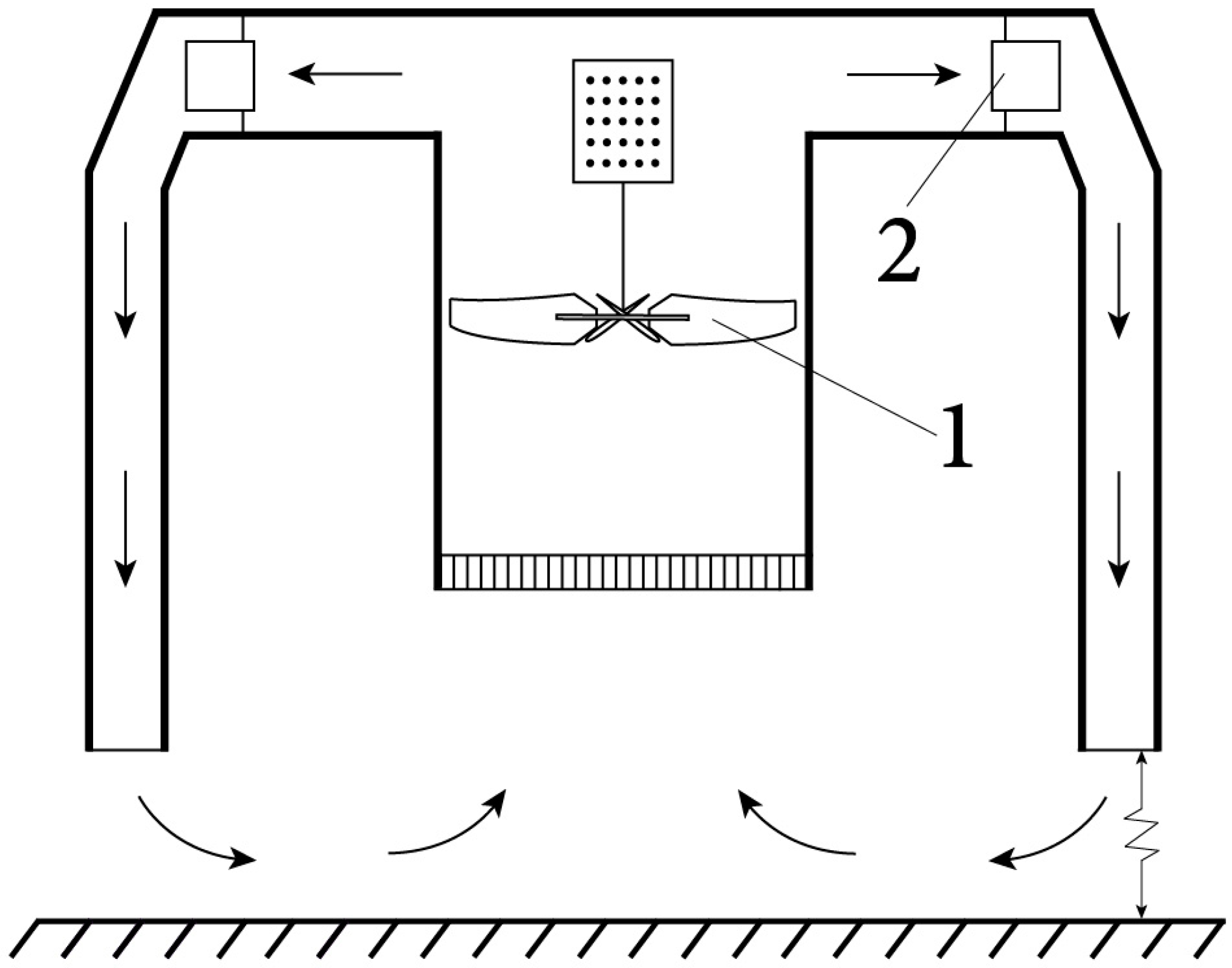
| 4 | Gallus et al. (2004) [42] | Wall-free, quasi-stationary vortex | Top-mounted fan | Guide vanes | Creation of forced downward flow and vortex structure movement |
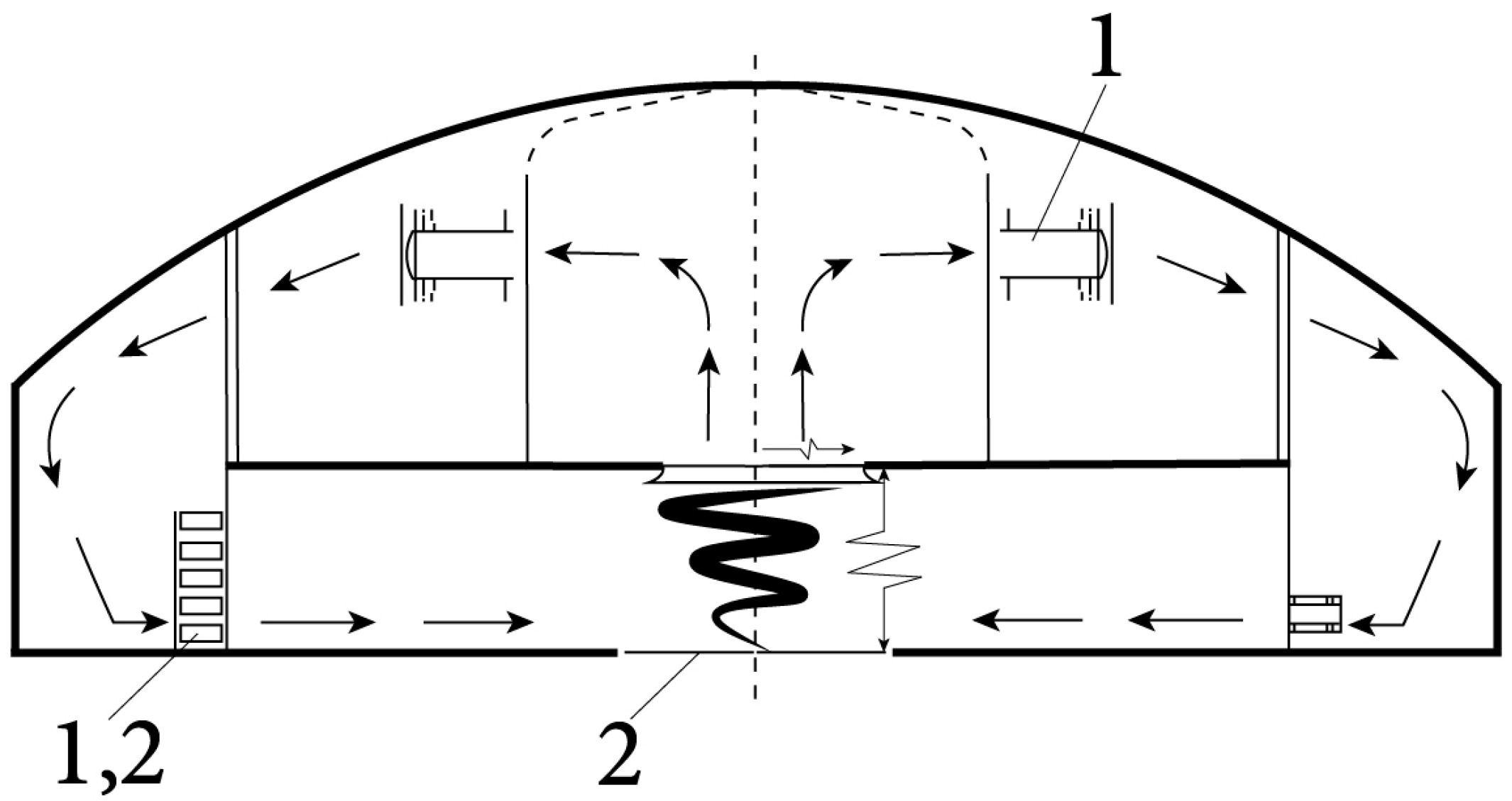
| 5 | Refan and Hangan (2016) [49] | Quasi-wall-free, quasi-stationary vortex | Large number of fans | Adjustable blades | Creation of required velocity gradients and vortex structure movement |
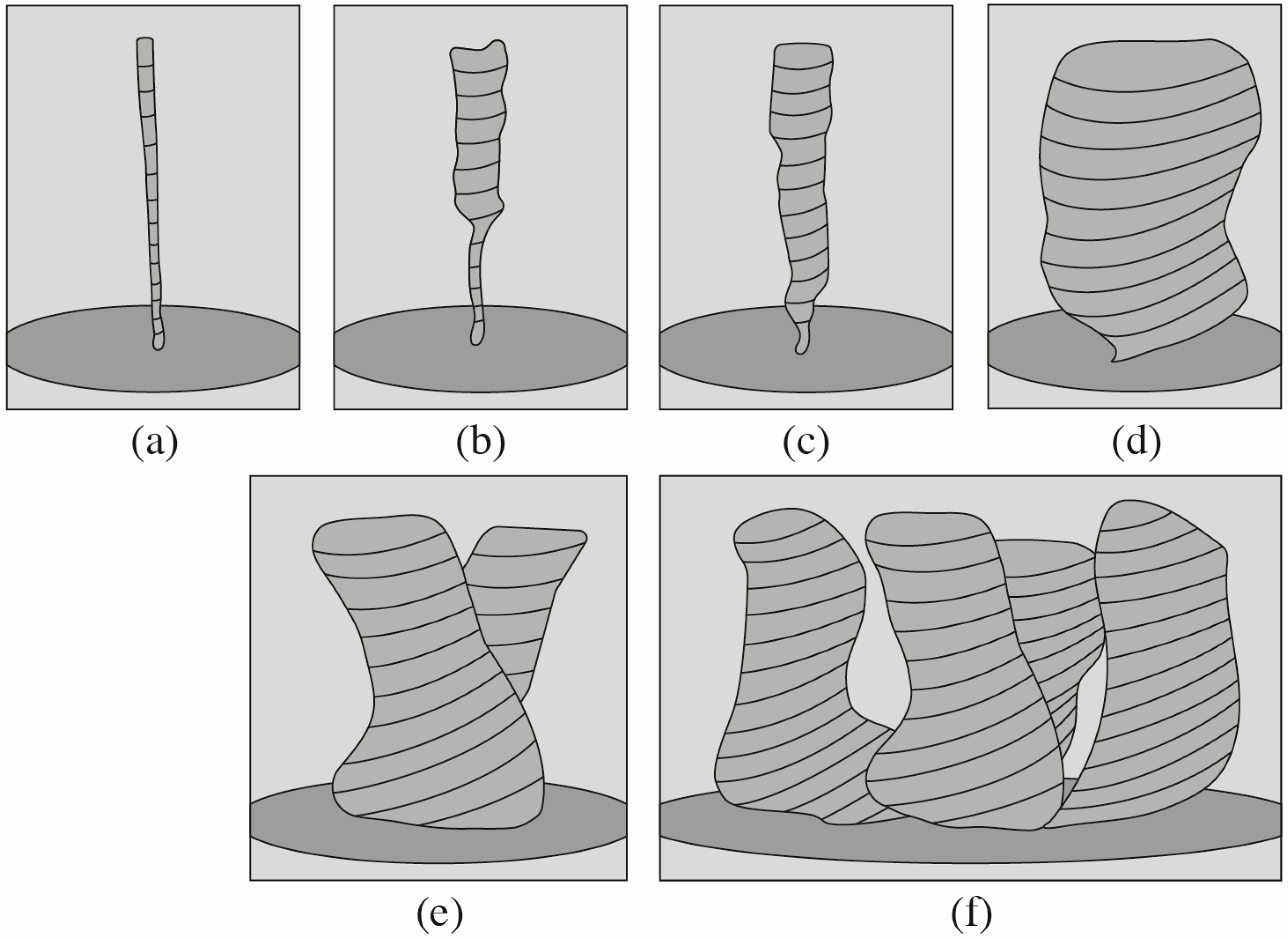
| 6 | Varaksin et al. (2008) [54] | Wall-free, non-stationary vortex | Buoyancy-driven convection | Absent | Possibility to study of non-stationary vortex generation, stability, etc. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varaksin, A.Y.; Ryzhkov, S.V. Physical Modeling of Structure and Dynamics of Concentrated, Tornado-like Vortices (A Review). Aerospace 2024, 11, 800. https://doi.org/10.3390/aerospace11100800
Varaksin AY, Ryzhkov SV. Physical Modeling of Structure and Dynamics of Concentrated, Tornado-like Vortices (A Review). Aerospace. 2024; 11(10):800. https://doi.org/10.3390/aerospace11100800
Chicago/Turabian StyleVaraksin, Aleksey Yu., and Sergei V. Ryzhkov. 2024. "Physical Modeling of Structure and Dynamics of Concentrated, Tornado-like Vortices (A Review)" Aerospace 11, no. 10: 800. https://doi.org/10.3390/aerospace11100800
APA StyleVaraksin, A. Y., & Ryzhkov, S. V. (2024). Physical Modeling of Structure and Dynamics of Concentrated, Tornado-like Vortices (A Review). Aerospace, 11(10), 800. https://doi.org/10.3390/aerospace11100800







