1. Introduction
Information about wind is crucial for planning flights in civil aviation. Accurate wind data can improve flight safety and stability, which benefits airlines and helps reduce emissions. Traditional methods of measuring wind, such as weather satellites, weather radars, and sounding balloons, have shown excellent results and can detect wind fields over large areas. However, they also have certain limitations, such as weather radar measurements, which require certain conditions (such as precipitation, insects, and other non-meteorological objects). Sounding balloons are deployed at fixed stations at fixed frequencies and carry instruments that can accurately measure wind fields. However, due to the limitation of the release frequency and location of the balloon, the measured data also have a low temporal and spatial resolution [
1].
At present, airlines commonly utilize integrated weather forecasting and air traffic services to access essential weather data [
2]. The wind field at the altitude of civil aviation is a nonlinear dynamic system, and even minor deviations between the initial state and the boundary conditions can introduce uncertainty into forecast outcomes [
3]. The numerical weather forecast is based on the existing observed values and the analysis and calculation of the wind field based on various physical laws. In this way, the wind field can be accurately nowcasting. However, it must be noted that due to the complexity of processing and solving mathematical and physical equations, there are certain limitations in obtaining rapid wind field information, and usually only one or two calculations can be performed per day [
4]. Reanalysis data integrate diverse measurement methods through data assimilation to represent meteorological data in an atmospheric grid format [
5]. Reanalysis data do not have the constraints of publishing timely forecasts, allowing more time to collect observations and allowing improvements to past dataset rows, which allows reanalysis data to provide high-quality meteorological data [
6]. While the above method can provide accurate data, there are some limitations in current aviation forecasting, which cannot take into account the accuracy and real-time of civil aviation meteorological data.
Thus, it is essential to develop a method for real-time detection of the wind field. Ref. [
7] used Automatic Dependent Surveillance-Broadcast(ADS-B) data of single aircraft and multi-aircraft to solve the wind vector. It was assumed that the wind vector remained constant in a small area for a short time, and the true airspeed (TAS) of the aircraft remained constant but the heading angle was different. The inversion problem of wind vector and airspeed is transformed into circle fitting. Ref. [
8] focused on the improvement of the algorithm and further reduced the error using a novel particle filter proposed. Ref. [
1] combined the ADS-B data with the Enhanced Surveillance data from the Mode Select Beacon System (Mode S) downlink to invert the wind field, achieving good results. The wind data calculated by these methods have a small error, as well as benefits from the advantages of the real-time acquisition of ADS-B and Mode S data, thus improving the real-time performance of meteorological data. However, all the wind data are distributed along the flight path and cannot be spatially continuous, and there are large areas that cannot be effectively detected. To address this limitation, refs. [
9,
10] propose constructing a meteorological particle model, which generates meteorological particles for each wind observation value, reconstructs the wind field based on the generated numerous meteorological particles, and calculates the confidence. However, the proposed meteorological particle model does not provide wind predictions in areas with insufficient observations. Ref. [
11] introduces the use of Gaussian process regression (GPR) in machine learning to model the wind field and train the model with wind observation value as the input data. The model fits the Gaussian distribution characteristic of the wind field in both time and space to calculate the wind field at any given time and point in space. Subsequently, ref. [
12] investigated the problem of online estimation of the vertical wind profile at a given location using the GPR model. Ref. [
13] also used the GPR model and collected real-time ADS-B and Mode S data for wind field estimation, and allowed new data to be added for data assimilation. The current wind field prediction results could be calculated within 5 min. Ref. [
14] combined the polynomial chaos expansion method of the GPR model to further improve the prediction effect of the model, which also allowed data assimilation. Since the GPR model allows data assimilation, past data can be used by the model to more accurately reconstruct the wind field. However, each time the wind field is reconstructed, the model needs to train the newly added data to fit the new Gaussian process, and the training time is proportional to the amount of data, which limits the calculation speed of wind field reconstruction, and requires the model parameters to be iteratively optimized.
The current popular and efficient method across various disciplines is the use of deep neural networks. Ref. [
15] describes a WindAware system that uses an LSTM-based RNN network to implement a wind prediction system designed to provide immediate forecasts of wind and turbulence for UAVs. The proposed method is compared with multi-layer Perceptron (MLP) and XGBoost, and its performance in surface wind prediction is verified. Ref. [
16] proposes a physically inspired neural network designed to reconstruct wind fields using dispersed local wind speed measurements. The network is based on U-net structure and realizes horizontal wind field reconstruction with partial convolution. This method focuses on the immediate and short-term prediction of the wind field and has a better performance than the Meteo-Particle model. However, to enhance the input, it requires additional 6 h forecast data from the Global Forecast System and additional optimization of hyperparameters in the physical loss function. Current wind prediction methods based on deep neural networks primarily address wind data prediction in the wind power generation field, lacking methods applicable in aviation meteorology [
4]. There is also less research on a general method that can calculate and obtain a complete and accurate reconstructed wind field using only incomplete wind observations as the input. In addition, although there are methods to obtain incomplete wind field data through the inversion of the wind field using joint observation data from ADS-B and Mode S, the amount of data obtained is insufficient for training and testing deep learning networks. Therefore, one of the challenges to be addressed is how to obtain a large amount of data.
To address the aforementioned issues, this paper introduces a novel deep learning neural network model called the Vision Mamba Decoder (VMD), based on the State Space Model (SSM). This method represents an innovative approach by integrating the Vision Mamba model, which has recently demonstrated superior performance over the Vision Transformer network in the field of computer vision. VMD can overcome the challenge of real-time aerial monitoring with incomplete wind observation data. Using an encoder structure, the VMD extracts critical features from scattered wind observations along flight trajectories. The extracted features are then transformed into a high-dimensional space. The decoder not only performs feature fusion but also reduces dimensionality, enabling accurate and rapid reconstruction of the horizontal wind field.
In order to provide a comprehensive understanding of the proposed method, the subsequent sections of this paper will delve into its details.
Section 2 introduces the model architecture and data acquisition methods, while
Section 3 describes the experimental setup designed to validate the effectiveness of the method. Finally,
Section 4 summarizes the key findings and explores future directions for this research.
3. Results
This section introduces how to verify the VMD network proposed in this paper through experiments (including the details of setting each hyperparameter in the experiment), displays the final wind field reconstruction results, and evaluates the reconstruction results of the model through indicators, such as the MAE.
3.1. Experiment Settings
This experiment was conducted on the ERA5 dataset, and the input features and labels were obtained by using the method proposed in
Section 2.3. In the experiment, wind data from January 2018 to December 2021 at 225 hPa pressure heights were used for model training, and the wind data from 2022 were utilized to test the model. The wind data include the u and v components of the wind, which represent the magnitude of the wind speed component in the east–west and south–north directions, respectively. Spatially, the data were restricted to the range of 3 to 8 degrees east longitude and 49 to 54 degrees north latitude, split into a grid of latitude and longitude at 0.25 resolution.
In order to ensure the repeatability of the training dataset and the validation dataset (to avoid the randomness of each training, especially the validation), this paper sets the seed parameter, so that a fixed mask can be generated by setting the same seed before each training, which is beneficial to compare the experimental results on the validation set. The optimizer is set to Adamw with a learning rate of
, momentum parameter of 0.9, batchsize of 512, and weight decay of 0.05. The experiments were completed on a single NVIDIA Quadro RTX 5000 GPU with 1000 rounds of training, and the loss curves are shown in
Figure 1.
As can be seen in
Figure 1, the train loss curve shows a significant downward trend until 700 epochs and then train loss almost converges. The test loss curve shows a rapid convergence in the first 20 epochs, and the oscillation disappears and becomes stable after 600 epochs. This shows that the model can effectively learn and converge during the training of 1000 epochs, and there is no obvious overfitting phenomenon.
3.2. Presenting Results
In order to demonstrate the results of the model reconstruction, this section tests a set of data that is not in the training set, and the generated Mask has a random seed so that the results are not different from test to test.
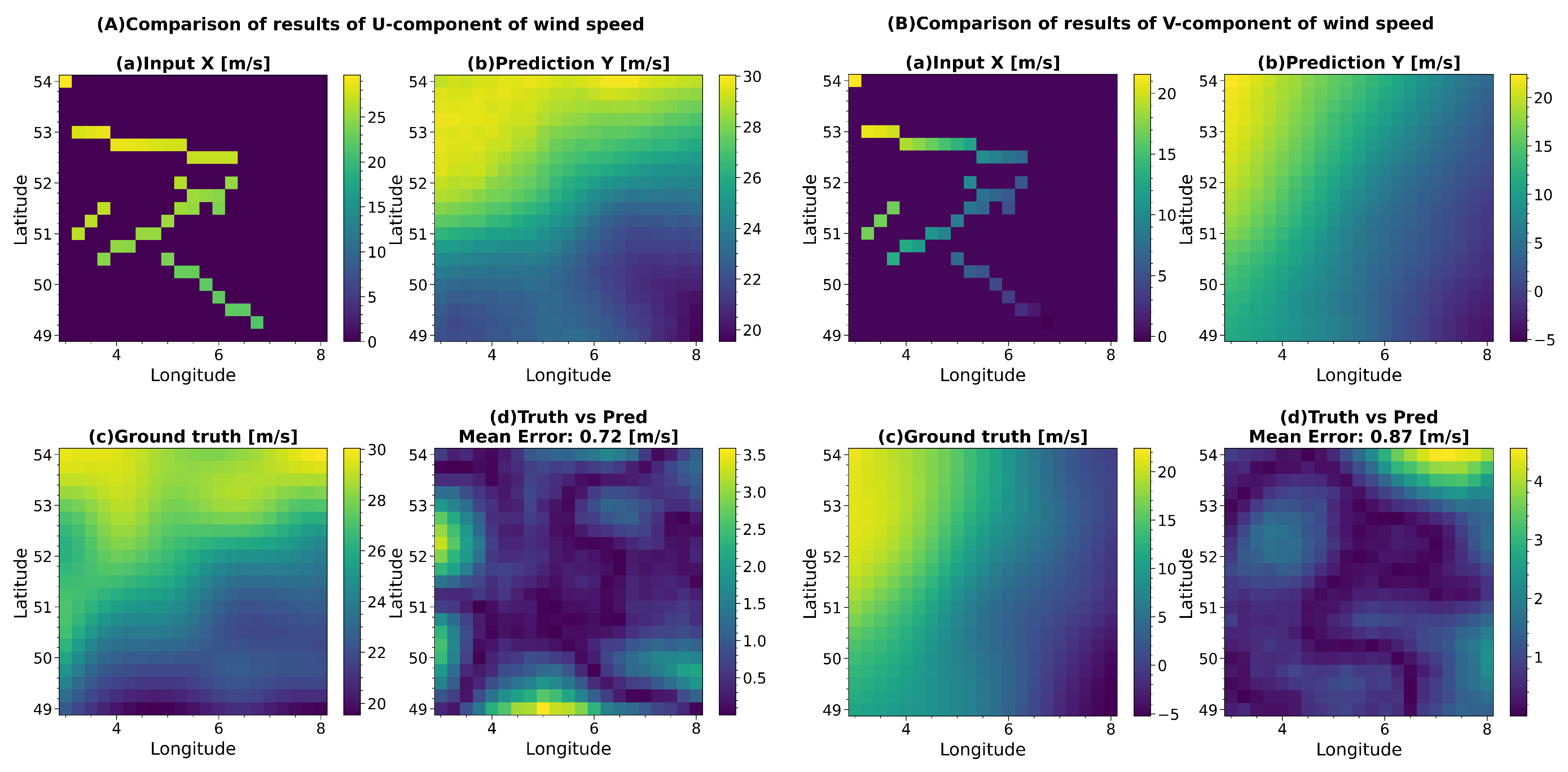
Figure 2 shows the result of the VMD output.
The reconstructed U and V components of the wind are presented in
Figure 2A and
Figure 2B, respectively. The subfigures a, b, and c in
Figure 2A,B represent the input data generated by real wind data masked with the random track, the model prediction results, and the real value, respectively. Subplot d shows the MAE between the predicted result and the ground truth. The mean error is the MAE of all data points in the current plot. All plots are in meters per second. Furthermore, the experimental data used in the figure comprise a pressure level of 300 hPa at 12:00 on 1 January 2022.
Images in
Figure 2 demonstrate that the reconstructed wind components U and V accurately represent the actual wind components. The model is able to yield effective and precise predictions even in areas with missing data (i.e., the areas covered by the Mask). In order to show the refactoring results more intuitively, the U and V components of the wind are also restored to the wind vector represented by the wind speed and wind direction, and the reconstructed wind field is plotted on the map, as shown in
Figure 3. The reconstructed wind field is plotted in
Figure 3 and bounded by the region included in the data (the airspace covers The Netherlands and Belgium, as well as western Germany), where the dark brown area is the continent, the light blue area is the ocean, and the green area indicates the area where the observations are present (that is, the unmasked area). Each arrow represents a reconstructed wind vector, which represents both direction and magnitude. Compared with
Figure 2,
Figure 3 can reflect the reconstruction results more intuitively.
Figure 3 shows the reconstruction results of transforming the U and V components of
Figure 2 into the wind vector field represented by wind speed and wind direction. It is more intuitive to see from
Figure 3 that the proposed model can effectively and accurately reconstruct the wind field. By comparing
Figure 2 with
Figure 3 (upper right corner of
Figure 3a,b, the prediction is northeast wind, the real is southeast wind), it can be seen that although there is a certain error in the prediction of V component of wind by the model, in the reconstructed wind vector field, the deviation between the reconstructed result and the real value is small. The VMD can effectively predict the wind speed and direction trends in the Mask area, and the errors of wind direction and wind speed are within an acceptable range.
However, when there is a dramatic change of wind in the Mask region, the model prediction results will produce certain errors.
Figure 4 shows two examples in the test set. The left figure of
Figure 4 shows an example when the regional atmospheric pressure imbalance leads to a large angle difference in the wind field, and the right figure of
Figure 4 shows a situation when the northeast region is dominated by southwest wind, the southwest region is composed of northwest wind and southwest wind, and the two winds meet in the middle region to produce an area with wind speed close to 0 but unstable wind direction. It can be seen from
Figure 4 that the model can still effectively predict the overall trend of the wind field distribution under such challenges. However, it is hard to avoid that there are some errors in the prediction of wind speed and direction in the mask region far from the observed value.
3.3. Robustness Testing
To verify the robustness of the model (sensitivity under various test conditions), five tests were conducted based on the data from 2022. For ease of explanation, here is a detailed description of the sub-datasets used for each test. Subset 1 contains the data for February, May, August, and November 2022, which are segmented according to pressure level to generate 37 datasets at different pressure levels. Subset 2 is sampled at a pressure level of 300 hPa in 2022. Subset 3 uses the same dataset as Subset 2 but manually limits the number of pseudo-tracks of the Mask region. Subset 4 is the subset sampled at 300 hPa on the 1st and 15th of September, October, November, and December 2022 at 12:00. Subset 5 is the subset sampled at 300 hPa at 12:00 on on 1st day of each month from January to October 2018.
3.3.1. Pressure Level
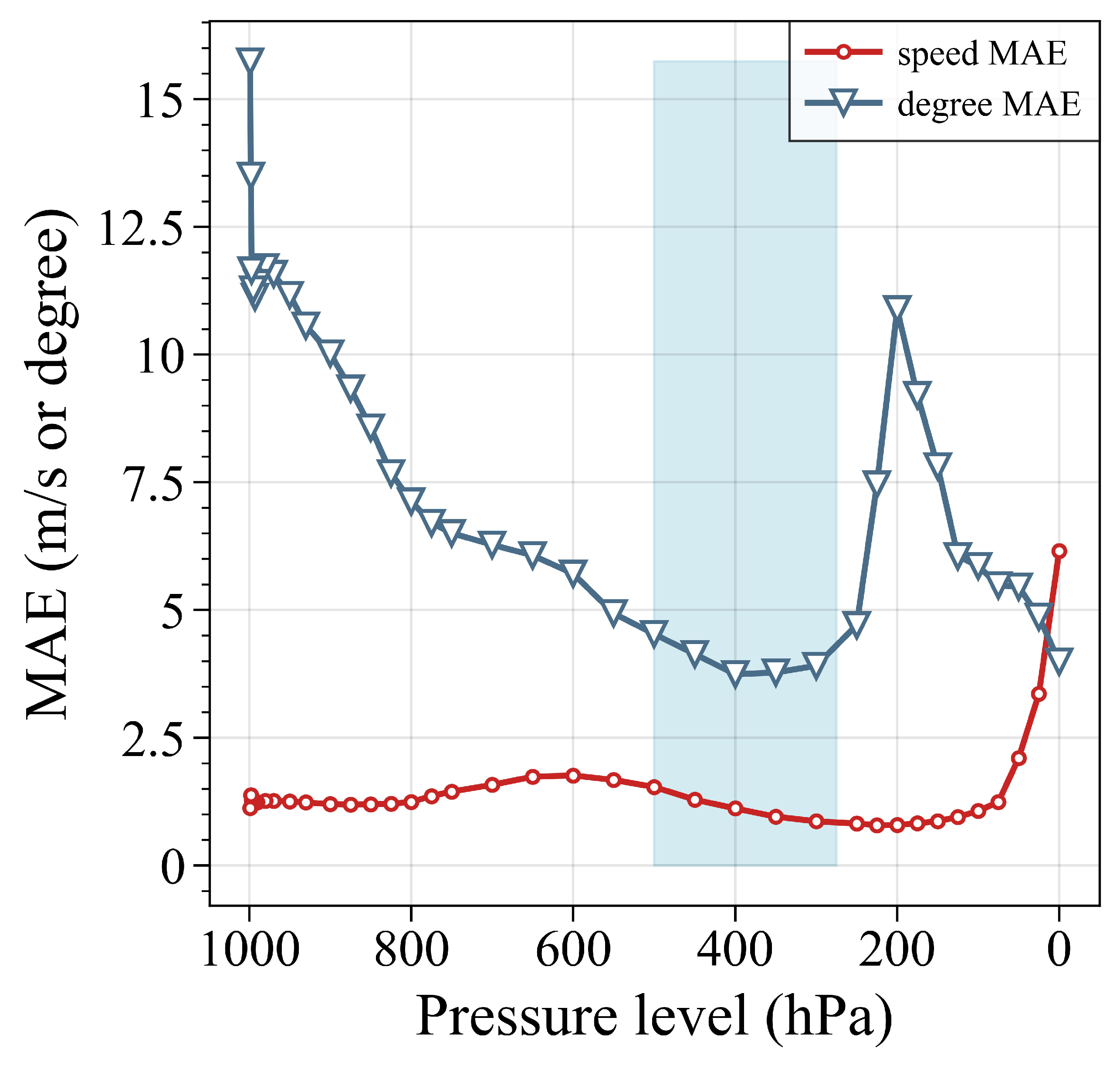
Firstly, the sensitivity of the model to pressure level was tested. The tests were conducted on Subset 1, where the data were spaced 2 months apart to avoid seasonal effects on the results. In
Figure 5, the error curve of wind speed and wind direction is drawn with the pressure level as the horizontal coordinate and the MAE as the vertical coordinate, in which the pressure level is arranged from 1000 hPa to 1 hPa (corresponding to the altitude from low to high to facilitate intuitive viewing), across 100 m to 58,000 m above sea level, approximately. The blue area in
Figure 5 indicates the possible pressure level of common civil aircraft during flight, that is, 225 hPa to 500 hPa. This altitude range is studied more in this paper.
It can be seen from
Figure 5 that the error of wind direction is greatly affected by the pressure level, especially in the low-altitude area. However, in the blue region, the error distribution of wind speed and wind direction is not significantly affected by the change of pressure level, and the MAE shows a slight decreasing trend with the increase in altitude. The VMD network’s reconstruction effect is optimal at the typical cruising altitude of civil aviation, with wind direction and the speed MAE reaching their lowest values.
3.3.2. Distance Interval
The model was tested on Subset 2 to verify the reconstruction effect of the model on horizontal wind fields in common civil aviation altitude airspace. The performance of the proposed model on Subset 2 is recorded in
Table 2.
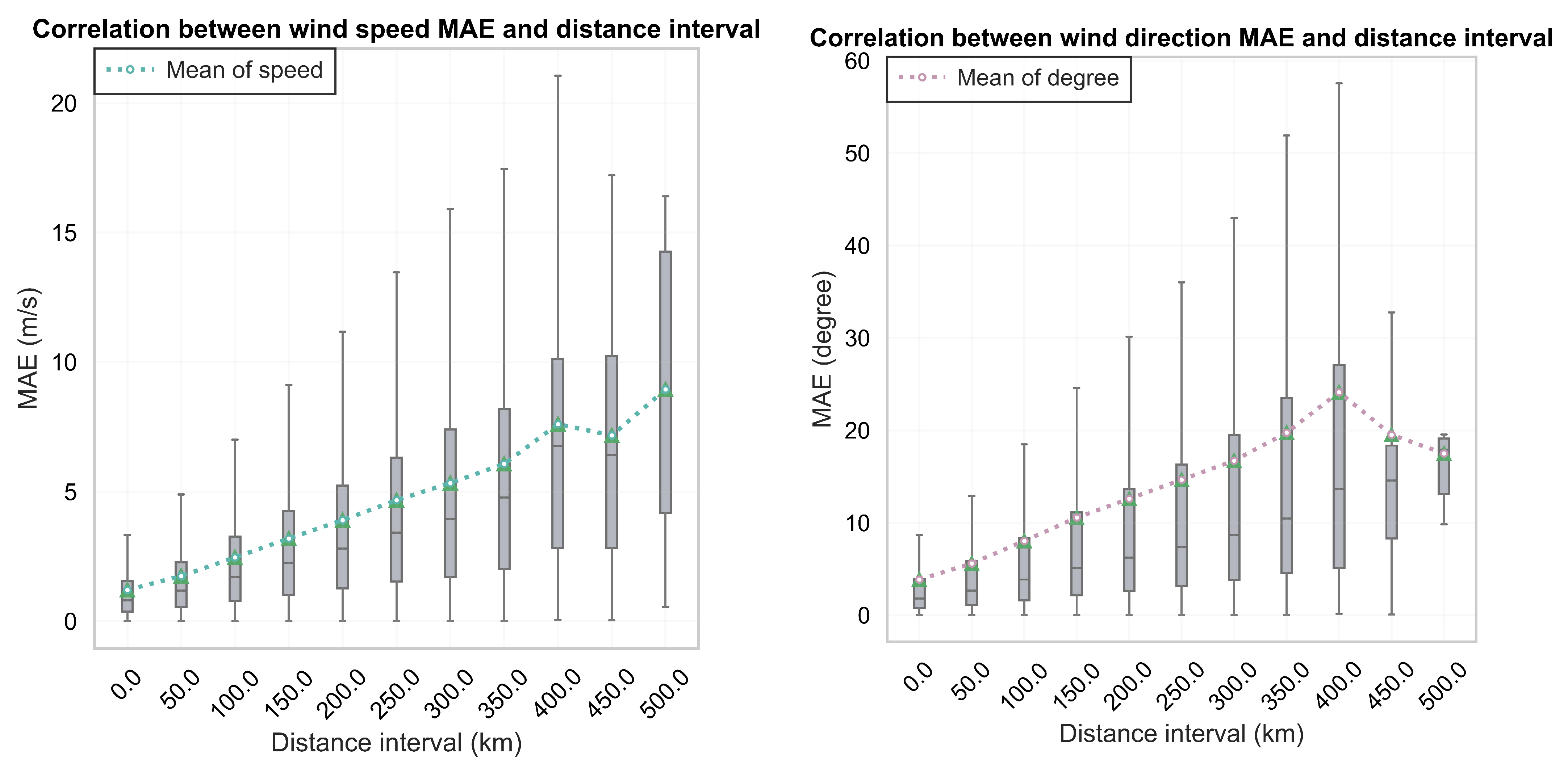
Considering that the model forecasts and reconstructs the wind field based on the existing data, the magnitude of the error may have a certain correlation with the minimum distance interval between the predicted position and the existing observed position (i.e., input X). The results of each reconstruction were statistically analyzed, and the distance interval and the corresponding MAE value in each prediction were recorded. The correlation between MAE and distance interval was plotted based on the statistical results with a step of 50 km interval.
Figure 6 shows the correlation between speed direction and distance interval.
As can be seen from
Figure 6, the overall trend of the forecast error mean curve increases with the increase in the distance interval from the known observation position, regardless of wind speed or wind direction. However, the prediction of wind direction seems to have better generalization ability. When the distance interval is greater than 400 km, the error of wind direction is significantly reduced.
3.3.3. Number of Pseudo-Track
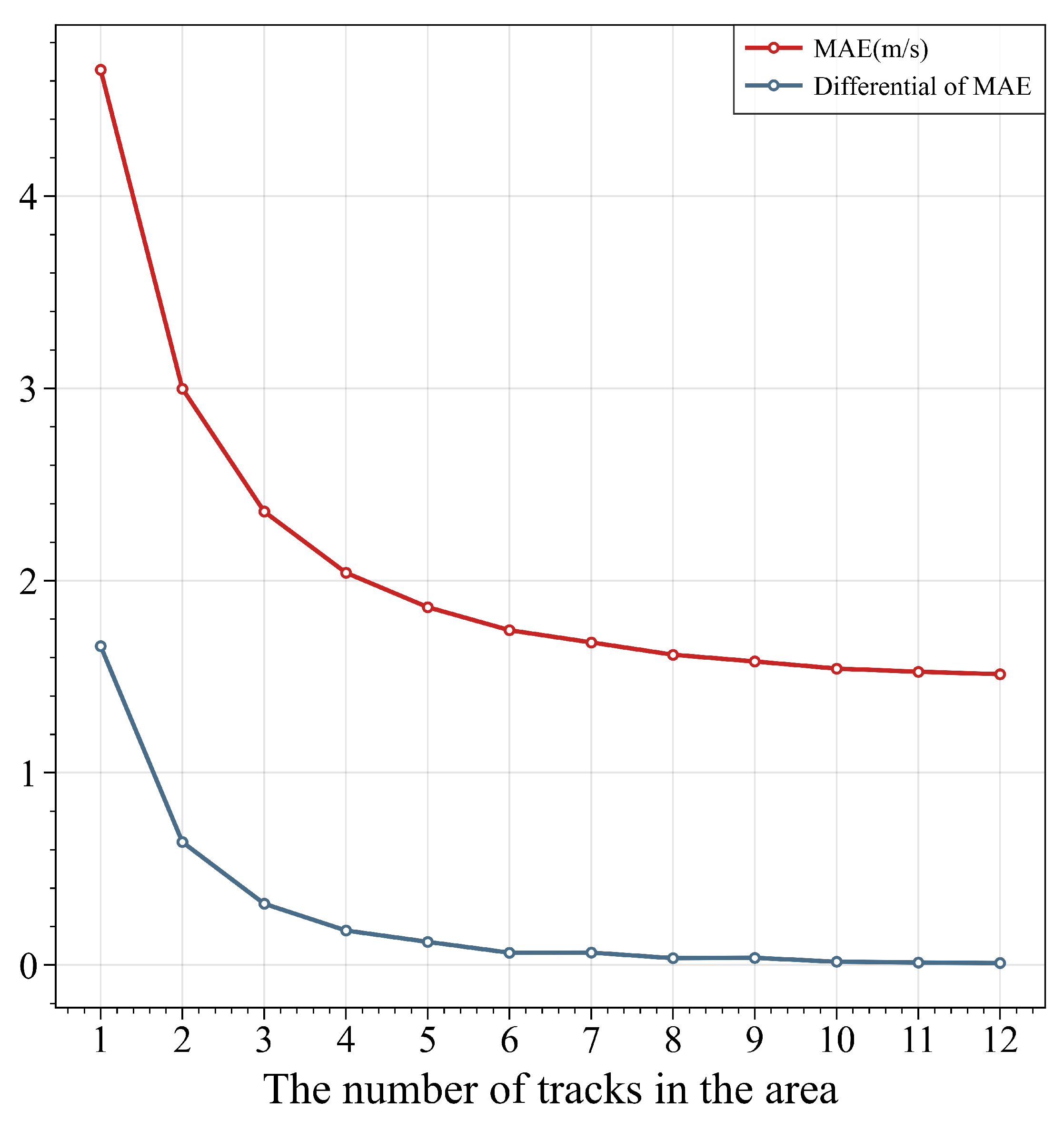
Considering that the number of tracks in airspace is uncertain, the model should be tested several times with the number of tracks as a variable to verify the sensitivity of the model to the number of tracks. The model was tested using Subset 3, manually setting the number of tracks from 1 to 12, and the results are shown in
Figure 7. The MAE curve in
Figure 7 represents the result of the wind speed reconstruction MAE as the number of tracks increases. The differential of the MAE is the gradient calculated for the MAE, which represents the speed of MAE’s decline. It can be seen from
Figure 7 that, at first, the MAE decreases dramatically as the number of tracks increases. When the number of tracks increases to more than 5, the decrease in MAE tended to be stable, and the gradient almost tended to 0. The MAE no longer declined significantly with the number of tracks.
3.3.4. Comparison
Furthermore, in order to illustrate the accuracy of the prediction results of the proposed model, the proposed model was compared with the GPR model and PINN model proposed in [
16,
20], respectively. To ensure the fairness of the comparison, testing was carried out on the same dataset as the GPR and PINN models, corresponding to Subsets 4 and 5, respectively.
Table 3 and
Table 4 show a comparison of the VMD vs. GPR and VMD vs. PINN.
Although the error of the VMD is larger than that of the GPR and PINN at some test dates, by comparing
Table 3 and
Table 4, the error of wind speed and direction of the VMD is about 33.8 % and 48.2 % smaller on average than that of the GPR, and about 19.1% and 38.6% smaller than that of the PINN.
3.4. Discussion
This study introduces and validates the VMD network for reconstructing wind fields. The model utilizes incomplete wind observation data to reconstruct the complete horizontal wind field. By training on the ERA5 dataset, the VMD network can extract features from incomplete wind data along the flight trajectory. These features are then decoded and upsampled to reconstruct a complete horizontal upper-air wind field. This study conducted various tests on different samples of the dataset, including sensitivity tests for the pressure level, distance interval, number of pseudo-tracks, and comparison with other models. The test results indicate that the VMD network performs well at the typical cruising altitudes of civil aviation, with the MAE of wind speed and wind direction being less than 2.5 m/s and 5 degrees, respectively. When compared with the GPR model and PINN network, the proposed VMD model demonstrates superior performance on the same dataset.
In areas with significant wind changes, the model’s predictions may be biased. When we tested the distance interval and amount of pseudo-track sensitivity, we found that errors increased with larger distance intervals or a smaller number of tracks. This happened because, in the Mask region, the wind speed and direction are no longer uniform and can change significantly, leading the model to make incorrect wind field predictions. To reduce this error, we can increase the number of cases of complex weather in the model training set. This will help the model learn correlations between data from large distance intervals, allowing it to predict wind field distribution from a macroscopic perspective rather than focusing on local features. Another approach is to introduce a wider range of observations, including expanding the data from X, Y, and Z axes, to provide more information for the prediction.
4. Conclusions
This paper developed a new VMD network to reconstruct a wind field across the entire airspace from incomplete wind data. The approach involved generating random tracks and applying a Mask operation to the ERA5 reanalysis dataset to create a large number of training data similar to the track. The model was evaluated on a validation set separate from the training set, yielding an MAE of 1.83 m/s for wind speed and 5.78 degrees for wind direction. When compared to the GPR model and PINN network, the VMD model reduced wind speed errors by 33.8% and 48.2%, respectively, and direction errors by 19.1% and 38.6%, respectively. The experiment demonstrates that the VMD model can efficiently and accurately reconstruct the horizontal wind field.
In future studies, we plan to use actual ADS-B and S-mode-combined observational data, which were the main focus of this study. Additionally, we aim to further extend the reconstruction dimension in the vertical direction so that the model can reconstruct a wind field in three-dimensional space. With further optimization, this method has the potential to provide comprehensive real-time meteorological data for the aviation and meteorological fields, ultimately enhancing the safety and efficiency of flights.