An Improved Approach for Reducing the Dimensionality of Wing Aerodynamic Optimization Considering Longitudinal Stability
Abstract
1. Introduction
- Gradient-based algorithm(e.g., Sequential quadratic programming algorithm (SQP), BFGS quasi-Newton algorithm, conjugate gradient algorithm, etc.)This type of optimization algorithm has a fast solution speed. Combining with the adjoint method [4,5,6] can effectively solve the wing aerodynamic optimization problem at high subsonic and transonic cruise conditions [7,8,9]. However, for addressing multi-extremum problems, it is possible to fall into a local optimum due to the algorithm’s inherent limitations.
- Gradient-free algorithm(e.g., Genetic algorithm (GA), simulated annealing method (SA), particle swarm optimization algorithm (PSO), etc.)Some of these optimization algorithms have proved their good global search capabilities in practice. Nonetheless, these algorithms require a great deal of aerodynamic evaluation during optimization, which will significantly increase the time and resource cost [10].
- Develop optimization strategies to enhance high-dimensional problem adaptabilityIntroducing low-fidelity sample data [25,26,27,28,29] or gradient information [30,31,32,33] into the surrogate-based optimization algorithm to establish the surrogate model has been proven effective. Combining parallel computing technology to develop a parallel infilling strategy [34,35,36] to maximize the usage of high-performance computers’ large-scale parallel computing capabilities
- Research into methods to reduce the dimensionality of optimization problems
- Methods based on the analysis of dataVariable screening can minimize the number of design variables by finding the most pertinent variables to the design problem and eliminating those that are less pertinent [37,38]. However, this method reduces the design space, and correlations of omitted variables may surface later in the optimization.Dimensionality reduction [39] can capture potential patterns in variables in a reduced space without deleting any variables, therefore enabling optimization to be performed in a reduced space [40,41,42,43]. Some nonlinear dimensionality reduction methods [44,45] are also progressively applied to aerodynamic optimization
- Methods based on aerodynamic characteristics
2. Methodology
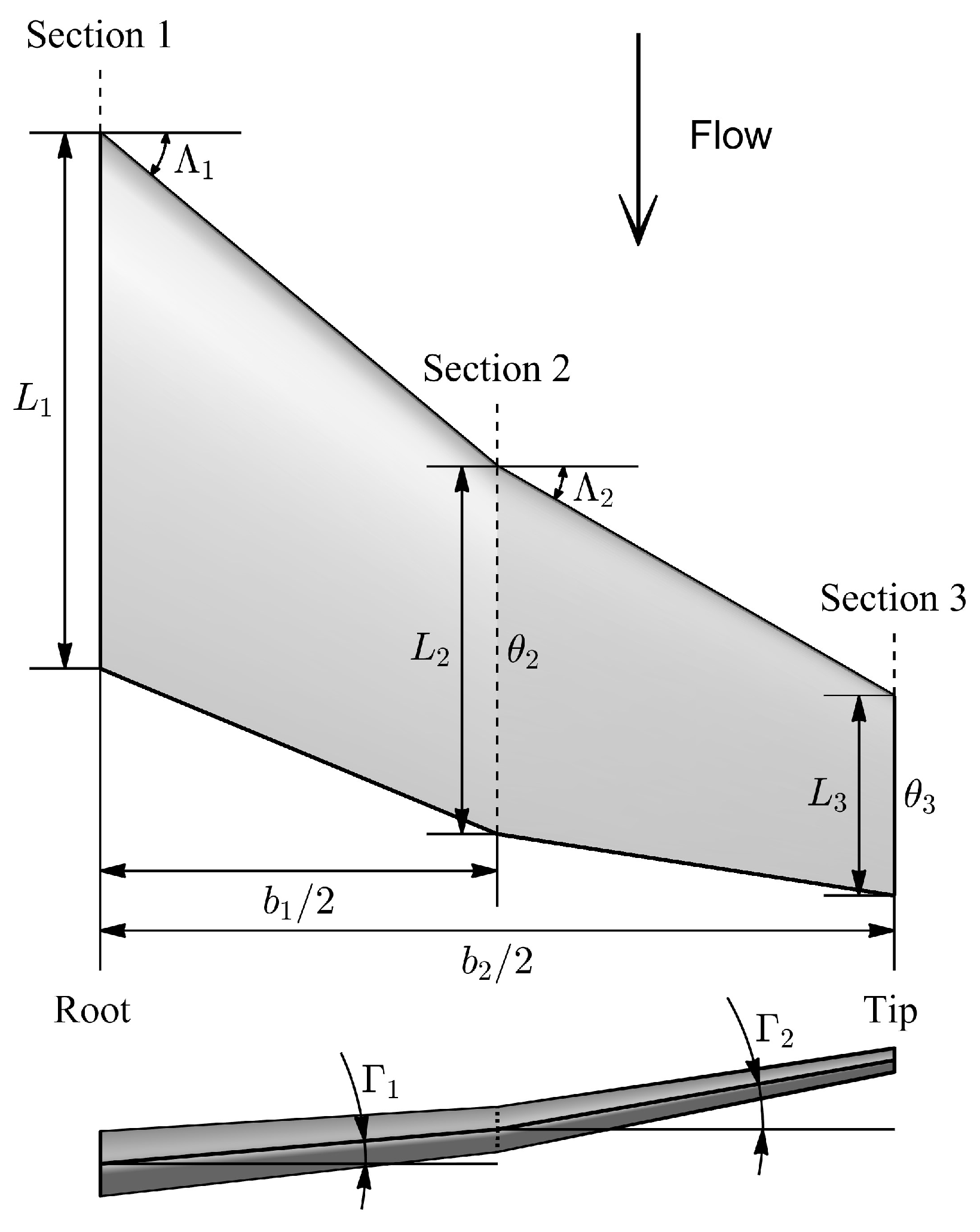
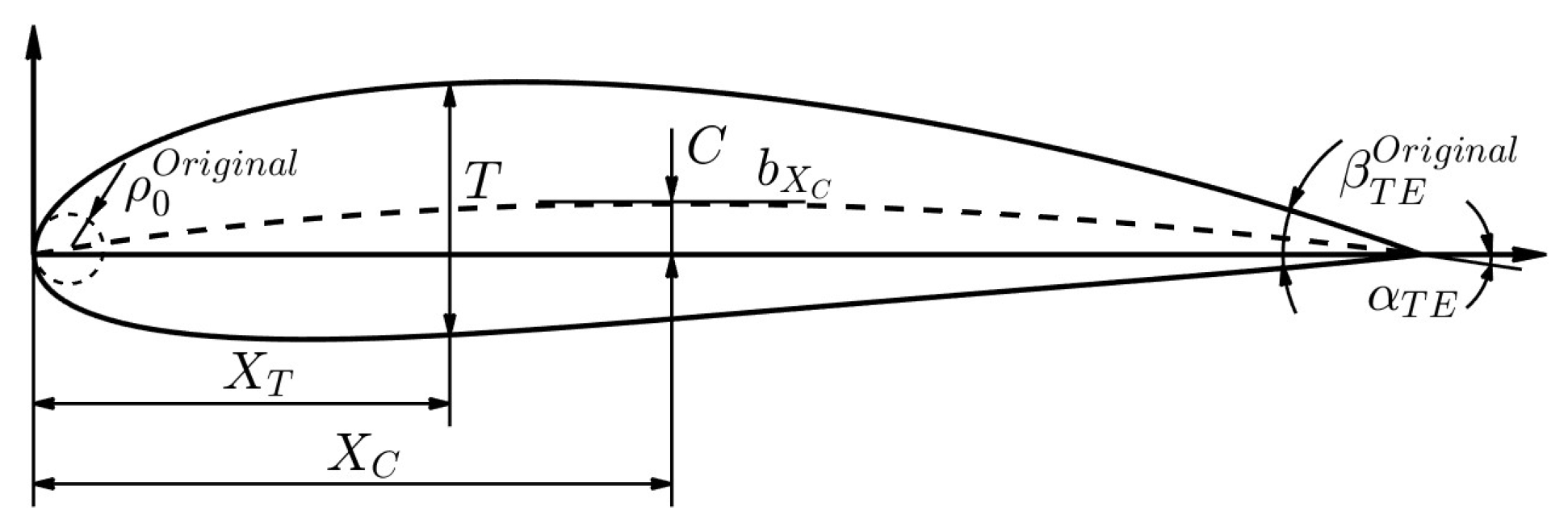
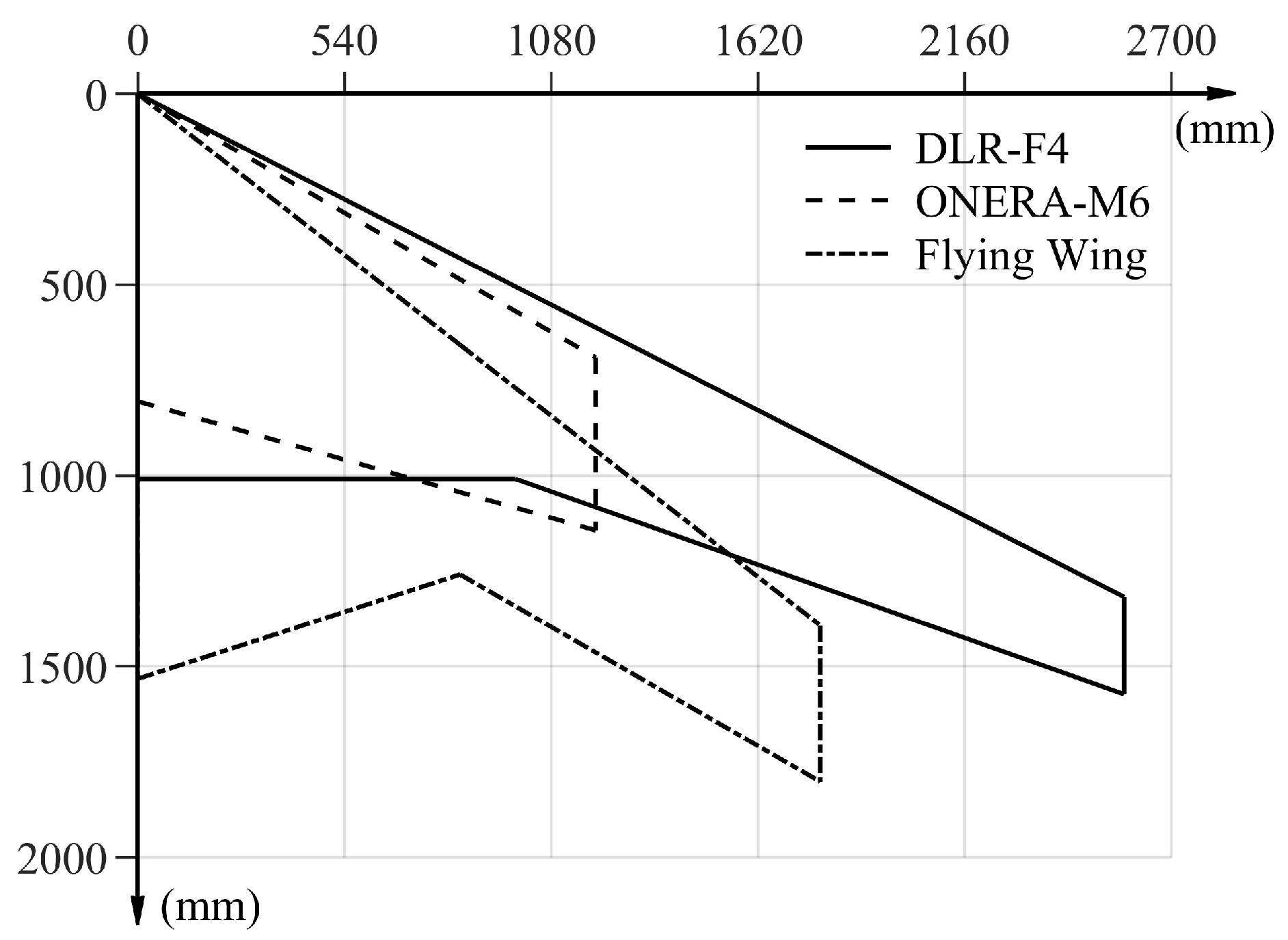
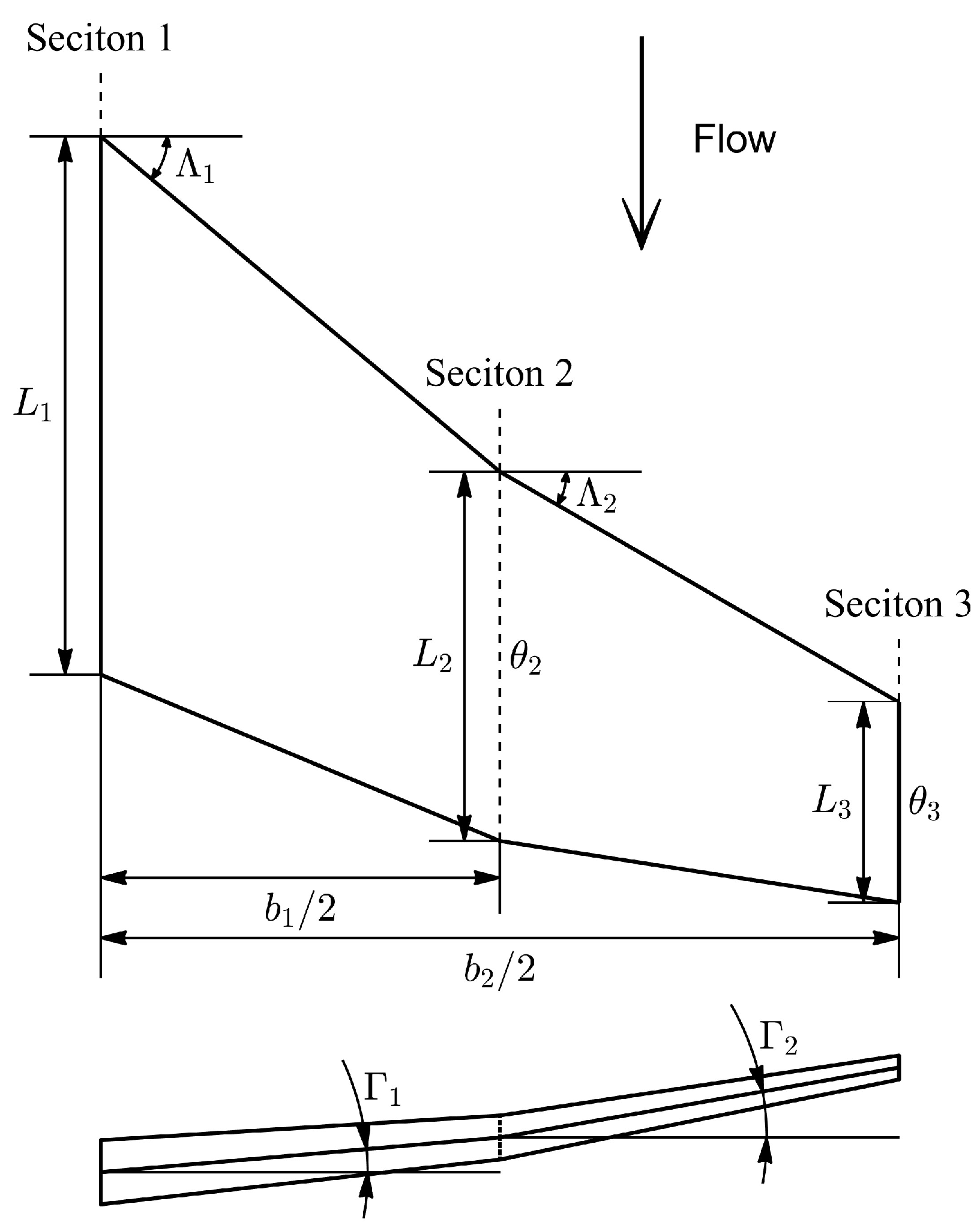
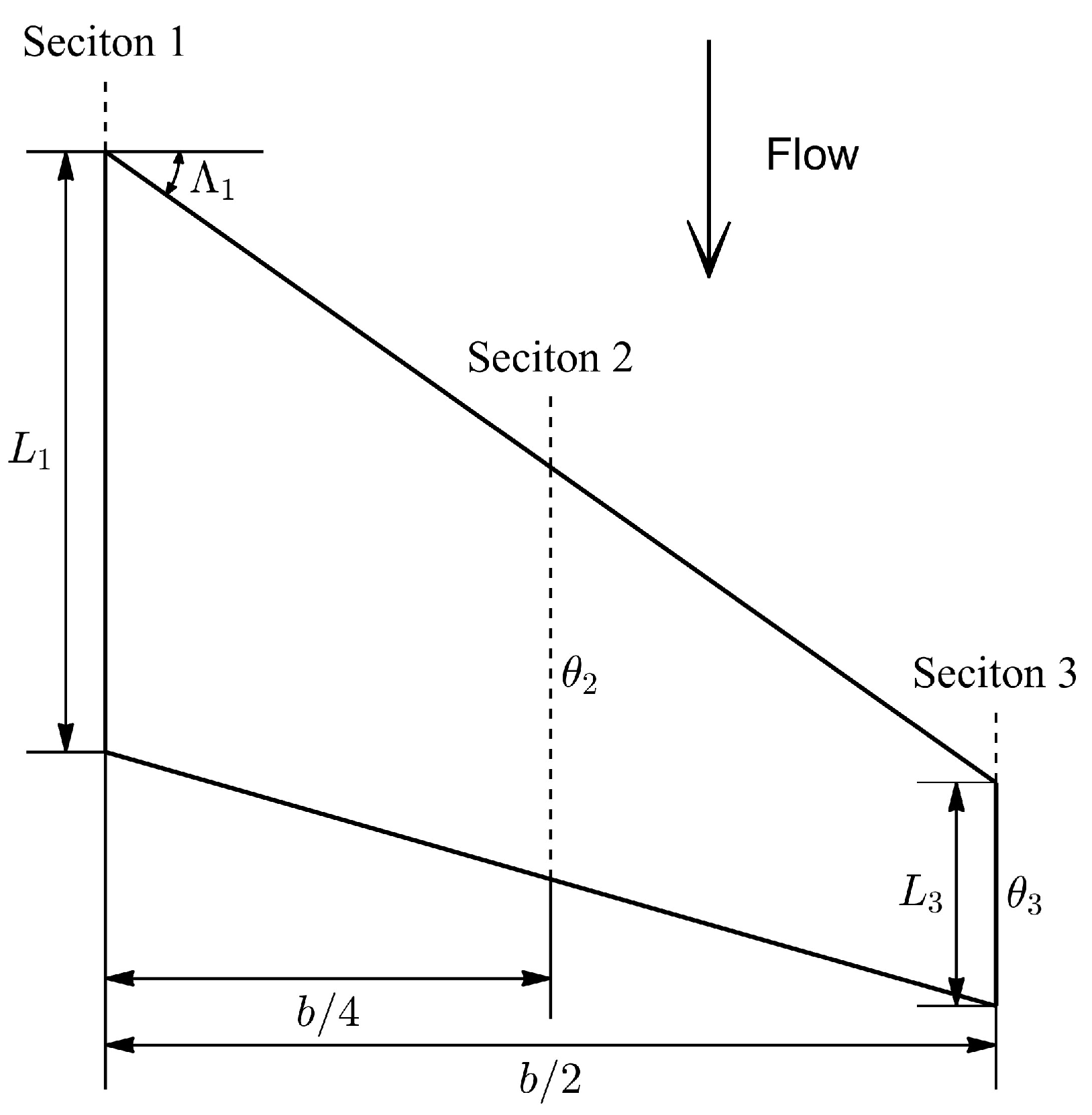
2.1. Geometric Parameterization
- Chordwise location of the maximum camber ()
- Maximum camber ()
- Camber line curvature on the location of maximum camber ()
- The angle between the camber line and the chord line on the trailing edge ()
- Chordwise location of the maximum thickness ()
- Maximum thickness ()
- Dimensionless quantity of the leading-edge radius ()
- Dimensionless quantity of the trailing edge boat-tail angle ()
2.2. Problem Definition and Methods for Reducing Dimensions
2.2.1. The Traditional Aerodynamic-Based Method Based on Camber-Thickness Decoupling
- is a variable set composed of all variables that describe the wing planform.
- is a variable set composed of all variables that describe the camber of the airfoil section, is the wing section identifier.
- is a variable set composed of all variables that describe the thickness of the airfoil section.
- Fix and perform optimization ,
- Under the optimal result of 1 (, ), execute optimization
- The application scope is uncertain because of the unclear definition of low angle of attack and small camber-thickness (Assumptions of the thin-wing theory).
- The total time of two lower-dimensional optimizations may not be less than that of a higher-dimensional optimization.
2.2.2. The Improved Approach Based on Decoupling Analysis
- can be decoupled from each other in the objective function .
- hardly contributes to the constraint function .
- For any values of , .
- For any values of , .
- For any values of , .
2.3. Aerodynamic Analysis
2.4. Dynamic Adjustment of the Center of Gravity
2.5. Surrogate-Based Optimization Algorithm
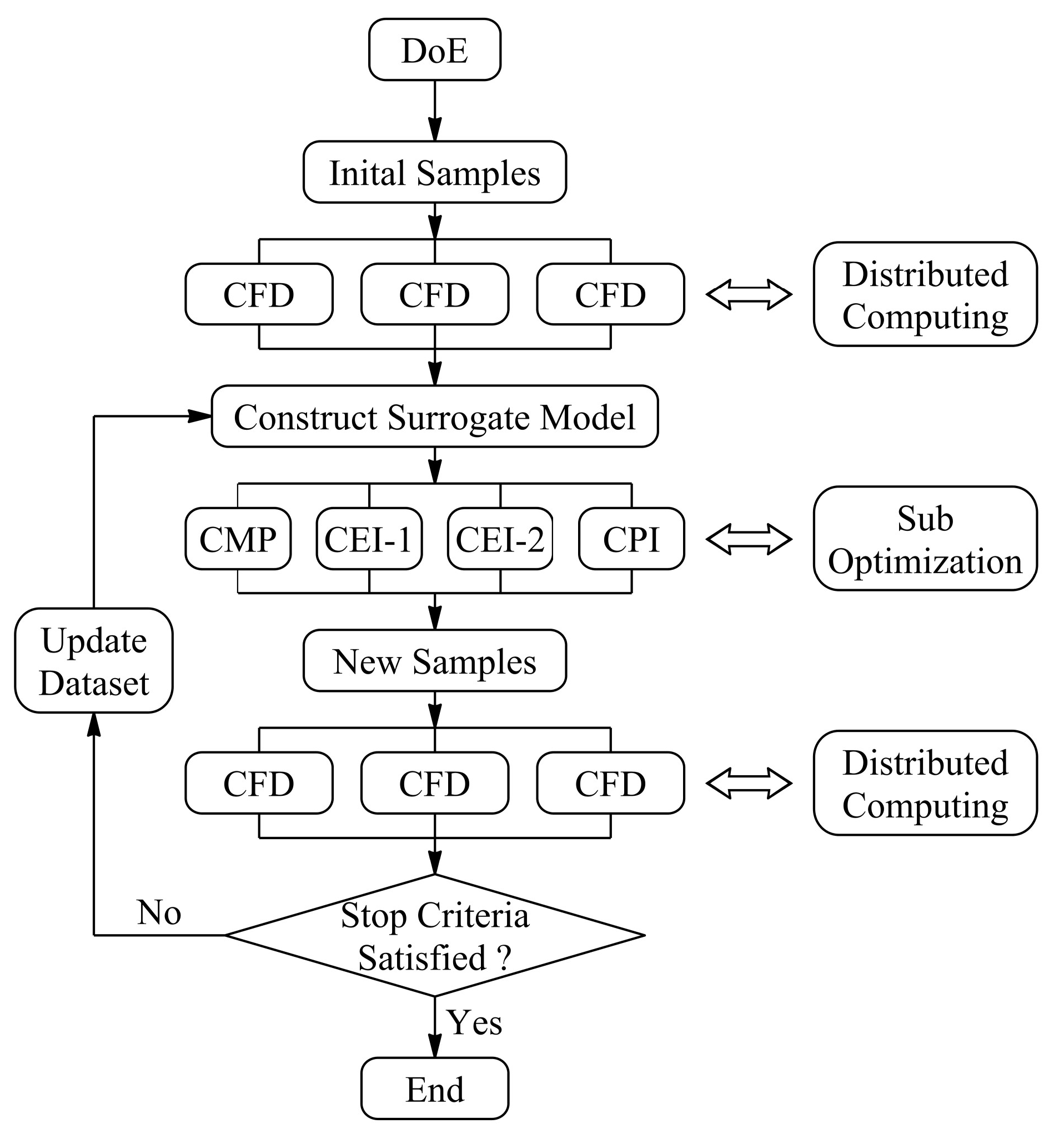
2.5.1. Algorithm Framework
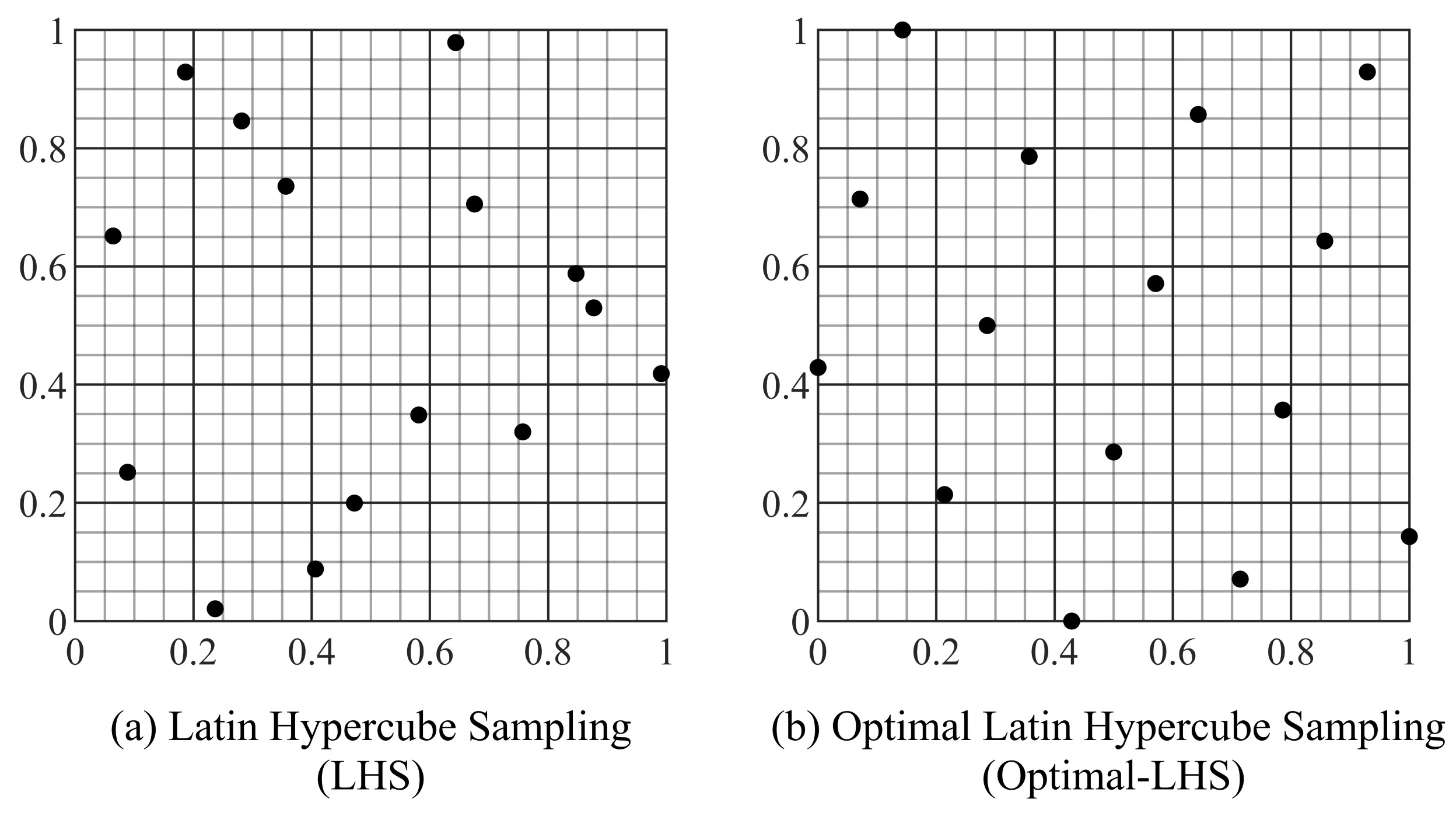
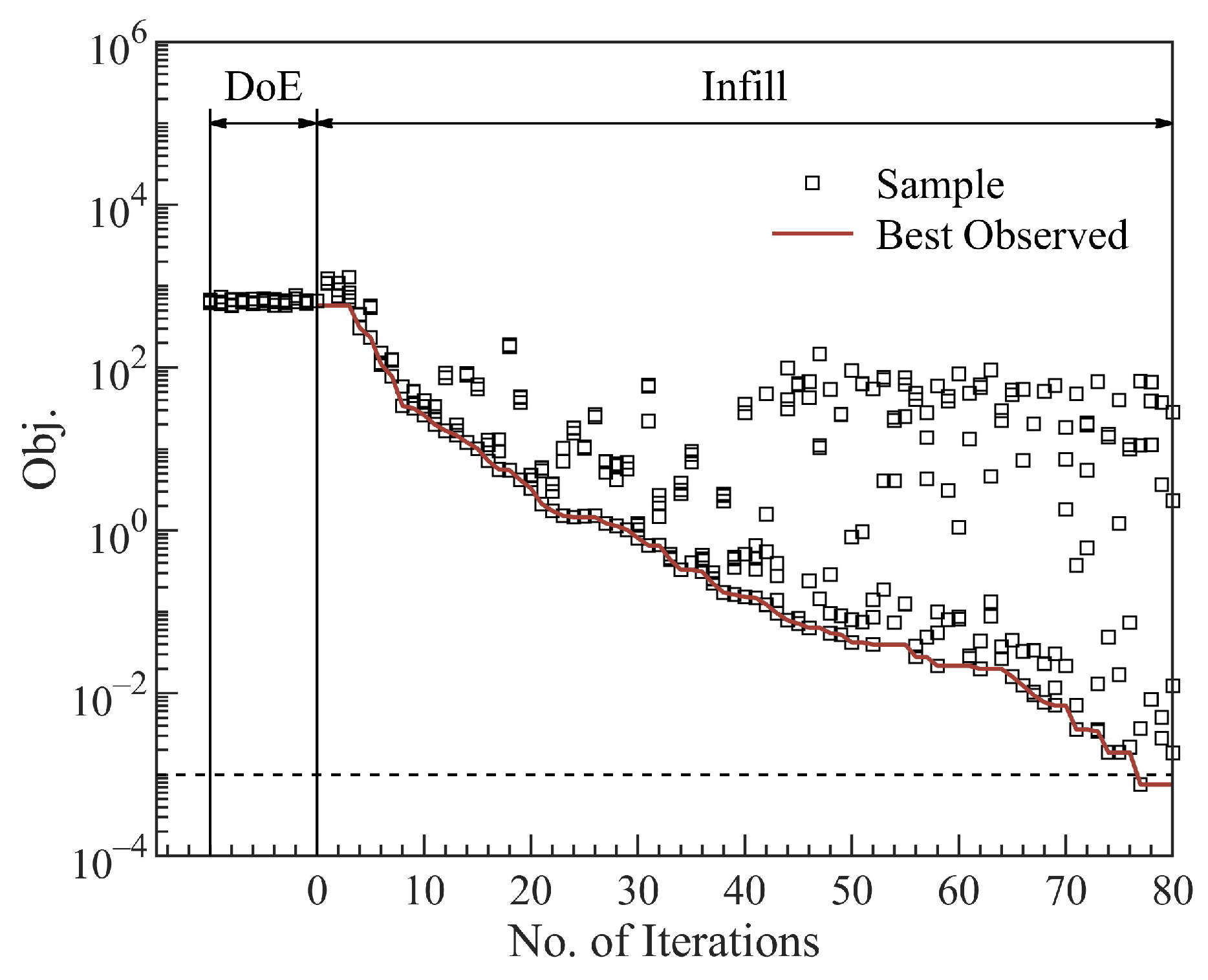
- Generate initial samples by the design of experiments (DoE). The Optimal-LHS method derived from the LHS method ensures a high level of uniformity in design space-filling, as Figure 8 shows.
- Evaluate samples by CFD with distributed computing, and the response values of objective and constraint functions are obtained.
- Construct surrogate models (Kriging model).
- Evaluate new samples by CFD with distributed computing, and the response values of objective and constraint functions are obtained.
- Return to step (3), add new samples to the dataset, and update the surrogate model. Repeat the preceding steps until the resulting sample converges to the local or global optimal solution.
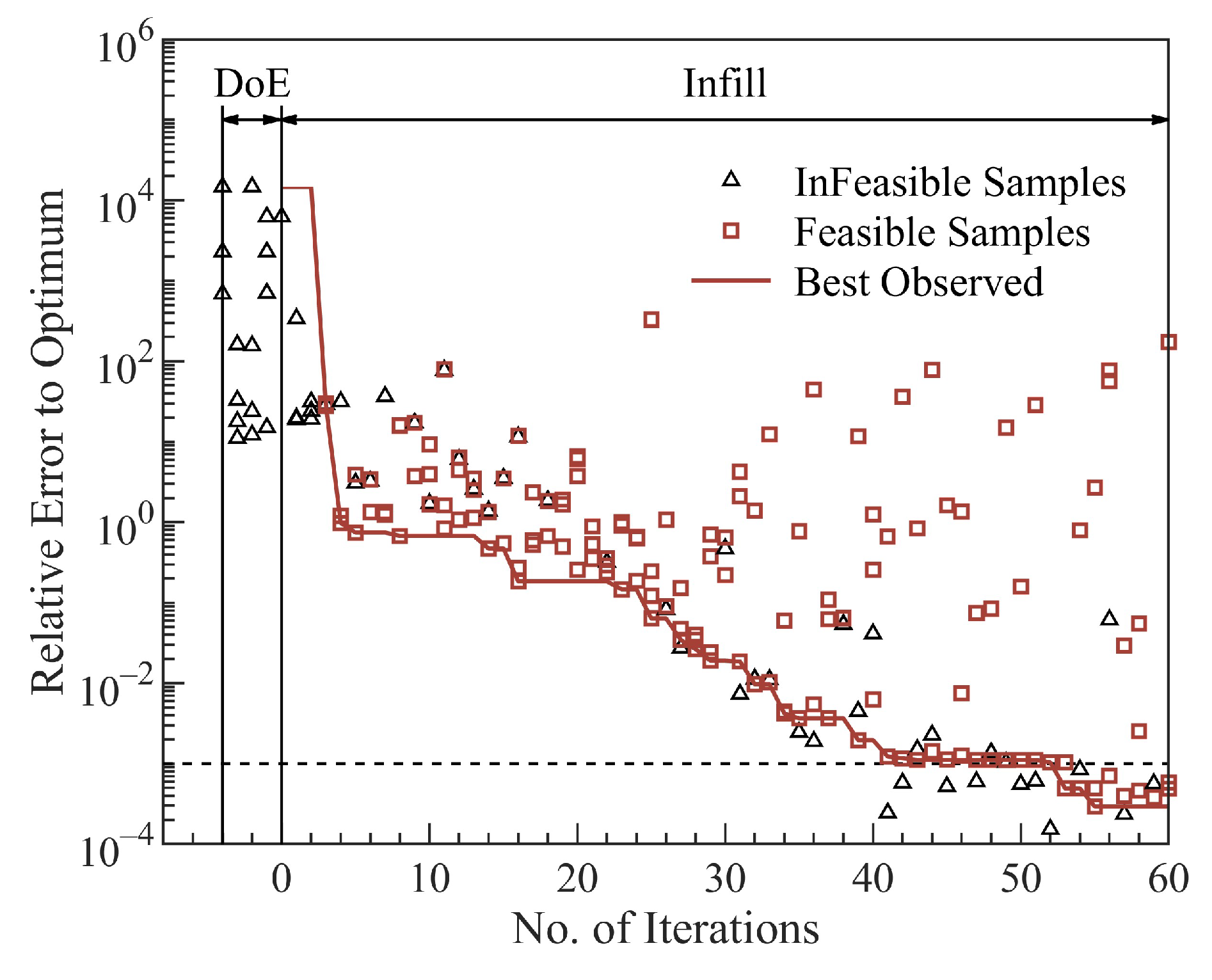
2.5.2. Constrained Global Optimization Test Case of a G9 Function
2.5.3. Unconstrained Global Optimization Test Case of a Sum-Squares Function
2.6. Sensitivity Analysis of Variance
3. Analysis Based on the Traditional Method
- Generate 300 samples by the Optimal-LHS method.
- Evaluate each sample at by CFD.
- Define the longitudinal static stability margin and automatically adjust the CG position. at are used as the response values to build the surrogate model:
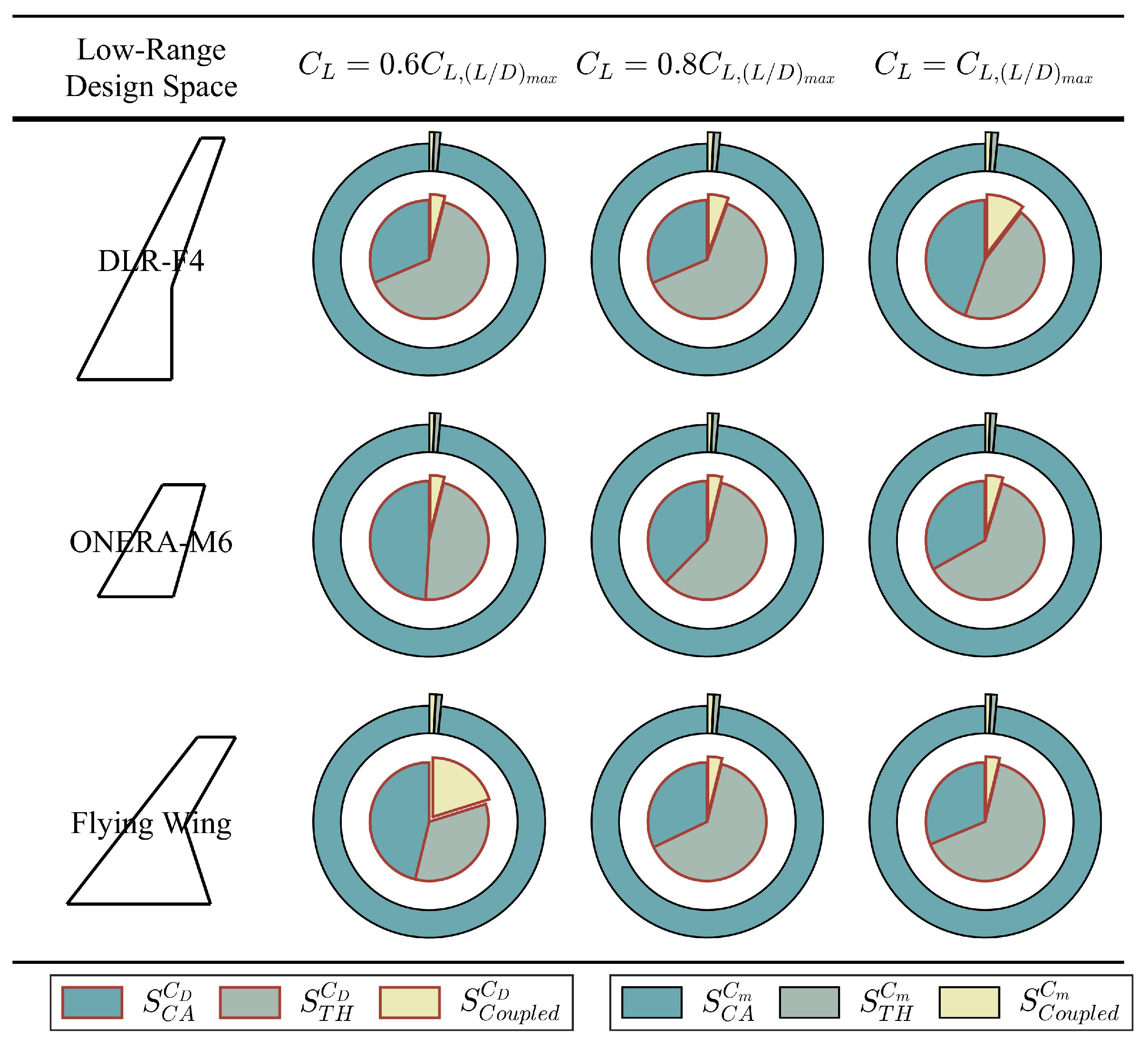
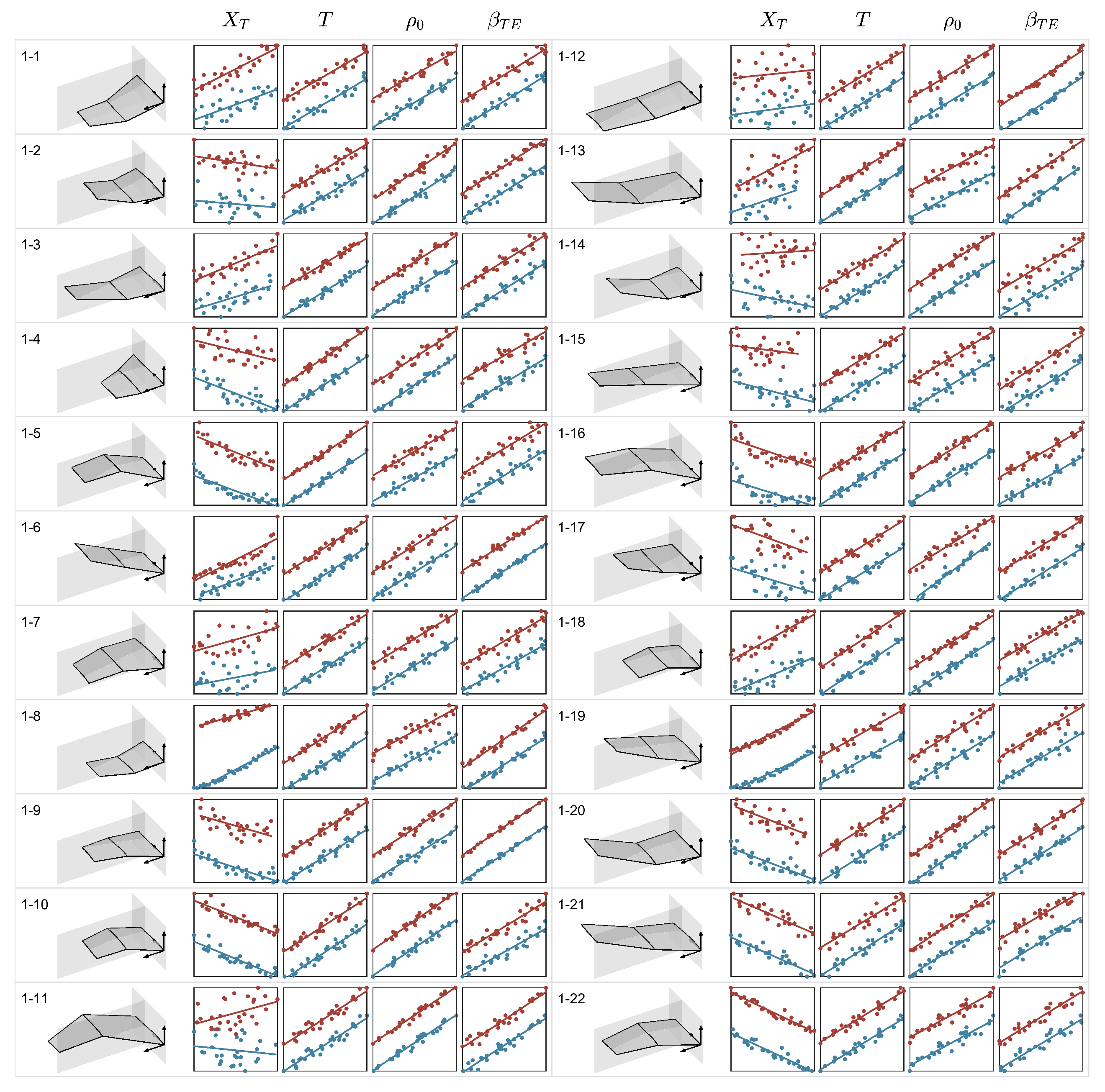
- Based on ANOVA analysis, in are obtained, where:means the sum of the main effects ofmeans the sum of the main effects ofmeans the interaction effect between and
- In wide-range design spaces, the interaction effect between and in the objective function cannot be ignored.
- In low-range design spaces, the interaction effect between and in the objective function appears unimportant.
- In both wide-range and low-range design spaces, hardly contributes to the constraint function .
- The applicable range is ambiguous since the definitions of low angle of attack and small camber-thickness are unclear. This section demonstrates that this method became possible due to the drastic reduction of the design space.
- To reach the same objective, two lower-dimensional optimizations may not take less time than one higher-dimensional optimization.
- In contrast to some rapid aerodynamic evaluation methods (e.g., vortex lattice method) that only require the data of the camber in the wing, the CFD-RANS method requires the complete data of thickness and camber. This means that before we start the first low-dimensional optimization (planform and camber optimization), we need to assign values to thickness variables for which the logic of the assignment is unclear.
4. Complete Derivation of the Improved Approach
- Verify that thickness variables can be decoupled from each other in the objective function , and hardly contributes to the constraint function . Where is the wing section identifier.
- Establishing a data-driven aerodynamic characteristics model analyzing the correlations between and objective function .
4.1. Verification of Decoupling of Thickness Variables
- Generate 100 samples by the Optimal-LHS method.
- Evaluate each sample at by CFD.
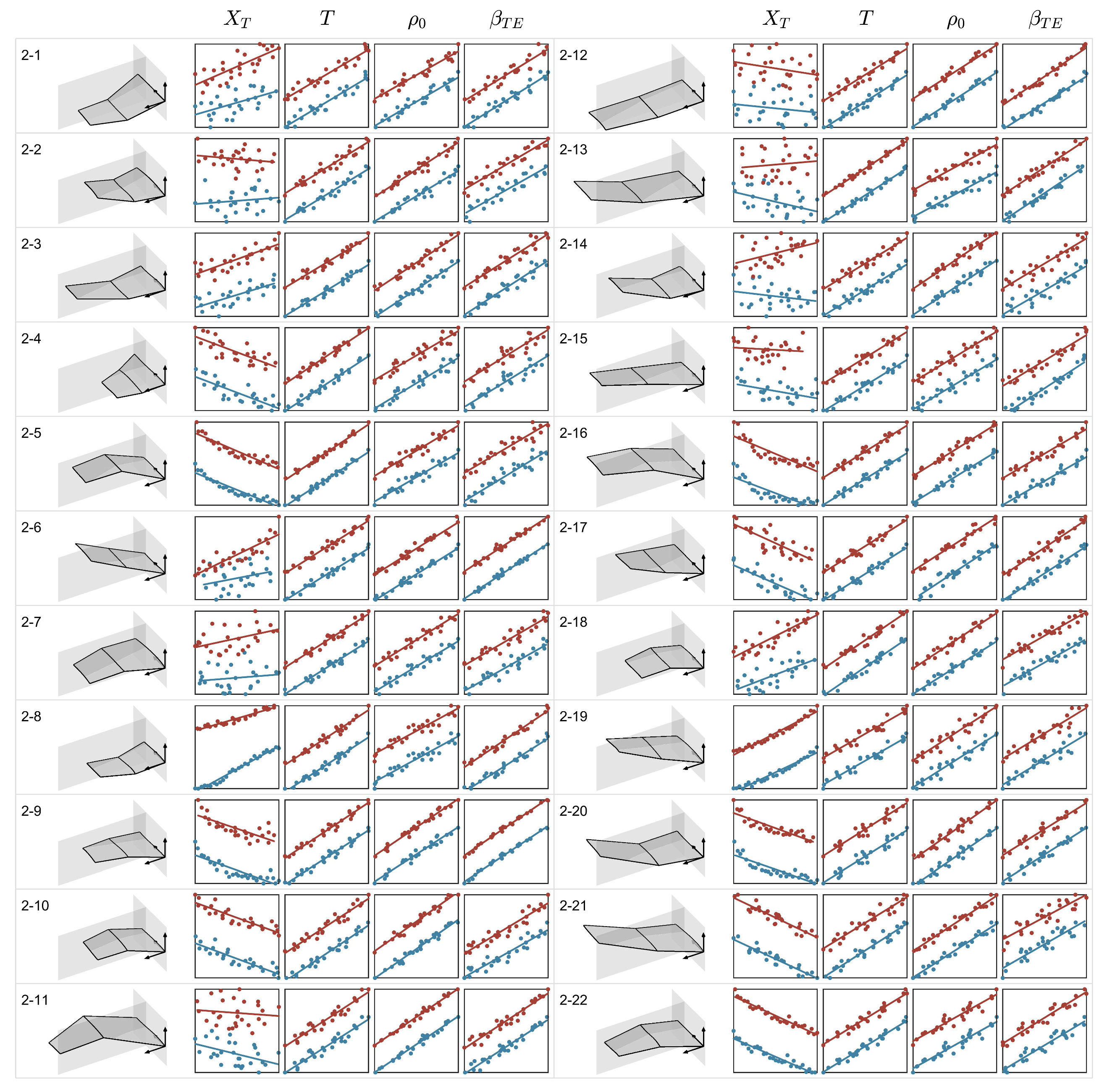
- at are used as the response values to build the surrogate model:where represents the wing section identifier.
- Based on ANOVA analysis, in are obtained.
- Define the longitudinal static stability margin and automatically adjust the CG position. at are used to analyze the magnitude of the influence of thickness variables on constraint function.
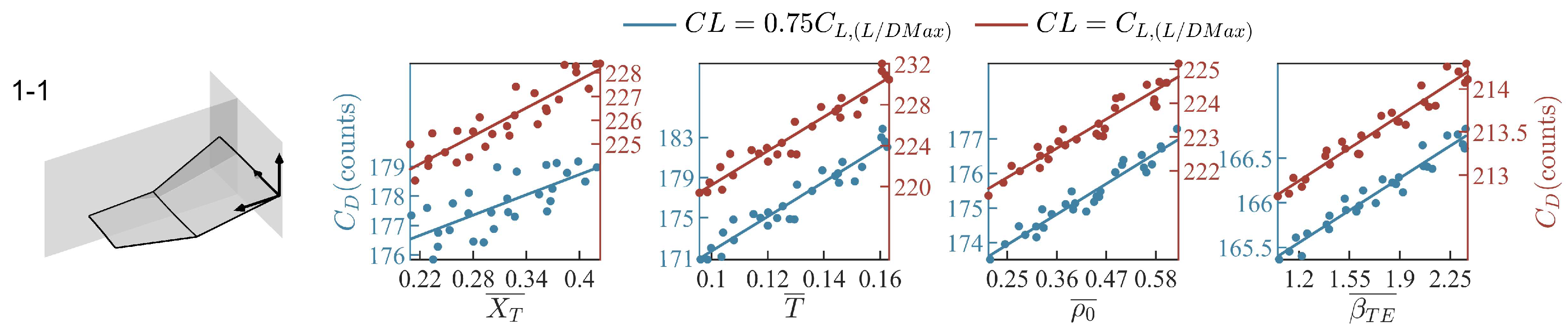
- can be decoupled from each other in the objective function . (we consider negligible below about 5%)
- hardly contributes to the constraint function .
4.2. Establishment of the Data-Driven Aerodynamic Characteristics Model
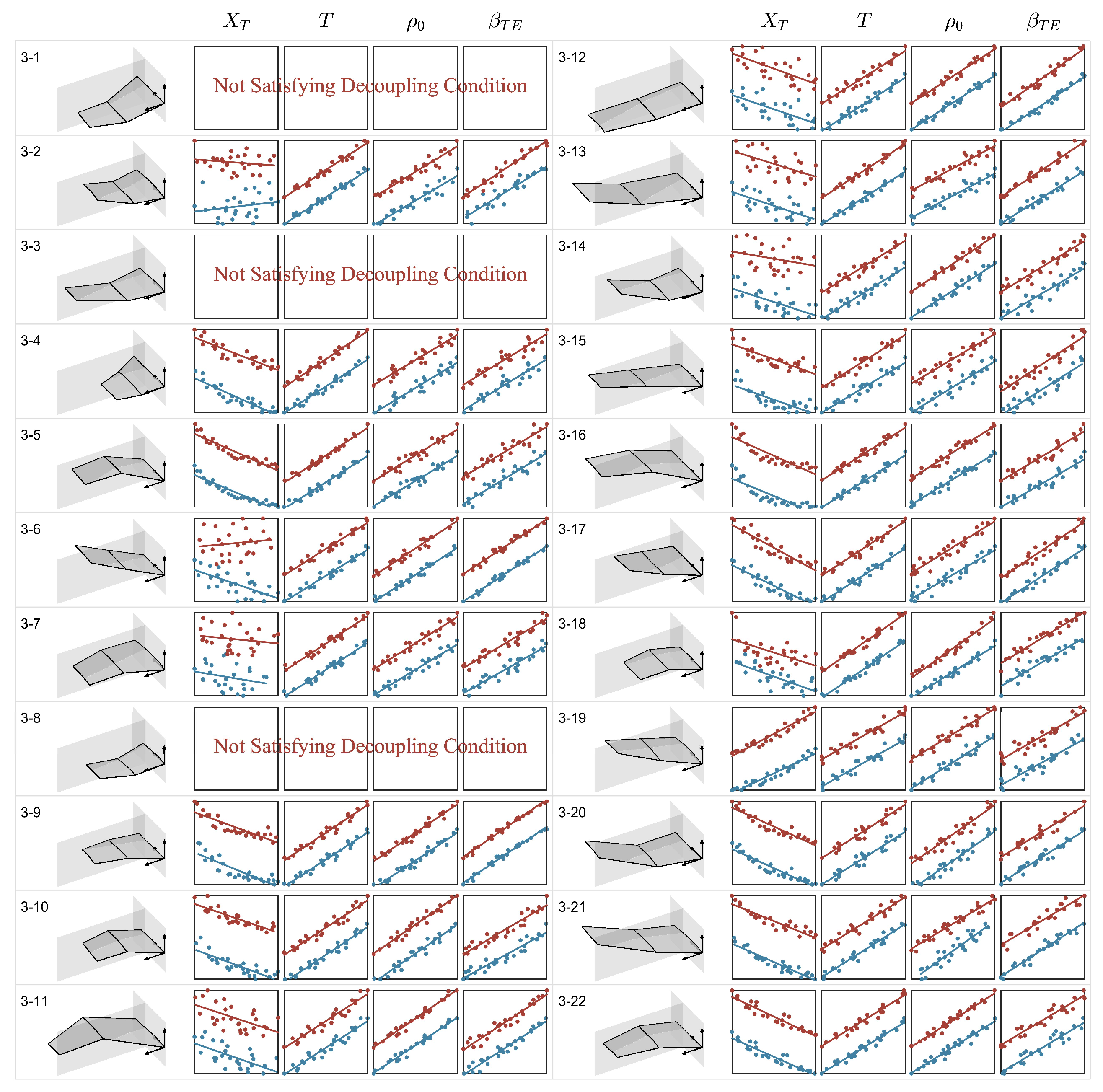
- are used as design variables (3 sections, a total of 3 variables) to generate 28 samples by the Optimal-LHS method, while the remaining thickness variables are generated randomly. Combine wing camber surfaces to form wing shapes.
- Evaluate each sample at by CFD.
- at are used as the response values to build the surrogate model:
- Based on ANOVA analysis, in are obtained, where:
- First-order fit and , where:
- For any values of , .
- For any values of , .
- For any values of , .
4.3. Application Scope
- There is no regional flow separation on the upper and lower surfaces of the wing.
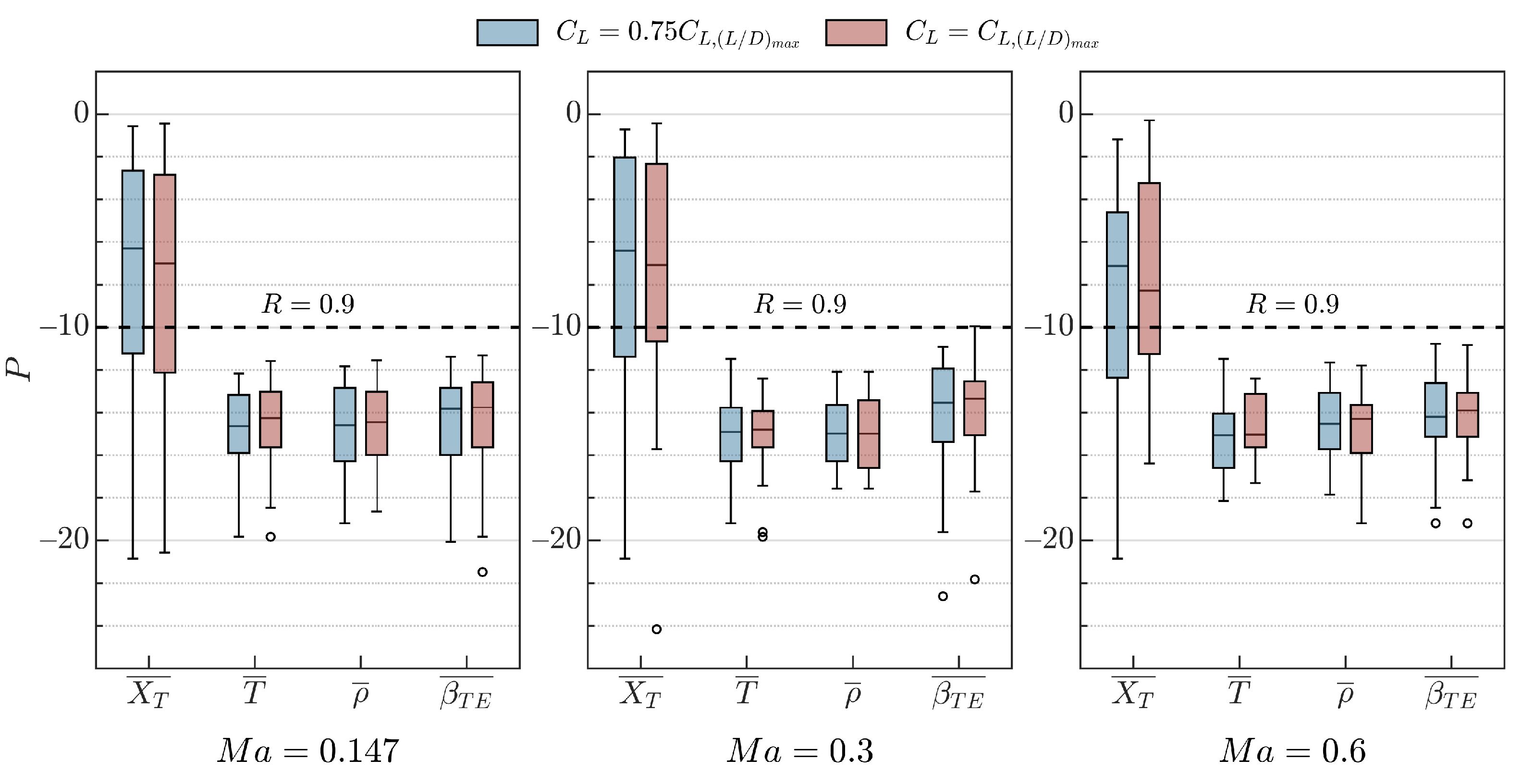
- The coupling () of is not greater than about 5%.
- The correlation coefficient () between and objective function is greater than about 0.9.
- Mach number ()
- Design lift coefficient ()
- Leading-edge sweepback ()
- The IGP method’s parameters. On the basis of design space containing 95% of the airfoils in the Profili airfoil library:
5. Validation by Surrogate-Based Aerodynamic Optimization
5.1. Determination of Full-Dimensional and Reduced-Dimensional Optimization
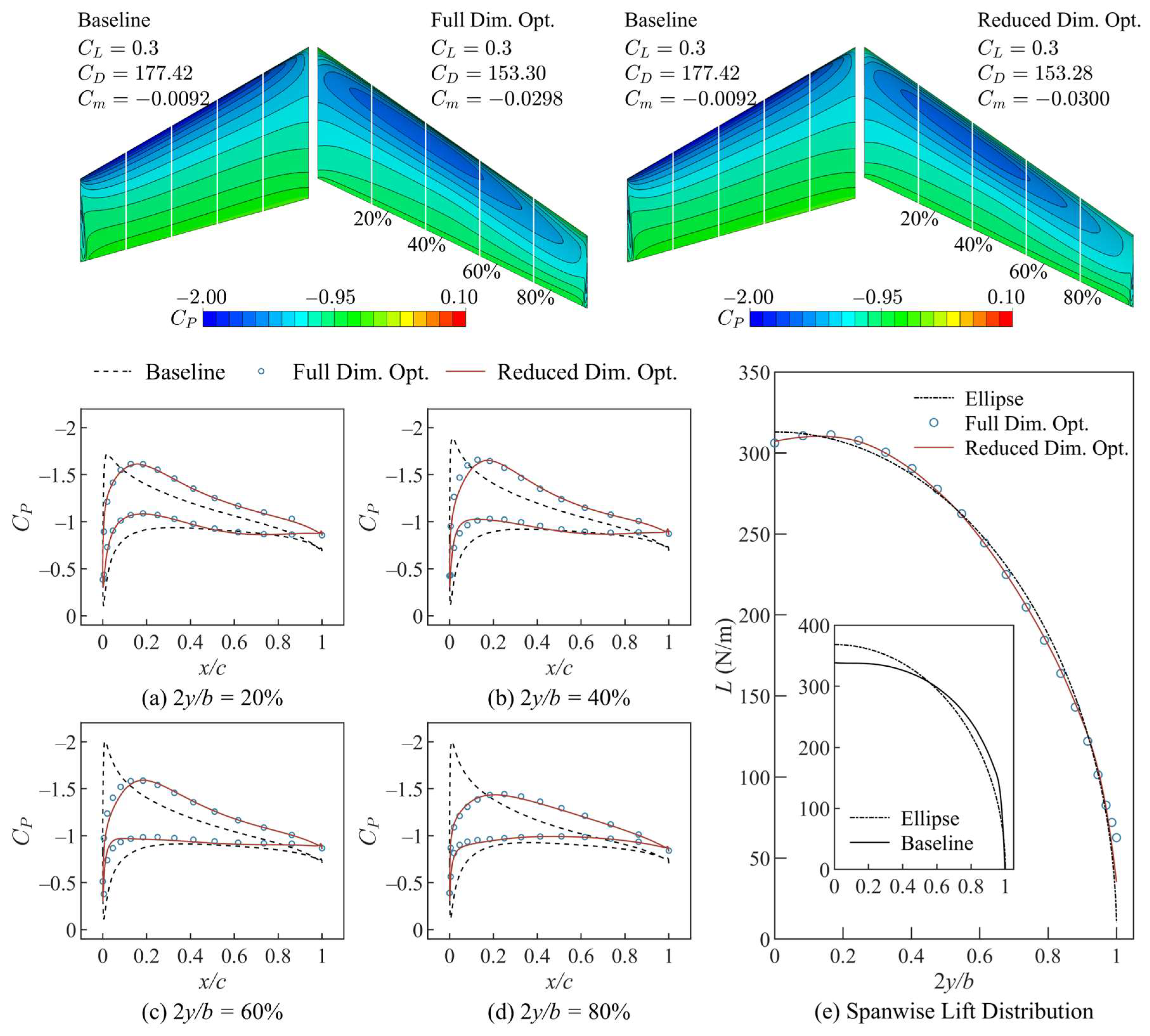
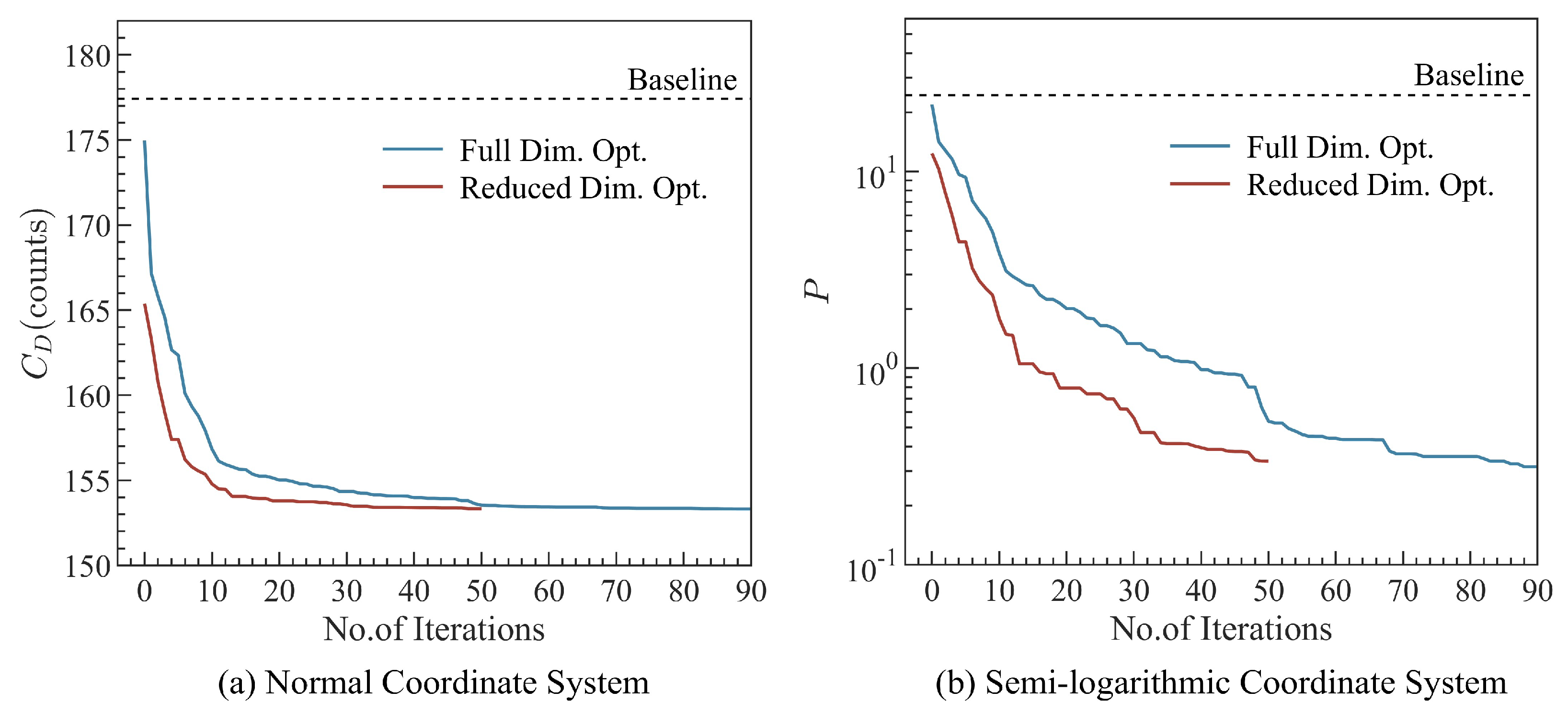
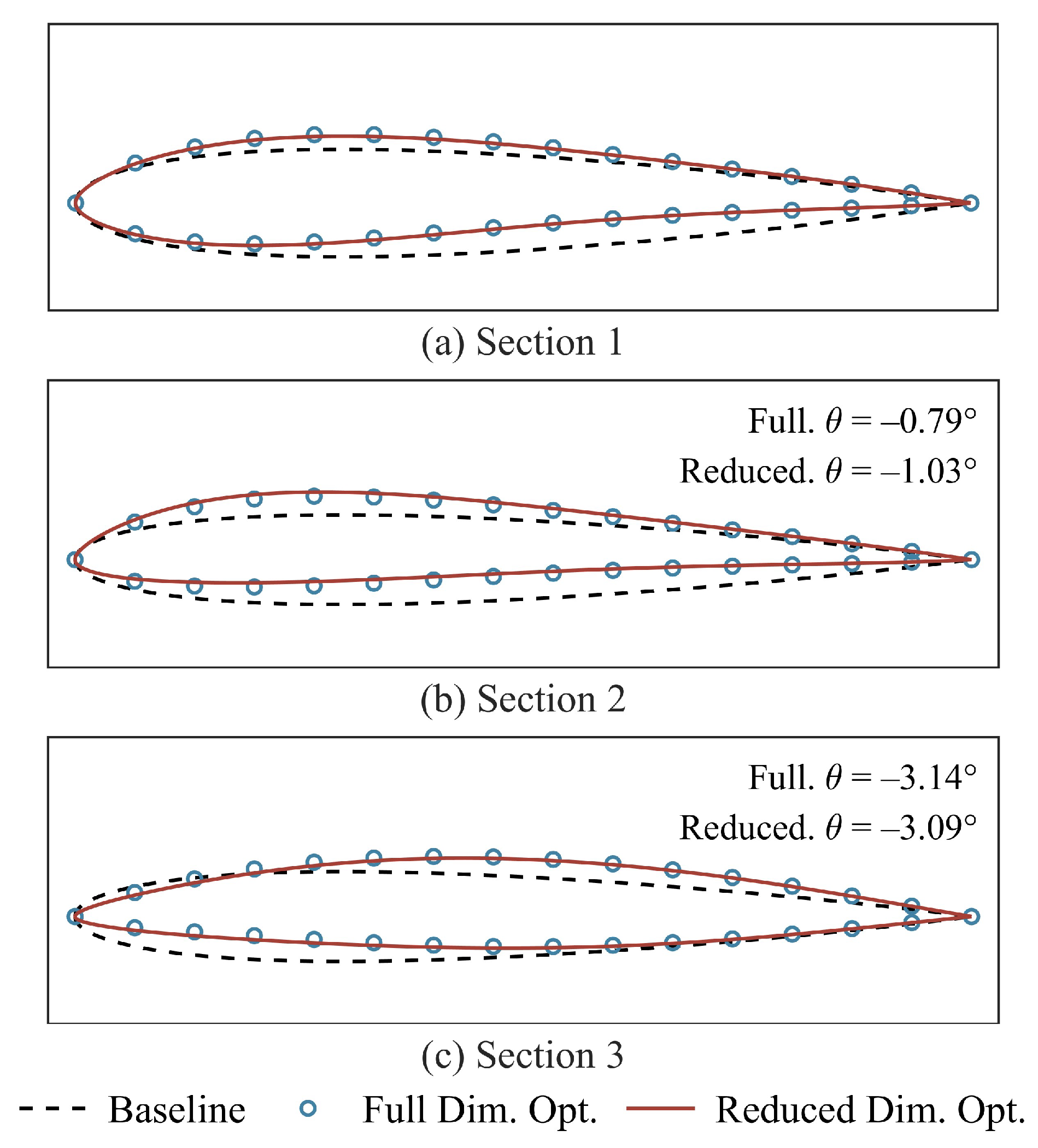
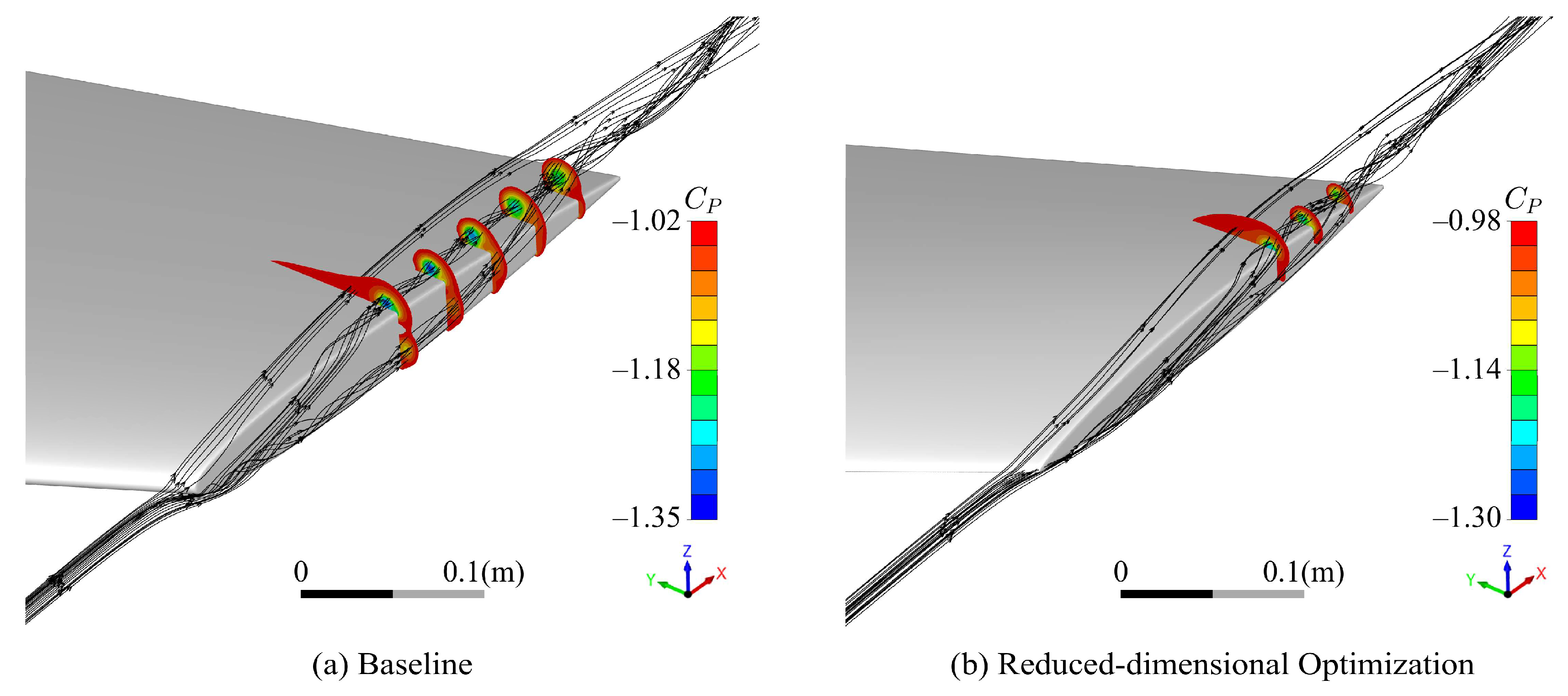
5.2. Optimization Results
6. Conclusions
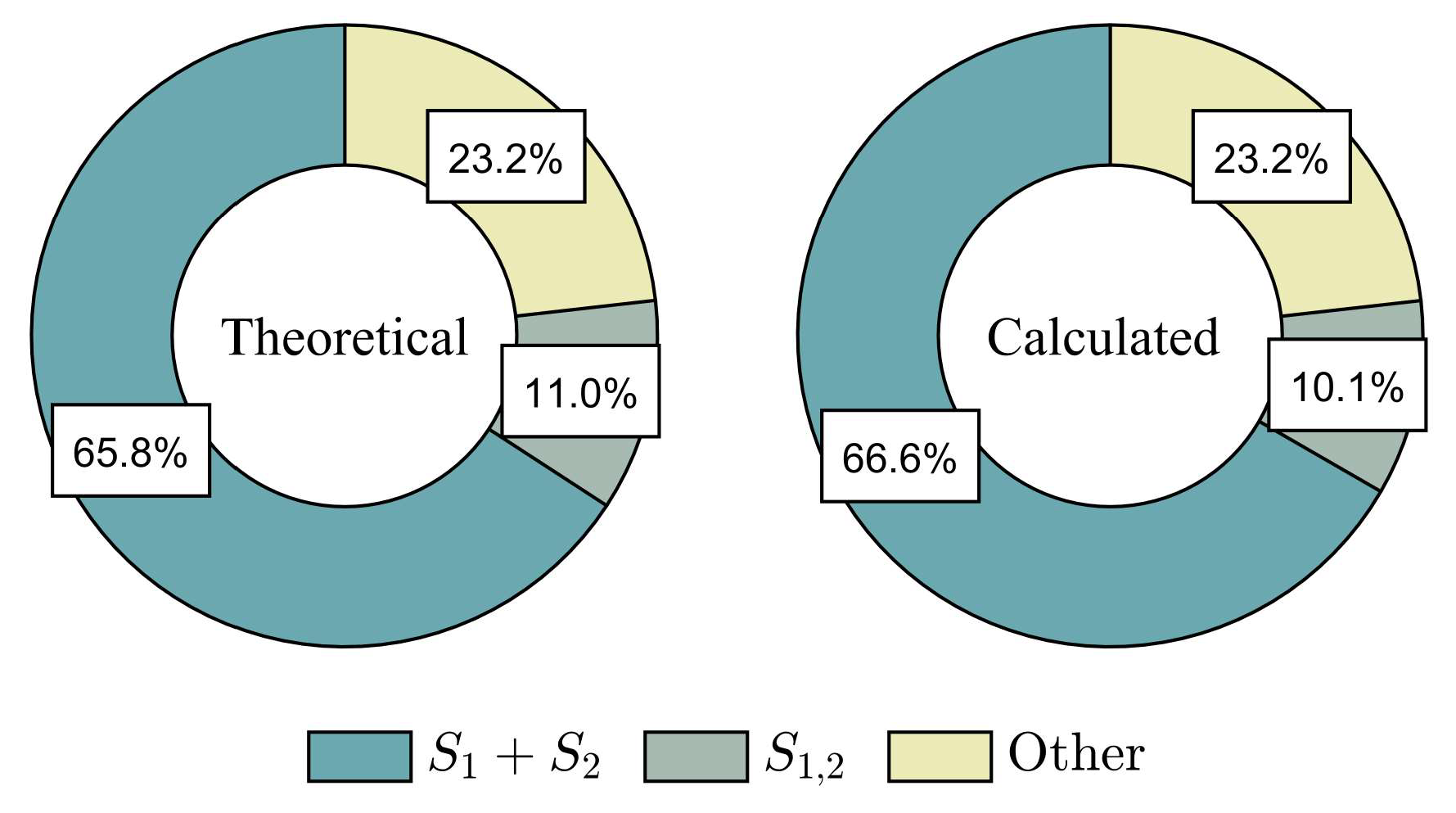
- In the design space encompassing about 95% of the Profili airfoil library, camber and thickness variables in the objective function are strongly coupled. As the design space is drastically reduced to 40%, decoupling can be achieved gradually. The constraint function is determined primarily by the wing planform and camber variables.
- For each configuration with varied planform and camber variables in a particular , , and design space, thickness variables () in the objective function can be decoupled separately, while the influence of thickness variables in the constraint function is kept to a tiny order of (longitudinal static stability margin is 3.5%).
- With the conclusions in (1) (2) and the data-driven aerodynamic characteristics model, it is possible to first identify certain thickness variables () according to the minimization based on the structural requirements. The dimension reduction amounts to (where represents the number of wing sections). As the number of wing sections increases, the effect of dimension reduction becomes more pronounced.
- In the aerodynamic optimization of an ONERA-M6 wing, the reduced-dimensional optimization (21-dimensional) utilizing the improved approach and the full-dimensional optimization (30-dimensional) have a consistent optimization effect (compared with the baseline, is reduced by about 13.6%). The results have a uniform planform and highly similar average shape of wing sections. The application of the improved approach accelerates the optimization process by an average of 43%. The values of determined by the improved approach are consistent with the results of full-dimensional optimization, which proves the accuracy of the aerodynamic characteristics model in reverse.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| angle of attack | |
| wingspan | |
| camber line curvature on the location of maximum camber | |
| maximum camber | |
| a variable set composed of all variables that describe sections’ camber | |
| center of gravity | |
| drag coefficient | |
| lift coefficient | |
| lift coefficient at maximum lift-to-drag ratio | |
| pitch moment coefficient | |
| pressure coefficient | |
| longitudinal static stability margin | |
| chord length | |
| lift-drag ratio | |
| Mach number | |
| sensitivity indices, indicates the effect of design variables on the function | |
| wing area | |
| maximum thickness | |
| a variable set composed of all variables that describe sections’ thickness | |
| velocity | |
| a variable set composed of all variables that describe the wing planform | |
| chordwise location of the maximum camber | |
| chordwise location of the maximum thickness | |
| the angle between the camber line and the chord line on the trailing edge | |
| dimensionless quantity of the trailing edge boat-tail angle | |
| dihedral angle | |
| leading-edge sweep angle | |
| dimensionless quantity of the leading-edge radius | |
| twist angle |
References
- Jameson, A.; Vassberg, J. Computational Fluid Dynamics for Aerodynamic Design—Its Current and Future Impact. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8 January 2001. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA/CR-2014-218178; NASA: Washington, DC, USA, 2014. [Google Scholar]
- Han, Z.H.; Xu, C.Z.; Qiao, J.L. Recent progress of efficient global aerodynamic shape optimization using surrogate-based approach. Acta Aeronaut. Astronaut. Sin. 2020, 41, 25–65. (In Chinese) [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Jameson, A. Optimum Aerodynamic Design Using CFD and Control Theory. In Proceedings of the 12th Computational Fluid Dynamics Conference, San Diego, CA, USA, 19 June 1995. [Google Scholar] [CrossRef]
- Kenway, G.K.W.; Mader, C.A.; He, P. Effective Adjoint Approaches for Computational Fluid Dynamics. Prog. Aerosp. Sci. 2019, 110, 100542. [Google Scholar] [CrossRef]
- Lyu, Z.; Martins, J.R.R.A. Aerodynamic Design Optimization Studies of a Blended-Wing-Body Aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef]
- Lyu, Z.; Kenway, G.K.W.; Martins, J.R.R.A. Aerodynamic Shape Optimization Investigations of the Common Research Model Wing Benchmark. AIAA J. 2015, 53, 968–985. [Google Scholar] [CrossRef]
- He, X.; Li, J.; Mader, C.A. Robust Aerodynamic Shape Optimization—From a Circle to an Airfoil. Aerosp. Sci. Technol. 2019, 87, 48–61. [Google Scholar] [CrossRef]
- Giannakoglou, K.C. Design of Optimal Aerodynamic Shapes Using Stochastic Optimization Methods and Computational Intelligence. Prog. Aerosp. Sci. 2002, 38, 43–76. [Google Scholar] [CrossRef]
- Schmit, L., Jr.; Farshi, B. Some Approximation Concepts for Structural Synthesis. In Proceedings of the 14th Structures, Structural Dynamics, and Materials Conference, Williamsburg, VA, USA, 20 March 1973. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N. Metamodels for Computer-Based Engineering Design: Survey and Recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Simpson, T.W.; Booker, A.J.; Ghosh, D. Approximation Methods in Multidisciplinary Analysis and Optimization: A Panel Discussion. Struct. Multidiscipl. Optim. 2004, 27, 302–313. [Google Scholar] [CrossRef]
- Viana, F.A.C.; Simpson, T.W.; Balabanov, V. Special Section on Multidisciplinary Design Optimization: Metamodeling in Multidisciplinary Design Optimization: How Far Have We Really Come? AIAA J. 2014, 52, 670–690. [Google Scholar] [CrossRef]
- Liu, J.; Han, Z.; Song, W. Comparison of infill sampling criteria in kriging-based aerodynamic optimization. In Proceedings of the 28th Congress of the International Council of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012. [Google Scholar] [CrossRef]
- Parr, J.M.; Keane, A.J.; Forrester, A.I.J. Infill Sampling Criteria for Surrogate-Based Optimization with Constraint Handling. Eng. Optim. 2012, 44, 1147–1166. [Google Scholar] [CrossRef]
- Cox, D.D.; John, S. A Statistical Method for Global Optimization. In Proceedings of the 1992 IEEE International Conference on Systems, Man, and Cybernetics, Chicago, IL, USA, 18–21 October 1992. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Han, Z.H. Research progress on Kriging model and proxy optimization algorithm. J. Aeronaut. Astronaut. 2016, 37, 3197–3225. (In Chinese) [Google Scholar] [CrossRef]
- Liu, F.; Han, Z.H.; Zhang, Y. Surrogate-Based Aerodynamic Shape Optimization of Hypersonic Flows Considering Transonic Performance. Aerosp. Sci. Technol. 2019, 93, 105345. [Google Scholar] [CrossRef]
- Liu, B.; Liang, H.; Han, Z.H. Surrogate-based aerodynamic shape optimization of a morphing wing considering a wide Mach-number range. Aerosp. Sci. Technol. 2022, 124, 107557. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J.; Bressloff, N.W. Design and Analysis of “Noisy” Computer Experiments. AIAA J. 2006, 44, 2331–2339. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Survey of Modeling and Optimization Strategies to Solve High-Dimensional Design Problems with Computationally-Expensive Black-Box Functions. Struct. Multidiscipl. Optim. 2010, 41, 219–241. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S. Hierarchical kriging model for variable-fidelity surrogate modeling. AIAA J. 2012, 50, 1885–1896. [Google Scholar] [CrossRef]
- Park, C.; Haftka, R.T.; Kim, N.H. Remarks on Multi-Fidelity Surrogates. Struct. Multidiscipl. Optim. 2017, 55, 1029–1050. [Google Scholar] [CrossRef]
- Giselle Fernández-Godino, M.; Park, C.; Kim, N.H. Issues in deciding whether to use multifidelity surrogates. AIAA J. 2019, 57, 2039–2054. [Google Scholar] [CrossRef]
- Brevault, L.; Balesdent, M.; Hebbal, A. Overview of Gaussian process based multi-fidelity techniques with variable relationship between fidelities, application to aerospace systems. Aerosp. Sci. Technol. 2020, 107, 106339. [Google Scholar] [CrossRef]
- Han, Z.H.; Xu, C.Z.; Zhang, L. Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids. Chin. J. Aeronaut. 2020, 33, 31–47. [Google Scholar] [CrossRef]
- Dwight, R.; Han, Z.H. Efficient Uncertainty Quantification Using Gradient-Enhanced Kriging. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4 May 2009. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S.; Zimmermann, R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
- Song, C.; Song, W.; Yang, X. Gradient-enhanced hierarchical kriging model for aerodynamic design optimization. J. Aerosp. Eng. 2017, 30, 04017072. [Google Scholar] [CrossRef]
- Han, Z.H.; Zhang, Y.; Song, C.X. Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization. AIAA J. 2017, 55, 4330–4346. [Google Scholar] [CrossRef]
- Sóbester, A.; Leary, S.J.; Keane, A.J. A parallel updating scheme for approximating and optimizing high fidelity computer simulations. Struct. Multidiscipl. Optim. 2004, 27, 371–383. [Google Scholar] [CrossRef]
- Liu, J.; Song, W.P. Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models. Struct. Multidiscipl. Optim. 2017, 55, 925–943. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z.H.; Zhang, Y. Efficient Global Optimization Using Multiple Infill Sampling Criteria and Surrogate Models. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8 January 2018. [Google Scholar] [CrossRef]
- Painchaud-Ouellet, S.; Tribes, C.; Trépanier, J.Y. Airfoil shape optimization using a nonuniform rational b-splines parametrization under thickness constraint. AIAA J. 2006, 44, 2170–2178. [Google Scholar] [CrossRef]
- Song, W.; Keane, A.J. Surrogate-based aerodynamic shape optimization of a civil aircraft engine nacelle. AIAA J. 2007, 45, 2565–2574. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative. J. Mach. Learn. Res. 2009, 10, 13. [Google Scholar]
- Ghisu, T.; Parks, G.; Jarrett, J.; Clarkson, P. Accelerating Design Optimization Via Principal Components Analysis. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10 September 2008. [Google Scholar] [CrossRef]
- Toal, D.J.J.; Bressloff, N.W.; Keane, A.J.; Holden, C.M.E. Geometric filtration using proper orthogonal decomposition for aerodynamic design optimization. AIAA J. 2010, 48, 916–928. [Google Scholar] [CrossRef]
- Ghoman, S.; Wang, Z.; Chen, P.; Kapania, R. A POD-Based Reduced Order Design Scheme for Shape Optimization of Air Vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23 April 2012. [Google Scholar]
- Ghoman, S.S.; Wang, Z.; Chen, P.C. Hybrid optimization framework with proper-orthogonal-decomposition-based order reduction and design-space evolution scheme. J. Aircr. 2013, 50, 1776–1786. [Google Scholar] [CrossRef]
- Viswanath, A.; Forrester, A.I.J.; Keane, A.J. Dimension reduction for aerodynamic design optimization. AIAA J. 2011, 49, 1256–1266. [Google Scholar] [CrossRef]
- Lukaczyk, T.W.; Constantine, P.; Palacios, F. Active Subspaces for Shape Optimization. In Proceedings of the 10th AIAA Multidisciplinary Design Optimization Conference, National Harbor, MD, USA, 13 January 2014. [Google Scholar] [CrossRef]
- Abbott, I.H.; Von Doenhoff, A.E. Theory of Wing Sections: Including a Summary of Airfoil Data; Dover Publications Inc.: New York, NY, USA, 1959; pp. 65–66. [Google Scholar]
- Berkenstock, D.; Alonso, J.J.; Lessard, L. A Convex Optimization Approach to Thin Airfoil Design. In Proceedings of the 2022 AIAA Aviation and Aeronautics Forum and Exposition, Chicago, IL, USA, 1 July 2022. [Google Scholar] [CrossRef]
- Wei, C.; Huang, J.; Song, L. Study on a Rapid Aerodynamic Optimization Method of Flying Wing Aircraft for Conceptual Design. Int. J. Aerosp. Eng. 2022, 2022, 5775355. [Google Scholar] [CrossRef]
- Lu, X.; Huang, J.; Song, L. An Improved Geometric Parameter Airfoil Parameterization Method. Aerosp. Sci. Technol. 2018, 78, 241–247. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6 January 1992. [Google Scholar]
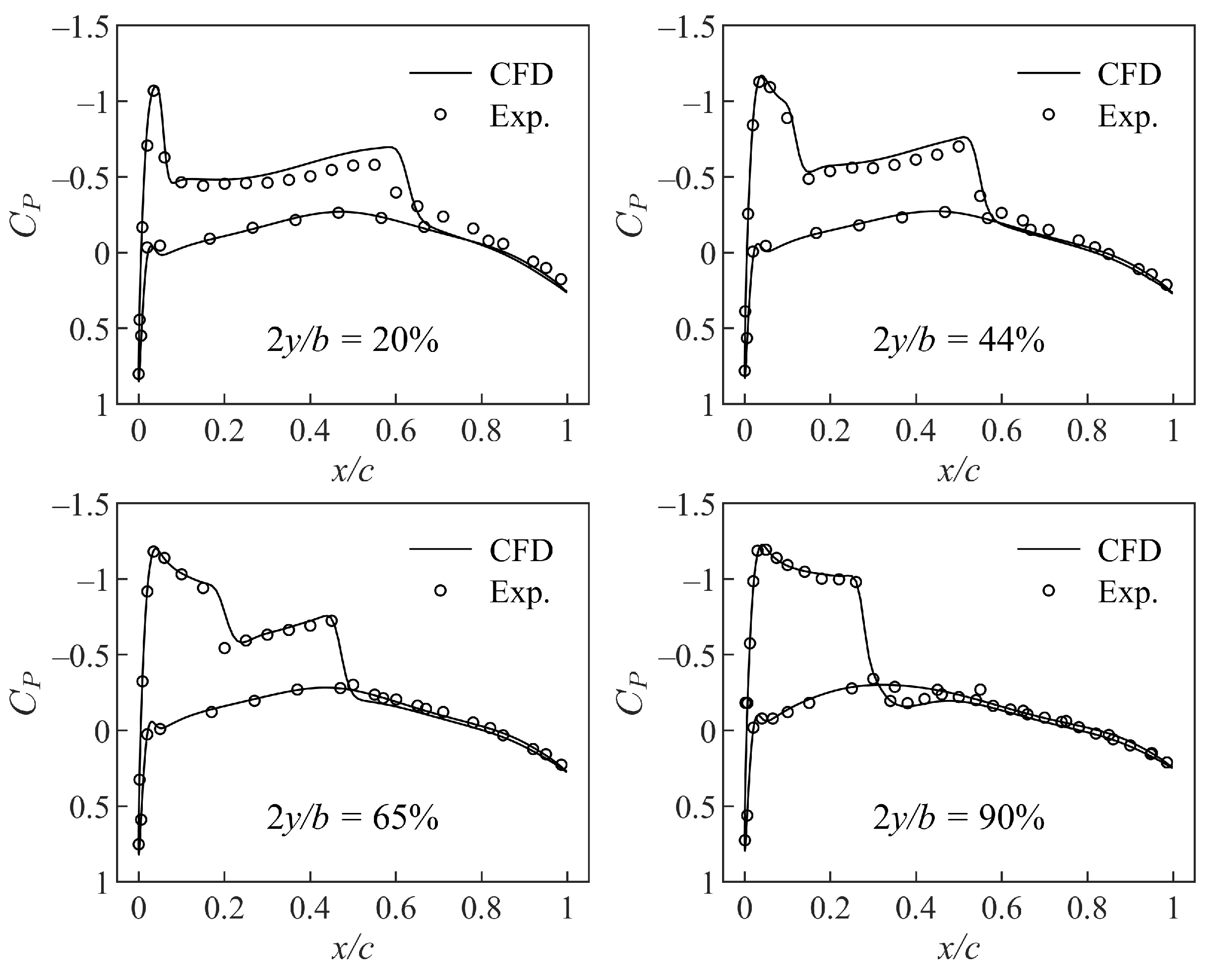
- Schmitt, V.; Charpin, F. Pressure Distributions on the ONERA-M6-Wing at Transonic Mach Numbers, Experimental Data Base for Computer Program Assessment; AGARD AR-138; NATO: Brussels, Belgium, 1979. [Google Scholar]
- Wolhart, W.D.; Thomas, D.F., Jr. Static Longitudinal and Lateral Stability Characteristics at Low Speed of Unswept-Midwing Models Having Wings with an Aspect Ratio of 2, 4, or 6; NACA-TN-4077; NASA: Washington, DC, USA, 1957. [Google Scholar]
- Saltelli, A.; Sobol, I.M. About the use of rank transformation in sensitivity analysis of model output. Reliab. Eng. Syst. Saf. 1995, 50, 225–239. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]

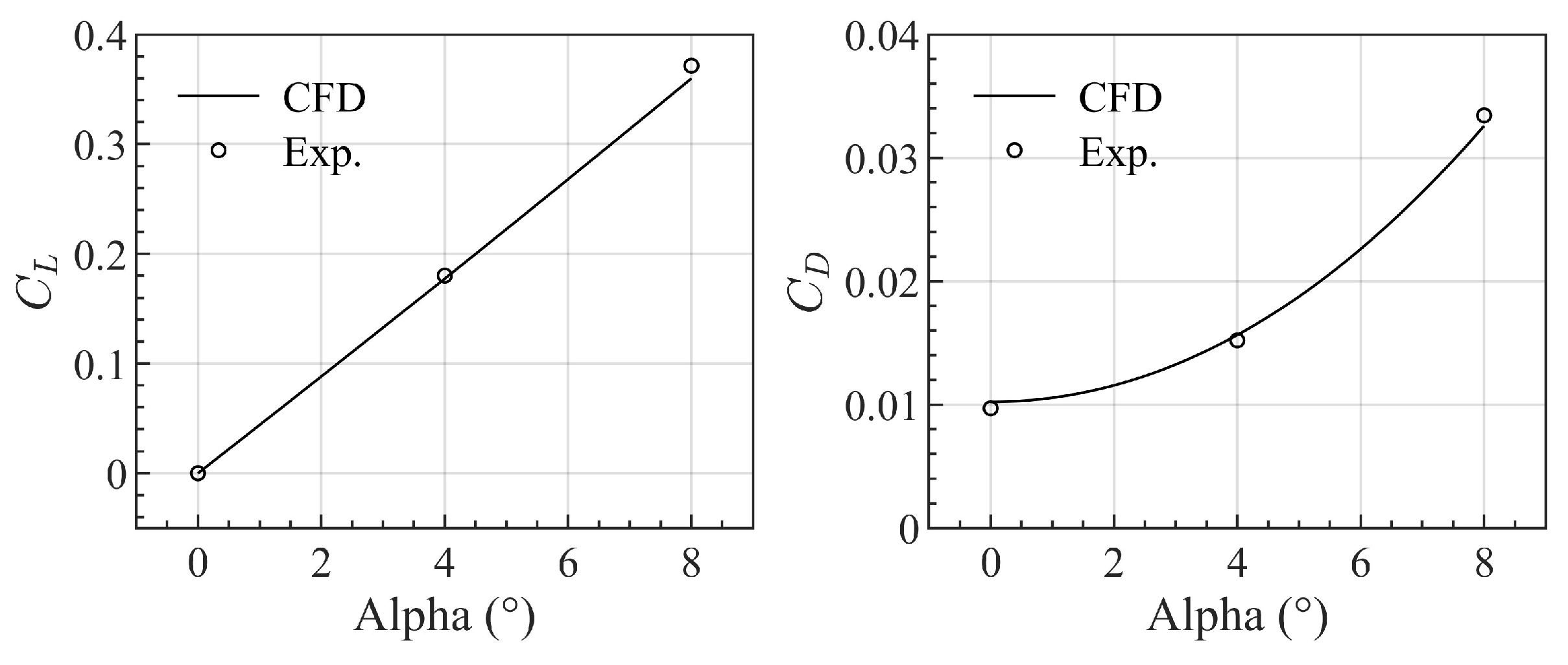


| Baseline | Lower Limit | Upper Limit | Range | |
|---|---|---|---|---|
| 805.9 | 644.7 | 967.1 | ±20% | |
| 453.3 | 362.6 | 544.0 | ±20% | |
| 1196.3 | 837.4 | 1555.2 | ±30% | |
| 30 | 0 | 45 | / | |
| 0 | −4 | 2 | / | |
| 0 | −8 | 2 | / | |
| 0 | −15 | 15 | / | |
| Section 1,2,3 | / | IGP (4 camber parameters) | ||
| Configuration | Flow Conditions | Number of Samples (Existent Flow Separation) | |
|---|---|---|---|
| 1 | 0 | ||
| 17 | |||
| 3 | 0 | ||
| 13 | |||
| 8 | 21 | ||
| 1 | |||
| Baseline | Full-Dimensional (30 Variables) | Reduced-Dimensional (21 Variables) | |
|---|---|---|---|
| 805.9 | [0.85, 1.15] Baseline | Same as Full-dimensional | |
| 453.3 | [0.85, 1.15] Baseline | ||
| 1196.3 | [0.85, 1.15] Baseline | ||
| 30 | [−5, 5] + Baseline | ||
| 0 | [−4, 2] | ||
| 0 | [−8, 2] | ||
| Section 1 | NACA 0012 | IGP 8 parameters | IGP 5 parameters () |
| Section 2 | NACA 0008 | ||
| Section 3 | NACA 0008 |
| No. | Number of CFD Evaluations | Total Time Cost (h) | Average Time Saved (%) | Optimal Results | (%) | at Optimum (%) | |||
|---|---|---|---|---|---|---|---|---|---|
(Counts) | |||||||||
| Baseline | 0.3 | 177.42 | −0.0092 | ||||||
| Full- dimensional | 1 | 60 + 360 | 45.5 | 0.3 | 153.34 | −0.0300 | 13.57 | 0.024 | |
| 2 | 60 + 360 | 45.6 | 0.3 | 153.30 | −0.0298 | 13.59 | 0.024 | ||
| 3 | 60 + 360 | 45.3 | 0.3 | 153.31 | −0.0299 | 13.59 | 0.020 | ||
| Reduced- dimensional | 1 | 60 + 200 | 25.8 | 42.96 | 0.3 | 153.37 | −0.0299 | 13.56 | 0.016 |
| 2 | 60 + 200 | 26.2 | 0.3 | 153.37 | −0.0299 | 13.56 | 0.002 | ||
| 3 | 60 + 200 | 25.8 | 0.3 | 153.28 | −0.0300 | 13.61 | 0.013 | ||
| No. | ||||||
|---|---|---|---|---|---|---|
| Baseline | 805.9 | 453.3 | 1196.3 | 30 | ||
| Full- dimensional | Both in 1,2,3 runs | 685.0 | 385.3 | 1375.7 | 35 | −2.25% |
| Reduced- dimensional | Both in 1,2,3 runs | 685.0 | 385.3 | 1375.7 | 35 | −2.25% |
| No. | ||||
|---|---|---|---|---|
| Full- dimensional | Both in 1,2,3 runs | 0.12, 0.10, 0.10 | 0.16, 0.16, 0.16 | 1.50, 1.50, 1.50 |
| (Determine by optimization) | ||||
| Reduced- dimensional | Both in 1,2,3 runs | 0.12, 0.10, 0.10 | 0.16, 0.16, 0.16 | 1.50, 1.50, 1.50 |
| (Determine by the improved approach) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, B.; Huang, J.; Lu, X.; Wu, Y.; Liu, J. An Improved Approach for Reducing the Dimensionality of Wing Aerodynamic Optimization Considering Longitudinal Stability. Aerospace 2024, 11, 80. https://doi.org/10.3390/aerospace11010080
Ji B, Huang J, Lu X, Wu Y, Liu J. An Improved Approach for Reducing the Dimensionality of Wing Aerodynamic Optimization Considering Longitudinal Stability. Aerospace. 2024; 11(1):80. https://doi.org/10.3390/aerospace11010080
Chicago/Turabian StyleJi, Boqian, Jun Huang, Xiaoqiang Lu, Yacong Wu, and Jingjiang Liu. 2024. "An Improved Approach for Reducing the Dimensionality of Wing Aerodynamic Optimization Considering Longitudinal Stability" Aerospace 11, no. 1: 80. https://doi.org/10.3390/aerospace11010080
APA StyleJi, B., Huang, J., Lu, X., Wu, Y., & Liu, J. (2024). An Improved Approach for Reducing the Dimensionality of Wing Aerodynamic Optimization Considering Longitudinal Stability. Aerospace, 11(1), 80. https://doi.org/10.3390/aerospace11010080







