Design and Machining of a Spherical Shell Rotor for a Magnetically Levitated Momentum Ball
Abstract
1. Introduction
2. Structure and Working Principle
2.1. Magnetically Levitated Momentum Ball
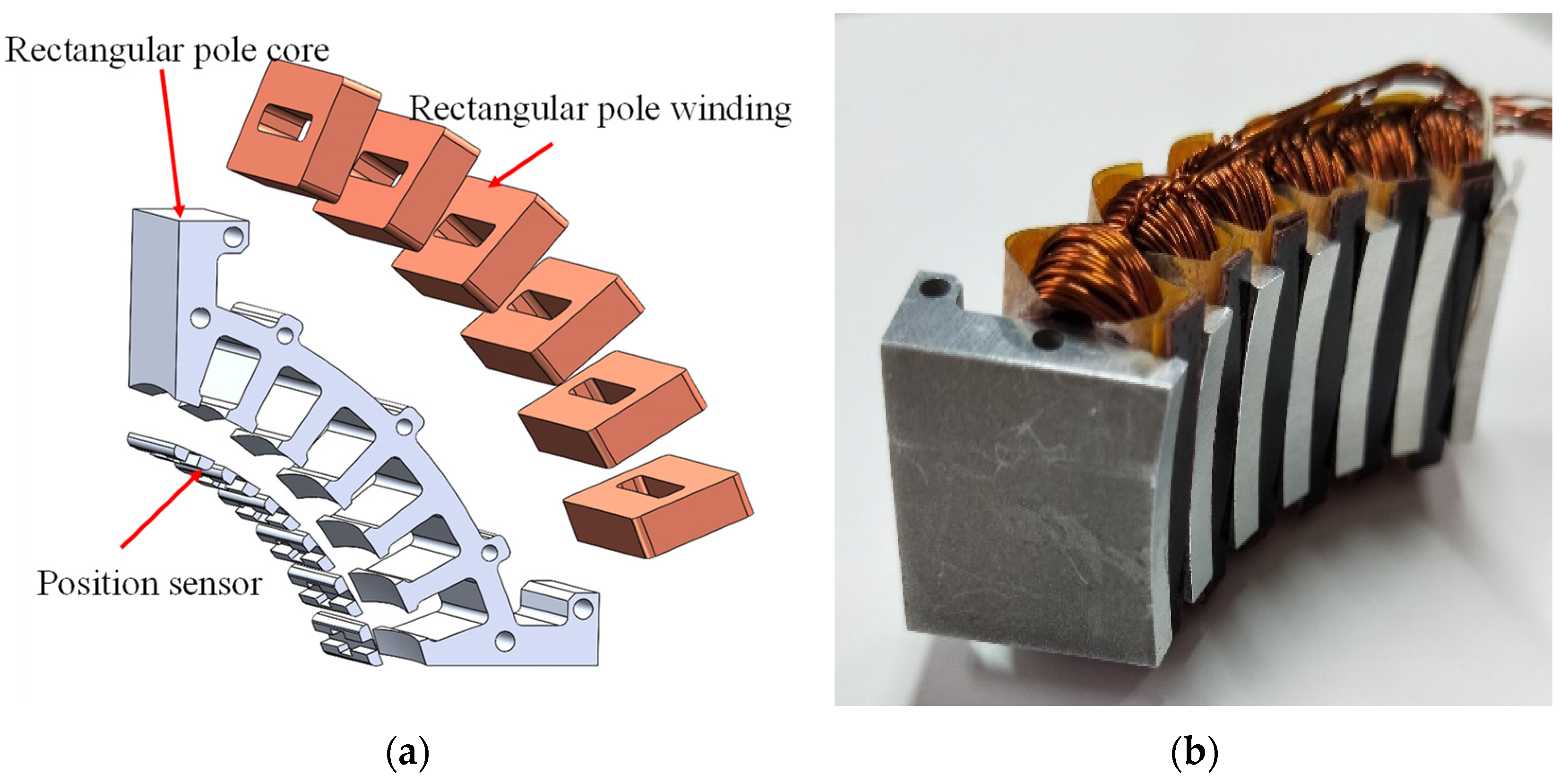
2.1.1. Right-Angled Magnetic Pole System
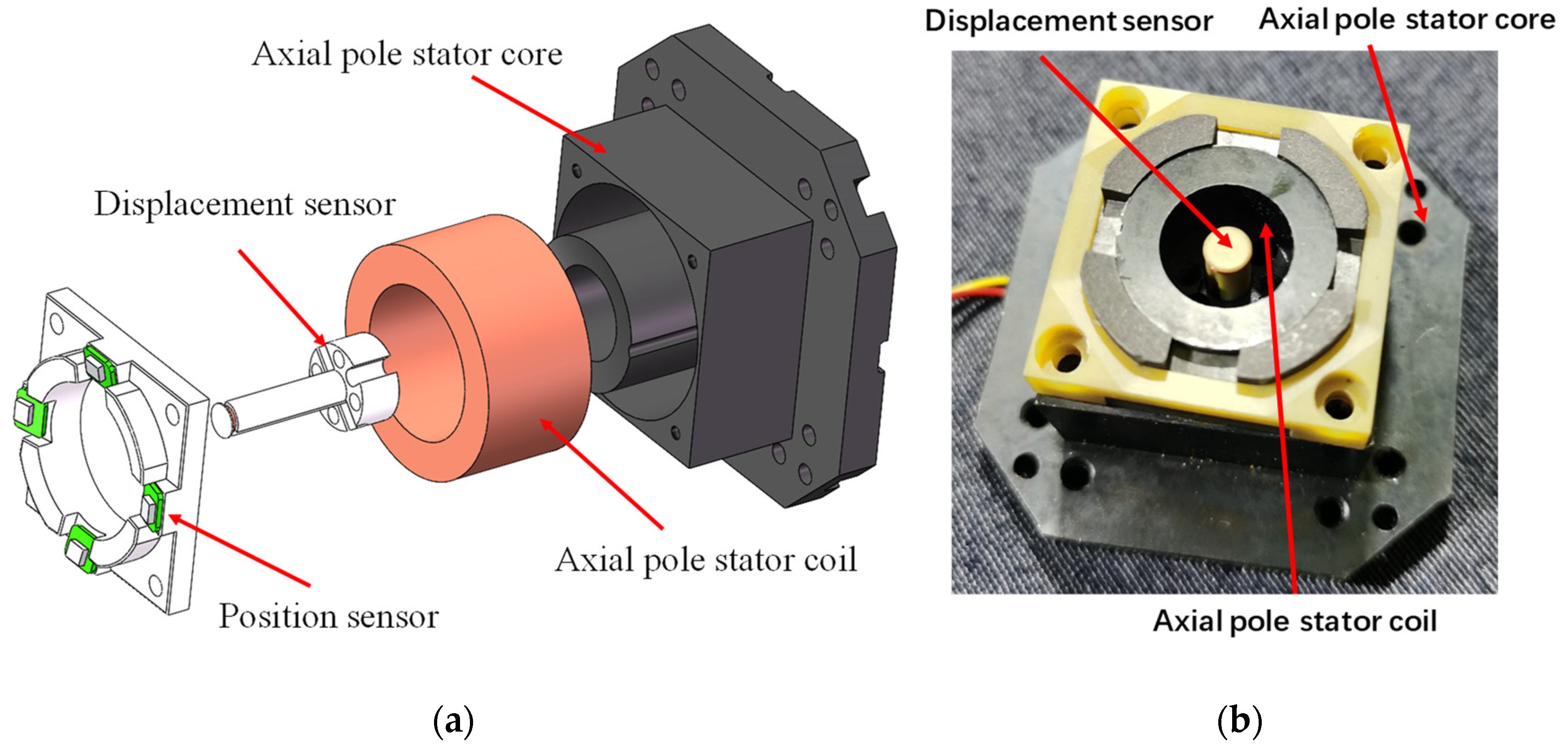
2.1.2. Axial Magnetic Pole System
2.1.3. Rotor Systems
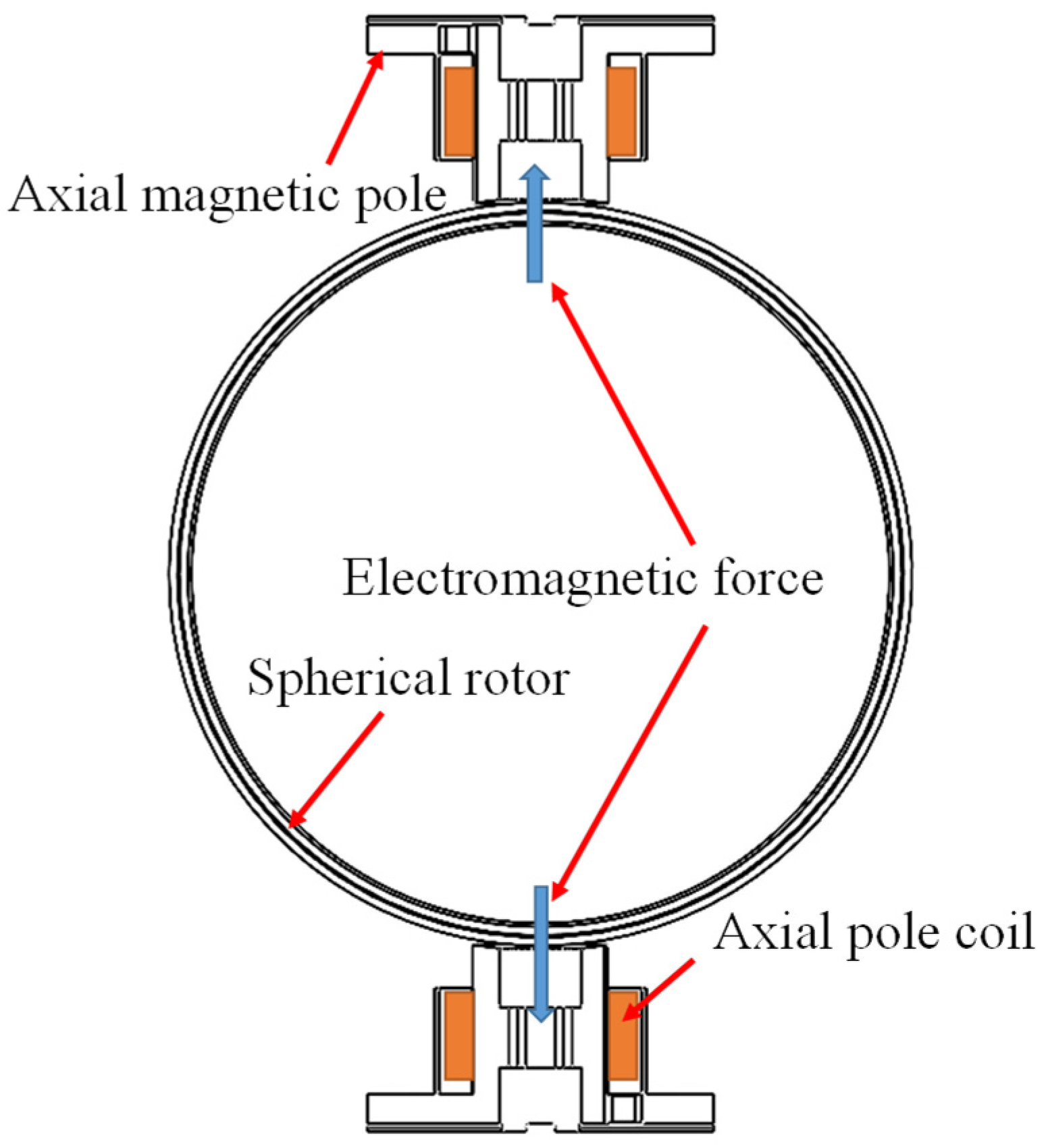
2.2. Principle of Operation
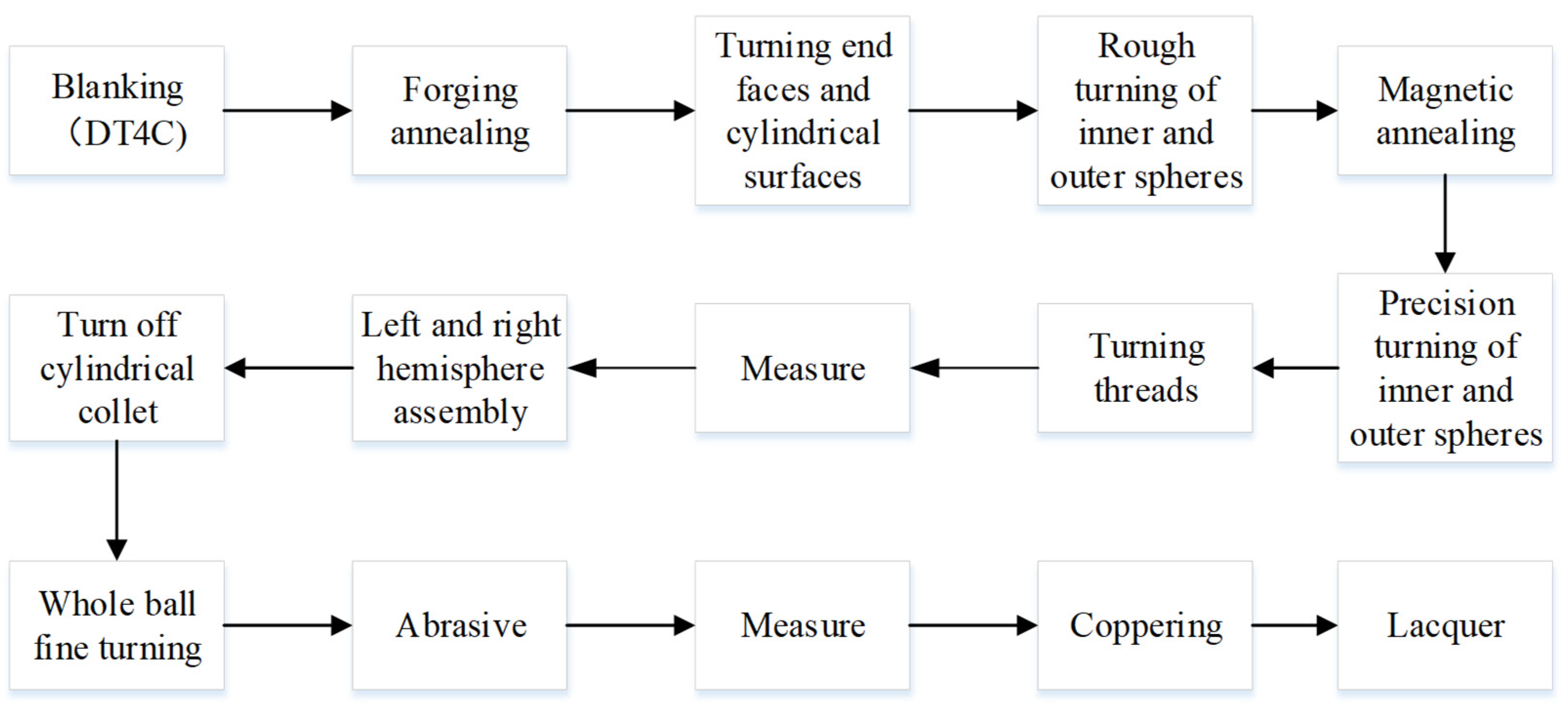
3. Processing Analysis
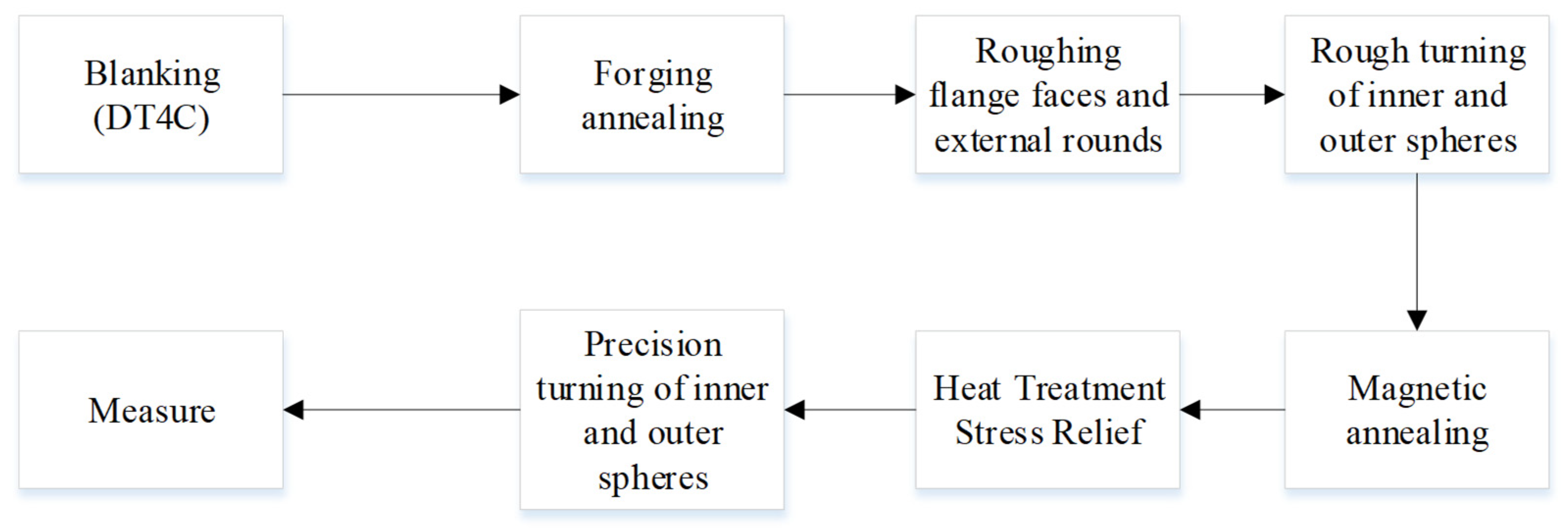
3.1. Process Optimization
3.2. Design of Machining Parameters
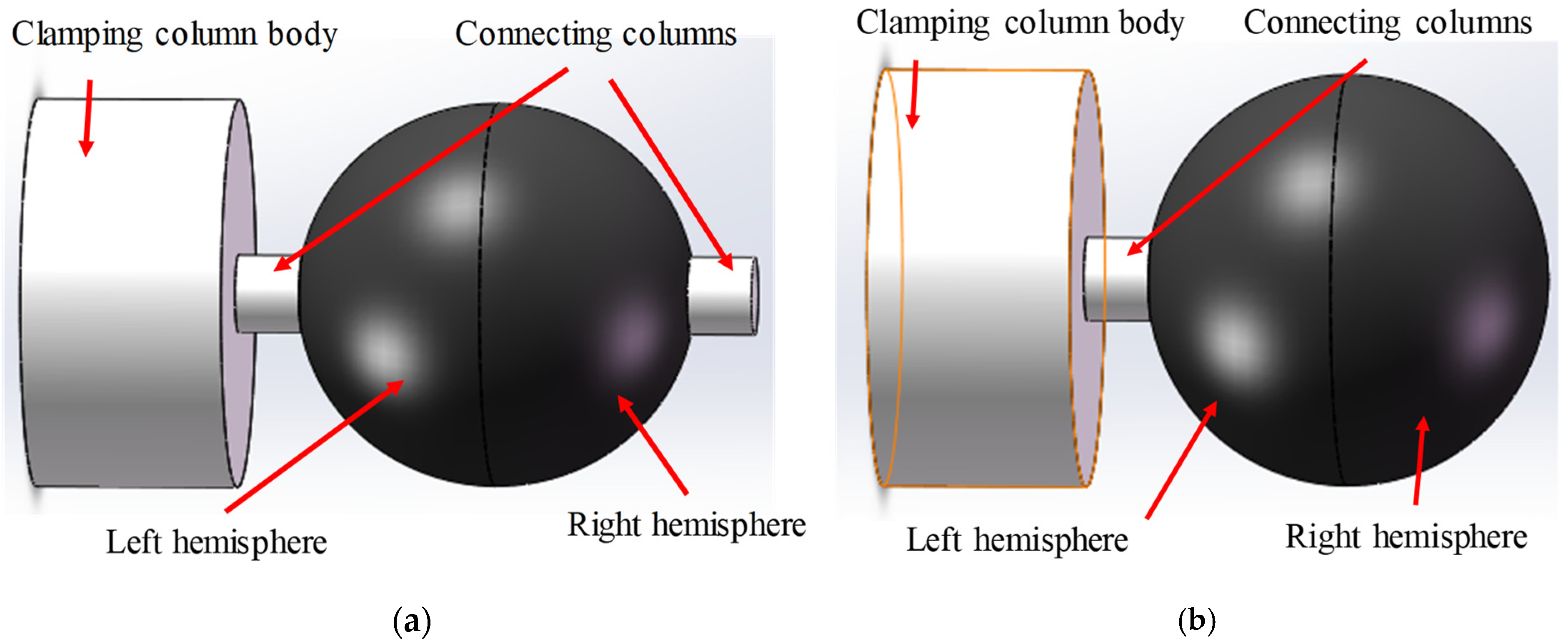
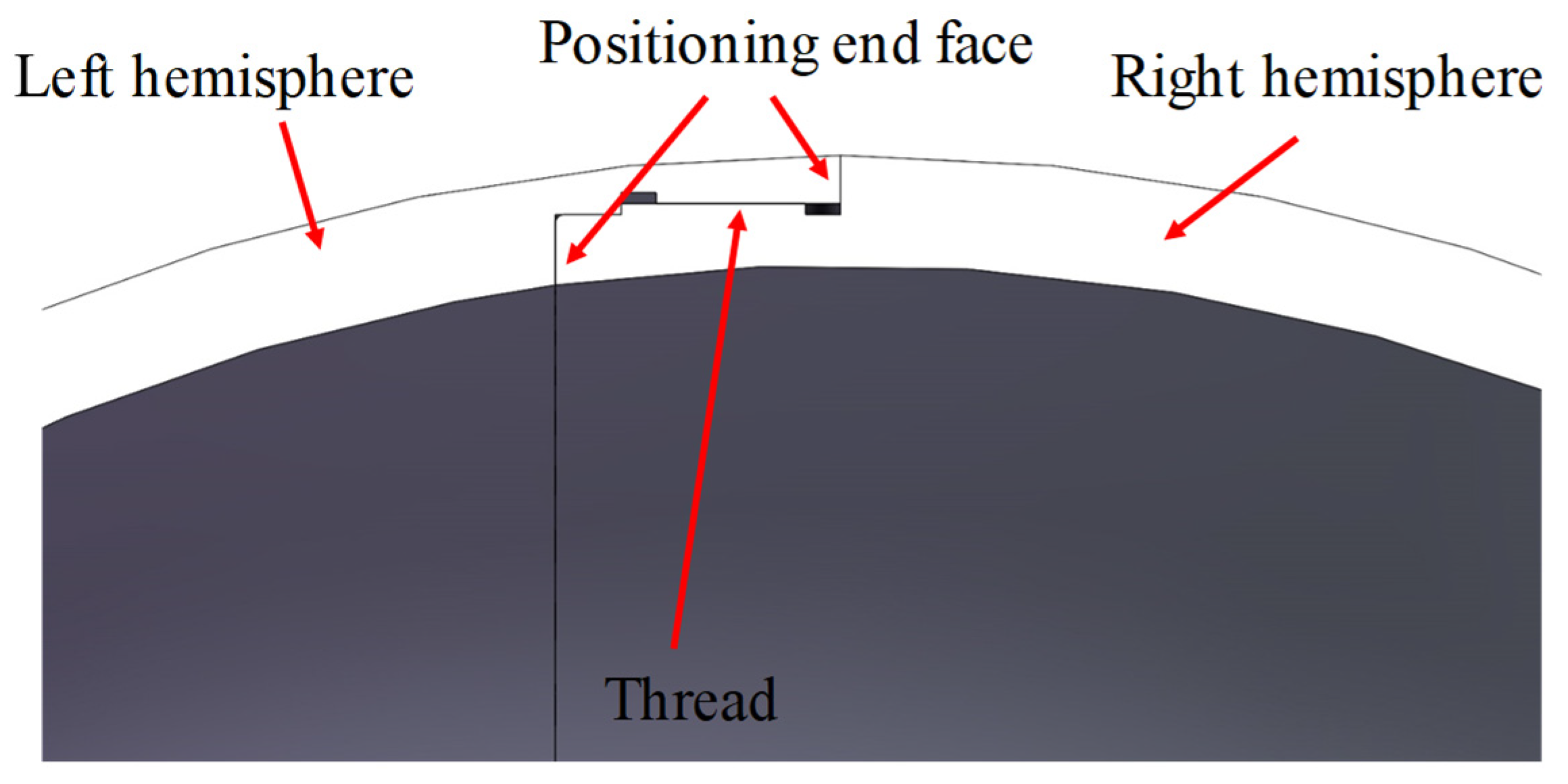
3.2.1. Workpiece Clamping
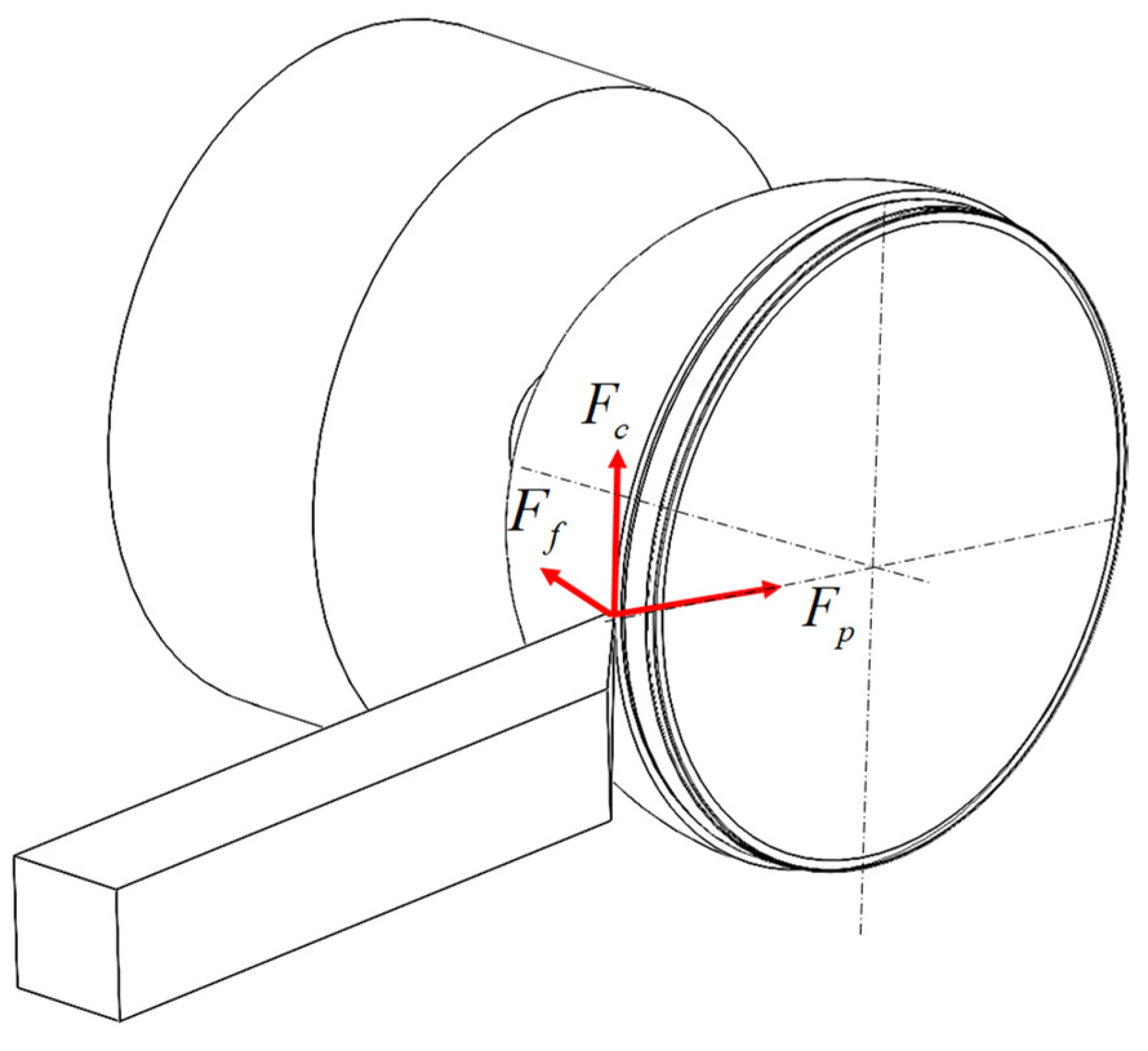
3.2.2. Force Analysis
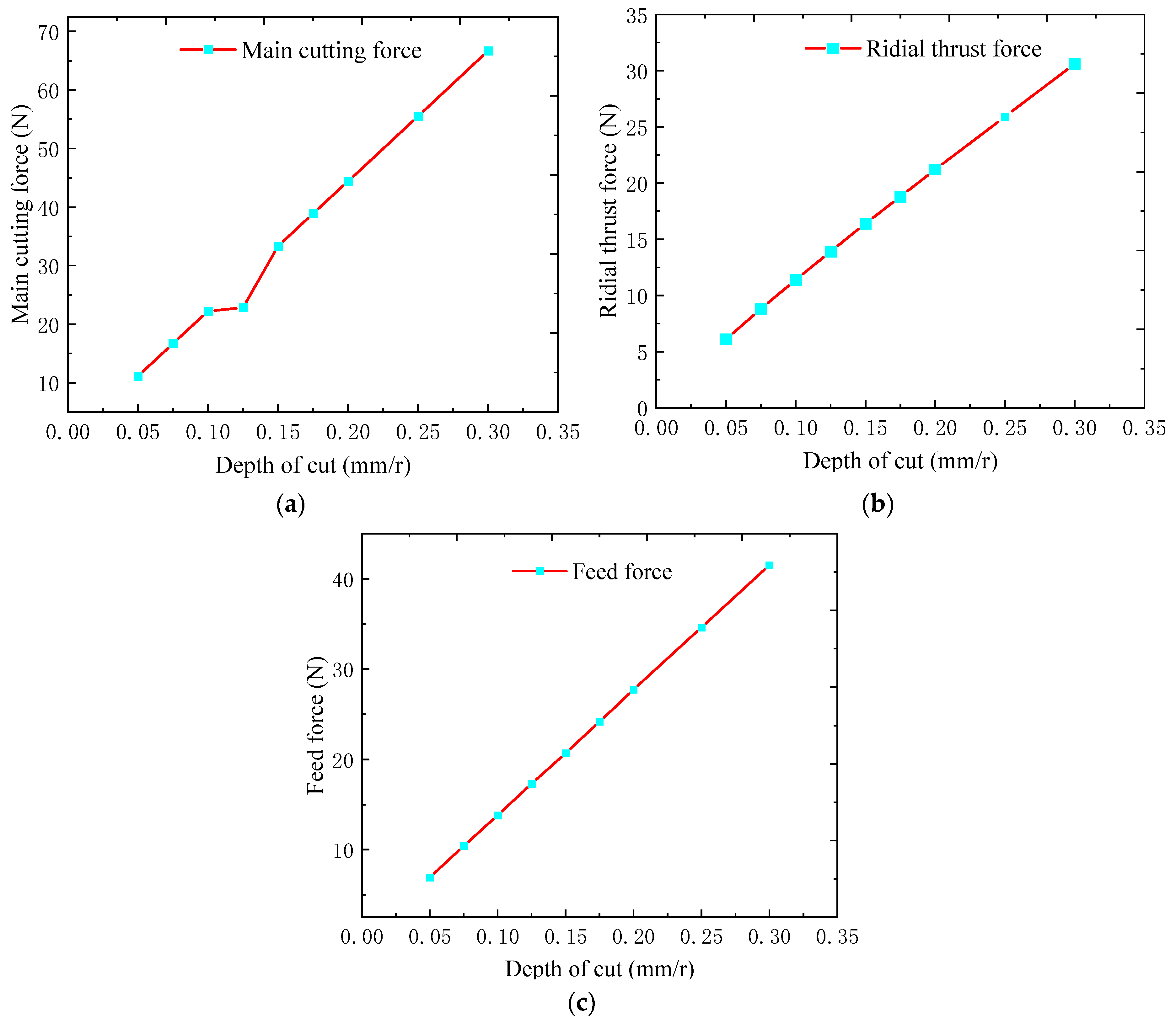
3.2.3. Cutting Force Calculation
- , , are the indexes of the influence of the amount of backdraft on the main cutting force , backdraft force and feed force , respectively;
- , , are the indices of the influence of feed force on the main cutting force , backdraft force , feed force , respectively;
- , , are the indices of the influence of cutting speed on the main cutting force , backdraft force , and feed force , respectively;
- , , are the total correction coefficients for the main cutting force , backdraft force and feed force when the calculation conditions are different from the experimental conditions, respectively.
- is the correction coefficient of the front angle to the main cutting force , back eating force and feed force respectively;
- is the correction coefficient of the main deflection angle to the main cutting force , back eating force and feed force respectively;
- correction factor for camber angle to main cutting force , back draft force , feed force , respectively;
- is the correction coefficient of the tip radius to the main cutting force , back eating force and feed force , respectively;
- is the correction factor for the back face wear to the main cutting force , back draft force and feed force respectively.
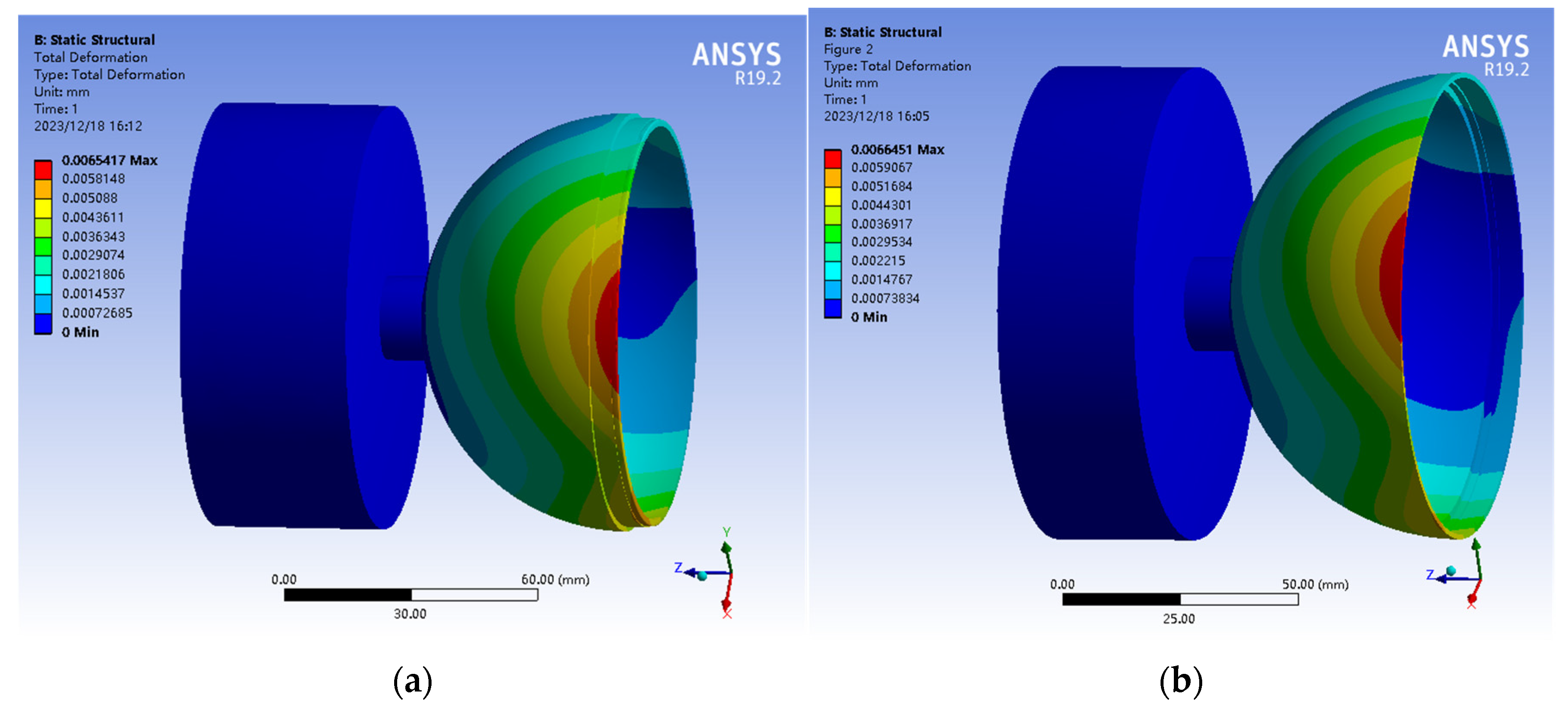
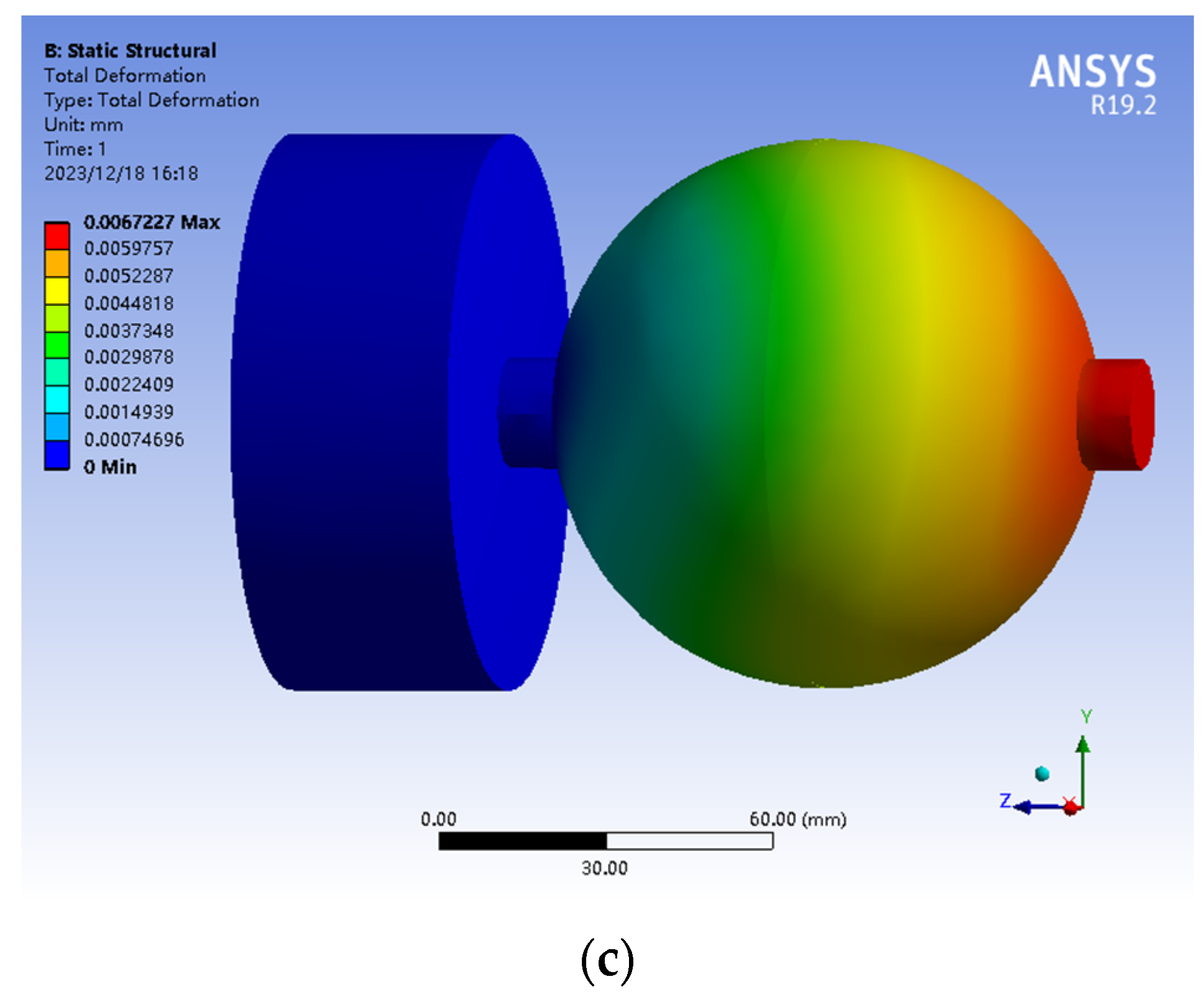
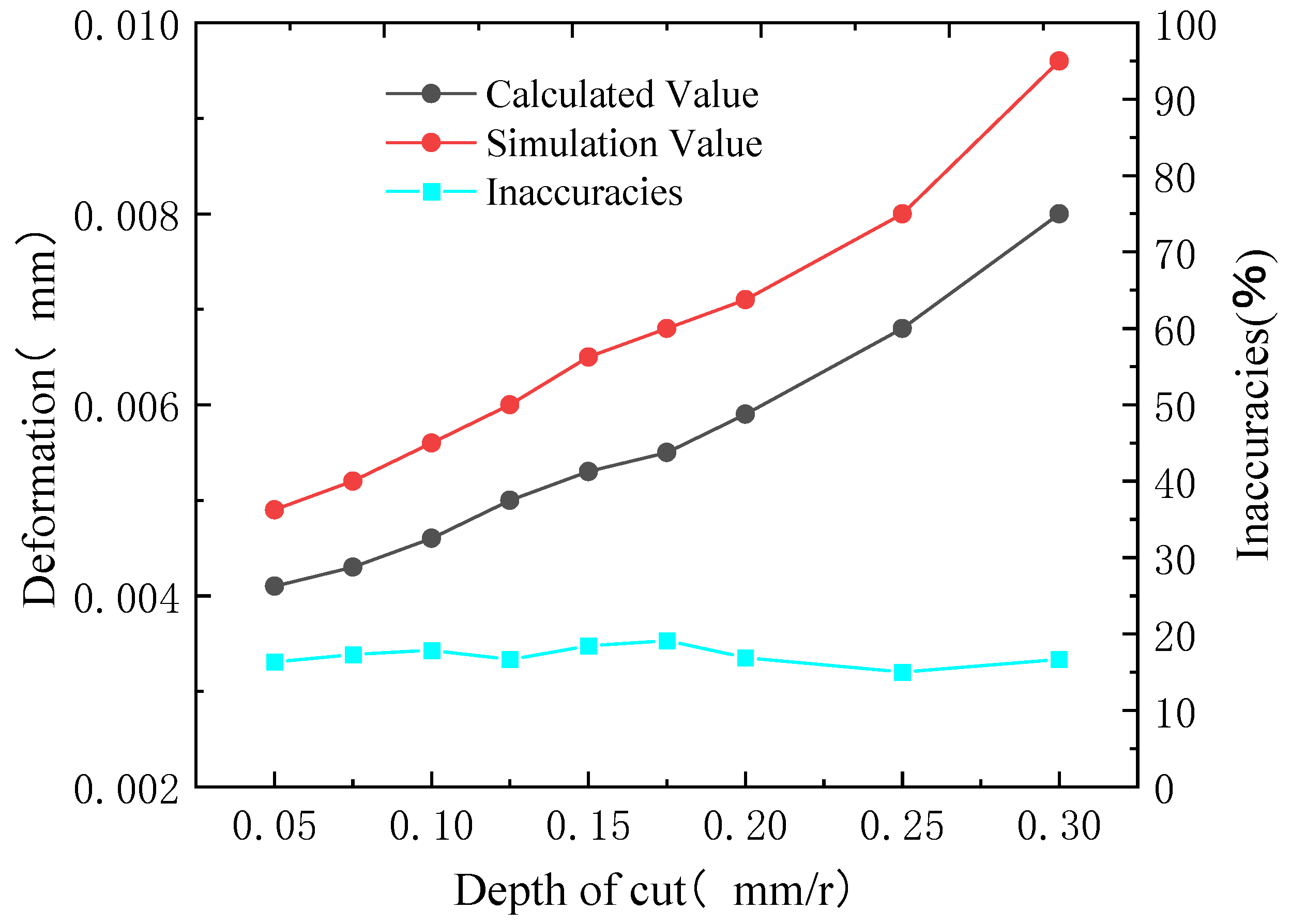
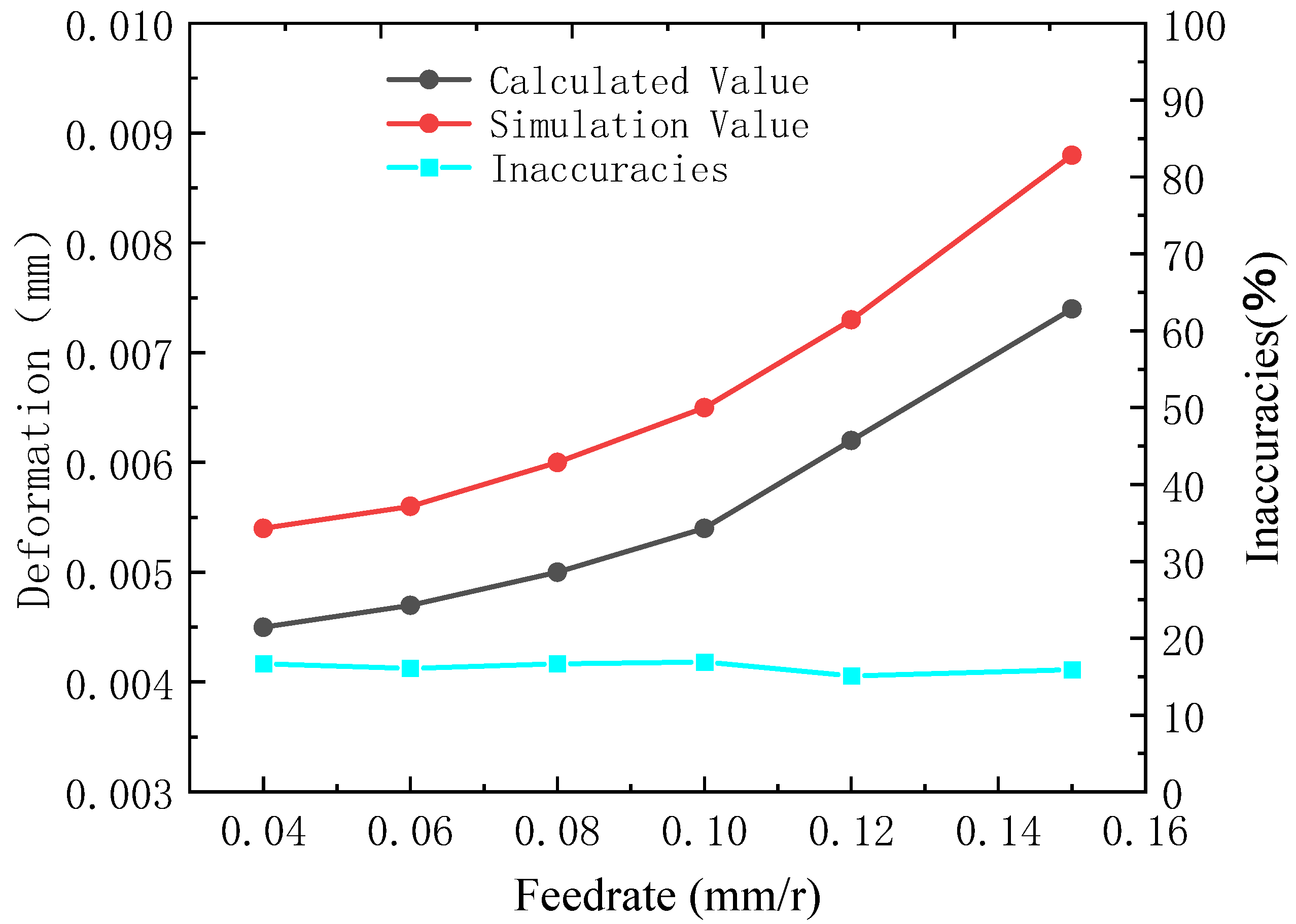
3.2.4. Finite Element Simulation Analysis
4. Experimental Measurements
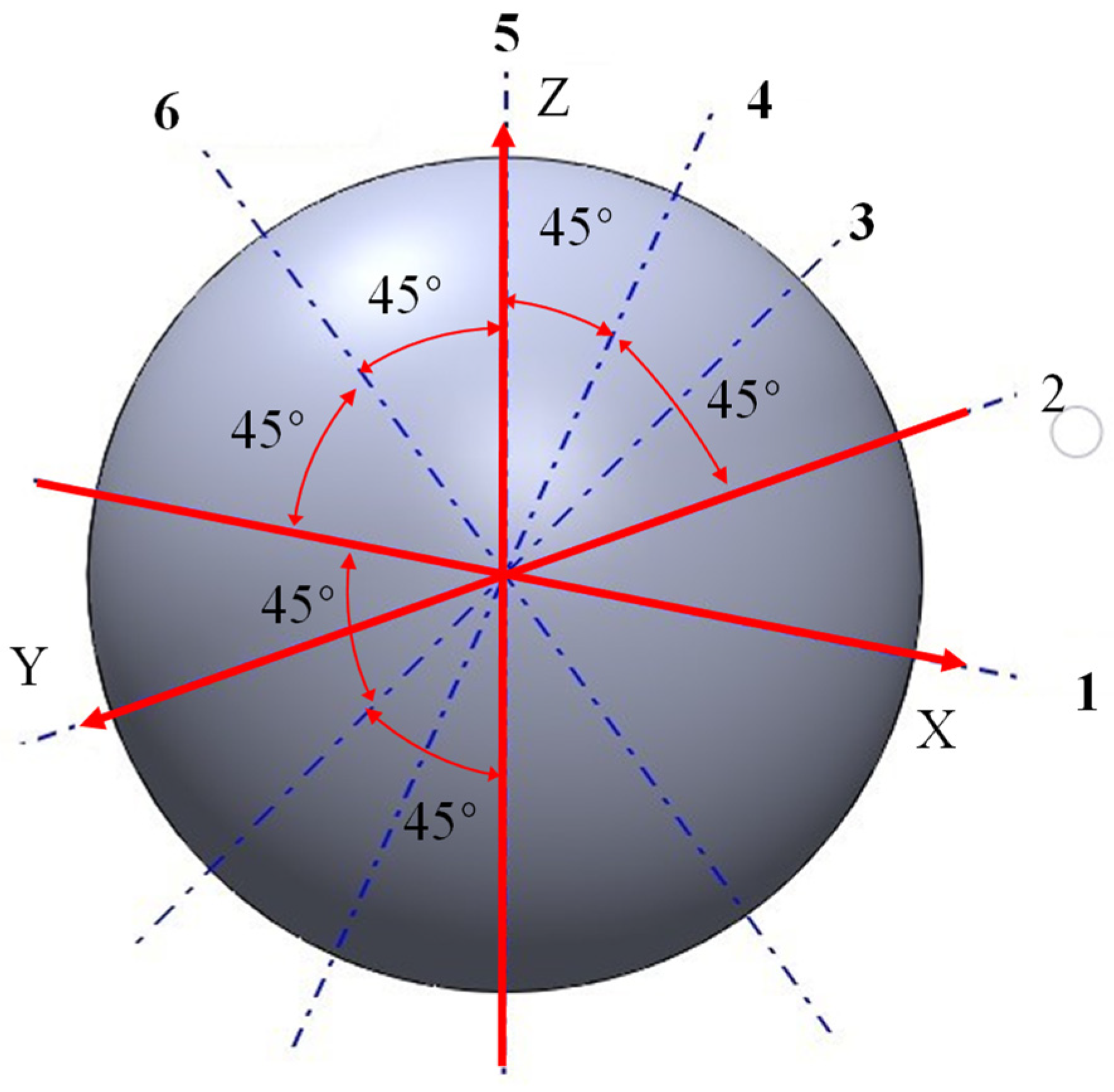
4.1. Static Balance Test
4.2. Dynamic Balance Measurement Experiment
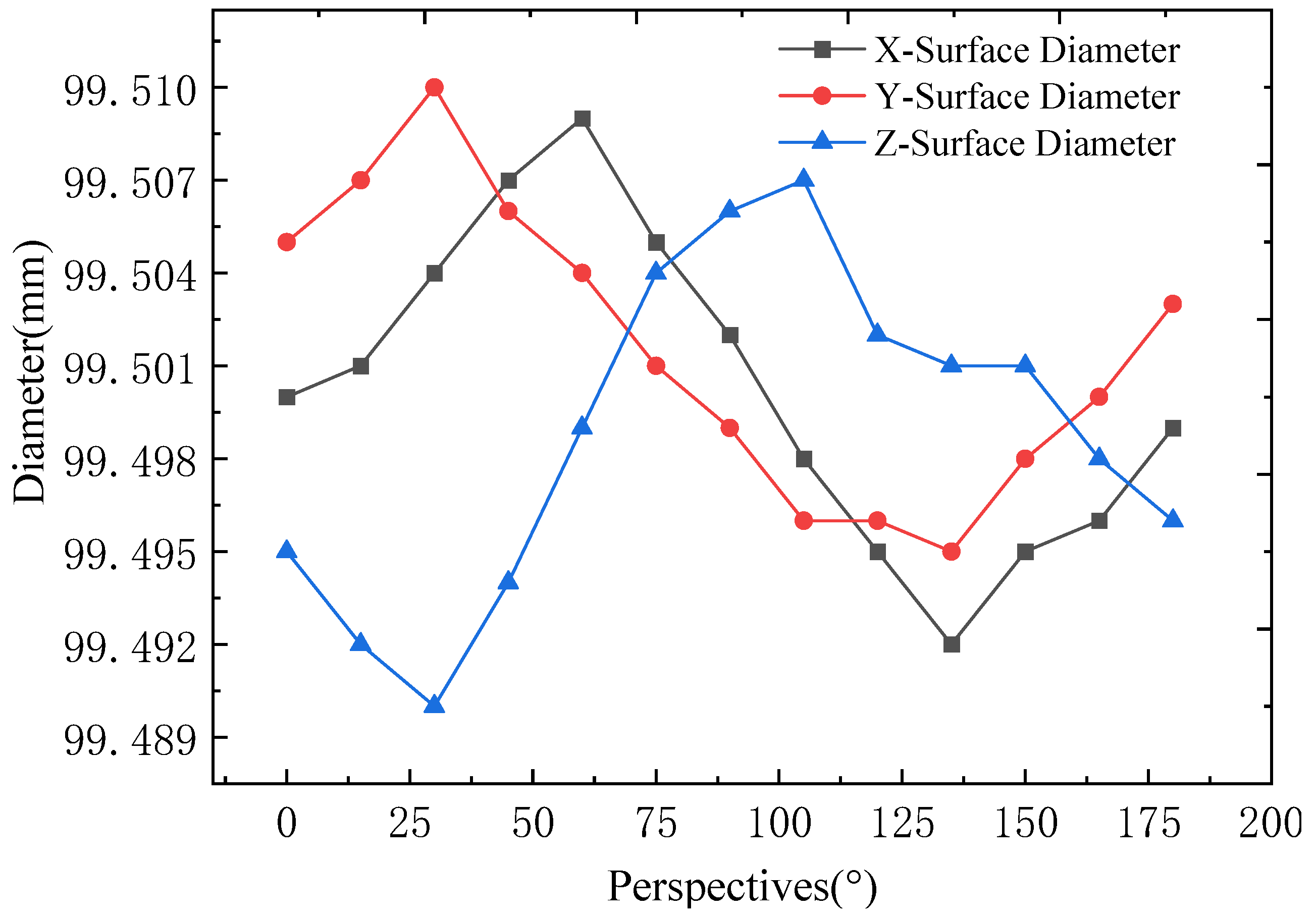
4.3. Diameter Measurement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ismail, Z.; Varatharajoo, R. A study of reaction wheel configurations for 3-axissatellite attitude control. Space Res. 2010, 15, 750–759. [Google Scholar] [CrossRef]
- Ormsby, R.D. Capabilities and limitations of reaction spheres for attitude control. ARS J. 1961, 31, 808–812. [Google Scholar] [CrossRef]
- Feng, H.W.; Fang, J.C. Modal Analysis and Experimental Study of high-speed rotor for Maglev control torque Gyroscope. Chin. J. Inertia Technol. 2005, 5, 74–77. [Google Scholar]
- Brown, C.D. Elements of Spacecraft Design. AIAA 2002, 5, 68. [Google Scholar]
- Wertz, J.R.; Larson, W.J. Space Mission Analysis and Design; Microcosm, Inc.: Torrance, CA, USA, 1992; pp. 1–18. [Google Scholar]
- Haeussermann, W. The Spherical Control Motor for Three Axis Attitude Control of Space Vehicles; NASA TM X-50071; NASA: Washington, DC, USA, 1959. [Google Scholar]
- De Weck, O.L. Reaction Wheel Disturbance Analysis; MIT SSL Memo: Cambridge, MA, USA, 1998; pp. 150–160. [Google Scholar]
- Tyc, G.; Staley, D.A.; Whitehead, W.R. GyroWheel TM-an innovative new actuator/sensor for 3-axis spacecraft attitude control. In Proceedings of the 13th Annual AIAA Conference on Small Satellites, Logan, UT, USA, 23–26 August 1999; pp. 1–13. [Google Scholar]
- Zhu, L.; Guo, J.; Gill, E. Review of reaction spheres for spacecraft attitude control. Prog. Aerosp. Sci. 2017, 91, 67–86. [Google Scholar] [CrossRef]
- Maini, A.K.; Agrawal, V. Satellite Technology: Principles and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Seyfart, G. Design, Construct, and Evaluate a Spherical Induction Robot; Carnegie Mellon University: Pittsburgh, PA, USA, 2016. [Google Scholar]
- Kong, J.X.; Zheng, Y.C.; Wang, X.K. Fixture Design Based on Magneto-rheological Fluids for Thin Wall Spherical Shell Precision Machining. In Proceedings of the Global Conference on Digital Design and Manufacturing Technology, Hangzhou, China, 23–25 January 2011; pp. 215, 315–319. [Google Scholar]
- Jing, K. Precision machining of thin-walled spherical shells based on magnetorheological fluid strengthening. Adv. Mater. Rerearch 2012, 381, 6–10. [Google Scholar]
- Mahajan, D.; Tajane, R. A Review on Ball Burnishing Process. Int. J. Sci. Res. Publ. 2013, 3, 1–8. [Google Scholar]
- Samołyk, G. Numerical analysis of a forging process for producing a hollow ball from tube. Adv. Sci. Technol. Res. J. 2018, 12, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.-Y.; Xian, H.-F.; Wang, W.-R.; Wang, X.-J.; Wu, Y.; Huang, S.-Z.; Zhao, X.-W. Improvement of the machining process of aluminum spherical shell. Sci. Technol. Innov. 2020, 23, 176–177. [Google Scholar]
- Samołyk, G.; Winiarski, G. Analysis of single-operation cold forging of a hollow ball from a tubular billet. Int. J. Adv. Manuf. Technol. 2019, 103, 3045–3056. [Google Scholar] [CrossRef]
- Samołyk, G.; Winiarski, G. Selected aspects of a cold forging process for hollow balls. Int. J. Adv. Manuf. Technol. 2022, 119, 2479–2494. [Google Scholar] [CrossRef]
- An, Q.; Kollmann, F.G. A general theory of finite deformation of viscoplastic thin shells. Acta Mech. 1996, 117, 47–70. [Google Scholar] [CrossRef]
- Duan, Z.; Li, C.; Ding, W.; Zhang, Y.; Yang, M.; Gao, T.; Cao, H.; Xu, X.; Wang, D.; Mao, C.; et al. Milling Force Model for Aviation Aluminum Alloy: Academic Insight and Perspective Analysis. Chin. J. Mech. Eng. 2021, 34, 18. [Google Scholar] [CrossRef]
- Arnaud, L.; Gonzalo, O.; Seguy, S.; Jauregi, H.; Peigné, G. Simulation of low-rigidity part machining applied to thin-walled structures. Int. J. Adv. Manuf. Technol. 2011, 54, 479–488. [Google Scholar] [CrossRef]
- Stephenson, D.A.; Agapiou, J.S. Metal Cutting Theory and Practice, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2005; pp. 100–112. [Google Scholar]















| Makings | Durometer (HB) | Tensile Strength (MPa) | Saturation Density (B/T) | Permeability (μ/(mH·m−1)) |
|---|---|---|---|---|
| pure iron (DT4C) | 50–80 | 313.6 | 234 | 41.8–62.8 |
| 45 steel | 207 | 600 | 89 | 52 |
| stainless steels | 187 | 520 | 40 | 16.3 |
| 10 steel | 137 | 335 | 193 | 47–58 |
| Processing Conditions | Parameters |
|---|---|
| Hardness (HBS) | 220 |
| Front Angle | 10° |
| Back Angle | 7° |
| Main declination Angle | 75° |
| Tool Cutting Edge Inclination Angle | 0° |
| Tip radius | 0.5 mm |
| Cutting speed | 90 m/min |
| Axis of Rotation | Unbalanced Mass (g) |
|---|---|
| 1 | 0.014 |
| 2 | 0.011 |
| 3 | 0.014 |
| 4 | 0.013 |
| 5 | 0.012 |
| 6 | 0.015 |
| Axis of Rotation | Unbalanced Mass (g) |
|---|---|
| 1 | 0.015 |
| 2 | 0.016 |
| 3 | 0.014 |
| 4 | 0.015 |
| 5 | 0.017 |
| 6 | 0.014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Zhang, Y.; Niu, Y.; Zhao, Y.; Guan, S.; Wang, Z.; Wu, T. Design and Machining of a Spherical Shell Rotor for a Magnetically Levitated Momentum Ball. Aerospace 2024, 11, 61. https://doi.org/10.3390/aerospace11010061
Ma L, Zhang Y, Niu Y, Zhao Y, Guan S, Wang Z, Wu T. Design and Machining of a Spherical Shell Rotor for a Magnetically Levitated Momentum Ball. Aerospace. 2024; 11(1):61. https://doi.org/10.3390/aerospace11010061
Chicago/Turabian StyleMa, Limei, Yongheng Zhang, Yuli Niu, Yong Zhao, Shaoya Guan, Zijing Wang, and Tuoda Wu. 2024. "Design and Machining of a Spherical Shell Rotor for a Magnetically Levitated Momentum Ball" Aerospace 11, no. 1: 61. https://doi.org/10.3390/aerospace11010061
APA StyleMa, L., Zhang, Y., Niu, Y., Zhao, Y., Guan, S., Wang, Z., & Wu, T. (2024). Design and Machining of a Spherical Shell Rotor for a Magnetically Levitated Momentum Ball. Aerospace, 11(1), 61. https://doi.org/10.3390/aerospace11010061






