Correlation Studies of Different Decoupled Two-Scale Simulations for Lattice Structures
Abstract
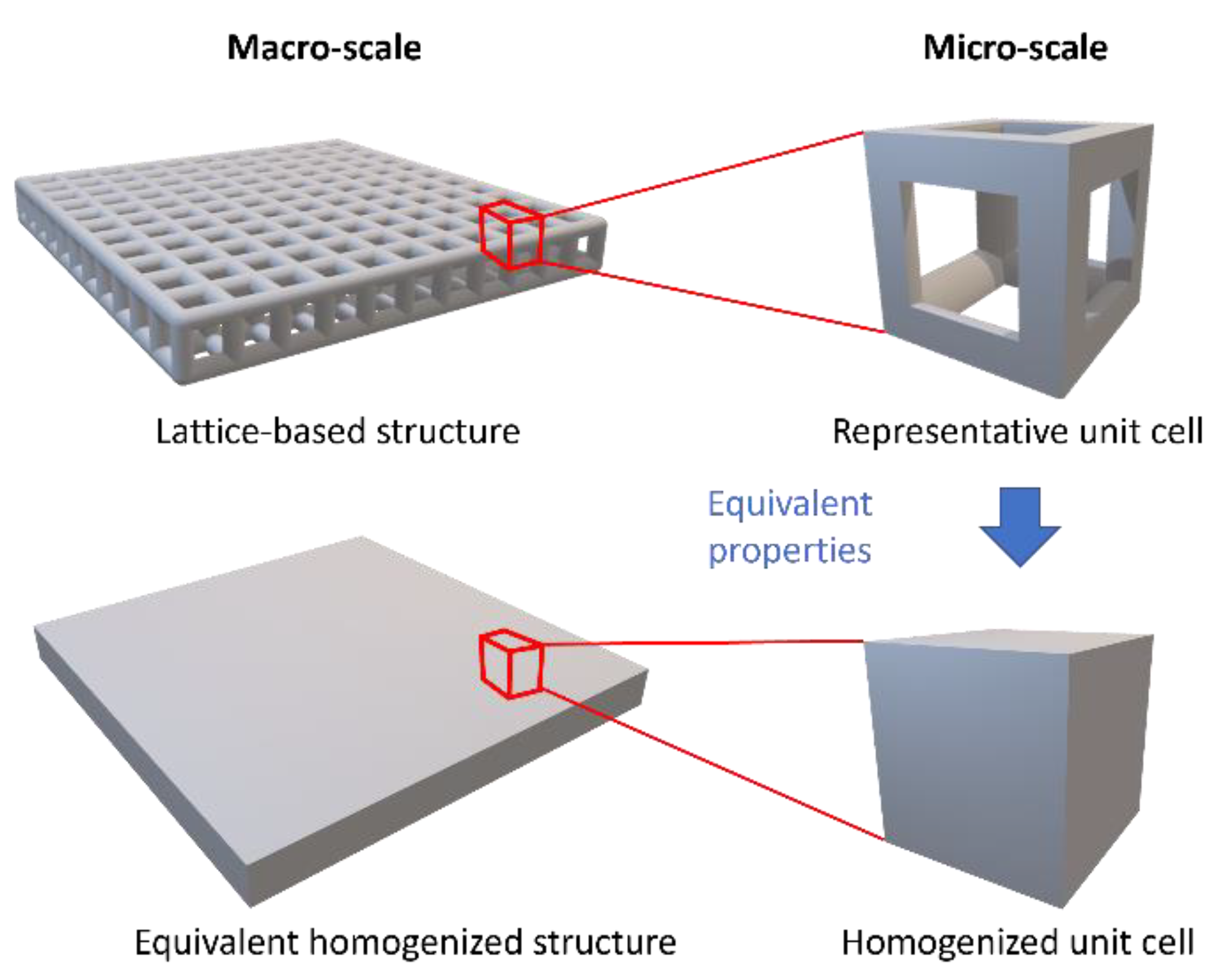
:1. Introduction
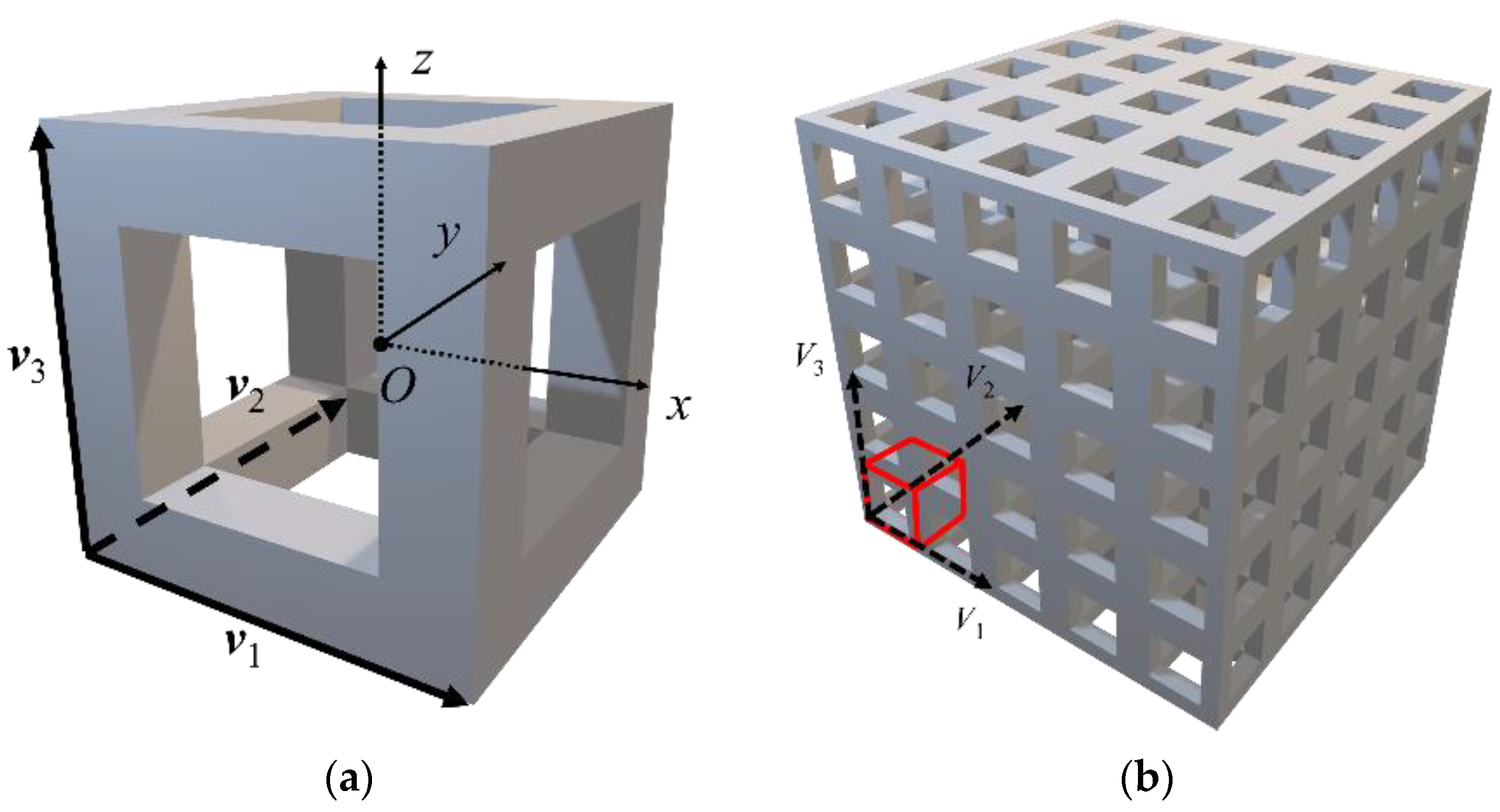
2. Numerical Procedures for Two-Scale Analysis
2.1. Computational Homogenization Method for Plates
- (1)
- The microscopic stress in the PUC is calculated by assigning the macroscopic unit strain or curvature (ex. ) for the microscale problem defined by Equation (1).
- (2)
- The components of effective stiffness tensor are obtained by calculating the macroscopic resultant force and moment with Equation (3) (ex. in the case of ).
2.2. Computational Homogenization Method for Solids
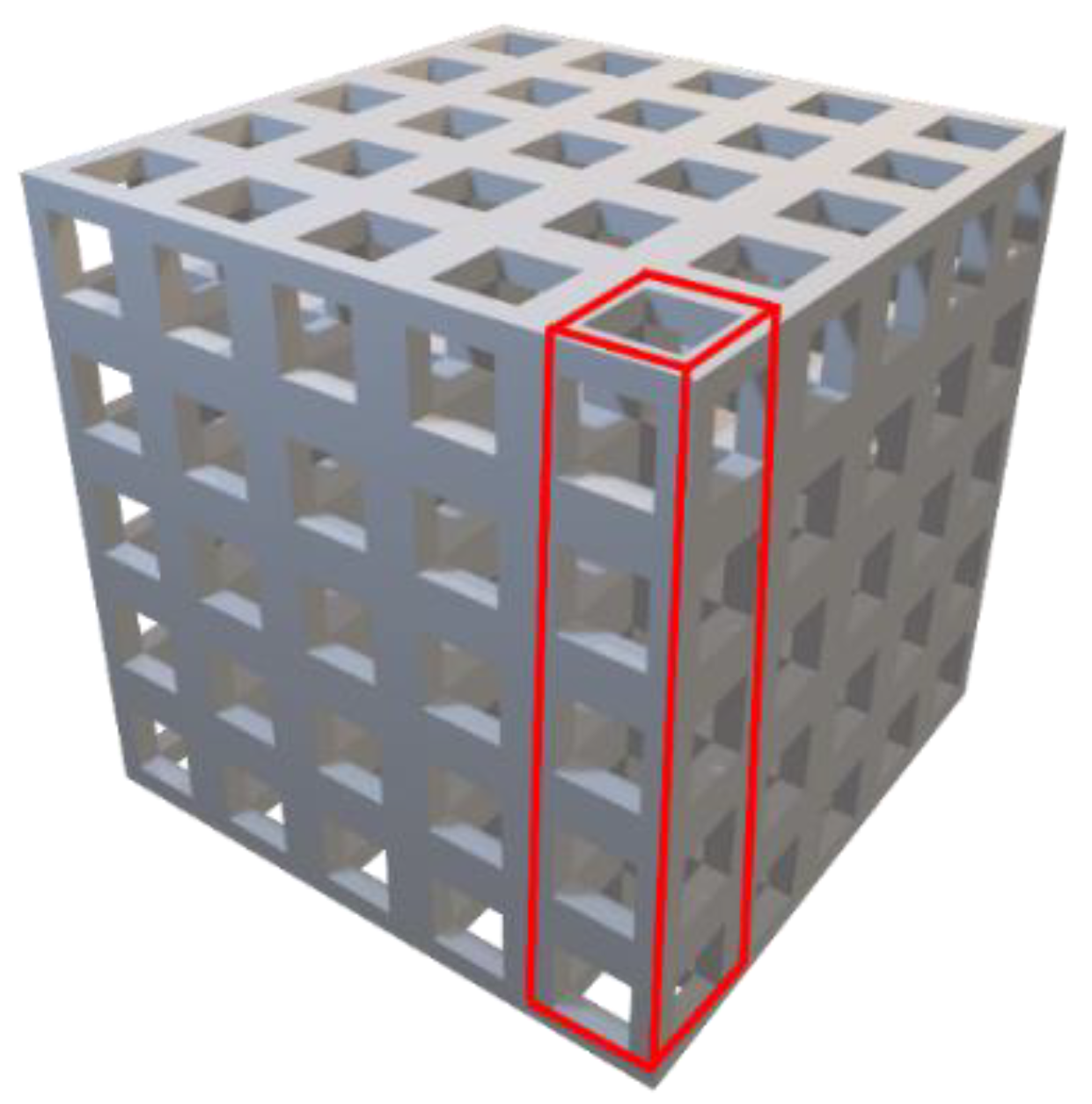
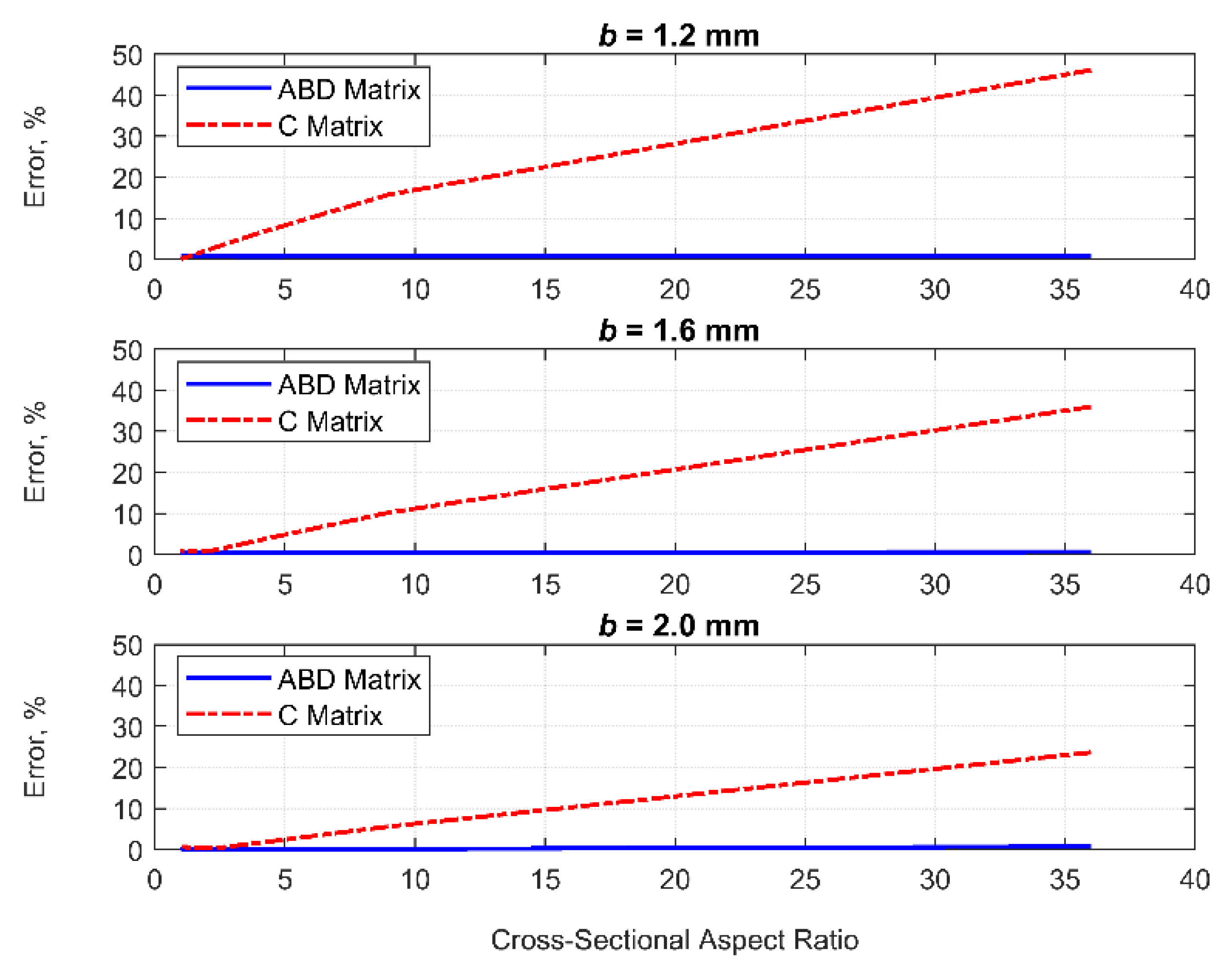
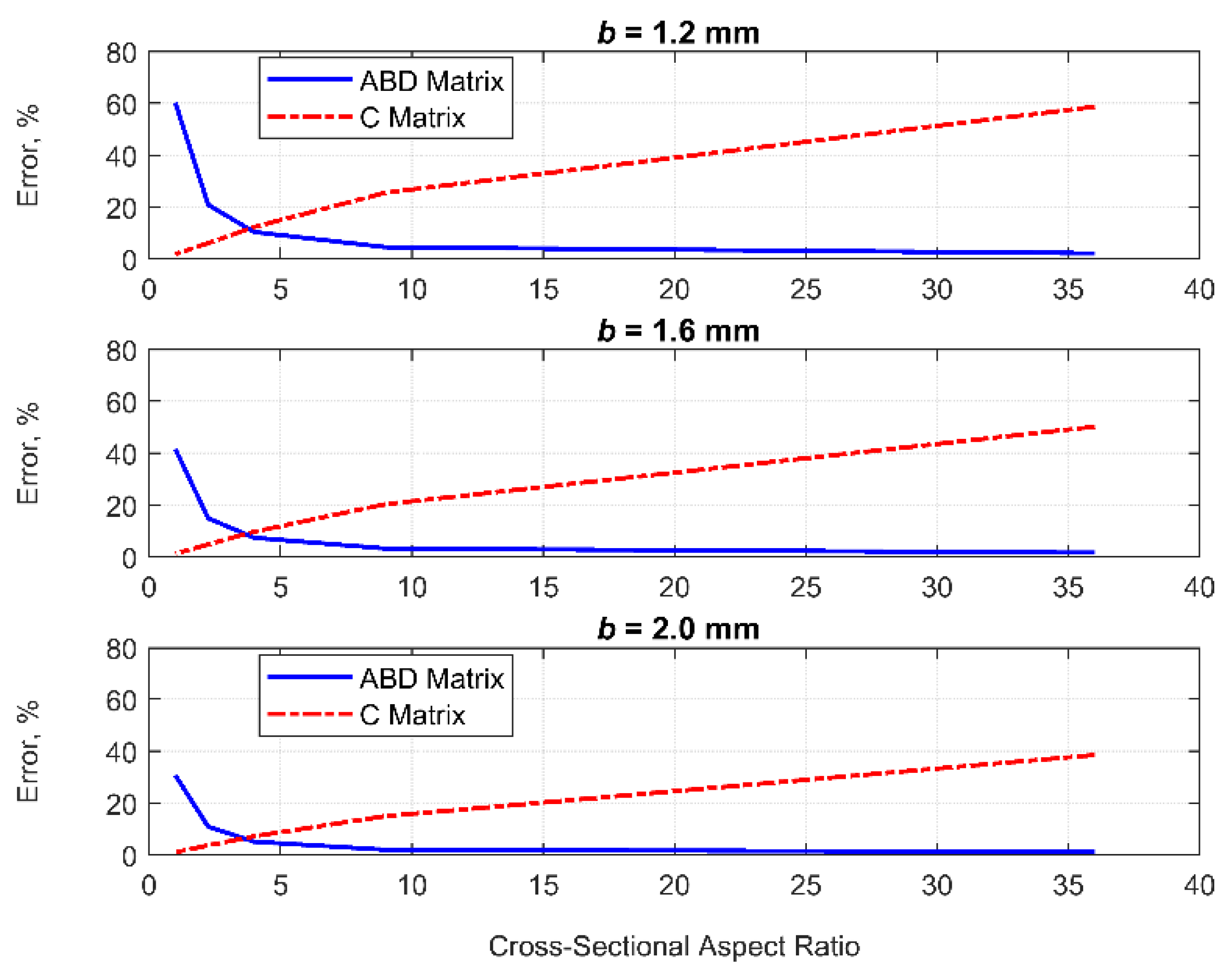
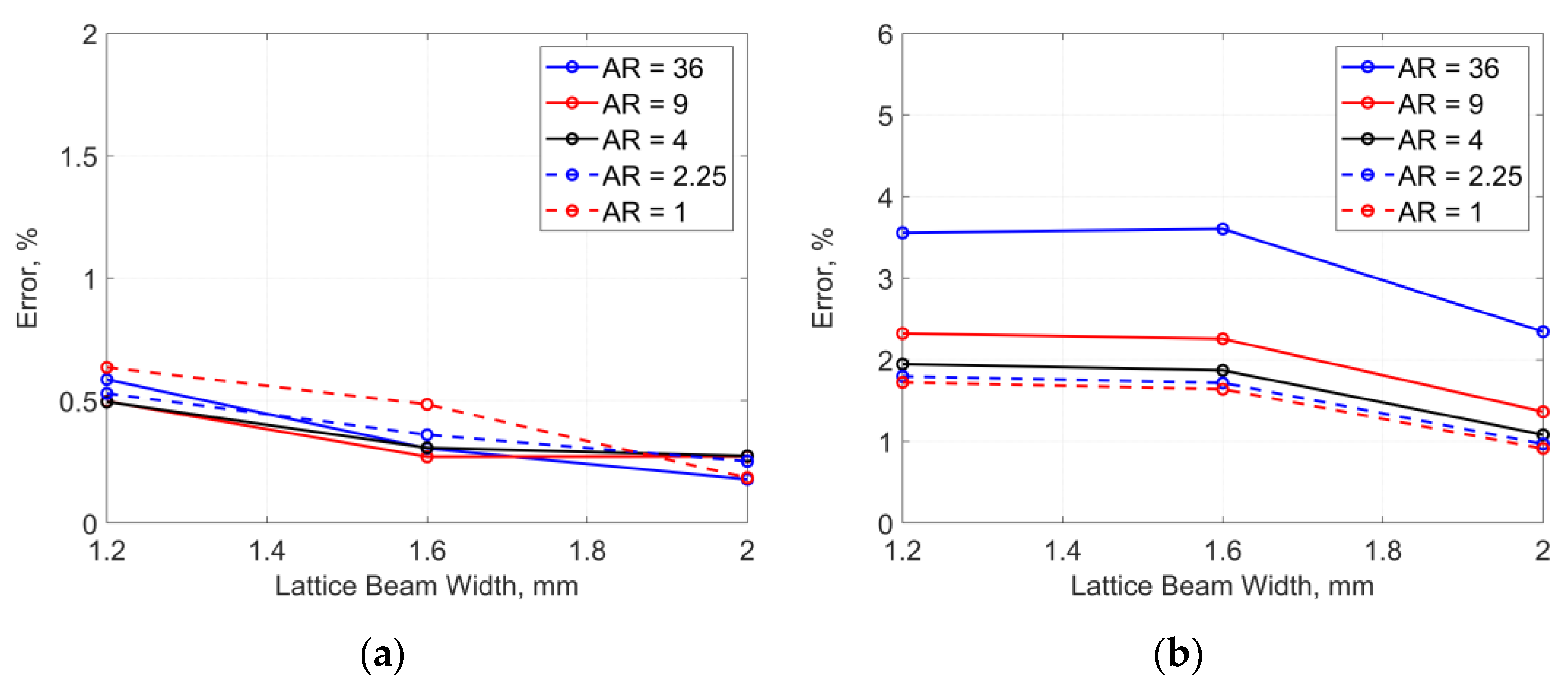
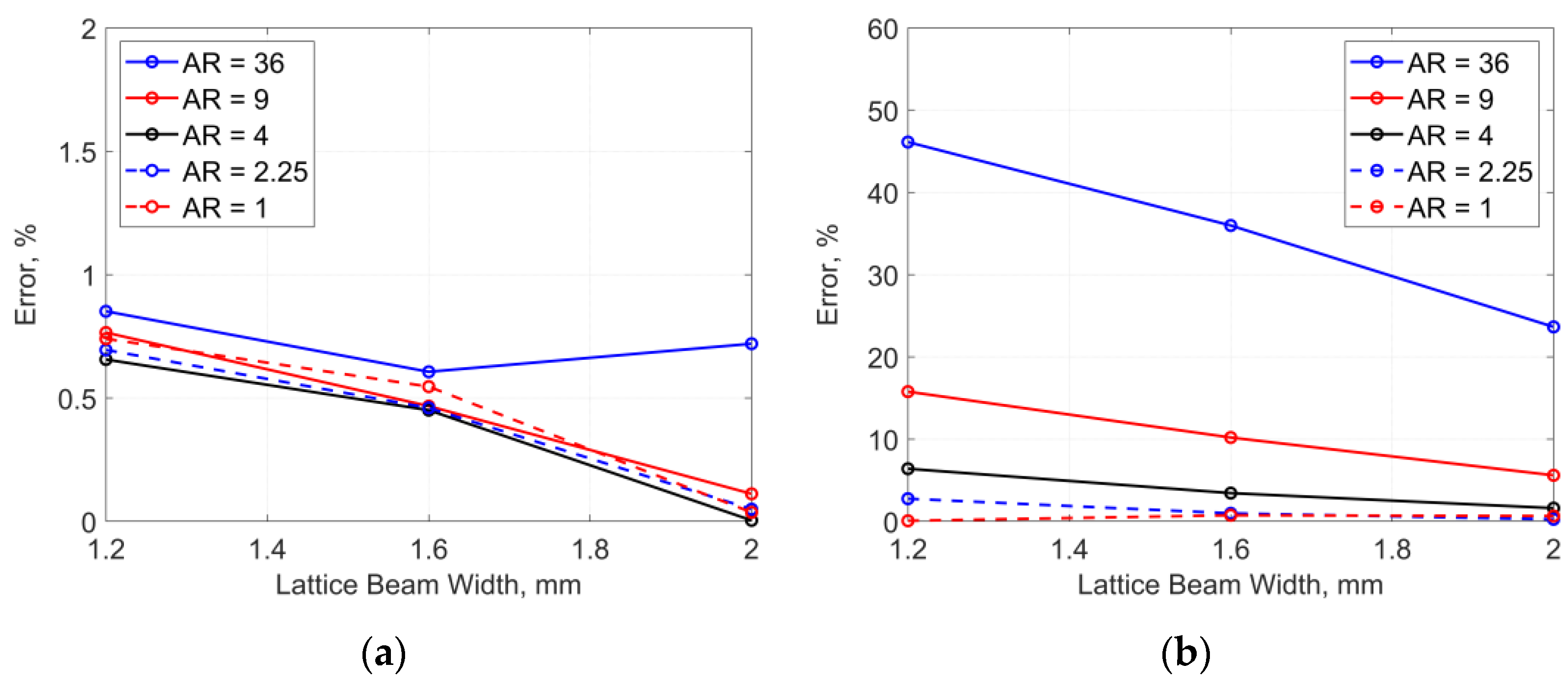
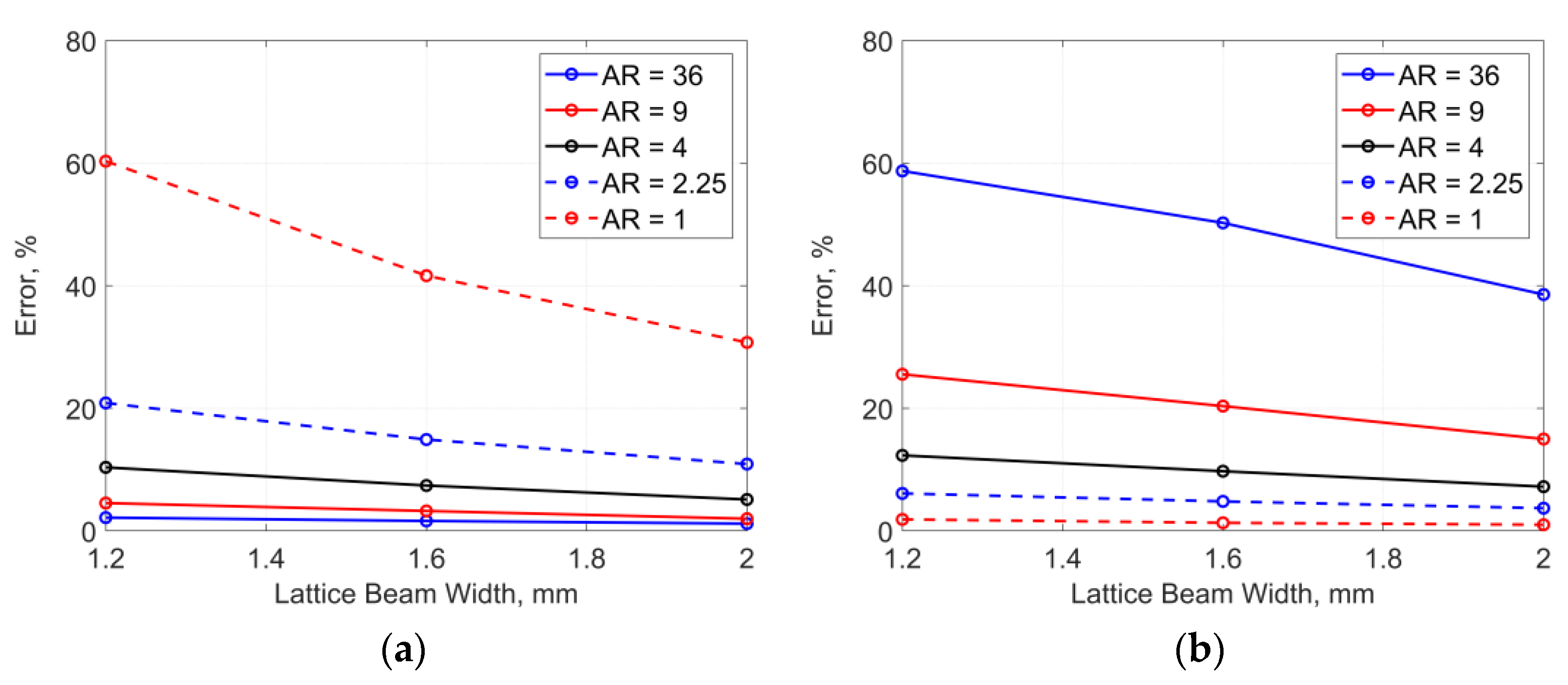
3. Correlation Study of Different Homogenization Approaches for Lattice-Based Structures
4. Conclusions
- (1)
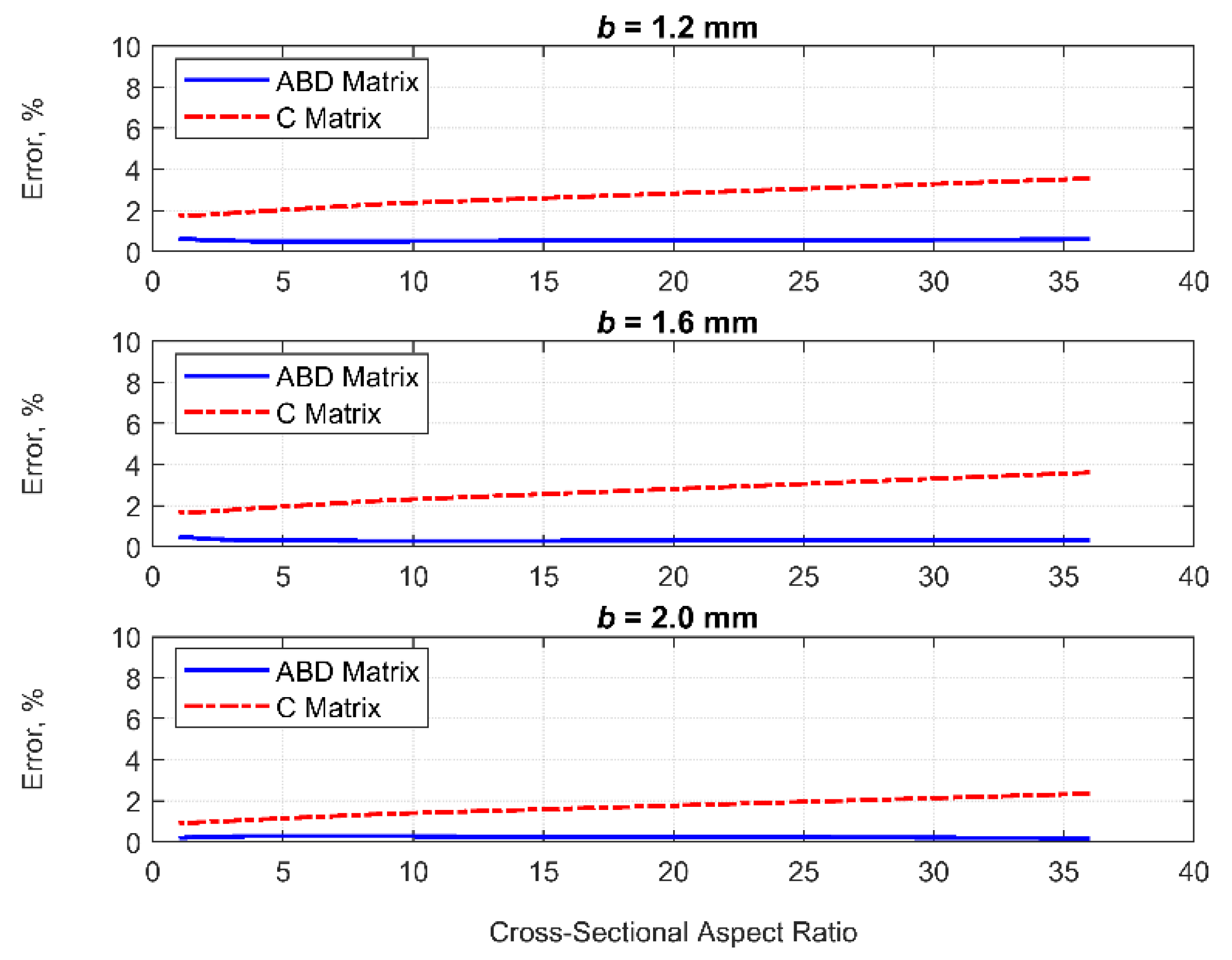
- Tensile stiffness can be estimated by both homogenizations with reasonable accuracy even if the assumptions in periodic conditions are violated. Therefore, one can choose both homogenization approaches for cost-effective analysis of lattice structures if a focus is on tensile responses;
- (2)
- Predictions of bending and torsional stiffnesses by both homogenizations can provide enough accuracy within a certain threshold. Also, the validity range would be extended if a unit cell of lattices has a higher filling rate. Hence, these homogenizations can still be used for finite periodic arrays of lattices within the threshold.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical Metamaterials at the Theoretical Limit of Isotropic Elastic Stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical Design and Multifunctional Applications of Chiral Mechanical Metamaterials: A Review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Qureshi, A.; Li, B.; Tan, K.T. Numerical Investigation of Band Gaps in 3D Printed Cantilever-in-Mass Metamaterials. Sci. Rep. 2016, 6, 28314. [Google Scholar] [CrossRef]
- Tan, K.T.; Huang, H.H.; Sun, C.T. Blast-Wave Impact Mitigation Using Negative Effective Mass Density Concept of Elastic Metamaterials. Int. J. Impact Eng. 2014, 64, 20–29. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Lin, W.; Qin, Q.H. A Novel Two-Dimensional Mechanical Metamaterial with Negative Poisson’s Ratio. Comp. Mater. Sci. 2020, 171, 109232. [Google Scholar] [CrossRef]
- Ye, M.; Gao, L.; Li, H. A Design Framework for Gradually Stiffer Mechanical Metamaterial Induced by Negative Poisson’s Ratio Property. Mater. Des. 2020, 192, 108751. [Google Scholar] [CrossRef]
- Bauer, J.; Meza, L.R.; Schaedler, T.A.; Schwaiger, R.; Zheng, X.; Valdevit, L. Nanolattices: An Emerging Class of Mechanical Metamaterials. Adv. Mater. 2017, 29, 1701850. [Google Scholar] [CrossRef]
- Yuan, S.; Shen, F.; Bai, J.; Chua, C.K.; Wei, J.; Zhou, K. 3d Soft Auxetic Lattice Structures Fabricated by Selective Laser Sintering: Tpu Powder Evaluation and Process Optimization. Mater. Des. 2017, 120, 317–327. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. Slm Lattice Structures: Properties, Performance, Applications and Challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, Y.; Xiao, R.; Bai, Y.; Song, C.; Wang, D. Evaluation of Topology-Optimized Lattice Structures Manufactured Via Selective Laser Melting. Mater. Des. 2018, 143, 27–37. [Google Scholar] [CrossRef]
- Mizzi, L.; Attard, D.; Gatt, R.; Farrugia, P.S.; Grima, J.N. An Analytical and Finite Element Study on the Mechanical Properties of Irregular Hexachiral Honeycombs. Smart Mater. Struct. 2018, 27, 105016. [Google Scholar] [CrossRef]
- Gibson, L.J. Cellular Solids. MRS Bull. 2003, 28, 270–274. [Google Scholar] [CrossRef]
- Ashby, M.F. The Properties of Foams and Lattices. Philos. T. R. Soc. A 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, Ultrastiff Mechanical Metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Hao, L.; Hussein, A.; Young, P.; Raymont, D. Advanced Lightweight 316l Stainless Steel Cellular Lattice Structures Fabricated Via Selective Laser Melting. Mater. Des. 2014, 55, 533–541. [Google Scholar] [CrossRef]
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S.; Zamani, D. On the Fatigue Behavior of Additive Manufactured Lattice Structures. Theor. Appl. Fract. Mech. 2019, 100, 225–232. [Google Scholar] [CrossRef]
- Shen, J.; Liu, K.; Zeng, Q.; Ge, J.; Dong, Z.; Liang, J. Design and Mechanical Property Studies of 3d Re-Entrant Lattice Auxetic Structure. Aerosp. Sci. Technol. 2021, 118, 106998. [Google Scholar] [CrossRef]
- Chen, Y.J.; Scarpa, F.; Liu, Y.J.; Leng, J.S. Elasticity of Anti-Tetrachiral Anisotropic Lattices. Int. J. Solids. Struct. 2013, 50, 996–1004. [Google Scholar] [CrossRef]
- Caillerie, D.; Nedelec, J.C. Thin Elastic and Periodic Plates. Math. Method. Appl. Sci. 1984, 6, 159–191. [Google Scholar] [CrossRef]
- Kohn, R.V.; Vogelius, M. A New Model for Thin Plates with Rapidly Varying Thickness. Int. J. Solids. Struct. 1984, 20, 333–350. [Google Scholar] [CrossRef]
- Kohn, R.V.; Vogelius, M. A New Model for Thin Plates with Rapidly Varying Thickness. II: A Convergence Proof. Q. Appl. Math. 1985, 43, 1–22. [Google Scholar] [CrossRef]
- Kohn, R.V.; Vogelius, M. A New Model for Thin Plates with Rapidly Varying Thickness. III: Comparison of Different Scalings. Q. Appl. Math. 1986, 44, 35–48. [Google Scholar] [CrossRef]
- Lewinski, T.; Telega, J.J. Plates, Laminates, and Shells: Asymptotic Analysis and Homogenization; World Scientific: Singapore, 2000; Volume 52. [Google Scholar]
- Schmitz, A.; Horst, P. A Finite Element Unit-Cell Method for Homogenised Mechanical Properties of Heterogeneous Plates. Compos. Pt. A Appl. Sci. Manuf. 2014, 61, 23–32. [Google Scholar] [CrossRef]
- Terada, K.; Hirayama, N.; Yamamoto, K.; Muramatsu, M.; Matsubara, S.; Nishi, S. Numerical Plate Testing for Linear Two-Scale Analyses of Composite Plates with in-Plane Periodicity. Int. J. Numer. Methods Eng. 2016, 105, 111–137. [Google Scholar] [CrossRef]
- Yoshida, K.; Nakagami, M. Numerical Analysis of Bending and Transverse Shear Properties of Plain-Weave Fabric Composite Laminates Considering Intralaminar Inhomogeneity. Adv. Compos. Mater. 2017, 26, 135–156. [Google Scholar] [CrossRef]
- Tsushima, N.; Higuchi, R. Stiffness and Strength Evaluation of Lattice-Based Mechanical Metamaterials by Decoupled Two-Scale Analysis. Mater. Today Commun. 2022, 31, 103598. [Google Scholar] [CrossRef]
- Terada, K.; Kikuchi, N. Nonlinear Homogenization Method for Practical Applications. Am. Soc. Mech. Eng. Appl. Mech. Div. AMD 1995, 212, 1–16. [Google Scholar]
- Tan, V.B.C.; Raju, K.; Lee, H.P. Direct Fe2 for Concurrent Multilevel Modelling of Heterogeneous Structures. Comput. Method Appl. M. 2020, 360, 112694. [Google Scholar] [CrossRef]
- Raju, K.; Tay, T.E.; Tan, V.B.C. A Review of the Fe2 Method for Composites. Multiscale Multidiscip. Model. Exp. Des. 2021, 4, 1–24. [Google Scholar] [CrossRef]
- Terada, K.; Kato, J.; Hirayama, N.; Inugai, T.; Yamamoto, K. A Method of Two-Scale Analysis with Micro-Macro Decoupling Scheme: Application to Hyperelastic Composite Materials. Comput. Mech. 2013, 52, 1199–1219. [Google Scholar] [CrossRef]
- Tsushima, N.; Arizono, H.; Tamayama, M. Geometrically Nonlinear Flutter Analysis with Corotational Shell Finite Element Analysis and Unsteady Vortex-Lattice Method. J. Sound Vib. 2022, 520, 116621. [Google Scholar] [CrossRef]
- Tsushima, N.; Tamayama, M.; Arizono, H.; Makihara, K. Geometrically Nonlinear Aeroelastic Characteristics of Highly Flexible Wing Fabricated by Additive Manufacturing. Aerosp. Sci. Technol. 2021, 117, 106923. [Google Scholar] [CrossRef]
- Tsushima, N.; Saitoh, K.; Arizono, H.; Nakakita, K. Structural and Aeroelastic Studies of Wing Model with Metal Additive Manufacturing for Transonic Wind Tunnel Test by Naca 0008 Example. Aerospace 2021, 8, 200. [Google Scholar] [CrossRef]
- Tsushima, N.; Yokozeki, T.; Su, W.; Arizono, H. Geometrically Nonlinear Static Aeroelastic Analysis of Composite Morphing Wing with Corrugated Structures. Aerosp. Sci. Technol. 2019, 88, 244–257. [Google Scholar] [CrossRef]
- White, D.A.; Kudo, J.; Swartz, K.; Tortorelli, D.A.; Watts, S. A Reduced Order Model Approach for Finite Element Analysis of Cellular Structures. Finite Elem. Anal. Des. 2023, 214, 103855. [Google Scholar] [CrossRef]
- Coenen, E.W.C.; Kouznetsova, V.G.; Geers, M.G.D. Computational Homogenization for Heterogeneous Thin Sheets. Int. J. Numer. Methods Eng. 2010, 83, 1180–1205. [Google Scholar] [CrossRef]
- Geers, M.G.D.; Coenen, E.W.C.; Kouznetsova, V.G. Multi-Scale Computational Homogenization of Structured Thin Sheets. Model. Simul. Mater. Sc. 2007, 15, S393. [Google Scholar] [CrossRef]
- Higuchi, R.; Yokozeki, T.; Nagashima, T.; Aoki, T. Evaluation of Mechanical Properties of Noncircular Carbon Fiber Reinforced Plastics by Using Xfem-Based Computational Micromechanics. Compos. Pt. A Appl. Sci. Manuf. 2019, 126, 105556. [Google Scholar] [CrossRef]
- Higuchi, R.; Aoki, R.; Yokozeki, T.; Okabe, T. Evaluation of the in-Situ Damage and Strength Properties of Thin-Ply Cfrp Laminates by Micro-Scale Finite Element Analysis. Adv. Compos. Mater. 2020, 29, 475–493. [Google Scholar] [CrossRef]
- Systems, D. Abaqus 2019 Documentation; Simulia Corp.: Providence, RI, USA, 2019. [Google Scholar]
- ANSYS Inc. Ansys Mechanical User’s Guide; ANSYS Inc.: Southpointe Canonsburg, PA, USA, 2013. [Google Scholar]
- Desalvo, G.J.; Gorman, R.W. Ansys Engineering Analysis System User’s Manual; Swanson Analysis Systems: Houston, PA, USA, 1989. [Google Scholar]
- Banerjee, B.; Chen, Z.J.; Kathirgamanathan, A.; Das, R. Comparison of Ansys Elements Shell181 and Solsh190; Industrial Research Limited: Lower Hutt, New Zealand, 2011. [Google Scholar]
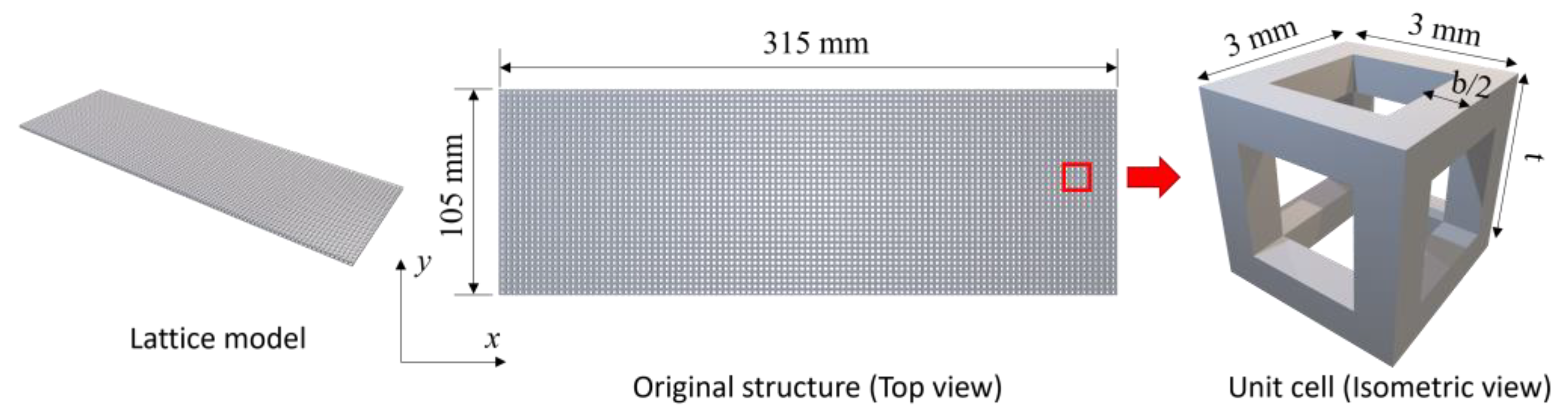


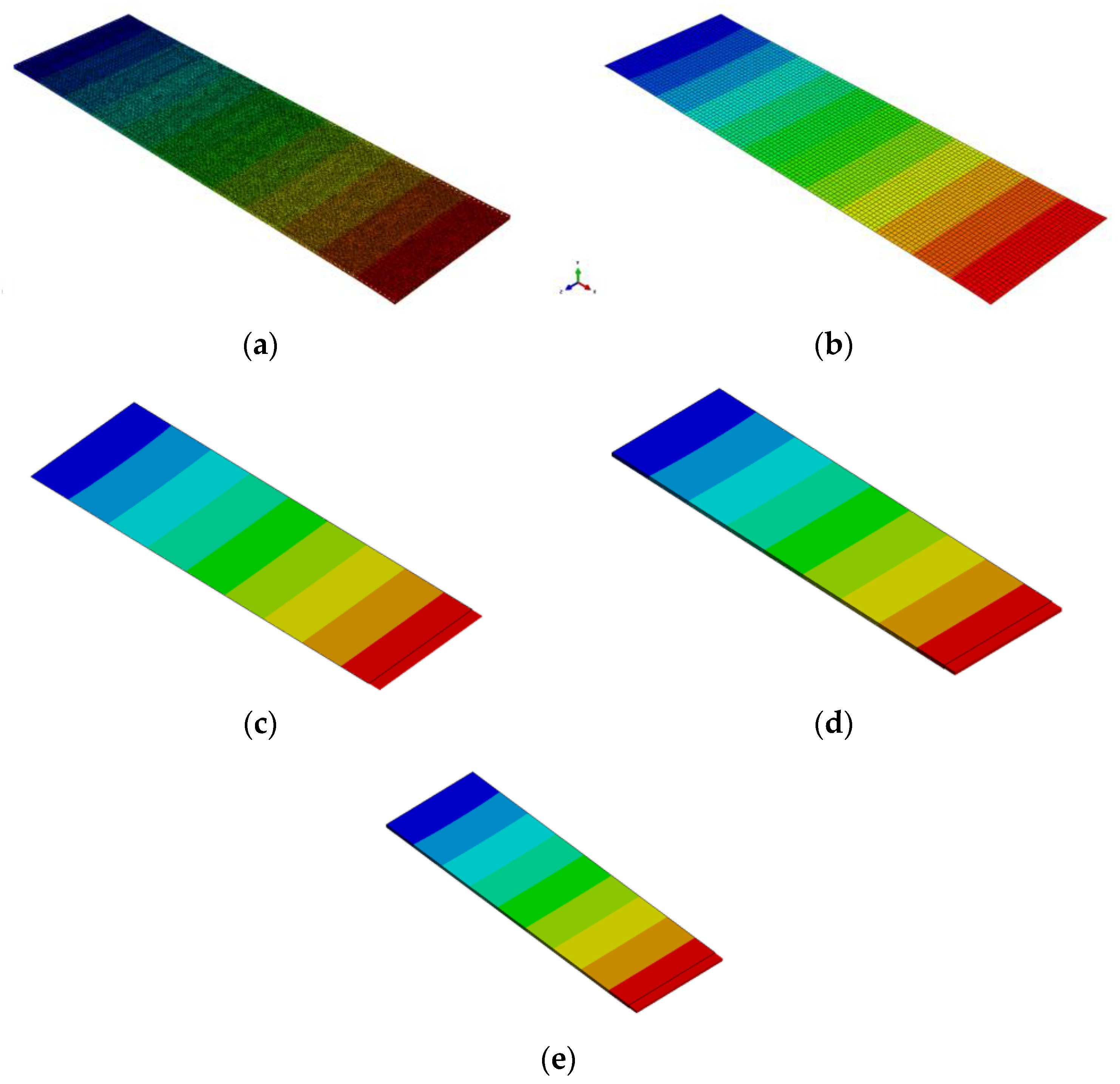
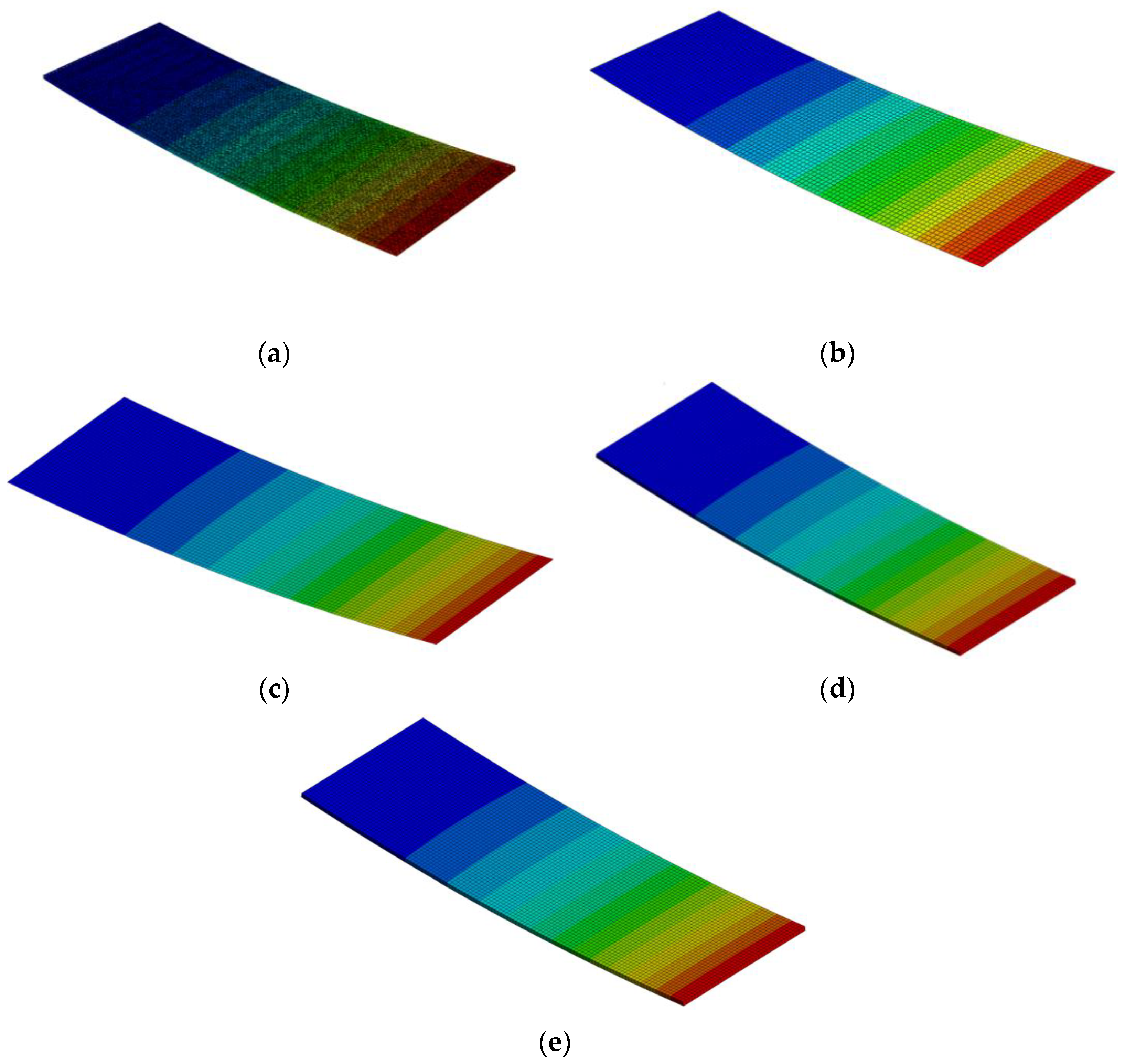
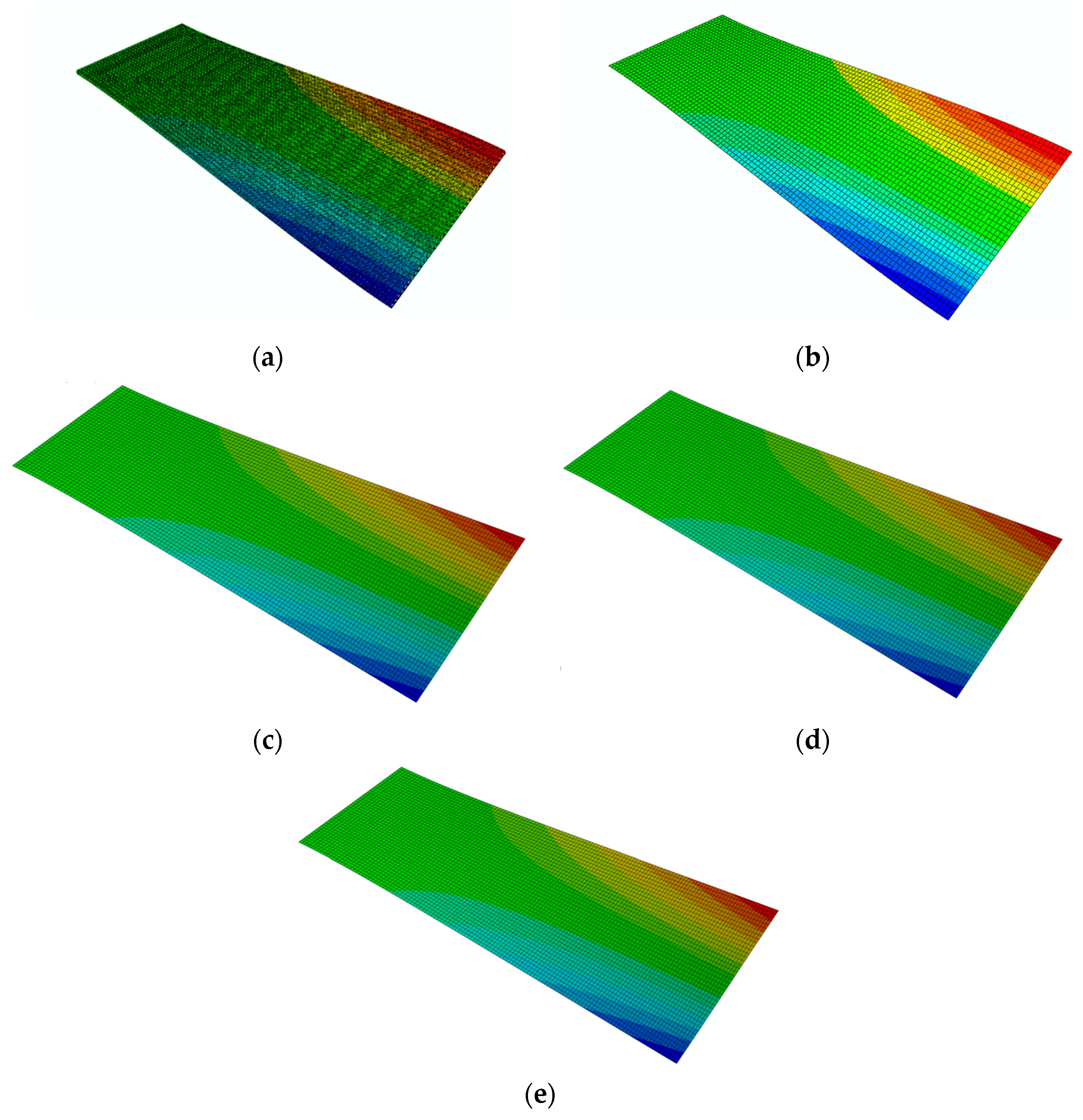

| Model | b, mm | Resultant Load, N |
|---|---|---|
| Detailed | 1.2 | 512.32 |
| Shell (ABD matrix) | 515.35 (0.59%) | |
| Shell (C matrix) | 527.83 (3.03%) | |
| Solsh (C matrix) | 527.88 (3.04%) | |
| Solid (C matrix) | 527.85 (3.03%) | |
| Detailed | 1.6 | 939.60 |
| Shell (ABD matrix) | 963.06 (2.50%) | |
| Shell (C matrix) | 994.68 (5.86%) | |
| Solsh (C matrix) | 994.84 (5.88%) | |
| Solid (C matrix) | 994.74 (5.87%) | |
| Detailed | 2.0 | 1575.1 |
| Shell (ABD matrix) | 1585.6 (0.67%) | |
| Shell (C matrix) | 1625.4 (3.19%) | |
| Solsh (C matrix) | 1626.0 (3.23%) | |
| Solid (C matrix) | 1625.7 (3.21%) |
| Model | b, mm | Resultant Moment, N·mm |
|---|---|---|
| Detailed | 1.2 | 12.903 |
| Shell (ABD matrix) | 13.013 (0.85%) | |
| Shell (C matrix) | 6.9361 (46.24%) | |
| Solsh (C matrix) | 6.9204 (46.37%) | |
| Solid (C matrix) | 6.9189 (46.38%) | |
| Detailed | 1.6 | 20.038 |
| Shell (ABD matrix) | 20.520 (2.41%) | |
| Shell (C matrix) | 13.133 (34.46%) | |
| Solsh (C matrix) | 13.065 (34.80%) | |
| Solid (C matrix) | 13.133 (34.46%) | |
| Detailed | 2.0 | 27.704 |
| Shell (ABD matrix) | 28.234 (1.91%) | |
| Shell (C matrix) | 21.630 (21.92%) | |
| Solsh (C matrix) | 21.417 (22.69%) | |
| Solid (C matrix) | 21.633 (21.91%) |
| Model | b, mm | Resultant Moment, N·mm |
|---|---|---|
| Detailed | 1.2 | 9.0123 |
| Shell (ABD matrix) | 9.2158 (2.26%) | |
| Shell (C matrix) | 3.7271 (58.64%) | |
| Solsh (C matrix) | 3.6902 (59.05%) | |
| Solid (C matrix) | 3.6699 (59.28%) | |
| Detailed | 1.6 | 23.019 |
| Shell (ABD matrix) | 23.442 (1.84%) | |
| Shell (C matrix) | 11.645 (49.41%) | |
| Solsh (C matrix) | 11.541 (49.86%) | |
| Solid (C matrix) | 11.473 (50.16%) | |
| Detailed | 2.0 | 41.934 |
| Shell (ABD matrix) | 41.549 (0.92%) | |
| Shell (C matrix) | 25.644 (38.85%) | |
| Solsh (C matrix) | 25.424 (39.37%) | |
| Solid (C matrix) | 25.266 (39.75%) |
| b, mm | Width, mm | Thickness, mm | Resultant Load, N | ||
|---|---|---|---|---|---|
| Detailed | Shell (ABD Matrix) | Solid (C Matrix) | |||
| 1.2 | 108 | 3 | 526.996 | 530.083 (0.59%) | 545.720 (3.55%) |
| 54 | 6 | 533.166 | 535.813 (0.50%) | 545.540 (2.32%) | |
| 36 | 9 | 535.078 | 537.723 (0.49%) | 545.490 (1.95%) | |
| 27 | 12 | 535.843 | 538.677 (0.53%) | 545.470 (1.80%) | |
| 18 | 18 | 536.225 | 539.631 (0.64%) | 545.460 (1.72%) | |
| 1.6 | 108 | 3 | 987.637 | 990.646 (0.30%) | 1023.210 (3.60%) |
| 54 | 6 | 999.829 | 1002.53 (0.27%) | 1022.384 (2.26%) | |
| 36 | 9 | 1003.39 | 1006.47 (0.31%) | 1022.151 (1.87%) | |
| 27 | 12 | 1004.82 | 1008.44 (0.36%) | 1022.061 (1.72%) | |
| 18 | 18 | 1005.54 | 1010.41 (0.48%) | 1022.017 (1.64%) | |
| 2.0 | 108 | 3 | 1633.99 | 1631.08 (−0.18%) | 1672.289 (2.34%) |
| 54 | 6 | 1647.24 | 1642.77 (−0.27%) | 1669.681 (1.36%) | |
| 36 | 9 | 1651.11 | 1646.60 (−0.27%) | 1668.957 (1.08%) | |
| 27 | 12 | 1652.69 | 1648.52 (−0.25%) | 1668.685 (0.97%) | |
| 18 | 18 | 1653.49 | 1650.44 (−0.18%) | 1668.556 (0.91%) | |
| b, mm | Width, mm | Thickness, mm | Resultant Moment, N·mm | ||
|---|---|---|---|---|---|
| Detailed | Shell (ABD Matrix) | Solid (C Matrix) | |||
| 1.2 | 108 | 3 | 13.2743 | 13.3873 (0.85%) | 7.154 (46.11%) |
| 54 | 6 | 33.9294 | 34.189 (0.77%) | 28.579 (15.77%) | |
| 36 | 9 | 68.6652 | 69.1156 (0.66%) | 64.272 (6.40%) | |
| 27 | 12 | 117.475 | 118.291 (0.69%) | 114.240 (2.75%) | |
| 18 | 18 | 257.200 | 259.103 (0.74%) | 257.020 (0.07%) | |
| 1.6 | 108 | 3 | 20.9876 | 21.1148 (0.61%) | 13.439 (35.97%) |
| 54 | 6 | 59.6814 | 59.9601 (0.47%) | 53.598 (10.19%) | |
| 36 | 9 | 124.748 | 125.31 (0.45%) | 120.463 (3.43%) | |
| 27 | 12 | 216.184 | 217.178 (0.46%) | 214.066 (0.98%) | |
| 18 | 18 | 477.997 | 480.607 (0.55%) | 481.534 (0.74%) | |
| 2.0 | 108 | 3 | 28.8551 | 29.0628 (0.72%) | 22.034 (23.64%) |
| 54 | 6 | 92.8346 | 92.9382 (0.11%) | 87.637 (5.60%) | |
| 36 | 9 | 199.988 | 199.98 (0.00%) | 196.772 (1.61%) | |
| 27 | 12 | 350.387 | 350.214 (0.05%) | 349.517 (0.25%) | |
| 18 | 18 | 780.946 | 780.662 (0.04%) | 786.025 (0.65%) | |
| b, mm | Width, mm | Thickness, mm | Resultant Moment, N·mm | ||
|---|---|---|---|---|---|
| Detailed | Shell (ABD Matrix) | Solid (C Matrix) | |||
| 1.2 | 108 | 3 | 9.37778 | 9.58021 (2.16%) | 3.873 (58.70%) |
| 54 | 6 | 17.9976 | 18.8126 (4.53%) | 13.402 (25.53%) | |
| 36 | 9 | 30.1893 | 33.3146 (10.35%) | 26.474 (12.31%) | |
| 27 | 12 | 42.0466 | 50.8146 (20.85%) | 39.482 (6.10%) | |
| 18 | 18 | 52.3985 | 83.9939 (60.30%) | 51.423 (1.86%) | |
| 1.6 | 108 | 3 | 23.9114 | 24.2967 (1.61%) | 11.901 (50.23%) |
| 54 | 6 | 52.9161 | 54.6308 (3.24%) | 42.151 (20.34%) | |
| 36 | 9 | 92.9082 | 99.7746 (7.39%) | 83.874 (9.72%) | |
| 27 | 12 | 132.062 | 151.731 (14.89%) | 125.723 (4.80%) | |
| 18 | 18 | 166.669 | 236.039 (41.62%) | 164.490 (1.31%) | |
| 2.0 | 108 | 3 | 42.5185 | 43.017 (1.17%) | 26.130 (38.54%) |
| 54 | 6 | 109.803 | 111.973 (1.98%) | 93.362 (14.97%) | |
| 36 | 9 | 201.765 | 212.075 (5.11%) | 187.237 (7.20%) | |
| 27 | 12 | 292.105 | 323.915 (10.89%) | 281.315 (3.69%) | |
| 18 | 18 | 372.514 | 486.983 (30.73%) | 368.809 (0.99%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsushima, N.; Higuchi, R.; Yamamoto, K. Correlation Studies of Different Decoupled Two-Scale Simulations for Lattice Structures. Aerospace 2023, 10, 723. https://doi.org/10.3390/aerospace10080723
Tsushima N, Higuchi R, Yamamoto K. Correlation Studies of Different Decoupled Two-Scale Simulations for Lattice Structures. Aerospace. 2023; 10(8):723. https://doi.org/10.3390/aerospace10080723
Chicago/Turabian StyleTsushima, Natsuki, Ryo Higuchi, and Koji Yamamoto. 2023. "Correlation Studies of Different Decoupled Two-Scale Simulations for Lattice Structures" Aerospace 10, no. 8: 723. https://doi.org/10.3390/aerospace10080723
APA StyleTsushima, N., Higuchi, R., & Yamamoto, K. (2023). Correlation Studies of Different Decoupled Two-Scale Simulations for Lattice Structures. Aerospace, 10(8), 723. https://doi.org/10.3390/aerospace10080723






