Design of a Hydrogen Aircraft for Zero Persistent Contrails
Abstract
1. Introduction
2. Materials and Methods
2.1. Identifying Contrail Persistence Regions
2.1.1. The Contrail Formation and Persistence Conditions
2.1.2. Mapping Contrail Persistence Regions
2.2. Modeling Redesigned Aircraft
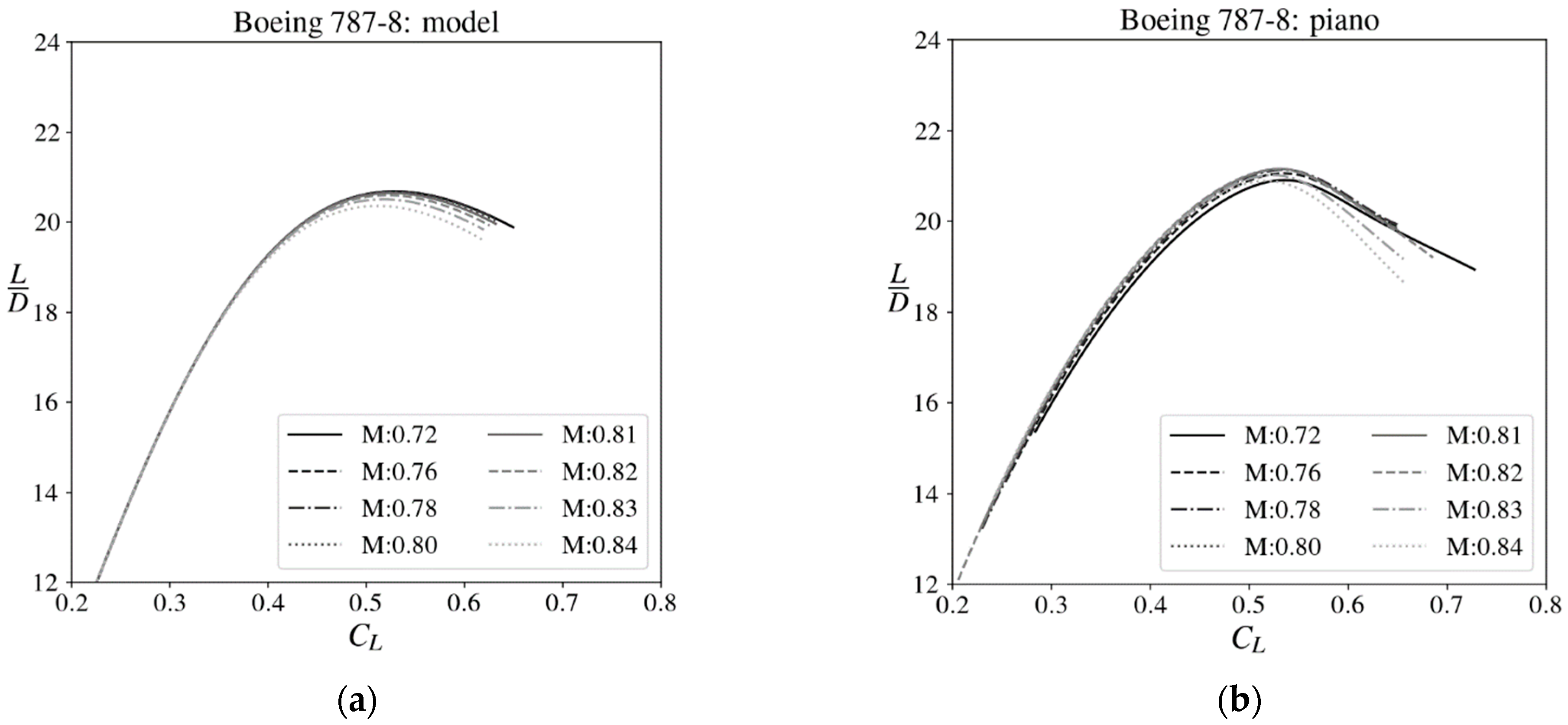
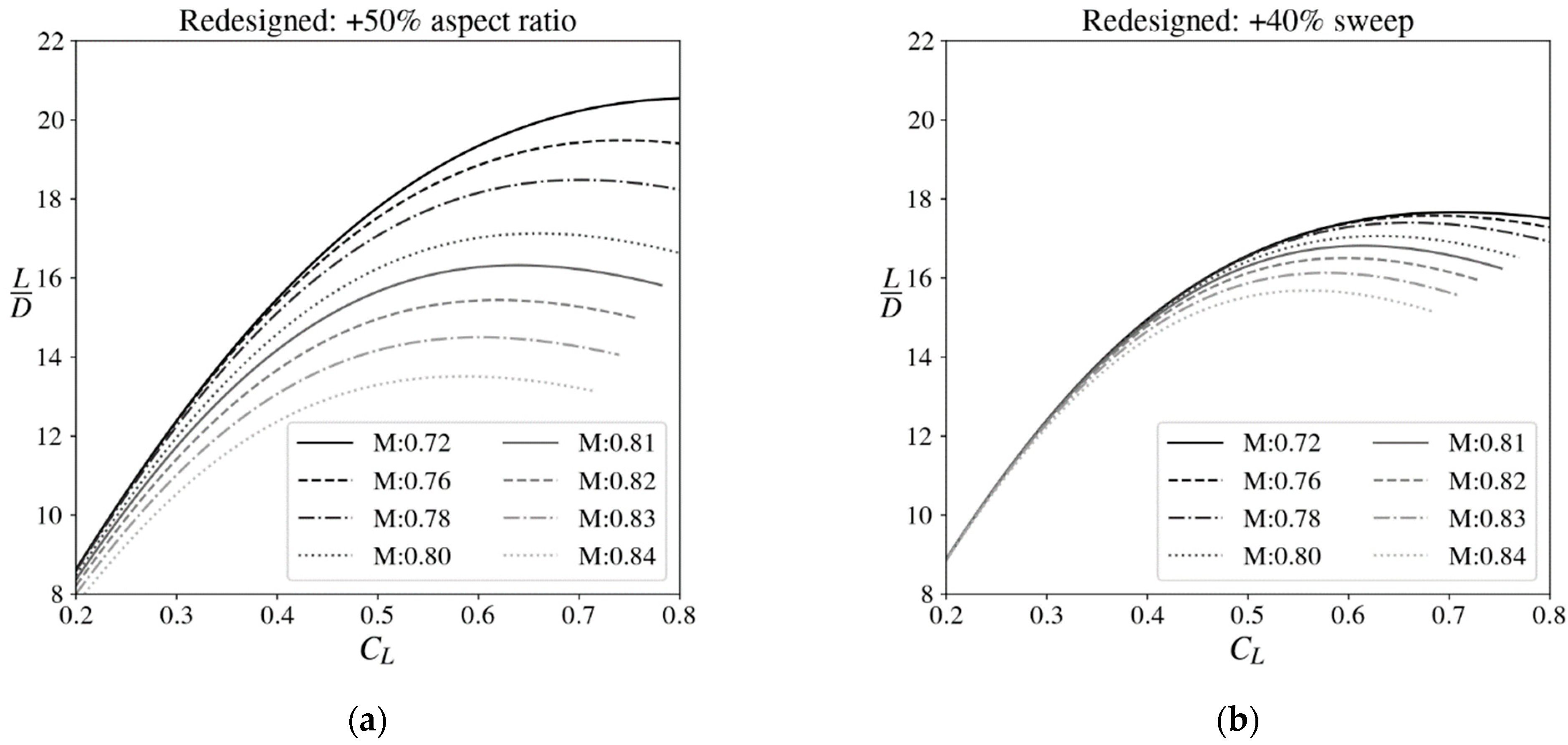
2.2.1. Developing a Theory-Based Drag Polar Model for Redesigned Wings
The Zero-Lift Drag Coefficient
The Induced Drag Coefficient
The Effect of Camber and Wing Twist
The Compressible Drag Component
The Complete Drag Model (Table 2)
| Incompressible Components | Compressible Component | ||
|---|---|---|---|
| Coefficient | k1 | ||
| Equation | (6) | (9) | (10) |
| Dependencies | |||
Drag Polars for Redesigned Wing Geometry
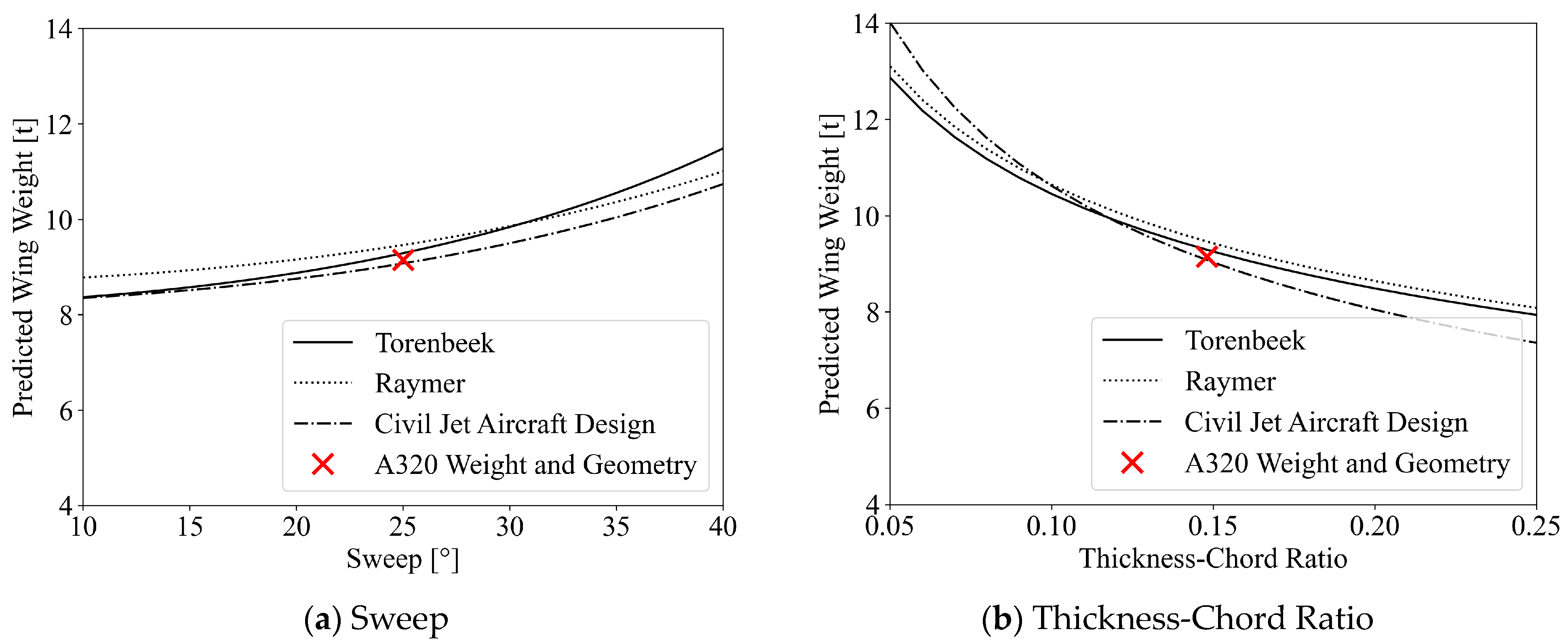
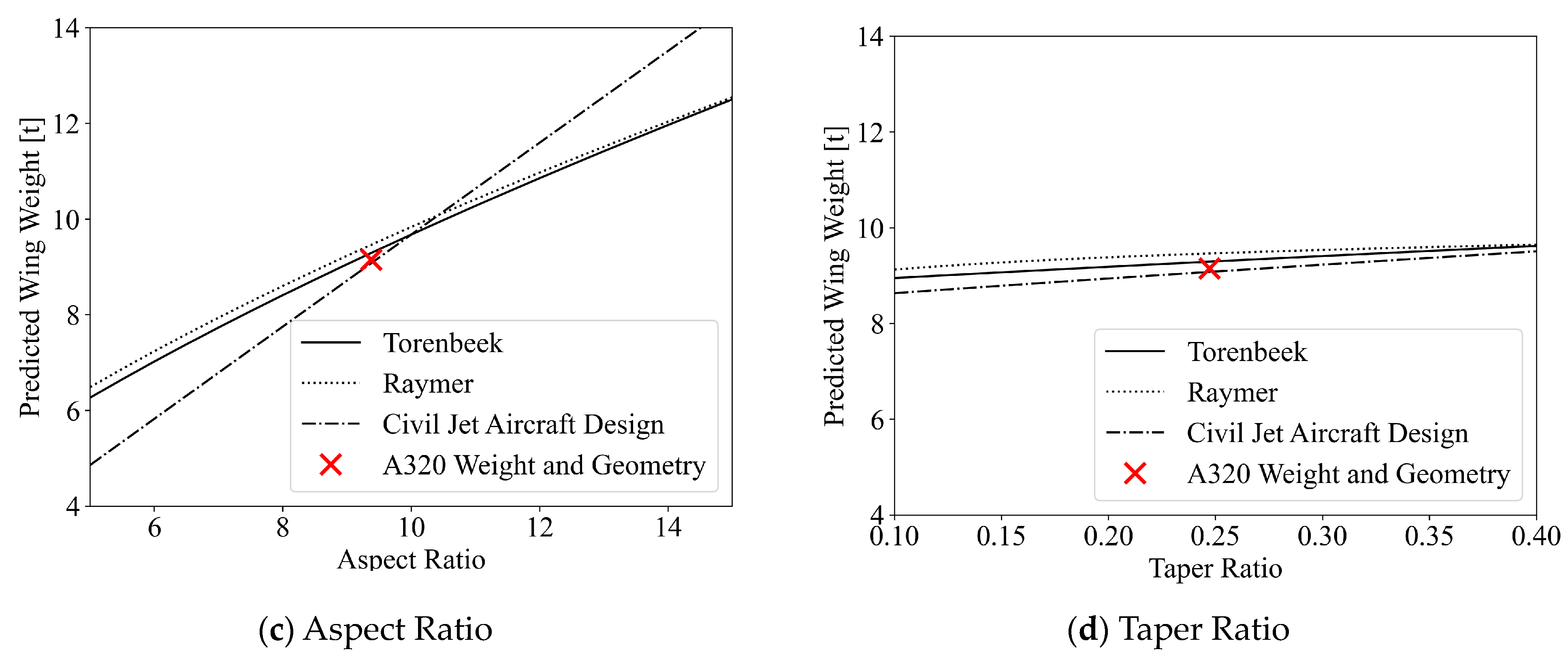
2.2.2. Estimating the Weight of Redesigned Wings
2.2.3. Modelling Hydrogen Aircraft
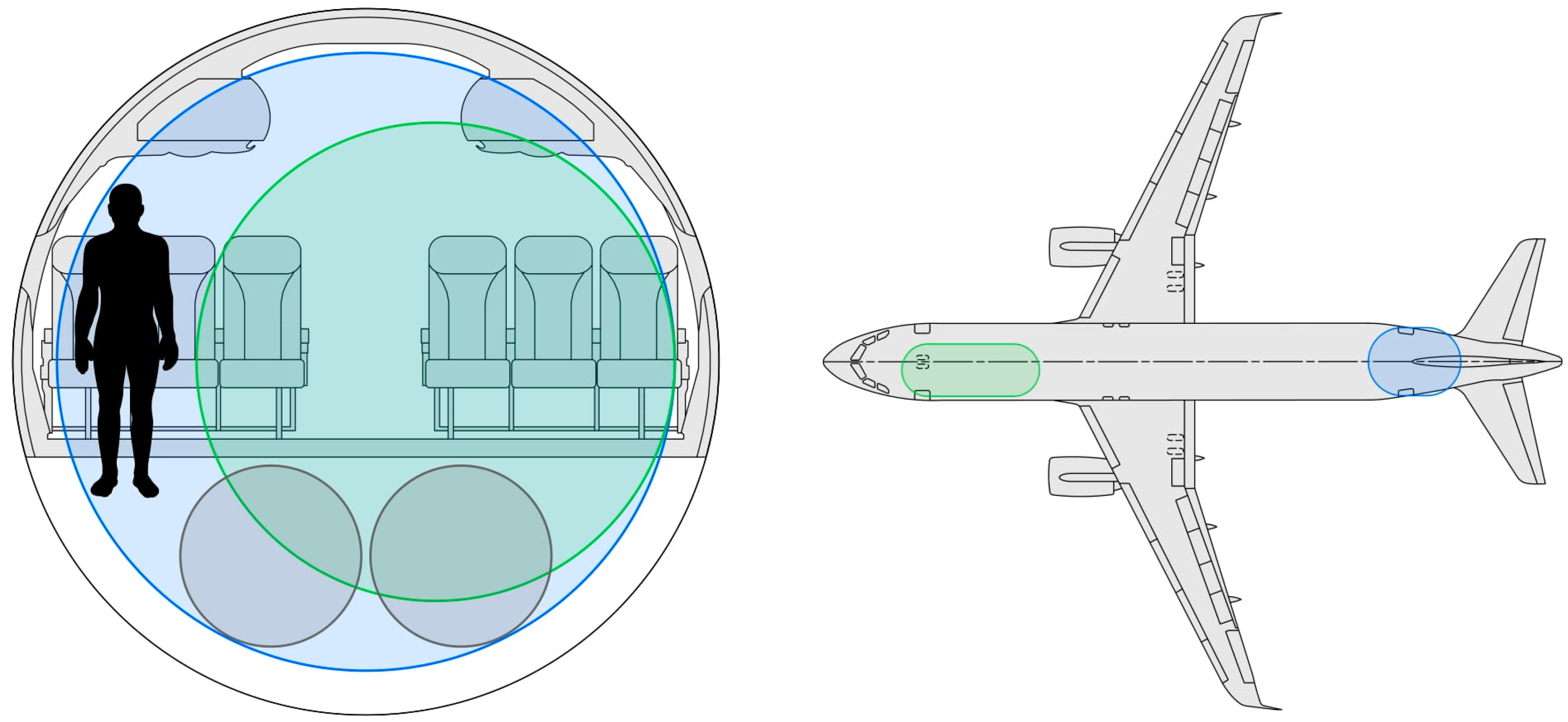
Sizing Liquid Hydrogen Tanks
Effect of Hydrogen on Weight Distribution
Effect of Hydrogen on Operating Point and Contrails
3. Results and Discussion
3.1. Performance of Redesigned Hydrogen Aircraft
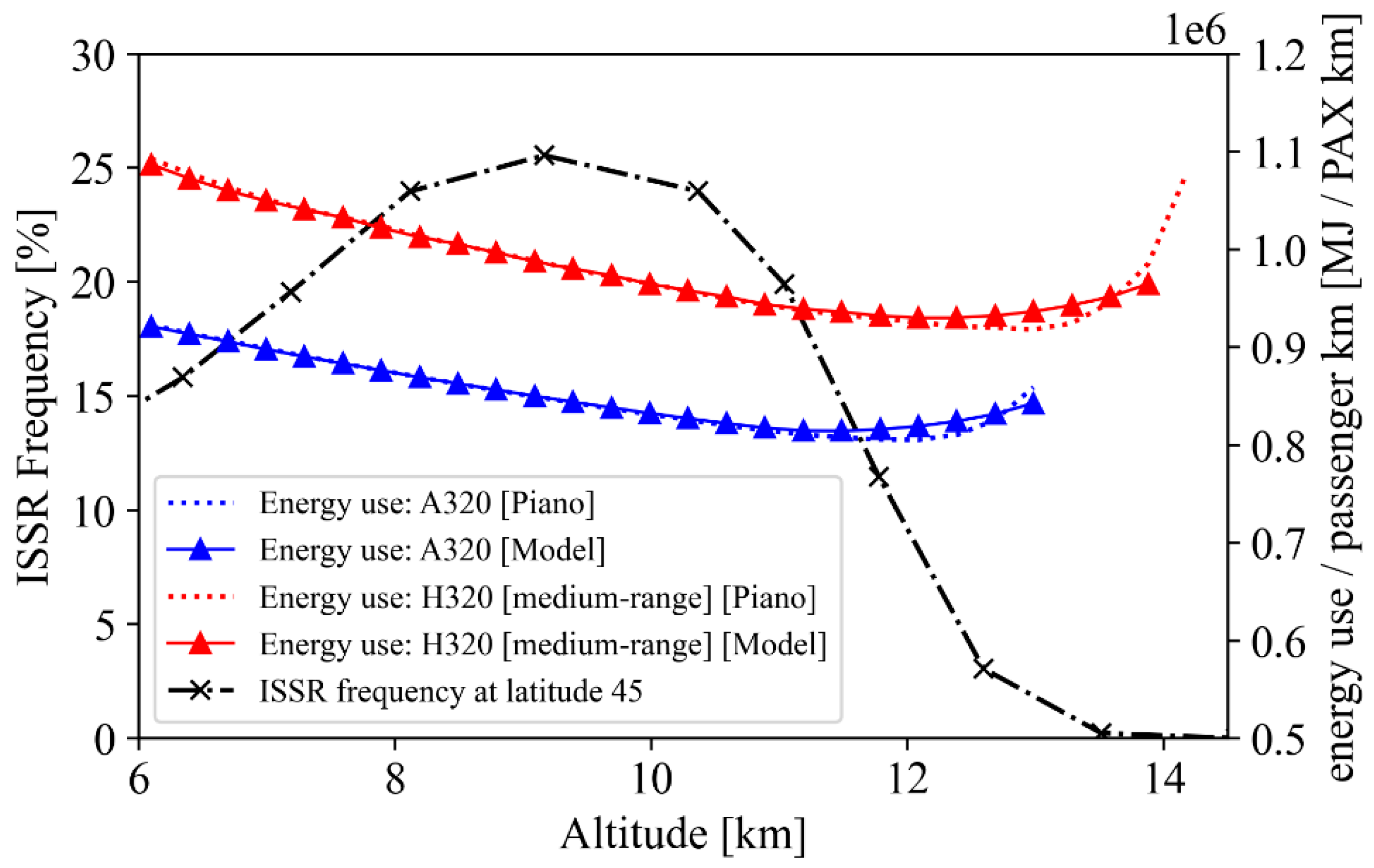
3.1.1. Modeling Aircraft Fuel Burn and Contrails
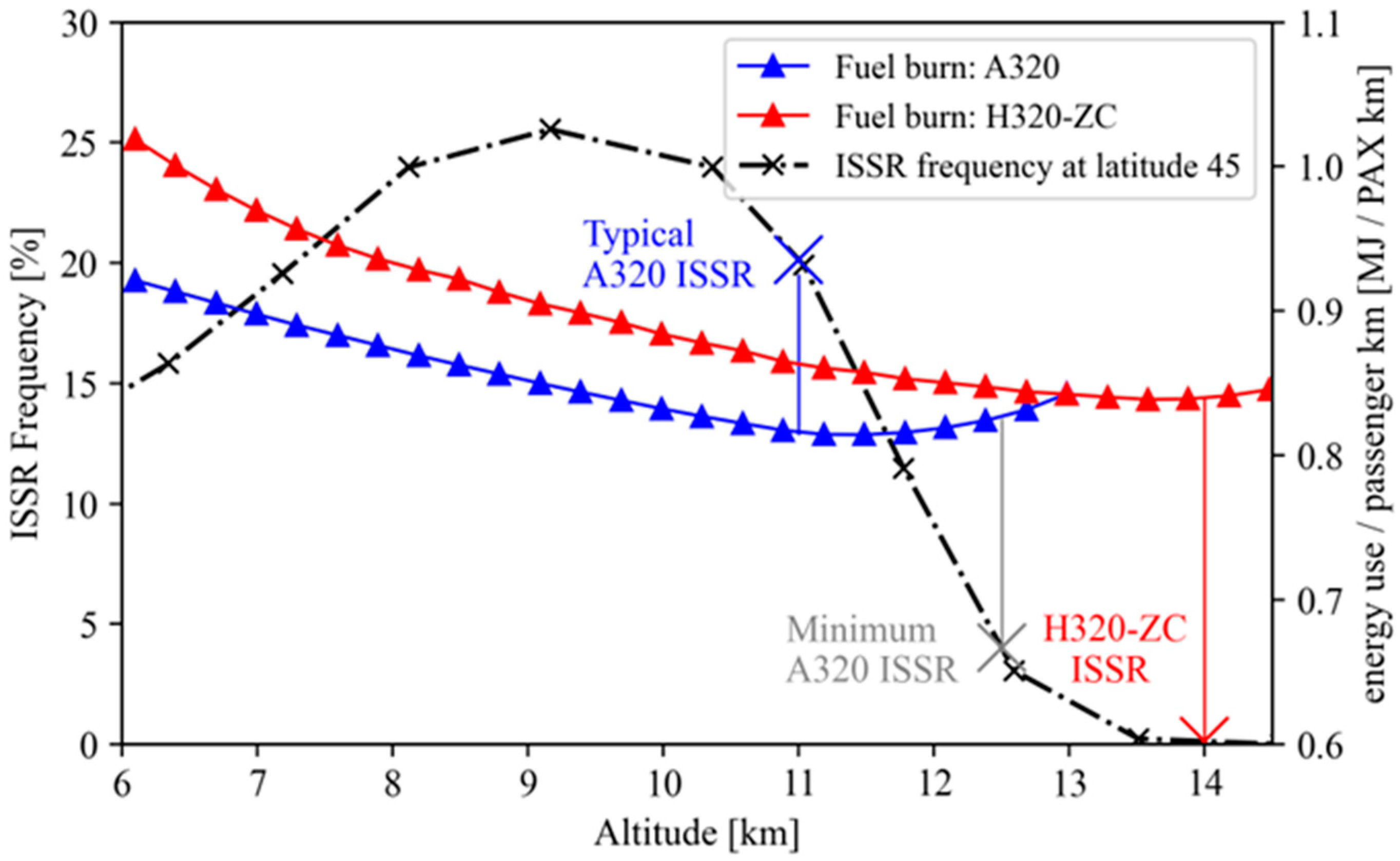
3.1.2. Modeling a Hydrogen Aircraft for Best Performance with Zero Contrails
3.2. Discussion of the Zero Contrails Hydrogen Aircraft Design
3.2.1. Contrails and Energy Use
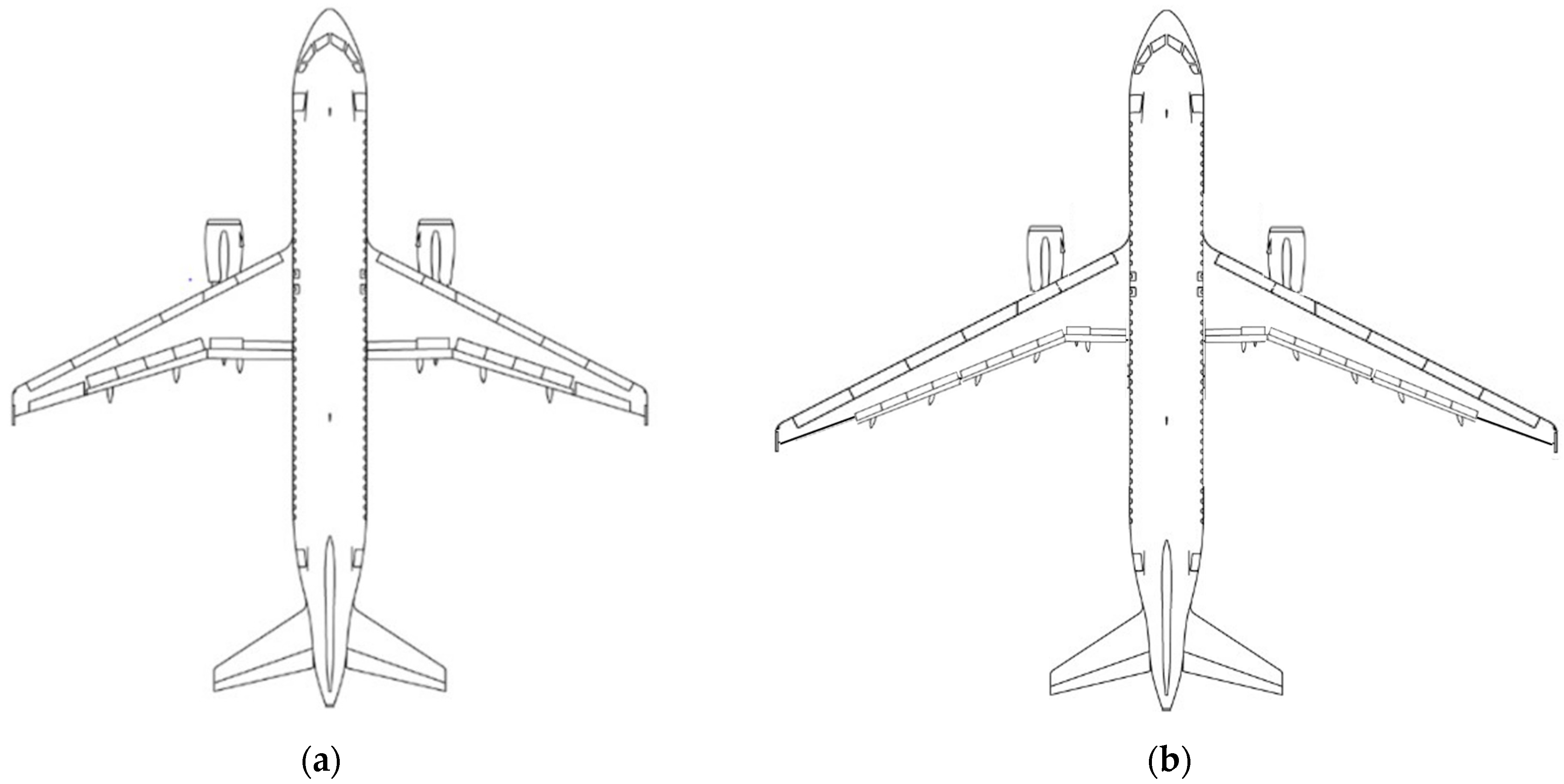
3.2.2. Wing Weight and Strength
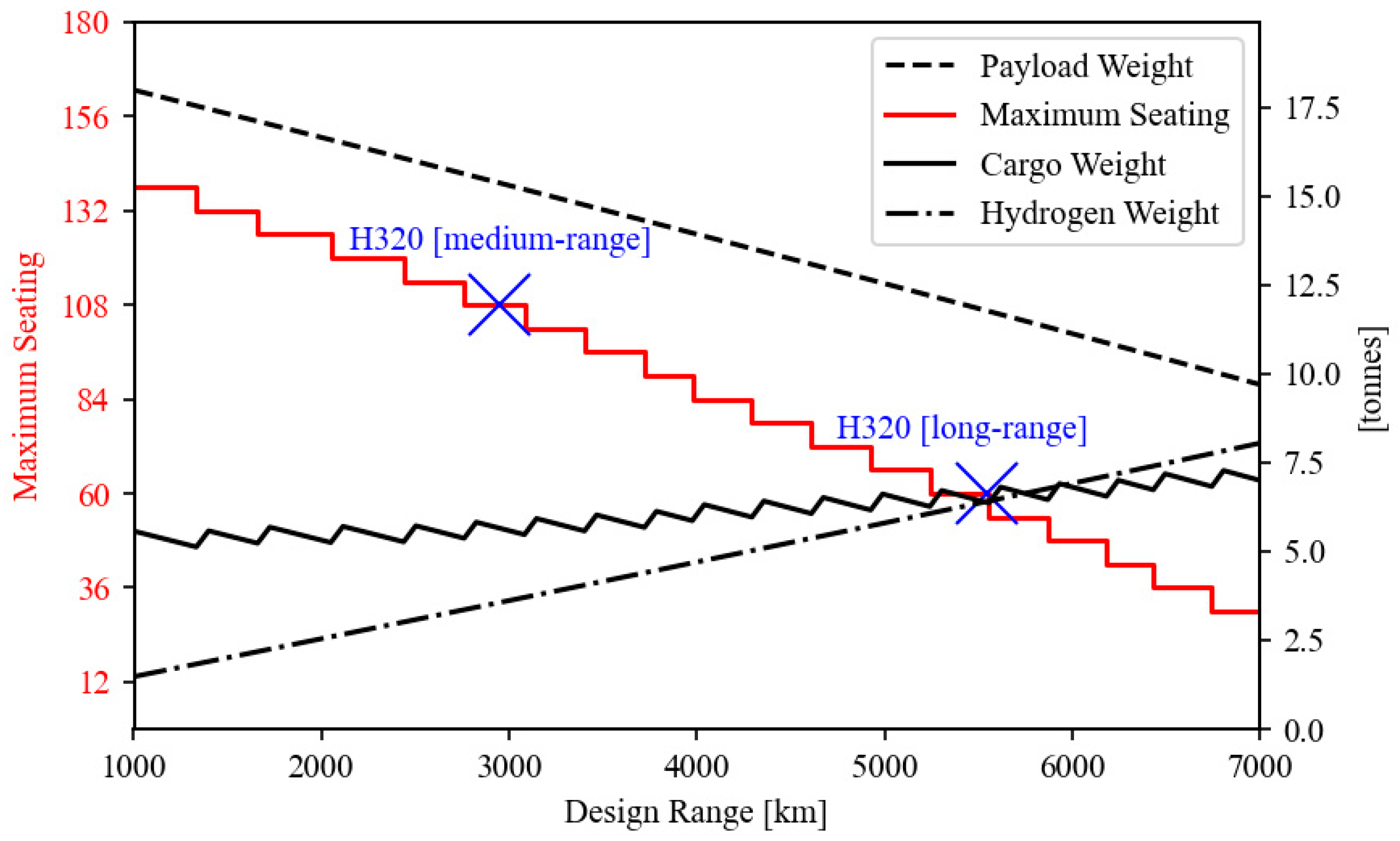
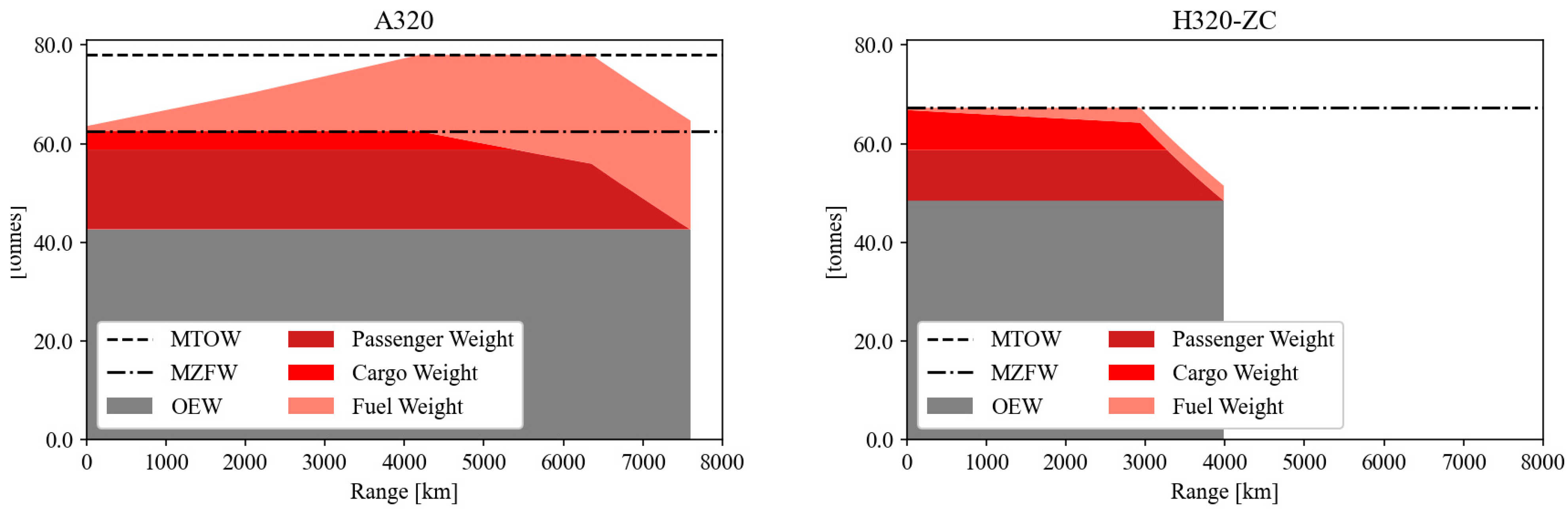
3.2.3. Payload, Range, and Feasibility
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AR | aspect ratio |
| B | wing span, m |
| BPR | engine bypass ratio by mass, kg kg−1 |
| c | wing chord, m |
| CD | drag coefficient |
| zero-lift drag coefficient | |
| skin friction coefficient | |
| d | fuselage diameter, m |
| FPR | fan pressure ratio |
| g | acceleration due to gravity, m s−2 |
| H | fuel burn parameter, m |
| induced drag coefficient | |
| L/D | lift to drag ratio |
| l | fuselage length, m |
| LCV | low calorific value, MJ kg−1 |
| Mach number | |
| critical Mach number | |
| drag-divergence Mach number | |
| M jet | jet Mach number |
| MTOW | maximum take-off weight, tons |
| MZFW | maximum zero-fuel weight, tons |
| P013 | bypass stagnation pressure downstream of fan, Pa |
| R | inertia relief, tons |
| Re | Reynolds number |
| rp | overall pressure ratio |
| RH | relative humidity |
| wing area, m2 | |
| wetted area of component, m2 | |
| SFC | specific fuel capacity, kg s−1 N−1 |
| t | wing thickness, m |
| T013 | bypass stagnation temperature downstream of fan, K |
| T02 | engine inlet stagnation temperature, K |
| T2 | engine inlet static temperature, K |
| Tjet | jet temperature, K |
| TR | taper ratio |
| ULF | ultimate load factor |
| V | aircraft speed, m s−1 |
| Wfuel | weight of fuel burned during a flight mission, tons |
| Wwing | weight of aircraft wings, tons |
| γ | heat capacity ratio |
| ηcycle | cycle efficiency |
| ηpropulsive | propulsive efficiency |
| ηoverall | overall engine efficiency |
| ηc | combustor isentropic efficiency |
| ηt | turbine isentropic efficiency |
| λ | wing sweep angle, ° |
Appendix A. Modeling Turbofan Efficiency
| Engine Parameter | Value | Source |
|---|---|---|
| Overall Pressure Ratio (rp) | 27.3 | [43] |
| Fan Pressure Ratio | 1.7 | Estimate |
| Bypass Pressure Ratio | 5.7 | [44] |
| Combustor Outlet Temperature | 1585 K | [45] |
| Fan Efficiency | 92% | [46] |
| Compressor Isentropic Efficiency | 89% | Estimate |
| Turbine Isentropic Efficiency | 85% | Estimate |
| Transfer Efficiency | 90% | Estimate |
| Inlet Diameter | 1.735 m | [47] |
Appendix A.1. Cycle Efficiency
Appendix A.2. Propulsive Efficiency
Appendix A.3. Overall Efficiency
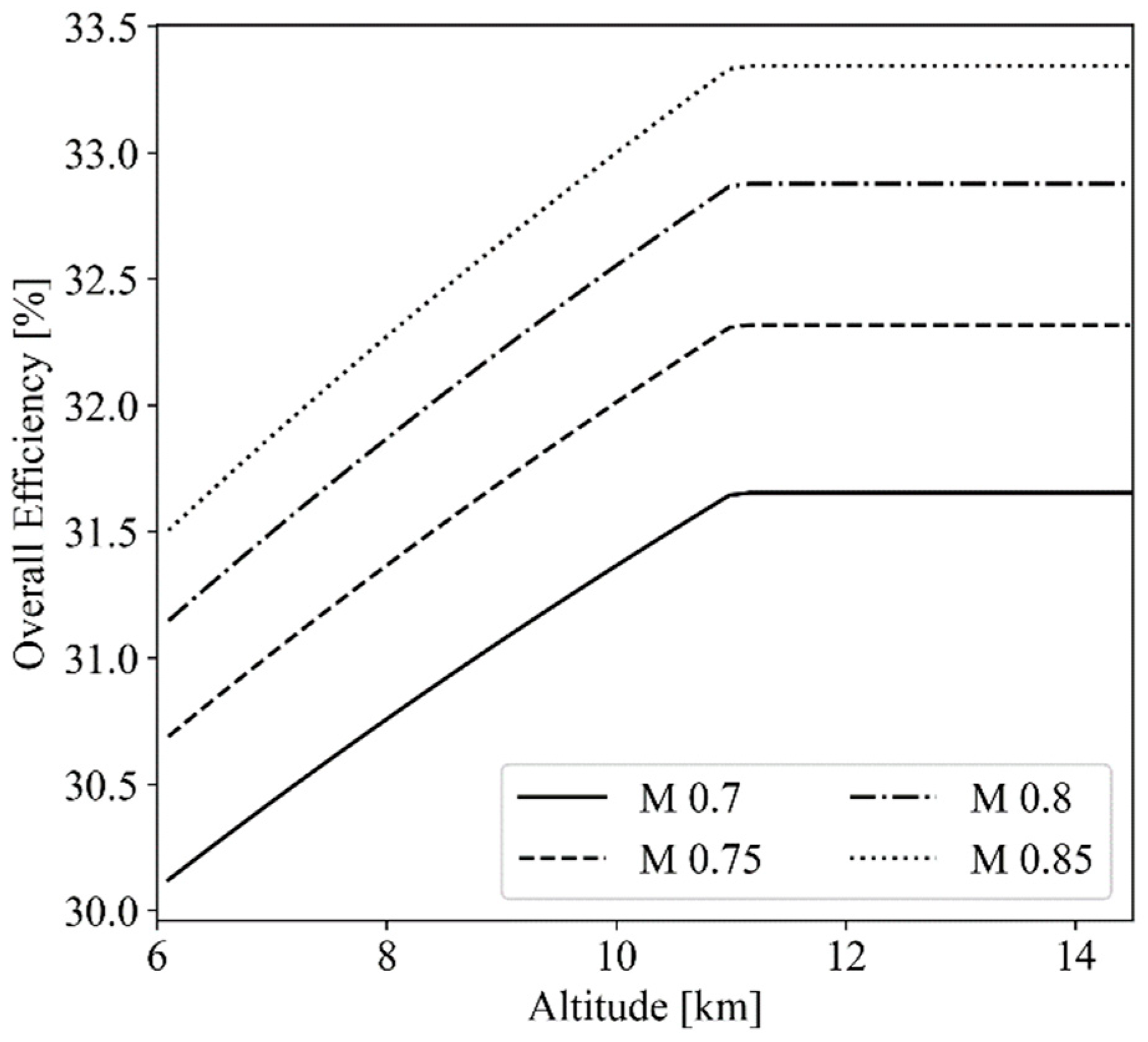
References
- Murcray, W.B. On the Possibility of Weather Modification by Aircraft Contrails. Mon. Weather Rev. 1970, 98, 745–748. [Google Scholar] [CrossRef]
- Lee, D.S.; Fahey, D.W.; Skowron, A.; Allen, M.R.; Burkhardt, U.; Chen, Q.; Dohert, S.J.; Freeman, S.; Forster, P.M.; Fuglestvedt, J.; et al. The Contribution of Global Aviation to Anthropogenic Climate Forcing for 2000 to 2018. Atmos. Environ. 2021, 244, 117834. [Google Scholar] [CrossRef] [PubMed]
- Kärcher, B. Formation and Radiative Forcing of Contrail Cirrus. Nat. Commun. 2018, 9, 1824. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, E. Die Entstehung von Eisnebel aus den Auspuffgasen von Flugmotoren. Schriften Der Dtsch. Akad. Der Luftfahrtforsch. 1941, 5, 1–15. Available online: https://elib.dlr.de/107948/ (accessed on 30 August 2022).
- Appleman, H. The Formation of Exhaust Condensation Trails by Jet Aircraft. Bull. Am. Meteorol. Soc. 1953, 34, 14–20. [Google Scholar] [CrossRef]
- Jensen, E.K. Environmental Conditions Required for Contrail Formation and Persistence. J. Geophys. Res. 1998, 103, 3929–3936. [Google Scholar] [CrossRef]
- Scholz, D. Design of a Hydrogen Passenger Aircraft–How much “Zero-Emission” is Possible? In Proceedings of the Hamburg Aerospace Lecture Series (AeroLectures, DGLR, RAeS, VDI, ZAL, HAW Hamburg), Hamburg, Germany, 19 November 2020. [Google Scholar] [CrossRef]
- Newbury, S. FlyZero Academic Programme Research Recommendations and Findings. Aerospace Technology Institute: FlyZero, 2022. Available online: https://www.ati.org.uk/wp-content/uploads/2022/03/FZO-ACA-REP-0056-Academic-Programme-Research-Findings.pdf (accessed on 29 August 2022).
- Hambling, D. Cloud Control. New Sci. 2021, 249, 41–43. [Google Scholar] [CrossRef]
- Molloy, J.; Teoh, R.; Harty, S.; Koudis, G.; Schumann, U.; Poll, I.; Stettler ME, J. Design Principles for a Contrail-Minimizing Trial in the North Atlantic. Aerospace 2022, 9, 375. [Google Scholar] [CrossRef]
- Contrail-Induced Global Warming: Why the Aviation Industry Needs to Be Thinking Beyond Carbon Emissions. Cranfield University. 2021. Available online: https://www.cranfield.ac.uk/alumni/communications/alumni-news/2021/0428-why-the-aviation-industry-needs-to-be-thinking-beyond-carbon-emissions (accessed on 6 December 2022).
- Job, S.; Brocklehurst, H.; Kumar, N.; Minshull, J. FlyZero Lifecycle Impact: Further Work on Climate Science and Material Impacts. Aerospace Technology Institute: FlyZero, 2022. Available online: https://www.ati.org.uk/wp-content/uploads/2022/03/FZO-STY-POS-0034-Lifecycle-Impact.pdf (accessed on 29 August 2022).
- Yin, F.; Grewe, V.; Gierens, K. Impact of Hybrid-Electric Aircraft on Contrail Coverage. Aerospace 2020, 7, 147. [Google Scholar] [CrossRef]
- Postma-Kurlanc, A.; Leadbetter, H.; Pickard, C. Hydrogen Infrastructure and Operations: Airports, Airlines and Airspace. Aerospace Technology Institute: FlyZero, 2022. Available online: https://www.ati.org.uk/wp-content/uploads/2022/03/FZO-CST-POS-0035-Airports-Airlines-Airspace-Operations-and-Hydrogen-Infrastructure.pdf (accessed on 29 August 2022).
- Noppel, F.; Singh, R. Contrail Avoidance in the Aircraft Design Process. Aeronaut. J. 2008, 112, 733–737. [Google Scholar] [CrossRef]
- Reutter, P.; Neis, P.; Rohs, S.; Sauvage, B. Ice Supersaturated Regions: Properties and Validation of ERA-Interim Reanalysis with IAGOS in Situ Water Vapour Measurements. Atmos. Chem. Phys. 2020, 20, 787–804. [Google Scholar] [CrossRef]
- Minnis, P. Contrails. In Encylopedia of Atmospheric Sciences; Elsevier: Amsterdam, The Netherlands, 2002; pp. 509–520. ISBN 9780122270901. [Google Scholar]
- Piano’s Aircraft Database. Lissy’s Ltd. Available online: https://www.lissys.uk/dbase.html (accessed on 11 October 2020).
- ERA-Interim Database. European Centre for Medium-Range Weather Forecasts. Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (accessed on 5 November 2021).
- Goff, J.A. Saturation Pressure of Water on the New Kelvin Temperature Scale; Transactions of the American Society of Heating and Ventilating Engineers, American Society of Heating and Ventilating Engineers: New York, NY, USA, 1946; pp. 95–122. [Google Scholar]
- Cavcar, A.; Cavcar, M. Approximate Solutions of Range for Constant Altitude–Constant High Subsonic Speed Flight of Transport Aircraft. Aerosp. Sci. Technol. 2004, 8, 557–567. [Google Scholar] [CrossRef]
- Kroo, I. Drag Due to Lift: Concepts for Prediction and Reduction. Annu. Rev. Fluid Mech. 2001, 33, 587–617. [Google Scholar] [CrossRef]
- Nita, M.; Scholz, D. Estimating the Oswald Factor from Basic Aircraft Geometrical Parameters; Deutscher Luft-und Raumfahrtkongress 2012, Document ID: 28142; Hamburg University of Applied Sciences Aero–Aircraft Design and Systems Group, Berliner Tor 9: Hamburg, Germany, 2012. [Google Scholar]
- Lock CN, H. The Ideal Drag Due to a Shock Wave. Parts I and II. Aeronautical Research Council, Technical Report Issue 2512. 1951. Available online: https://reports.aerade.cranfield.ac.uk/bitstream/handle/1826.2/3677/arc-rm-2512.pdf (accessed on 29 August 2021).
- Poole, D.; Allen, C.; Rendall, T. Objective Function and Constraints for Robust Transonic Aerofoil Optimization. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. AIAA Paper 2017-0360, January 2017. [Google Scholar] [CrossRef]
- Grasmeyer, J. Multidisciplinary Design Optimisation of a Transonic Strut-Braced Wing Aircraft. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. AIAA Paper 99-16010, January 1999. [Google Scholar] [CrossRef]
- Mason, W.H. Analytic Models for Technology Integration in Aircraft Design. In Proceedings of the Aircraft Design, Systems and Operations Conference, Dayton, OH, USA, 17–19 September 1990. AIAA Paper 90-3262, September 1990. [Google Scholar] [CrossRef]
- Jenkinson, L.R.; Simpkin, P.; Rhodes, D. Civil Jet Aircraft Design; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar]
- Boeing 787-8 Piano File. Lissys Ltd. Available online: https://www.lissys.uk/samp1/b787.html (accessed on 30 August 2022).
- Boeing 787 Dreamliner Specs. ModernAirliners.com. Available online: https://modernairliners.com/boeing-787-dreamliner/boeing-787-dreamliner-specs/ (accessed on 30 August 2022).
- Raymer, D.P. Aircraft Design: A Conceptual Approach; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992. [Google Scholar]
- Torenbeek, E. Synthesis of Subsonic Airplane Design; Delft University Press: Delft, The Netherland, 1982. [Google Scholar]
- Gudmundsson, S. Anatomy of the Airfoil. In General Aviation Aircraft Design; Butterworth-Heinemann: Oxford, UK, 2014; pp. 235–297. [Google Scholar] [CrossRef]
- Flügel, Transporter, Masserelevante Daten; LTH Masseanalyse–Deutsche Aerospace Airbus: Hamburg, Germany, 1993; Technical Report 501 52-01, 1993.
- ASME Boiler and Pressure Vessel Code; American Society of Mechanical Engineers: New York, NY, USA, 2019; ISBN 9780791873564.
- Klell, M. Storage of Hydrogen in the Pure Form. In Handbook of Hydrogen Storage: New Materials for Future Energy Storage; Wiley-VCH Verlag GmbH Co.: Weinheim, Germany, 2010; Chapter 1. [Google Scholar]
- New Aviation, Propulsion, Knowledge and Innovation Network–Full Report. Heathrow Airport. 2022. Available online: https://www.heathrow.com/content/dam/heathrow/web/common/documents/company/about/future-flight-challenge/NAPKIN%20Long%20Report%20221028.pdf (accessed on 17 January 2023).
- Aircraft Characteristics, Airport and Maintenance Planning. Airbus Customer Services. Available online: https://www.airbus.com/sites/g/files/jlcbta136/files/2021-11/Airbus-Commercial-Aircraft-AC-A320.pdf (accessed on 20 August 2022).
- Human Silhouette. Wikimedia Commons. Available online: https://commons.wikimedia.org/wiki/File:SVG_Human_Silhouette.svg (accessed on 30 August 2022).
- Husemann, M.; Schaefer, K.; Stumpf, E. Flexibility within Flight Operations as an Evaluation Criterion for Preliminary Aircraft Design. J. Air Transp. Manag. 2018, 71, 201–214. [Google Scholar] [CrossRef]
- Seeckt, K.; Scholz, D. Jet versus Prop, Hydrogen versus Kerosene for a Regional Freighter Aircraft; Deutscher Luft-und Raumfahrtkongress, Deutsche Gelleschaft für Luft: Aachen, Germany, 2009; Document ID: 121195. [Google Scholar]
- European Union Aviation Safety Agency. Aircraft Engine Emissions Databank. 2021. Available online: https://www.easa.europa.eu/domains/environment/icao-aircraft-engine-emissions-databank (accessed on 30 August 2022).
- Roux, E. (Ed.) Réacteurs Simple et Double Flux: Données Caractéristiques; 2007; ISBN 9782952938006. Available online: http://elodieroux.com/EditionsElodieRouxEngines.html (accessed on 30 June 2023).
- Yin, F.; Rao, A.G. Performance Analysis of an Aero Engine with Inter-Stage Turbine Burner. Aeronaut. J. 2017, 121, 1605–1626. [Google Scholar] [CrossRef]
- CFM56-7: An In-Depth Look at the New Industry Leader. CFM International. 1996. Available online: https://www.cfmaeroengines.com/press-articles/cfm56-7-an-in-depth-look-at-the-new-industry-leader/ (accessed on 30 June 2023).
- CFM56 Brochure. CFM International. 2017. Available online: https://www.cfmaeroengines.com/wp-content/uploads/2017/09/Brochure_CFM56_fiches_2017.pdf (accessed on 30 June 2023).
- Airbus A320 R2 Door. Wikimedia Commons. Available online: https://commons.wikimedia.org/wiki/File:Airbus_A320_R2_Door.png (accessed on 31 August 2022).


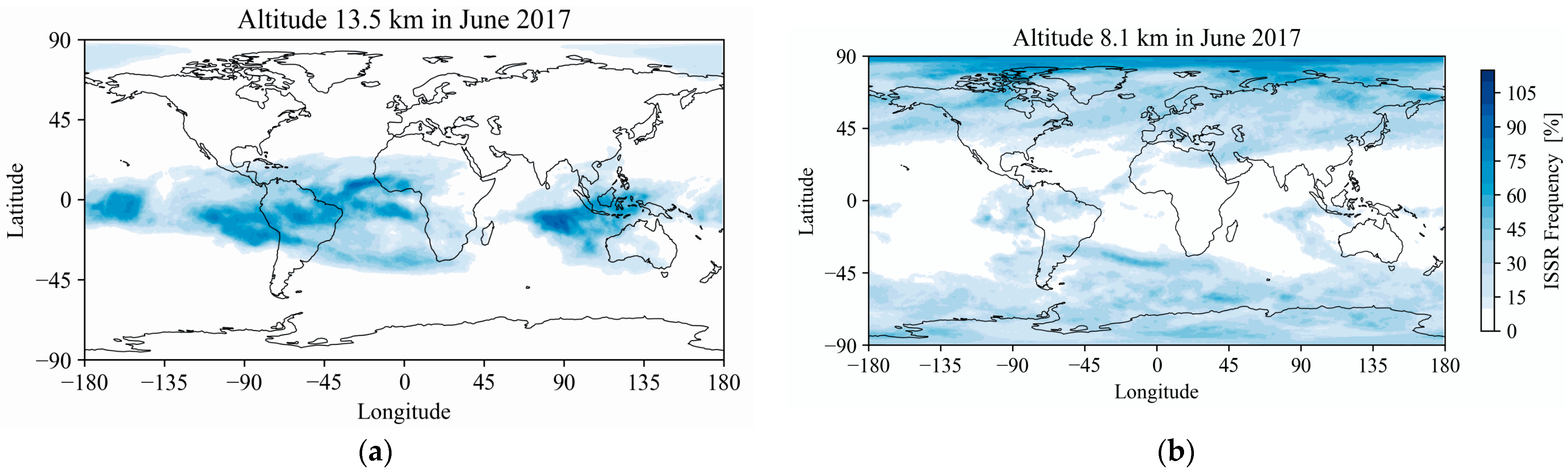
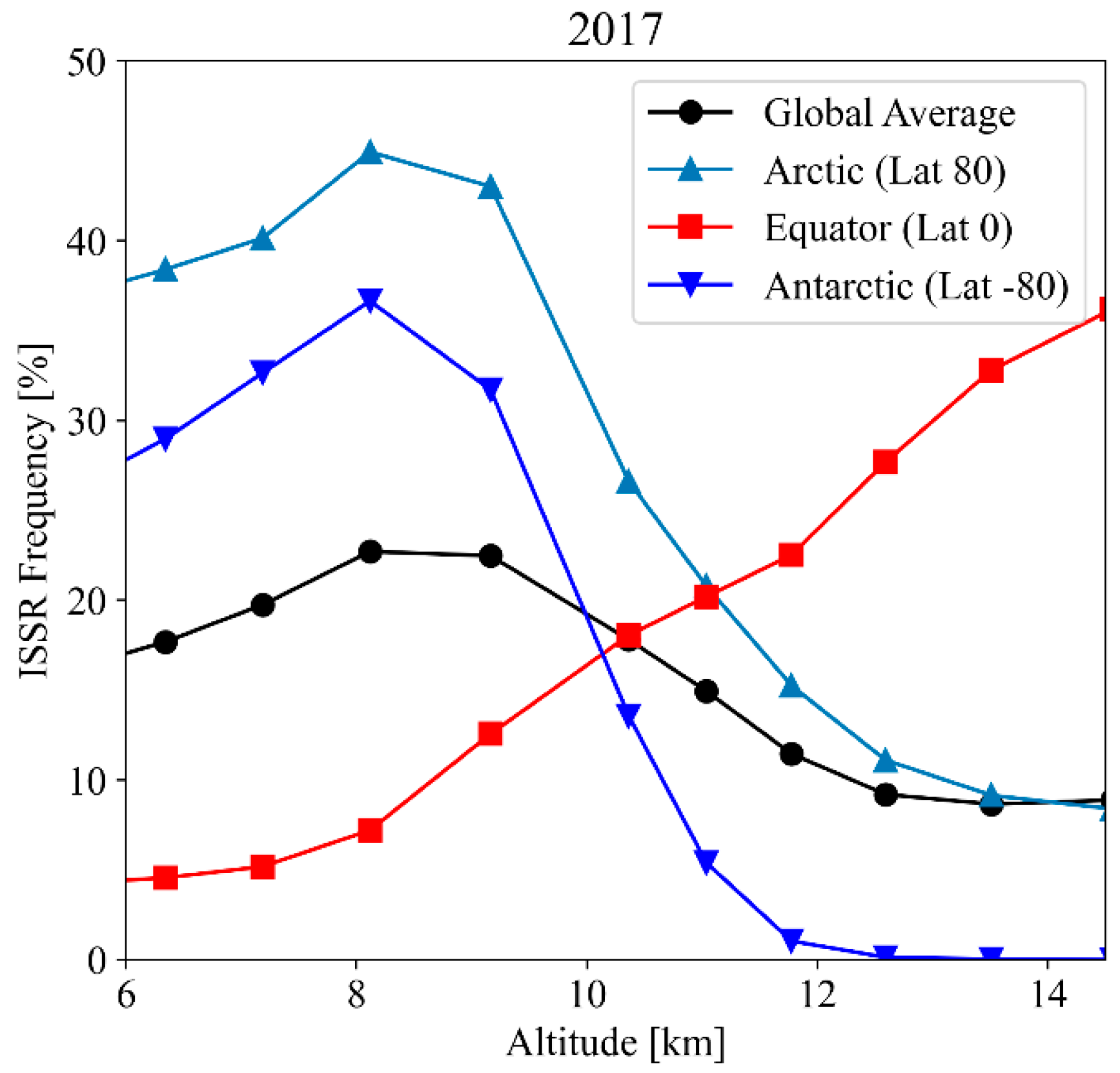





| Operating Region | Latitude Range | Cruise Altitude | ISSR Frequency at This Altitude | ISSR Frequency at Current Altitudes |
|---|---|---|---|---|
| Equatorial, Low-altitude | Between −25° and 25° | 6 km | 3–5% | 10–20% |
| Non-Equatorial, High-altitude | Greater than 35° or less than −35° | 14 km | 0–2% | 10–25% |
| Aircraft | Thickness-Chord Ratio | Fuselage Diameter | Fuselage Length | Wing Span | Wing Area | Aspect Ratio | Wing Sweep |
|---|---|---|---|---|---|---|---|
| A320 | 0.148 | 4.05 | 37.57 | 34.1 | 124.8 | 9.4 | 25 |
| B787-8 | 0.111 | 5.88 | 56.72 | 60.12 | 360.5 | 8.9 | 32 |
| Model | Torenbeek | Raymer | Civil Jet Aircraft Design |
| Estimate | 9.29 tons | 9.46 tons | 9.08 tons |
| Error | 1.5% | 3% | 0.7% |
| Aircraft | Thickness-Chord Ratio | Aspect Ratio | Wing Sweep | Wing Area | Cruise Altitude at Maximum Range | Energy Use at Maximum Range [MJ/PAX-km] | ISSR Frequency at Maximum Range |
|---|---|---|---|---|---|---|---|
| A320 | 0.148 | 9.4 | 25° | 124 m2 | 11.5 km | Approximately 0.80 | Approximately 15% |
| H320 | 0.148 | 9.4 | 25° | 124 m2 | 12.5 km | Approximately 0.93 | Approximately 4% |
| H320-ZC | 0.1 | 15 | 25° | 124 m2 | 14 km | Approximately 0.83 | Negligible |
| Aircraft | A320—at maximum altitude at 45% fuel | H320 | H320-ZC |
| Average ISSR Frequency | −80% | −96% | Negligible |
| Energy Use per Passenger-km | +6% | +15% | +5% |
| Cruise Altitude | 12.5 km | 13.5 km | 14 km |
| Objective | Results |
|---|---|
| Assess the dependence of contrail persistence regions on altitude, latitude, and longitude |
|
| Determine how retrofitting a conventional aircraft with in-fuselage hydrogen tanks affects contrails and performance at low-contrails altitudes |
|
| Redesign the wings of a hydrogen aircraft for minimal fuel burn at a zero-contrails operating altitude and Mach number. |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barton, D.I.; Hall, C.A.; Oldfield, M.K. Design of a Hydrogen Aircraft for Zero Persistent Contrails. Aerospace 2023, 10, 688. https://doi.org/10.3390/aerospace10080688
Barton DI, Hall CA, Oldfield MK. Design of a Hydrogen Aircraft for Zero Persistent Contrails. Aerospace. 2023; 10(8):688. https://doi.org/10.3390/aerospace10080688
Chicago/Turabian StyleBarton, David I., Cesare A. Hall, and Matthew K. Oldfield. 2023. "Design of a Hydrogen Aircraft for Zero Persistent Contrails" Aerospace 10, no. 8: 688. https://doi.org/10.3390/aerospace10080688
APA StyleBarton, D. I., Hall, C. A., & Oldfield, M. K. (2023). Design of a Hydrogen Aircraft for Zero Persistent Contrails. Aerospace, 10(8), 688. https://doi.org/10.3390/aerospace10080688






