Abstract
Quantum radar is a novel detection method that combines radar and quantum technologies. It exceeds the detection threshold and poses a threat to conventional stealth targets. This work aims to derive the expression of the quantum radar cross-section of a new complex target. The calculation formula of QRCS was derived after introducing the relative photon parameters and vector dot product. Subsequently, a comprehensive optimization model of quantum stealth and lift–drag ratio based on a genetic algorithm was proposed for the waverider warhead. During the optimization process, we proposed an optimization method with the objective function of the QRCS pioneering design value and achieved better outcomes than the optimization method using the average value in terms of QRCS performance and lift–drag ratio in the important azimuths of the waverider. By changing the design variables of the waverider warhead and using this new optimization method, the QRCS of the waverider in the forward and lateral angles were minimized, remarkably improving the aerodynamic performance of the waverider. Similarly, the optimization results show that the proposed design value optimization method is feasible.
1. Introduction
Quantum radar is a new detection technique that integrates radar and quantum technologies. It maximizes the quantum features of electromagnetic waves to break through the detection threshold and has broad application prospects [1].
The radar cross section (RCS) is a physical quantity that characterizes the intensity of the electromagnetic wave scattering caused by the target when subjected to radar wave irradiation, and it is also a significant indicator in stealth design [2,3]. Because quantum radar differs from traditional radar in terms of a working system, radar, and target action mechanism [4], the concept of traditional RCS is no longer relevant. Therefore, there is a need to identify a novel physical quantity to measure the scattering of incident photons by target atoms. For the first time, a team of Professor Marco Lanzagorta [5,6,7] suggested the concept of quantum radar cross section (QRCS) by combing the theory of quantum electrodynamics. Similar to RCS, QRCS is a physical quantity utilized to measure the electromagnetic scattering intensity of a target under quantum radar wave irradiation. Brandsema et al. [6,7,8] optimized the QRCS expression and provided a general expression form of QRCS, which can be used to numerically calculate the target QRCS. At the same time, they derived two-dimensional flat targets (rectangular flat, circular flat, and triangular flat) analytical QRCS expression to confirm the numerical calculation results; they also simulated the planar target QRCS of the photon in different modes. Lin [9] et al. proposed a QRCS calculation method for plate-shaped targets and conducted a numerical verification. This numerical method has high computational efficiency and can be applied in QRCS computation of the ideal conductor plate with an arbitrary shape. Liu et al. [10,11] analyzed the QRCS of the corner reflectors under single-photon incidence by determining quantum radar equations. Fang et al. [12,13] discovered the difference between the QRCS and RCS of the cube in the primary lobe and analyzed the reasons. They speculated that this new macroscopic quantum phenomenon can be applied in the detection and identification of stealth weapons and the field of biomedicine. Chen et al. [14] investigated the single-photon and two-photon QRCS of a single surface based on the cylindrical model. Significant in-depth studies on 2D targets have been undertaken, building a mature theoretical and numerical foundation for the above research, but QRCS for 3D targets mostly focuses on the numerical calculation of simple targets.
Elsewhere, Liu et al. [15] proposed the design theory of waverider aircraft with a variable Mach number and tight flow field based on a conical basic flow field and analyzed the shape and aerodynamic characteristics of the waverider with variable Mach number and tight cone. Consequently, they discovered that the waverider with a tight flow field has good waverider performance under wide flying Mach number conditions. Yu et al. [16] proposed an inverse waverider design approach under strong geometric constraints based on the concept of generating shock waves with arbitrary shapes. The results showed that the proposed waverider design method exhibits high flexibility and can adhere to the actual design of a hypersonic vehicle in terms of geometric constraints and aerodynamic performance. Zhao et al. [17] discussed the design methods of two types of fixed sweep waverider and found that the high-speed aerodynamic performance of the pointed wing waverider is better than that of the general tight conical waverider. Chen et al. [18] proposed a new design method for the snout waverider and discovered that under non-viscosity-free conditions, the waverider with a small volume ratio has a larger lift–drag ratio.
Despite the notable progress in the quantum radar scattering properties of targets, optimization in the field of quantum stealth of complex targets remains limited in the existing research, and the quantum stealth design of warheads is also a new research direction. In order to counter the threat posed by quantum radar to waverider, we will conduct a new optimization research.
First, we derive a formula for quantum radar scattering cross section for complicated targets. The model of the waverider warhead is then obtained using the parametric design process. At the same time, a genetic algorithm-based optimization model of QRCS and the lift–drag ratio of complex target based is constructed, and a creative optimization approach based on the QRCS design value is given. The method described above is utilized to optimize the waverider body, confirming the feasibility of the proposed complete optimization method. The results demonstrate that by altering design variables including the position and inclination of the control points, the overall performance of quantum stealth and lift–drag ratio can be significantly improved. Furthermore, a new waverider with the best main direction QRCS and lift–drag ratio can be obtained by optimizing the QRCS design value objective function. Therefore, our findings provide an effective comprehensive optimization tool. The research opens up a new method for the comprehensive optimization of quantum stealth of the waverider, and makes a contribution to the direction of countering quantum radar.
2. The Concept and Simplified Expression of the Quantum Radar Cross-Section
Defining the Cartesian coordinate system , and for any point on the target surface, is the angle between the incident wave and the axis Z, is the angle between the projection of the incident wave at plane and the axis X. Similarly, is the angle between the scattered wave and the axis Z, and is the angle between projection of the scattered wave at plane and the axis X.
For any target, the analytical expression of its quantum radar cross section (QRCS) is presented by [8]:
where denotes the orthogonally projected area of the target in each incidence, and is the total interference distance. , is the distance from a transmitter to an atom on the surface of an object, and is the distance from the atom to the receiver. Then we have:
Presumably, the incident photon wave vector is pointing from a distance to the origin of the coordinates, and the reflected photon wave vector is pointing away from the origin of the coordinates. denotes the incident wave vector of the photon, and represents the scattered wave vector of the photon.
Substituting , , it yields:
where denotes the position vector of the nth atom. Since and are not dependent on the position of the atoms, they can be taken out in front of the summation. Setting photon parameters , (1) is written as:
The summation in (4) is transformed into an integral form, and its Fourier form is given. If the incident wave of the photon irradiates a certain point on the target surface without considering diffraction, the scattered wave of the photon on the above point only exists in the normal space of the tangent plane. The occlusion factor function represent the integral region:
When dealing with targets, it is cumbersome to use numerical integration, and the finite element method is adopted for calculation. The following is the conversion process from a direct integral solution to a finite element solution.
The surface should be divided into triangular facets. represents the normal vector of a plane element. , denote the vectors on both sides of the triangle, thus leaving the area of the surface element
represents the center of the element. Putting (4) and (6) and together, we obtain:
where M denotes the number of surface elements of the target surface. Equation (7) does not consider occlusion. If the occlusion is considered, should be added to (7). Subsequently, (7) is expressed as:
where:
Equation (9) refers to the final simplified expression of the 3D target’s QRCS.
As mentioned above, this paper derives a formula that can be used to compute the quantum radar scattering cross-section of complex targets. The main idea is to transform the model into a plane element form, calculate the contribution of each triangular plane element to the entire target scattering in the formula, and use the shielding factor to screen out the contribution plane element before calculating the outcome. After importing the grid file of the model, create a MATLAB program based on this to achieve the objective of target quantum radar simulation.
3. The Concept of Conical Flow Equation
The design process of the waverider in this paper is as follows: the Taylor-Maccoll equation is used to get the conical flow field, and then the leading edge line is defined on the shock surface. Finally, the lower surface is obtained by using the lower surface curve and a certain ratio.
According to the continuity equation, no rotation condition and Euler equation of conical flow, Taylor-Maccoll equation under axisymmetric condition can be obtained:
where is the critical velocity, is the radial velocity component of the conic ray, is the angle between the ray from the apex of the conic and the axis of the conic, and is the specific heat ratio.
4. Research Methods
In this section, we will perform parametric modeling and optimization design of a waverider aircraft. First, we describe the geometry of the cone-guided waverider, as well as the value range of its design variables and the initial value content. Subsequently, two types of optimization objective functions are described, one of which uses a special calculation method for the mean value of QRCS. In addition, Isight was utilized to design a multi-objective optimization method for the waverider, and a new shape was obtained by adjusting the design variables. In addition, we will compare the optimization effects of QRCS and lift–drag ratio of the waverider aircraft, respectively, under the condition of two objective functions.
4.1. Parametric Design and Design Variables
CATIA modeling software was first applied to design and draw a cone-guided waverider. Figure 1 shows the modeling of the waverider drawn.
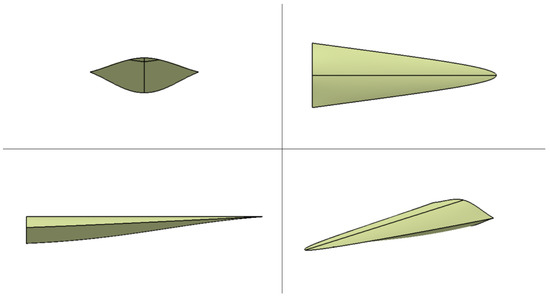
Figure 1.
Schematic diagram of the waverider warhead.
As shown in Figure 2, the original length, width, and height of this type of waverider are 1488 mm, 523 mm, and 168 mm, respectively.
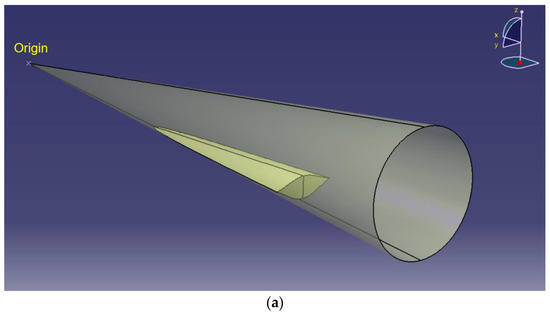
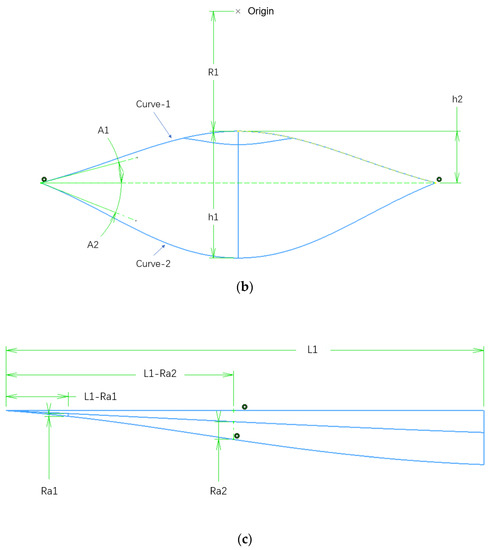
Figure 2.
Waverider warhead design and design variables. (a,b,c) Cross section of Figure 3.
Figure 2 shows the parametric design method of the waverider warhead. Because of its high flight Mach number, a straight line with a slope of 0.126 was used and the X-axis was taken as the rotation axis to establish a conical surface to meet the aerodynamic performance at this flight speed.
In Figure 2b, we took the intercept R1 from the origin along the negative direction of the z-axis and took the vertex of Curve-1 at this position. Both endpoints of Curve-1 and Curve-2 intersect the conic surface, and the vertical distance between the endpoint and the vertex of Curve-1 is h2. We stretched Curve-1 to a conic surface along the X-axis to form the leading edge line and the upper surface of the waverider warhead. Additionally, the tangent angle between Curve-1 and Curve-2 and the horizontal line were set as A1 and A2, respectively.
In Figure 2c, the lower surface was obtained by setting a certain ratio to Curve-2. First, points on the ratio L1-Ra1 (12%) and L1-Ra2 (48%) of the length of the waverider were selected, respectively. The YZ plane passing through these two points was selected as the reference plane. The two planes and the leading edge line intersected at points A and B, as shown in Figure 3. The distance between the two intersections and the ZX plane was divided by the distance between C and the ZX plane to obtain two corresponding ratios. Curve-2 was copied to two points A and B, and then the width and height of Curve-2 were scaled based on these two ratios to obtain the first type of Curve, hence its other endpoint always remained on the ZX plane. Finally, the height of the first curve was scaled by the ratios Ra1 and Ra2 respectively to obtain the second curve, which is the guideline used to generate the surface. Therefore, the shape of the lower surface of the waverider can be controlled here by the ratio Ra1 and Ra2.
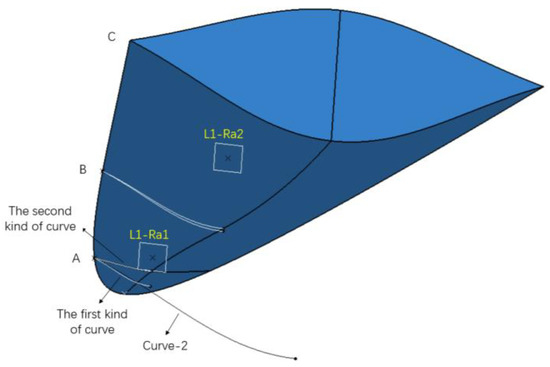
Figure 3.
Lower surface curve multiplied by ratio setting.
Table 1 presents the design variables, constraints, and initial values of the waverider warhead used in this paper.

Table 1.
Design variables, initial values, and constraints of the waverider.
A total of 8 design variables are set in Table 1, and the minimum and maximum values of each design variable are the constraint conditions of the waverider warhead. Through the setting of these parameters and the changes made to them, the shape, QRCS, and lift–drag ratio of the waverider vehicle were affected, providing a good start for the subsequent joint optimization effect.
4.2. The Setting of Optimization Method and Objective Function
The analysis of QRCS and lift–drag ratio features of the waverider vehicle was realized through optimization. Using the optimization method described below, the shape of the new waverider can be optimized to minimize the QRCS of the waverider and increase the lift–drag ratio. For this optimization problem, a mathematical model should first be established.
We set the QRCS calculation conditions for the waverider warhead as follows: the pitch angle of 0°, the azimuth angle ranging from 0–90°, and the photon frequency of 1.27 GHz. For the azimuth angle irradiated by quantum radar, the azimuth angle in the head and side of the target in a small range is a relatively important detection angle. For the aerodynamic simulation of the waverider, the calculation conditions were set as follows: Mach number 8.1, pressure 2.85 kPa, and angle of attack 4°, as a result, we realized a reliable aerodynamic simulation capability of the waverider.
Therefore, we set an objective function that considers head-to-side QRCS (QRCS design value) as the main factor in quantum radar stealth and superposition it with the lift–drag ratio, as well as a function that considers the mean value of QRCS of azimuth angle 0–90° and superposition it with the lift–drag ratio, to optimize this waverider aircraft. Then, we compared the quantum stealth and lift–drag ratio of the two optimization conditions. In addition, the minimum value of the objective function was defined as the optimal solution of the optimization process.
The objective function of the comprehensive optimization of QRCS design value and the lift–drag ratio of this multi-objective optimization is:
where, , is the design value of QRCS, which respectively use the specific gravity of 0.48, 0.15, and 0.37 in the QRCS mean value of azimuth , and . is the lift–drag ratio and is the number of cycles. As shown, we primarily optimized the head-to-side and side-to-side quantum radar stealth, thus this objective function sets a higher proportion in the QRCS average value of the azimuth angle of and .
The comprehensive optimization objective function of average QRCS and the lift–drag ratio is:
where, is the average QRCS.
The design variables are:
The optimization method we used was constructed based on the Isight function; the Multi-Island genetic algorithm was adopted in the optimization algorithm setting. The joint optimization of QRCS and lift–drag ratio can be realized after setting the objective function and a certain weight in the optimizer (Figure 4). Multi-island genetic algorithm is a distributed optimization technique. It extends the genetic algorithm to the framework of multiple “islands” and simulates the migration and communication of populations through the concept of “migration”, so that the populations of each island can constantly accept new genes, so as to obtain better search performance. It can effectively improve the search efficiency of GA, avoid local optimal solutions, and support multi-objective optimization.
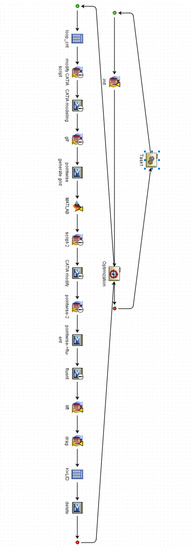
Figure 4.
Isight multi-objective optimization flow chart.
The population crossover probability is 0.8, mutation probability is 0.01, the population size is 8, 12 islands, and 14 generations.
From the Figure 4, it is not difficult to see the comprehensive optimization process we set up. First, the initial file path and optimization module was established before setting up the process in the optimization module. The general process involved: modifying the parameters of the model and making changes to the outside; the surface of the waverider warhead was then divided into a triangular grid. The MATLAB program designed by the formula in this paper was used to compute the target QRCS and output the results. A flow field model for the waverider was generated before using pointwise to divide it into a grid used in flow (Figure 5). Eventually, the lift–drag ratio was calculated in fluent, and the subsequent cycle was executed until the optimization task was completed.
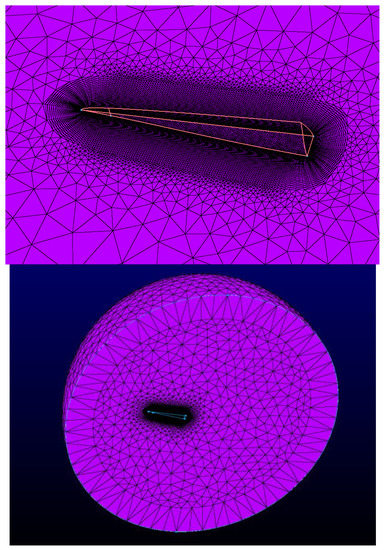
Figure 5.
Grid division of flow field.
5. Analysis and Optimization of the Waverider
First, we verified the accuracy of the QRCS calculation formula derived in this paper. Specifically, our QRCS calculation method of the waverider was compared with the QRCS calculation method derived by predecessors [12] at different vertical angles and azimuth angles. The simulation results are shown in Figure 6.
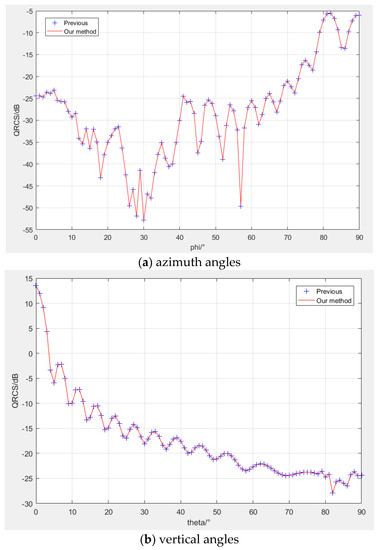
Figure 6.
The QRCS simulation results of the waverider are compared between the two calculation methods at different angles.
From the Figure 6, we found that our QRCS calculation method is basically consistent with the QRCS results obtained by previous methods under different azimuth and vertical angles. In addition, in terms of calculation time, the calculation method used in this paper and the previous method need 141.3 s and 245.6 s, respectively, to get Figure 6a, and 141.7 s and 246.2 s, respectively, to get Figure 6b. Therefore, the calculation method of QRCS proposed in this paper has obvious advantages in calculation time.
5.1. Optimization of the Objective Function Using QRCS Design Values
Through the above simulation work, we respectively obtained the comprehensive optimization results represented by the QRCS design value and QRCS average value. Figure 7 shows the quantum radar simulation using QRCS design value, obtained by considering a certain weight of QRCS means value in three ranges.
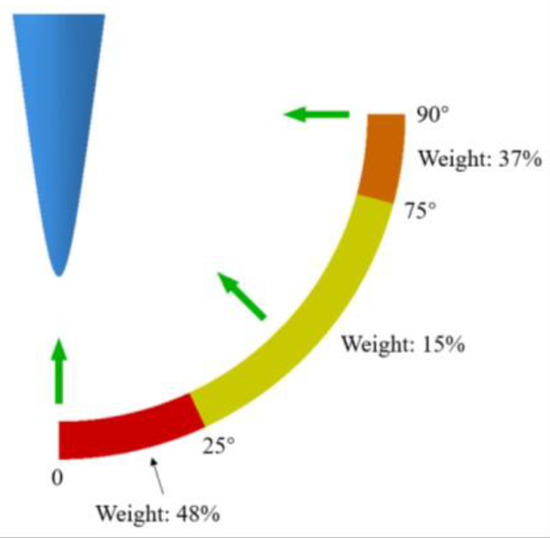
Figure 7.
Quantum radar simulation form using QRCS design values.
First, we analyzed the objective function of the QRCS design value mentioned above and obtained comprehensive optimization results.
As shown in Figure 8, 1345 cycles were performed in the optimization process of the design value of QRCS, and in the 1227th cycle, consequently, we obtained the minimum value of QRCS design value and the function optimal solution using the design value (green dot). From the optimization trend of QRCS design value, the trend line (light blue) shows an apparent downward trend with the increasing number of cycles, reaching the bottom in approximately 1050 cycles, before starting to increase. This indicates that the quantum stealth optimization of this waverider has obtained the best local performance. In addition, Table 2 shows that the design value of the optimized waverider QRCS decreases from the initial −10.1 dB to −20.2 dB, and the minimum position (1227 times) was similar to the position of the optimal objective function. Therefore, this paper has achieved desired results in the optimization of QRCS design value.
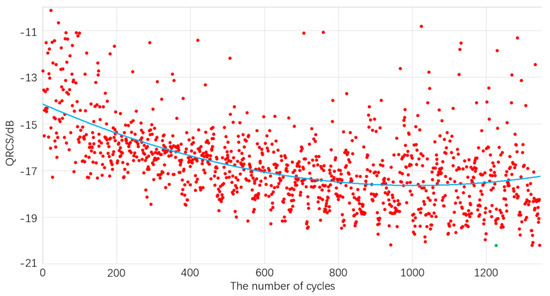
Figure 8.
Trend diagram of QRCS design value optimization.

Table 2.
Comparison of QRCS design values and K before and after optimization.
Figure 9 shows the optimization of lift–drag ratio K for the waverider warhead using the objective function of the design value. It is not difficult to identify that the waverider completed the convergence faster in the area of the lift–drag ratio, particularly in the first 200 cycles; however, the waverider maintained a high position without major changes after 600 cycles. From the trend line of the lift–drag ratio, the waverider also reached the extreme value earlier and stopped increasing. Therefore, in the optimization of the lift–drag ratio, the limit of the design parameter category in this paper has been reached.
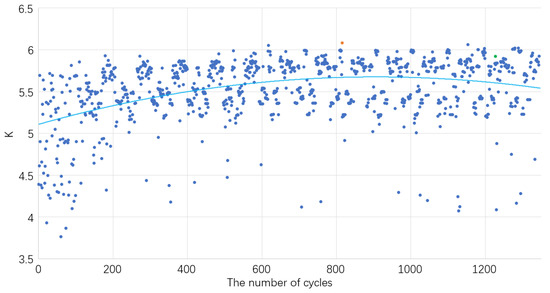
Figure 9.
Optimization trend chart of the lift–drag ratio using an objective function with design values.
Table 2 intuitively presents the design value of QRCS before and after optimization. It is not difficult to note that the lift–drag ratio K of the warhead at the optimal objective function significantly improved compared to the initial situation. Despite being slightly lower than the point at the highest lift–drag ratio in the optimization process (orange point, 820 cycles), the coupling problem was small and without a significant impact on the QRCS design value.
Based on the changing trend of the objective function in Figure 10, it is not difficult to observe that with an increasing number of cycles, the objective function also has an obvious decrease and convergence process (from −7.94 to −14.919). The trend line shows an obvious convergence phenomenon; in 1227 cycles (green dot), the objective function reached the minimum.
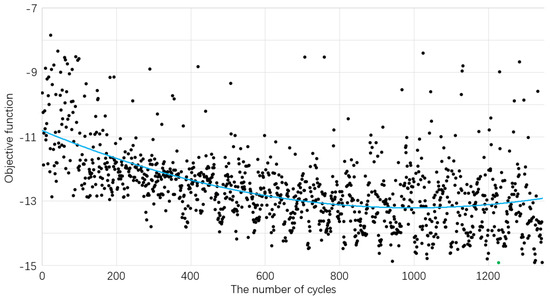
Figure 10.
Shows the trend of the objective function using the design values.
In Figure 11 and Figure 12, and Table 3, we have shown the shape changes of the optimized waverider warhead and compared it with the original warhead. From the change in the shape of the warhead, it has a significantly flattened shape and is also pointed at the leading edge. From the changes of design parameters, its design variables including h1, h2, and A2 were significantly reduced, thus can be considered that these parameters have a relatively large impact on its QRCS or the calculation results of its lift–drag ratio K. In addition, a few parameters did not significantly change after optimization, and therefore such parameters were not the major variables affecting the optimization we described.
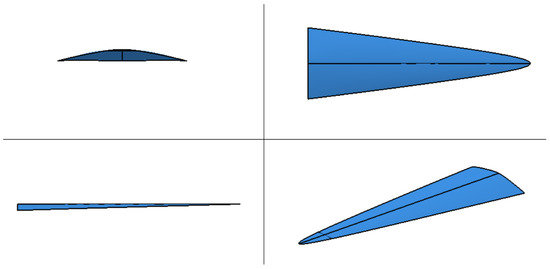
Figure 11.
Waverider warhead optimized using design values.
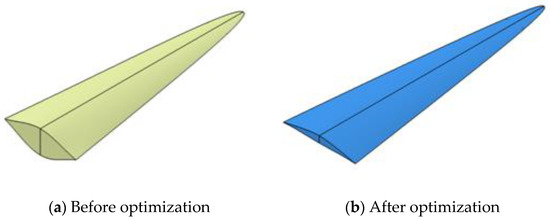
Figure 12.
Comparison of waverider warhead before and after optimization.

Table 3.
Parameter changes of the waverider before and after optimization.
The effect of some parameters on the design value of the QRCS can be intuitively understood from Figure 13. As for QRCS in Figure 13b changing with h2, although it presents an irregular shape, the decrease in h2 is also conducive to the realization of quantum radar stealth. The feature of Figure 13c is that angle A2 decreases with an increasing number of cycles, which is also favorable for QRCS reduction. It can be seen from these phenomena that these parameters can significantly affect the design value of the waverider QRCS. As for Figure 13d, QRCS presents irregular changes with increasing ratio Ra1, and there is no regular trend. Therefore, Ra1 is not the major variable affecting the design value of QRCS.
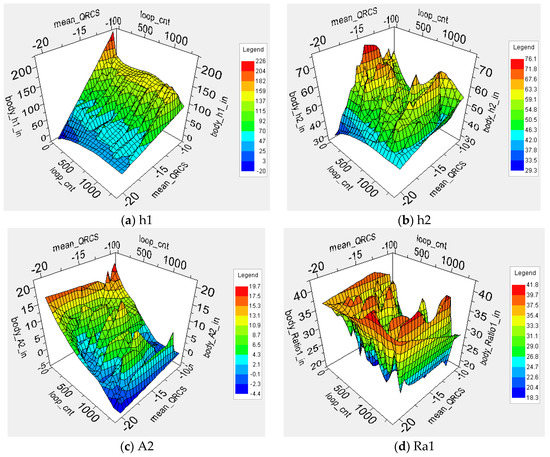
Figure 13.
Influence of different parameters on the design value of QRCS.
Figure 14 shows the static pressure distribution of the non-optimized and optimized waverider warhead during hypersonic flight. Both of them generated higher pressure at the lower surface and lower pressure at the upper part. Although the pressure on the lower surface of the optimized waverider was lower than that without optimization, the position with large pressure was concentrated at the front position with a large angle to the horizontal direction, resulting in a significant increase in the resistance at this position, and a decrease after optimization. Thus, the lift–drag ratio was significantly higher than that of the former.
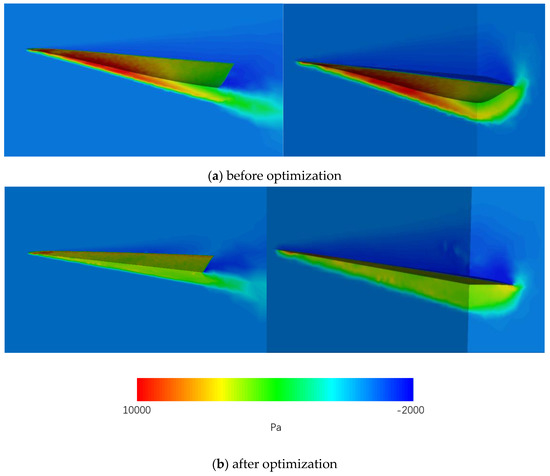
Figure 14.
Comparison of pressure distribution of the waverider before and after optimization.
5.2. Optimization of the Objective Function Using the QRCS Mean Value
In this section, we use the objective function of the mean QRCS to optimize the design of this waverider warhead. This will be performed by taking the average QRCS of the azimuth angle and the lift–drag ratio as the optimization objective. The simulation results are shown below.
Figure 15 and Table 4 present the optimization trend using the mean QRCS and the comparison between the mean QRCS of the optimized waverider warhead and the initial value respectively. In the 1131st cycle of this optimization process, we obtained the minimum value of the QRCS mean value and the optimal solution of the function using the design value (green dot).
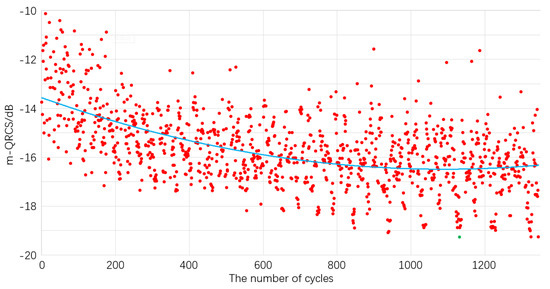
Figure 15.
Optimization trend chart using QRCS mean value.

Table 4.
Comparison of average QRCS before and after optimization.
From the optimization trend of the average QRCS, the trend line shows an obvious downward trend with the increasing number of cycles, reaching the bottom in this process; this indicates that the quantum stealth optimization of this waverider warhead has the best stealth performance against quantum radar. Meanwhile, Table 5 shows that the average value of the optimized waverider QRCS decreases from −10.457 dB to −19.271 dB, reducing by nearly 9 dB.

Table 5.
Parameter changes of the waverider with the mean value of QRCS after optimization.
The minimum position of the average value of the QRCS (1131 times) was similar to that of the optimal position of the objective function. These phenomena are similar to the case with the objective function of the design value. The above content suggests that the optimization method we used also achieved satisfactory results on the average QRCS.
Figure 16 shows the optimization of lift–drag ratio K using the objective function of QRCS mean value. In 879 cycles (orange point), the lift–drag ratio K reached its maximum value; however, the trend of the lift–drag ratio did not increase afterward; the trend line had reached the top, indicating the best optimization of the lift–drag ratio K under this condition. In addition, with the optimal objective function of the QRCS mean (green dot), the lift–drag ratio was lower than the highest point, hence the design contradiction brought by this optimization was significant compared to the former.
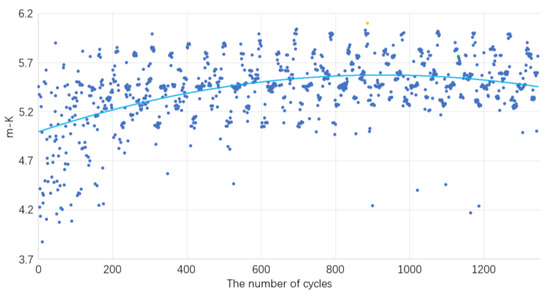
Figure 16.
Trend diagram of the lift–drag ratio optimization using the objective function of QRCS mean value.
Table 4 also presents that the maximum value of the lift–drag ratio K obtained under this condition was about 0.34 higher than the value of K with optimal objective function; this is larger than the difference brought by the design value of QRCS. Although the value of K was lower when the objective function is optimal, it remained significantly higher than the initial value. Therefore, it also plays a good lift–drag ratio optimization effect.
Figure 17 shows the variation trend of the objective function using the mean value of QRCS. With the increasing number of cycles, the objective function also has an obvious decline and convergence process. From the trend line, there is an apparent convergence phenomenon, and in 1131 cycles (green dot), the objective function reaches the minimum value; therefore, the objective function optimization under this condition meets the expectation.
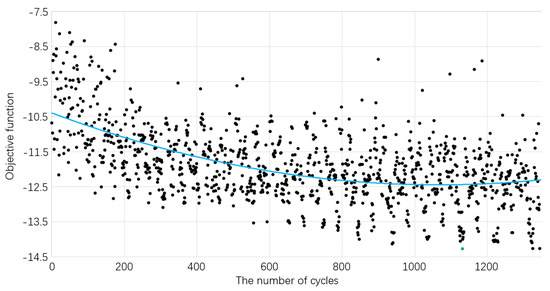
Figure 17.
Trend chart of the objective function using QRCS mean value.
Figure 18 and Table 5 show the shape changes of the waverider warhead optimized using the average value of QRCS. From the change of the shape of the warhead, its shape was also remarkably flattened, and its lower surface was relatively flat. This result is different from the case of using the design value optimization. From the changes in design parameters, h1, h2, A2, and other design variables were significantly reduced; in addition, some parameters did not significantly change, which is similar to the former. In nutshell, the design variables used in this paper can play a more important role in comprehensive target optimization.
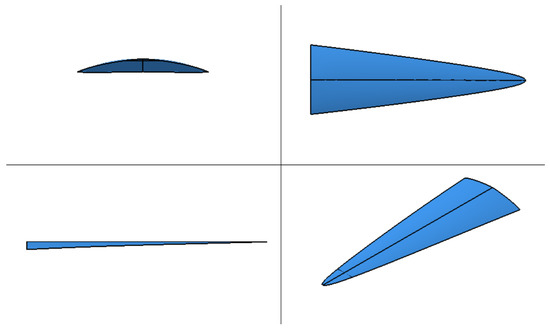
Figure 18.
The waverider warhead optimized using the QRCS mean value.
Figure 19 shows the simulation results of the flow field of the waverider optimized with the mean value. It also generates relatively large pressure on the lower surface and has a good lift effect; however, it is still slightly lower than that of the waverider optimized with the design value.
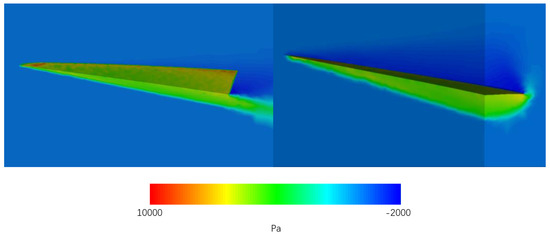
Figure 19.
Pressure distribution of the optimized waverider.
5.3. Comparison of Optimization of Two Objective Functions
Figure 20 shows the comparison of QRCS optimization of the waverider using two objective functions in different azimuth angles. From the perspective of different azimuth angles, the two optimization methods showed obvious reduction compared to the initial time in most angles, only within the range of azimuth angles 25–37°, there was no large difference in these QRCS. When we compared the QRCS curves of the two optimization methods, the QRCS obtained using the objective function of the design value was slightly lower than the result obtained using the average value at the position of the azimuth angle 0–25°. When the design value was 75–90°, the QRCS obtained using the design value was higher when the design value was close to 90°, and the rest of the time was lower than the outcome of using the mean value optimization.
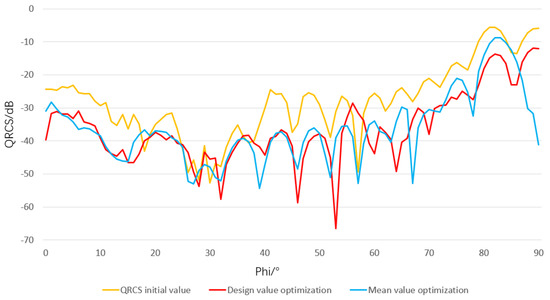
Figure 20.
Comparison of QRCS optimization effects using two objective functions.
Table 6 and Table 7 show QRCS mean value variation of different azimuths after optimization. We found that the QRCS with the azimuth 0–25° obtained by the QRCS design value optimization method was −35.9 dB, which was not only 8.1 dB lower than the initial case, but also 0.6 dB lower than the case with the mean value optimization. As for the mean value of QRCS in the 75–90° region, the mean value of QRCS optimized using the design value was 7.6 dB and 2.1 dB lower than the initial value and the mean value optimized, respectively. As for the optimization of the lift–drag ratio, this optimization method can obtain a higher lift–drag ratio. Therefore, the new optimization method proposed in this paper is better than the latter in both aspects.

Table 6.
Comparison of the lift–drag ratio optimized using QRCS average value.

Table 7.
Changes in QRCS mean values of different azimuths after optimization with the two methods.
From the above content, the basic idea of QRCS design value is to focus the optimization on the two regions with azimuth angles of 0–25° and 75–90°. Furthermore, to avoid increasing the QRCS of other azimuth angles, this paper specifies a small proportion for the mean QRCS of these azimuth angles. This also ensures that the rest of the azimuth QRCS can also be appropriately reduced. Therefore, this paper obtained a better result in the optimization of quantum radar stealth at main angles by adopting the objective function optimization method of QRCS design values.
From the standpoint of aerodynamics, because the optimization approach using average value needs to consider all angles, there will be a large coupling effect, increasing the contradiction in design performance. In this work, the optimization method based on design value can reduce this design contradiction, allowing the waverider to perform better in terms of quantum stealth and lift–drag ratio. In summary, the objective function optimization method of QRCS design values proposed has obtained satisfactory outcomes in the comprehensive optimization of quantum radar stealth and lift–drag ratio.
6. Conclusions
In conclusion, this paper first deduced the QRCS formula of complex targets using the method of vector dot product and shielding factor. Subsequently, the waverider was designed and parameterized, before establishing a comprehensive optimization model of QRCS and lift–drag ratio of complex targets based on a genetic algorithm. Further, we proposed an optimization method using the design value of QRCS. Comprehensive optimization of the waverider was compared with the proposed optimization method using the average objective function. Notably, the proposed optimization method of quantum stealth and the lift–drag ratio is feasible. The experimental results showed that the comprehensive performance of quantum stealth and lift–drag ratio can be substantially improved by changing the waverider shape and adjusting the design variables including the position and inclination of the control points. Due to the reduction in the design constraints, a new type of waverider geometry with the best major direction QRCS and the best lift–drag ratio can be obtained using the optimization method of the objective function of QRCS design value. This performance is superior to the method that uses the average value of QRCS. Therefore, it is possible to realize a comprehensive optimization of QRCS and lift–drag ratio by changing the shape of the waverider body and using the QRCS design value. The research in this paper opens up a new method for the comprehensive optimization of quantum stealth of wave waverider and makes a contribution to the direction of countering quantum radar.
Author Contributions
Conceptualization, S.L. and M.Y.; Methodology, S.L.; Software, S.L.; Validation, S.L. and M.Y.; Formal Analysis, S.L.; Investigation, Z.M.; Resources, Z.M.; Data Curation, S.L.; Writing—Original Draft Preparation, S.L.; Writing—Review & Editing, J.H.; Visualization, J.H.; Supervision, J.H.; Project Administration, M.Y.; Funding Acquisition, Z.M. and M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (Grant No. 61976014). Fundamental Research Funds for the Central Universities. National Natural Science Foundation of China (Grant No. 12004027).
Data Availability Statement
Data sharing does not apply to this article as no new data were created or analyzed in this study.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
References
- Brandsema, M.J.; Lanzagorta, M.; Narayanan, R.M. Equivalence of classical and quantum electromagnetic scattering in the far-field regime. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 58–73. [Google Scholar] [CrossRef]
- Sang, J.H. Aircraft Stealth Technology; Aviation Industry Press: Beijing, China, 2015. [Google Scholar]
- Ji, J.Z.; Huang, P.L.; Ma, Y.P.; Zhang, S.J. Stealth Principle; Beihang University Press: Beijing, China, 2018. [Google Scholar]
- Malik, M.; Magaña-Loaiza, O.S.; Boyd, R.W. Quantum-secured imaging. Appl. Phys. Lett. 2012, 101, 241103. [Google Scholar] [CrossRef]
- Lanzagorta, M. Quantum radar cross section. Proceedings of the Quantum Optics Conference. SPIE Photonics Eur. 2010, 77270K. [Google Scholar]
- Brandsema, M.J.; Narayanan, R.M.; Lanzagorta, M. Design considerations for quantum radar implementation. In Proceedings of the SPIE Conference on Radar Sensor Technology XVIII, Baltimore, MD, USA, 29 May 2014; Volume 90770T. [Google Scholar]
- Brandsema, M.J.; Narayanan, R.M.; Lanzagorta, M. Analytical formulation of the quantum electromagnetic cross section. In Proceedings of the SPIE Conference on Radar Sensor Technology XX, Baltimore, MD, USA, 12 May 2016; Volume 98291H. [Google Scholar]
- Brandsema, M.; Narayanan, R.; Lanzagorta, M. Theoretical and Computational Analysis of the Quantum Radar cross Section for Simple Geometric Targets; Quantum Information Science; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Lin, Y. Calculation of quantum radar scattering cross section of flat structures. Guid. Fuze 2014, 35, 50–53. [Google Scholar]
- Liu, K.; Xiao, H.T.; Fan, H.Q.; Fu, Q. Analysis of quantum radar cross section and its influence on target detection performance. IEEE Photonics Technol. Lett. 2014, 26, 1146–1149. [Google Scholar]
- Liu, K.; Xiao, H.T.; Fan, H.Q. Analysis and simulation of quantum radar cross section. Chin. Phys. Lett. 2014, 31, 034202. [Google Scholar] [CrossRef]
- Fang, C.H. The simulation and analysis of quantum radar cross section for three-dimensional convex targets. IEEE Photonics J. 2018, 10, 7500308. [Google Scholar] [CrossRef]
- Fang, C.; Tan, H.; Liu, Q.F.; Tao, L.; Xiao, L.; Chen, Y.; Hua, L. The calculation and analysis of the bistatic quantum radar cross section for the typical 2-D plate. IEEE Photonics J. 2018, 10, 7500614. [Google Scholar] [CrossRef]
- Chen, K.; Chen, S.X.; Wu, D.W.; Wang, X. Analysis of quantum radar cross section of curved surface target. ACTA Opt. Sinica 2016, 36, 1227002-1. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Wen, X.; Ding, F. Novel osculating flowfield methodology for wide-speed range waverider vehicles across variable Mach number. Acta Astronaut. 2019, 162, 60–167. [Google Scholar] [CrossRef]
- Yu, K.; Xu, J.; Gong, H.; Li, R.; Liu, S. Inverse design methodology of cone-derived waverider based on pre-defined shock wave under strong geometric constraints. Acta Astronaut. 2019, 159, 527–539. [Google Scholar] [CrossRef]
- Zhao, Z.T.; Huang, W.; Yan, B.B.; Yan, L.; Zhang, T.T.; Moradi, R. Design and high speed aerodynamic performance analysis of vortex lift waverider with a wide-speed range. Acta Astronaut. 2018, 151, 848–863. [Google Scholar] [CrossRef]
- Chen, L.L.; Guo, Z.; Deng, X.L.; Hou, Z.X.; Wang, W.K. Investigation on a Novel Waverider Design Method. Adv. Aeronaut. Sci. Eng. 2019, 10, 1674–8190. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).