Abstract
Visualization methods have always been used to inspect flows that are invisible to the naked eye. Seedless velocimetry has been regarded as an alternative to other intrusive quantitative methods and adapted to fit many applications in the industrial or scientific field. Schlieren image velocimetry (SIV) uses the general working principle of a schlieren system to acquire flow images, while relying on a particle image velocimetry (PIV)-like algorithm to obtain quantitative data related to the studied flow. The test case of this study consists of a turbulent round exhaust jet generated by a micro-thruster that uses as a propellent. Mapping the local velocities of the flow is achieved by initially performing a lagrangian tracking method which makes use of a direct image correlation algorithm. These results are then compared to the velocity map obtained from a kymograph applied to a series of images. The velocity profiles obtained through SIV will be compared to the velocity profile of the jet provided by the CFD simulation. The schlieren investigation of the jet’s local velocity map is set to determine the thruster’s capabilities, and conclude if the thruster reaches the desired Mach for which it has been designed.
1. Introduction
The schlieren image velocimetry (SIV) method presents implementation similarities with the particle image velocimetry (PIV) method. The PIV visualization method relies on tracking particles introduced in the studied flow to generate the instantaneous velocity field, through the acquisition of two consecutive images recorded with short-time delay. The results are obtained by image cross correlation. PIV can be considered an artificial-tracking mechanism [1] due to the tracking of particles’ movement based on the supposition that the particles follow the flow perfectly, and not tracking the flow itself. The PIV method can prove to be extremely challenging or even impossible to apply to certain types of flow, such as the electrohydrodynamic and compressible flows, which are the issues arising from the selection of the particles and their spreading mechanism [2].
Moreover, SIV is performed through cross correlating consecutive schlieren images recorded with a short-time delay. The schlieren optical system allows for the recording of images of the optical inhomogeneities present in the studied medium, which are revealed by the deviation of the light. In the case of a turbulent jet, the eddies formed within the flow are considered SIV’s “tracer particles”. Therefore, the latter method represents a more direct tracking mechanism using flow elements to describe the flow’s velocity, and thus can be considered as “self-seeded” [1].
There are many studies regarding the implementation of the SIV method on different test cases. Papamoschou [3] demonstrated that it is possible to acquire velocity information regarding high-speed flows when inquiring about the global convective velocity of a supersonic shear layer using a pulsed light and a short camera exposure time, while Fu [4] and Wu [5] provided the solution of using a high-speed image acquisition system to extract velocities from the image sequence. The post-processing algorithms are very similar to PIV algorithms and in most cases, if the application allows it, the cross correlation of the images is performed in a commercially available PIV software with predefined and already optimized functions.
The field of quantitative schlieren spreads across a large application variety, and the experimental methods differ based on the desired outcome. Partially similar to the present paper, Jonassen et al. determined the velocity field of an axisymmetric, helium jet by applying the schlieren image cross correlation through a commercially available PIV software [6]. Other studies regarding SIV on axisymmetric turbulent jet plumes were conducted by Kegerise and Settles on a turbulent-free convection plume [7]. More recently, Settles et al. described the kymograph method as a means to determine an asymmetrical jet’s centerline velocity more accurately, in a study concentrating on determining the velocity field of a turbulent helium jet in air, and comparing its results to the ones obtained by applying the BOS method on the same jet [8].
There are many quantitative schlieren methods available, for example, background oriented schlieren (BOS), which was implemented to compute flow-field information. Relevant papers covering the BOS technique are represented by Raffel [9], Elsinga [10], Scarano [11], and Settles [8]. Others used shadowgraph images and correlated them to obtain quantitative information regarding different types of flows, such as the jet structure of pulsating water, velocity field analysis [12], or to perform velocity measurements in a cavitating microchannel for two-phase flow configuration [13]. Other experiments, such as [10,14] or [15], use the calibrated color-schlieren method, providing data comparison between quantitative schlieren methods.
The present study concentrates on obtaining velocity information regarding a turbulent exhaust jet dispersing through air by applying different post-processing mechanisms. The gap addressed by the paper is the comparison between Settles’ and Liberzon’s new kymograph method and conventional velocity mapping mechanisms.
Morales [2] describes the process of gathering velocity information on different jet plumes, a free air jet, and various small-engines exit jets by performing a lagrangian tracking of the flow elements revealed by schlieren imaging. The tracking of the elements was conducted manually in this case due to their continuously distorting geometries. A comparison between different cut-offs is also applied, resulting in favor of the vertical and focused schlieren methods, which resulted in the author having a more similar path to the Monte Carlo simulation conducted for the free air jet. The Monte Carlo simulation and direct velocity measurements data obtained by Fellouah et al. [16] were used for constructing the free air jet’s ideal velocity profile. Fellouah et al. [16] used a hot wire rake to measure the velocity distribution of a very similar jet and used the recorded data to generate the velocity profile function describing the velocity profile at certain radial and axial displacements from the nozzle.
The conclusion regarding the lagrangian SIV method applied here is that the lagrangian method provides very little information regarding the velocity distribution, and thus is recommended to be used along with another method to provide proper sampling. The centerline velocity profile, however, must be generated by the application of the Abel transform, given the path averaging character of the axisymmetric flow.
The present paper presents the results from a conducted study regarding a lagrangian tracking performed in a similar manner as [2], compared to the kymograph method described by [8]. The accuracy of these two methods is determined by relating them to the results obtained through a CFD simulation of the exhaust jet.
By mapping the centerline velocity of the exhaust jet, the performance of the nozzle generating the exhaust jet can be confirmed without introducing additional intrusive velocity measurement probes.
The speed at the exit of the nozzle is determined by CFD to be around the magnitude of 1200 m/s, and thus continues past Mach 3.5. The performance of the jet can be determined from its axisymmetric character, whereas its geometry and flow structure can be analyzed from the visualized integrated plane.
2. Experimental Setup
The purpose of this paper is to describe the velocity distribution of an exhaust jet, generated by a micro-thruster designed to be used in space applications. More information regarding the development of the micro-thruster can be found in [17].
This turbulent jet exiting the thruster is encapsulated in a vacuum chamber that only allows for optical access through two parallel glass windows with a smaller diameter than the parabolic mirrors of the schlieren system. The exhaust jet is fully developed in air at normal conditions at the moment the schlieren images were recorded.
The schlieren system used is a U-turn schlieren, very similar to the classical Z-type system, using two parabolic mirrors, a circular knife edge, and 3 mm × 3 mm LED as a light source. The system is placed in a U-shape manner due to the geometrical constraints of the vacuum chamber and the surrounding laboratory environment.
The light source needs to be adequately chosen in order for the images to reveal the flow’s turbulent elements, which will make performing a lagrangian tracking method possible. Another important factor to account for is the type of knife edge used. Even if in other types of quantitative studies, a vertically or horizontally placed knife edge can present the advantage of eliminating density gradients from one of the two directions (x or y, depending on the reference axis system and the type of knife edge used), making calculations of the deflection angle (that in the end yields the density field values) easier, in the case of the lagrangian tracking, the overall coherence of the jet must be ensured. The exhaust jet needs to contain black and white elements in the entire image of the flow field for a consistent and more accurate tracking. For this consideration, a circular knife edge has been chosen. The images were acquired with the setup from Figure 1 and the equipment described in Table 1.
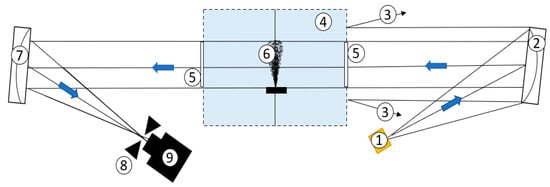
Figure 1.
The U-turn schlieren setup: 1—light source; 2—first parabolic mirror; 3—rays reflected back by the vacuum chamber’s outer casing; 4—vacuum chamber; 5—circular glass windows; 6—exhaust jet; 7—second parabolic mirror; 8—circular knife edge; 9—CCD camera.

Table 1.
Schlieren equipment used to record images of the exhaust jet.
3. Lagrangian Tracking Method
The main goal behind the lagrangian tracking method is to provide a way to track coherent elements present in the flow field. Direct cross correlating schlieren images cannot be performed due to the presence of incoherent elements whose geometries vary significantly, making them impossible to be distinguished from one frame to another. Moreover, the tracking algorithm can get side-tracked due to the coherent elements shapeshift, even if it happens with a lower magnitude than in the incoherent elements case, which can make the element’s path very difficult to reconstruct, if not impossible.
For the first five steps of the image pre-processing plan, described in Figure 2, designated MATLAB functions were used. (The source code for this section is available for download, uploaded as Supplementary Material for this paper). The multilevel threshold’s result developed by [18] can be observed in Figure 3a, and it is applied by following the mechanism described in [2] on image histograms containing pixel intensities, separated into three regions (Figure 3b). A single level threshold provides a good visualization of half the flow’s features, as explained by [19], while applying it on three different levels allows for the separation of the light and dark elements from the gray regions. The three levels applied are: Pixel intensity of 1—for black pixels, 128—gray pixels, 255—white pixels.
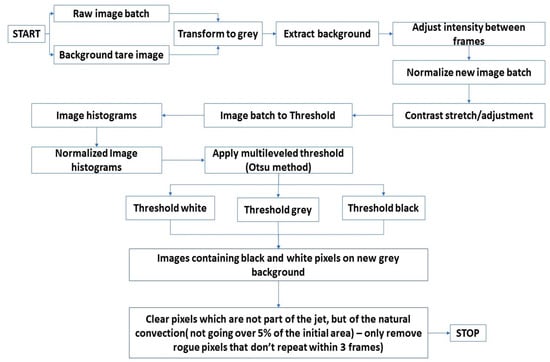
Figure 2.
Image pre-processing plan for the lagrangian tracking method.
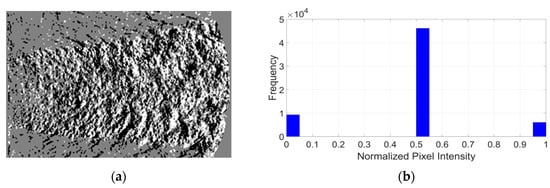
Figure 3.
(a) Multilevel threshold applied by R. Morales [2] to a rocket exhaust jet test image after background subtraction; (b) histogram of the normalized pixel intensities corresponding to (a) [2].
The exhaust jet studied in this paper is encapsulated in the opened vacuum chamber and exits with a very high temperature, not dispersing fast enough for the background of the frames to remain as a series of neutral gray-colored pixels after background subtraction is applied. Therefore, the boundary between the jet and the background is distinguishable, but “rogue” elements are still present after threshold application. These elements represent a source of error and need to be identified and removed.
From Figure 4a, one can observe that the first part of the jet, the closest one to the thruster, appears to be darker and with little to no distinctive elements to track. The area is not sufficiently populated with tracking elements and the sufficient data sampling condition is not fulfilled; therefore, the SIV method can be applied starting at 34 mm away from the micro-thruster and ending at the superior limit of the vacuum chamber’s glass window.
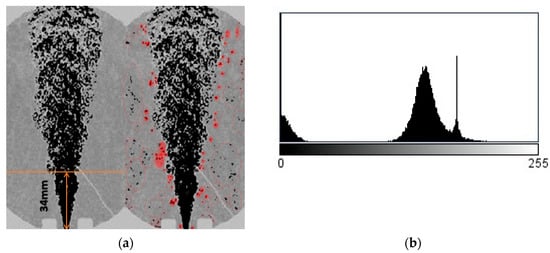
Figure 4.
Image with noise and its histogram: (a) Frame after the additional pre-processing step (right), frame before excluding spurious tracking elements (left); (b) image histogram depicting the contrast plateau of the frame after applying the threshold, generated by ImageJ [20] software.
The data sampling condition is given by the central limit theorem [21] and requires a number of at least 30 samples per investigated jet region to present sufficient data sampling.
Another important issue present in the lagrangian method is the data lost through image binarization, which does not allow for accounting for any subpixel displacements. Therefore, some displacement measurements will have a -pixel error. The tracking of different color elements is performed separately. They are first visually identified, and then an edge-detection algorithm to define their shape contour is applied. The contour’s geometry is important since it must be used to determine the element’s centroid, which provides a reference position for the element.
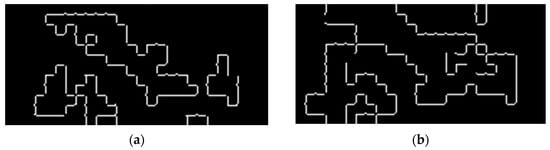
Figure 5.
Element contour generated by the “Roberts” [22] edge-detection filter: (a) Element in the first frame; (b) the same element in the second consecutive frame.
The Roberts edge-detection filter highlights regions of high-spatial frequency, which usually belong to edges. The Roberts edge-detection algorithm finds edges where the pixel intensity is maximum, using the Roberts approximation to the derivative [23].
Although regarded as very noise-sensitive, it was considered to be the perfect fit as it requires a very clear pixel delimitation to construct the edges. This method is applied here to better account for element displacement and its shape shift. If the recording speed is adequate, then the geometry of most tracked elements will remain the same or at least very similar. However, in the case that it fluctuates significantly, the velocity at that point can be erroneously determined due to the unfitting determination of the element’s centroid.
Figure 5 presents a coherent element that appears in several consecutive frames, but whose shape shifting magnitude is higher than expected. Its shape in the first frame is presented in Figure 5a, and the deformation suffered in the second frame is presented in Figure 5b. This issue will transform into an error in the reconstruction of the element’s path since the path is built upon centroid localization and tracking.
The center of mass of the element was found with help from the Regionprops/Centroid function in MATLAB, which returns the coordinates for the center of mass of each element in every frame analyzed. This error can be drastically reduced if the recording speed of the camera is high enough to keep the elements in a similar shape in order to accurately account for their movement. A compromise between reducing the time to account for the shift in geometry and the increasing error generated by recording a smaller pixel displacement with a 1-pixel error must be considered.
Further post-processing might be needed if the edge-detection filter does not describe the element as a closed region. One can try additional preset filters or develop a custom filter in the attempt to close the edges of the elements. The same process is applied to both black and white elements.
The path reconstruction’s last step involved cross correlating consecutive images to establish each element’s path and behavior. The velocities are obtained by cross correlating pairs of two consecutive images. However, 10 frames are used to perform element tracking, which is necessary to solve for the adequate sample size in each region, considering possible new elements to track developed throughout the frame progression, especially in the regions closer to the nozzle’s exit. The assumption that the thruster runs at nominal regime through the 10 frames is made based on the short frame separation time.
4. Schlieren Kymograph Method
The image processing for the kymograph method follows the same path found in Figure 2, stopping before the Otsu threshold. The kymograms are obtained from an image batch of 100 images. A sequence of consecutive frames is found in Figure 6a,b. Figure 6c presents the coordinates considered for the kymograph. It can be observed that the circular knife edge had a very small diameter in contrast to the image. The differences in density found in various areas of the jet make choosing the cut-off very difficult, since the jet disperses with its axial direction.

Figure 6.
(a,b) Consecutive schlieren images used to acquire kymographs; (c) coordination system of the jet (where x represents the distance from the exit nozzle to the mirror limit, and d/2 is on the vertical center axis of the micro-thruster).
The circular knife cut-off was 50%. Although it is the one suggested by most fundamental studies, such as [24], which focuses on the schlieren method evolution as being the ideal cut-off percentage, it has proved to be slightly higher than necessary for this type of jet.
The kymographic concept is covered by Settles and Liberzon [8]. The same process used in [8] to obtain the kymograms is also applied to the present study. The kymogram results from the use of the ImageJ software. To obtain a kymogram, one must open an image stack in ImageJ by pressing Select File > Import > Image Sequence. The kymogram is generated by drawing a line with the dimension of 1-pixel across the center of the jet. In the present case, the center of the jet is determined by physically measuring the thruster’s position relative to the front screws which frame it, and then transforming the distance into pixels according to a magnification factor, allowing for the placement of a proper center axis. The straight line is drawn with the Straight-Line tool. Thereafter, the KymoRescliceWide module is used to extract an image with the resolution of 1-pixel x the length of the image from each image present in the image stack. These new generated images are then placed sequentially as rows, forming the kymogram.
In the present study, the center of images from 1–100 are stacked to form the jet’s centerline kymogram, as pictured in Figure 7. This center represents a 1-pixel vertical line positioned at d/2, as seen in Figure 6c, and ends at x (the top of the visualization window).
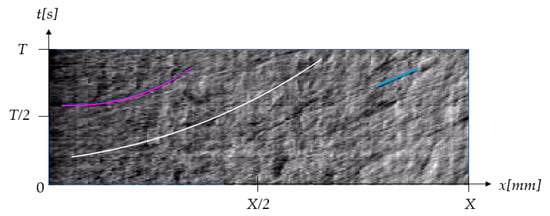
Figure 7.
Kymograms of the jet’s centerline velocity.
The kymograph presents curves which describe the dislocation of the centerline element as a function of time (from frame sequence) and distance (from the thruster to the top of the window).
The centerline kymogram found in Figure 7 has a very poor resolution caused by the high-acquisition rate used by the high-speed camera and the fact that it only covers 100 frames. However, the curves are identifiable and data regarding velocity distribution in the jet have been extracted. The white curve represents the center axis jet velocity, the pink represents the displacement of a turbulent element, while the straight lines, such as the blue one represents a shallower turbulent element observed by schlieren. Ref. [8] mentions the fact that the higher the slope of the curve in the kymogram, the lower the speed of the element it represents. The small blue line segment represents a turbulent element with low speed found at the top extremity of the jet, where turbulent elements tend to linger more within the schlieren image sequence. Therefore, this method quantifies for the velocity, as the graph provides the dependence of distance with time.
The kymograph curves represented in Figure 7 have been fitted using the ImageJ software. The curves have been identified by applying the Roberts filter in order to highlight the differences in pixel intensities, and then manually placing points of interest, which created the presented curves. The curves shown in Figure 7 are highlighted in colors for the ease of observation.
However, the velocity data from the kymogram are manually subtracted, as described in [8], by placing a line segment on the original curve, obtaining the centroid and computing the of the indicated point.
Manually extracting data from kymograms and performing lagrangian tracking is very time consuming. The number of points investigated was enough to determine a velocity distribution trend, which is further discussed in comparison to the other method applied to the jet in question.
5. CFD Considerations
The experimental installation was designed to validate the feasibility of gaseous hydrogen and oxygen mixture for small-scale thrusters. It consists of a small-size thruster placed inside an experimentation chamber and connected to oxygen and hydrogen lines. The thruster was designed for a nominal value of 1 N in vacuum conditions, with an expansion ratio of 50 and a nominal mass flow of 0.3 g/s. Several tests were conducted in atmospheric and vacuum condition to determine the performance of the experimental model at near and stoichiometric mixtures. The thruster geometry consists of a convergent–divergent nozzle with a minimal section of less than 1 mm.
In order to estimate the thruster’s performances and to determine the magnitude of the flow field at the thruster outlet, a 3D numerical simulation was conducted using ANSYS CFX. The computational model was created in order to reproduce the geometry of the chamber, of the thrusters, and the relative placement of these elements. The thruster’s inner geometry was modeled in order to account for the outlet of the combustion chamber and the convergent divergent nozzle. The flow around the external geometry of the thrusters is of lesser importance; therefore, in order to lower the computational demand, a conic wall was used for the outer geometry of the experimental model, as can be seen in Figure 8. The overall dimensions of the computational model were determined by the experimental chamber dimensions, which has a cylindrical shape.
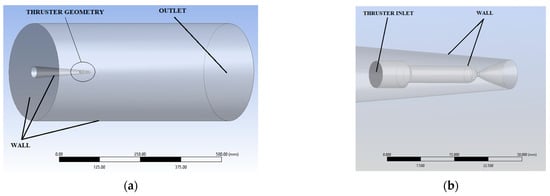
Figure 8.
(a) Fluid volume; (b) thruster’s interior geometry.
The numerical grid was generated using ICEM software. The grid is of the structured hexahedral type with a smaller dimension for the thruster’s inside volume and the vicinity of the thruster outlet as can be determined from Figure 9. The grid independence was checked in terms of resulted y+ values, which were in the suggested intervals for the turbulence model used.

Figure 9.
(a) Numerical grid for thruster internal flow; (b) numerical grid for fluid volume.
The numerical case was set based on measurements for the respective test, and thus the total mass flow was set at 0.27 g/s. In order to reduce the complexity of the numerical simulation and lower the computational demand, the combustion process was not modeled. The combustion process was considered complete at the volume inlet, with the working fluid composed of water vapor forming the complete reaction of gaseous H2 and O2. The temperature was determined using the CEARun software for a stoichiometric reaction of gaseous hydrogen and oxygen resulting in a value of 3450 K. The fluid used for this simulation was a mixture of H2O, H2, O2, and N2 in order to simulate the interaction between the water vapors and ambient air.
The boundary conditions for this study are presented in Table 2. Inlet boundary conditions were set for the thruster inlet (fixing the mass flow, total temperature and chemical components of the fluid, water vapor in this case), opening conditions for the fluid volume outlet (fixing the temperature, pressure and chemical components). For the thruster and experimental chamber walls, adiabatic no slip conditions were used. Reynolds-averaged Navier–Stokes (RANS) simulations were conducted using the K-ε turbulence model due to its known performance for high-turbulent flows.

Table 2.
Boundary conditions.
For convergent criteria, three parameters were monitored: Residuals, mass flow imbalance, and the reaction on the thruster walls. The residuals target was fixed at 1 × 10−6 reaching at least 1 × 10−4 for each parameter. The mass flow imbalance was less than 1% with the reaction force on the thruster walls almost constant (variation less than 1% over several hundred iterations). The numerical results were compared with experimental data in terms of thruster pressures and thrust measurements, validating the numerical study.
6. Results
The lagrangian tracking method provided limited data related to the jet’s velocity due to the small number of coherent elements available in the images. Relevant sampling of traceable turbulent elements starts at 34 mm away from the jet and deforms less as it progresses to the upper visual limit, which can be found at 122 mm away from the thruster. The 0–34 mm jet section returned only two coherent traceable elements, marked with an yellow x, as represented in Figure 10.
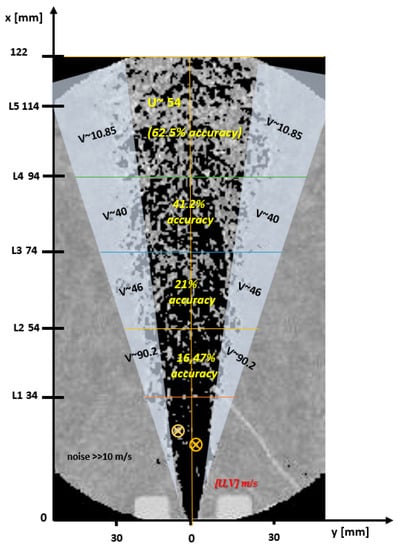
Figure 10.
U- and V-averaged velocity values per regions of interest, generated through lagrangian tracking.
A comparison with the CFD obtained velocity confirms the hypothesis that the most accurate estimation will be possible at a certain distance from the jet’s exit, where the velocity of the jet is in good agreement with the image acquisition rate.
The results of the lagrangian tracking present a low traceability rate. The spatial resolution is very poor, and it is believed that the velocity values start converging toward the CFD obtained profile somewhere after 120 mm away from the thruster, where the tracked elements have a lower velocity and suffer less deformation, which makes them easier to track. This leads to the belief that the error is smaller in that area.
The points in which the velocity is equal to 10 [m/s] represent the elements that displaced their center with exactly 1 mm on the x-axis and y-axis, respectively, and most of the time these elements are represented by a singular pixel. Therefore, the 1-pixel elements with 10 m/s displacement will not be considered as relevant for the present study, representing another limitation of this system.
In some local points, the velocity value results are higher than the CFD velocity profile due to the possible tracking errors that resulted from a confusion made by the cross-correlation algorithm between the flow elements and the continuously moving pixels in the background. Other errors may appear due to element deformation in time that might be viciously traced in some areas where the velocity profile does not fit the acquisition rate.
Figure 9 presents the accuracy map of the method, which is calculated by averaging each point found in the investigated area.
A drop in the V velocity values, as represented in Figure 10, can be observed with the increase in the distance from the thruster to the upper visual limit. This is caused by the jet’s significant drop in the energy of the jet as a result of the developing jet elements, which then tend to float after reaching a certain height. The maximum V velocity for each section is depicted due to the fact that the CFD model does not account for the turbulence of the jet. In order to reach a fair comparison regarding the movement of the elements, a better CFD turbulence model should be used in future studies.
The lagrangian tracking method proved to be effective only in the last two sections of the jet that appear in the schlieren images (between lines 4 and 6), rendering a more precise measurement of the jet plumes. The central axis velocity could not be found given the low acquisition rate and the path-averaging character of the method.
According to other literature studies, such as the one represented in [2], the accuracy of the lagrangian tracking method can be placed anywhere between 20% and 100%, depending on the character of the studied flow. In the present study, by only considering results from the last two CFD sections that appear in the schlieren images (from 94 mm to 122 mm away from the thruster), a mean accuracy of the measurements is found to be equal to 62.5% (locally calculated for each point in comparison to the CFD mean jet axis velocity profile presented in the mentioned sections, and then averaged).
In the other sections of the jet represented in the schlieren images, the accuracy drops significantly and the data obtained become irrelevant, for example, in the last section of the jet, the accuracy value is below 20%.
The 62.5% accuracy does not represent a generally good data accuracy, but does present a higher element traceability than other types of investigated axisymmetric jets [2].
To better describe the axisymmetric jet’s velocity profiles and account for its 3D character, an Abel Inverse Transform, similar to the [25], but applied to the velocity field, will be performed in a future study.
The maximum velocity of the jet that resulted from CFD is 1124 m/s. For recording the elements motion in the exit area of the thruster, an acquisition rate equal to at least 300.000 fps is needed. This acquisition rate can be achieved with a PIV-like system, incorporating a dual-frame high-speed camera.
The lines of interest along the jet’s developing path, considered for this study are pictured in Figure 11 and are explained further.
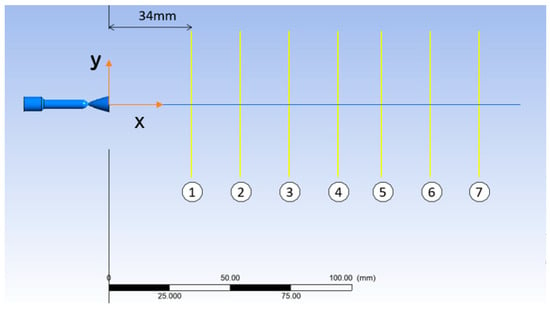
Figure 11.
Lines that divide the jet into six sections of interest, starting at line 1 and ending with line 7 from the CFD simulation.
The graph in Figure 12 represents the Gaussian-like mean U velocity profile found on the lines that section the jet, as showcased in Figure 10, while the graph found in Figure 12 presents the anti-symmetrical character of the mean V velocity profile, the jet’s structure is inclined in opposite senses at the left, respectively the right of the centerline, indicating that the lateral component will have different signs.
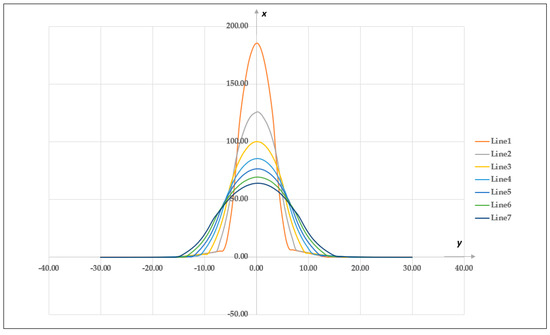
Figure 12.
CFD obtained—U velocity profiles along the seven jet lines presented in Figure 10, in the same coordinate system.
Sections start on line 1, placed at 34 mm away from the thruster and continue to divide the jet in new, equally spaced 20 mm sections. It is implied that any U velocity value fitted in between the two lines found on the graph in Figure 12, and also belonging to the sections described, is a valid local value of the flow velocity. Similar to the V velocity profiles, presented in Figure 13. From the velocity profiles, it is noticeable that the jet’s axial symmetry does not only refer to its geometry which can be observed in the schlieren images, but also to the fact that it should disperse in a very similar manner on the outskirts, where the turbulent elements are easier to follow through the lagrangian tracking method.
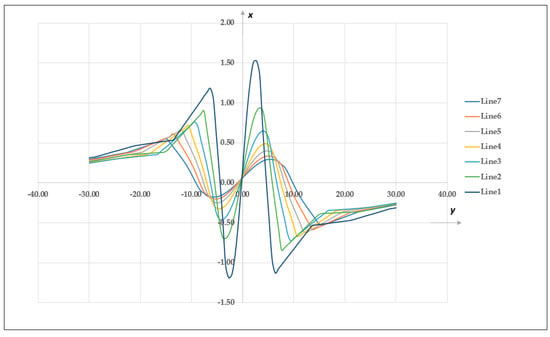
Figure 13.
CFD obtained—V velocity profiles along the seven jet lines presented in Figure 11, in the same coordinate system.
The CFD profile presented in Figure 14 provides information regarding the jet’s center axis velocity. The same information can be extracted from jet kymograms.
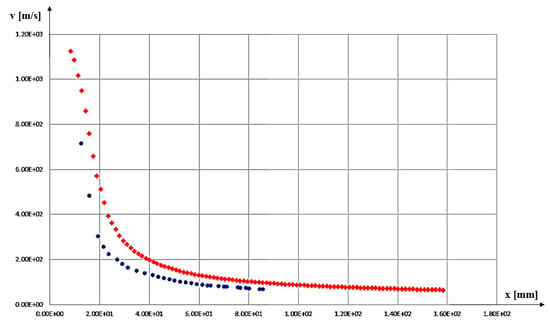
Figure 14.
Overlay of the kymograph resulted velocity profile (blue series) and the CFD profile (red series).
The jet axis kymogram analyzed is represented in Figure 6 by a white curve. Velocity on the axis itself was extracted by manually performing dx/dt in some points found on the designated curve.
The kymogram velocity profile reveals a maximum velocity higher than the one presented by the CFD model. A 30% error has been registered at the first point of the kymograph. This large error only refers to the area close to the thruster, where schlieren methods fail due to the large values of density, which presents issues in correctly identifying the starting point of the velocity profile curve found on the kymogram.
The overall accuracy of the kymograph method improves after the first point, but in its extremity, the velocity values seem to drop faster than the CFD provided curve. The accuracy of the method has been proven to be over 80% in areas located at 60 cm away from the thruster. The graph for this section overlays very well with the CFD velocity profile, as it can be seen in Figure 14. The first point of the kymograph curve is considered to be an error, resulting in a maximum velocity of the jet equal to 1460 m/s, and is not included in Figure 14. The kymograph velocity profile stops at nearly 85 cm from the thruster, where the curve begins to be harder to identify due to the density drop.
7. Conclusions and Future Work
Through this study, an estimate of the velocity profile of an exhaust jet has been achieved. The methods provided data on velocity in sections where they better fit the experiment’s settings. The lagrangian tracking performed better in sections where the jet was described by plumes. Tracking turbulent elements in a 3D jet was demonstrated to have a very poor overall accuracy, in some cases dropping as low as 30%. The 62.5% accuracy that resulted from lagrangian tracking can be improved by better adapting the acquisition rate to the flow’s overall velocity. Another option is to record images at different acquisition rates, especially dedicated to a particular jet section, which has a particular velocity range and density. A MATLAB code can be created to identify and track turbulent elements and further use an adaptive algorithm, which can be applied to account for their deformation in time. Comparing this method to the CFD velocity profile only applies in the upper sections, as one is line-averaged and the other represents the jet’s center axis velocity profile. A live post-processing script can also be deployed, as edge-detection in real time is a valid option and other computational needs only depend on the post-processing system’s performances.
The kymograph method offered more accurate and reliable results, with a very high accuracy, compared to the lagrangian tracking. This method can be improved in the context of the present jet by lowering the acquisition rate to be able to record images with better resolution, which will help in identifying and describing the curve from the generated kymograph.
The accuracy of the two schlieren methods applied is calculated by comparison to the data obtained from the CFD simulation.
However, the CFD data have been compared to experimental data gathered by sensors measuring the total mass flow and output thrust. The results of the numerical simulation revealed a 4% error when compared to the experimental data in terms of velocity magnitude at the nozzle outlet, representing slightly lower values for the numerical simulations.
In the present study, the lagrangian tracking method proved to be useful in jet plumes, but was not relevant for the jet’s center axis, despite the fact that the method was improved using the designated correlating functions for coherent element tracking. The kymograph method proved to be a better fit for determining the centerline velocity, while being quite difficult to apply to other jet areas without the automation of the post-processing mechanism. Nevertheless, it generated results within a 20% error when compared to CFD.
The error magnitude found in the schlieren methods exceeds by far the error magnitude found in the CFD simulation. Therefore, the calculated accuracy of the schlieren methods can be considered relevant even when taking into account the CFD error.
Future work aims at a fully experimental characterization of the studied jet by applying quantitative schlieren methods. Apart from the already mentioned aspects, a study regarding a calibrated color-filter schlieren to determine the jet’s temperature profile is underway. The resulted values of the aimed parameters (velocities, pressures, temperatures) will be used to assess the performances of the micro-thruster, without intruding the flow.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/aerospace10070576/s1. The image processing code is attached to this paper as supplementary material and can be downloaded here.
Author Contributions
Software, E.G.P.; validation, E.G.P.; experimental setup, J.V., E.G.P. and R.E.N.; writing—original draft preparation, E.G.P.; writing—review and editing, E.G.P. and R.E.N.; supervision, T.P. and V.A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Acknowledgments
This work was carried out through the “Nucleu” Program, within the framework of the National Plan for Research, Development and Innovation 2023-2026, supported by the Romanian Ministry of Research, Innovation and Development, project number PN23.12.06.02.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Biswas, S. Physics of Turbulent Jet Ignition; Springer International Publishing AG (part of Springer Nature): Cham, Switzerland, 2018. [Google Scholar]
- Morales, R. Lagrangian Schlieren Image Velocimetry Measurements in Exhaust Plumes, Partial Report. Master’s Thesis, New Mexico Institute of Mining and Technology, Socorro, Mexico, 2018. [Google Scholar]
- Papamoschou, D. A two-spark schlieren system for very high velocity measurement. Exp. Fluids 1989, 7, 354–356. [Google Scholar] [CrossRef]
- Wu, S.; Fu, Y. Quantitative analysis of velocity distribution from schlieren images. In Proceedings of the 8th International Symposium on Flow Visualization, Sorrento, Italy, 1–4 September 1998. [Google Scholar]
- Wu, Y. Detection of velocity distribution of a flow field using sequences of schlieren images. Opt. Eng. 2001, 40, 1661. [Google Scholar] [CrossRef]
- Jonassen, D.; Settles, G.S. Schlieren “PIV” for turbulent flows. Opt. Eng. 2006, 44, 190–207. [Google Scholar] [CrossRef]
- Kegerise, M.; Settles, G.S. Schlieren image-correlation velocimetry and its application to. In Proceedings of the 9th International Symposium on Flow Visualization, Edinburgh, UK, 22–25 August 2000. [Google Scholar]
- Settles, G.S.; Liberzon, A. Schlieren and BOS velocimetry of a round turbulent helium jet in air. Opt. Lasers Eng. 2022, 156, 107104. [Google Scholar] [CrossRef]
- Raffel, M. Background-Oriented Schlieren (BOS) techniques. Exp. Fluids 2015, 56, 60. [Google Scholar] [CrossRef]
- Elsinga, G.E.; van Oudheusden, B.W.; Scarano, F.; Watt, D.W. Assessment and application of quantitative schlieren methods: Calibrated color schlieren and background oriented schlieren. Exp. Fluids 2003, 36, 309–325. [Google Scholar] [CrossRef]
- Scarano, F.; Benocci, C.; Riethmuller, M.L. Pattern recognition analysis of the turbulent flow pas a backward facing step. Phys. Fluids 1999, 11, 3808–3818. [Google Scholar] [CrossRef]
- Mauger, C.; Méès, L.; Michard, M.; Lance, M. Velocity measurements based on shadowgraph-like image correlations in a cavitating micro-channel flow. Int. J. Multiph. Flow 2014, 58, 301–312. [Google Scholar] [CrossRef]
- Zelenak, M.; Foldyna, J.; Scucka, J.; Hloch, S.; Riha, Z. Visualization and measurement of high-speed pulsating and continuous water jets. Measurement 2015, 72, 1–8. [Google Scholar] [CrossRef]
- Elsinga, G.E.; van Oudheusden, B.W.; Scarano, F.; Watt, D.W. Assesment and application of quantitative schlieren methods with bi-directional sensitivity: CCS and BOS. In Proceedings of the PSFVIP-4, Chamonix, France, 3–5 June 2003. [Google Scholar]
- Hargather, M.; Settles, G.S. A comparison of three quantitative schlieren techniques. Opt. Lasers Eng. 2012, 50, 8–17. [Google Scholar] [CrossRef]
- Fellouah, H.; Ball, C.; Pollard, A. Reynolds number effects within the development region of a turbulent round free jet. Int. J. Heat Mass Transf. 2009, 52, 3943–3954. [Google Scholar] [CrossRef]
- Nicoară, R.E.; Vilag, J.; Suciu, C.; Vilag, V. Experimental testing of small H2/O2 thrusters in atmospheric and vacuum condition. In Proceedings of the 7th Edition of the Space Propulsion Conference, Online, 15 March 2021. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Gonzales, R.; Woods, R.; Eddins, S. Digital Image Processing Using Matlab; Gatesmark Publishing: Knoxville, TN, USA, 2009. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Ganti, A. Investopedia. Available online: https://www.investopedia.com/terms/c/central_limit_theorem.asp (accessed on 25 April 2023).
- Roberts, L. Machine Perception of 3-D Solids, Optical and Electro-Optical Information Processing; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Available online: https://www.mathworks.com/help/images/ref/edge.html (accessed on 25 April 2023).
- Settles, G.S. Schlieren and Shadowgraph Techniques; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Liu, X.; Wang, X.; Zhao, X.; Xiao, P.; Liu, Y.; He, J. An improved inversion algorithm to reconstruct 2D temperature fields of long sparks with high-speed schlieren technique. Measurement 2021, 180, 109620. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).