Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine
Abstract
1. Introduction
2. Methods
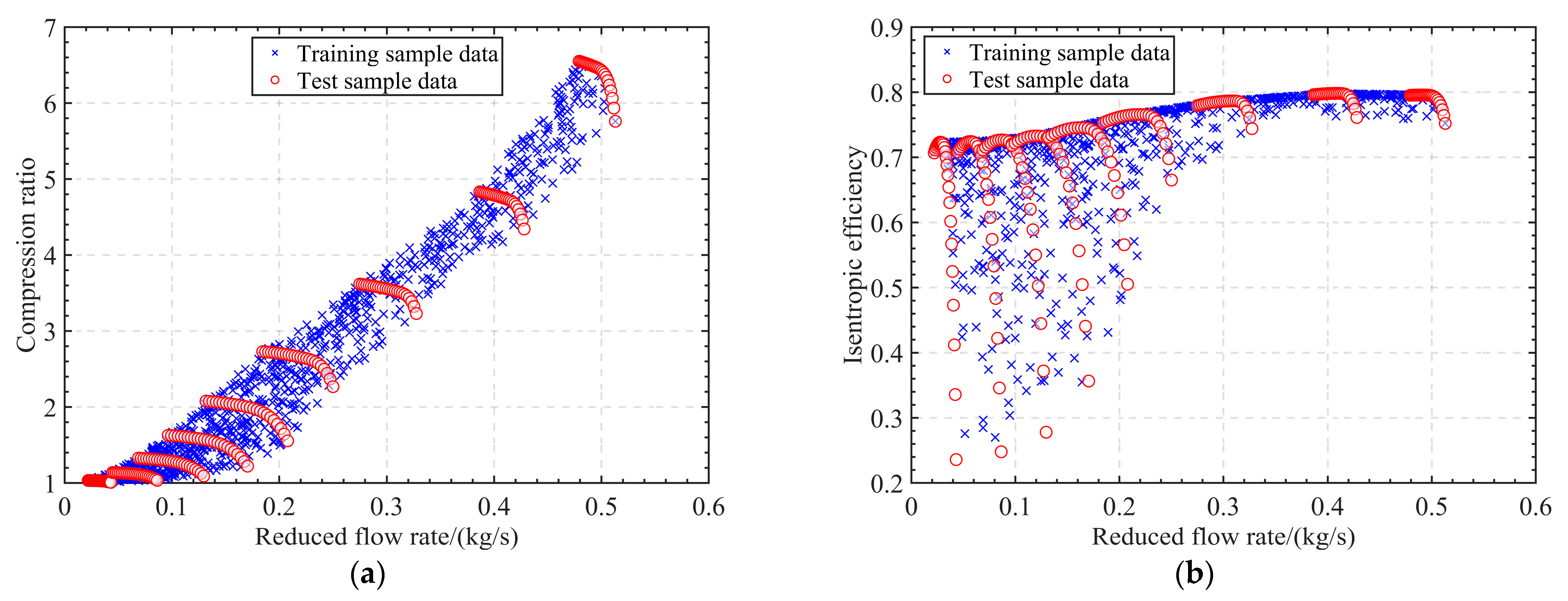
2.1. Data Processing of Compressor Characteristics
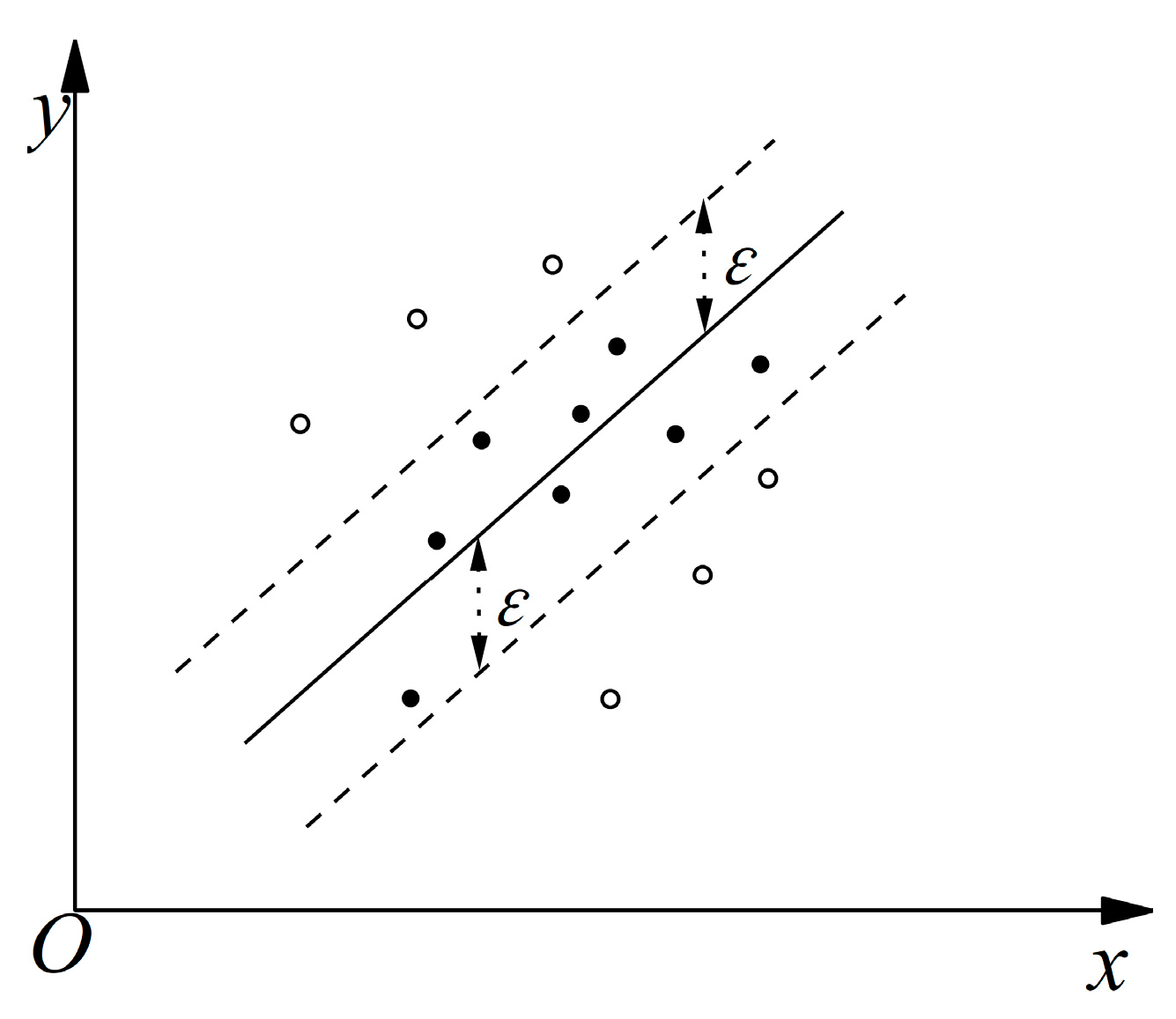
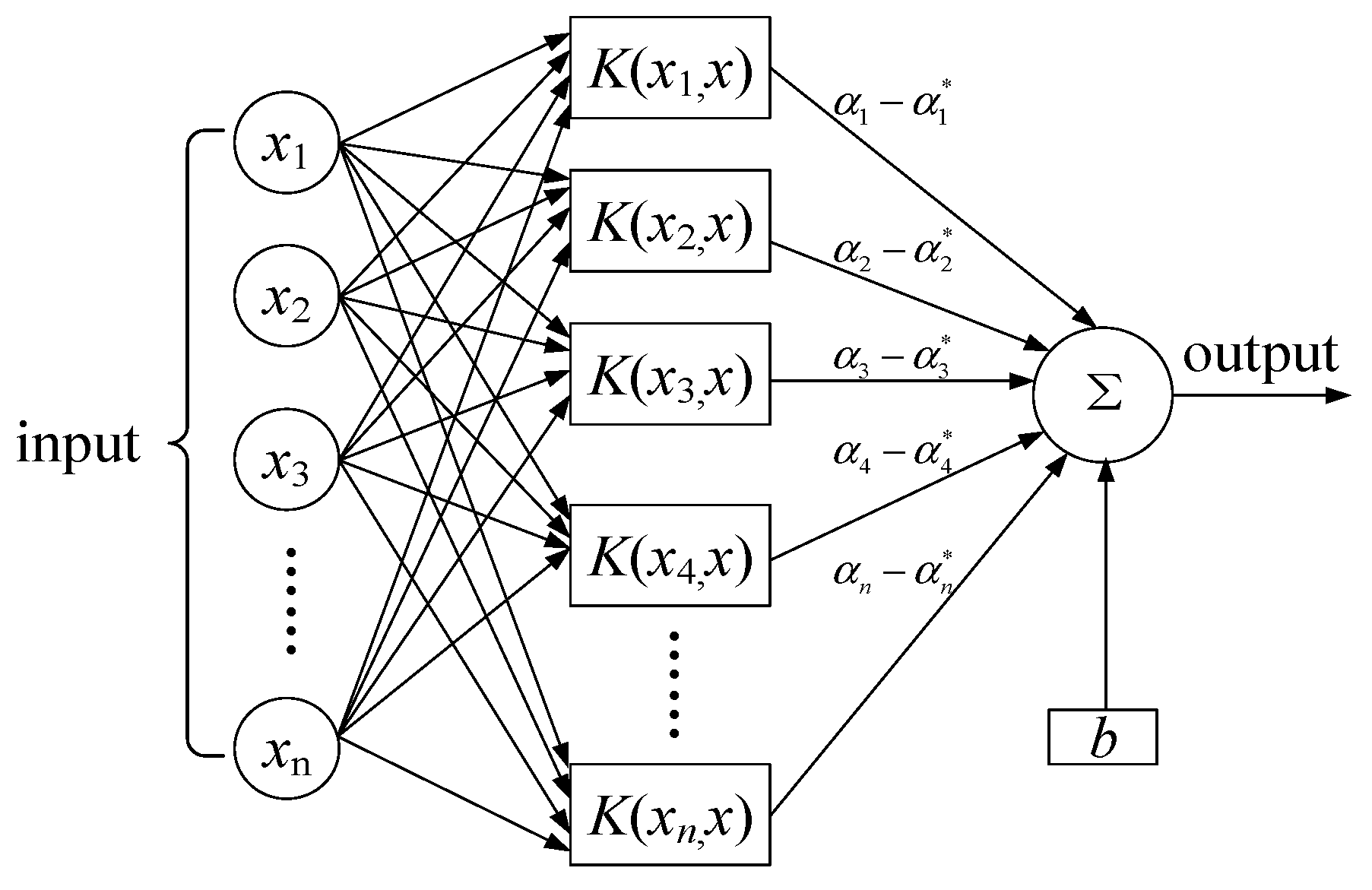
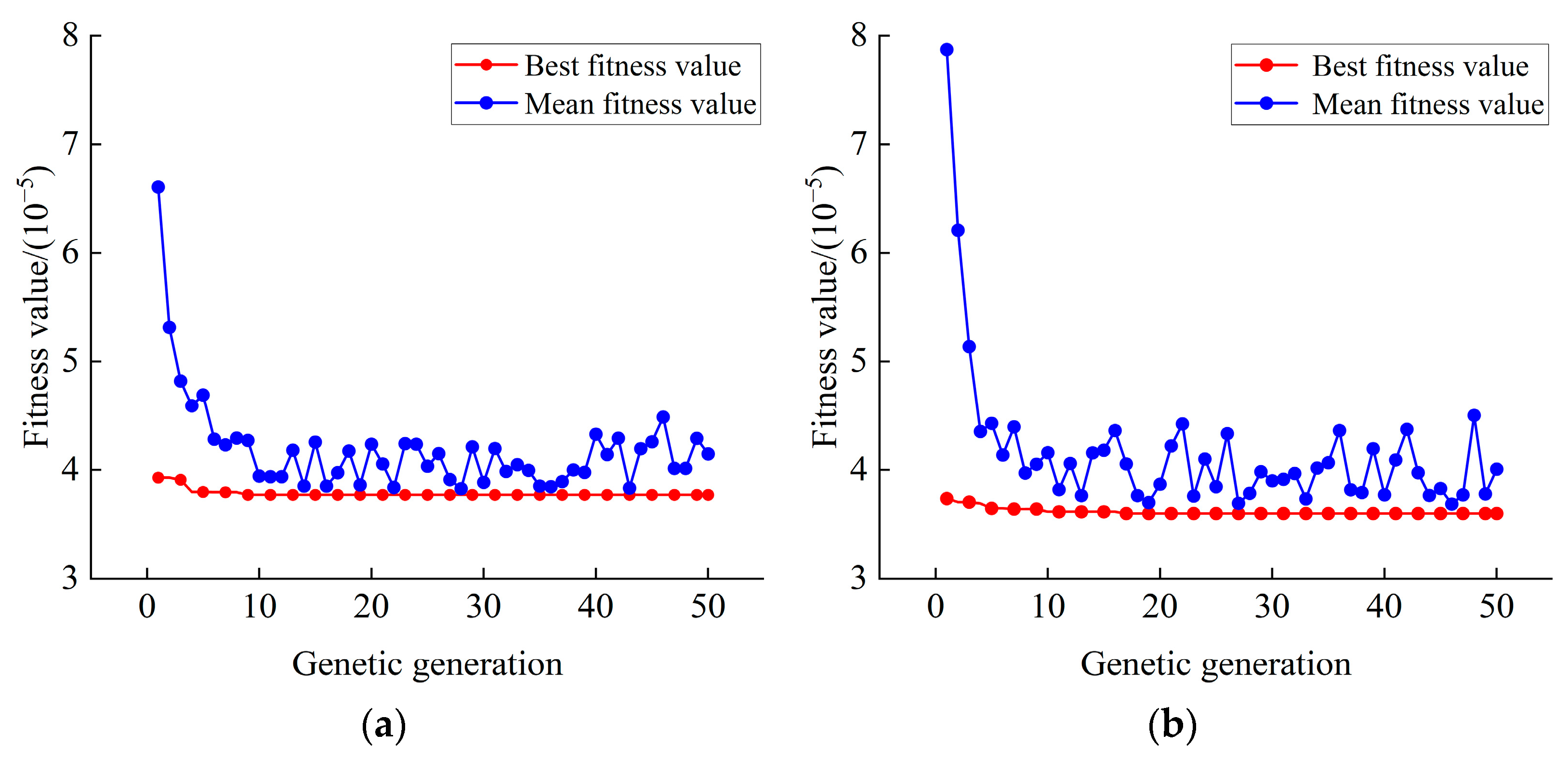
2.2. GA-SVM
2.3. Evaluation Indicators
3. Results
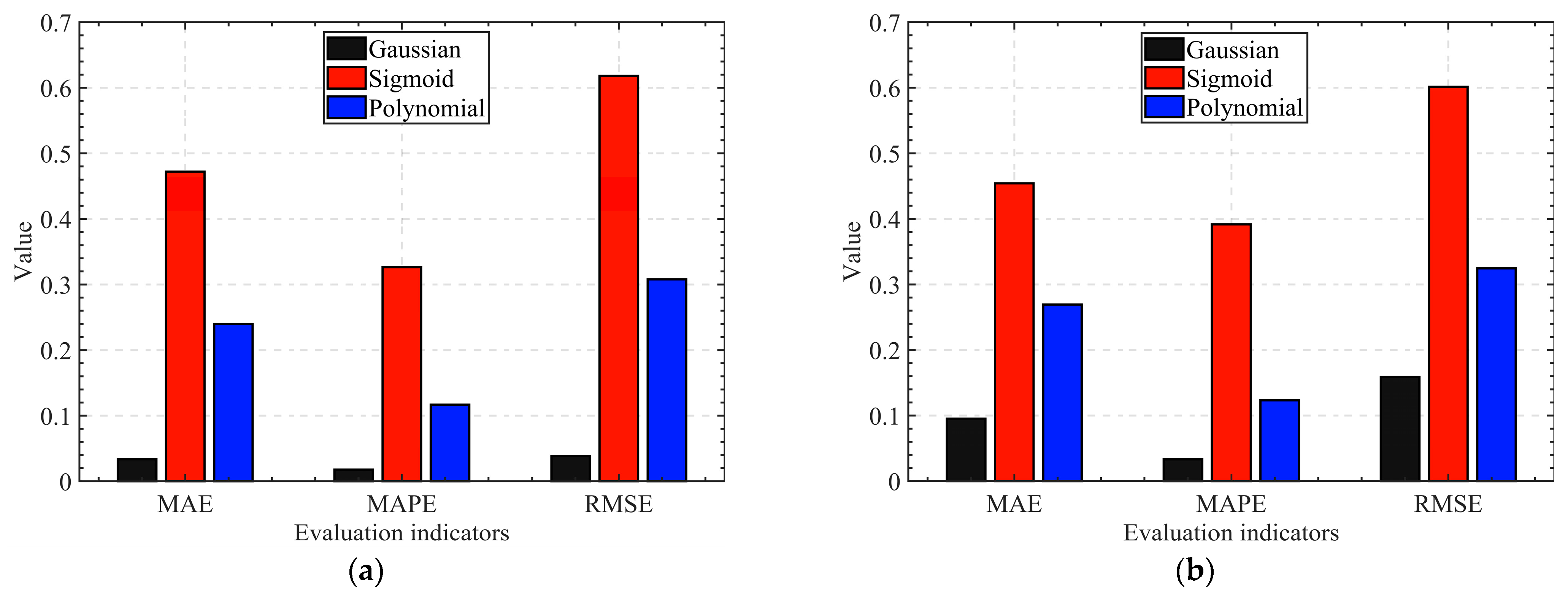
3.1. Kernel Function Selection
3.2. Interpolation Method
3.3. Preliminary Comparison of Prediction Models
3.4. Further Comparison of the GA-SVM and GA-BPNN
3.5. Optimization of Original Data
4. Conclusions
- (1)
- As SVM is used for compressor performance prediction, Gaussian kernel functions can achieve high prediction accuracy. Preliminary training and testing of 200 sets of training sample data and 25 sets of test sample data were carried out. The MAE, MAPE, and RMSE of the predicted results for the training sample are 0.0337, 0.0177, and 0.0385, respectively. The MAE, MAPE, and RMSE of the predicted results for the test sample are 0.0952, 0.0334, and 0.1589, respectively. These two sets of evaluation indicators are superior to the sigmoid kernel function and the polynomial kernel function.
- (2)
- The training samples obtained using the linear interpolation method were found to be more accurate, corresponding to a higher prediction accuracy of the GA-SVM. At this point, the GA-SVM kernel coefficient for predicting compression ratio is 36.7785, and the penalty factor is 99.9012; the GA-SVM kernel coefficient for predicting isentropic efficiency is 257.0136, and the penalty factor is 99.7891.
- (3)
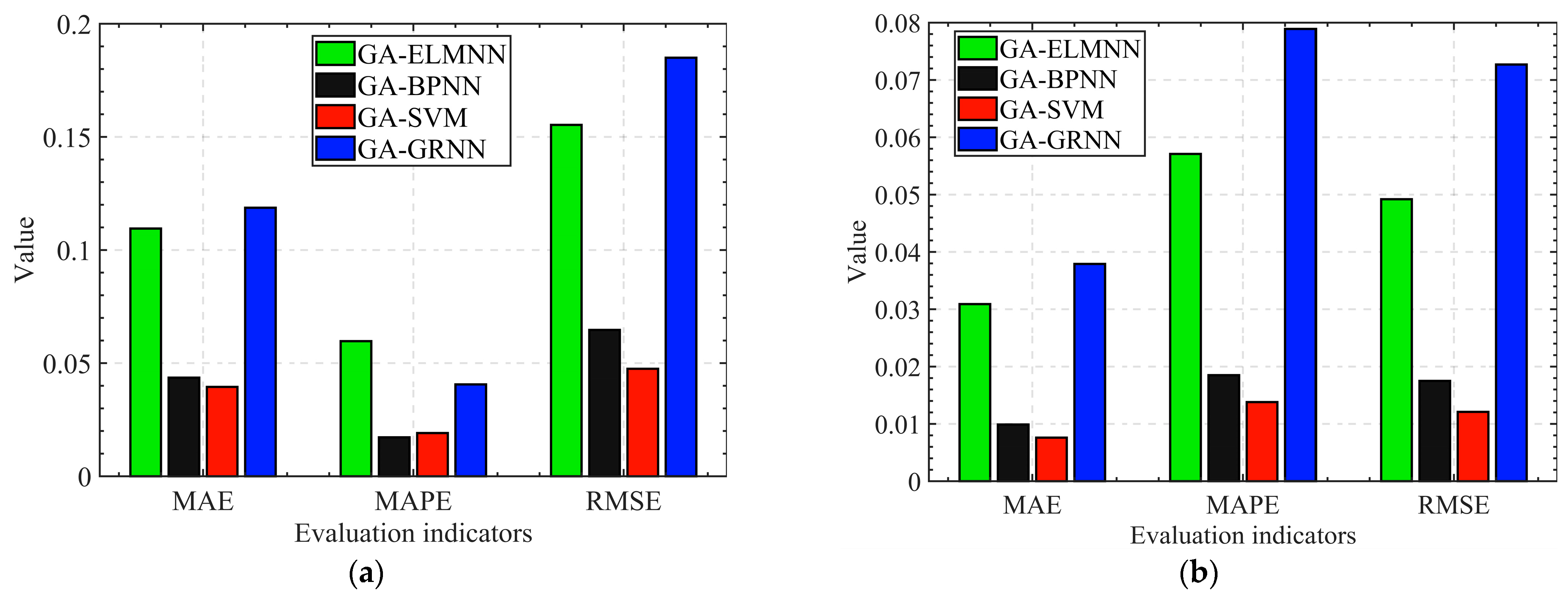
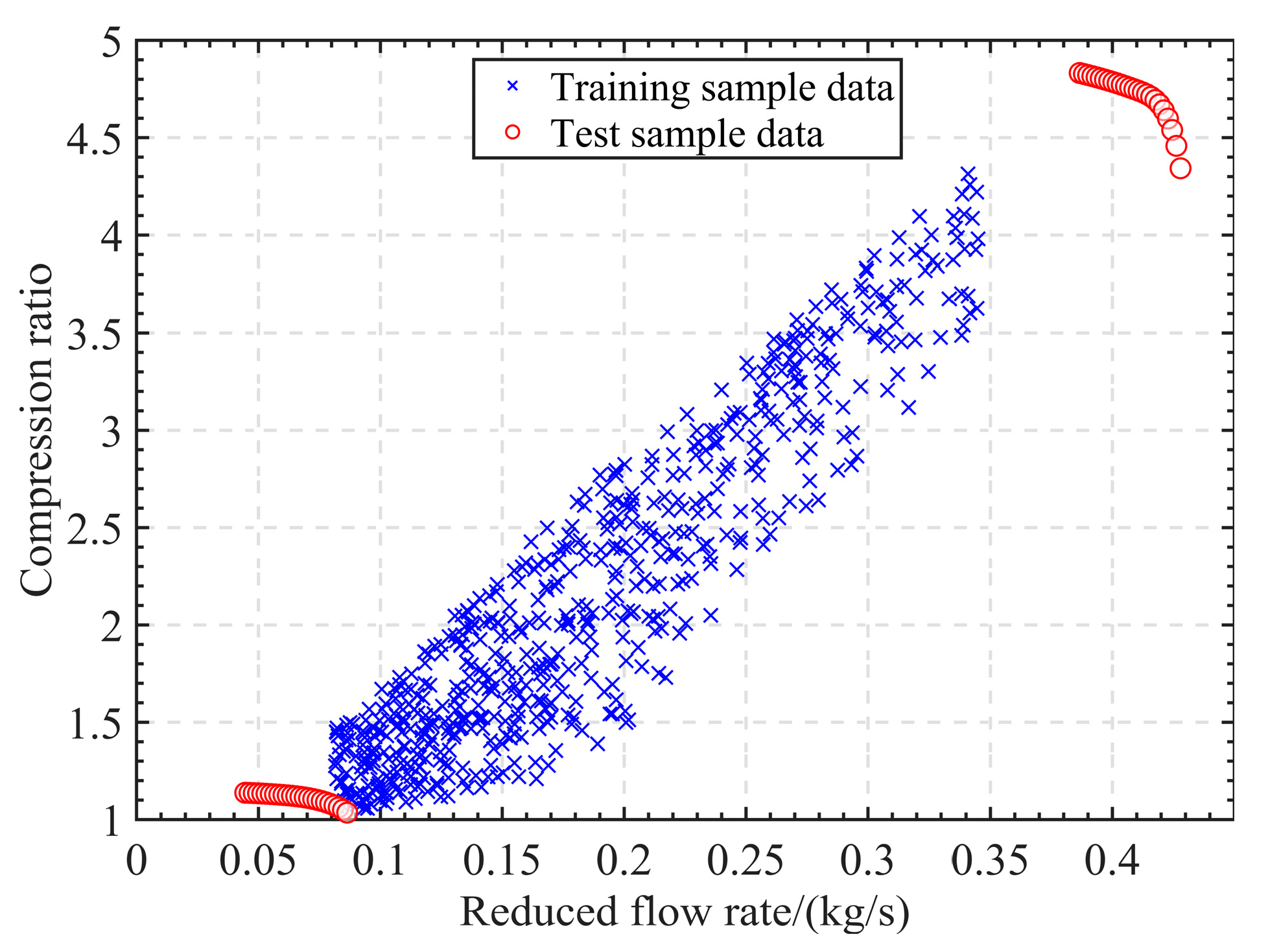
- Train four models using 1000 initial training samples from Section 3.2. The GA-SVM and GA-BPNN have significantly better prediction accuracy in compression ratio and isentropic efficiency than the GA-ELMNN and GA-GRNN. The MAPE of GA-SVM predicted compression ratio results is slightly higher than GA-BPNN, and all other performance indicators are better than GA-BPNN. In addition, the GA-SVM and GA-BPNN also outperform the GA-ELMNN and GA-GRNN in terms of extrapolation performance. In data sensitivity analysis, GA-SVM and GA-BPNN can maintain almost unchanged accuracy when the training sample sizes are 600, 800, and 1000.
- (4)
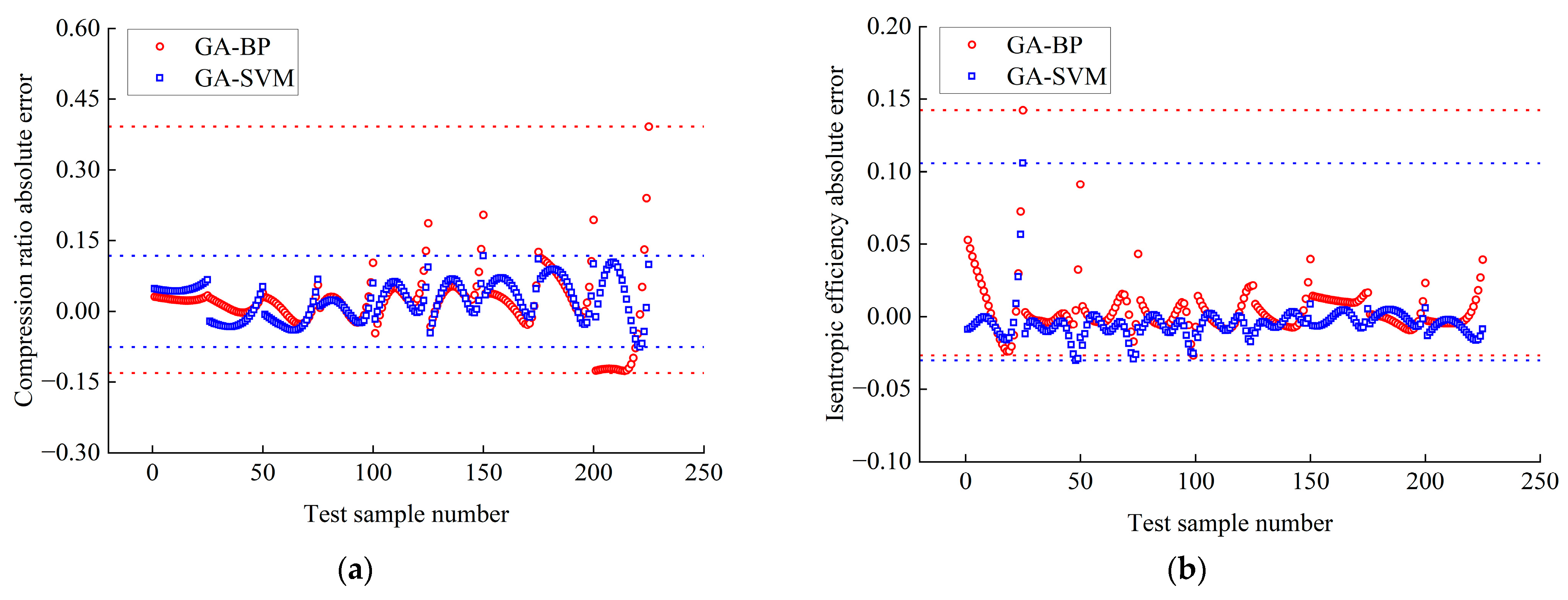
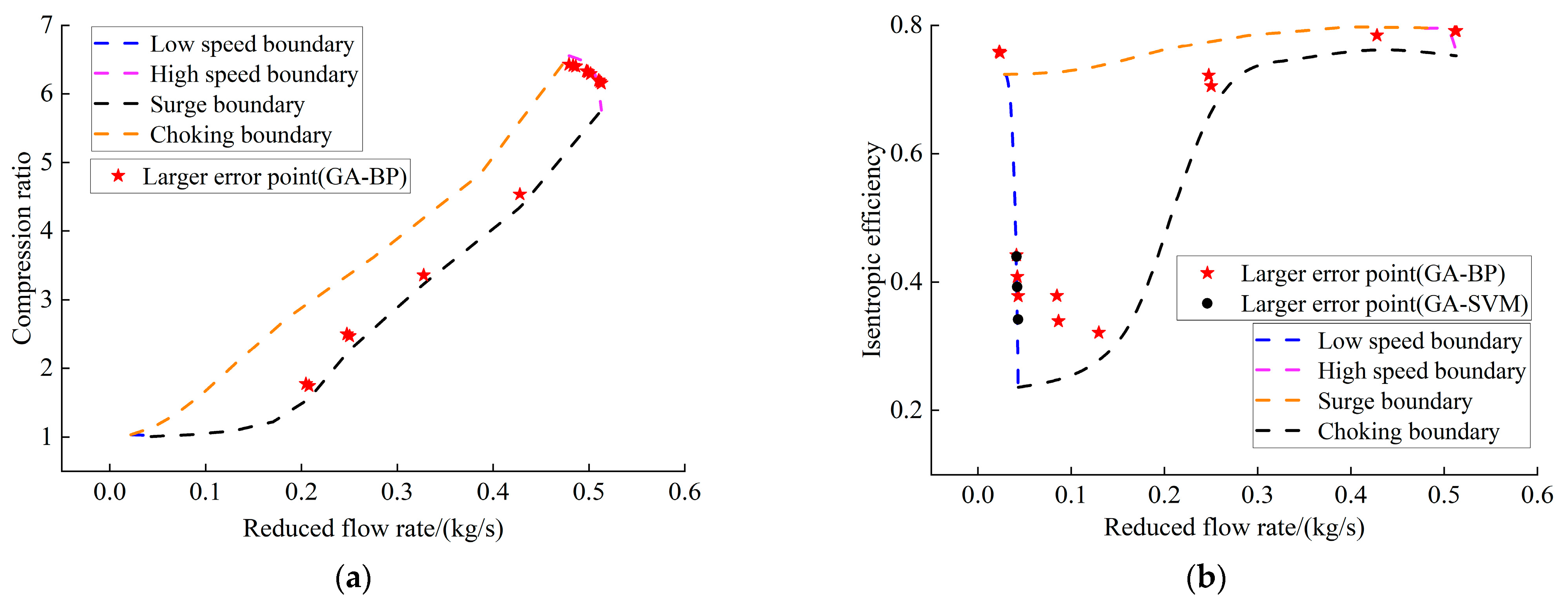
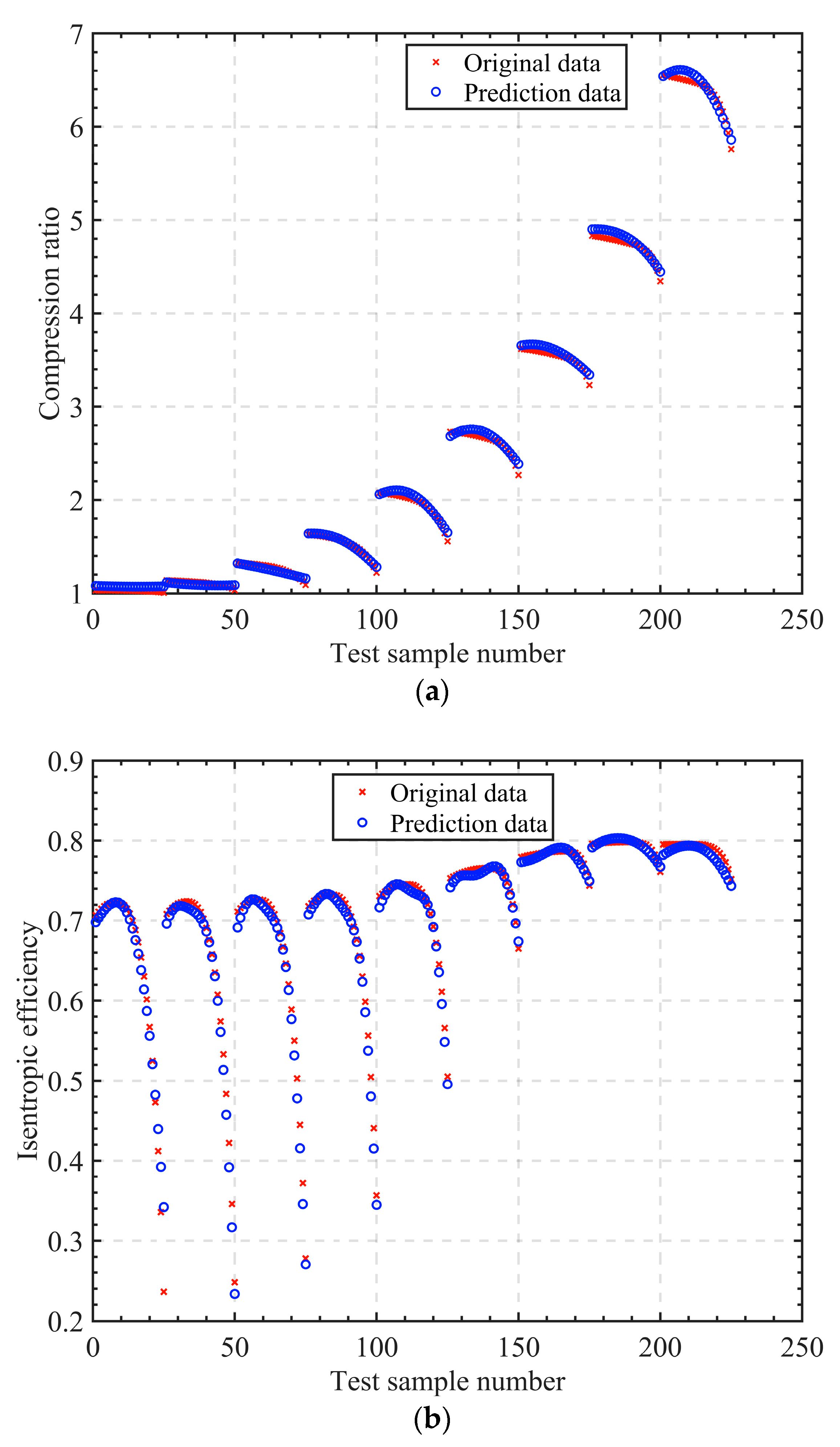
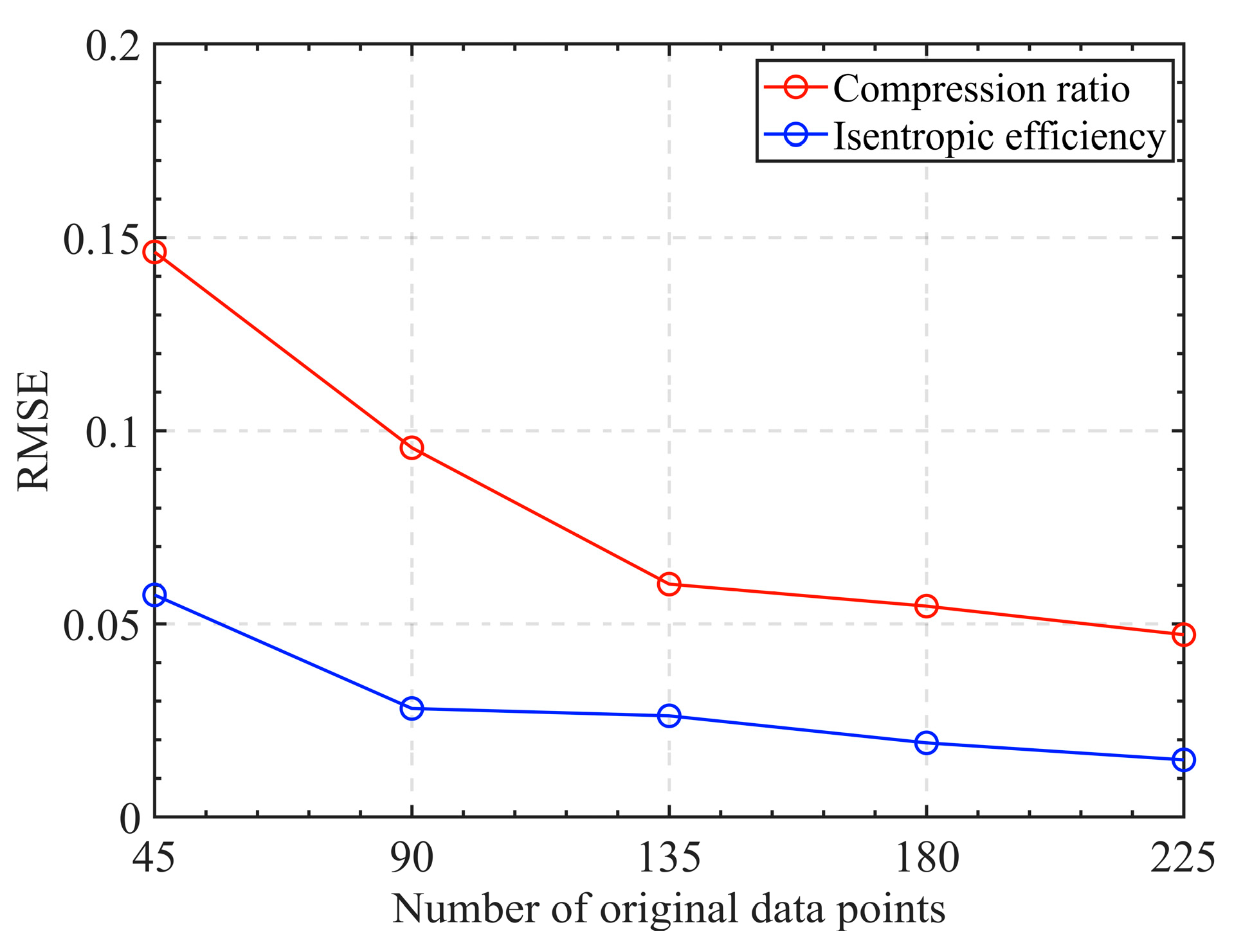
- Analyzing the error size of 225 test data points from GA-SVM and GA-BPNN, it was found that the error band of the GA-BPNN was larger than that of the GA-SVM in terms of the compression ratio and isentropic efficiency prediction results. The GA-SVM needs to be more accurate in predicting boundary data points. After comprehensive comparison and detailed analysis, the generalization of the GA-SVM is better than the GA-BPNN. Furthermore, reducing the number of original data points to 135 still allows the GA-SVM to maintain a high level of predictive accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Chen, J.; Cheng, J.; Xiang, H. Aerodynamic Optimization of Transonic Rotor Using Radial Basis Function Based Deformation and Data-Driven Differential Evolution Optimizer. Aerospace 2022, 9, 508. [Google Scholar] [CrossRef]
- Xin, R.; Zhai, J.; Liao, C.; Wang, Z.; Zhang, J.; Bazari, Z.; Ji, Y. Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine. J. Mar. Sci. Eng. 2022, 10, 985. [Google Scholar] [CrossRef]
- Kovač Kralj, A. Improving Electricity Generation The Product Reaction Loop and the Use of Exhaust Gas for Co-Product Production Using Polyethylene Waste and Flue Gas or Wood. Processes 2022, 10, 2251. [Google Scholar] [CrossRef]
- Kurzke, J.; Riegler, C. A New Compressor Map Scaling Procedure for Preliminary Conceptional Design of Gas Turbines. In Turbo Expo: Power for Land, Sea, & Air; ASME: New York, NY, USA, 2000. [Google Scholar]
- Huang, S.; Yang, C.; Chen, H.; Zhou, N.; Tucker, D. Coupling impacts of SOFC operating temperature and fuel utilization on system net efficiency in natural gas hybrid SOFC/GT system - ScienceDirect. Case Stud. Therm. Eng. 2022, 31, 101868. [Google Scholar] [CrossRef]
- Zhong, M.P. Analysis and optimum design for the transient thermal process of a two-stage compressor under alternating working conditions. Appl. Therm. Eng. 2016, 103, 28–37. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, S.M. Prediction of a Compressor’s Performance Based on Data and Neural Networks. Therm. Turbine 2017, 46, 158–163. [Google Scholar]
- Huang, W.; Chang, J.; Sun, Z.B. Characteristic Curve Prediction of Compressor Based on MEA-BP Neural Network. J. Chongqing Univ. Technol. (Nat. Sci.) 2019, 33, 67–74. [Google Scholar]
- Xie, X.Y.; Lu, Y.M.; Wang, X.F.; Wang, W. Simulation investigation on dynamic performance of single shaft gas turbine based on different compressor characteristic curve prediction methods. J. Eng. Therm. Energy Power 2021, 36, 26–34. [Google Scholar]
- Fang, Y.L.; Liu, D.F.; He, X.; Yu, L.W.; Deng, Z.M. Research on the precise step fitting method of compressor characteristic map. Gas Turbine Exp. Res. 2019, 32, 21–27. [Google Scholar]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. A component map tuning method for performance prediction and diagnostics of gas turbine compressors. Appl. Energy 2014, 135, 572–585. [Google Scholar] [CrossRef]
- Ghorbanian, K.; Gholamrezaei, M. An artificial neural network approach to compressor performance prediction. Appl. Energy 2009, 86, 1210–1221. [Google Scholar] [CrossRef]
- Zheng, H.T.; Pan, F.M.; Yang, R. Performance calculation of compressor based on object-oriented method. J. Aerosp. Power 2014, 29, 140–145. [Google Scholar]
- Lu, X.K.; Zhang, S.J.; Chi, J.L.; Wang, B. Research on the Fitting Method of Compressor Performance Curve based on Genetic Algorithm. J. Eng. Therm. Energy Power 2022, 37, 105–109. [Google Scholar]
- Fei, J.; Zhao, N.; Shi, Y.; Feng, Y.; Wang, Z. Compressor performance prediction using a novel feed-forward neural network based on Gaussian kernel function. Adv. Mech. Eng. 2016, 8, 1687814016628396. [Google Scholar] [CrossRef]
- Gholamrezaei, M.; Ghorbanian, K. Compressor map generation using a feed-forward neural network and rig data. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 97–108. [Google Scholar] [CrossRef]
- Zhou, W.; Lu, S.; Huang, J.; Pan, M.; Chen, Z. A Novel Data-Driven-Based Component Map Generation Method for Transient Aero-Engine Performance Adaptation. Aerospace 2022, 9, 442. [Google Scholar] [CrossRef]
- Ying, Y.; Xu, S.; Li, J.; Zhang, B. Compressor performance modelling method based on support vector machine nonlinear regression algorithm. R. Soc. Open Sci. 2020, 7, 191596. [Google Scholar] [CrossRef]
- Jiang, A.W.; Xie, S.S. Method to achieving compressor characteristics based on support vector machine (SVM) and particle swarm optimization (PSO). J. Aerosp. Power 2010, 25, 2571–2577. [Google Scholar]
- Xu, S.Y.; Ying, Y.L.; Zhou, H.Y.; JIN, Y.F.; XIE, Q.Y. Expression of Compressor Characteristic Line Based on Artificial Bee Colony Optimization Support Vector Machine Parameters. Gas Turbine Technol. 2020, 33, 24–33. [Google Scholar]
- Du, X.; Zhou, K.; Cui, Y.; Wang, J.; Zhou, S. Mapping Mineral Prospectivity Using a Hybrid Genetic Algorithm–Support Vector Machine (GA–SVM) Model. ISPRS Int. J. Geo-Inf. 2021, 10, 766. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Duan, H.; Yin, X.; Kou, H.; Wang, J.; Zeng, K.; Ma, F. Regression prediction of hydrogen enriched compressed natural gas (HCNG) engine performance based on improved particle swarm optimization back propagation neural network method (IMPSO-BPNN). Fuel 2023, 331, 125872. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Shi, C.; Ge, Y.; Wang, S.; Yang, J. Development of cyclic variation prediction model of the gasoline and n-butanol rotary engines with hydrogen enrichment. Fuel 2021, 299, 120891. [Google Scholar] [CrossRef]
- Ji, C.; Wang, H.; Shi, C.; Wang, S.; Yang, J. Multi-objective optimization of operating parameters for a gasoline Wankel rotary engine by hydrogen enrichment. Energy Convers. Manag. 2021, 229, 113732. [Google Scholar] [CrossRef]
- Shen, W.; Guo, X.; Wu, C.; Wu, D. Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm. Knowl.-Based Syst. 2011, 24, 378–385. [Google Scholar] [CrossRef]
- Jing, L.L.; Yu, Y.Q. GNSS-IR soil moisture inversion method based on GA-SVM. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 486–492. [Google Scholar]
- Wang, H.; Ji, C.; Yang, J.; Ge, Y.; Wang, S. Implementation of a novel dual-layer machine learning structure for predicting the intake characteristics of a side-ported Wankel rotary engine. Aerosp. Sci. Technol. 2023, 132, 108042. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Su, T.; Shi, C.; Ge, Y.; Yang, J.; Wang, S. Comparison and implementation of machine learning models for predicting the combustion phases of hydrogen-enriched Wankel rotary engines. Fuel 2022, 310, 122371. [Google Scholar] [CrossRef]









| Parameters | Compression Ratio (Linear) | Compression Ratio (Cubic) | Isentropic Efficiency (Linear) | Isentropic Efficiency (Cubic) |
|---|---|---|---|---|
| 99.9012 | 87.5251 | 99.7891 | 99.2186 | |
| 36.7785 | 34.3228 | 257.0136 | 284.2515 | |
| RMSE | 0.0475 | 0.0466 | 0.0121 | 0.0124 |
| MAE | 0.0395 | 0.0398 | 0.0076 | 0.0081 |
| MAPE | 0.0191 | 0.0203 | 0.0138 | 0.0145 |
| Predictive Variable | Model | GA-ELMNN | GA-BPNN | GA-SVM | GA-GRNN |
|---|---|---|---|---|---|
| Compression ratio | training time (s) | 216.3 | 1626.3 | 218.5 | 677.5 |
| test time (s) | 0.74 | 1.38 | 0.71 | 0.87 | |
| Isentropic efficiency | training time (s) | 1479.5 | 3127.9 | 1421.4 | 1536.7 |
| test time (s) | 0.78 | 2.21 | 1.01 | 0.89 |
| Model | GA-ELMNN | GA-BPNN | GA-SVM | GA-GRNN |
|---|---|---|---|---|
| RMSE | 0.1754 | 0.0844 | 0.0609 | 0.1627 |
| MAE | 0.1453 | 0.0655 | 0.0372 | 0.1406 |
| MAPE | 0.05 | 0.0273 | 0.0159 | 0.0651 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, L.; Liu, R.; Miao, X.; Chen, Y.; Li, S.; Ji, H. Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine. Aerospace 2023, 10, 558. https://doi.org/10.3390/aerospace10060558
Zhong L, Liu R, Miao X, Chen Y, Li S, Ji H. Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine. Aerospace. 2023; 10(6):558. https://doi.org/10.3390/aerospace10060558
Chicago/Turabian StyleZhong, Lingfeng, Rui Liu, Xiaodong Miao, Yufeng Chen, Songhong Li, and Haocheng Ji. 2023. "Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine" Aerospace 10, no. 6: 558. https://doi.org/10.3390/aerospace10060558
APA StyleZhong, L., Liu, R., Miao, X., Chen, Y., Li, S., & Ji, H. (2023). Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine. Aerospace, 10(6), 558. https://doi.org/10.3390/aerospace10060558






