Thermal Simulations of Drilling of Cryogenic Lunar Soils Containing Water Ice
Abstract
1. Introduction
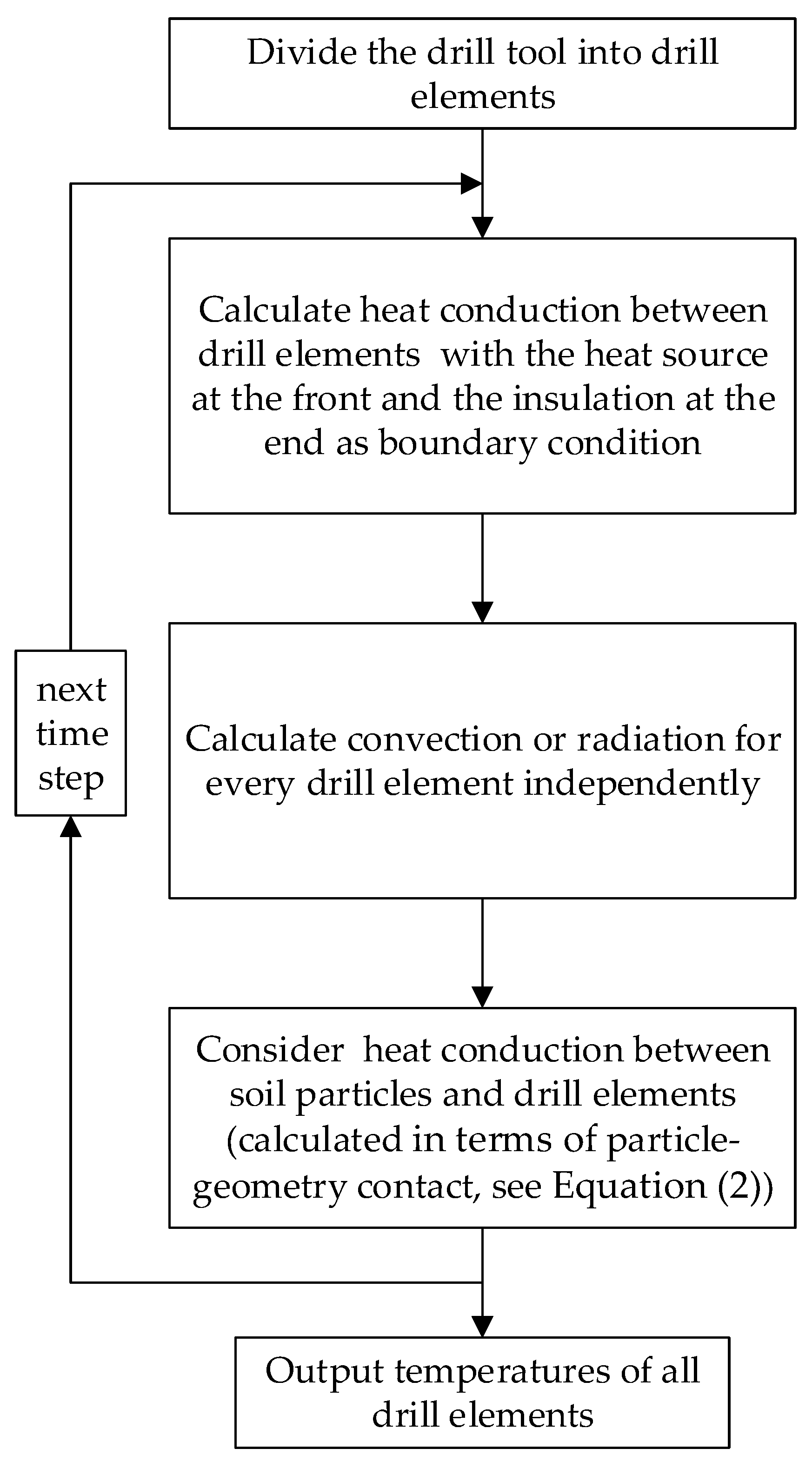
2. Model
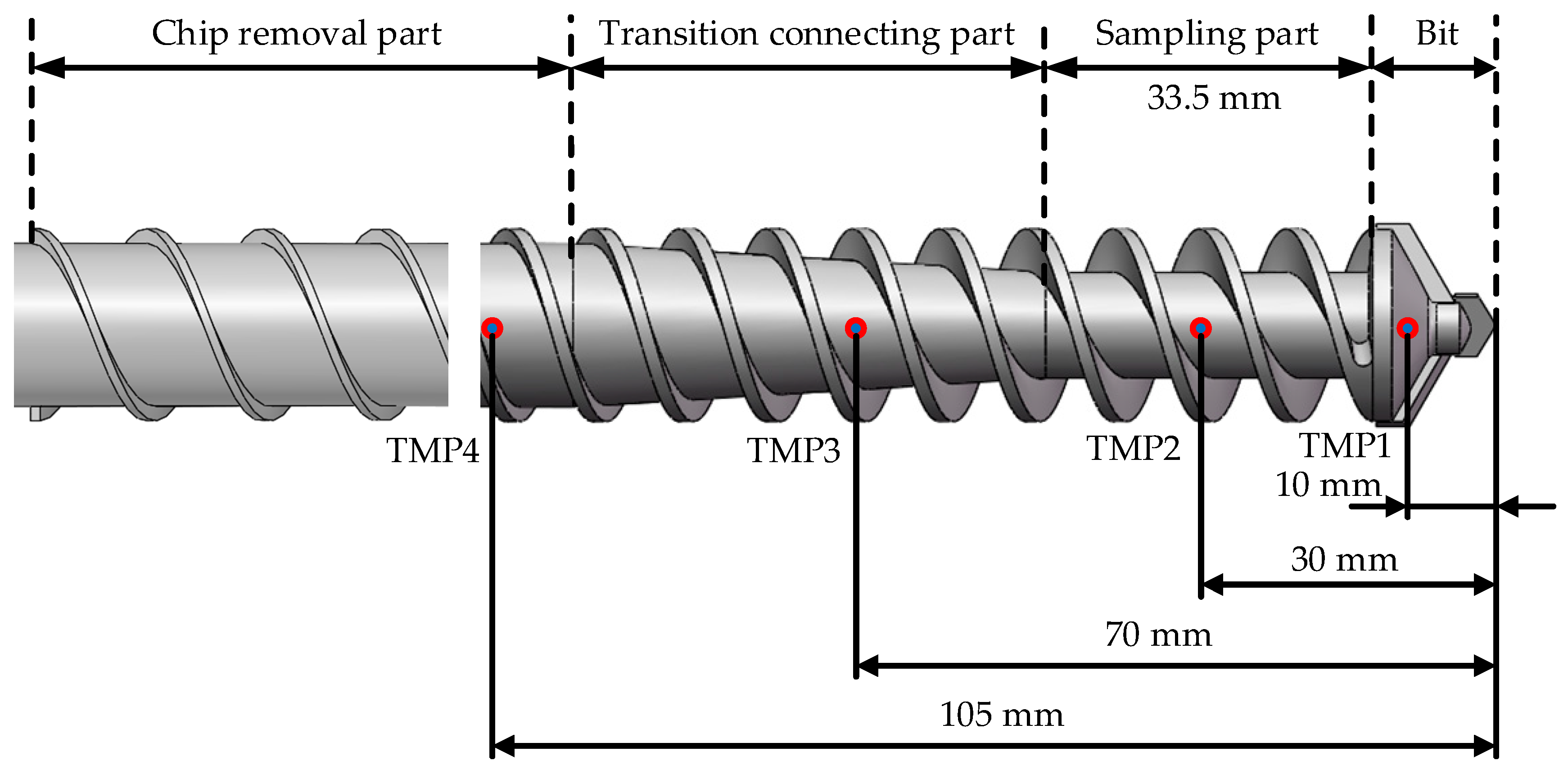
3. Experiment
- Weigh all kinds of particle sizes of anorthosite and basalt and place them in the oven for drying (more than 8 h);
- According to the different materials’ different particle size ratio configurations, put them into the blender for uniform mixing;
- After the mixing of dry soil, the mixing of water into the samples should be allocated according to dry soil and different water content;
- After the completion of mixed water configuration, leave the homogenized seal to stand for 6 to 8 h;
- Use a press to compact the sample five times to the required compactness;
- Sample the samples after compaction to verify the actual moisture content of the samples after preparation;
- Transfer the samples to the secondary refrigeration freezer (−80 °C) for storage after 6–8 h of primary refrigeration (−30 °C). The samples need to undergo secondary refrigeration for 6–8 h before use.
4. DEM Thermal Simulations Based on Experimental Conditions
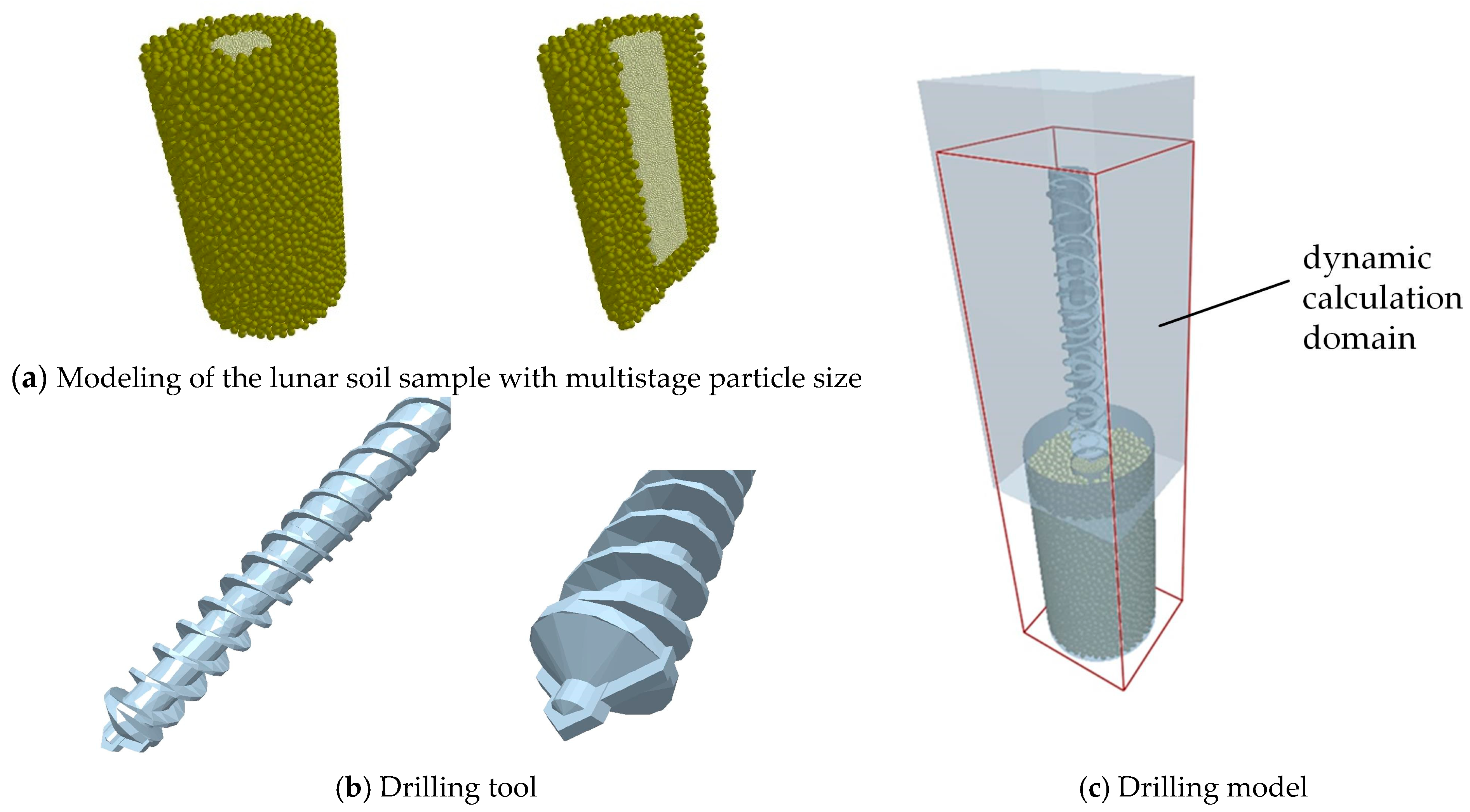
4.1. DEM Model
4.2. Simulation Parameters
- ETCs of the simulated lunar soil were measured. The measured values were the calibration targets.
- The levels of the three factors (i.e., the three parameters that required calibration, specifically particle thermal conductivity, shear modulus, and diameter) were determined, and the CCD matrix was obtained.
- DEM simulations were conducted to measure the ETC of the granular assembly according to the parameters in the CCD matrix.
- The function describing the relationship between these factors and ETC was fitted using variance analysis based on the results of step 3.
- The parameters that provided the fitting results closest to the calibration targets were determined via optimization. These parameters were used as the simulation parameters.
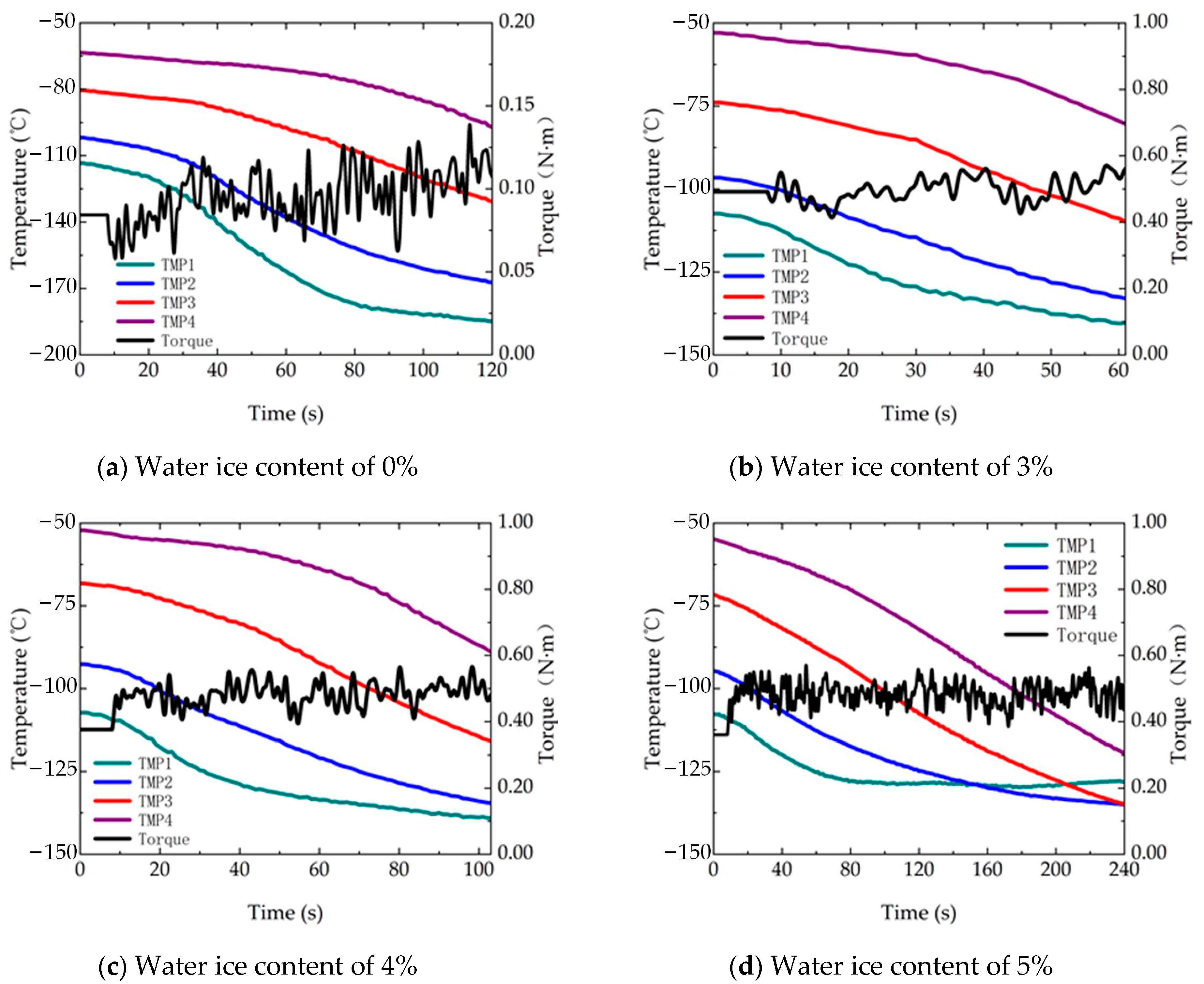
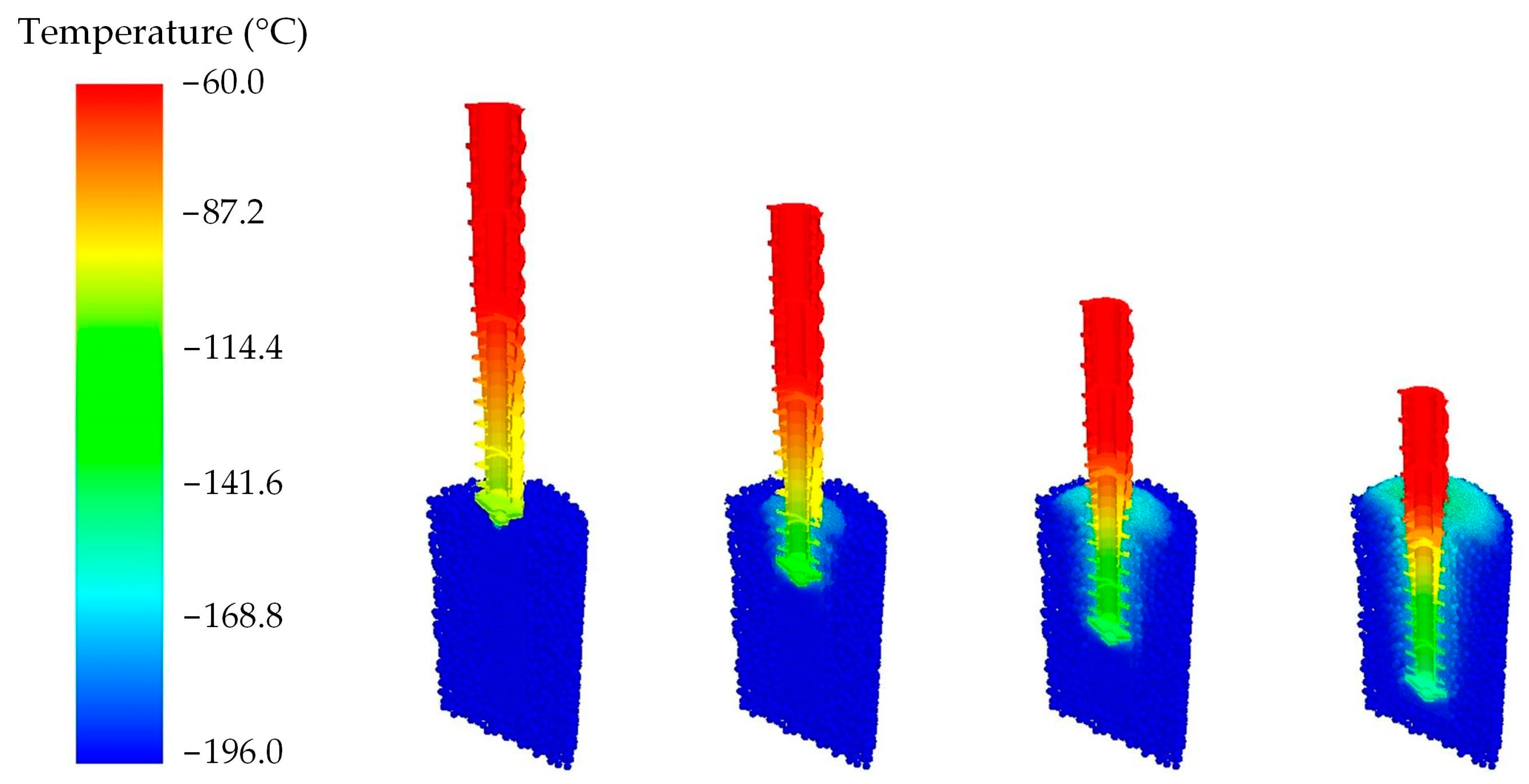
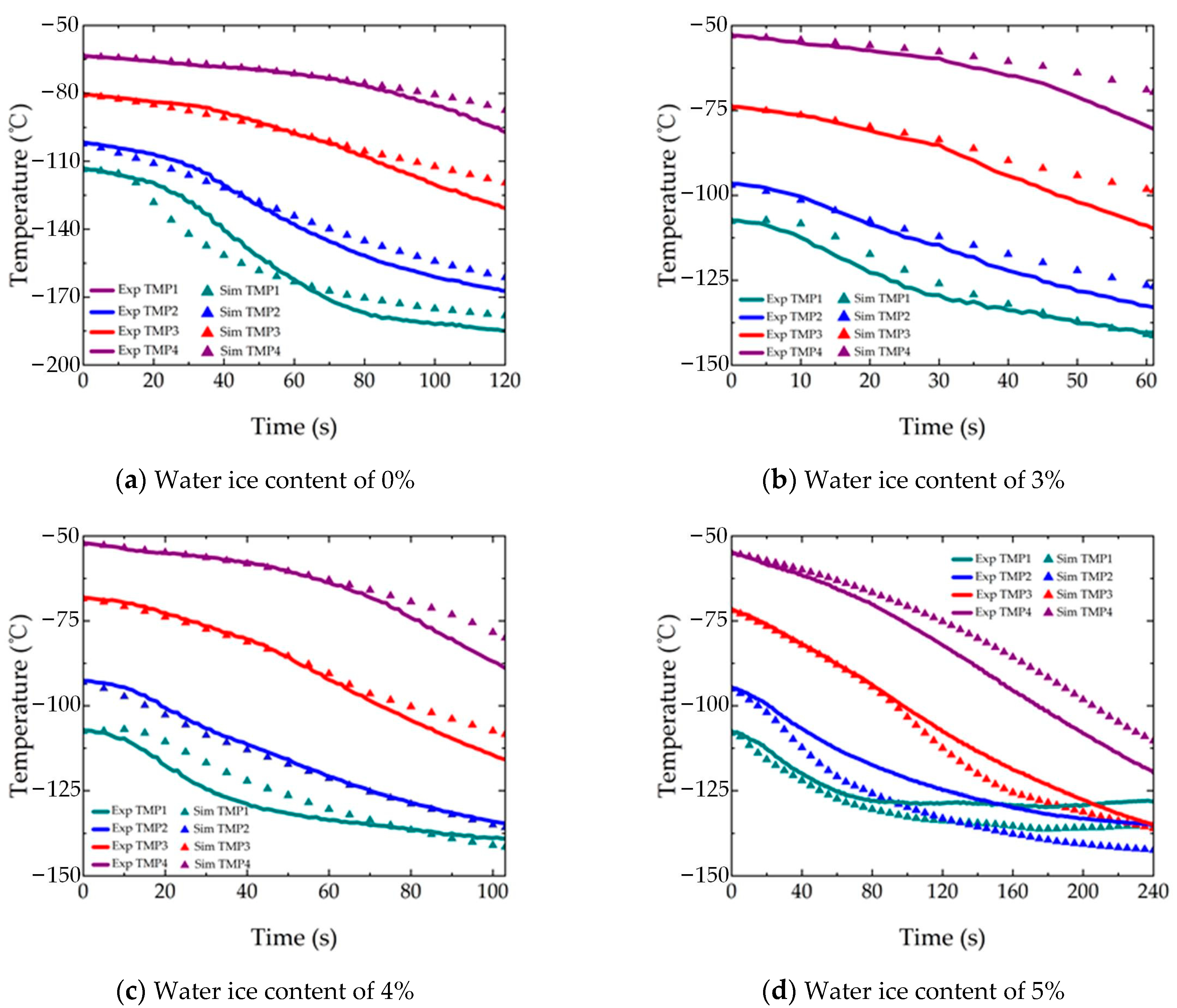
4.3. Results and Analysis
5. DEM Thermal Simulation in a Vacuum
5.1. Drilling Model and Parameter Modification in a Vacuum
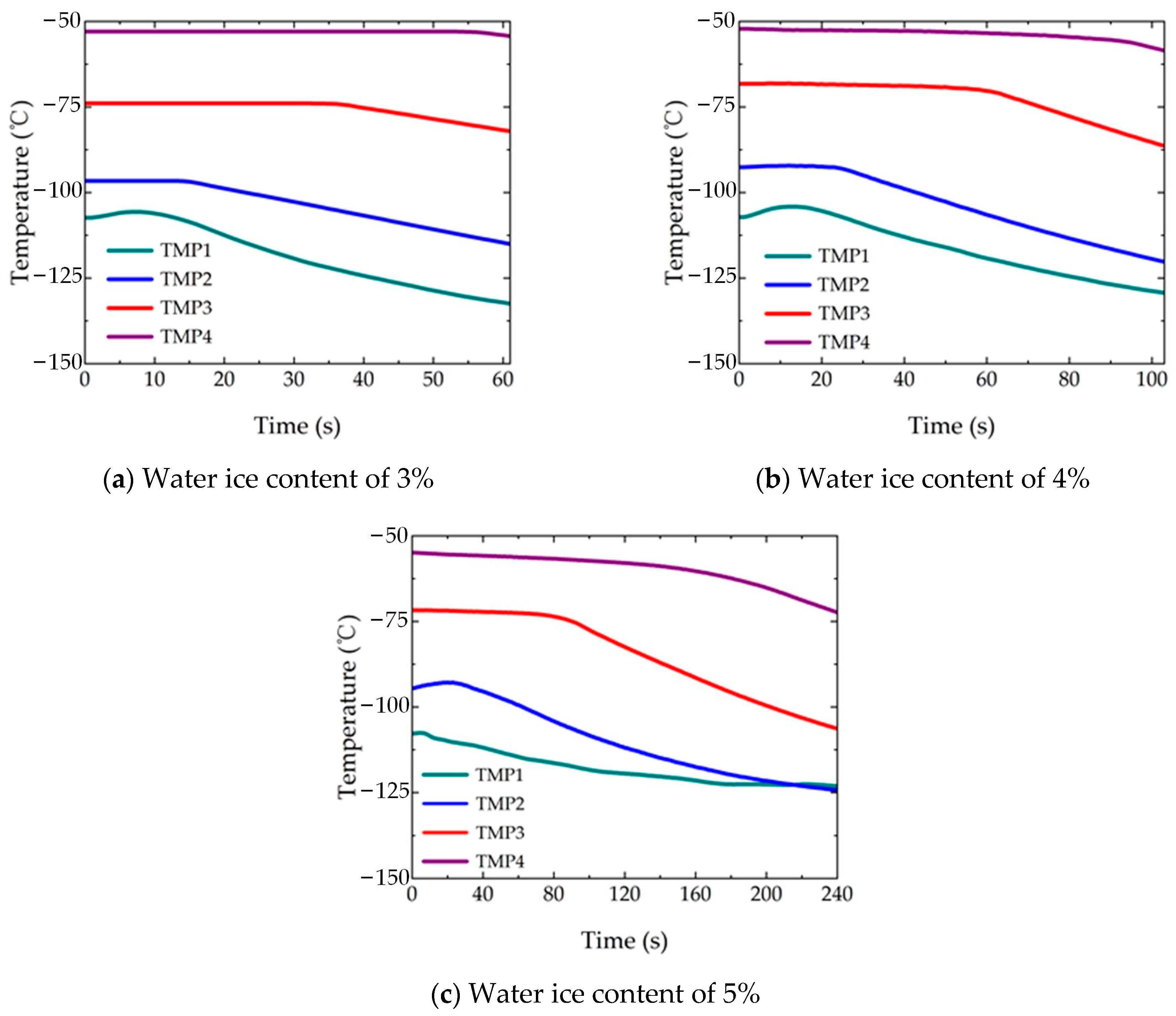
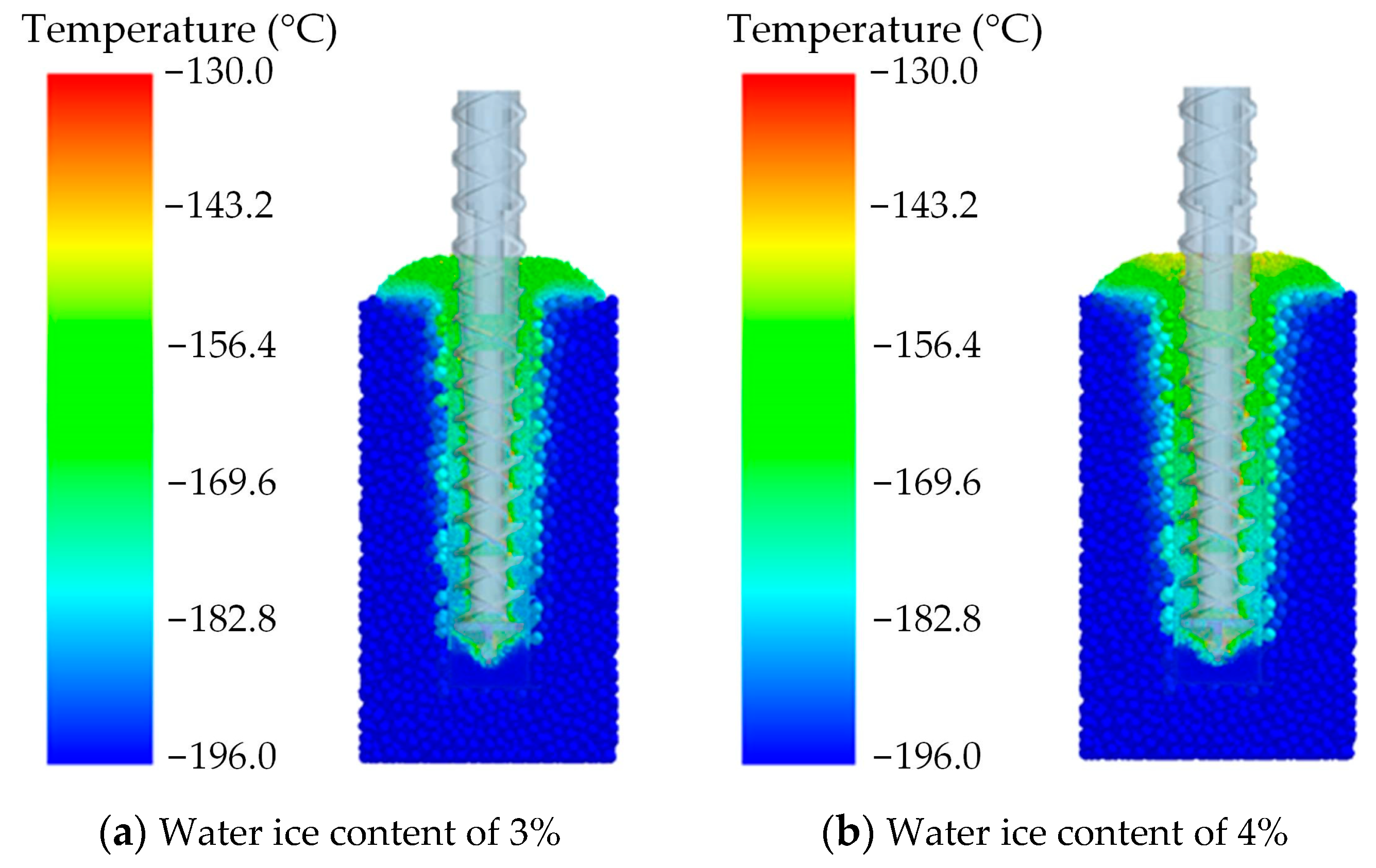
5.2. Results and Analysis
6. Conclusions
- Using parameter calibration, a DEM heat transfer model for drilling cryogenic simulated lunar soil with water ice was established.
- Cryogenic drilling experiments were carried out, and the drilling temperatures of dry soil and lunar soil with the water ice content in the 3–5% range in reasonable procedures assisted by vibration excitation were obtained.
- The thermal simulation of drilling in cryogenic lunar soils with water ice was carried out, and the maximal error was approximately 10 °C, compared with the corresponding experimental results, validating the feasibility and accuracy of the DEM model. The results showed that lunar soil has an obvious cooling effect on the drilling tool, and the temperature of the drilling tool tended to stabilize with drilling. The temperature of lunar soil mainly increased near the drilling tool and during chip removal, which has a small influence range and was within an acceptable range.
- By modifying the model, the drilling simulations of cryogenic lunar soils with water ice in a vacuum were carried out. The results indicated that for reasonable drilling procedures assumed in this paper, compared with the experimental results obtained at atmospheric pressure, the temperature of the drilling tool increased by approximately 10–20 °C, and the maximal temperature in the sampled area increased by approximately 6–8 °C. Furthermore, the contribution of the water ice sublimation-based escape could be safely neglected.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, T.; Wang, B.; Wei, H.; Zhang, Y.; Chao, C.; Xu, K.; Ding, X.; Hou, X.; Zhao, Z. Review on planetary regolith-sampling technology. Prog. Aerosp. Sci. 2021, 127, 100760. [Google Scholar] [CrossRef]
- Liu, T.X.; Zhou, J.; Liang, L.; Zhao, Y.; Cao, D.Q. Investigation of effect of stones on lunar regolith drilling using DEM. Comput. Geotech. 2021, 131, 103958. [Google Scholar] [CrossRef]
- Tang, J.; Yang, T.; Chen, X.; Zhang, Z.; Tian, Y.; Zhang, W.; Jiang, S. Mechanical Characteristics of Lunar Regolith Drilling and Coring and Its Crawling Phenomenon: Analysis and Validation. Aerospace 2022, 9, 709. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, Z.; Liu, S.T.; Li, J.L.; Ding, X.L.; Yin, S.; Wang, G.X.; Lai, X.M. Design and experimental performance verification of a thermal property test-bed for lunar drilling exploration. Chin. J. Aeronaut. 2016, 29, 1455–1468. [Google Scholar] [CrossRef]
- Zhang, T.; Ding, X.L. A thermal model for predicting the drilling temperature in deep lunar regolith exploration. Appl. Therm. Eng. 2018, 128, 911–925. [Google Scholar] [CrossRef]
- Zhang, T.; Ding, X.L.; Liu, S.T.; Xu, K.; Guan, Y.S. Experimental technique for the measurement of temperature generated in deep lunar regolith drilling. Int. J. Heat Mass Tranf. 2019, 129, 671–680. [Google Scholar] [CrossRef]
- Cui, J.S.; Hou, X.Y.; Wen, G.L.; Liang, Z.W. DEM thermal simulation of bit and object in drilling of lunar soil simulant. Adv. Space Res. 2018, 62, 967–975. [Google Scholar] [CrossRef]
- Cui, J.S.; Hou, X.Y.; Wen, G.L.; Liang, Z.W. Thermal simulation of drilling into lunar rock simulant by discrete element method. Acta Astronaut. 2019, 160, 378–387. [Google Scholar] [CrossRef]
- Liu, D.Y.; Zhang, H.; Yang, S.; Yin, C.; Zhang, J.B.; Sun, Q.C.; Lai, X.M. Lunar polar drilling sampling technique. J. Deep Space Explor. 2020, 7, 278–289. (In Chinese) [Google Scholar]
- Vargas, W.L.; McCarthy, J.J. Stress effects on the conductivity of particulate beds. Chem. Eng. Sci. 2002, 57, 3119–3131. [Google Scholar] [CrossRef]
- Vargas, W.L.; McCarthy, J.J. Thermal expansion effects and heat conduction in granular materials. Phys. Rev. E 2007, 76, 041301. [Google Scholar] [CrossRef] [PubMed]
- El Shamy, U.; De Leon, O.; Wells, R. Discrete Element Method Study on Effect of Shear-Induced Anisotropy on Thermal Conductivity of Granular Soils. Int. J. Geomech. 2013, 13, 57–64. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.; Moscardini, M.; Kamlah, M.; Liu, S.L. A DEM-based heat transfer model for the evaluation of effective thermal conductivity of packed beds filled with stagnant fluid: Thermal contact theory and numerical simulation. Int. J. Heat Mass Tranf. 2019, 132, 331–346. [Google Scholar] [CrossRef]
- Gong, Z.; Wu, Y.; Zhu, Z.G.; Wang, Y.; Liu, Z.Y.; Xu, W.X. DEM and dual-probability-Brownian motion scheme for thermal conductivity of multiphase granular materials with densely packed non-spherical particles and soft interphase networks. Comput. Methods Appl. Mech. Eng. 2020, 372, 113372. [Google Scholar] [CrossRef]
- Lee, D.; Pham, K.; Kang, M.; Park, S.; Choi, H. Stepwise DE/FE combined approach for estimating effective thermal conductivity of frozen spherical particulate media. Comput. Geotech. 2020, 128, 103837. [Google Scholar] [CrossRef]
- Calvet, T.; Vanson, J.M.; Masson, R. A DEM/FFT approach to simulate the effective thermal conductivity of granular media. Int. J. Therm. Sci. 2022, 172, 107339. [Google Scholar] [CrossRef]
- Yan, C.Z.; Wei, D.S.; Wang, G. Three-dimensional finite discrete element-based contact heat transfer model considering thermal cracking in continuous-discontinuous media. Comput. Methods Appl. Mech. Eng. 2022, 388, 114228. [Google Scholar] [CrossRef]
- Li, M.X.; Tang, D.W.; Quan, Q.Q.; Zhao, Z.J.; Guo, F.; Meng, L.Z.; Deng, Z.Q. Investigation on the ultimate uplift capacity for asteroid exploration in drilling anchoring process: Numerical modelling and DEM simulation. Adv. Space Res. 2021, 67, 3026–3036. [Google Scholar] [CrossRef]
- Wang, T.Z.; Quan, Q.Q.; Xu, Y.; Yu, H.Y.; Tang, D.W.; Deng, Z.Q. Study the influence of anchoring parameters on asteroid drilling anchoring with discrete element simulation. Adv. Space Res. 2023, 71, 816–828. [Google Scholar] [CrossRef]
- Pelech, T.; Barnett, N.; Dello-Iacovo, M.; Oh, J.; Saydam, S. Analysis of the stability of micro-tunnels in lunar regolith with the Discrete Element Method. Acta Astronaut. 2022, 196, 1–12. [Google Scholar] [CrossRef]
- Pitcher, C.; Alkalla, M.; Pang, X.; Gao, Y. Development of the Third Generation of the Dual-Reciprocating Drill. Biomimetics 2020, 5, 38. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.N.; Tao, L.J.; Zhang, W.W.; Tang, J.Y.; Pang, Y.; Jiang, S.Y. Analysis of the lunar regolith sample obstruction in the Chang’E-5 drill and its improvement. Adv. Space Res. 2022, 69, 2248–2258. [Google Scholar] [CrossRef]
- Liu, T.X.; Liang, L.; Zhao, Y.; Cao, D.Q. Equivalent boundary model of lunar soil drilling simulation by DEM. J. Terramechanics 2020, 91, 85–95. [Google Scholar] [CrossRef]
- Liu, T.X.; Zhou, J.; Liang, L.; Bai, Z.F.; Zhao, Y. Effect of drill bit structure on sample collecting of lunar soil drilling. Adv. Space Res. 2021, 68, 134–152. [Google Scholar] [CrossRef]
- Cui, J.; Kui, L.; Zhang, W.; Zhao, D.; Chang, J. Simulation of Drilling Temperature Rise in Frozen Soil of Lunar Polar Region Based on Discrete Element Theory. Aerospace 2023, 10, 368. [Google Scholar] [CrossRef]
- Zhao, D.; Cheng, Z.; Zhang, W.; Cui, J.; Wang, H. Numerical Modeling of Thermal Behavior during Lunar Soil Drilling. Aerospace 2023, 10, 472. [Google Scholar] [CrossRef]
- Wang, X.W.; Ma, H.Z.; Li, B.; Li, T.J.; Xia, R.; Bao, Q.B. Review on the research of contact parameters calibration of particle system. J. Mech. Sci. Technol. 2022, 36, 1363–1378. [Google Scholar] [CrossRef]
- Deng, Z.Q.; Cui, J.S.; Hou, X.Y.; Jiang, S.Y. Calibration of Discrete Element Heat Transfer Parameters by Central Composite Design. Chin. J. Mech. Eng. 2017, 30, 419–427. [Google Scholar] [CrossRef]
- Gupta, A.; Kavakbasi, B.T.; Dutta, B.; Grabowski, B.; Peterlechner, M.; Hickel, T.; Divinski, S.V.; Wilde, G.; Neugebauer, J. Low-temperature features in the heat capacity of unary metals and intermetallics for the example of bulk aluminum and Al3Sc. Phys. Rev. B 2017, 95, 094307. [Google Scholar] [CrossRef]
- Formisano, M.; De Sanctis, M.C.; De Angelis, S.; Carpenter, J.D.; Sefton-Nash, E. PROSPECTING the Moon: Numerical simulations of temperature and sublimation rate of a cylindric sample. Planet. Space Sci. 2019, 169, 8–14. [Google Scholar] [CrossRef]
- Metzger, P.T.; Zacny, K.; Morrison, P. Thermal Extraction of Volatiles from Lunar and Asteroid Regolith in Axisymmetric Cranka-Nicolson Modeling. J. Aerosp. Eng. 2020, 33, 04020075. [Google Scholar] [CrossRef]



| Mineral Class (Proportion) | Particle Size Range | Proportion |
|---|---|---|
| Anorthosite (70%) | 0.025–0.05 mm | 31.568% |
| 0.05–0.075 mm | 6.797% | |
| 0.075–0.1 mm | 10.545% | |
| 0.25–0.5 mm | 10.545% | |
| 0.5–1 mm | 10.545% | |
| Basalt (30%) | 0.025–0.05 mm | 13.502% |
| 0.05–0.075 mm | 2.920% | |
| 0.075–0.1 mm | 4.526% | |
| 0.25–0.5 mm | 4.526% | |
| 0.5–1 mm | 4.526% |
| No. | Water Ice Content | Rotational Speed (rpm) | Feed Rate (mm/min) | WOB (N) | Impact Frequency (Hz) | Impact Energy (J) | Drilling Depth (mm) | Time (s) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 wt% | 120 | 50 | -- | 0 | 0 | 100 | 120 |
| 2 | 3 wt% | 120 | 98.4 | 190 | 5 | 2 | 100 | 61 |
| 3 | 4 wt% | 120 | 58.3 | 190 | 5 | 2 | 100 | 103 |
| 4 | 5 wt% | 120 | 25.0 | 190 | 5 | 2 | 100 | 240 |
| Parameters | Values |
|---|---|
| Particle thermal conductivity (W/m·K) | 2.1/6.2/8.1/10.0 [27,28] |
| Particle specific heat (J/kg·°C) | 200.0/257.5/277.7/297.9 |
| Particle diameter (mm) | 1.0/3.6 |
| Number of particles | 56,102 |
| Particle density (kg/m3) | 3 × 103 |
| Particle shear modulus (Pa) | 4 × 107 |
| Particle Poisson’s ratio | 0.25 |
| Geometry thermal conductivity (W/m·K) | 12.7 (−100 °C) [29] |
| Geometry specific heat (J/kg·°C) | 376 (−100 °C) [29] |
| Geometry density (kg/m3) | 7.85 × 103 |
| Geometry shear modulus (Pa) | 8 × 1010 |
| Geometry Poisson’s ratio | 0.25 |
| Friction coefficient between particles | 0.48 |
| Friction coefficient between particle and geometry | 0.5 |
| Drilling depth (mm) | 100 |
| Rotational speed (rpm) | 120 |
| Feed rate (mm/min) | 50/98.4/58.3/25.0 |
| Initial temperature (°C) | −196 |
| Air convection coefficient (W/m2·K) | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Chen, B.; Liu, S.; Zhao, D.; Zhang, W. Thermal Simulations of Drilling of Cryogenic Lunar Soils Containing Water Ice. Aerospace 2023, 10, 510. https://doi.org/10.3390/aerospace10060510
Cui J, Chen B, Liu S, Zhao D, Zhang W. Thermal Simulations of Drilling of Cryogenic Lunar Soils Containing Water Ice. Aerospace. 2023; 10(6):510. https://doi.org/10.3390/aerospace10060510
Chicago/Turabian StyleCui, Jinsheng, Baoxian Chen, Sibo Liu, Deming Zhao, and Weiwei Zhang. 2023. "Thermal Simulations of Drilling of Cryogenic Lunar Soils Containing Water Ice" Aerospace 10, no. 6: 510. https://doi.org/10.3390/aerospace10060510
APA StyleCui, J., Chen, B., Liu, S., Zhao, D., & Zhang, W. (2023). Thermal Simulations of Drilling of Cryogenic Lunar Soils Containing Water Ice. Aerospace, 10(6), 510. https://doi.org/10.3390/aerospace10060510






