Sectional Leading Edge Vortex Lift and Drag Coefficients of Autorotating Samaras
Abstract
1. Introduction
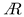 ), since with higher
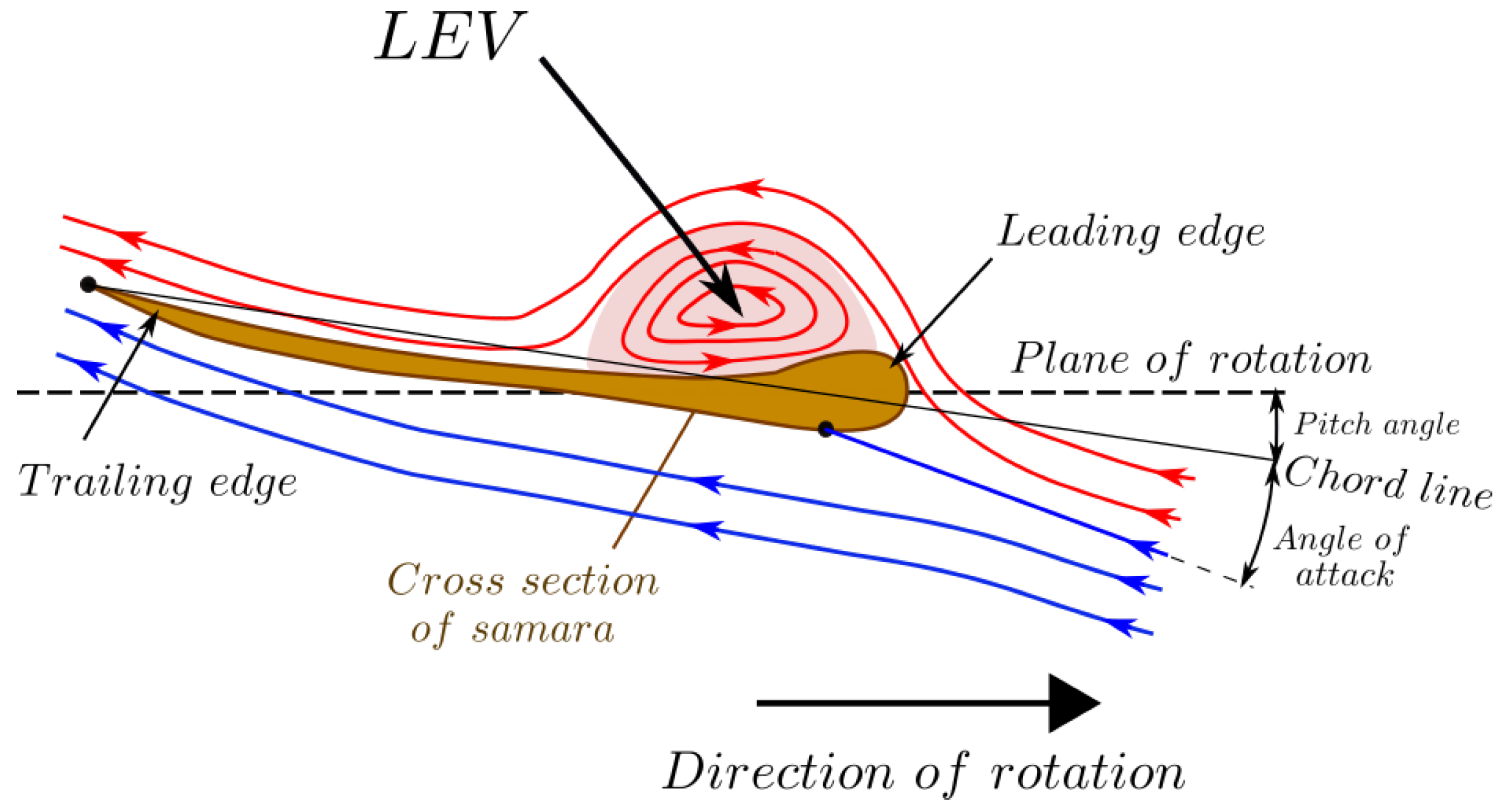
), since with higher 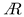 , also scales up, leading to a LEV that cannot be stabilised [38,40,41]. All of these conditions together mean that the LEV tends to be restricted to flight conditions of low Reynolds number (the Reynolds number () is a measure of the ratio of inertial to viscous forces) of or lower. In contrast, helicopters have high aspect ratio blades and operate at too high Reynolds numbers to maintain a stable LEV.
, also scales up, leading to a LEV that cannot be stabilised [38,40,41]. All of these conditions together mean that the LEV tends to be restricted to flight conditions of low Reynolds number (the Reynolds number () is a measure of the ratio of inertial to viscous forces) of or lower. In contrast, helicopters have high aspect ratio blades and operate at too high Reynolds numbers to maintain a stable LEV.2. Sectional Lift and Drag Coefficient Models
2.1. The Normal Force Model
2.2. The Polhamus Model
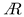 = 4.38 and having NACA0005 aerofoil as a cross-section. Similarly, if the analysis is extended to a range of aspect ratios then the variation of and can be calculated, as illustrated in Figure 4. The NACA0005 aerofoil was used as it has a similar thickness to chord ratio as to a natural samara cross-section, as shown in Figure 5, despite the fact that the natural samara possesses a complex aerofoil that is extremely thin with a thick leading edge and with a rugged profile [19].
= 4.38 and having NACA0005 aerofoil as a cross-section. Similarly, if the analysis is extended to a range of aspect ratios then the variation of and can be calculated, as illustrated in Figure 4. The NACA0005 aerofoil was used as it has a similar thickness to chord ratio as to a natural samara cross-section, as shown in Figure 5, despite the fact that the natural samara possesses a complex aerofoil that is extremely thin with a thick leading edge and with a rugged profile [19].2.3. Adapted 2D Polhamus Model

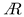 = 4 wing and for a periodic wake without flapping [67].
= 4 wing and for a periodic wake without flapping [67].3. Samara Numerical Model
4. Assessment of LEV Lift Models Using Data from the Literature
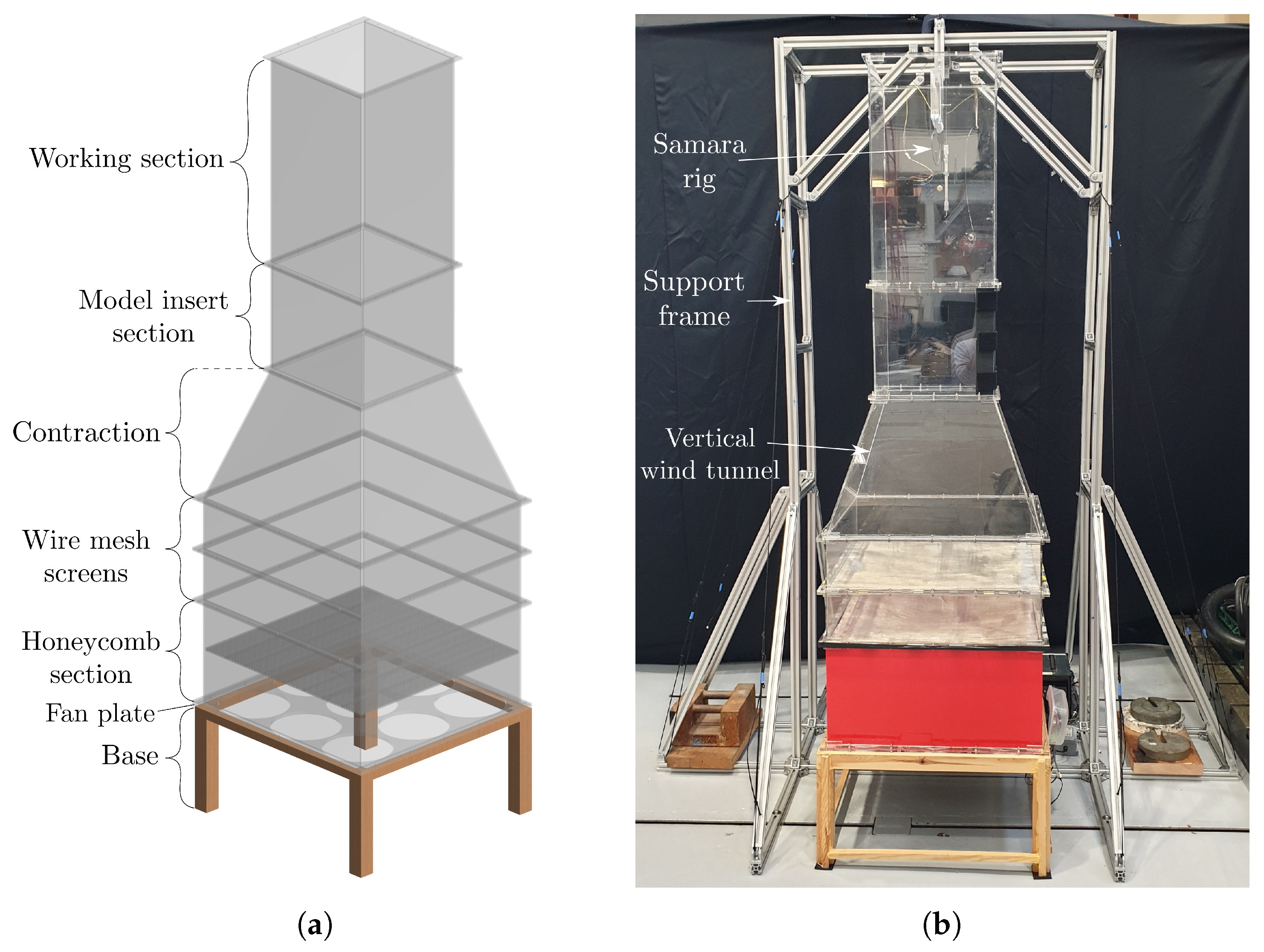
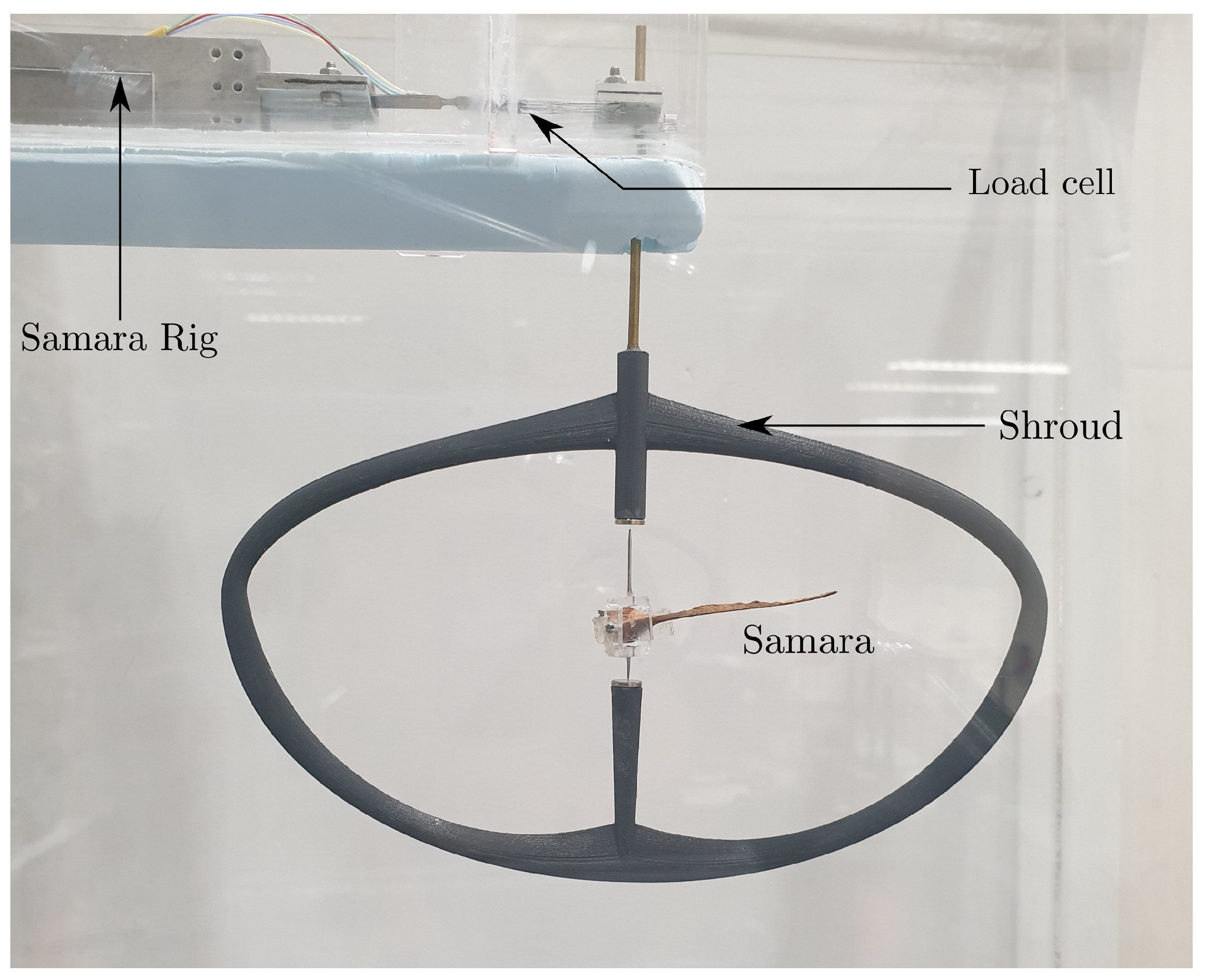
5. Description of Wind Tunnel Experiments
6. Results and Discussion
6.1. Numerical Analysis of Sycamore A Using the Normal Force Model
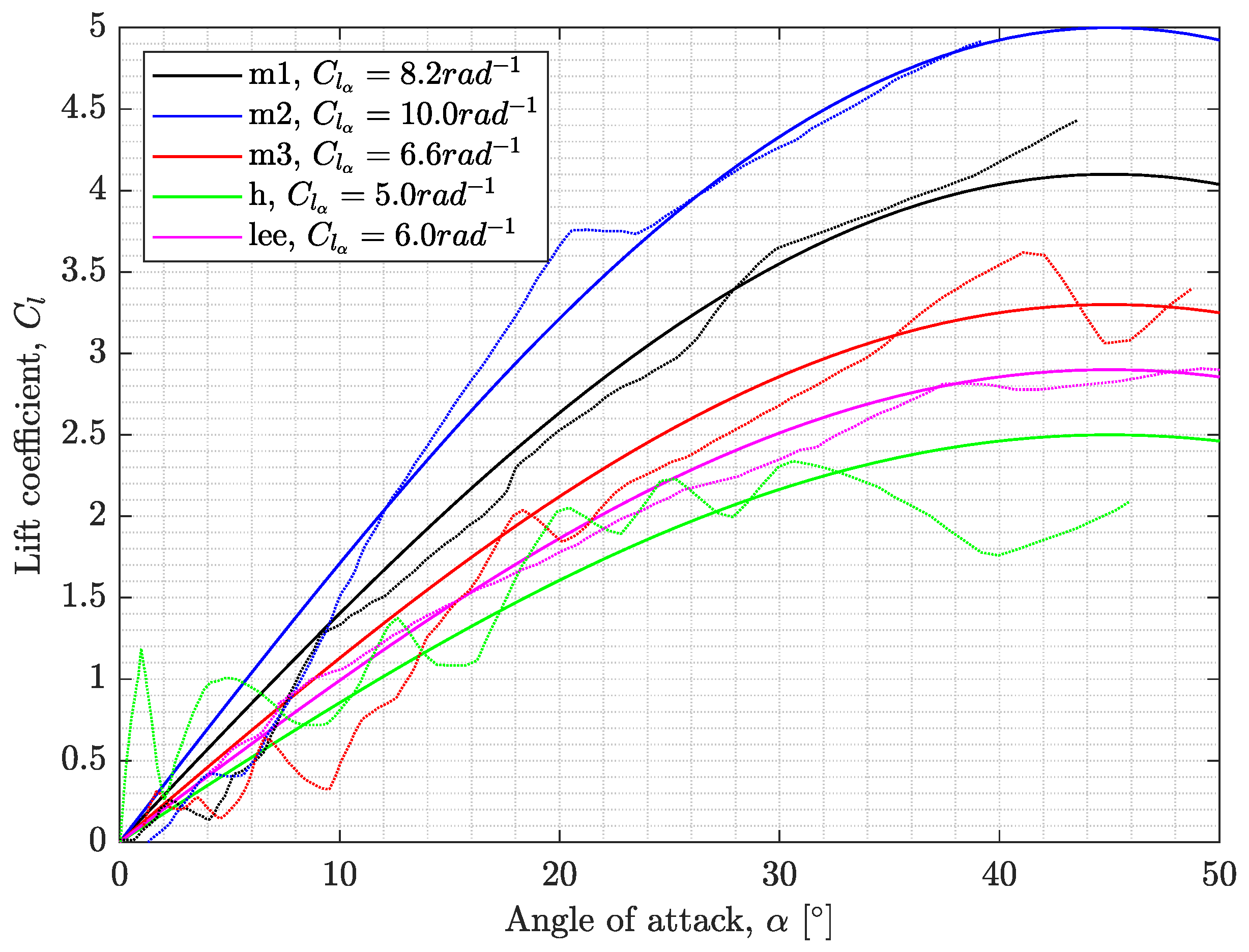
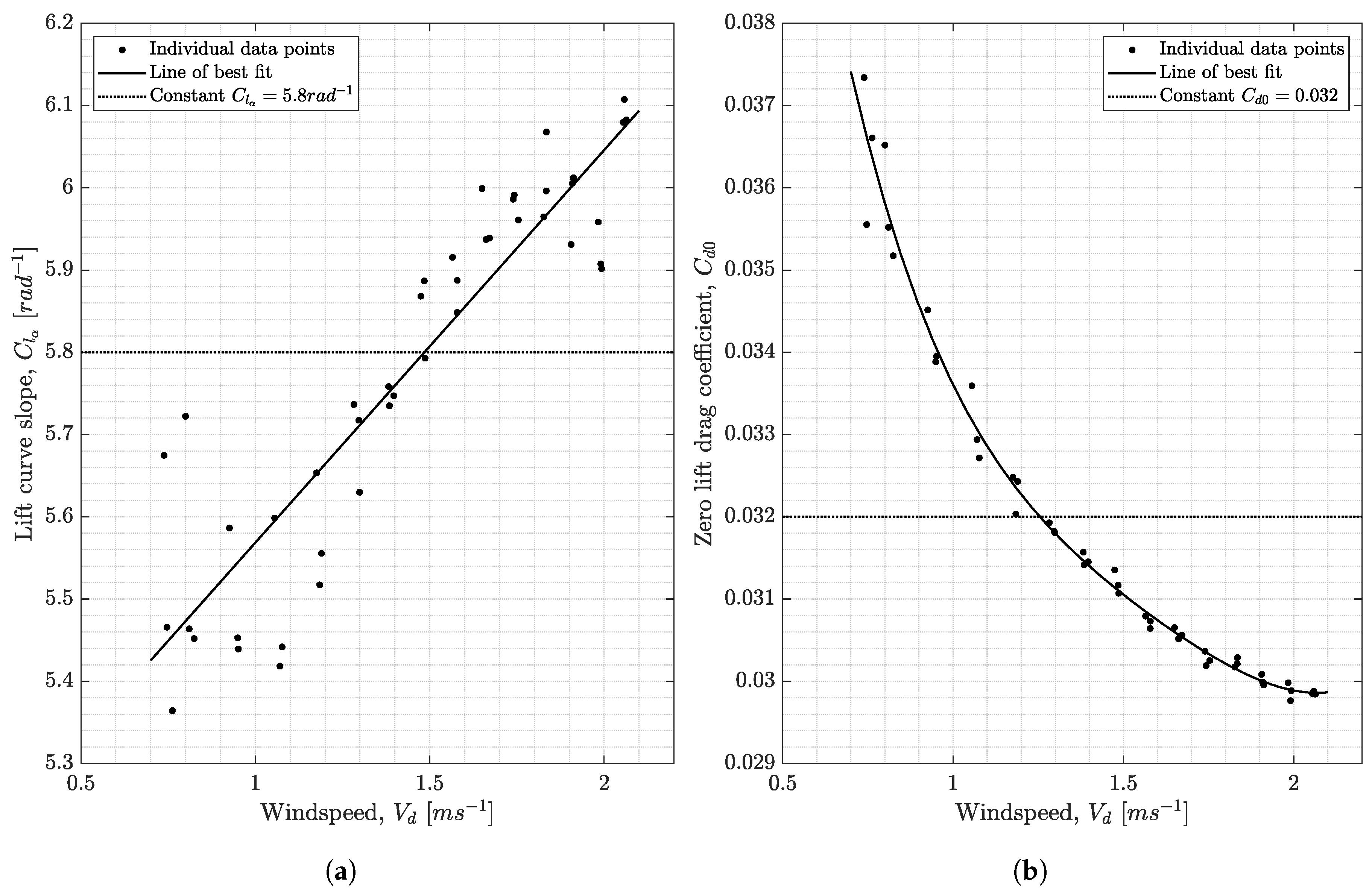
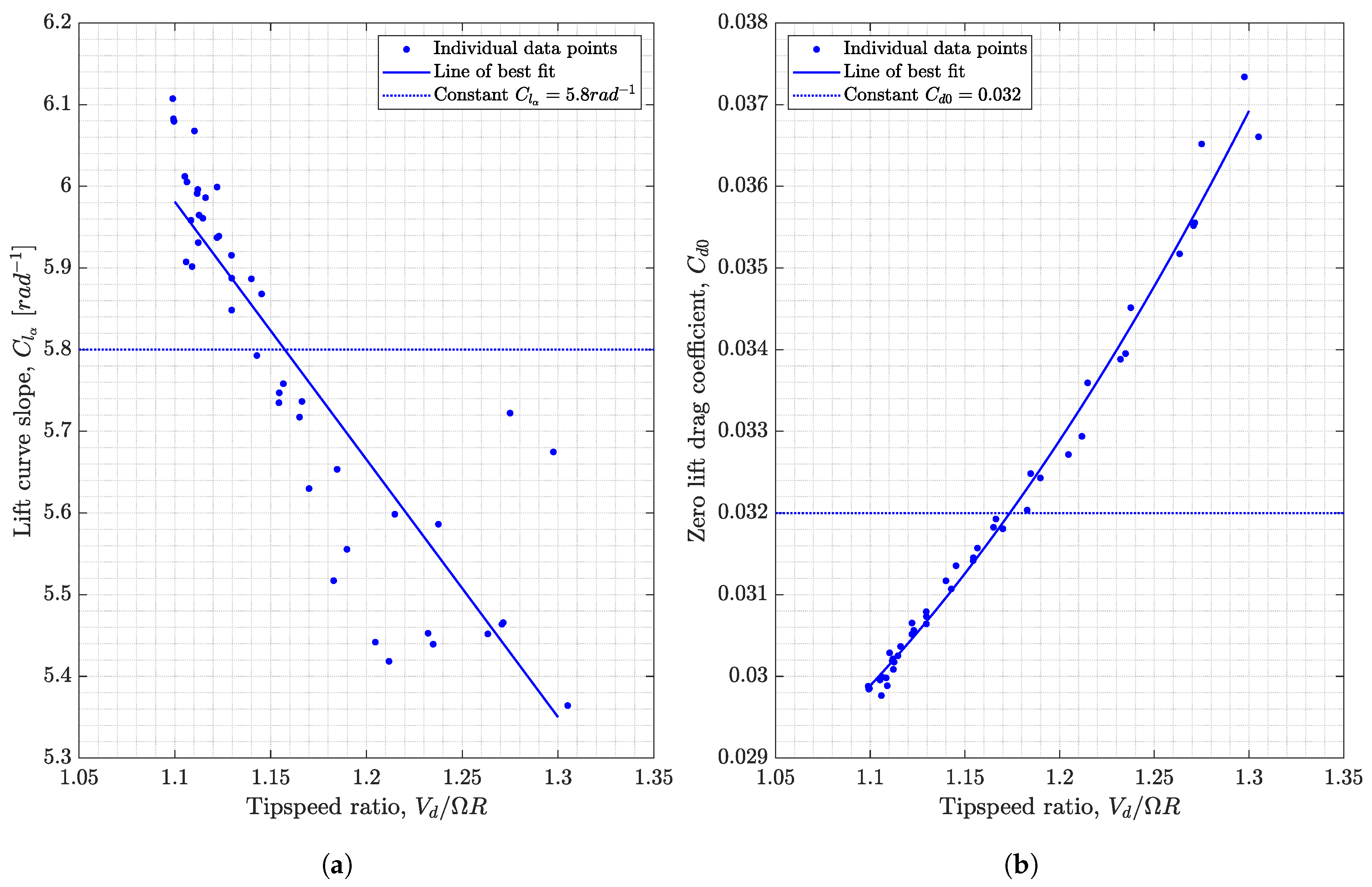
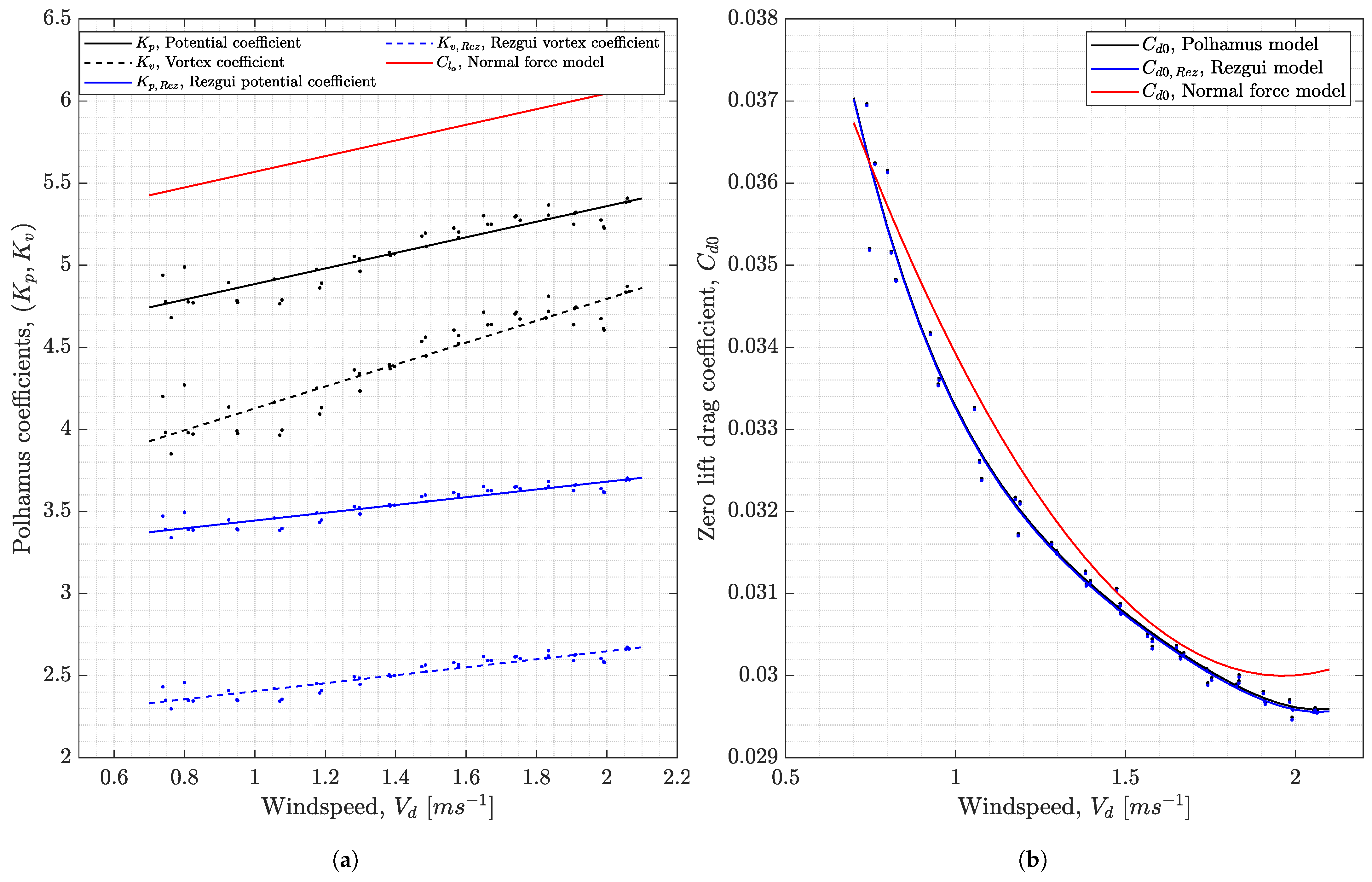
6.2. Predicting Lift Curve Slope and Zero-Lift Drag Coefficient for Each Experimental Data Point
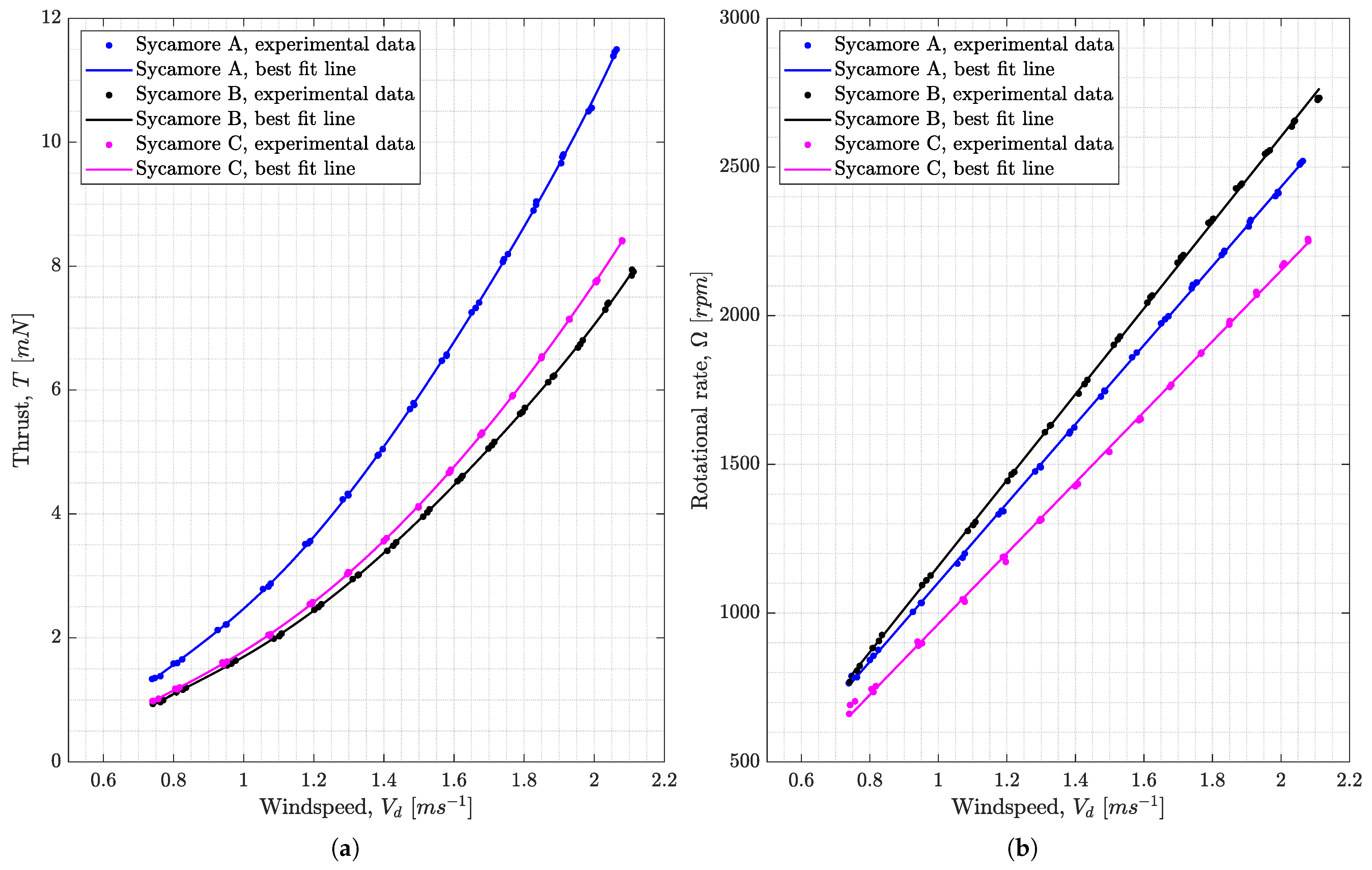
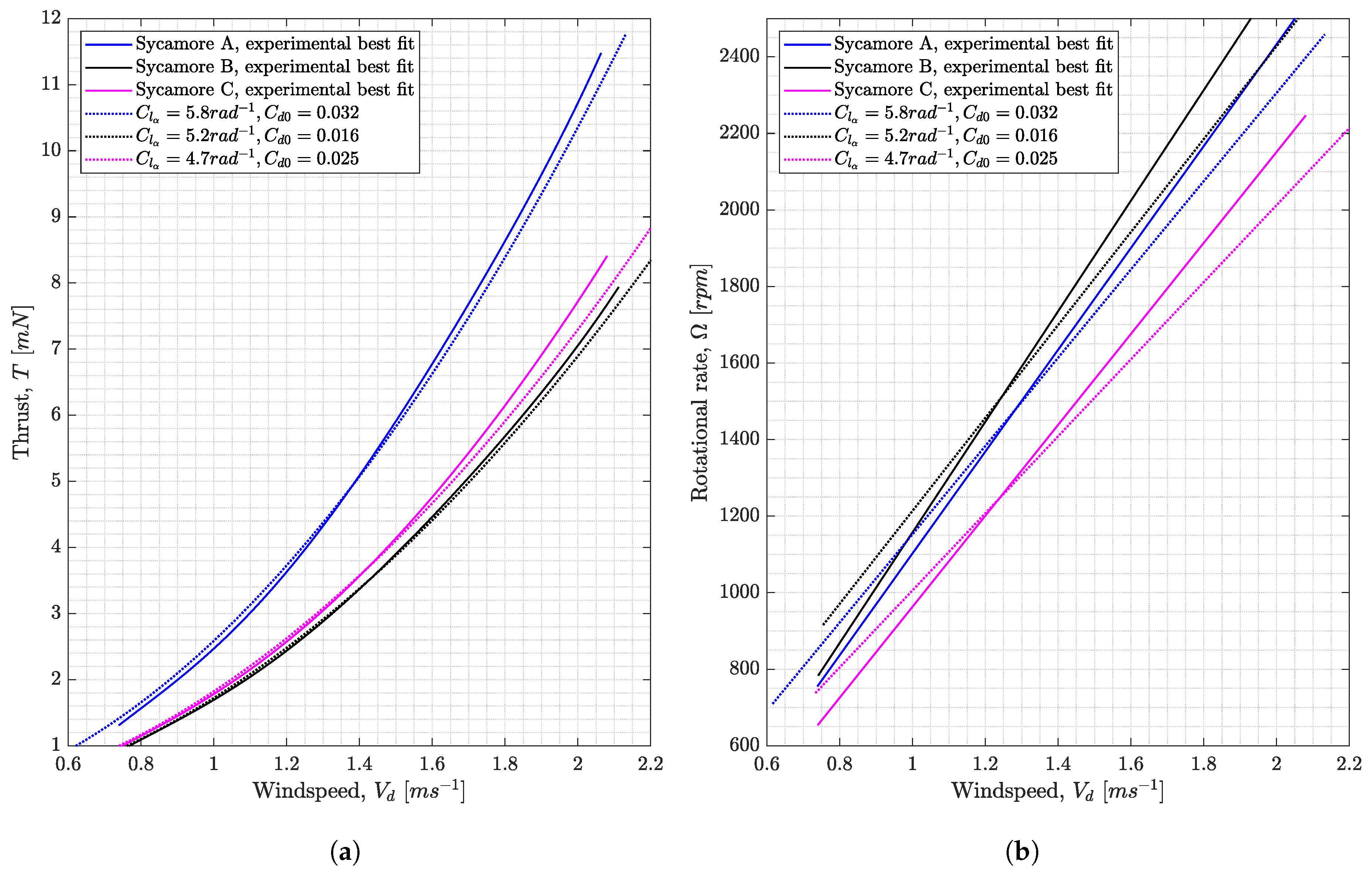
6.3. Numerical Analysis for Sycamore B and C
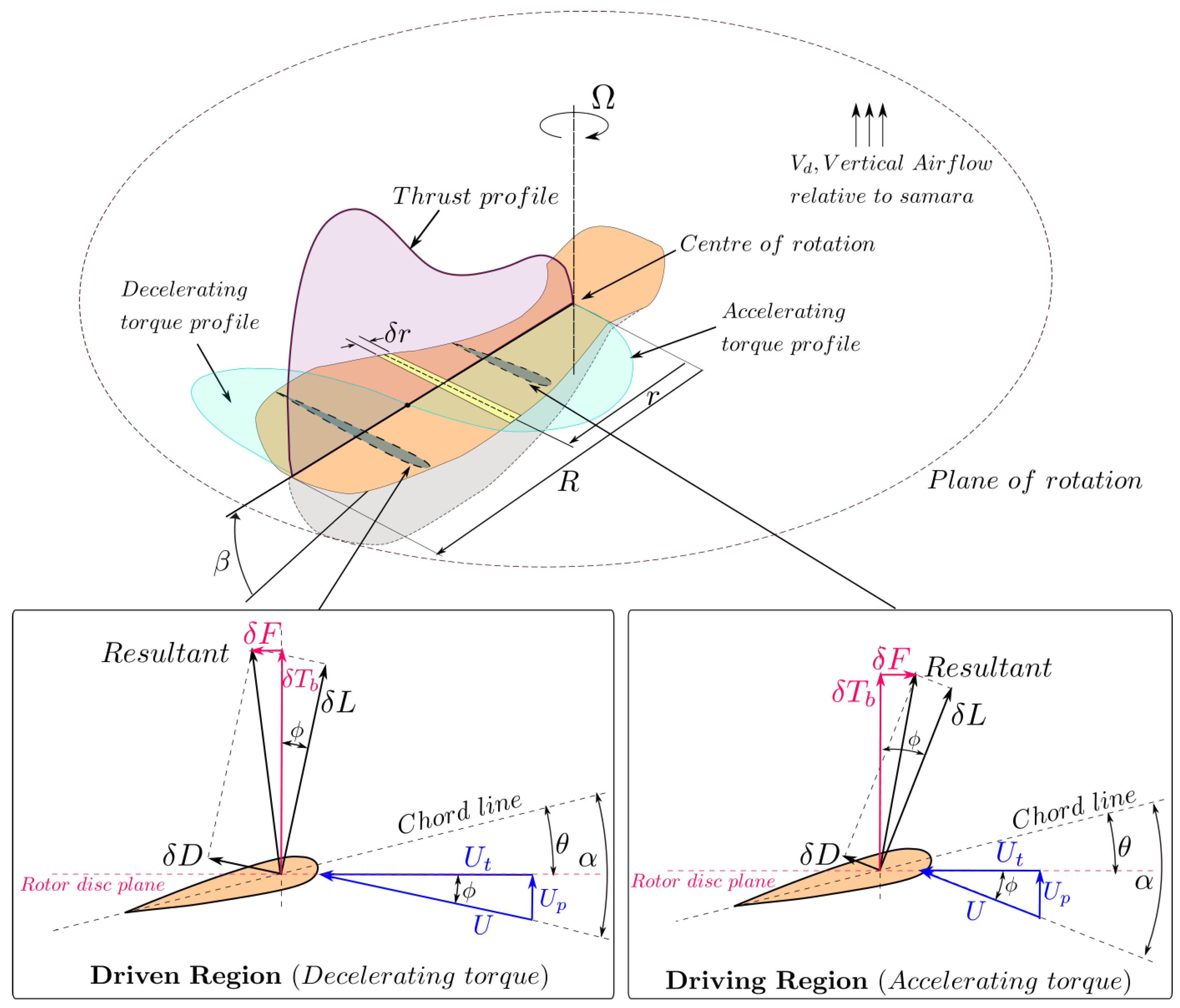
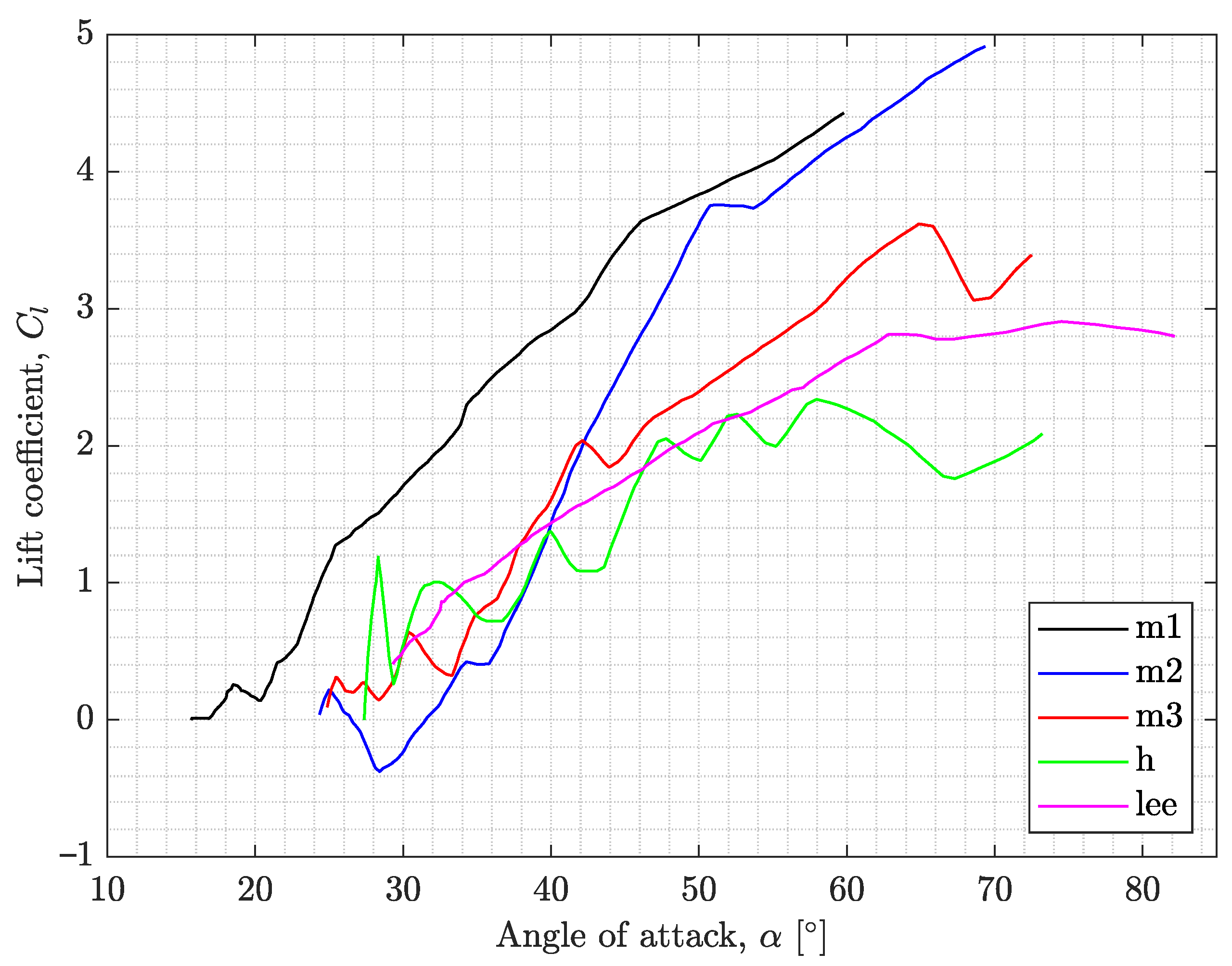
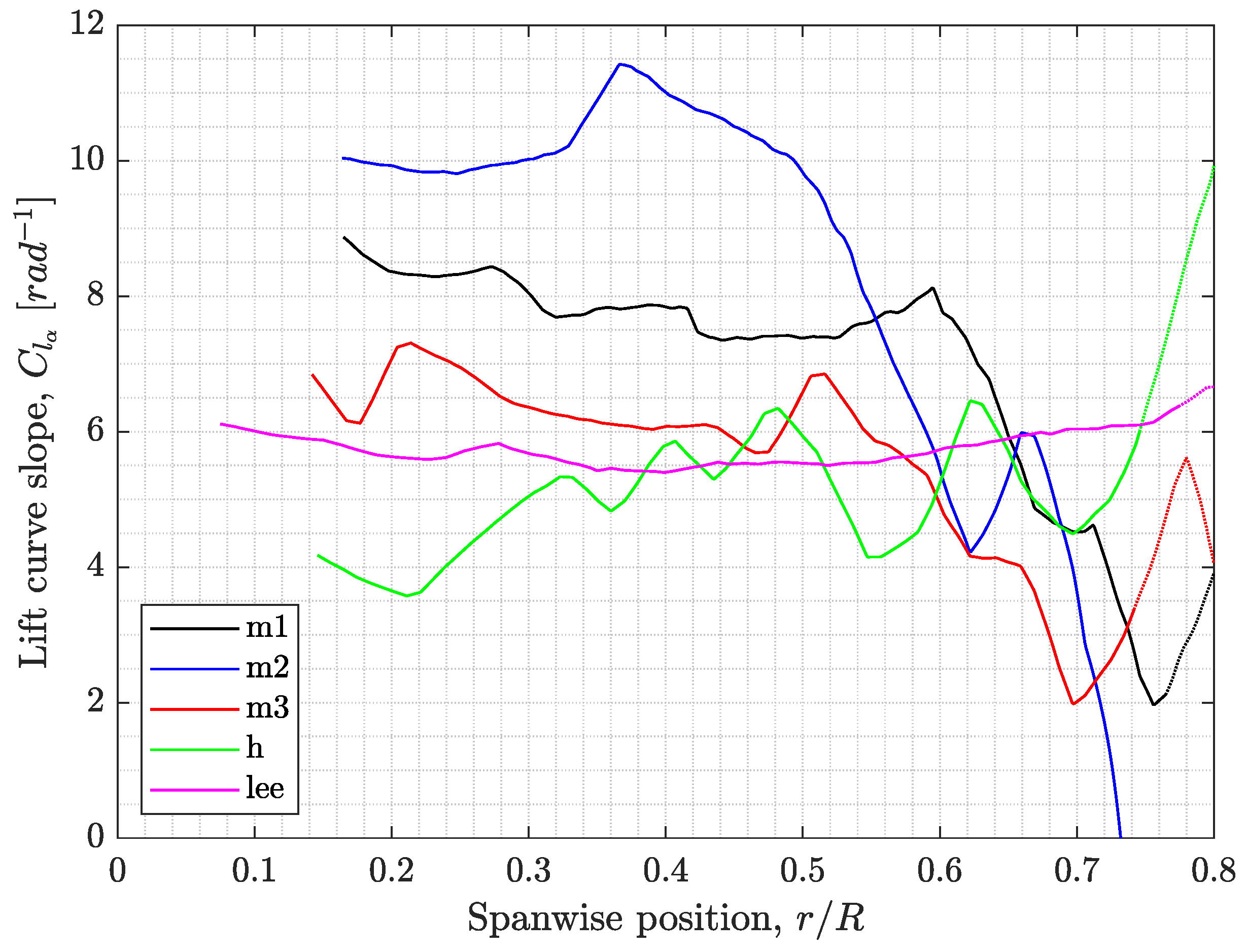
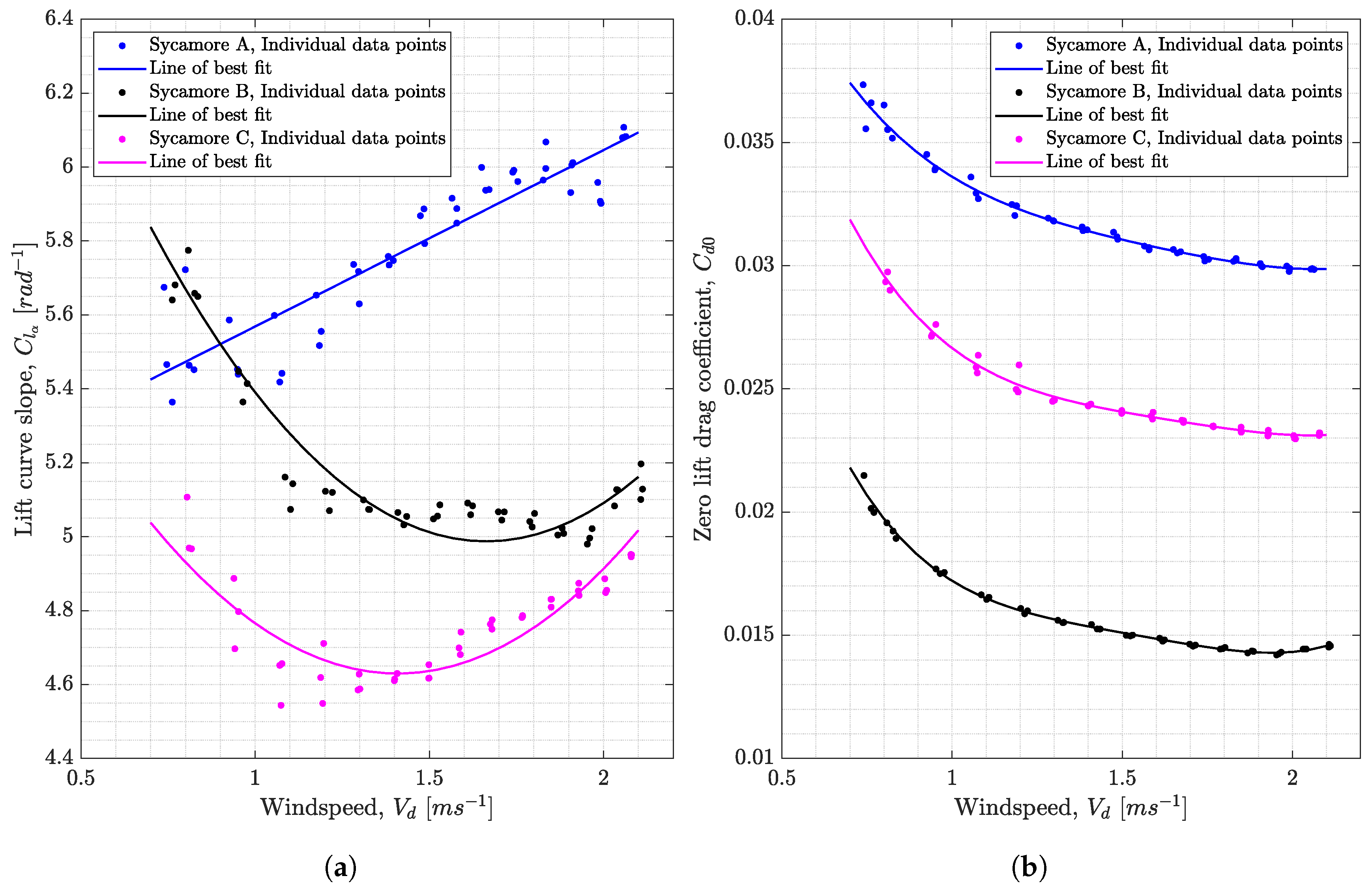
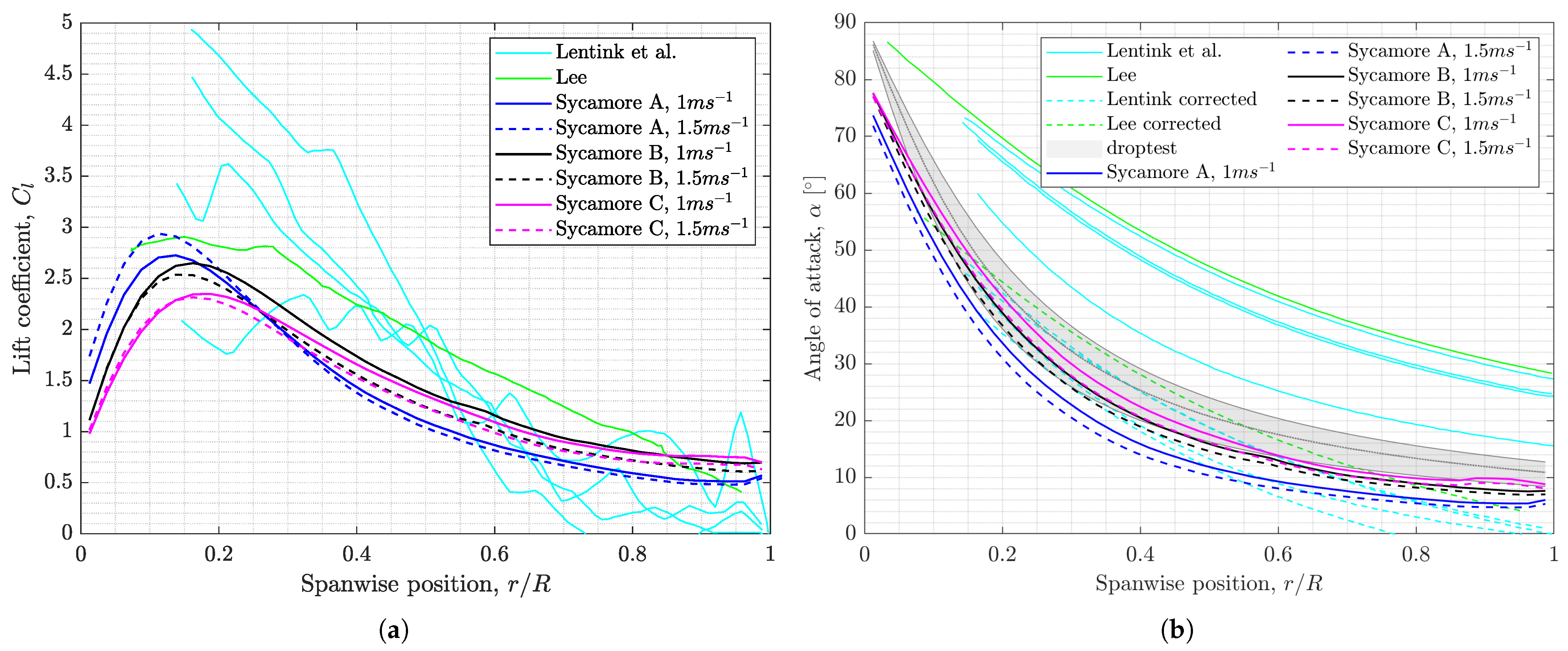
6.4. Sectional Lift and Drag Coefficients of Sycamore A, B, and C
6.5. Numerical Analysis with Polhamus Model
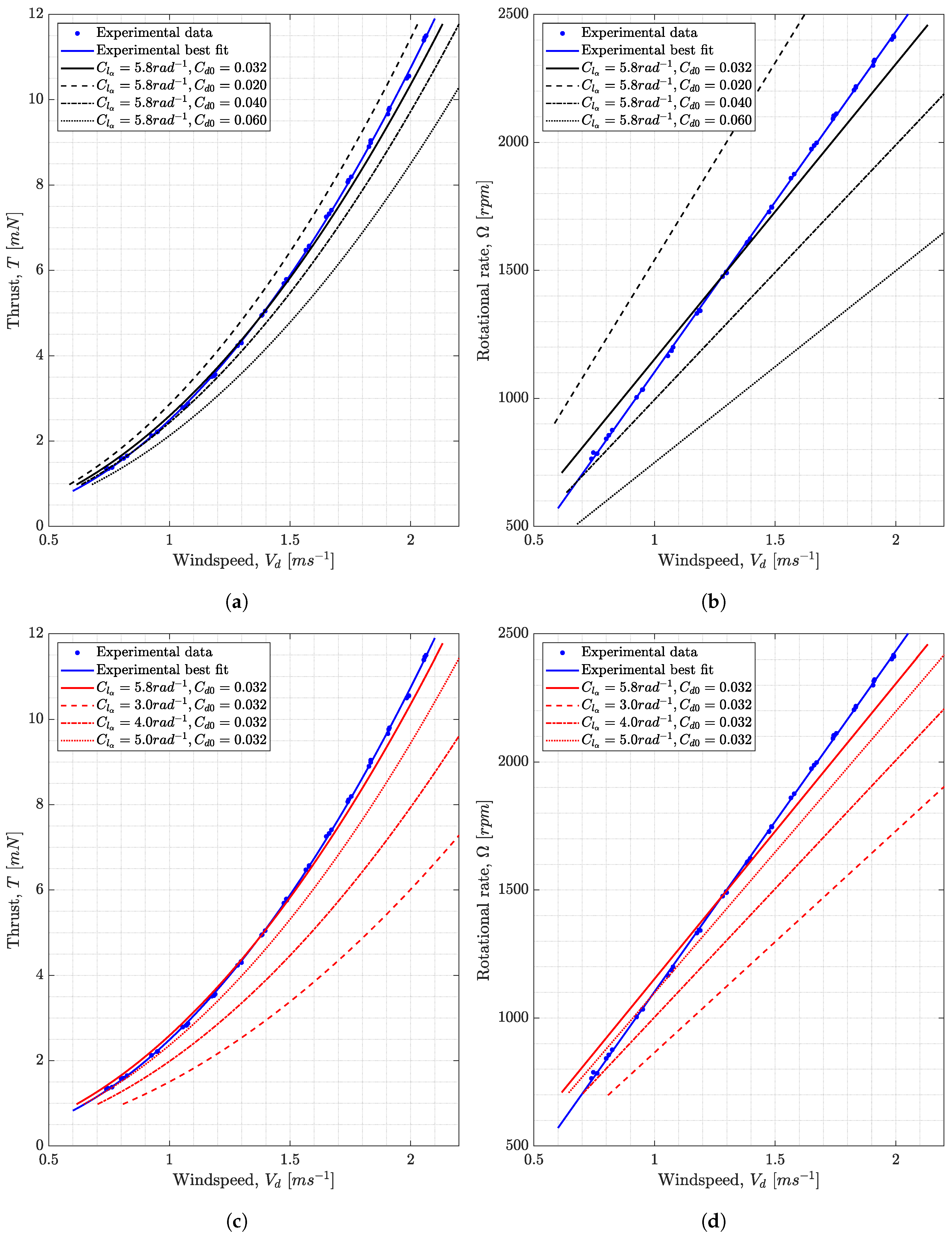
 . Therefore, the SNM was run with the Polhamus model and normal force drag model and the values of , and were estimated, to match the measured individual thrust and rotor speed data points of Sycamore A.
. Therefore, the SNM was run with the Polhamus model and normal force drag model and the values of , and were estimated, to match the measured individual thrust and rotor speed data points of Sycamore A. varying from to . The disparity between the Polhamus coefficients could be attributed to the fact that Figure 4 shows the calculated and values, whereas Figure 24 presented the computed coefficients using the BEM.
varying from to . The disparity between the Polhamus coefficients could be attributed to the fact that Figure 4 shows the calculated and values, whereas Figure 24 presented the computed coefficients using the BEM. varying from to . These aspect ratios are close to that of Sycamore A, which is
varying from to . These aspect ratios are close to that of Sycamore A, which is  = 3.88.
= 3.88. (as shown in Figure 4), which was evaluated in advance using crude assumptions (e.g., non-rotating rectangular wing). These shortfalls must be further addressed and refined if such a model is to be used in describing the of samaras with LEV.
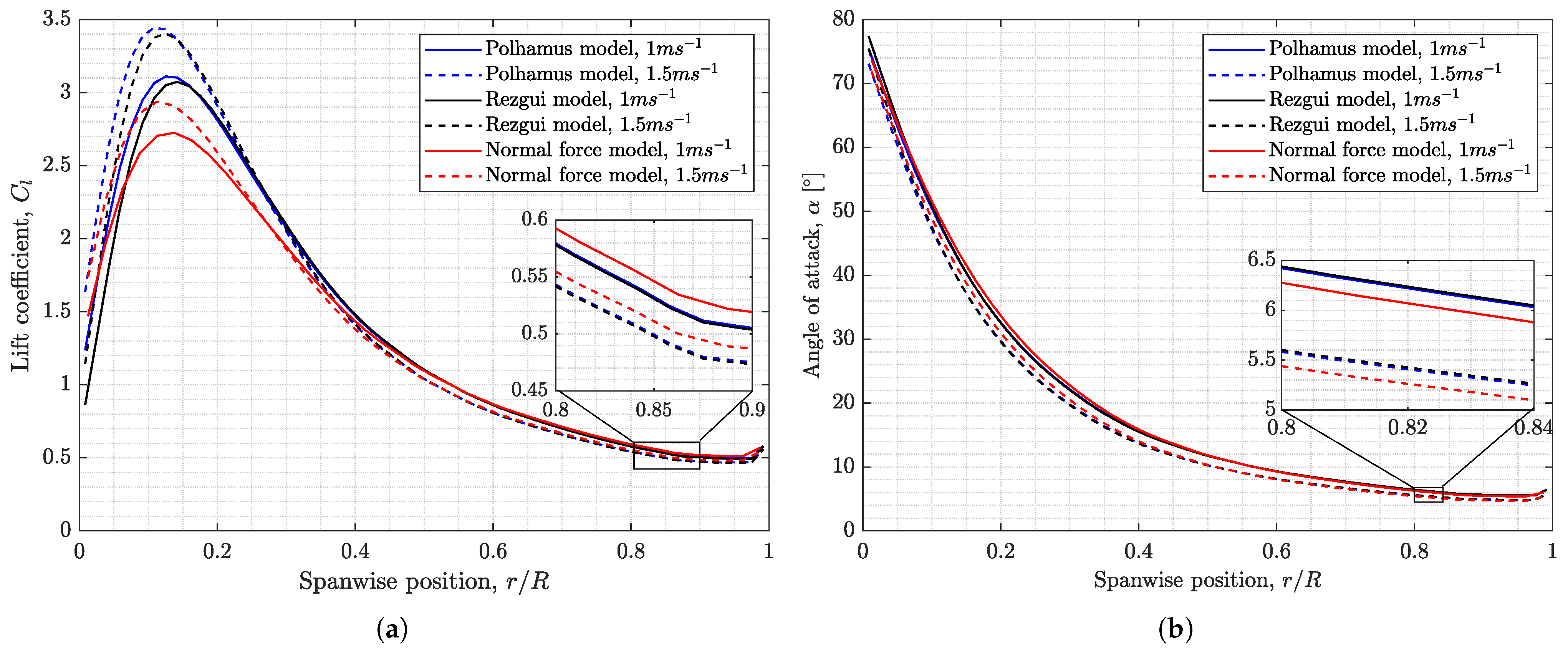
(as shown in Figure 4), which was evaluated in advance using crude assumptions (e.g., non-rotating rectangular wing). These shortfalls must be further addressed and refined if such a model is to be used in describing the of samaras with LEV.6.6. Sectional Lift and Drag Coefficients of Different Models
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEM | Blade Element-Momentum |
| LEV | Leading Edge Vortex |
| SNM | Samara Numerical Model |
References
- Norberg, R.Å. Autorotation, self-stability, and structure of single-winged fruits and seeds (samaras) with comparative remarks on animal flight. Biol. Rev. 1973, 48, 561–596. [Google Scholar] [CrossRef]
- Azuma, A.; Okuno, Y. Flight of a samara, Alsomitra macrocarpa. J. Theor. Biol. 1987, 129, 263–274. [Google Scholar] [CrossRef]
- Minami, S.; Azuma, A. Various flying modes of wind-dispersal seeds. J. Theor. Biol. 2003, 225, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Walker, J. The aerodynamics of the samara: Winged seed of the maple, the ash and other trees. Sci. Am. 1981, 245, 226–238. [Google Scholar] [CrossRef]
- Guries, R.P.; Nordheim, E.V. Flight characteristics and dispersal potential of maple samaras. For. Sci. 1984, 30, 434–440. [Google Scholar]
- Ladera, C.L.; Pineda, P.A. The physics of the spectacular flight of the Triplaris samaras. Lat.-Am. J. Phys. Educ. 2009, 3, 11. [Google Scholar]
- McCutchen, C. The spinning rotation of ash and tulip tree samaras. Science 1977, 197, 691–692. [Google Scholar] [CrossRef]
- Green, D.S. The terminal velocity and dispersal of spinning samaras. Am. J. Bot. 1980, 67, 1218–1224. [Google Scholar] [CrossRef]
- Pirie, M.D.; Klitgaard, B.B.; Pennington, R.T. Revision and biogeography of Centrolobium (Leguminosae-Papilionoideae). Syst. Bot. 2009, 34, 345–359. [Google Scholar] [CrossRef]
- Liu, W.; Ouyang, Y.; Wan, C. Flavonoids of the genus of Acer: A mini review. Asian J. Chem. 2013, 25, 7075–7078. [Google Scholar] [CrossRef]
- van Gelderen, C.J.; van Gelderen, D.M. Maples for Gardens: A Color Encyclopedia; Timber Press: Portland, OR, USA, 1999. [Google Scholar]
- Kwon, B.G.; Sohn, M.H. Effects of the CG Positions on the Autorotative Flight of Maple Seeds. Int. J. Aeronaut. Space Sci. 2022, 23, 241–254. [Google Scholar] [CrossRef]
- Varshney, K.; Chang, S.; Wang, Z.J. The kinematics of falling maple seeds and the initial transition to a helical motion. Nonlinearity 2011, 25, C1. [Google Scholar] [CrossRef]
- Nathan, R.; Katul, G.G.; Horn, H.S.; Thomas, S.M.; Oren, R.; Avissar, R.; Pacala, S.W.; Levin, S.A. Mechanisms of long-distance dispersal of seeds by wind. Nature 2002, 418, 409–413. [Google Scholar] [CrossRef]
- Johnson, W.C. Estimating dispersibility of Acer, Fraxinus and Tilia in fragmented landscapes from patterns of seedling establishment. Landsc. Ecol. 1988, 1, 175–187. [Google Scholar] [CrossRef]
- Glauert, H. A General Theory of the Autogyro; Technical report; HM Stationery Office: Richmond, UK, 1926.
- Lee, A.Y.; Bryson, A.E., Jr.; Hindson, W.S. Optimal landing of a helicopter in autorotation. J. Guid. Control Dyn. 1988, 11, 7–12. [Google Scholar] [CrossRef]
- Sipe, T.W.; Linnerooth, A.R. Intraspecific variation in samara morphology and flight behavior in Acer saccharinum (Aceraceae). Am. J. Bot. 1995, 82, 1412–1419. [Google Scholar] [CrossRef]
- Azuma, A.; Yasuda, K. Flight performance of rotary seeds. J. Theor. Biol. 1989, 138, 23–53. [Google Scholar] [CrossRef]
- Lentink, D.; Dickson, W.B.; Van Leeuwen, J.L.; Dickinson, M.H. Leading-edge vortices elevate lift of autorotating plant seeds. Science 2009, 324, 1438–1440. [Google Scholar] [CrossRef]
- Birch, J.M.; Dickinson, M.H. Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 2001, 412, 729–733. [Google Scholar] [CrossRef] [PubMed]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, C. An indicial-Polhamus aerodynamic model of insect-like flapping wings in hover. WIT Trans. State-Art Sci. Eng. 2006, 4, 606–665. [Google Scholar]
- Ford, C.P.; Babinsky, H. Lift and the leading-edge vortex. J. Fluid Mech. 2013, 720, 280–313. [Google Scholar] [CrossRef]
- Seter, D.; Rosen, A. Theoretical and experimental study of axial autorotation of simple rotary decelerators. J. Aircr. 2014, 51, 236–248. [Google Scholar] [CrossRef]
- Seter, D.; Rosen, A. Study of the vertical autorotation of a singlewinged samara. Biol. Rev. 1992, 67, 175–197. [Google Scholar] [CrossRef]
- Rezgui, D.; Arroyo, I.H.; Theunissen, R. Model for sectional leading-edge vortex lift for the prediction of rotating samara seeds performance. Aeronaut. J. 2020, 124, 1236–1261. [Google Scholar] [CrossRef]
- Nabawy, M.R.; Crowther, W.J. The role of the leading edge vortex in lift augmentation of steadily revolving wings: A change in perspective. J. R. Soc. Interface 2017, 14, 20170159. [Google Scholar] [CrossRef]
- Lentink, D.; Dickinson, M.H. Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Exp. Biol. 2009, 212, 2705–2719. [Google Scholar] [CrossRef]
- Willmott, A.P.; Ellington, C.P.; Thomas, A.L. Flow visualization and unsteady aerodynamics in the flight of the hawkmoth, Manduca sexta. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1997, 352, 303–316. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Taylor, G.K.; Thomas, A.L. Smoke visualization of free-flying bumblebees indicates independent leading-edge vortices on each wing pair. In Animal Locomotion; Springer: Berlin/Heidelberg, Germany, 2010; pp. 249–259. [Google Scholar]
- Thomas, A.L.; Taylor, G.K.; Srygley, R.B.; Nudds, R.L.; Bomphrey, R.J. Dragonfly flight: Free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms, controlled primarily via angle of attack. J. Exp. Biol. 2004, 207, 4299–4323. [Google Scholar] [CrossRef]
- Warrick, D.R.; Tobalske, B.W.; Powers, D.R. Lift production in the hovering hummingbird. Proc. R. Soc. B Biol. Sci. 2009, 276, 3747–3752. [Google Scholar] [CrossRef]
- Muijres, F.; Johansson, L.C.; Barfield, R.; Wolf, M.; Spedding, G.; Hedenstrom, A. Leading-edge vortex improves lift in slow-flying bats. Science 2008, 319, 1250–1253. [Google Scholar] [CrossRef] [PubMed]
- Shyy, W.; Liu, H. Flapping wings and aerodynamic lift: The role of leading-edge vortices. AIAA J. 2007, 45, 2817–2819. [Google Scholar] [CrossRef]
- Eldredge, J.D.; Jones, A.R. Leading-edge vortices: Mechanics and modeling. Annu. Rev. Fluid Mech. 2019, 51, 75–104. [Google Scholar] [CrossRef]
- Jardin, T.; David, L. Spanwise gradients in flow speed help stabilize leading-edge vortices on revolving wings. Phys. Rev. E 2014, 90, 013011. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Lua, K.B.; Lim, T. Aspect ratio effects on revolving wings with Rossby number consideration. Bioinspir. Biomim. 2016, 11, 056013. [Google Scholar] [CrossRef] [PubMed]
- Harbig, R.R.; Sheridan, J.; Thompson, M.C. Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 2013, 717, 166–192. [Google Scholar] [CrossRef]
- Phillips, N.; Knowles, K.; Bomphrey, R.J. The effect of aspect ratio on the leading-edge vortex over an insect-like flapping wing. Bioinspir. Biomim. 2015, 10, 056020. [Google Scholar] [CrossRef]
- Usherwood, J.R.; Ellington, C.P. The aerodynamics of revolving wings II. Propeller force coefficients from mayfly to quail. J. Exp. Biol. 2002, 205, 1565–1576. [Google Scholar] [CrossRef]
- Salcedo, E.; Treviño, C.; Vargas, R.O.; Martínez-Suástegui, L. Stereoscopic particle image velocimetry measurements of the three-dimensional flow field of a descending autorotating mahogany seed (Swietenia macrophylla). J. Exp. Biol. 2013, 216, 2017–2030. [Google Scholar] [CrossRef]
- Limacher, E.; Rival, D.E. On the distribution of leading-edge vortex circulation in samara-like flight. J. Fluid Mech. 2015, 776, 316–333. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, E.J.; Sohn, M.H. Mechanism of autorotation flight of maple samaras (Acer palmatum). Exp. Fluids 2014, 55, 1718. [Google Scholar] [CrossRef]
- Arroyo, I.H.; Rezgui, D.; Theunissen, R. Analytical model for leading-edge vortex lift on rotating samara seeds: Development and validation. In Proceedings of the 2016 RAeS Applied Aerodynamics Conference, Bristol, UK, 19–21 July 2016. [Google Scholar]
- Lee, I.; Choi, H. Scaling law for the lift force of autorotating falling seeds at terminal velocity. J. Fluid Mech. 2018, 835, 406–420. [Google Scholar] [CrossRef]
- Arranz, G.; Gonzalo, A.; Uhlmann, M.; Flores, O.; García-Villalba, M. A numerical study of the flow around a model winged seed in auto-rotation. Flow Turbul. Combust. 2018, 101, 477–497. [Google Scholar] [CrossRef]
- Holden, J.R.; Caley, T.M.; Turner, M.G. Maple seed performance as a wind turbine. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1304. [Google Scholar]
- Bai, S.; Chirarattananon, P. Design and take-off flight of a samara-inspired revolving-wing robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 6070–6076. [Google Scholar]
- Rabault, J.; Fauli, R.A.; Carlson, A. Curving to fly: Synthetic adaptation unveils optimal flight performance of whirling fruits. Phys. Rev. Lett. 2019, 122, 024501. [Google Scholar] [CrossRef] [PubMed]
- Zakaria, M.Y.; Dos Santos, C.R.; Dayhoum, A.; Marques, F.; Hajj, M.R. Modeling and prediction of aerodynamic characteristics of free fall rotating wing based on experiments. In Proceedings of the International Conference on Aerospace Sciences and Aviation Technology. The Military Technical College, Cairo, Egypt, 9–11 April 2019; pp. 1–15. [Google Scholar]
- Rao, M.; Hoysall, D.C.; Gopalan, J. Mahogany seed–a step forward in deciphering autorotation. Curr. Sci. 2014, 106, 1101. [Google Scholar]
- Usherwood, J.R.; Ellington, C.P. The aerodynamics of revolving wings I. Model hawkmoth wings. J. Exp. Biol. 2002, 205, 1547–1564. [Google Scholar] [CrossRef] [PubMed]
- Birch, J.M.; Dickson, W.B.; Dickinson, M.H. Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Exp. Biol. 2004, 207, 1063–1072. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Gotz, K.G. Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Exp. Biol. 1993, 174, 45–64. [Google Scholar] [CrossRef]
- Dickson, W.B.; Dickinson, M.H. The effect of advance ratio on the aerodynamics of revolving wings. J. Exp. Biol. 2004, 207, 4269–4281. [Google Scholar] [CrossRef]
- Deng, X.; Schenato, L.; Wu, W.C.; Sastry, S.S. Flapping flight for biomimetic robotic insects: Part I-system modeling. IEEE Trans. Robot. 2006, 22, 776–788. [Google Scholar] [CrossRef]
- Taha, H.E.; Hajj, M.R.; Beran, P.S. State-space representation of the unsteady aerodynamics of flapping flight. Aerosp. Sci. Technol. 2014, 34, 1–11. [Google Scholar] [CrossRef]
- Berman, G.J.; Wang, Z.J. Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 2007, 582, 153–168. [Google Scholar] [CrossRef]
- Walker, S.M.; Taylor, G.K. A semi-empirical model of the aerodynamics of manoeuvring insect flight. J. R. Soc. Interface 2021, 18, 20210103. [Google Scholar] [CrossRef] [PubMed]
- Polhamus, E.C. A Concept of the Vortex Lift of Sharp-Edge Delta Wings Based on a Leading-Edge-Suction Analogy; Technical report; NASA Langley Research Center: Hampton, VA, USA, 1966.
- Traub, L.W. Analysis and estimation of the lift components of hovering insects. J. Aircr. 2004, 41, 284–289. [Google Scholar] [CrossRef]
- Tornado; “Tornado, A Vortex Lattice Method implemented in MATLAB”. Available online: http://tornado.redhammer.se/ (accessed on 17 December 2022).
- Muijres, F.T.; Spedding, G.R.; Winter, Y.; Hedenström, A. Actuator disk model and span efficiency of flapping flight in bats based on time-resolved PIV measurements. Exp. Fluids 2011, 51, 511–525. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Taylor, G.K.; Lawson, N.J.; Thomas, A.L. Digital particle image velocimetry measurements of the downwash distribution of a desert locust Schistocerca gregaria. J. R. Soc. Interface 2006, 3, 311–317. [Google Scholar] [CrossRef]
- Nabawy, M.R.; Crowther, W.J. A quasi-steady lifting line theory for insect-like hovering flight. PLoS ONE 2015, 10, e0134972. [Google Scholar] [CrossRef]
- Jones, R.T. Correction of the Lifting Line Theory for the Effect of the Chord; Technical report; National Advisory Committee for Aeronautics: Langley Field, VA, USA, 1941.
- Mahmuddin, F. Rotor blade performance analysis with blade element momentum theory. Energy Procedia 2017, 105, 1123–1129. [Google Scholar] [CrossRef]
- Benini, E.; Toffolo, A. Optimal design of horizontal-axis wind turbines using blade-element theory and evolutionary computation. J. Sol. Energy Eng. 2002, 124, 357–363. [Google Scholar] [CrossRef]
- Jung, B.; Rezgui, D. Flight Performance of an Autorotating Samara with varying windspeed. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 2111. [Google Scholar]
- Jung, B.K. Investigation into the Flight Performance of an Autorotating Samara with Varying Flight Conditions. Ph.D. Thesis, University of Bristol, Bristol, UK, 2022. [Google Scholar]
- Leishman, G.J. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Coleman, T.F.; Li, Y. An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Lee, I. Numerical Study of a Freely-Falling Maple Seed. Ph.D. Thesis, Seoul National University, Seoul, Republic of Korea, 2016. [Google Scholar]
- Anderson, J. Fundamentals of Aerodynamics, 5th ed.; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- BitFenix; BitFenix Spectre PRO fans 230 mm. Available online: https://www.bitfenix.com/products/fan/spectre-pro/spectre-pro-specs/ (accessed on 12 December 2022).
- Smd Sensors; S100 (0.2 N and 0.4 N) Load Cells. Available online: https://www.smdsensors.com/products/type/s100-0-2-0-4-n-load-cell/ (accessed on 12 December 2022).
- National Instruments; NI-9237 Strain and Load Module. Available online: https://www.ni.com/en-gb/support/model.ni-9237.html (accessed on 12 December 2022).
- Okamoto, M.; Yasuda, K.; Azuma, A. Aerodynamic characteristics of the wings and body of a dragonfly. J. Exp. Biol. 1996, 199, 281–294. [Google Scholar] [CrossRef]
- Nabawy, M.R.; Crowther, W.J. On the quasi-steady aerodynamics of normal hovering flight part II: Model implementation and evaluation. J. R. Soc. Interface 2014, 11, 20131197. [Google Scholar] [CrossRef] [PubMed]
- Winslow, J.; Otsuka, H.; Govindarajan, B.; Chopra, I. Basic understanding of airfoil characteristics at low Reynolds numbers (104–105). J. Aircr. 2018, 55, 1050–1061. [Google Scholar] [CrossRef]
- Laitone, E. Wind tunnel tests of wings at Reynolds numbers below 70,000. Exp. Fluids 1997, 23, 405–409. [Google Scholar] [CrossRef]
- Broadley, P.; Nabawy, M.R. An experimental investigation of Reynolds number effects on the aerodynamics of insect-like revolving wings. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0307. [Google Scholar]
- Levy, D.E.; Seifert, A. Simplified dragonfly airfoil aerodynamics at Reynolds numbers below 8000. Phys. Fluids 2009, 21, 071901. [Google Scholar] [CrossRef]
- Okamoto, M.; Sasaki, D.; Kamikubo, M.; Fujii, R. Disappearance of Vortex Lift in Low-Aspect-Ratio Wings at Very-low Reynolds Numbers. Trans. Jpn. Soc. Aeronaut. Space Sci. 2019, 62, 310–317. [Google Scholar] [CrossRef]

 , rectangular wing using Tornado. A fourth order polynomial was used as the line of best fit.
, rectangular wing using Tornado. A fourth order polynomial was used as the line of best fit.
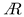 , rectangular wing using Tornado. A fourth order polynomial was used as the line of best fit.
, rectangular wing using Tornado. A fourth order polynomial was used as the line of best fit.


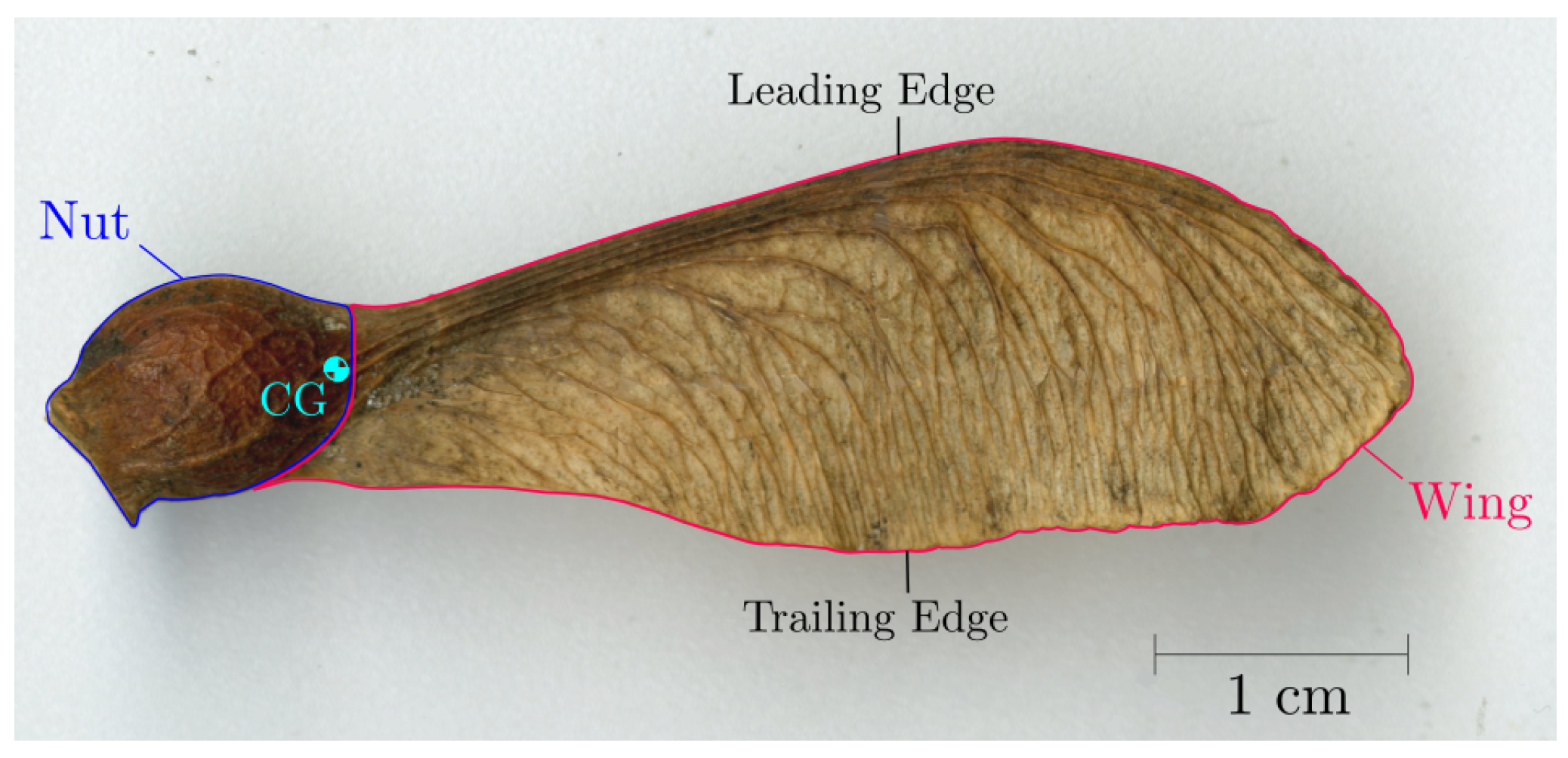
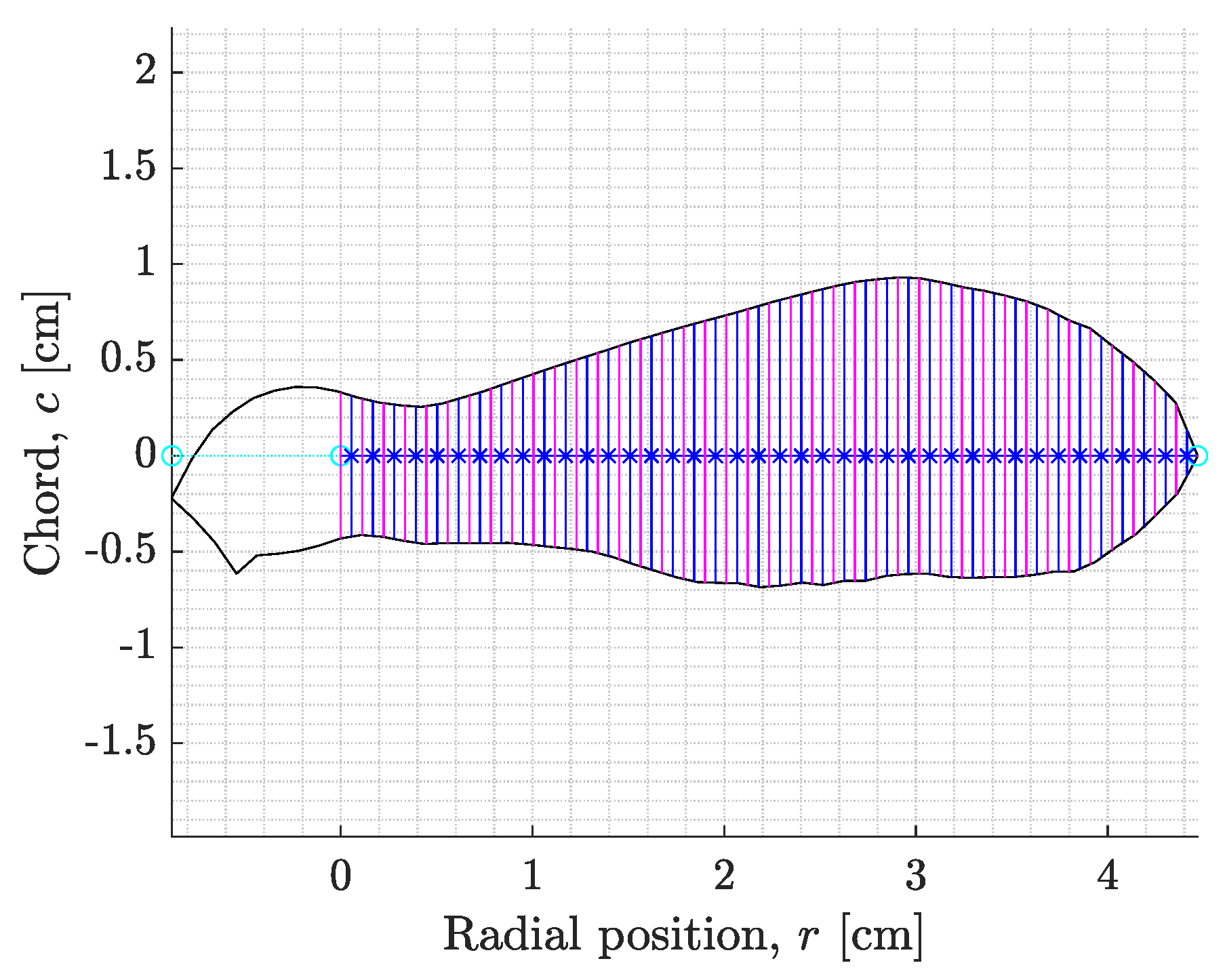
 is the aspect ratio of the blade. Sycamore A, 4.47 cm,
is the aspect ratio of the blade. Sycamore A, 4.47 cm, 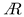 = 3.88; Sycamore B, 3.82 cm,
= 3.88; Sycamore B, 3.82 cm, 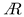 = 4.37; Sycamore C, 3.97 cm,
= 4.37; Sycamore C, 3.97 cm, 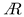 = 3.35, (b) rotor hub with graphical illustrations of the pitch, , and coning, , angle.
= 3.35, (b) rotor hub with graphical illustrations of the pitch, , and coning, , angle.
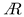 is the aspect ratio of the blade. Sycamore A, 4.47 cm,
is the aspect ratio of the blade. Sycamore A, 4.47 cm, 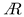 = 3.88; Sycamore B, 3.82 cm,
= 3.88; Sycamore B, 3.82 cm, 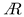 = 4.37; Sycamore C, 3.97 cm,
= 4.37; Sycamore C, 3.97 cm, 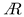 = 3.35, (b) rotor hub with graphical illustrations of the pitch, , and coning, , angle.
= 3.35, (b) rotor hub with graphical illustrations of the pitch, , and coning, , angle.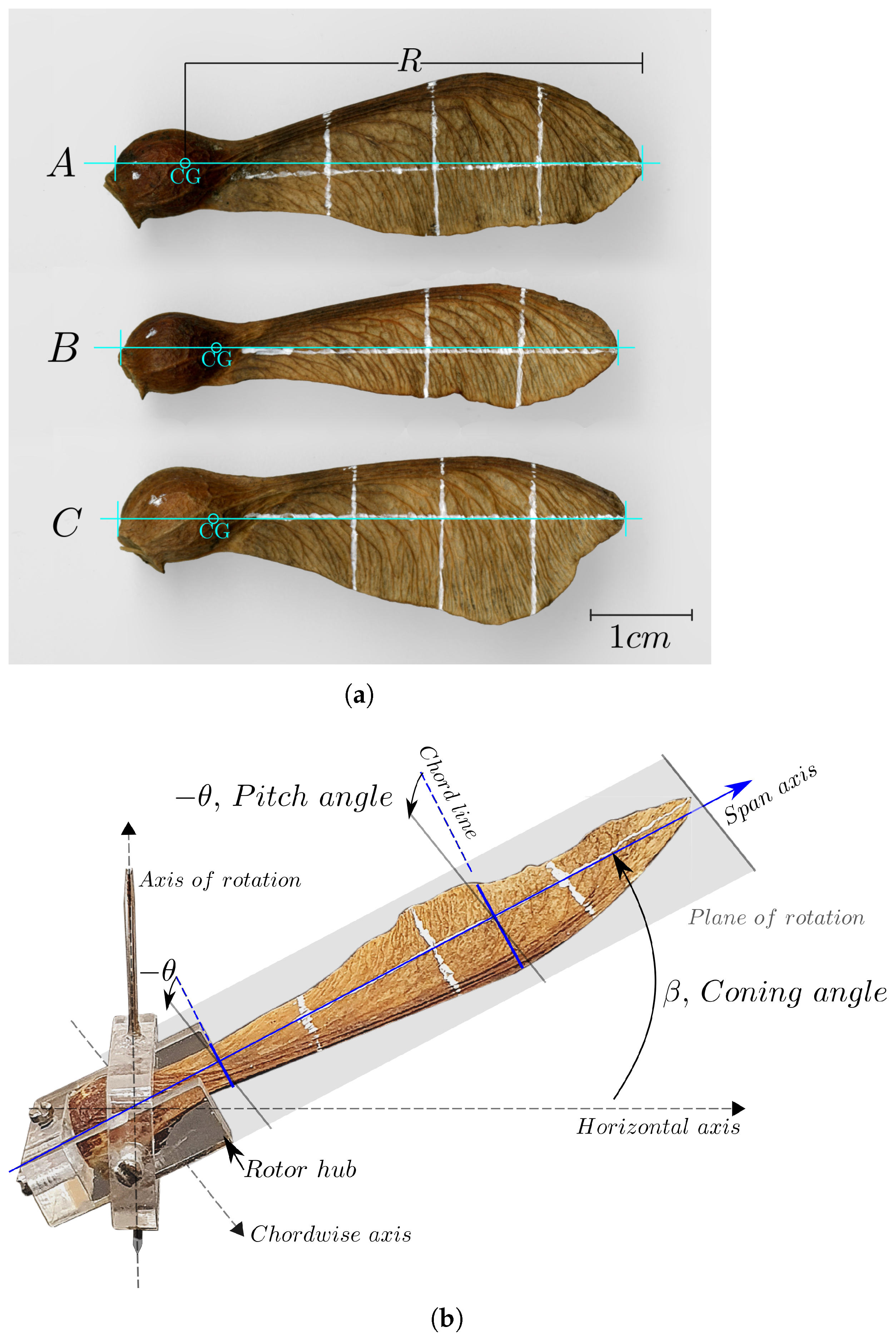


| h | |||||
|---|---|---|---|---|---|
| −17.3 | −29.2 | −23.8 | −27.3 | −25.3 |
| Rotor Parameters | Values | Flight Parameters | Values |
| Number of Blade (B) | 1 | Thrust (T) | Variable |
| Blade mass (m) | 232 mg | Windspeed () | Variable |
| Blade radius (R) | 4.47 cm | Omega () | Variable |
| Blade mean chord () | 1.15 cm | Pitch angle () | |
| Twist () | Coning () | ||
| Normal force model parameters | Values | ||
| Lift curve slope () | 3.0∼5.8 rad | ||
| Zero-lift drag coefficient () | 0.015∼0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, B.K.; Rezgui, D. Sectional Leading Edge Vortex Lift and Drag Coefficients of Autorotating Samaras. Aerospace 2023, 10, 414. https://doi.org/10.3390/aerospace10050414
Jung BK, Rezgui D. Sectional Leading Edge Vortex Lift and Drag Coefficients of Autorotating Samaras. Aerospace. 2023; 10(5):414. https://doi.org/10.3390/aerospace10050414
Chicago/Turabian StyleJung, Byung Kwon, and Djamel Rezgui. 2023. "Sectional Leading Edge Vortex Lift and Drag Coefficients of Autorotating Samaras" Aerospace 10, no. 5: 414. https://doi.org/10.3390/aerospace10050414
APA StyleJung, B. K., & Rezgui, D. (2023). Sectional Leading Edge Vortex Lift and Drag Coefficients of Autorotating Samaras. Aerospace, 10(5), 414. https://doi.org/10.3390/aerospace10050414






