Preliminary Aero-Elastic Optimization of a Twin-Aisle Long-Haul Aircraft with Increased Aspect Ratio

Abstract

This paper presents a preliminary study on the improvement of the fuel efficiency of a civil transport aircraft, focusing on the aero-elastic optimization of an increased aspect ratio wingbox. The wing is stretched, increasing its aspect ratio, and a trade-off between the improved aerodynamic efficiency and the structural mass identifies an optimal aspect ratio for such aircraft. The aeroelastic optimization is performed with NeOPT, a structural optimizer for conceptual and preliminary design phases. The analysis considers different materials and structural solutions for the wingbox and tackles aeroelastic constraints, such as flutter and aileron efficiency, from the preliminary design phases. The fuel consumption of the sized aircraft is evaluated with a simplified approach that provides an indication of the fuel efficiency. The results show how a composite wing with increased aspect ratio can save up to 6.9% of fuel burnt with respect to the baseline aluminum wing. The results are extended at fleet level, achieving a 2-million-ton cut in CO₂ emissions and a saving of USD 1.28 million on fuel-related costs.

1. Introduction

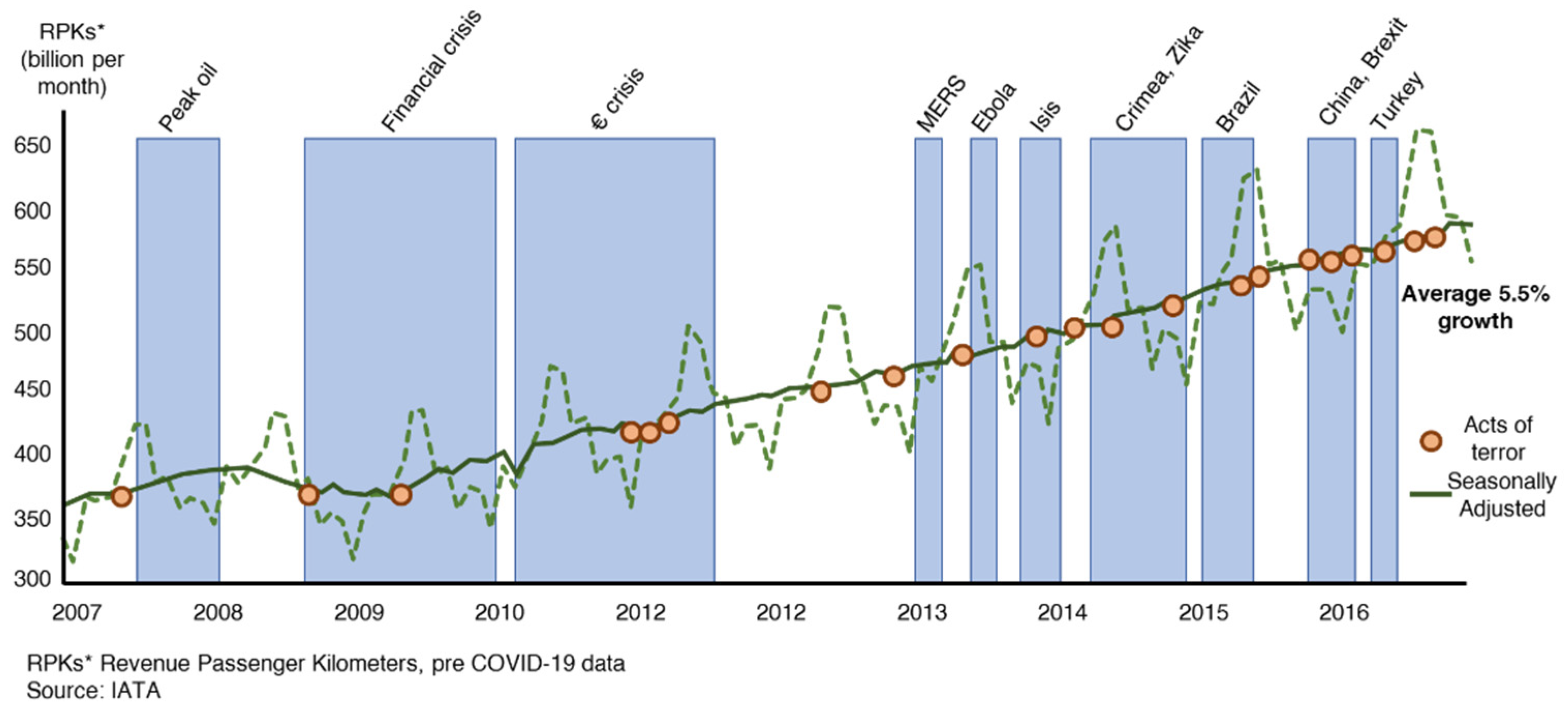
Air transportation is a market which grows constantly, by 5% each year (pre COVID-19), although acts of terror, financial crises, pandemics and other global events have reduced the circulation of people across the years, as Figure 1 shows. In a similar way, the goods traffic and logistics increased as well.

To satisfy the increasing payload demand (passengers and goods), airliners are increasing their fleets, making the skies an even more crowded place: the world’s aircraft fleet is expected to increase from the current 25,900 to 47,080 by 2040 [2].

More flying aircraft means more related emissions, which is in opposition to the objectives stated by the European Union Flightpath 2050 [3], among which is a 75% cut in CO₂ pollution. This contradiction creates a challenging situation where the aeronautical industries are asked to invert the emission trend in an expanding market. Current technologies, such as composite materials, biofuels, new engine options and many others, provide an improvement in the efficiency of aircraft, but they are not sufficient to invert the emissions trend. To achieve this ambitious goal, new technologies must be adopted concurrently with breakthrough aircraft configurations. The investigation of new configurations is reflected in the effort of the scientific and industrial communities: many studies have concentrated on the study of the Blended Wing Body (BWB) [4,5,6,7,8,9], the Truss Braced Wing (TBW) gained popularity as well [10,11,12,13], a more exotic V-shaped configuration was presented and is under development [14], as well as the box wing or PrandtPlane configuration [15,16,17,18] and many others.

Despite the maximum range usually being one of the Top-Level Aircraft Requirements (TLAR), it can be used as a Key Performance Indicator (KPI), together with the fuel consumption embedded into the classical Breguet Equation (1) for turbofan aircraft, to highlight the potential areas of improvement that can be considered to evaluate and compare the overall performance of similar aircraft:

$$R=\frac{V_{TAS}}{g}\left(\frac{L}{D}\right)\frac{1}{SFC}ln\left(\frac{W_{initial}}{W_{initial}-W_{Fuel burnt}}\right)$$

(1)

While the Breguet formula represents an approximation valid for cruise conditions and cannot represent the full consumption of an aircraft for its entire mission profile, it is often used to compare different aircraft configurations in trade-off analyses such as in the current application. It is possible to identify three main areas that directly impact on the efficiency: the propulsive term (SFC), the aerodynamic efficiency term $\left(\frac{L}{D}\right)$ and a structural efficiency term $\left(\frac{W_{initial}}{W_{initial}-W_{Fuelburnt}}\right)$.

The first player to be addressed to improve the aircraft fuel consumption while decreasing the emissions at the same time is the propulsion efficiency. It must be admitted that during recent decades, the engine manufacturers have carried out impressive work to significantly improve the efficiency of engines [19]. Further steps are now under development aiming at the use of synthetic fuels and, more challengingly, hydrogen [20,21]. These aspects are not discussed in this paper.

Concerning the second area of interest, i.e., the aerodynamic efficiency, there are two possibilities: adopting a radically different configuration, such as, for example, Blended Wind Body or Truss-Braced Wing, or improving the classical tube and wing configuration. The second option is the one considered here. Current transport aircraft are characterized by a maximum aerodynamic efficiency, expressed as L/D, at cruise speed, with wings based on supercritical airfoils and thickness ratios (t/c) ranging from 15% to 12%, aspect ratio ranging from 8 to 11 and a typical C_L in cruise around 0.5–0.6. A suitable way to improve aerodynamic efficiency is by reducing the drag by means of the increase in aspect ratio. Indeed, it must be remembered that, for the wing only, the drag coefficient in the subsonic regime can be written as

$${\mathrm{C}}_{\mathrm{D}}={\mathrm{C}}_{\mathrm{D}0}+\frac{{\mathrm{C}}_{\mathrm{L}}^2}{\pi \mathsf{\Lambda }e}$$

(2)

where C_D0 is the drag coefficient at zero lift, $\mathsf{\Lambda }$ is the aspect ratio and e the Oswald coefficient, respectively. The induced drag of a long-range transport at cruise conditions represents approximately 30% of the total drag, so it is very clear why reducing the induced drag is of capital importance in increasing the aerodynamic efficiency, and therefore the global efficiency, to reduce emissions.

The integrated and holistic nature of the aircraft design, however, does not allow the application of a few substantial configuration modifications without incurring a multidisciplinary trade-off: for example, the increase in the aspect ratio (aerodynamic performance improvement) has a drawback, which is the increase in the wing bending moment and therefore the increase in the structural mass fraction, needed to withstand higher loads. Indeed, the recent interest in strut-braced aircraft configuration represents a means to minimize the mass penalty due to the very high aspect ratio. Moreover, high and ultra-high aspect ratio wings are naturally more exposed to aero-elastic phenomena, such as flutter, torsional divergence and control reversal. An integrated approach allows all these cross effects to be considered, including the capability to predict the aeroelastic behavior since the conceptual design phase is a must. Recently, two European projects funded under the Cleansky 2 program called RHEA and U-HARWARD studied new wing configurations. The second one, led by POLIMI, is focused on the investigation on future high and very high aspect ratio aircraft [22,23] with a special emphasis on three-wing configurations: cantilever wing, strut-braced wing and folding wingtip. The research activity covers the main aspects of conceptual, preliminary and high-fidelity analysis. The work presented here contributes to this project with the development of advanced tools for enhanced fidelity structural models to predict the impact of high aspect ratio cantilever wings, taking into account advanced materials and aeroelastic requirements.

Finally, increasing the wing aspect ratio means extending the wingspan, and this could be prevented by the fact that aviation companies limit the wingspan due to the size of existing airports, formulated in terms of different categories: ARC (Airport Reference Code) and ADG (Airplane Design Group) [24]. Boeing, to overcome this limitation, introduced for the B777X family the folding wingtip mechanism, where the last 10% of the wing can be folded up when on the ground, reducing the total wingspan from 71.75 m to 64.85 m so as to be classified with ARC code E on the ground while having an actual ARC code F in flying conditions, but this solution introduces a weight penalty due to the mechanism.

The last area to be investigated among the ones previously introduced to improve the global efficiency is represented by the structural efficiency term.

Thanks to their lightweight and strength properties, in recent decades composite materials have offered the possibility of exploring new design spaces to limit the mass increase due to the span extensions, and the latest industrial applications can be found in the Boeing 787 and Airbus A350 families, where the wing is entirely realized with composite materials. A historical perspective on the application of composites in aviation can be found in [25]. However, together with the potential mass saving using composites due to the favorable stiffness-to-density ratio, it must be considered that due to their high strength characteristics, the final structures show higher deformability, increasing the potential risks of aeroelastic issues. The impact of composite materials on the structural design of a brand new aircraft must be considered from the early design phases (conceptual-preliminary design); their behavior must be described with proper tools to fully characterize the aero-servo-elastic properties of the aircraft and to fully exploit the potential of the materials to achieve the best structural layout without any aeroelastic issues.

One of the challenges from the aircraft design perspective is to implement the capability to correctly predict the sensitivity with respect to the design variables described above, taking into consideration that most of the calculations are based on approximated formulas based on statistical estimations. In [26], an interesting study is reported that corrects the approximated formulas commonly used during the conceptual design phase that are able to estimate the sensitivity of the design point due to the variations in MTOW, aspect ratio and use of composites. In particular, a revised formula to estimate the structural weight has been proposed. Despite the verification of the proposed new formula using long-range and short–medium-range aircraft data having been successfully demonstrated, it must be pointed out that only a revised structural mass estimation is proposed, while other effects, such as the impact of wing deformability on aerodynamics, the effect of structural flexibility on stability derivatives and flutter or control reversal, need to be addressed as well. However, to allow these kinds of structural response estimations, it is necessary to introduce a structural model, even if simplified, that usually is not available in the common tools used during the conceptual design phase.

Fully convinced of the importance of bringing at least a flavor of aeroelasticity from the initial design phase, due to the increased flexibility of modern aircraft, since 2007 POLIMI started developing a design suite called NeoCASS [27,28,29,30], one of the first physical-based conceptual design tools. The main goals at the basis of NeoCASS developments are the following: to define a simple but realistic structural model allowing the relevant aeroelastic characteristics to be captured through very fast analysis runs; to implement an automatic structural model generation to be embedded into the typical procedures adopted during the conceptual design phase; and to make the process fully transparent for the user to minimize the need for special competences in terms of structural finite element and aeroelastic analysis. The main advantage of this approach, together with the aeroelastic prediction capabilities, is the availability of a physically based structural weight estimation that does not require pre-existent statistics, which are unavailable in the case of new technologies or unconventional aircraft configurations. The (minimum) mass of the structure is exactly the weight of the material needed to sustain the applied loads.

These initial requirements necessitated the adoption of a simplified finite element model, i.e., a stick model for the structure, based on beams elements, together with a Vortex Lattice Model (VLM) or a Doublet Lattice Model (DLM) for steady and unsteady calculations, respectively. The use of stick models was introduced when the computational cost was still a barrier to the extended application of numerical methods; however, stick models are used even today, especially for the identification of the critical dynamic loads, such as the ones related to the gust response calculations. The main difference between the approach proposed in NeoCASS and the one typically adopted in industries is the following: in NeoCASS, the stick finite element model is adopted since the initial structural sizing carried out during the conceptual design, based on the full set of loads requested by the certification rules. In doing so, the structural mass estimation is physically based, corresponding to the mass requested to sustain the loads, together with the due aeroelastic verifications. In industry, the structural sizing is not performed at the conceptual design level, where only a rough estimation of the masses is carried out based on statistical data. Once the conceptual design is completed, resulting in one or few best candidate aircraft configurations, for each one a global finite element model (GFEM) is produced to start the structural sizing process. Once completed, the GFEM model is condensed into a stick model to generate the full set of dynamic loads. With this traditional approach, any realistic aeroelastic evaluation can be performed only at the end of the conceptual and preliminary design phases, meaning that any unexpected behavior requires a second design loop, usually producing a weight penalty to be corrected. In the last 10 years, many tools for the conceptual and preliminary design stages were developed in academy and industry: PROTEUS was developed at TU-Delft [31], ATLASS is the Gulfstream’s tool [32], Bombardier developed its own methodology [33], EMWET [34] is another example of this suite’s class, just to cite some examples. Some of them need the availability of a GFEM model, many of them are based on the use of a commercial finite element software, limiting the practical applications at the conceptual level where there is the need to analyze hundreds or maybe thousands of configurations. In the novel approach adopted by NeoCASS, the stick model is automatically generated at the beginning of the design loop, starting from a limited number of geometrical data describing the aircraft, and sizing the aircraft on the basis of the real load conditions dictated by the certification rules, such as CS23 or CS25 [35]. It covers all the conceptual and preliminary design phases, starting from a simple geometrical module and providing a realistic mass and stiffness distribution for the structural elements, while the non-structural masses are still computed with statistical models. The simplified models adopted, together with the automatism introduced to create them and all the requested fluid–structure interfaces, make the use of NeoCASS fully compatible with the tools adopted for the conceptual design phase. In particular, it can be connected to any L0 conceptual design tool to define the optimal aircraft configuration, providing a very accurate and physically based structural mass calculation, fully compliant with the aeroelastic requirements and avoiding any statistical estimation.

The need to speed up the automatic sizing process forced a few simplifications to be introduced into the NeoCASS suite concerning the structural models, limited to isotropic or quasi-isotropic materials, such as in the case of the composite materials considered, such as black aluminum. This limits the capability to fully capture the structural coupling due to the fibers’ orientation. Moreover, during the analysis of unconventional configurations, such as of BWB or strut-braced wings, the model based on beams only is not able to fully capture the actual structural behavior, so the need for 3D modelling capability becomes a must. For this reason, the sizing approach underwent a major revision in recent years. A new optimization module called NeOPT [36,37,38], based on the novel concept of the wingbox meta-model [39], was created and the existing solvers were improved [40], especially the structural model employed to describe the slender structure of composite wings.

The combination of NeoCASS and NeOPT now provides a single environment, single model design suite that is physically based, and the sizing of the wingbox is performed through its semi-analytical representation (meta-model) of the wingbox allowing any structural and aeroelastic responses to be taken into account, such as, among others, failure and buckling, flutter, control effectiveness and gust responses, with or without the adoption of active control technologies, such as maneuver and gust load alleviation systems.

The main scope of this paper is to introduce the capabilities of the NeOPT module and to use it to estimate the sensitivity of the range and fuel burn of a typical long-range transport aircraft with respect to the increase in aspect ratio and to the structural concept and material adopted. The paper is organized as follows: Section 2 describes the optimization and analysis framework; Section 3 introduces an application of the methodology, represented by the investigation of a typical twin-aisle long-haul aircraft; Section 4 finally reports the final conclusions and outlooks. Nomenclature and abbreviations can be found after the conclusions.

2. Aero-Servo-Elastic Optimization and Analysis Framework

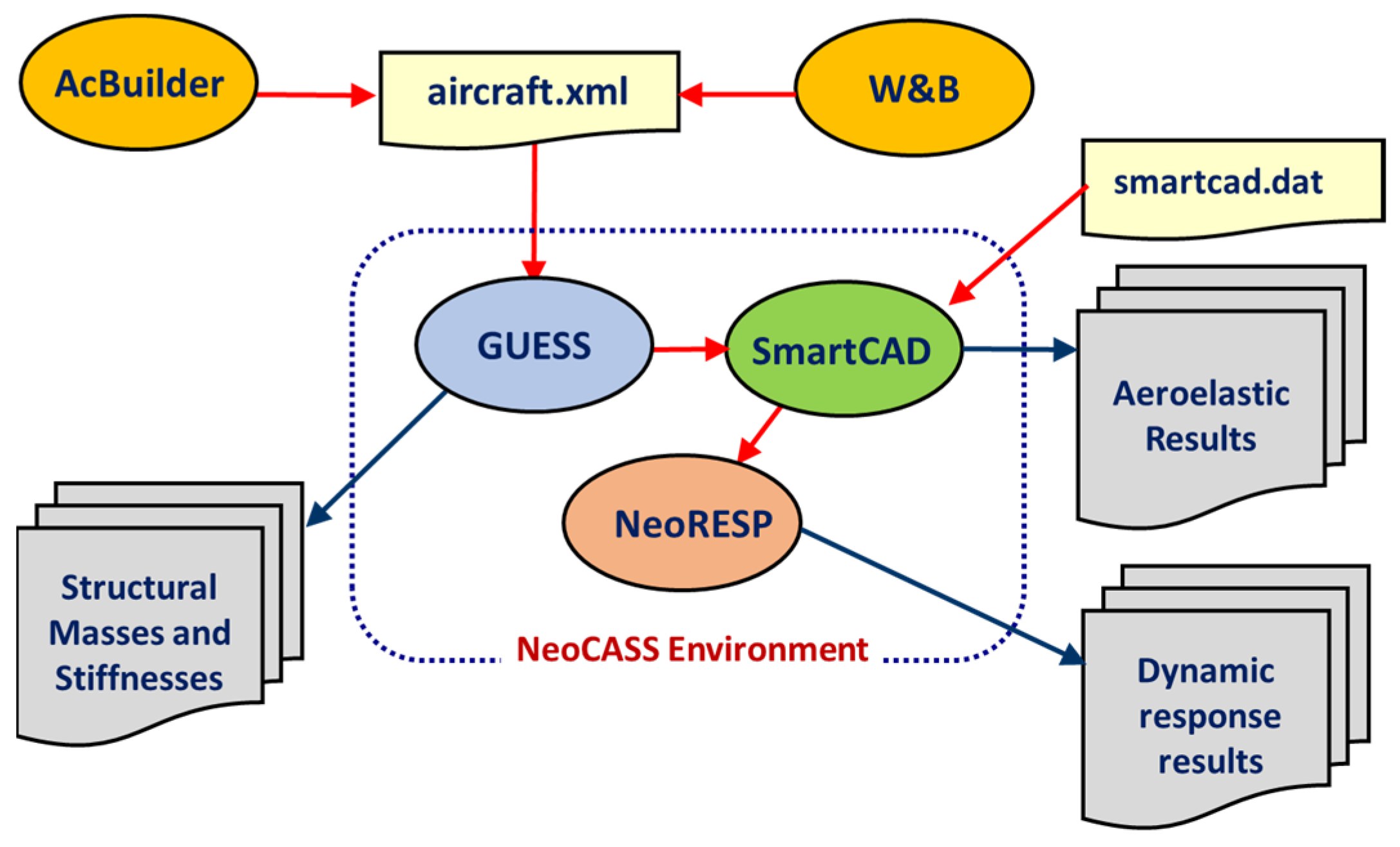
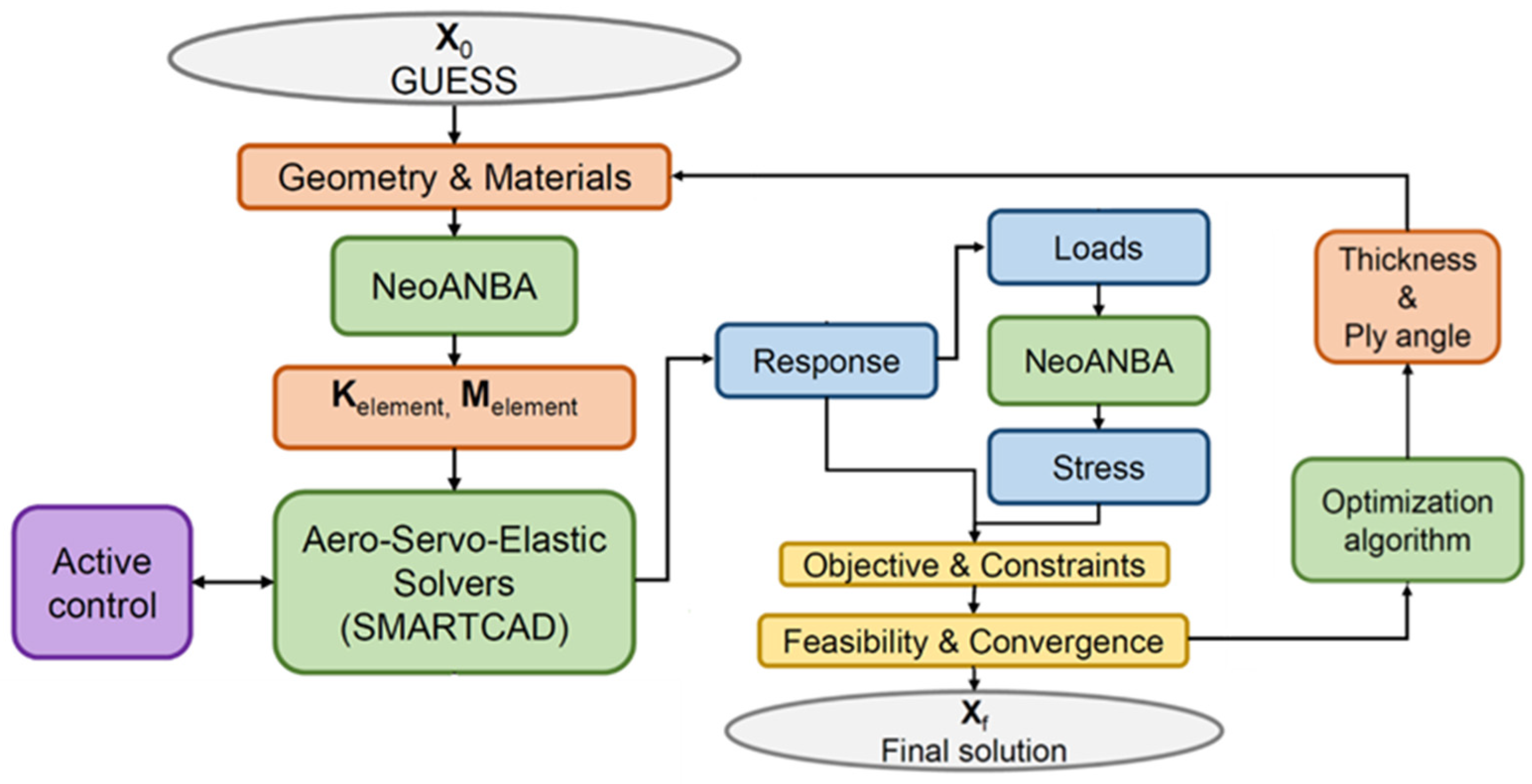
Figure 2 shows a schematic overview of NeoCASS suite. It is composed of three main modules, named GUESS, SmartCAD and NeoRESP. The first one is designed to provide the initial structural sizing of the aircraft, on the basis of a limited set of geometrical properties together with the structural design philosophy selected by the user. The sizing process is performed on the basis of the actual sizing maneuvers specified by the certification rules adopted, for example CS 23 and CS 25 or by a simplified set of user-defined sizing maneuvers. The second module, named SmartCAD, is the aeroelastic kernel, including a family of solvers to provide the complete set of aeroelastic analyses, such as aeroelastic trim, flutter and control reversal. Both GUESS and SmartCAD adopt the approach of frozen maneuvers to solve the trim problems, solving the equilibrium equations as pure algebraic systems of equations not considering the time evolution of loads. The third module is named NeoRESP and allows any generic response problem to be solved, including gust response, in the frequency domain and by recovering the time responses by the inverse Fourier Transform, as well as generating state–space models to design and implement different kinds of active control systems, such as the ones for maneuver and gust load alleviation.

There are two other separate modules to enrich the NeoCASS environment, namely AcBuilder and Weight and Balance (W&B). The first one helps the user to define in a parametric way the initial geometry of the aircraft under analysis, while the second one implements a classical weight and balance process to estimate the different aircraft weights on the basis of statistical formulas. This raw mass distribution is used as an initial point for the sizing performed with the GUESS module, where the structural components of the aircraft are sized to withstand the loads computed with a set of rigid trim analyses.

The analyses carried out by the NeoCASS modules require a definition of a simplified but complete finite element aeroelastic model and dedicated structural and aerodynamic solvers. The model is a stick one, so based on the use of beams elements only, while two aerodynamic modules are available, Vortex Lattice and Double Lattice modules for steady and unsteady aerodynamic computations are used, respectively.

It is important to underline two aspects. First, the generation of the aeroelastic model is fully automatic and does not require any major intervention from the user. Thanks to the simplified geometrical description, the use of a dedicated preprocessor for the meshing generation is not required. The model generated includes the structural elements, based on a three-nodes nonlinear finite volume beam model [41], the aerodynamic panels as well the interface nodes to provide the correct fluid–structure interface.

Second, NeoCASS does not include any tool for the optimal definition of the design point and the related aircraft configuration, which is read as an assigned input and used as is. In other words, there is not any internal loop designed to optimize or change the aircraft configuration. Only the structural design variables, such as the thickness of the structural elements, are updated during the sizing process. In this view, NeoCASS could be interfaced to any conceptual design tool to provide, once requested, the physically based evaluation of the structural mass as well as the aeroelastic impact of the structural flexibility on the main performance indices.

As already anticipated in the introduction, GUESS performs a physical-based fully-stress design of the aircraft, with some limitations to speed up the procedure and generate the aeroelastic models in fully automatic way: the wingbox is assumed to be rectangular and symmetric, the material considered is isotropic, the load envelope is composed of rigid trim analyses and the derivative of the loads with respect to the design variable is not directly considered.

These issues are faced and overcome by the new NeOPT module, which performs a refined optimization of the wingbox sized by GUESS. This is now possible thanks to the meta-model approach introduced in [39]: it is a semi-analytical description of the wingbox, where the 3D geometrical and physical properties of the component are arranged so that different analysis model can be managed with a single set of information, and the results obtained in one domain can be easily transferred to other domains. The wingbox is represented with higher fidelity without increasing its complexity in terms of the FEM model. Moreover, the sizing can be performed by exploiting all the solvers available in NeoCASS, considering dynamic load conditions, such as gust and control input, and the flutter analysis to impose the aero-servo-elastic stability of the aircraft.

One of the features of the meta-model is its interface with NeoANBA, which is a 2D cross-sectional solver that provides the full 6 × 6 beam stiffness matrix of any hollow section composed of isotropic and/or of orthotropic materials. Beyond the fully coupled stiffness matrix, NeoANBA provides the stress distribution of each element for unit loads, and since the method is linear, it is possible to find the cross-sectional stress state for any combination of internal loads obtained with the stick model [39].

2.1. Design Space and Variables

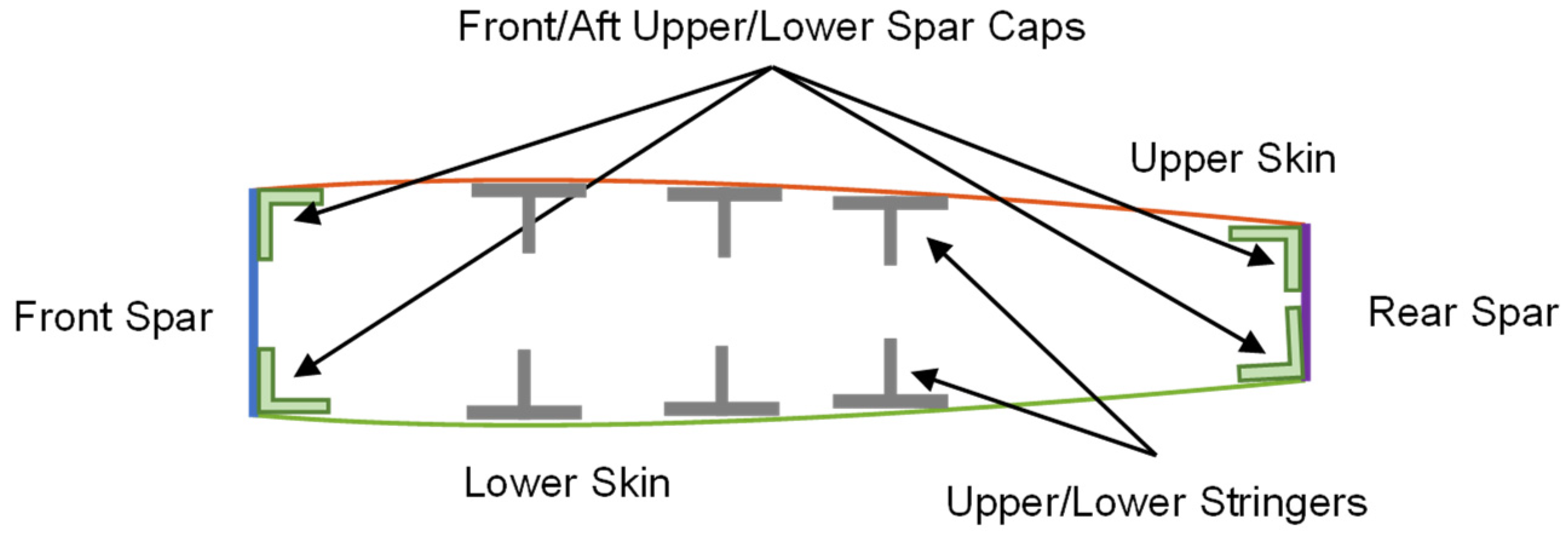
Figure 3 shows a typical wingbox section together with all the structural elements that can become potential design variables. In the simplest case, i.e., with just one cell, there are ten elements characterizing the wingbox structural behavior: upper and lower skins (1–2), front and rear spars (3–4), upper and lower front and rear spar caps (5–6–7–8), and finally upper and lower stringers (9–10). To limit the variability of the section shapes for stringers and spars, we consider only L- and T-shaped sections in the case of spar caps and stringers, respectively. Moreover, following the best practices that link the thickness of the panels to that of the longitudinal elements connected to them, the stringer and spar cap dimensions are parametrized on their thickness. From the optimization point of view, in the most general case the thicknesses of all ten structural elements can be assumed as design variables during the optimal sizing process, section by section spanwise. However, this decision is in the hands of the user. Indeed, it is possible to simplify the optimization process by limiting the total number of design variables by applying a variable-linking approach, where two or more design variables are linked together. For example, if we assume a pure symmetric wingbox with geometrical and structural behavior, we can force all the upper and lower structural elements properties to be the same, for a total of four design variable for each section. When the thickness of a structural element is used as a design variable, it is considered free (to assume any value), while in the other case it is considered fixed, equal to the corresponding linked one. If composite materials are employed, an additional variable can be introduced, i.e., the laminate orientation with regards to the beam axis. It is a unique design variable since the laminate of the upper and lower skin are rotated together symmetrically or asymmetrically. When composite materials are employed, the stacking sequence is a priori defined in terms of the total thickness percentage and orientation of each ply, hence the unique design variable is the thickness of the laminate and its orientation in the case of symmetric or asymmetric section layouts.

NeOPT includes a set of pre-defined layouts of the wingbox sections, summarized in

Table 1. Available section variable linking (* if intermediate spars are present).

Layout Name	Upper Skin	Lower Skin	Upper Stringer	Lower Stringer	Front Spar	Aft Spar	Spar Caps	Mid Spar *	Upper Skin Orientation	Lower Skin Orientation
ISO4	free	=upper skin	free	=upper stringer	free	=front spar	all equal	free *	−	−
COMP4	free	=upper skin	free	=upper stringer	free	=front spar	all equal	free *	−	−
ISO7	free	free	free	free	free	free	all equal	free *	−	−
COMP7	free	free	free	free	free	free	all equal	free *	−	−
ISO10	free	free	free	free	free	free	all free	free *	−	−
COMP10	free	free	free	free	free	free	all free	free *	−	−
ASYM4	free	=upper skin	free	=upper stringer	free	=front spar	all equal	free *	free	=upper skin
ASYM7	free	free	free	free	free	free	all equal	free *	free	=upper skin
ASYM10	free	free	free	free	free	free	all free	free *	free	=upper skin
SYM4	free	=upper skin	free	=upper stringer	free	=front spar	all equal	free *	free	=—upper skin
SYM7	free	free	free	free	free	free	all equal	free *	free	=—upper skin
SYM10	free	free	free	free	free	free	all free	free *	free	=—upper skin

, that the user can adopt to model the wing under design. The name of each available layout of sections includes the type of material (ISO or COMP for aluminum alloy or composite materials, respectively) and the total number of resulting design variables. In the case of composite materials including their orientation among the design variables, the names are SYM or ASYM, in the case of symmetric or asymmetric laminates for upper and lower skins, followed once again by the total number of design variables.

The second level of variable linking is applied in the spanwise direction, the wing is divided into patches where the design variables are kept constant. An example is provided in Figure 4, where the wingbox is divided into five patches. The total number of design variables is equal to the number of patches multiplied by the number of section variables.

2.2. Objective Function and Constraints

Despite the conventional objective of the optimization being the minimization of the structural mass, it must be pointed out that any analysis response or any combination of them can be used as an objective as well. At the same time, any pure structural or aeroelastic responses can be considered as constraints to impose specific requirements. In general, a generic inequality constraint g can be formulated as follows:

$$g\left(x\right)<0$$

(3)

Of special interest are the constraints regarding the buckling loads and the flutter constraint.

The stresses are used to analytically evaluate the buckling of each component following the approach proposed in [42,43]. The buckling indexes (BI) are evaluated as a combination of the axial (x), shear (xy) and bending (b) loading of the element, as in Equation (4). The critical (cr) value for each force component is evaluated starting from the element size and the material characteristics.

$$BI=1-\left(\frac{-N_x}{N_{x cr}}+\frac{\left|N_{xy}\right|}{N_{xy cr}}+\frac{N_b}{N_{b cr}}\right)$$

(4)

The failure of the components depends on the nature of the materials: if they are isotropic, the Von Mises’s criterion is used, otherwise the Tsai–Hill criterion is applied. Furthermore, whichever response obtained with an aero-servo-elastic analysis can be used as an additional constraint, as in the case of the flutter or in the case of control surfaces with minimum efficiency.

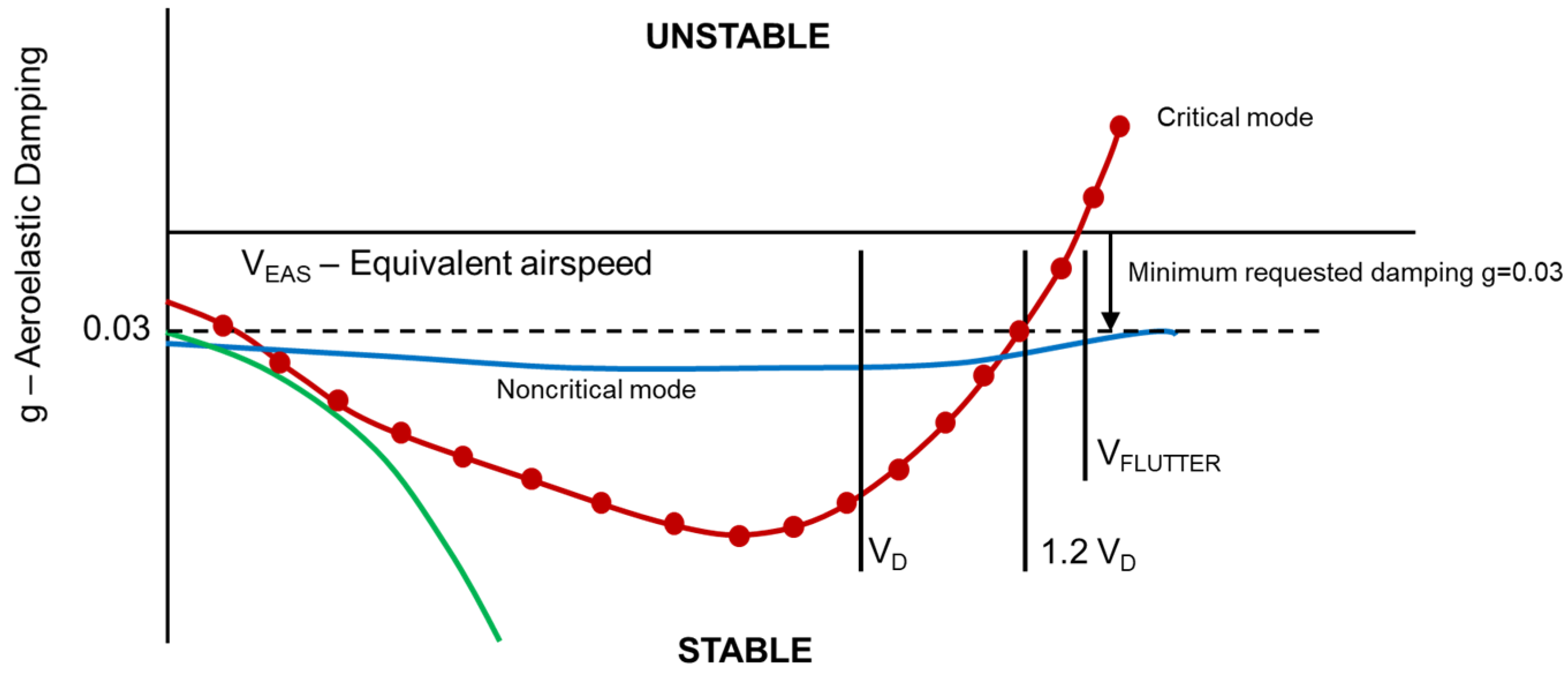
For flutter constraints, it must be recalled that the flutter analysis implemented in NeoCASS is based on a special implementation of a classical p-k method [44], whose typical results are represented by the so-called V-g and V-frequency plots representing the trend of the eigenvalues of the aeroelastic problem with respect the flight speed, solved in an iterative way. Figure 5 sketches a typical flutter result in terms of an aeroelastic damping trend, showing the minimum values requested by the certification rules. The flutter constraint is then imposed by shaping the minimum, negative value of aeroelastic damping for the entire flight envelope for all the critical mode shapes.

2.3. The MDO Problem Solved in NeOPT

NeOPT is an optimizer that solves a generic constrained optimization problem in the form of Equation (5), namely, “find the design variables x that minimize the objective function f, and x has to be in the search space S that satisfies the response constraint g and is limited by an upper and lower bound (ub/lb)”:

$$\underset{x}{\min }f\left(\mathit{x}\right)\mathit{s}.t.\mathit{x}\in S;\mathit{S}:\{\mathit{x}\in {\mathbb{R}}^n\mathit{s}.t.\mathit{g}\left(\mathit{x}\right)\le 0\cap {\mathit{x}}_{\mathit{lb}}\le \mathit{x}\le {\mathit{x}}_{\mathit{ub}}\}$$

(5)

Figure 6 shows the workflow adopted by NeOPT: the design variables x, described further on, are processed with a finite-element cross-sectional solver (NeoANBA) [38,39], which provides the stiffness and mass matrices of the beam elements describing the wingbox. This solver is based on the ANBA theory [45], where the cross section is modelled with panels (skins and spars) and concentrated area elements (stringers and spar caps).

Then, the built-in aero-servo-elastic solvers included into the aeroelastic kernel called SMARTCAD are used to evaluate the structural responses and the loads are used to evaluate the cross-sectional stress distribution to analytically evaluate the constraints. The feasibility and convergence criteria are evaluated by the optimization algorithm, providing the new set of design variables that is used in the next optimization step. Since NeoCASS is Matlab-based, all the features developed in NeOPT are written in the same coding environment and the optimizer used is the Matlab built-in fmincon, with the Sequential Quadratic Programming (SQP) options. It is a gradient-based optimization method that computes the gradient by finite differences.

At this point, it is possible to perform the first level of variable linking, exploiting a predefined set of section layouts listed and described in Table 1, where it is described if a design variable is free or it is linked to another one for the selected section layout. If intermediate spars are present, their thickness is described by a single and free design variable.

The framework is entirely developed inside NeoCASS, hence any kind of analysis can be used to obtain the internal force distribution used to evaluate the constraints. In the optimization, multiple sets of loads coming from different analyses can be used together to evaluate the worst-case failure and buckling index for a given component, and typically trim analysis and dynamic gust are considered simultaneously. The available solutions are listed hereafter (in brackets the equivalent Nastran solution).

▪

Static solution (SOL101);

▪

Elastic trim (SOL144);

▪

Flutter analysis (SOL145);

▪

Dynamic Aeroelastic solution (SOL146);

▪

State-Space analysis (Not Available).

The latest analysis option is crucial when active control technologies (such as maneuver and gust load alleviation or flutter suppression) are considered in the optimization loop since the control synthesis is easier to apply in the time domain.

Before starting the optimization, a selection of the worst-case load conditions is performed through the classic 2D plots in different monitoring stations by picking the maneuvers that provide the most critical values for the bending–torsion and bending–shear envelope spanwise, therefore reducing the number of analyses required during the refined optimization loop without losing significant load conditions.

3. Application to a Twin-Aisle Long-Haul Aircraft

This section summarizes the results obtainable with the approach proposed in this paper when applied to a typical twin-aisle long-haul family aircraft. It is divided into three parts: Firstly, the baseline aluminum aircraft is designed, starting from scratch and using as reference an existing airplane, then a comparative analysis between the baseline aircraft and the equivalent with a composite wing is performed by keeping the same geometry. Finally, the sensitivity of the overall performances for both iso- and orthotropic wingboxes with regards to the aspect ratio is obtained. It must be remembered that in conceptual design it is important to identify the impact of a design choice on the overall design of the aircraft; for this reason, a fast but reliable study changing some of the wingbox’s macro parameters is performed in this section, not aiming at defining the optimal design configuration but more oriented at better understanding the impact of adopting increased aspect ratios and composite wings for this class of aircraft.

3.1. The Baseline Aircraft

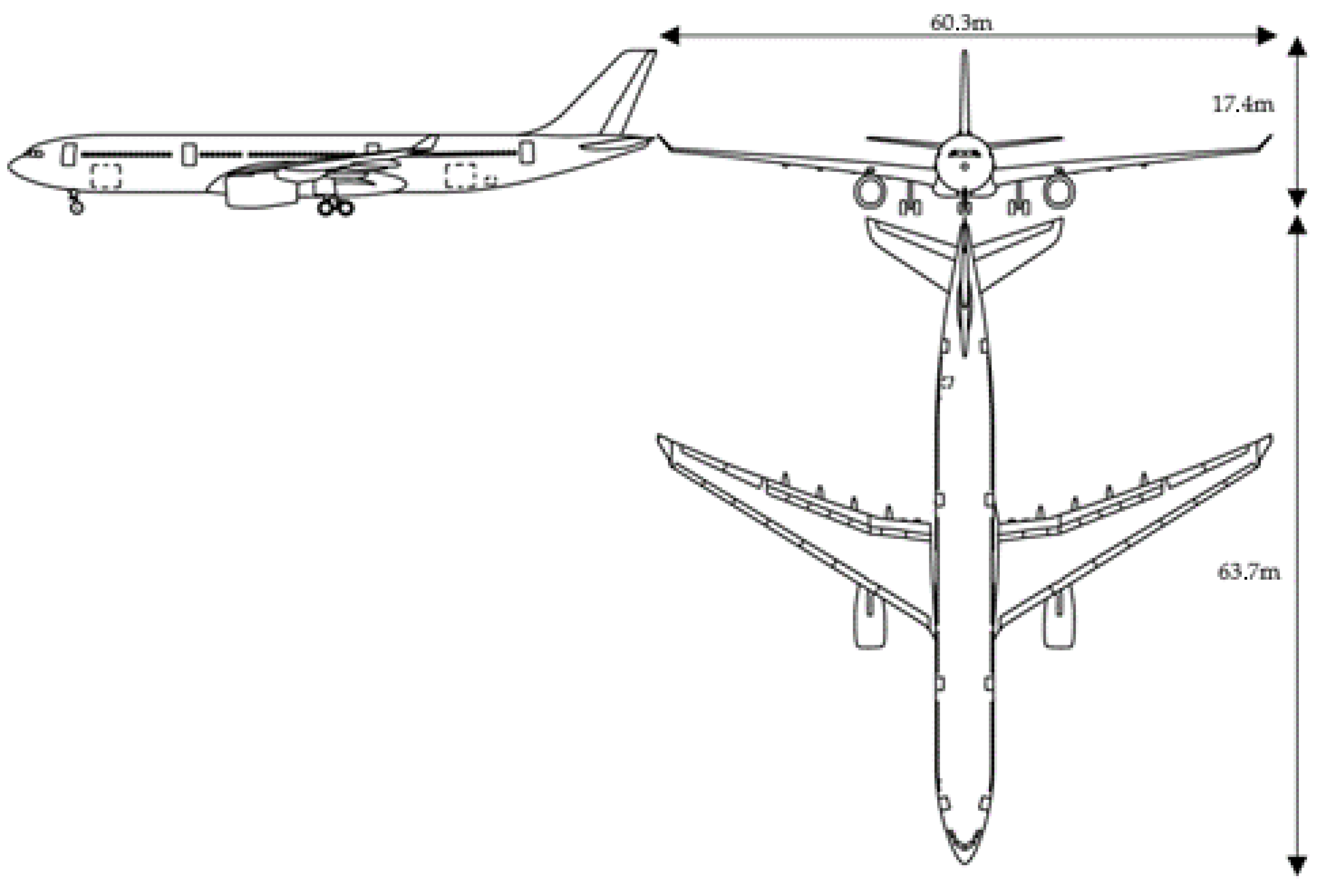
The reference aircraft used in this study is inspired by the publicly available data describing the Airbus A330-300 [46] to define a generic aircraft, renamed here as Twin-Aisle Long-Haul (TALH) to avoid any kind of relation and confusion with the actual commercial aircraft. The only data used are the external dimensions in Figure 7 and engine mass, used to produce the AcBuilder model in Figure 8a and the equivalent stick model in Figure 8b. The main hypothetical characteristics of the TALH aircraft are listed in

Table 2. TALH main characteristics.

Number of passengers	300
Wing area	366.7 m2
Aspect ratio	9.17
Max range	10,200 km
Max cruise altitude	13,100 m
Max Operating Mach number	0.87
Max Operating Speed (EAS)	175 m/s
Cruise speed at FL 380 (TAS)	244.91 m/s
Cruise speed (EAS)	127.5 m/s
Max lift coefficient in take-off configuration	2.1
Max lift coefficient in landing configuration	2.5
Max lift coefficient in clean wing configuration	1.75
Clean lift curve slope	5.7 1/rad

.

The aircraft is entirely made of aluminum, the wingbox is located between 25.5% and 64% of the root chord and between 25% and 61% of the tip chord. The wing elements are divided into five patches as in Figure 4.

The wingbox is described with two section layouts available among the ones in Table 1: ISO7 and ISO10. The aluminum alloy properties are listed in

Table 3. Aluminum alloy properties.

Material	E11 (GPa)	E22 (GPa)	G12 (GPa)	ν12 (-)	ρ (kg/m3)	σmax (MPa)
AL7075-T6	72	72	27.69	0.3	2800	430

.

The sizing conditions in terms of trim maneuvers are listed in

Table 4. Maneuver conditions used to size the aircraft.

ID	Type	CS	N	z(m)	Mach
1–4	Pull-up	25.331	2.5	0/8061/0/12,250	0.514/0.87/0.375/0.87
5–8	Push-down	25.331	−1.0	0/8061/0/12,250	0.514/0.87/0.375/0.87
9	Flap max down	25.345 a1	2.0	0	0.329
10	Static Gust for landing configuration	25.345 a2	1.0	0	0.329
11–16	Aft movement of pitch control at VA, VC, VD URDD5 (positive and negative)	25.331 b1	1.0	0	0.357/0.375/0.514
17/20/23/26	Sideslip max rudder (positive and negative)	25.351 a	1.0	0	0.357/0.226
18/21/24/27	Sideslip overswing (positive and negative)	25.351 b	1.0	0	0.357/0.226
19/22/25/28	Sideslip maneuver 15° (positive and negative)	25.351 c	1.0	0	0.357/0.226
29/31	Aileron abrupt maximum deflection at $\mathrm{V}\mathrm{A}=\sqrt{{\mathrm{N}}_{max}}\ast \mathrm{V}\mathrm{S}$ (positive and negative)	25.349	1.0	0	0.357
30/32	Aileron abrupt deflection + 2/3 max load factor (positive and negative)	25.35	1.7	0	0.357

, they are automatically defined on the basis of the CS25 certification rules [35]. The related trim loads are multiplied by a 1.5 safety factor before the evaluation of the constraints.

In addition to the structural constraints evaluated for the maneuvers set, a no-flutter constraint was imposed for three different altitudes of 0 m, 8061 m (≈26,500 ft) equivalent to the corner point in n-V flight envelope diagram and the cruise altitude of 11,582 m (≈38,000 ft).

The sizing process of the baseline aluminum aircraft leads to a wingbox mass of 9639.55 kg for the ISO7 section and 9553.53 kg for the ISO10 section, highlighting how a higher number of design variables on the cross section helps to obtain a lighter structure. The ISO10 wingbox’s mass obtained so far is used as a reference value for next investigations.

3.2. The Composite Baseline Aircraft

Thanks to the high strength-to-weight and stiffness-to-weight ratios, composite materials can be exploited to design lighter structures. The baseline aircraft wingbox has been re-designed considering the possible adoption of composite materials. The only component modified during this process is the wingbox itself, the remaining part of the aircraft as well as the non-structural masses were kept identical to the baseline ones.

As shown for the isotropic wingbox, two different cross-section layouts were used (COMP7 and COMP10). Moreover, a test considering the laminate orientation as a design variable (COMP7 ASYM) was performed to evaluate the potential mass saving introduced with the aeroelastic tailoring by controlling the laminate orientation angle. The section layout characteristics are described in Table 1.

Two different stacking sequences were employed, one is quasi-isotropic (LAM1) and the other one (LAM2) has a larger amount of fiber in the 0° direction. The two stacking sequences are illustrated in Figure 9a,b, while

Table 5. Carbon Fiber Uni-Directional (CFUD) properties from [48].

Material	E11 (GPa)	E22 (GPa)	G12 (GPa)	ν12 (-)	ρ (kg/m3)	σmax (MPa)
CFUD	135	10	5	0.3	1500	1500

lists the characteristics of the carbon fiber unidirectional ply (CFUD). The difference between the two stacking sequences is that the 90° plies in LAM1 are converted into 0° plies in LAM2. The choice of using uni-directional plies instead of other fabric types was made to replicate the automated fiber-placing process adopted for the realization of a large aeronautical structure with a non-conventional plies orientation [47].

The sizing was performed considering the same load conditions and aeroelastic stability requirements used for the aluminum aircraft, and the results obtained are shown in

Table 6. Wingbox masses and their variation w.r.t. ISO10 solution for the baseline aircraft.

	Mass (kg)	Δ% w.r.t ISO10
ISO7	9639.55	+0.90
ISO10	9553.53	-
COMP7 LAM1	6957.19	−27.18
COMP10 LAM1	6770.72	−29.13
COMP7 LAM1 ASYM	6815.47	−28.66
COMP7 LAM2	5352.07	−43.98

: composite wingboxes are lighter than the aluminum ones, thanks to their better strength/mass and stiffness/mass ratios. As for the aluminum case, it is possible to see how a larger number of design variables saves more structural mass. Furthermore, the additional laminate’s orientation design variable allows for an asymmetric orientation of the upper/lower laminate skins: this introduces a wash-out effect that decreases the wing root bending moment thanks to the bending–torsion coupling of the beam stiffness matrix, this can be noted by comparing the solutions named COMP7 LAM1 and COMP7 LAM1 ASYM, where the better orientation of the material led to a 141.72 kg mass saving. The impact of the fiber placement is noted as well from comparing the results obtained with the COMP7 LAM1 and COMP7 LAM2 solutions: fibers orthogonal to the beam axis are less relevant and their contribution to the wing stiffness is negligible, as in the case of LAM2, which leads to a wingbox that is 23% lighter in relation to the same solution obtained with COMP7 LAM1.

3.3. The Sensitivity to Increased Aspect Ratio

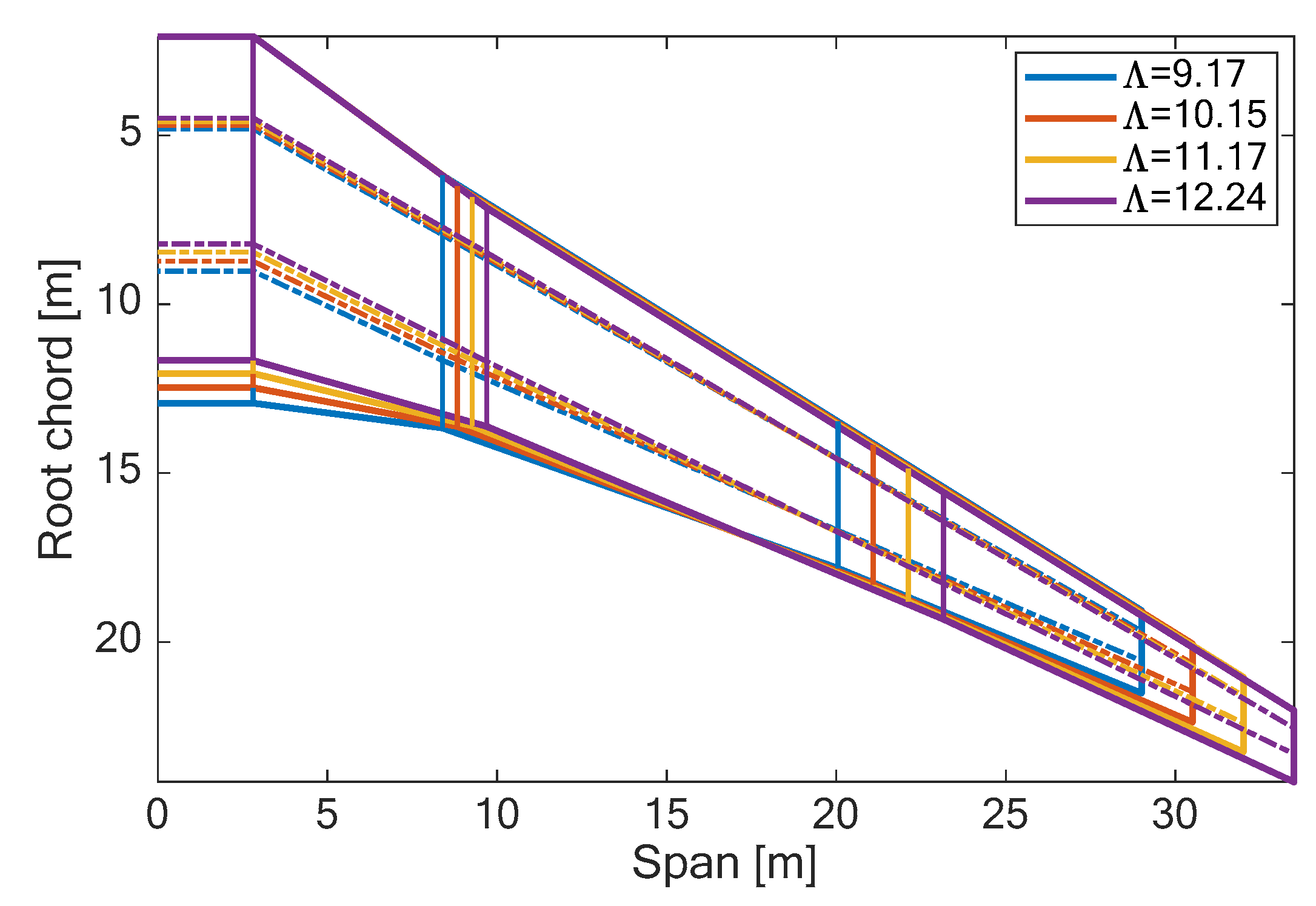
So far, the conceptual design showed that more efficient structures can be realized with composite materials. This section performs a parametric study by increasing the wing’s aspect ratio (Λ), keeping constant the projected area and the taper ratio. Remembering that $\mathsf{\Lambda }=\frac{wing spa{n}^2}{wing area}$ and by freezing the wing area, it is possible to obtain the relation between the aspect ratio and wingspan.

This topic receives huge interest from the aeroelastic community [22,23] because an increase in the aspect ratio leads to better aerodynamic performance by reducing the induced drag, but it increases the wing root bending moment, which can be considered the most relevant KPI for wingbox sizing. For this reason, a limited population of aircraft models has been generated with increasing wing aspect ratios by stretching the wing planform geometry of the baseline aircraft while keeping the wing area, leading edge sweep and taper ratio constant, as shown in Figure 10. It must be highlighted that the impact of changing wing geometry on other onboard devices is not considered in this study. Just as an example, the increase in the wing aspect ratio results in reduced available space inside the wingbox, which could require a completely different landing gear configuration, for example, fuselage-mounted landing gear, which adds additional complexity to the analysis. Moreover, the change in the position of the wing caused by the stretching process of the planform could potentially lead to a change in the position of the center of gravity. However, considering that this change is small, it is assumed that the cg is located at a fixed position in each aircraft model, making the trim process easy. Finally, most importantly, any change in the relevant aircraft parameters would require the re-definition of the design point diagram, taking advantage of the snowball effects. However, the super simplification adopted here is justified by the fact that the main goal of this paper is to demonstrate the reliability of the tool presented in generating trade-off studies that can fully capture the structural mass sensitivities in compliance with the aeroelastic requirements dictated by the certification rules and not to present an optimal aircraft configuration. Indeed, the tool NeOPT, part of the NeoCASS suite, must be coupled to classical L0 aircraft conceptual design tools to generate optimal aircraft configurations that are fully compliant with the aeroelastic requirements from the early design phases, avoiding later design corrections and their related weight penalties.

The aspect ratio is modified as in

Table 7. Numerical values of the wings considered and their relative variation w.r.t. Λ = 9.17.

Wing Area (m2)	Wingspan (m)	Λ (-)	Δ Span %	Δ Λ %
366.7	58	9.17	-	-
366.7	61	10.15	+5.17	+10.69
366.7	64	11.17	+10.34	+21.81
366.7	67	12.24	+15.51	+33.48

and the result is represented in Section 3.4. For each wing, the wingbox nondimensional position is maintained, i.e., the front spar position at the root is at 25.5% of the root chord and 25% of the tip chord, while the rear spar is placed at 64% of the root chord and 61% of the tip chord. This leads to a preliminary location of the elastic axis, coincident with the nodal line placed at 44.6% of the root chord and 43% of the tip chord. The spars are planar, meaning that no kinks are present between the fuselage intersection and the wing tip, the only kink present is the one between the carrythrough and the external part of the wingbox.

The obtained aircraft family was sized following the same procedure used for the baseline aircraft (Λ = 9.17), using the same constraints, load conditions and objective function.

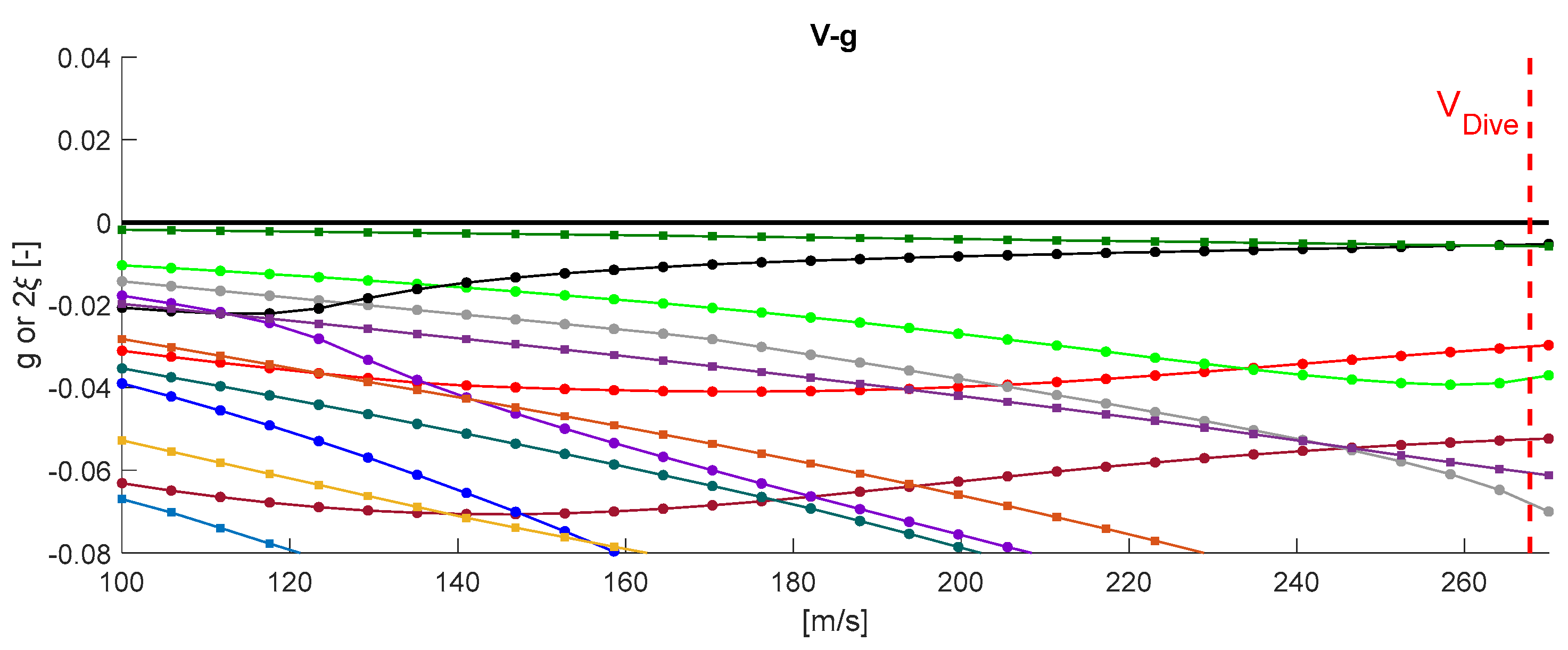
As an example of the flutter constrain implementation, Figure 11 shows the evolution of the damping of the aeroelastic modes vs. the airspeed (V-g plot) for the COMP7 LAM2 Λ = 12.24 case: it is possible to see that the aircraft is dynamically stable at the corner point altitude (8061 m) until the maximum Mach number and dynamic pressure. Similar results have been achieved for all the configurations studied.

The sizing is performed for a family of 24 aircraft, considering the four aspect ratios and the six cross sections and material layout.

Table 8. Wingboxes mass and relative variation with respect to Λ = 9.17 with the same section layout and ISO10 layout.

Section Type		Λ = 9.17	Λ = 10.15	Λ = 11.17	Λ = 12.24
ISO7	Mass (kg)	9640	10,597	11,700	14,201
	Δ wrt Λ = 9.17 (%)	0.00	+9.94	+21.38	+47.32
	Δ wrt Λ = 9.17 ISO10 (%)	+0.90	+10.93	+22.47	+48.64
ISO10	Mass (kg)	9554	10,419	11,422	13,594
	Δ wrt Λ = 9.17 (%)	0.00	+9.05	+19.56	+42.29
	Δ wrt Λ = 9.17 ISO10 (%)	0.00	+9.05	+19.56	+42.29
COMP7 LAM1	Mass (kg)	6957	7859	8778	10,142
	Δ wrt Λ = 9.17 (%)	0.00	+12.96	+26.18	+45.77
	Δ wrt Λ = 9.17 ISO10 (%)	−27.18	−17.74	−8.11	6.15
COMP10 LAM1	Mass (kg)	6771	7696	8395	9752
	Δ wrt Λ = 9.17 (%)	0.00	+13.67	+23.98	+44.03
	Δ wrt Λ = 9.17 ISO10 (%)	−29.13	−19.44	−12.13	2.07
COMP7 LAM1 ASYM	Mass (kg)	6815	7740	8357	9340
	Δ wrt Λ = 9.17 (%)	0.00	+13.56	+22.62	+37.05
	Δ wrt Λ = 9.17 ISO10 (%)	−28.66	−18.99	−12.52	−2.23
COMP7 LAM2	Mass (kg)	5352	5648	6082	7318
	Δ wrt Λ = 9.17 (%)	0.00	+5.54	+13.63	+36.74
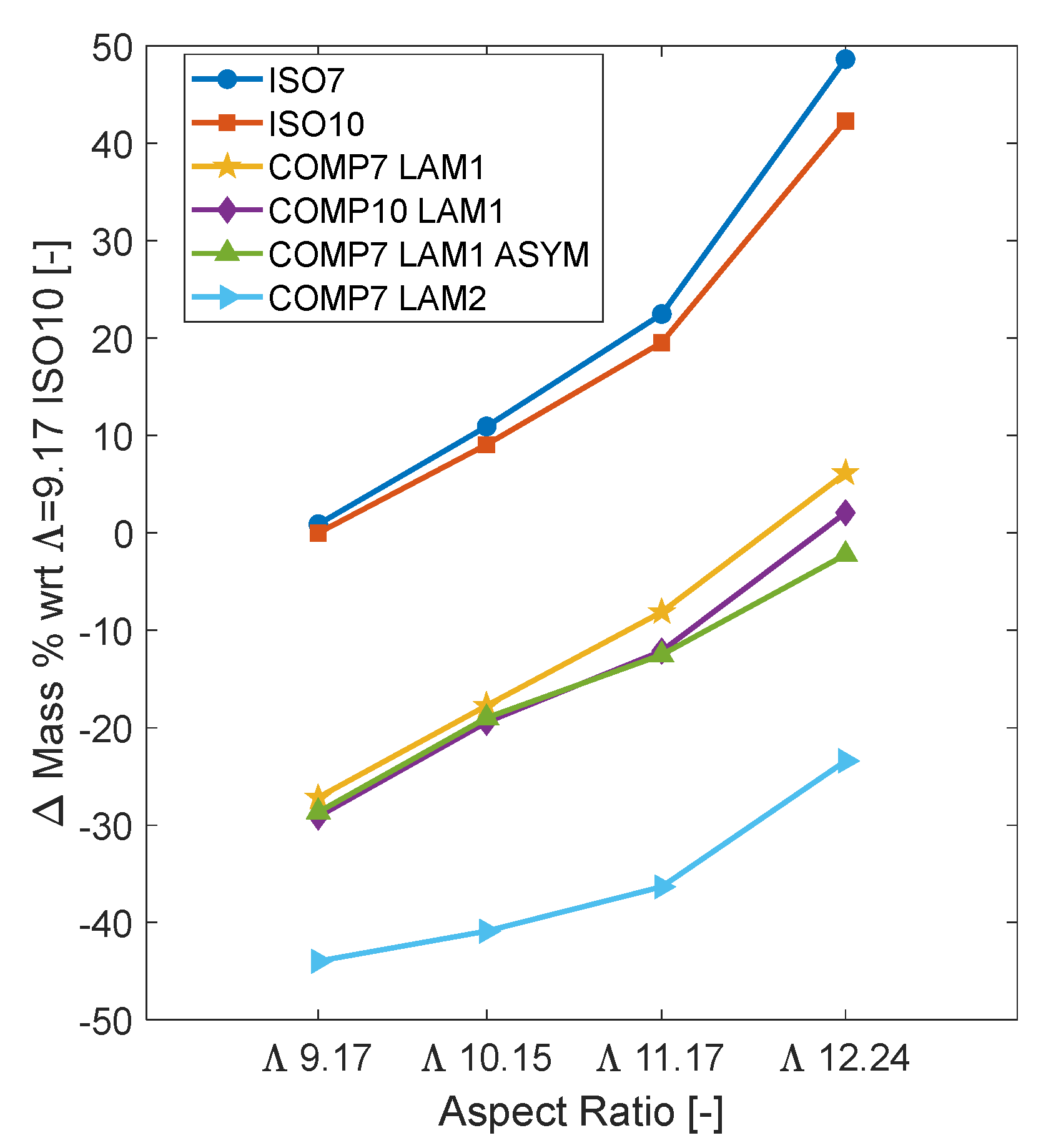
	Δ wrt Λ = 9.17 ISO10 (%)	−43.98	−40.88	−36.34	−23.40

shows results of the sizing for the right wingbox: for each section layout and aspect ratio there are three values reported: the first row represents the structural mass of the wingbox, the second row is the percentual variation of the mass with respect to the solution obtained for the same section layout in the baseline configuration (Λ = 9.17) and the last row represent the mass’ percentual variation with respect to the baseline solution obtained with the ISO10 layout, which is the lightest aluminum wingbox.

As expected, when increasing the aspect ratio, the mass increases for two main reasons: the first one is because the span is increased and hence the arm for the bending moment is also increased, which is the most relevant internal force for the structural sizing of the wing. The second one is due to the fact that stretching the wing and keeping the same percentual position in the chord direction for the spar reduces the sizes of the wingbox, hence more material is needed to restore the stiffness loss due to geometrical effects.

The results of Table 8 are graphically reported in the diagrams of Figure 12a,b. The left plot shows how the evolution of the mass is mainly clustered depending on the material used, in this case the aluminum is the heavier solution, while LAM2 is the lightest and LAM1 assumes intermediate values. The difference in the results obtained for the two different stacking sequences is due to the 10% oriented at 90° for the LAM1, which results in a penalty mass with respect to LAM2. As seen for the baseline aircraft, by increasing the aspect ratio it is possible to better appreciate the effect of the aeroelastic tailoring comparing the COMP7 LAM1 (yellow star marker in Figure 12a,b) solution with COMP7 LAM1 ASYM (green lower triangle marker in Figure 12a,b). For the second solution, the orientation of the laminate is a design variable, and the optimizer creates a wash-out effect that passively alleviates the maneuver load. This is translated into a mass reduction with respect to the results obtained for the solution where the orientation is fixed. In terms of relative variation with respect to the baseline solution, the mass varies following a more homogeneous trend.

The diagram in Figure 13 shows the relative variation of the wingbox’s mass with regards to the solution obtained with the ISO10 layout, which is the lightest solution for aluminum. Composite materials allow an increase in the aspect ratio without increasing the wingbox mass with respect to a conventional aluminum solution; indeed, the COMP7 LAM1 ASYM and LAM2 structural mass for an aspect ratio of 12.24 is lower than the mass obtained for the ISO10 layout for the baseline aircraft.

3.4. Overall Performances Estimation

The results obtained so far show an increase in mass for the aspect ratio extension from Λ = 9.17 to Λ = 12.24, which would mean a worsening of the fuel efficiency if only the structural performance is considered. However, the aspect ratio increasing leads to better aerodynamic performances by reducing the induced drag term, so it is of particular interest to estimate its impact in terms of overall performance and potential emissions reduction. To do so, the induced drag coefficient is now quantified with an inviscid computation, i.e., Morino’s method implemented in ALIS [49], an in-house 3D panel method solver, that adopts Trefftz’s plane for this calculation. Then, Breguet’s range equation is rewritten with the non-dimensional coefficient and the drag term is decomposed in a constant term C_D0, containing viscous drag, and the induced term C_Di. 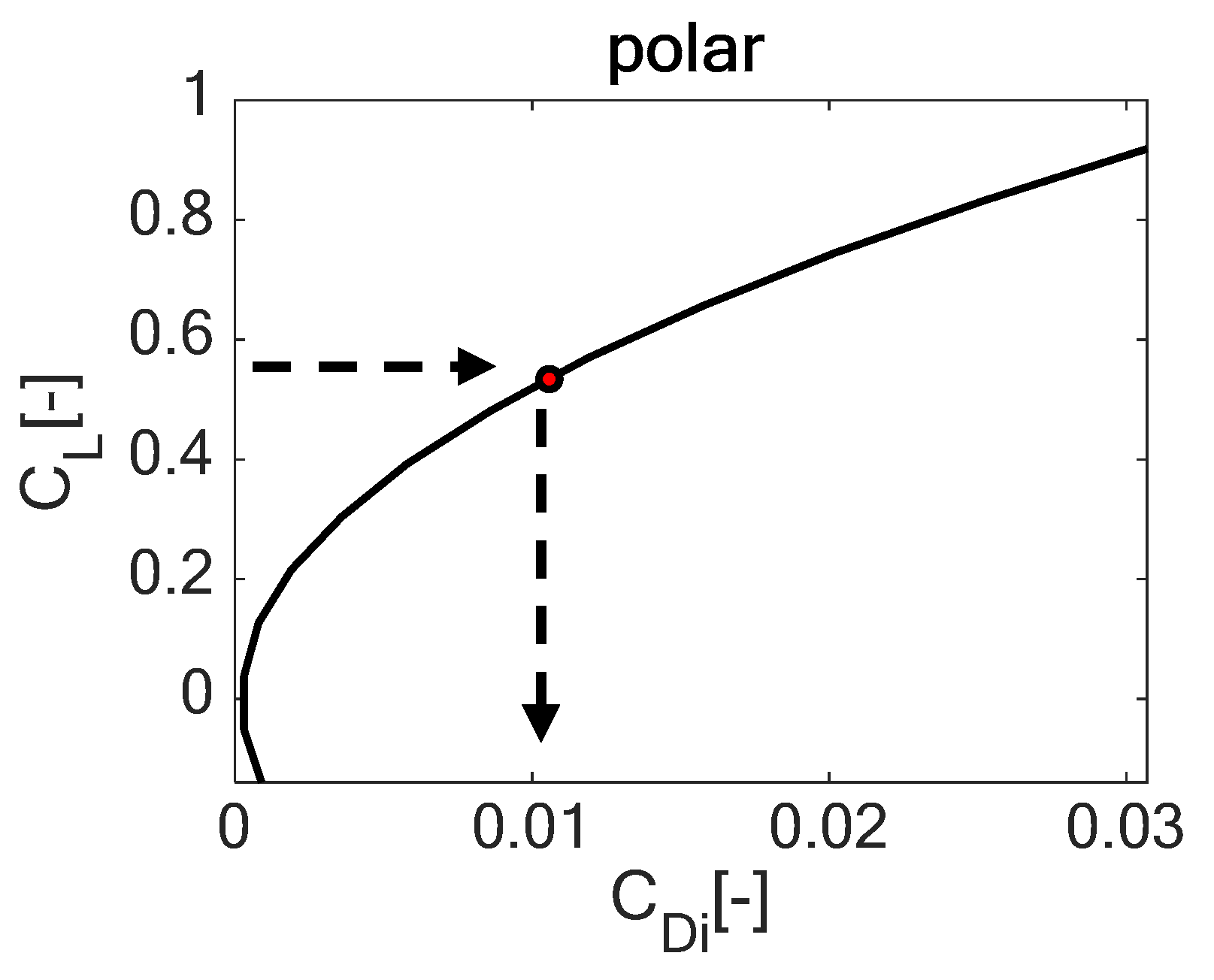The C_D0 is assumed to be equal to 0.018 like for the CERAS [50], and is kept constant since the wetted wing area is not modified and the lift coefficient C_L value is the one obtained to equilibrate the weight of the aircraft for an intermediate value between W₁ (MTOW = OEW + payload + fuel) and W₂ (OEW + payload), namely W₁ − 0.5W_fuel. Once the lift coefficient is obtained, it is possible to evaluate the induced drag term by interpolating the polar curve, as is graphically shown in Figure 14.

The fuel weight, the velocity and the specific fuel consumption are fixed in this study, and the airspeed is not modified to avoid the dependency of the SFC on this parameter. Indeed, the SFC increases with the airspeed and finding the optimal point for the flight speed and SFC values is beyond the aim of this work, which is focused on the structural sizing.

$$R=\frac{V_{TAS}}{g}\frac{C_L}{C_{D0}+C_{Di}}\frac{1}{SFC}ln\frac{W_1}{W_2}$$

(6)

Breguet’s equation can be solved for the fuel weight imposing the range, as in Equation (7). In this case, the lift coefficient, and hence the induced drag term, directly depend on the current actual weight, which is a function of the fuel weight itself. In the following, a 10,000 km route is considered. The SFC is assumed to be $15.4\frac{g}{kN s}$ for each engine.

$$\frac{V_{TAS}}{g}\left(\frac{C_L\left({\mathit{W}}_{\mathit{f}\mathit{u}\mathit{e}\mathit{l}}\right)}{C_{D0}+C_{Di}\left(C_L\right({\mathit{W}}_{\mathit{f}\mathit{u}\mathit{e}\mathit{l}}\left)\right)}\right)\frac{1}{SFC}ln\left(\frac{W_2+{\mathit{W}}_{\mathit{f}\mathit{u}\mathit{e}\mathit{l}}}{W_2}\right)-R=0$$

(7)

The results obtained in terms of range and fuel consumption are reported in

Table 9. Fuel burnt (t) on a 10,000 km route, in brackets the variation with respect to Λ = 9.17 with the same section layout.

	Λ = 9.17	Λ = 10.15	Λ = 11.17	Λ = 12.24
ISO7	128.055 (-)	125.920 (−1.67%)	123.998 (−3.17%)	123.471 (−3.58%)
ISO10	127.995 (-)	125.797 (−1.72%)	123.824 (−3.26%)	123.138 (−3.80%)
COMP7 LAM1	126.056 (-)	123.966 (−1.66%)	122.071 (−3.16%)	120.970 (−4.04%)
COMP10	125.913 (-)	123.852 (−1.64%)	121.831 (−3.24%)	120.751 (−4.10%)
COMP7 LAM1 ASYM	125.936 (-)	123.879 (−1.63%)	121.800 (−3.29%)	120.476 (−4.34%)
COMP7 LAM2	124.861 (-)	122.398 (−1.97%)	120.292 (−3.66%)	119.196 (−4.54%)

and plotted in Figure 15a,b. The punctual values are fitted with a third-order polynomial curve fitting, which provides an indication of the evolution of the two performance indexes for higher aspect ratios. For each configuration, the performance index has a convex or concave shape, meaning that it is possible to find a stationary point where the KPI is minimized, as for the fuel consumption, or maximized, as for the range. The position of the stationary point depends on the structural layout adopted, but in general it is between Λ = 12 and Λ = 12.5 for all the solutions obtained.

The vertical dashed line represents the aspect ratio value that limits the current aerodrome reference code (ARC) [24] of the Airbus A330–300, this must be considered in the conceptual design phase because the ARC can be a limiting factor for the aspect ratio increase. In this case, 65 m is the maximum span of the ARC E aircraft class and is equivalent to an aspect ratio of 11.52, but a further extension of the span up to more than 67 m can lead to performance improvement.

Both the plots show that it is possible to obtain a maximum for the range and a minimum for the fuel consumption, considering an aspect ratio higher than the maximum studied. The most promising solution among the ones studied is achieved with the COMP7 LAM2 solution for an aspect ratio of 12.24.

Table 10. Environmental and economic impact quantitative analysis: comparison between the baseline aluminum configuration, the same Λ but realized with composite materials and the most promising composite solution with Λ = 12.24. A 10,000 km route is considered.

Configuration	Fuel Burnt per Flight (t)	Fuel Saving per Fight (t)	Fuel Cost Reduction per Flight (USD)	CO2 Avoided per Flight (t)	Fuel Cost Reduction per AC per Year (million USD)	CO2 Avoided per AC per Year (t)
Λ 9.17 ISO10	127.995	-	-	-	-	-
Λ 12.24 ISO10	123.138	4.857	5456	15.635	1.993	5706.91
Λ 9.17 COMP7 LAM2	124.861	3.134	3511	10.088	1.281	3682.12
Λ 12.24 COMP7 LAM2	119.196	8.799	9890	28.323	3.609	10,337.90

presents the environmental impact and a limited economic impact on the fuel-related direct costs of using composite materials instead of aluminum alloy, and the impact of an aspect ratio increase.

The usage of composite materials (COMP7 LAM2) in the same wing configuration provides a fuel saving of 3.134 tons (−2.4%) with respect to the aluminum solution (ISO10). A detailed evaluation of how this fuel reduction impacts the emission would require a dedicated tool. Here, a simplified approach is reported while waiting for the implementation of this new tool. Considering an emission factor of $9.75\frac{\mathrm{kg} C{O}_2}{gall}$ [51], equivalent to $3.219\frac{\mathrm{kg} C{O}_2}{\mathrm{kg} fuel}$ with an averaged fuel density of $0.8\frac{\mathrm{kg}}{{\mathrm{m}}^3}$, the CO₂ avoided is 10.088 tons for each flight. From an economical perspective, saving 3.134 tons of fuel with a fuel cost of 143 USD/bbl (average fuel price for the first semester of 2022 [52]), equivalent to $1.124\frac{USD}{\mathrm{kg} fuel}$, corresponds to USD 3511 saved on a 10,000 km route, considering the full availability of the aircraft during the year and one journey per day (365 flights), the total year’s fuel cost saving is around USD 1.28 million per year per aircraft.

The same comparison can be made considering the obtained minimum fuel consumption for the LAM2 layout with an aspect ratio of 12.24.

The results obtained in the most performant solution (LAM2 Λ = 12.24) at fleet level, e.g., considering 200 aircraft, would lead to more than 2 million tons of CO₂ avoided in one single year. Since it is difficult to quantify the emission, as an example a natural-gas-fired thermo-electric power plant [53], that supplies 1.8 million families and produces 5 tWh, considering an average yearly energy consumption of 2700 kWh for a 3–4 people family, produces a similar amount of CO₂.

3.5. Other Aeroelastic Constraints

The optimization so far presented was performed considering structural (failure and buckling) and aeroelastic (flutter) constraints, helping the designer to identify the most promising solution among the considered ones. The adopted constraints do not directly impose stiffness requirements on the wing, in fact the wing is designed to withstand loads and to be stable across the flight envelope. This may lead to a very efficient wing from the structural point of view, but one that is too flexible to properly handle the aircraft. At this point, the design can be refined by introducing other constraints or requirements to the design and evaluating how much penalty structural mass has to be added to satisfy different requirements.

A typical example of this is the efficiency of the aileron (Equation (8)), which may end in a control reversal that must be avoided and that can be defined as

$$\eta =\frac{C_{l\partial {\delta }_{aileron,flexible}}}{C_{l\partial {\delta }_{aileron,rigid}}}$$

(8)

Thanks to its adaptability, NeOPT can include this constraint in the optimization and evaluate how much this additional limitation would cost in terms of structural mass; an additional optimization of the Λ 12.24 COMP7 LAM2 solution is performed.

The constraint is implemented as in Equation (8), and it is imposed in two different flight points: in cruise condition (Mach = 0.83 and EAS = 127.5 m/s) it must be ${\eta }_{cruise}>0.5$ and at the corner point (Mach = 0.87 and EAS = 175 m/s) ${\eta }_{corner point}>0.3$. These constraints are added to the ones already used for the previous optimizations and the results are presented in

Table 11. Comparison between previous optimization and the one considering aileron efficiency.

Λ 12.24 COMP7 LAM2 Constraints	Wingbox Mass (kg)	${\mathit{\eta }}_{\mathit{c}\mathit{r}\mathit{u}\mathit{i}\mathit{s}\mathit{e}}$	${\mathit{\eta }}_{\mathit{c}\mathit{o}\mathit{r}\mathit{n}\mathit{e}\mathit{r}\mathit{p}\mathit{o}\mathit{i}\mathit{n}\mathit{t}}$
Trim, flutter	7318.40	8%	−5%
Trim, flutter, aileron efficiency	7939.43	58%	33%

, where it appears that a structural mass increase of 8.5% is required to satisfy the aileron efficiency constraint.

Table 11 clearly shows how not considering stiffness constraints, such as the aileron effectiveness, may lead to a poor design that may jeopardize the aircraft, as in the case of Λ 12.24 COMP7 LAM2 that experiences control reversal at the corner point. This latest example highlights the importance of performing aeroelastic sizing during the conceptual design, where performance constraints (aileron efficiency) may considerably increase (8.5%) the structural wing’s structural mass. The problem can be also faced by adding high-speed ailerons in the inner wing (not discussed in this work). However, this latest option shows how crucial the aeroelasticity is in conceptual design, justifying or driving design choices that have huge impacts on the wing configuration, in this case a stiffer and heavier wing or a wing with an additional control surface, which in any case adds something in terms of structural mass or secondary masses (actuation system and control surface mass). A structural weight estimation based on simple statistical data cannot capture all these aspects, which become more and more important in the design of future, more flexible aircraft.

4. Conclusions

This work presented an evolution of the conceptual design tool known as NeoCASS, including the newly implemented NeOPT suite that improves the wing structural description. This allows orthotropic material to be considered during the conceptual design phases, proposing a physical-based analyses approach to evaluating the CS25 compliant loads to be used during the sizing. The importance of properly evaluating the stiffness properties is highlighted in the paper, showing how the coupling effects generated by tailoring the laminate’s orientation can save additional mass with respect to a quasi-isotropic wingbox. Moreover, the approach allows us to analyze unusual configurations, such as the high aspect ratio cantilevered wings, in a fast and reliable way and relying on physical-based aeroelastic simulations.

The application of this design methodology to a Twin-Aisle Long-Haul aircraft, similar to an Airbus A330, showed how the usage of composite materials is convenient with respect to the aluminum for the design of high aspect ratio aircraft. For different aspect ratios, a mean value of 2.8% fuel can be saved by exploiting composite materials, while 4.1% can be saved by increasing the aspect ratio for the layout of different sections.

In the most promising case, an increased span (+15.51%) and the usage of composite materials can save up to 2022 kg for the wingbox. Considering an operational cruise of 10,000 km, for the identified solution the fuel consumption is reduced by 8.799 t, which is reflected in a direct cost saving of USD 9890 and 10,337.90 t of CO₂ avoided.

The NeOPT package provides the designer a tool to use between the conceptual and preliminary design stages, using low- to medium-fidelity tools that are sufficient to obtain a realistic mass and stiffness distribution following CS/EASA 25 regulations concerning the loads, the flutter behavior and other aeroelastic constraints. The procedure is highly automatable and fast to set up, moreover the computational cost can be calculated with a notebook.

The implementation of a dedicated tool for the calculation of emissions which also extends the Breguet approach, limited to the cruise phase, to the complete mission is now under focus.