Abstract
The flow through the stator vanes of a variable geometry turbocharger turbine can reach supersonic conditions and generates a shock wave on the stator vanes, which has a potential impact on the flow loss as well as on unsteady aerodynamic interaction. The shock wave causes a sudden increase in pressure and can lead to boundary separation and strong excitation force, besides pressure fluctuation in the rotor blades. Thus, in this study, the flat surface of the vanes of a commercial variable geometry turbocharger turbine has been modified to analyze the effects of two grooved surfaces configuration using CFD simulations. The results reveal that the grooves change the turbine efficiency, especially at higher speed, where the increase in the efficiency is between 2% and 6% points. Additionally, the load fluctuation around the rotor leading edge can be reduced and minimize the factors that compromise the integrity of the turbine. Furthermore, the grooves reduce the supersonic pocket developed on the suction side of the vane and diminish the shock wake intensity. Evaluating the effectiveness of the available energy usage in the turbine, on the one hand, at lower speed, the fraction of energy at the inlet destinated to produce power does not change significantly with a grooved surface on the stator vanes. On the other hand, at higher speed and higher pressure ratio with 5 grooves occurs the most effective approach of the maximum energy.
1. Introduction
Turbochargers are a key component for energy recovery in power systems, especially in the transport sector where the turbine can provide approximately one third of the compressor power [1]. Also, turbochargers can be found in the aviation industry [2] in the auxiliary power units (APUs) where the configuration depends on the space within the fuselage of aircraft or large helicopters for electrical power generation. Some works present different APUs configuration as an alternative to conventional systems where some arrangements are based on a hybrid propulsion configuration, i.e., with a more strongly electric concept, reducing the source of pollution [3,4]. Radial turbines can be used in environmental control system (ECS) or in high-altitude fuel cell [1,5] aircraft operation due to the high pressure ratios involved [6,7].
Variable geometry turbine (VGT) turbochargers can vary the flow area by adjusting the opening of the stator vanes, and thus the flow entering the rotor to optimize the energy according to their operating point. Nevertheless, under certain operational conditions, the area formed by the vanes is reduced to increase the velocity of the exhaust gases entering the rotor [8] and resulting in high Mach numbers and the development of shock waves in the stator [9]. This evidence has been portrayed in some papers where the behavior of the shock waves is studied, as in [10,11]. The location of the shock waves depends on the blade geometry , appearing in the throat formed between the vanes or on the suction side (SS) of the vanes.
According to the study of Zhao et al. [9] in a turbine with the vanes at a closed position and high inlet pressure, a shock wave appears near the throat of the nozzle, followed by another shock wave on the SS.
The shock wave developed on the stator vane can extend to the rotor leading edge (LE), cause high unstable loading on the blades [12], and worsen with increasing pressure ratio [13]. The interaction of the shock wave with the rotor blades generates flow instability in the form of pressure fluctuations at the rotor trailing edge (TE) [14], besides of the decrease in the efficiency [15,16] and increasing the possibility of high cycle fatigue fracture [17,18,19,20]. Rubechini et al. [21] found that the strength of the unsteady interaction is related to the shock wave pattern at the region between the nozzle and the rotor. Such pattern depends on the nozzle geometry. These shock waves can be weakened by small changes in the stator geometry, as was reported in the work of Sonoda et al. [22] by a locally high concave curvature and a small groove on the pressure surface (PS) near the TE, which lead to a double shock structure and reduce the TE loss and shock loss. Yang et al. [23] analyzed the used “split sliding guide vane” (SSGV) to weaken the leakage flow and shock intensity of the traditional stator vanes. Thus, the global performance of the turbine was improved, especially at small guide vane openings, reporting and increase of 12% and a decrease of 57% of the vanes clearance leakages flow. Therefore, the attenuation of shock waves in stator and rotor channels are important, being more so in the stator due to the interaction with the rotor itself. An attenuation approach is proposed by Chaudhuri et al. [24] employing simple staggered geometries within a channel simulating the stator itself. Following a similar working pattern, exposed cylinders are presented one by one generating a curve similar to the curve described by a 2D airfoil, which also generate attenuation by splitting the wave into several oblique waves [25]. Lei et al. [26] studied, by using an experimental methodology and numerical modelling in CFD, the behaviour of the shock wave in a linear turbine nozzle with a and without a grooved surface. Comparing the smooth and the grooved surface, the authors found that by applying interstitials, the normal shock wave changes to an oblique shock wave followed by a low intensity normal shock wave . The first shock wave decreases the upstream flow velocity and pressure distortion downstream of the vane. In addition, at high PR, the shock wave can be effectively mitigated.
Zhao et al. [27] analysed, by means of CFD and experimental tests, the alterations of the shock wave structure by using different grooves configuration in a turbine nozzle, where the depth, width and number of the grooves vary. The results show that the single strong shock was converted into a multiple shock wave structure with weaker intensity, decreasing the shock wave loss and reducing the aerodynamic excitation [28]. Varying the grooves width and depth causes minor changes in shock wave intensity and wake loss.
As mentioned above, many studies use CFD as a valuable and reliable tool to characterize the internal turbine aerodynamics [29,30] even at off-design operational points. Such points can encompass extremely low mass flow rates with the turbine operating at negative efficiency [31] or high pressure ratios reaching the choked flow [32].
In order to investigate the flow behaviour of a radial turbine with and without grooved vanes, at off-design conditions with high pressure ratios (PRs) reaching choked flow, CFD simulations are performed in this work. The first section of this work describes the selected geometries. Then, a mesh independence analysis is presented. In addition, the performance parameters of the original geometry and of the grooved surface are compared. Finally, the analysis of the flow field in the stator including pressure profiles, and a study of the exergy in each region of the computational domain are presented.
2. Geometry Description
The turbine with variable geometry of a turbocharger used in automotive diesel engine of 2 L has been selected for this study. The original geometry of the stator vanes was modified to generate two different groove configurations. The groove width, depth, and height are 0.7 mm, 0.15 mm, and 1.9 mm, respectively, which were kept constant for the two configurations changing only the number of grooves as depicts Figure 1. It is important to remark that the height of the grooves does not cover the hole vane height and are centered from the 50% stator span. Furthermore, the location of the grooves along the chord covers the region where the supersonic pocket and the shock wave is developed, as was previously study by Tiseira et al. [32,33]. Comparing both configurations, the vanes with 11 grooves contain the locations of the same grooves as the configuration with 5 grooves plus one groove downstream and five grooves upstream. The CFD domain is built of the following regions, the inlet and outlet ducts, the volute, stator and rotor as illustrates the Figure 2 indicating also the location of the inlet and outlet prove section used to evaluate the performance parameters. The inlet duct length is equal to six duct diameters resulting in a length of 200 mm, while the outlet duct length corresponds to nine duct diameters, that is equal to 400 mm being long enough to set the experimental measurement section in the computational domain. The probe sections are placed at the same location of experimental measurement probes [34], which are located according to turbocharger gas stand test code [35]. The most important geometrical parameters of the stator and rotor are presented in Table 1.
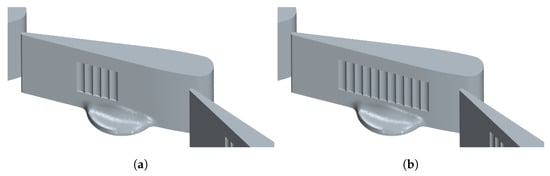
Figure 1.
Stator geometry with different grooved surfaces. (a) Geometry with 5 grooves. (b) Geometry with 11 grooves.
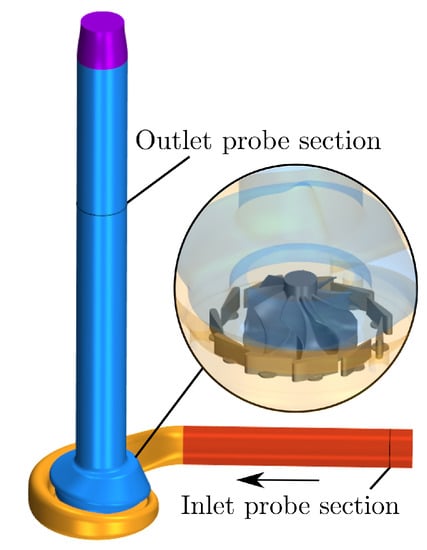
Figure 2.
CFD domain regions.

Table 1.
Geometrical characteristics of the turbine.
3. Numerical Method
The steady Reynolds-averaged Navier-Stokes (RANS) and unsteady Reynolds-averaged Navier-Stokes (URANS) solver from the commercial CFD software Star-CCM+ 2021.1.1 (Build 16.02.009-R8) has been used to model the internal flow behavior. The simulations were run on the cluster of the Universitat Politècnica de València, which consists of 99 nodes, the total computing power of the cluster is 50 TFLOPS. The fluid passing through the turbine has been considered as air and assumed as ideal and compressible gas. To calculate the subsonic and supersonic conditions reached according to the operational point the density-based solver is selected [36,37]. Furthermore, the Weiss-Smith preconditioned Roe’s Flux Difference Splitting (ROE FDS) scheme is chosen for evaluating inviscid fluxes in the coupled flow model. The CFD domain is solved in two steps; the RANS model, considering a frozen rotor, mixing plane interfaces, and moving reference frame for simulating motion of the rotor, is first used as a precursor, and then URANS model, using rigid body motion to consider the motion of the wheel. This procedure reduces the computational cost. In order to determine the turbulent eddy viscosity, the turbulence model k- SST model [38] is chosen with compressibility correction and Durbin scale limiter for realizability. The k- SST model is widely recommended, and well-validated for radial turbomachinery in the literature [39,40,41,42,43] under subsonic, transonic and supersonic conditions [19,44,45]. For the URANS simulations the time step size has been selected as the time that takes the turbine wheel to rotate depending on the rotational speed [31,46]. Some authors as Galindo et al. [47] use to define the time step, but as the differences are less than 1% as shown in Table 2 and to reduce the computational cost the rotation was selected to define the time step. This size corresponds to 180 time steps per rotor revolution. To bring each time step to convergence 20 inner iterations steps were necessary and applying a low CFL number. The residuals of inner iterations, the mass flow, and efficiency were evaluated to look at the convergence. For lower speed cases, the convergence has been attained after about three rotor revolutions, while for higher speed cases, it has been attained after about eight revolutions. The numerical simulations are carried out with 10% VGT opening and two reduced speeds, 3882 rpm/ and 8421 rpm/, which will be designated hereinafter as the lower and the higher speeds, respectively. These rotational speeds are selected based on two aspects. First, the study of Tiseira et al. [32] used these speeds to analyze the development of sonic conditions at the stator. Second, automotive turbocharger turbines can reach these speeds under specific engine operating conditions as tip-in and full-load working points [48]. Regarding the boundary conditions, the pressure at the inlet duct has been set as a constant and non-reflecting total inlet pressure with a value of 3.0 bar and 5.5 bar, whose corresponding PR will be labeled as the lower and the higher PR, respectively. The outlet pressure at the outlet duct is set as a constant static pressure with radial equilibrium and non-reflecting with a value of 1 bar. The total inlet temperature set as a boundary condition is relatively low, 340.55 K, and the walls are considered adiabatic in accordance with previous numerical and experimental testsRegarding to the pressure at the inlet duct, a total inlet pressure of 3.0 bar and 5.5 bar is imposed, whose corresponding PR will be labeled as the lower and the higher PR, respectively. The outlet pressure at the outlet duct has a value of 1 bar. The total inlet temperature set as a boundary condition is relatively low, 340.55 K, and the walls are considered adiabatic in accordance with previous numerical and experimental tests [32,49].

Table 2.
Differences in the performance parameters of the case at higher PR when using and to define the time step.
The planes at the inlet and outlet probe sections depicted in Figure 2 are used to evaluate the performance parameters. Furthermore, the planes shown in Figure 3 are selected to determine the stator efficiency and to carry out an exergy analysis presented in the following sections. It is essential to highlight that the region between the stator outlet’s and rotor inlet’s boundaries corresponds to the denoted vaneless space in this work.
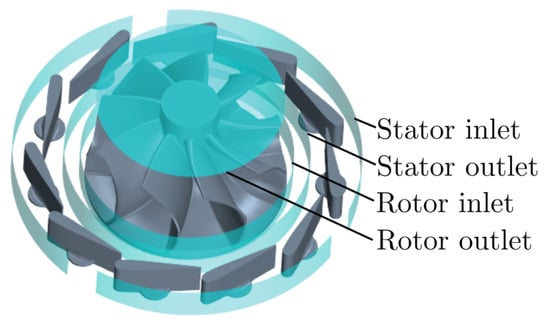
Figure 3.
Selected planes to specify the inlet and outlet of the stator and rotor.
4. Mesh Analysis
A mesh independence study has been carried out to ensure valid results of the turbine performance and the flow profile on the stator vanes. The different configurations has been discretized by means of a unstructured polyhedral mesh [50]. The case of lower speed and higher PR with 11 grooves in the stator surface is selected for this mesh independece study. The inlet and outlet duct are meshed using an extruded mesh and kept for the different mesh densities, changing only the density of the regions of the stator and rotor, that will be denoted as core, and the number of prism layers for the boundary layer.
The Mach number at two points in the vaneless space, one at the middle of the vaneless space, Point A, and the other close to the expected shock wave at a radial position of R = 26.08 mm, Point B, based in previous studies by Tiseira et al. [32,33] as depicts Figure 4 are considerate to compare the different mesh densities.
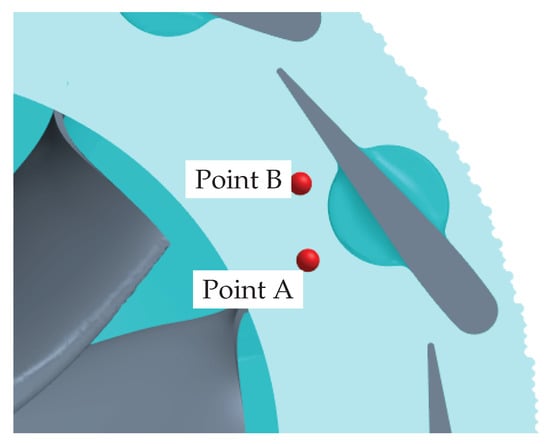
Figure 4.
Selected points to evaluate the Mach number. Point A (at the middle of the stator vaneless space) and Point B (at a radial distance of R = 26.08 mm).
The mass flow rate and the turbine power have been evaluated, as well as, the static pressure on the grooves and the density gradient, used to visualize the shock wave as show Figure 5 and Figure 6. The initial mesh parameters correspond to the mesh used for the case without grooves and will be referred to as the mesh with the coarser core and 15 layers in the boundary layer. Thus, the core is refined from this case, and the number of layers in the boundary layer is changed.
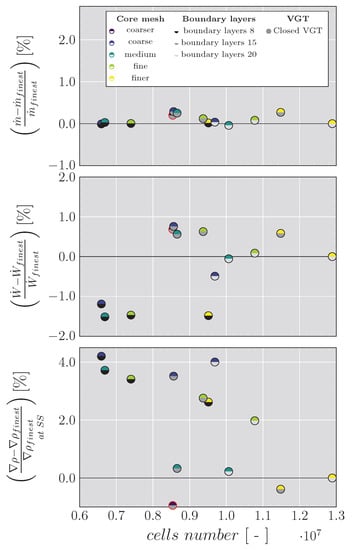
Figure 5.
Mesh analysis Part A. The red dot corresponds to the mesh parameters used with the case without grooves.
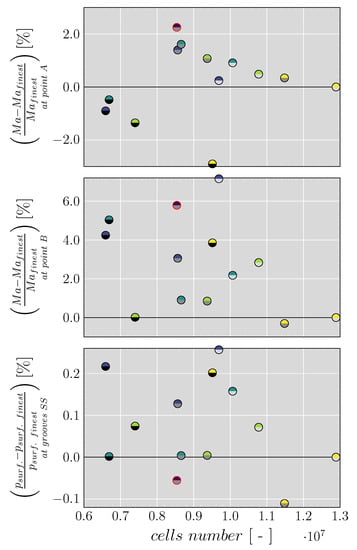
Figure 6.
Mesh analysis Part B. The red dot corresponds to the mesh parameters used with the case without grooves.
In order to reach a compromise between results precision and computational cost and according to the results presented in Figure 5 and Figure 6, the best options are the medium core mesh with 15 or 20 cells in the boundary layer, since the results obtained are very close to the case with the finer mesh and are less computationally expensive. To select between the medium core mesh with 15 and 20 cells in the boundary layer, the grid convergence index (GCI) [51] is calculated with respect to the finer mesh as shows Table 3. The final chosen mesh corresponds to the medium mesh with 10 million cells and 20 cells in the boundary layer and depicted in Figure 7. It presents a lower GCI, implying a lower error in all variables, especially in the mass flow rate and turbine power. In order to capture adequately the behavior of the viscous sublayer, the selected mesh has a non-dimensional distance to the centroid of the first layer of cells close to the walls () lower than 1. Other aspects of the mesh quality are presented in Table 4, where a skewness angle of 0 indicates a perfectly orthogonal mesh and cells with a skewness angle greater than 85 are considered bad cells, the volume change in the regions of the computational domain is greater than 0.01 (lower values are considered bad cells) and the cell quality is close to 1.0, which is the value of a perfect cell [36].

Table 3.
Mesh independence study.
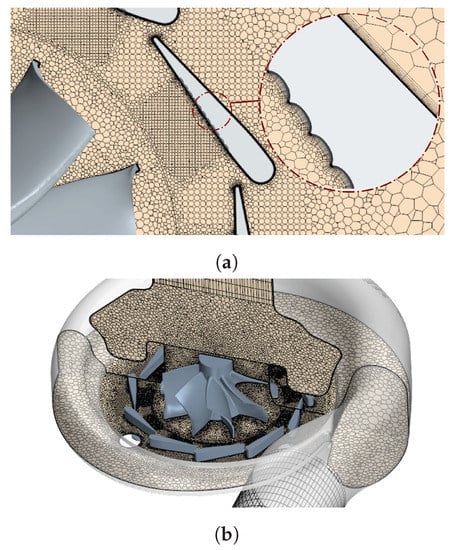
Figure 7.
View of the selected mesh to evaluate the effects of a grooved surface in the stator vanes. (a) Top view. (b) 3D view.

Table 4.
Average values of different mesh quality parameters.
5. Performance Characteristics
As was mentioned in a previous section, to evaluate the performance of the turbine with grooved surface in the stator vanes, two rotational speed, 3882 rpm/ (lower speed) and 8421 rpm/ (higher speed) and two PR, lower and higher has been selected besides of set the vanes at a closed position (10% VGT). Figure 8 shows the reduced mass flow and the total-to-static efficiency of the different operational points for the three stator configurations and calculated using Equations (1)–(3).
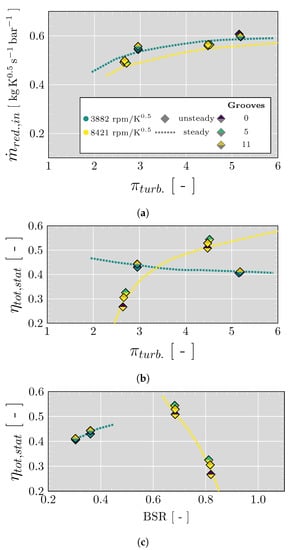
Figure 8.
Turbine map based on steady results of the original stator geometry (0 grooves) and unsteady results with and without grooved surface; Steady: Dashed lines; Unsteady: Markers. (a) Reduced mass flow map. (b) Efficiency vs. expansion ratio map. (c) Efficiency vs. blade-speed-ratio (BSR) map.
The results correspond to the unsteady and steady simulations. The steady simulations correspond only to the case of the stator without grooves and are shown only to mark the trend of the turbine map. Figure 8a shows that there is not a significant change in the reduced mass flow due to the presence of the grooved surface in the stator vanes and only a slight difference at higher speed and lower PR but less than 2%. Nevertheless, the grooved surface has an impact on the turbine efficiency at higher speed rather than at lower speed, as depicts Figure 8b,c. Table 5 is presented to see better the changes. An improvement in the efficiency can be achieved with the configuration of 11 grooves and an even better one with 5 grooves at higher speed and both PR. The major difference occurs at higher speed and lower PR with an increase of 3.0% points for the case of 11 grooves and 5.0% points for the case of 5 grooves. At the same speed but at higher PR the rise in the efficiency is 2.0% points and 3.0% points for 11 grooves and 5 grooves, respectively. Table 5 also reveals that the presence of the grooves has a slight impact on the total to total pressure ratio of the stator, as the velocity of the flow at the stator outlet decrease with the presence of the grooves and taking into account that the function of the vanes is to direct the flow toward the rotor, where the major expansion takes place to produce shaft work. Furthermore, the stator efficiency calculated using Equations (4) and (5) slightly decrease with the increase of grooves. At higher speed and lower PR, the efficiency decreases by 6% points and 8% points with 5 grooves and 11 grooves, respectively. While at higher speed and higher PR the drop is just 1% points and 3% points with 5 grooves and 11 grooves, respectively. Nevertheless, this penalty in the stator efficiency is compensated with the improvement in the turbine total-to-static efficiency due to the effects of the grooves on the shock waves that will be analyzed in the following sections, together with other aspects of the stator flow profile. Furthermore, the regions where the efficiency is evaluated and that are depicted in Figure 3 present a flow conditions quite complex and even more downstream of stator affecting the report of the losses.

Table 5.
Pressure ratio and performance of the turbine and stator for the evaluated cases with and without grooved surface; URANS simulations.
6. Analysis of the Stator Flow features
In the following part, the Mach number, pressure profile, and numerical Schlieren are evaluated to gain insight into the relationship between the shock wave structure and the groove surface geometry and the impact on the turbine performance.
6.1. Influence of Grooved Vanes on the Flow Profile
The Mach number profile has been evaluated at 50% stator span together with the stator vane pressure profile for the cases reaching choking conditions, corresponding to the points of higher PR at higher and lower speed. Figure 9 depicts how the supersonic region connecting the stator vane and the rotor entry shrink as the grooves number increase, resulting in the detachment of the supersonic pocket of the stator and the rotor for the case of 11 grooves. Nevertheless, the supersonic region closer to the vane SS extends more upstream and downstream than the original configuration for the cases at higher speed and remains without significant variation at lower speed. Furthermore, the wake at the vane TE increases as the number of grooves increases, generating a lower velocity region that contributes to the reduction or detachment of the aforementioned supersonic pocket connecting the stator and rotor of the neighboring vane. Thus, the unsteady behavior of the wake has a beneficial effect on the flow profile and with it on the efficiency [52,53]. The pressure disturbances can be clearly seen in Figure 9 representing the static pressure distribution on the vane surface [27]. In Figure 9a the pressure drop on the SS of the vane starting at the LE is due to the acceleration of the flow, at 0.44 relative chord length flow reaches the sonic conditions () and continues accelerating until 0.6 relative chord length, where the pressure suddenly rise due to the presence of the shock wave as will be show further and the flow decelerates, going back to at 0.68 relative chord length and then to subsonic conditions. Due to the presence of grooves, Figure 9b depicts that the pressure on the SS with 5 grooves drops 4% compared with the original configuration at 0.07 relative chord length. From the LE, the pressure profile follows the same trend as the case without grooves until 0.48 relative chord length where the pressure sink. A pressure peak takes place at 0.52 relative chord length, followed by four other peaks that match the number of grooves and with the presence of small shock waves. At 0.6 relative chord length, where the case without grooves presents the lower pressure on the SS, the pressure increases by 15%. The pressure profile of the vanes with 11 grooves presents a signification variation, as shown in Figure 9c, where the pressure disturbances extend from 0.3 to 0.78 relative chord length, while the supersonic pocket only cover the region between 0.4 and 0.66 relative chord length. At 0.07 relative chord length the pressure drops 4% compared with the original configuration. Then, from 0.07 until the first groove at 0.3 relative chord length, the flow starts to accelerate less than the original configuration, as depicted in the lower slope of the pressure profile. Furthermore, at 0.6 relative chord length, where the point of lower pressure is located in the original configuration and just before the shock wave, the pressure increases 26% and marked in the Mach number contour with less intensity for the case of 11 grooves. From another perspective, the vane load around 0.6 relative chord length decrease with a grooved surface. Furthermore, the pressure jump caused by the shock wave in the smooth vanes decreases and changes to several peaks with the grooved vanes, as was mentioned above. Comparing the pressure jump of the original geometry with the most significant jump in the 5 and 11 grooves configuration is possible to observe a decrease of 45% and 67%, respectively. Another aspect to highlight is that in the region before the shock wave, the Mach number in the case without grooves is higher than in the grooved vanes cases. Thus, the shock waves on the grooved vanes are less intense and generate less entropy, improving the turbine efficiency.
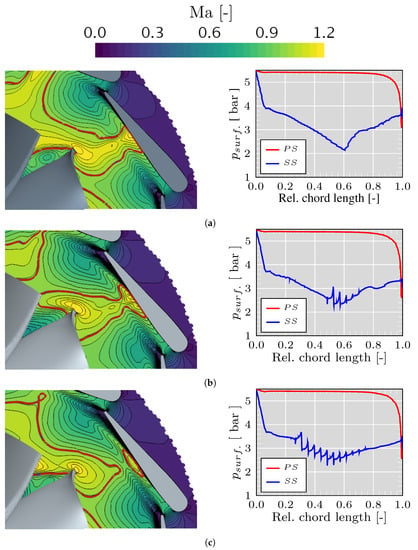
Figure 9.
Mach number and stator vane pressure profile snapshots of URANS simulations at 50% span of the stator passage with closed VGT position at higher speed and higher PR; red line: . (a) Geometry with 0 grooves (original configuration). (b) Geometry with 5 grooves on the stator vanes. (c) Geometry with 11 grooves on the stator vanes.
Analyzing the case of lower speed and higher PR as depicts Figure 10 is possible to observe how the presence of a grooved surface modified the Mach number contour, presenting a reduction around the middle of the supersonic region at the throat formed by the relative position of the rotor blade and the stator vane. Furthermore, this reduction is also caused by the effects of the wake of the adjacent stator vane TE [54,55], as the flow reduce the velocity after passing by the grooves. Close to the SS, the supersonic region of the case without grooves extends from 0.3 to 0.73 relative chord length. In contrast, in the 5 and 11 grooves cases, the starting position does not change significantly but expands until 0.84 and 0.87 relative chord length, respectively, representing an increase of 30% for the 5 grooves and 32% for the case of 11 grooves. For the configuration of 5 and 11 grooves, before of the acceleration of the flow on the SS, the flow accelerates when passing close to the geometry throat formed by the convergent passage between the vanes [28] reaching , as depict Figure 10b,c. Nevertheless, this acceleration is particular for the time step depicted in these figures. Furthermore, in Figure 10c the whole passage presents an instantaneous choked flow. The presence of sonic conditions in this region is due to the wake at the TE that slows down and compresses the surrounding of the entering flow. Pressure profiles show the effect of the grooved surface compared with the original configuration, presenting a similar behavior as the case of higher speed and higher PR. Figure 10a depicts the pressure fall for the original configuration until 0.62 relative chord length followed by a sudden rise. Comparing the original geometry with the case of 5 and 11 grooves at the same chord position, the static pressure decreases 18% and 24%, respectively, as shown in the pressure profiles in Figure 10b,c. Upstream at 0.15 relative chord length, the pressure on SS of the smooth vanes drops 8% when using grooved vanes. Furthermore, the highest pressure pick occurs after passing the first groove, followed by a sudden fall in the pressure. The pressure disturbances match the number of grooves affecting the velocity profile. Comparing the pressure jump of the original geometry with the most significant jump in the 5 and 11 grooves configuration is possible to observe a decrease of 39% and 56%, respectively.
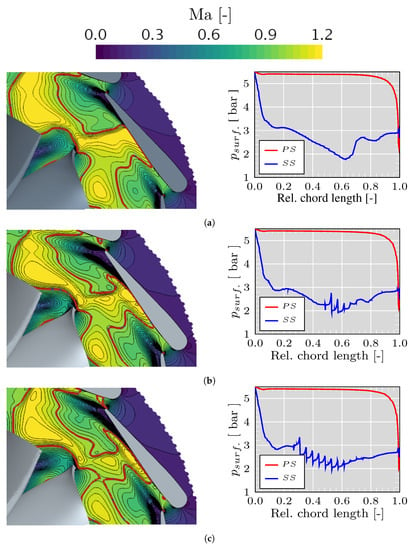
Figure 10.
Mach number and stator vane pressure profile snapshots of URANS simulations at 50% span of the stator passage with closed VGT position at lower speed and higher PR; red line: . (a) Geometry with 0 grooves (original configuration). (b) Geometry with 5 grooves in the stator vanes. (c) Geometry with 11 grooves in the stator vanes.
According to Tiseira et al. [33] the low rotational speed can cause the development of a supersonic region close to the turbine wheel inlet, analyzing the system in the relative reference frame for rotation. Nevertheless, due to the presence of grooves the size of the region decrease for the case with 5 grooves and disappear for the case with 11 grooves, representing just a small increase in the efficiency of 0.4% and 0.5% points. At higher speed the flow remains subsonic in all cases.
6.2. Shock Wave Structure in Grooved Surface Vanes
For a deeper analysis of the effects of the grooved surface on the vaneless space flow profile, numerical Schlieren has been carried out for one blade passing for the two analyzed reduced speeds at higher PR. At higher speed and higher PR, the Schlieren images in Figure 11 show that normal shock wave pattern change to a less intense wave when increasing the number of grooves, and a multiple shock structure is generated. The main shock remains practically at the same position as in the original configuration near 0.6 relative chord length. For the case of 5 grooves, two front leg shock waves are developed before the main shock. A third and fourth small shock waves are presented downstream; the last shock wave is not possible to distinguish in the Schlieren image due to its low intensity but is visible in the pressure profile depicted in Figure 9, thus the number of shock waves match with the number of grooves [26]. The configuration of 11 grooves also presents multiple shock waves. First, around the middle of the vane five shock waves of weak intensity stay close to the stator SS without extending to the rotor. Then an orthogonal shock wave where the main shock is expected in the original configuration is presented, followed by other five shock waves of low intensity. Furthermore, the rotor still contributes to the formation of a throat when goes by the stator vane shock, but with a weaker intensity for the case of 5 grooves and disappears for the case of 11 grooves due to the sudden disturbance generated by the the change of flow area.


Figure 11.
Transient numerical schlieren for closed VGT opening at 50% span of the stator passage with higher simulated PR and higher speed; left side: Original geometry; middle: Geometry with 5 grooves in the stator; right side: Geometry with 11 grooves in the stator.
At lower speed, the shock wave is leaned backward, slightly varying its angle depending on the rotor blade position and presents an increase in the intensity compared with the case at higher speed [33]. This shock wave appears at 0.62 relative chord length, and even with 5 or 11 grooves on the stator vanes, the shock wave has a longer extension toward the rotor compared with the cases of higher speed as depicted in Figure 12. The intensity of the shock wave is depressed when increasing the grooves number. Besides, a multiple shock structure consisting of a series of small waves are generated from each groove. The presence of these waves can be seen more clearly in the pressure profiles in Figure 10 than in the Schlieren image due to the intensity and the limitation of a highly detailed flow structure that can provide the URANS simulation, especially in the boundary layer [55,56]. Furthermore the moving rotor blade encounters locally supersonic speed, resulting in the formation of shock waves in the relative frame.


Figure 12.
Transient numerical schlieren for 10% VGT opening at 50% span of the stator passage with higher simulated PR and lower speed; left side: Original geometry; middle: Geometry with 5 grooves in the stator; right side: Geometry with 11 grooves in the stator. (a) rotor blade passing. (b) rotor blade passing. (c) rotor blade passing. (d) rotor blade passing.
The Schlieren images also support the results presented in Table 5 regarding the diminishing of the stator efficiency as the shock waves in cases of grooved surface are confined in the region delimiting the outlet of the stator. In contrast, the shock wave in the case without grooves interacts with the rotor, as was mentioned before, downstream of the limiting stator outlet plane.
The weakening of the intensity of the standing shock wave at both speeds can contribute to diminishing losses close to the rotor. Furthermore, at higher speed, the presence of load fluctuation around the rotor LE, as reported by Tiseira et al. [33], can be reduced and minimize the factors that compromise the integrity of the turbine [57,58].
For the cases with a grooved surface, it is possible to observe the presence of a shock wave at the convergent section between the vanes, only between a time of 50% and 75% blade passing. The shock wave has a higher intensity for the case of 11 grooves than 5 grooves, as shown in Figure 12 and in the Mach number contours of Figure 10.
6.3. Effects on the Rotor Blade
After analyzing the impact of the grooves on the stator and vaneless space reducing the supersonic pocket and the intensity of the shock waves, this section focus on the effects on the rotor evaluating the blade loading. The blade loading provides the work on the turbine shaft and is determined based on the pressure difference between the PS and SS. Thus, Figure 13 presents the blade loading at lower and higher speed, both at higher PR. At lower speed, the blade loading of the three stator vanes geometries presents the same trend in the first middle part of the vane as shown in Figure 13a. Furthermore, the spike in the blade loading is due to the stator SS shock wave striking the blade LE [20,28], besides the formation of shock waves in the relative frame. In the region between 0.7 and 0.9 relative chord length, the load improves more in the case of 5 grooves than in the case of 11 grooves. In contrast, the differences are insignificant at the rest of the chord length, explaining the slight variation in the turbine efficiency presented in Figure 8b. At higher speed, Figure 13b depicts how the use of grooves on stator vanes increases the blade loading and can avoid the blade loading oscillates between negative and positive values every time a stator vane is passed as was reported in the study of Tiseira et al. [33], especially in the case of 5 grooves, which presents a rise in the turbine efficiency of 3% points, followed by the case of 11 grooves with an increase of 2% compared with the original configuration.
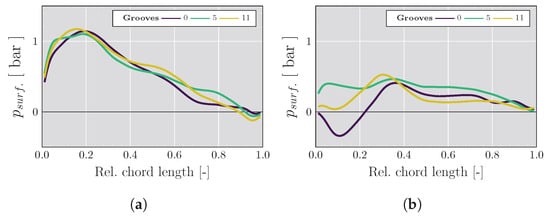
Figure 13.
Rotor blade loading at 50% span with closed VGT position. (a) Lower speed and higher PR. (b) Higher speed and higher PR.
6.4. Exergy Analysis
For the cases of lower and higher PR and both at lower and higher speed, with and without grooved surface, the exergy in each region of the computational domains has been evaluated. The planes that limits the regions in the stator and rotor are depicted in Figure 3 similar to the study carry out by Tiseira et al. [32]. The specific exergy flow of a perfect gas is defined by the Equation (6),
where h is the specific enthalpy (subscript t denotes the total quantity), s is the specific entropy and is the dead state temperature, Here, the ambient conditions are used as dead state with and . In order to obtain the net exergy passing through a control surface the Equation (7) has been used, where is the density of the fluid, is the velocity vector of the fluid and is the unit normal vector of .
The normalized exergy change through the inlet duct and volute is negligible for all the cases as depicts Figure 14a. Comparing the cases with grooved surfaces against those without grooves under the same operational conditions, one has the following results. At lower speed and lower PR, the normalized exergy change in the stator increases by 8.2% and 15.4% for the case of 5 grooves and 11 grooves, respectively. Nevertheless, the gain in the stator due to the presence of grooves is penalized in the vaneless space as the flow decelerates. Thus, the exergy decreases by 2.8% and 13.5% for the cases of 5 and 11 grooves, respectively. When the flow goes through the rotor, the changes in the exergy compared with the case without grooves are neglected. In the cases of higher speed and lower PR, where the flow does not reach sonic conditions in the stator vane, the exergy increase in the stator is higher than in the cases at lower speed and lower PR. The configurations of 5 and 11 grooves present a rise of 38.2% and 27.5%, respectively. Nevertheless, exergy variation in the vaneless space shows a drop of 38.6% and 53.4% for 5 and 11 grooves, respectively, while the fraction corresponding to the rotor can increase by 25.4% and 22.8%.
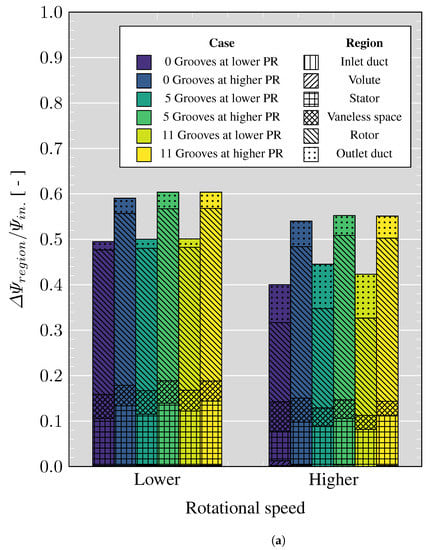
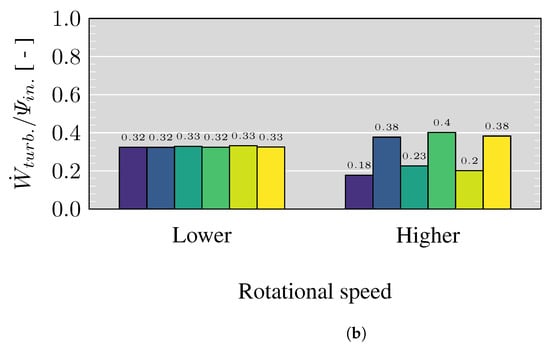
Figure 14.
Exergy analysis for the evaluated operational points; lower: 3882 rpm/; higher: 7456 rpm/. (a) Distribution of the normalized overall exergy in the turbine domain. (b) Comparison of the turbine power with respect to the exergy at the inlet probe plane.
Focusing on the cases at higher PR and the two selected rotational speed, whose Mach number and density gradient profiles were analyzed in the previous section, the exergy fraction in each region of the computation domain with grooved surface on the stator vanes present the following variation concerning the original geometry. At lower speed, the energy usefulness in the stator increases 4.6% and 7.6% for the configuration of 5 and 11 grooves, respectively. In the vaneless space, the geometry with 5 grooves presents a particularity compared with the rest of the cases. The normalized exergy change increases by 8.7%, which is reflected in the stator efficiency shown in Table 5. While in the 11 grooves configuration drops by 2.2%. In the rotor, despite the reduction in the shock wave intensity on the stator vane that influences the rotor performance, the changes represent less than 0.5% compared with the original geometry. At higher speed and higher PR, the 5 and 11 grooves cases present in the stator an increase of the energy quality of 8.2% and 15.9%, respectively. Furthermore, the exergy variation in the vaneless space presents a degradation of 23.0% and 40.2% for 5 and 11 grooves, respectively, as a consequence of the flow distortion produced by the grooves and the wake increase at the TE. Then as a consequence of the reduction of the supersonic conditions in the vaneless space that affect the rotor, the normalized amount of work obtainable in this region can increase by 8.7% and 7.7%.
The fluid leaving the rotor contains a considerable portion of flow exergy, especially at higher speed. Increasing the PR at lower speed increases the exergy in the outlet region, while at higher speed decreases. Furthermore, the exergy budget grows with the grooves up to 16.7%; except for the case of higher speed and higher PR, where the exergy change decreases by 22.4% and 13.5% using 5 and 11 grooves, respectively.
Figure 14b presents the ratio of the turbine power over the exergy flow at the inlet probe section, which represents the effectiveness of available energy usage in the system. At lower speed the fraction of energy at the inlet destinated to produce power does not change significantly with a grooved surface on the stator vanes and is also reflected in the small change in the efficiency depicted in Figure 8b and Table 5. The maximum change relating to the original configuration occurs with the 5 grooves geometry at higher speed and lower PR, presenting an increase of 27.3%, followed by the case of 11 grooves with a rise of 13.3% at the same operational conditions. Furthermore, the most significant approach of the maximum energy corresponds to the configuration of 5 grooves at higher speed and higher PR.
The exergy analysis reveals that turbine efficiency does not reflect effective energy usage in the system. Furthermore, this analysis shows excellent potential to improve the available energy usage in the turbine system. From Figure 14b, we observe that the effectiveness of available energy usage at higher speed and lower PR passed from 0.18 to 0.23 using 5 grooves on the stator vanes, which has a turbine efficiency of 32% against the 27% of the original configuration.
One can highlight that the use of grooves to take advantage of available energy at the turbine inlet, reducing the impact of the irreversibility generated by the shock waves, has a more significant effect at higher speed than at lower speed.
7. Conclusions and Findings
The stator vanes of the variable geometry turbine have been modified, changing the flat surface of the stator SS to a grooved surface with 5 and 11 grooves. Analyzing the turbine performance, the change in the reduced mass flow generated by the grooved surface is insignificant. Nevertheless, the grooves’ presence impacts the turbine efficiency, especially at higher speed, rising to 5.8% points. On the one hand, the total to static efficiency of the turbine increases, but on the other hand, the stator efficiency slightly decreases with the rise of grooves.
At higher PR increasing the number of the grooves, the supersonic region connecting the stator vane and the rotor entry becomes smaller. Furthermore, the wake at the vane TE increases, affecting the supersonic region of the neighboring vane along with the shock wave contributing to the rise in the efficiency presented in the turbine map but decreasing the stator efficiency. The presence of grooves generates pressure peaks on the vane SS, which are related to small shock waves. The number of pressure peaks matches the number of grooves. Additionally, the pressure jump of the original geometry can be decreased up to 67%.
The numerical Schlieren images reveal that the shock wave pattern on the grooved vanes at higher speed is less intense, generating a multiple shock structure. The main shock normal to the SS remains practically at the same position as in the original configuration. At higher and lower speeds, the intensity of the shock wave decreases with increasing the number of grooves. The weakening of the intensity of the standing shock wave at both speeds can contribute to diminishing losses close to the rotor. Furthermore, at higher speed, the load fluctuation around the rotor LE can be reduced, and minimize the factors that compromise the integrity of the turbine.
The blade loading has been evaluated to analyze the impact of the flow profile on the rotor blade when using a grooved surface in the stator at high PR. At lower speed, the blade loading of the two grooved vanes geometries improves after the middle part of the vane, especially in the case of 5 grooves. This result justifies the slight variation in the turbine efficiency. At higher speed, the blade loading rises, and the oscillation between negative and positive values is prevented due to the use of grooves, justifying the increase in the turbine efficiency up to 3%.
An exergy analysis was carried out to quantify the potential for achieving the maximum possible work of the turbine. The exergy change is more significant when using 11 than 5 grooves at lower speed and lower PR, especially in the stator with an increase of 15.4%. On the contrary, in the cases of higher speed and lower PR, where the flow does not reach sonic conditions in the stator vane, the exergy increase in the stator is higher than in the cases at lower speed and lower PR rising to 38.2%. Considering the cases at higher PR, first at lower speed stand out the configuration with 11 grooves with an increase in the energy potential of 7.6%, a decrease of 2.2%, and a slight rise of 0.5% in the stator, vaneless space, and rotor, respectively. While at higher speed, the 5 grooves geometry represents a better choice than the 11 grooves. Thus, the exergy change in the regions mentioned above increases by 8.2%, a reduction of 23.0%, and a rise of 8.7%.
Evaluating the effectiveness of the available energy usage in the turbine at lower speed, the fraction of energy at the inlet destined to produce power does not change significantly with a grooved surface on the stator vanes, which is reflected in an insignificant change in the efficiency. On the contrary, the most significant approach of the maximum energy occurs at higher speed and higher PR with 5 grooves. Thus, using grooves to take advantage of available energy at the turbine inlet, reducing the impact of the irreversibility generated by the shock waves, has a more significant effect at higher speed than lower speed.
Author Contributions
Conceptualization, J.G., A.T., R.N., L.B.I. and J.D.E.; methodology, L.B.I. and J.D.E.; software, J.D.E.; formal analysis, J.D.E.; investigation, J.D.E.; resources, R.N.; data curation, J.D.E.; writing—original draft preparation, J.G., A.T., R.N., L.B.I. and J.D.E.; writing—review and editing, J.G., A.T., R.N., L.B.I. and J.D.E.; supervision, A.T. and L.B.I. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been partially supported by the Subprograma de Formación de Profesorado Universitario (FPU). Ministerio de Universidades. FPU18/02628.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank Luis Miguel García-Cuevas for his support in the theoretical and programming part.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| Notations | |
| D | Rotor diameter |
| Mach Number | |
| Mass Flow | |
| Reduced Mass Flow | |
| N | Rotational speed |
| p | Pressure or order of accuracy |
| r | radial coordinate or refinement factor ratio |
| Entropy generation rate per unit volume | |
| T | Temperature |
| t | Time |
| Non-dimensional wall distance | |
| Power | |
| Abbreviations | |
| BSR | Blade speed ratio |
| CFD | Computational Fluid Dynamics |
| GCI | Global Convergence Index |
| LE | Leading Edge |
| PR | Pressure Ratio |
| PS | Pressure Side |
| RANS | Reynolds Average Navier Stokes |
| SS | Suction Side |
| TE | Trailing Edge |
| URANS | Unsteady Reynolds Average Navier Stokes |
| VGT | Variable Geometry Turbine |
| Greek symbols | |
| Stator Blade Angle | |
| Difference | |
| Relative error | |
| Efficiency | |
| Corresponding Pressure Ratio | |
| Density | |
| Subscripts | |
| Turbine Inlet Section | |
| Reduced Numbers | |
| Relative Value | |
| Stator or Rotor Blade Surface | |
| Total or Stagnation Conditions | |
| Total-To-Static Value | |
References
- Kerviel, A.; Pesyridis, A.; Mohammed, A.; Chalet, D. An evaluation of turbocharging and supercharging options for high-efficiency Fuel Cell Electric Vehicles. Appl. Sci. 2018, 8, 2474. [Google Scholar] [CrossRef]
- Bruensicke, W.; Cholvin, R. The turbocharger function in the light aircraft field. In Proceedings of the General Aviation Aircraft Design and Operations Meeting, Wichita, KS, USA, 25–27 May 1964; pp. 1–9. [Google Scholar] [CrossRef]
- Jiménez-Espadafor Aguilar, F.J.; Vélez Godiño, J.A. Innovative power train configurations for aircraft auxiliary power units focused on reducing carbon footprint. Aerosp. Sci. Technol. 2020, 106, 106109. [Google Scholar] [CrossRef]
- Cheng, K.; Qin, J.; Sun, H.; Dang, C.; Zhang, S.; Liu, X.; Bao, W. Performance assessment of an integrated power generation and refrigeration system on hypersonic vehicles. Aerosp. Sci. Technol. 2019, 89, 192–203. [Google Scholar] [CrossRef]
- Abu Kasim, A.F.B.; Chan, M.S.C.; Marek, E.J. Performance and failure analysis of a retrofitted Cessna aircraft with a Fuel Cell Power System fuelled with liquid hydrogen. J. Power Sources 2022, 521, 230987. [Google Scholar] [CrossRef]
- Lück, S.; Wittmann, T.; Göing, J.; Bode, C.; Friedrichs, J. Impact of Condensation on the System Performance of a Fuel Cell Turbocharger. Machines 2022, 10, 59. [Google Scholar] [CrossRef]
- Desantes, J.M.; Novella, R.; Pla, B.; Lopez-Juarez, M. Effect of dynamic and operational restrictions in the energy management strategy on fuel cell range extender electric vehicle performance and durability in driving conditions. Energy Convers. Manag. 2022, 266, 115821. [Google Scholar] [CrossRef]
- Huayin, T. Application of Variable Geometry Turbine on Gasoline Engines and the Optimisation of Transient Behaviours. Ph.D. Thesis, University of Bath, Bath, UK, 2016. [Google Scholar]
- Zhao, B.; Sun, H.; Shi, X.; Qi, M.; Guo, S. Investigation of using multi-shockwave system instead of single normal shock for improving radial inflow turbine reliability. Int. J. Heat Fluid Flow 2018, 71, 170–178. [Google Scholar] [CrossRef]
- Lei, X.; Qi, M.; Sun, H.; Shi, X.; Hu, L. Study on the Interaction of Clearance Flow and Shock Wave in a Turbine Nozzle; SAE Technical Paper 2017-01-10; SAE: Warrendale, PA, USA, 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Qi, M.; Zhang, H.; Zhao, B. Shock, Leakage Flow and Wake Interactions in a Radial Turbine With Variable Guide Vanes. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Kawakubo, T. Unsteady Rotor-Stator Interaction of a Radial-Inflow Turbine With Variable Nozzle Vanes. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea and Air, Glasgow, UK, 14–18 June 2010; pp. 2075–2084. [Google Scholar] [CrossRef]
- Sato, W.; Yamagata, A.; Hattori, H. A Study of Aerodynamic Excitation Forces on a Radial Turbine Blade Due to Rotor-Stator Interaction. In Proceedings of the Institution of Mechanical Engineers—11th International Conference on Turbochargers and Turbocharging, London, UK, 13–14 May 2014; Woodhead Publishing: Oxford, UK, 2014; pp. 389–398. [Google Scholar]
- Yang, D.; Lao, D.; Yang, C.; Hu, L.; Sun, H. Investigations on the Generation and Weakening of Shock Wave in a Radial Turbine With Variable Guide Vanes. In Turbomachinery, Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; ASME: New York, NY, USA; Volume 2D, pp. 1–9. [CrossRef]
- Hu, L.; Yang, C.; Sun, H.; Zhang, J.; Lai, M. Numerical Analysis of Nozzle Clearance’s Effect on Turbine Performance. Chin. J. Mech. Eng. 2011, 24, 618–625. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, C.; Hu, L.; Sun, H.; Yi, J.; Eric, C.; Shi, X.; Engeda, A. Understanding of the Interaction between Clearance Leakage Flow and Main Passage Flow in a VGT Turbine. Adv. Mech. Eng. 2015, 7, 652769. [Google Scholar] [CrossRef]
- Liu, Y.; Lao, D.; Liu, Y.; Yang, C.; Qi, M. Investigation on the effects of nozzle openings for a radial turbine with variable nozzle. In Proceedings of the SAE 2014 World Congress & Exhibition, Detroit, MI, USA, 8–10 April 2014; Volume 1, pp. 1–8. [Google Scholar] [CrossRef]
- Hu, L.; Sun, H.; Yi, J.; Curtis, E.; Morelli, A.; Zhang, J.; Zhao, B.; Yang, C.; Shi, X.; Liu, S. Investigation of nozzle clearance effects on a radial turbine: Aerodynamic performance and forced response. In Proceedings of the SAE 2013 World Congress & Exhibition, Detroit, MI, USA, 16–18 April 2013; Volume 1, pp. 1–11. [Google Scholar] [CrossRef]
- Paniagua, G.; Yasa, T.; De La Loma, A.; Castillon, L.; Coton, T. Unsteady strong shock interactions in a transonic turbine: Experimental and numerical analysis. J. Propuls. Power 2008, 24, 722–731. [Google Scholar] [CrossRef]
- Chen, H. Turbine wheel design for Garrett advanced variable geometry turbines for commercial vehicle applications. In 8th International Conference on Turbochargers and Turbocharging; Woodhead Publishing: Sawston, UK, 2006; pp. 317–327. [Google Scholar] [CrossRef]
- Rubechini, F.; Marconcini, M.; Arnone, A.; Del Greco, A.S.; Biagi, R. Special Challenges in the CFD Modeling of Transonic Turbo-Expanders. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition; ASME: San Antonio, TX, USA, 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Sonoda, T.; Arima, T.; Olhofer, M.; Sendhoff, B.; Kost, F.; Giess, P.A. A Study of Advanced High-Loaded Transonic Turbine Airfoils. J. Turbomach. 2004, 128, 650–657. [Google Scholar] [CrossRef]
- Yang, D.; Wang, K.; Wang, H.; Zhang, Q.; Lei, X.; Hu, L. An Investigation of the Performance and Internal Flow of Variable Nozzle Turbines with Split Sliding Guide Vanes. Machines 2022, 10, 1084. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Hadjadj, A.; Sadot, O.; Glazer, E. Computational study of shock-wave interaction with solid obstacles using immersed boundary methods. Int. J. Numer. Methods Eng. 2012, 89, 975–990. [Google Scholar] [CrossRef]
- Wan, Q.; Eliasson, V. Numerical Study of Shock Wave Attenuation in Two-Dimensional Ducts Using Solid Obstacles: How to Utilize Shock Focusing Techniques to Attenuate Shock Waves. Aerospace 2015, 2, 203–221. [Google Scholar] [CrossRef]
- Lei, X.; Qi, M.; Sun, H.; Hu, L. Investigation on the Shock Control Using Grooved Surface in a Linear Turbine Nozzle. J. Turbomach. 2017, 139, 121008. [Google Scholar] [CrossRef]
- Zhao, B.; Qi, M.; Sun, H.; Shi, X.; Ma, C. Experimental and Numerical Investigation on the Shock Wave Structure Alterations and Available Energy Loss Variations With a Grooved Nozzle Vane. J. Turbomach. 2019, 141, 051001. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, L.; Sun, H.; Yang, C.; Shi, X.; Yi, J.; Curtis, E.; Engeda, A. Numerical Investigation of a Novel Approach for Mitigation of Forced Response of a Variable Geometry Turbine During Exhaust Braking Mode. In Microturbines, Turbochargers and Small Turbomachines, Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; ASME: New York, NY, USA, 2016; Volume 8. [Google Scholar] [CrossRef]
- Zhang, S.; Ding, S.; Liu, P.; Qiu, T. Effect of Hot Streak on Aerothermal Performance of High Pressure Turbine Guide Vane under Different Swirl Intensities. Aerospace 2022, 9, 579. [Google Scholar] [CrossRef]
- Bhide, K.; Siddappaji, K.; Abdallah, S.; Roberts, K. Improved Supersonic Turbulent Flow Characteristics Using Non-Linear Eddy Viscosity Relation in RANS and HPC-Enabled LES. Aerospace 2021, 8, 352. [Google Scholar] [CrossRef]
- Serrano, J.R.; Gil, A.; Navarro, R.; Inhestern, L.B. Extremely low mass flow at high blade to jet speed ratio in variable geometry radial turbines and its influence on the flow pattern a CFD analysis. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; 2017; pp. 1–13. [Google Scholar] [CrossRef]
- Tiseira, A.; García-Cuevas, L.M.; Inhestern, L.B.; Echavarría, J.D. Development of Choked Flow in Variable Nozzle Radial Turbines. Int. J. Engine Res. 2021, 23, 1388–1405. [Google Scholar] [CrossRef]
- Tiseira, A.; Dolz, V.; Inhestern, L.B.; Echavarría, J.D. Choking dynamic of highly swirled flow in variable nozzle radial turbines. Aerosp. Sci. Technol. 2022, 122, 107396. [Google Scholar] [CrossRef]
- Serrano, J.R.; Garcia-Cuevas, L.M.; Inhestern, L.B.; Mai, H.; Rinaldi, A.; Sanchez, A.M. Methodology to Evaluate Turbocharger Turbine Performance at High Blade to Jet Speed Ratio Under Quasi Adiabatic Conditions. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; pp. 1–14. [Google Scholar] [CrossRef]
- SAE Engine Power Test Code Committee. Turbocharger Gas Stand Test Code; Ground Vehicle Standard; SAE International: Warrendale, PA, USA, 1995; pp. 1–12. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software. STAR-CCM + 2019.1 User Guide Release version 14.02.010-R8. pp. 26–7402. Available online: https://www.plm.automation.siemens.com/global/es/products/simcenter/STAR-CCM.html (accessed on 27 March 2023).
- Wheeler, A.P.S.; Korakianitis, T.; Banneheke, S. Tip-Leakage Losses in Subsonic and Transonic Blade Rows. J. Turbomach. 2012, 135, 011029. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.; Hansen, T. CFD simulation of turbomachinery flows—Verfication, validation and modelling. In Proceedings of the ECCOMAS 2004—European Congress on Computational Methods in Applied Sciences and Engineering, Jyväskylä, Finland, 24–28 July 2004; pp. 1–14. [Google Scholar]
- Simpson, A.T.; Spence, S.W.T.; Watterson, J.K. A Comparison of the Flow Structures and Losses Within Vaned and Vaneless Stators for Radial Turbines. J. Turbomach. 2009, 131, 1–15. [Google Scholar] [CrossRef]
- Galindo, J.; Fajardo, P.; Navarro, R.; García-Cuevas, L.M. Characterization of a radial turbocharger turbine in pulsating flow by means of CFD and its application to engine modeling. Appl. Energy 2013, 103, 116–127. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, M.; Pan, L.; Deng, K.; Wu, X.; Wang, C. Gasdynamic behaviours of a radial turbine with pulsating incoming flow. Energy 2021, 218, 119523. [Google Scholar] [CrossRef]
- Galindo, J.; Serrano, J.R.; García-Cuevas, L.M.; Medina, N. Twin-entry turbine losses: An analysis using CFD data. Int. J. Engine Res. 2021, 23, 1180–1200. [Google Scholar] [CrossRef]
- Zhao, B.; Qi, M.; Sun, H.; Shi, X.; Ma, C. A comprehensive analysis on the structure of groove-induced shock waves in a linear turbine. Aerosp. Sci. Technol. 2019, 87, 331–339. [Google Scholar] [CrossRef]
- Ananthakrishnan, K.; Govardhan, M. Influence of fillet shapes on secondary flow field in a transonic axial flow turbine stage. Aerosp. Sci. Technol. 2018, 82–83, 425–437. [Google Scholar] [CrossRef]
- Galindo, J.; Hoyas, S.; Fajardo, P.; Navarro, R. Set-Up Analysis and Optimization of CFD Simulations for Radial Turbines. Eng. Appl. Comput. Fluid Mech. 2013, 7, 441–460. [Google Scholar] [CrossRef]
- Galindo, J.; Serrano, J.R.; García-Cuevas, L.M.; Medina, N. Using a CFD analysis of the flow capacity in a twin-entry turbine to develop a simplified physics-based model. Aerosp. Sci. Technol. 2021, 112, 106623. [Google Scholar] [CrossRef]
- Serrano, J.R.; Arnau, F.J.; De la Morena, J.; Gómez-vilanova, A.; Guilain, S.; Batard, S. A methodology to calibrate gas-dynamic models of turbocharged petrol engines with variable geometry turbines and with focus on dynamics prediction during tip-in load transient tests. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, 21–25 September 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Serrano, J.R.; Tiseira, A.; García-Cuevas, L.M.; Inhestern, L.B.; Tartoussi, H. Radial turbine performance measurement under extreme off-design conditions. Energy 2017, 125, 72–84. [Google Scholar] [CrossRef]
- Mendonça, F.; Clement, J.; Palfreyman, D.; Peck, A. Validation of unstructured CFD modelling applied to the conjugate heat transfer in turbine blade cooling. In Proceedings of the ETC_8-198, European Turbomachinery Conference, Graz, Austria, 24–28 April 2008. [Google Scholar]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Asghar, M.A.; Liu, Y.; Cui, J.; Lu, L. Investigation of Unsteady Flow Interactions in a Transonic High Pressure Turbine Using Nonlinear Harmonic Method. Energies 2018, 11, 342. [Google Scholar] [CrossRef]
- Li, L.; Tan, W.; Zhang, J.; Han, G.; Zhang, Y. Unsteady Effects of Wake on Downstream Rotor at Low Reynolds Numbers. Energies 2022, 15, 6692. [Google Scholar] [CrossRef]
- Zhao, B.; Qi, M.; Zhang, H.; Shi, X. Investigation on effects of shock wave on vortical wake flow in a turbine nozzle cascade. Aerosp. Sci. Technol. 2020, 98, 105690. [Google Scholar] [CrossRef]
- Bian, X.; Wang, Q.; Su, X.; Yuan, X. Interaction mechanisms of shock waves with the boundary layer and wakes in a highly-loaded NGV using hybrid RANS/LES. Chin. J. Aeronaut. 2020, 33, 149–160. [Google Scholar] [CrossRef]
- Léonard, T.; Gicquel, L.Y.M.; Gourdain, N.; Duchaine, F. Steady/Unsteady Reynolds-Averaged Navier–Stokes and Large Eddy Simulations of a Turbine Blade at High Subsonic Outlet Mach Number. J. Turbomach. 2014, 137, 041001. [Google Scholar] [CrossRef]
- Hancock, B.J.; Clark, J.P. Reducing Shock Interactions in Transonic Turbine via Three-Dimensional Aerodynamic Shaping. J. Propuls. Power 2014, 30, 1248–1256. [Google Scholar] [CrossRef]
- Zhao, B.; Shi, X.; Sun, H.; Qi, M.; Song, P. Effects of grooved vanes on shock wave and forced response in a turbocharger turbine. Int. J. Engine Res. 2021, 22, 805–814. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).