Abstract
This paper presents a methodology for designing a highly reliable Air Traffic Management and Control (ATMC) methodology using Neural Networks and Peer-to-Peer (P2P) blockchain. A novel data-driven algorithm was designed for Aircraft Trajectory Prediction (ATP) based on an Autoencoder architecture. The Autoencoder was considered in this study due to its excellent fault-tolerant ability when the input data provided by the GPS is deficient. After conflict detection, P2P blockchain was used for securely decentralized decision-making. A meta-controller composed of this Autoencoder, and P2P blockchain performed the ATMC task very well. A comprehensive database of trajectories constructed using our UAS-S4 Ehécatl was used for algorithms validation. The accuracy of the ATP was evaluated for a variety of data failures, and the high-performance index confirmed the excellent efficiency of the autoencoder. Aircraft were considered in several local encounter scenarios, and their trajectories were securely managed and controlled using our in-house Smart Contract software developed on the Ethereum platform. The Sharding approach improved the P2P blockchain performance in terms of computational complexity and processing time in real-time operations. Therefore, the probability of conflicts among aircraft in a swarm environment was significantly reduced using our new methodology and algorithm.
1. Introduction
Air Traffic Management and Control (ATMC) is one of the most critical issues in aviation transportation [1]. The safety and efficiency of aviation transportation require advanced path planning systems. Various strategies have been designed for path planning to manage airspace [2], traffic flow [3], and capacity [4]. Path planning methods can be categorized into two classes, namely representation and coordinate-related techniques [5]. Representation techniques are based on c-space and include cell decomposition [6], roadmaps [7], potential fields [8], and Voronoi diagrams [9]. The coordinate [10] and non-coordinate techniques are based on various algorithms such as evolutionary models [11], genetic algorithms [12,13], particle swarm optimization [14], and ant colony optimization [15].
Vulnerabilities in an ATMC system, due to faults and failures [16], can result in catastrophic aerial collisions [17]. Safe airspace allocation, therefore, has a key role in ATMC performance [18]. Coordinate-based methodologies have shown very good efficiency in airspace allocation. Linear programming [19], control theory [20,21], meta-heuristic algorithms [22], evolutionary techniques [23], and machine learning [24] models are the most well-known and widely used approaches. The fault-tolerance feature [25] must be considered a fundamental criterion for the design and development of ATMC systems in order to improve safety requirements. Among the above-mentioned methodologies, those based on artificial intelligence (especially deep learning algorithms) have proven their extraordinary ability for fault detection [26], air traffic management [27], control [28], and collision avoidance.
The ATMC system mainly works based on “future trajectories” [29]. By relying on advanced trajectory prediction algorithms, very good decisions can be made, which greatly improves the efficiency of trajectory planning, and thus the performance of the ATMC [30,31]. The first requirement is the design of an accurate Aircraft Trajectory Prediction (ATP) model. Many deterministic and probabilistic approaches have been investigated for the ATP model [24,32,33,34,35]. Among these, data-driven algorithms have shown the best performance, particularly when they are provided with a rich dataset [36]. Hence, the first aim of this paper was to design an ATP model based on deep Neural Network architectures. Among them, the Autoencoder algorithm has shown excellent functionality and results for vehicle trajectory prediction. Vehicle (automobile) trajectory prediction with a variational Autoencoder [37], vessel (ship) trajectory prediction using a dual linear Autoencoder [38], and aircraft trajectory prediction using a deep Autoencoder [39] are some examples of very good utility and performance of the Autoencoder. Among the advantages of the Autoencoder, its fault tolerance feature remains its main and outstanding specification [40]. In other words, the Autoencoder can perform accurate trajectory prediction despite deficient (possibly wrong) data obtained from the GPS. This is the reason why we have therefore selected an Autoencoder algorithm for our UAS-S4 trajectory prediction.
In addition to predicting future trajectories, a decision-making algorithm is also needed to manage and control aircraft to avoid collisions. In essence, ATMC is a distributed mission and a central coordinator cannot perform this task properly. By considering a single air traffic controller for a specific flight area, the ATMC system may have difficulties in crowded flight zones. Moreover, reliability issues that arise from failures (dues to miscommunications, adversarial attacks, delayed control commands, or overloaded zones) confirm the advantages of decentralized over centralized approaches [41].
Local broadcast methodology, control zones, trigger, and Peer-to-Peer (P2P) blockchain are among the most widely used fault-tolerant methodologies [42]. Local broadcast uses an efficient and simple algorithm, but it cannot be applied on a grided airspace topology [43]. The control zones approach is fault-tolerant in the case of many agent failures (with high probability), but a global knowledge of aircraft trajectory is required [44]. The trigger strategy can tolerate many agent failures without requiring knowledge of its topology, but in some cases is less efficient than that of control zones [45].
Basically, a vehicle’s movement in an environment requires dynamic path planning, as each vehicle’s trajectory affects another one. Therefore, a consensus algorithm is needed for analyzing collected trajectory data, and path planning while minimizing the risk of conflict between vehicles. The most successful consensus algorithms have been developed based on deterministic, randomized, leader-free, and leader-based methodologies. Deterministic approaches may not solve the consensus problem due to a single communication failure in an asynchronous environment. Randomized methodologies are not suggested for critical tasks such as air traffic management due to safety issues. The leader-based methodology is more vulnerable than others in the case of cybersecurity attacks. Leader-free methodology outperforms others if the safety issue is the main concern. We need Blockchain as the most reliable infrastructure for implementing a leader-free consensus algorithm.
P2P blockchain is the most secure decentralized coordination methodology that allows the consensus model to make fully collective decisions [46]. As the ATMC system needs a concursus algorithm for reliable airspace allocation, blockchain based on the P2P topology can safely perform this task. Although its high computational complexity is its drawback, by relying on fast processors and desired GPS data collection time, P2P blockchain outperforms other methodologies.
Among the P2P strategies, Linear Consensus Protocol has been widely used for decentralized management and control of network dynamic agents. However, it is sensitive in realistic operation when faults and failures occur on sensors and actuators (hard failures), and when faced with Adversarial or Sybil attacks (soft failures) [47]. Hence, blockchain technology was developed to provide a decentralized, scalable, and secure P2P decision-making system. Ethereum can provide a platform for creating Smart Contracts not only for financial transactions [48], but also for swarm robots [49], multi-agent UAV moving management [50], and others. Our customized Smart Contract based on the Ethereum framework manages and controls aircraft future trajectories, relying on trajectories predicted by the Autoencoder.
The paper is organized as follows. Section 2 presents the Air Traffic Management problem statement. The methodology for aircraft trajectory prediction using an Autoencoder algorithm with our ATP model and the implementation of the P2P blockchain for the ATMC are presented in Section 3. Section 4 is devoted to the results, including representing the accuracy of the ATP model under data failure, and the performance of the Smart Contract designed for the ATMC. Finally, Section 5 provides a general discussion, conclusions, and recommendations for future work.
2. Problem Statement
Assume a flight area composed of airspace-like cubes, with several aircraft flying through their desired trajectories. Figure 1 shows the assumed flight area, constructed by cubes , in which and are the number of cubes along the axes, respectively.
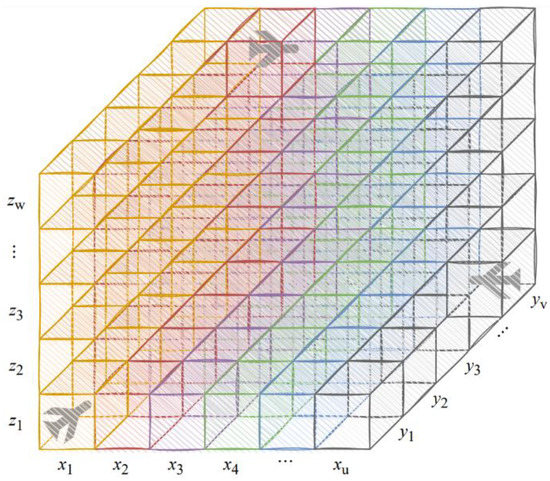
Figure 1.
Flight area composed of cubic airspaces.
According to Figure 1, there is no limitation to the cube size. The cube size is in which they are positive integers. The figure is rendered colourful in order to well illustration the airspace which is composed of small cubes. Aircraft might be found in cubes according to their latitude, longitude, and altitude, and they pass through airspaces following their individual trajectories. To avoid aerial collisions, aircraft should never be in the same airspace. Hence, traffic management must allocate safe coordinates to aircraft. To improve safety while reducing costs, long-term series of allocation is needed in time. Producing such long-term series makes the prediction of future aircraft trajectories an essential requirement for efficient allocation. For the prediction of future aircraft trajectory, it is assumed that aircraft fly in their air corridors, as shown in Figure 2. Considering that GPS data (which includes latitude, longitude, altitude, heading, speed, and time of the aircraft) at a given time is available, a model can therefore be used to predict the aircraft’s future trajectories for the next time steps.
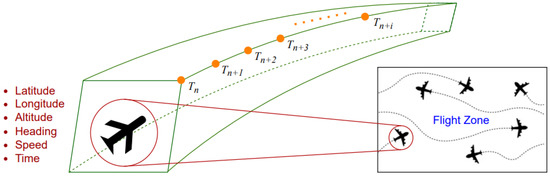
Figure 2.
Aircraft Trajectory Prediction for Air Traffic Management.
By using such predicted trajectories (the first objective), future airspace coordinates that minimize the risk of conflict (the second objective) can be allocated to an aircraft by relying on its determined cube-based path. These objectives highlight the need for efficient methodologies for accurate trajectory prediction and reliable airspace allocation.
3. Methodologies
This section presents the methodologies for realizing accurate trajectory prediction and traffic management. To satisfy the first objective, a data-driven model based on a Neural Network was designed for trajectory prediction. Then, to meet the second objective, a blockchain-based protocol was designed for airspace allocation to ensure safe and efficient traffic management.
3.1. Trajectory Prediction
A temporal latent Autoencoder [51] was used as the benchmark algorithm to develop the Aircraft Trajectory Prediction (ATP) model. This Autoencoder is an unsupervised protocol that not only removes noise from the GPS data but also reconstructs compressed data. Following strong dependencies among training data, it can also perform good-quality predictions even when data is deficient. These outstanding features make this Autoencoder an essential tool in fault-tolerant prediction strategies. Figure 3 shows the Autoencoder architecture that has been considered for the ATP model.
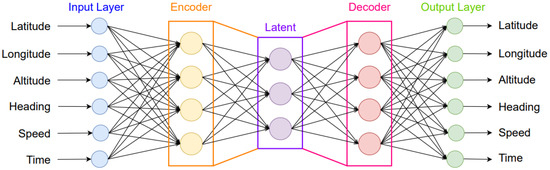
Figure 3.
The Autoencoder architecture for fault-tolerant aircraft trajectory prediction [51].
As shown in Figure 3, the data provided by the GPS (i.e., latitude, longitude, altitude, heading, speed, and time) is fed to the input layer, which then fully propagates it through the Encoder layer that reduces the dimensions of the input data. The Latent layer in the middle of the architecture produces the “Code”, which is fully passed to the Decoder layer. The Decoder is the mirror of the Encoder; its role is to enlarge the Code dimensions, and thereby prepare the full-dimension data for the Output layer. The robustness of the Autoencoder varies with the number of neurons in the Latent layer. The Autoencoder is trained to predict future trajectories even when some elements in the input vector are not well measured. For instance, in Figure 3, by considering 3 neurons in the Latent layer, in the worst case, the Autoencoder will still be able to predict trajectories in the case where there are 3 missing inputs.
The principles of how the Autoencoder works are described next. Let us consider two Euclidean spaces, decoded GPS data , and encoded GPS data . Using decoder , and encoder transfer functions, and , where both functions are multilayer perceptrons [52]. For encoded and decoded data samples, the following statement holds:
where is the encoded and is the decoded GPS data. Training this Autoencoder requires a critical function to evaluate the quality of the training. This task is performed using a predetermined probability distribution over the encoder transfer function , and a quality function associated with trajectory reconstruction, such that measures the difference between and . Therefore, the loss function that must be minimized by solving this optimization problem using the gradient technique can be mathematically represented as follows [52]:
Next, by considering the reference distribution for {} such as [52]:
where is the Dirac measure.
By considering L2 loss: as the Autoencoder quality function (norm 2), the optimal Autoencoder would be formulated as the following least-square optimization problem [52]:
The hyperparameters of the trained Autoencoder for ATP were fine-tuned by minimizing the optimization criteria given in Equation (4). The trajectories predicted by the Autoencoder can then be used for airspace allocation and traffic management.
3.2. Airspace Allocation
By using predicted trajectories, a receding-horizon lattice planner was developed for dynamic airspace allocation [53]. A Consensus Protocol must confirm that an aircraft will not be in a conflicting (possible collision) zone in any future steps [36]. To guarantee separation between aircraft, the Peer-to-Peer (P2P) topology [54] shown in Figure 4 was used as a decentralized Consensus Protocol based on blockchain technology.
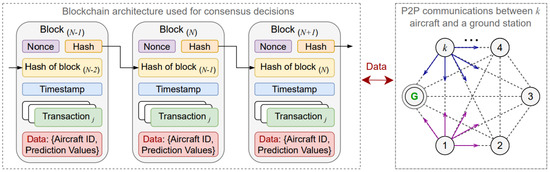
Figure 4.
P2P blockchain architecture that supports smart contracts for the consensus protocol.
Regardless of blockchain methodology, utilizing the P2P topology provides robust communication in case of data loss. Blockchain is an outstanding methodology for coming up with wrong data. Hence, using the blockchain methodology, which is developed based on P2P topology, not only provides robustness in case of data loss but also in case of wrong data (predicted by the Autoencoder) due to adversarial attacks. The Ethereum-based Smart Contract [55] executes Block(N+1) that allows aircraft to follow their trajectories if there is no conflict between the trajectories predicted by their corresponding Autoencoders.
As illustrated on the right-hand side of Figure 4, a ground station and k aircraft are assumed, which are fully connected and communicate with each other, and a P2P topology is therefore constructed. Each aircraft can be considered an “agent”, and is equipped with an Autoencoder that can be used to predict its future trajectories. Each aircraft submits its predicted trajectory (using its own Autoencoder) to the blockchain by itself. In the order word, each aircraft is an agent that creates a node on the P2P blockchain topology. All aircraft should confirm the future trajectories of the others relying on the previous executed block in the blockchain that contains all aircraft future trajectories in the last timestamp. The ATP is performed decentralized, and its values are shared among agents through the P2P topology. Blockchain methodology keeps trajectory data private and only allows identified aircraft to read and write the data on the chain. Each aircraft is considered a node and must individually act as an agent, share its data with others nodes, and write it on the blockchain. Block(N+1) is executed when the Smart Contract confirms that there is no conflict between aircraft relying on the Autoencoders and Block(N). Secured data mainly includes the aircraft identifier (ID) [1 − k], and its predicted trajectories which are stored in Block(N+1). This process is performed on-chain, relying on the previous block hash (“data encryptor”), the added number to the hash (“nonce”), exact time execution (“timestamp”), and j number of agreements for trajectory predictions (“transactions”). Trajectory Data are logged once an aircraft enters a district, and lasts as long as it exists in the corresponding districts.
Increasing the number of aircraft in a flight zone is a real challenge. Sharing data among many aircraft increases both the computational complexity and the error rate for a Smart Contract. Sharding means we consider aircraft in some classes regarding their close locations. The Smart Contract cannot execute new blocks quickly, and it may fail in the Block execution for unnecessary agreement. The concept of Sharding (scaling of the blockchain network) allows the Smart Contract to categorize aircraft into multiple districts (sub-flight zones) in terms of their locations. The ground station communicates with the districts through sharding and each of which oversees the path planning for aircraft, as shown in Figure 5.
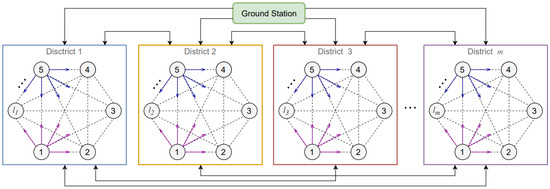
Figure 5.
Sharding a flight zone into several districts for edge computing in each sub-flight zone.
Figure 5 illustrates the P2P communication topology between aircraft. The flight zone is sharded by considering m districts. Each district creates a sub-flight zone that contains agents (aircraft), where indicates the number of sub-flight zones (districts). In other words, aircraft in a flight zone are sharded into sub-flight zones according to their locations. Worth mentioning that nodes 1 to 5 in each district are unique. For instance, node number 1 in district number 1 is not the same as node number 1 in district number 2, and each one represents the node corresponding to a particular aircraft.
The ground station does not communicate directly with the aircraft, but instead calls Smart Contract for the required data that are obtained from each individual district. The sharding methodology can reduce the computational complexity of the Smart Contract while reducing the error rate due to failed agreements associated with unnecessary encounter situations. The following section explains and discusses these improvements from a numerical perspective.
4. Results and Discussion
To test and validate the methodology presented in this study, aircraft trajectories were generated using our UAS-S4 flight dynamics model [56,57], and its corresponding controller [58]. This aircraft is pictured in Figure 6, and its specifications are listed in Table 1. A number of 1820 flight trajectories containing 218,400 samples (i.e., ) were generated and used for the training, testing, and validation of our newly designed Autoencoder.

Figure 6.
Hydra Technologies UAS-S4 Ehecatl.

Table 1.
The UAS-S4 geometrical and flight data specifications.
Weighting vectors were initialized, and then a batch normalization was performed by recentering and rescaling the input data with the aim to obtain a fast and stable trajectory prediction [59]. Regularization was also performed, as a means to reduce the magnitudes of regressed trajectories [60]. The hyperparameters were tuned [61]; with a Code size of (vector), the system could be tolerant in the case of faults or failures of three out of all six elements of the input vector .
For the encoder, 4 and 5 numbers of nodes were considered, and the decoder architectures were the same as those of the encoder. The Mean Absolute Error (MAE) was determined as the loss function. Table 2 presents the prediction accuracy, and precision of the Autoencoder, which is compared with the Long Short-Term Memory (LSTM) [36] under four different data failure combinations.

Table 2.
The Fault-tolerant Autoencoder and LSTM trajectory prediction accuracy and precision comparison.
According to Table 2, the LSTM shows slightly better performance than the Autoencoder only in the absence of failure. However, when these methods use deficient data (e.g., latitude, altitude, and speed failure), the Autoencoder shows very good prediction accuracy (91.2%), while the LSTM shows a much worse prediction accuracy (58.7%). These results confirm the excellent fault-tolerant ability of the Autoencoder. Worth mentioning that the training trajectories data were generated using the simulator while random disturbances such as wind shear, wind gusts, and turbulences were considered in the simulation process. In accordance with Table 2, 98.7% prediction accuracy in the test phase confirms the generalizability of the Autoencoder for trajectory prediction even in case of unknown disturbances dues to climate changes.
Moreover, the Autoencoder performance is dependent on its architecture (number of neurons in the Encoder, Latent, and Decoder) as shown in Table 3. For this purpose, we considered different feasible numbers of neurons for Encoder, Latent, and Decoder to determine which number gives the best performance.

Table 3.
The Autoencoder performance considering different number of neurons in the architectures.
Table 3 shows that using 2 neurons in the Latent layer when 3 elements (i.e., latitude, altitude, and speed) in the input vector were lost (had failures) resulted in the Code generating failure, and dramatic prediction accuracy reduction (shown in red). It is worth noting that the use of 4 neurons in the Encoder layer can provide better data for coding than using 5 neurons. Prediction Accuracy (shown in green) confirms that the best Autoencoder architecture is composed of 3 neurons in the Latent layer, and 4 neurons in the Decoder and Encoder layers.
Relying on the given fault-tolerant Autoencoder for trajectory prediction, 120 UAS-S4s were arranged in a flight zone, in which each had its own location, heading, and speed. Their future trajectories were managed and controlled using the Smart Contract. A private chain combining the “consensus layer” with the “contract layer” was designed for ATMC decision-making, based on proof of time and Smart Contract approaches, respectively. We considered the Linear Consensus Protocol (LCP) as the baseline and compared its performance to the performance of our Smart Contract-based Consensus Protocol (SCCP). Both methodologies were analyzed in cases of “soft” failures (Sybil Attacks and Adversarial Attack). In order to improve Smart Contract performance to avoid unnecessary encounter situations, the Sharding methodology was used to design several sub-flight zones. Table 4 shows the error rate while different Consensus Protocols were managing the UAS-S4′s trajectories and different attacks were imposed on the aircraft.

Table 4.
ATMC error rate when consensus protocols control and manage traffic.
According to the Error Rate shown in Table 4, when soft attacks are not imposed, the Linear Consensus Protocol (LCP) methodology can perform the ATMC task with the smallest error rate (5.3%). However, the superiority of the Smart Contract-based Consensus Protocol (SCCP) and Sharding-SCCP over the LCP becomes obvious when Sybil Attacks and Adversarial Attacks are considered. Under such conditions, the SCCP showed an 18.6% error rate, while the LCP almost collapsed (83.2% error rate). Sharding improved the SCCP performance (down to a 15.4% error rate). The following section elaborates on and summarizes these results.
For the reliability evaluation, we considered the error rate as the performance index. The error rates due to block execution failures were measured, while various consensus protocols were approaching adversarial attacks. Worth mentioning that the randomized consensus methodology is not utilized in the comparison study due to its inherent safety weakness for performing the ATM critical task. The block execution error rates were 2.24%, 2.09%, and 0.87% when deterministic, leader-based, and leader-free consensus methodologies were in charge, respectively. These error rate values confirm the leader-free blockchain methodology is more reliable than other consensus protocols while approaching adversarial attacks.
The probability of UAS conflicts after airspace allocation might be analyzed as a critical dynamic performance. A total of 100 UAS-S4s were operated at (altitude), (latitude), and (longitude), by utilizing 16 shards to ensure safe performance. Figure 7 illustrates the probability of conflicts among three UAS-S4s in a specific sub-flight zone under two protocols, the LCP (a) and blockchain (b).
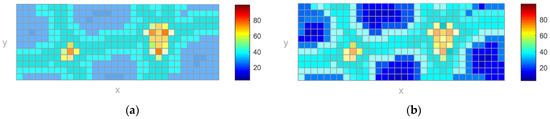
Figure 7.
Probability of UASs conflicts using Linear Consensus Protocol LCP (a) and blockchain (b).
Figure 7 is extracted from the 10th shard, where 3 UASs have conflicts within 3.84 km2. A comparison between plot (a) for the LCP and plot (b) with blockchain confirms that the blockchain performance was better than that of the LCP in terms of the probabilities of conflicts and safety. The average probability of conflicts was 33.1% for the LCP and 26.7% for the blockchain. In addition, the LCP does not give safe zones, while the blockchain approach offers a substantial number of such zones.
5. Conclusions
A reliable Air Traffic Management and Control (ATMC) was designed based on an Autoencoder, and a Smart Contract on the Ethereum blockchain. The Autoencoder was designed to predict future flight trajectories despite partial failures in the GPS data. It has shown excellent prediction accuracy when tested with deficient data obtained from the GPS. The impact of the number of neurons used in the Autoencoder’s hidden layers on its performance was investigated. The number of neurons in the Latent layer determined the threshold robustness for the Autoencoder when it is faced with deficient data. Relying on the predicted trajectories using this fault-tolerant Autoencoder, a Consensus Protocol was designed for Air Traffic Management and Control (ATMC). A Smart Contract based on Ethereum blockchain was designed to perform the ATMC task. The Smart Contract Consensus Protocol (SCCP), and a Sharding SCCP showed very good performance under Sybil Attacks and Adversarial Attacks. The designed ATMC system composed of the Autoencoder, and the Smart Contract Consensus Protocol showed very good robustness in cases of data failures or attacks.
Author Contributions
Conceptualization, S.M.H. and S.A.H.; methodology, S.M.H. and S.A.H.; software, S.M.H. and S.A.H.; validation, S.M.H., S.A.H., R.M.B. and G.G.; formal analysis, S.M.H., S.A.H., R.M.B. and G.G.; investigation, S.M.H. and S.A.H.; resources, R.M.B. and G.G.; data curation, S.M.H.; writing—original draft preparation, S.M.H.; writing—review and editing, R.M.B. and G.G.; visualization, S.M.H.; supervision, R.M.B. and G.G.; project administration, R.M.B.; funding acquisition, R.M.B. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSERC within the Canada Research Chairs program, which made possible the realization of this research and the publication of this paper. Ruxandra Botez is the Canada Research Chair Tier 1 Holder in Aircraft Modeling and Simulation New Technologies.
Data Availability Statement
Not applicable.
Acknowledgments
Special thanks are due to the Natural Sciences and Engineering Research Council of Canada (NSERC) for the Canada Research Chair Tier 1 in Aircraft Modeling and Simulation Technologies funds. We would also like to thank Odette Lacasse and Oscar Carranza for their support at ETS, as well as Hydra Technologies’ team members Carlos Ruiz, Eduardo Yakin, and Alvaro Gutierrez Prado in Mexico. Finally, we wish to express our appreciation to the Canada Foundation for Innovation CFI, the Ministère de l’Économie et de l’Innovation and Hydra Technologies for their support of the acquisition of the UAS-S4 at the LARCASE.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Nomenclature
| A | Decoded GPS data |
| B | Encoded GPS data |
| E | Encoder transfer function |
| D | Decoder transfer function |
| Number of steps for future trajectory prediction | |
| Number of executed agreements | |
| Number of aircraft in a flight zone before sharding | |
| Number of aircraft in a flight zone after sharding | |
| L | Autoencoder loss function |
| Number of districts that provide sub-flight zones after sharding | |
| Number associated with a block in the chain | |
| Q | Autoencoder quality function |
| Time during which the aircraft is in step n |
References
- Lygeros, J.; Tomlin, C.; Sastry, S. On controller synthesis for nonlinear hybrid systems. In Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No. 98CH36171), Tampa, FL, USA, 18 December 1998; IEEE: Piscataway, NJ, USA; Volume 2, pp. 2101–2106.
- Murrieta-Mendoza, A.; Demange, S.; George, F.; Botez, R. Performance DataBase creation using a level D simulator for Cessna Citation X aircraft in cruise regime. In Proceedings of the IASTED Modeling, Identification and Control Conference, Innsbruck, Austria, 16–17 February 2015; pp. 818–826. [Google Scholar]
- Murrieta Mendoza, A.; Bunel, A.; Botez, R.M. Aircraft vertical reference trajectory optimization with a RTA constraint using the ABC algorithm. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; p. 4208. [Google Scholar]
- Murrieta-Mendoza, A.; Romain, C.; Botez, R.M. Commercial aircraft lateral flight reference trajectory optimization. IFAC-PapersOnLine 2016, 49, 1–6. [Google Scholar] [CrossRef]
- Petres, C.; Pailhas, Y.; Patron, P.; Petillot, Y.; Evans, J.; Lane, D. Path planning for autonomous underwater vehicles. IEEE Trans. Robot. 2007, 23, 331–341. [Google Scholar] [CrossRef]
- Geraerts, R. Planning short paths with clearance using explicit corridors. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AL, USA, 4–8 May 2021; IEEE: Piscataway, NJ, USA; pp. 1997–2004.
- Yang, K.; Sukkarieh, S. 3D smooth path planning for a UAV in cluttered natural environments. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA; pp. 794–800. [Google Scholar]
- Nash, A.; Koenig, S.; Tovey, C. Lazy Theta*: Any-angle path planning and path length analysis in 3D. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; Volume 24, pp. 147–154. [Google Scholar]
- Wilburn, J.N.; Perhinschi, M.G.; Wilburn, B.K. Implementation of a 3-Dimensional Dubins-Based UAV Path Generation Algorithm. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 5232. [Google Scholar]
- Murrieta-Mendoza, A.; Botez, R.M. Methodology for vertical-navigation flight-trajectory cost calculation using a performance database. J. Aerosp. Inf. Syst. 2015, 12, 519–532. [Google Scholar] [CrossRef]
- Boughari, Y.; Botez, R.; Ghazi, G.; Theel, F. Evolutionary Algorithms for Robust Cessna Citation X Flight Control; No. 2014-01-2166; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Patron, R.F.; Kessaci, A.; Botez, R.M. Flight trajectories optimization under the influence of winds using genetic algorithms. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 4620. [Google Scholar]
- Hashemi, S.M.; Barati, S.; Talati, S.; Noori, H. A genetic algorithm approach to optimal placement of switching and protective equipment on a distribution network. J. Eng. Appl. Sci. 2016, 11, 1395–1400. [Google Scholar]
- Murrieta-Mendoza, A.; Ruiz, H.; Kessaci, S.; Botez, R.M. 3D reference trajectory optimization using particle swarm optimization. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017; p. 3435. [Google Scholar]
- Murrieta-Mendoza, A.; Hamy, A.; Botez, R.M. Four-and three-dimensional aircraft reference trajectory optimization inspired by ant colony optimization. J. Aerosp. Inf. Syst. 2017, 14, 597–616. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Menhaj, M.B.; Amani, A.M. Reconfigurable Fault-Tolerant Control by Linear quadratic Virtual Actuator under Control Signal Constraint. J. Eng. Appl. Sci. 2006, 11, 1998–2004. [Google Scholar]
- Perhinschi, M.G.; Moncayo, H. Artificial immune system for comprehensive and integrated aircraft abnormal conditions management. Adv. Comput. Intell. Auton. Aerosp. Syst. 2018, 147–218. [Google Scholar]
- Patrón, R.F.; Kessaci, A.; Botez, R.M. Horizontal flight trajectories optimisation for commercial aircraft through a flight management system. Aeronaut. J. 2014, 118, 1499–1518. [Google Scholar] [CrossRef]
- Patrón RS, F.; Botez, R.M.; Labour, D. Vertical profile optimization for the Flight Management System CMA-9000 using the golden section search method. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; IEEE: Piscataway, NJ, USA; pp. 5482–5488. [Google Scholar]
- Hashemi, S.M.; Botez, R.M.; Grigorie, L.T. Adaptive fuzzy control of chaotic flapping relied upon lyapunov-based tuning laws. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020; p. 3193. [Google Scholar]
- Hashemi, S.; Botez, R. Nonlinear adaptive fuzzy control of uncertain chaotic click mechanism flapping-wing. In CASI AERO 2019 (Laval, QC, Canada, 14–16 May 2019); Canadian Aeronautics and Space Institute: Ottawa, ON, USA, 2019. [Google Scholar]
- Boughari, Y.; Ghazi, G.; Botez, R.M.; Theel, F. New Methodology for Optimal Flight Control Using Differential Evolution Algorithms Applied on the Cessna Citation X Business Aircraft—Part 1. Design and Optimization. INCAS Bull. 2017, 9, 31. [Google Scholar]
- Boughari, Y.; Botez, R.M.; Ghazi, G.; Theel, F. Flight control clearance of the Cessna Citation X using evolutionary algorithms. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 510–532. [Google Scholar] [CrossRef]
- Ghazi, G.; Botez, R.M.; Bourrely, C.; Turculet, A.-A. Method for calculating aircraft flight trajectories in presence of winds. J. Aerosp. Inf. Syst. 2021, 18, 442–463. [Google Scholar] [CrossRef]
- Hashemi, S.; Abyari, M.; Barati, S.; Tahmasebi, S.; Talati, S. A proposed method to controller parameter soft tuning as accommodation FTC after unknown input observer FDI. J. Eng. Appl. Sci. 2016, 11, 2818–2829. [Google Scholar]
- Coulter, N.; Moncayo, H. An Online Machine Learning Paradigm for Spacecraft Fault Detection. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021; p. 1339. [Google Scholar]
- Degas, A.; Islam, M.R.; Hurter, C.; Barua, S.; Rahman, H.; Poudel, M.; Ruscio, D.; Ahmed, M.U.; Begum, S.; Rahman, M.A. A Survey on Artificial Intelligence (AI) and eXplainable AI in Air Traffic Management: Current Trends and Development with Future Research Trajectory. Appl. Sci. 2022, 12, 1295. [Google Scholar] [CrossRef]
- Perez, A.E.; Moncayo, H.; Moguel, I.; Perhinschi, M.G.; Al Azzawi, D.; Togayev, A. Development of Immunity Based Adaptive Control Laws for Aircraft Fault Tolerance. In Proceedings of the Dynamic Systems and Control Conference, 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 46186, p. V001T03A001. [Google Scholar]
- van Iersel, Q.G.; Murrieta Mendoza, A.; Felix Patron, R.S.; Hashemi, S.M.; Botez, R.M. Attack and Defense on Aircraft Trajectory Prediction Algorithms. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 4027. [Google Scholar]
- Ghazi, G.; Botez, R.M.; Domanti, S. New methodology for aircraft performance model identification for flight management system applications. J. Aerosp. Inf. Syst. 2020, 17, 294–310. [Google Scholar] [CrossRef]
- Ghazi, G.; Gerardin, B.; Gelhaye, M.; Botez, R.M. New adaptive algorithm development for monitoring aircraft performance and improving flight management system predictions. J. Aerosp. Inf. Syst. 2020, 17, 97–112. [Google Scholar] [CrossRef]
- Ghazi, G.; Botez, R.M.; Maniette, N. Cessna Citation X takeoff and departure trajectories prediction in presence of winds. J. Aerosp. Inf. Syst. 2020, 17, 659–681. [Google Scholar] [CrossRef]
- Delahaye, D.; Puechmorel, S.; Tsiotras, P.; Féron, E. Mathematical models for aircraft trajectory design: A survey. In Air Traffic Management and Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 205–247. [Google Scholar]
- Dancila, R.; Botez, R. New flight trajectory optimisation method using genetic algorithms. Aeronaut. J. 2021, 125, 618–671. [Google Scholar] [CrossRef]
- Patrón RS, F.; Botez, R.M. Flight trajectory optimization through genetic algorithms for lateral and vertical integrated navigation. J. Aerosp. Inf. Syst. 2015, 12, 533–544. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Botez, R.M.; Grigorie, T.L. New reliability studies of data-driven aircraft trajectory prediction. Aerospace 2020, 7, 145. [Google Scholar] [CrossRef]
- Neumeier, M.; Betsch, M.; Tollkühn, A.; Berberich, T. Variational autoencoder-based vehicle trajectory prediction with an interpretable latent space. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC); IEEE: Piscataway, NJ, USA, 2021; pp. 820–827. [Google Scholar]
- Murray, B.; Perera, L.P. A dual linear autoencoder approach for vessel trajectory prediction using historical AIS data. Ocean. Eng. 2020, 209, 107478. [Google Scholar] [CrossRef]
- Zeng, W.; Xu, Z.; Cai, Z.; Chu, X.; Lu, X. Aircraft trajectory clustering in terminal airspace based on deep autoencoder and gaussian mixture model. Aerospace 2021, 8, 266. [Google Scholar] [CrossRef]
- Ivanovic, B.; Leung, K.; Schmerling, E.; Pavone, M. Multimodal deep generative models for trajectory prediction: A conditional variational autoencoder approach. IEEE Robot. Autom. Lett. 2020, 6, 295–302. [Google Scholar] [CrossRef]
- Nasreen, M.; Ganesh, A.; Sunitha, C. A study on Byzantine fault tolerance methods in distributed networks. Procedia Comput. Sci. 2016, 87, 50–54. [Google Scholar] [CrossRef]
- Burke, E.K.; Burke, E.K.; Kendall, G.; Kendall, G. Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Liu, M. Robotic online path planning on point cloud. IEEE Trans. Cybern. 2015, 46, 1217–1228. [Google Scholar] [CrossRef]
- Maurer, A.; Tixeuil, S. Containing byzantine failures with control zones. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 362–370. [Google Scholar] [CrossRef]
- Zegers, F.M.; Hale, M.T.; Shea, J.M.; Dixon, W.E. Event-triggered formation control and leader tracking with resilience to byzantine adversaries: A reputation-based approach. IEEE Trans. Control Netw. Syst. 2021, 8, 1417–1429. [Google Scholar] [CrossRef]
- Mokhtar, A.; Murphy, N.; Bruton, J. Blockchain-based multi-robot path planning. In Proceedings of the 2019 IEEE 5th World Forum on Internet of Things (WF-IoT); IEEE: Piscataway, NJ, USA, 2019; pp. 584–589. [Google Scholar]
- Cheng, Z.; Zhao, L.; Shi, Z. Decentralized Multi-UAV Path Planning Based on Two-Layer Coordinative Framework for Formation Rendezvous. IEEE Access 2022, 10, 45695–45708. [Google Scholar] [CrossRef]
- Buterin, V. A next-generation smart contract and decentralized application platform. White Pap. 2014, 3, 36. [Google Scholar]
- Castelló Ferrer, E. The blockchain: A new framework for robotic swarm systems. In Proceedings of the Future Technologies Conference; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1037–1058. [Google Scholar]
- De Campos MG, S.; Chanel, C.P.; Chauffaut, C.; Lacan, J. Towards a Blockchain-Based Multi-UAV Surveillance System. Front. Robot. AI 2021, 8, 557692. [Google Scholar] [CrossRef]
- Nguyen, N.; Quanz, B. Temporal latent auto-encoder: A method for probabilistic multivariate time series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 9117–9125. [Google Scholar]
- Michelucci, U. An introduction to autoencoders. arXiv 2022, arXiv:2201.03898. [Google Scholar]
- Andersson, O.; Ljungqvist, O.; Tiger, M.; Axehill, D.; Heintz, F. Receding-horizon lattice-based motion planning with dynamic obstacle avoidance. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC); IEEE: Piscataway, NJ, USA, 2018; pp. 4467–4474. [Google Scholar]
- Alladi, T.; Chamola, V.; Sahu, N.; Guizani, M. Applications of blockchain in unmanned aerial vehicles: A review. Veh. Commun. 2020, 23, 100249. [Google Scholar] [CrossRef]
- Alharby, M.; Van Moorsel, A. Blockchain-based smart contracts: A systematic mapping study. arXiv 2017, arXiv:1710.06372. [Google Scholar]
- Hashemi, S.M.; Botez, R.M. Support Vector Regression Application for the Flight Dynamics New Modelling of the UAS-S4. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 2576. [Google Scholar]
- Kuitche, M.; Yañez-Badillo, H.; Botez, R.; Hashemi, S. Stabilisation, tracking and disturbance rejection control design for the UAS-S45 Bálaam. Aeronaut. J. 2022, 126, 1474–1496. [Google Scholar] [CrossRef]
- Hashemi, S.; Botez, R. Lyapunov-based robust adaptive configuration of the UAS-S4 flight dynamics fuzzy controller. Aeronaut. J. 2022, 126, 1187–1209. [Google Scholar] [CrossRef]
- Hashemi, S.; Hashemi, S.A.; Botez, R.M.; Ghazi, G. A Novel Air Traffic Management and Control Methodology using Fault-Tolerant Autoencoder and FP2P Blockchain Application on the UAS-S4 Ehécatl. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 2190. [Google Scholar]
- Hashemi, S.; Hashemi, S.A.; Botez, R.M.; Ghazi, G. Attack-tolerant Trajectory Prediction using Generative Adversarial Network Secured by Blockchain Application to the UAS-S4 Ehécatl. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 2192. [Google Scholar]
- Hashemi, S.M.; Botez, R.M. A Novel Flight Dynamics Modeling Using Robust Support Vector Regression against Adversarial Attacks. SAE Int. J. Aerosp. 2023, 16, 19. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).