Safety and Efficiency Evaluation Model for Converging Operation of Aircraft and Vehicles
Abstract
1. Introduction
2. Rules for Separation Establishment between Aircraft and Vehicle
3. Aircraft and Vehicle Convergence Safety Assessment Model Set-Up
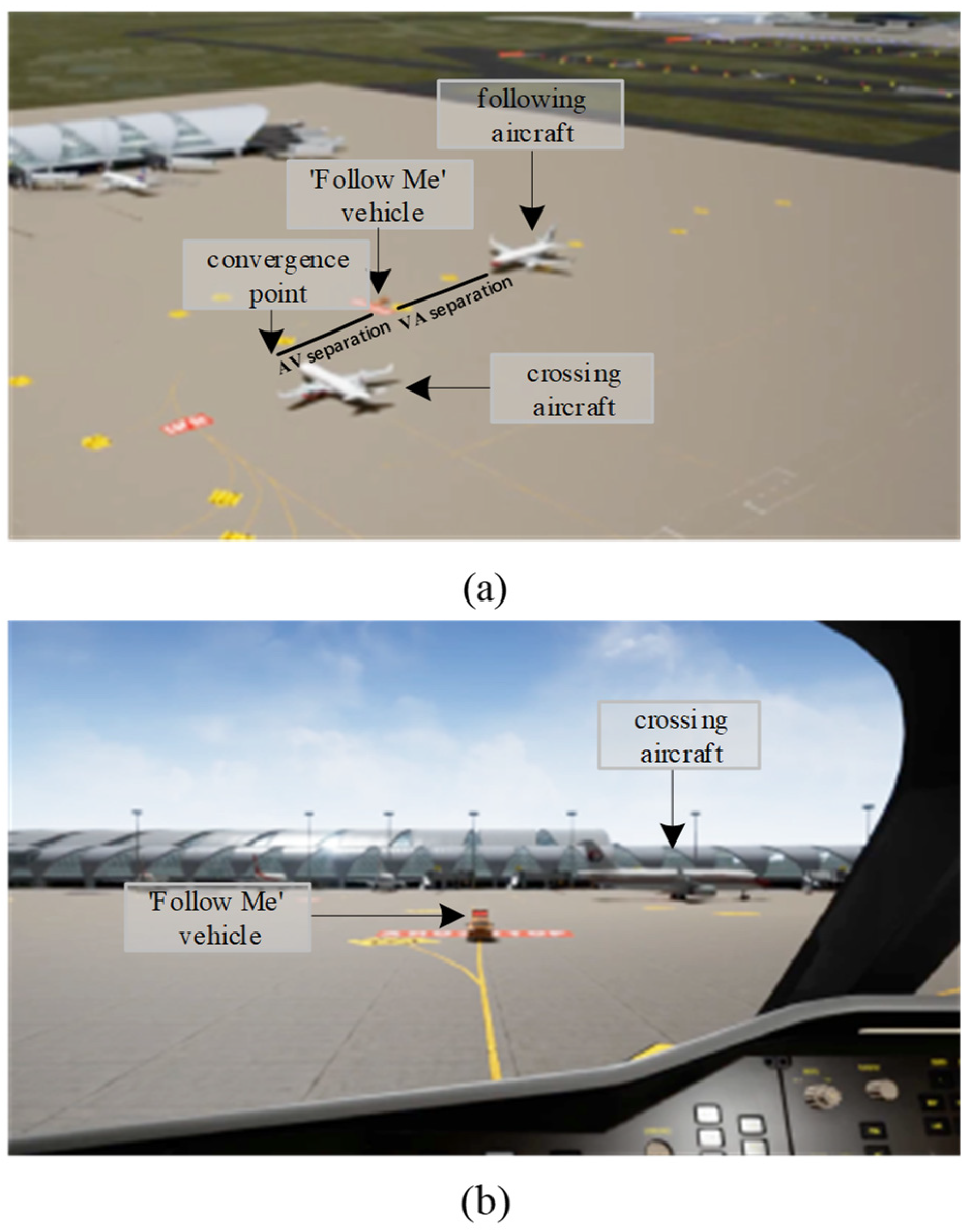
3.1. An Abstract Description of the Convergence Operation Process
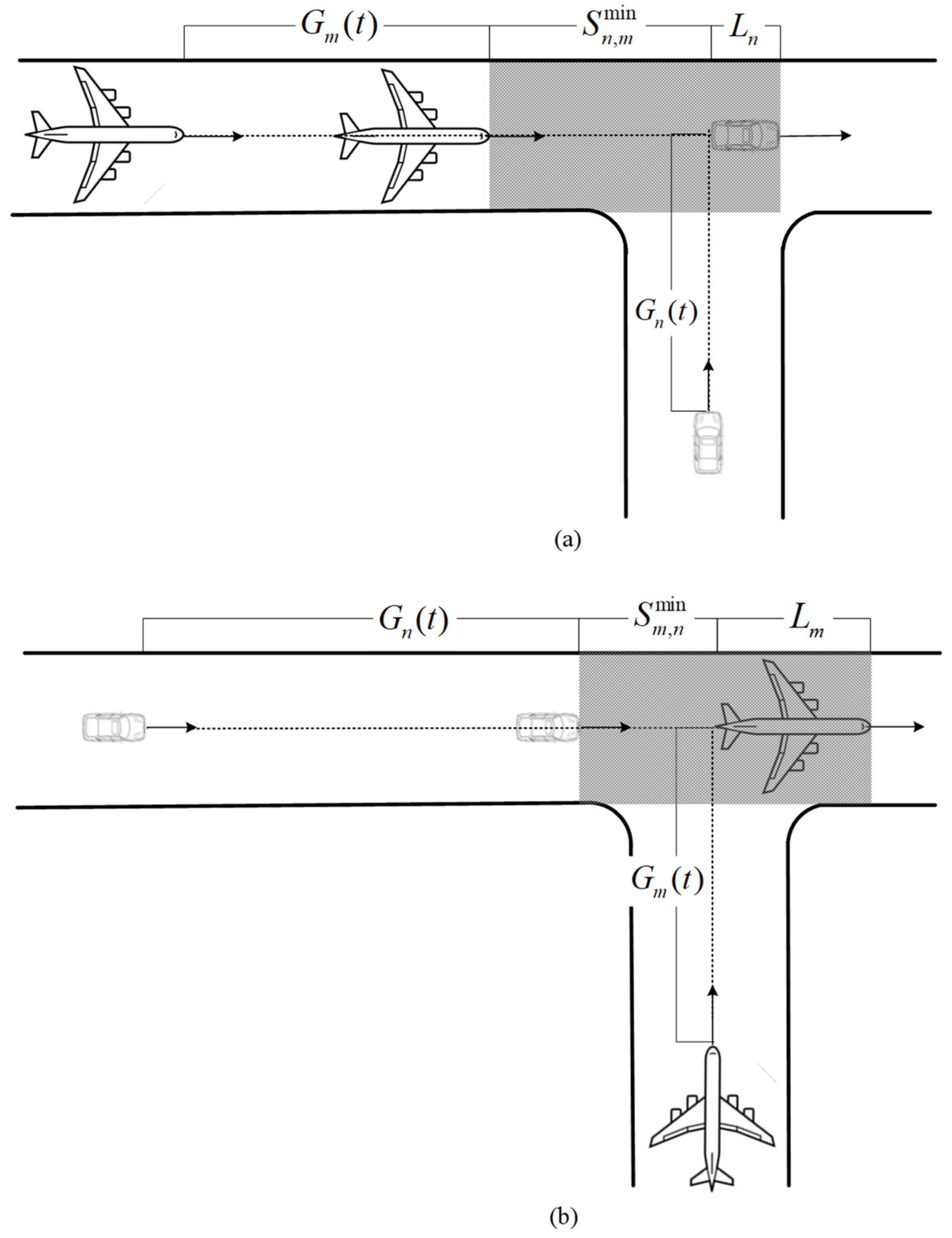
3.2. Vehicle and Aircraft Cross-Motion Regulations
3.3. Vehicle and Aircraft Cross-Motion Safety Assessment
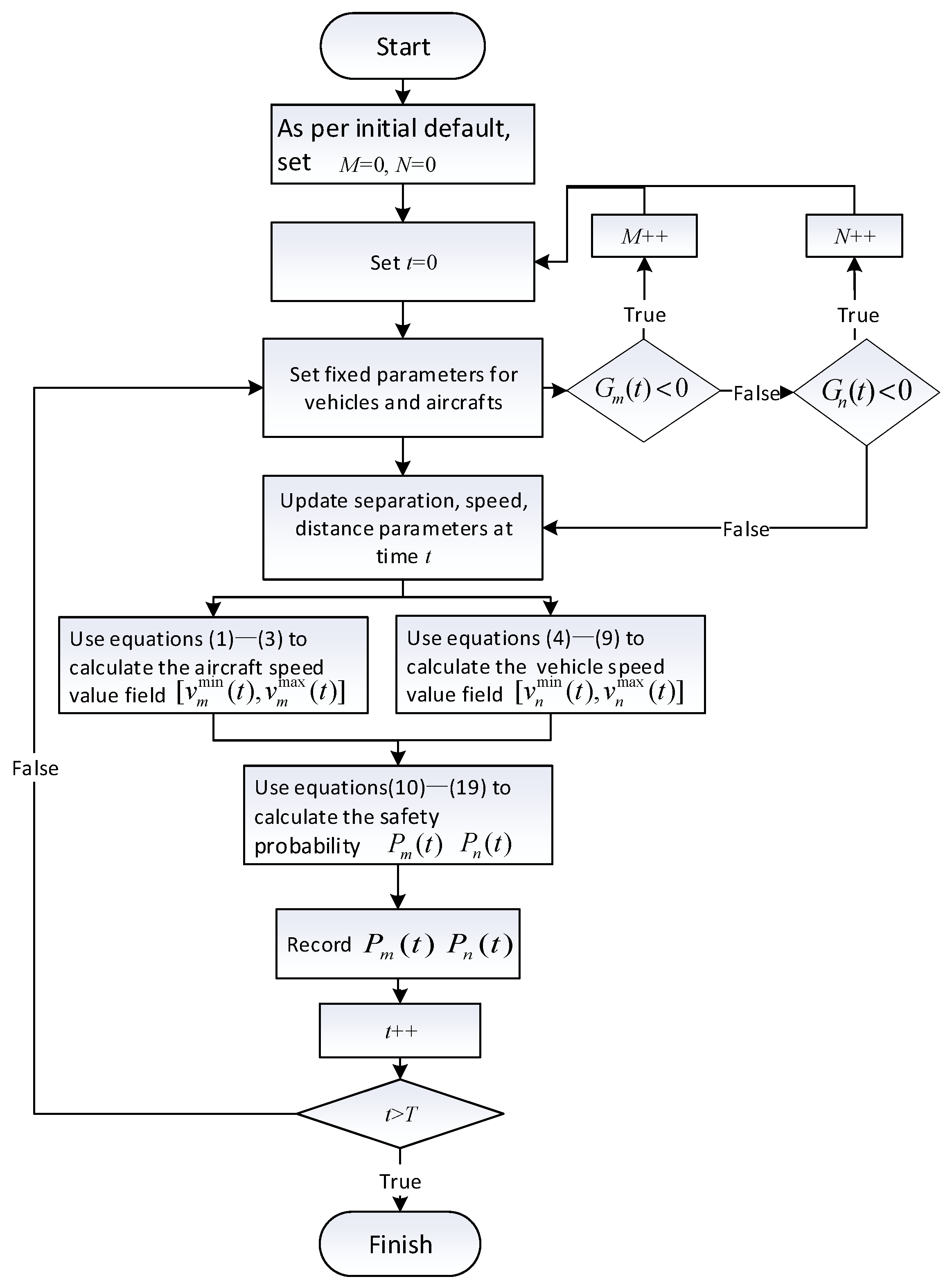
4. Safety Assessment Simulation Design and Data Analysis
4.1. Simulation Platform Set-Up
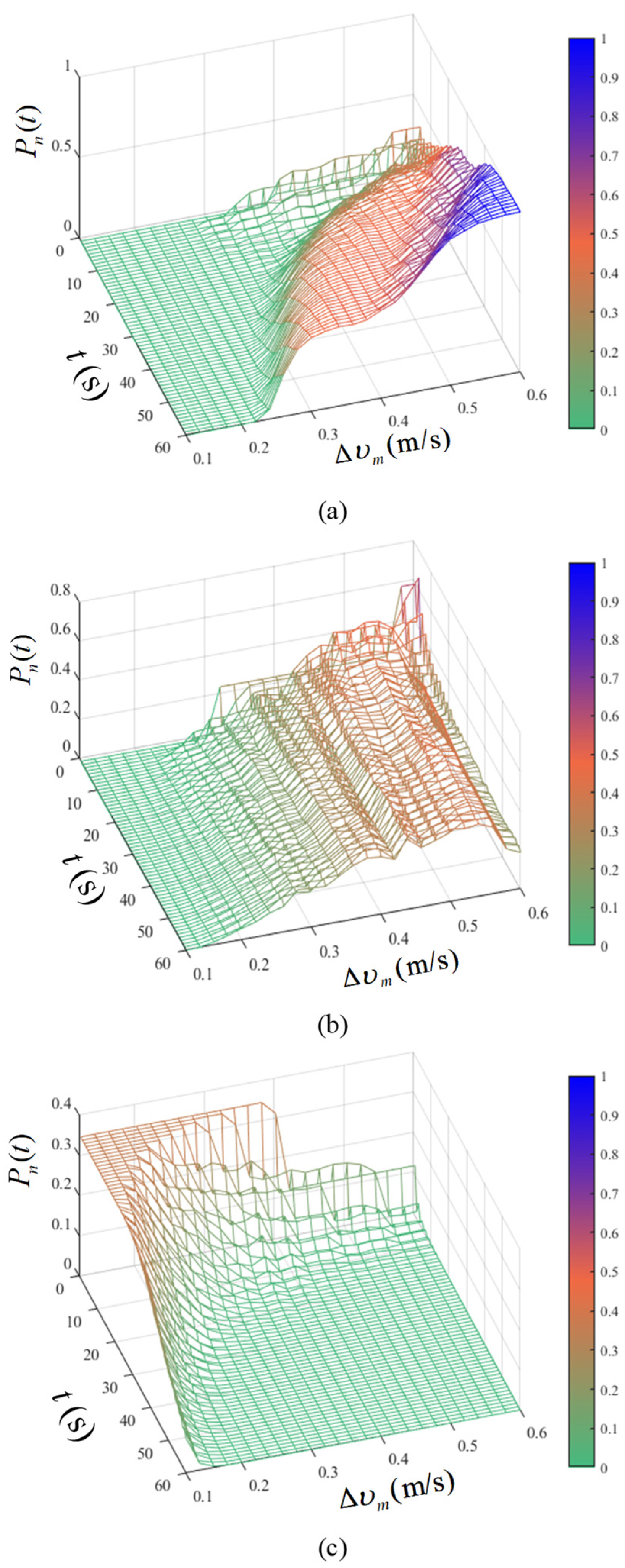
4.2. Safety Assessment in the Case of the Vehicle Passing an Intersection First
4.3. Safety Assessment in the Case of the Aircraft Passing an Intersection First
4.4. Safety Assessment Comparison and Discussion
- (1)
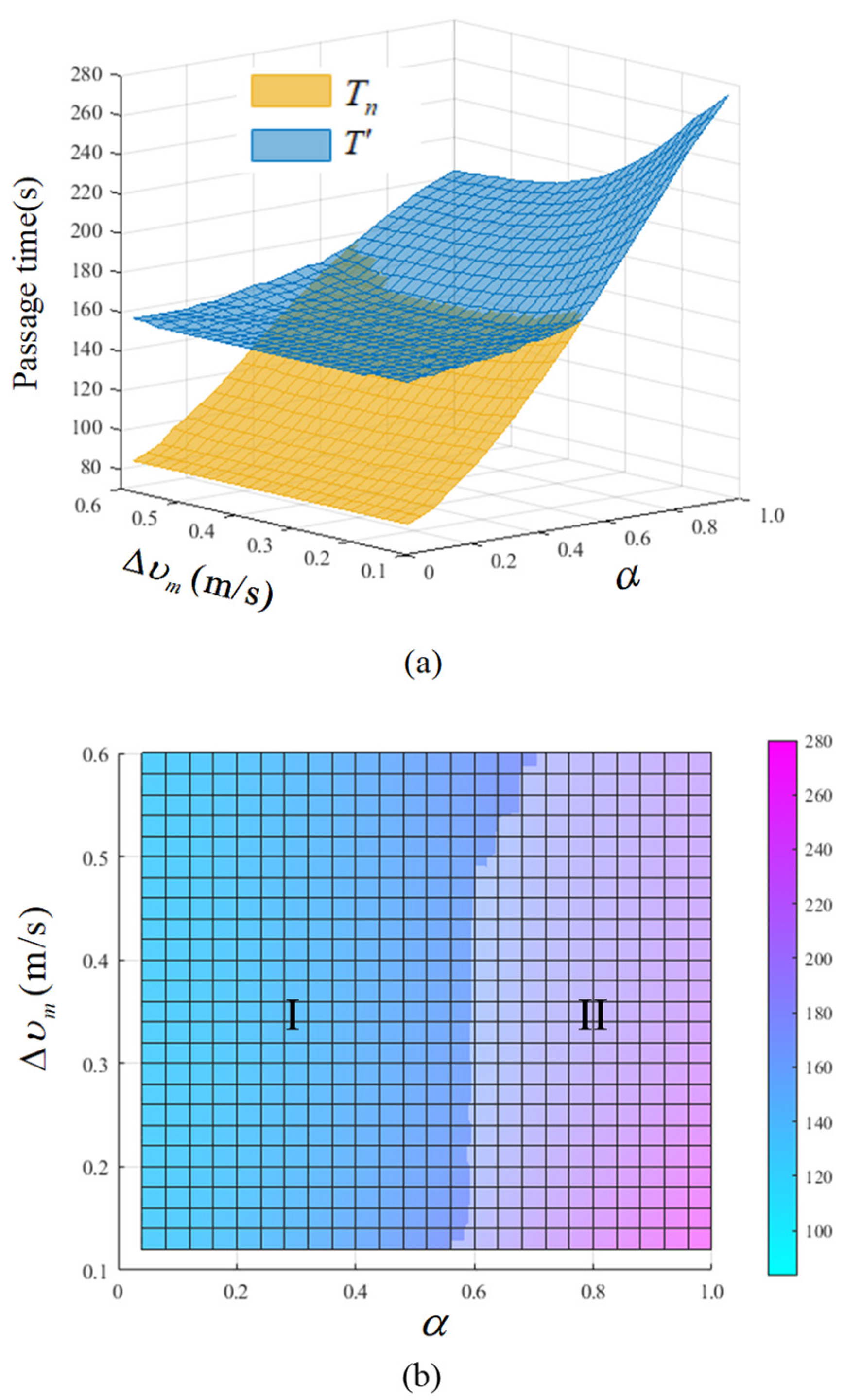
- When , it is safer for the vehicle to cross the intersection first, but whether it can do so without colliding with an aircraft depends on how the aircraft regulates its speed. If the aircraft’s speed change is minimal, there is a 100% chance of a collision at the crossing. In actual operation, when vehicles completely ignore aircraft due to poor visibility caused by fog or when the driver cannot observe aircraft due to the occlusion of terminals and obstacles, the controller should notify the pilot promptly to observe and slow down in time and remind pilots to adjust speed to avoid vehicles before reaching critical road intersection.
- (2)
- When , the safety of an aircraft passing an intersection is slightly higher than it is for a vehicle, indicating that when the vehicle safety sensitivity is low, the interval adjustment is relatively slow and both the vehicle and the aircraft have a chance to pass the intersection safely. However, the approach to the intersection will stimulate the deceleration behavior of the vehicle, thus forming the priority passage of aircraft under vehicle avoidance.
- (3)
- When , the safety probability value of the aircraft passing the intersection first is the highest. Vehicles respond sensitively to the position of the aircraft, slowing down in time and gradually increasing the separation of the two to ensure safety, thus forming the process of vehicles maintaining a low speed and following the aircraft through the intersection in turn.
- (4)
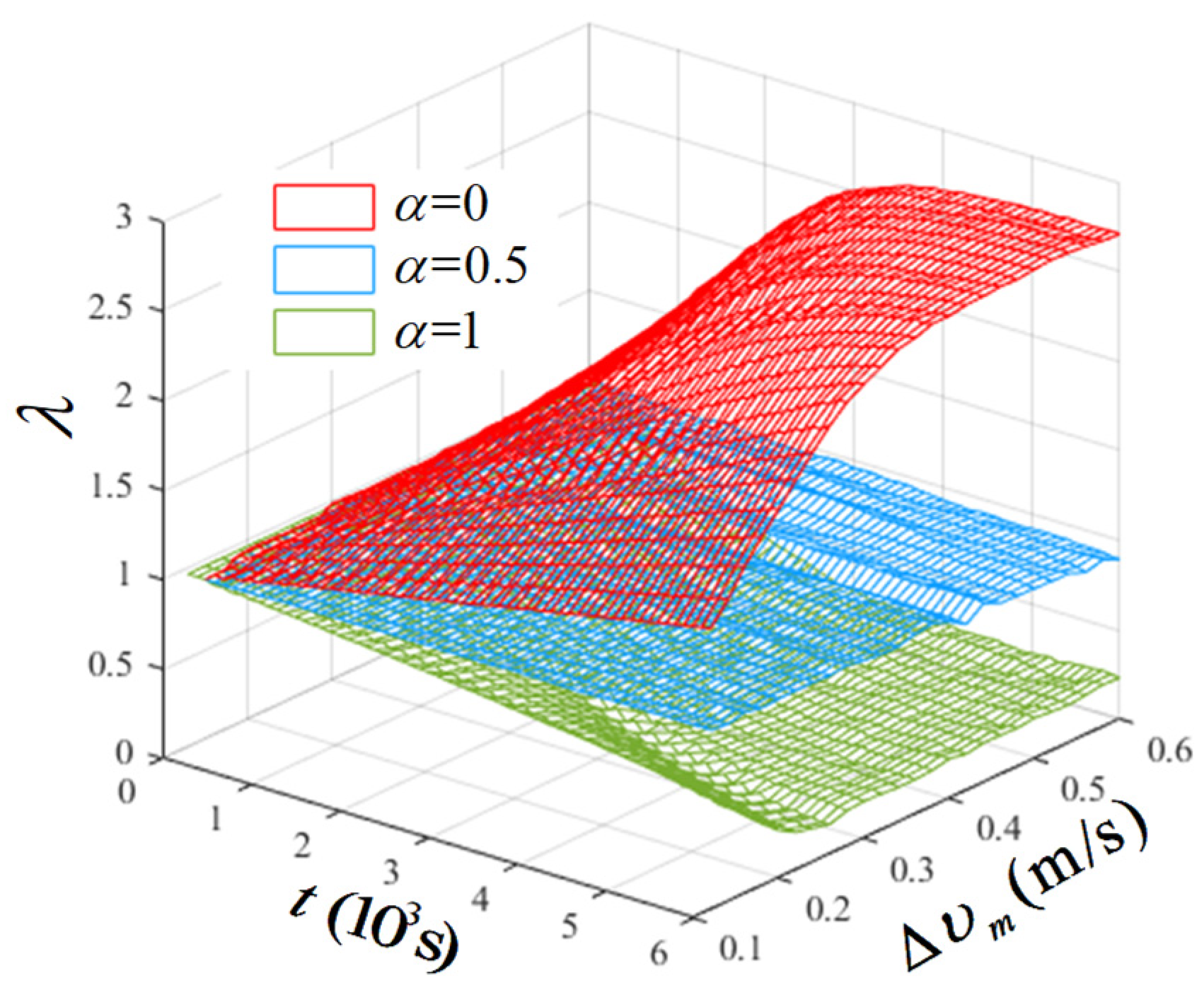
- The relationship between and the safety probability of cross-motion of a mixed vehicle and an aircraft is essentially positive, suggesting that the pilot’s capacity to adjust the speed and the proper amplification of the speed range can be beneficial to the separation establishment and operational safety. Additionally, the operational risk can be raised by the existing driving strategy of steady-speed taxiing, which is primarily advocated by different airline divisions to maintain taxiing stability.
5. Mixed Traffic Flow Capacity and Efficiency Analysis
6. Conclusions
- Vehicle safety sensitivity is inversely proportional to the probability of vehicle priority passing through the intersection without conflict and is directly proportional to the probability of aircraft priority passing through. The safety sensitivity of vehicles is inversely proportional to the passing efficiency and is directly proportional to the passing ratio of aircraft.
- Vehicle safety sensitivity and deceleration rules determine the passage order of vehicles and aircraft in a short local scope and affect the passage proportion of vehicles and aircraft in the long-term multi-area range.
- The increase and decrease in aircraft taxiing speed are proportional to safety and efficiency, which indicates that even if the control rules stipulate that the driver should take the initiative to take measures, the pilot’s initiative of separation and speed adjustment should not be removed.
- A mixed traffic flow with higher safety and efficiency, better stability, and balanced locomotive proportion can be achieved when .
- To further improve the safety of airport operations, it is possible to consider reducing the factors that contribute to the unsafe conditions of vehicle and aircraft operations during the airport planning stage. For example, expanding the airport area to reduce congestion during operations [40]. Another option is to optimize the airport runway and taxiway structures using the minimum distance model [41] after adjusting the appropriate parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Department of Development Planning, Civil Aviation Administration of China. 2021 National Civil Transport Airport Production Statistics Bulletin. 2022. Available online: http://www.caac.gov.cn/XXGK/XXGK/TJSJ/202203/P020220328389410591630.pdf (accessed on 10 April 2022).
- Jiang, L. Study on Apron Operation Safety of Special Vehicle. Civ. Aviat. Manag. 2014, 8, 73–74. [Google Scholar]
- Guo, B.; Wang, Z.J.; Pan, Y.J. The control of the aircraft ground collision or scratch risk. Civ. Aviat. Manag. 2017, 2, 105–112. [Google Scholar]
- Braaksma, J.P.; Shortreed, J.H. Improving Airport Gate Usage with Critical Path. Transp. Eng. J. ASCE 1971, 97, 187–203. [Google Scholar] [CrossRef]
- Cheung, A.; Ip, W.H.; Lu, D.W.; Lai, C.L. An aircraft service scheduling model using genetic algorithms. J. Manuf. Technol. Manag. 2005, 16, 109–119. [Google Scholar] [CrossRef]
- Mao, X.Y.; Mors, T.A.; Ac, M.; Roos, N. Agent-based scheduling for aircraft deicing. In Proceedings of the 18th Belgium-Netherlands Conference on Artificial Intelligence, Namur, Belgium, 5–6 October 2006; Benelux Association for Artificial Intelligence(Namur, Belgium), 2006; pp. 229–236. [Google Scholar]
- Heng, H.J.; Yan, X.D. Implementing airport special vehicles scheduling algorithm with multi-objective optimisation. Comput. Appl. Softw. 2016, 33, 238–242. [Google Scholar]
- Padrón, S.; Guimarans, D.; Ramos, J.J.; Fitouri-Trabelsi, S. A bi-objective approach for scheduling ground-handling vehicles in airports. Comput. Oper. Res. 2016, 71, 34–53. [Google Scholar] [CrossRef]
- Zhang, J.H.; Meng, Q.S. Scheduling optimization of airport special vehicle based on improved FCM and krill herd algorithm. Mach. Tool Hydraul. 2018, 46, 112–117. [Google Scholar]
- Wang, Z.R.; Li, Y.; Hei, X.H.; Meng, H.N. Research on airport refueling vehicle scheduling problem based on greedy algorithm. In Proceedings of the International Conference on Intelligent Computing 2018: Intelligent Computing Theories and Application, Wuhan, China, 15–18 August 2018; pp. 717–728. [Google Scholar]
- Zaninotto, S.; Gauci, J.; Farrugia, G.; Debattista, J. Design of a Human-in-the-Loop Aircraft Taxi Optimisation System Using Autonomous Tow Trucks. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 2931. [Google Scholar]
- Liu, Y.; Zhang, J.; Ding, C.; Bi, J. Modeling and heuristic algorithm of ground ferry vehicle scheduling in large airports. In Proceedings of the 19th COTA International Conference of Transportation, Nanjing, China, 6–8 July 2019; pp. 159–170. [Google Scholar]
- Zhao, Z.; Hu, L.; Qian, Y.Y.; Jin, H.; Jia, A.P. Research on Optimal Allocation Method of Aircraft Towing Rules Based on Multi-agent. J. Syst. Simul. 2022, 34, 113–125. [Google Scholar]
- Sun, D.G.; Sun, J.; Wang, M.; Kang, Q. Application of the improved Bow-tie risk analysis technology in civil airport safety. J. Saf. Sci. Technol. 2010, 6, 85–89. [Google Scholar]
- Wilke, S.; Majumdar, R.A.; Ochieng, W.Y. Airport surface operations: A holistic framework for operations modeling and risk management. Saf. Sci. 2014, 63, 18–33. [Google Scholar] [CrossRef]
- Fei, C.G.; Pan, W.P. Research on safety risk evaluation for electric special vehicle running on airport apron. Mod. Electron. Tech. 2017, 40, 34–38. [Google Scholar]
- Wang, Y.G.; Gao, Y.H. On the safety risk analysis and countermeasures of apron in large and medium sized airports. J. Saf. Environ. 2018, 18, 1716–1722. [Google Scholar]
- Zhao, X.; Malasse, O.; Buchheit, G. Verification of safety integrity level of high demand system based on Stochastic Petri Nets and Monte Carlo Simulation. Reliab. Eng. Syst. Saf. 2019, 184, 258–265. [Google Scholar] [CrossRef]
- Wang, Y.G.; Zuo, X.Y.; Xing, D.J. Risk evaluation on prevention and control of aircraft damage events owing to airport reason. J. Saf. Sci. Technol. 2020, 16, 165–171. [Google Scholar]
- Tong, X.Z. Hangzhou Airport Apron sector operation innovation mode. China High New Technol. 2020, 13, 85–86. [Google Scholar]
- Hu, X.; Lodewijks, G. Detecting fatigue in car drivers and aircraft pilots by using non-invasive measures: The value of differentiation of sleepiness and mental fatigue. J. Saf. Res. 2020, 72, 173–187. [Google Scholar] [CrossRef]
- Liu, B.F.; Tang, X.P.; Zhang, F. Risk assessment study for driverless special vehicles in airport flight area. Sci. Technol. Rev. 2021, 39, 83–91. [Google Scholar]
- Wang, X.L.; Yin, H. Identification of key conflict points in airport airfield area based on betweenness and degree entropy. J. Saf. Sci. Technol. 2022, 18, 236–242. [Google Scholar]
- Song, I.; Cho, I.; Tessitore, T.; Gurcsik, T.; Ceylan, H. Data-driven prediction of runway incursions with uncertainty quantification. J. Comput. Civ. Eng. 2018, 32, 04018004. [Google Scholar] [CrossRef]
- Zeng, H.; Zhang, H.M.; Ren, B.; Cui, L.; Wu, J. Aviation safety prediction method research based on improved LSTM model. Syst. Eng. Electron. 2022, 44, 569–576. [Google Scholar]
- Wang, X.L.; Yin, H.; He, M. Potential Conflicts Prediction of Mobile in the Airport Airfield Area Based on LSTM. J. Beijing Univ. Aeronaut. Astronaut. 2022. Available online: https://www.doc88.com/p-98839603750911.html (accessed on 28 November 2022).
- Cai, C.; Wu, K.; Yan, Y. Rapid detection and social media supervision of runway incursion based on deep learning. Int. J. Innov. Comput. Appl. 2018, 9, 98–106. [Google Scholar] [CrossRef]
- Lyu, Z.L.; Chen, L.Y. SA-FRCNN: An Improved Object Detection Method for Airport Apron Scenes. Trans. Nanjing Univ. Aeronaut. Astronaut. 2021, 38, 571–586. [Google Scholar]
- Zhu, X.P.; Zhang, T.X.; Li, J.J.; Xu, H. Wingtip Detection-Based Aircraft Gate Taxi-in Conflict Determination. J. Saf. Environ. 2022. Available online: http://www.cnki.com.cn/Article/CJFDTotal-AQHJ20221116005.htm (accessed on 10 December 2022).
- Yang, K.; Kang, R. Research on Taking off and Landing Separation of Aircrafts in Airport Category II Operation. Adv. Eng. Sci. 2019, 51, 217–225. [Google Scholar]
- Kang, R.; Yang, K. Risk assessment model of aircraft opposite taxiing conflict. China Saf. Sci. J. 2021, 31, 39–45. [Google Scholar]
- Kang, R.; Chen, J.; Yang, K. Probabilistic Model for the Crossover Convergence of Taxiing Aircraft. J. Ordnance Equip. Eng. 2019, 40, 115–118+150. [Google Scholar]
- Yang, K.; Yang, H.Y.; Zhang, J.W.; Kang, R. Effects on Taxiing Conflicts at Intersections by Pilots’ Sensitive Speed Adjustment. Aerospace 2022, 9, 288. [Google Scholar] [CrossRef]
- Order of the Ministry of Transport, PRC No.30. Civil Aviation Air Traffic Management Rules. 2017. Available online: http://xxgk.mot.gov.cn/jigou/fgs/201712/P020180116563208004963.pdf (accessed on 29 September 2017).
- Luo, J. Aerodrome Control; Civil Aviation Press: Beijing, China, 2013. [Google Scholar]
- Aircraft Pilot Guide-Ground Operations:AC-91-FS-2014-23, Department of Flight Standards, Civil Aviation Administration of China, Beijing. 2014. Available online: http://www.caac.gov.cn/XXGK/XXGK/GFXWJ/201811/P020181127316789533888.pdf (accessed on 11 October 2014).
- Zhao, L.; Liu, H.X. Study on Relationship Between Driving Behavior Characteristics and Personality Traits. J. Saf. Sci. Technol. 2016, 12, 171–178. [Google Scholar]
- Wei, T.Z.; Lin, M.; Li, C.X.; Zhu, Z.S.; Liu, H.X.; Zhu, D. Study of Driver’s Hazard Perception and Discriminant Model based on Covert Hazard. J. Saf. Sci. Technol. 2021, 17, 175–181. [Google Scholar]
- Kang, R.; Yang, K. Assessment on Cross Conflict of Vehicle and Aircraft Considering Driving Modes. J. Saf. Sci. Technol. 2023, 19, 218–223. [Google Scholar]
- Kazda, A.; Sedláčková, A.N.; Bračić, M. Expropriation and airport development. Civ. Environ. Eng. 2020, 16, 282–288. [Google Scholar] [CrossRef]
- Havel, K.; Balint, V.; Novak, A. A number of conflicts at route intersections—Rectangular model. Commun. Sci. Lett. Univ. Žilina 2017, 19, 145–147. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Yang, H.; Zhang, J.; Kang, R. Safety and Efficiency Evaluation Model for Converging Operation of Aircraft and Vehicles. Aerospace 2023, 10, 343. https://doi.org/10.3390/aerospace10040343
Yang K, Yang H, Zhang J, Kang R. Safety and Efficiency Evaluation Model for Converging Operation of Aircraft and Vehicles. Aerospace. 2023; 10(4):343. https://doi.org/10.3390/aerospace10040343
Chicago/Turabian StyleYang, Kai, Hongyu Yang, Jianwei Zhang, and Rui Kang. 2023. "Safety and Efficiency Evaluation Model for Converging Operation of Aircraft and Vehicles" Aerospace 10, no. 4: 343. https://doi.org/10.3390/aerospace10040343
APA StyleYang, K., Yang, H., Zhang, J., & Kang, R. (2023). Safety and Efficiency Evaluation Model for Converging Operation of Aircraft and Vehicles. Aerospace, 10(4), 343. https://doi.org/10.3390/aerospace10040343





