1. Introduction
As a new type of aircraft, the stratospheric airship relies on buoyancy to balance the influence of gravity to realize the long-term flying and stationing in near space at the altitude of 20 km [
1,
2,
3,
4]. As a new type of Earth observation and surveillance platform, the stratospheric airship, compared with satellites and unmanned aerial vehicles (UAV), has many outstanding advantages, such as a large task load and long-term stationing in the air [
5] The stratospheric airship is widely used in Earth observation, regional surveillance, navigation and positioning, comprehensive early warning detection, electronic reconnaissance, confrontation, communication, and relay and has high military use and civil value. Therefore, the development of the stratospheric airship has great strategic value and significance.
The motion mode can well reflect the disturbed motion mode of the aircraft, and modal analysis uses the corresponding means to analyze the disturbed motion characteristics of the aircraft [
6]. Motion mode analysis plays an important role in aircraft design. It provides the corresponding theoretical basis for the overall optimization of the aircraft, flight quality analysis, and flight control system design, and it forms a set of mature analysis methods [
7]. As a new type of aircraft, the stratospheric airship has obvious differences in its flight mechanism and flight characteristics compared to airplanes and other aircrafts. Therefore, it is necessary to conduct in-depth research on the motion mode of the stratospheric airship according to its characteristics.
Many scholars have carried out related technical research on the motion mode analysis of the stratospheric airship. Khoury [
8] provided the motion mode analysis method of a low-altitude airship according to its motion characteristics; Ouyang et al. [
9] took the “Zhiyuan 1” stratospheric verification airship as the research object, studied the disturbed motion of the airship in detail, and described the motion mode of the airship. Li et al. [
10] analyzed the motion modes of a Skyship-500 airship through simulations and experiments and provided the characteristic root distribution at different flight speeds; Liu et al. [
11] took the stratospheric airship with a volume of 500 m
3 as the research object, calculated the eigenvalues of the disturbed motion of the airship, and analyzed the influence of flight speed on the motion mode and kinetic characteristics of the airship; Yang et al. [
12] systematically studied the motion modes of the stratospheric airship and provided the modal characteristics of longitudinal motion and lateral motion; Wang [
13] revealed the influence of flight speed on the motion mode of an airship through analyzing the pole distribution and frequency characteristics of the airship at typical flight speeds. Liu [
14] described the process of stratospheric airship mode calculation in detail and provided the correlation mechanism of flight speed change on airship motion mode; Miao [
15] took the 1000 m
3 stratospheric verification airship as the research object, introduced the free motion characteristics of the airship at typical flight speeds, and simulated and analyzed the control response characteristics of the airship; Wang [
16] introduced the motion mode characteristics of the V-shaped new concept stratospheric airship and calculated the motion mode of the airship under typical working conditions; Wang et al. [
17] analyzed the characteristics of the longitudinal motion modes of the stratospheric airship from the perspective of stability and provided the modes sensitive to the longitudinal motion; Anshul et al. [
18] conducted the trim and stability analysis of an airship with bifurcation techniques and provided the pole distribution diagram in different motion states; Wu et al. [
19] analyzed and calculated the motion mode and dynamic characteristics of an airship driven by a new type of driving system with Matlab according to the characteristics of the “buoyant-slider” driven airship; Zhang [
20] took GoodYear ZP4K as the research object, analyzed the characteristics of the longitudinal and lateral mode motion of the airship, and provided the generation mechanism of the pendulum motion mode; Liu [
21] analyzed the influence of different motion models on the motion modes of airship under the conditions of straight and level flight at a constant speed and pointed out the root cause of the difference of motion modes. Yuan [
22] proposed a control strategy combining model prediction, sliding mode control, and extended state observer for the space trajectory tracking of a stratospheric airship under state constraints, input saturation, and position disturbance and carried out a corresponding simulation analysis; Huang [
23] analyzed the impact of external environmental changes on buoyant gas, airship mass, and internal and external pressure differences; Liu [
24] proposed the corresponding dynamic model of a stratospheric airship according to the different description methods of aerodynamic parameters; Li [
25] carried out dynamic modeling and a longitudinal stability analysis for a stratospheric airship with a double-hull configuration and gave the simulation results of pole distribution and handling characteristics; Gobiha [
26] carried out dynamic modeling for an autonomous flying airship and used the established nonlinear 6 DOF model to simulate and evaluate the motion characteristics of the airship.
To summarize, the analysis of the current literature research on the motion modes of the stratospheric airship basically focuses on the determination of the overall scheme of the airship and the motion modes at typical flight speeds. In the actual engineering practices, except when the flight speed affects the motion mode of the stratospheric airship, the locations of the center of mass and the center of buoyance, aerodynamic characteristics, and other parameters of the airship will also have a greater impact on the motion mode of the stratospheric airship; even the impact is subversive. At the same time, compared with the airplane, the stratospheric airship has a large volume and a complex structure, so it is difficult to ensure that all the parameters of the airship in the design, production, and assembly process are testable and to ensure the closed-loop control of the airship technology in the full state and the whole process with the existing design means and process; under the influence of the external environment during the flight, there is great uncertainty between the actual flight state and the theoretical design state in terms of the related parameters of the airship. Therefore, it is necessary to carry out in-depth research on the influence of the perturbation of the key parameters such as the center of mass, the center of float, and the aerodynamic characteristics of the stratospheric airship on the motion mode. Such research can provide corresponding technical support for the overall optimization, the design of the flight control system, and the stable flight of the stratospheric airship. Therefore, the main goal of this paper is to focus on the uncertainty of key parameters such as the center of mass, the center of buoyancy, and the aerodynamic characteristics during the manufacturing and flight test of the stratospheric airship and analyze the influence of the perturbation of these key parameters on the motion mode. The effects of these key parameters on the motion stability, damping characteristics, and frequency change trend of each motion mode of the airship are investigated to optimize the overall design of the stratosphere airship flight control system.
The paper is organized as follows: in
Section 2, the description of the nonlinear model and the linearized model of the disturbed motion of the stratospheric airship are given; in
Section 3, the motion modes of the stratospheric airship at a typical flight speed is analyzed; in
Section 4, the influence of the key parameters of the stratospheric airship on motion modes is analyzed in detail; finally, the influence of the key parameters of the stratospheric airship on motion modes is summarized.
4. Motion Mode of Stratospheric Airship
4.1. Description of Motion Mode
The so-called mode, namely the vibration mode of motion, is an inherent property of the time-invariant system. The mode is the most basic independent unit of the motion of the system, and the total motion of the system is a linear combination of the modes. The motion mode embodies the free motion characteristics of the airship after being disturbed, and it is the basic component of the disturbed motion of the airship. The motion mode reflects the law of motion variables changing with time and the amplitude ratio of variables and phase relationship between variables. The assignment of the motion parameters in a certain mode has a fixed proportional relationship, and the phase difference between motion parameters is also constant [
32].
The motion of the airship is the linear combination of different eigenvalues in the corresponding motion modes, and the influence of eigenvectors and initial values is reflected in the weight of different motion modes. Under the condition of the same initial value in the same mode, the performance of the corresponding motion parameters is determined by the relative sizes of eigenvectors.
4.2. Characteristics of Motion Mode
According to the corresponding time scale of the six-DOF motion of the airship, the motion of the airship can be divided into long-term motion and short-term motion. The long-term motion is used to describe the translation of the center of mass of the airship, and the short-term motion is used to describe the attitude change process of the airship. The mode of the short-term motion is more representative for the description of the motion characteristics of the airship and plays a leading role in the influence of the flight quality of the airship. Therefore, we further analyze the short-term motion of the airship below.
- (1)
Pitching Channel
The characteristic equation of the pitching channel of the airship can be derived according to the linear model of the longitudinal motion:
wherein ,
wherein represents the derivative of normal aerodynamic coefficient; represents the derivative of pitch damping moment coefficient; represents the derivative of pitch attitude moment coefficient.
From the characteristic equation, it can be seen that the motion mode of the pitching channel is composed of a monotone damping mode and a second-order oscillation convergence mode; the frequency of the second-order oscillation mode is determined by , and the damping is determined by .
- (2)
Yaw Channel
The characteristic equation of the yaw channel of the airship can be derived according to the linear model of the lateral motion:
wherein , .
wherein represents the derivative of lateral aerodynamic coefficient; represents the derivative of the yaw aerodynamic stabilization coefficient; and respectively represent the derivatives of yaw damping force and damping force moment coefficients.
From the characteristic equation above, it can be seen that the motion mode of the yaw channel for the stratospheric airship is a second-order oscillation convergence mode; the change of and affects the damping effect of the motion mode; the change of , , , and affects the frequency of the motion mode; upon the large damping of the mode, the second-order oscillation mode transforms into two one-order inertia damping modes.
- (3)
Analysis of Difference between Pitch Motion Mode and Yaw Motion Mode
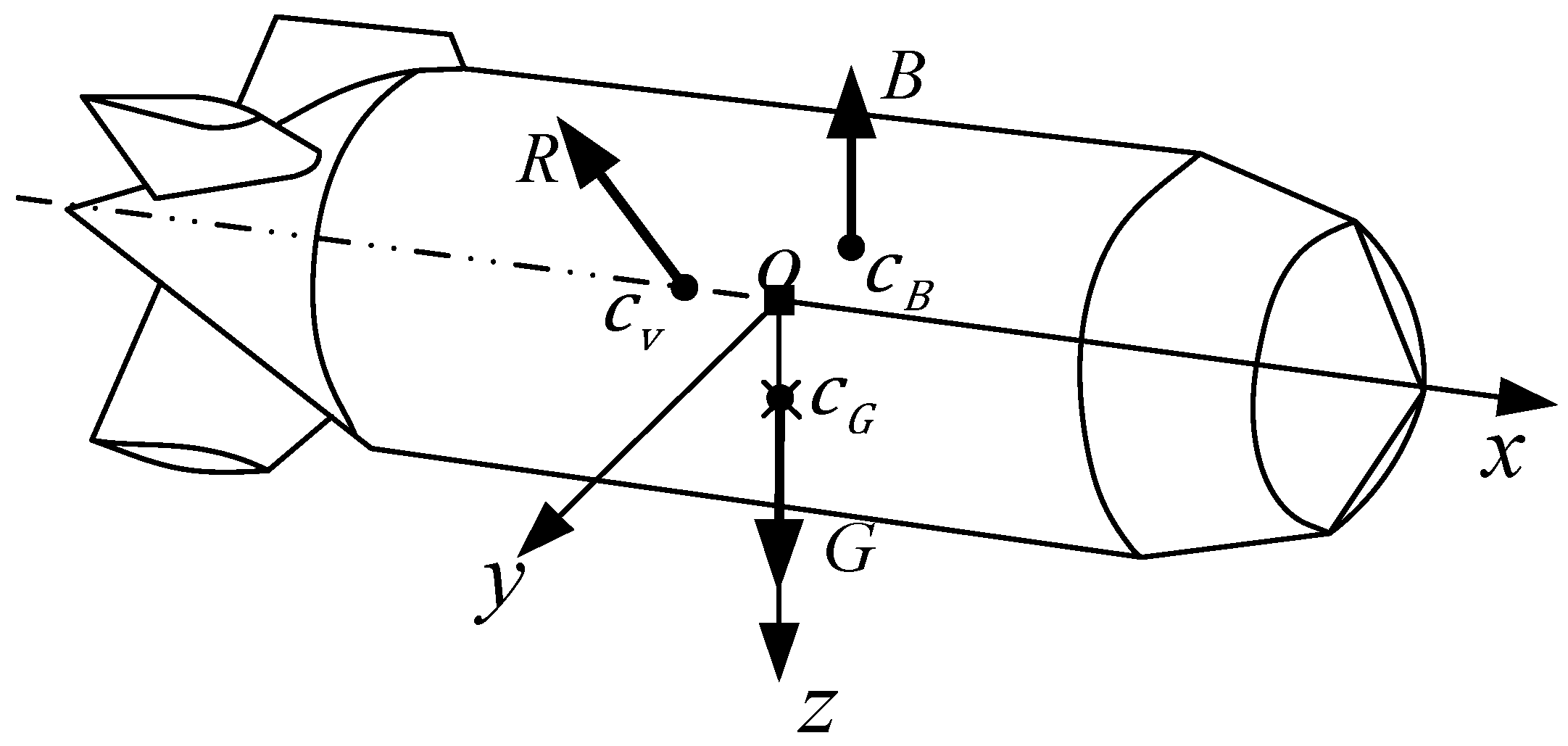
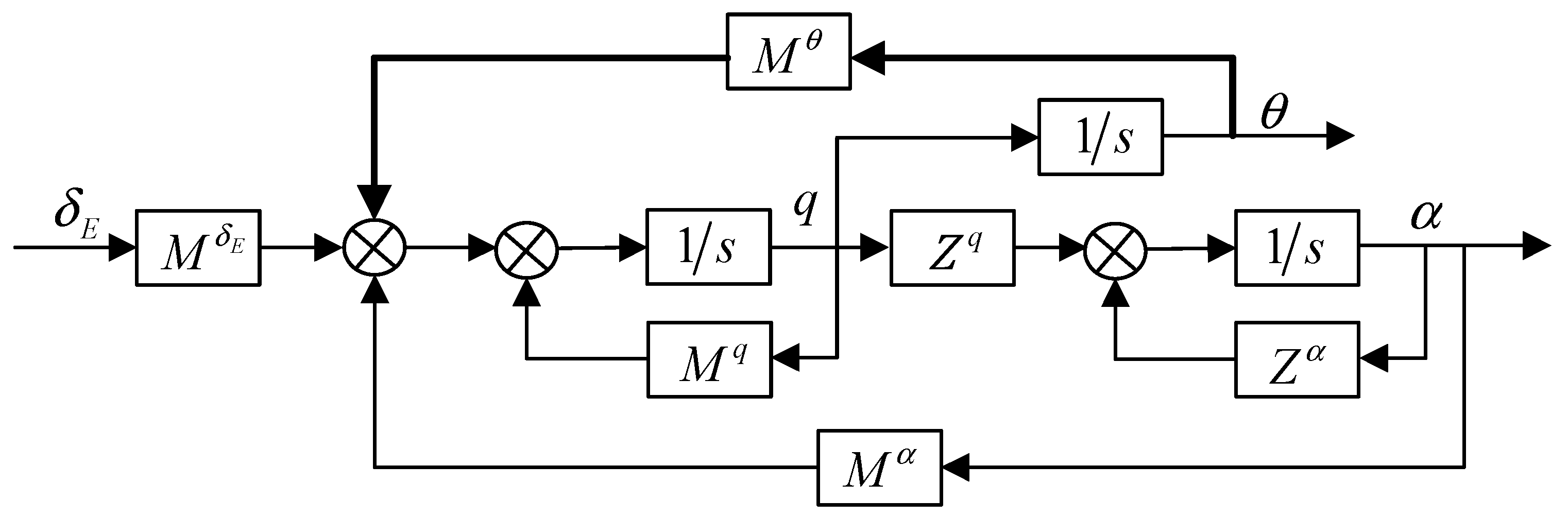
From the above analysis of the pitch motion mode and yaw motion mode, it can be seen that the pitch motion mode is quite different from the yaw motion mode of the airship. The pitch attitude angle motion mode is composed of an inertial damping mode and a second-order oscillation convergence mode, while the yaw rate motion mode is composed of a second-order oscillation mode and adds an integration link on the basis of the second-order oscillation mode, thus resulting in unstable motion modes. According to the longitudinal motion linearized model, the internal state structure diagram of the pitch channel can be obtained in order to further analyze the roots, as shown in
Figure 2.
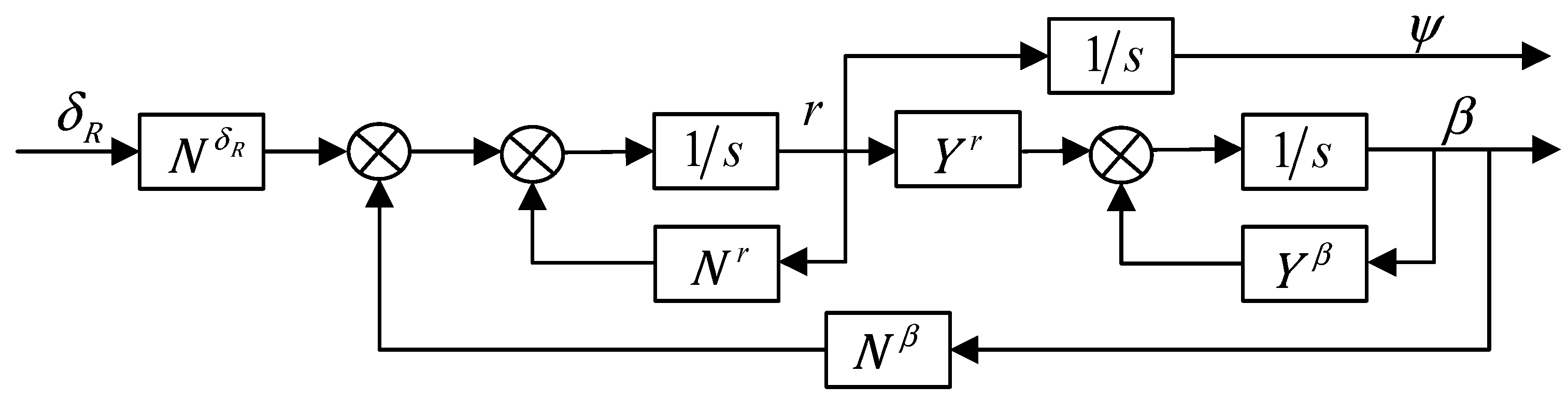
The internal state structure diagram of the yaw channel of airship can be derived according to the linear model of the lateral motion, as shown in the
Figure 3:
Comparing the internal state structure diagrams of the airship’s pitch channel and yaw channel, it can be found that the attitude angle forms a negative feedback loop through in the internal state structure diagram of the pitch channel, but there is no feedback loop of attitude angle in the internal state structure diagram of the yaw channel. The fundamental reason for this phenomenon is that the center of mass of the airship is located directly below the coordinate system of the airship hull and the gravity will produce a moment to feed the motion information of the pitch angle back to the system during the attitude motion, while the gravity will not produce any moment in the horizontal plane, so the motion information of the yaw angle cannot be fed back to the system. Similarly, when the center of buoyancy is above the body center and the attitude of the airship changes, the buoyance force will generate a torque through the center of buoyancy and feed the information of pitch attitude angle back to the system.
5. Influence of Key Parameter Perturbation on Motion Mode
5.1. Moment of Aerodynamic Stabilization
For high-speed and high-dynamic aircrafts such as missiles and airplanes, the moment of aerodynamic stability plays a crucial role in the motion modes of the pitch channel and yaw channel. The value and polarity of the moment determine the frequency of motion mode and the stability of the motion, and the parameter perturbation has a great influence on the kinetic characteristics of the system. Since the airship belongs to the category of low-speed and low-dynamic aircrafts, there is a big difference between the airship and a high-dynamic aircraft; therefore, it is necessary to study the influence of the aerodynamic stability moment perturbation on the disturbed motion mode of the airship.
- (1)
Pitching Channel
According to the state equation of the pitching channel, the characteristic equation of short-term motion of pitch channel can be obtained:
By factoring the equation above, the short-term motion modes of the pitch channel can be obtained and consist of a first-order inertial damping mode and a second-order oscillatory convergence mode. The corresponding characteristic equation is shown as follows:
wherein represents the frequency of the first-order inertial damping mode; and respectively denote the damping and frequency of the second-order oscillation convergence mode.
Then, the calculation formula of pitch aerodynamic stability moment
is shown as follows:
wherein represents the angle of attack; represents the perturbation coefficient of pitch aerodynamic stability moment, .
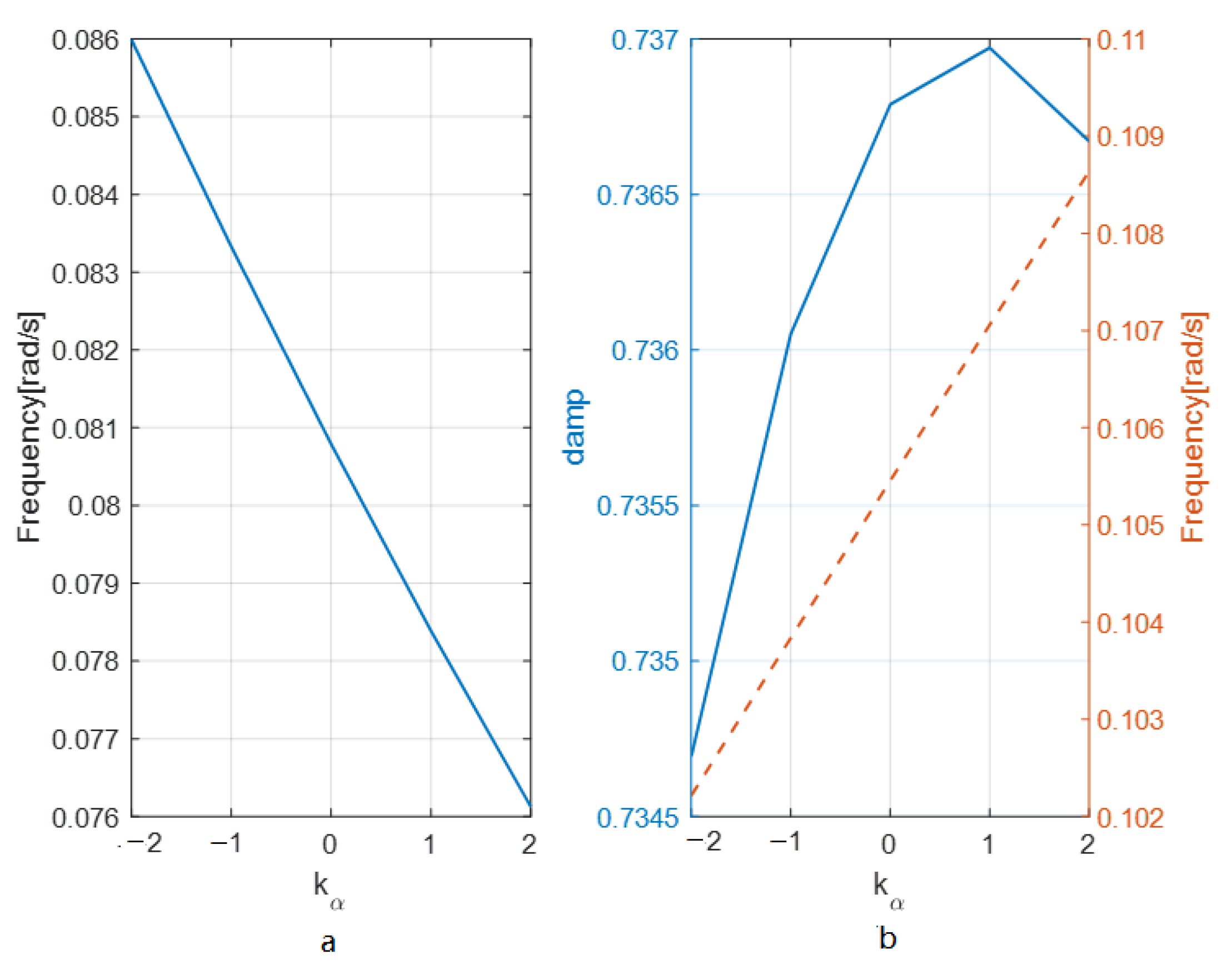
In the perturbation range of the selected pitch aerodynamic stability moment, the change curves of the key parameters of the pitching channel in different motion modes with the perturbation of the pitch aerodynamic stability moment can be calculated, respectively, as shown in the
Figure 4.
Figure 4a depicts the frequency change curves of the first-order inertial damping mode under the perturbation of the pitch aerodynamic stability moment, while
Figure 4b depicts the damping and frequency change curves of the second-order oscillation convergence mode under the perturbation of the pitch aerodynamic stability moment. As can be seen from the above figures, with the increase of the perturbation coefficient of the pitch aerodynamic stability moment, the frequency of the first-order inertial damping mode will gradually decrease, while the damping and frequency of the second-order oscillation convergence mode will increase. However, the change amplitude of the above data shows that the influence on the disturbed motion mode of the pitching channel is very small and can be ignored. Therefore, the influence of the pitch aerodynamic stability moment can be ignored in the analysis of the pitching channel disturbed motion mode.
According to the above analysis conclusions, the characteristic equation of the pitch channel disturbed motion can be simplified as follows:
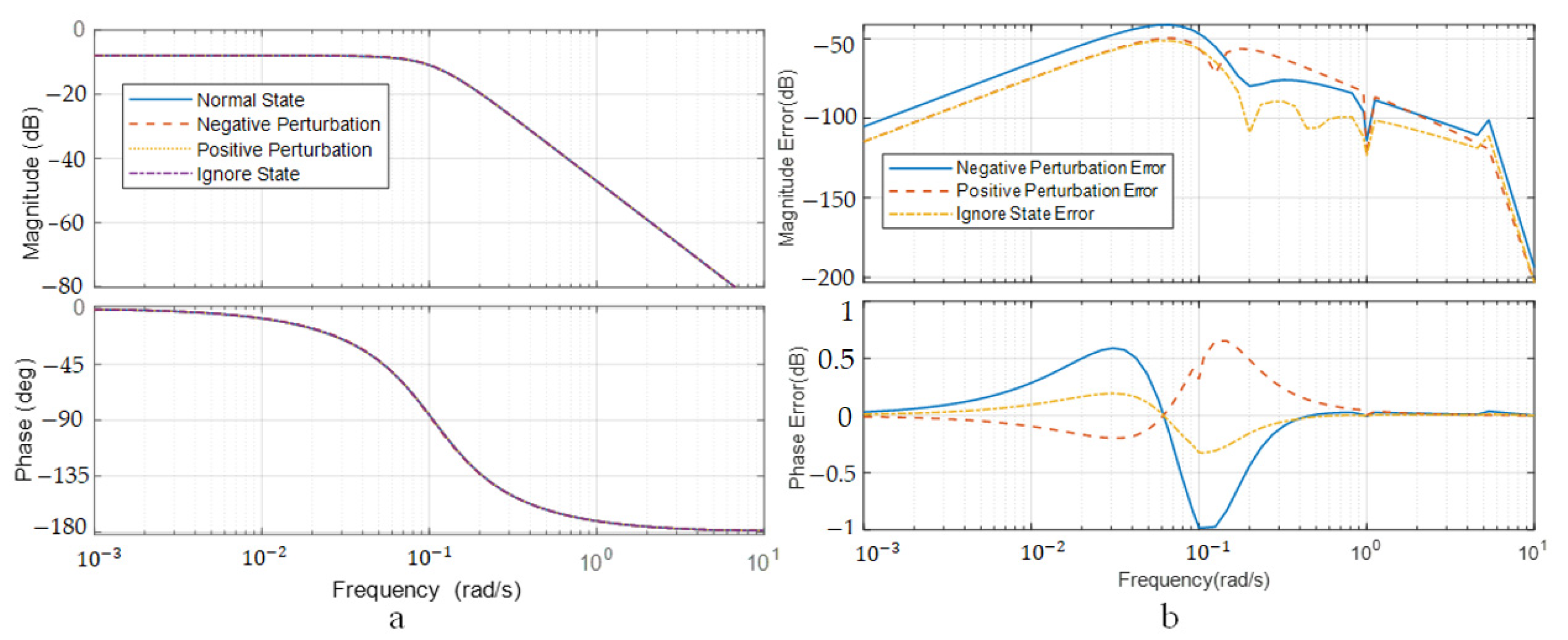
To further illustrate the influence of the pitch aerodynamic stability moment perturbation on the pitching motion mode of the stratospheric airship and to verify the rationality and validity of the assumption that the influence of pitch aerodynamic stability moment can be ignored in the mode analysis, the Bode plot and deviation curve under the state of pitch aerodynamic stability moment perturbation are respectively presented in
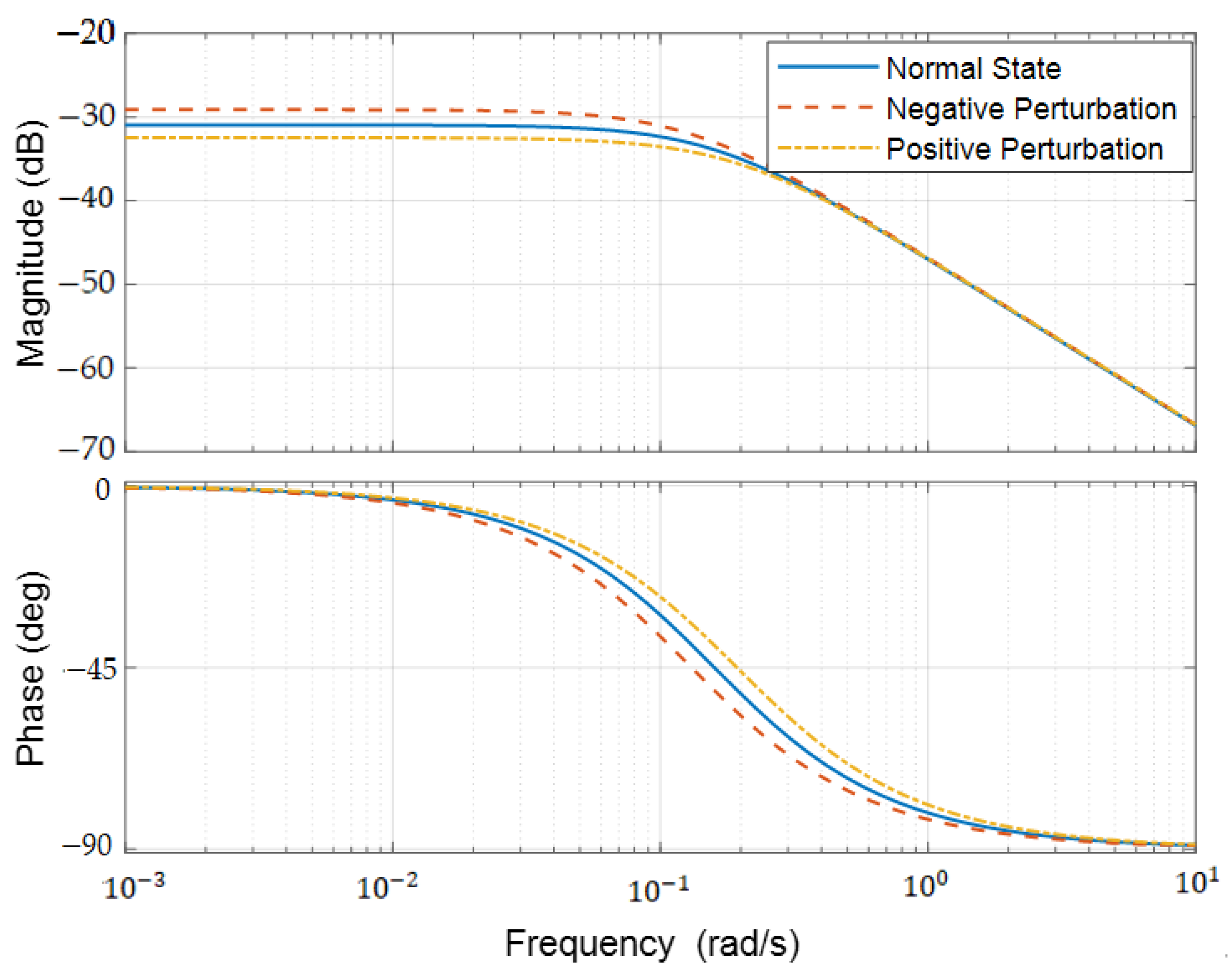
Figure 5.
Figure 5a depicts the Bode plot of the pitching channel in the perturbation state of the pitch aerodynamic stability moment, and
Figure 5b depicts the amplitude frequency and phase frequency deviation curves of the pitching channel in the perturbation state of the pitch aerodynamic stability moment. The above figures show that the amplitude-frequency characteristics and phase-frequency characteristics of the corresponding system are basically unchanged in the perturbation state of the pitch aerodynamic stability moment; the amplitude-frequency and phase-frequency deviation in the pitch aerodynamic stability moment perturbation state are in a small range relative to the nominal state. Therefore, the influence of the pitch aerodynamic stability moment can be ignored during the analysis of the motion mode of the pitch channel. This is the huge difference between the stratospheric airship and the high-speed and high-dynamic aircrafts in terms of pitch disturbed motion.
- (2)
Yaw Channel
As mentioned above, the short-term motion mode of yaw channel can be described with a second-order oscillation mode, and the corresponding characteristic equation is shown as follows:
wherein and denote the damping and frequency of the yaw channel short-term motion mode, respectively.
Then, the calculation formula of the yaw aerodynamic stability moment
is shown as follows:
wherein represents the angle of slideslip; represents the perturbation coefficient of the yaw aerodynamic stability moment, .
In the perturbation range of the selected yaw aerodynamic stability moment, the change curves of the key parameters of the yaw channel in different motion modes with the perturbation of the yaw aerodynamic stability moment can be calculated respectively, as shown in
Figure 6.
Figure 6a depicts the frequency characteristic curve of the yaw channel motion mode under the perturbation of the yaw aerodynamic stability moment, while
Figure 6b depicts the damping characteristic curve of the yaw channel motion mode under the perturbation of the yaw aerodynamic stability moment. As can be seen from the above figures, the yaw disturbed motion is stable when the yaw aerodynamic stability moment is perturbed within the specified range; with the increase of the perturbation coefficient of the yaw aerodynamic stability moment, the frequency of the yaw disturbed motion mode will also increase; in the whole change process, however, the damping of the yaw disturbed motion is always one, indicating that the disturbed motion is overdamped, and the second-order oscillation convergence mode transforms into two inertia damping modes. The comparison result of the change amplitude of the above data shows that the frequency of the yaw disturbed motion mode increases with a small amplitude when the pitch aerodynamic stability moment is perturbed, and therefore, the influence of the yaw aerodynamic stability moment on the yaw disturbed motion is minimal and can be ignored.
According to the above analysis conclusions, the characteristic equation of the yaw channel disturbed motion can be simplified as follows:
The above equation shows that the yaw motion mode can be simplified into two first-order inertial damping modes, whose characteristics are related to the derivative of the lateral aerodynamic coefficient and the derivative of the yaw damping moment coefficient, respectively.
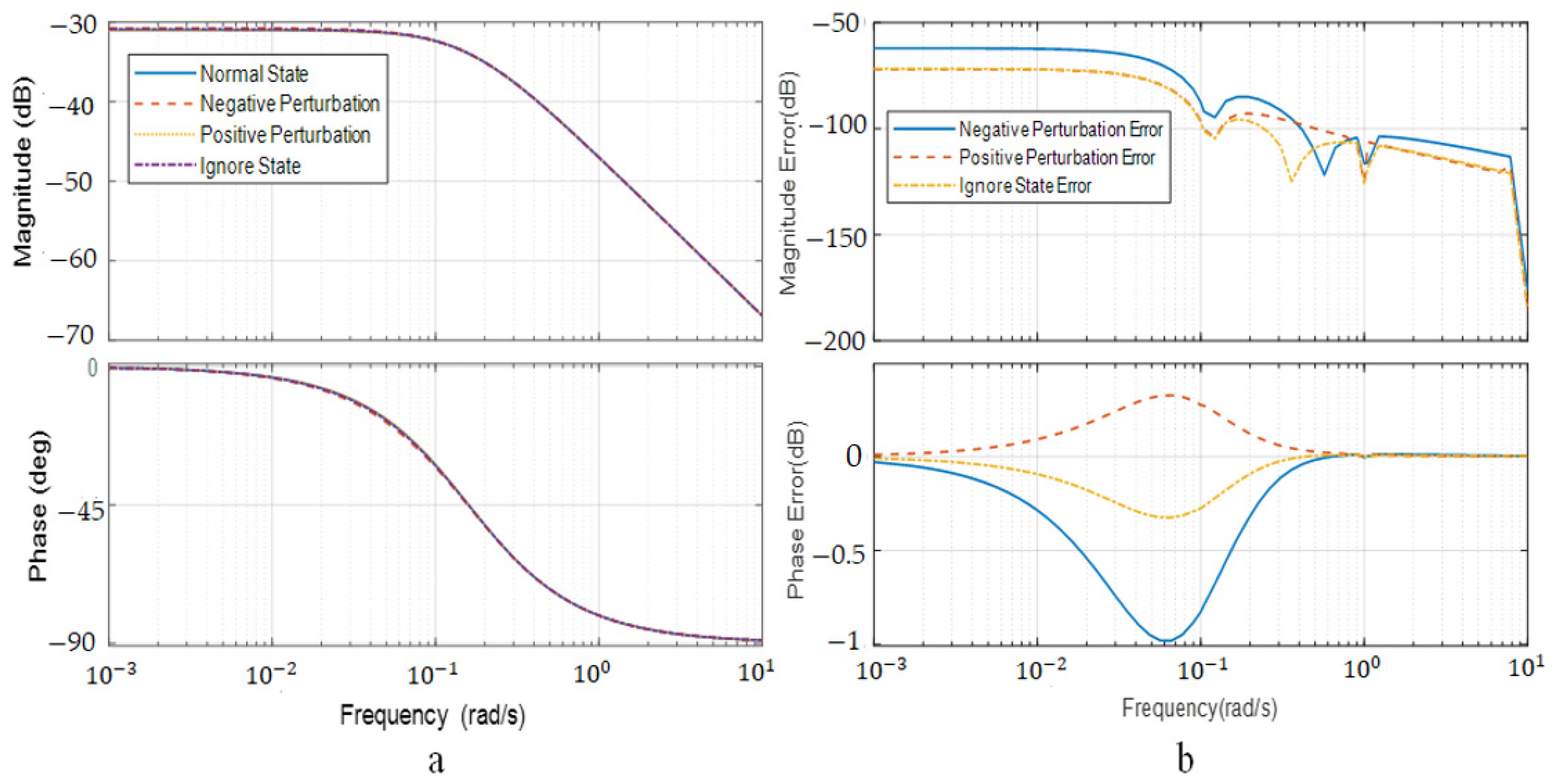
To further illustrate the influence of the yaw aerodynamic stability moment perturbation on the yaw motion mode of the stratospheric airship and to verify the rationality and validity of the assumption that the influence of yaw aerodynamic stability moment can be ignored in the mode analysis, the Bode plot and deviation curve under the state of yaw aerodynamic stability moment perturbation are respectively presented in
Figure 7.
Figure 7a depicts the Bode plot of the yaw channel in the perturbation state of the yaw aerodynamic stability moment, and
Figure 7b depicts the amplitude frequency and phase frequency deviation curves of the yaw channel in the perturbation state of the yaw aerodynamic stability moment. The above figures show that the amplitude-frequency characteristics and phase-frequency characteristics of the corresponding system are basically unchanged in the perturbation state of the yaw aerodynamic stability moment; the amplitude-frequency and phase-frequency deviation in the yaw aerodynamic stability moment perturbation state are in a small range relative to the nominal state. Therefore, the influence of the yaw aerodynamic stability moment can be ignored during the analysis of the motion mode of the yaw channel. This is the huge difference between the stratospheric airship and the high-speed and high-dynamic aircrafts in terms of yaw disturbed motion.
5.2. Location of Mass Center
The mass centers of aircrafts such as missiles and airplanes are basically distributed uniformly inside the aircrafts around the carrier coordinate systems. Therefore, the mass center of the aircraft can be well-configured to the origin of the carrier coordinate system so that the gravity only has an effect on the motion of the mass center of the aircraft and will not have any effect on the attitude motion. Due to the special structure layout, the mass center of the airship does not overlap with its center of body; its gravity will have a great influence on the attitude motion of the airship with the change in the location of the mass center, resulting in the great differences of the airship’s pitching motion mode from that of missiles and airplanes.
5.2.1. Axial Location
- (1)
Pitching Channel
According to the linearized model, the perturbation in the axial location of the mass center mainly affects
in the state transition matrix, as shown in the equation below:
wherein represents the derivative of the pitch aerodynamic damping moment coefficient; represents the dynamic pressure; represents the characteristic area; represents the characteristic length; represents the axial of the airship’s mass center; represents the airship’s trim axial velocity.
It can be seen from the above equation that when other parameters are unchanged and the axial location of the airship’s mass center is perturbed in a positive way, the damping of the second-order oscillation convergence mode will increase; otherwise, the damping of the second-order oscillation convergence mode will decrease.
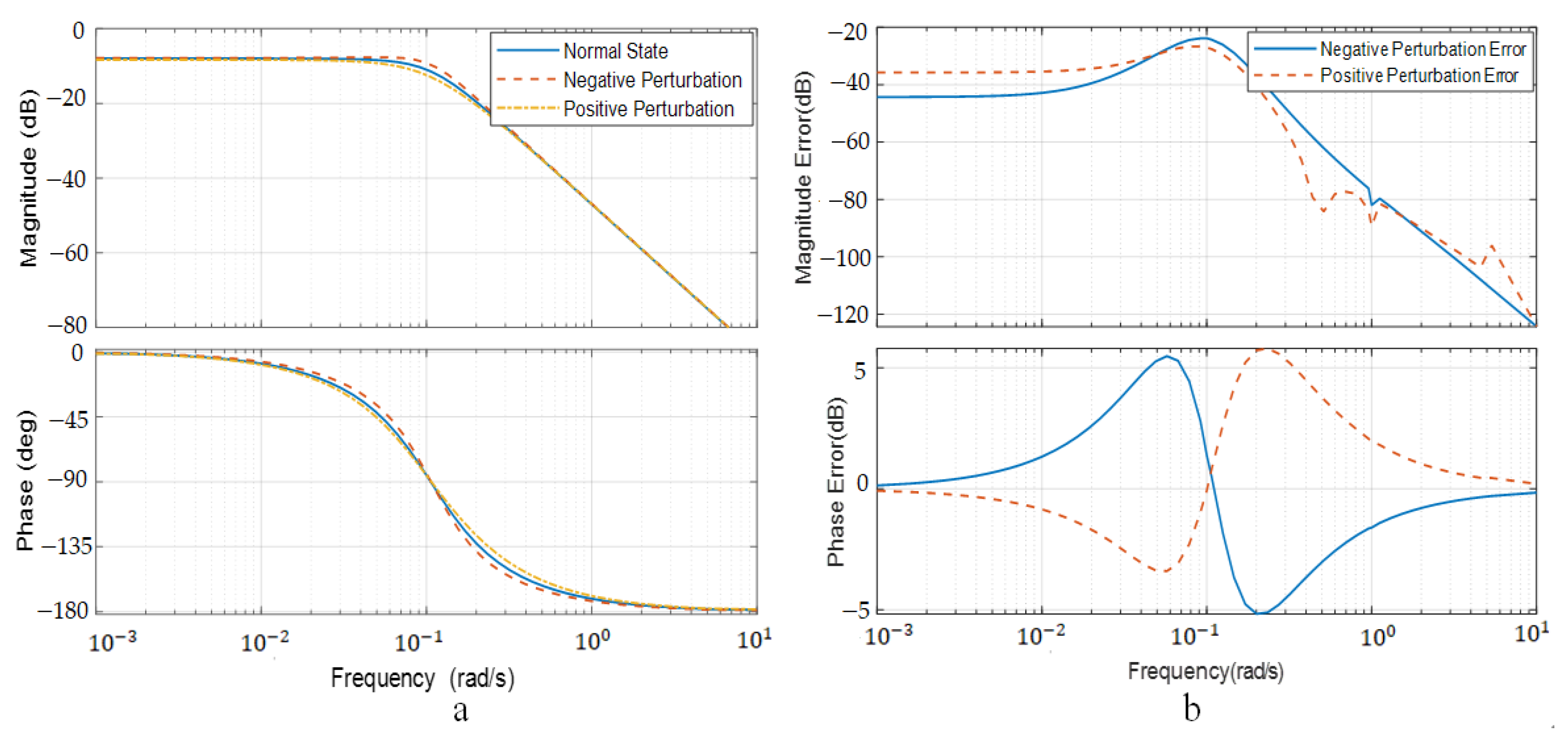
According to the requirements of the overall scheme, the change range of the axial location of mass center shall be from −10 m to 10 m; then, the Bode plot and deviation curve of the perturbation boundary of the airship’s pitch angle motion in the axial location and that in nominal state are shown in the
Figure 8.
The influence of the change in axial location of mass center on the pitching channel disturbed motion modes of the stratospheric airship is shown in
Figure 9.
Figure 8a depicts the Bode plot of the pitching channel with axial location perturbation of the mass center;
Figure 8b depicts the amplitude frequency and phase frequency deviation curves of the pitching channel with axial location perturbation of the mass center;
Figure 9a depicts the curve of the influence of the axial location perturbation of the mass center on the frequency of the first-order inertia damping motion mode of the pitching channel;
Figure 9b depicts the damping and frequency characteristic curves of the second-order oscillatory convergence mode of the pitching channel under the axial location perturbation of the mass center. It can be seen from
Figure 8 and
Figure 9 that the axial location perturbation of the mass center has a great influence on the damping of the pendulum motion mode but has little influence on the frequency of the pendulum motion and the frequency of the first-order inertia damping mode. Moreover, the damping increases linearly with the axial location of the mass center.
- (2)
Yaw Channel
According to the yaw channel linear model,
can be described as:
wherein represents the derivative of yaw aerodynamic damping moment.
It can be seen from the above equation that the axial location perturbation of mass center will affect . When the axial location of the airship’s mass center is perturbed in a positive way, will increase; otherwise, will decrease. As mentioned earlier, the yaw motion mode of the airship can be described as two first-order inertia damping modes, which determines the frequency of one of the modes so that the axial location perturbation of the mass center will directly affect the moment-dependent motion mode.
The Bode plot of the corresponding yaw motion in the perturbation boundary of the axial location of the mass center is shown in
Figure 10.
It can be seen from the Bode plot that the influence of the axial location of the mass center on the motion mode of the yaw channel is consistent with the results of the previous analysis: the axial location of the mass center mainly affects the dominant motion mode of the yaw motion and has a relatively obvious influence on the motion characteristics of the yaw motion within the middle- and low-frequency bands.
5.2.2. Vertical Location
The main flight mode of the stratospheric airship is horizontal flight. Due to the inherent characteristics of gravity, the vertical location perturbation of the mass center mainly affects the motion mode of pitching channel in the disturbed motion. As mentioned earlier, the motion mode of the stratospheric airship’s pitch channel can be composed of an inertia damping mode and an oscillation convergence mode, the latter of which is usually referred to as the “pendulum effect” mode. The fundamental cause of the stratospheric airship pendulum effect mode is that the mass center of the airship does not overlap with the body center, and the mass center of the airship that lies under the system so that the attitude disturbance of the airship in the pitch and roll direction can quickly converge.
When the overall aerodynamic layout is determined, the key parameter affecting the pendulum motion mode is
, and such a parameter not only determines the frequency of the pendulum motion but also has a certain impact on the damping of the pendulum motion. According to the linearized model, we can see that:
wherein and respectively represent the vertical projections of the center of buoyancy and the center of mass of the airship; and respectively denote the buoyancy and gravity of the airship.
In order to better analyze the influence of the center of mass on the pendulum motion, it can be assumed that the center of buoyancy coincides with the body center; in this case, both the weight and the mass center location of the airship will not only affect the frequency of the pendulum motion, but the mass center location of the airship will also affect the stability of the pendulum motion. In order to ensure the stability of the pitch motion mode, the center of mass of the airship shall be generally required to be located below the body center.
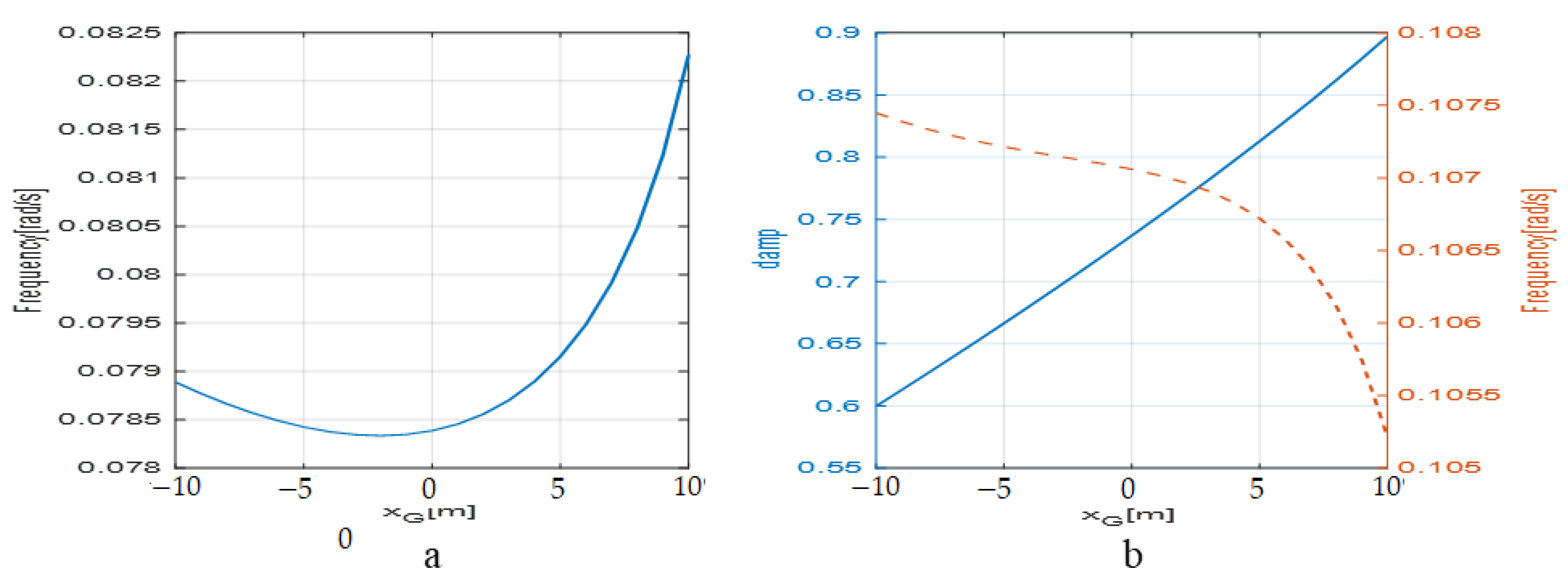
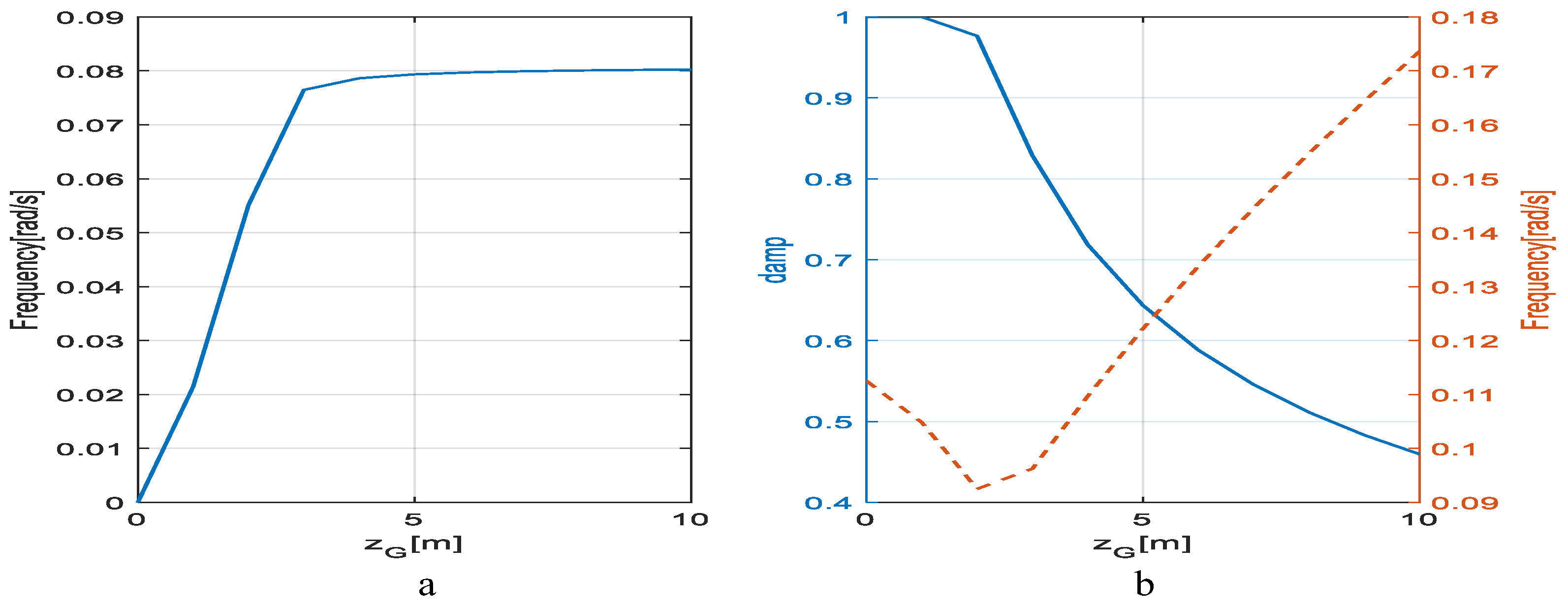
The vertical location of mass center is selected to vary in the range of 0 m to 10 m. The influence of the change in the vertical location of mass center on the disturbed motion mode of the stratospheric airship’s pitch channel is shown in
Figure 11.
Figure 11a depicts the frequency characteristic curve of the first-order inertia damping mode of the pitching channel affected by the vertical perturbation of the mass center;
Figure 11b depicts the damping and frequency characteristic curves of the second-order oscillation convergence mode of the pitching channel affected by the vertical perturbation of the mass center. The left figure above depicts the frequency change curve of the first-order inertia damping mode of the pitching channel with the vertical location perturbation, and the right figure above depicts the parameter change curve of the second-order oscillation convergence mode of the pitching channel with the vertical location perturbation. As can be seen from the left figure, when the vertical location of the mass center is less than 3 m, the frequency of the first-order inertia damping mode increases linearly with the increase of the vertical location; after the vertical location is larger than 3 m, the frequency of the first-order inertia damping mode remains essentially the same. As can be seen from the right figure, when the vertical location is larger than 3 m, the second-order oscillation convergence mode will linearly increase with the increase of the vertical location, while the damping will decrease with the increase of vertical location.
In conclusion, the change in the vertical location of the mass center has a large effect on the motion modes of the pitching channel and a negligible effect on the motion modes of the yaw channel. The above simulation results show that when the vertical location is set in the range between 3 and 8 m, the second-order oscillation convergence mode has better damping characteristics and moderate frequency characteristics, while the first-order inertia damping mode has a small frequency change.
5.3. Location of Buoyant Center
In the aerodynamic modeling process of airship, it is generally assumed that the center of buoyancy is located at the body center; in this way, the buoyancy force does not produce any moment on the airship, and the change of buoyancy force will only affect the motion characteristics of the airship’s center of mass but has no effect on the attitude motion characteristics. Therefore, the buoyancy force has no effect on the short-term motion modes. In the process of engineering implementation, it is difficult to configure the airship’s center of the buoyancy at its body center, and therefore, it is necessary to study the influence of the center of the buoyancy on the motion mode of the stratospheric airship when it does not coincide with the body center.
According to the linear model of the stratospheric airship, the axial location perturbation of the center of the buoyancy has little effect on the airship’s motion modes; this is because the buoyancy has the same characteristics as gravity, and the vertical location perturbation of the center of the buoyancy has a great influence on the pitch disturbed motion mode of the airship but little influence on the yaw disturbed motion mode. Therefore, we only need to consider the influence of the vertical location perturbation of the center of the buoyancy on the pitching channel of the airship when analyzing the influence of the buoyant center perturbation.
According to the linearized model, the associated coupling effect of the buoyant center is shown in the following equation.
Similar to the vertical center of mass, the vertical perturbation of the buoyant center affects the frequency of the pendulum motion mode of the airship. The above equation shows that when the vertical location of the airship’s buoyant center is above the body center, the vertical location perturbation of the buoyant center will not only increase the frequency of the pendulum motion but also increase the stability of the pendulum motion; otherwise, the frequency and stability of pendulum motion will be reduced. When the vertical location of the buoyant center is below the vertical location of the mass center, the pendulum motion is unstable.
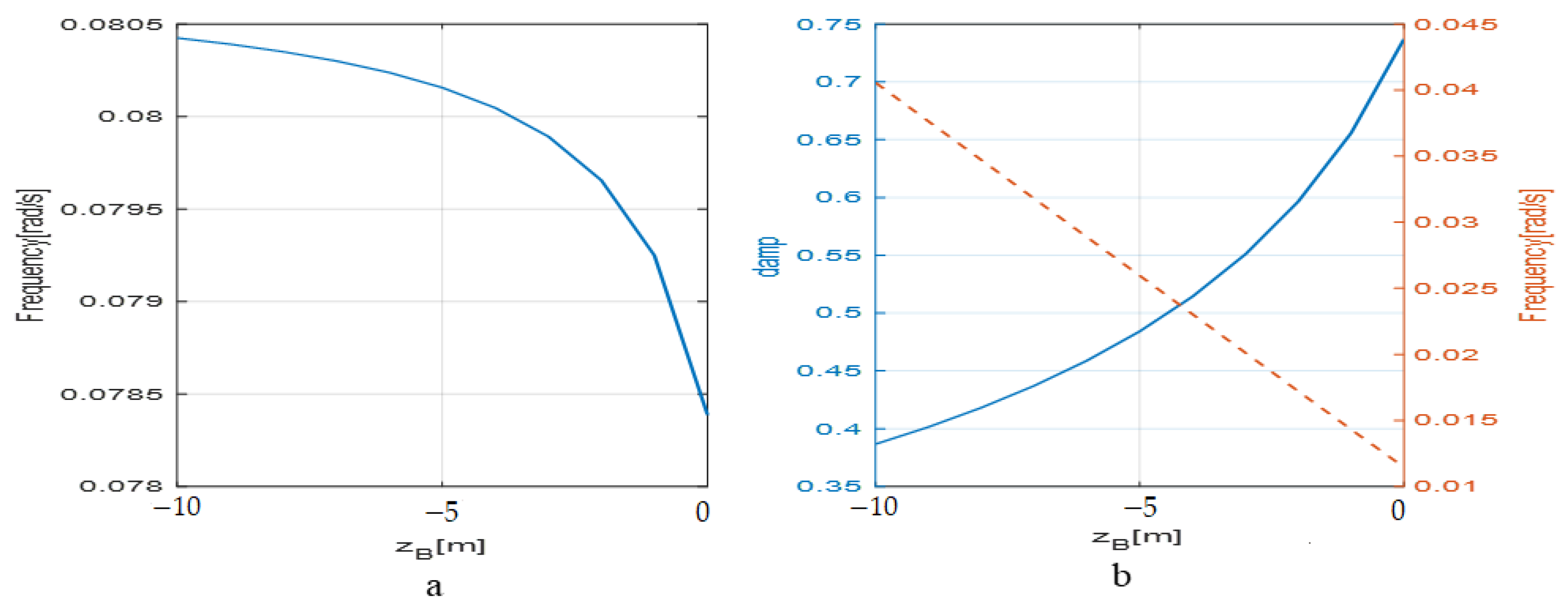
According to the requirements of the overall scheme, the vertical perturbation boundary of the buoyant center was selected to simulate and analyze the influence of the perturbation on the disturbed motion mode of the pitching channel; the corresponding curves are shown in
Figure 12.
Figure 12a depicts the frequency characteristic curve of the first-order inertia damping mode of the pitching channel affected by the vertical perturbation of the buoyant center;
Figure 12b depicts the damping and frequency characteristic curves of the pendulum motion mode of the pitching channel affected by the vertical perturbation of the buoyant center. As can be seen from the figures above, the frequency of the first-order inertia damping mode increases with an increase in the distance of the buoyant center deviating from the body center, but the frequency will increase with the decrease of the damping in the pendulum motion mode. As can be seen from the data change amplitude, the buoyant center perturbation mainly affects the characteristics of the pendulum motion mode and has little effect on the first-order inertia damping mode. Moreover, when the buoyant center perturbation is controlled within 3 m, the pendulum motion has better damping characteristics and moderate frequency characteristics.